Long-range mechanical signaling in biological systems

Abstract

Cells can respond to signals generated by other cells that are remarkably far away. Studies from at least the 1920’s showed that cells move toward each other when the distance between them is on the order of a millimeter, which is many times the cell diameter. Chemical signals generated by molecules diffusing from the cell surface would move too slowly and dissipate too fast to account for these effects, suggesting that they might be physical rather than biochemical. The non-linear elastic responses of sparsely connected networks of stiff or semiflexible filament such as those that form the extracellular matrix (ECM) and the cytoskeleton have unusual properties that suggest multiple mechanisms for long-range signaling in biological tissues. These include not only direct force transmission, but also highly non-uniform local deformations, and force-generated changes in fiber alignment and density. Defining how fibrous networks respond to cell-generated forces can help design new methods to characterize abnormal tissues and can guide development of improved biomimetic materials.

1. Introduction

The idea that cells can signal to other cells at a distance and that the basics of this signal might be mechanical rather than chemical can be traced back a century ¹. This article provides some examples in which long-range force transmission is an important factor in tissue morphogenesis and other biological processes. In contrast to the strain fields in simple elastic continuum materials such as those formed by flexible polymers, where the strain magnitude decays rapidly from the point of force following a power law, the force transmission in biological materials relies on the presence of fibrous networks with large mesh sizes and stiff filaments. The physical properties of these dilute networks include shear strain-stiffening ^{2, 3}, alignment in the stress direction ^{4, 5}, non-affine deformations ^{6, 7}, and anomalous, strain-dependent Poisson’s ratios ⁸, each of which can contribute to force transmission. These effects are considered in a summary of the key theoretical models that can account for long-range force transmission in networks formed by semiflexible or stiff biopolymers.

2. Background

2.1. Experimental evidence for long-range force transmission.

Studies published in the 1920s showed that when nerves were severed and then placed into cell culture media of various kinds, the cells emerged from the damaged nerve and spread or grew in a random radial fashion if the nerve end was placed in liquid or if a single nerve was placed in a dilute blood clot. However, if two nerve ends were placed near each other in a blood clot, the cells at first emerged randomly, but then rapidly moved toward each other to make a line of new tissue connecting the two previously separated nerve ends. Even earlier there was evidence that the growth of neural tissue was influenced by a stimulatory fibrillation ⁹ and various studies at that time tested the hypotheses that the signals leading to spatial guidance of nerve cells were primarily chemical, electrical, or mechanical (reviewed in ¹⁰). The possibility of mechanical guidance was not limited to neural cells, and these early studies showed that two triangular islands of fibroblasts, placed mms away from each other within blood plasma clots acted as “suction pumps” (“saugenpumpen”) to draw cells from each island to the other ¹.

Later studies showed that the traction stresses exerted by different cell types in collagen gels varied over a large range and that, perhaps paradoxically, the fastest moving cells, such as neutrophils or neuronal growth cones, exerted the least force, whereas fibroblasts generated much more force than was required for them to locomote. As a result, explants of fibroblasts distant from each other could reorganize and align collagen fibers between them over a distance of a cm ^{11, 12}.

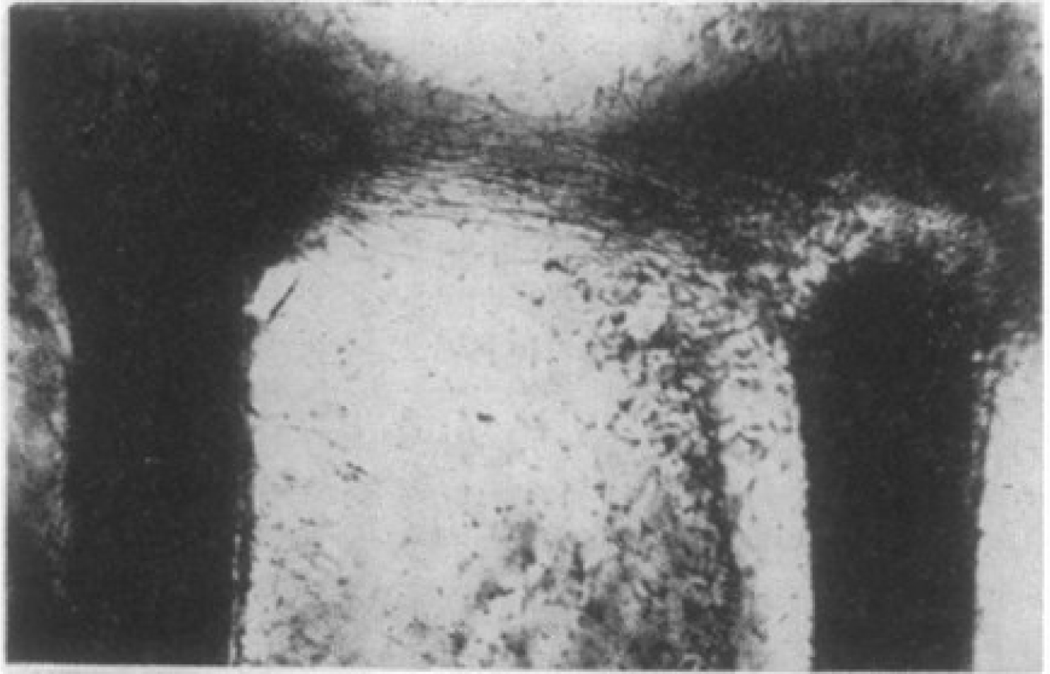
An example of the pattern formed by cells, largely fibroblasts, emerging from two severed nerves placed in a blood clot is shown in Figure 1. Although the magnification of this image is not given in the original report, the diameter of a typical adult rat nerve is approximately 0.5 mm, ¹³ so the distance between the two cut nerves is more than 1 mm. Immediately between the nerve ends, the cells grew toward each other; in other positions where the side of one nerve end faced away from the other, the growth was random. This pattern of growth was described as being due to an “attraction field” emanating from the cluster of cells at the nerve ends growing into the matrix. The nature of this attraction has been the subject of much debate ^{14, 15}. A related quantitative study placed pairs of small embryonic chick heart pieces, consisting mainly of fibroblasts, at different distances to each other within a mixture of embryonic fluid and a fibrin gel formed from chicken blood plasma. This study showed that the fibroblasts placed tension on the fibrin strands within the clot, and that as the tissue pieces grew, the cells preferentially moved to the space between adjacent tissue pieces and aligned the fibers in between ¹⁴. Calculating the probability that cells from adjacent tissue pieces made oriented bridges between them led to a measure of the attraction field incidence, I, as a function of the Initial distance, d, between tissues pieces within the clot. Remarkably, I depended inversely on d², and approached zero only at d between 3.5 and 4 mm. This distance is far too large to support spatial gradients of chemical signals that might be generated between the cell clusters. The large length scale and the power-law decay suggested that the signal might be physical. Whether this signal is the force that the cells exert on the matrix and transmit to the distant cell or spatial patterning of the matrix as cells pull on the fibrin or collagen fibers in the extracellular matrix (ECM) is not obvious, since cells can respond to both forces at the membrane and to the topography and the stiffness of the fibers in their substrate.

Figure 1.

Two rat nerves were severed and then placed in a blood plasma clot. The regenerating cell at the top form a bridge from one nerve end to the other. From 1.

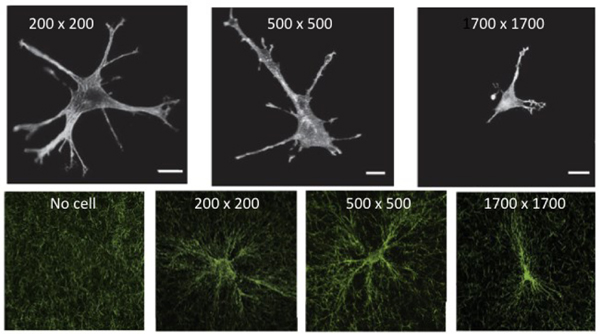
Measurements of individual cells on the surface of thin collagen gels have revealed more clearly the distances over which a cell can sense mechanical signals and how the contractile energy of the cell, as well its ability to chemically modify the matrix, reorient the fiber network structure ¹⁶. Figure 2A shows the morphology of a single fibroblast, of average diameter approximately 50 μm, placed on collagen gels contained within rigid square frames of length 200 μm, 500 μm, or 1700 μm ¹⁷. The cells within the 200 μm x 200 μm frame extend multiple processes toward all sides of the frame. The number of extensions decreases when the frame length is 500 μm and is close to 2 when the frame length is 1700 μm, similar to the shape of the cell in an infinitely large gel. These results are consistent with the hypothesis that the cell extends protrusions toward a rigid boundary that is near enough to the force it develops on the network so that the strain field propagates to the rigid boundary, and therefore the cell feels more resistance in that direction and moves toward it. If the boundary is more than ~ 800 μm away, the cell no longer feels resistance from the boundary, and the number of branches decreases, leading to a bipolar cell. During the hours that the cell accommodates to its substrate, it is also remodeling it. Figure 2B shows how the collagen gel surrounding the contractile cell is reorganized. The collagen fibers tend to concentrate near the cell edges and to align in parallel with the cell extensions ¹⁷.

Figure 2.

(A) Morphology of 3T3 fibroblasts in grids with opening widths of 200 μm, 500 μm, and 1700 μm visualized by rhodamine phalloidin staining for actin filaments. (B) Cell-induced alignment of collagen networks. After remodeling by cells, collagen fibers imaged by confocal reflectance microscopy were aligned parallel to cell extensions. Scale bar: 20 μm. From 17.

Cells are capable of altering their surrounding mechanical environment, which can alter the perceived mechanical force transduction of surrounding cells. Specifically, the local stiffness near a contractile cell in a collagen or fibrin gel can be higher than the average stiffness far away from the cell ^{16, 18, 19}. Since many cell types respond to substrate stiffness ²⁰, often by moving to areas of increased stiffness (see section 3.2), these changes in surrounding matrix mechanical properties due to local stiffening may directly alter nearby cell behavior. A cell’s ability to sense long-range forces from other cells is also modulated by its environment. For example, if a cell in a fiber network can feel a rigid boundary, then it is likely also to respond to another cell pulling within the same matrix. When mesenchymal stem cells were sparsely cultured on fibrin gels, they generated strain fields larger than 5 times the cell diameter, similar to the field generated by fibroblasts in collagen gels, and they oriented their long axes toward each other if they were less than 400 μm away. On the surface of the gel, they formed ribbon-like aggregates, whereas on rigid substrates they aggregated randomly ¹⁸.

2.2. Models for long-range force transmission.

Multiple mechanisms can explain the apparent traction field around cells in a fibrous matrix. The simplest might be that a single fiber connects two cells, and as one cell pulls on the fiber, the adjacent cell immediately feels the force when the fiber is pulled taught. This is unlikely to be the case in biomimetic systems, because the mesh size of collagen and fibrin gels at physiologically realistic concentrations is less than one micron, and fibers long enough to directly connect two distant cells have not been identified, and if they existed would be part of a 3D network, rather than free long filaments. If the cell responds to a force, then that force is propagated through a series of fibers and crosslinks that form a force chain long enough to span between cells. This mechanism is well supported theoretically ²¹, and predicts that long-range strain fields are possible only in stiff polymer networks and not in hydrogels formed by flexible polymers.

Alternatively, the cell responds to the alignment in the fiber networks caused by the neighboring contractile cell. The reorganization has two spatial aspects. The fiber density increases when the fibers align, thereby providing a higher concentration of adhesive sites for cell receptors, and the directionality of the aligned fiber bundles provides a spatial cue for the adhesive steps during cell motility ²². An additional mechanism involves the nonlinear elasticity of fibrous networks. Unlike linear elastomers, for which the elastic modulus is independent of strain, networks of semiflexible and rigid biopolymers stiffen with increasing shear strain ^{3, 23}, as caused by the contractile cell ²⁴. Whether long-range mechanical signaling results from strain-stiffening per se ²⁵ or requires the long fibers typically present in strain-stiffening materials ²⁶ is still unresolved and might depend on the specific system.

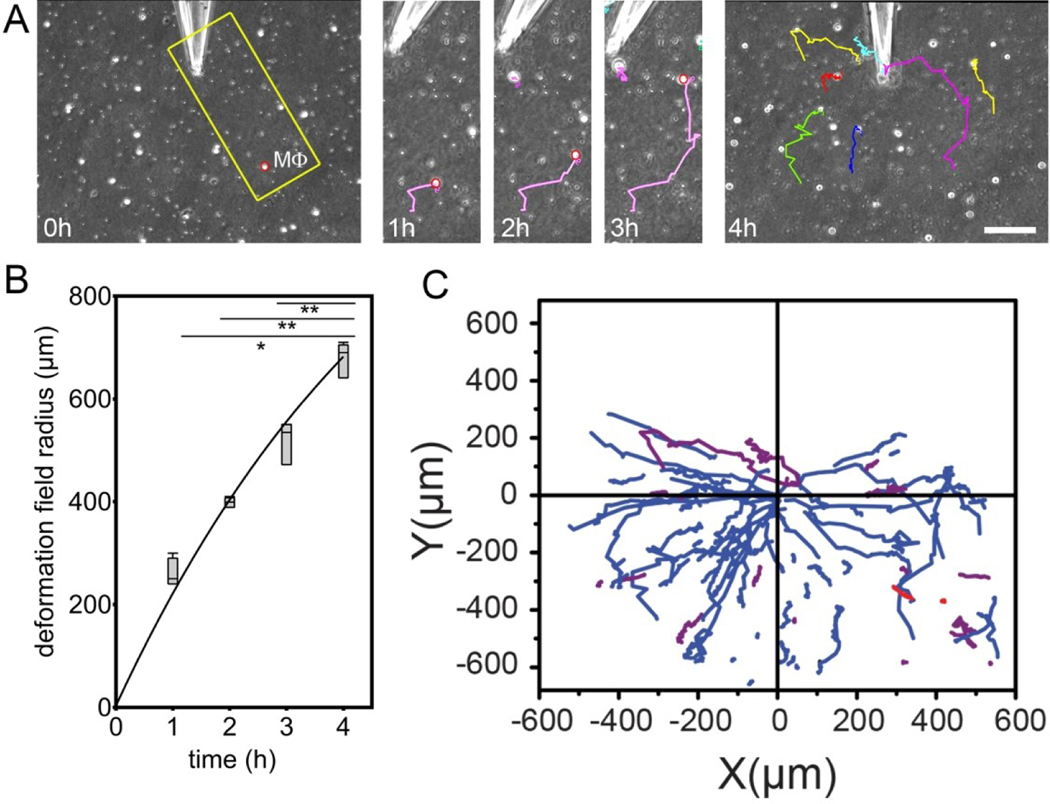
One recent study shows that, despite the doubts raised by the originator of the attraction field hypothesis ¹⁵ it is in some cases the force itself to which a cell responds to initiate its movement toward a point of local force generation. Pakshir et al ²⁷ studied how macrophages respond when a contractile fibroblast deforms a collagen matrix on which both cell types are placed. They found that macrophages migrated persistently toward the contractile cell even when they were hundreds of microns, or many cell diameters away. Initial studies placed a single myofibroblast in the middle of a mm scale collagen matrix and monitored how macrophages that were initially distributed throughout the matrix moved. When macrophages were within 600 microns they moved persistently toward the contracting cell. This study alone does not unambiguously imply reaction to a force, because chemical gradients and fiber alignments are still possible attracting stimuli. However, if the matrix was aligned by the cell and then chemically fixed before the macrophages were deposited, they no longer moved persistently toward the cell, even in the presence of some fiber alignment. Even more strikingly, the contractile fibroblast in the center of the matrix could be replaced by a microneedle that applied directional forces of the same magnitude as the myofibroblast. This force was sufficient to create strain fields that extended hundreds of microns away from the point of force, and macrophages within this strain field moved persistently toward the force, as seen in Figure 3. It was proposed that macrophages mechanosense the velocity of matrix local displacement as supported by the following evidence. (i) Fibrous matrices enable long-range transmission of tensile forces generated by contractile fibroblasts, which in turn triggers migration of macrophages over distances 20–40 times larger than their diameters. (ii) Static mechanical cues, such as pre-aligned collagen or collagen condensation are neither required nor sufficient to trigger the migration of macrophages. (iii) Dynamic changes in the deformation of the collagen matrix are required to attract migratory macrophages above a critical matrix strain velocity.

Figure 3.

Macrophages (Mϕ) are attracted by local pulling events in collagen ECM. (A) Mϕ were seeded onto collagen ECM with microneedles inserted 5 μm into the 200 μm thick collagen gel. Lateral collagen deformation was performed by using negative pressure to pull collagen fibers into the tip. Mϕ migration was tracked from phase contrast movies. Scale bar: 100 μm. (B) Deformation field growth with time. (C) Mϕ trajectories are plotted with respect to distance from the microneedle.

3. Long-range force transmission in biological materials: tissues, cells, and artificial matrices

In this section, we review long-range force transmission in the contexts of various physiological tissues, in cells, as well as in artificial matrices and biomaterials.

3.1. Tissues

Within biological tissues, long-range force transmission becomes necessary for physiological processes early in development. A well-conserved example is the mechanical stimulation that is necessary for generating epithelial tubule branching structures, such as in the case of the mammalian lungs, intestines, or kidney ^{28, 29}. For example, branching behavior of the developing lung epithelium is synchronized between distant parts of the lung ²⁹. This process is carefully coordinated by contractions of the developing smooth muscle surrounding the airway epithelium and the resulting fluctuations in transmural pressure within the epithelial tubules. This leads to regulated pressures experienced by the airway epithelium that regulate the synchronized branching morphogenesis ^{30, 31}. Similar sorts of patterning are possible in generating other epithelial patterns. For instance, in vitro studies have demonstrated that epithelial cells maintain and contract type I collagen within the ECM to successfully transmit forces between cells up to 600 μm away to generate and maintain a tubule-like patterning ³². A similar dependence on Col-I fiber orientation is shown in branching morphogenesis in mammary gland maturation, as epithelial cells migrate along axially oriented collagen fibers in the stromal fat pad. In vitro experiments further suggest that this epithelial cell–type I collagen fiber relationship is both causal, as aligned Col-I fibers are necessary to direct epithelial cell orientation, and interdependent, as the epithelial cells are also capable of axially aligning the fibers of their substrate via RhoA/ROCK-mediated contractions ³³. Following development, these matrix-aligning forces must then be carefully regulated for epithelial patterning to be maintained, as uncontrolled epithelial cell contractility can lead to tumor initiation and progression ³⁴.

In addition to playing a role in developing tissue structures, long-range force transmission can be involved in normal tissue function and homeostasis. This is perhaps best exemplified in musculoskeletal tissues, where mechanical loads are transmitted to allow for locomotion of the body. The cells within these tissues experience these loads as well, as mechanical strain is transmitted to the resident fibroblasts and fibroblast nuclei ^{35, 36}. However, tendons also exhibit the ability to transmit forces from the cell to the macroscale tendon ECM as unloaded tendons are able to contract the macroscale tendon ECM to restore tension ^{37, 38}. The specific ECM components and organization in addition to cell types within different musculoskeletal tissues result in tissue-specific macro- to micro-scale strain transfer ¹⁶. Force transmission within musculoskeletal tissues is disrupted by tissue injury, either through overloading or a puncture injury ^{35, 36}. Alterations in force transmission alone can lead to disease progression in these tissues. For example, increasing collagen crosslinks within the cartilage extracellular matrix via lysyloxidase overexpression can directly lead to osteoarthritis progression at a similar scale and rate to surgically-induced osteoarthritis progression ³⁹.

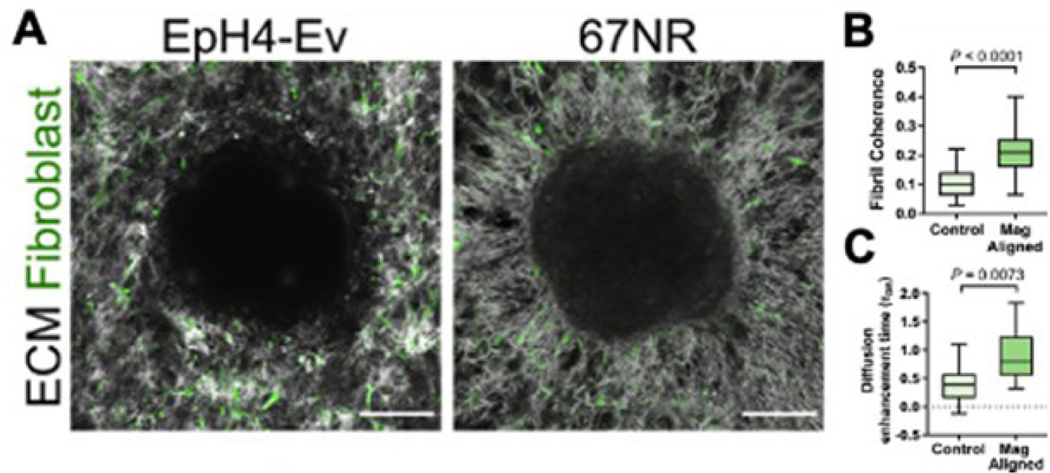
Long-range mechanical force transmission plays a role in the progression of various diseases, such as cancer ⁴⁰. For example, cancer cells are capable of generating sufficiently high force to align the nearby ECM fibrils, which promotes cell migration and diffusion of cancer growth factors away from the tumor microenvironment (Figure 4) ⁴¹. This effect was validated by growing cancer cell spheroids on collagen gels to observe the mechanical effect the spheroids had on the surrounding ECM and fibroblasts and by investigating how matrix alignment alters diffusion, as shown in Figure 4. Also, the rearrangement of ECM fibers further increases cancer cell stiffness and, therefore, the traction forces that the cell puts on the surrounding ECM, creating a positive feedback loop ⁴².

Figure 4.

A. Morphology of collagen ECM and fibroblasts surrounding a non-metastatic EpH4-Ev spheroid and a metastatic 67NR spheroid, demonstrating increased alignment surrounding the metastatic spheroid. B,C. Magnetically-controlled increased fiber alignment to model the effect of the cancerous spheroid results in increased rates of diffusion of exosome-sized particles. From 3.

While the importance of long-range force transmission within tissues is becoming more appreciated, continued understanding of how long-range force transmission guide tissue development, homeostasis, and disease progression is necessary for the development of future beneficial therapies and tissue engineering solutions that recapitulate normal tissue mechanical behavior.

3.2. Cells

Assessing long-range force transmission to cells is important for understanding how cells within tissues interpret their mechanical environment and use it to regulate their behavior. Cells transduce mechanical force from their surroundings via integrins, cytoskeleton filaments, and cytoskeletal-nucleus mechanical tethers, such as the LINC complex ^{43, 44}. A cell’s interpretation of its mechanical surrounding is not a passive process. Rather, the cells are constantly probing their surrounding ECM by pulling it with actomyosin fibers anchored via focal adhesions to the matrix ⁴⁵. Moreover, cells maintain a significant amount of prestress within themselves in order to prime themselves for understanding their mechanical environment ⁴⁵.

Cell interpretation of their mechanical environment is necessary for guiding and regulating cell behavior. For instance, the mechanical properties of the environment alone can lead to altered differentiation states in stem cells ⁴⁶. This regulatory role occurs most directly because varying ECM stiffnesses and applied mechanical forces are transmitted to the nucleus resulting in shape changes that alter gene transcription ⁴⁷. In addition to matrix stiffness alone, anisotropy of the substrate also directs cell phenotype and stem cell fate towards an anisotropic (i.e., fibrillar collagen-producing) lineage ⁴⁸. The ECM mechanical environment regulates how the cells interact with their substrate by increasing focal adhesion and stress fiber density on stiffer substrates ^{49, 50}. Beyond focal adhesion and stress fiber density and organization, there is a lack of understanding of the mechanisms by which cells interpret mechanical cues from the ECM. However, it has been hypothesized that substrate stiffness is estimated by cells probing deformation fields in the surrounding fibrous ECM, whereby fiber buckling would lead to decreased interpreted compressive stiffness ⁵¹. This fiber buckling amplifies cell contraction and increases their mechanosensitivity ⁵².

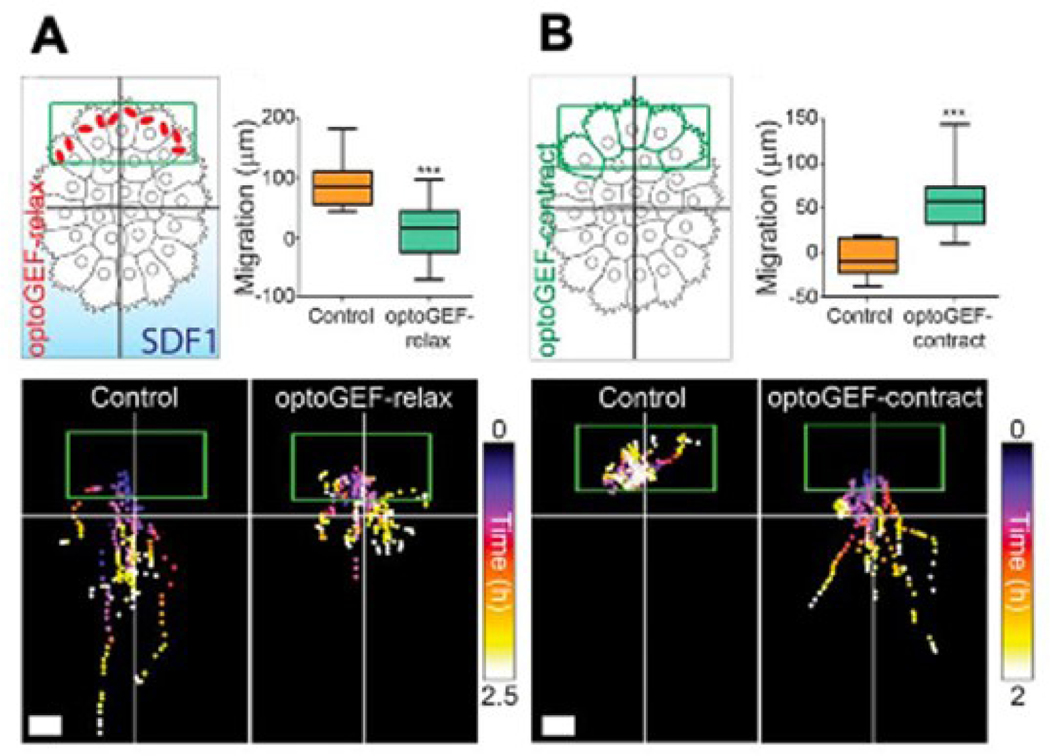
While the mechanism of cell transduction of long-range forces is not fully understood, it is known that it plays a role in cell processes through direct involvement in the process or in a regulatory role. One such example of a cell process is cell migration, where cells apply forces to their substrate in order to move themselves along. Specifically, long-range tensile forces are necessary to coordinate collective cell migration, as tensile forces at the front of invasive cell cohorts displace and align the ECM in order to create tracks along which the cells can migrate ⁵³. Long-range forces can also be transmitted intracellularly to drive collective cell migration during development, as forces at the rear of a neural crest cell group work to push the cell collective forward (Figure 5) ⁵⁴. In addition to coordinating cell migration patterns, force transmission directly regulates this process. Durotaxis is the migration of cells as guided by rigidity gradients, whereby cells generally migrate in the direction of greater matrix stiffness in a cell type-specific manner ⁵⁵. In addition to relatively static rigidity gradients, cells can also be guided along migratory paths by application of mechanical strain, which elicits a non-monotonic migration response in the direction of applied strain ⁵⁶. Thus far, durotaxis is less understood than other methods of guided cell migration such as chemotaxis. Continued investigation of durotaxis is essential for basic science understanding of cell behaviors but also has direct clinical relevance, as migration in response to mechanical stiffness gradients play a large role in cancer cell migration/metastasis as described previously ^{41, 42}. Specifically, cancer cells exhibit increased durotactic migratory potential on softer substrates, possibly reminiscent of the increased migratory capability of cancer cells as they metastasize away from the primary tumor ⁵⁷.

Figure 5.

A. Neural crest cell group treated with SDF1 gradient to induce migration, with migratory behavior abolished via relaxing contractility at the rear of the cell group via optoGEF-relax. B. Neural crest cell group without SDF1 begins to directionally migrate when contractility at the rear side of the group is induced via optoGEF-contract. From 2.

Another example of long-range forces playing a role in cell behavior is in distant cell communication, as cells are capable of communicating via mechanical signals transmitted through the extracellular matrix ⁵⁸. Specifically, the nonlinear elastic nature of fibrous matrices has been demonstrated to be a necessary ECM component for this communication to take place ²¹. One example of such communication is exemplified in the macrophage-fibroblast relationship, as fibroblast signal through force perturbations in the ECM to the local resident macrophages. Interestingly, application of forces to the ECM is sufficient to initiate macrophage migration in the direction of these forces, as discussed previously ²⁷. It is also worth noting that long-range force transmission is necessary to elicit the assembly of multicellular structures and patterns ^{32, 59}. Long-range force transmission can also affect intercellular biochemical communication. Specifically, it has been shown that long-range forces are capable of altering the physical structure of the ECM to increase rates of diffusion and, therefore, enhance cell-cell biomechanical communication ^{60, 61}.

3.3. Artificial Matrices and Biomaterials

After addressing long-range force transmission within cells and tissues, it is necessary to acknowledge how these concepts are translated to artificial matrices and biomaterials. Artificial matrices include materials that are largely or entirely synthetic, such as self-assembling block copolymer networks ⁶², with biomaterials being engineered materials made primarily from biological macromolecules such as fibrin, collagen, or glycosaminoglycans. Matrix stiffness and organization can be carefully modulated to observe the effects of these parameters on force transmission across matrices via fiber buckling and tensioning ⁶³. The stiffness of the individual fibers can also be tuned, whereby fibers of lower stiffness are more easily recruited by cellular traction forces, which promotes focal adhesion formation ⁶⁴. It is important to note that the process of focal adhesion formation is multi-faceted and complex, as it is a dynamic process that is regulated by signaling cascades that are modulated by the cell’s surrounding mechanical environment ⁶⁵. Moreover, these processes also guide the formation of different types of stress fibers (i.e., dorsal or ventral), which are determined by spatial relation to the cell nucleus. These different types of stress fibers also have differing roles in cell contractility, as dorsal stress fibers typically do not contain myosin while ventral stress fibers do ⁶⁶.

Given that many in vitro experiments are performed on artificial matrices, it is also important to understand how long-range force transmission may play a role in these experiments. When culturing cells on matrices of specific stiffness, it is possible that the cells modulate the matrix stiffness by pulling on their local fibers and causing them to stiffen with increasing strain. Moreover, this result may be compounded as the resulting stiffer fibrous matrix promotes greater cell force generation ⁶⁷. The porosity of the matrix can also affect what the cell is sensing, and the density of adhesion sites on artificial matrices might affect the interpreted mechanical stiffness ⁶⁸. Relatedly, it is known that shorter fiber lengths can limit the amount of traction a cell can generate, leading to altered force generation and, therefore, altered cell spreading and migration ⁶⁹. In addition to static mechanical cues, it is also important to consider how dynamic matrix loading is attenuated as it reaches the level of the cell, though this is dependent on the type of strain that is being applied to the sample ⁷⁰. Moreover, there is continued debate over how the matrix allows for strain attenuation at the level of the cell ⁷¹. While cells may misinterpret mechanical cues that the artificial matrix is designed to impart to them, it is also important to consider that these cells may not directly sense these mechanical cues as the cells degrade and remodel matrix as well as deposit new ECM in the surrounding area within hours of being seeded on the substrate ^{72, 73}. It is also possible that cells generate strain fields that go beyond the matrix in their immediate vicinity, and so respond to barriers at the distal side of matrices, such as the stiff frames present in Figure 2, or a rigid surface like bone or tissue culture plastic that underlies the ECM or a gel. Therefore, the appropriate thickness of a fibrous gel requires the consideration of long-range force transmission ^{74, 75}.

Overall, artificial matrices and biomaterials provide a tool for increased understanding of how mechanical forces are transmitted through fibrous networks. They also provide a tool for culturing cells within environments that closely recapitulate their physiological mechanical environment. Continued use and understanding of force transmission within these artificial matrices and biomaterials will allow for mechanistic understanding of long-range force transmission in physiological cells and tissues.

4. Modeling the mechanical behavior of biomaterials

In native states, cells of different types are usually surrounded by a three-dimensional (3D) fibrous microenvironment whose local physical properties can impact many important cellular functions including migration and proliferation ⁷⁶. The local physical properties of the fibrous microenvironment, in turn, depend on different factors including the collagen concentration, initial stiffness, degree of strain stiffening, pore size, cross-linking, degradability, viscosity, and plasticity ^{8, 67, 77–81}. In experimental systems, it is often difficult to isolate the potential contribution of each factor, and thus the impact of each factor cannot be separately investigated. To fill this gap, many computational models have been developed. In silico models offer the following features that can help us to better understand the mechanics of fibrous networks: (1) each physical parameter can be independently varied, allowing decoupling of different mechanisms and assessing the contribution of each of them to the overall mechanical behavior, (2) simulations can be carried out much faster compared with experiments and they can be easily shared and replicated, (3) computational models enable us to measure the cell-generated force from the experimentally measured displacement field, and (4) simulations can reveal new perspectives of biological phenomena and therefore suggest new experiments.

4.1. Linear analysis

In this section, we first present the theoretical prediction from the linear elastic framework on how the strain field generated by a contractile cell decays with distance from the cell. We will then compare the strain field with the one generated within a fibrous nonlinear network to show the effect of material nonlinearity on the range of displacement propagation. Assume a spherical cell with a radius r₀ within a linear elastic matrix. Assuming that u₀ is the cell-generated radial displacement at the cell-matrix interface (r = r₀), our goal is to determine the matrix displacement field u as a function of the distance from the cell center r = r₀. To this end, we need to solve the mechanical equilibrium in the matrix

$$\frac{d{\sigma }_{\text{r}}}{dr}+\frac{2}{r}\left({\sigma }_{\text{r}}-{\sigma }_{\theta }\right)=0$$ (1)

where σ_r and σ_θ are the radial stress and hoop stress, respectively. For linear elastic materials, σ_r and σ_θ are related to the radial and hoop strains ε_r and ε_θ as follows

$${\sigma }_{\text{r}}=\frac{E}{(1+v)(1-2v)}\left[(1-v){\epsilon }_{\text{r}}+2v{\epsilon }_{\theta }\right]$$ (2)

$${\sigma }_{\theta }=\frac{E}{(1+v)(1-2v)}\left[{\epsilon }_{\theta }+v{\epsilon }_{\text{r}}\right]$$ (3)

where E and v are the elastic modulus and Poisson’s ratio of the matrix, respectively. The strains ε_r and ε_θ for a linear material are defined in terms of the radial displacement u as follows

$${\epsilon }_{\text{r}}=\frac{du}{dr},{\epsilon }_{\theta }=\frac{u}{r}$$ (4)

Substituting equations (2–4) into equation (1), the mechanical equilibrium can be written in the following form

$$\frac{d^{2}u}{d{r}^2}+\frac{2du}{rdr}-\frac{2u}{r^2}=0$$ (5)

To solve the above differential equation, we need two boundary conditions. Considering that the displacement u at the cell-matrix interface and far from the cell are respectively u₀ and zero, the two boundary conditions are given as follows

$$u\left(r_0\right)=u_0,u(\infty )=0$$ (6)

which yields the following solution for equation (5)

$$u=u_0{\left(\frac{r_0}{r}\right)}^2$$ (7)

With the displacement field at hand from equation (7), the strain and stress fields can be determined from equations (2–4)

$${\epsilon }_{\text{r}}=-2\frac{u_0}{r}{\left(\frac{r_0}{r}\right)}^3,{\epsilon }_{\theta }=\frac{u_0}{r}{\left(\frac{r_0}{r}\right)}^3$$ (8)

$${\sigma }_{\text{r}}=-\frac{2E{u}_0}{(1+v)r}{\left(\frac{r_0}{r}\right)}^3,{\sigma }_{\theta }=\frac{2E{u}_0}{(1+v)r}{\left(\frac{r_0}{r}\right)}^3$$ (9)

Equation (7) shows that the displacement decay in linear materials is proportional to 1/r² and the stress/strain decay is proportional to 1/r^{3 5, 51, 82, 83}. However, experimental results from 3D particle tracking microscopy experiments reveal that the cell-generated displacement field decays significantly slower within collagen fibrous matrices ⁶⁷ due to the long-range transmission of mechanical forces within these matrices which will be later discussed.

4.2. Nonlinear (strain-stiffening) response of fibrous matrices

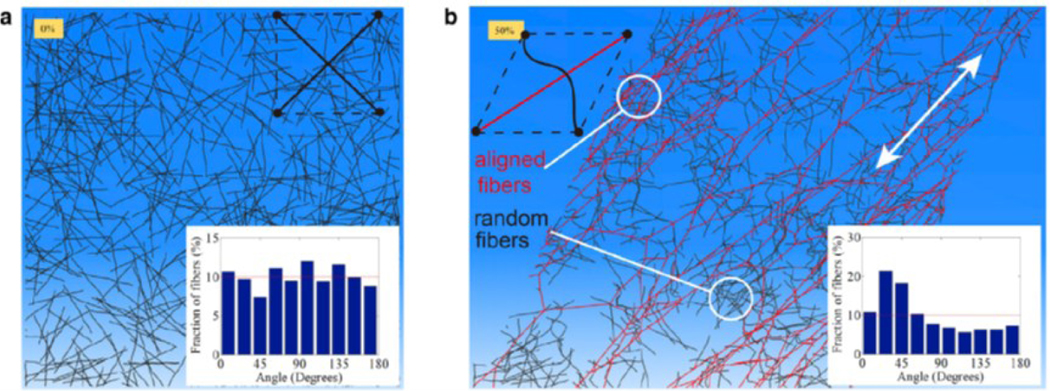
A large fraction of biological materials is composed of fibrous networks whose mechanical properties, unlike linear hydrogels, change as they are deformed under cell-generated forces. When fibrous networks are mechanically loaded, forces are carried by individual fibers, which can lead to translation, rotation, and deformation of each fiber ⁸⁴. As a result, the deformation field of fibrous networks can be highly nonaffine, i.e., the displacement field at the microscale does not match the deformation field at the scale of the bulk material ⁷ which in turn generates a nonhomogeneous local strain field entirely different from the far-field imposed strain ^{6, 84–86}. This feature of fibrous networks leads to unique behaviors in tension, compression, and shear. Specifically, when loaded, individual fibers in the network tend to rotate and align along the direction of the maximum principal strain. The rotation and alignment of fibers can cause unusual behaviors in fibrous network materials including strain stiffening and long-range force transmission which distinguish them from linear elastic hydrogels. For example, as an initially isotropic fibrous collagen network undergoes large deformations, there is a set of collagen fibers that is reorganized and aligned in the direction of the maximum principal strain when the matrix is stretched in this direction beyond a critical strain ^{5, 87} (Fig. 6). While this set of fibers reorients and aligns in the maximum principal stretch direction causes strain stiffening, there is another set of fibers that experiences compression and buckles in the minimum principal stretch direction ^{5, 67}. The stress-strain relationship becomes even more complicated with the presence of cells within the network and/or when the network is loaded multiaxially ^{8, 88}. Note that the alignment of collagen fibers can lead to local stiffening of the matrix, while cells sense and actively respond to this local stiffening by promoting their contractility leading to a positive feedback loop between cells and the ECM ^{67, 76, 89, 90}.

Figure 6.

Discrete fiber simulations of an initially random (isotropic) fiber network before (a) and after (b) 50% shear strain. The inset in (a) shows that fibers are isotropically distributed in all directions in the initial configuration. The inset in (b) shows that after the shear deformation, more fibers are aligned in the 45o orientation which coincides with the direction of the maximum principal stretch 8.

As the stress and strain fields generated by a contractile cell decay with distance from the cell, it is clear that large fiber alignment in the collagen matrix is confined to a region surrounding the cell, while far away from the cell the stress and strain fields are small enough to be approximated with linear elasticity. Sander ⁹¹ determined the critical distance from the cell above which the cell-generated stress and strain fields can be approximated using linear elasticity. Below the critical distance, collagen fibrous networks exhibit significant nonlinear strain stiffening behavior that cannot be captured by linear elastic models as shown in Figure 7. Using two-dimensional discrete fiber network simulations, Onck et al. ⁴ showed that the nonlinear strain stiffening behavior of fibrous networks lies in the rearrangement of the network rather than in its constituent fibers. Similarly, using realistic network architectures of collagen-I networks, Stein et al., ⁹² demonstrated that the nonlinear behavior of collagen fibrous networks can be entirely explained by the alignment of collagen fibers in the direction of tensile stress, as opposed to entropic stiffening of individual collagen fibers.

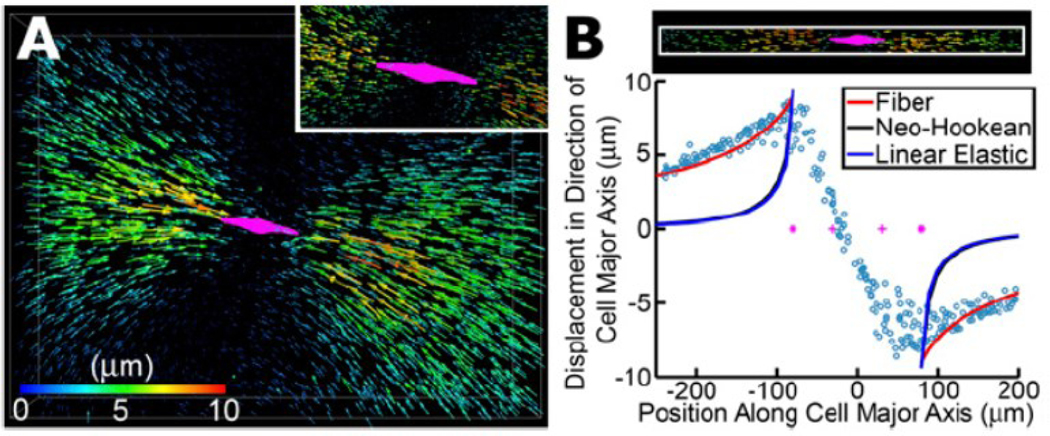
Figure 7.

Long-range force transmission within a three-dimensional collagen network. (A) Deformation field generated by an MDA-MB-231 breast cancer cell within a three-dimensional collagen network. Each arrow represents the displacement of a fluorescent bead covalently bonded to collagen fibers. 4,000 of 12,000 tracked bead displacements are shown. Arrows are rendered at four times their true size. The cell is shown in magenta. The inset shows a zoomed-in view where all displacement vectors are rendered at their true scale. (B) Bead displacements along the long axis of the cell are plotted as a function of their position along the long axis of the cell. Coordinate (0,0) represents the center of the cell. Solid lines are fits to the experimental data (circles) using three different material models: fibrous model (red) 57, nonlinear hyperelastic neo-Hookean model (black), and linear elastic model (blue).

Note that while individual collagen fibers show significant strain stiffening in tension to resist extension, they buckle and soften in compression ^{25, 93, 94}. The stiffening of collagen fibrous networks in tension and their softening in compression ^{88, 95} can also lead to negative normal stresses when collagen networks undergo shear deformations ⁹⁴. When an initially isotropic fibrous network (with fibers equally distributed in all directions) undergoes shear deformations, we can assume that an equal number of fibers are stretched and compressed. If the fibrous network is made of linear fibers that show the same resistance against tension and compression, sliding one plat with respect to the other in shear deformations only generates shear (tangential) stresses and not normal stresses (that tend to pull the plates together or push them apart). However, if the fibrous network is made of collagen fibers, since the tensile force generated by the stretched fibers is significantly higher than the compressive force of those under compression, a net tensile force is generated that tends to pull the plates together ⁹⁴. This negative normal stress can be also observed in discrete fiber simulations of collagen networks in shear tests where the negative normal stress increases quadratically with shear strain ^{92, 96}.

Another striking property of fibrous networks is their capability to transmit forces over relatively long distances. The alignment of collagen fibers in the direction of tension and the subsequent stiffening of the network ^{80, 97, 98} can lead to long-range transmissions of mechanical forces within fibrous collagen matrices ^{26, 52}. For example, when cells contract in a fibrous network, the displacement can be felt as far as 20 times the cell size, which is significantly high compared with the force-transmission range in linear hydrogels. As a result, cells can sense other cells located at distances ~20 times their size in 3D collagen fibrous matrices. Note that the alignment of collagen fibers by the cellular tensile forces and the subsequent long-range force transmission can be even lead to the formation of collagen tracts between neighboring cells through which cells can mechanically interact with each other within the matrix ^{61, 99, 100}. To capture the above physical behaviors of fibrous network materials, there are mainly two schools of models: (i) discrete fiber network models, and (ii) continuum models. As their names imply, the major difference between these two types of models is whether the fibers are treated discretely or as a continuum. In the following section, we look into these two different types of models and review their strengths and weaknesses.

4.3. Discrete fiber networks

Discrete fiber networks explicitly consider the geometry of individual fibers and the microstructure of the network (Figure 8. (a–d)). Fibers in the model are connected to each other when they intersect. This construction mimics the structure of natural fibrous networks. When a discrete fiber network is loaded, mechanical forces are transmitted through fibers and crosslinks, leading to displacement and rotation of individual fibers. The discrete fiber network intrinsically captures the non-affine deformation of the fibrous network and is therefore widely used to study the impact of fiber microstructure on the mechanical behavior of fibrous network materials. To construct a discrete fiber network, the following two major specifications of networks should be considered: (i) the microstructure of the network, and (ii) the constitutive models of individual fibers.

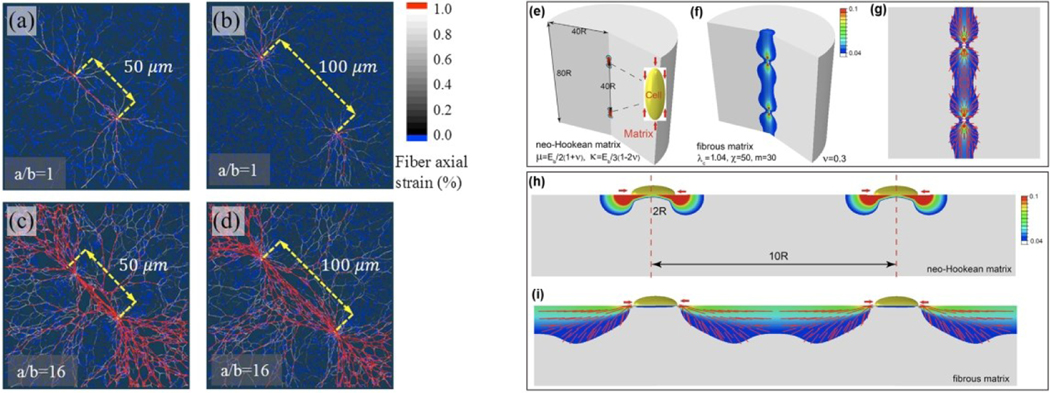
Figure 8.

(a-d) Numerical results from discrete network fiber simulations show the interaction between two cells with different center-to-center distances at 90% cell contraction 77. When the distance is 50 μm, cells of all aspects ratios mechanically interact by forming collagen tracts (a and c). However, as the separation distance increases, only cells with high aspect ratios (d) can mechanically interact with each other, while no visible collagen tracts are observed for circular cells (b). (e-i) Numerical results from continuum models 8. Contour plots of the maximum principal strain in three-dimensional matrices for linear isotropic materials (e) and fibrous materials (f). Vector plots of the maximum principal strain which coincides with the orientation of the collagen fibers after cellular contraction (g). Contour plots of the maximum principal strain on two-dimensional matrices for linear isotropic materials (h) and fibrous materials (i).

4.3.1. Network generation.

Since the topology of in vivo fibrous networks (e. g., collagen, fibrin networks) are not well established, many models have either employed imaging-based networks or artificially generated networks. Using images of a 3D collagen network, Stein et al. confirmed that the alignment of fibers, instead of nonlinearity of individual fibers, lead to the strain-stiffening of the whole network ⁹². Ma et al. used confocal reflectance microscopy images of cells and their surrounding network of collagen fibers to generate the structure of the fibrous network and identified that the presence of fibers is critical for the long-range force transmission ²⁶. Sander et al. used confocal microscopy data for a collagen-I network to propose a critical radius within which the fibers are aligned due to the cell contraction ⁹¹. While using real network images has a clear advantage in clinical relevance, it suffers in practice from artifacts from imaging techniques and segmentation algorithms. For example, fibers at different depths could be misidentified to be crosslinked. Imaging at the nano- and micro- scales are also difficult to segment due to limits on the resolution.

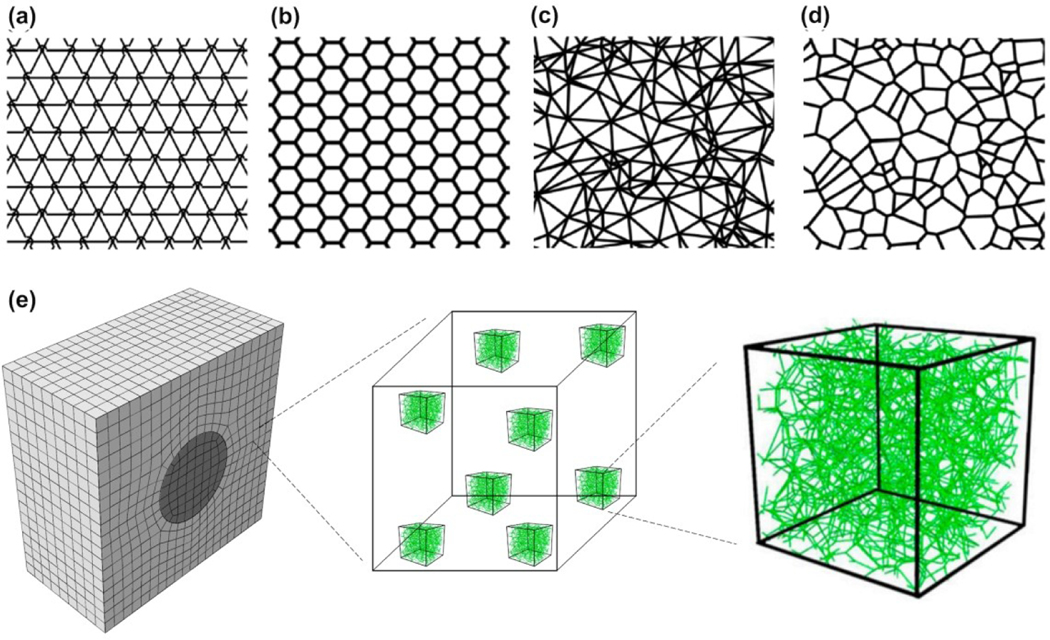
Due to these difficulties in imaging-based models, many studies use models that are artificially created. The networks can be generated by either introducing randomness in a periodic network, or randomly placing fibers in a domain according to a preset rule. In the first category, for example, Arzash et al. studied the fiber networks in the ropelike limit using periodic 2D triangular and hexagonal lattices (Figures 9a and 9b) ¹⁰¹. They eliminated fibers randomly to match the connectivity (i. e., the number of fibers joined at one crosslink) with the real biopolymer networks, and to remove the unphysical effects of network-spanning fibers. In the second category, for example, the Delaunay networks are constructed by placing N random points in a box and triangulating them in a way that there is no point inside the circumferencecircle of any triangle, which maximizes the smallest angle among all triangulations of the given point set (Figure 9c) ⁸⁴. Another example is the Voronoi network which is a derivative of the Delaunay networks by connecting the circumcircles (Figure 9d) ¹⁰¹.

Figure 9.

Different networks for discrete fiber simulations. (a) A triangular lattice network. The arc denotes that one of the three crossing fibers is detached from the cross-link which reduces the local connectivity from 6 to 4. (b) A hexagonal lattice which has a local connectivity of 3. (c) A Delaunay network with a nonuniform local connectivity which has the average local connectivity of 6. (d) A Voronoi network which has a local connectivity of 3.

With many discrete models developed for fibrous network materials, the freedom of choice in network geometry raises potential issues on the clinical relevance of the results and their implications. Humphries et al. compared dual, Voronoi, growth, and perturbed networks and found all these network geometries are able to capture the long-range mechanical communications ⁶¹. However, the response heterogeneity, fiber alignment, and substrate displacement fields are sensitive to the network choice. Aghvami et al. showed that low connectivity and rotational freedom of the fibers in the network is critical for the enhanced long-range mechanosensing ¹⁰². As the networks are generated randomly, larger variations of mechanical response were also observed with the same type of networks. This shows the importance of the choice of network geometry and further validation of the model by comparing it with experiments in multi-axial testing.

4.3.2. Fiber mechanical properties.

In addition to the geometry of the network, the constitutive model of individual fibers also plays an important role in the mechanical response of the network. One of the most frequent choices is linear elastic beams. When deformed, the strain energy is given by

$$U=\frac{1}{2}\int EI{\left({\nabla }^{2}u\right)}^{2}ds+\frac{1}{2}\int EA{(dl/ds)}^{2}ds$$ (10)

where E denotes the Young’s modulus, A represents the cross-sectional area of the beam, and Iindicates the moment of inertia. The ratio I/A indicates the easiness of bending the fiber. When the fiber is long and thin with large Iand small A, it is easier to bend the fiber than to stretch it. When compressed, the fibers (modeled as elastic beams) will buckle due to instability, leading to the softening of the whole network. In some studies, the fibers are modeled as wavy structures with curvatures. This resembles the shape of fibers observed in many experiments. These filaments are assumed to be stress-free in the initial wavy state and when loaded, the work required for the deformation of the network is stored as bending strain energy in each fiber. Onck et al. studied modeling wavy fibers and concluded that despite quantitative differences, the general behavior is qualitatively similar ⁴.

4.4. Anisotropic strain-stiffening continuum models

Recently, several continuum models have been developed to capture the long-range force transmission in fibrous networks (Figure 8(e–i)). While the discrete fiber networks can explicitly illustrate the mechanism of fiber realignment, they are computationally complex. Moreover, since the networks are generated randomly, the results are statistical, making it difficult to reproduce the results. Continuum models are simpler with fewer parameters and deterministic without randomness, making them a convenient tool to model experiments. Wang et al. ⁵ developed a constitutive continuum model by incorporating the fact that the fibrous materials stiffen preferentially along the directions of tensile principal stretches. The model is developed based on discrete fiber simulations that show aligned fibers stiffen the network anisotropically along the loading direction (Figure 6). The strain energy density of the matrix in this model can be written as

$$W=\underset{ randomlyalignedfibers}{\underbrace{\frac{\mu }{2}\left({\overline{I}}_1-3\right)+\frac{k}{2}{(J-1)}^2}}+\underset{ alignedfibers}{\underbrace{{\displaystyle {\sum }_{a=1}^{3}f\left({\lambda }_a\right)}}}$$ (11)

where the first part captures the isotropic mechanical behavior of randomly distributed fibers using a hyperelastic neo-Hookean material, and the second part captures the alignment of fibers which causes strain-stiffening along the principal stretch directions. μ and k respectively denote the initial shear and bulk moduli, Ī₁ is the first invariant of the deviatoric part of the Cauchy-Green tensor, j denotes the determinant of the deformation gradient tensor, and λ_a (a = 1,2,3) represents the principal stretches. In equation (11), f is a non-linear function which rises sharply as λ_a increases, capturing the anisotropic strain-stiffening induced by fiber alignment. Wang et al. ⁵ showed that the ability of the material to anisotropically stiffen along the loading direction is essential to capture the long-range force transmission. However, the specific form of the constitutive equation is not crucial as long as it captures the orientational anisotropy and stiffening that naturally arise along the principal directions upon loading. Using the strain energy function in equation (11), the radial stress in equation (2) can be obtained in the following form (see reference ⁵)

$${\sigma }_{\text{r}}=\frac{E}{(1+v)(1-2v)}\left[(1-v){\epsilon }_{\text{r}}+2v{\epsilon }_{\theta }\right]+E_{\text{f}}{\epsilon }_{\text{r}}$$ (12)

where E_f represents the stiffening response of collagen matrices in tension. Substituting σ_r (from equation (12)) and σ_θ (from equation (3)) into the equilibrium equation (1) yields the following equation

$$[1+\frac{(1+v)(1-2v)}{(1-v)}\frac{E_{\text{f}}}{E}]\left(\frac{d^{2}u}{d{r}^2}+\frac{2du}{rdr}\right)-\frac{2u}{r^2}=0$$ (13)

Solving equation (13) with the boundary conditions (6) yields the following solution

$$u=u_0{\left(\frac{r_0}{r}\right)}^n$$ (14)

where

$$n=\frac{1}{2}\left(\sqrt{\frac{9+\chi }{1+\chi }}+1\right),\chi =\frac{(1+v)(1-2v)}{(1-v)}\frac{E_{\text{f}}}{E}$$ (15)

Note that for E_f/E ≫ 1 (strong fibrous response), the exponent n→1 and therefore equation (14) shows a slow decay of displacement, whereas for an isotropic material (E_f/E≪ 1), n→2 which yields equation (7).

This continuum model has been successfully used to explain and predict the force transmission in collagen matrices with different microstructures ¹⁰⁰. Hall et al. ⁶⁷ used single-cell traction force measurements for breast cancer cells embedded within 3D collagen matrices. As expected, the displacements are highest in the matrix near the two tips of the cell along the long axis of the cell. While the isotropic neo-Hookean hyperplastic model predicted a quick decay of the displacement field with distance from the cell, the experimentally measured displacement field decays significantly slower and can be only captured by the above continuum model (Figure 7B). With the help of the computational model, Hall et al. ⁶⁷ identified that the cells are able to generate sufficient strain to locally align and stiffen the surrounding collagen matrix, which in turn positively feedbacks to the cell to enhance the generation of cell contractile force.

In addition to discrete fiber network and continuum models, multiscale models have been also used to study the mechanics of fibrous matrices ^{103, 104}. These multiscale models use both continuum and discrete fiber network frameworks to simulate material behavior at different scales. At the macroscopic scale, these multiscale models use a continuum framework, but instead of using a constitutive equation to relate the stress to the strain, discrete fiber network simulations at the microscopic scale are used at the locations where the stress-strain relationships needed for the continuum simulation ¹⁰⁵. Note that continuum and multiscale models can also enable us to approximate cell-generated traction forces within fibrous collagen environments ^{67, 83, 100}. Historically, in methods for measuring cell-generated forces, cells are cultured on a linear elastic hydrogel with known mechanical properties and we use the experimentally-measured displacement field generated on the surface of the hydrogel together with a linear elastic constitutive model to calculate cell traction forces. As discussed earlier, the linear elastic model, however, cannot capture the mechanical behavior of collagen fibrous matrices and thus cannot be used to measure cell-generated forces within these physiologically more relevant environments.

5. Conclusions

Physical signals allow cells to sense the presence of other cells at distances much larger than are possible by diffusing chemical signals. These physical signals include direct transmission of force from one cell to another, as well as cell traction-generated changes in the alignment, density and stiffness of the extracellular matrix. Long-range force transmission in biological materials appears to require the unique, nonlinear responses of fibrous networks such as those that form the extracellular matrix and the intracellular cytoskeleton. There is much still to learn, both experimentally and theoretically, about how fibrous networks respond to the forces generated in biological tissues, and understanding these principles can lead to better methods for characterizing soft tissues and to improved biomimetic materials.