Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Aug 12;61(8):3752–3757. doi: 10.1021/acs.jcim.1c00652

New Features of the Open Source Monte Carlo Software Brick-CFCMC: Thermodynamic Integration and Hybrid Trial Moves

H Mert Polat †,‡,, Hirad S Salehi ‡, Remco Hens ‡, Dominika O Wasik §, Ahmadreza Rahbari ‡, Frédérick de Meyer †,, Céline Houriez , Christophe Coquelet , Sofia Calero §,∥, David Dubbeldam ⊥, Othonas A Moultos ‡, Thijs J H Vlugt ‡,*
PMCID: PMC8385706  PMID: 34383501

Abstract

graphic file with name ci1c00652_0004.jpg

We present several new major features added to the Monte Carlo (MC) simulation code Brick-CFCMC for phase- and reaction equilibria calculations (https://gitlab.com/ETh_TU_Delft/Brick-CFCMC). The first one is thermodynamic integration for the computation of excess chemical potentials (μex). For this purpose, we implemented the computation of the ensemble average of the derivative of the potential energy with respect to the scaling factor for intermolecular interactions (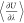Inline graphic). Efficient bookkeeping is implemented so that the quantity 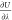Inline graphic is updated after every MC trial move with negligible computational cost. We demonstrate the accuracy and reliability of the calculation of μex for sodium chloride in water. Second, we implemented hybrid MC/MD translation and rotation trial moves to increase the efficiency of sampling of the configuration space. In these trial moves, short Molecular Dynamics (MD) trajectories are performed to collectively displace or rotate all molecules in the system. These trajectories are accepted or rejected based on the total energy drift. The efficiency of these trial moves can be tuned by changing the time step and the trajectory length. The new trial moves are demonstrated using MC simulations of a viscous fluid (deep eutectic solvent).

Introduction

Recently, we presented Brick-CFCMC,1 an open source molecular simulation code for the calculation of phase- and reaction equilibria using state-of-the-art force field-based Monte Carlo (MC) simulations in different ensembles, such as the NVT, the NPT, grand-canonical, the reaction, and the Gibbs ensembles. Brick-CFCMC uses the Continuous Fractional Component Monte Carlo (CFCMC) method2−6 for molecule exchanges. This method involves a fractional molecule whose interactions with the surrounding molecules are scaled using a continuous scaling factor, λ, from zero interactions with the surroundings (λ = 0) to full interactions with the surroundings (λ = 1).2 The CFCMC method considerably improves the insertion or deletion of molecules while allowing for a direct computation of chemical potentials and partial molar properties.5,7−10 Brick-CFCMC has been used in many studies, especially for the computation of gas solubilities in solvents.5,6,11,12

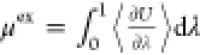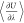We present the implementation of new features, namely, the computation of excess chemical potentials (μex) using thermodynamic integration (Inline graphic)13,14 and hybrid MC/MD trial moves. This allows for the calculation of μex by integrating the average derivative of potential energy with respect to the interaction scaling factor (Inline graphic). Using μex, activity coefficients of species can be computed.15,16 Brick-CFCMC can already calculate μex using the probability distribution of the scaling factor p(λ) of fractional molecules.1,8 This method requires the probabilities p(λ = 0) and p(λ = 1). A weight function is required to ensure a flat probability distribution of λ.2,17 Although this method works efficiently for small molecules, we found that it is difficult for large and/or strongly polar molecules because (1) the probability distribution of λ can be sensitive to the changes in the biasing function, and (2) the biasing function can be very large for ionic systems (e.g., of the order of 100kBT). Therefore, a flat distribution of the observed probability of λ is challenging to achieve in a single simulation, resulting in a large uncertainty for the computed μex. It is more convenient to calculate μex of large and/or strongly polar molecules using thermodynamic integration because it eliminates the need for sampling the full λ-space with equal probabilities in a single simulation. With thermodynamic integration, Inline graphic can be computed from several independent simulations at different fixed values of λ (or a limited range of λ-values) or by sampling the whole λ-space in a single simulation. 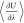We implemented efficient bookkeeping, so the instantaneous value of Inline graphic is updated after every MC trial move. Therefore, the ensemble average Inline graphic is computed with negligible computational cost. Alternatively, the weighted histogram analysis (WHAM) method,18,19 the Bennett acceptance ratio (BAR) method,20 and the multistate Bennett acceptance ratio (MBAR) method21 may also be used for the computation of μex using postprocessing of simulation data.22

In the CFCMC method, trial moves are attempted to reinsert the fractional molecule at a random position in the simulation box. Additionally, trial moves are attempted to transform the fractional molecule into a whole molecule, while a randomly selected whole molecule is transformed into a fractional molecule (at the same value of λ).6 These trial moves help sampling the λ-space more efficiently, as well as thermalizing the system. However, for viscous liquids with strong intermolecular interactions, such as ionic liquids and deep eutectic solvents (DES),11 the sampling of configuration space is not efficiently performed by single-molecule trial moves, even if the aforementioned trial moves are carried out. It is well-known that single-molecule trial moves are not efficient in inducing collective motion in a dense fluid.23,24 A variety of advanced techniques have been developed and reported in the literature for improving the sampling of configuration space in MC simulations. Well-known examples of such techniques are the smart MC algorithm by Rossky et al.,23 force bias MC by Pangali et al.,25 multiparticle MC moves by Moucka et al.,26 and hybrid MC by Duane et al.27 We have implemented hybrid MC/MD trial moves for translation and rotation of molecules (conceptually similar to Duane et al.27) in Brick-CFCMC. We chose to have separate hybrid translation and rotation moves because combining these two trial moves were found to be less efficient.28 In these trial moves, short Molecular Dynamics (MD) simulations are performed in the NVE ensemble, where Newton’s equations of motion are integrated according to the computed resultant force or torque on each molecule. A schematic representation of the hybrid translation trial move is shown in Figure 1. The hybrid trial moves are performed collectively, meaning all molecules are translated or rotated at every MD time step, using a time-reversible (and area-preserving) integrator. During the hybrid trial moves, all molecules are kept rigid (intramolecular degrees of freedom are sampled differently in Brick-CFCMC1). Therefore, translations are applied to the centers of mass of the molecules, and rigid-body rotations are performed around the centers of mass. The short MD trajectories generated by the hybrid trial moves are accepted or rejected with a probability proportional to the Boltzmann factor of the total energy of the system13

graphic file with name ci1c00652_m008.jpg 1

where o and n denote the old and new (initial and final) configurations of the MD trajectory, and ΔU and ΔK are the differences in potential energy and kinetic energy (translational or rotational), respectively, between the old and new configurations. β is defined as 1/(kBT), where kB is the Boltzmann constant, and T is the absolute temperature.

Figure 1.

Figure 1

Open in a new tab

Schematic representation of (a) a conventional translation trial move and (b) a hybrid translation trial move. The conventional translation move attempts to displace a single randomly selected molecule in the simulation box in a random direction, while the hybrid translation trial move displaces all the molecules simultaneously, according to the magnitude and direction of the resultant forces acting on the molecules, using a short MD trajectory in the NVE ensemble. The length of the short MD trajectory as well as the time step Δt can be adjusted to have a required acceptance probability. These trial moves increase the efficiency of the simulations significantly in the equilibration of the system and the sampling of configuration space;23,24 see also Figure S4 of the Supporting Information. The red and gray atoms represent oxygen and hydrogen atoms, respectively. This figure was created with iRASPA.29

Brick-CFCMC with these major new features can be downloaded from https://gitlab.com/ETh_TU_Delft/Brick-CFCMC.

Implementation

In the CFCMC method, intermolecular LJ and electrostatic interactions are scaled differently as a function of λ. The scaling of LJ and electrostatic interactions is denoted by λLJ and λel, respectively, and both are functions of λ. It is important to note that λLJ and λel should be continuous functions of λ and that electrostatics are fully switched off (λel = 0) before scaling down the LJ interactions.30 Details of this scaling are provided in the Supporting Information. 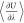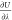In Brick-CFCMC, the value of Inline graphic can only be computed for one charge-neutral group of fractional molecules; however, this group can contain several different molecules or ions. For example, a fractional group can consist of both a sodium ion (Na+) and a chloride ion (Cl–), so that thermodynamic integration directly results in the excess chemical potential of sodium chloride μNaClex. Analytic expressions for Inline graphic were derived for intermolecular Lennard-Jones and electrostatic potentials. For the LJ potential, terms were derived for truncated, for truncated and shifted, and for tail corrections. Analytic expressions for derivatives of electrostatic potentials may seem trivial at first sight because for linear charge scaling Inline graphic is proportional to λ.28 It is important to note that such a scaling may lead to overlaps between atoms for low values of λel. 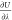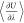For this reason, we have used an offset for interatomic distances which makes the computation of Inline graphic numerically stable (but leading to more complex expressions). For electrostatic interactions, we derived analytic expressions for the Wolf method,31 for the damped and shifted version of the Wolf method,32−34 and for the Ewald summation.35 These analytic expressions can be found in the Supporting Information. The computation of Inline graphic can be switched on with the respective keyword in the input files as described in the manual of Brick-CFCMC. 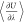The value of Inline graphic is computed in Brick-CFCMC for every MC trial move. 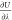The software prints the values of Inline graphic as a function of λ to a file. We implemented the thermodynamic integration with efficient bookkeeping so that the computation of Inline graphic has negligible additional computational cost as the number of fractional molecules in the simulation box is low compared to the total number of molecules. Thermodynamic integration can be performed by postprocessing computed values of Inline graphic using a tool provided with Brick-CFCMC. Brick-CFCMC also provides values for Inline graphic that can be read directly into alchemlyb,36 and we have verified that identical excess chemical potentials are obtained.

The velocity Verlet algorithm37,38 is used to integrate the equations of motion in hybrid translation trial moves. In hybrid rotation trial moves, the quaternions of molecules need to be integrated simultaneously with the angular velocities. The NOSQUISH algorithm of Miller et al.39 is used for the integration of equations of motion. The algorithms used for both the hybrid translation and hybrid rotation trial moves are symplectic (area-preserving) and time-reversible.13,39 Details of these algorithms as implemented in Brick-CFCMC can be found in the Supporting Information. For the hybrid trial moves, for efficiency reasons, the electrostatic forces/torques needed to create the short MD trajectories are always computed using the damped, shifted Wolf potential,32 for which the damping parameter and cutoff radius (independent of the cutoff for electrostatic energies) can be provided in the simulation input. The fact that the actual interaction potential (e.g., the Ewald summation) is different is accounted for in the acceptance rules.40

Case Studies

To validate the implementation of thermodynamic integration and hybrid MC/MD trial moves, we present two case studies. Using the new thermodynamic integration feature in Brick-CFCMC, we computed the excess chemical potential of infinitely diluted sodium chloride in water at 298 K and 1 bar in the NPT ensemble. For water molecules, the SPC/E41 force field was used, while for NaCl molecules, the Joung-Cheatham42 force field was used. The force field and simulation details are provided in the Supporting Information. It is important to note that with the CFCMC technique we could not achieve a flat probability distribution of λ in a single simulation, and multiple simulations were needed in which the λ-space is confined. The weight function and the probability distribution of λ of this simulation are shown in Figure S2 of the Supporting Information. Using the thermodynamic integration, we performed 102 different MC simulations of NaCl/water solutions at different and fixed values of λ. In Figure 2, 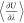Inline graphic of NaCl in water as a function of λ is shown. Using the thermodynamic integration, μNaClex was calculated as −741.7 kJ mol–1. This value is consistent with the literature as it is within the chemical accuracy (≈ 4 kJ mol–1)43 of previous simulations (−742 kJ mol–1).44 Note that −741.7 kJ mol–1 corresponds to ca. –300kBT, so it is expected that a single CFCMC simulation sampling the full λ-space will not be sufficient to overcome this free energy difference. The results show that the calculation of μex using our implementation of thermodynamic integration is an accurate and reliable method for strongly polar molecules. μNaCl computed using thermodynamic integration is also consistent with the experiments (−743 kJ mol–1)45 in the literature. We also simulated the same system using the Ewald summation for electrostatics instead of the damped and shifted version of the Wolf method. In this case, μNaClex was computed as −739.2 kJ mol–1, showing that thermodynamic integration with the Ewald summation yields results nearly identical to those obtained by the damped and shifted version of the Wolf method. We also tested the number of data points in λ-space that are needed for an accurate calculation of μNaCl. Table 1 shows the computed values of μNaClex for different numbers of data points in λ-space. These results show that the number of data points can be decreased from 102 to 19 without loss in accuracy.

Figure 2.

Figure 2

Open in a new tab

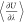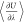Value of Inline graphic as a function of λ for infinitely diluted NaCl in water at 298 K and 1 bar. The values of Inline graphic were collected from 102 independent simulations at different and fixed values of λ. The red circles and the blue line represent the values of Inline graphic and the fitted spline, respectively. μNaClex was computed as −741.7 kJ mol–1 from the integration of a fitted spline. The inset schematically shows a NaCl fractional group in water. Modifying the scaling factor λ by dλ changes the strength of the interactions between the fractional group and the surrounding molecules, allowing for the computation of Inline graphic. In the inset, the red and gray atoms represent the oxygen and hydrogen of water, while the green and purple atoms represent chloride and sodium ions, respectively.

Table 1. Computed Values of μNaClex Using Thermodynamic Integration for Different Numbers of (Equidistant) λ Pointsa.

no. of λ points μNaClex [kJ mol–1]
102 –741.70.3
52 –741.90.3
36 –741.90.3
27 –742.00.5
22 –742.10.8
19 –742.60.8
9 –751.32.8
Open in a new tab
a

Spline fitting was used for the numerical integration. The subscripts in the second column show uncertainties computed as one standard deviation.

To increase the efficiency of the hybrid trial moves, it is recommended that the size of the MD time step Δt is specified according to the maximum average displacement of molecules and an acceptance probability of ca. 50%. Therefore, for each system, short test simulations should be performed to obtain the optimal time step size. In Figure 3, the acceptance probability and the average displacement are presented for the hybrid translation trial move as a function of time step size, for a system of choline chloride/urea deep eutectic solvent at 323 K and 1 bar. It can be observed that based on the acceptance probability of 50% and the maximum average displacement, the optimal time step size is obtained as 0.0075 and 0.0095 ps, respectively. Therefore, a value within this range is deemed efficient for the hybrid translation trial move of this system. It is important to note that a time step of 0.001 ps is typically used for reasonable energy conservation in MD simulations of this system, which is significantly smaller.46,47 The time step size and the trajectory length can be specified independently for the hybrid translation and hybrid rotation trial moves. A similar procedure to the one for hybrid translation trial move can be followed for hybrid rotation trial moves. It is important to note that the optimal time step size depends on the length of the MD trajectory (specified as 5 time steps in the simulations of Figure 3). In principle, longer MD trajectories result in smaller values for the optimal time step size (and vice versa). Short test simulations can be conducted to determine the optimal values of the time step and the number of time steps. For a detailed study on how to choose the optimal number of time steps and the integration time step size, the reader is referred to ref (48). To show the effect of hybrid MD trial moves, we have conducted simulations of choline chloride/urea DES for various fractions of hybrid trial moves in a cubic simulation box at 323 K, starting from random initial configurations. In Figure S4 of the Supporting Information, the running potential energy is shown as a function of the number of MC steps. Clearly, the use of hybrid MD trial moves significantly facilitates equilibration of the system.

Figure 3.

Figure 3

Open in a new tab

Average acceptance probabilities (red) and molecule displacements (blue) for the hybrid translation trial move as a function of time step size, for a choline chloride/urea deep eutectic solvent at 338.15 K and 1 bar. Five time steps are used as trajectory length for all simulations. The lines are drawn to guide the eye.

Conclusions

We present new features implemented in the Brick-CFCMC simulation code for phase and reaction equilibria. We implemented thermodynamic integration for the calculation of μex. With efficient bookkeeping, we compute Inline graphic which can then be integrated to obtain μex. We show the accuracy and reliability of this method by computing the excess chemical potential of NaCl (μNaClex) in water at infinite dilution. Analytic derivatives of all interaction potentials with respect to the scaling factor for intermolecular interactions are provided. Our results showed that the computed value of the excess chemical potential μNaCl is in agreement with simulations and experiments from the literature. We also implemented hybrid translation and rotation trial moves to increase the efficiency of the equilibration and configuration space sampling of the system. These trial moves collectively translate/rotate all molecules in the simulation box by performing short MD simulations in the microcanonical ensemble, according to the computed forces/torques on every molecule. These short MD simulations are accepted or rejected based on the Boltzmann factor of the total energy difference. We showed how the optimum time step size of the MD trajectory can be obtained using the simulation of a deep eutectic solvent system as an example.

Data and Software Availability. Brick-CFCMC, its source code, and many examples are freely available from gitlab (https://gitlab.com/ETh_TU_Delft/Brick-CFCMC).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.1c00652.

  • Detailed explanation of implementation of thermodynamic integration method; analytic expressions for derivatives of potential energy with respect to scaling factors for intermolecular interactions; detailed explanation of implementation of hybrid trial moves; and simulation details for case studies (PDF)

This work was supported by the Carbon Capture Utilization and Storage R&D program from TotalEnergies S.E. Exploration & Production. We are grateful for the support by NWO Exacte Wetenschappen (Physical Sciences) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organisation for Scientific Research, NWO). T.J.H.V. acknowledges NWO-CW (Chemical Sciences) for a VICI grant.

The authors declare no competing financial interest.

Supplementary Material

ci1c00652_si_001.pdf (604.2KB, pdf)

References

  1. Hens R.; Rahbari A.; Caro-Ortiz S.; Dawass N.; Erdos M.; Poursaeidesfahani A.; Salehi H. S.; Celebi A. T.; Ramdin M.; Moultos O. A.; Dubbeldam D.; Vlugt T. J. H. Brick-CFCMC: Open Source Software for Monte Carlo Simulations of Phase and Reaction Equilibria Using the Continuous Fractional Component Method. J. Chem. Inf. Model. 2020, 60, 2678–2682. 10.1021/acs.jcim.0c00334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Shi W.; Maginn E. J. Continuous Fractional Component Monte Carlo: An Adaptive Biasing Method for Open System Atomistic Simulations. J. Chem. Theory Comput. 2007, 3, 1451–1463. 10.1021/ct7000039. [DOI] [PubMed] [Google Scholar]
  3. Shi W.; Maginn E. J. Improvement in molecule exchange efficiency in Gibbs ensemble Monte Carlo: Development and implementation of the continuous fractional component move. J. Comput. Chem. 2008, 29, 2520–2530. 10.1002/jcc.20977. [DOI] [PubMed] [Google Scholar]
  4. Rosch T. W.; Maginn E. J. Reaction Ensemble Monte Carlo Simulation of Complex Molecular Systems. J. Chem. Theory Comput. 2011, 7, 269–279. 10.1021/ct100615j. [DOI] [PubMed] [Google Scholar]
  5. Rahbari A.; Garcia-Navarro J. C.; Ramdin M.; van den Broeke L. J.; Moultos O. A.; Dubbeldam D.; Vlugt T. J. H. Effect of Water Content on Thermodynamic Properties of Compressed Hydrogen. J. Chem. Eng. Data 2021, 66, 2071–2087. 10.1021/acs.jced.1c00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rahbari A.; Hens R.; Ramdin M.; Moultos O.; Dubbeldam D.; Vlugt T. J. H. Recent advances in the continuous fractional component Monte Carlo methodology. Mol. Simul. 2021, 47, 804–823. 10.1080/08927022.2020.1828585. [DOI] [Google Scholar]
  7. Rahbari A.; Hens R.; Nikolaidis I. K.; Poursaeidesfahani A.; Ramdin M.; Economou I. G.; Moultos O. A.; Dubbeldam D.; Vlugt T. J. H. Computation of partial molar properties using continuous fractional component Monte Carlo. Mol. Phys. 2018, 116, 3331–3344. 10.1080/00268976.2018.1451663. [DOI] [Google Scholar]
  8. Rahbari A.; Hens R.; Dubbeldam D.; Vlugt T. J. H. Improving the accuracy of computing chemical potentials in CFCMC simulations. Mol. Phys. 2019, 117, 3493–3508. 10.1080/00268976.2019.1631497. [DOI] [Google Scholar]
  9. Rahbari A.; Poursaeidesfahani A.; Torres-Knoop A.; Dubbeldam D.; Vlugt T. J. H. Chemical potentials of water, methanol, carbon dioxide and hydrogen sulphide at low temperatures using continuous fractional component Gibbs ensemble Monte Carlo. Mol. Simul. 2018, 44, 405–414. 10.1080/08927022.2017.1391385. [DOI] [Google Scholar]
  10. Poursaeidesfahani A.; Hens R.; Rahbari A.; Ramdin M.; Dubbeldam D.; Vlugt T. J. H. Efficient Application of Continuous Fractional Component Monte Carlo in the Reaction Ensemble. J. Chem. Theory Comput. 2017, 13, 4452–4466. 10.1021/acs.jctc.7b00092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Salehi H. S.; Hens R.; Moultos O. A.; Vlugt T. J. H. Computation of gas solubilities in choline chloride urea and choline chloride ethylene glycol deep eutectic solvents using Monte Carlo simulations. J. Mol. Liq. 2020, 316, 113729. 10.1016/j.molliq.2020.113729. [DOI] [Google Scholar]
  12. Dawass N.; Wanderley R. R.; Ramdin M.; Moultos O. A.; Knuutila H. K.; Vlugt T. J. H. Solubility of Carbon Dioxide, Hydrogen Sulfide, Methane, and Nitrogen in Monoethylene Glycol; Experiments and Molecular Simulation. J. Chem. Eng. Data 2021, 66, 524–534. 10.1021/acs.jced.0c00771. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Frenkel D.; Smit B.. Understanding Molecular Simulation, 2nd ed.; Elsevier: San Diego, CA, 2002; Vol. 1, 10.1016/B978-0-12-267351-1.X5000-7. [DOI] [Google Scholar]
  14. Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300. 10.1063/1.1749657. [DOI] [Google Scholar]
  15. Mester Z.; Panagiotopoulos A. Z. Mean ionic activity coefficients in aqueous NaCl solutions from molecular dynamics simulations. J. Chem. Phys. 2015, 142, 044507. 10.1063/1.4906320. [DOI] [PubMed] [Google Scholar]
  16. Kussainova D.; Mondal A.; Young J. M.; Yue S.; Panagiotopoulos A. Z. Molecular simulation of liquid–vapor coexistence for NaCl: Full-charge vs scaled-charge interaction models. J. Chem. Phys. 2020, 153, 024501. 10.1063/5.0012065. [DOI] [PubMed] [Google Scholar]
  17. Wang F.; Landau D. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. 10.1103/PhysRevLett.86.2050. [DOI] [PubMed] [Google Scholar]
  18. Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. 10.1002/jcc.540130812. [DOI] [Google Scholar]
  19. Grossfield A.WHAM: The weighted histogram analysis method. http://membrane.urmc.rochester.edu/wordpress/?page_id=126 (accessed 2021-08-06).
  20. Bennett C. H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  21. Shirts M. R.; Chodera J. D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Beauchamp K.; Chodera J.; Naden L.; Shirts M.; Martiniani S.; Stern C.; McGibbon R. T.; Gowers R.; Dotson D.. choderalab/pymbar. 2019. https://doi.org/10.5281/zenodo.3559263 (accessed 2021-08-10).
  23. Rossky P.; Doll J.; Friedman H. Brownian dynamics as smart Monte Carlo simulation. J. Chem. Phys. 1978, 69, 4628–4633. 10.1063/1.436415. [DOI] [Google Scholar]
  24. Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; 10.1093/oso/9780198803195.001.0001. [DOI] [Google Scholar]
  25. Pangali C.; Rao M.; Berne B. On a novel Monte Carlo scheme for simulating water and aqueous solutions. Chem. Phys. Lett. 1978, 55, 413–417. 10.1016/0009-2614(78)84003-2. [DOI] [Google Scholar]
  26. Moučka F.; Rouha M.; Nezbeda I. Efficient multiparticle sampling in Monte Carlo simulations on fluids: Application to polarizable models. J. Chem. Phys. 2007, 126, 224106. 10.1063/1.2745293. [DOI] [PubMed] [Google Scholar]
  27. Duane S.; Kennedy A.; Pendleton B. J.; Roweth D. Hybrid Monte Carlo. Phys. Lett. B 1987, 195, 216–222. 10.1016/0370-2693(87)91197-X. [DOI] [Google Scholar]
  28. Nejahi Y.; Barhaghi M. S.; Schwing G.; Schwiebert L.; Potoff J. Update 2.70 to “GOMC: Gpu Optimized Monte Carlo for the simulation of phase equilibria and physical properties of complex fluids. SoftwareX 2021, 13, 100627. 10.1016/j.softx.2020.100627. [DOI] [Google Scholar]
  29. Dubbeldam D.; Calero S.; Vlugt T. J. H. iRASPA: Gpu-accelerated visualization software for materials scientists. Mol. Simul. 2018, 44, 653–676. 10.1080/08927022.2018.1426855. [DOI] [Google Scholar]
  30. Pham T. T.; Shirts M. R. Identifying low variance pathways for free energy calculations of molecular transformations in solution phase. J. Chem. Phys. 2011, 135, 034114. 10.1063/1.3607597. [DOI] [PubMed] [Google Scholar]
  31. Wolf D.; Keblinski P.; Phillpot S.; Eggebrecht J. Exact method for the simulation of Coulombic systems by spherically truncated, pairwise r–1 summation. J. Chem. Phys. 1999, 110, 8254–8282. 10.1063/1.478738. [DOI] [Google Scholar]
  32. Fennell C. J.; Gezelter J. D. Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. J. Chem. Phys. 2006, 124, 234104. 10.1063/1.2206581. [DOI] [PubMed] [Google Scholar]
  33. Waibel C.; Feinler M. S.; Gross J. A Modified Shifted Force Approach to the Wolf Summation. J. Chem. Theory Comput. 2019, 15, 572–583. 10.1021/acs.jctc.8b00343. [DOI] [PubMed] [Google Scholar]
  34. Hens R.; Vlugt T. J. H. Molecular Simulation of Vapor–Liquid Equilibria Using the Wolf Method for Electrostatic Interactions. J. Chem. Eng. Data 2018, 63, 1096–1102. 10.1021/acs.jced.7b00839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ewald P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 369, 253–287. 10.1002/andp.19213690304. [DOI] [Google Scholar]
  36. Dotson D.; Beckstein O.; Wille D.; Kenney I.; Wu Z.; shuail; Lee H.; trje3733; Lim V.; Barhaghi M. S.; Hsu W.-T.. alchemistry/alchemlyb: 0.4.2; 2021. https://doi.org/10.5281/zenodo.4973744 (accessed 2021-08-10).
  37. Verlet L. Computer ”Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. 10.1103/PhysRev.159.98. [DOI] [Google Scholar]
  38. Swope W. C.; Andersen H. C.; Berens P. H.; Wilson K. R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. 10.1063/1.442716. [DOI] [Google Scholar]
  39. Miller T.; Eleftheriou M.; Pattnaik P.; Ndirango A.; Newns D.; Martyna G. Symplectic quaternion scheme for biophysical molecular dynamics. J. Chem. Phys. 2002, 116, 8649–8659. 10.1063/1.1473654. [DOI] [Google Scholar]
  40. Vlugt T. J. H.; Martin M.; Smit B.; Siepmann J. I.; Krishna R. Improving the efficiency of the configurational-bias Monte Carlo algorithm. Mol. Phys. 1998, 94, 727–733. 10.1080/002689798167881. [DOI] [Google Scholar]
  41. Berendsen H.; Grigera J.; Straatsma T. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
  42. Joung I. S.; Cheatham T. E. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Kroes G.-J. Towards chemically accurate simulation of molecule–surface reactions. Phys. Chem. Chem. Phys. 2012, 14, 14966. 10.1039/c2cp42471a. [DOI] [PubMed] [Google Scholar]
  44. Benavides A.; Aragones J.; Vega C. Consensus on the solubility of NaCl in water from computer simulations using the chemical potential route. J. Chem. Phys. 2016, 144, 124504. 10.1063/1.4943780. [DOI] [PubMed] [Google Scholar]
  45. Hamer W. J.; Wu Y. Osmotic Coefficients and Mean Activity Coefficients of Uni-univalent Electrolytes in Water at 25°C. J. Phys. Chem. Ref. Data 1972, 1, 1047–1100. 10.1063/1.3253108. [DOI] [Google Scholar]
  46. Perkins S. L.; Painter P.; Colina C. M. Molecular Dynamic Simulations and Vibrational Analysis of an Ionic Liquid Analogue. J. Phys. Chem. B 2013, 117, 10250–10260. 10.1021/jp404619x. [DOI] [PubMed] [Google Scholar]
  47. Celebi A. T.; Vlugt T. J. H.; Moultos O. A. Structural, Thermodynamic, and Transport Properties of Aqueous Reline and Ethaline Solutions from Molecular Dynamics Simulations. J. Phys. Chem. B 2019, 123, 11014–11025. 10.1021/acs.jpcb.9b09729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Hens R.Molecular Simulation of Phase and Reaction Equilibria: Software and Algorithm Development. Ph.D. thesis, Delft University of Technology, 2020; 10.4233/uuid:41c32a8f-2db7-4091-abb5-4d6a5e596345. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci1c00652_si_001.pdf (604.2KB, pdf)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES