Abstract
Sarcopenia is a geriatric syndrome characterized by significant loss of muscle mass. Based on a commonly used definition of the condition that involves three measurements, different subclinical and clinical states of sarcopenia are formed. These states constitute a partially ordered set (poset). This paper focuses on the analysis of longitudinal poset in the context of sarcopenia. We propose an extension of the generalized linear mixed model and a recoding scheme for poset analysis such that two submodels - one for ordered categories and one for nominal categories, that contain common random effects can be jointly estimated. The new poset model postulates random effects conceptualized as latent variables that represent an underlying construct of interest - susceptibility to sarcopenia over time. We demonstrate how information can be gleaned from nominal sarcopenic states for strengthening statistical inference on a person’s susceptibility to sarcopenia.
Keywords: muscle mass, aging, longitudinal analysis, poset, Health ABC
1. Introduction
This paper was motivated by longitudinal data collected for subclinical and clinical states in sarcopenia. Proposed by Irwin Rosenber in 1989 [1], the term sarcopenia (Greek sarx or flesh + penia or loss) was used to denote the condition of age-related decrease of muscle mass. The meaning of the term has evolved and broadened over the years since to have substantial overlap with the physical phenotype of frailty [2] . Despite debates about the distinction between the two terms [3, 4], it would be fair to say that sarcopenia is now recognized as a geriatric syndrome signified by age-related progressive and generalized loss of skeletal muscle mass and strength. Although the term sarcopenia has become part of the medical lexicon to suggest age-related muscle loss and low muscle performance, there is still no broadly accepted clinical definition, nor are there consensus diagnostic criteria. Recent developments in the operational definition of sarcopenia focused on three measurements - muscle mass, gait speed, and grip strength. Particularly, the European Working Group on Sarcopenia in Older People (EWGSOP) uses a definition [5] that can be visualized by Figure 1(a). It can be seen that the diagnostic classification involves the dichotomization of the three measures. Thus, the different states of sarcopenia can be cross-classified with labels in {1, … , 8}, and mapped into the partially ordered set (poset), which is represented by the Hasse diagram in Figure 1(b). The EWGSOP recognizes three stages of sarcopenia - presarcopenia (muscle loss without decrease in strength or performance), sarcopenia (muscle loss with either decrease in strength or performance), and severe sarcopenia (muscle loss with decrease in both strength and performance) [5]. Presarcopenia represents the condition in which significant loss of muscle mass has occurred, but muscle strength and performance are largely intact. The relationship between muscle mass and strength is not linear, in that strength may be preserved even when substantial tissue loss has occurred [6]. Individuals with presarcopenia (state {5}, Fig. 1(b)), however, are much more likely to transition to full sarcopenia (defined as states {6, 7, 8} per EWGSOP) than persons with intact muscle mass (e.g., states {2}, {3}, {4}).
Figure 1.
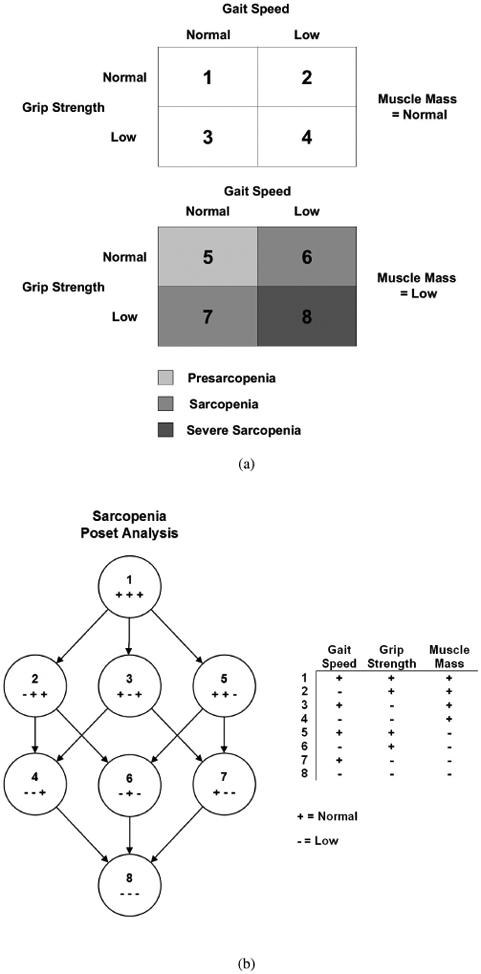
(a) Classification of sarcopenia states from EWGSOP criteria, (b) poset representation of sarcopenia states in (a). An arrow from category 1 to category 2 indicates that 1 dominates 2, and so on.
While a diagnostic classification of sarcopenia (with versus without) as a geriatric syndrome has generated considerable interest, the examination of progression of sarcopenia through various stages of the condition in older adults has not received as much attention. For example, there may exist subclinical states of sarcopenia and individuals in some specific subclinical states are more vulnerable than others in eventually developing sarcopenia. Subclinical states are important because intervening in earlier stages of sarcopenia may be able to reverse or decelerate the condition. For example interventions intended to prevent the onset of full sarcopenia, such as exercise and nutrition programs, can be directed towards the persons with greatest risk of progression. Additionally, various risk factors are likely to interact with the subclinical states, forming different risk profiles and progression possibilities.
Longitudinal data are key to understanding disease progression, which may occur in any direction. Longitudinal analysis of a mix of ordered and unordered states related to sarcopenia, as depicted in Figure 1(b), is necessary to elucidate the natural history of sarcopenia and evaluate risk factors for understanding strategies to prevent, delay, or treat sarcopenia. Unfortunately, models for poset are few and far-between, let alone longitudinal models.
Using longitudinal data, in this paper we study how different states of sarcopenia, both subclinical and clinical, as defined by the EWGSOP criteria, progress over time through the lens of poset. Our intention is to delineate risk factors that drive the dynamic of the disease over an extended period of time. The methodology for the analysis of subclinical states of sarcopenia represents a longitudinal generalization of the poset formulation in [7]- i.e., we extend the generalized fixed effects linear model for poset to mixed linear model such that random effects are used to explain correlations between sarcopenia states within the same individual over time. The extension is non trivial because unlike the fixed effects model for poset in cross-sectional setup [7], of which linear submodels could be individually applied to the ordered and unordered categories, in the extended model the common random effect terms cut across different submodels - some ordered and some unordered - for the poset of sarcopenia states. Therefore all submodels have to be estimated jointly.
Additionally, we integrated both ordinal and nominal item response theory (IRT, [11]) into the poset model such that the random effect terms can be interpreted as latent constructs that represent an individual’s propensities of progressing to sarcopenia over time. The benefits of the extended poset method can be summarized as follows: First, via the common random effect (latent variable), the method allows information to be gleaned from the nominal categories for enhancing inference in the ordered categories. Second, the method features a recoding scheme for the poset categories, which allows commonly available software to be applied to longitudinal poset data. Finally, the integrated IRT models permit better interpretation of results including the latent variable as sarcopenia susceptibility. We illustrate these benefits using a data set from the Health ABC study that contained 10-year follow up observations on sarcopenia status for n=3,075 older adults, aged 70-79 years at baseline [9].
The paper is organized as follows: First we provide some background to poset and describe the methodology of poset modeling. Next we describe the integration of IRT models into generalized linear mixed model and the data analysis example. We conclude with a discussion.
2. Method
2.1. Partially Ordered Set Theory
Unlike ordinal responses, where a rank order exists for all response categories, in partially ordered set (poset), some categories cannot be directly compared. We first establish some basic notation. A poset (P, ⪯) is reflexive (a ⪯ a), antisymmetric (if a ⪯ b and b ⪯ a, then a = b), and transitive (if a ⪯ b and b ⪯ c, then a ⪯ c). In this paper we only consider finite poset P. When a ⪯ b, we say that b dominates a. Two distinct elements a and b in P are comparable if a ⪯ b or b ⪯ a. Otherwise, they are incomparable.
An element a ∈ P is maximal (minimal) if there is no element b ∈ P such that a ⪯ (⪰)b. In a finite poset -i.e., when P is finite, there is always at least one maximal element and one minimal element. A chain in a poset (P, ⪯) is a totally ordered subset C of P, whereas an antichain is a set A of pairwise incomparable elements. A chain is a maximal chain if no other chain contains (covers) it. Similarly, we can define a maximal antichain. For example, in Figure 3 (b), the set {2,3,5} forms a maximal antichain. We further define a weak order between subsets S1 and S2 in P if any element in S2 is dominated by some element in S1 and no element in S2 dominates any element in S1. We call it S1 weakly dominates S2. A set of subsets is called totally weakly ordered if pairwise subsets are weakly ordered. Similarly, we define a strong order between S1 and S2 if every element in S1 dominates all the elements in S2 and say that S1 strongly dominates S2.
Figure 3.
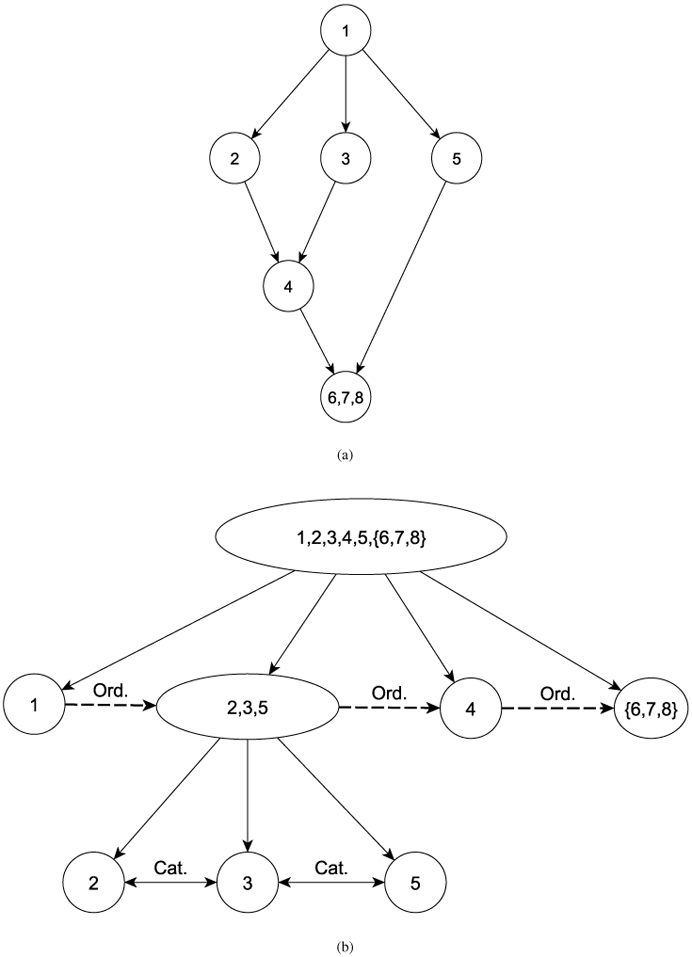
(a) Poset structure of real data example in HABC, (b) Conditional partition and model for poset categories in (a).
2.2. Poset partition
Two key results - poset partition and subitem recoding - are required for setting up the longitudinal model for poset. The first result, as proved in [7] and labeled as the conditional partition theorem, states that finite poset can be partitioned into antichains that are totally weakly ordered. The procedure for obtaining the totally weakly ordered set is to iteratively remove the maximal elements in a poset and the reduced poset. Using Figure 1(b) again as example, denote the poset by P which has the maximal element {1}. By removing {1}, the set P \ {1} now contains the set {2, 3, 5} as its maximal elements. By continuing to remove the maximal elements, we can derive the following 4 antichains that are totally weakly ordered: {1}, {2, 3, 5}, {4, 6, 7}, and {8}. The sets form a partition of P. In general, for a specific poset category k ∈ P, the conditional partition procedure results in a sequence of nested partitions, each identifies the category k within a specific set within the partition.
When the conditional partition theorem is applied to data, generalized linear model (GLM) analysis can be incorporated into the analysis. It can be shown that if there are K categories in the poset response set, then there exist K − 1 independent equations, each corresponding to an identifiable GLM ([7]). For totally weakly ordered sets, it is suggested that the cumulative ordinal model be applied, and for comparing categories within antichain, the multinomial logistic regression. If the various models do not share common regression coefficients, then the maximum likelihood procedure separately maximizes each individual model loglikelihood. Accordingly, existing software programs for estimation - multinomial or cumulative ordinal regression alike- can be directly applied to each individual model.
For the purpose of illustration, we continue to use the sarcopenia example in Figure 1(b). Here P = {1, 2, 3, 4, 5, 6, 7, 8}. Figure 2 shows the corresponding poset structure. Applying the GLM poset approach cross-sectionally to the poset, one would fit an ordinal model (e.g., cumulative logit regression) to the ordered categories - {1} ⪰ {2, 3, 5} ⪰ {4, 6, 7} ⪰ {8}, and two separate multinomial logit model respectively to {2},{3},{5}, and {4,},{5}, {7}.
Figure 2.
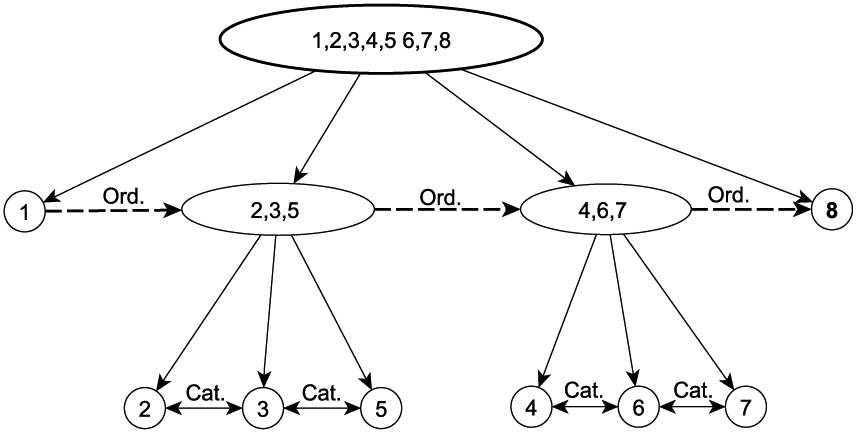
Conditional partition and model for poset in sarcopenia example (Figure 1(b)). Ord=Ordinal model; Cat=Categorical model
2.3. Mixed effect poset model and subitem recoding
As an extension to the poset generalized linear model [7] for analyzing longitudinal data, we propose to include random effects into the generalized linear model for poset. In longitudinal studies, the introduction of random effects for each individual, denoted by θi (could be a vector) for the ith person (i = 1, ⋯ , I), takes into account the correlation between the repeated measurements from the same individual over time. Like the generalized mixed model, the poset likelihood for the mixed effect model is formed by integrating out the common random effect θ. The addition of the common random effect complicates model structure as well as estimation procedure because now the submodels cannot be separately estimated. We first formalize the model and then describe a solution that allows estimation of the longitudinal poset using generic linear mixed model programs.
To fix notation, assume the response Yit for individual i at timepoint t (t = 1, ⋯ , T) takes a labeling value in the poset P = {1, ⋯ , K}. Note that these values are not necessarily ordered in poset; they only serve as labels for the poset category. We also assume that a set of covariates Xit, possibly time-varying, is also available. From the partition result in [7], denote the sequence of nested conditional partitions identified for the response k ∈ P by , , ⋯ such that . Here , and , and ∪ represents the union of sets of elements over the partition. Thus, qk + 1 is the total number of partitions associated with response category k. Denote the sets to which the response k belong by , ⋯ , , where , , ⋯ , . By definition, .
For example, in Figure 1(b), for the poset category 4, , , , ; , , and .
Denote the vector of responses Yit by Yi. The form for generalized linear mixed model (GLMM) for poset responses follows the same general matrix form of GLMM for categorical and continuous responses:
| (1) |
with g(.) denotes the link function, β the coefficients of the fixed effects, θi the random effects, and Xi and Zi respectively the design matrices for the fixed effects β and the random effects θi.
Given the random effects θi, the conditional probability of observing the poset response category yit = k ∈ P at time t is given by
| (2) |
Rewrite the response pattern in Yit over time as a T-vector taking some values k ∈ P. The overall likelihood for the longitudinal mixed model can be expressed as
| (3) |
where f (θi) is the density function of random effects. Here we assume that θi ~ N(0, G), where G is the covariance matrix for the random effects.
The GLMM is a flexible tool for handling longitudinal data in which different individuals have different number of observations, and that the timings of the observations are not necessarily the same [8]. Particularly, the maximum likelihood procedure only uses available responses in the data. We devised a recoding scheme for poset responses to take advantage of this important property of the GLMM - first treated an outcome at a specific timepoint as response to a single “item”, then recoded the poset response such that the single-item response is transformed into multiple responses to sub-items that were conditionally independent given the random effects. Some of the subitem responses would necessarily be coded as missing (NA). They would not be made available for the maximum likelihood procedure for GLMM and thus not appear in the likelihood equation.
To understand how the recoding scheme works, we continue to use the illustrative example from the sarcopenia example in Figure 1(b). The outcome variable (sarcopenia status) has 8 poset categories and per the structure of the poset in Figure 2 there would be 3 recoded subitem responses. The first subitem represents the 4-category ordered responses {1} ⪰ {2, 3, 5} ⪰ {4, 6, 7} ⪰ {8}; the second the 3 unordered categories {2,3,5}, and the third the unordered categories {4,6,7}. Table 1 shows the coding scheme for these 8 categories in the poset, with NA representing missing value. We distinguish between the two types of subitem responses by labeling them Unordered (U) and ordered (O) respectively using superscripts.
Table 1.
Recoding scheme for sarcopenia example.
| Category | Subitem 1 | Subitem 2 | Subitem 3 |
|---|---|---|---|
| 1 | 1O | NA | NA |
| 2 | 2O | 1U | NA |
| 3 | 2O | 2U | NA |
| 4 | 3O | NA | 1U |
| 5 | 2O | 3U | NA |
| 6 | 3O | NA | 2U |
| 7 | 3O | NA | 3U |
| 8 | 4O | NA | NA |
Superscripts (U) and (O) are respectively used to indicate unordered and ordered categories; dummy coding is used and the category labeled 1U is used as reference.
Proposition 1. When the subitem responses using the above recoding scheme of the poset response categories are assumed to be conditionally independent given the random effects in the GLMM, the multivariate likelihood evaluated using the subitem responses is identical to that of the longitudinal poset model specified in Equation 3.
The proof is given in an appendix. The result is a generalization of the work in [10] to a longitudinal setting.
3. Application: Sarcopenia in Older Adults
3.1. Latent Variable Based Longitudinal Poset Model for Sarcopenia Study
The mixed poset model described above lacks specific features appropriate for the sarcopenia study and requires modifications. First, the random effects θ are individual but not time-specific. While the linear and additive random effects θ in Equation 1 can be interpreted as a general susceptibility to a disease, it is difficult to interpret θ as a person-specific latent construct if one expects this construct to change over time, as in the sarcopenia study. Second, within our poset formulation, unordered categories, which are non-directional, cannot be directly related to the random effects, which also appear in the model for the ordered response. To solve the dilemma, we analyzed the longitudinal poset responses under a latent variable framework. We specified a multidimensional latent variable θi = (θit) for individual i to represent a construct of susceptibility to sarcopenia, which is allowed to vary over time points. Within-person correlation is modeled by the covariance in the distribution of θi. By borrowing tools from the psychometric literature, specifically the IRT and related existing software [12], we incorporated the ordered and unordered responses within the latent variable framework for multivariate poset responses. Some preliminary background for both the ordinal and nominal IRT models is provided in an appendix.
Specifically, we focus on IRT models [13] by treating the poset responses to subitems as multivariate responses of different modes (ordered and unordered) given a specific timepoint, and the repeated measurements over time as multidimensional data. For our longitudinal poset analysis of the sarcopenia data, instead of using all 8 categories as defined in Figure 1(b), we followed the EWGSOP definition and grouped together the three states 6, 7, and 8. Figure 3(a) shows a reformatted poset that is consistent with this definition, and Figure 3(b) shows the poset analytic submodels derived from the reformatted poset. The recoding scheme resulted in two subitems - one ordered and one nominal.
For response Yijt from individual i to subitem j at time t that contains ordered responses labeled 1, … , M, the following cumulative ordinal model [14] was applied:
| (4) |
with
| (5) |
where i = 1, … , I, j = 1 , … , J, T = 1, … , T, and k = 1, …, M.
The slope parameter is a weight function for ordered category k of an subitem for the latent variable θit. The parameter djtk, which is item- and category-specific, is called the intercept parameter. We note that while the cumulative item response model is the most commonly used model, other ordinal item response models such as the sequential model [15] are also possible.
Model 4-5 is not identified; we will discuss identifiability constraints after model presentation. On the other hand, for nominal (unordered) response with category k, k = 1, … , L, we followed the multinomial logistic model (see Appendix 1) [13]:
| (6) |
in which
| (7) |
For both the ordinal and nominal models, the latent trait vector for an individual follows a normal distribution:
| (8) |
where bt is the mean of the latent variable at time t, and G is a covariance matrix. In the unordered model 7, the category-specific parameters correspond to the “scoring” function (explained below) that orients the direction of the unordered categories to that of the latent variable. To identify the nominal model [17, 13], we set , ; cjt1 = 0, and ∑k cjtk = 0. Furthermore, the scale of θ is identified by setting one of the means in bt to zero and the diagonal entries in G to unity. Off-diagonal elements of G are unconstrained for capturing correlation between within-person responses.
Several important remarks need to be made here for clarification of the model. First, we assume that θi = (θit), t = 1, ⋯ , T is multidimensional. This flexibility allows the separation the two sources of correlation: within-individual correlation over time, as captured by the covariance matrix G, and correlation across subitem responses of the same individual within a given timepoint, as captured by the random effect θit.
Second, besides the item-specific slope parameter , which is constrained to be positive, the nominal model included a multiplicative weight parameter for the latent variable in Equation 7. The motivation for including is that it offers a way for researchers to glean information about the direction of ordering of the nominal categories from the data. Drawing experience from the psychometric literature, the random effects θ in the response models 4 - 6 has a clear interpretation– it is a person-specific effect that signifies the propensity of progressing to sarcopenia, or susceptibility to the condition. For example, in the ordinal model 4, a higher value of θ means a higher propensity for being in a worse sarcopenia state. The distribution of sarcopenia susceptibility is allowed to vary over time in mean (bt in Equation 8) as one expects susceptibility to increase over time. The model set up thus requires θ in the nominal model 6 to retain the same interpretation as that in the ordinal model, necessitating an ordering (as estimated from the data) of the nominal categories. Using the language from IRT, the scoring function [13] has the following interpretation for poset categories: higher value of suggests higher order of that category on the scale [0, L − 1].
Because the scoring function values are not simultaneously estimable with the other item parameters, ANOVA-style contrast matrices are used to reparametrize them into estimable contrasts[19]. A particular linear-Fourier contrast matrix was used by [13, 20] to provide a smooth transition between the full-rank nominal model and a constrained model of which some linear coefficients are set to zero (see Appendix 1). Other contrasts have been used in the past, e.g., polynomials or deviation contrasts[19]. The Fourier basis, from our experience, is more flexible. As argued in [13], if the data indicate another order, estimated values of may be less than zero or exceed L − 1. In practice, prior knowledge and preliminary analysis could be used to guide setting up the initial order for the nominal categories so that the fitted model would yield admissable values of for the efficient determination of the appropriate order.
The determination of the order for the poset model is especially important when covariates are included into both the ordinal and nominal submodels. In such a case, covariates enter as fixed effects into both models 4-5 and 6-7. For example, let X denotes the set of covariates and βt the vector of regression coefficients. Then Equation 7 becomes
| (9) |
where βt is a vector of regression coefficients. In the current application, the same set of covariates will be used for the ordinal and nominal models.
A third remark regards constraints on the model, for example, whether or not the respective “item” parameters a, d and c in the models 4 and 9 are allowed to vary over time points. In other words, whether or not one would assume that the subitem parameters are invariant across time. In general, it is not possible to allow both the parameters characterizing the distributions of the latent variables θ and all subitem parameters to be freely estimated without constraint; the model would be unidentified. One can fix the distribution of θ to be invariant over time and allow the subitem parameters to vary over time, an approach that we did not adopt, as it seems unlikely that individual θ value, indicating extent of susceptibility to sacropenia, is invariant over time. Instead we conceptualized θ = (θt) as a T-dimensional latent variable and fixed all intercept parameters in the ordered and nominal model to be time-invariant. - e.g., dkt = dk in Equation 4, and ctk = ck in Equation 9. Scoring functions are also constrained to be equal across timepoints. Equality constraints can also be imposed on slope parameter and/or the regression coefficients βt (e.g., in Equation 9). In those cases, goodness-of-fit indexes can be used to compare constrained and unconstrained models.
A final remark concerns the estimation procedure. Model estimation was implemented using flexMIRT [12, 25], in which poset responses took the form of mixed-mode (ordinal and nominal) responses to subitems over time. The multiple responses were handled under the aforementioned latent variable IRT model. The overall likelihood (Equation 3), which involves high dimensional integration, needs to be optimized. Traditional methods such as the EM would take a long time to complete. We instead opted to use the Metropolis-Hastings Robbins-Monro [22] for all estimation.
3.2. Data Sample and poset method
We used longitudinal data (n = 3,075) from the Health, Aging, and Body Composition (Health ABC) Study [9] and applied the poset analysis. At baseline (yr1) the age range of the participants was 70-79 years; 49% were male and 41% were African American. Additional study details have been published [23]. Briefly, data from the following study years - 1, 2, 3, 4, 5, 6, 8, and 10 were considered. For the three variables used in producing the sarcopenia status variable - appendicular lean mean (ALM, in kg), is the sum of bone-free lean tissue in the arms and legs was standardized for height (m2), ALM < 7.23 kgm−2 for men and < 5.67 kgm−2 for women were defined as low; grip strength (in kg) < 30(20) for men (women) and gait speed (in ms−1) < 0.8 for both genders were respectively defined as low; see Table 5 in [5]. Because not all variables were measured every year for all participants, we did not include year 3 and 5 data. Previously identified risk factors for sarcopenia [24, 9] - BMI, bodily pain, diabetes status at baseline, physical activity, age, gender, and race, were included as covariates.
Participants with missing visits were included in the analysis under the assumption that the missing values were missing-at-random (MAR). Only visits with observed values were included into the likelihood equation. To minimize the potential bias due to missing values that may violate the MAR, we employed several strategies to handle missing values. First, following [9], we excluded n = 147 participants that had no follow up data. Individuals with incomplete measurements for defining sarcopenia state were also excluded. Second, we did not exclude deceased participants such that data collected prior to their deaths were included. Missing value due to death hence did not enter into the model for statistical inference. Unless death was directly related to the three variables defining sarcopenia, which we believed was unlikely, the potential bias due to missing values from death should be minimal. Compared to death, missingness directly related to poor gait (e.g., poor locomotion prevented a participant to come to clinic for measurement) or grip or low ALM, could be a more serious issue because in these cases, missingness in the outcome was associated with the value of the outcome - in other words, data were missing not at random (MNAR). In general, without auxillary information, it is impossible to tell what mechanism exactly leads to missingness. MNAR models requires strong assumptions and were not considered in the current analysis.
Finally we examined the missing value patterns and data distribution by sarcopenic states by time both using the 8-category poset and the EWGSOP-guided poset. For yr8 data, we found suspiciously low sample sizes for state 2 and 4. For example, for state 2, n=23 at yr8, compared to n=122 and n=143 at yr6 and yr10 respectively. This may be an artifact of a different measurement protocol (home measurement vs clinic measurement) implemented in yr8. A decision was made to exclude yr8 data. As a result, data from 5 unequally-spaced time points - yr1, yr2, yr4, yr6, and yr10, were eventually included in our analysis. As previously mentioned, to circumvent the issue that the time points are not equally spaced and the potentially changing risk to sarcopenia over time, for each individual susceptibility to sarcopenia is modeled by a 5-dimensional latent variable with unstructured covariance across dimensions and variances set to unity. The mean of θ at time point 3 (yr4), which had a relatively large sample size, was set to zero as reference.
3.3. Results
A total of n=2,742 participants were included into yr1. Because of missing values and attrition, the following 4 time points respectively contained n=2,603, n=2,286, n=1,875, and n=1,410 participants.
We compared four models (M1-M4) cross-classified by the two conditions: slope parameters for the ordered/unordered poset component models across time-points were constrained to be equal (yes/no). For each model, the following 3 conditions for covariates were also included for comparison: no covariates, with covariates with regression coefficients not constrained over time, and with covariates and regression coefficients constrained to be invariant over time. Both AIC and BIC values showed that the best model was the one with constrained slope parameters for the ordered and unordered model (M4) and included covariates with constraint (Table 2). Here we only report result from the best model.
Table 2.
Goodness-of-fit for fitted models
| Model | No covariate | Covariate | Covariate(fixed) | |||
|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | |
| M1 | 45919 | 46121 | 37624 | 38034 | 37131 | 37374 |
| M2 | 48343 | 48521 | 37297 | 37683 | 36212 | 36432 |
| M3 | 49144 | 49322 | 37137 | 37523 | 37464 | 37684 |
| M4 | 48377 | 48531 | 37899 | 37261 | 36051 | 36247 |
M1=No constraint on slope in both ordered and nominal model; M2= Slope in ordered model constrained over time; M3= Slope in nominal model constrained over time; M4=Slope in both ordered and nominal model constrained over time. Covariate (fixed)=regression coefficients constrained to be invariant over time. Values for the best model are indicated in bold.
Table 3 shows the estimated means of the latent variable over the time points and their correlations. As expected, susceptibility to sacropenia tends to increase over the years, with the smallest increment over the first two time points (yr1 and yr2). Correlations between susceptibility across two neighboring time points are in the range 0.67 to 0.71, suggesting that sarcopenia risks for various time points are highly correlated.
Table 3.
Estimated latent distributions for 5 time points
| Correlation | Time 1 | Time 2 | Time 3 | Time 4 | Time 5 |
|---|---|---|---|---|---|
| 1.00 | |||||
| 0.71 | 1.00 | ||||
| 0.67 | 0.69 | 1.00 | |||
| 0.61 | 0.63 | 0.67 | 1.00 | ||
| 0.50 | 0.51 | 0.54 | 0.57 | 1.00 | |
| Mean | −0.27 (0.01) | −0.20 (0.01) | 0.00 | 0.15 (0.01) | 0.32 (0.01) |
Standard errors of mean estimates are in parentheses. The 5 time points refer to Years 1, 2, 4, 6, and 10.
The intercept parameters dk in the ordinal model take the values 0.53, −5.00, and −5.58. Estimation with time- and category-specific led to large unstable estimates in some cases. A decision was therefore made to fix across categories and time. The resulting procedure yielded an estimated value 3.69 for a(o). For the nominal model, the scoring functions were such that the first and last response categories (respectively {2} and {5}) were respectively set at 0 and 2 and the category {3} was estimated to attain values 0.14, 0.04, 0.67, 0.96, 1.31 over time. This suggests that the nominal response categories should be aligned with the direction of θ in the order {2}, {3}, and {5} without exception. This result also suggests that being in category {5} (normal gait and grip but low muscle mass) portends higher risk to progress to sarcopenia than categories {2} and {3}, which both have normal lean muscle mass. See also distribution of θ across states in Discussion.
Table 4 shows the regression coefficients for the fixed effects. BMI contains 5 categories (from low to high) and was treated as continuous. A positive coefficient for a categorical predictor suggests higher likelihood of a worse sarcopenic state. Therefore being older, diabetic, and having pain are all associated with higher likelihood of becoming sarcopenic. The negative coefficient for BMI is somewhat surprising, but see [26]. To further investigate the effect of BMI, we plotted the distributions of BMI by sarcopenic class. The trends were found to be similar for different time points, therefore we only show the graphs for the first (yr1) and last (yr10) (Figure 4). It can be seen that more severe sarcopenic states have lower BMI in general, with mean BMI of the best state (no sarcopenia, labeled 1) at around a BMI of 28 kgm−2. The relationship seems to vary within the first four states {1},{2},{3}, and {4}, while the presarcopenia state {5} and sarcopenia states {6, 7, 8} all have BMIs below 25 kgm−2. The negative coefficient of BMI is likely to be attributed to the differential distributions over better and poorer states. Admittedly, the complex relationship between BMI and sarcopenia [27], the latter of which is defined by both function and muscle mass, may not be well represented by a single linear regression coefficient. Of note, we examined whether how BMI was modeled could affect the other estimates by removing it completely from the model. The regression results, in terms of significance of the other variables, remained unchanged.
Table 4.
Results of the proposed poset generalized linear mixed effects model.
| Variable | Estimate (SE) | p-value |
|---|---|---|
| Race | −0.34 (0.03) | < 0.001 |
| Gender | 0.29 (0.03) | < 0.001 |
| Age | 0.79 (0.04) | < 0.001 |
| BMI | −1.53 (0.05) | < 0.001 |
| Diabetes | 0.12 (0.02) | < 0.001 |
| PA | −0.06 (0.04) | 0.13 |
| Bodily pain | 0.18 (0.03) | < 0.001 |
Abbreviation: BMI=Body mass index, PA=Physical activity, SE=Standard error; Respective reference category for variables Race, Gender, Diabetes,and Bodily pain: White, Male, No diabetes, No bodily pain
Figure 4.

Distributions of BMI across sarcopenic states at (a) First time point (yr1), (b) last time point (yr10).
Besides BMI, other modifiable factors contribute to the risk of progressing to sarcopenia. For example, diabetes is a significant risk factor. Having diabetes increases the risk of progressing into worse sarcopenic states with the odds ratio of exp(0.12) = 1.13. The odds ratio for bodily pain is exp(0.18) = 1.20, representing an increase of 20% in risk of progressing into worse sarcopenic state when pain is present.
4. Discussion
Body composition changes as part of the normal aging process. Starting at around age 50, muscle mass declines by approximately 8% per decade. At around age 70, the loss of muscle mass accelerates to 15% per decade [28]. The onset of sarcopenia is insidious and reflects the gradual nature of muscle loss. Rather than experiencing a sudden impairment, those persons who become sarcopenic experience a progressive decline in strength and functioning that mirrors the steady loss of muscle mass [29]. Thus an understanding of preconditions for the syndrome and the various subclinical states of the syndrome is important. In this paper, we view subclinical sarcopenic states as posets and propose a novel longitudinal poset models for data analysis. Although the current approach bears some resemblance to the hidden Markov poset model described in [30] in terms of fitting a mixed model to data, the two poset approaches are methodologically rather different; the hidden Markov approach basically reordered the categories of the poset and does not separately consider nominal and ordered categories.
There are several contributions of the longitudinal poset analysis. First, it allows a general framework for analyzing a large class of responses in a longitudinal setting. The clinical application demonstrates the possibility of the poset approach for analyzing subclinical states. Second, the approach allows information to be gleaned from the nominal categories to enhance inference in the ordered responses via random effects (latent variables). Traditional analysis such as collapsing unordered categories into a single category would miss an opportunity to exploit information within unordered categories for improving predictive modeling. Distinct from how random effects are typically used in longitudinal analysis, here we adopt a psychometric viewpoint in the context of latent variable and interpret the quantity θ as a susceptibility factor for an older adult to develop into sarcopenia.
To visualize the relationship between the latent variable θ and the sarcopenic states, we plotted the distribution of θ by sarcopenic states at the first and the last time point (Figure 5). The almost monotonic relationship between θ and the sarcopenic states provides support to the susceptibility interpretation. Importantly, according to this poset analysis result, state 4, which has deficits in functions (both gait and grip strength) but not lean mass, has a higher susceptibility to sacropenia than state 5, which has low muscle mass but normal function. The ordering between the two states is consistent at baseline and at the last time point. The poset analysis reveals the high risk associated with older adults with seemingly normal muscle mass but low functions. This implies that older adults with early signs of functional deficit is likely to be as of high risk for developing sacropenia as older adults with low muscle mass. Figure 5 also suggests that from the poset analysis states 6, 7, 8 are quite similar, both at baseline and the last time point, offering support for the EWGSOP definition of sarcopenia that collapses these 3 states into one. It is also interesting to note that the distribution of θ for State 1 (normal) has substantial variance at yr1, implying that different individuals in the normal state actually may have rather different risk of progressing to sarcopenia over time. This may be an artifact of θ being modeled as a vector of T = 5 dimensions- information was borrowed across later time points for retrospectively shaping the value of θ at the first time point through the covariance matrix G. Notably state 2, 3, and 5 have increasing means in θ, which is consistent with the ordering estimated from the scoring function. The variances of these states however are all relatively small, especially when compared to state 1.
Figure 5.
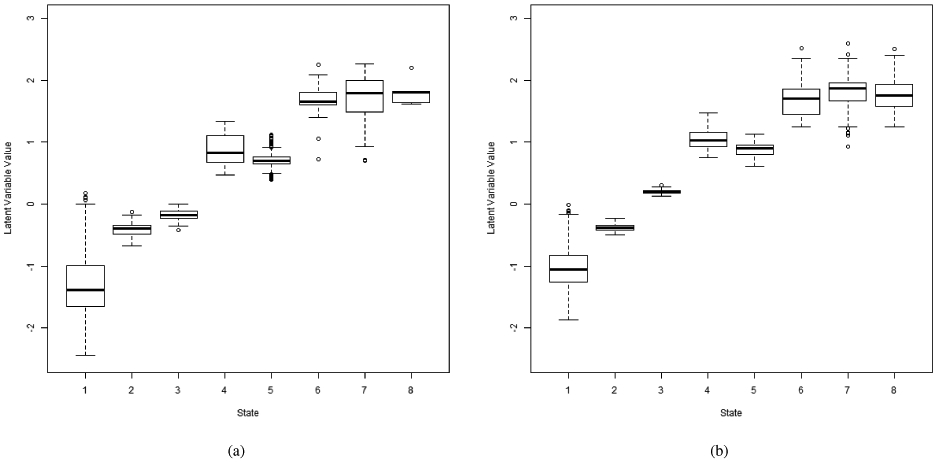
Distributions of latent variable θ by sarcopenic states at (a) first time point (yr1), (b) last time point (yr10).
As suggested by a referee, we also examined the robustness of the poset model by collapsing the states 2, 3, and 5 into one state and conducted an ordinal item response model analyses. The estimated latent distribution using collapsed categories showed similar patterns to that of the poset model. For example, estimated means across time points 1 through 5 had respective values of −0.26, −0.21, 0.00, −0.03, 0.08. The correlation between the latent variables ranged from 0.51 to 0.69, compared to the range of 0.50 to 0.71 in Table 3. Significant and non significant results (p < .05) in the regression analysis using collapsed categories remained unchanged.
The current article has a few limitations. First the procedure for establishing a weak order in a poset by iteratively removing the maximal (minimal) elements does not always lead to a unique partitioned solution. A simple example is to change ⪰ to ⪯ to in the sarcopenia example. Figure 6 shows the resulting poset, the structure of which is different from that depicted in Figure 3(a). The non-uniqueness of poset may lead to interpretation issue. We suggest using substantive knowledge for choosing the appropriate poset representation. Additionally, collapsing poset elements can also be considered for reducing the complexity of the GLMM and improve interpretability of results.
Figure 6.
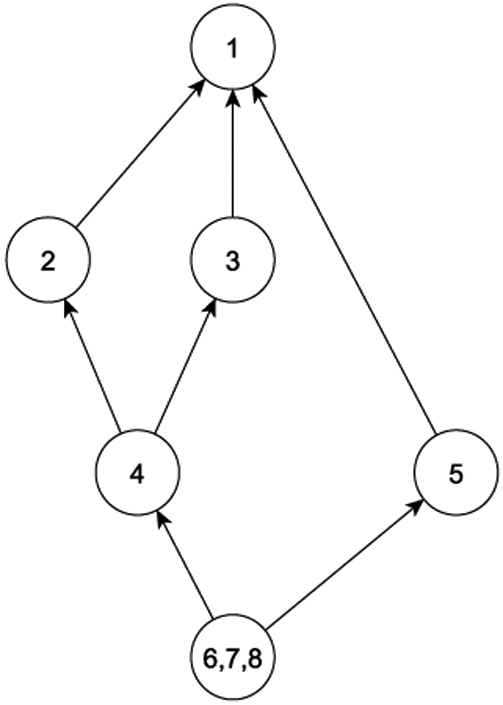
Alternative representation of weakly ordered poset for Health ABC sarcopenia data.
Another limitation, as pointed out by a referee, is that the poset definition in the sarcopenia application requires all three measurements - muscle mass, gait and grip, to be present. Missing any one of the measurements could result in missing classification. Furthermore, as explained in the method section, the MAR assumption for missing value also has limitation as missing values due to death or health reasons may not be truly missing at random. Readers should consider potential bias in the results due to violation of the MAR assumption.
Another limitation is that in this study we use the same linear fixed effects for both the nominal and ordinal model and also assume no time by predictor interaction. For example, the effect of BMI on sarcopenic state was summarized using a single regression coefficient, as discussed in the Results section. Note that in the current approach, in order to identify the model, we allow the latent variable to change over time and constrain some items parameters. This approach may not be applicable to other types of poset analysis such as subgroup analysis in cohorts with shorter period of followup. Poset items may behave differently across groups. In that case, one may use the latent variable as a device to account for intra-person observations, test for poset item parameter invariance across groups, and adjust the model to accommodate differential item behaviors. We will further explore such alternative models.
Acknowledgement
This study is funded by the following grant: NSF SES-1220549, NIH 1UL1TR001420-01, and P30AG21332.
Appendix
Appendix 1: Background for (cross-sectional) ordinal and nominal item response models
Item response models are designed for multiple categorical item responses (dichotomous, polytomous, and nominal) that are “caused” by an underlying individual-specific latent trait, often denoted by θi where i is the index for individual. The distribution of latent trait is often assumed to follow a normal distribution N(0, G) where G is the variance. For identification of the scale, G is set to a fixed value. Different link functions are possible in IRT models. For illustration purpose, we only use the logistic link here.
First we introduce the item response model for ordered categories. Without loss of generality, assume each item uniformly contains M ordered categories, labeled 1, ⋯ , M. For the response Yij of individual i to item j, j = 1, ⋯ , J, the cumulative model (called graded response model in the psychometric literature) can be written as:
| (10) |
With
| (11) |
where k = 1, …, M.
The parameter djk are ajk, k = 1, ⋯ , M are respectively called the intercept and discrimination parameters. Constrained models are possible – for example, ajk = aj.
The nominal (unordered) item response model [16] is less commonly used in the literature. Following the previous notation, we label the (unordered) responses k, k = 1, …, L. The basic nominal model can be written as:
| (12) |
in which
| (13) |
and
| (14) |
Identification constraints such as aj1 = cj1 = 0 are used to identify the model. In order to set up a more flexible framework to handle more complex data such as multidimensionality in latent trait, [13] offered a new parameterization of the basic nominal model. The new parameterization involves the separating the a parameter into a single discrimination parameter for all categories and a category-specific scoring function for all the responses. Specifically,
| (15) |
where aj is the single discrimination parameter which is common for all response categories, and is the category-specific scoring function. The following constraint is imposed for identification: , , and cj1 = 0. The advantages of the new parameterization include both better parameter interpretation and easier generalization to multidimensional latent trait.
Another feature added to the basic model from [13] is the use of a smoothing, either through polynomial or Fourier basis for the a and c parameters so those parameters across response categories would be “smoothly changing”. Let and c = (ck) (subscript j suppressed). The Fourier basis for the a and c parameters takes the form:
| (16) |
and
| (17) |
where α and η are vectors of length L − 1, and
| (18) |
in which fki = sin[π(i − 1)(k − 1)/(L − 1)], and α1 = η1 = 1. Restricted models where some α2, ⋯ , αL−1 are set to zero are also possible. See [13] for details of further generalization to multidimensional models in which θi is a vector of length > 1.
For both the ordinal and nominal IRT models, the conditional likelihoods given θ are formed by the product of the likelihoods of the individual item responses under the assumption of conditional (local) independence given θ. The overall likelihood is then formed by integrating out the latent variable.
Appendix 2: Proof of Proposition 1
Proof. We follow the notation in Section 2.3. The conditional partition sets associated with category k are denoted by , ⋯ , , and the corresponding sets that category k belongs by , ⋯ , . By definition, .
The joint density of observing a specific poset category k is given by
| (19) |
When the poset categories k = 1, ⋯ , K are recoded as subitem responses, each of the conditional probabilities , ⋯ , corresponds to the probability of a subitem response Y* that was not coded as NA. Denote this subset by and the subset of NA responses to the subitems by . The conditional probability of observing the sequence , ⋯ , in Equation 19 is given by
| (20) |
The equality is the result of the conditional independence requirement of the subitem responses.
On the other hand, the ML procedure in GLMM directly evaluates the probability of the response pattern of the subitems for category k given by . Under the conditional independence and missing data assumption of GLMM, this probability is evaluated as , which is the same as the right hand side in Equation 20.
References
- 1.Rosenberg IH. Summary comments. American Journal of Clinical Nutrition 1989; 50: 1231S–1233S. [Google Scholar]
- 2.Bandeen-Roche K, Xue Q, Ferrucci L, Walston J, Guralnik JM, Chaves P, Zeger SL, Fried LP. Phenotype of frailty: Characterization in the women’s health and aging studies. Journal of Gerontology: Biological Sciences and Medical Sciences 2006; 3: 262–266. [DOI] [PubMed] [Google Scholar]
- 3.Cruz-Jentoft AJ, Michel J-P. Sarcopenia: A useful paradigm for physical frailty. European Geriatric Medicine 2013; 4: 102–105. [Google Scholar]
- 4.Bauer JM, Sieber CC. Sarcopenia and frailty: A clinician’s controversial point of view. Experimental Gerontology 2008; 43: 674–678. [DOI] [PubMed] [Google Scholar]
- 5.Cruz-Jentoft AJ, Baeyens JP, Bauer JM, Boirie Y, Cederholm T, Landi F, Martin FC, Michel J-P, Rolland Y, Schneider SM, Topinkova E, Vandewoude M, Zamboni M. Sarcopenia: European consensus on definition and diagnosis. Age and Ageing 2010; 39: 412–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goodpaster BH, Park SW, Harris TB, Kritchevsky SB, Nevitt M, Schwartz AV, Simonsick EM, Tylavsky FA, Visser M, Newman AB. The loss of skeletal muscle strength, mass, and quality in older adults: the health, aging and body composition study. 2006. Journal of Gerontology A: Biological Sciences and Medical Sciences. 2006; 61(10):1059–64. [DOI] [PubMed] [Google Scholar]
- 7.Zhang Q, Ip E. Generalized Linear Model for Partially Ordered Data. Statistics in Medicine 2012; 31: 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.McCulloch CE, Searle SR, Neuhaus JM. Generalized, linear, and mixed models (2nd ed.) Hoboken, NJ: Wiley and Son, 2008. [Google Scholar]
- 9.Murphy RA, Ip EH, Zhang Q, Boudreau RM, Cawthon PM, Newman AB, Tylavsky FA, Visser M, Goodpadter BH, Harris TB. Transition to sarcopenia and determinants of transitions in older adults: A population-based study. Journal of Gerontology A: Biological Sciences and Medical Sciences 2014; 69: 751–758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ip EH, Chen S, Quandt S. Analysis of multiple partially ordered responses to belief items with Dont Know option. Psychometrika 2016; 81:483–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lord FM. Applications of item response theory to practical testing problems. Mahwah, NJ: Lawrence Erlbaum Associates Inc, 1980. [Google Scholar]
- 12.Houts CR, Cai L. flexMIRT R users manual version 3.5: Flexible multilevel multidimensional item analysis and test scoring. 2016; Chapel Hill, NC: Vector Psychometric Group. [Google Scholar]
- 13.Thissen D, Cai L, Bock RD. The nominal categories item response model. In: Nering ML, Ostini R, ed. Handbook of polytomous item response theory models. Abingdon: Routledge; 2010:43–75. [Google Scholar]
- 14.Semejima F. Estimation of latent ability using a response pattern of graded scores. 1969; Psychometrika Monograph Supplement, No. 17. [Google Scholar]
- 15.Tutz G. Sequential item response models with an ordered response. British Journal of Mathematical and Statistical Psychology 1990; 43: 39–55. [Google Scholar]
- 16.Bock RD. Estimating item parameters and latent ability when responses are scored in two or more latent categories. Psychometrika 1972; 37: 29–51. [Google Scholar]
- 17.Thissen D, Steinberg L. A response model for multiple-choice items. Psychometrika 1984;49: 501–519. [Google Scholar]
- 18.Muraki E. A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement 1992; 16: 159176. [Google Scholar]
- 19.Thissen D, Steinberg L. A taxonomy of item response models. Psychometrika 1986;51: 567577. [Google Scholar]
- 20.Thissen D, Cai L. Nominal categories models. In: van der Linden WJ ed.Handbook of item response theory: Vol. 1. Boca Raton, FL: Chapman Hall/CRC: 2015: 51–73. [Google Scholar]
- 21.Thissen D, Steinberg L, Mooney JA. Trace lines for testlets: A use of multiple-categorical-response models. Journal of Educational Measurement 1989;26: 247–260. [Google Scholar]
- 22.Cai L. (2010b). High-dimensional exploratory item factor analysis by a Metropolis-Hastings Robbins-Monro algorithm. Psychometrika, 2010: 75:33–57.. [Google Scholar]
- 23.Visser M, Goodpaster BH, Kritchevsky SB, et al. Muscle mass, muscle strength, and muscle fat infiltration as predictors of incident mobility limitations in well-functioning older persons. Journal of Gerontology A: Biological Sciences and Medical Sciences 2005; 60: 324–333. [DOI] [PubMed] [Google Scholar]
- 24.Cesari M, Penninx BW, Pahor M, et al. Inflammatory markers and physical performance in older adults: the InCHIANTI study. Journal of Gerontology A: Biological Sciences and Medical Sciences 2004; 59: 242–248. [DOI] [PubMed] [Google Scholar]
- 25.Cai L. flexMIRT R version 3.51: Flexible multilevel multidimensional item analysis and test scoring [Computer software]. 2017; Chapel Hill, NC: Vector Psychometric Group. [Google Scholar]
- 26.Bales CW, Buhr G. Is obesity bad for older persons? A systematic review of the pros and cons of weight reduction in later life. Journal of the American Medical Director Association 2008; 9:302312. [DOI] [PubMed] [Google Scholar]
- 27.Buch S, Carmeli E, Boker LK, Marcus Y, Shefer G, Kis O, Berner Y, Stern N, Muscle function and fat content in relation to sarcopenia, obesity and frailty of old age An overview, Experimental Gerontology 2016; 76: 25–32. [DOI] [PubMed] [Google Scholar]
- 28.Grimby G, Saltin B. The ageing muscle. Clinical Physiology and Functional Imaging 1983;3: 209–218. [DOI] [PubMed] [Google Scholar]
- 29.Yu SCY, Khow KSF, Jadczak D, Visvanathan R. Clinical Screening Tools for Sarcopenia and Its Management. Current Gerontology and Geriatrics Research 2016; Article ID 5978523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ip E, Zhang Q, Rejeski J, Harris T, S K. Partially ordered mixed hidden markov model for the disablement process of older adults. Journal of the American Statistical Association 2013; 108: 370–384. [DOI] [PMC free article] [PubMed] [Google Scholar]


