Vocal fold dynamics in a synthetic self-oscillating model: Intraglottal aerodynamic pressure and energy

Abstract

Self-sustained oscillations of the vocal folds (VFs) during phonation are the result of the energy exchange between the airflow and VF tissue. Understanding this mechanism requires accurate investigation of the aerodynamic pressures acting on the VF surface during oscillation. A self-oscillating silicone VF model was used in a hemilaryngeal flow facility to measure the time-varying pressure distribution along the inferior-superior thickness of the VF and at four discrete locations in the anterior-posterior direction. It was found that the intraglottal pressures during the opening and closing phases of the glottis are highly dependent on three-dimensional and unsteady flow behaviors. The measured aerodynamic pressures and estimates of the medial surface velocity were used to compute the intraglottal energy transfer from the airflow to the VFs. The energy was greatest at the anterior-posterior midline and decreased significantly toward the anterior/posterior endpoints. The findings provide insight into the dynamics of the VF oscillation and potential causes of some VF disorders.

I. INTRODUCTION

Self-sustained oscillations of the vocal folds (VFs) are the result of the coupling between the aerodynamic energy, which is transferred to the VFs, biomechanical structure of the VFs, and acoustic loading of the vocal tract.¹ The rate of energy transfer from the fluid to the VF tissue is correlated with the pressure and velocity fields within the glottis (i.e., the opening between the VFs).^2,3 Because the glottis forms a time-varying orifice during phonation, high-fidelity temporal and spatial resolution of the intraglottal pressure and velocity are needed to elucidate the mechanism of the energy transfer.^4,5 Understanding the fundamentals of energy exchange provides insight into the physics of VF oscillation and vocal efficiency in normal and pathological conditions.⁶

Glottal velocity fields have been widely studied using static and dynamic VF models,^7–17 excised larynges,^18–21 and computational approaches,^22–30 with a review of the literature found in Mittal et al.³¹ Surprisingly, there is little work that has connected the observed fluid flow phenomena with the resultant pressure loading at sufficient spatial and temporal resolutions to provide direct insight into the energy exchange process. Initial work used static VF models in steady flow,^32–36 identifying that the glottal pressure reached a local minimum for divergent orientations. Subsequent work investigated the influence of features, such as inferior/superior VF angles^36–38 and inlet and exit VF radii,^39–41 on the pressure field. While providing significant spatial resolution of the VF surface pressure, the use of static geometries in steady flow, commonly justified by invoking the quasi-steady assumption,⁴² neglects temporal dependencies in the flow. Successive work has shown that the quasi-steady assumption overlooks key fluid dynamics, particularly during the opening and closing phases when flow accelerations are very high.^16,43–45

During the closing phase of a modal phonatory cycle, the glottis forms a divergent channel. The resultant adverse pressure gradient gives rise to complex flow behavior, including variations in the flow separation point,⁴⁶ formation and propagation of vortices within the glottis,^21,47–49 and flow asymmetries. This phenomenon has been observed using particle image velocimetry (PIV) in studies with static,¹² dynamically driven,¹⁵ and self-sustained oscillating⁵⁰ models of the VFs as well as in an excised canine larynx.⁵¹ The resultant pressure loading has been investigated by exploring a theoretical solution for the asymmetric pressure loading.^52–54 Although this empirical approach was derived from unsteady, driven VF oscillations, the model implementation relied upon a quasi-steady assumption and further neglected three-dimensional effects and supraglottal geometry (i.e., the ventricular folds), which have subsequently been shown to be important in determining the development of flow asymmetries.^55,56

Finally, despite the fairly common use of two-dimensional VF model geometries, which are extruded in the anterior-posterior direction, the three-dimensionality of the VFs has been shown to have a significant influence on VF surface pressure loadings,⁵⁷ exhibiting a lower pressure drop than that observed for two-dimensional models, and giving rise to anterior-posterior variations in the pressure loading. Unfortunately, these effects have largely been investigated in static models with steady flow. A notable exception measured the unsteady, three-dimensional intraglottal pressure loading in self-oscillating excised VFs, investigating the dependence of both anterior-posterior pressure gradients and unsteady effects.⁵⁸ It was found that the intraglottal pressure reached negative gauge values only along the midline of the VFs and not at the anterior and posterior edges. However, the diameter of the pressure sensors used to acquire the intraglottal pressure was relatively large (2.36 mm) compared to the inferior-superior and anterior-posterior VF dimensions [$\mathcal{O}(10\hspace{0.17em}\hspace{0.17em}\text{mm})$], leading to poor spatial resolution of the flow and obfuscating some of the key dynamical behaviors.

Nevertheless, similar results have been observed using computational models of the VFs undergoing self-sustained oscillations.^59,60 Early efforts³ validated the computational model kinematics with synthetic silicone VF models to investigate the aerodynamic energy exchange during oscillation. The results provided insight into the net energy transfer from the airflow to the VF tissue, which was found to be positive, validating a previously proposed theory that the energy transfer from the fluid to the VF must be greater during opening than closing to produce self-sustained oscillations.⁵ However, modeling VF contact is highly challenging in numerical investigations, which can influence the accuracy of the oscillation dynamics.

Despite the extensive efforts devoted to resolving the intraglottal aerodynamic pressure during VF oscillation, temporal and spatial variations in the pressure have still not been accurately quantified. This deficiency arises from the challenging environment of voiced speech production, where tight geometric constraints, in tandem with the high-frequency of the VF oscillations, pose significant challenges.⁶¹ Recently, a new approach that employs synthetic, self-oscillating VF models in a hemilaryngeal configuration was developed and validated for accurately measuring the intraglottal aerodynamic pressures during oscillation.⁶¹ The self-oscillating VF model captures both the three-dimensional and unsteady flow effects, addressing the shortcomings of many previous investigations.

The objective of this work is to investigate the intraglottal aerodynamic pressure distributions in a hemilaryngeal self-oscillating silicone model during the non-collision phase of VF oscillation. The model is incorporated into a novel flow facility that enables, for the first time, both temporal and spatial resolution of the intraglottal pressure waveform during the opening and closing phases of the phonatory cycle. The pressure field is then used to investigate the energy exchange from the airflow to the VFs. The flow facility and measurement procedure are described in Sec. II. The results and discussion are presented in Sec. III. Finally, Sec. IV is left for the conclusions.

II. METHODS

A. Hemilaryngeal flow facility

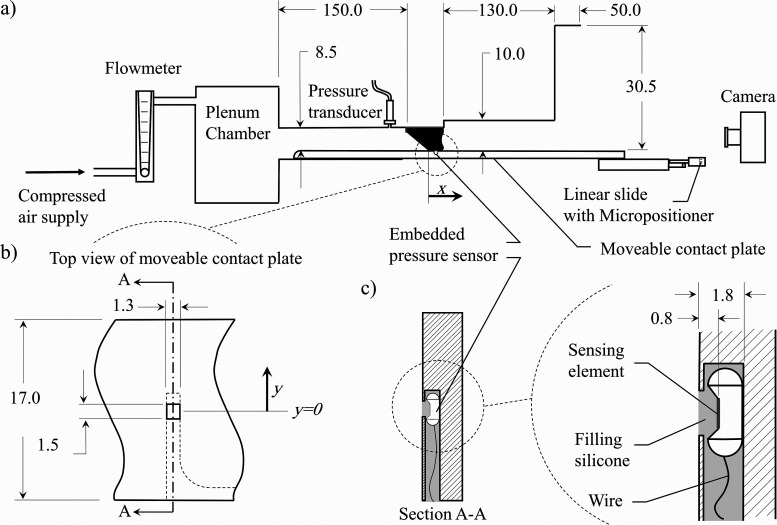
A synthetic, self-oscillating silicone model of the VFs was used in a hemilaryngeal flow facility to acquire the intraglottal pressure distribution in both the inferior-superior and anterior-posterior directions. The geometry of the VF model and experimental setup was similar to that used in prior work (see Sec. 3.1 in Motie-Shirazi et al.⁶¹) and is shown in Fig. 1(a).

FIG. 1.

(a) The schematic of the experimental flow facility. (b) A close-up top view of the contact plate and relative position of the pressure sensor. (c) The schematic of section A-A on the left, showing the pressure sensor orientation inside the channel beneath the contact plate, and a close-up view of the sensor on the right, displaying its relative location to the contact surface. All dimensions are in mm.

Briefly, a constant pressure source provided flow through a Dwyer RMC 101-SSV inline flow meter (Dwyer, Michigan City, IN, USA), which measured the time-averaged flow rate. On exiting the flow meter, the flow entered a 0.03 m³ plenum chamber with a cross-sectional area of 0.06 m², whose inner walls were insulated acoustically by foam. The plenum chamber was connected to a model trachea, which was comprised of a 213.0 mm² area rectangular channel that was 150.0 mm long. The design of the subglottal tract connecting the plenum chamber to the VFs was chosen based on previous work, showing that subglottal acoustic loading effects can be captured using a large volume plenum chamber connected to a constant area tracheal tube according to the specified dimensions.^62,63 The subglottal pressure was monitored with a Kulite ET-3DC pressure transducer (Kulite, Leonia, NJ).

The VF model was mounted in a hemilaryngeal configuration by placing it in a bracket at the exit of the model trachea. The wall against which the VF oscillated extended the length of the tracheal tract and could be moved in the inferior-superior direction. This is referred to as the contact plate [see Figs. 1(a) and 1(b)]. A Millar Mikro-Cath pressure sensor (Millar, Houston, TX) was embedded in a channel beneath the contact plate [see Figs. 1(b) and 1(c)]. A 1.50 mm × 1.30 mm window, located above the sensing element of the sensor, connected the channel to the contact surface; therefore, the pressure at the surface was transferred to the transducer. The sensing element was a piezoresistive type with dimensions of 1.0 mm × 1.0 mm and was placed 0.8 mm beneath the surface of the contact plate [see Fig. 1(c)]. The channel was then filled with Smooth-On Dragon Skin 10 silicone (Smooth-On Inc, Macungie, PA) to provide a smooth level surface against which the VF model vibrated. The channel continued beneath the surface of the contact plate over the entire distance of the inferior-superior direction to allow electrical access for the sensor wires.

Calibration of the silicone-embedded pressure sensor was performed by submerging it at variable depths in water and comparing the hydrostatic pressure with the pressure recorded by the transducer. A one-to-one linear relationship between the hydrostatic and measured pressure was found with a maximum error of 0.03 kPa.⁶¹ Although the calibration method did not consider the contribution of shear stress to the pressure recorded by the sensor, it can be shown that if steady flow through parallel channels is assumed, the wall shear stress will be 3 orders of magnitude lower than the intraglottal static pressure and is, therefore, negligible. The frequency bandwidth of the embedded pressure sensor was measured to be at least 3.8 kHz,⁶¹ which was suitable to resolve the unsteady intraglottal aerodynamic pressure signal. Moreover, studying the pressure sensor response to a dynamic load showed that the silicone encasing the sensor produced a critically damped response such that ancillary wave propagation within the silicone decayed quickly and did not affect the aerodynamic pressure measures.

High-speed video (HSV) of the VF kinematics was acquired with a Photron AX200 charge-coupled device (CCD) camera (Photron, Tokyo, Japan) at 20 000 frames-per-second and a resolution of 640 pixels × 480 pixels. The camera was positioned superiorly to the VF exit. An Elicar V-HQ Macro 90 mm f 2.5 lens (Jaca Corporation, Tokyo, Japan) provided a field of view measuring 48.0 mm × 36.0 mm. The HSV, subglottal pressure, and intraglottal pressure signals were all synchronized and acquired using a custom LabVIEW Virtual Instrument program (National Instruments Corporation, Austin, TX). The subglottal and intraglottal pressure signals were recorded on a National Instruments PCIe-6321 data acquisition card at 80 kHz for a duration of 0.75 s.

A vocal tract was added to the flow facility at the VF exit to include the acoustic loading effects as shown in Fig. 1(a). The geometry of the vocal tract was idealized based on the vocal tract geometry of the vowel /o/, which was reported from the magnetic resonance imaging of the vocal tract.⁶⁴ The supraglottal channel had a constant length of 26.2 mm in the anterior-posterior direction and a total height of 180.0 mm in the inferior-superior direction. The medial-lateral width varied over two discrete, connected sections. The first section (exiting the glottis) had a height of 130.0 mm and a width of 10.0 mm (262.0 mm² cross-sectional area), which then transitioned to the second section, which measured 50.0 mm long with a width of 30.5 mm (917.0 mm² cross-sectional area).

Four identical contact plates were employed for the measurements with each containing an embedded pressure sensor at a different location in the anterior-posterior direction; one is positioned at the anterior-posterior midline [see Fig. 1(b)] with the subsequent contact plates equally spaced every 1.78 mm in the anterior direction. The coordinate system is defined such that x = 0 corresponds to the location of the inferior edge of the glottis when the VF is at rest, and x values indicate the distance in the inferior-superior direction. The y coordinate is aligned with the anterior-posterior direction with y = 0 indicating the anterior-posterior midline. The pressure sensors in the four contact plates were located at $y=0,\hspace{0.17em}\hspace{0.17em}1.78,\hspace{0.17em}\hspace{0.17em}3.56$, and 5.34 mm. A Thorlabs PT1 linear slide (Thorlabs, Newton, NJ) adjusted the contact plate in the inferior-superior (x) direction to enable pressure acquisition at any location along this direction. The area over which the pressure was measured was 1.50 mm × 1.30 mm in the anterior-posterior and inferior-superior directions, respectively [see Fig. 1(b)]. The linear slide had a positional accuracy of 0.0254 mm.

B. VF model

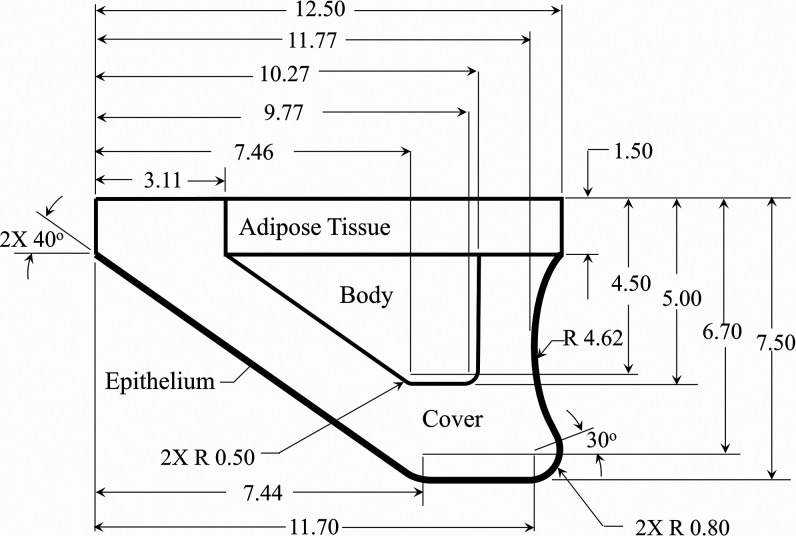
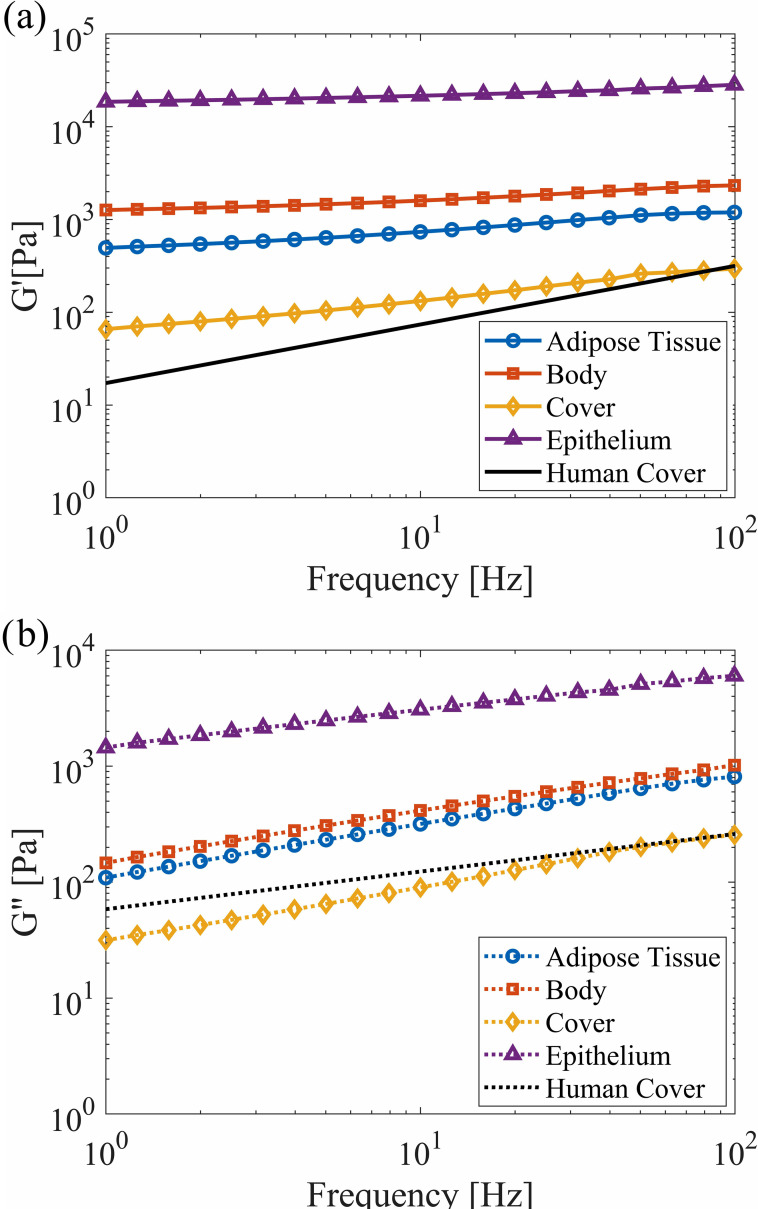
The dimensions of the VF model, layer composition, and silicone mixture ratios used for each layer were the same as those in prior work,⁶¹ with the dimensions and layer thicknesses shown in Fig. 2. The VF profile was extruded in the anterior-posterior direction to a length of 17.0 mm. The modulus of elasticity of each silicone layer was newly quantified using a TA Instruments AR 2000 Rheometer (TA Instruments, New Castle, DE) to improve the accuracy at the low moduli of interest. Cylindrical samples with a diameter of 60.0 mm and a thickness of 1.0 mm were created from the same batch of each silicone mixture as for the VF layers. The elastic ($G\prime$) and viscous ($G″$) shear moduli were measured by performing a frequency sweep from 1 to 100 Hz, which was the upper limit of the instrument, at a 1% strain. The results are presented in Fig. 3 and compared with values from human VF cover measurements.⁶⁵ Good agreement with the physiological data was found.

FIG. 2.

The geometry and dimensions of the synthetic VF model. All dimensions are in mm.

FIG. 3.

(Color online) (a) The elastic ($G\prime$) and (b) viscous ($G″$) shear moduli of different layers of the VF model with corresponding values for human VFs (Ref. 65). The axes are plotted on a logarithmic scale.

The complex modulus of elasticity ($E^{*}$) of an isotropic material is related to the complex shear modulus ($G^{*}=G\prime +iG″$) and Poisson's ratio (ν) by

$$E^{*}=2G^{*}(1+\nu ).$$ (1)

Poisson's ratio has been measured to be $\approx 0.4$ for different mixture ratios of silicone at 1% strain.⁶⁶ Using these relationships, the magnitude of the complex modulus of elasticity at a frequency of 100 Hz was computed for each layer and is reported in Table I, alongside the range of physiological values. The physiological magnitudes present the Young's modulus of elasticity when tensile^67–69 and indentation^70,71 tests were performed, and report the complex modulus of elasticity obtained using dynamic mechanical analysis⁷² and rheology^65,73,74 measurements. A good agreement is found between the physiological and synthetic values. The silicone type and mixture ratios of each layer are also presented in Table I. The mixture ratio of A:B:thinner represents the ratios of part A and part B of the Smooth-On Ecoflex 0030 (EF) or Dragon Skin 10 (DS; Smooth-On Inc, Macungie, PA) silicone to thinner.

TABLE I.

The moduli of elasticity of the physiological and silicone VF models for each layer. Smooth-On Ecoflex 0030 and Dragon Skin 10 silicone mixtures (Smooth-On Inc, Macungie, PA) are denoted by EF and DS, respectively.

Layer	Physiological range (kPa)	Silicone VF model (kPa)	Silicone ratio (Type of silicone)
Adipose tissue	1–10 (Ref. 67)	4.04	1:1:4 (EF)
Body	1.5–50 (Refs. 68, 70, 72)	7.13	1:1:2 (EF)
Cover	1–8 (Refs. 65, 69, 71, 73, 74)	1.10	1:1:7 (EF)
Epithelium	$\text{Not}\hspace{0.17em}\hspace{0.17em}\text{measured}$	81.10	1:1:1 (DS)

C. Pressure measurement procedure

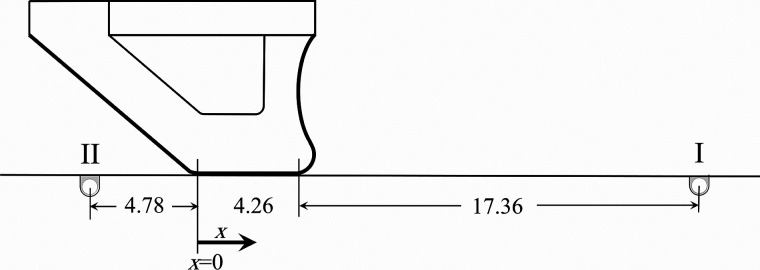
During VF oscillation, each of the movable contact plates was independently inserted and positioned such that the pressure sensor was located superior to the VF. The contact plate was then moved in the inferior direction in increments of 0.254 mm. The unsteady intraglottal pressure at each location was acquired by the pressure sensor. Figure 4 shows the initial and final positions (I and II) of the sensor relative to the VF model at rest. Note that the airflow caused the VF to bulge slightly in the superior direction such that contact did not occur at the exact glottal midpoint of the rest position of the VF model. After sampling for 0.75 s at each location, which produced about 120 cycles for an oscillation frequency of 160 Hz, the waveforms were then phase-averaged based on synchronizing the intraglottal data with the unsteady subglottal pressure recorded with the Kulite pressure transducer (Kulite, Leonia, NJ).

FIG. 4.

The schematic of the initial (I) and final (II) positions of the pressure sensor moving with the contact plate relative to a stationary VF model. All dimensions are in mm.

III. RESULTS AND DISCUSSION

A. Oscillation dynamics

VF oscillation dynamics were investigated with a medial prephonatory compression of 0.75 mm, which resulted in a medial prephonatory pressure of 1.25 kPa. These are, respectively, the medial distance, which the VF is deformed into the hemilaryngeal plate when it is in a static configuration, and the resulting static pressure (see Motie-Shirazi et al.⁶¹ for further details). The onset pressure of the VF model was measured to be 1.70 kPa. The intraglottal pressure measurements were performed at a mean subglottal pressure of $p_{\text{sub}}=2.20\hspace{0.17em}\hspace{0.17em}\text{kPa}$. The mean flow rate was measured to be $338\hspace{0.17em}\hspace{0.17em}\text{mL}/\mathrm{s}$. The fundamental frequency of oscillation was 160 Hz yielding a period (T) of 6.25 ms. The subglottal pressure was kept constant when the four individual contact plates were employed. The mean flow rate and frequency variation were 2.8% and 1.2%, respectively, as the different plates were used. Because of this slight change in the frequency, all of the measured pressure waveforms at the four anterior-posterior locations were normalized to a frequency of 160 Hz.

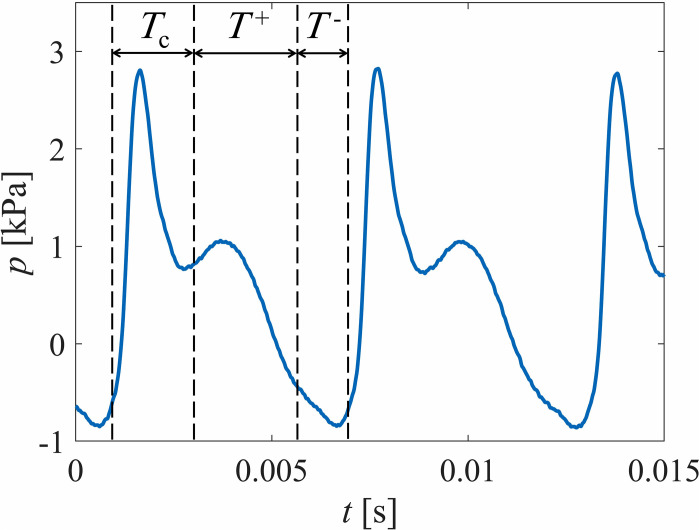
Figure 5 shows a kymogram plot of an oscillation cycle at the mid anterior-posterior location extracted from the HSV. At this location, the open quotient ($\text{OQ}=T_{\text{open}}/T$) was calculated to be $\simeq 0.78$ and the speed quotient ($SQ=T^{+}/T^{-}$) was $\simeq 2.09$, where $T_{\text{open}}$, T, T⁺, and T^- are defined in Fig. 5. Both the OQ and SQ are in the physiological ranges for human VFs.^75,76 Hence, the current VF model geometry and configuration provides a significant advantage over prior efforts because of the ability to replicate the robust dynamics of contact. In addition, the maximum glottal width and glottal area were calculated to be 0.67 mm and 8.45 mm², which are physiologically accurate.^77,78

FIG. 5.

(Color online) The kymogram at the mid anterior-posterior location of the VF model. The solid and dashed lines identify the sinusoidal functions that were respectively fitted to the inferior edge of the VF during closing and the superior edge during opening via the least-squares regression (Ref. 65).

The onset pressure and flow rate of the synthetic model were higher than the physiological values.⁷⁹ This behavior has been observed in previous investigations with hemilaryngeal configurations.^58,80,81 In addition, a relatively high medial prephonatory compression was required to get robust contact in the synthetic models, which also increased the onset pressure and flow rate. In spite of the higher subglottal pressures, the VF kinematics are representative of the physiological motion.

B. Pressure measurements

The time-varying pressure waveforms were measured in the inferior-superior direction in increments of 0.254 mm as described in Sec. II C. The inferior and superior glottal boundaries were carefully identified by employing a previously proposed technique⁸³ for identifying contact that monitors the electrical resistance between the VF and contact plate. The details can be found in Motie-Shirazi et al.⁶¹ Figure 6 presents three successive cycles of the unsteady intraglottal pressure, measured at the inferior-superior center of the contact region and the anterior-posterior midline.

FIG. 6.

(Color online) The successive cycles of the intraglottal pressure waveforms with the key phases identified.

The time intervals of the different phases were extracted from the synchronized HSV and are labeled in Fig. 6. The intraglottal pressure waveform at the contact region showed a double-peak pattern, consistent with earlier findings.^61,80,81 The sharp peak with the highest pressure magnitude occurs as a result of the VF impact during the contact phase, denoted by T_c in Fig. 6. It is followed by a second peak with a lower pressure magnitude, which corresponds to the aerodynamic pressure rising as the VFs begin to open (T⁺) and the sensor is exposed to the subglottal pressure. This is followed by a decrease in pressure as the flow begins to accelerate. After reaching the maximum opening, the glottis begins to close (T^-), with continued flow acceleration and decreasing pressure until shortly before the closure when the pressure rises. A more detailed description of these general behaviors can be found in previous studies.^61,81 In Sec. III C, the spatial variations in the unsteady aerodynamic pressure are discussed. Note that the intraglottal pressure distribution and energy exchange during the collision phase of the current model are reported and discussed in a separate publication.⁸⁴

C. Aerodynamic pressure

1. Opening phase

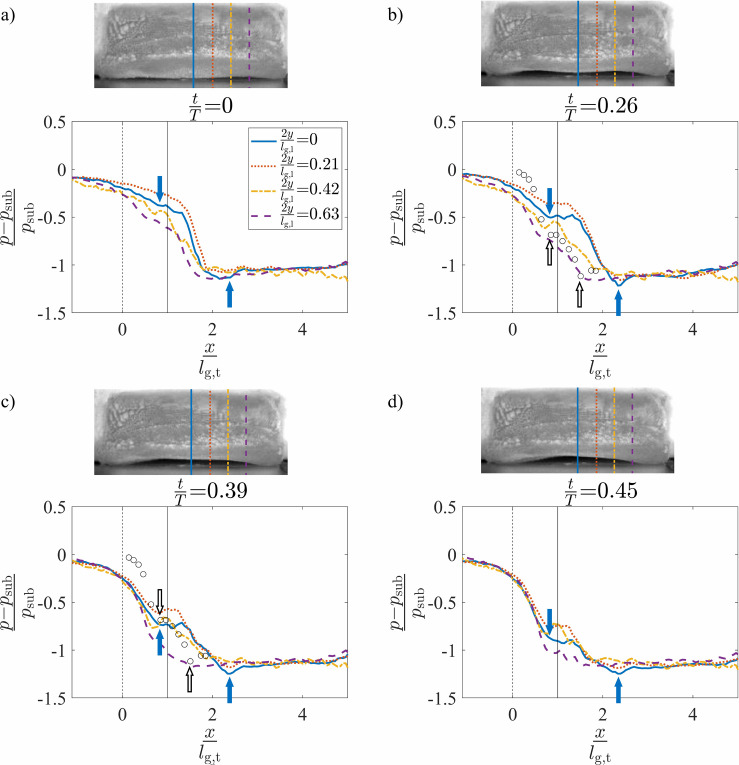
The spatial variation of the intraglottal aerodynamic pressure in the inferior-superior direction was computed as the normalized pressure drop relative to the mean subglottal pressure, $p_{\text{sub}}$. This is expressed as $(p-p_{\text{sub}})/p_{\text{sub}}$. Figures 7(a)–7(d) present the surface pressure measurements at the four anterior-posterior locations and four different instances in time during the glottal opening, corresponding to the normalized times of $t/T=0$, 0.26, 0.39, and 0.45, respectively. The distance from the midline, y [see Fig. 1(b)], is normalized by the glottal half length in the anterior-posterior direction, which was $l_{g,l}/2=0.85\hspace{0.17em}\hspace{0.17em}\text{mm}$. The abscissa indicates the distance from the inferior glottal margin when the VF is at rest and the medial prephonatory compression is not applied, normalized by the inferior-superior glottal thickness of $l_{g,t}/2=4.26\hspace{0.17em}\hspace{0.17em}\text{mm}$ (see Fig. 4). The inset images are a superior view of the VF orientation at the corresponding times and denote the anterior-posterior position of the four pressure measurements by the corresponding line types. At the VF midline, the VF opening began at $t/T=0$ and ended at $t/T=0.52$. The dashed vertical lines $x/l_{g,t}=0$ and $x/l_{g,t}=1$ indicate the locations of the inferior and superior boundaries, respectively, of the glottis when the VF is at rest.

FIG. 7.

(Color online) The normalized intraglottal pressure drop versus the normalized inferior-superior distance plotted at four positions in the anterior-posterior direction and normalized times of (a) $t/T=0$, (b) $t/T=0.26$, (c) $t/T=0.39$, and (d) $t/T=0.45$. The times coincide with a convergent glottal configuration. The solid arrows indicate the glottal entrance and exit at $2y/l_{g,l}=0.0$. Each inset presents a superior view of the VF orientation at the same instance in time. The dashed and solid vertical lines at $x/l_{g,t}=0$ and $x/l_{g,t}=1$, respectively, identify the glottal entrance and exit when the VF is in its rest configuration. The pressure measurements from the steady flow, static investigations (Ref. 57) are included as hollow circles in subplots (b) and (c) with the glottal margins indicated by hollow arrows.

A video showing the progression of the intraglottal pressure distributions throughout the oscillatory cycle is included as supplementary material.⁸⁵ The still images of Fig. 7 are extracted from this video, as well as those discussed in Sec. III C 2 for the divergent orientations.

During the opening of the glottis (see Fig. 7), the mean subglottal pressure decreased as the flow accelerated through the glottis. Note that for Figs. 7(b)–7(d), the pressure within the glottal region plateaus before sharply decreasing. This can be explained by the viscous losses within the glottis being balanced by the total acceleration of the flow. The minimum pressure then occurred at the glottal exit, where the glottal gap width was the smallest. The location of the glottal entrance and exit along the midline of the VF are noted in Fig. 7 by the successive solid arrows. Comparing these locations across Figs. 7(b)–7(d) shows that the glottal entrance and exit were largely stationary during the opening phase of the VF oscillation. Nevertheless, the consistent shift in the location of the superior edge of the VF (the minimum pressure location) relative to the static position of the superior VF edge indicates the presence of superior VF bulging during oscillation.

The intraglottal pressure measurements were compared with the prior results acquired along the midline of the three-dimensional static VF models in steady flow,⁵⁷ represented as circles in Figs. 7(b) and 7(c). The static models had a 10° convergence angle and fixed medial-lateral glottal width of 0.8 mm. For comparison, the estimated location of the glottal entrance in the current self-oscillating model was aligned with the glottal entrance in the prior static model investigations. The inferior-superior distances were normalized by each corresponding inferior-superior glottal thickness, which were 4.26 and 3.00 mm, respectively. The glottal entrance and exit of the static model are indicated with the hollow arrows in Figs. 7(b) and 7(c). The location of the glottal exit did not match because the glottal thickness of the synthetic model increased during oscillation, as described above, but was fixed for the static model. The intraglottal pressure profiles in these models are very similar with a change in the slope at the entrance and a drop in the pressure at the glottal exit. Similar behavior has been reported in static models with convergent glottal profiles.^{32,36,37,41,86}

Unsteady flow effects can be observed by comparing the temporal progression of the intraglottal pressure waveform during the glottal opening, which are presented sequentially in Figs. 7(a)–7(d). The mean intraglottal pressure, p_m, decreased at all of the anterior-posterior locations as the glottis was opening. Figure 8 shows the variation of the mean intraglottal pressure, p_m, at the four anterior-posterior locations as a function of the normalized time during the glottal opening. This contradicts the oft-employed quasi-steady assumption that is invoked when investigating pressure-flow relationships through static VF models. As the glottal area increases during opening, the quasi-steady assumption ensures that the intraglottal pressure remains constant because the glottal velocity is not a function of the glottal area. In contrast, the increased subglottal pressure that builds up during the glottal closing results in a temporally accelerating flow field, which produces a significant decrease in the magnitude of the intraglottal pressure. Whereas previous work has identified the existence of high flow acceleration during opening,¹⁸ these findings correlate the flow velocity with the intraglottal pressure field.

FIG. 8.

(Color online) The mean intraglottal pressure at the four different anterior-posterior locations as a function of normalized time.

The unsteady intraglottal pressure distribution varied in the anterior-posterior direction. During the later stages of opening [Figs. 7(c) and 7(d)], the pressure magnitude at the entrance of the glottis remained largely constant in time at the anterior-posterior midline, whereas at the more anterior positions of $2y/l_{g,l}=0.21$ and 0.42, it increased slightly before subsequently decreasing in time. At $2y/l_{g,l}=0.63$, the pressure is significantly lower for all inferior-superior positions. These variations are likely due to the three-dimensional geometry, which drives three-dimensional flow behavior as has been previously observed.⁵⁷ Note that the pressure values in the self-oscillating and static models could not be directly compared because the models did not have identical geometries, and the shape of the self-oscillating model continuously varied in time during the VF oscillation.

2. Closing phase

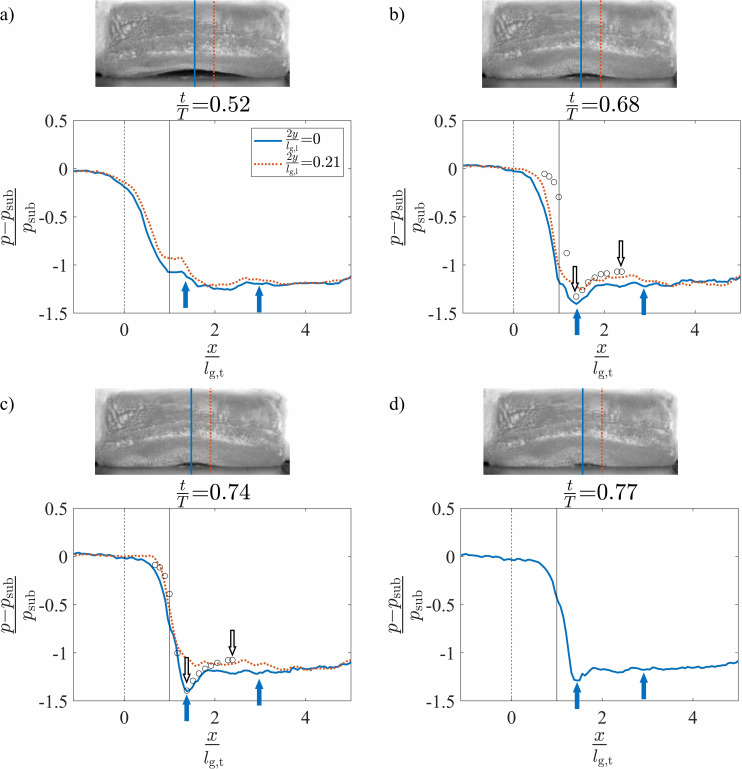
The spatial variation of the normalized intraglottal pressure drop during the glottal closing is plotted in Figs. 9(a)–9(d) at four normalized times of $t/T=0.52$, 0.68, 0.74, and 0.77, respectively. The pressure profiles are not presented at $2y/l_{g,l}=0$ and 0.21 because closure at these locations has already occurred at the selected times. Similarly, $2y/l_{g,l}=0.21$ is not plotted in Fig. 9(d) for the same reason. A clear divergent profile was present during the closing phases of oscillation, as was observed in the kymogram of Fig. 5 and a kymogram extracted from the position $2y/l_{g,l}=0.21$ (not shown for brevity). For kymograms extracted at the more anterior/posterior positions of $2y/l_{g,l}=0.42$ and 0.63, the propagation of the mucosal wave and resultant divergent profile were not as pronounced.

FIG. 9.

(Color online) The normalized intraglottal pressure drop versus the normalized inferior-superior distance plotted at four positions in the anterior-posterior direction and normalized times of (a) $t/T=0.52$, (b) $t/T=0.68$, (c) $t/T=0.74$, and (d) $t/T=0.77$. The times coincide with a divergent glottal configuration. The solid arrows indicate the glottal entrance and exit at $2y/l_{g,l}=0.0$. Each inset image presents a superior view of the VF orientation at the same instance in time. The dashed and solid vertical lines at $x/l_{g,t}=0$ and $x/l_{g,t}=1$, respectively, identify the glottal entrance and exit when the VF is in its rest configuration. The pressure measurements from the steady flow, static investigations (Ref. 57) are included as hollow circles in subplots (b) and (c) with the glottal margins indicated by hollow arrows.

The glottal entrance and exit at the midline of the VF are indicated by the solid arrows in Figs. 9(b)–9(d). The entrance locations were identified based on the assumption that the pressure will be a minimum at the glottal entrance (the minimum glottal area) when the glottis assumes a divergent orientation. At the beginning of the glottal closing when $t/T=0.52$ [Fig. 9(a)], the glottis was largely a uniform channel and, thus, it was difficult to identify the precise location of the glottal entrance. In this state, the glottal entrance was presumed to be at the same position as found at the other times during closing because as can be seen in Figs. 9(b)–9(d), this location did not change significantly over time. Downstream of the minimal glottal area, pressure recovery occurred in the divergent glottal channel. The precise location of the glottal exit was estimated by assuming that the glottal thickness remained equal to the value found for the convergent glottal orientation as described in Sec. III C 1. In addition, the shifted location of the glottal entrance relative to the convergent phase denotes the increased superior bulging in the divergent profile.

The intraglottal pressures are compared in Fig. 9 with the prior results of the steady flow through three-dimensional static VF models with a 10° divergent glottal profile and fixed medial-lateral glottal width of 0.8 mm.⁵⁷ The intraglottal pressure distributions obtained from the static model investigations at anterior positions of $2y/l_{g,l}=0.50$ and 0.0 (Ref. 57) are plotted as hollow circles in Figs. 9(b) and 9(c), respectively. For comparison, the divergent angle of the self-oscillating VF model was estimated from the recorded HSV during the closing phase of the glottis based on the known medial-lateral displacement of the inferior and superior edges (see the VF edges at T^- in Fig. 5) and the inferior-superior thickness of the medial surface when at rest. It was found that at an anterior position of $2y/l_g=0.21$, a divergent angle of ∼10° occurred at $t/T=0.68$ [Fig. 9(b)] and for an anterior position of $2y/l_g=0$, the divergence angle was ∼10° at $t/T=0.74$ [Fig. 9(c)]. Reasonable agreement is observed between the static and dynamic pressure profiles, which is not surprising as unsteady effects resulting from the flow acceleration are not anticipated to be as significant during the latter phases of the phonatory cycle. The magnitude of the minimum pressure was lower at the middle when compared to the anterior/posterior positions, again, indicating the presence of three-dimensional flow behavior.

The temporal variation of the intraglottal pressure during the glottal closing was observed by comparing the temporal evolution of the minimum pressure peak, which occurs at the minimal glottal area. As the VFs closed, this value decreased as the minimum glottal area became smaller and the subsequent pressure loss across the glottis increased. However, it is interesting to note that immediately preceding the closure, at $t/T=0.77$, the minimum pressure increased despite the continued decrease in the glottal area [see the insets of Figs. 9(c) and 9(d)]. This increase in the minimal pressure can be explained by an increase in the viscous pressure loss when the glottal orifice becomes very small at the end of the closing, resulting in a decrease in the flow velocity and, consequently, a rise in the pressure. This is an important observation that is not captured by static VF investigations.

D. Aerodynamic power

The power transferred to the VF is approximately equal to the product of the normal force applied on the VF glottal surface and normal component of the surface velocity.³ The inferior-superior motion of the VF could not be tracked in this study because the HSV of the VF oscillations was only recorded from a superior point of view. Nevertheless, studies with excised⁸⁷ and synthetic⁸⁸ VFs showed that the maximum glottal displacement and velocity in the inferior-superior direction are at most 20% of those in the medial-lateral direction. Therefore, the difference between the magnitude of the total velocity (i.e., the resultant velocity vector comprising both the medial-lateral and superior-inferior components) and the purely medial-lateral component of velocity is at most 2%. Accordingly, considering only the medial-lateral component instead of the total normal velocity in the power transfer calculation, results in only a 2% error. It was also found that viscous forces applied on the VF have a minor influence on the transferred power.³ Therefore, the medial-lateral component of the velocity and intraglottal aerodynamic pressure were used to estimate the power transfer.

At each of the four anterior-posterior locations, the medial-lateral component of the glottal surface velocity was estimated from kymogram plots at the same position where the pressure measurements were acquired. The kinematics of the visible medial boundary of the VF, which is the superior edge during the opening and inferior edge during the closing, was determined using a previously proposed least-squares regression approach. The medial surface dynamics were specified according to

$$l_{gf,w}(t)=\sum _{n=0}^N{C}_n\hspace{0.17em}\hspace{0.17em}\text{sin}\left(\frac{2\pi }{T}t+{\varphi }_n\right),$$ (2)

where $l_{gf,w}$ is the fitted value of the glottal width, N is the number of sinusoidal terms, and C_n and ${\varphi }_n$ are constants found by applying the least-squares regression to the glottal width in time.⁸² The temporal history of the glottal width was extracted from the kymogram plots by defining a constant threshold value. The least-squares regression was then applied to the opening and closing phases of the glottal cycle to determine the sinusoidal fits—one during the glottal opening and the other during the glottal closing.

It was found that including four coefficient terms in Eq. (2) was sufficient for accurately resolving the medial surface kinematics, resulting in an R² value of 0.98 during the glottal opening and 0.99 during glottal closing. Fitted functions overlaid on the kymogram are displayed in Fig. 5.

The magnitude of the glottal surface velocity in the medial direction ($v_g$) was then estimated by computing the derivative of the functions at each instance in time. This assumes that the medial VF surface velocity is equal to the superior edge velocity during opening and the inferior edge velocity during closing. Although admittedly an approximation, it provides a first-order estimate of the VF surface velocity. Because the VF surface velocity could not be estimated outside the glottal region, the power transfer was only investigated within the glottis. The sensitivity of the glottal surface velocity to the choice of threshold value was investigated by varying the threshold value over a range that corresponded to what was visually identified as the upper and lower limits of the glottal edge. The error in the computed surface velocity over this range of threshold values was found to be less than 18%.

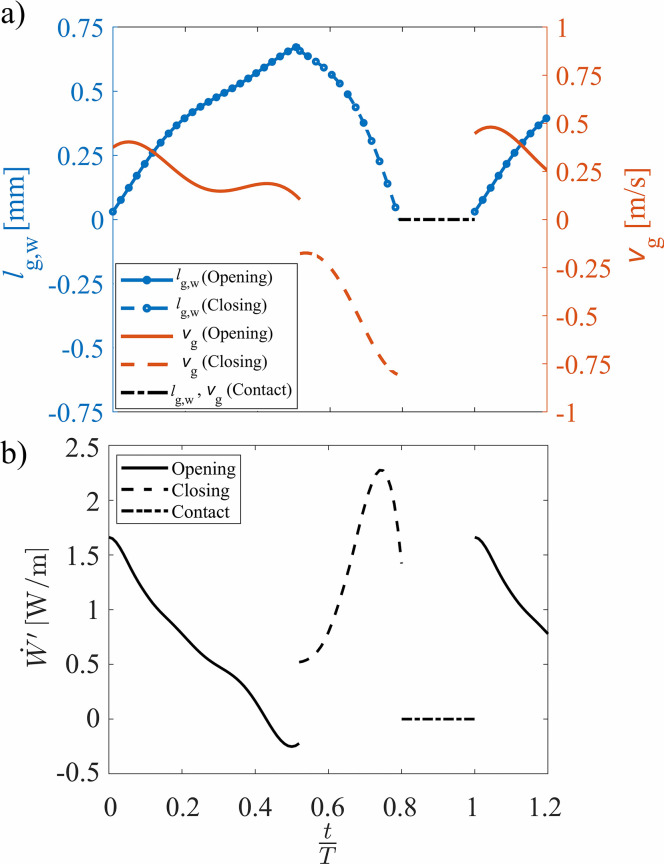
The medial VF displacement and surface velocity are presented in Fig. 10(a) as a function of the time normalized by an oscillation period. The lines with circles represent the medial-lateral glottal width during opening and closing with the ordinate axis on the left showing the magnitude. The lines without symbols are the corresponding medial surface velocities as represented by the ordinate axis on the right. The dashed-dotted line identifies the contact phase when the VF was closed and the displacement and velocity were zero.

FIG. 10.

(Color online) The temporal change in (a) the glottal width and velocity calculated from the fitted curves to the extracted kymogram, and (b) the power per unit anterior-posterior length, at $2y/l_{g,l}=0.0$ during the glottal opening phase, closing phase, and contact.

At each of the anterior-posterior locations, the time-varying aerodynamic power per unit anterior-posterior length ($\dot{W}\prime$), denoted by the prime superscript, during opening and closing of the glottis was calculated by multiplying the VF surface velocity with the integral of the pressure between the inferior and superior margins of the glottis, according to

$${{\dot{W}}^{\prime }}_k(t)=v_g(t){\int }_{x_{{\text{inf}}_k}}^{x_{{\text{sup}}_k}}{p}_k(x,t)\hspace{0.17em}\mathrm{d}x,$$ (3)

where p(x,t) indicates the intraglottal pressure at the inferior-superior location of x at time t. The limits $x_{\text{inf}}$ and $x_{\text{sup}}$ denote the locations of the inferior and superior edges of the VF, which were estimated based on the pressure distributions during the opening and closing phases, using the method explained in Secs. III C 1 and III C 2. The subscript k varies from one to four and corresponds to the four anterior-posterior positions at which the pressure was acquired. When computing the power, it is implicitly assumed that the intraglottal pressure remains unchanged across the medial-lateral direction of the glottal channel. This is a simplification that neglects cross-channel pressure differences, which may arise due to flow separation, vortex propagation, etc. The contribution of this assumption to the overall measurement error is considered in the subsequent discussion on measurement uncertainty.

The time dependence of ${\dot{W}}^{\prime }$ at the midline of the VF is plotted in Fig. 10(b). During the glottal opening, the intraglottal power was initially positive because the spatial average of the intraglottal pressure was in phase with the surface velocity and they are both positive in magnitude, indicating the transfer of energy from the airflow to the VF. The power transfer became negative during the last 10% of the opening phase as the spatial average of the intraglottal gauge pressure became negative while the surface velocity was still positive, denoting that energy began to be transferred from the VF back to the fluid even as the glottis was still opening. This is a unique behavior that arises from the unsteady flow acceleration and is not captured by quasi-steady investigations. A discontinuity is observed in Fig. 10 when the VF transitioned from the opening to closing phase. This is due to the assumption that the medial surface velocity is equal to the velocity at the superior VF edge during opening and the inferior edge during closing. During the closing phase, both the intraglottal pressure and velocity were negative, which lead to a positive power transfer, indicating that the direction of the energy transfer was again from the fluid to the VF. The power initially increased during the closing phases; however, immediately preceding closure, the power rapidly decreased as seen in Fig. 9(d).

Although the mechanics of the energy transfer have been studied numerically,^5,54,89 computationally,³ and in driven synthetic VF models,¹⁷ they have never been explored experimentally in self-oscillating VFs. Comparison of the current measurements with prior investigations using a two-dimensional computational model³ and a driven synthetic VF model¹⁷ reveal similar behavior with an initially positive power transfer, which subsequently decreased, reaching a negative value as the glottis reached maximum opening [compare Fig. 10(b) to Fig. 12 in Ref. 3 and Fig. 13 in Ref. 17]. However, during the closing phase, the power in the computational and driven model investigations reached more negative values at the beginning of the closing phase and then increased, becoming positive only at the end of the closing phase. This difference is likely because both previous works computed the power transfer over the entire VF, whereas the current investigation only considered the power transfer within the glottis. One important feature of the power transfer, which was not captured by the computational and driven models, was the sharp drop in power immediately preceding the VF closure, which was due to the result of increased pressure losses arising from viscous effects as the glottal orifice becomes very small. This is likely because in the computational investigation,³ the collision phase was not modeled (i.e., the minimum medial-lateral glottal width was 0.2 mm), thereby likely altering the aerodynamic behavior during the glottal closure and subsequent opening. In the driven model,¹⁷ a Bernoulli flow assumption was used to obtain the pressure field, which neglected the viscous effects of the flow and was not able to predict the pressure rise at the end of the closing phase.

The variation of the intraglottal aerodynamic energy transfer as a function of the anterior-posterior position was also investigated. The aerodynamic energy transferred per unit anterior-posterior length ($W\prime$) during the opening and closing of one VF oscillation was calculated by integrating the power per unit length over time as

$${W^{\prime }}_k={\int }_{t_{i_k}}^{t_{e_k}}{{\dot{W}}^{\prime }}_k(t)\hspace{0.17em}\mathrm{d}t,$$ (4)

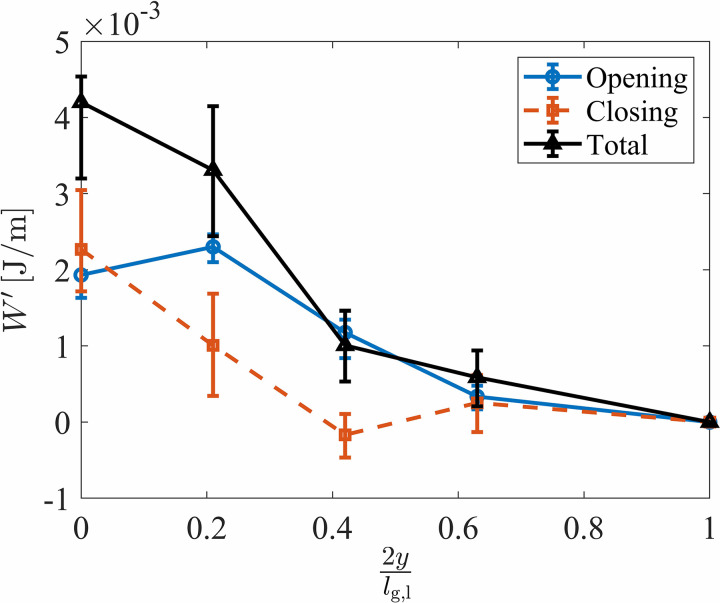
where t_i and t_e are the times corresponding to the start and end of the opening or closing of the glottis at the specified anterior-posterior location as denoted by the subscript k. The total aerodynamic energy per unit length at the four anterior-posterior directions is shown in Fig. 11 along with the respective contributions from the opening and closing phases. The total aerodynamic energy transfer was positive across the entire anterior-posterior length, indicating that throughout an oscillation cycle, net energy is transferred from the fluid to the VF across the anterior-posterior direction. However, the total energy per unit length decreased significantly from the midline to the anterior edge, indicating that the majority of the energy exchange occurs at the middle of the VFs. The total energy at the location of $2y/l_{g,l}=0.63$ was only 14% of the value at the midline. These findings further reinforce the importance of considering the three-dimensional effects.

FIG. 11.

(Color online) The aerodynamic energy per unit anterior-posterior length computed during the glottal opening and closing and the total aerodynamic energy transferred over the entire phonatory cycle as a function of the anterior-posterior location. The markers denote the mean value, and the bars indicate the error bounds.

It is interesting to note that while the midpoint experienced largely the same amount of positive energy transfer during both opening and closing, the more anterior locations exhibit a marked increase in energy transfer during the opening versus closing phases. The energy during opening increased from the midline to $2y/l_{g,l}=0.21$ because of the increased intraglottal pressure at this same location as observed in Figs. 7(a)–7(d). It is believed that this anterior-posterior variation in the intraglottal pressure was because of the three-dimensional flow behavior that occurred.

The total energy transferred to the VF within the glottis can be computed by assuming a linear variation between the energy at each anterior-posterior location, which goes to zero at the anterior-posterior edge, and integrating the energy over the anterior-posterior direction. Note that because the pressure field was assumed to be symmetric about the anterior-posterior midline, the energy was only computed over half of the VF length and then multiplied by two. The aerodynamic energy transfer, W, during the opening and closing phases, as well as the total amount were found to be

$$W_{\text{opening}}=17.52\hspace{0.17em}\hspace{0.17em}\mu \mathrm{J},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{W}_{\text{closing}}=8.29\hspace{0.17em}\hspace{0.17em}\mu \mathrm{J},W_{\text{Total}}=25.81\hspace{0.17em}\hspace{0.17em}\mu \mathrm{J},$$

respectively.

The net energy transfer was positive during both the opening and closing, which is in contrast with previous numerical³ and driven VF model¹⁷ observations, although only the intraglottal power transfer was considered in the current work. Nevertheless, these findings satisfy the required condition for obtaining self-sustained oscillations, i.e., the net energy to the VF must be positive during an oscillation cycle.⁵ The energy transfer per unit length at the anterior-posterior midline accounted for $\approx 45\%$ of the total energy transfer to the VFs with the middle third of the glottis accounting for over 80% of the total aerodynamic energy transfer. Whereas earlier work⁵⁷ has highlighted how the surface pressure is influenced by the anterior-posterior variations, the energy transfer is found to be even more centrally concentrated along the glottal midline as the result of the multiplicative relationship between the decreased pressure and surface velocity at the anterior-posterior endpoints. The concentration of the energy transfer in the middle of the VF also suggests that more energy is also dissipated along the midline, which coincides with where VF fatigue and damage are most likely to occur.^90,91 This may help explain the prevalence of some VF pathologies, such as polyps and nodules, in the mid anterior-posterior direction of the VFs.⁹²

The variation in energy transfer due to the inferior-superior VF limits over which the aerodynamic pressure is considered has implications for reduced-order VF models as well because, historically, they only consider the contribution to the intraglottal energy transfer from the medial-lateral force and velocity components⁹³ as in the current work. Discrepancies due to the approximation of the medial surface velocity in the current investigations are also likely to influence the energy exchange.

It is interesting to note that the aerodynamic power per unit anterior-posterior length [see Fig. 10(b)], when multiplied by the total glottal length of 17.0 mm, yields a maximum value of $\sim \mathcal{O}(0.01W)$, which is consistent with prior lumped-element modeling efforts.^54,89 Note that the work of Zañartu et al.⁸⁹ reports a similar value for the power transfer, which is shown in Fig. 5 of that article, although the associated text reports an incorrect value due to a typographical error. In addition, values reported in prior numerical³ and driven VF studies¹⁷ are of the same order of magnitude as those found in the current work. However, they report slightly higher values for the power transfer because they computed the power transferred over the entire VF inferior-superior thickness, whereas the current study only considers the power transfer within the glottis.

The total error of the energy calculations resulted from errors in the surface velocity estimation and intraglottal pressure measurements. The pressure measurement error was comprised of two parts. The inaccuracy consisted of the sensor calibration error, which was measured to be 0.03 kPa and is explained in Sec. II, and the error resulting from the difference between the measured pressure on the hemilaryngeal plate and the actual aerodynamic pressure on the surface of the VF. Studies with static VF models with a uniform glottis in a hemilaryngeal configuration⁹⁴ showed that the pressure along the VF surface was consistently lower than the pressure measured on the hemilaryngeal plate. This difference was shown to be as high as 10% of the subglottal pressure. In addition, flow separation may occur when the glottis forms a divergent profile, which changes the intraglottal pressure field.^21,46,48,51 Studies with static VF models with a 10° divergent glottal profile, which is approximately the maximum divergence angle observed in the current study, showed that the pressure change due to flow separation on the surface of the VFs was less than 5% of the subglottal pressure.³⁴ Therefore, the total error of the intraglottal pressure measurement can be conservatively estimated to be approximately 11% and 16% of the subglottal pressure during the opening and closing phases of the VF, respectively. The error in the VF surface velocity was a combination of the error caused by neglecting the inferior-superior velocity component, which was estimated to be less than 2%, and the error of tracking the medial edge of the VF using the method introduced above. The latter error was evaluated by changing the threshold of the pixel intensity used to identify the VF medial boundary and employing the acquired time-varying surface velocity at each threshold intensity value in the energy calculations. The resultant error was found to be approximately 13%. The total measurement error that the aforementioned parameters introduced into the energy calculations were computed and are presented with error bars in Fig. 11.

Finally, it should be reiterated that the current approach for investigating the role of the aerodynamic power transfer uses a physical, synthetic VF model in a hemilaryngeal orientation. Although the current models were designed to ensure robust contact, they still suffered from a small amount of out-of-plane anterior-posterior motion, which is a common challenge with silicone VF models. The subglottal pressure was also higher in magnitude than the normal speech configurations. This arose because of a combination of the hemilaryngeal arrangement, which is known to produce higher subglottal pressures, and the medial compression, which was applied to the physical models. The measurement of the intraglottal pressure along the medial wall also neglects the cross-channel pressure differences that may arise from flow separation, etc., as previously discussed. Consequently, whereas most of these effects are expected or shown to have a minor influence on the results, care should be taken to consider the results in the context of these assumptions.

IV. CONCLUSIONS

An investigation of the intraglottal aerodynamic pressure was performed with a synthetic self-oscillating VF model in a hemilaryngeal orientation. The key oscillation features of the model were found to have physiologically relevant values.

The intraglottal pressure distribution was found to be highly dependent on the unsteady and three-dimensional effects. The unsteady flow effects were reflected by the intraglottal gauge pressure becoming negative during the later stages of the glottal opening, a feature not captured by the prior static VF, steady-flow investigations. This influenced the energy exchange process, decreasing the total amount of energy transferred from the fluid to the VF during the opening phase.

The net aerodynamic energy transfer of the fluid to the structure was also positive during the closing phase, although it was less positive than during opening, thereby satisfying the necessary energy-exchange requirement for successful VF oscillation.⁵ Immediately preceding the VF closure, the energy exchange decreased precipitously as the intraglottal pressure increased as the result of viscous losses through the narrowing glottal aperture.

Significant variations in the intraglottal aerodynamic pressure were observed between the midline and the anterior locations along the VF surface. Similarly, the aerodynamic energy transfer varied in the anterior-posterior direction with over 80% of the aerodynamic energy transfer occurring over the middle third of the VF surface. This supports the idea that VF damage occurs along the middle third of the VF length because of the increased dissipation of energy within this region.