Recent Developments in Free Energy Calculations for Drug Discovery

Abstract

The grand challenge in structure-based drug design is achieving accurate prediction of binding free energies. Molecular dynamics (MD) simulations enable modeling of conformational changes critical to the binding process, leading to calculation of thermodynamic quantities involved in estimation of binding affinities. With recent advancements in computing capability and predictive accuracy, MD based virtual screening has progressed from the domain of theoretical attempts to real application in drug development. Approaches including the Molecular Mechanics Poisson Boltzmann Surface Area (MM-PBSA), Linear Interaction Energy (LIE), and alchemical methods have been broadly applied to model molecular recognition for drug discovery and lead optimization. Here we review the varied methodology of these approaches, developments enhancing simulation efficiency and reliability, remaining challenges hindering predictive performance, and applications to problems in the fields of medicine and biochemistry.

Introduction

Modern drug development requires screening over vast regions of chemical space to identify potential binders against a protein target. This approach is costly in time and material resources (DiMasi et al., 2016). Even after identification of potential ligands from initial screening assays, further refinement must be carried out to improve binding properties, ensure that off target effects are minimized, and optimize pharmacokinetic properties. Evaluation of binding free energies through virtual screening has shown promise in efficiently narrowing the chemical search space for candidate compounds and streamlining the process of lead compound optimization. Outside of the pharmaceutical field, binding affinity predictions find additional uses in protein engineering, and guide the rational design of mutations altering enzyme substrate/product specificity (Kaushik et al., 2018; Li Y. et al., 2019; Bhati et al., 2019; Ono et al., 2020; Chen et al., 2021), structural stability (Aldeghi et al., 2018; Jandova et al., 2018; Pourjafar-Dehkordi et al., 2019; Martin et al., 2020), and catalytic efficiency (Xue et al., 2019; Wang K. et al., 2020).

Here we discuss recent developments and applications of molecular dynamics to calculate absolute binding free energies in protein-ligand binding interactions. Through utilization of the Molecular Mechanics Poisson Boltzmann Surface Area (MM-PBSA) (Cheatham et al., 1998; Srinivasan et al., 1998; Kollman et al., 2000; Gohlke and Case, 2004; Yang et al., 2011; Miller et al., 2012; Wang et al., 2016; Wang et al., 2018a), Linear Interaction Energy (LIE) (Aqvist et al., 1994; Aqvist and Marelius, 2001; Aqvist et al., 2002; Gutierrez-de-Teran and Aqvist, 2012), and absolute alchemical methods (Kirkwood, 1935; Zwanzig, 1954; Kirkwood, 1967; Bennett, 1976; Straatsma and McCammon, 1991; Gilson et al., 1997; Boresch et al., 2003; Shirts, 2012), researchers are able to evaluate biomolecular interactions that drive molecular recognition at atomic resolution and derive accurate predictions for binding free energies. These methods rigorously account for conformational dynamics and solvent interactions that are key to protein-ligand interactions and absent in coarser-grained approaches such as ligand docking. The value in these methods for advancing drug discovery is highlighted by their widespread application. Within the last 20 years the number of citations for each method has grown from a small handful to several thousand, notably the MM-PBSA method was found in over 2,000 citations in the last year (Figure 1). These three methods differ in their treatment of solvent and required simulation data, either involving only the end point states of bound and unbound species, or demanding simulation of a complete binding pathway traversing intermediate states between the end points for determination of binding free energy. These differences result in trade-offs between predictive accuracy and computational cost that must be weighed by the user to select the best approach for their application. In this review, discussion of approaches for the calculation of relative binding free energies is skimmed over as having been recently reviewed elsewhere (Cournia et al., 2017; Song and Merz, 2020). We focus on describing the fundamental principles of each method, recent developments enhancing their usability by improving accuracy and computational efficiency, and successful applications in drug discovery projects.

FIGURE 1.

Citation counts for each method over the past 20 years. The development and utilization of molecular simulation to guide drug discovery has grown dramatically in recent years. The MM-PBSA method, which balances simulation rigor, high speed, and minimal setup complexity to allow high throughput screening, has seen extensive application reaching over 2,000 citations in 2020. Steep computational costs and challenges in generalizing protocols to work on broad sets of protein-ligand systems have limited the usage of absolute alchemical and LIE based approaches.

Free Energy Calculation Approaches

Molecular Mechanics Poisson Boltzmann Surface Area

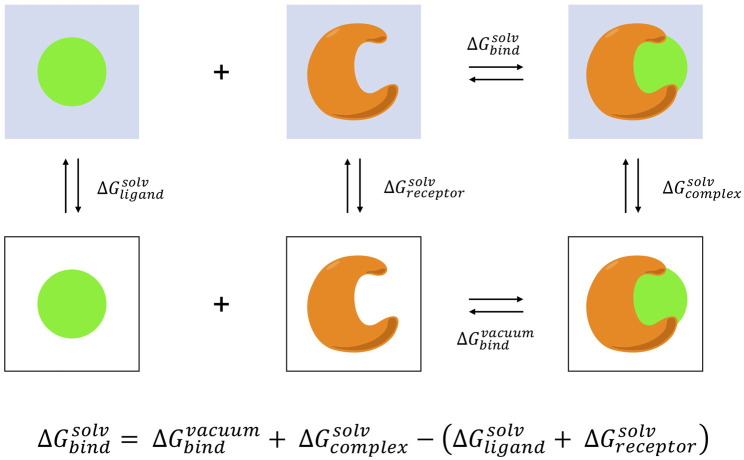
The MM-PBSA method as applied to small molecule binding is an end-point method estimating the binding free-energy difference between the protein-ligand complex and the separate unbound components, the complex, ligand, and protein alone (Sharp and Honig, 1990; Cheatham et al., 1998; Srinivasan et al., 1998; Kollman et al., 2000; Gohlke and Case, 2004; Yang et al., 2011; Miller et al., 2012; Genheden and Ryde, 2015; Wang et al., 2016; Wang et al., 2019a) (Figure 2). MM-PBSA provides a balanced approach characterized by improved rigor and accuracy over molecular docking, and with reduced computational demands compared to pathway methods such as alchemical transformations that require involved experimental setup to sample intermediate states through the decoupling of ligand interactions (Rastelli et al., 2010; Hou et al., 2011; Slynko et al., 2014; Sun et al., 2014). In addition to only requiring end-point data, a further approximation with MM-PBSA that enables efficient free-energy calculation is the utilization of implicit solvation. By coarse-graining solvent as a continuum with uniform dielectric constant the treatment of solvent interactions is greatly simplified. However, this may lead to difficulties modeling highly charged ligands and recent works have focused on minimizing these errors (Wang et al., 2019a).

FIGURE 2.

MM-PBSA thermodynamic cycle. The binding free energy in aqueous environment is calculated as the difference between the sum of binding in vacuum and solvating the complex with solvating the receptor and ligand individually. The information necessary to complete this cycle can be obtained by decomposing a single trajectory into the ensemble desolvated receptor, ligand, and complex configurations, and computing the solvation free energies for each state with the Poisson-Boltzmann equation. Normal mode analysis can be performed to determine the contribution of entropy to the binding process.

Two main approaches are employed to generate the data for MM-PBSA binding energy predictions with both starting from molecular dynamics (MD) simulation in explicit solvent: multiple trajectories with the three components, complex, apo receptor, and ligand separately, or a single trajectory with the bound protein-ligand complex that is divided into the three components afterward (Kollman et al., 2000; Wang et al., 2016). MD is carried out with explicit solvation to maximize accuracy of conformational sampling, and frames are post-processed by removal of solvent and ion molecules. The converged trajectory is evaluated with each frame as an individual sample point to generate ensemble averages and uncertainty values for the energy quantities. The single-trajectory approach is favored for its straightforward implementation and cancellation of covalent energy errors as conformations for the complex and separated receptor and ligand are based on shared configurations. However, the single-trajectory method may not be optimal due to its reliance on the problematic assumption that ligand binding does not involve large-scale conformational changes (Lee and Olson, 2006; Wang et al., 2016). The multi-trajectory approach is better suited for binding events associated with large conformation changes, but is noted to produce noisier estimates and require longer simulation time to reach convergence as the complex and individual components can sample diverged conformations (Swanson et al., 2004; Yang et al., 2011).

The binding free energy between the ligand (L) and receptor (R) is defined as:

$$\Delta G_{bind}=G_{RL}-G_R-G_L$$

The difference in free energy between the complex and individual components can be decomposed into enthalpic (ΔH) and entropic (-TΔS) terms evaluating changes in bonding interactions and conformational disorder with binding. The enthalpic energy term can be approximated as the gas-phase molecular mechanics energy (ΔE_MM) and solvation free energy (ΔG_solv). The configurational entropy (−TΔS) can be estimated with the normal mode or quasi-harmonic analysis (Yang et al., 2011; Kassem et al., 2015), but is often omitted due to high computational cost and difficulty obtaining convergence.

$$\Delta G_{bind}=\Delta H-T\Delta S\approx \Delta E_{MM}+\Delta G_{solv}-T\Delta S$$

ΔE_MM is computed from the molecular mechanics force field and consists of the covalent energy (ΔE_covalent), electrostatic energy (ΔE_elec), and van der Waals dispersion and repulsion energy (ΔE_vdW). The covalent term includes changes in bonds (ΔE_bond), angles (ΔE_angle), and torsion (ΔE_torsion) energies.

$$\Delta E_{MM}=\Delta E_{\mathrm{cov}alent}+\Delta E_{elec}+\Delta E_{vdW}$$

$$\Delta E_{\mathrm{cov}alent}=\Delta E_{bond}+\Delta E_{angle}+\Delta E_{torsion}$$

ΔG_solv describes the contribution of polar and non-polar interactions to the transfer of the ligand from gas phase to solvent. The polar solvation component (ΔG_polar) specifies the interaction energy of the solute’s charge distribution in the continuum solvent and is found by evaluation of the Poisson-Boltzmann equation (PBE) (Perutz, 1978; Warwicker and Watson, 1982; Bashford and Karplus, 1990; Davis and McCammon, 1990; Jeancharles et al., 1991; Gilson, 1995; Honig and Nicholls, 1995; Edinger et al., 1997; Luo et al., 1997; Luo et al., 2002; Sharp and Honig, 2002; Lu and Luo, 2003; Tan et al., 2006; Cai et al., 2009; Wang et al., 2009; Ye et al., 2009; Cai et al., 2010; Wang et al., 2010; Wang and Luo, 2010; Ye et al., 2010; Cai et al., 2011; Hsieh and Luo, 2011; Botello-Smith et al., 2012; Wang et al., 2012; Liu et al., 2013; Wang et al., 2013; Wang et al., 2017). The non-polar solvation term (ΔG_non-polar) measures the energy from the solute forming a cavity in the solvent and the van der Waals interactions at the cavity interface between solute and solvent (Wagoner and Baker, 2006; Tan et al., 2007), so that the total solvation free energy can be expressed as:

$$\Delta G_{solv}=\Delta G_{polar}+\Delta G_{non-polar}$$

The basis of the PBE is the Poisson equation with dielectric distribution ε(r), electrostatic potential distribution φ(r), and fixed atomic charge density ρ(r), where each function is dependent on the solute atom position vector (r).

$$\mathrm{\nabla }\epsilon \left(r\right)\mathrm{\nabla }\phi \left(r\right)=-4\pi \rho \left(r\right)$$

To account for electrostatic interactions from ionic salt molecules in the solution, the electrostatic potential (φ(r)) is solved with the PBE with the additional terms λ(r) representing the ion-exclusion function set to 0 inside the Stern layer and molecular interior and 1 outside, and salt-related term f(φ(r)) that depends on the electrostatic potential, the valence (z_i), electron charge (e), bulk concentration (c_i), and temperature (T), with summation over all ion types (i).

$$\mathrm{\nabla }\epsilon \left(r\right)\mathrm{\nabla }\phi \left(r\right)+\lambda \left(r\right)f\left(\phi \left(r\right)\right)=-4\pi \rho \left(r\right)$$

$$f\left(\phi \left(r\right)\right)=4\pi {\displaystyle \sum _i^n{z}_{i}e{c}_i}\exp \left(-\frac{z_{i}e\phi \left(r\right)}{k_{B}T}\right)$$

The PBE can be linearized for easier numerical computation under conditions where the ionic strength and electric field are both weak. The linear PBE equation includes the modified Debye-Hückel parameter (κ²), solvent dielectric constant (ε_solv), and solution ionic strength (I) where I = z²c.

$$\mathrm{\nabla }\epsilon \left(r\right)\mathrm{\nabla }\phi \left(r\right)-{\epsilon }_{solv}{k}^2\phi \left(r\right)=-4\pi \rho \left(r\right)$$

$$k^2=\frac{8\pi e^{2}I}{{\epsilon }_{solv}{k}_{B}T}$$

MM-PBSA is often used in tandem with the closely related Molecular Mechanics Generalized Born Surface Area (MM-GBSA) approach as both utilize the same set of inputs for the prediction of binding free energies with continuum solvation (Chen et al., 2016; Wang et al., 2019b). The difference between the methods lies in the calculation of ΔG_polar where the GB model is based on an analytical expression approximating the PBE. This leads to large speed improvements, but predictive performance is generally reduced compared to PBE, though this is system dependent (Genheden and Ryde, 2015; Chen et al., 2016). The GB equation is composed of terms describing solute atoms as spheres with partial charge (q), internal dielectric (ε) and solvent dielectric (ε₀), distance between particles i and j (r_ij), and the effective Born radius (α).

$$\Delta G_{GB}=-\left(\frac{1}{\epsilon }-\frac{1}{{\epsilon }_0}\right){\displaystyle \sum _{i,j}\frac{q_i{q}_j}{f_{GB}}}$$

$$f_{GB}=\sqrt{r_{ij}^2+{\alpha }_i{\alpha }_j\exp \left(-\frac{r_{ij}^2}{4{\alpha }_i{\alpha }_j}\right)}$$

ΔG_non-polar has classically been determined as proportional to the solute’s solvent accessible surface area (SASA) (Wagoner and Baker, 2006; Tan et al., 2007) as:

$$\Delta G_{non-polar}^{SA}=\gamma \ast SASA+b$$

The surface tension constant (γ) describing the free energy of forming a cavity in water and the offset (b) are determined empirically and set as constants for all solute molecules. These variables are assigned as γ = 0.00542 kcal/mol-A² and b = 0.92 kcal/mol in the AMBER package (Case et al., 2005; Miller et al., 2012; Case et al., 2020). Alternative methods with atom-specific surface tension constants have also been explored (Eisenberg and McLachlan, 1986; Ooi et al., 1987).

More updated methods to resolve ΔG_non-polar incorporate the van der Waals dispersion free-energy as a separate term, treating the process as two events where a cavity is created and the non-polar solute is inserted into the cavity (Tan et al., 2007). The separation of terms additionally allows individual scaling of the cavity formation and dispersion terms as a function of solute size. ΔG_cavity is calculated with similar linear regression as the classical ΔG_non-polar equation with SASA replaced with solvent accessible volume (SAV) and the attractive dispersion energy is computed through surface-integration. The updated scaling factors are set as γ = 0.0378 kcal/mol-A³ and b = -0.569 kcal/mol in the AMBER package (Case et al., 2005; Miller et al., 2012; Case et al., 2020).

$$\Delta G_{non-polar}^{CD}=\Delta G_{dispersion}+\Delta G_{cavity}$$

$$\Delta G_{cavity}=\gamma \ast SAV+b$$

Molecular Mechanics Poisson Boltzmann Surface Area Developments and Benchmarks

Improvements to the MM-PBSA method include more rigorous treatment of the dielectric constants and electrostatic polarization for better predictive accuracy on highly charged ligands, faster PB solvers, extension to pKa calculation, and novel schemes for determination of entropy. Scaling of the solute dielectric constant to tune the screening of electrostatic interactions in the non-polar protein environment is found to have a critical, receptor-dependent role on predictive accuracy (Hu and Contini, 2019). Heterogenous dielectric values are applied to implicit membrane models where the dielectric is discretely varied with membrane depth (Greene et al., 2019), and with Gaussian dielectric to smoothly distribute the interface over protein cavities (Hazra et al., 2019). Integration of a Gaussian based model for molecular volume and surface area determination with the Gaussian dielectric distribution removes sharp surfaces separating the solute and solvent for a surface free approach to MM-PBSA calculation (Chakravorty et al., 2019). Electronic polarization effects can be incorporated through the use of polarizable force fields such as AMOEBA, this is implemented in the boundary integral PBE solver PyGBe (Cooper, 2019). Combination of the polarizable Drude oscillator force field with PBSA lowers RMSE from 2.5 kcal/mol with the standard CHARMM36 force field to 0.8 kcal/mol in calculation of solvation free energies for 70 molecules in addition to reducing errors in alanine scanning (Aleksandrov et al., 2018). Coupling PBE calculation with Monte Carlo sampling of protonation states is applied to estimation of protonation free energies leading to pKa values within 2.05 pKa units RMSE of experiment using the Drude-PB method and within ∼0.8 pKa units RMSE using PypKa. (Aleksandrov et al., 2020; Reis et al., 2020). There are also updates to the PBE solvers through geometric multigrid on CPU allowing massively parallel scaling to 100 CPUs and a grid size of 10⁹ (Womack et al., 2018) and GPU implementation leading to ∼100 times speed up compared to CPU (Qi and Luo, 2019). Introduction of analytical interface and surface regulation for the immersed interface method is proposed to improve stability and convergence and GPU implementation leads to 20 times speed up (Wei et al., 2019b). Regularization methods are investigated under the matched interface and boundary framework for proper treatment of charge singularities for higher numerical accuracy (Lee et al., 2021). Finally extensions of the harmonic average method are proposed for fully taking advantage of the dense data parallelism to enhance the performance of PBE solvers on GPU platforms (Wei et al., 2019a). Ensemble MM-PBSA calculation through use of multiple independent trajectories and maintenance of an explicit ligand hydration shell on the bromodomain-containing protein 4 system, a key regulator of transcription, showed robust reproducibility (Wright et al., 2019). Menzer et al. (2018) implement a confining potential on ligand external degrees of freedom and higher order cumulant expansion terms for average receptor-ligand interaction energies for more effective treatment of entropy.

A number of recent benchmarks identify best-practices to achieve optimal accuracy and directly compare MM-PBSA with other binding free energy prediction methods to highlight its advantages and disadvantages in drug discovery. When testing of MM-PBSA was performed on over 250,000 ligands for the GPCR superfamily following docking (Yau et al., 2019; Yau et al., 2020), utilization of a single energy minimized structure is found to be the most computationally efficient method for virtual screening. In prediction of binding free energies and correct binding pose from 55 protein-RNA complexes, MM-PBSA (r_p −0.510) shows slightly lower performance than MM-GBSA (r_p −0.557) (Chen F. et al., 2018). Molecular mechanics 3-dimensional reference interaction site model (MM-3D-RISM) is shown to have similar predictive performance as MM-PBSA, but differs in decomposition of polar and non-polar solvation energies (Pandey et al., 2018). Mishra and Koca (2018) investigate the effects of simulation length, VDW radii sets, and combination with QM Hamiltonian on MM-PBSA predictions of protein-carbohydrate complexes. The conditions with optimal agreement to experiment are found to be 10 ns simulation with the mbondi radii set, and PM6 DFT method with QM resulting in the highest correlation of 0.96. Entropic effects are further studied by Sun et al. (2018) through comparison of normal mode analysis (NMA) and interaction entropy on over 1,500 protein-ligand systems with varying force fields. The most accurate results are obtained with the truncated NMA method, but due to high computational costs the authors recommend the interaction entropy approach instead, and force field choice made only minor differences. Enhanced sampling methods including aMD and GaMD are compared to conventional MD with MM-PBSA on protein-protein recognition, although the enhanced sampling methods are beneficial in encouraging exploration of conformational space, they do not improve binding affinity predictions on the timescales tested (Wang et al., 2019b). The effect of including a small number of explicit water molecules and performing NMA for entropy calculation is examined for the bromodomain system (Aldeghi et al., 2017). Using a limited number of solvent molecules (∼20) and entropy estimate improved MM-PBSA accuracy, although performance does not surpass absolute alchemical approaches the results came at significantly lower compute requirements.

The ease of performing MM-PBSA analysis and balance of speed and accuracy make it a popular method to use as an initial filter to rank drug candidates. Estimation of binding affinities with MM-PBSA for small-molecule protein-protein interaction inhibitors is automated with the farPPI web server (Wang Z. et al., 2019) and prediction of changes in protein-DNA binding affinities upon mutation with the Single Amino acid Mutation binding free energy change of Protein-DNA Interaction (SAMPDI) web server (Peng et al., 2018). Furthermore, due to its reliability MM-PBSA is often used as a baseline comparison or in combination with alternative methods for higher performance. Machine learning methods based on extracting protein-ligand interaction descriptors as features from MD simulation are compared to MM-PBSA on the tankyrase system (Berishvili et al., 2019). Machine learning also accelerates pose prediction methods based on short MD simulation combined with MM-PBSA through the Best Arm Identification method to obtain the correct binding pose with minimal number of runs (Terayama et al., 2018). QM approaches allow more accurate consideration of nonbonded electrostatic interactions, but their usage is limited by high computational costs. This problem is addressed through fragment-based methods where localized regions of the protein-ligand system are treated with QM and the more global effects of solvation, entropy, and conformational sampling are evaluated through MM-PBSA analysis (Wang Y. et al., 2018; Okimoto et al., 2018; Okiyama et al., 2018; Okiyama et al., 2019).

LIE

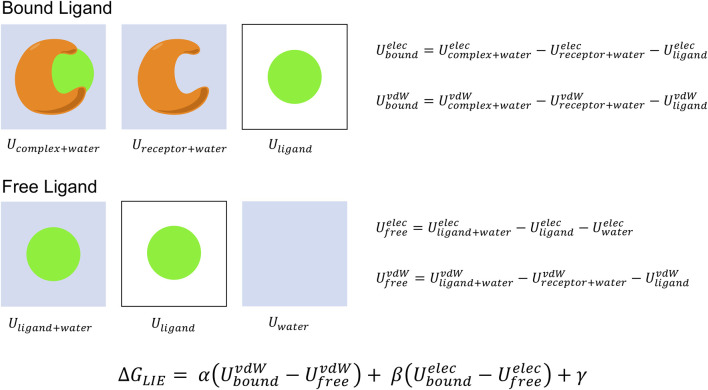
The Linear Interaction Energy (LIE) approach is another end-point method that predicts absolute binding free energies based on the change in free-energy from transferring the ligand from the solvated receptor-bound state to the aqueous free state (Aqvist et al., 2002; Gutierrez-de-Teran and Aqvist, 2012) (Figure 3).

$$\Delta G_{bind}\left(lig\right)=\Delta G_{solv}^{bound}\left(lig\right)-\Delta G_{solv}^{free}\left(lig\right)$$

FIGURE 3.

LIE binding free energy calculation. The binding free energy is computed from force field energy estimates of the differences in van der Waals and electrostatic energies for the ligand bound to the protein and free in solvent environment. The system dependent LIE parameters α and β are empirically determined and used to scale the non-polar and coulombic interaction energies to have minimal error with respect to available experimental data. The final term γ acts as an optional offset parameter to further tune the model. LIE requires no post-processing and can be completed from a single trajectory.

This process considers binding in terms of the van der Waals (vdW) energy from creating the cavity in the target environment for the ligand and the electrostatic energy between the molecule and the environment. With that objective, LIE estimates ΔG_bind by an ensemble approach where two MD simulations are performed, with the ligand bound in the solvated protein and ligand free in solution, and the difference in VDW and electrostatic interactions between the ligand and environment in each case is measured (Aqvist et al., 1994; Hansson et al., 1998; Aqvist and Marelius, 2001).

$$\Delta G_{bind}=\left(\Delta G_{bound}^{polar}-\Delta G_{free}^{polar}\right)+\left(\Delta G_{bound}^{non-polar}-\Delta G_{free}^{non-polar}\right)=\Delta \Delta G_{bind}^{polar}+\Delta \Delta G_{bind}^{non-polar}$$

The molecular mechanics force field applied in MD provides potential energies (U) composed of polar and non-polar components that can be converted into free-energies. The linear response approximation where averages of the electrostatic interaction energies between the ligand and environment is utilized to determine the polar term. The second term ${\langle U_{lig-env}^{elec}\rangle }_{off}$ representing the potential electrostatic energy from conformations sampled with interactions between ligand and environment turned off is a negligible constant, and is generally ignored (Gutierrez-de-Teran and Aqvist, 2012).

$$\Delta G_{solv}^{elec}=\frac{1}{2}\left\{{\langle U_{lig-env}^{elec}\rangle }_{on}+{\langle U_{lig-env}^{elec}\rangle }_{off}\right\}=\frac{1}{2}{\langle U_{lig-env}^{elec}\rangle }_{on}$$

The scaling factor ½ is replaced with the variable β, and the polar component for LIE free-energy calculation considering bound and free ligand simulation is:

$$\Delta G_{bind}^{polar}=\beta \left({\langle U_{lig-env}^{elec}\rangle }_{bound}-{\langle U_{lig-env}^{elec}\rangle }_{free}\right)=\beta \Delta \langle U_{lig-env}^{elec}\rangle$$

Non-polar interactions including hydrophobic packing and van der Waals interactions are derived from the Lennard-Jones potential force field term. Due to the observed linear correlation of solvation free energies for non-polar compounds with solute size, and similar linear scaling for average van der Waals interaction energies with solute size, LIE assumes that average van der Waals energies can be directly employed to capture non-polar binding contributions with a similarly formed estimate as the polar component (Aqvist et al., 1994).

$$\Delta G_{bind}^{non-polar}=\alpha \left({\langle U_{lig-env}^{vdW}\rangle }_{bound}-{\langle U_{lig-env}^{vdW}\rangle }_{free}\right)=\alpha \Delta \langle U_{lig-env}^{vdW}\rangle +\gamma$$

The set of three empirical parameters: α to scale the vdW interaction energies (Wang et al., 1999), β to scale coulombic interaction energies (Åqvist and Hansson, 1996; Hansson et al., 1998), and γ as an optional offset constant (Almlof et al., 2004), are all freely tunable. These parameters are known to be system dependent and must be calibrated based on available experimental data (Almlof et al., 2007; van Dijk et al., 2017). Scaling of the model parameters is assumed to account for factors known to impact ΔG_bind but that are not explicitly declared including intramolecular energies, entropic confinement, desolvation effects, etc. The completed LIE estimation is based on force-field averaged energies and enables calculation of binding free energies solely through sampling of potential energies between the ligand and solvent or protein environments without post-processing

$$\Delta G_{bind}=\alpha \Delta \langle U_{lig-env}^{vdW}\rangle +\beta \Delta \langle U_{lig-env}^{elec}\rangle +\gamma$$

LIE Developments and Benchmarks

As the least computationally expensive method, LIE is uniquely suited for high-throughput screening and recent efforts are devoted toward the direction of improving predictive accuracy, even if the calibrated parameters are system dependent. To this end, multiple alterations to the base LIE protocol are proposed to more rigorously account for polar and entropic interactions by including additional terms, combining LIE results with PBSA (Huang et al., 2020) or alchemical calculations, and utilizing ensemble docking poses with iterative LIE models. The extended linear interaction energy method (ELIE) introduced by He et al. includes the PBSA terms for the polar solvation energy, non-polar solvation energy, and entropic contribution and individual scaling factors for each (He et al., 2019). Performance of ELIE in the Cathepsin S D3R 2017 Grand Challenge is found to show improved RMSE (1.17 kcal/mol) compared to MM-PBSA (3.19 kcal/mol) (He et al., 2019). Further benchmarking on 8 drug targets with a series of congeneric ligands to examine the application of ELIE to drug lead optimization demonstrates that ELIE (0.94 kcal/mol RMSE) can approach the accuracy of Free Energy Perturbation (FEP)/Thermodynamic Integration (TI) (1.08/0.96 kcal/mol RMSE) methods when using receptor-specific parameters. The authors find that 25 ns MD simulations show optimal accuracy as it generally decreases with longer simulation (Hao et al., 2020). The performance of LIE in host-guest systems is also evaluated on 4 host families (cucurbiturils, octa acids, β-cyclodextrin) with an array of 49 chemically diverse guests. The base LIE is modified to include host strain energy, and parameters are found to be transferable between the different host systems, notably resulting in binding predictions with RMSE below 1.5 kcal/mol through only a few nanoseconds of simulation (Montalvo-Acosta et al., 2018). Ngo et al. estimate HIV-1 protease inhibitor binding affinities with a modified LIE that includes a polar interaction term obtained from PBE, training on 22 samples and testing on a set of 11 ligands demonstrates good performance with 1.25 kcal/mol RMSE and 0.83 Pearson correlation (Ngo et al., 2020a). Proteins with flexible active sites may bind ligands in multiple orientations, this requires estimation of binding affinity from multiple poses weighted by their frequency to account for the contributions from each potential binding mode. Rifai et al. evaluate binding of inhibitors to malleable Cytochrome P450s with an iterative weighing approach where each training compound is sampled with multiple simulations starting from different binding poses and LIE parameters are determined from Boltzmann weighing individual trajectory results (Rifai et al., 2020). Further accuracy is obtained by combining LIE with alchemical simulations to consider the ligand solvation free energies. Direct comparison of LIE with MM-PBSA on the SIRT1 system with a set of 27 inhibitors finds that both methods produce comparable Pearson correlations of 0.72 for LIE and 0.64 for MM-PBSA indicating good predictive value in ranking inhibitors, LIE is advantageous in requiring shorter simulation due to slow convergence of the MM-PBSA polar term (Rifai et al., 2019). The two-domain LIE (2D-LIE) approach is introduced to predict the binding free energy between protein domains and applied to computing cellulase kinetics (Schaller et al., 2021).

Absolute Alchemical Simulations

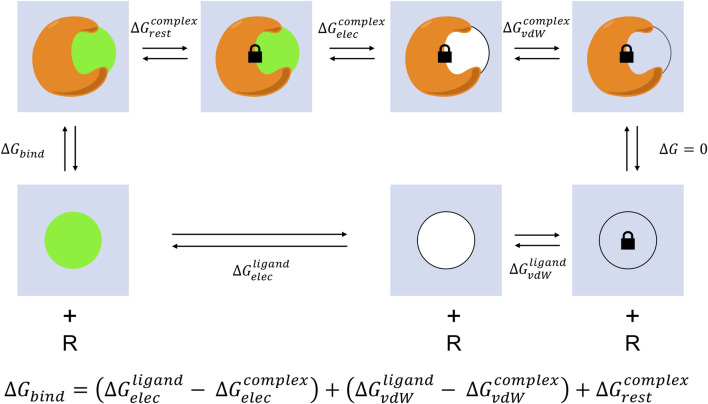
End-point free energy prediction methods generally lack the ability to account for entropic and solvent effects, which play significant roles in protein-ligand interactions (Mobley and Dill, 2009), except for methods that explicitly compute end-state free energies such as the Mining Minima method (Head et al., 1997; Luo et al., 1999; Luo and Gilson, 2000; Mardis et al., 2001; Chen et al., 2004; Chang et al., 2007; Moghaddam et al., 2011). Capturing receptor conformation changes driven by ligand binding, water-mediated hydrogen-bonding, or solvent exchange that occurs as the ligand crowds the binding pocket are critical to rigorously estimate the free energy difference between the ligand bound and unbound states (Mobley et al., 2007). Pathway simulations tracking the MD trajectory of the ligand binding or unbinding event enable the computing of these effects, but come at high computational cost and increased simulation complexity (Woo and Roux, 2005; Lee and Olson, 2006; Gan and Roux, 2009) (Figure 4). The most direct approach to account for entropy and solvent effects in binding would be to simulate the receptor (R) and ligand (L) together and count the frequency of bound (RL) and unbound (R + L) conformations.

$$R+L\rightleftharpoons RL$$

FIGURE 4.

Absolute alchemical simulation thermodynamic cycle. Two trajectories are completed to model the unbinding process. The simulations start from the complex of protein-ligand bound and end with receptor and unbound ligand (top track), and from ligand alone in solvent to ligand removed (bottom track). The ligand is transformed through a series of unphysical states to decouple electrostatic and van der Waals interactions with the surrounding environment to reach the final state where it no longer interacts with the initial system. The binding free energy prediction is the sum of the coulombic and non-polar energies involved in the transformation eliminating protein-ligand interactions. A restraint is typically included to prevent the ligand from exiting the active site while the binding interactions keeping the protein and ligand together are scaled off in order to aid convergence, this is corrected for with an additional transformation progressively turning on the restraints for the complex track and an analytical correction for the ligand track.

The ratio of bound to unbound states is an equilibrium constant (K_eq) that can be input into the Gibbs free energy equation where the Boltzmann constant (k_b) and temperature (T) are multiplied with the natural log of K_eq to calculate the binding free energy (ΔG_bind).

$$K_{eq}=\frac{\left[RL\right]}{\left[R\right]\left[L\right]}$$

$$\Delta G_{bind}=-k_{b}T\ln K_{eq}$$

In practice, it is not possible to estimate the equilibrium constant as the binding and unbinding events rarely occur within the timescales accessible with current simulation methods, leading to insufficient sampling. To bypass this sampling limitation, alchemical approaches modeling the gradual decoupling of electrostatic and van der Waals interactions between the ligand and receptor have been utilized to simulate the transition between ligand bound and unbound states without the need to physically capture the process (Zwanzig, 1954). The basis of this calculation is the thermodynamic cycle describing in one leg the removal of ligand from the complex, and in a parallel leg the removal of the ligand from solvent (Boresch et al., 2003). The end states with receptor alone and solvent alone interconvert with zero free energy difference as the ligand is absent from both systems, leaving the last transition between ligand in solvent to ligand bound to receptor solvable with knowledge of the free energy costs in transferring the ligand out of the receptor and out of solvent. This is typically performed through the Zwanzig equation also known as Exponential Averaging (EXP) or Free Energy Perturbation (FEP).

$$\Delta {\text{G}}_{\text{AB}}=-k_{b}T\ln {\langle -\frac{1}{k_{b}T}\left(U_B-U_A\right)\rangle }_A$$

EXP calculates the difference in potential of the end states using the ensemble of one simulated end state; however, this method is susceptible to bias in the free energies estimated due to poor phase space overlap of the end states (Lu et al., 2003).

Since free energy is a state function, its difference between states in the closed thermodynamic cycle is independent of the pathway taken, this includes non-physical intermediates that cannot be observed experimentally. The sampling of non-physical intermediate states is described by the parameter λ spanning from 0 where no perturbation has occurred to 1 where the ligand is fully decoupled from the environment and gives rise to the name alchemical. A drawback of the approach is the need for many intermediate states to guarantee accuracy of the simulation. The potential energies are computed for each intermediate state, and the free energy differences are calculated through thermodynamic integration by evaluating the integral of the ensemble averaged derivatives of potential energy with respect to λ (Kirkwood, 1935; Kirkwood, 1967; Shirts and Pande, 2005; Bruckner and Boresch, 2011b; a;de Ruiter et al., 2013).

$$U\left(\lambda \right)=\lambda U_0+\left(1-\lambda \right)U_1$$

$$\Delta G={\int }_0^1<\frac{d{U}_{\lambda }}{d\lambda }{>}_{\lambda }d\lambda$$

Standard alchemical transformations are carried out in two stages, first with scaling ligand atom partial charges to model decoupling of electrostatics, and next with the van der Waals interactions (Shirts, 2012; Klimovich et al., 2015). These two transformations are performed separately to avoid singularity artifacts that arise from atomic overlap created by strong attractive electrostatic interactions drawing atoms lacking steric bulk over others (Beutler et al., 1994; Klimovich et al., 2015). It is also necessary to utilize an alternative “softcore” Lennard-Jones potential coupled to the λ window during the van der Waals scaling. Linear scaling with the standard Lennard-Jones potential leads to numerical instabilities at λ endpoints due to the severe repulsive forces calculated on overlapping atoms and contributes to poor phase space overlap with neighboring windows (Steinbrecher et al., 2007; Steinbrecher et al., 2011). An example “softcore” potential is illustrated as a function of the λ window and configuration (x), and contains the tunable parameters α, m, n, and standard terms for the distance where the pair-wise potential is 0 (σ) and the distance separating the atoms (r) (Hornak and Simmerling, 2004; Steinbrecher et al., 2011; Giese and York, 2018).

$$U\left(\lambda ,x\right)=4\epsilon {\lambda }^n\left[{\left(\alpha {\left(1-\lambda \right)}^m+{\left(\frac{r}{\sigma }\right)}^6\right)}^{-2}-{\left(\alpha {\left(1-\lambda \right)}^m+{\left(\frac{r}{\sigma }\right)}^6\right)}^{-1}\right]$$

Further considerations involving the direction of the alchemical transformation, the utilization of restraints, the treatment of charge neutralization, λ window scheduling, procedure to select data samples that are both uncorrelated and equilibrated, and method to calculate free energy differences between the intermediate states must be made to ensure simulation stability and minimize variance in final free energy determination with the alchemical perturbation. The above factors all play some roles in the accuracy of the simulated free energies but are often not easy to decide a priori. Sampling of the physiologically relevant binding pose is essential to obtaining accurate values, initializing the alchemical transformation from an experimentally determined complex and modeling ligand decoupling generally maintains the ligand in the most applicable configurations (Klimovich et al., 2015). Theoretically there should be no difference beginning from the opposite end point state with an empty active site and having the ligand grown in; however, this may require longer simulation time as the ligand can easily get trapped in local minima away from the true binding pose and sample irrelevant states. The ligand may leave the binding pocket as the interactions with the receptor are scaled, hindering convergence (Mobley et al., 2006).

This is prevented by attaching restraints, which are later corrected for with an additional penalty term, to hold the ligand in the binding pocket. Two types of restraint schemes are common, the first involves imposing a single virtual bond between the ligand and receptor which is analytically corrected for by the formula

$$\Delta G_{restra\mathrm{int}}=-k_{b}T\ln \left[\frac{8{\pi }^2{V}^0{K}_r^{1\text{/}2}}{{\left(2\pi k_{b}T\right)}^{1\text{/}2}}\right]$$

where V⁰ is the standard state volume and K_r the force constant (Roux et al., 1996; Gilson et al., 1997; Mann and Hermans, 2000; Harger et al., 2017). An alternative restraining approach, the 6DOF method introduced by Boresch et al. (Boresch et al., 2003), enforces stricter adherence to a defined pose through one distance, two angular, and three dihedral restraints. Restraining the ligand to a single orientation expedites convergence, but may frustrate sampling of appropriate conformations not directly captured in the crystal structure, leading to overestimation of binding affinities (King et al., 2021). The 6DOF restraint correction is calculated with the following equation

$$\Delta G_{restra\mathrm{int}}^{6DOF}=-k_{b}T\ln \left[\frac{8{\pi }^2{V}^0{\left(K_r{K}_{\theta A}{K}_{\theta B}{K}_{\varphi A}{K}_{\varphi B}{K}_{\varphi C}\right)}^{\frac{1}{2}}}{r_{a,A,0}^2\sin {\theta }_{A,0}\sin {\theta }_{B,0}{\left(2\pi k_{b}T\right)}^3}\right]$$

where r_a,A,0 is the restrained distance, θ_A,0 and θ_B,0 are the two restrained angles, and K’s are the force constants (Boresch et al., 2003).

The transformation of charged ligands demands corrections to maintain neutrality in the simulation box as the ligand partial charges are scaled (Lin et al., 2014). Due to the usage of periodic boundary conditions, excess charges are propagated through all cells and cause errors in charge distribution (Hunenberger and McCammon, 1999; Anwar and Heyes, 2005; Hub et al., 2014). This issue can be managed by performing the partial charge scaling simultaneously on a specified counter-ion (Dixit and Chipot, 2001; Wallace and Shen, 2012; Chen W. et al., 2018), or through the correction scheme introduced by Rocklin et al. (Rocklin et al., 2013) based on an additional PB calculation to account for periodic finite-size effects.

The number and length of λ windows governs the variability of the free energy calculation (Shirts and Pande, 2005; Pham and Shirts, 2011). Increased sampling reduces the variance, but may not be worthwhile due to the added simulation costs. Rather than equally spacing the λ windows, a better strategy would be to more densely sample regions where transitions are non-linear near the end points of the van der Waals scaling stage and reduce sampling in more linear regions such as the electrostatic scaling. Datapoints from the beginning of each λ window are not yet equilibrated and sequential datapoints are autocorrelated, contamination with these energy values will distort the final free energy prediction (Chodera, 2016). Straightforward solutions to these problems would be to discard all data from the first half of the λ window and to only process energy values with large intervals (King et al., 2021). More sophisticated methods that aim to conserve as many datapoints as possible include the usage of automated equilibration detection based on reverse cumulative averaging (Yang et al., 2004) and subsampling of energies based on the calculated statistical inefficiency (Chodera, 2016), this can be performed with the pymbar (Shirts and Chodera, 2008) package written by the Chodera group. Lastly, thermodynamic integration is known to produce results with high variability due to the numerical integration over highly non-linear functions. The Bennett Acceptance Ratio (Bennett, 1976) (BAR) approach minimizes variance in the calculation of free energy by accounting for energies in neighboring states (Lu et al., 2003). The BAR calculation self-consistently solves for the free energy (C) that satisfies the relations where i and j are consecutive states and U is the potential energy from a selected state.

$$\Delta G=\ln \frac{{\Sigma }_{j}f\left(U_i-U_j+C\right)}{{\Sigma }_{j}f\left(U_j-U_i+C\right)}+C$$

$$\Delta G=C$$

$$f\left(x\right)=\frac{1}{1+e^x}$$

However, this method can face the same issues as EXP/FEP if there is no overlap between neighboring states. This has been extended to the Multistate Bennett Acceptance Ratio (Shirts and Chodera, 2008) (MBAR) method addressing the critical issues in BAR and produces the lowest variance of all free energy estimators by using energy differences from all λ windows (Paliwal and Shirts, 2011).

Absolute Alchemical Simulations Developments and Benchmarks

A major impediment to the usage of alchemical simulations is their complicated setup and data processing for ligand decharging and vdW removal stages. Updates to the popular molecular dynamics packages NAMD (Chen H. et al., 2020) and AMBER (Lee et al., 2020a; He et al., 2020) enable GPU accelerated calculation of the $\frac{d{U}_{\lambda }}{d\lambda }$ term necessary for thermodynamic integration or energy cross terms for sampling conformations at different lambda values for MBAR computation. To support high-throughput alchemical screening and improved reproducibility, a number of software packages automate the experimental setup in preparing the simulation files with appropriately decoupled ligand topologies and output the final binding free energy prediction after processing the trajectories. These include the VMD plugin BFEE (Fu et al., 2018), the python tool BAT.py (Heinzelmann and Gilson, 2021) for AMBER, the CHARMM-GUI Free Energy Calculator (Kim et al., 2020), the web platform Biomolecular Reaction and Interaction Dynamics Global Environment (Senapathi et al., 2020) (BRIDGE) for GROMACS, and Flare (Kuhn et al., 2020).

Improvements in simulation efficiency have allowed faster sampling of protein-ligand binding conformations and exploration of longer timescales to more comprehensively capture the significant perturbations that occur from ligand decoupling in absolute alchemical simulations. Giese et al. (Giese and York, 2018) utilize the simple but effective parameter interpolated thermodynamic integration (PI-TI) scheme where intermediate lambda states are defined by scaling the ligand molecular mechanic parameters, this allows taking full advantage of the standard GPU accelerated MD integrators and existing Hamiltonian replica exchange methods (HREMD) without the need to implement any alchemical specific code. Validation of this study examined pKa predictions on a double strand RNA system resulting in an error within 1.2 pKa units. Monte Carlo methods based on making unphysical, Boltzmann weighed rotamer and torsion moves lead to greater conformational sampling and crossing of energy barriers that would necessitate substantial simulation time in MD. Pure MC (Cabeza de Vaca et al., 2018; Qian et al., 2019) and the hybrid MC/MD method Binding modes of Ligands Using Enhanced Sampling (BLUES) involving random ligand rotations, relaxation with MD, and final acceptance or rejection through nonequilibrium Monte Carlo are demonstrated to have greater binding mode sampling efficiency than standard MD. Hamiltonian replicas parallelize sampling backbone torsions of T4 lysozyme (Jiang et al., 2018) and solvent exchange in the cytochrome P450 binding site (Jiang, 2019) to speed convergence within 1 ns in the latter study. In cases where no reliable experimental structure with ligand bound is available, the generalized replica exchange with solute tempering (gREST) + FEP (Oshima et al., 2020) approach where protein-ligand interactions are weakened through simulation at high temperature to force refinement of ligand binding orientation or Alchemical Grid Dock (Minh, 2020) method can be performed to obtain high quality binding poses. Alternative lambda schedules aimed at reducing the number of intermediate windows to simulate without sacrificing low variance are introduced by Konig et al. (Konig et al., 2020) with enveloping distribution sampling and addition of a restraint energy distribution function in the screening of SARS-CoV-2 protease inhibitors (Li et al., 2020). Entropic bottlenecks caused by order/disorder transitions that inhibit convergence can be avoided by biasing the simulation with the integrated logistic function away from the transition regions (Pal and Gallicchio, 2019). Metadynamics methods utilizing a history dependent bias potential to drive sampling of unexplored conformations are used for the theophylline-RNA complex to get within 0.02 kcal/mol of experiment (Tanida and Matsuura, 2020). The Gaussian algorithm enhanced FEP (GA-FEP) method is used to guide the design of Phosphodiesterase-10 inhibitors and overcomes poor sampling by fitting the observed energies to a multivariate Gaussian distribution to extrapolate better converged energy values for downstream BAR calculation (Li Z. et al., 2019). Dual resolution models where the active site portions of the protein are modeled with full atom representation and other regions as coarse grained showed significant speedup with only minor loss in accuracy compared to the all-atom model for the lysozyme system binding with di-N-acetylchitotriose (Fiorentini et al., 2020). Sakae et al. (Sakae et al., 2020) demonstrate a modified alchemical approach starting with unrestrained ligand for broader sampling of binding poses and bypass the need to exhaustively enumerate all potential binding modes. The DeepBAR method applies generative modeling to construct sample conformations of the cucurbit[7]uril host-guest system for the BAR analysis without the need for intermediate state sampling to achieve higher computational efficiency (Ding and Zhang, 2021).

Advances in finite size and charge treatment schemes have improved accuracy in computing decharging energies, and new formulations for the evaluation of “soft-core” atoms lead to greater numerical stability and reduced variability in vdW removal. The poor representation of electronic polarization in molecular simulation makes binding affinity prediction for charged and titratable molecules challenging. Standard MD simulation is unable to model dielectric screening effects that alter the strength of ligand partial charges as it transitions between the polar solvent environment to the non-polar protein active site (King et al., 2021). We demonstrate that scaling the dielectric constant with the MBAR/PBSA continuum solvent model provides a convenient method to reproduce the effects of charge polarization without requiring any modification to the MD integrator. RMSE for the predicted binding affinities of inhibitors for urokinase plasminogen activator is reduced from 3.2 kcal/mol with standard alchemical simulation to 0.89 kcal/mol with MBAR/PBSA (King et al., 2021). The AMOEBA polarizable force field that incorporates electronic polarization through induced dipoles, atomic dipoles, and quadrupole terms is applied to the lead optimization of the MELK inhibitor IN17 (Harger et al., 2019). In the SAMPL7 TrimerTrip host-guest blind challenge, utilization of the AMOEBA force field shows excellent results with 7/8 samples having errors within 2 kcal/mol (Laury et al., 2018; Shi et al., 2020; Amezcua et al., 2021). The commonly used approach to maintain charge neutrality through co-alchemical ions is shown not to fully eliminate charge artifacts in periodic simulation boxes due to localized differences in electrostatic potentials and solvent densities for the distant ion and bound ligand (Ohlknecht et al., 2020b). Continuum-electrostatics calculations (Ohlknecht et al., 2020a) and the “Warp-Drive” (Ekimoto et al., 2018) method of simultaneously perturbing the protein-ligand complex and a distant unbound ligand are proposed to more accurately correct for finite-size effects. Difficulty in modeling the extraction of charged ligands from deeply buried binding sites with potential of mean force (PMF) methods is addressed with the AlchemPMF protocol where steric obstructions along the physical pathway are alchemically removed, resulting in improved binding free energy estimates on HIV-1 integrase and telomeric DNA G-quadruplex (Cruz et al., 2020). Li et al. (Li and Nam, 2020) develop the Gaussian repulsive soft-core potential to produce a linear hybrid Hamiltonian with respect to lambda to allow improved simulation efficiency over the standard separation-shifted potential that generates non-linear Hamiltonians. Extension of smooth-step soft-core potentials that are composed of monotonically increasing polynomial functions that have the desirable end-point values enable one-step alchemical transformations by overcoming the issues of end-point catastrophe, particle collapse, and large gradient jumps (Lee et al., 2020b).

Benchmarks of alchemical simulations demonstrate their utility and high accuracies. The SAMPL6 and SAMPL7 challenges (Rizzi et al., 2020) feature several entries examining alchemical approaches for CB[8] and tetra-methylated octa-acids host-guest systems with comparison to umbrella sampling (Han et al., 2018; Nishikawa et al., 2018), TrimerTrip host-guest system with comparison of AM1-BCC and RESP charge schemes (Huai et al., 2020), and evaluation of GAFF and CGenFF force fields (Khalak et al., 2020). Novel applications of alchemical simulation include the estimation of binding affinity change upon protein mutation through the ensemble thermodynamic integration with enhanced sampling (TIES) approach on the fibroblast growth factor receptor 3 (FGFR3), notably simulations without enhanced sampling are unable to capture conformational changes driven by protein mutation in the binding site (Bhati et al., 2019). PMF methods based on utilizing restraints to physically pull the ligand out of the binding site are directly compared to absolute alchemical approaches on the HIV-1 integrase system by Deng et al. (Deng et al., 2018), the final results show similar performance with absolute errors in the range of 1.6–4.3 kcal/mol for alchemical and 1.5–3.4 kcal/mol for PMF. The authors add that the alchemical approach supports simpler setup as they do not need to geometrically define the pathway for the ligand to exit the binding site. Loeffler at al. (Loeffler et al., 2018) validate alchemical simulation results from different software packages in the calculation of hydration free energies and determine that the tested packages (AMBER, CHARMM, GROMACS, and SOMD) produce consistent free energies. The scale of alchemical simulations is growing dramatically by harnessing cloud computing (Zasada et al., 2020). The report of massive-scale simulation of 301 HIV-1 integrase inhibitors on the IBM World Community Grid (Xia et al., 2019) highlights how the availability of distributed computing is enabling high-throughput FEP screening.

Applications to Drug Discovery

Usage of free energy calculations is propelling pharmaceutical research. Work performed on a broad range of disease topics including understanding the mechanism for drug actions, optimizing binding affinities against target molecules, and identification of potential inhibitors from libraries demonstrate the importance of these tools. We survey practical applications of modern free energy calculations with attention on works with exemplary accuracy or data contribution, and further detail usage of free energy calculations on a range of biomedical targets. Recent work coupling simulation prediction with experimental validation is of exceptional interest. These studies provide a direct benchmark on the utilization of free energy methods rather than post-hoc analysis that may not generalize well to real-world problems. Secondly, efforts to complete screening campaigns and validation of free energy predictions contribute valuable datasets that can guide the development of future methods such as machine learning models that are prominently dependent on access to ample and diverse data.

Achieving chemical accuracy of below 1 kcal/mol error is still not typical with free energy calculations. Studies utilizing the end state methods MM-PBSA or LIE generally show high errors, a consequence of coarse graining solvent, electrostatic, and entropic interactions. Alternative metrics of Pearson correlation, measuring the linear association between simulation and experimental binding free energies, or Spearman correlation, where the ranked relationship between predicted and experimentally measured values are analyzed, are better suited to compare the performance of end state methods as they capture the ability of the models to select a small number of candidate drug compounds with the highest potential. For example in evaluating ligand binding to the purinergic platelet receptor P2Y₁₂R, MM-PBSA shows absolute RMSE values over 6 kcal/mol from experimental measurements, but is still able to capture the correct trend in ligand binding affinities with Pearson correlation of 0.79 (Greene et al., 2016). In another work MM-PBSA shows RMSE for the Thrombin system at 4.26 kcal/mol, but highly accurate Pearson correlation of 0.86 (Wang et al., 2016). Several studies utilizing alchemical methods progress toward the threshold of chemical accuracy, and lay the groundwork for best practices to follow in future works. Aldeghi et al. achieve 1.54 kcal/mol RMSE with absolute binding free energy calculation on the bromodomain-containing protein 4 system through usage of Hamiltonian-exchange dynamics on top of standard sampling protocols (Aldeghi et al., 2017). Low MUE of 0.83 kcal/mol is achieved by Kuhn et al. in the prediction of relative affinities by carrying out the alchemical transformation in both directions with independent simulations to eliminate the effects of hysteresis (Kuhn et al., 2020). In studies where relative binding affinities are converted to absolute binding free energies, calibration of model predictions can be performed through scaling the average of the predicted binding free energies to equal the average of the experimental binding free energies (Wang et al., 2015; de Oliveira et al., 2019).

SARS-CoV-2

The emergence of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has caused a global health crisis with over 2 million deaths worldwide, compelling rapid drug development for potential therapeutics. Several major protein targets have been identified for inhibition of SARS-CoV-2 function and surveyed through molecular simulation for predicted binding affinity with repurposed and novel drugs, these include the RNA dependent RNA polymerase (Procacci et al., 2020; Wakchaure et al., 2020) (RdRp) that replicates the RNA genome, the main protease (Macchiagodena et al., 2020b; Ngo et al., 2020b; Chowdhury et al., 2020; Gupta et al., 2020; Gupta and Zhou, 2020; Jukic et al., 2020; Li et al., 2020; Milenković et al., 2020; Tejera et al., 2020; Aghaee et al., 2021; Bhardwaj et al., 2021) (3CL M^pro) that mediates replication and transcription, the spike protein (Patil et al., 2021) involved in initiating infection by penetrating the host cell, S-adenosyl-methionine dependent methyltransferase (Sk et al., 2020) (nsp16) that adds the 5′-cap to mRNA essential for stability, envelope protein (Dey et al., 2020) that is involved in virion assembly and budding, Papain-like protease that functions in viral replication and immune response evasion (Bosken et al., 2020), and the host serine protease TMPRSS2 (Singh et al., 2020) that primes the spike protein. Alanine scanning is combined with MM-PBSA to identify the hot-spot binding residues GLU166 and GLN189 on M^pro as critical sites for inhibitors to target (Aghaee et al., 2021). Since only partial structures of the spike protein bound to the receptor protein angiotensin converting enzyme 2 (ACE2) exist, homology modeling is performed to structurally evaluate interactions mediating the spike protein ACE2 complex. MM-PBSA alanine scanning at the interface is utilized to determine the set of residues vital to the tight binding interaction. 5 residues disordered in the crystal structure, VAL445, THR478, GLY485, PHE490, and SER494, are identified to be crucial for ACE2 specificity (Sakkiah et al., 2020). By analyzing the binding poses obtained during MD simulation with hydroxychloroquine, Procacci et al. propose an inhibitor with improved potency for M^pro by restructuring polar contacts on the ligand for greater hydrophobic packing surface area (Procacci et al., 2020). El Hassab et al. perform fragment based drug design and link together generated fragments binding to RdRp (El Hassab et al., 2020). Potential vaccine candidates derived from B-cell and T-cell epitopes from the spike protein have their binding stability assessed through MD simulation (Das and Chakraborty, 2020).

The push for the rapid development of potential therapeutics for SARS-CoV-2 leaves many of these studies as exploratory in nature, predicting free energies of binding or ranking potential ligands without corresponding experimental data. These studies can be used in the future to benchmark these free energy techniques when the experimental data becomes available. However, we do want to highlight studies that have experimental data to compare with. One particular study evaluates the repurposing of FDA-approved drug molecules as M^Pro protease inhibitors using a workflow that combines docking, 100 ns molecular dynamics using a conventional force field, 5 ns molecular dynamics using a neural network derived pseudo-quantum mechanical/molecular mechanical force field (ANI), and finally MM-PBSA to refine the field of 1,615 molecules down to 9 molecules. Ten molecules out of 62 that were obtained after initial docking have experimental data for inhibition activity ranging in active (3), moderately active (3), and inactive (4). Out of the final set of nine selected molecules, two molecules are in the active range, one is moderately active, and no inactive molecules were selected. The study is cognizant of potential missed active molecules during the docking step and the loss of three active/moderately molecules during subsequent steps, but does not further evaluate the details for the loss of those molecules (Gupta and Zhou, 2020). An additional study looks at potential inhibitors for 3CL protease using Hamiltonian replica exchange and non-equilibrium alchemical simulations. The binding free energy of 21 potential inhibitors is calculated with four molecules having experimental data to compare to, three of the molecules having error within 2 kcal/mol and one with 5 kcal/mol (Macchiagodena et al., 2020b).

Cancer

Anti-cancer therapeutics are a significant target for molecular simulation. Studies have evaluated potential small molecule or peptide inhibitors and interrogated the binding interactions of known drug-protein interactions. Novel data representation is applied to the investigation of tankyrase inhibitors targeting the Wnt pathway using a workflow that combines docking and machine learning scoring to filter through a library of 1.7 million potential inhibitors down to 174 molecules, Downstream QSAR screening using ADMET and physico-chemical features further reduces the number to 17 molecules. A subset of selected molecules is chosen to simulate using molecular dynamics calculating binding free energy using MM-PBSA and FEP with MBAR, which show reasonable agreement to experimental assays for two tested molecules (Berishvili et al., 2020). Another study of note is the calculation of binding free energy for inhibitors of the p53-MDMX/MDM2 interactions. The use of FEP with BAR results in mean absolute error (MAE) of 0.816 kcal/mol and root mean squared error (RMSE) of 1.064 kcal/mol for a set of five inhibitors targeting p53-MDMX interaction; however, for MDM2 and a set of 14 molecules the resulting MAE is 3.08 kcal/mol. Furthermore, the simulation of apo MDM2 structure to improve sampling of conformational states is used to generate a free energy landscape and free energy correction that improves the MAE to 1.95 kcal/mol and RMSE to 2.83 kcal/mol (Singh and Li, 2020). Additional studies overview the dissociation mechanism of GDP from Cdc42 which modulates cell migration and polarity (Kang et al., 2019). The AMOEBA polarizable force field is used to predict covalent and non-covalent inhibitors of fructose-bisphosphate aldolase A (Qi et al., 2019). The following works are reported to identify promising drug candidates, such as assessing the delivery of the antitumor agent paclitaxel via cell penetrating peptides (Wei et al., 2021), methotrexate analogs against drug resistant human dihydrofolate reductase (Rana et al., 2020), inhibitors for Adenosine A₃ receptor (Lagarias et al., 2019), and peptide inhibitors against epidermal growth factor receptor (Tavakoli and Ganjalikhany, 2019) identify promising drug candidates. Simulation of lactate dehydrogenase A found overexpressed in the tumor environment (Jafary et al., 2019), kinesin spindle protein inhibition with (+)-morelloflavone (Ogunwa et al., 2019), chemosensitizing caryophyllene sesquiterpenes with doxorubicin on P-glycoprotein (Di Sotto et al., 2020), and inhibitor binding to the transcription silencing G-quadruplex element of the oncogene c-MYC (Chen B. et al., 2020) demonstrate the broad range of cancer targets. Other works of interest find altered inhibitor binding interactions with mutant anaplastic lymphoma kinase involved in lung cancer (Xiao et al., 2019), activated Cdc42-associated kinase 1 inhibitors (Granadino-Roldan et al., 2019), small molecules binding to the MUSHASHI family of RNA binding proteins (Minuesa et al., 2019), and negative regulation of STXBP4 on the Hippo pathway (Vargas et al., 2020).

Neurodegenerative Diseases

Many studies have been performed on neurodegenerative disorders, with major focus on understanding Alzheimer’s disease. Thai et al. demonstrate how MM-PBSA can rapidly facilitate drug development by first predicting strong multipotent binding of CID 9998128 with Aβ₄₂ peptide, Aβ₄₂ fibrils, and β-secretase, then performing in vitro assays confirming that the compound inhibits Aβ fibril formation (Thai et al., 2018). Other works include the development of positron emission tomography/single photon emission computed tomography probes targeting Aβ for imaging (Kawai et al., 2018), rational design of anti-Aβ antibodies (Greene et al., 2018), small molecule inhibitors targeting Aβ fibrils (Ngo et al., 2019; Gupta and Dasmahapatra, 2020), β-sheet breaker peptides to interfere with amyloid fibril assembly (Shuaib et al., 2019), and structural modeling of aspartyl protease γ-secretase in complex with Aβ peptides (Hitzenberger and Zacharias, 2019). Further study of neurodegenerative disease involves fragment docking of reversible covalent inhibitors on calpain, a calcium dependent cysteine protease, whose overexpression has been correlated with neurodegenerative disorders (Zhang H. et al., 2019). The study uses FEP/λ-REMD as well as Site-Identification by Ligand Saturation to enhance the FEP calculations for a set of ten α-ketoamides. This results in an overall Pearson correlation of 0.85 compared to experiment; however, the correlation changes when categorizing these into covalent (0.84) and non-covalent (0.41) states, suggesting that only the covalent state is useful for inhibition (Zhang H. et al., 2019). Additional studies explore the identification and design of inhibitors against Caspase 8 involved in neural cell death (Ahmad et al., 2019) and evaluate novel 1,4-diazepane containing ligands as σ-receptor ligands with antioxidant and neuroprotective properties (Zampieri et al., 2020).

Antibacterials and Antivirals

Innovation in the field of antibacterial discovery is driven by greater computing power allowing screening of larger compound libraries and more accurate assessment of binding affinities. This is necessary to overcome the challenges in the rise of infectious bacterial strains resistant to long-established antibiotics. MM-PBSA and bioassays are combined to guide discovery of antimicrobial compounds derived from petroleum ether extracts of Peperomia blanda on methylthioadenosine phosphorylase, highlighting an effective pipeline for isolating novel compounds and identifying potential targets (Al-Madhagi et al., 2019). Recent studies examine the effects of mutations on ligand binding to guanine riboswitches found to be potential antibacterial targets (Chen et al., 2019), the discovery of ligands targeting the virulence factor thermolysin from Bacillus thermoproteolyticus (Lamazares et al., 2021), selective inhibition of bacterial RNA polymerase via the nucleoside analog pseudouridimycin (Rabbad et al., 2019), berberine as an inhibitor of the multidrug efflux system MexXY-OprM found in aminoglycoside resistant Pseudomonas (Laudadio et al., 2019), inhibition of Pseudomonas aeruginosa quorum signaling and biofilm formation by targeting anthranilate-CoA ligase (Shaker et al., 2020), and inspection of cruzain inhibitor binding modes to develop more potent treatments for Chagas disease caused by Trypanosoma cruzi (Martins et al., 2018). The lung disease tuberculosis, caused by the bacteria Mycobacterium tuberculosis, is targeted with indolizines to inhibit enoyl[acyl-carrier] protein reductase (Venugopala et al., 2019), virtually screened for inhibitors against the polyphosphate kinase Rv2984 that carries out the essential reaction producing inorganic polyphosphate (Shahbaaz et al., 2019), and simulated with induced fit docking of outer membrane protein A (OmpATb) to discover inhibitors blocking pore-forming activity.

Development of effective antiviral drugs is necessary to combat pandemic viruses and emerging pathogenic agents. Antiviral therapies typically inhibit the machinery specifically involved in viral replication, but this selectivity is difficult to achieve as viruses hijack the host cell proteins for replication and drugs inhibiting these processes will also damage the host cells. A second obstacle is that the high rate of viral replication leads to rapid development in drug resistance. Structural evaluation of residues critical to forming ligand binding interactions such as hydrogen bonds and hydrophobic packing has provided insight to guide the design of inhibitors against HIV, influenza, Ebola, Dengue, and HPV. HIV infection leads to destruction of CD4⁺ T cells and development of Acquired Immunodeficiency Syndrome. There are currently no available treatments to cure HIV, but therapeutics can control HIV progression. Binding affinity predictions are applied to elucidate the binding mode of inhibitors targeting HIV-1 protease and understand mutant protease resistance mechanisms (Li et al., 2018; Wang R.-G. et al., 2020; Wang and Zheng, 2020). In particular, the work of Li et al. looks at ten inhibitors for the HIV-1 protease and compares MM-PB/GBSA methods for calculation of free energy using conventional and polarizable force fields as well as the scaling of the interior dielectric constant. The optimization of the dielectric constants results in an RMSE of 1.43 kcal/mol in MM-PBSA with correlation coefficient of 0.87 and an RMSE of 6.62 kcal/mol in MM-GBSA with a correlation of 0.78 (Li et al., 2018). Further work has targeted HIV-1 reverse transcriptase through large scale virtual screening to yield 4 compounds for experimental validation (Zhang et al., 2016). Influenza viral infection causes respiratory illnesses commonly called the flu that can lead to death. Work on antivirals to treat influenza includes utilizing amantadine probes to block influenza M2 proton channels to prevent virus replication (Tzitzoglaki et al., 2020), analyzing the effects of the hemagglutinin mutations on binding affinity to human receptors (Zhou et al., 2018), screening inhibitors for the PB2 protein of influenza RNA polymerase to inhibit generation of RNA primers essential for replication (Pham et al., 2020), optimizing neuraminidase inhibitors as lead compounds (Yu et al., 2019), and characterizing potential influenza polymerase inhibitors (Pérez-Sánchez et al., 2021). Ebola causes hemorrhagic fever and molecular interactions between the monoclonal antibody ADI-15946 and the Ebola GPcl receptor is studied (Hou and Zhang, 2020). Dengue is a tropical illness transmitted by mosquitoes, it is targeted with thioguanine small molecule inhibitors for the NS2B/NS3 protease (Hariono et al., 2019) and antiviral peptides binding to the envelope protein domain III (Isa et al., 2019). Therapies treating human papillomavirus targeting the E6 oncoprotein complex are also evaluated (Ricci-Lopez et al., 2019).

Integral Membrane Proteins

The application of molecular dynamics in the prediction of binding affinities has expanded to include more challenging systems than typical proteins in aqueous environment. Successful simulation of integral membrane proteins usually includes the interactions of the protein with the surrounding lipid bilayer to model the non-polar setting. A major difficulty with the addition of the lipid molecules is their slow relaxation timescales impairing convergence. Corey et al. validate the application of free energy calculations with protein-lipid interactions and address the sampling issue by utilizing the coarse-grained Martini v2 force field (Corey et al., 2019). G-protein coupled receptors (GPCRs) are an important drug target due to their roles in recognizing extracellular signals and converting them into intracellular responses. Profiling of inhibitors against subsets of GPCRs including cannabinoid receptors (Jung et al., 2018; Ji et al., 2020; Yang et al., 2020), biphenyl scaffolds targeting free fatty acid receptors (FFAR1/FFAR4) involved in diabetes (Zhang X. et al., 2019), and CXCR4 (Shen et al., 2019) yield potential candidates for future experiment and insight into the interactions forming the binding interface. A study of the complement component fragment 5a receptor (C5aR) system explores the binding of two protein ligand inhibitors (Sahoo et al., 2018). Particular interest in this system arises from the simultaneous binding at multiple binding sites for a single ligand. These binding interactions are explored using MM-PBSA to elucidate important residues at differing sites. The residues predicted to have central impact are consistent with experimental mutational analysis (Sahoo et al., 2018). Additionally, GPCR dimerization is also studied with the TGR5 system through PMF computations using umbrella sampling and MM-PBSA. Computational results corroborate experimental FRET experiments in revealing residue hot spots at the 1/8 interface for dimerization inhibitors to target (Waschenbach et al., 2020). The mechanism of opioid pain suppression is examined through simulation of fentanyl with the Gluoeobacter violaceus ligand-gated ion channel. The study indicates that the fentanyl-binding induced conformational changes inhibit conduction through the channel (Faulkner et al., 2019).

Nucleic Acids

Nucleic acids carry genetic data and regulate cell processes. Study of binding affinity predictions with DNA or RNA generally requires use of different force fields than those used for protein systems, but otherwise involves the same logic and data processing. Deng (Deng, 2019) compares the double decoupling and PMF approaches in the consideration of small molecule inhibitors in complex with G-quadruplex DNA, and finds that both approaches have errors within 2 kcal/mol of the experimentally determined binding free energies. Further work with DNA includes investigation of alkaloid binding to human telomeric G-quadruplex (Deng et al., 2019), umbrella sampling of catabolite activator protein to identify DNA binding induced conformation changes (Prabhakant et al., 2020), binding of the antiviral netropsin in the DNA minor groove (Zhang et al., 2018), examination of Z-DNA stability with modified cytosine bases (Vongsutilers et al., 2020), and binding recognition and allosteric mechanism of tryptophan-responsive regulatory protein-DNA (Mariadasse et al., 2020). Simulation of RNA features the prediction of riboswitch binding affinities (Hu et al., 2020) and in silico screening of aptamers targeting hepatitis B surface antigen (Sabri et al., 2019).

Peptides

Peptides are short chains of amino acids that can function as therapeutic drugs, biosensors, and catalysts. Peptide sequences are often optimized to achieve a desired conformation capable of binding and inhibiting target proteins similarly to small molecule inhibitors, with the advantage that peptides can bind larger surface areas for greater specificity than small molecules. Simulation and in silico design of peptides has been performed to generate cyclic lead compounds against the hormone resistin through the alchemical method to optimize selectivity (Chi and Vargas, 2020), construct peptide inhibitors derived from the LEDGF/P75 protein against HIV1 integrase receptor (Kilburg and Gallicchio, 2018), investigate differences in free energy profiles of cell penetrating peptides on DOPC model lipid bilayers to characterize penetration efficiency (Her Choong and Keat Yap, 2020), and identify determinants for peptide binding to the PSM9 PDZ domain found in synaptic junctions (Harish et al., 2019).

Metal Ions

Metal ions are coordinated by metalloproteins to catalyze reactions that are challenging to achieve with conventional organic chemical methods. They are important in oxygen transfer, redox reactions, and free radical capture. Additional roles for metal ions involve their ability to stabilize highly charged interactions such as those with the DNA phosphate backbone. Accurate representation of metal ions in molecular simulation is limited by the complications of polarization effects that are not captured in conventional force fields, suboptimal treatment of metal ion ligation to amino acid residues through restraints, and lack of well-tested force field parameters in comparison to those available for organic molecules. Even with these difficulties, study of metal ion binding with molecular simulation is constantly advancing. Jing et al. (Jing et al., 2018) utilize a polarizable force field to demonstrate that selective binding of Ca²⁺ and Mg²⁺ arises from many-body polarization effects. Improved parameterization of Zn²⁺ ions coordinating to Asp/Glu (Macchiagodena et al., 2020a) and His/Cys (Macchiagodena et al., 2019) enables more reliable simulation of zinc binding proteins, binding free energies of Mg²⁺ coordination with nucleoside di- and tri-phosphates such as ADP and ATP are studied with polarizable force fields (Walker et al., 2020), and an optimized 12-6-4 potential incorporating charge-induced dipole interactions allows accurate binding free energy calculation of Co²⁺ and Ni²⁺ to the enzyme glyoxalase I (Song et al., 2020). The impact of zinc ions on O6-methylguanine DNA methyl transferase DNA binding activity (Gharouni et al., 2021) and effects of sodium or calcium ions on calprotectin dimerization (Gheibi et al., 2019) is investigated.

Biomedical Studies

A host of other biomedical applications outside the major categories discussed above have also been published in recent years. Cataract formation occurs through human γD-Crystallin aggregation and application of MD shows that the steroid lanosterol binds to hydrophobic surface regions near the C-terminal region to protect against dimerization (Kang et al., 2018). Inhibitors are identified to target the JAMM deubiquitinylases Rpn11 and CSN5 that remove covalently attached ubiquitins from proteins to regulate homeostasis (Kumar et al., 2018). Free energy calculation is used to study adenosine deaminase abnormal function as reported in rheumatoid arthritis (Tian et al., 2018), the ricin catalytic subunit found in the chemical weapon ricin (Botelho et al., 2020), the tyrosine phosphatase PTP-CPS4B involved in Streptococcus pneumonia metabolic signaling (Zaman et al., 2021), and clusters formed by uric acid and melamine that contribute to renal dysfunction (Chattaraj and Paul, 2020). Escherichia coli pathogenesis has been discovered to be driven by colonization factor I fimbriae binding to the Lewis A glycan epitope found in the small intestine (Mottram et al., 2018). The recognition mechanism for highly charged inorganic phosphate by phosphate binding protein has been studied with the polarizable forcefield AMOEBA to resolve the protonation state of the bound phosphate (Qi et al., 2018). Diabetes is a metabolic disease characterized by the inability to regulate blood sugar levels. Therapeutics have been explored through liver fructose 1,6-bisphosphate inhibitors to control gluconeogenesis-mediated overproduction of glucose (Proenca et al., 2020) and dipeptidyl peptidase 4 inhibitors to block degradation of incretins that stimulate decrease of blood glucose (Rahman et al., 2020). Half-life extension of insulin determir by complex formation with human serum albumin has been examined as a platform for drug delivery (Ryberg et al., 2020). Further studies assess the role of conformational changes in AcrB transporter contributing to multidrug resistance (Matsunaga et al., 2018), transport of cholesterol by the Aster-A protein (Moesgaard et al., 2020), and reduction of chronic inflammation by treatment with the peptide KCF18 binding to TNF-α and interleukin-6 (Jiang et al., 2019). Investigation into other areas includes adaptive immune response through toll-like receptor activity when bound to diprovocim (Su et al., 2019) and stability when complexed with lipopolysaccharide or neoseptin3 (Tafazzol and Duan, 2019), cooperative binding of heat shock protein 70 with piperine (Zazeri et al., 2020), agonists and antagonist binding to androgen receptor triggering different conformational changes (Azhagiya Singam et al., 2019), and the binding pathway of benzamidine to mutant trypsin protease through enhanced ligand sampling (Shao and Zhu, 2019).

Non-Pharmaceutical Applications

Research in the fields of biotechnology and plant biology is also aided by molecular simulations. Studies of interaction mechanisms between the germination stimulant karrikins binding to their receptor KAI2 (Zhang et al., 2020) and 4-hydroxyphenulpyruvate dioxygenase inhibitors functioning as herbicides is reported (Fu et al., 2019). Manufacture of commercially valuable polyketides, secondary metabolites synthesized by multi-domain polyketide synthase complexes, has been investigated via comparison of thioesterase binding affinity to cyclized products to understand product release mechanisms of the antifungals amphotericin and nystatin (Wang et al., 2021). Binding free energy analysis is also used to elucidate the molecular basis of ketoreductase chain length and regiospecificity (Serapian and van der Kamp, 2019; Zhao et al., 2020). Potential insecticides targeting the ecdysone receptor to disrupt growth are identified (Horoiwa et al., 2019).

Conclusion

Prediction of binding free energies via molecular simulation is playing a key role in accelerating drug development efforts by reducing the time and experimental effort required to establish functional pharmaceuticals. The growing number of successful applications highlights the utility of these computational methods. MM-PB/GBSA is recommended for initial stages of virtual screening where ranking of large number of candidates is performed due to its balance of improved reliability over molecular docking and speed. LIE can be alternatively used when the number of candidates is extremely high and simulation speed is prioritized as it bypasses the post-processing steps required for MM-PB/GBSA at the cost of some accuracy. In later stages of drug optimization where fewer simulations are necessary due to a narrowed range of candidates, alchemical methods are suggested due to their greater rigor in considering interactions with explicit solvent and conformational entropy. Challenges in reaching adequate conformational sampling, overly simplistic treatment of electronic polarization, and deficiencies in force field parameterization still must be addressed. Active research in these areas is ongoing, knowledge of the rapid development of current approaches and their elevated performance compared to studies completed only a few years ago inspires confidence that the grand challenge of accurate binding free energy prediction is achievable in the near future.

Author Contributions

EK: Literature search and drafted the review; EA: Additional literature search and revision; RL: Designed the structure and supervised the review. All authors critically revised the manuscript.

Funding

The work was supported by the National Institute of Health/NIGMS (GM093040 and GM130367 to RL).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.