Highlights
-
•
Theoretical model has been validated through single-bubble sonochemistry.
-
•
Optimum bubble temperature for production of oxidants.
-
•
Numerical simulations of sonochemical synthesis of nanoparticles.
-
•
FEM calculation of an acoustic field in a sonochemical reactor.
Keywords: Numerical simulation, Bubble dynamics model, OH radical, Single-bubble sonochemistry, Optimum bubble temperature, Sonochemical synthesis of nanoparticles
Abstract
Numerical simulations for sonochemistry are reviewed including single-bubble sonochemistry, influence of ultrasonic frequency and bubble size, acoustic field, and sonochemical synthesis of nanoparticles. The theoretical model of bubble dynamics including the effect of non-equilibrium chemical reactions inside a bubble has been validated from the study of single-bubble sonochemistry. By the numerical simulations, it has been clarified that there is an optimum bubble temperature for the production of oxidants inside an air bubble such as OH radicals and H2O2 because at higher temperature oxidants are strongly consumed inside a bubble by oxidizing nitrogen. Unsolved problems are also discussed.
1. Introduction
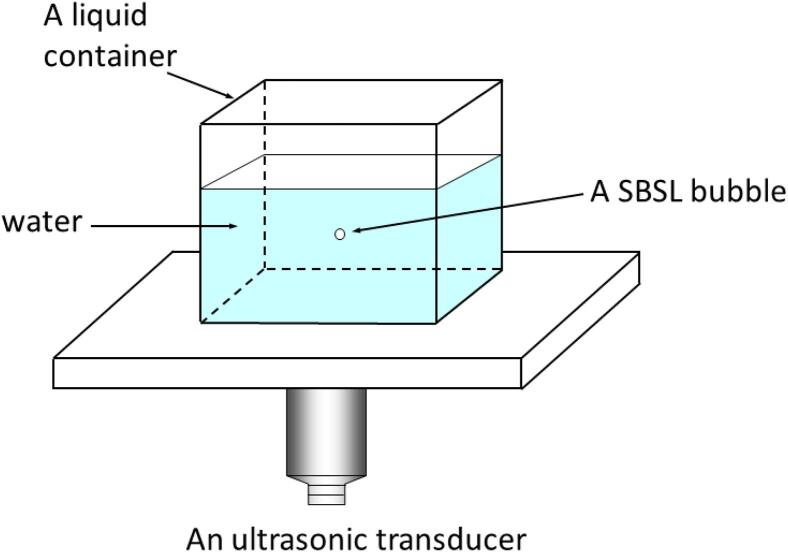
About 30 years ago when I started research in sonochemistry and sonoluminescence, reproducibility in experiments in sonochemistry was much poorer than that in recent years [1]. The turning point was the development in research on single-bubble sonoluminescence (SBSL) after the discovery by Gaitan and Crum in 1990 [2]. SBSL is a light emission phenomenon from a stably pulsating bubble trapped near the pressure antinode of a standing ultrasonic wave (Fig. 1) [2], [3], [4], [5], [6]. In 1991, Barber and Putterman [6] reported in Nature that SBSL pulse width is smaller than 100 ps. After the report, many physicists (including myself) started research on SBSL [3], [4], [5]. The considerable development in SBSL research in the following 10 years was reviewed by Brenner, Hilgenfeldt, and Lohse [4] in 2002.
Fig. 1.
An experimental apparatus for a single-bubble system [3]. Copyright (2004), with permission from Taylor & Francis.
Triggered by the research of SBSL, collaboration between chemists, physicists and ultrasonic engineers in sonochemical experiments has increased [1]. As a result, reproducibility in sonochemical experiments has been considerably improved [1], [7]. For example, pre-degassed water is used in an ultrasonic cleaning bath in which a beaker or a flask for sonochemical experiment is immersed in order to prevent the temporal variation of acoustic intensity due to degassing of water in the bath [8]. Another example is the use of impedance matching circuit to prevent the reflection of electric power from the ultrasonic transducer [9], [10].
Another development in sonochemical research triggered by the SBSL research is numerical simulations of sonochemical reactions inside a bubble [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28]. The first paper on numerical simulations of sonochemical reactions is probably by Kamath, Prosperetti, and Egolfopoulos [11] in 1993. There has been considerable development in numerical simulations of sonochemical reactions since then. The numerical simulations have revealed many mechanisms in sonochemistry. In the present review, various numerical simulations for sonochemistry are discussed.
2. Bubble dynamics model
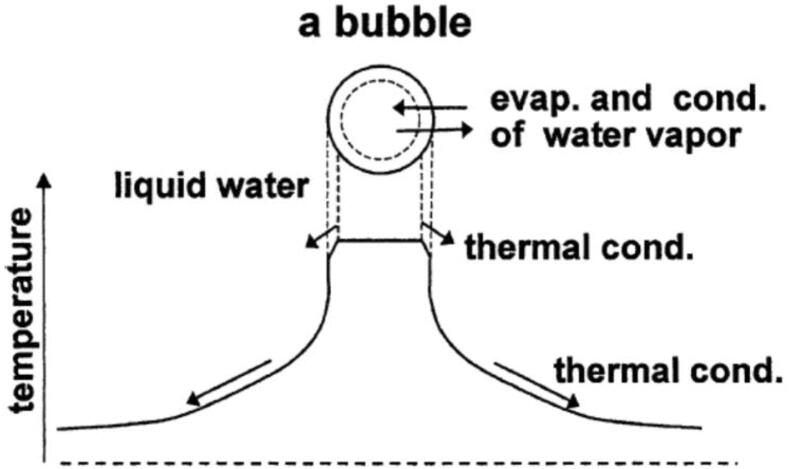
At the beginning of the SBSL research, it was believed that a spherical shock wave is formed inside a collapsing bubble [3], [4], [29], [30], [31]. When the spherical shock wave is converged at the bubble center, temperature at the bubble center increases very sharply to about 106 K, which was thought to be responsible for the short pulse of SBSL light [29]. However, following researches have revealed that shock wave formation inside a collapsing bubble is unlikely because temperature near the bubble wall is lower than that near the bubble center by thermal conduction between the heated bubble interior and the surrounding liquid [3], [4], [23], [32], [33], [34], [35]. Lower temperature near the bubble wall results in smaller speed of sound near the bubble wall compared to that near the bubble center. In other words, the sound-speed increases as the distance from the bubble wall increases toward the bubble center. For the shock wave formation, pressure disturbances radiated inwardly from the bubble wall should overtake the previously radiated pressure disturbances. However, as a pressure disturbance moves with the speed of sound plus the radial fluid velocity, the pressure disturbance never overtake the previously radiated pressure disturbances because a typical bubble collapse is not so violent to overcome the adverse sound-speed gradient for the shock wave formation [35].
Actually, according to the numerical simulations of fundamental equations of fluid dynamics inside a collapsing bubble, the temperature and pressure inside a collapsing bubble are nearly spatially uniform [23]. Thus, in the theoretical model discussed in the present review, temperature is assumed to be spatially uniform inside a bubble except at the thermal boundary layer near the bubble wall (Fig. 2) [19].
Fig. 2.
The bubble dynamics model [19]. Reprinted from Ultrasonics, vol. 42, K. Yasui, T. Tuziuti, and Y. Iida, Optimum bubble temperature for the sonochemical production of oxidants, pp. 579–584, Copyright (2004), with permission from Elsevier.
In the model [10], [12], [16], [18], [21], [36], the following effects are taken into account; thermal conduction inside and outside a bubble, non-equilibrium evaporation and condensation of water vapor at the bubble wall, non-equilibrium chemical reactions inside a bubble, variation of liquid temperature at the bubble wall and corresponding changes of physical properties of the liquid such as saturated vapor pressure, surface tension, latent heat of evaporation, thermal conductivity, viscosity, etc. As the equation of bubble dynamics (temporal evolution of bubble radius), modified Keller equation is used, in which effect of liquid compressibility is taken into account to the first order [10], [36]. With regard to chemical reactions inside an air bubble, 93 chemical reactions and their backward reactions are taken into account involving N2, O2, H2O, OH, H, O, HO2, H2O2, O3, N, HNO2, HNO, HNO3, NO, NO2, and N2O [18].
3. Single-bubble sonochemistry
For usual experiments of sonochemistry, direct comparison between theory and experiment is practically very difficult because there are many uncontrollable factors in the experiments such as temporal variation in number and size of bubbles as well as that of acoustic field in a sonochemical reactor, spatial movement of bubbles, etc. [10], [37], [38]. It is practically very difficult to know the exact values of number of bubbles as well as their size distribution. In 2002, Didenko and Suslick [39] experimentally reported the production rate of OH radicals from a SBSL bubble, which is called single-bubble sonochemistry. The experiment of single-bubble sonochemistry has enabled one to compare theory with experiment because the number of a bubble was fixed and the pressure amplitude of ultrasound was experimentally measured as well as the maximum bubble radius at the bubble expansion [39].
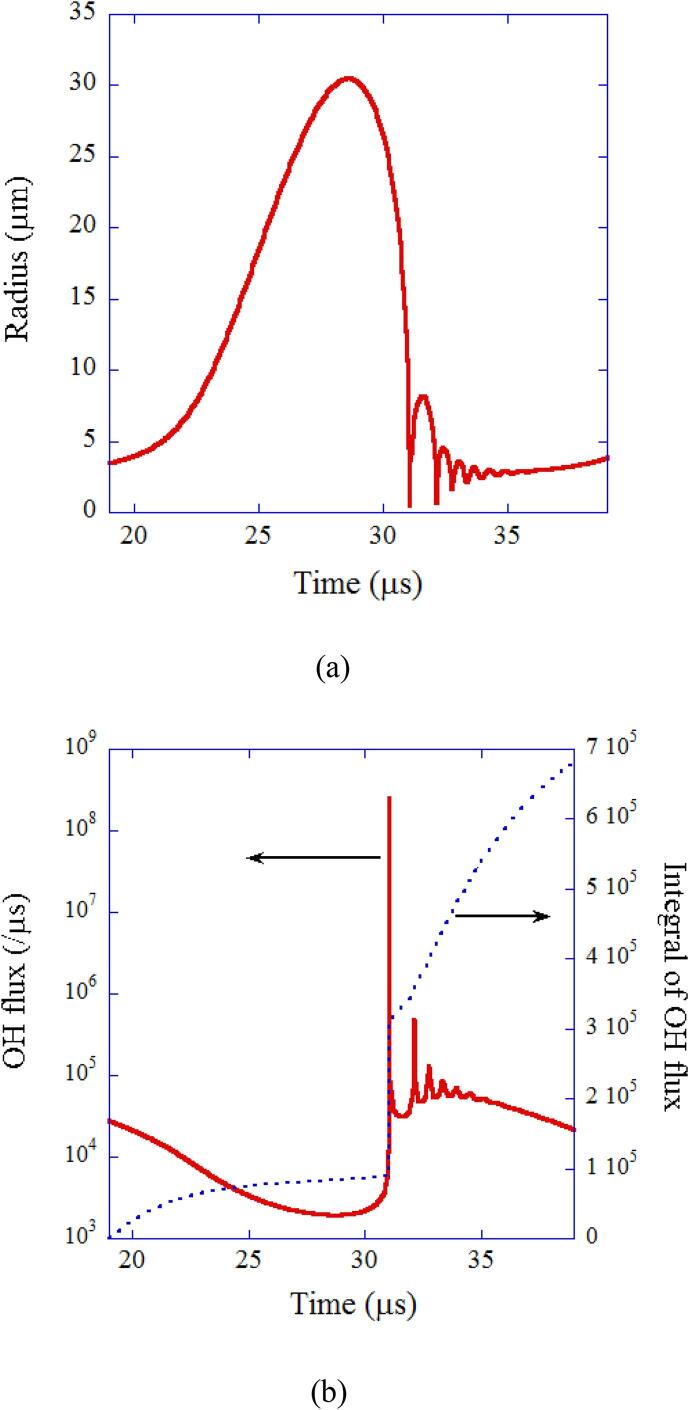
The results of numerical simulations under the condition of single-bubble sonochemistry are shown in Fig. 3, Fig. 4 [21]. During the rarefaction phase of ultrasound, a bubble expands (Fig. 3 (a)). At the compression phase of ultrasound, a bubble collapses very violently, which is called Rayleigh collapse [4], [10]. There are two reasons for the violent collapse of a bubble [10]. One is the spherical geometry of the bubble collapse. According to the continuity of liquid, speed of ingoing liquid increases as the radius from the bubble center decreases because the surface area of a spherical liquid shell decreases. The other is the inertia of the ingoing liquid toward the bubble.
Fig. 3.
The calculated results for one acoustic cycle when a SBSL bubble in a steady state in water at 3 °C is irradiated by an ultrasonic wave of 52 kHz and 1.52 bar in frequency and pressure amplitude, respectively [21]. The ambient bubble radius is 3.6 μm. (a) The bubble radius. (b) The dissolution rate of OH radicals into the liquid from the interior of the bubble (solid line) and its time integrals (dotted line). Reprinted from J. Chem. Phys., vol. 122, K. Yasui, T. Tuziuti, M. Sivakumar, and Y. Iida, Theoretical study of single-bubble sonochemistry, 224706, Copyright (2005), with the permission of AIP Publishing.
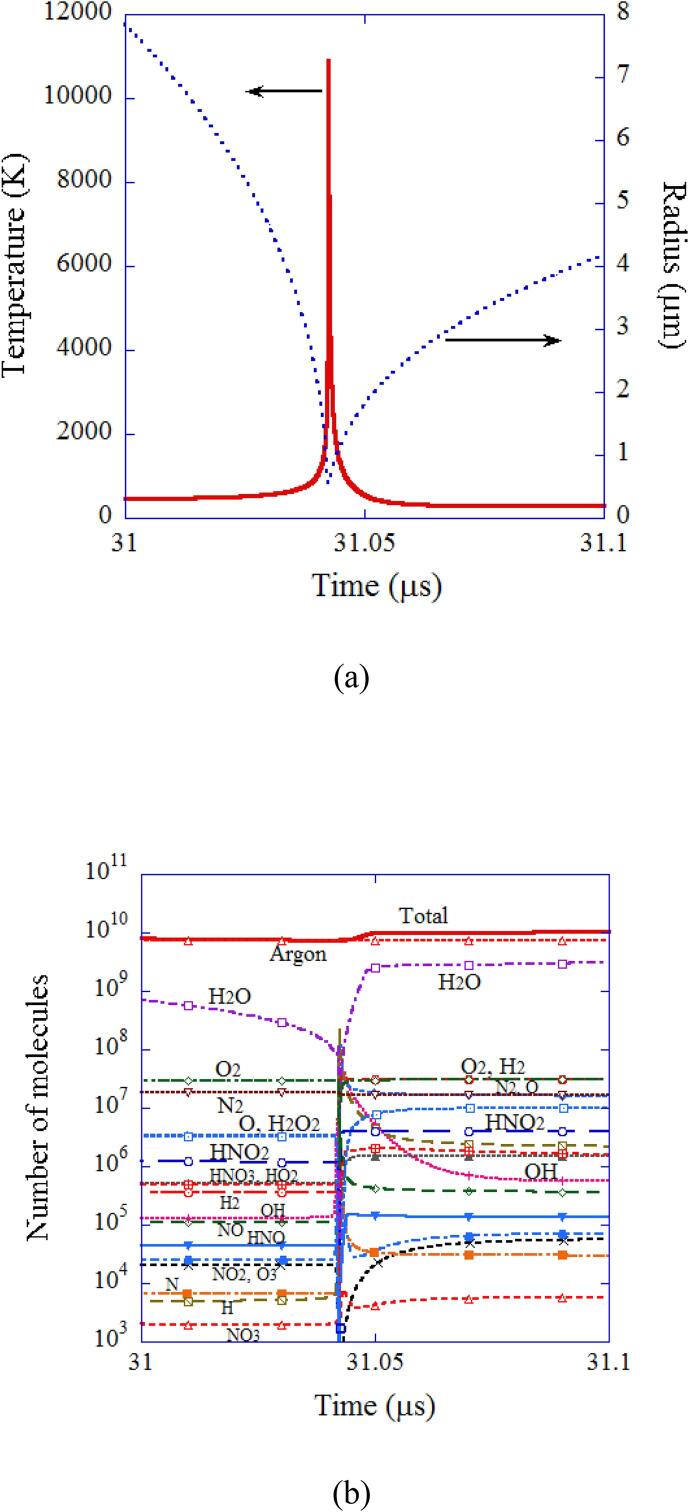
Fig. 4.
The calculated results for a SBSL bubble in a steady state at around the end of the bubble collapse only for 0.1 μs [21]. (a) The bubble radius and the temperature inside a bubble. (b) The number of molecules inside a bubble. Reprinted from J. Chem. Phys., vol. 122, K. Yasui, T. Tuziuti, M. Sivakumar, and Y. Iida, Theoretical study of single-bubble sonochemistry, 224706, Copyright (2005), with the permission of AIP Publishing.
At the end of the violent bubble collapse, temperature and pressure significantly increase due to quasi-adiabatic compression of a bubble where “quasi-“ means that appreciable amount of thermal conduction takes place between the heated interior of a bubble and the surrounding liquid [10], [12]. As a result, water vapor is dissociated inside a bubble and OH radicals are created. Here, an argon bubble is studied because nitrogen is burned inside an initial air bubble by the high bubble temperature. Then, nitrogen and oxygen are changed to water soluble species such as HNOx and NOx which gradually dissolve into water. Accordingly, only chemically inactive species argon remains inside a SBSL bubble because a SBSL bubble repeats expansion and violent collapse more than 104 times per second. This is called argon rectification hypothesis which has been validated both experimentally and theoretically [4], [40].
In the present numerical simulations, the dissolution rate of chemical species such as OH radicals are also numerically calculated [21]. The result for OH radicals is shown in Fig. 3 (b) [21]. The time integral of the OH flux is also shown by dotted line in Fig. 3 (b). It is seen that the calculated amount of OH radicals dissolved into the surrounding liquid in one acoustic cycle is , which nearly agrees with the experimental result of [21], [39]. Thus it is concluded that the theoretical model for single-bubble sonochemistry has been almost validated.
The results of numerical simulation at around the end of the bubble collapse are shown as a function of time only for 0.1 μs in Fig. 4 [21]. At the end of the violent bubble collapse, temperature sharply increases to 10900 K (Fig. 4 (a)). As a result, many molecules present inside a bubble except argon are dissociated inside the strongly heated bubble. The chemical products such as OH radicals present inside a SBSL bubble before the end of the violent collapse are produced at the previous violent collapse. When the bubble is cooled after the end of the violent collapse, many chemical species are produced inside a bubble again (Fig. 4 (b)).
4. Influence of ultrasonic frequency
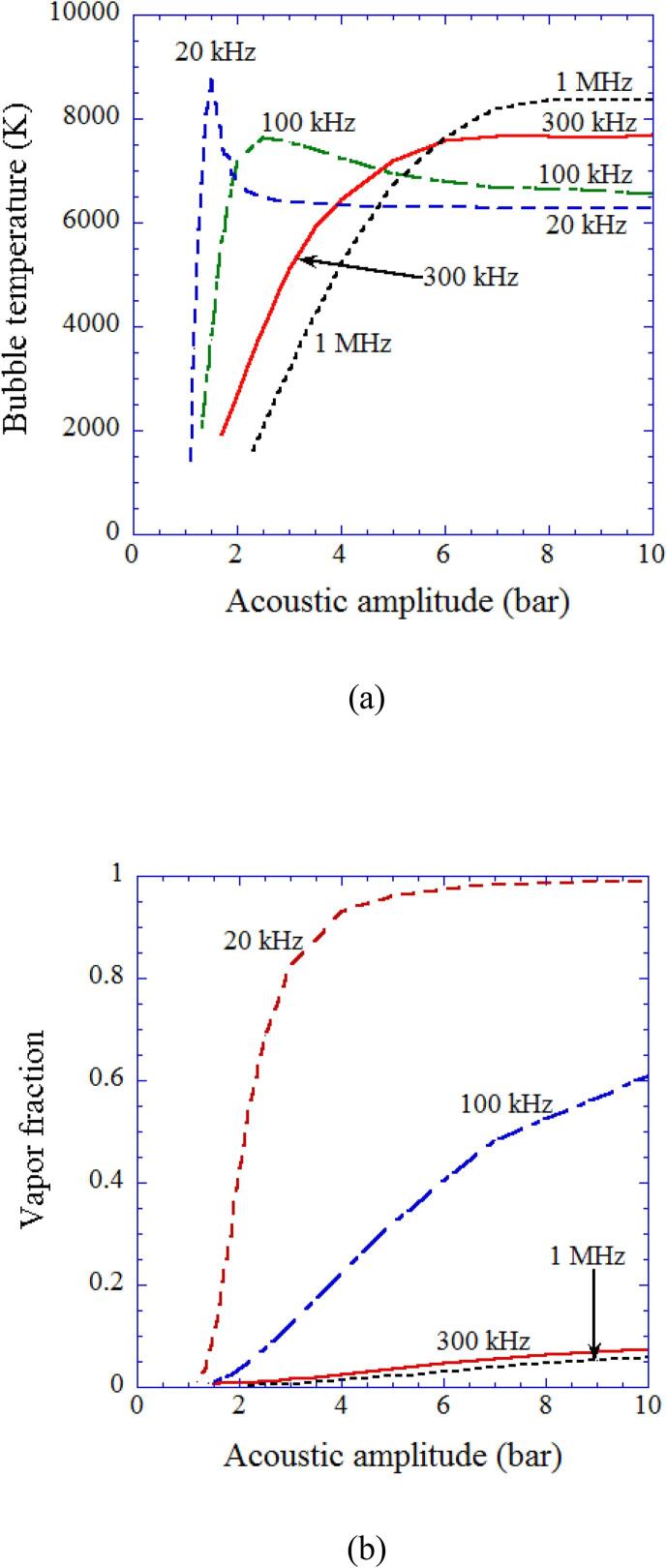
Using the theoretical model validated through the study of single-bubble sonochemistry [10], [12], [16], [18], [21], [36], influence of ultrasonic frequency on sonochemical reactions inside an air bubble is studied by numerical simulations (Fig. 5, Fig. 6, Fig. 7) [25]. For relatively low ultrasonic frequencies of 20 kHz and 100 kHz, there is a peak in bubble temperature as a function of acoustic amplitude which is the pressure amplitude of ultrasound (Fig. 5 (a)). The reason is as follows [25]. As the acoustic amplitude increases, a bubble expands more and the amount of water vapor entering a bubble by evaporation increases. As a result, the amount of water vapor trapped inside a bubble at the end of the violent collapse increases. It should be noted that condensation of water vapor at the bubble wall during the violent bubble collapse is strongly in non-equilibrium due to the high speed of the bubble collapse [41]. Thus the amount of water vapor trapped inside a bubble at the end of the bubble collapse increases as the amount of water vapor entering a bubble during bubble expansion increases. In other words, the vapor fraction, which is a mole fraction of water vapor inside an air bubble, increases as the acoustic amplitude increases (Fig. 5 (b)). Too much vapor fraction decreases the bubble temperature because water vapor has a larger molar heat than that of air and the endothermic heat of vapor dissociation cools the bubble considerably [16], [25], [42]. This is the reason for the existence of the peak in bubble temperature for 20 kHz and 100 kHz in Fig. 5 (a). For higher ultrasonic frequencies, the vapor fraction at the end of the violent collapse is very small due to shorter time for bubble expansion caused by shorter acoustic period. Thus, the bubble temperature increases as the acoustic amplitude increases although it is saturated at relatively high acoustic amplitudes [25].
Fig. 5.
The calculated result as a function of acoustic amplitude for various ultrasonic frequencies (20 kHz, 100 kHz, 300 kHz, and 1 MHz) for the first collapse of an isolated spherical air bubble [25]. The ambient bubble radii are 5 μm for 20 kHz, 3.5 μm for 100 and 300 kHz, and 1 μm for 1 MHz. (a) The temperature inside a bubble at the final stage of the bubble collapse. (b) The molar fraction of water vapor inside a bubble at the end of the bubble collapse. Reprinted from J. Chem. Phys., vol. 127, K. Yasui, T.Tuziuti, T. Kozuka, A. Towata, and Y.Iida, Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound, 154502, Copyright (2007), with the permission of AIP Publishing.
Fig. 6.
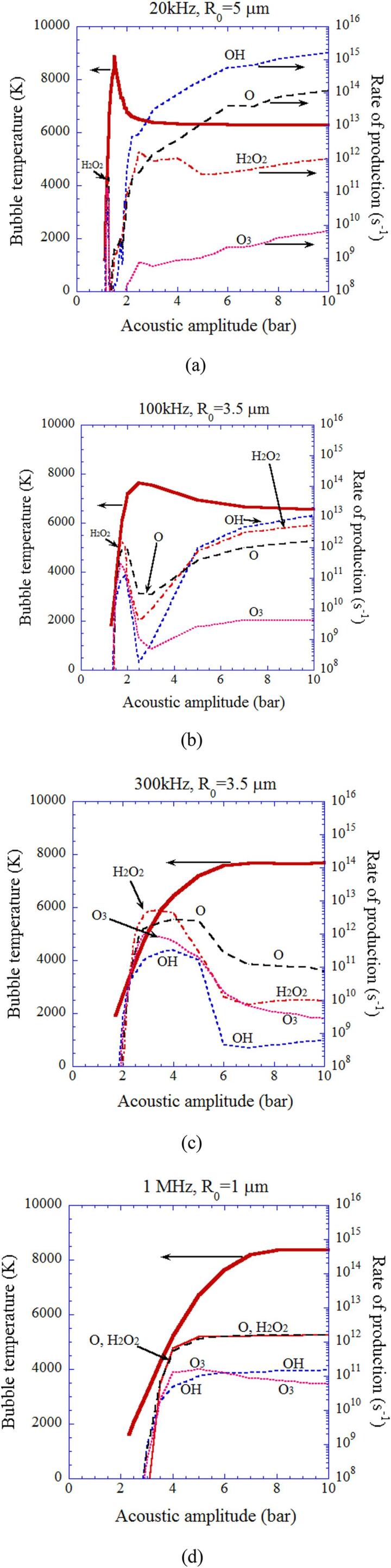
The rate of production of each oxidant inside an isolated spherical air bubble per second calculated by the first bubble collapse as a function of acoustic amplitude with the temperature inside a bubble at the end of the bubble collapse (the thick line): (a) 20 kHz and R0 = 5 μm. (b) 100 kHz and R0 = 3.5 μm. (c) 300 kHz and R0 = 3.5 μm. (d) 1 MHz and R0 = 1 μm [25]. Reprinted from J. Chem. Phys., vol. 127, K. Yasui, T. Tuziuti, T. Kozuka, A. Towata, and Y.Iida, Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound, 154502, Copyright (2007), with the permission of AIP Publishing.
Fig. 7.
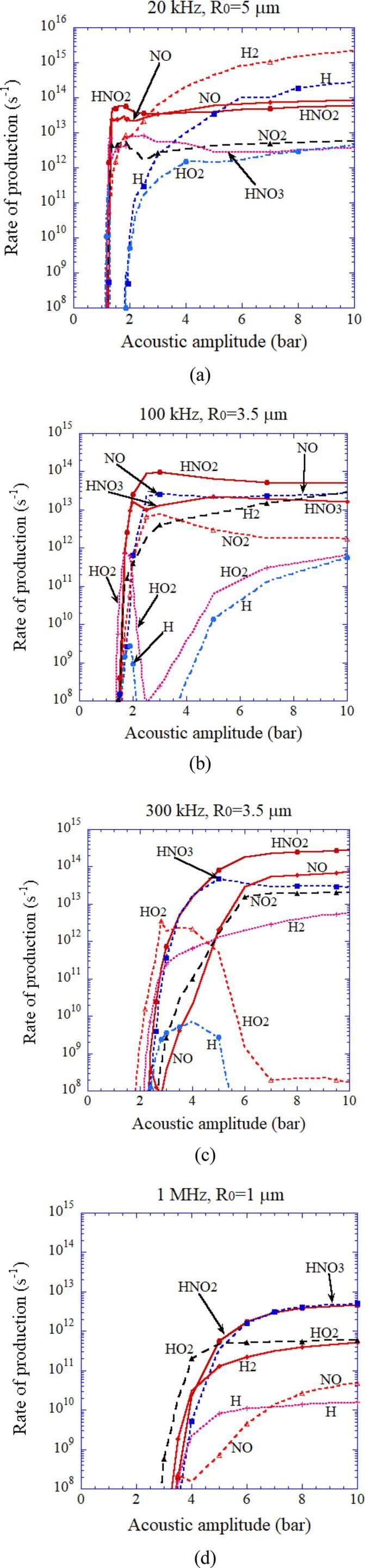
The rate of production of other main chemical species inside an isolated spherical air bubble per second calculated by the first bubble collapse as a function of acoustic amplitude [25]. (a) 20 kHz and R0 = 5 μm. (b) 100 kHz and R0 = 3.5 μm. (c) 300 kHz and R0 = 3.5 μm. (d) 1 MHz and R0 = 1 μm. Reprinted from J. Chem. Phys., vol. 127, K. Yasui, T. Tuziuti, T. Kozuka, A. Towata, and Y. Iida, Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound, 154502, Copyright (2007), with the permission of AIP Publishing.
In Fig. 6, the rate of production of oxidants such as OH and O radicals as well as H2O2 and O3 inside an air bubble in water per second calculated by the first collapse are shown with the temperature inside a bubble at the end of the violent collapse as a function of acoustic amplitude for various ultrasonic frequencies [25]. When the bubble temperature is higher than 7000 K except for the case of 1 MHz, the amount of oxidants produced inside an air bubble is relatively small because the oxidants are strongly consumed inside an air bubble by oxidizing nitrogen (N2) [19], [25]. As a result, under the condition, large amounts of HNOx and NOx are produced inside an air bubble (Fig. 7) [25]. For the ultrasonic frequency of 1 MHz, oxidants are not so much consumed inside an air bubble even at higher temperature than 7000 K because of the much shorter duration of high temperature due to the small size of a bubble (R0 = 1 μm, where R0 is the ambient radius which is the bubble radius when ultrasound is absent). The typical size of a bubble at each ultrasonic frequency is determined according to the experimental data [43], [44] for active bubbles, which is probably determined by the shape instability of a bubble at each ultrasonic frequency [26], [45].
5. Influence of bubble size
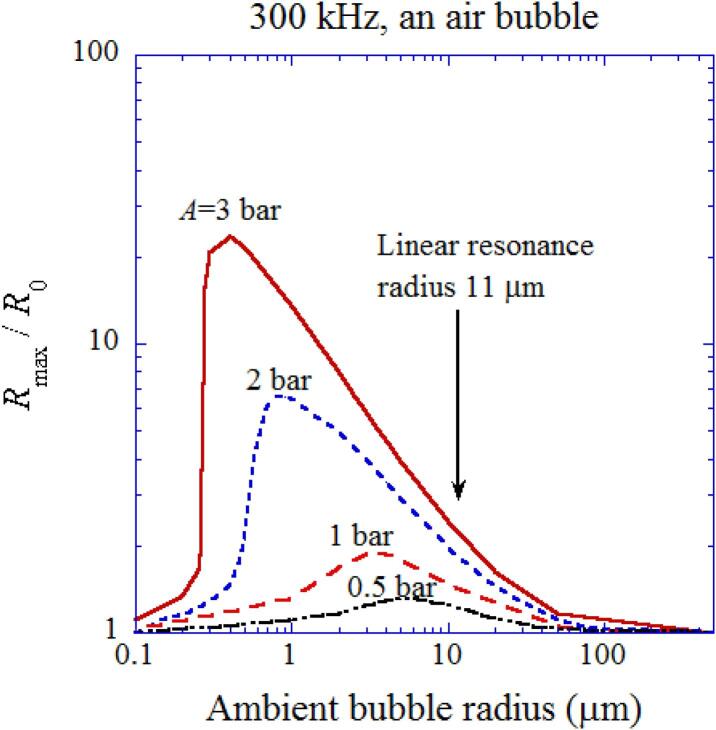
The influence of ambient bubble radius (R0) is discussed [26]. In typical experiments of sonochemistry, the acoustic amplitude is relatively high such as more than 1 atm (=1.013 bar = 1.013 × 105 Pa) [10]. Accordingly, the bubble pulsation is strongly nonlinear (non-sinusoidal) as already seen in Fig. 3 (a) [21]. At 300 kHz, the linear resonance radius of a bubble is about R0 = 11 μm [10], [26]. However, the peak in the expansion ratio (Rmax/R0, where Rmax is the maximum bubble radius at the bubble expansion) is at significantly smaller R0 than the linear resonance radius due to the nonlinearity of the bubble pulsation (Fig. 8) [26]. As the acoustic amplitude increases, the peak of the expansion ratio shifts to smaller R0, which is called the nonlinear resonance radius [10]. Even at acoustic amplitude as low as 0.5 bar, the nonlinear resonance radius is considerably smaller than the linear resonance radius.
Fig. 8.
The calculated expansion ratio () as a function of ambient bubble radius for various acoustic amplitudes at 300 kHz [26]. Both the horizontal and vertical axes are in logarithmic scale. Reprinted from J. Chem. Phys., vol. 128, K. Yasui, T. Tuziuti, J. Lee, T. Kozuka, A. Towata, and Y. Iida, The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions, 184705, Copyright (2008), with the permission of AIP Publishing.
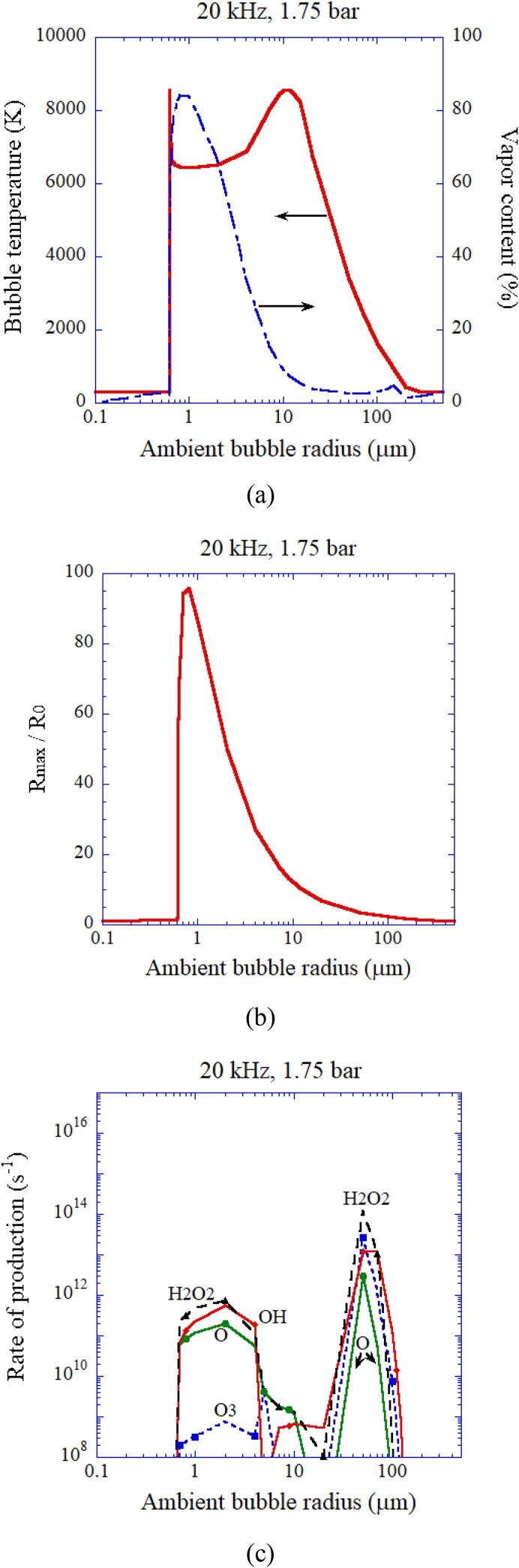
In Fig. 9, the calculated results are shown as a function of ambient radius of an air bubble at 20 kHz and 1.75 bar in ultrasonic frequency and acoustic amplitude, respectively [26]. As in the case of Fig. 5, the bubble temperature is relatively low when the vapor fraction at the end of the bubble collapse is relatively high (Fig. 9 (a)). From Fig. 9 (b), the nonlinear resonance radius is 0.8 μm, which is more than two orders of magnitude smaller than the linear resonance radius of 164 μm at 20 kHz. As in the case of Fig. 6, the rate of production of oxidants becomes relatively low when the bubble temperature is higher than 7000 K (Fig. 9 (c)). The range of ambient bubble radius for an active bubble is from the Blake threshold radius of 0.63 μm at 1.75 bar to near the linear resonance radius of 164 μm [26]. The Blake threshold is threshold for large expansion of a bubble at relatively low ultrasonic frequency [46].
Fig. 9.
The calculated result as a function of ambient bubble radius of an air bubble at 20 kHz and 1.75 bar in ultrasonic frequency and acoustic amplitude, respectively [26]. The horizontal axis is in logarithmic scale. (a) The peak temperature (solid) and the molar fraction of water vapor (dash dotted) inside a bubble at the end of the bubble collapse. (b) The expansion ratio (). (c) The rate of production of each oxidant with the logarithmic vertical axis. Reprinted from J. Chem. Phys., vol. 128, K. Yasui, T. Tuziuti, J. Lee, T. Kozuka, A. Towata, and Y. Iida, The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions, 184705, Copyright (2008), with the permission of AIP Publishing.
6. Acoustic field
In usual experiments of sonochemistry which is a multibubble system, not only chemical reaction-rates in each bubble but also spatial distribution of number density of bubbles and acoustic amplitude are relevant to the total sonochemical activity [47], [48], [49], [50], [51], [52], [53]. In this section, numerical simulations of an acoustic field (spatial distribution of acoustic amplitude) are discussed [53].
In this section, the commercially available FEM (finite element method) software has been utilized (PAFEC-vibroacoustics, PACSYS Ltd.). In the software, the coupling of the acoustic field and the vibration of the reactor’s wall has been taken into account. For details, please see Ref. [53].
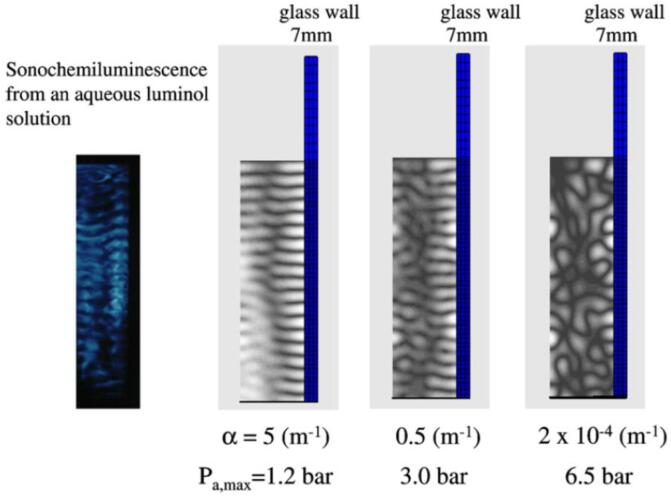
In the present FEM formulation, complex bulk modulus of the liquid is used in order to take into account the attenuation of ultrasound. In Fig. 10, the results of the FEM calculations on the spatial distribution of acoustic amplitude are shown for various attenuation coefficients of ultrasound [53]. The ultrasonic frequency is 100 kHz and the internal dimensions of the rectangular liquid container is 7 cm × 7 cm × 20 cm. The liquid (water at 20 °C) height is 13.9 cm. Only a half plane of the rectangular container is shown in Fig. 10. For comparison, the photograph of sonochemiluminescence from an aqueous solution is shown for the corresponding half plane [53], [54]. The calculated result for the attenuation coefficient of (m−1) corresponds to the case when no bubble exists in the liquid. In this case, the side wall of the liquid container vibrates strongly due to high acoustic amplitude. It results in the very complex spatial pattern of an acoustic field as seen in Fig. 10 because vibrating side wall radiates strong acoustic (ultrasonic) waves into the liquid [53].
Fig. 10.
The calculated spatial distribution of the acoustic amplitude for glass wall (7 mm in thickness) for various attenuation coefficients of ultrasound [53]. The photograph of sonochemiluminescence from an aqueous luminol solution has been also shown for the corresponding half plane. Reprinted from Ultrason. Sonochem., vol. 14, K. Yasui, T. Kozuka, T. Tuziuti, A. Towata, Y. Iida, J. King, and P. Macey, FEM calculation of an acoustic field in a sonochemical reactor, pp. 605–614, Copyright (2007), with permission from Elsevier.
When the attenuation coefficient is (m−1), the calculated spatial distribution of acoustic amplitude is similar to the spatial pattern of sonochemiluminescence. For the both images, horizontal stripes of pressure antinodes and nodes in the standing wave are clearly seen as well as a vertical line of a pressure node. When the attenuation coefficient is (m−1), some horizontal stripes of the standing-wave pattern are disconnected. Thus it is concluded that the actual attenuation coefficient of ultrasound in a bubbly liquid under ultrasound is in the range of 0.5 – 5 (m−1) [53].
When the side glass wall is thin (2 mm in thickness), the side wall nearly freely vibrates under ultrasound. Thus, there is a vertical line of pressure node near the side wall in this case (Fig. 11) [53]. It should be noted that the liquid surface is always a pressure node because the liquid surface vibrates freely.
Fig. 11.

The calculated spatial distribution of the acoustic amplitude for glass wall with internal friction (2 mm in thickness) [53]. The attenuation coefficient is 5 m−1. Reprinted from Ultrason. Sonochem., vol. 14, K. Yasui, T. Kozuka, T. Tuziuti, A. Towata, Y. Iida, J. King, and P. Macey, FEM calculation of an acoustic field in a sonochemical reactor, pp. 605–614, Copyright (2007), with permission from Elsevier.
7. Sonochemical synthesis of nanoparticles
Although sonochemical synthesis of nanoparticles has been intensively studied experimentally [55], [56], [57], [58], [59], [60], [61], [62], there are few numerical simulations on this topic probably because of the complex nature of the particle synthesis [63], [64], [65]. Kordylla et al. [66] performed excellent numerical simulations of sonocrystallization which is crystallization under ultrasound. In the first part of this section [63], numerical simulations of sonochemical production of BaTiO3 nanoparticles are discussed using a model developed from the model of Kordylla et al. [66].
Dang et al. [67], [68], [69] experimentally reported sonochemical synthesis of BaTiO3 nanoparticles. The starting materials were BaCl2 and TiCl4 in aqueous solution at pH14 in which Ar gas was dissolved. The aqueous solution was irradiated with ultrasound at 20 kHz using an ultrasonic horn for 20 min at 80 °C. Then BaTiO3 nanoparticles were formed, which were spherical aggregates consisting of spherical nanocrystals of 5–10 nm in diameter. The diameter of an aggregate was 100–400 nm depending on the initial concentration of BaCl2 and TiCl4 [67]. Surprisingly, crystal axes of BaTiO3 nanocrystals were aligned in an aggregate, which was confirmed by the selected area electron diffraction (SAED) pattern [68], [69]. In other words, an aggregate of BaTiO3 nanocrystals is mesocrystal which has been intensively studied since 2005 [70], [71], [72], [73], [74], [75]. With simple mechanical stirring instead of ultrasound irradiation, BaTiO3 particles were produced only after 8 h and they were neither mesocystals nor aggregates but larger particles with irregular shape [67], [68], [69].
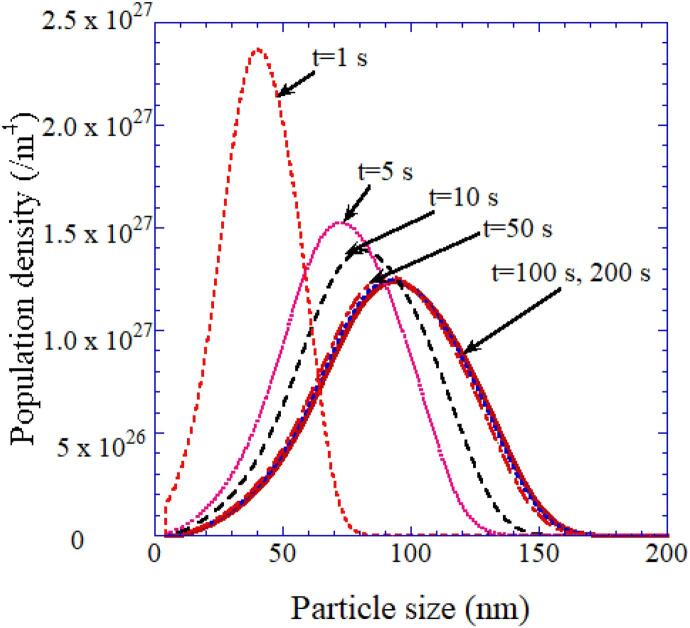
Firstly, aggregation process is numerically simulated using two different models [63]. One is the normal model used in aerosol dynamics that any particles aggregate when they collide. The other is a new model that only primary particle (a single nanocrystal) aggregates with other particles (any aggregates or a primary particle). According to the numerical simulations, the normal model results in the peak at the size of a primary particle (5–10 nm) in the size distribution of particles (aggregates) [63]. It disagrees with the experimental result of the peak at around 100 nm for the initial concentration of BaCl2 and TiCl4 of 0.4 mol/L [67]. On the other hand, the new model results in the peak at around 100 nm, which agrees with the experimental result (Fig. 12) [63], [67]. Thus, it is suggested that only primary particles (or possibly only small aggregates) aggregate with other particles.
Fig. 12.
The calculated results on temporal development of sonochemically synthesized BaTiO3 particle (aggregate) size-distribution when the initial concentration of BaCl2 and TiCl4 is 0.4 mol/L [63]. Reprinted from Ultrason. Sonochem., vol. 18, K. Yasui, T. Tuziuti, and K. Kato, Numerical simulations of sonochemical production of BaTiO3 nanoparticles, pp. 1211–1217, Copyright (2011), with permission from Elsevier.
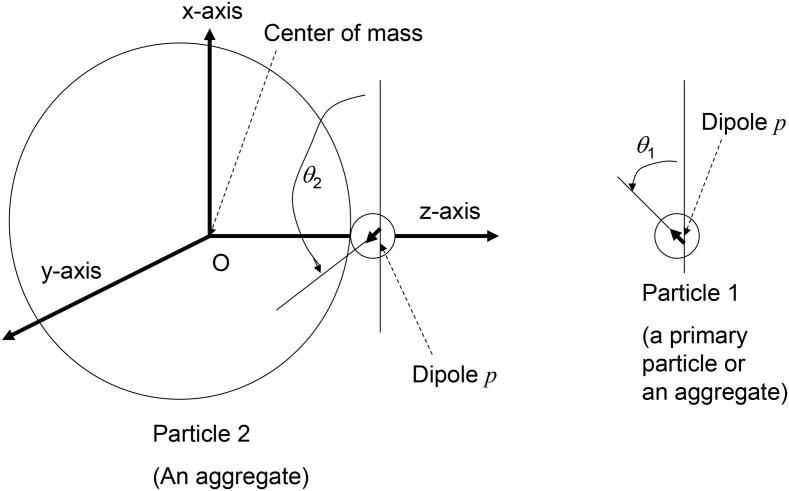
Then, what is the reason for such restriction in aggregation? Furthermore, what is the reason for the alignment of crystal axes in an aggregate? In order to study the mechanisms, numerical simulations of collisions of particles are performed using the Newton’s equation of translational motion and the equation of rotation of particles (Fig. 13) [64], [76]. For the equation of translational motion, electric dipole–dipole interaction, repulsive double layer interaction with zeta potential of −40 mV, and attractive interaction due to hydrogen bond between –OH on the surface of BaTiO3 nanocrystals are considered [64]. The magnitude of electric dipole moment in a primary particle (a single BaTiO3 nanocrystal) of 10 nm in diameter is assumed as 69.6 D (=2.32 × 10−28 (C m)) from the condition of tetragonal crystal structure stabilized by adsorbate-induced charge screening [64], [77]. Without adsorbate-induced charge screening, 10 nm BaTiO3 nanocrystals become cubic crystal structure due to the size effect caused by the increased free energy of tetragonal crystal structure by depolarization field [77]. For the equation of rotation, the following torques are considered; torque due to electric dipole–dipole interaction, van der Waals torque, torque due to friction caused by viscosity of the liquid, torque due to dynamic friction when the two particles are attached, and random torque causing the rotational Brownian motion [64].
Fig. 13.
Configuration of a collision between two particles [76]. Reprinted with permission from J. Phys. Chem. C, vol. 116, K. Yasui and K. Kato, Dipole-dipole interaction model for oriented attachment of BaTiO3 nanocrystals: a route to mesocrystal formation, pp. 319–324, Copyright (2012), American Chemical Society.
For a collision between an aggregate and a primary particle (or an aggregate), only the nearest primary particles are considered for the electric dipole–dipole interaction because the Debye length is only 0.3 nm at pH 14 in the experiment (Fig. 13) [64], [67], [68], [69], [76]. For the rotational motion, electric dipole–dipole interaction makes a pair of dipoles in antiparallel. On the other hand, van der Waals torque makes a pair of dipoles in parallel or antiparallel because van der Waals torque solely makes a pair of optical axes (due to the anisotropy in dielectric constant) aligned [78], [79].
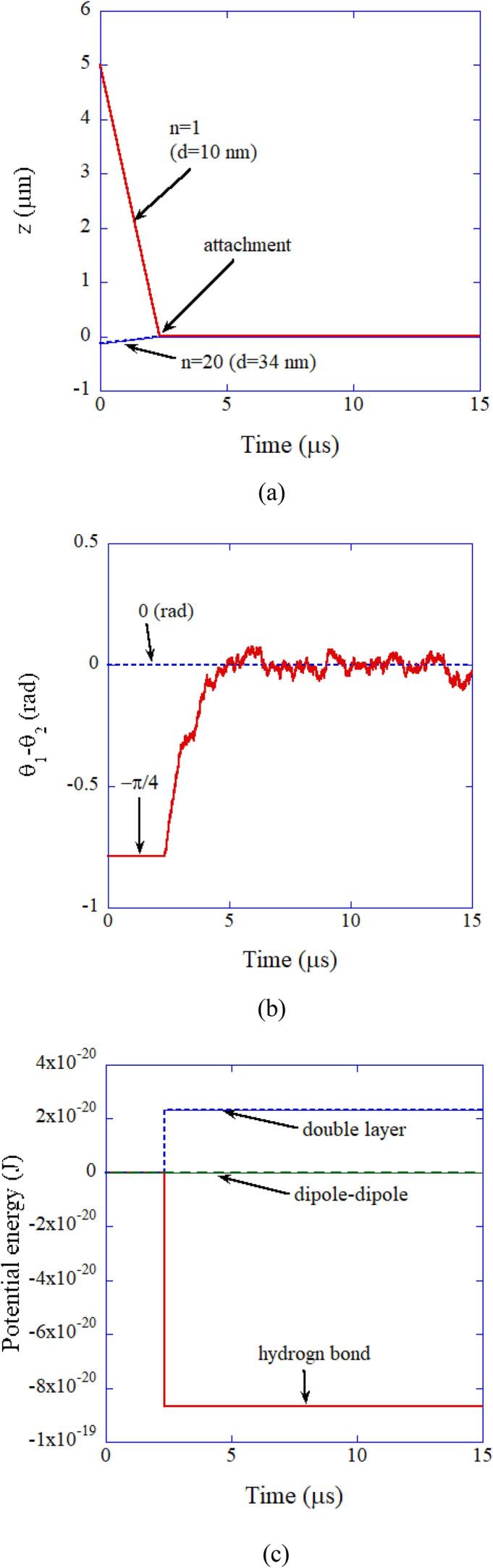
In Fig. 14, the result of numerical simulation on the collision between a primary particle (10 nm) and an aggregate (34 nm) consisting of 20 primary particles is shown [64]. The two particles are attached by attractive interaction due to hydrogen bond at time 2.3 μs. The two dipoles are aligned in parallel due to van der Waals torque. In other words, the crystal axes are aligned by van der Waals torque.
Fig. 14.
The result of the numerical simulation on the collision between a primary particle (n = 1, d = 10 nm) and an aggregate (n = 20, d = 34 nm) consisting of 20 primary particles of 10 nm in diameter in aqueous solution at pH 14 as a function of time for 15 μs [64]. (a) The position of each particle. (b) The relative angle of the two dipoles. (c) The potential energy. Reprinted from Ultrason. Sonochem., vol. 35, K. Yasui and K. Kato, Numerical simulations of sonochemical production and oriented aggregation of BaTiO3 nanocrystals, pp. 673–680, Copyright (2017), with permission from Elsevier.
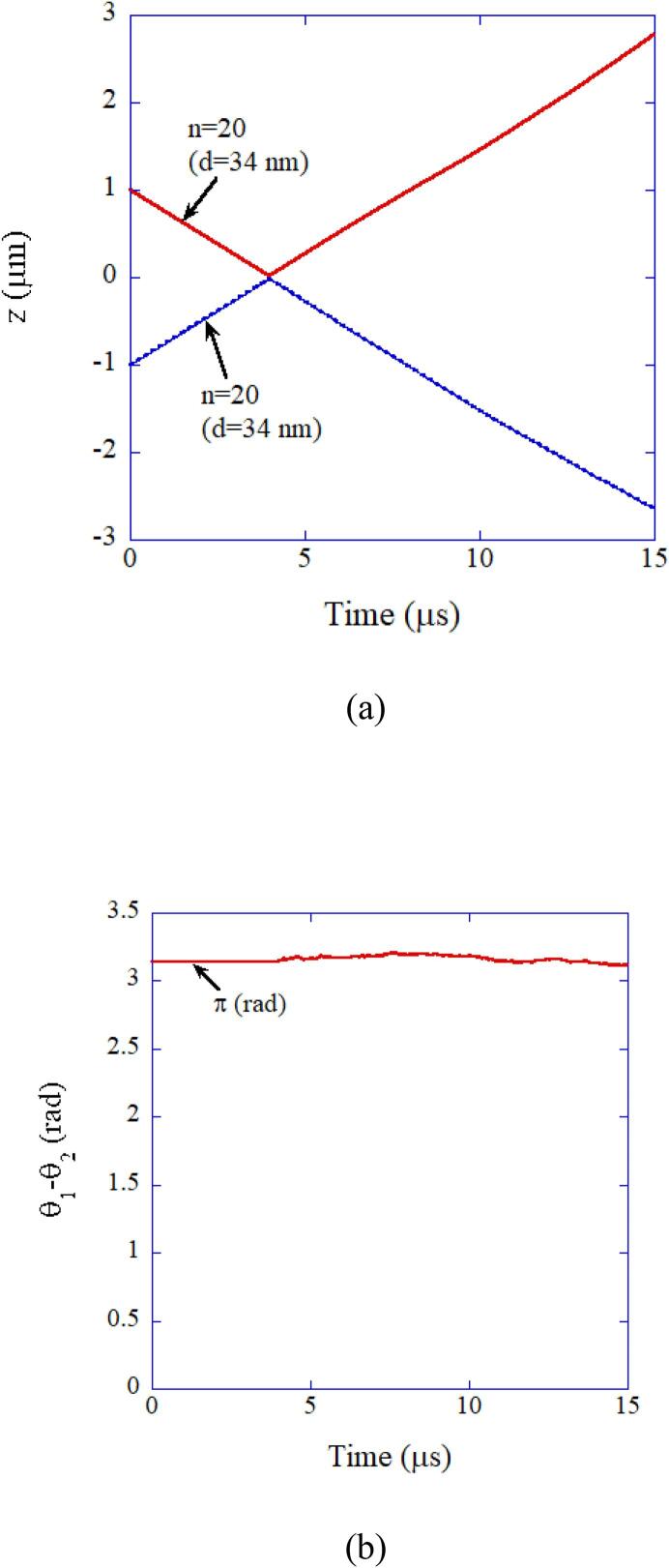
In Fig. 15, the result of numerical simulation on the collision between two aggregates (34 nm) consisting of 20 primary particles is shown [64]. The two aggregates never attach each other due to repulsive double-layer interaction. As the repulsive double-layer interaction is stronger for larger particles, larger aggregates than n = 20 never aggregate. This is the reason for the success of the new model of aggregation in Fig. 12 [63], [64].
Fig. 15.
The result of the numerical simulation on the collision between two aggregates (n = 20, d = 34 nm) consisting of primary particles of 10 nm in diameter [64]. (a) The position of each particle. (b) The relative angle of the two dipoles. Reprinted from Ultrason. Sonochem., vol. 35, K. Yasui and K. Kato, Numerical simulations of sonochemical production and oriented aggregation of BaTiO3 nanocrystals, pp. 673–680, Copyright (2017), with permission from Elsevier.
8. Unsolved problems
In sections 3–5, chemical reactions inside a bubble are numerically simulated, and chemical reactions in the liquid phase are not simulated. One of the unsolved problems in numerical simulations for sonochemistry is the chemical reactions in the liquid phase outside a bubble [80], [81], [82], [83], [84]. The important questions are as follows. What is the lifetime of O radicals in the liquid phase [10], [37]? What is the role of O atoms in sonochemical reactions in the liquid phase?
Another unsolved problem is the effect of bubble–bubble interaction on sonochemical reaction rates [85], [86]. In a multibubble system, bubble pulsation is strongly influenced by the presence of surrounding bubbles because each bubble radiates acoustic (ultrasonic) waves into the surrounding liquid, which is called bubble–bubble interaction [85], [86], [87], [88], [89], [38], [90], [91], [92]. The important questions are as follows. What is the chemical activity of bubble clusters [93], [94], [95]? What is the role of bubble-shape instability on chemical activity [93], [96]? For numerical simulations of bubble clusters, large parameter scans are required such as bubble size distribution, bubble number density, ultrasonic frequency and pressure amplitude, etc. [97], [28]. Furthermore, chemical kinetic model has been continuously updated [98], [99], and numerical simulations for sonochemistry using updated chemical kinetic model are required. Numerical simulations with complex chemical kinetics in the presence of hydrocarbons should also be performed in future [100], [101], [102].
With regard to an acoustic field, role of Anderson localization of an acoustic (ultrasonic) wave in a bubbly liquid is to be studied [103], [104]. Some experiments on sonoluminescence (SL) have indicated that spatial localization of SL intensity occurs when there are some visibly large bubbles in the liquid [105]. On the other hand, in the absence of visibly large bubbles, the spatial distribution of SL intensity is rather uniform [105]. It suggests that Anderson localization of acoustic waves occurs when there are some visibly large bubbles in a cavitating liquid.
9. Conclusion
The bubble dynamics model including the effect of non-equilibrium chemical reactions inside a bubble has been validated through the study of single-bubble sonochemistry [21], [39]. Numerical simulations based on the model have revealed that there is an optimum bubble temperature for production of oxidants inside an air bubble because at higher temperature oxidants are strongly consumed inside an air bubble by oxidizing nitrogen [18], [19], [25], [26]. Numerical simulations of sonochemical production of nanoparticles as well as spatial distribution of acoustic amplitude in a sonochemical reactor are also discussed [53], [63], [64]. Finally, unsolved problems are described.
CRediT authorship contribution statement
Kyuichi Yasui: Conceptualization, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The author would like to thank his collaborators in his research.
References
- 1.H. Nomura, S. Koda, What is sonochemistry?, in: F.Grieser, P.Choi, N. Enomoto, H. Harada, K. Okitsu, K. Yasui (Eds.), Sonochemistry and the Acoustic Bubble, Elsevier, Amsterdam, 2015, pp. 1-9, 10.1016/B978-0-12-801530-8.00001-3.
- 2.D.F. Gaitan, L.A. Crum, Observation of sonoluminescence from a single, stable cavitation bubble in a water glycerin mixture, in: M.F. Hamilton, D.T.Blackstock (Eds.), Frontiers of Nonlinear Acoustics, Proc. 12th ISNA, Elsevier Appl. Sci. Pub., 1990, pp. 459-463.
- 3.Yasui K., Tuziuti T., Sivakumar M., Iida Y. Sonoluminescence. Appl. Spectrosc. Rev. 2004;39(3):399–436. doi: 10.1081/ASR-200030202. [DOI] [Google Scholar]
- 4.Brenner M.P., Hilgenfeldt S., Lohse D. Single-bubble sonoluminescence. Rev. Mod. Phys. 2002;74(2):425–484. doi: 10.1103/RevModPhys.74.425. [DOI] [PubMed] [Google Scholar]
- 5.Young F.R. CRC Press; Boca Raton: 2005. Sonoluminescence. [Google Scholar]
- 6.Barber B.P., Putterman S.J. Observation of synchronous picosecond sonoluminescence. Nature (London) 1991;352(6333):318–320. doi: 10.1038/352318a0. [DOI] [Google Scholar]
- 7.Koda S., Kimura T., Kondo T., Mitome H. A standard method to calibrate sonochemical efficiency of an individual reaction system. Ultrason. Sonochem. 2003;10(3):149–156. doi: 10.1016/S1350-4177(03)00084-1. [DOI] [PubMed] [Google Scholar]
- 8.Tuziuti T., Yasui K., Sivakumar M., Iida Y., Miyoshi N. Correlation between acoustic cavitation noise and yield enhancement of sonochemical reaction by particle addition. J. Phys. Chem. A. 2005;109(21):4869–4872. doi: 10.1021/jp0503516. [DOI] [PubMed] [Google Scholar]
- 9.Asakura Y. In: Sonochemistry and the Acoustic Bubble. Grieser F., Choi P., Enomoto N., Harada H., Okitsu K., Yasui K., editors. Elsevier; Amsterdam: 2015. Experimental methods in sonochemistry; pp. 119–150. [DOI] [Google Scholar]
- 10.Yasui K. Acoustic Cavitation and Bubble Dynamics, Springer, Cham. Switzerland. 2018 doi: 10.1007/978-3-319-68237-2. [DOI] [Google Scholar]
- 11.Kamath V., Prosperetti A., Egolfopoulos F.N. A theoretical study of sonoluminescence. J. Acoust. Soc. Am. 1993;94(1):248–260. doi: 10.1121/1.407083. [DOI] [Google Scholar]
- 12.Yasui K. Alternative model of single-bubble sonoluminescence. Phys. Rev. E. 1997;56(6):6750–6760. doi: 10.1103/PhysRevE.56.6750. [DOI] [Google Scholar]
- 13.Gong C., Hart D.P. Ultrasound induced cavitation and sonochemical yields. J. Acoust. Soc. Am. 1998;104(5):2675–2682. doi: 10.1121/1.423851. [DOI] [Google Scholar]
- 14.Storey B.D., Szeri A.J. Water vapour, sonoluminescence and sonochemistry. Proc. R. Soc. Lond. A. 2000;456(1999):1685–1709. doi: 10.1098/rspa.2000.0582. [DOI] [Google Scholar]
- 15.Storey B.D., Szeri A.J. A reduced model of cavitation physics for use in sonochemistry. Proc. R. Soc. Lond. A. 2001;457(2011):1685–1700. doi: 10.1098/rspa.2001.0784. [DOI] [Google Scholar]
- 16.Yasui K. Effect of liquid temperature on sonoluminescence. Phys. Rev. E. 2001;64 doi: 10.1103/PhysRevE.64.016310. [DOI] [PubMed] [Google Scholar]
- 17.Yasui K. Effect of volatile solutes on sonoluminescence. J. Chem. Phys. 2002;116(7):2945–2954. doi: 10.1063/1.1436122. [DOI] [Google Scholar]
- 18.Yasui K., Tuziuti T., Iida Y., Mitome H. Theoretical study of the ambient-pressure dependence of sonochemical reactions. J. Chem. Phys. 2003;119(1):346–356. doi: 10.1063/1.1576375. [DOI] [Google Scholar]
- 19.Yasui K., Tuziuti T., Iida Y. Optimum bubble temperature for the sonochemical production of oxidants. Ultrasonics. 2004;42(1-9):579–584. doi: 10.1016/j.ultras.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 20.Yuan L. Sonochemical effects on single-bubble sonoluminescence. Phys. Rev. E. 2005;72 doi: 10.1103/PhysRevE.72.046309. [DOI] [PubMed] [Google Scholar]
- 21.Yasui K., Tuziuti T., Sivakumar M., Iida Y. Theoretical study of single-bubble sonochemistry. J. Chem. Phys. 2005;122 doi: 10.1063/1.1925607. [DOI] [PubMed] [Google Scholar]
- 22.Yasui K., Tuziuti T., Iida Y. Dependence of the characteristics of bubbles on types of sonochemical reactors. Ultrason. Sonochem. 2005;12(1-2):43–51. doi: 10.1016/j.ultsonch.2004.06.003. [DOI] [PubMed] [Google Scholar]
- 23.An Y. Mechanism of single-bubble sonoluminescence. Phys. Rev. E. 2006;74 doi: 10.1103/PhysRevE.74.026304. [DOI] [PubMed] [Google Scholar]
- 24.Hauke G., Fuster D., Dopazo C. Dynamics of a single cavitating and reacting bubble. Phys. Rev. E. 2007;75 doi: 10.1103/PhysRevE.75.066310. [DOI] [PubMed] [Google Scholar]
- 25.Yasui K., Tuziuti T., Kozuka T., Towata A., Iida Y. Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound. J. Chem. Phys. 2007;127 doi: 10.1063/1.2790420. [DOI] [PubMed] [Google Scholar]
- 26.Yasui K., Tuziuti T., Lee J., Kozuka T., Towata A., Iida Y. The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions. J. Chem. Phys. 2008;128 doi: 10.1063/1.2919119. [DOI] [PubMed] [Google Scholar]
- 27.Merouani S., Hamdaoui O., Rezgui Y., Guemini M. Sensitivity of free radicals production in acoustically driven bubble to the ultrasonic frequency and nature of dissolved gases. Ultrason. Sonochem. 2015;22:41–50. doi: 10.1016/j.ultsonch.2014.07.011. [DOI] [PubMed] [Google Scholar]
- 28.Kalmar C., Klapcsik K., Hegedus F. Relationship between the radial dynamics and the chemical production of a harmonically driven spherical bubble. Ultrason. Sonochem. 2020;64 doi: 10.1016/j.ultsonch.2020.104989. [DOI] [PubMed] [Google Scholar]
- 29.Wu C.C., Roberts P.H. Shock-wave propagation in a sonoluminescing gas bubble. Phys. Rev. Lett. 1993;70(22):3424–3427. doi: 10.1103/PhysRevLett.70.3424. [DOI] [PubMed] [Google Scholar]
- 30.Moss W.C., Clarke D.B., White J.W., Young D.A. Hydrodynamic simulations of bubble collapse and picosecond sonoluminescence. Phys. Fluids. 1994;6:2979–2985. doi: 10.1063/1.868124. [DOI] [Google Scholar]
- 31.Kondic L., Gersten J.I., Yuan C. Theoretical studies of sonoluminescence radiation: radiative transfer and parametric dependence. Phys. Rev. E. 1995;52:4976–4990. doi: 10.1103/PhysRevE.52.4976. [DOI] [PubMed] [Google Scholar]
- 32.Vuong V.Q., Szeri A.J. Sonoluminescence and diffusive transport. Phys. Fluids. 1996;8:2354–2364. doi: 10.1063/1.869020. [DOI] [Google Scholar]
- 33.Yuan L., Cheng H.Y., Chu M.C., Leung P.T. Physical parameters affecting sonoluminescence: a self-consistent hydrodynamic study. Phys. Rev. E. 1998;57:4265–4280. doi: 10.1103/PhysRevE.57.4265. [DOI] [Google Scholar]
- 34.Cheng H.Y., Chu M.C., Leung P.T., Yuan L. How important are shock waves to single-bubble sonoluminescence. Phys. Rev. E. 1998;58:R2705–R2708. doi: 10.1103/PhysRevE.58.R2705. [DOI] [Google Scholar]
- 35.Vuong V.Q., Szeri A.J., Young D.A. Shock formation within sonoluminescence bubbles. Phys. Fluids. 1999;11(1):10–17. doi: 10.1063/1.869920. [DOI] [Google Scholar]
- 36.Yasui K. Variation of liquid temperature at bubble wall near the sonoluminescence threshold. J. Phys. Soc. Jpn. 1996;65(9):2830–2840. doi: 10.1143/JPSJ.65.2830. [DOI] [Google Scholar]
- 37.K. Yasui, Unsolved problems in acoustic cavitation, in: M.Asokkumar, F. Cavalieri, F. Chemat, K. Okitsu, A. Sambandam, K. Yasui, B. Zisu (Eds.), Handbook of Ultrasonics and Sonochemistry, Springer, Singapore, 2016, pp. 259-292. 10.1007/978-981-287-278-4_1.
- 38.Yasui K., Tuziuti T., Lee J., Kozuka T., Towata A., Iida Y. Numerical simulations of acoustic cavitation noise with the temporal fluctuation in the number of bubbles. Ultrason. Sonochem. 2010;17(2):460–472. doi: 10.1016/j.ultsonch.2009.08.014. [DOI] [PubMed] [Google Scholar]
- 39.Didenko Y.T., Suslick K.S. The energy efficiency of formation of photons, radicals and ions during single-bubble cavitation. Nature (London) 2002;418(6896):394–397. doi: 10.1038/nature00895. [DOI] [PubMed] [Google Scholar]
- 40.Lohse D., Brenner M.P., Dupont T.F., Hilgenfeldt S., Johnston B. Sonoluminescing air bubbles rectify argon. Phys. Rev. Lett. 1997;78(7):1359–1362. doi: 10.1103/PhysRevLett.78.1359. [DOI] [Google Scholar]
- 41.Yasui K. Effect of non-equilibrium evaporation and condensation on bubble dynamics near the sonoluminescence threshold. Ultrasonics. 1998;36(1-5):575–580. doi: 10.1016/S0041-624X(97)00107-8. [DOI] [Google Scholar]
- 42.Yasui K. Temperature in multibubble sonoluminescence. J. Chem. Phys. 2001;115(7):2893–2896. doi: 10.1063/1.1395056. [DOI] [Google Scholar]
- 43.Weninger K.R., Camara C.G., Putterman S.J. Observation of bubble dynamics within luminescent cavitation clouds: sonoluminescence at the nano-scale. Phys. Rev. E. 2001;63 doi: 10.1103/PhysRevE.63.016310. [DOI] [PubMed] [Google Scholar]
- 44.Lee J., Ashokkumar M., Kentish S., Grieser F. Determination of the size distribution of sonoluminescence bubbles in a pulsed acoustic field. J. Am. Chem. Soc. 2005;127(48):16810–16811. doi: 10.1021/ja0566432. [DOI] [PubMed] [Google Scholar]
- 45.Yasui K. Influence of ultrasonic frequency on multibubble sonoluminescence. J. Acoust. Soc. Am. 2002;112(4):1405–1413. doi: 10.1121/1.1502898. [DOI] [PubMed] [Google Scholar]
- 46.Yasui K. In: Sonochemistry and the Acoustic Bubble. Grieser F., Choi P., Enomoto N., Harada H., Okitsu K., Yasui K., editors. Elsevier; Amsterdam: 2015. Dynamics of acoustic bubbles; pp. 41–83. [DOI] [Google Scholar]
- 47.Kerboua K., Hamdaoui O. Void frcation, number density of acoustic cavitation bubbles, and acoustic frequency: a numerical investigation. J. Acoust. Soc. Am. 2019;146:2240–2252. doi: 10.1121/1.5126865. [DOI] [PubMed] [Google Scholar]
- 48.Okitsu K., Suzuki T., Takenaka N., Bandow H., Nishimura R., Maeda Y. Acoustic multibubble cavitation in water: a new aspect of the effect of a rare gas atmosphere on bubble temperature and its relevance to sonochemistry. J. Phys. Chem. B. 2006;110:20081–20084. doi: 10.1021/jp064598u. [DOI] [PubMed] [Google Scholar]
- 49.Sutkar V.S., Gogate P.R. Design aspects of sonochemical reactors: techniques for understanding cavitational activity distribution and effect of operating parameters. Chem. Engnrg. J. 2009;155:26–36. doi: 10.1016/j.cej.2009.07.021. [DOI] [Google Scholar]
- 50.Tudela I., Sáez V., Esclapez M.D., Díez-García M.I., Bonete P., González-García J. Simulation of the spatial distribution of the acoustic pressure in sonochemical reactors with numerical methods: a review. Ultrason. Sonochem. 2014;21(3):909–919. doi: 10.1016/j.ultsonch.2013.11.012. [DOI] [PubMed] [Google Scholar]
- 51.Servant G., Laborde J.-L., Hita A., Caltagirone J.-P., Gérard A. Spatio-temporal dynamics of cavitation bubble clouds in a low frequency reactor: comparison between theoretical and experimental results. Ultrason. Sonochem. 2001;8(3):163–174. doi: 10.1016/S1350-4177(01)00074-8. [DOI] [PubMed] [Google Scholar]
- 52.Mettin R., Luther S., Ohl C.-D., Lauterborn W. Acoustic cavitation structures and simulations by a particle model. Ultrason. Sonochem. 1999;6(1-2):25–29. doi: 10.1016/S1350-4177(98)00025-X. [DOI] [PubMed] [Google Scholar]
- 53.Yasui K., Kozuka T., Tuziuti T., Towata A., Iida Y., King J., Macey P. FEM calculation of an acoustic field in a sonochemical reactor. Ultrason. Sonochem. 2007;14(5):605–614. doi: 10.1016/j.ultsonch.2006.09.010. [DOI] [PubMed] [Google Scholar]
- 54.Hatanaka S.-ichi., Yasui K., Tuziuti T., Mitome H. Difference in threshold between sono- and sonochemical luminescence. Jpn. J. Appl. Phys. 2000;39(Part 1, No. 5B):2962–2966. doi: 10.1143/JJAP.39.2962. [DOI] [Google Scholar]
- 55.Gedanken A. Using sonochemistry for the fabrication of nanomaterials. Ultrason. Sonochem. 2004;11(2):47–55. doi: 10.1016/j.ultsonch.2004.01.037. [DOI] [PubMed] [Google Scholar]
- 56.Okitsu K., Cavalieri F. Sonochemical Production of Nanomaterials, Springer, Cham. Switzerland. 2018 doi: 10.1007/978-3-319-96734-9. [DOI] [Google Scholar]
- 57.Manickam S., Ashokkumar M., editors. Cavitation: A Novel Energy-Efficient Technique for the Generation of Nanomaterials. Pan Stanford; Singapore: 2014. [Google Scholar]
- 58.S. Anandan, M. Ashokkumar, Sonochemical preparation of monometallic, bimetallic and metal-loaded semiconductor nanoparticles, in: Pankaj, M. Ashokkumar (Eds.), Theoretical and Experimental Sonochemistry Involving Inorganic Systems, Springer, Dordrecht, 2011, pp. 151-169. 10.1007/978-90-481-3887-6_6.
- 59.Pollet B.G. The use of ultrasound for the fabrication of fuel cell materials. Intern. J. Hydrogen Energy. 2010;35(21):11986–12004. doi: 10.1016/j.ijhydene.2010.08.021. [DOI] [Google Scholar]
- 60.Muthoosamy K., Manickam S. State of the art and recent advances in the ultrasound-assisted synthesis, exfoliation and functionalization of graphene derivatives. Ultrason. Sonochem. 2017;39:478–493. doi: 10.1016/j.ultsonch.2017.05.019. [DOI] [PubMed] [Google Scholar]
- 61.Yu C., Yu J.C., He H., Zhou W. Progress in sonochemical fabrication of nanostructures photocatalysts. Rare Met. 2016;35:211–222. doi: 10.1007/s12598-016-0694-7. [DOI] [Google Scholar]
- 62.Dheyab M.A., Aziz A.A., Jameel M.S. Recent advances in inorganic nanomaterials synthesis using sonochemistry: a comprehensive review on iron oxide, gold and iron oxide coated gold nanoparticles. Molecules. 2021;26:2453. doi: 10.3390/molecules26092453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Yasui K., Tuziuti T., Kato K. Numerical simulations of sonochemical production of BaTiO3 nanoparticles. Ultrason. Sonochem. 2011;18(5):1211–1217. doi: 10.1016/j.ultsonch.2011.03.006. [DOI] [PubMed] [Google Scholar]
- 64.Yasui K., Kato K. Numerical simulations of sonochemical production and oriented aggregation of BaTiO3 nanocrystals. Ultrason. Sonochem. 2017;35:673–680. doi: 10.1016/j.ultsonch.2016.05.009. [DOI] [PubMed] [Google Scholar]
- 65.Yasui K., Kato K. In: Cavitation: A Novel Energy-Efficient Technique for the Generation of Nanomaterials. Manickam S., Ashokkumar M., editors. Pan Stanford; Singapore: 2014. Numerical simulations of nucleation and aggregation of BaTiO3 nanocrystals under ultrasound; pp. 381–414. [Google Scholar]
- 66.Kordylla A., Krawczyk T., Tumakaka F., Schembecker G. Modeling ultrasound-induced nucleation during cooling crystallization. Chem. Engnrg. Sci. 2009;64(8):1635–1642. doi: 10.1016/j.ces.2008.12.030. [DOI] [Google Scholar]
- 67.Dang F., Kato K., Imai H., Wada S., Haneda H., Kuwabara M. Characteristics of BaTiO3 particles sonochemically synthesized in aqueous solution. Jpn. J. Appl. Phys. 2009;48:09KC02. doi: 10.1143/JJAP.48.09KC02. [DOI] [Google Scholar]
- 68.Dang F., Kato K., Imai H., Wada S., Haneda H., Kuwabara M. A new effect of ultrasonication on the formation of BaTiO3 nanoparticles. Ultrason. Sonochem. 2010;17(2):310–314. doi: 10.1016/j.ultsonch.2009.08.006. [DOI] [PubMed] [Google Scholar]
- 69.Dang F., Kato K., Imai H., Wada S., Haneda H., Kuwabara M. Oriented aggregation of BaTiO3 nanocrystals and large particles in the ultrasonic-assisted synthesis. CrystEngComm. 2010;12:3441–3444. doi: 10.1039/c003587d. [DOI] [Google Scholar]
- 70.Coelfen H., Antnonietti M. Mesocrystals: inorganic superstructures made by highly parallel crystallization and controlled alignment. Angew. Chem. Int. Ed. 2005;44:5576–5591. doi: 10.1002/anie.200500496. [DOI] [PubMed] [Google Scholar]
- 71.Niederberger M., Coelfen H. Oriented attachment and mesocrystals: non-classical crystallization mechanisms based on nanoparticle assembly. Phys. Chem. Chem. Phys. 2006;8:3271–3287. doi: 10.1039/b604589h. [DOI] [PubMed] [Google Scholar]
- 72.Song R.-Q., Cölfen H. Mesocrystals – ordered nanoparticle superstructures. Adv. Mater. 2010;22(12):1301–1330. doi: 10.1002/adma.200901365. [DOI] [PubMed] [Google Scholar]
- 73.Fang J., Ding B., Gleiter H. Mesocrystals: syntheses in metals and applications. Chem. Soc. Rev. 2011;40:5347–5360. doi: 10.1039/c1cs15043j. [DOI] [PubMed] [Google Scholar]
- 74.Uchaker E., Cao G. Mesocrystals as electrode materials for lithium-ion batteries. Nano Today. 2014;9(4):499–524. doi: 10.1016/j.nantod.2014.06.004. [DOI] [Google Scholar]
- 75.Sturm E.V., Coelfen H. Mesocrystals: past, presence, future. Crystals. 2017;7:207. doi: 10.3390/cryst7070207. [DOI] [Google Scholar]
- 76.Yasui K., Kato K. Dipole-dipole interaction model for oriented attachment of BaTiO3 nanocrystals: a route to mesocrystal formation. J. Phys. Chem. C. 2012;116:319–324. doi: 10.1021/jp208848j. [DOI] [Google Scholar]
- 77.Yasui K., Kato K. Influence of adsorbate-induced charge screening, depolarization factor, mobile carrier concentration, and defect-induced microstrain on the size effect of a BaTiO3 nanoparticle. J. Phys. Chem. C. 2013;117:19632–19644. doi: 10.1021/jp312609j. [DOI] [Google Scholar]
- 78.Yasui K., Kato K. Oriented attachment of cubic or spherical BaTiO3 nanocrystals by van der Waals torque. J. Phys. Chem. C. 2015;119(43):24597–24605. doi: 10.1021/acs.jpcc.5b06798. [DOI] [Google Scholar]
- 79.Esquivel-Sirvent R., Schatz G.C. Van der Waals torque coupling between slabs composed of planar arrays of nanoparticles. J. Phys. Chem. C. 2013;117(10):5492–5496. doi: 10.1021/jp400581j. [DOI] [Google Scholar]
- 80.Torii T., Yasui K., Yasuda K., Iida Y., Tuziuti T., Suzuki T., Nakamura M. Generation and consumption rates of OH radicals in sonochemical reactions. Res. Chem. Intermed. 2004;30(7-8):713–721. doi: 10.1163/1568567041856918. [DOI] [Google Scholar]
- 81.Shibata T., Nishiyama H. Numerical study of chemical reactions in a surface microdischarge tube with mist flow based on experiment. J. Phys. D: Appl. Phys. 2014;47 doi: 10.1088/0022-3727/47/10/105203. [DOI] [Google Scholar]
- 82.Takeuchi N., Ando M., Yasuoka K. Investigation of the loss mechanisms of hydroxyl radicals in the decomposition of organic compounds using plasma generated over water. Jpn. J. Appl. Phys. 2015;54 doi: 10.7567/JJAP.54.116201. [DOI] [Google Scholar]
- 83.Guo X., Minakata D., Crittenden J. On-the fly kinetic Monte Carlo simulation of aqueous phase advanced oxidation processes. Environ. Sci. Technol. 2015;49(15):9230–9236. doi: 10.1021/acs.est.5b02034. [DOI] [PubMed] [Google Scholar]
- 84.Bruggeman P.J., Kushner M.J., Locke B.R., Gardeniers J.G.E., Graham W.G., Graves D.B., Hofman-Caris R.C.H.M., Maric D., Reid J.P., Ceriani E., Fernandez Rivas D., Foster J.E., Garrick S.C., Gorbanev Y., Hamaguchi S., Iza F., Jablonowski H., Klimova E., Kolb J., Krcma F., Lukes P., Machala Z., Marinov I., Mariotti D., Mededovic Thagard S., Minakata D., Neyts E.C., Pawlat J., Petrovic Z.L., Pflieger R., Reuter S., Schram D.C., Schröter S., Shiraiwa M., Tarabová B., Tsai P.A., Verlet J.R.R., von Woedtke T., Wilson K.R., Yasui K., Zvereva G. Plasma-liquid interactions: a review and roadmap. Plasma Sources Sci. Technol. 2016;25(5):053002. doi: 10.1088/0963-0252/25/5/053002. [DOI] [Google Scholar]
- 85.An Y. Formulation of multibubble cavitation. Phys. Rev. E. 2011;83 doi: 10.1103/PhysREvE.83.066313. [DOI] [PubMed] [Google Scholar]
- 86.Stricker L., Dollet B., Fernández Rivas D., Lohse D. Interacting bubble clouds and their sonochemical production. J. Acoust. Soc. Am. 2013;134(3):1854–1862. doi: 10.1121/1.4816412. [DOI] [PubMed] [Google Scholar]
- 87.Mettin R., Akhatov I., Parlitz U., Ohl C.D., Lauterborn W. Bjerknes forces between small cavitation bubbles in a strong acoustic filed. Phys. Rev. E. 1997;56:2924–2931. doi: 10.1103/PhysREvE.56.2924. [DOI] [Google Scholar]
- 88.Yasui K., Iida Y., Tuziuti T., Kozuka T., Towata A. Strongly interacting bubbles under an ultrasonic horn. Phys. Rev. E. 2008;77 doi: 10.1103/PhysRevE.77.016609. [DOI] [PubMed] [Google Scholar]
- 89.Yasui K., Lee J., Tuziuti T., Towata A., Kozuka T., Iida Y. Influence of the bubble-bubble interaction on destruction of encapsulated microbubble under ultrasound. J. Acoust. Soc. Am. 2009;126:973–982. doi: 10.1121/1.3179677. [DOI] [PubMed] [Google Scholar]
- 90.Yasui K., Towata A., Tuziuti T., Kozuka T., Kato K. Effect of static pressure on acoustic energy radiated by cavitation bubbles in viscous liquids under ultrasound. J. Acoust. Soc. Am. 2011;130(5):3233–3242. doi: 10.1121/1.3626130. [DOI] [PubMed] [Google Scholar]
- 91.Fan Y., Li H., Zhu J., Du W. A simple model of bubble cluster dynamics in an acoustic field. Ultrason. Sonochem. 2020;64 doi: 10.1016/j.ultsonch.2019.104790. [DOI] [PubMed] [Google Scholar]
- 92.Shen Y., Zhang L., Wu Y., Chen W. The role of the bubble-bubble interaction on radial pulsations of bubbles. Ultrason. Sonochem. 2021;73 doi: 10.1016/j.ultsonch.2021.105535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Mettin R., Cairos C., Troia A. Sonochemistry and bubble dynamics. Ultrason. Sonochem. 2015;25:24–30. doi: 10.1016/j.ultsonch.2014.08.015. [DOI] [PubMed] [Google Scholar]
- 94.Hatanaka S., Yasui K., Kozuka T., Tuziuti T., Mitome H. Influence of bubble clustering on multibubble sonoluminescence. Ultrasonics. 2002;40(1-8):655–660. doi: 10.1016/S0041-624X(02)00193-2. [DOI] [PubMed] [Google Scholar]
- 95.Yasui K. Multibubble sonoluminescence from a theoretical perspective. Molecules. 2021;26:4624. doi: 10.3390/molecules26154624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Hatanaka S., Mitome H., Yasui K., Hayashi S. Single-bubble sonochemiluminescence in aqueous luminol solutions. J. Am. Chem. Soc. 2002;124(35):10250–10251. doi: 10.1021/ja0258475. [DOI] [PubMed] [Google Scholar]
- 97.Hegedűs F., Klapcsik K., Lauterborn W., Parlitz U., Mettin R. GPU accelerated study of a dual-frequency driven single bubble in a 6-dimensional parameter space: the active cavitation threshold. Ultrason. Sonochem. 2020;67:105067. doi: 10.1016/j.ultsonch.2020.105067. [DOI] [PubMed] [Google Scholar]
- 98.Varga T., Olm C., Nagy T., Zsély I.G., Valkó É., Pálvölgyi R., Curran H.J., Turányi T. Development of a joint hydrogen and syngas combustion mechanism based on an optimization approach. Intern. J. Chem. Kinetics. 2016;48(8):407–422. doi: 10.1002/kin.2016.48.issue-810.1002/kin.21006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Turanyi T., Tomlin A.S. Analysis of Kinetic Reaction Mechanisms, Springer. Berlin. 2014 doi: 10.1007/978-3-662-44562-4. [DOI] [Google Scholar]
- 100.Suslick K.S., Flint E.B. Sonoluminescence from non-aqueous liquids. Nature (London) 1987;330(6148):553–555. doi: 10.1038/330553a0. [DOI] [PubMed] [Google Scholar]
- 101.Ciawi E., Rae J., Ashokkumar M., Grieser F. Determination of temperatures within acoustically generated bubbles in aqueous solutions at different ultrasound frequencies. J. Phys. Chem. B. 2006;110(27):13656–13660. doi: 10.1021/jp061441t. [DOI] [PubMed] [Google Scholar]
- 102.Warnatz J., Maas U., Dibble R.W. 2nd ed. Springer; Berlin: 1999. Combustion. [Google Scholar]
- 103.Leroy V., Bretagne A., Fink M., Willaime H., Tabeling P., Tourin A. Design and characterization of bubble phononic crystals. Appl. Phys. Lett. 2009;95 doi: 10.1063/1.3254243. [DOI] [Google Scholar]
- 104.Condat C.A., Kirkpatrick T.R. Resonant scattering and Anderson localization of acoustic waves. Phys. Rev. B. 1987;36(13):6782–6793. doi: 10.1103/PhysRevB.36.6782. [DOI] [PubMed] [Google Scholar]
- 105.Lee J., Yasui K., Tuziuti T., Kozuka T., Towata A., Iida Y. Spatial distribution enhancement of sonoluminescence activity by altering sonication and solution conditions. J. Phys. Chem. B 112. 2008;112(48):15333–15341. doi: 10.1021/jp8060224. [DOI] [PubMed] [Google Scholar]