Abstract
Chemical and biochemical processes generally suffer from extreme nonlinearities with respect to internal states, manipulated variables, and also disturbances. These processes have always received special technical and scientific attention due to their importance as the means of large-scale production of chemicals, pharmaceuticals, and biologically active agents. In this work, a general-purpose genetic algorithm (GA)-optimized neural network (NNARX) controller is introduced, which offers a very simple but efficient design. First, the proof of the controller stability is presented, which indicates that the controller is bounded-input bounded-output (BIBO) stable under simple conditions. Then the controller was tested for setpoint tracking, handling modeling error, and disturbance rejection on two nonlinear processes that is, a continuous fermentation and a continuous pH neutralization process. Compared to a conventional proportional-integral (PI) controller, the results indicated better performance of the controller for setpoint tracking and acceptable action for disturbance rejection. Hence, the GA-optimized NNARX controller can be implemented for a variety of nonlinear multi-input multi-output (MIMO) systems with minimal a-priori information of the process and the controller structure.
Keywords: Chemical, Biochemical, Nonlinear, Controller, Neural network, Genetic algorithm
Chemical, Biochemical, Nonlinear, Controller, Neural Network, Genetic Algorithm.
1. Introduction
Chemical and biochemical processes are among some of the most vital and yet nonlinear modern industrial processes under technical and scientific considerations. A variety of chemicals and active biological agents are produced in such systems [1, 2], while they are operated under extreme working standards to comply with stringent production regulations and a competitive global market.
Control of chemical and biochemical processes is a challenging task due to nonlinearities associated with their internal states, manipulated variables, and also disturbances [3] as well as their time variability [2], which is inherent to many chemical and biochemical systems [4, 5].
The controller design for nonlinear processes has been studied in numerous works. Fernández et al. [6] studied a simple but efficient technique for tracking optimal profiles with error minimization for nonlinear biochemical processes, which was based on linear algebra for the calculation of control actions. The performance of the designed controller was tested through simulations by adding parametric uncertainty and perturbations in the initial conditions.
Aguilar-López et al. [7] introduced an uncertainty-based observer with a polynomial structure capable of estimating the unknown modeling error of a continuous bioreactor coupled to a linear input-output controller. In Mailleret et al. [8], a nonlinear adaptive control and the global asymptotic stability of closed-loop system were investigated for a bioreactor with unknown kinetics. They verified their approach on a real-life wastewater treatment plant.
Artificial neural networks (ANNs) are general-purpose modeling tools that can be used for various applications, including static and dynamic modeling, clustering, and pattern recognition [9, 10, 11, 12]. ANN is useful in particular when modeling with fundamental governing equations is costly, time-consuming or both [13, 14].
Naregalkar and Subbulekshmi [15] proposed a novel approach using NARX (nonlinear auto-regressive with exogenous input) model and enhanced moth flame optimization (EMFO) for pH neutralization of wastewater. They evaluated their method in terms of integral squared error (ISE), integral absolute error (IAE), mean squared error (MSE), settling time, and peak overshoot.
del Rio-Chanona et al. [16] utilized an ANN model for dynamic modeling and optimization of a 15-day fed-batch process for cyanobacterial C-phycocyanin production. To generate additional datasets, they artificially introduced random noise to the original dataset. They also chose the change of state variables as training data output.
The lack of online information on some bioprocess variables and the presence of model and parametric uncertainties are important challenges for the control of such processes. To address these issues, Rómoli et al. [17] proposed an online state estimator based on a Radial Basis Function (RBF) neural network that feeds information to a controller, which was derived via a linear algebra-based design strategy.
Intelligent methods can also be used to control nonlinear chemical and biochemical processes. These approaches can compensate modeling errors, tackle the occurrence of disturbances, and advise optimal operation scenarios as control actions. Ünal et al. [18] reviewed different aspects of using artificial intelligence and evolutionary algorithms i.e., genetic algorithm (GA) and ant colony (AC) for PID controller tuning on real-time experimental setups. The performances of these three techniques were compared with each other using the criteria of overshoot, rise time, settling time, and root mean square (RMS) error of the trajectory. It was observed that the performances of GA and AC are better than that of Ziegler-Nichols technique.
Latha et al. [19] used particle swarm optimization (PSO) algorithm for tuning of a proportional-integral-derivative (PID) controller for a class of time-delayed stable and unstable process models. The dimension of the search space was only three tuning parameters of conventional PID controllers. They tested their approach in real-time on a nonlinear spherical tank system. The real-time result with PSO-tuned PID offered better results for reference tracking, multiple reference tracking, and disturbance rejection problems.
More recently, intensive studies have been conducted for designing the NARX network architecture to enhance modeling accuracy and versatility. In this regard, various methods have been proposed for activation function selection and network weights and biases tuning via optimization by different algorithms. Liu et al. [20] considered NARX neural networks for analysis and identification of noisy nonlinear magnetorheological (MR) damper systems. The accuracy of their results supports the use of this modeling technique for identifying irregular nonlinear models of MR dampers and similar devices. Rankovic et al. [21] developed a nonlinear model predictive control (NMPC) scheme, with the assumption that the object model is unknown. Therefore, they used a digital recurrent network (DRN) model instead to predict the future evolution of the system, which is essential for model predictive control. From their framework, one can infer that designing the network structure is crucial and complex.
Combination of NARX models with genetic algorithm has been used for forecasting, which subsequently can be used for decision making. Han et al. [22] utilized a NARX network for bitcoin price forecasting and concluded that genetic algorithm was effective to decide the architecture of the NARX neural network better than some other information criteria.
In a similar study to our work, Hernández-Alvarado et al. [23] used a neural NARX network to optimize PID controller gains for an underwater remotely operated vehicle in simulation and also in a real-time manner. They took into consideration two criteria to assess the performance of the controllers: position tracking error and energy consumption, leading to the conclusion that the proposed method obtained the best performance with less energy.
In this work, we propose a general-purpose neural network-based NARX controller, which does not rely on a predefined form of any conventional controller, but can emulate a PI action. We will show that the controller can be tuned on some simple data sets, and hence might be tuned in an online manner similar to Ziegler-Nichols closed-loop tuning procedure [24]. We evaluated the controller performance on a continuous fermentor model as a nonlinear single-input single-output (SISO) process. Furthermore, as the importance of pH in chemical and biochemical processes cannot be overemphasized, it has also been taken into consideration in this study as a highly nonlinear multi-input multi-output (MIMO) system.
After introducing the controller structure and elaborating on its stability conditions, the tuning procedure is described, which was done using genetic algorithm optimization of the network weights. In the results section, the performance of the controller is tested for setpoint tracking, modeling error, and disturbance rejection scenarios, and compared with a conventional PI controller.
2. NARX formulation
The nonlinear autoregressive model with exogenous input (NARX) is a time series model, which is represented as a function of the model output and one or more independent inputs all at several past time steps. In the predictive form, a NARX model can be represented by:
| (1) |
where y is the network output, u is the network input, and f can be any linear or nonlinear analytic function.
3. Neural network structure
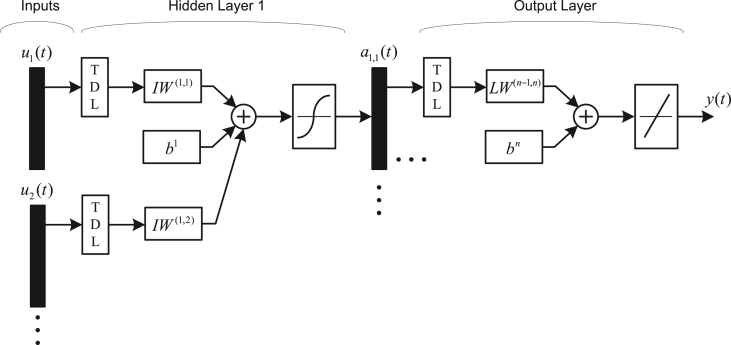
Artificial neural networks appear in a variety of architectures [11]. Specifically, the feedforward ANNs can be readily extended to the NARX networks with the introduction of tapped delay lines at the network input or even between layers, as shown in Figure 1. In this regard, the new architecture is called a neural NARX or NNARX network. In addition, such networks may have one or more feedback lines from outputs or hidden layers enclosing several layers of the network, which are not shown in Figure 1 since such feedback lines are not included in our NNARX approach. This structure offers several interesting characteristics including time series prediction and nonlinear input-output realization of dynamic systems.
Figure 1.
General structure of a NNARX feedforward neural network with tapped delay lines.
It is worthy of attention that this network is fully connected, which means there is a connection between every input and every neuron in each layer. The importance of these connections is controlled by the weight parameters, while bias parameters shift the network output to a suitable position. Typically, all weights and biases are regulated by any convenient optimization algorithm.
It must be also noted that Figure 1 refers to a specific structure of NARX networks that do not directly receive y output(s) as their inputs. In our case, y as the controller output (manipulated variable) is resolved in the closed-loop response of the process and does not directly appear as the network input.
In fact, many control schemes are a stable subset of linear or nonlinear dynamic systems. Therefore, a NNARX model can be utilized as a nonlinear parametric controller. As we will see in the results section, this structure may add integral effect to the control action, while it acts as an efficient nonlinear predictor. When combined together, these effects can be considered an inverse model controller with integral effect.
3.1. Proof of BIBO stability
According to the Gronwall Lemma [25], if are real nonnegative sequences for
| (2) |
Then
| (3) |
Theorem 1. The system (1) is bounded-input bounded-output (BIBO) stable with the initial conditions for if it is Lipchitz with the constants , and , .
Proof.
Consider and for simplification. Hence:
| (4) |
| (5) |
Hereand, ,
From the Gronwall Lemma we have
| (6) |
Since we supposed that the initial condition is bounded, we easily obtain
| (7) |
which according to the assumptions all terms are bounded, and this yields the required result.
4. NNARX controller tuning
Genetic algorithm (GA) is a heuristic optimization method inspired by the so-called evolution process in nature [26, 27] as it mimics the evolutionary operators: selection, crossover, and mutation to achieve a fitter population of solutions (individuals) over iterations (generations). The main advantages of this algorithm are that GA does not require calculating any derivatives. Hence in the case of the current problem, any sort of network topology and transfer function can be used without a-priori assumption on their exact formulations, which otherwise were needed for differentiation. On the other hand, as there are no derivates involved, the controller structure is not significantly affected by the noise effects if implemented on an actual process. Moreover, the error term(s) can be arbitrarily defined as a function of closed-loop response as utilized in this work. It must be emphasized that for higher-order systems (more delays and/or MIMO systems), the solution space grows tremendously, rendering classical gradient-based optimization methods inefficient.
The objective function for tuning is defined as the weighted sum of the mean squared errors (MSE) of the tracking tasks over time as:
| (8) |
| (9) |
where ei is the tracking error and ymi and yspi are the ith measured output and its respective setpoint. wis are arbitrary weights, which regulate the importance of the error terms. They are set to unity in this work.
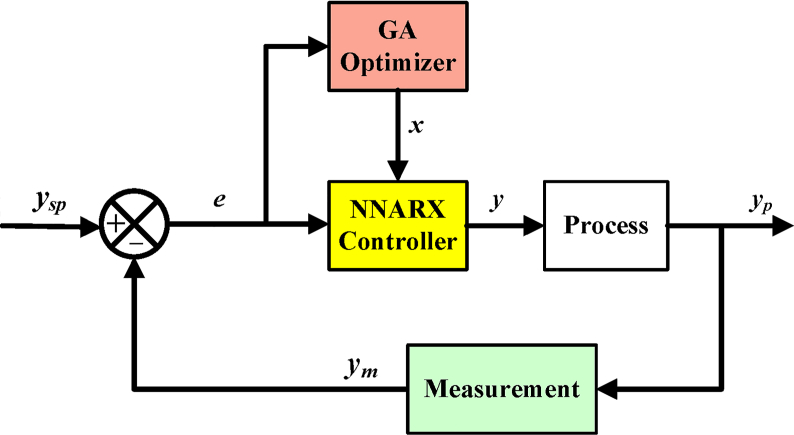
It must be emphasized that ei is the input to the NNARX controller, while the manipulated variables are the network outputs. On the other hand, the GA-optimizer receives MSE values for every individual, and returns the NNARX weight (and bias) values (x in Figure 2) to the network. The overall scheme of the closed-loop diagram is shown in Figure 2. Hence, the optimizer calls the closed-loop system model for a sufficiently large number of times until it concludes that no better solution can be found.
Figure 2.
General closed-loop structure of the control scheme with the GA-optimized NNARX.
5. PI controller tuning
For the sake of comparison, a PI controller is selected and tuned by model parameters. In this regard, a first-order plus time delay (FOPTD) model is fitted to the open-loop step response of the selected processes. The tests data and the results are given in Table 1. The regression was implemented via the sequential quadratic programming (SQP) approach to minimize MSE, which is defined similar to Eq. (8) but without the weight parameters. It must be emphasized that only process gain and time constant are fitted as the process time delay is considered to be equal to one sample time, which is a reasonable assumption, considering the response time of the measurement sensors.
Table 1.
Step response test parameters, regression results, and PI controller tuning parameters.
| Parameter | Fermentation Process | Neutralization process (Level) | Neutralization process (pH) |
|---|---|---|---|
| Step size | -0.01 (Dilution rate) | +5 ml/s (Acid) | +5 ml/s (Base) |
| Sample time | 0.1 h | 1 s | 1 s |
| Process gain (kp) | -31.9 | 0.92 | 0.60 |
| Process time constant () | 5.24 h | 196.2 s | 33.2 s |
| Process time delay () | 0.1 h | 1 s | 1 s |
| MSE | 1.15 × 10−4 | 1.50 × 10−6 | 1.76 × 10−3 |
| Proportional gain () | -0.274 | 53.2 | 13.9 |
| Integral time () | 2.4 | 16 | 16 |
| Derivative time () | - | - | - |
According to the Skogestad's SIMC PID tuning rule [28], the following formulas are suggested based on the FOPTD model parameters:
| (10) |
| (11) |
where kp, τ, and tD are process gain, time constant, and time delay, respectively. Also, kc and τI are controller proportional gain and integral time, respectively. It is apparent that the suggested controller is in the PI mode. Hence the derivative mode is deactivated ().
On the other hand, τc is the desired closed-loop time constant and the only tuning degree of freedom. Skogestad [28] suggests that a good trade-off can be obtained by choosing τc equal to process time delay. Hence, the values of 0.1 h and 1 s were initially used for the closed-loop time constant of the continuous fermentation and pH neutralization processes, respectively. However, these settings make the closed-loop response of both processes unstable. Hence, these values were modified to 0.5 h and 3 s as the closed-loop time constants of the studied processes, respectively.
6. Modeling
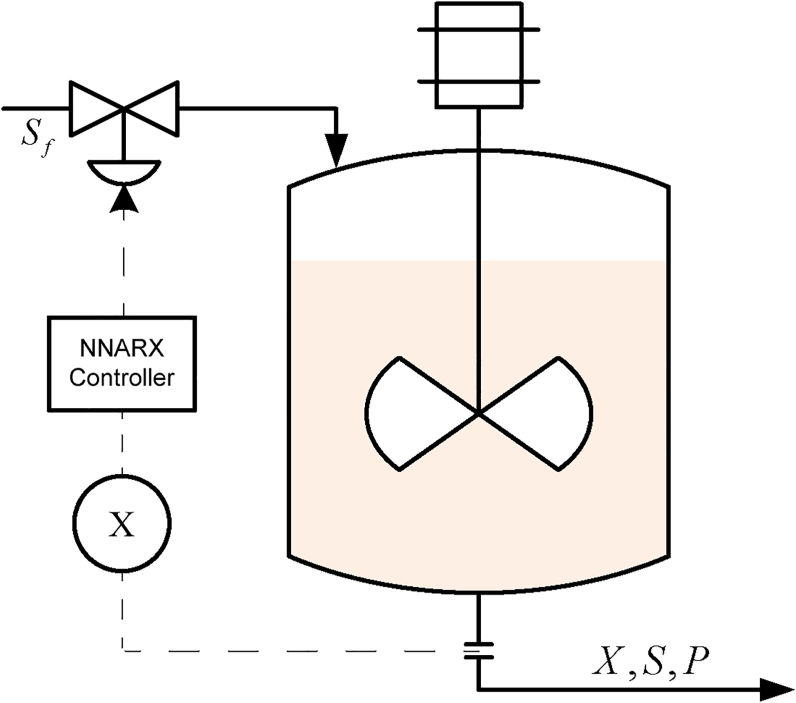
We have considered two typical nonlinear chemical and biochemical processes. The first process is a continuous fermentor in which the biomass (cell-mass) concentration in g/l is the controlled variable (plant output), while the manipulated variable (plant input) is the dilution rate, representing a nonlinear SISO system.
A rather simplified but general form of the process is shown in Figure 3 and represented by the following equations [29]:
| (12) |
| (13) |
| (14) |
| (15) |
where D is the dilution ratio, X is the cell-mass concentration, S is the substrate concentration, which is consumed by the microorganism, and Sf is the substrate concentration in the feed stream. P is the product concentration and Pm is the product saturation constant. is the cell-mass yield. α and β are kinetic parameters of the fermentation reaction. μ is the growth rate and μm is the maximum growth rate. Km and Ki are substrate saturation and inhibition constants, respectively [29]. The nominal parameter values are given in Table 2.
Figure 3.
Fermentation process diagram. X is the cell-mass concentration (measured variable), S is the substrate concentration, and P is the product concentration.
Table 2.
The nominal parameter values for the continuous fermentation process [29].
| Parameter | Value | Unit |
|---|---|---|
| D | 0.202 | 1/h |
| Ki | 22 | g/l |
| Km | 1.2 | g/l |
| P | 19.14 | g/l |
| Pm | 50 | g/l |
| S | 5.0 | g/l |
| Sf | 20.0 | g/l |
| X | 6.0 | g/l |
| Yx/s | 0.4 | g/g |
| α | 2.2 | g/g |
| β | 0.2 | 1/h |
| μm | 0.48 | 1/h |
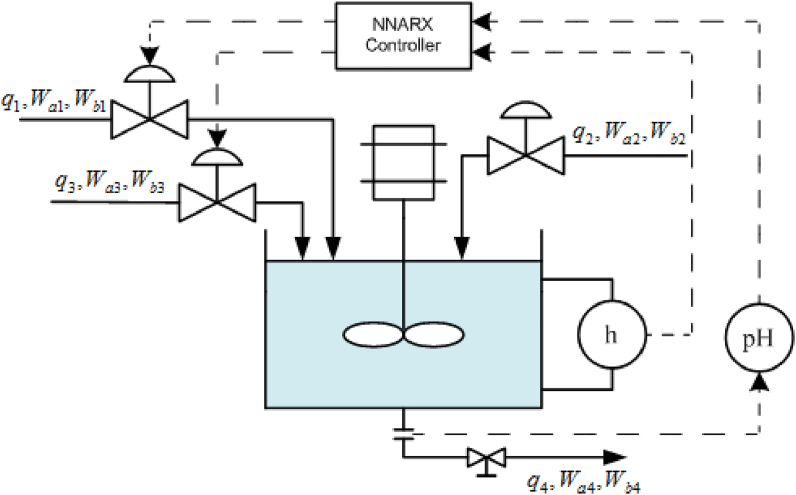
The second example is a neutralization process in which the liquid level of the tank and the effluent pH are the controlled variables, while acid and base flow rates are the manipulated variables. It is clear that this system is a MIMO process, as shown in Figure 4.
Figure 4.
Continuous pH neutralization process diagram.
The governing equations are given as follows:
| (16) |
| (17) |
| (18) |
where h is the liquid level in the neutralization tank, and A is the tank cross-section. CV is the outlet valve discharge coefficient, which is a constant in this work. q1, q2, and q3 are acid, buffer, and base flow rates, respectively. Wa1 to Wa4 and Wb1 to Wb4 are reaction invariants as described in Hu and Rangaiah [29].
The relation of pH with other variables is given by the following implicit algebraic equation [29]:
| (19) |
However, to circumvent the solution of such a nonlinear algebraic equation, the first derivative of Eq. (19) was calculated and simplified with respect to the derivative of pH. In this regard, another differential equation was added to the set of state equations:
| (20) |
where:
| (21) |
| (22) |
| (23) |
The nominal parameters for the neutralization process are given in Table 3.
Table 3.
The nominal parameter values for the continuous pH neutralization process [29].
| Parameter | Value | Unit |
|---|---|---|
| A | 207 | cm2 |
| CV | 8.75 | ml/cm/s |
| pK1 | 6.35 | - |
| pK2 | 10.25 | - |
| Wa1 | 3 × 10−3 | M |
| Wa2 | -3 × 10−2 | M |
| Wa3 | -3.05 × 10−3 | M |
| Wa4 | -4.32 × 10−4 | M |
| Wb1 | 0 | M |
| Wb2 | 3 × 10−2 | M |
| Wb3 | 5 × 10−5 | M |
| Wb4 | 5.28 × 10−4 | M |
| q1 | 16.6 | ml/s |
| q2 | 0.55 | ml/s |
| q3 | 15.6 | ml/s |
| h | 14.0 | cm |
| pH | 7.0 | - |
7. Simulation
The preliminary NNARX network structure was constructed by the Neural Network Toolbox-Simulink code generation facility [30]. The network was then modified in Simulink to suit the design required as a MIMO controller. The overall network structural parameters are given in Table 4. As shown in this table and earlier in Figure 1, several delays were introduced at the input layer. It is worthy of attention that this network is fully connected, which means there is a connection between every input and every neuron in each layer. As mentioned earlier, the importance of these connections is controlled by the weight parameters, which are regulated by the GA-optimizer. On the other hand, as the controller is designed around the steady state conditions for which , and in order to reduce the number of optimizing parameters, all bias parameters were permanently set to zero.
Table 4.
NNARX structural parameters.
| Parameter | Fermentation process | Neutralization Process |
|---|---|---|
| Number of hidden layers | 1 | 1 |
| Number of input delays | 4 (0:3) | 3 (1:3) |
| Number of hidden layer neurons | 2 | 2 |
| Hidden layer transfer function | tansig | tansig |
| Output layer transfer function | purelin | purelin |
| Preprocessing function | mapminmax | mapminmax |
| Postprocessing function | mapminmax_reverse | mapminmax_reverse |
| Sample time | 0.1 h | 1s |
Using one hidden layer is conventional in working with artificial neural networks [31] unless problem complexity necessitates adding one or more hidden layers [32]. The number of neurons is selected based on some trial and error. The number of delays is also selected based on the complexity of the process. It must be emphasized that the poles and zeros of the controller in the linear analogy are allocated by these delays, while they can generate integral and derivative actions, for which at least three delayed instances of the error are required.
It must be noted that this network requires just a few neurons in the hidden layer to obtain satisfactory results. This feature makes the optimization task faster and more efficient. The completed closed-loop structure was implemented and simulated in Simulink.
The MATLAB Global Optimization Toolbox was used for the optimization task [33]. The optimizer parameters are given in Table 5. For optimization and simulation, MATLAB and Simulink 2014a on a laptop with an Intel Core i5-3380 M (2.90 GHz) CPU with 6 GB RAM were used. It is worthy of attention that the number of optimizing parameters equals the weights of the designed NNARX controller. The lower and upper bounds on the optimizing parameters were set by some trial and error.
Table 5.
GA-Optimization parameters.
| Parameter | Fermentation Process | Neutralization Process |
|---|---|---|
| Number of optimizing parameters | 10 | 16 |
| Population size | 50 | 50 |
| Crossover fraction | 0.15 | 0.15 |
| Crossover function | crossovertwopoint | crossovertwopoint |
| Elite-count | 2 | 2 |
| Selection operator | Tournament | Tournament |
| Lower bound on weights | -1 | -2 |
| Upper bound on weights | 1 | 4 |
| Termination criteria | Average distance | Average distance |
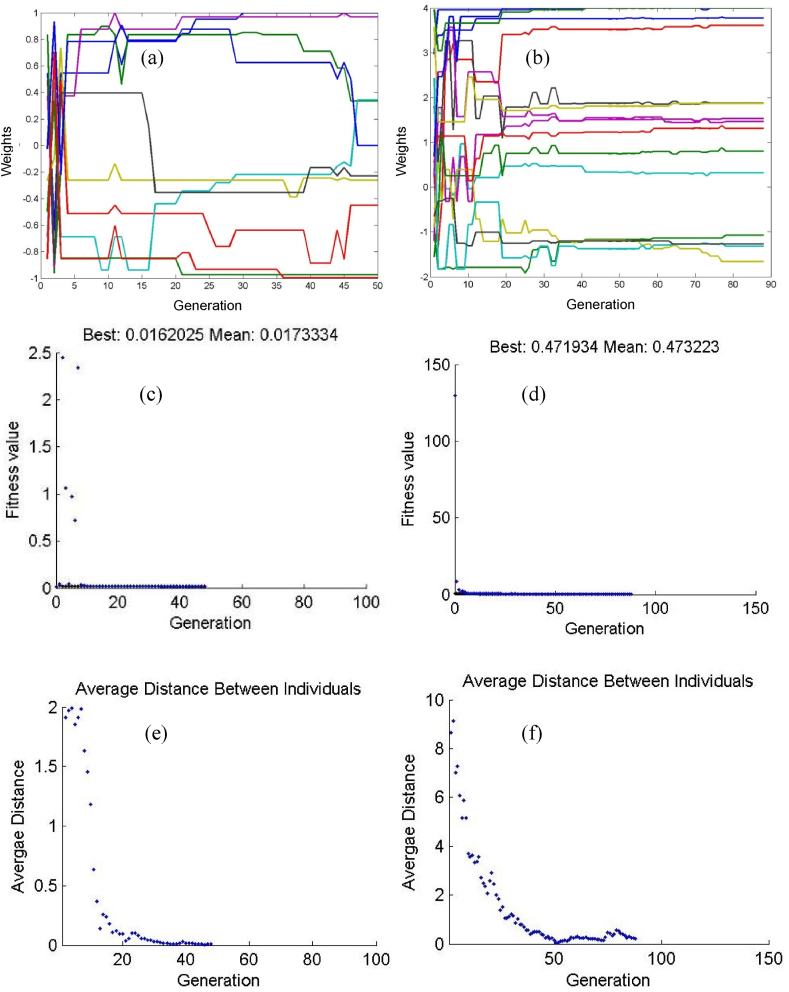
The summary of the optimization results is given Figure 5. For the continuous fermentation process, the optimization has terminated in exactly 50 generations (iterations) with the criterion that the average change in the fitness (objective function) values has fallen below a predefined limit (10−6). Similarly, for the neutralization process, the variations in the fitness values have reached a minimum in about 50 generations. However, the termination criterion (average change in the fitness values) has been satisfied after 88 generations. The variations in most of the weights have also dropped in about 50 generations. Careful tuning of genetic algorithm parameters (e.g., population size, selection function, crossover, and mutation operators) helps in finding at least the area in which the global optimum is expected to be found, and this is sufficient as long as the controller performance is concerned.
Figure 5.
Evolution of weights, change in fitness (objective function) values, and change in average distance between individuals (solutions) for the fermentation process (a, c, and e) and neutralization process (b, d, and f).
8. Results
In this section, the performance of the NNARX controller is assessed on the two nonlinear systems mentioned earlier. As for the case studies, first, setpoint tracking is investigated on both processes. Further, a modeling error is introduced to the formulation of the fermentation process. Finally, a disturbance in the form of an unwanted change in the buffer flow rate (q2) is introduced in the neutralization process. These changes are introduced at time
8.1. Setpoint tracking
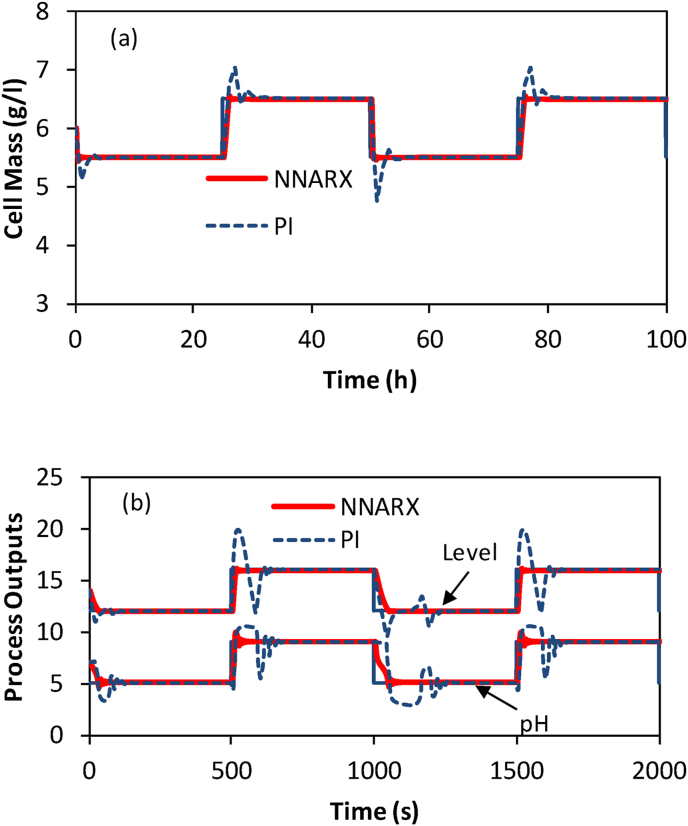
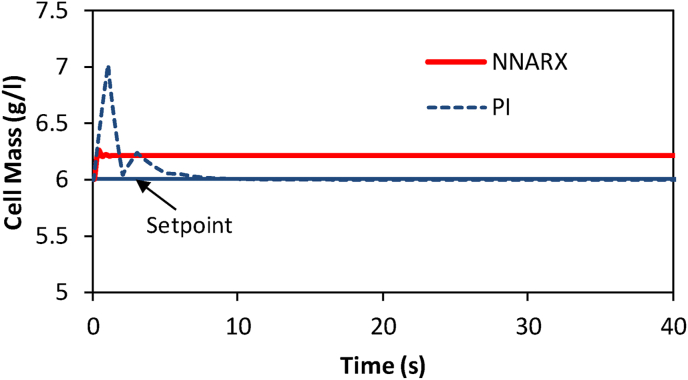
For the first analysis of the controller performance on the continuous fermentor, a square pulse train with a period of 50 h and amplitude of 0.5 g/l is introduced to the setpoint of cell-mass concentration with respect to its steady state value, as shown in Figure 6a. As can be seen, the tracking error is remarkably small, and the output (cell-mass concentration) promptly follows the setpoint with a slight overshoot incomparable to that of the PI controller.
Figure 6.
Setpoint tracking results for: (a) fermentation process, (b) neutralization process.
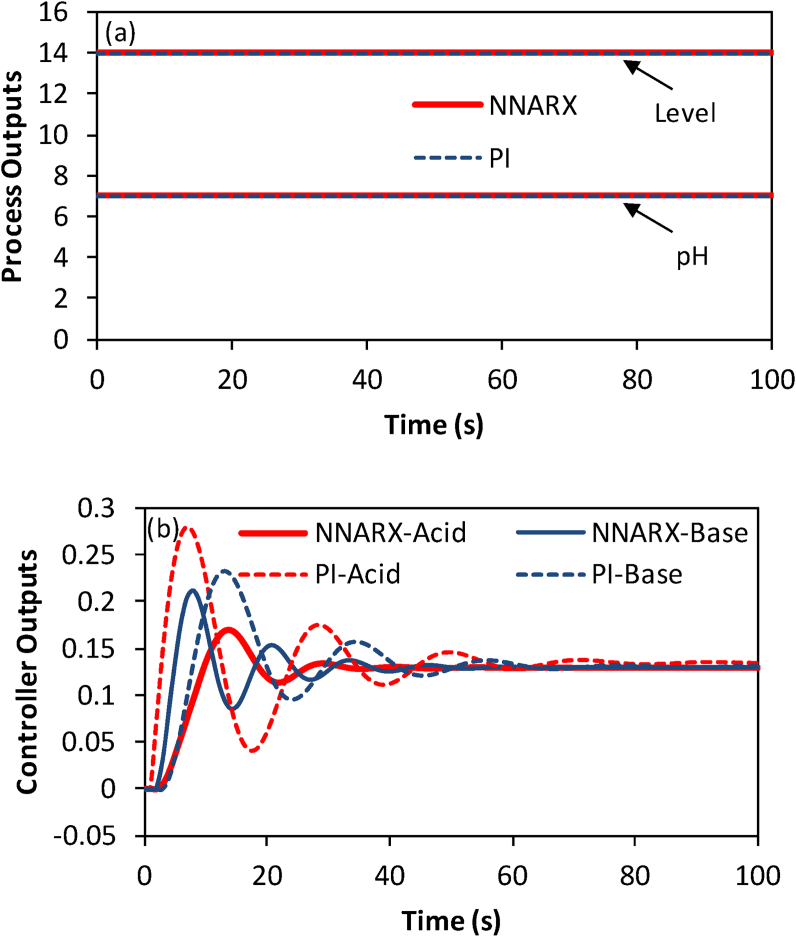
A similar test was carried out on the neutralization process in which a square pulse train with a period of 1000 s and amplitude of unity was introduced with respect to the steady state values of level and pH (Figure 6b). It is apparent that here also, the controller response is quite fast, and the offset is very small, while the overshoot is much smaller compared to that of the PI controller.
It is important to note that this offset-free response may suggest the integral action of the NNARX controller considering that an integral action in the discrete form is very similar to the NNARX structure with a linear transfer function.
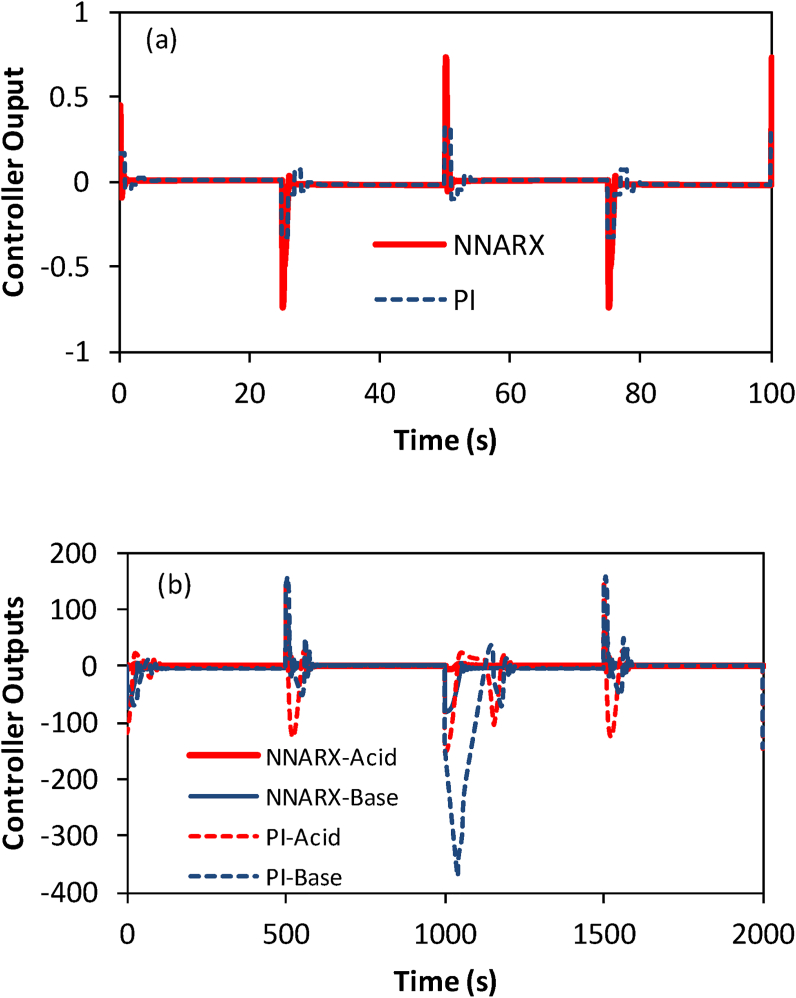
The variations in the manipulated variables (controller outputs) for the setpoint tracking problem are shown in Figure 7. The prompt setpoint tracking action of the NNARX controller for the fermentation process has come at the cost of aggressive changes in the manipulated variable (dilution rate in Figure 7a). However, for the neutralization process, the NNARX controller offers even smoother controlling actions compared to the PI controller, as can be seen in Figure 7b. Moreover, there is no sustained fluctuation in the manipulated variables, which is a desired behavior.
Figure 7.
Variations in the controller outputs for the setpoint tracking problem for: (a) fermentation process, (b) neutralization process.
8.2. Modeling error
For a test of modeling error, it is here assumed that the growth rate () is wrongfully calculated from the following equation instead of Eq. (15) based on which the NNARX controller was trained:
| (24) |
The simulation results are given in Figure 8. From this figure, one can infer that although the controller quickly reduces the tracking error, there has remained a small offset over time. Hence, for this problem, the PI controller is obviously superior.
Figure 8.
Results of including a modeling error in the fermentation process model.
8.3. Disturbance rejection
For another investigation, a disturbance in the form of an unmeasured change in the buffer flow rate (q2) is applied at time . At this moment, the buffer flow rate is reduced to 50% of its nominal value. It is noteworthy that a decrease in buffer value in any neutralization process increases process sensitivity, causing the controlling task more tedious. The results are shown in Figure 9. It is apparent from Figure 9a that the deviation from the setpoint value is small, but it must be admitted that the integral effect is slightly compromised. The changes in the manipulated variables (acid and base flow rates) are shown in Figure 9b, which shows mild fluctuations. Based on these results, the NNARX controller is able to tackle the relatively large unmeasured disturbance.
Figure 9.
Results of including a disturbance as an unmeasured change in the buffer flow rate (-50% of the nominal value) for the neutralization process: (a) process variables, (b) controller outputs.
8.4. Quantitative analysis
A quantitative analysis was carried out based on the integral absolute error (IAE) criterion:
| (25) |
As given in Table 6, the IAE values for the proposed NNARX controller are significantly smaller compared to the PI controller for setpoint tracking, especially for the neutralization process. However, the IAE values for modeling error and disturbance rejection are smaller for the PI controller due to the perfect integral action of this controller.
Table 6.
Integral absolute error (IAE) values for all the case studies.
| Process | Case study | IAE (NNARX) | IAE (PI) |
|---|---|---|---|
| Fermentation process | Setpoint tracking | 4.926 | 6.688 |
| Modeling error | 21.25 | 1.62 | |
| Neutralization process | Setpoint tracking (Level) | 248.5 | 764.2 |
| Setpoint tracking (pH) | 323.4 | 1095 | |
| Disturbance rejection (Level) | 9.962 | 0.1639 | |
| Disturbance rejection (pH) | 8.398 | 0.0544 |
9. Conclusion
In this work, a neural network-based nonlinear controller was tested on two nonlinear chemical and biochemical processes. The controller was tuned using genetic algorithm by running the closed-loop models for a sufficiently large number of times. There are at least two advantages of using GA as the training algorithm: 1) it does not require any knowledge of the neuron transfer function properties as opposed to gradient-based methods, which require exact derivatives of the transfer functions for back propagation, 2) GA is heuristically a global optimization method, and as we have seen in this problem, it is efficient in training dynamic neural networks, which are generally hard to train to an acceptable level of accuracy in a limited time.
The results indicated that the proposed NNARX controller enjoys a relatively simple but versatile structure. Moreover, it can be readily and quickly tuned with the minimum degree of richness in the information provided to the tuning algorithm. In this regard, the authors believe that the proposed method can be implemented in an online manner as well [34, 35]. In other words, it is possible that the process is started up without a-priori knowledge of the process, but the controller is tuned as the real-time process is in operation.
The NNARX controller action was not perfect for disturbance rejection for significant modeling errors. However, we expect that with the introduction of the measured disturbances as independent inputs to the controller, and also real-time optimization of the controller as it “flies”, the above-mentioned problems be alleviated.
Declarations
Author contribution statement
Bijan Medi: Conceived and designed the experiments; Performed the experiments; Wrote the paper.
Ayyob Asadbeigi: Analyzed and interpreted the data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
No data was used for the research described in the article.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Bennett B., Cole G. Institution of Chemical Engineers; 2003. Pharmaceutical Production: an Engineering Guide. [Google Scholar]
- 2.Bonvin D., François G. In: Coulson and Richardson's Chemical Engineering. fourth ed. Rohani S., editor. Butterworth-Heinemann; 2017. Chapter 11-Control and Optimization of Batch Chemical Processes; pp. 441–503. [Google Scholar]
- 3.Oravec J., Horváthová M., Bakošová M. Multivariable robust MPC design for neutralisation plant: experimental analysis. Eur. J. Contr. 2021;58:289–300. [Google Scholar]
- 4.Alford J.S. Bioprocess control: advances and challenges. Comput. Chem. Eng. 2006;30:1464–1475. [Google Scholar]
- 5.Pörtner R., Platas Barradas O., Frahm B., Hass V.C. In: Current Developments in Biotechnology and Bioengineering. Larroche C., Sanromán M.Á., Du G., Pandey A., editors. Elsevier; 2017. Advanced process and control strategies for bioreactors; pp. 463–493. [Google Scholar]
- 6.Fernández C., Pantano N., Rómoli S., Patiño D., Ortiz O., Scaglia G. 2016 IEEE Biennial Congress of Argentina (ARGENCON) IEEE; 2016. Controller design for tracking paths in nonlinear biochemical processes. [Google Scholar]
- 7.Aguilar-López R., Tec-Caamal E.N., Neria-González M.I. Observer-based control for uncertain nonlinear systems applied to continuous biochemical reactors. Math. Probl Eng. 2020;2020:6417860. [Google Scholar]
- 8.Mailleret L., Bernard O., Steyer J.-P. Nonlinear adaptive control for bioreactors with unknown kinetics. Automatica. 2004;40:1379–1385. [Google Scholar]
- 9.Derhami V., Mehrabi O. Action value function approximation based on radial Basis function network for reinforcement learning. J. Control. 2011;5:50–63. [Google Scholar]
- 10.Fatemi Moghadam A., Sharifi A., Teshnelab M. Prediction and identification of nonlinear rotary cement kiln system with neuro-fuzzy ANFIS network by using feature selection with genetic algorithm. J. Control. 2011;5:22–33. [Google Scholar]
- 11.Schmidhuber J. Deep learning in neural networks: an overview. Neural Network. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 12.Zohoori Zangeneh A., Teshnehlab M., Ahmadieh Khanesar M. Proposing interval activation functions in radial Basis function neural network to predict nonlinear dynamic systems. J. Control. 2016;9:1–25. [Google Scholar]
- 13.Forgione M., Piga D. Continuous-time system identification with neural networks: model structures and fitting criteria. Eur. J. Contr. 2021;59:69–81. [Google Scholar]
- 14.Medi B., Bahramian A., Nazari V. Synthesis and characterization of conducting polyaniline nanostructured thin films for solar cell applications. JOM. 2020;73:504–514. [Google Scholar]
- 15.Naregalkar A., Subbulekshmi D. In: Advances in Smart Grid Technology. Zhou N., Hemamalini S., editors. Springer; 2020. NARX-EMFO based controller optimization for pH neutralization in wastewater treatment; pp. 403–417. [Google Scholar]
- 16.del Rio-Chanona E.A., Manirafasha E., Zhang D., Yue Q., Jing K. Dynamic modeling and optimization of cyanobacterial C-phycocyanin production process by artificial neural network. Algal Res. 2016;13:7–15. [Google Scholar]
- 17.Rómoli S., Serrano M., Rossomando F., Vega J., Ortiz O., Scaglia G. Neural network-based state estimation for a closed-loop control strategy applied to a fed-batch bioreactor. Complexity. 2017;2017:9391879. [Google Scholar]
- 18.Ünal M., Ak A., Topuz V., Erdal H. Vol. 449. Springer; 2012. (Optimization of PID Controllers Using Ant colony and Genetic Algorithms). [Google Scholar]
- 19.Latha K., Rajinikanth V., Surekha P. PSO-based PID controller design for a class of stable and unstable systems. ISRN Artif. Intell. 2013;2013 [Google Scholar]
- 20.Liu Q., Chen W., Hu H., Zhu Q., Xie Z. An optimal NARX neural network identification model for a magnetorheological damper with force-distortion behavior. Front. Mater. 2020;7:10. [Google Scholar]
- 21.Rankovic V., Radulovic J., Grujovic N., Divac D. Neural network model predictive control of nonlinear systems using genetic algorithms. Int. J. Comput. Commun. 2014;7:540–549. [Google Scholar]
- 22.Han J.-B., Kim S.-H., Jang M.-H., Ri K.-S. Using genetic algorithm and NARX neural network to forecast daily bitcoin price. Comput. Econ. 2019:1–17. [Google Scholar]
- 23.Hernández-Alvarado R., García-Valdovinos L.G., Salgado-Jiménez T., Gómez-Espinosa A., Fonseca-Navarro F. Neural network-based self-tuning PID control for underwater vehicles. Sensors (Basel) 2016;16:1429. doi: 10.3390/s16091429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stephanopoulos G. Prentice-Hall; 1984. Chemical Process Control: an Introduction to Theory and Practice. [Google Scholar]
- 25.Holte J.M. MAA-NCS Meeting at the University of North Dakota. 2009. Discrete Gronwall lemma and applications. [Google Scholar]
- 26.Goldberg D.E. Addison-Wesley; Boston: 1989. Genetic Algorithms in Search, Optimization and Machine Learning. [Google Scholar]
- 27.Medi B., Kazi M.-K., Amanullah M. Nonlinear direct inverse method: a shortcut method for simultaneous calibration and isotherm determination. Adsorption. 2013;19:1007–1018. [Google Scholar]
- 28.Skogestad S. Simple analytic rules for model reduction and PID controller tuning. J. Process Contr. 2003;13:291–309. [Google Scholar]
- 29.Hu Q., Rangaiah G.P. Adaptive internal model control of nonlinear processes. Chem. Eng. Sci. 1999;54:1205–1220. [Google Scholar]
- 30.Mathworks . The MathWorks Inc.; 2014. Neural Network Toolbox 8.2. [Google Scholar]
- 31.Alimohammadi H., Alagoz B.B., Tepljakov A., Vassiljeva K., Petlenkov E. A NARX model reference adaptive control scheme: improved disturbance rejection fractional-order PID control of an experimental magnetic levitation system. Algorithms. 2020;13:201. [Google Scholar]
- 32.Akhtar M., Kraemer M.U.G., Gardner L.M. A dynamic neural network model for predicting risk of Zika in real time. BMC Med. 2019;17:171. doi: 10.1186/s12916-019-1389-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mathworks . The MathWorks Inc.; 2014. Global Optimization Toolbox 3.2.5 User Guide. [Google Scholar]
- 34.Michalewicz Z., Janikow C.Z., Krawczyk J.B. A modified genetic algorithm for optimal control problems. Comput. Math. Appl. 1992;23:83–94. [Google Scholar]
- 35.Varasteh F., Nazar M.S., Heidari A., Shafie-khah M., Catalão J.P.S. Distributed energy resource and network expansion planning of a CCHP based active microgrid considering demand response programs. Energy. 2019;172:79–105. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.