Abstract

Spinel LiMn2O4 has attracted wide attention due to its advantages of a high-voltage plateau, good capacity, environmental friendliness, and low cost. Due to different experimental synthesis methods and conditions, there are many intrinsic point defects in LiMn2O4. By means of first-principles calculations based on a reasonable magnetic configuration, we studied the formation energies, local structures, and charge compensation mechanism of intrinsic point defects in LiMn2O4. The formation energies of defects under the assumed O-rich equilibrium conditions were examined. It was found that O, Li, and Mn vacancies, Mn and Li antisites, and Li interstitial could appear in the lattice at some equilibrium conditions, but Mn interstitial is hard to form. The charge was compensated mainly by adjusting the oxidation state of Mn around the defect, except for the defects at the 8a Wyckoff site. The binding energies between point defects were calculated to shed light on the clustering of point defects. Furthermore, the diffusion of Li ions around the defects was discussed. Cation antisites led to a decrease of the Li diffusion barrier but O vacancy caused an increase of the barrier. This study provides theoretical support for understanding point defects in spinel LiMn2O4.
1. Introduction
Spinel LiMn2O4 is a typical manganese-based cathode material.1−3 Thackeray et al. first proposed it as a cathode material for lithium-ion batteries.4 In terms of battery performance, spinel LiMn2O4 has a high-voltage plateau (>4 V), good theoretical capacity density (148 mAh/g), and great thermal safety. More importantly, Mn has obvious advantages of low cost and nontoxicity. Consequently, LiMn2O4 is considered to be a substitute for layered LiCoO2 on the electrodes of lithium-ion batteries.5−8
The cubic spinel structure of LiMn2O4 belongs to the Fd3̅m space group. Oxygen atoms, which are at 32e sites, are arranged in a cubic close-packed arrangement, lithium ions are located at 8a tetrahedral sites, and manganese ions occupy half of the octahedral positions, which are 16d sites. The other half of the octahedral void is 16c sites, which reside halfway between neighboring tetrahedral sites and serve as a channel for the migration of Li.9−11 The average oxidation state of Mn in LiMn2O4 is +3.5, which is caused by a mixture of Mn3+ and Mn4+ in equal proportion, and its charge–discharge activity is the contribution of Mn3+/Mn4+ redox.12,13 The existence of the orbital-degeneracy Mn3+ ions will cause the Jahn–Teller (JT) effect during charging and discharging,14−16 leading to unique properties such as structural distortions and phase transitions. On this account, the spinel LiMn2O4 transforms into an orthogonal phase when the temperature drops below 280 K,17,18 and its magnetic ground state is antiferromagnetic (AFM).19−21
It is difficult to obtain the exact stoichiometric LiMn2O4 because of various synthetic methods and the synthetic environment. There would be various types of intrinsic point defects within the material, such as vacancies, interstitials, and metal antisite defects. Using powder X-ray diffraction and thermogravimetry analysis (TGA), Tarascon et al. found that some Mn ions are located in the tetrahedral sites of the spinel and a significant number of oxygens are lost,22 suggesting that Mn antisites and O vacancies appear in LiMn2O4. Paulsen et al. also found that a certain amount of metal ion antisite defects, i.e., the antisites of Li and Mn, exist in Li2MnO4 at a wide range of temperatures.23 Oh’s group first applied differential pulse polarography to analyze the dissolved Mn2+ ions, which are generated by the disproportionation reaction 2Mn3+ → Mn4+ + Mn2+ in the electrolyte.24 They found that Mn dissolution was the primary reason for the capacity loss. With the dissolution of Mn, Mn vacancies are present in the 16d octahedral sites.
Following the formation of defects in the lattice, the spatial geometric environment and chemical environment of the surrounding atoms will change. As a result, the structure and charge distribution of LiMn2O4 will change, which further affects the structure stability, charge voltage, and diffusion of ions in the material. Sugiyama et al. studied the effect of O vacancies (i.e., O deficiency) on the phase transition from cubic to the tetragonal phase of LiMn2O4 using differential scanning calorimetry (DSC), magnetic susceptibility, 7Li nuclear magnetic resonance, and electronic resistivity.25 Xia et al. studied the effects of Li defects and O vacancies on the structure and electrochemical properties of LiMn2O4.26 They found that the capacity loss rate of anoxic materials is much faster, which is related to the phase transition in the cyclic process, in comparison with intact LiMn2O4. Besides experimental studies on defect-related properties in cathode materials, theoretic calculations, especially first-principles methods based on density functional theory (DFT), have been demonstrated to be a powerful tool for addressing defects in solid.27,28 Some researchers have studied point defects in LiMn2O4 through computational methods.20,21,29−32 As early as the 1990s, Islam’s group have studied Li- and Mn-related interstitials and vacancies in LiMn2O4 using interatomic potential models.32 Koyama et al. studied O vacancy, Li and Mn interstitials, Mn antisite, and some defect complexes in LiMn2O4 using the first-principles method.29 They revealed that metal interstitials have lower formation energy compared with that of O vacancy. The excess Li are prone to occupy the 16d site other than the 16c site. Hoang has investigated cation point defects in LiMn2O4 in various possible charged states.20 Recently, Xiao et al. studied the effect of Li-excess (it is in fact antisite Li in their work) on the diffusion of Li in LiMn2O4 using first-principles calculations and found that the Li-excess configuration enhances the Li ion diffusivity by introducing two new kinds of fast Li migration channels.30
As mentioned above, point defects are common in LiMn2O4 and may affect the electrochemical performance of LiMn2O4. Although there are some studies on point defects in LiMn2O4 by experimental or/and theoretic calculation methods in the literature, point defects are still not understood. For example, how is the distribution of point defects? What are the effects of defects on the charge distribution and charge compensation in the delithiation process? And how is the migration of Li when defects exist in the lattice? On the other hand, previous theoretic calculations have not carefully dealt with the magnetism of Mn in the lattice, except for the work of Xiao et al.30 The spinel LiMn2O4 may have various magnetic configurations. Ouyang et al. considered the magnetic structures of LiMn2O4 with one ferromagnetic (FM) and two AFM arrangements of Mn ions. According to DFT calculations, they found that the AFM ordering of Mn chains along the [110] direction was more stable than other magnetic structures.18 Recently, Liu et al. conducted extensive work on LiMn2O4 with different structures and magnetic configurations to find its ground state.21 They used eight different AFM and two FM orders, including Ouyang’s structures, and found that the most stable structure is a highly symmetrical configuration with alternating AFM (↑↓↑↓) layer and FM layer along the [001] direction. Koyama et al. and Huang just assumed a simple high-spin FM configuration of Mn to investigate point defects in LiMn2O4.29,33 Different magnetic configurations will affect the ground-state structure of LiMn2O4 and further affect the properties of defects in the system. Therefore, to achieve accurate defect properties in LiMn2O4 computationally, it is better to investigate it based on a reasonable magnetic structure.
In this work, we use the first-principles calculation method based on DFT to comprehensively explore defect-related properties in spinel LiMn2O4. The formation energies of various isolated intrinsic point defects and the binding energies between point defects are calculated based on the lowest energy magnetic configuration proposed by Liu et al.21 Furthermore, Bader charges are calculated to shed light on charge compensation associated with the creation of defects. Finally, we discuss the effect of defects on the diffusion of lithium ions. It is noteworthy that point defects in semiconductors and insulators may occur in charged states, and the thermodynamics of charged defects in LiMn2O4 have already been investigated by Hoang based on a ferromagnetic spin configuration.20 Since the magnetic configuration used by Hoang is different from that of our work, we speculate that some conclusions on thermodynamics of charged point defects drawn from calculations based on the present magnetic configuration may be inconsistent with the results of Hoang. Therefore, we will study charged defects in LiMn2O4 in future work, but only neutral defects are considered in the present work.
2. Computational Methodology
DFT calculations were performed by the projector augmented wave (PAW) potential method, as implemented in the Vienna ab initio simulation package (VASP).34 The interactions between electrons are treated by the generalized gradient approximation of Perdew and Wang with the Hubbard parameter correction (GGA+U).35−38 The U values for the d-orbitals of Mn were set to 3.9 eV based on previous reports.39,40 The electronic configurations of 1s22s1, 3p63d54s2, and 2s22p4 are employed as valence electrons for Li, Mn, and O, respectively, and all the other electrons are treated as core electrons. The conventional cubic spinel unit cell with the AFM magnetic configuration reported by Liu et al. was taken as the initial structure. The energy cutoff for the plane wave was set as 500 eV. The Brillouin zone was sampled by 2 × 2 × 2 special k-points using the Monkhorst–Pack scheme for geometry optimization, and 4 × 4 × 4 for the calculations of total energies and electronic structures. Geometry relaxation was complete when the residual forces acting on every atom were less than 0.02 eV Å–1. Point defects were considered to have a low concentration in the bulk, so the cell volume and shape were fixed to the optimized crystal of bulk during the relaxation of defective lattice, and only atoms’ coordinates were fully relaxed.
The climbing image nudged elastic band (CINEB) method was used to investigate the minimum energy pathways of ion hopping from one lattice site to the adjacent positions.41,42 We insert five images during the CINEB calculation and the residual forces acting on every atom were less than 0.02 eV Å–1. To describe the electron charge transfer between ions in the material, this paper adopts the Bader charge analysis method based on the charge density calculation.43,44
3. Results and Discussion
3.1. Lattice and Magnetic Structure
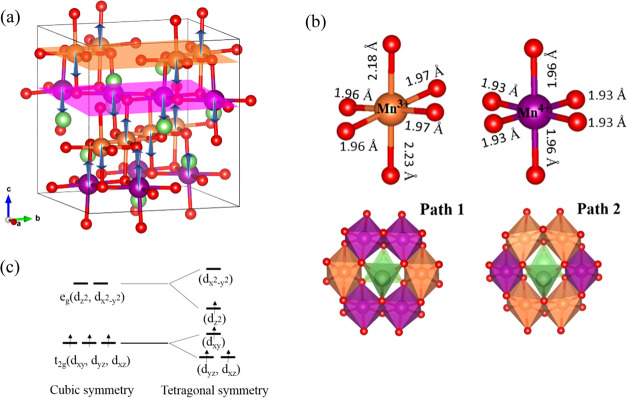
The ground-state structure of LiMn2O4 is a highly symmetrical configuration with alternating AFM (↑↓↑↓) layer and FM layer along the [001] direction, as predicted by Liu et al.21Figure 1a shows the ground structure of LiMn2O4. After structural optimization, the cubic cell transforms into a tetragonally distorted cell with a lattice elongation of 7% along the c direction. The calculated lattice parameters (a = b = 8.20 Å and c = 8.74 Å) are consistent with the experimental data (a = b = 8.11 Å and c = 8.65 Å)33 and previous calculated results (a = b = 8.20 Å and c = 8.76 Å; a = b = 8.22 Å and c = 8.76 Å).21,30 The spinel LiMn2O4 is thus an orthorhombic lattice instead of a cubic one. Due to the magnetic structure, there are two different Mn–O6 octahedral structures in the cell along the [001] direction. The specific octahedral structure and Mn–O bond length of the Mn–O6 octahedrons are shown in Figure 1b. The purple Mn–O6 octahedron is approximately a regular octahedron with the Mn–O bond length in the (001) plane being 1.93 Å and that in the c direction being 1.96 Å. However, the yellow Mn–O6 octahedron has a large distortion. The four Mn–O bonds in the (001) plane are almost equal (1.96–1.97 Å), but the other two Mn–O bonds along the c direction (2.23 and 2.18 Å) are longer than these in the (001) plane. As mentioned previously, Mn3+ ions can cause JT distortion and thus the yellow Mn layer is rationally judged as the Mn3+ layer. The calculated Mn–O distances in the JT distorted MnO6 octahedron agree well with the experimental data at 300 K (1.92 and 2.26 Å).45 The conclusion is further supported by the atom’s magnetic moments and Bader charges. The yellow Mn ion has a magnetic moment of 3.82 μB, while the purple Mn ion has about 3.13 μB. Note that the number of unpaired electrons of Mn4+ is less than that of Mn3+ (Figure 1c) and thus the yellow Mn is indeed in the + 3 state. Our calculated magnetic moments are consistent with the calculations by Liu et al.,21 who reported the magnetic moments of Mn3+ and Mn4+ to be 3.9 μB and 3.2 μB, respectively. We further find that the Bader charge around Li is +0.89 e, and the Bader charges for yellow and purple Mn are +1.71 e and +1.84 e, respectively. For oxygen, due to different Mn ions around it, we denote O on the Mn3+ layer as OMn3+. Similarly, the O on the Mn4+ layer is denoted as OMn4+. We find that the Bader charges of the two O are almost equal (the Bader charges of OMn3+ and OMn4+ are −1.09 e and −1.13 e, respectively).
Figure 1.
(a) Crystal and magnetic configurations of spinel-type LiMn2O4. Green spheres are Li, red spheres are O, yellow and purple spheres are Mn3+ and Mn4+, respectively. The blue arrows indicate the direction of the magnetic moment of Mn. The Mn ions are with AFM configuration in the Mn3+ layer and with FM configuration in the Mn4+ layer. (b) The structure of Mn4+-O6 and Mn3+-O6 octahedrons and two paths for Li migration that consist of different oxidation states of Mn ions. (c) Schematic representation of electron distribution in the 3d orbital of Mn ions.
The JT effect originates from the orbital degeneration of transition metal ions. In spinel LiMn2O4, Mn3+(t2g3, eg1) is a JT ion, which will cause distortion of the surrounding tetragonal lattice, but Mn4+(t2g3, eg0) is not a JT ion. We can clearly observe in Figure 2 that the eg orbital of Mn3+ atom in the spin-up channel splits into a dz2 orbital and dx2–y2 orbital, opening a gap of about 0.5 eV between them.18,19 The dz2 orbital is filled while the dx2–y2 orbital is unoccupied. This leads to a larger magnetic moment for Mn3+ compared with that of Mn4+. By comparing the projected DOS of Mn and O, it is found that the Mn-d and O-p orbitals are hybridized to form covalent bonds between O and Mn. The profiles of px and py of O in both Mn3+ and Mn4+ layers are almost identical, and thus, the bond status of trivalent and quadrivalent Mn–O are basically the same in the (001) plane. An additional covalent bond is formed just below the Fermi level by Mn3+-dz2 and O-pz, which makes the structure more stable.
Figure 2.
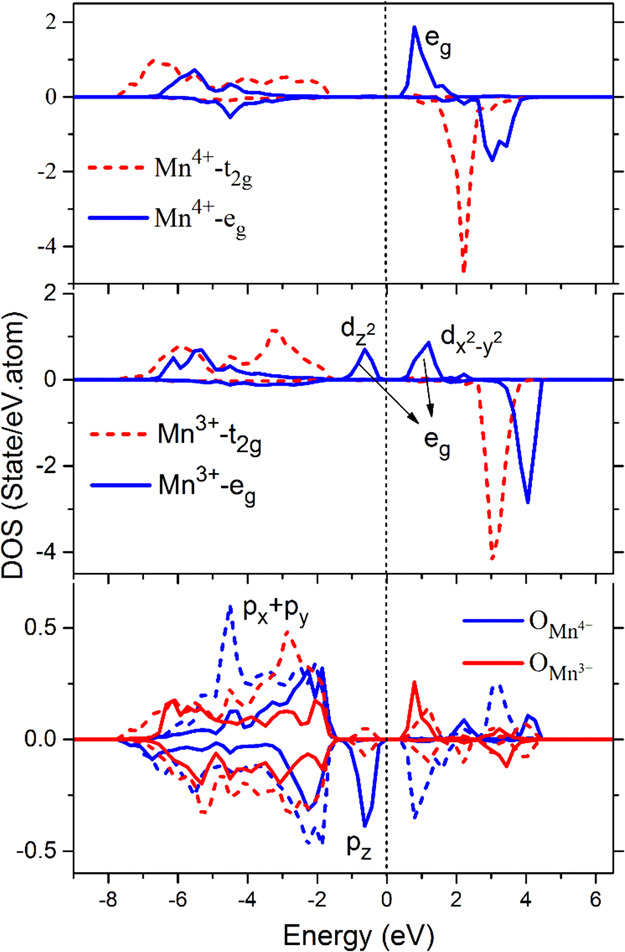
Projected density of states (DOS) of Mn-3d and O-2p. The solid and dashed lines in the upper panel represent Mn-eg and Mn-t2g orbitals, respectively. The O-pz (solid lines) and O-px,y orbitals (dashed lines) are shown in the lower panel. The zero of the energy is set to the Fermi level.
3.2. Isolated Point Defects
We then focus on single or isolated point defects in LiMn2O4. The following intrinsic defects are considered in this work: Li vacancy (VLi), Mn vacancy (VMn), O vacancy (VO), Li interstitial (ILi), Mn interstitial (IMn), Li antisite (LiMn), and Mn antisite (MnLi).
The formation energy of a point defect Ef is defined as
| 1 |
where Edefect and Ebulk are the total energies of the unit cell with and without the defect, respectively. The generation of defects involves adding atoms into or removing atoms from the unit cell. μi is the atomic chemical potential of species i, and ni is the number of atoms i added to (positive) or removed from (negative) the lattice to produce the defect. The atomic chemical potential can also be written as μi = μi0 + Δμi, where μi is the chemical potential of element i in its standard state. The standard states for Li and O are bcc Li and gaseous O2, respectively. As for Mn, we choose the structure of I43m, which has different magnetic moments, as the standard state based on the previous theoretic and experimental works.46
The atomic chemical potentials are constrained by thermodynamic equilibrium conditions with various phases containing Li, Mn, and O. The existence of the LiMn2O4 phase requires a constraint on the chemical potentials as
| 2 |
where ΔHf(LiMn2O4) is the enthalpy of formation of LiMn2O4. To calculate formation energies, one must obtain the values of Δμi (i = O, Li, and Mn). Another two linearly independent equations are needed in addition to eq 2. The synthesis processes of LiMn2O4 are usually in air;10,47,48 thus, we assume O2 is in equilibrium with the LiMn2O4 sample. In this case, the chemical potential of O is μo = μo0, corresponding to the O-rich condition. The third constraint can be found from the observed phases in experiments. LiMn2O4 is synthesized by heating the mixing of Li salts and Mn-based oxides in air and the impurity phases Mn2O3, Mn3O4, LiMnO2, and Li2MnO3 are generally present in the resulting samples.47 Moreover, MnO2 may also be present because it usually served as a reactant in some synthesis experiments.10,48 So, the third limiting condition for chemical potentials can be derived from one of the five phases: monoclinic Li2MnO3 and LiMnO2, cubic Mn2O3, tetragonal Mn3O4, and MnO2. For instance, if LiMn2O4, O2, and Mn2O3 are in equilibrium with each other, we get
| 3 |
Here, ΔHf(Mn2O3) is the enthalpy of formation of Mn2O3. The calculated formation enthalpies of LiMn2O4, Li2MnO3, LiMnO2, Mn2O3, Mn3O4, and MnO2 are shown in Table S1 and the atomic chemical potentials under various equilibrium conditions are in Table S2.
Table 1 lists defect formation energies at various O-rich equilibrium conditions. For vacancies, there are two kinds of Mn and O vacancies in LiMn2O4. We mark them as VMnIII, VMn, VOIII, and VO (superscripts III and IV indicate that atoms on the Mn3+ and the Mn4+ layers are removed to generate vacancies, respectively). For antisite defects, there is only one case of Mn antisite (a Mn locates in the Li site) and two types of Li antisites (a Li ion substitutes Mn3+ or Mn4+, denoted as LiMnIII or LiMn). The 16c Wyckoff site is the interstitial site for Li or Mn, which locates in the midpoint between two neighboring Li ions. The interstitials can occur in both the Mn3+ and the Mn4+ layers, and we also use III and IV to denote different interstitials of Li and Mn.
Table 1. Calculated Formation Energies Ef of Intrinsic Defects in LiMn2O4 under Some O-Rich Equilibrium Conditionsa.
|
Ef (eV) |
|||||
|---|---|---|---|---|---|
| defects | a | b | c | d | e |
| VLi | 1.22 | 0.46 | 0.38 | –0.09 | –0.22 |
| VMnIII | 0.22 | 0.60 | 0.64 | 0.88 | 0.94 |
| VMnIV | –0.13 | 0.25 | 0.29 | 0.53 | 0.59 |
| VOIII | 2.28 | 2.28 | 2.28 | 2.28 | 2.28 |
| VOIV | 2.30 | 2.30 | 2.30 | 2.30 | 2.30 |
| LiMnIII | –1.43 | –0.29 | –0.17 | 0.54 | 0.73 |
| LiMnIV | –1.22 | –0.08 | 0.04 | 0.75 | 0.94 |
| MnLi | 2.84 | 1.70 | 1.58 | 0.87 | 0.68 |
| ILiIII | 1.28 | 2.04 | 2.12 | 2.59 | 2.72 |
| ILiIV | 1.00 | 1.76 | 1.84 | 2.31 | 2.44 |
| IMnIII | 4.14 | 3.76 | 3.72 | 3.48 | 3.42 |
| IMnIV | 3.98 | 3.60 | 3.56 | 3.32 | 3.26 |
a, b, c, d, and e represent the LiMnO2, Li2MnO3, MnO2, Mn2O3, Mn3O4 phases that coexist with O2 and LiMn2O4, respectively. The negative values of formation energies indicate that LiMn2O4 would spontaneously form defects, and therefore, the assumption of local equilibrium under those conditions indicates instability.
As we choose the O-rich condition, an environment that is more close to the experimental operation condition, to determine the chemical potentials for each of the elements, the formation energy of O vacancies is irrelevant to the equilibrium conditions. As shown in Table 2, the formation energies of VOIII and VO are almost equal (2.28 and 2.30 eV), which are higher than that of other metal cation vacancies. Koyama et al. studied oxygen vacancy and metal interstitials in LiMn2O4 through the local spin density approximation (LSDA) and ultrasoft pseudopotentials based on FM configuration.29 They reported that VO has a formation energy of 2.17 eV when the chemical potential of oxygen is determined by the equilibrium between Mn2O3 and MnO2. We also calculated the formation energy of VO under the same conditions and found the value to be 1.81 eV. The difference may originate from the fact that we use different calculation methods and magnetic configurations of LiMn2O4 compared with Koyama’s work.
Table 2. Distance dX-O between the Center of Defect X and Its Surrounding O Atomsa.
| 8a |
16d |
16c |
||||
|---|---|---|---|---|---|---|
| defects | VLi | MnLi | LiMnIII | VMnIV | IMnIV | ILiIV |
| dX-O (Å) | 2.00(×4) | 2.04(×4) | 2.17(×2) | 2.33(×2) | 1.96(×4) | 1.93(×2) |
| 2.07(×4) | 2.21(×4) | 2.02(×2) | 2.14(×2) | |||
| 2.40(×2) | ||||||
The values in parentheses indicate the number of X–O “bonds”.
The formation energy of VLi is in the range of −0.22 to 1.22 eV, depending on the equilibrium conditions. It is found that the formation energy of VLi is negative (−0.09 eV at condition d and −0.22 eV at condition e). A negative formation energy indicates that the system would spontaneously form defects, and therefore, the assumption of local equilibrium under those conditions indicates instability. Strictly speaking, the atomic chemical potentials are limited in a range that avoids the formation of competitive phases containing Li, O, and Mn. As for Mn vacancies, the formation energy of VMn is relatively low. The formation of VMnIV is lower by 0.35 eV than that of VMn; thus, Mn vacancies are more likely to form in the Mn4+ layer. Note that the formation energy of VMnIV is negative (−0.13 eV) at condition a, the environment that LiMn2O4, O2, and LiMnO2 are in equilibrium with each other. Again, this indicates that the material would be unstable in the presence of O2 and LiMnO2.
The formation energies for vacancies are not very much high, and thus, they would appear in LiMn2O4 at a detectable concentration in the synthesis process. Tarascon et al. used the TGA measurement to test the effect of annealing temperatures on the oxygen content.22 They found that at 1000°C, LiMn2O4 even has a reversible oxygen loss of 5% and forms LiMn2O3.8. Kanno et al. synthesized tetragonal spinel LiMn2O4 by quenching from 920°C, and the time-of-flight (TOF) neutron powder diffraction measurement shows that 3.5% O vacancies are generated and no significant stoichiometric composition deviation was observed at Li 8a and Mn 16d sites.49
As for cation antisites, namely, LiMnIII, LiMn, and MnLi, we found that the formation energies of Li antisites were lower than that of the Mn antisite under most equilibrium conditions. The formation energy of MnLi is lower than that of Li antisites, just only under condition e. The calculated formation energies of these cation antisites do not exceed 3.0 eV and thus MnLi and LiMn are likely to appear in LiMn2O4, as revealed by several experiments.22,33,47,50 Paulsen and Dahn have investigated in detail the phase diagram and the stability region of the Li–Mn–O spinel between 400 and 800 °C by various experimental methods23. They found that the thermodynamic stable phases in the range of 400–880 °C are only the spinel with the composition Li1+xMn2–xO4+δ (δ < 0.02). If the temperature is above 800°C, the stable Li–Mn–O spinel is Li1–xMn2+xO4. In other words, LiMn and MnLi antisites generally appear in LiMn2O4 and make the spinel more stable.
Among interstitial defects, i.e., an external Li or Mn atom entering the empty 16c site, the formation energies of Li interstitials are moderate (1.0–2.44 eV for ILiIV and 1.28–2.72 eV for ILi). Thus, the Li insertion process of LiMn2O4 is feasible and LiMn2O4 has the ability to accommodate extra Li ions. Moreover, the excess Li ions tend to occupy the 16c site of the Mn4+ layer. Yamada et al. found that excess Li would be preferably inserted into the interstitial 16c sites under reducing experimental conditions, forming tetragonal Li1+xMn2O4.51 Gummow et al. also reported that tetragonal lithiated spinel Li2Mn2O4 can be synthesized under appropriate reducing conditions.52 As for Mn interstitial, the formation energy of it is so high that it is hard to form at the assumed equilibrium conditions.
The occurrence of defects can result in a local structural change. We show the distance between the defect X with the most stable configuration and its surrounding O atoms in Table 2. The bond length of O–Li in pristine LiMn2O4 is 2.00 Å. We found that VLi had no significant influence on the original Li–O4 tetrahedron, as the distance of VLi–O is still 2.0 Å. When a Mn substitutes a Li to form MnLi, the length of Mn–O bonds in the Mn–O4 tetrahedron is 2.04 Å, slightly larger than the bond length of O–Li. VMnIV causes the original Mn–O6 octahedron to expand. The distance of VMn–O is 2.33 Å in the direction of c-axis and 2.21 Å in the a/b plane, while the bond lengths of Mn4+–O are 1.96 and 1.93 Å in defect-free LiMn2O4. The outward relaxation of O is due to the missing of strong covalent bonds between O and Mn. LiMnIII mainly affects the O atoms in the Mn3+ plane. The four Mn3+–O bonds in the (001) plane are 1.96–1.97 Å, but the distances of LiMn–O are elongated to 2.07 Å. For interstitial defects at the 16c site, the newly formed Mn–O6 octahedron in the Mn4+ layer distorts slightly (two Mn–O bonds with a length of 2.02 Å and four Mn–O bonds with a length of 1.96 Å). In addition to O atoms being affected by the 16c Mn, we found that there was a repulsion for the adjacent 8a Li ions due to the Coulomb repulsive interaction between the interstitial Mn and Li cations, which increased the distance of 16c IMnIV and 8a Li from 1.88 to 2.23 Å. ILi also affects its neighboring 8a Li, but the Coulomb repulsion effect is less compared with the case of Mn interstitial. The distance between Li (8a) and Li (16c) is 2.13 Å, which is 0.1 Å lower than the distance of Li (8a) and IMnIV(16c). The occurrence of VO causes the Li ion to directly deviate from the oxygen defect, resulting in a distance of VOIII–Li to be 2.40 Å. Consequently, the other three Li–O bonds in the formed Li–O3 unit due to the removal of a O atom are decreased to 1.89 Å.
3.3. Electronic Structure Analysis
When defects are generated in the lattice, atom’s charge will rearrange, and charge compensation to the defects occurs. To understand the charge transfer between atoms when a defect exists, the Bader charges are calculated and shown in Table 3. If an exotic Mn is embedded into the 16c octahedral site, the interstitial Mn then bonds with its surrounding six oxygen atoms. The charge transfer in the lattice with an interstitial defect of IMn is mainly realized by changing the oxidation state of the lattice 16d Mn on the opposite side of the new bonding oxygen. That is to say, charge compensation in the case of Mn interstitial is carried out by the six Mn on the 180° IMn–O–Mn chain. By checking the Mn–O6 octahedron in which the Bader charge of Mn decreased by 0.13 e, we found that it shows noticeable distortion. For the embedding of the low valence element of Li in the 16c site to form ILi, the Bader charge of Mn in the direction of b-axis is decreased by 0.15 e. The VO defect at the 32e site causes the reduction of the two Mn4+ bonded with the missing O to Mn3+ directly, as the Bader charge of the two Mn decreased by 0.20 e.
Table 3. Change in Bader Charges ΔQ of the Atoms Near Some Isolated Defects.
| |
8a |
16d |
16c |
32e | ||||
|---|---|---|---|---|---|---|---|---|
| defects | VLi | MnLi | LiMn | VMn | IMn | ILi | VO | |
| ΔQ (e) | Mn | +0.13 | +0.13 | –0.13 | –0.15 | –0.20 | ||
| O | +0.14 | –0.05 | +0.05 | +0.17 | –0.02 | –0.07 | –0.02 | |
When a defect occurs in the 16d site (VMn and LiMn), it can be considered that the high-valence Mn is replaced by a low-valence element. At this time, the nearest Mn3+ (for LiMnIII, there are two Mn3+ and, for VMn, there are four Mn3+) is oxidized to Mn4+ for charge compensation, as its Bader charge is increased by 0.13 e in the two cases. Thus, VMn or LiMn gives rise to an increase in Mn4+ ions and subsequently a decrease in Mn3+ ions. As a result, the JT distortion around the defects is suppressed and the stability of the spinel structure is increased. The powder neutron-diffraction study, which did not detect any structural phase transition from 4 to 290 K, verified the stability of Li-substituted spinel LiMn1.96Li0.04O4.53
However, if the defect is in the 8a site (VLi and MnLi), it affects the Bader charge of the O in the X–O4 tetrahedron directly (again, here, X represents the defect) and has no obvious effects on the charge of the surrounding Mn ions. Especially for VLi, the charge of the surrounding O decreased by 0.14 e.
The charge transfer in the defective lattice is further illustrated by the DOS of the eg state of Mn. As can be seen from Figure 3, in the case of ILi, IMn, and VO, the original Mn4+ around defects is reduced to Mn3+, which is manifested by the split of the eg orbital and the formation of a low-energy dz2 orbital below the Fermi level. For the defects of VMn and LiMn, charge compensation is carried out by the surrounding Mn3+ oxidation to Mn4+. These two kinds of defects can reduce the JT distortion around the defects, and the original dz2 orbital also disappears.
Figure 3.
DOS of the eg orbital of Mn around some point defects. The Fermi energy is set at zero.
3.4. Defect pairs
The electrostatic and elastic interactions between point defects may cause the clustering or association of some defects. Thus, in this section, we investigate the interactions between some point defects.
The binding energy Eb between isolated defects A and B is defined as follows
| 4 |
Ef(AB) is the formation energy when defects A and B exist in the nearest-neighbor mode, and Ef(A) and Ef(B) are the formation energies of isolated defects A and B, respectively. The above definition shows that if the binding energy is negative, defects A and B have an attractive interaction; otherwise, defects A and B show a repulsive interaction. We choose the lowest energy configuration of the defect pair to calculate the formation energies of defect pairs and the corresponding binding energies between point defects.
The formation energies of some defect pairs under our considered thermodynamic equilibrium conditions are shown in Table S3. It is found that the formation energies of defect pairs VLi–VLi, VMnIII–VLi, MnLi–VLi, LiMn–VLi, LiMnIII–LiMn, MnLi–MnLi and MnLi–LiMnIII are less than 1.0 eV under some equilibrium conditions; thus, these defect pairs may occur in LiMn2O4 with detectable concentrations in the experimental synthesis process. Defect pairs IMn–VLi and VOIV–VLi in some cases have moderate formation energy (1.0 – 1.6 eV), indicating the two defect pairs may also appear in the LiMn2O4. However, the pairs of Mn vacancy, O vacancy, and IMn–VMnIII are hard to form due to their high formation energy, especially for O vacancy. Among these defect pairs, we pay particular attention to the cation exchange defect, i.e., the MnLi–LiMn defect pair because cation mixing is common in cathode materials.39,54,55The formation energy of MnLi–LiMnIII is 0.81 eV. Therefore, a considerable concentration of Li/Mn exchange defect can be observed in LiMn2O4 samples prepared by various experimental methods. By using the X-ray diffraction technique, Tarascon et al. reported that the amount of Li/Mn mixing can reach 10% in LiMn2O4 powders.22
Then, we consider the binding energy between point defects. The binding energy is independent of the atomic chemical potentials and is listed in Table 4.
Table 4. Binding Energy Eb between Some Isolated Point Defects.
| defect pair | VLi–VLi | VMnIII–VLi | VOIV–VLi | LiMnIII–VLi | IMnIV–VLi | IMnIII–VMn |
|---|---|---|---|---|---|---|
| Eb (eV) | –0.05 | 0.18 | –0.60 | 0.07 | –1.76 | –2.01 |
| defect pair | MnLi–VLi | MnLi–MnLi | VMnIII–VMn | LiMnIII–LiMn | LiMnIII–MnLi | VOIII–VO |
| Eb (eV) | –0.44 | –0.47 | 1.93 | 0.85 | –0.60 | 0.24 |
We observe that the interaction between VLi is rather weak, as the binding energy between VLi is −0.05 eV. This finding is consistent with the nature of the ionic bond for Li, and thus, Li vacancies are prone to distribute in the lattice randomly. The pair LiMnIII–VLi also shows a small binding energy (0.07 eV), so the Li antisite has a weak repulsive interaction with Li vacancy. IMn–VLi, VOIV–VLi,MnLi–VLi, MnLi–MnLi, IMn–VMnIII, and LiMn–MnLi have obviously negative binding energies, indicating that the defect pairs are more stable than the corresponding isolated defects. The exchange defect of MnLi–LiMn has a large attractive effect. The binding energy between MnLi and LiMnIII is −0.60 eV, and thus the two types of defects tend to cluster. The clustering of cation exchange defects is also found in other cathode materials, such as in LiFePO4.56 IMn and VLi have an extremely high binding energy (−1.76 eV), showing a strong agglomeration phenomenon. So, Li vacancies are prone to be formed near the Mn interstitial. O vacancies tend to be separated, as the binding energy between them is positive (0.24 eV). The binding energy of the LiMn antisite is 0.85 eV, hinting that LiMn would not be clustering. There is a strong repulsion between VMn–VMnIV, as the binding energy between VMn and VMnIV, is a significant positive value (1.93 eV). The result is in accordance with the finding that VMn–VMnIV has relatively high formation energy.
The Frenkel defect can be regarded as a kind of defect pair, namely an interstitial in 16c site plus a vacancy near it. Our calculated results show that the Li-Frenkel is unstable. After the structural relaxation for the Li-Frenkel, it was found that the Li atom at the 16c site moves back to its original 8a site, forming the pristine lattice again. This suggests that the generation of Li-Frenkel in LiMn2O4 is impossible. For the Mn-Frenkel defect, i.e., the defect pair IMn–VMn, the lowest energy configuration is IMnIII–VMn with a binding energy of −2.01 eV, showing significant attraction between IMn and VMn. So, the 16c Mn atom tends to approach the lattice 16d site if there is a Mn vacancy around it.
Huang et al. investigated the local structure of Li and O in oxygen-deficient tetragonal LiMn2O4 with a spherical aberration-corrected scanning transmission electron microscope (STEM) and first-principles calculations.33 They revealed that Li ions move away from their ideal positions due to the presence of oxygen vacancies, resulting in defect complexes formed by Li and O vacancies. Their finding is consistent with our result that VOIV and VLi have a strong attractive interaction. Koyama et al. studied O vacancy and interstitials of Li and Mn in the cubic LiMn2O4 by first-principles calculations based on FM configuration.29 They revealed that when a Mn interstitial is placed at the 16c site, the configuration that a Li atom near the interstitial moves into the other neighboring 16c site has low energy compared with the simple interstitial lattice structure. That is, Li vacancy is prone to form near the interstitial Mn. The present finding that IMn and VLi have a strong attractive interaction is qualitatively in accordance with the conclusion of Koyama et al.
3.5. Diffusion of Li in LiMn2O4
Diffusion of Li is an important elementary step in the charge/discharge process in electrode materials. As for LiMn2O4, the diffusion of Li is mediated via the vacancy mechanism, which is composed of a series of jumps of Li ions between two 8a sites through a 16c site. In this section, we discuss the effect of point defects on the migration of Li ions.
After a Li vacancy is generated, the neighboring Li atom is allowed to migrate to the vacancy site through a ‘ring’ consisting of six Mn3+/Mn4+ ions, that is, the Li ion jumps over the 16c octahedron sharing edges with six Mn–O6 octahedrons. Usually, there are two kinds of Mn6 rings, as depicted in Figure 1b. We named the diffusion path that composes of four Mn4+ and two Mn3+ in the Mn6 ring as Path 1. The center of the 16c site in Path 1 is located on the Mn3+ layer. The path involves migration across the Mn6 ring composed of two Mn4+ and four Mn3+ is named Path 2 in which the 16c site is located on the Mn4+ layer. We use the CINEB method with five images to study the diffusion behavior of Li going through the two different diffusion paths. We first investigate the diffusion of Li in pristine LiMn2O4. The calculated migration barrier of Li is shown in Figure 4a. Due to the different oxidation states of Mn in Path 1 and Path 2, the volume of the 16c octahedron and the electrostatic interaction between Mn and the migrated Li are different. We clearly observe different Li diffusion barriers for the two paths (0.35 eV for Path 1 and 0.68 eV for Path 2). Our calculated diffusion barriers are generally in agreement with the previous theoretic values based on the same magnetic configuration.21,30 Xiao et al. reported that the migration barrier is 0.38 eV for Path 1,30 and a barrier of 0.23 eV for Path 1 and 0.70 eV for Path 2 were reported by Liu et al.21 We also found that a metastable configuration is reached when Li diffuses via Path 2. This configuration corresponds to the migrated Li at the 16c position in the center of the Mn6 ring. By comparison of the two paths, it is obvious that Li ions can easily diffuse through the path with more Mn4+ ions. The reason for the lower migration barrier of Li in Path 2 can be attributed to the electrostatic interaction between cations. Compared with Mn3+, Mn4+ has a smaller electron cloud range, and thus, Mn4+ ions have a small Coulomb repelling effect on the mobile Li ions. Thus, if the symmetry is consistent, the higher the Mn4+ ratio, the lower the migration barrier of Li. We further speculate that a higher oxidized ion substituting a Mn in the Mn6 ring would increase the Li diffusion kinetics in spinel LiMn2O4.
Figure 4.
Calculated diffusion barriers of Li along different paths. (a) Li diffusion in pristine LiMn2O4; (b) Li diffusion in LiMn2O4 with a MnLi defect; (c) Li diffusion in LiMn2O4 with a LiMn defect; and (d) Li diffusion in LiMn2O4 with VO. The inset shows the six-membered ring in the diffusion paths. Orange, purple, and green balls represent Mn3+, Mn4+, and Li, respectively.
Then, we consider the effects of point defects on the migration of Li. For this purpose, the defects with the lowest energy in each type are only considered, and Li vacancy is generated in the neighboring of the defect to study the migration process. The interstitials are not considered because they are located in the 16c site and hence block the diffusion of Li. The defects considered here are MnLi, LiMnIII, and VO, which are commonly observed in experiments.
The calculated energy barriers of Li migration in the lattice with defects of MnLi, LiMn, and VO are shown in Figure 4b,c,d, respectively. One should note that in some cases the Mn6 ring in the diffusion path is different from that of pristine LiMn2O4 because of charge transfer. The six-membered rings in the migration paths of the defective cell are also shown in the inset of Figure 4b,c,d. MnLi is the defect that a Mn is in a Li site (8a site), which does not change the oxidation state of Mn of the diffusion ring. The diffusion energy barriers for Li migrating through Paths 1 and 2 are 0.27 and 0.65 eV, respectively. Compared with Li diffusion in defect-free LiMn2O4, it is revealed that MnLi leads to a decrease in the diffusion barrier of Li slightly. As for the antisite LiMn, Li is prone to substitute Mn3+. In this case, the Mn6 ring in the diffusion channel is changed to a Mn5Li ring, that is to say, the ring is composed of five Mn ions and one Li ion. The diffusion barriers of Path 1 and Path 2 are 0.25 and 0.46 eV, respectively. The diffusion barrier of Li is reduced by 0.1 or 0.22 eV in comparison with that of Li diffusion in perfect LiMn2O4. This is because the Coulomb repulsive interaction of Li–Li is much weaker than that of Li–Mn3+. Xiao et al. have studied Li diffusion in Li-excess LiMn2O4 by first-principles calculations.30 They found that when a Mn3+ in the Mn6 ring is replaced by a Li, the diffusion barrier of Li is 0.24 or 0.29 eV, depending on the atomic arrangement of Mn4+, Mn3+, and Li+ in the ring. The presently calculated diffusion barrier of Path 1 is in good agreement with their result.
When an anion defect (i.e., O vacancy) is present in the lattice, Li ions around it have a strong tendency to move outward from the VO defect, and the previous study has shown that two Mn4+ around it are reduced to Mn3+. In this case, the Mn6 ring in the diffusion path is also different from the Mn6 ring of the perfect lattice, as shown in Figure 4d. The energy barriers for Li migrating through Path 1 (0.97 eV) and Path 2 (1.0 eV) are almost equal. The higher diffusion barrier in the case of VO is mainly caused by the charge distribution of the Mn ring in the diffusion path. Both Path 1 and Path 2 in the case of VO are asymmetrically arranged in the Mn ring and have a high ratio of Mn3+ ions, and this causes much more serious JT distortion and coulombic repulsion between Mn and migrated Li.
By studying the influence of point defects on the diffusion energy barrier of Li, we found that both LiMn and MnLi antisites can effectively reduce the diffusion energy barrier, but VO results in an increase of diffusion barrier significantly. One should be aware that the kinetics process for Li migration is not only determined by the migration barrier but also by the concentration of point defects in the lattice. Consequently, if the antisite defects or the cation mixing is at a high concentration, they could promote Li diffusion kinetics. From an experimental point of view, 10% cation mixing could be achieved by adjusting the synthesis conditions.22 Such defect concentration is relatively considerable and it is possible to measure the diffusion kinetics of Li ions in LiMn2O4 samples with cation mixing. Hence, cation mixing is beneficial for improving the charge/discharge rate of LiMn2O4.
4. Conclusions
In summary, defect properties of spinel LiMn2O4 were studied by means of first-principles calculations based on a reasonable magnetic configuration. The formation energies of intrinsic defects of vacancies, interstitials, and cation antisites were calculated under assumed equilibrium conditions and the binding energies of some defect pairs were calculated to determine the clustering of some point defects. Charge distribution and compensation involving the creation of defects were also investigated. The present work reveals that O, Mn, and Li vacancies, Mn and Li antisites, and Li interstitial may exist in LiMn2O4, but their concentrations are sensitive to experimental conditions and thermal history. The defect pairs IMnIV–VLi,VO–VLi, MnLi–VLi, MnLi–MnLi, IMnIII–VMn, and LiMnIII–MnLi are more stable than corresponding isolated defects. The charge compensation associated with the creation of defects was also determined according to Bader charges. We found that the compensation was mainly achieved through the redox of the surrounding Mn3+/Mn4+, except for the case of defects at the 8a site. Finally, the diffusion of Li ions around defects was studied. It was found that O vacancy significantly increased the diffusion barrier of Li. In contrast, the antisite defects, i.e., LiMn and MnLi, decreased the Li diffusion barrier obviously. Our theoretical studies provide clear information on the defect properties in LiMn2O4 on the atomic scale and could help in adjusting the performance of spinel LiMn2O4 from defect engineering.
Acknowledgments
This work was funded by the Sino-German Center for Promotion of Science (Grant No. GZ 1528) and Guangxi Key Laboratory of Information Materials (201013-K).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01162.
The calculated formation enthalpies of LiMn2O4, Li2MnO3, LiMnO2, Mn2O3, MnO2, and Mn3O4 (Table S1); the calculated chemical potentials of Li and Mn at some equilibrium conditions (Table S2); and the calculated formation energies of defect pairs with the lowest energy configuration (Table S3) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bäuerlein P.; Herr R.; Kloss M.; Kümpers J.; Maul M.; Meissner E. Advanced lithium ion cells with lithium manganese spinel. J. Power Sources 1999, 81–82, 585–588. 10.1016/S0378-7753(99)00226-8. [DOI] [Google Scholar]
- Gummow R. J.; Kock A. D.; Thackeray M. M. Improved capacity retention in rechargeable 4 V lithium/lithium-manganese oxide (spinel) cells. Solid State Ionics 1994, 69, 59–67. 10.1016/0167-2738(94)90450-2. [DOI] [Google Scholar]
- Guyomard D.; Tarascon J. M. The carbon/Li1+xMn2O4 system. Solid State Ionics 1994, 69, 222–237. 10.1016/0167-2738(94)90412-X. [DOI] [Google Scholar]
- Thackeray M.; David W.; Bruce P.; Goodenough J. B. Lithium insertion into manganese spinels. Mater. Res. Bull. 1983, 18, 461–472. 10.1016/0025-5408(83)90138-1. [DOI] [Google Scholar]
- Manev V.; Banov B.; Momchilov A.; Nassalevska A. LiMn2O4 for 4 V lithium-ion batteries. J. Power Sources 1995, 57, 99–103. 10.1016/0378-7753(95)02227-9. [DOI] [Google Scholar]
- Prabaharan S.; Saparil N. B.; Michael S.; Massot M.; Julien C. Soft-chemistry synthesis of electrochemically-active spinel LiMn2O4 for Li-ion batteries. Solid State Ionics 1998, 112, 25–34. 10.1016/S0167-2738(98)00219-7. [DOI] [Google Scholar]
- Son J.; Kim H. G.; Park Y. New preparation method and electrochemical property of LiMn2O4 electrode. Electrochim. Acta 2004, 50, 453–459. 10.1016/j.electacta.2004.04.048. [DOI] [Google Scholar]
- Zhang S.; Jow T. Optimization of synthesis condition and electrode fabrication for spinel LiMn2O4 cathode. J. Power Sources 2002, 109, 172–177. 10.1016/S0378-7753(02)00063-0. [DOI] [Google Scholar]
- Takada T.; Hayakawa H.; Enoki H.; Akiba E.; Slegr H.; Davidson I.; Murray J. Structure and electrochemical characterization of Li1+xMn2–xO4 spinels for rechargeable lithium batteries. J. Power Sources 1999, 81–82, 505–509. 10.1016/S0378-7753(98)00225-0. [DOI] [Google Scholar]
- Rouse G.; Masquelier C.; Rodriguez-Carvajal J.; Hervieu M. Cubic Orthorhombic Transition in the Stoichiometric Spinel LiMn2O4. Electrochem. Solid-State Lett. 1999, 2, 6–8. 10.1149/1.1390716. [DOI] [Google Scholar]
- Ram P.; Gören A.; Carlos M.; Ferdov S.; Silva M. M.; Singhal R.; Costa C. M.; Lanceros-Mendez S. Improved performance of rare earth doped LiMn2O4 cathodes for lithium-ion battery applications. New J. Chem. 2016, 40, 6244–6252. 10.1039/C6NJ00198J. [DOI] [Google Scholar]
- Liu T.; Dai A.; Lu J.; et al. Correlation between manganese dissolution and dynamic phase stability in spinel-based lithium-ion battery. Nat. Commun. 2019, 10, 4721 10.1038/s41467-019-12626-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei S. M. Small polaron migration in LixMn2O4: From first principles calculations. Phys. Lett. A 2009, 373, 2796–2799. 10.1016/j.physleta.2009.05.071. [DOI] [Google Scholar]
- Karim A.; Fosse S.; Persson K. A. Surface structure and equilibrium particle shape of the LiMn2O4 spinel from first-principles calculations. Phys. Rev. B 2013, 87, 075322 10.1103/PhysRevB.87.075322. [DOI] [Google Scholar]
- Nakayama M.; Nogami M. A first-principles study on phase transition induced by charge ordering of Mn3+/Mn4+ in spinel LiMn2O4. Solid State Commun. 2010, 150, 1329–1333. 10.1016/j.ssc.2010.05.006. [DOI] [Google Scholar]
- Rodríguez-Carvajal J.; Rousse G.; Masquelier C.; Hervieu M. Electronic crystallization in a lithium battery material: columnar ordering of electrons and holes in the spinel LiMn2O4. Phys. Rev. Lett. 1998, 81, 4660–4663. 10.1103/PhysRevLett.81.4660. [DOI] [Google Scholar]
- Singh G.; Gupta S. L.; Prasad R.; Auluck S.; Gupta R.; Sil A. Suppression of Jahn-Teller distortion by chromium and magnesium doping in spinel LiMn2O4: A first-principles study using GGA and GGA+U. J. Phys. Chem. Solids 2009, 70, 1200–1206. 10.1016/j.jpcs.2009.07.001. [DOI] [Google Scholar]
- Ouyang C. Y.; Shi S. Q.; Lei M. S. Jahn–Teller distortion and electronic structure of LiMn2O4. J. Alloys Compd. 2009, 474, 370–374. 10.1016/j.jallcom.2008.06.123. [DOI] [Google Scholar]
- Lee Y. K.; Park J.; Lu W. Electronic and Bonding Properties of LiMn2O4 Spinel with Different Surface Orientations and Doping Elements and Their Effects on Manganese Dissolution. J. Electrochem. Soc. 2016, 163, A1359–A1368. 10.1149/2.0991607jes. [DOI] [Google Scholar]
- Hoang K. Understanding the electronic and ionic conduction and lithium over-stoichiometry in LiMn2O4 spinel. J. Mater. Chem. A 2014, 2, 18271–18280. 10.1039/C4TA04116J. [DOI] [Google Scholar]
- Liu W. W.; Wang D.; Wang Z.; Deng J.; Zhang Y.; Lau W.-M. Influence of magnetic ordering and Jahn–Teller distortion on the lithiation process of LiMn2O4. Phys. Chem. Chem. Phys. 2017, 19, 6481–6486. 10.1039/C6CP08324B. [DOI] [PubMed] [Google Scholar]
- Tarascon J.; McKinnon W.; Coowar F.; Bowmer T.; Amatucci G.; Guyomard D. Synthesis conditions and oxygen stoichiometry effects on Li insertion into the spinel LiMn2O4. J. Electrochem. Soc. 1994, 141, 1421–1431. 10.1149/1.2054941. [DOI] [Google Scholar]
- Paulsen J.; Dahn J. Phase diagram of Li–Mn–O spinel in air. Chem. Mater 1999, 11, 3065–3079. 10.1021/cm9900960. [DOI] [Google Scholar]
- Dong H. J.; Shin Y. J.; Oh S. M. Dissolution of Spinel Oxides and Capacity Losses in 4 V Li/LixMn2O4 Cells. J. Electrochem. Soc. 1996, 143, 2204–2211. 10.1149/1.1836981. [DOI] [Google Scholar]
- Sugiyama J.; Atsumi T.; Hioki T.; Noda S.; Kamegashira N. Nonstoichiometry and defect structure of spinel LiMn2O4−δ. J. Power Sources 1997, 68, 641–645. 10.1016/S0378-7753(96)02595-5. [DOI] [Google Scholar]
- Xia Y.; Sakai T.; Fujieda T.; Yang X. Q.; Sun X.; Ma Z. F.; Mcbreen J.; Yoshio M. Correlating Capacity Fading and Structural Changes in Li1+yMn2-yO4-δ Spinel Cathode Materials: A Systematic Study on the Effects of Li/Mn Ratio and Oxygen Deficiency. J. Electrochem. Soc. 2001, 148, A723–A729. 10.1149/1.1376117. [DOI] [Google Scholar]
- Wang J.; Du Y.; Xu H.; Jiang C.; Kong Y.; Sun L.; Liu Z.-K. Native defects in LiNH2: A first-principles study. Phys. Rev. B 2011, 84, 024107 10.1103/PhysRevB.84.024107. [DOI] [Google Scholar]
- Wang J.; Du Y.; Sun L. Understanding of hydrogen desorption mechanism from defect point of view. Natl. Sci. Rev. 2018, 5, 318–320. 10.1093/nsr/nwx114. [DOI] [Google Scholar]
- Koyama Y.; Tanaka I.; Adachi H.; Uchimoto Y.; Wakihara M. First principles calculations of formation energies and electronic structures of defects in oxygen-deficient LiMn2O4. J. Electrochem. Soc. 2003, 150, A63–A67. 10.1149/1.1522720. [DOI] [Google Scholar]
- Xiao W.; Xin C.; Li S.; Jie J.; Gu Y.; Zheng J.; Pan F. Insight into fast Li diffusion in Li-excess spinel lithium manganese oxide. J. Mater. Chem. A 2018, 6, 9893–9898. 10.1039/C8TA01428K. [DOI] [Google Scholar]
- Xu B.; Meng S. Factors affecting Li mobility in spinel LiMn2O4- A first-principles study by GGA and GGA+U methods. J. Power Sources 2010, 195, 4971–4976. 10.1016/j.jpowsour.2010.02.060. [DOI] [Google Scholar]
- Ammundsen B.; Rozière J.; Islam M. S. Atomistic Simulation Studies of Lithium and Proton Insertion in Spinel Lithium Manganates. J. Phys. Chem. B 1997, 101, 8156–8163. 10.1021/jp971413y. [DOI] [Google Scholar]
- Huang R.; Ikuhara Y. H.; Mizoguchi T.; Findlay S. D.; Kuwabara A.; Fisher C. A. J.; Moriwake H.; Oki H.; Hirayama T.; Ikuhara Y. Oxygen-vacancy ordering at surfaces of lithium manganese(III,IV) oxide spinel nanoparticles. Angew. Chem. 2011, 123, 3109–3113. 10.1002/ange.201004638. [DOI] [PubMed] [Google Scholar]
- Kresse G. G.; Furthmüller J. J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Yue W. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. 10.1103/PhysRevB.45.13244. [DOI] [PubMed] [Google Scholar]
- Wang Y.; Perdew J. P. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 1991, 44, 13298–13307. 10.1103/PhysRevB.44.13298. [DOI] [PubMed] [Google Scholar]
- Anisimov V. I.; Zaanen J.; Andersen O. K. Band Theory and Mott Insulators: Hubbard U Instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. 10.1103/PhysRevB.44.943. [DOI] [PubMed] [Google Scholar]
- Shiiba H.; Zettsu N.; Nakayama M.; Oishi S.; Teshima K. Defect formation energy in spinel LiNi0.5Mn1.5O4-δ using Ab initio DFT calculations. J. Phys. Chem. C 2015, 119, 9117–9124. 10.1021/acs.jpcc.5b01661. [DOI] [Google Scholar]
- Kitchaev D.; Peng H.; Liu Y.; Sun J.; Perdew J. P.; Ceder G. Energetics of MnO2 polymorphs in density functional theory. Phys. Rev. B 2016, 94, 045132 10.1103/physrevb.93.045132. [DOI] [Google Scholar]
- Henkelman G.; Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- Henkelman G.; Uberuaga B. P.; Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
- Tang W.; Sanville E.; Henkelman G. A grid-based Bader analysis algorithm without lattice bias. J. Phys.: Condens. Matter 2009, 21, 084204 10.1088/0953-8984/21/8/084204. [DOI] [PubMed] [Google Scholar]
- Sanville E.; Kenny S. D.; Smith R.; Henkelman G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. 10.1002/jcc.20575. [DOI] [PubMed] [Google Scholar]
- Yamaguchi H.; Yamada A.; Uwe H. Jahn-Teller transition of LiMn2O4 studied by x-ray-absorption spectroscopy. Phys. Rev. B 1998, 58, 8–11. 10.1103/PhysRevB.58.8. [DOI] [Google Scholar]
- Sliwko V.; Mohn P.; Schwarz K. The electronic and magnetic structures of alpha - and beta -manganese. J. Phys: Condens. Matter 1994, 6, 6557–6564. 10.1088/0953-8984/6/32/017. [DOI] [Google Scholar]
- Tarascon J.; Coowar F.; Amatuci G.; Shokoohi F.; Guyomard D. The Li1+xMn2O4C system Materials and electrochemical aspects. J. Power Sources 1995, 54, 103–108. 10.1016/0378-7753(94)02048-8. [DOI] [Google Scholar]
- Strobel P.; Rousse G.; Ibarra-Palos A.; Masquelier C. Disproportionation of stoichiometric LiMn2O4 on annealing in oxygen. J. Solid State Chem. 2004, 177, 1–5. 10.1016/S0022-4596(03)00189-0. [DOI] [Google Scholar]
- Kanno R.; Kondo A.; Yonemura M.; Gover R.; Kawamoto Y.; et al. The relationships between phases and structures of lithium manganese spinels. J. Power Sources 1999, 81–82, 542–546. 10.1016/S0378-7753(99)00103-2. [DOI] [Google Scholar]
- Gao Y.; Dahn J. R. Thermogravimetric analysis to determine the lithium to manganese atomic ratio in Li1+xMn2-xO4. Appl. Phys. Lett. 1995, 66, 2487–2489. 10.1063/1.113143. [DOI] [Google Scholar]
- Yamada A. Lattice instability in Li (LixMn2–x)O4. J. Solid State Chem. 1996, 122, 160–165. 10.1006/jssc.1996.0097. [DOI] [Google Scholar]
- Gummow R. J.; Thackeray M. M. An Investigation of Spinel-Related and Orthorhombic LiMnO2 Cathodes for Rechargeable Lithium Batteries. J. Electrochem. Soc. 1994, 141, 1178–1182. 10.1149/1.2054893. [DOI] [Google Scholar]
- Verhoeven V. W. J.; Mulder F. M.; Schepper I. M. d. Influence of Mn by Li substitution on the Jahn–Teller distortion in LiMn2O4. Phys. B 2000, 276–278, 950–951. 10.1016/S0921-4526(99)01272-7. [DOI] [Google Scholar]
- Seo D.-H.; Lee J.; Urban A.; Malik R.; Kang S.; Ceder G. The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials. Nat. chem. 2016, 8, 692–697. 10.1038/nchem.2524. [DOI] [PubMed] [Google Scholar]
- Chen J.; Graetz J. Study of antisite defects in hydrothermally prepared LiFePO4 by in situ X-ray diffraction. ACS Appl. Mater. Interfaces 2011, 3, 1380–1384. 10.1021/am200141a. [DOI] [PubMed] [Google Scholar]
- Chung S. Y.; Choi S. Y.; Yamamoto T.; Ikuhara Y. Atomic-scale visualization of antisite defects in LiFePO4. Phys. Rev. Lett. 2008, 100, 125502 10.1103/PhysRevLett.100.125502. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.