Water/Oil Emulsions with Controlled Droplet Sizes for In Vitro Selection Experiments

Abstract

In the early history of life, RNA might have had many catalytic functions as ribozymes that do not exist today. To explore this possibility, catalytically active RNAs can be identified by in vitro selection experiments. Some of these experiments are best performed in nanodroplets to prevent diffusion between individual RNA sequences. In order to explore the suitability for the large-scale in emulsio selection of water-in-oil emulsions made by passing a mixture of mineral oil, the emulsifier ABIL-EM90, and a few percent of an aqueous phase through a microfluidizer, we used dynamic light scattering to characterize the size of aqueous droplets dispersed throughout the oil. We found that seven or more passes through the microfluidizer at 8000 psi with close to half molar inorganic salts and 10% polyethylene glycol produced droplets with sizes below 100 nm that were ideal for our purposes. We also identified conditions that would produce larger or smaller droplets, and we demonstrate that the emulsions are stable over weeks and months, which is desirable for different types of in vitro selection experiments.

Introduction

Early stages of life may have relied on catalytic RNAs (ribozymes) to sustain biochemical functions, such as self-replication, before encoded protein synthesis allowed the emergence of today’s DNA/RNA/protein organisms.¹⁻⁴ To test how that stage of life could have functioned, researchers are aiming to generate ribozymes with central biochemical functions in such a system. In vitro selection experiments are the only known method to identify new catalytic RNAs (ribozymes) that do not exist today in nature.⁵⁻⁷ The starting points for in vitro selection experiments are large RNA libraries with randomized regions, usually containing 10¹⁴–10¹⁶ different sequences.⁸⁻¹³ A tiny fraction of the library molecules fold into structures that form a catalytic pocket and catalyze a desired reaction. To isolate these ribozymes, the library molecules are incubated with a substrate molecule such that catalytically active molecules tag themselves with the substrate. A “handle” at the substrate then allows isolating the active molecules. The catalytically active molecules are amplified by reverse transcription, PCR amplification, and transcription. The resulting RNA library is consequently enriched in catalytically active sequences. Multiple cycles of selection and enrichment are carried out until the pool is dominated by active sequences. Only then can individual, catalytically active RNA molecules be cloned and characterized.^5,6

A serious limitation for such experiments is that the catalyzed reaction needs to result in the self-tagging of the catalytically active library molecule, so that the active molecules can be isolated from the library of inactive molecules. Therefore, these classical methods do not allow the direct selection of catalysts that generate freely diffusing reaction products. One may, however, identify such catalysts if one can compartmentalize the library molecules. The compartments should separate each single RNA molecule from all others, so that the reaction products from active library molecules can be tagged in a separate step within the same compartment. The compartments can be aqueous droplets of water-in-oil emulsions. These have been used for in emulsio evolution.^14,15

Water-in-oil emulsions have been used for the evolutionary optimization of both ribozymes^14,16−20 and proteins.²¹⁻²³ All these previous in emulsio evolution experiments, however, started from an existing, active ribozyme or protein, so that sampling a combinatorial space of less than 10⁸ was sufficient to generate improved ribozymes and proteins. To identify new catalysts from random sequences, a much larger number of individual library molecules need to be sampled. The critical problem is how to generate a sufficient number of small aqueous droplets with a sufficiently narrow size distribution. One study optimized an existing ribozyme from a library with a high complexity (9 × 10¹⁴) in an emulsion.¹⁹ However, the emulsion had droplets with a broad size distribution and each droplet contained on average 30 library molecules, which limited the selective power. As an alternative, one might employ chip-based microfluidic devices, which are able to generate extremely narrow droplet size distributions. These, however, are currently limited to about 10⁸ droplets,¹⁶⁻¹⁸ which are inadequate when about 10¹²–10¹⁶ different library sequences are necessary to identify a new ribozyme from a random sequence.⁷⁻¹³

One must conclude, therefore, that the identification of new ribozymes from a completely random sequence in emulsions will require at least 10¹² small droplets, with most droplets hosting no more than one library molecule. To generate emulsions with such large droplet numbers along with a suitable size distribution, a promising technique is the use of a microfluidizer. This apparatus presses a raw emulsion mixture through an orifice with a defined geometry, generating defined shear forces. Emulsion volumes of hundreds of milliliters can be produced easily, and repeated passes of this emulsion through the microfluidizer can generate a narrow size distribution.²⁴

The formulation of the emulsion is critically important for the success of in emulsio selection experiments because the emulsifier needs to be compatible with the catalysts in the droplets, and the emulsion needs to be stable over the course of the experiment. A number of different emulsifiers have been used for evolution experiments.^14,17,20,25 The proprietary, siloxane-based emulsifier ABIL EM-90 in mineral oil, was particularly useful for in emulsio evolution experiments because it facilitated enzymatic activity better than other emulsifiers.²⁶ This formulation and slight variations were used in several in emulsio evolution experiments,^18,19 and it is the one chosen for the present study.

We have used a microfluidizer-generated emulsion successfully for the direct in emulsio selection of a ribozyme that generates freely diffusing guanosine 5’-triphosphate (GTP) from guanosine and cyclic trimetaphosphate.²⁷ The emulsion had a droplet size distribution with a diameter of around 150 nm, small enough that most droplets contained one ribozyme (or none): at this droplet diameter, one molecule per droplet corresponds to a concentration of about 1 μM in the aqueous phase. The emulsion used heavy mineral oil as the matrix, the siloxane-based emulsifier ABIL EM-90, and a 5% aqueous phase. Inside the compartments (droplets), active library molecules were tagged at their 3′-terminus using a highly optimized ribozyme that tags RNA 3′-termini with 6-thio-modified GTP (6sGTP).²⁸ This sulfur tag was used to isolate active pool molecules on polyacrylamide gels containing covalently immobilized mercury.²⁹⁻³¹ An effective complexity of 1.6 × 10¹⁴ different sequences with 150 randomized positions was covered. After 12 rounds of this selection procedure, five clusters with biochemical activity for nucleoside triphosphorylation dominated the RNA library. The most active ribozyme for the production of GTP from guanosine and cyclic trimetaphosphate was characterized in more detail and shown to mediate an 18,000-fold rate enhancement over the uncatalyzed reaction. This is the first case of the in emulsio selection of a ribozyme from a completely random sequence.

The measurement of droplet sizes is important to characterize in emulsio selection systems and to help in the design of optimal emulsions for different selection experiments. This measurement is not trivial because light microscopy does not resolve the sizes of images of droplets that are smaller than the wavelength of visible light. The droplets may show up and be seen as points of light, like stars in the sky; but as with stars, there is no information about the size of each point. One possible strategy could be static light scattering, which measures the intensity of light scattering as a function of conditions; but among other challenging requirements, one must prepare and know very accurately a wide range of concentrations. This is tedious in any case and particularly difficult for highly viscous solvents in which it is difficult to ensure homogeneity. An alternative we deemed more attractive is dynamic light scattering (DLS), which measures the diffusion of the small droplets through oil. These measurements are tedious for emulsions in viscous oil because the droplet’s diffusion is slow and outside the range anticipated by commercial instruments that are optimized to deal with aqueous solutions. Here, we use a home-made setup for DLS to measure the autocorrelation function of DLS over times long enough to deal with highly viscous emulsions.

Our analysis shows the effect of multiple passes of the emulsion through the microfluidizer and describes the droplet size as a function of the microfluidizer pressure, the addition of various amounts of polyethylene glycol (PEG), and the incorporation of inorganic salts. We also investigated droplet stability over time from hours to months. The Results section outlines conditions that we found to be promising for the in emulsio selections of either RNAs or proteins from large sequence libraries.

Experimental Methods

Preparation of the Raw Mixture Used to Make Emulsions

The oil phase of the emulsion was generated by mixing 4% (v/v) of the emulsifier ABIL EM90 (Evonik), with 96% (v/v) heavy mineral oil (Fisher O122-1). Because both liquids are viscous, they were measured by weight with 1.78 g (4.47% w/w) of ABIL EM90 and 39.6 g (95.53% w/w) of mineral oil. The oil phase was stirred at least 15 min at room temperature and degassed in oil vacuum until bubbling ceased. The mineral oil phase was then cooled on an ice bath for 10 min while stirring gently. An aqueous solution containing 100 mM MgCl₂, 200 mM KCl, 50 mM Tris/HCl pH 8.3, and PEG 20,000 at the desired concentration [usually 0 or 10% (w/v) but occasionally others] was added to the oil phase and stirred for 5 min before loading this raw emulsion into the prepared microfluidizer. A few experiments tested the result of using different salt concentrations, as specified in the Results. The aqueous phase amounted to 5% of the final emulsion volume.

Preparation of the Fine Emulsion

A microfluidizer (Microfluidics, M110L) with a Z-shaped channel and a diameter at the narrowest section of 0.1 mm (Microfluidics, H10Z, 100 μm) was prepared by rinsing with 50 mL of heavy mineral oil (Fisher, O122-1), adjusting the pressure to the value needed for a specific experiment (2000–12,000 psi), and cooling the microfluidizer cell with an ice bath. The ice-cold raw emulsion was loaded into the glass inlet of the microfluidizer, and the pressure valve was opened. The first piston stroke (∼6 mL) was discarded, and all the subsequent piston strokes were pooled. Immediately after the last stroke was collected, the emulsion was cooled by rotating it in the ice bath for 5 min. The contents were loaded again into the glass inlet of the microfluidizer for the next pass. The emulsion turned white immediately after the first pass but was slightly transparent after seven passes. The final emulsion was slightly red when viewed by looking through the emulsion but appeared slightly blue when light was reflected off the emulsion. Unless otherwise noted, the emulsion was passed seven times through the microfluidizer cell. Critical to the measurement is the knowledge of the viscosity of the oil. The oil viscosity (0.20 mPa s) at the temperature of the DLS was determined using a falling ball viscometer³² and was consistent with the manufacturer’s specifications. The index of the refraction of the oil was 1.41. The resulting fine emulsion was stored overnight at room temperature prior to DLS measurement the following day. Some early efforts chilled the samples overnight, but that was determined to be unnecessary and, given what we learned later, may have been counterproductive.

Sample Preparation for DLS Measurements

The fine emulsion had to be diluted to be suitable for DLS measurements. The mineral oil used for dilution was saturated with water by vortexing for about a minute and was then centrifuged at 2000g for 2 min. This water-saturated mineral oil was used to make 1:300 and 1:600 dilutions. The mixture was slowly inverted about 10 times. To disrupt possible aggregates of emulsion droplets, the diluted emulsion was processed five times in a hand-held glass tissue homogenizer while withdrawing the piston very slowly to minimize the formation of bubbles. The samples were transferred into quartz “fluorescence” cuvettes of dimensions 1 × 1 × ∼4 cm with four clear sides and a Teflon stopper. Quartz is not essential to work at 532 nm, but it does have low luminescence and may offer superior quality.

Laser Illumination for DLS

A Coherent Verdi neodymium ion laser, with single transverse and single longitudinal modes, frequency doubled to 532 nm, was used. The beam traveled about 1.5 m before entering the sample chamber through a small aperture (but one large enough to accommodate small movements of the beam without clipping). This eliminates stray light produced in the laser itself. The beam was then reflected 90° upward to pass vertically through the sample cuvette, which was set on its side, so that the transmitted beam could avoid the cuvette stopper and escape from the box through another small aperture and be captured with a nonreflecting beam stop. This cuvette was tilted just enough to steer any reflections from cell windows away from the detector. The interior of the box had a low reflectivity, black coating. The beam polarization at the sample was horizontal and perpendicular to the direction of the detector. A small, round aperture of slightly less than 1 mm diameter was positioned about 2 cm from the cuvette. That aperture, along with the incident beam diameter, defined the scattering volume, which was kept away from the cell walls, except for a few control efforts, not discussed here. The solid angle detected was defined by a rectangular aperture, at 90° from the vertical incident beam, of about 2 mm by 3 mm located 20 cm distant at the entrance to a subtractive, double monochromator (Spex 1672 Doublemate). The detection bandwidth was 4 nm. The optical path of the scattered light was enclosed by an opaque cylinder. In the path of the scattered light, there was a polarizer. There was also an additional aperture acting as a baffle, one large compared to the scattered beam, but blocking some possible reflections. The entire laser and detection apparatus was on a vibration-isolated optical table in a darkened “tent” with some control of air movement and temperature and modest air filtering. Due to these precautions, background light was negligible, both at the laser wavelength and at any other wavelengths. The efforts were overkill for the main measurements but reassuring for certain controls. For example, there was no reason to expect depolarized scattering, but preliminary measurements searched for a depolarized signal by rotating the polarizer to pass vertically polarized light. Any depolarized signal was undetectable. All the subsequent measurements detected polarized scattering with the polarizer oriented horizontal, parallel to the incident beam polarization. Most measurements were made with an unfocused incident beam, but some preliminary tests used a lens to focus the light into the cuvette. Two lenses were tried, one of 100 mm focal length and one of 500 mm. The cuvette was not necessarily at the focus; it could be just at a reduced beam size. We used laser powers ranging from a few milliwatts up to half a watt, but for optimal signal-to-noise, we settled on about 100–200 mW in an unfocused beam. The laser is most stable at powers above 1 W, so neutral attenuators were employed. Some preparations scattered more strongly than others and that influenced the power used. With focused beams, we used less power.

Detection of the DLS Signals

After passing through the double monochromator, photons were detected by an Amperex TUVP56 photomultiplier tube (PMT) with an S-20 photocathode. This ancient 13-stage design is capable of high gain, good for photon counting, and it is specially designed to tolerate exceptionally high anode currents up to one full ampere for a short time, given adequate interdynode capacitance. While it is not really linear at that level, it works well at milliamp output currents (or equivalent photon count rates) that would exceed the capacity of most other tubes. We operated at modest gain and then passed the output pulses through a 10-fold amplifier to a discriminator and thence to a multichannel scalar (MCS) (a PC plug-in board: MCA-3 P7882, FAST ComTec GmbH) that accumulated photon counts for a time bin and then advanced to the next bin. A second output from the discriminator was sent to a frequency/pulse counter, so that we could monitor the scattered intensity in real time. The measurements reported here were made using a 0.5 ms dwell time per bin in the MCS. Preliminary measurements with both longer and much shorter dwell times revealed 0.5 ms to offer a good balance between having sufficient resolution to measure the correlation times of interest and the desire to have a long record for calculating the autocorrelation. The record length for a single measurement run accumulated in the MCS was 2¹⁹ samples (524,288), which for a 0.5 ms dwell time is about 4.37 min. Multiple such “runs”, typically about 20 or more, were recorded for each particular sample. Photons recorded per 0.5 ms bin in a single run ranged from as many as three thousand (rarely) down to as few as one hundred, in order to explore the effect of changing the laser flux, PMT high voltage, and discriminator settings, but were mostly around one thousand counts per bin. At that count rate, the random “shot” noise from photon statistics would impose a 3% uncertainty for the number recorded in each single bin. With half a million bins being summed to calculate each point of the autocorrelation, the fluctuations imposed by photon statistical shot noise were negligible and did not affect the autocorrelation at any delay time after zero. The shot noise does contribute to the 0-time datum of the autocorrelation but that was excluded from curve fitting. Extensive efforts to find correlations due to variation in the laser or the beam propagation to the sample by detecting scattering from ground glass failed at levels well below the signals of interest. What in the sample itself might introduce random or systematic deviations into the autocorrelation and why it was useful to average many separate autocorrelation curves are discussed below.

Calculation of the Autocorrelations

The calculation of the autocorrelation off-line in a PC proceeded by first calculating the mean of the 2¹⁹ samples in the data file and subtracting that mean from the data value at each sample bin. Then, the resulting value for any particular number of photon counts in a bin was multiplied by itself for the time 0 autocorrelation and added to a sum associated with delay 0. Then that same number was multiplied by the photon count for the next sample bin and added to a running sum for the time delay of one unit. The number was then multiplied by the numbers for as many successive delay times as desired, and each product was added to a running sum associated with that particular time delay. All of this was repeated for each of the 2¹⁹ data points. The sum for each delay was divided by the number of products contributing to it. In the ideal case, with uniform small nanodrops, the autocorrelation should decay from some initial values to zero according to a single exponential function.³³ Typically, autocorrelations were computed out to 5000 or 10,000 delay times, far longer than the persistence time of fluctuations in the scattered intensity, which were in the range of 40–200 bins for the half-life. Such long times test whether the autocorrelation at long times is close to zero with random scatter above and below zero. The autocorrelation traces are normalized so that the 0-delay point is equal to 1. Actual curve fitting used some appropriate initial portions of the full autocorrelation. If one fits 10,000 points, statistical tests of the goodness of fit will report that a fit is very good if it fits well the last 9000 points, perhaps all zeroes, no matter how poorly it fits the relevant initial portion. Fitting the decay of the autocorrelation to any model was accomplished using our own version of the Marquardt method taken from the Bevington’s classic text on data analysis.³⁴ Several possible models were considered; some were much more complicated than single exponentials. Bevington’s FORTRAN programs were converted to C code some 40 years ago and adapted for personal computers not long after that. We might not do it that way if we were starting today, but the code has served some of us for decades.

Results

Except where noted otherwise, results are reported in terms of a diameter calculated directly from the lifetime of a single exponential fit to the initial decay of the autocorrelation, usually with a very small constant offset that may be positive or negative. The characteristic particle diameter can be estimated from the lifetime using a formula that is found in any treatment of DLS for Rayleigh scattering; we cite the one we rely upon.³³ For our conditions, it reduces to the following

where d is the diameter in nm and τ is the lifetime in milliseconds.³³ This equation includes a factor of 2 for homodyne detection and otherwise needs only the scattering vector and a viscosity for the oil, which is very close to 200 times that of water. The temperature must be known because it affects the oil viscosity and was 22.6 ± 0.5 °C.

Some preliminary measurements were made on aqueous solutions containing standardized latex spheres (Polysciences, 64 ± 10 and 200 ± 12 nm). In these cases, because the solvent was water, the channel dwell time needed to be a hundred times shorter and shot noise was a larger issue—but we could compensate by averaging more runs. The measurements of any standard agreed well with the manufacturer’s claimed particle diameter. Various small distortions of the autocorrelation discussed below were not seen in the aqueous solutions, consistent with our inference that working with viscous oil can be somewhat problematic. Nor were there any such distortions in measurements at several different wavelengths of the fluorescence of rhodamine 6G in ethanol, which remained precisely constant to better than one part per thousand in numerous trials, aside from a gradual decrease in amplitude due to “bleaching” of the dye.

Effect of Multiple Passes through the Microfluidizer

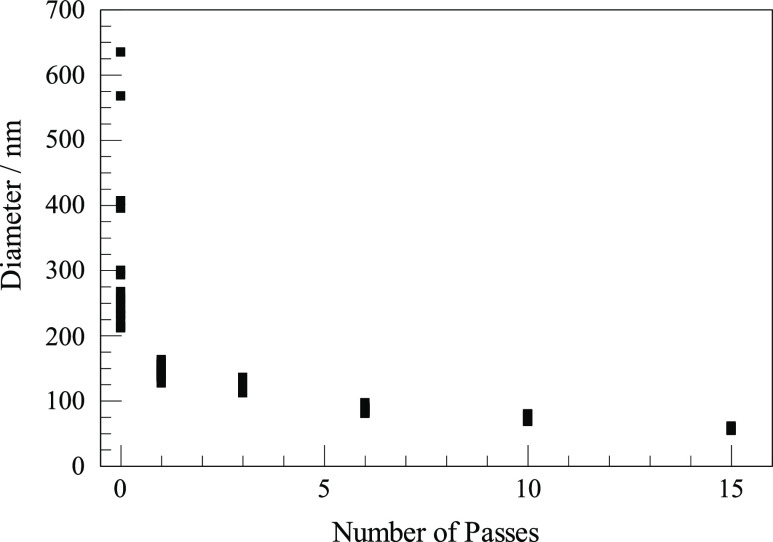
We tested emulsions after 0, 1, 3, 6, 10, and 15 passes through the microfluidizer. The results are shown in Figure 1 for emulsions made at 8000 psi with our standard salt concentrations and 10% PEG at 300:1 dilution. Each of the six instances is represented in the figure by 16–19 points, each derived from fitting a single DLS measurement run to a single exponential fit to the first three half-lives (almost 90%) of the decay of the count signal. Except for the measurement on the raw mixture with no pass at all through the microfluidizer, the 16–19 points largely overlap in the figure, and from them, one may estimate a mean size and derive some notion of variation. The conditions used were favorable for making emulsions. It is quite possible that emulsions made at much lower pressure or with less favorable composition would benefit from more passes, but we did not investigate lower pressures for this test. The 0-pass mixture (the raw emulsion before passing through the microfluidizer) was not close to being a uniform emulsion, but it did have some variations in refractive index that result in light scattering as they diffuse through the observation volume. The autocorrelations for that mixture varied widely, with lifetimes differing by more than a factor of 3. Figure 1 gives convincing reassurance that more passes are better. It also shows that after six or more passes, DLS measurements on a single sample became quite reproducible. Figure 1, by itself, does not show that another preparation under the same conditions would produce nearly identical autocorrelations. On the other hand, the fact that different preparations using different numbers of passes showed such a nice, smooth trend suggested that repeating any case would give similar results. Most importantly, Figure 1 demonstrates that the DLS measurements were reproducible when we did have a true emulsion and that averaging one or two dozen measurements for any one sample was useful and sufficient for our purposes.

Figure 1.

Diameters inferred from the decay of autocorrelation measurements fit to single exponentials for six emulsions, each prepared by a different number of passes through the microfluidizer.

Adequacy of a Single Exponential Fit

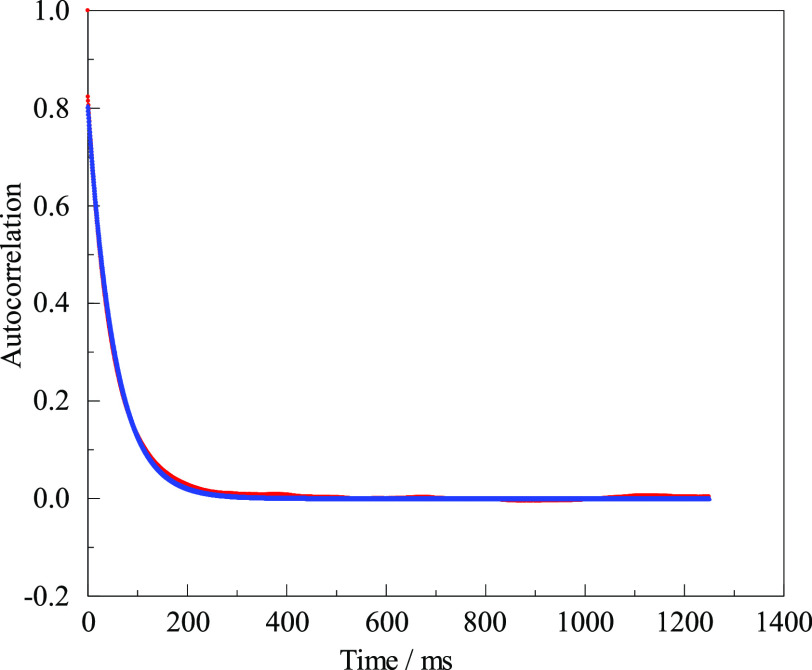
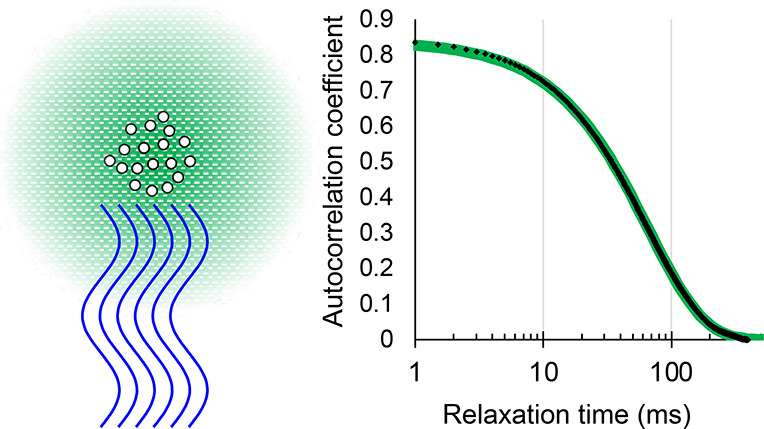
If an emulsion consisted of perfectly uniform droplets, each with a diameter much less than the wavelength of the laser light, and if there were no instrumental artifacts, the autocorrelation trace would be a perfect single exponential decaying to zero at long times. There will be an extra signal in the time zero bin due to photon shot noise, but the exponential should fit from the next point to the end of the file and can be extrapolated back to zero time to yield an initial amplitude. In reality, no emulsion is perfectly homogeneous. We ruled out the above-mentioned artifacts related to the laser or to vibrations, but there might still be other problems related to the sample itself. Figure 2 compares an autocorrelation trace with a single exponential fit that has only two free parameters: an initial amplitude and a time constant for the decay.

Figure 2.

Autocorrelation function of a representative DLS experiment. Data (red) are compared to a fit (blue) of the form 0.80 exp(−time/54.4 ms). Only the first quarter of the full length is plotted.

There are no lines in Figure 2, just 2500 data points and 2500 fit points. The emulsion was made at 8000 psi and 10% PEG. The measurement was made after we had some experience. Otherwise, it was selected arbitrarily. (The same data appear later as the last point in Figure 4 and the first point in Figure 5 under the specified conditions.) In many circumstances, this would be considered a superb fit, but there are slight deviations. The autocorrelation in Figure 2 is the average of 25 runs, totaling more than 2²³ samples of the scattered intensity, with each of the sample measurements involving many hundreds of photon counts. If the figure can be examined closely, one may detect slight discrepancies below 0.01 in amplitude. There is a slight excess of data above fit for times near or below about 20 ms. There is also a slight excess at long times, say 100–300 ms. There is a slight deficiency of data below fit near 50 ms. This behavior is universal (so long as shot noise is reduced sufficiently) and is presumably the evidence for the variation in droplet sizes. There are also slight “bumps” or variations in the data above the fit near 400, 700, and 1200 ms, along with a “dip” near 900 ms. There may be smaller “bumps” and “dips” elsewhere. Features like these did not become more prominent by averaging multiple runs; they appeared at random times in one run and were minimized by averaging multiple runs, but they could be large enough in rare cases to have a small effect even on the average of several runs.

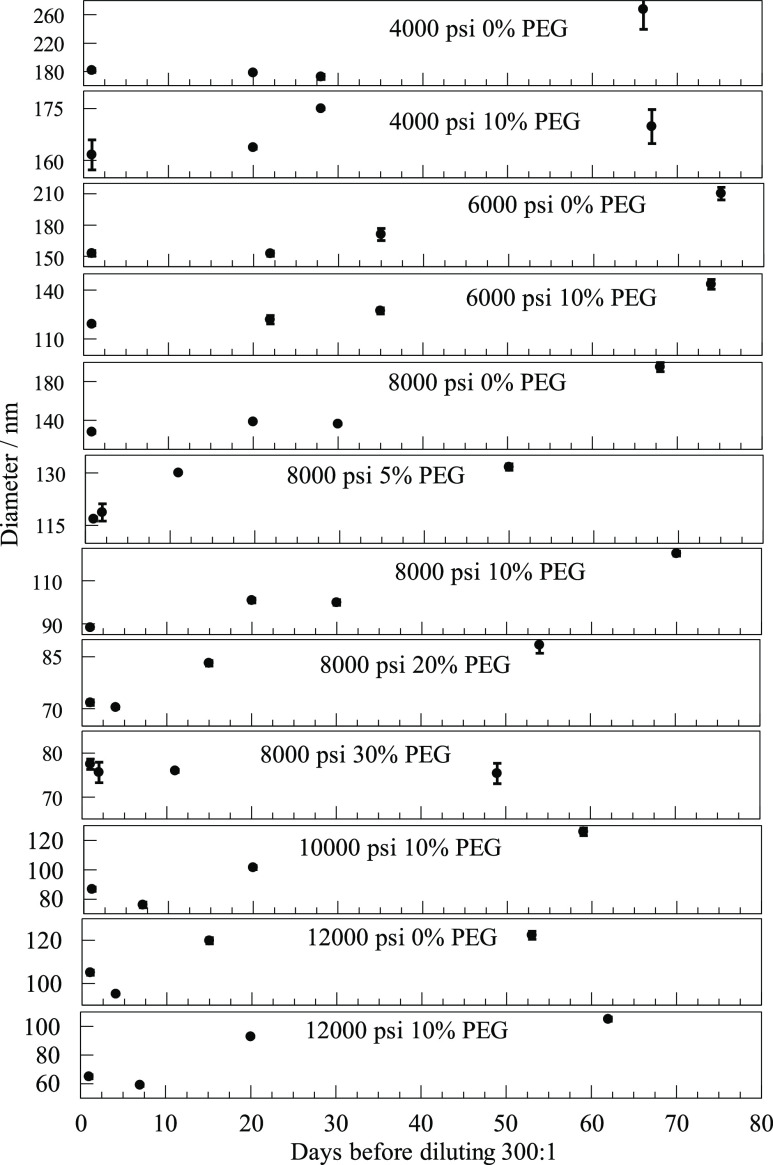
Figure 4.

Diameters inferred from the lifetimes of exponential fits to the initial decay of autocorrelations for dilutions made from stock emulsions after various delays for different pressures and PEG concentrations. The graphs illustrate that for many combinations of pressure and PEG concentration, the diameters determined from the autocorrelation functions remain almost the same over the course of several weeks.

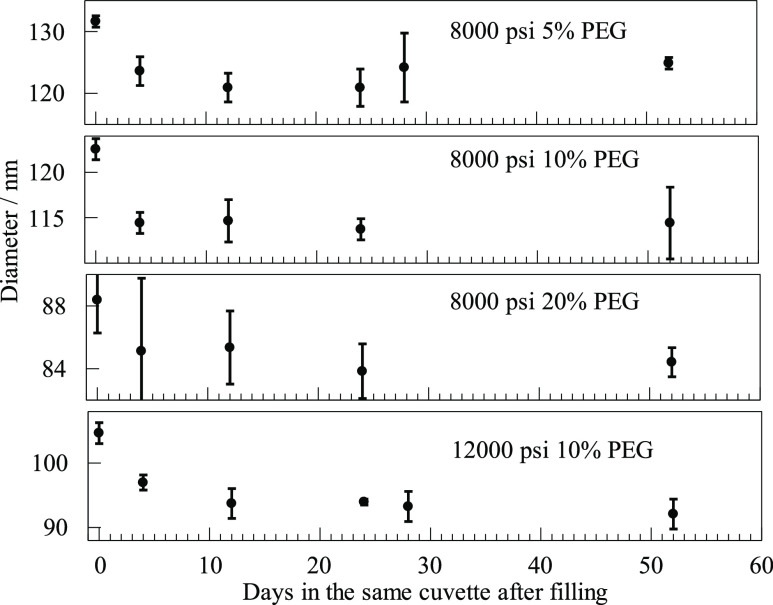
Figure 5.

Diameters inferred from single exponential fits to the initial decay of autocorrelations for emulsions kept undisturbed in cuvettes for many days after dilution.

One final discrepancy is not evident in Figure 2. The data set is very slightly offset above the fit. A statistically better fit was obtained if we fit to a constant 0.0021 plus an exponential. The amplitude remained 0.80, but the lifetime was reduced from 54.4 to 53.8 ms. There must have been slow or rare changes in the average scattered intensity. We return to the matter of possible small artifacts in the Supporting Information. For now, it suffices to compare diameters typical of different emulsions obtained by the best fits to single exponentials with small constant offsets.

Effect of Various Pressures and Different Amounts of PEG

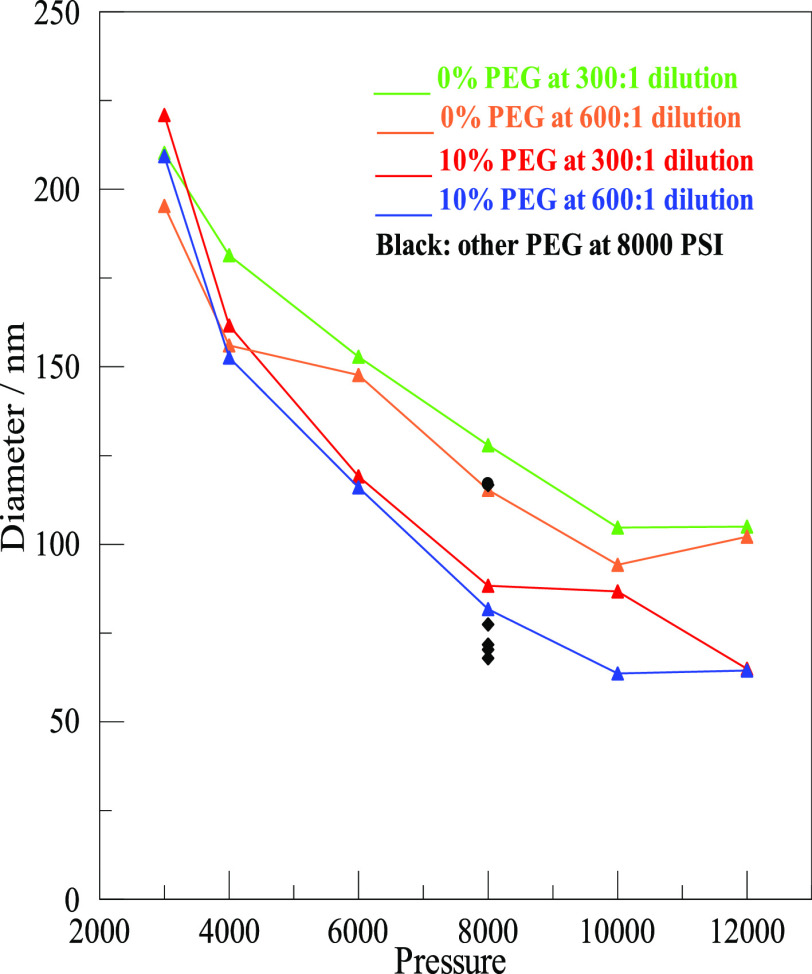
The central goal of our study was to explore the effect of different pressures for the microfluidizer and different concentrations of PEG on the size of nanodrops. A summary is shown in Figure 3. The numerical values of the data points with estimates of their uncertainties are given in Tables S1 and S2 of the Supporting Information. The two prominent inferences we can make from Figure 2 are that higher pressures produced smaller droplets and that adding some amount of PEG, shown in the bottom two lines, also gave smaller droplets. Emulsions without PEG are shown in the top two lines. Uncertainties were mostly near 1 or 2% but were higher at 4000 psi and especially at 3000 psi. The 0% PEG at 6000 psi and 600:1 dilution also had a larger than usual uncertainty of 4%. The listed uncertainties were relevant to the repeatability of the autocorrelations on the same sample over a couple of hours. The obvious displacement of two other points from where it appears they should be was around 10%, which was more than the uncertainty in fitting. Factors that involve such a real, but still modest, variation in either the samples or the measurement conditions, as in these cases, appeared to be rare. Working at 12,000 psi was the upper limit of what was comfortable with the microfluidizer.

Figure 3.

Average diameters of nanodrops as a function of pressure, both with and without PEG, and at two different dilutions. The concentration of PEG (w/v) in the aqueous phase and the dilution of the emulsion for DLS measurement are given in the inset. At 8000 psi, the black symbols are for additional PEG concentrations, as detailed in the text.

Shown in Figure 3 are two different dilutions of the samples of each stock emulsion. After storing the emulsion overnight, dilutions of 300:1 or 600:1 were made the following morning before DLS measurements were carried out 1–6 h later. The results for samples prepared at a dilution of 300:1 are shown in the top, green, line and the third, red, line. Results for 600:1 dilution are displayed on the second, orange, line and the bottom, blue, line. The lines connect points but have no other significance. There was a pronounced tendency for the 600:1 dilution to give slightly smaller diameters than the 300:1 dilutions. The small effect of this dilution, even if real, would be irrelevant to the matter of finding optimal conditions for generating desirable droplets for in vitro selection. Possible sources for the small effect are described in the second- and third-last paragraph of the discussion. Having established that 8000 psi was a reasonable pressure, additional PEG concentrations were tested at that pressure for both dilutions. They are shown in the figure as black dots. For all PEG concentrations, the 600:1 dilution had slightly smaller diameters. Both dilutions for 5% fell close to the second line. The two points for dilutions of 20% PEG and two more for 30% PEG all fell below the bottom line. They were quite close together, pretty much overlapping. It seemed that beyond 20%, or even 10%, further increasing PEG did very little to further reduce diameters. In fact, these particular preparations gave slightly larger diameters for 30% PEG than those for 20% PEG. The data for all the 300:1 dilutions are also displayed as a three-dimensional bar graph in Figure S1 in the Supporting Information.

Effect of Small Inorganic Salts

We explored the effect of varying the concentrations of inorganic salts. All the samples used for other measurements employed identical salt compositions. Here, we compare four different preparations. Three incorporated 10% PEG but had only 200 mM KCl, 100 mM MgCl₂, or Tris/HCl at pH 8.5. (The preparations for other works included all three of these additives.) The slightly alkaline pH of 8.5 was chosen because a pH higher than neutral makes it easier for ribozymes to catalyze base-catalyzed reactions, for example, via the deprotonation of a hydroxyl group in preparation for a nucleophilic attack. A fourth sample was prepared by mixing just water with the oil and the emulsifier, with no salt and no PEG. All four preparations passed the microfluidizer seven times at 8000 psi and were then diluted 300:1 for DLS studies. The droplet sizes for the four situations are listed in Table 1.

Table 1. Diameters Inferred from the Initial Decay of Autocorrelations for Different Salts.

sample composition	diameters in nm
200 mM KCl	104.7 ± 0.2
100 mM MgCl2	188 ± 3
Tris/HCl at pH 8.5	166 ± 1
plain water	(337 ± 28) see text

The preparations listed in Table 1 showed larger sizes than did the usual salt composition, which had a diameter near 88 nm. Salts of small ions had a profound effect. The preparation with just water, emulsifier, and oil, with no salts at all, and no PEG, did not result in anything resembling exponentially decaying autocorrelations, indicative of proper DLS from nanoparticles. There was evident inhomogeneity in the mixture that resulted in light scattering, but seven passes were not sufficient to produce nanodrops uniform enough to be well characterized by an average diameter. Still, there was some autocorrelation that persisted for a time more or less equivalent to a diameter near 337 nm. Additional control studies measuring DLS for either pure oil or pure water processed through the microfluidizer, with or without various additives, all gave scattering weaker by about 2 orders of magnitude, with no correlations at all on the millisecond time scale.

Stability of Emulsions over Many Weeks

Passes through the microfluidizer to form “stock” emulsions were carried out the same day the oil was mixed with emulsifier, water, and other additives. The stock was stored overnight before portions were diluted for DLS. Measurements made the same day as the dilutions, day 1, meaning one day after the stock was prepared, are reported in Figure 3. We retained the stocks at room temperature and chose 12 of those to dilute and investigate again days or weeks later. These delayed measurements are reported in Figure 4 along with the values from Figure 3 that appear again as measurements on day 1. Dilutions at 300:1 were prepared from the stock in the morning of the listed day, and 20 DLS measurement runs, or more, were made later that same day.

Figure 4 combines 12 plots covering more than 2 months of storage. They are arranged so that the pressure used in the microfluidizer increases downward. Within each pressure group, the PEG used increases downward. Note that the scales of the vertical ordinates are expanded greatly by different amounts and offset in order to display the variability observed. Every plot has four data points, the first of which is for the datum in Figure 3. Each point has an error bar that indicates the scatter in that day’s autocorrelation fits. In most cases, the error bars are barely discernible.

Comparing the 12 plots, one sees that changes over weeks were modest. The emulsions remained suitable for in emulsio selection experiments. The trends that higher pressures and some amounts of PEG decreased nanodrop sizes were confirmed. In two cases, the second dilution and the DLS measurement listed were made only 1 day after the first, and they turned out almost identical, but so did some made a month later. There is a long-term trend toward slightly larger drop sizes. Perhaps there was some aggregation.

Stability of Diluted Emulsions over Many Weeks

We wondered whether emulsions would be more or less stable after dilution. Four of the 300:1 dilutions were saved after the last DLS measurements reported in Figure 4. Three samples were for 8000 psi pressure at different PEG concentrations, and the fourth was for 12,000 psi at 10% PEG. These four were diluted from stocks and measured on the same day, which was 49–75 days after the stock had been prepared with the microfluidizer. The four were then measured at various times over another 2 months. The samples in their cuvettes were handled carefully, kept undisturbed in the horizontal position in which they were mounted in the laser beam, and certainly not remixed. They were the last dilutions prepared from their stock emulsions. Measured diameters are shown in Figure 5. The vertical scales are expanded another two to four times compared to the most expanded scales of Figure 4. On these scales, error bars of two percent are evident, and in a couple of cases, they are about 4%.

In Figure 5, we see an initial decrease in the autocorrelation decay time. It is under 10%, but it is still more than most error bars. (These initial data points are also high as the final points in Figure 4.) After the initial drop, correlation times remained pretty much unchanged for many weeks. This figure has no hint of the upward drift noted in Figure 4. If that trend in Figure 4 were to be attributed in whole or in part to a slight tendency toward aggregation, perhaps further aggregation would be inhibited by dilution. Perhaps dilution even reduces some existing aggregation.

We also used these four samples to test the effect of a temperature change. On day 17 after dilution, the temperature was lowered to about 15 °C and the samples were given time to equilibrate. The temperature was then allowed to increase during the day, and samples were remeasured at intervals. Autocorrelation lifetimes increased at reduced temperatures, almost doubling at the lowest temperature. This is readily explained by the expected change in viscosity of the oil. These points are not included in Figure 5 because temperatures were different for different samples and varied over the day. The point is that there was a change as expected, but even after that rude treatment, when temperatures returned to the usual value and when samples were measured again on day 24 and later, samples had recovered and behaved exactly as they always had.

Discussion

In order to explore the suitability of emulsions made by passing a mixture of mineral oil, 4% (v/v) of the emulsifier ABIL-EM90, and a few percent of an aqueous phase through a microfluidizer for large-scale in emulsio selection experiments, we used DLS to characterize the size of aqueous droplets dispersed throughout the oil. DLS measures the time variation of the intensity of light scattered into a small solid angle in some direction. A sufficiently small scattering center will scatter light in all directions as a point source. Light emitted from neighboring droplets interferes in constructive and destructive ways. (This is homodyne DLS, which is what we had.) When this emission is viewed at a distance (perhaps on the ceiling of a darkened lab), there is a random pattern of light and dark “speckles”. If the scattering is from ground glass kept stationary, the pattern remains fixed. If the ground glass is moved or if the scattering is from small droplets, which move, then the speckles move. The motion of such patterns past the limiting aperture of the detection system causes the detected signal intensity to vary. The motion is random on long time scales, but any instantaneous signal level persists for a time before increasing or decreasing. The persistence time depends upon the velocity of the scattering centers. For sufficiently small droplets that diffuse, the velocity depends upon their size and the viscosity of the medium through which they move.

In order to characterize the scattered light, we used a laser at 532 nm, parallel polarization, strict elimination of any wavelength different from 532 nm, strict elimination of “background scattering” of laser light, detection by photon counting, and the subsequent offline computation of autocorrelation functions and curve fitting to measure the “persistence” times characteristic of the movement of our tiny nanodrops. In order to have any scattered light at all in DLS, there must be a difference in the index of refraction between some sort of nanoparticles and some medium through which those particles move. In order to apply the simple theory we use, the droplets must be more or less spherical and they must be considerably smaller than the wavelength. This is the Rayleigh theory. (Note that texts that discuss this theory usually characterize a small “particle” by its radius not by its diameter.) Once these conditions are satisfied, our DLS requires the knowledge of only two parameters, the scattering vector and the oil viscosity. The scattering vector depends upon the wavelength of the monochromatic laser beam, the index of the refraction of the oil medium, and the 90° scattering angle. Most notably, the concentration of droplets need not be known. It only needs to be high enough to give a measurable signal and low enough to avoid multiple scattering. The high viscosity of the oil results in diffusion that is about 200 times slower than it would be in water. This makes it easier to collect enough photons to reduce the random shot noise of photon collection. On the other hand, it does require a long time to sample the diffusive motion well enough to determine what the characteristic time is, and it presents other challenges. More or less adequate measurements with the MCS could be made in a few minutes. We wished, however, to achieve more precision and to look for subtle effects. For that reason, we collected data on each sample for 90 min or more.

We assume that the emulsifier is essential; we did not test without it except for just a couple of controls using pure water or pure oil; and it was not our goal to compare alternative emulsifiers. Inorganic salts were very helpful in making smaller and more uniform droplets. PEG, likewise, improved uniformity and reduced sizes. Using DLS, we learned what conditions will consistently prepare droplets with diameters near or below 100 nm in diameter.

Meleson et al. found that the droplet size distribution of a raw emulsion that passed through a microfluidizer becomes more narrow and approaches a consistent diameter as the number of passes increases, with a less change after the number of passes exceeds about five.²⁴ In agreement with their finding, Figure 1 shows decreasing nanodrop sizes with increasing numbers of passes and a trend toward a limiting value. There is also less variation among multiple autocorrelation measurements of the same sample in the DLS measurements after more passes. Figure 1 emphasizes a typical diameter that characterizes most of the emulsion. Not evident there, but likely over the first several passes, is a disproportionate reduction in a small number of larger nanodrops that diffuse very slowly.

About seven passes were adequate to produce emulsions with nanodrops small enough to compartmentalize ribozyme or enzyme reactions for in vitro selection experiments, as long as one uses reasonable pressures and some amounts of PEG along with appropriate inorganic salts. More passes would be justified if there were a compelling need for smaller sizes; we standardized on seven passes. Note that what are reported in Figure 1 are multiple DLS measurements of a single sample preparation for each number of passes. Different preparations under the same conditions likely result in similarly sized emulsion droplets, given the smooth overall trends in Figure 3 and the regularities seen in Figure 1. We did not make extensive efforts to compare multiple preparations made under identical conditions, but it may be worth mentioning that in our initial efforts to determine optimal conditions for making the DLS measurements and calculating the autocorrelation functions, we did prepare and measure several more preparations at 8000 psi and 0 or 10% PEG that agree quite well with what we report. Since these had minor variations (such as chilling overnight), we do not consider them suitable for rigorous comparison, but they did convince us that at the level of reproducibility needed for the purpose of finding suitable conditions, nothing would be gained by exhaustive efforts to determine whether multiple preparations are repeatable to 2, 4, or 6%.

Each autocorrelation curve was characterized by a best fit to a single exponential decay. Figure 2 shows an example of such a fit and reports the small effect of allowing a tiny offset. Long-time offsets for autocorrelations for the subsequent figures were calculated separately as the mean of data points starting six or more half-lives from the beginning. Then, with that value fixed as a constraint on the asymptote of the exponential decay, the best fit to a single exponential plus that offset was calculated for the initial three half-lives, which account for 87.5% of the decay. All of the results in Figure 3 were also fit to four half-lives and most were fit to five half-lives. That made little difference. Using three half-lives was more critical for the heterogeneous emulsions treated in Figure 1, so we continued the practice for consistency. Using three half-lives of the decay for the fit did lead to slightly shorter times and smaller diameters, mostly by about 1 or 2%. The main result was the finding that for this emulsifier and this microfluidizer, pressures near 8000 psi and about 10% PEG are convenient and for many purposes optimal.

The identification of conditions useful for producing nanodrops of various specific sizes is likely to be of use in future work, whether that work involves more in emulsio selection or efforts in other biological or material research. For the successful in emulsio selection cited in the Introduction, conditions were used that generated nanodroplets about 150 nm in diameter. The aqueous volume in the first round of selection was 17.5 mL, resulting in a total of 10¹⁶ droplets. Since the concentration of the RNA library in this first selection round was 0.5 μM, about 5 × 10¹⁵ RNA sequences were tested. (The number of ribozymes in each droplet should obey Poisson statistics, so that in order to have most drops containing no more than one ribozyme, one must tolerate at least as many having none at all.) The selection procedure actually resulted in an effective complexity of 1.6 × 10¹⁴ different sequences; this is less than the total number of RNA library sequences because an average of 30 copies were used for each RNA library sequence. This was sufficient to identify five RNA sequence clusters with catalytic activity for the triphosphorylation of guanosine to generate GTP, and it was, therefore, a successful in emulsio selection from a very large, random library. In addition to considerations on the complexity of the library, one needs to evaluate how many product molecules would need to be generated in a given emulsion droplet in order to tag successful RNA library sequences. In the case of the mentioned in emulsio selection, the droplet diameter was such that a single product molecule (6-thio GTP) would correspond to a 1 μM concentration in that particular droplet. That concentration was sufficient to mediate the tagging of library molecules with the thio modification and, therefore, the isolation of active library molecules.

In a few cases, specifically some expected to produce uniform, small nanodrops, the single exponential was sufficient so far as statistical goodness-of-fit tests could discern. In most cases, however, as in Figure 2, data suggest that a single exponential plus a constant is not completely accurate. That is to be expected. The emulsion is never really homogeneous. The DLS should result in an autocorrelation curve that is the sum of many exponential decays. It might be tempting to think that each particle size contributes its own decay curve, but that is false. Recall that it is the interference between neighboring particles that produces the speckles we observe. Particularly sized nanodrops do not interfere only with others of their own size. They interfere with other nanodrops of all sizes. This leads to a different exponential decay for each possible combination. This and related matters are discussed further in the Supporting Information. There are additional considerations that affect the form of the predicted autocorrelation. Small droplets within the Rayleigh range (especially those less than 60 nm) scatter with an intensity proportional to the sixth power of the diameter. There must be a large number of small nanodrops for them to become visible in the autocorrelation. Large droplets (especially those above about 120 nm) scatter with an intensity that can not only fall below that sixth power dependence but also actually decrease. We found that we could obtain statistically better fits by allowing for a Gaussian distribution of times that suggested a 15–25 nm full width at half-maximum range of diameters, but this is not to be taken too seriously as a wide variety of sums of exponentials will fit the autocorrelation. Furthermore, there are real concerns that even when small artifacts can have no significant effect on fits to a single exponential, they can completely frustrate attempts to fit more complex functions with more free parameters.

One of the advantages of collecting data in strings of half a million bins and then collecting 20 or more such strings is that one may examine the autocorrelation of each run and discard anything that is obviously distorted. Typically, one run out of a series of a couple dozen would be discarded. Figure 2, however, is from a series in which all 25 runs were averaged together and no run was deleted. We wanted to err on the side of accepting marginal data rather than risk imposing some prejudice, so our policy was to reject only runs with very evident bumps or dips. Any sum of exponentials must decay monotonically and fairly smoothly. As regards the fitting, we obtained essentially the same diameter whether we fit each run and averaged those fitting parameters, as could be done with Figure 1, or we averaged all the autocorrelations together before fitting, as in Figure 2, or we averaged about six to eight runs and fit that group, then did the same for more groups, and then averaged the parameters. We preferred the last method. It reduced the influence of minor distortions, while also offering a simple way to find a suitable uncertainty (error bar) to report, which was the total range encompassing all the fits. The error bars offer some confidence in the fitting, but nothing more. We were interested in exploring factors that would reduce droplet sizes by 50%, not in trying to reduce uncertainties from 3 to 1%. Small distortions or artifacts would be reduced if we averaged 500 runs over about 40 h of data collection for each sample. Aside from being tedious, the effort would have no significant effect on the general behavior of the initial decay that reveals the typical size of the droplets.

The presence of substantial concentrations of salts (near half molar ionic strength) in the aqueous phase appeared to be essential for making homogeneous emulsions of small sizes with the emulsifier we used, as shown in Table 1. The salt conditions we used elsewhere were those needed for our selection experiments, so we did not explore variations beyond this one exercise. The low-salt conditions all produced larger diameters. Even those could be small enough for our purposes, and it is likely that more passes, higher pressures, or more PEG could compensate somewhat for reduced salt.

One goal of the project was to test how long stock emulsions can be stored. If the DLS measurements were little affected, it is likely that other works could be carried out at convenient times over some weeks. The measurements shown in Figure 4 showed that a given emulsion gave much the same diameter for nanodrops whether it was diluted and measured the day after it was made or diluted and then measured many weeks later. There were no instances of decreasing sizes after a week. There was some trend toward slightly larger diameters over months. Even then sizes remain adequate for purposes of in emulsio selection experiments. The figure suggests that PEG promoted stability over long times. The largest fractional changes are seen in limiting cases, such as low pressure without PEG or the smallest droplets. The largest diameter increases in Figure 4 would correspond to doubling the volume.

After dilution, nanodrop sizes were, if anything, even more stable, as illustrated in Figure 5. Since the sample for each of the four conditions was left in its cuvette undisturbed at room temperature and in the same orientation used for measurements, this is good evidence for the reliability of DLS. It is unlikely that changes in measurements would exactly compensate changes in the emulsions over weeks after the small initial decrease. The emulsions appeared robust, and DLS seemed reliable.

Let us consider, next, some possible causes for small deviations in the diameters from where we might expect them in Figures 3–5. A major concern is the matter of changes in temperature of a few tenths of a degree. The fact that variations were as small as they were is a strong evidence that temperature was controlled quite well. Still, a few particular points deviated from where they might be expected to lie by more than the uncertainty of any one DLS measurement. In most cases, a couple tenths of a degree variation in temperature would account for the deviation. It is also possible that temperatures rose slightly during each day. Electronics were turned on at the start of each day and produced heating, so did the personnel working around the optical table. This might account for a couple of the percent variation in diameter. Figure 3 shows that 600:1 dilution almost always led to slightly smaller diameters than 300:1 dilution. That may be intrinsic, but it is also true that both dilutions were prepared within a few minutes of each other early on a given day. We then routinely measured the 300:1 dilutions first and the 600:1 dilutions a few hours later in order to keep measurement conditions as similar as possible within each group. This, however, may mean that the temperature was a fraction of a degree warmer by the time we got to the 600:1 dilutions. That would have resulted in faster diffusion and a slightly smaller apparent diameter.

We monitored temperature and never saw variations as large as 0.5 °C, but if there were rare excursions as large as 0.5 °C, that would be enough to explain even the biggest, rare deviations. Most notably, it would be enough to account for the high initial diameters seen in Figure 5 and for the subsequent decrease on what may have been on cooler days. These initial values were all measured on the same day. These diameters were also the values for the last days for the same samples in Figure 4, which were also high and contribute to the slow upward trend in the diameter. The apparent increase in diameter in Figure 4, however, did not depend upon just the final measurement. Most instances included two or more points showing the increase. It is unlikely that temperature varied on different days to produce that trend with no example trending in the opposite direction. Consequently, temperature variations were unlikely to account for all of the (quite small) apparent variation in diameters, although they must have contributed. Aggregation may also have contributed. Uncertainties also vary and suggest occasional problems other than temperature variations.

To summarize, we were able to reduce common “dirt effects” so that they did not affect the major trends reported, which were those pressures near or above 8000 psi and about 10% PEG along with seven or more passes through the microfluidizer provided the nanodroplets needed for in emulsio selection experiments. It would be nice to be able to offer detailed assessments of the distribution of nanodrop sizes, but size distributions cannot be determined using only the autocorrelations we recorded, no matter how precisely those are measured. A more comprehensive theoretical understanding is essential, of course, but it is also necessary to have some additional information either from another source altogether or from DLS measurements that use more than a single scattering vector. This could involve multiple wavelengths or detection at more than a single angle or both. Some more issues involved in thinking about distributions of droplet sizes are addressed in the Supporting Information, along with additional thoughts about experimental problems involved in working with viscous oils.

Conclusions

In order to characterize water-in-oil emulsions for in vitro selection experiments, we measured emulsion droplet sizes by DLS. This technique measures the diffusion of the small aqueous droplets through oil. Our analysis shows the effect of multiple passes of the emulsion through the microfluidizer and describes the droplet size as a function of the microfluidizer pressure over the range of 3000–12,000 psi, the addition of various amounts of PEG, and the incorporation of inorganic salts. We also demonstrated that the nanodrops in our emulsions were stable for many weeks with no special storage requirements. We outline conditions that we found to be promising for in emulsio selection experiments.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c03445.

• Key data, discussion of distributions of nanodrop sizes, and further thoughts on the challenges of working with viscous emulsions or solutions (PDF)

The authors declare no competing financial interest.