Examination of the Butler Equation for the Surface Tension of Liquid Mixtures

Abstract

The classical Butler equation used to describe surface tension and the surface composition of liquid mixtures is revisited. A straightforward derivation is presented, separating basic chemical thermodynamics and assumptions proper to Butler’s model. This model is shown to conceal an approximation not recognized by other researchers. The shortcoming identified consists of not allowing surface standard values to vary with surface tension by virtue of the changing composition. A more rigorous equation is derived and shown to yield the Butler equation in case of incompressible surface phases. It is concluded that the Butler equation slightly overestimates ideal surface tensions. Butler’s surface-phase concentrations of the surface-active component are also slightly overestimated in the surface-active component dilute range, being just underestimated at higher concentrations. Despite this, Butler’s model stands as a very good standard due to its versatility.

Introduction

Predicting the surface tension and the composition of layers overlying liquid mixtures has been the goal of much research over more than a century.^1,2 The renowned Gibbs adsorption isotherm²⁻⁵ (GAI) is a fundamental equilibrium equation that is the foundation stone of this field of inquiry. However, in the case of a binary mixture, GAI only links the surface tension to the relative adsorption, which is the difference between adsorption of one component and that of the other.⁵ Among the milestones in this pursuit, the Butler equation⁶ published in 1932 is of the foremost influence. Indeed, it was not only the first workable proposal for estimating both the surface composition and surface tension but also the starting point for the advancements due to Hoar and Melford,⁷ Sprow and Prausnitz,⁸ and Kaptay.⁹ This notwithstanding, it has been claimed by Rusanov¹⁰ and by Santos and Reis^11,12 that Butler’s model is not so rigorous as generally regarded. Furthermore, it has been emphasized by different authors^3,13 that molecular-thermodynamic models must be validated against the GAI, a condition that Radke³ suspects that is not met by the Butler equation. Present examination of the Butler equation was prompted by Kaptay’s⁹ recently improved derivation that removed some, not all, previous reservations to its acceptance. A straightforward derivation of the Butler equation is advanced in terms of formal chemical thermodynamics. Properties of the ideal surface region proposed by Butler are carefully examined since the ideal model for liquid mixtures has proven very useful to describe the essential features of mixtures.¹⁴ It will be shown that indeed Butler’s original and subsequently improved derivations conceal an approximation, namely, that the chosen standard state for describing surface energy changes with varying compositions is not a constant.

Based on a previous thermodynamic development,^11,12 an equation for the surface tension of ideal liquid mixtures is concisely derived. This alternative approach accounts for the variation of standard chemical potentials with changing surface tension from its value for a pure component to its current value at the composition of interest. Remarkably, the alternative equation reduces to the classical Butler equation for incompressible surface phases, as claimed by Rusanov¹⁰ on different grounds. A quantitative evaluation of the effect of this hidden approximation is presented for the molecular mixture, water–ethanol, at 298.15 K and for the metallic liquid alloy, cooper–tin, at 1400 K and is shown to be insignificant.

Butler Equation

Formal Thermodynamics Derivation

Considering a physical planar surface phase¹⁵ of molecular components A and B at fixed temperature T and pressure p that is in thermodynamic equilibrium with an underlying liquid phase, the differential of the surface-phase Gibbs energy is

1

where G stands for Gibbs energy, S for entropy, V for volume, γ for surface tension, A for surface area, and μ_i and n_i for chemical potential and the amount of the substance, respectively, of component i = A, B. The superscript “s” denoting the surface phase is only attached to properties whose equilibrium values are different in both phases.

It follows from eq 1 that

2

3

The variation of surface Gibbs energy with the composition at constant T and p can be established from eq 3 by applying the rule of partial differentiation to introduce an extra restriction. This gives

4

It has been shown^2,16−18 that the derivative (∂A/∂n_B^s)_T,p,nA is the partial molar surface area of B designed for conditions of constant T and p, and denoted¹⁸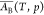

5

Inserting eqs 2, 3, and 5 into eq 4 leads to

6

Equation 6 is not new, but now it has been concisely derived using classical thermodynamics only. This is an important step because the Butler equation is based on it. Furthermore, it is noted that eq 6 is identical to eq 21e of ref (2), eq 13 of ref (9), and eq 2d of ref (19) although a misprint certainly occurred in the last two equations, where A appears as an extra constraint in the partial derivative of G^s. For simplicity, the following shorthand is introduced

7

In the bulk phase, μ_B is described by

8

where R is the gas constant and f_B is the rational activity coefficient of B at mole fraction x_B; an asterisk denotes a pure-component property. Hence, the standard state is the pure liquid B.

The equilibrium condition between the surface and bulk phases requires the uniformity of μ_B so that from eqs 6 and 8, and considering eq 7, one obtains

9

Equation 9 is valid over the full composition range. Since f_B = 1 for x_B = 1, then

10

By noting that g_B = (∂G/∂n_B)_T,p,nA = μ_B, it follows from eq 10 that g_B^*,s ≠ g_B = μ_B^*.

Subtracting eq 10 from eq 9 yields

11

12

It is remarked that proceeding from eqs 6 to 12 required only well-established chemical thermodynamics (see eq 8) and the phase-equilibria thermodynamics expressed in eq 9. Hence, eq 12 is a rigorous expression for the dependence of surface tension on the mixture composition at constant T and p that does not involve any approximation or extra thermodynamic assumption.

Butler’s original contribution was to put forward an equation for the difference (g_B^s – g_B). Assuming that this difference can be expressed by an equation similar to eq 8, for changes with the composition at fixed T and p, Butler⁶ proposed the following expression

13

where g_B^0,s is the corresponding standard-state value.

From eqs 6, 7, and 13, one obtains

14

Using the artifact g_B^0,s = g_B + g_B^0,s – g_B and recalling eq 10, eq 14 leads to

15

Hence, this approach implicitly assumes a surface standard chemical potential, μ_B^0,s, having the form

16

However, Butler considered g_B^0,s to be a constant, independent of the surface-phase composition and thus equal to g_B. Therefore, from eqs 12 and 13 one obtains the commonly accepted form of the Butler equation

17

In accordance with this treatment, Butler’s standard chemical potential, μ_B^0,s(Butler), becomes

18

It is interesting to note that Butler’s approach still makes some allowance for a change in the value of the surface standard chemical potential with varying surface compositions.

It is emphasized that in the abovementioned derivation of the Butler equation, no assumption was made regarding the surface-phase thickness, in agreement with the improved derivation of the Butler equation recently achieved by Kaptay⁹ without assuming a surface monolayer. This notwithstanding, why some authors^3,10−12 have argued that the Butler equation still contains an approximation? If so, it must be found in a hidden assumption within eq 13. To clarify this matter, the focus is directed to Butler’s ideal surface phase.

The ideal model¹⁴ acquires special relevance in surface thermodynamics because experimentally, the surface-region composition is not easily accessible.²⁰⁻²² Since for an ideal liquid mixture according to Raoult’s law, x_B^(ideal) = x_B, then the corresponding ideal surface phase should be defined so that x_B^s(ideal) = x_B. These equalities hold for equilibrium attained from the joint conditions μ_B^(ideal) = μ_B and μ_B^(real) = μ_B.²³

According to Butler, the ideal model for the surface region is obtained from eq 13 by setting f_B^s = 1

19

and from eq 17

20

To progress, pure molar and ideal partial molar surface areas need to be modeled.²⁴ Usually, they are calculated from well-known relationships as proportional to some power of the pure molar volume^2,8,9,11,19 or the partial molar volume in the ideal bulk phase.^2,8,9,19 Since the latter does not vary with the composition, then 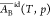= A_B^* and eq 20 simplifies to

21

Noting that an analogous expression holds for component A

22

equating eqs 21 to 22 allows the estimate Butler’s surface-phase composition by solving the nonexplicit expression^25,26

23

where r_A/B = A_A^*/A_B.

Butler’s ideal surface tensions are then obtained by inserting these x_B^s values in eq 21.

Alternatively, solving eq 21 for x_B^s and eq 22 for x_A and considering that x_A^s + x_B = 1, a nonexplicit equation is obtained for the calculation of γ^id. Using these values in eq 21 gives x_B^s. In fact, this alternative way is the most frequently employed. However, it is not certain that Butler’s ideal surface-phase compositions thus calculated, and which should be used in eq 19, match those of the corresponding real surface phase. In other words, it is legitimate to look for hidden assumptions in the modern derivation of ideal Butler equations leading to eqs 21 and 22. In addition to equating 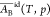in eq 20 to A_B, there is no guarantee that the standard value g_B^id,0,s in eq 19 is rigorously composition independent. Indeed, at fixed T and p, standard states in the ideal surface phase with composition x_B should be the pure liquid components under the surface tension of the ideal mixture at that composition because, as demonstrated by Rudisill and LeVan,¹³ only these pure-component standard states satisfy the GAI.

Finally, it is noticed that G^s in eq 1 is defined as the Legendre transform of the surface-phase internal energy, U^s, with respect to the variables T and p, G^s = U^s – TS^s + pV^s. Guggenheim²⁷ made a different choice by introducing the surface-phase transformed Gibbs energy, herein denoted G’^s, defined as G’^s = U^s – TS^s + pV^s – γA = G^s – γA. However, it is paradoxical that using the differential of G’^s does not lead to the useful Butler equation.

Hidden Approximation

The suspected variation of g_B^id,0,s with the composition can be estimated using the Taylor formula for a single variable around g_B, which provides a sound mathematical answer to this question. Its application gives

24

Differentiation of eq 10 in order of γ_B^* gives

25

The Gibbs–Duhem equation for the surface phase of pure liquid B is²⁷

26

Division by dγ_B^* at fixed T and p gives

27

Hence, eq 25 simplifies to

28

Singling out the first summation term in eq 24 and considering eq 28 leads to

29

By noting that (∂A_B^*/∂γ_B)_T,p > 0 is a thermodynamic requirement for a stable surface phase,²⁸ even disregarding the higher-order terms of Taylor expansion, one concludes that g_B^id,0,s ≠ g_B for x_B^s < 1. In other words, Butler’s assumption of constant standard states g_i while the composition is changed at fixed T and p conceals a presumably small approximation.

On the other hand, Butler’s approach leading to eq 20 for γ^id does not provide a clue to calculate 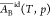, which has been considered constant and equal to A_B^*. However, using an advanced thermodynamic treatment,¹⁸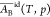 and 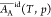have been calculated for the system water (A)–ethanol (B) at 298 K and shown to vary slightly with the composition. Over the full range from pure water to pure ethanol, 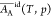increases 6% and 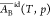decreases 2% (see Table S2 of ref (18)).

Alternative Equation

Ideal Surface Phase

According to the Lewis–Randall formulation of chemical thermodynamics, the chemical potential of B in a bulk ideal mixture is

30

It is reasonable to base the formulation of surface ideality on the following expression¹¹⁻¹³

31

Then, at equilibrium

32

Turning to the Taylor formula, standard chemical potentials become related as follows

33

Separating the first term and considering eq 27 give

34

Assuming constant surface thickness of a pure liquid, it is shown in the Supporting Information that^4,11

35

and

36

Inserting the latter result into eq 34 leads to

37

Recalling the series expansion

38

and setting the variable x as

39

one finds that

40

Finally, combining eqs 32 and 40 gives

41

Bearing in mind that e^(c In z) = z^c, eq 41 is transformed into

42

where (∂A_B^*/∂p) can be estimated using the model-based eq S7.

Since an analogous equation holds for x_A^s and recalling x_A + x_B^s = 1, γ^id can be computed from the resulting nonexplicit expression and thereby the surface-phase composition calculated. Although eqs 40 and 42 are not new,¹¹ the foregoing proof is shorter. Note that this alternative approach is not amenable to yield an explicit equation for γ^id as eq 21 nor an equation for x_B similar to eq 23, which are both proper to Butler’s approach.

Results and Discussion

Considering a given binary system at fixed T, p, and x_B, it is clear that calculated values for x_B^s and γ^id depend on the chosen model, the Butler equation, or the alternative equation. However, these models are not too dissimilar. Indeed, inasmuch as ln(1 – x) ≈ −x for |x| < 1, x being given by eq 39, eq 41 reduces to eq 21, a fact appreciated by other authors,^29,30 and consequently x_B (Butler’s approach) ≈ x_B^s (alternative approach). Considering eqs 39, S9, and S10, this equivalence is best for binary systems of components with not significantly different surface tensions, large molar volumes, and low isothermal compressibilities. This same outcome arises from retaining only the first term of Taylor expansion in eq 33, which amounts to considering (∂A_B/∂p)_T null (see eq 36). Equivalently, in view of eqs 28 and 35, (∂g_B^*,s/γ_B)_T,p = 0 for an incompressible surface phase so that from eq 29, g_B^id,0,s = g_B, which is Butler’s nonstated assumption. This is an important result on the account of Rusanov’s harsh criticism of Butler’s model “because it involves compressible bulk phases and incompressible monolayer”.¹⁰ It is underlined that the alternative model makes provision for compressible surface phases. Present arguments have been based on ideal surface properties that provide reference values for estimating excess quantities. Excess surface tensions γ^E = γ – γ^id are linked to surface-phase activity coefficients.³¹ Hence, any approximation made while computing Butler’s ideal surface tension values will be included in Butler’s activity coefficients to describe real surfaces.

Comparison of Models

Two binary systems were used to compare ideal surface tension and the surface composition predicted by Butler’s and alternative equations. Labeling B as a surface-active constituent, the examined systems are water (A)–ethanol (B) at 298.15 K, which is a mixture of molecular liquids, and the liquid alloy cooper (A)–tin (B) at 1400 K. Molar surface areas of the pure components were estimated on the basis of hexagonally close-packed disks in a monolayer of close-packed equal spheres (packing factor f_i(hcp) = 1.091);^7,32 additional calculations were made using the packing factor for cubic cells f_i(cc) = 1.000, as recommended by Kaptay^19,33 for simple liquid metals, and which is also employed for molecular liquids.⁸ The required physical data for water and ethanol (refs (34−36)) and for copper and tin (refs (37−39)) are presented in Table S1. For Butler’s model values, x_B^s was calculated using eq 23, and then eq 21 was employed to obtain γ^id. For the alternative model values, an equivalent procedure was used, namely, resorting to eq 42 and its analogue for x_A and solving x_A^s + x_B = 1 for γ^id. Plots of ideal surface tension (f_i(hcp) = 1.091) and the difference between surface compositions, expressed as % deviation, calculated by both models against the bulk concentration are shown in Figures 1 and 2, respectively, for both binary systems.

Figure 1.

Ideal surface tension, γ^id, versus the bulk mole fraction of component B, x_B. Solid lines for the alternative model and broken lines for Butler’s model. Surface packing factor f_i(hcp) = 1.091.

Figure 2.

Difference between estimated surface mole fractions by the alternative and Butler’s equation expressed as % deviation from the alternative model. Surface packing factor f_i(hcp) = 1.091.

Figure 1 shows that Butler’s ideal surface tensions are marginally larger than those calculated with the alternative equation. Consequently, the corresponding excess surface tensions are slightly different.

The unexpected behavior observed in Figure 2 deserves some clarification. Indeed, solving eq 21 for Butler’s x_B^s values, dividing by eq 42 for the alternative x_B values, and taking logarithms and resorting to the series expansion 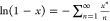(|x| ≤ 1 and x given by eq 39), yield

43

Analysis of eq 43 shows that the first term on the r.h.s. is positive and the remainder negative; the magnitude of the remainder decreases with increasing x_B since (γ^id – γ_B^*) varies between (γ_A – γ_B^*) and zero. Therefore, x_B(Butler) < x_B^s(alternative) for low x_B values and opposite for large x_B values. Moreover, since these differences are negligible, particularly for x_B ≥ 0.2, one may conclude that Butler’s model introduces unimportant errors in the calculated surface-phase compositions.

The impact of the adopted packing factor on theoretical calculations of ideal surface tensions was evaluated for both representative binary systems. The outcome of this analysis is condensed in Figure 3, which shows that a smaller f_i entails smaller γ^id values as well as smaller differences between alternative and Butler’s models. The generally small differences depend on the composition, being imperceptible at high concentrations of the surface-active component. The chemical nature of the mixture components having a noteworthy effect on γ^id estimates which depend on the computed molar surface areas, that are calculated using f_i values. In sum, for both binary systems, γ^id (Butler, f_i = 1) > γ^id (alternative, f_i = 1) > γ^id (Butler, f_i = 1.091) > γ^id (alternative, f_i = 1.091), despite an overall modest impact of the packing factor value on the reliability of Butler’s model.

Figure 3.

Effect of the packing factor f_i-value on the difference between calculated ideal surface tensions by the alternative and Butler’s models, expressed as % deviation from the alternative model for (⧫), f_i(hcp) = 1.091 and (●), f_i(cc) = 1.000.

Finally, one may speculate about the major factor contributing to the deviation of Butler’s model from the alternative approach herein presented. Clearly, it is the isothermal compressibility of the pure compounds, which is of the order of 1 GPa^–1 for molecular liquids,⁴⁰ while not amounting to more than a few 0.01 GPa^–1 for liquid metals.⁴¹ The magnitude difference between isothermal compressibilities offsets the pure-component surface tension differences γ_H2O^* – γ_EtOH = 49.72 mN m^–1 and γ_Cu^* – γ_Sn = 801 mN m^–1, resulting in minor deviations of γ^id and x_B^s for both systems.

Conclusions

The Butler equation merits a good score in this examination. As widely acknowledged, it has provided a good basis to estimate the surface tension and the surface-phase composition of planar liquid mixtures. The Butler equation is, herein, deduced using formal thermodynamics allowing the disclosure of an underlying hidden approximation. This consists of implicitly assuming that in the thermodynamic description of surface phases at fixed T and p, the standard-state values of mixture constituents are not affected by the surface tension variation that accompanies composition changes. An alternative equation allowing for the effect of surface tension on surface standard chemical potentials is worked out. It is shown that it reduces to the conventional Butler equation when molar surface areas of the pure components are not affected by surface tension or pressure variations. Interestingly, this conclusion corroborates Rusanov’s¹⁰ inference that the Butler equation is only exact for incompressible surface phases.

Summing up, even though imperfect, the Butler equation has the advantage of providing an explicit and mathematically simple expression for the surface tension of liquid mixtures. This feature has allowed various surface phenomena to be successfully modeled^{2,19,26,42−46} while employing the Butler equation. It has been, herein, demonstrated that it can continue to be confidently applied because of the small, largely inconsequent numerical errors involved.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02606.

• Derivation of eqs 35 and 36 and physical properties of water and ethanol at 298.15 K and of liquid metal copper and tin at 1400 K (Table S1) (PDF)

Author Contributions

^† M.S.C.S.S. and J.C.R.R. contributed equally. This manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.