Effect of Internal Architecture on the Assembly of Soft Particles at Fluid Interfaces

Abstract

Monolayers of soft colloidal particles confined at fluid interfaces are at the core of a broad range of technological processes, from the stabilization of responsive foams and emulsions to advanced lithographic techniques. However, establishing a fundamental relation between their internal architecture, which is controlled during synthesis, and their structural and mechanical properties upon interfacial confinement remains an elusive task. To address this open issue, which defines the monolayer’s properties, we synthesize core–shell microgels, whose soft core can be chemically degraded in a controlled fashion. This strategy allows us to obtain a series of particles ranging from analogues of standard batch-synthesized microgels to completely hollow ones after total core removal. Combined experimental and numerical results show that our hollow particles have a thin and deformable shell, leading to a temperature-responsive collapse of the internal cavity and a complete flattening after adsorption at a fluid interface. Mechanical characterization shows that a critical degree of core removal is required to obtain soft disk-like particles at an oil–water interface, which present a distinct response to compression. At low packing fractions, the mechanical response of the monolayer is dominated by the outer polymer chains forming a corona surrounding the particles within the interfacial plane, regardless of the presence of a core. By contrast, at high compression, the absence of a core enables the particles to deform in the direction orthogonal to the interface and to be continuously compressed without altering the monolayer structure. These findings show how fine, single-particle architectural control during synthesis can be engineered to determine the interfacial behavior of microgels, enabling one to link particle conformation with the resulting material properties.

Colloidal particles are ideal building blocks to obtain micro- and nanostructured materials whose properties can be tailored by engineering interparticle interactions.^1,2 Using soft colloids, the coupling between particle architecture and deformability in different environments (e.g., in bulk suspensions or following confinement at interfaces, under different temperature or pH conditions, etc.) enables a rich behavior and imparts functionalities unattainable with mechanically rigid, i.e., “hard”, particles.^3,4 Microgels, colloidal particles comprising an internally cross-linked network formed by a water-soluble polymer, have emerged as a prominent choice with facile synthesis and versatile applications.⁵⁻⁷ Among the latter, materials comprising microgel monolayers confined at solid or fluid interfaces, such as air–water or oil–water interfaces, present both high potential and important challenges. The versatility in their assembly and their responsiveness enable microgel monolayers to be used as substrates for cell culture and harvesting,⁸ or in sensing,⁹ optics,¹⁰ and patterning¹¹ applications. Additionally, self-assembly at fluid interfaces and transfer to solid substrates allow using microgel monolayers as tunable nanolithography masks,^12,13 whereas the direct use of microgels at the fluid interface can be exploited to obtain smart responsive foams¹⁴ or emulsions.¹⁵

In spite of the practical interest, currently, there are no fundamental guidelines that connect synthesis procedures in bulk with the resulting single-particle properties and collective behavior of the microgels upon interfacial adsorption. Moreover, it is still unclear how different three-dimensional (3D) shapes of the microgels in suspension translate into their new morphology at the interface and how their bulk mechanical properties are transferred to the interface.¹⁶⁻¹⁹

The vast majority of microgels are prepared by one-pot precipitation polymerization, which leads to the formation of particles with a radially decreasing cross-linking density profile in bulk aqueous suspensions.^20,21 As the particles adsorb to a fluid interface, surface tension and the different solubility of the polymer in the two phases cause a reconfiguration of the polymer network.²²⁻²⁴ These standard microgels flatten out at the interface, with the more loosely cross-linked polymer chains at the particle periphery creating a thin corona, which surrounds the particle within the interfacial plane. Nowadays, various synthetic procedures allow realizing microgels with different architectures, such as homogeneously cross-linked^25,26 or hollow ones.^23,27−30 The case of hollow microgels, that is, particles made of a polymeric shell surrounding an empty core, is particularly appealing. Their peculiar responses to swelling and compression in 3D,³¹⁻³³ specifically relating to the conformation and retention of the inner cavity, poses untapped opportunities to tailor their assembly at fluid interfaces.

In this article, we address the general question of how the internal architecture of a microgel affects its bulk and interfacial properties by selecting and characterizing a model system that allows us to tune the particle inner structure from the one of a standard batch-synthesized microgel to a hollow one. To this end, we synthesize core–shell microgels, where the inner microgel core can be chemically degraded in a controlled fashion.²⁸ We experimentally and numerically follow the progressive removal of the core and evidence how it affects both the swelling–deswelling transition in bulk and the particle morphology at the interface. We then focus on the collective response of hollow microgels under compression at the interface. In particular, our final hollow particles present a significantly thinner and softer shell compared to those in existing literature,^{23,29,33−35} which discloses a rich mechanical and structural behavior. Overall, our approach allows precisely linking single-particle properties to their interfacial assembly in order to tailor the two-dimensional (2D) assembly of soft colloids.

Results and Discussion

Characterization of the Hollow Microgels in Bulk

Core Degradation

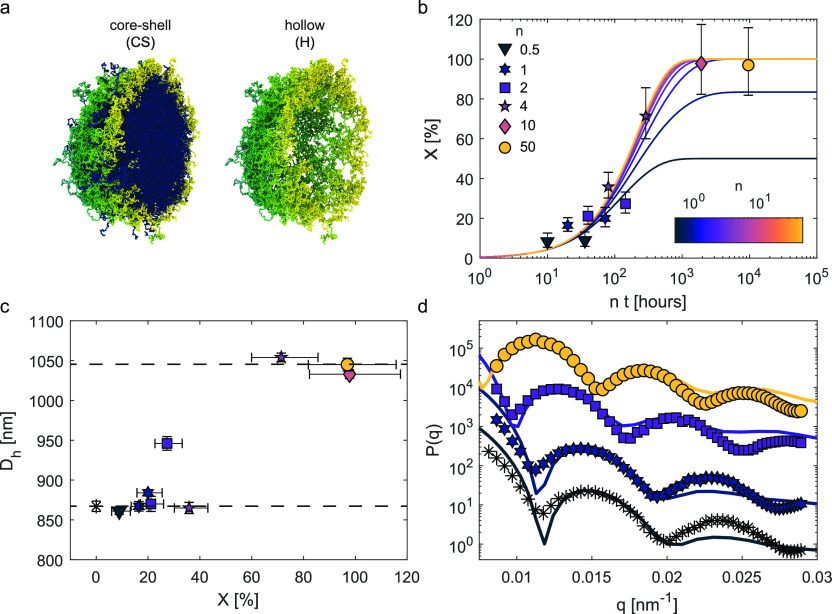
The hollow microgels used in this study are synthesized by means of a two-step polymerization procedure, followed by a degradation process.²⁸ We first obtain a standard microgel by free-radical precipitation polymerization using DHEA as a cross-linker, and afterward, we grow a second polymeric shell on top using methylenebis(acrylamide) (BIS) as a cross-linker, forming a core–shell particle with a thin interpenetrated network in the interfacial region (see Materials, Models, and Methods for a detailed description of the synthesis). By exposing the core–shell (CS) microgels to NaIO₄, the DHEA cross-linkers in the core (C) can be degraded, leading to the progressive formation of hollow (H) microgels, as represented by the simulation snapshots of Figure 1a.

Figure 1.

Core–shell and hollow microgels in bulk aqueous suspensions: core degradation process. (a) Simulation snapshots of the cross section of a core–shell microgel before and after the removal of the inner core. The core with the DHEA cross-linker is colored in blue, and the outer shell with the BIS cross-linker is colored in green/yellow. (b) Extent of core removal X as a function of n·t, where n is the NaIO₄ to DHEA molar ratio and t is the reaction time. The symbols indicate the values of X estimated from the experimental form factors (see Materials, Models, and Methods), whereas the lines show eq 2 fitted to the experimental X for different values of n. (c) Hydrodynamic diameter D_h of core–shell microgels as a function of the extent of core removal X. The horizontal dashed lines emphasize the sudden transition to a larger dimension upon removal of a critical core fraction. (d) Experimental (symbols) and numerical (lines) form factors as a function of the wavenumber q. The experimental form factors are for n·t = 0, 20, 144, and 9600, whereas the numerical ones are calculated for different number densities of the core microgel: ρ ≈ 0.08, 0.06, and 0.01 σ^–3 (from the bottom to the top), where σ, representing the monomer size, is the unit length in the simulations. The yellow circles correspond to the hollow microgel (X = 100%). The form factors are arbitrarily shifted along the y-axis for visual clarity. The symbols in (c) and (d) correspond to the same values of n shown in (b), with * black symbols indicating the core–shell microgel prior to core removal (n = 0).

We study the kinetics of the degradation of the core as a function of the time t and the initial NaIO₄ to DHEA molar ratio 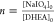via ex situ static light scattering (SLS) and dynamic light scattering (DLS) measurements. In particular, we vary n in the range of 0.5–50 and t in the range of 20–192 h and define the degree of core removal as 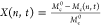. Here, M_c⁰ and M_c(n,t) are the mass of the core before and after the reaction with NaIO₄, respectively. These are estimated from the microgels’ radial density profiles, which we extract by fitting the form factors for different values of n and t, as described in Materials, Models, and Methods and reported in Figures S1 and S2. The symbols in Figure 1b represent the experimental X(n,t) for different values of n. When plotted against the product n·t, X exhibits a sigmoidal trend, with larger n·t leading to increasingly higher X up to n·t ≃ 10³ h, after which X reaches a plateau at ≃100%.

To rationalize such kinetics, we model the degradation of the core as a bimolecular and stoichiometric reaction between the vicinal diol group in the DHEA polymer network and NaIO₄.²⁸ The reaction DHEA_(s) + NaIO_4(l) → C_(l) leads to a soluble product C_(l) that is washed out during the postreaction cleaning step. By assuming the reaction follows a first-order kinetics with respect to the concentration of both DHEA and NaIO₄, perfect mixing within the reaction vessel, and a 1:1 linear correlation between the degree of core removal and the cleavage of the vicinal diol in the DHEA molecules, X is prescribed by the following differential equation:

1

where k is the reaction rate constant. This equation admits two analytical solutions depending on whether n = 1 or n ≠ 1:

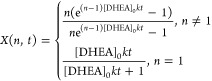2

It is important to remark that, within this framework, for a given initial DHEA concentration [DHEA]₀, varying n is not equivalent to varying t as X(n,t) is not a function of the product n·t. This emphasizes the importance of studying the effects of varying both n and t separately. Nonetheless, for n ≫ 1, X(n,t) can be approximated to a sole function of the product n·t as X(n,t) ∼ (e^nkt – 1)/e^nkt.

The fitting of the experimental X(n,t) with eq 2 is plotted in Figure 1b against n·t, giving an excellent description of the experimental data (R² = 0.96) with a value of k = 1.33 × 10^–2 ± 4 × 10^–3 m³ mol^–1 h^–1.

The degree of core removal correlates with the microgels’ hydrodynamic diameter D_h, as measured by DLS. The standard DHEA-cross-linked (core) microgels prior to the growth of the BIS shell have D_h = 640 nm at 22 °C (blue triangle in Figure S3). After the second polymerization step, the D_h of the core–shell particle reaches 870 nm (22 °C). We then calculate the thickness of the BIS shell as (D_h(CS) – D_h(C))/2, obtaining a value of 115 nm. After reaction with NaIO₄, D_h remains roughly constant up to X ≃ 40%, after which it rapidly increases, reaching a plateau at ≃1050 nm for X ≃ 70%, as schematically represented by the two dashed horizontal lines in Figure 1c. This is in agreement with the plateau observed for the degree of core removal in Figure 1b and indicates that the dissolution of the core allows for an increased swelling of the pNIPAM network in the shell.²⁸ In particular, this behavior reveals that a critical number of cross-links needs to be cleaved in order to allow the rearrangement of the outer polymer shell. This observation differentiates our study from previous ones in which hollow particles are synthesized by the dissolution of a rigid core and in which much thicker shells are typically obtained.^23,29 The fitting of the form factors indicates that the cleaved polymer leaves the microgel cores, which is also confirmed by measurement of the dry volume of polymer by atomic force microscopy (AFM) presented later on.

To further support these findings on the core dissolution, we perform a study in which we verify the compatibility of the form factors extracted experimentally at different degradation stages with those calculated from a numerical model for hollow microgels. The model that best reproduces the experimental data at the highest X is determined by adjusting the size of the inner cavity and the monomer density of the polymeric shell in the simulations. A faithful comparison is achieved, as shown in Figure 1d, for a hole radius that comprises 75% of the core–shell microgel size (compared to 74 ± 2% from the DLS measurements) and an outer shell having an average monomer density of about half that of the standard microgel used for the core particle (see Materials, Models, and Methods and Supporting Information, Figures S12–S15).

Since it is not possible to reproduce the chemical degradation procedure numerically, we mimic this process by taking the hollow model just described, inserting a standard microgel in the central cavity (representing the inner DHEA-cross-linked microgel), and subsequently removing a certain number of monomers from the inner core, leading to a decrease of its density (see Materials, Models, and Methods and Figure S16). As shown in Figure 1d, the analysis of the form factors confirms the trend we observe in experiments as a function of X, with the first peak of the form factor shifting to smaller wavenumbers and the simultaneous appearance of the third peak in the range of examined wavenumbers. Although we do not explicitly include polydispersity in the simulations, the present model is able to qualitatively reproduce the experimental form factors and, in particular, to capture the relative positions of the peaks detected by SLS.

Temperature Response

Numerical simulations offer us further insights on the internal structure of the microgels upon core degradation by studying their temperature response. In order to substantiate the numerical results with experiments, we perform DLS and SLS measurements below and above the pNIPAM’s volume phase transition temperature (VPTT) of 35 °C (Figures S3–S5). At 40 °C, when pNIPAM is in a collapsed state, D_h decreases from 520 nm (for X = 0%) to 490 nm (for X ≃ 100%, Figure S3). This indicates that above the VPTT, upon degrading the core particle, the outer shell does not buckle into the particle interior, despite being very thin (≃15 nm). Nonetheless, the swelling ratio D_h(22 °C)/D_h(40 °C) for a hollow microgel (2.1 ± 0.05) is higher than that for the initial core–shell particle (1.66 ± 0.04) because D_h(22 °C) increases with n·t and thus X.

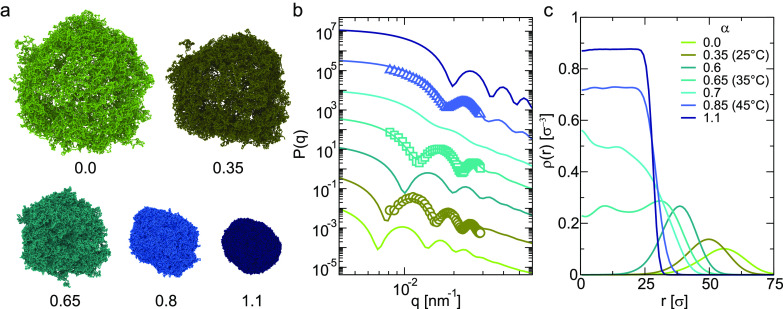
The temperature response of the hollow microgels (i.e., with X ≃ 100%) emerging from the SLS measurements is fully captured by the simulations, where the entire range of effective temperatures can be accessed by varying the parameter α of a solvophobic potential (see Materials, Models, and Methods). Figure 2a displays representative simulation snapshots, showing the transition from a fully swollen microgel to a collapsed one at α = 1.1. It is evident by the snapshots that, due to their intrinsic structure and the reduced density of the shell, these hollow microgels appear more anisotropic and fluffy than the corresponding standard microgels.²¹

Figure 2.

Responsiveness of the hollow microgels across the VPT. (a) Simulation snapshots of hollow microgels as a function of the effective temperature α. (b) Experimental (symbols) and numerical (lines) form factors for different effective temperatures. The values of α = 0.35, 0.65, and 0.85 correspond to T = 25, 35, and 45 °C, respectively. The comparison is performed by matching the positions of the first peak of P(q), yielding an estimate of the bead size used in the simulations σ = 8.25 nm. The form factors are arbitrarily rescaled on the y-axis for visual clarity. (c) Density profiles as a function of the distance from the center of mass of the hollow microgel in units of σ for different values of the effective temperature α.

The alignment with real units is obtained by matching the first peak of the numerical form factor onto the experimental one at T = 25 °C and by adopting the same rescaling factor for the other temperatures.²¹ The comparison, reported in Figure 2b, shows an almost perfect agreement between the form factors of model and laboratory microgels, which is thus realized for α = 0.35, 0.65, and 0.85 corresponding to T = 25, 35, and 45 °C, respectively. In particular, we note how the curves progressively shift to higher wavevectors, consistently with the decrease in particle size measured with DLS (Figure S4). Most importantly, we find a crossover at α = 0.7, roughly corresponding to 36–37 °C, where the form factor has a smoother shape before exhibiting sharp peaks at higher α values.

Having established the correspondence between experimental and numerical form factors, we examine the calculated radial density profiles to confirm the effective formation of hollow microgels below the VPTT. Figure 2c indeed shows a polymer density profile characterized by a Gaussian-like shell, with a cavity occupying most of the extension of the microgel. However, from around 35 °C, the cavity in the center of the microgel starts to be filled by the polymer chains. Above the VPTT, the hollow particles collapse into a dense globule so that the shape of the density profiles resembles those of standard microgels at high temperatures.²¹

Below the VPTT, the volume occupied by the cavity in our hollow microgels corresponds to roughly 40% of the particle size. This markedly differs from other hollow microgels described in literature,^{23,29,33−35} which are usually obtained by removal of a hard core. In such cases, the size of the cavity is significantly smaller, with a volume occupied by the cavity ranging from ≈1.8 to 6.2%. This has the consequence that, typically, the cavity is also retained at high temperatures, despite a slight size reduction. Indeed, the full shrinkage of the hole is no longer energetically convenient due to the penalty in the elastic bending energy that the thick shell would have to experience.²³ Therefore, the reported strategy allows for synthesizing hollow microgels, which possess a much thinner shell and a correspondingly larger cavity.

Hollow Microgels at Fluid Interfaces

Individual Microgels

To ultimately rationalize how a given internal polymeric structure of the microgels affects their 2D assembly at fluid interfaces, we begin by analyzing the conformation that individual particles acquire after adsorption.

An indirect measurement of the 3D shape of the microgels at the oil–water interface is obtained by visualizing the colloids after deposition from the liquid interface onto a solid substrate. AFM imaging allows for a precise quantification of the height profiles of dried microgels. Following previous works,^24,36 we correlate the profiles measured in this condition with the conformation the microgels had at the interface prior to deposition.

Figure 3a reports typical 3D profiles of isolated microgels deposited on the solid substrate before and after the core degradation process. The reconstructed height profiles at various degrees of core degradation are reported in Figure 3b. Untreated core–shell microgels (i.e., X = 0%) display the characteristically common “core–corona” morphology comprising a denser and thicker core and a more spread-out polymer layer (or corona) of decreasing thickness.²² Upon increasing X, the height profiles reveal that the microgel flattens and its extension on the interfacial plane increases. In other words, upon removal of the internal polymer network, the microgels become more deformable, and the outer shell, less and less constrained by the reduction of cross-links in the core, can further stretch and expand at the interface. Ultimately, a totally different profile is obtained for the hollow particle (X ≃ 100%), which takes up a flat disk-like shape at the interface, with a maximum thickness of around 15 nm after deposition. In all cases, an external corona composed by the outermost polymer chains, which spread out on the interfacial plane, is found around the microgels, as it is clearly shown by AFM phase images (Figure S6 and Figure 5a).

Figure 3.

Core–shell and hollow microgels at the liquid interface. (a) 3D profiles of dried core–shell (left) and hollow (right) microgels as obtained by AFM imaging after deposition onto a silicon wafer from the hexane–water interface. (b) Experimental height profiles for different X (%). The shaded regions correspond to the standard deviations of the height profiles calculated on around 10 particles. (c) Average and standard deviation of the microgels Young’s modulus obtained from AFM nanoindentation measurements as a function of X. (d) Simulations snapshots of a standard (left) and a hollow (right) microgel adsorbed at a oil–water interface. (e,f) Numerical density profiles on the plane of the interface ρ(ζ) (e) and across the interface ρ(z) (f) for a hollow microgel and for a standard core–corona microgel; for ρ(z), negative z corresponds to the oil phase.

Figure 5.

Collective behavior of hollow microgels at the oil–water interface. (a) AFM phase images showing the microgels’ conformation at different values of the surface pressure Π. Scale bar: 2 μm. (b) Compression isotherms reporting the surface pressure Π versus the center-to-center distance d_cc in the particle monolayer. The dashed lines separate the three different regimes (see main text). The first part of the compression curve is fitted to eq 5. Inset: hexatic order parameter ψ₆ as a function of d_cc. The black dotted line indicates the diameter of a single particle at the liquid interface prior to compression (D_i⁰).

This conformation differs from others reported in literature, where hollow particles with a thicker shell with respect to the ones investigated here preserve a small cavity even when absorbed at the interface.²³ Instead, it may resemble at a first sight that of ultralow cross-linked (ULC) microgels, which are synthesized in the absence of cross-linkers.^37,38 However, although a flattening of the particle is observed for both our hollow microgels and ULC microgels, in the present case, it appears to be much more pronounced with respect to what was observed, for instance, in ref (37).

Furthermore, the change in morphology observed during core degradation is different from the effect of reducing the cross-linker concentration in standard batch-synthesized microgels. For the latter particles, decreasing the internal cross-linking density also results in an increased spreading at the interface together with a concomitant decrease of the maximum height.^39,40 However, in that case, the height profile retains a Gaussian-like shape, which remains overall qualitatively similar for different cross-linking degrees.²⁴

A closer look at the height profiles for our microgels reveals that their maximum height decreases up to 3 times the initial height already for only ≈40% of core removal, suggesting that, for X ≳ 40%, a critical number of cross-links in the internal polymer network are cleaved and the particle stiffness rapidly decreases.

A more direct measure of the mechanical properties of the microgels is obtained by AFM nanoindentation experiments, measured in water after particle deposition from the oil–water interface (see Materials, Models, and Methods). The data in Figure 3c, complemented by Figure S8, display a marked reduction of the particles’ Young’s modulus, which correlates well with the change in morphology. For X ≈ 40%, the particles have lost most of their internal stiffness and can consequently spread more at the interface under the action of the interfacial tension. Finally, the height profiles also indicate that the core degradation is associated with a loss of polymer; that is, the cleaved polymers leave the inner part of the particle. As the dry height profile of the microgels is a direct representation of polymer mass distribution, their integral represents the particle total dry mass. In Figure S7, we show that the evolution of the height profiles corresponds to a mass loss, again correlated to the decrease in particle stiffness.

In simulations, we compare the particle morphology of a standard and a hollow microgel. Simulation snapshots are reported in Figure 3d and Figure S9 and immediately illustrate the difference between the two architectures. The microgel density profiles projected onto the plane of the interface ρ(ζ) (see Materials, Models, and Methods for its definition), reported in Figure 3e, closely mirror the experimentally measured ones after deposition (Figure 3b). In particular, these confirm a similar distribution of the polymer network between core–shell particles and standard microgels, whereas for the hollow ones, the numerically extracted shape compares well to that obtained experimentally. In Figure 3f, we also report the profiles across the interface ρ(z). Here, as opposed to the case of the standard microgel, which shows different protrusions in oil and water, the hollow microgel is essentially confined within the interface where it forms a uniform thin layer, barely protruding into either fluid. A comparison between simulations and experiments shows that the extension of the microgel across the interface obtained from simulations is about few σ, comparing quite well with the experimental height in Figure 3b.

Finally, we characterize the extent of the in-plane deformation at the oil–water interface relative to the bulk size by the ratio D_i⁰/D_h, where D_i is the particle diameter at the interface as measured by AFM phase images or extracted from the simulations. The core–shell microgels have a stretching ratio of 1.7 ± 0.1, whereas the hollow microgels reach a value of 2.4 ± 0.1, following the same trend of the values extracted from the numerical simulations (1.4 and 1.9, respectively).

2D Assembly and Response upon Compression

After examining their single-particle conformation at the oil–water interface, we study 2D assemblies of the hollow microgels to link their architecture with their 2D phase behavior and response upon interfacial compression. To this purpose, we spread microgels at a hexane–water interface in a custom-built Langmuir trough and transfer monolayers onto a solid substrate under continuous compression, as detailed in the Materials, Models, and Methods section.

Figure 4 reports the microgels’ conformation within a monolayer upon increasing compression of the liquid interface, as revealed by AFM height images. At low pressures (up to Π ≈ 15 mN·m^–1), the microgels deform in a limited manner (see height profiles in Figure 4b): both the cross-sectional area within the interface plane and the height of each microgel remain approximately constant. In this compression range, microgels organize into a hexagonal assembly and show no appreciable deformation. We hypothesize that increasing compression in this regime mostly affects the outermost polymer chains, which occupy all the available space between the particles (see discussion below). These observations are also captured by the numerical simulations results reported in Figure 4c,d. Here, the radial compression is progressively carried out on single hollow microgels (see Materials, Models, and Methods). The numerical density profiles, both on the plane of the interface (Figure 4c) and across the interface (Figure 4d), are essentially not affected if D_i/D_i⁰ ≲ 5% (corresponding to Π ≲ 15 mN·m^–1 in the experiments), resembling in all respects the profile of an uncompressed particle. However, at higher Π, the rearrangement of the polymeric network involves the whole microgel. For Π > 20 mN·m^–1, the hollow microgels significantly deform to accommodate the increased pressure: the cross-sectional area decreases, while the height of the deposited microgels increases (Figure 4b). At this level of compression, part of the polymer chains desorb from the interface and the particle expands in the third dimension, perpendicularly to the interface. This extension in the third dimension is clearly visible in the ρ(z) profiles of the simulated microgels reported in Figure 4d. Furthermore, as more clearly evidenced from phase images shown in Figure 5a, in this regime, the particles also deform within the interface plane, with the outer polymer chains that fill the voids between the particles’ cores to fully occupy the available space at the interface.

Figure 4.

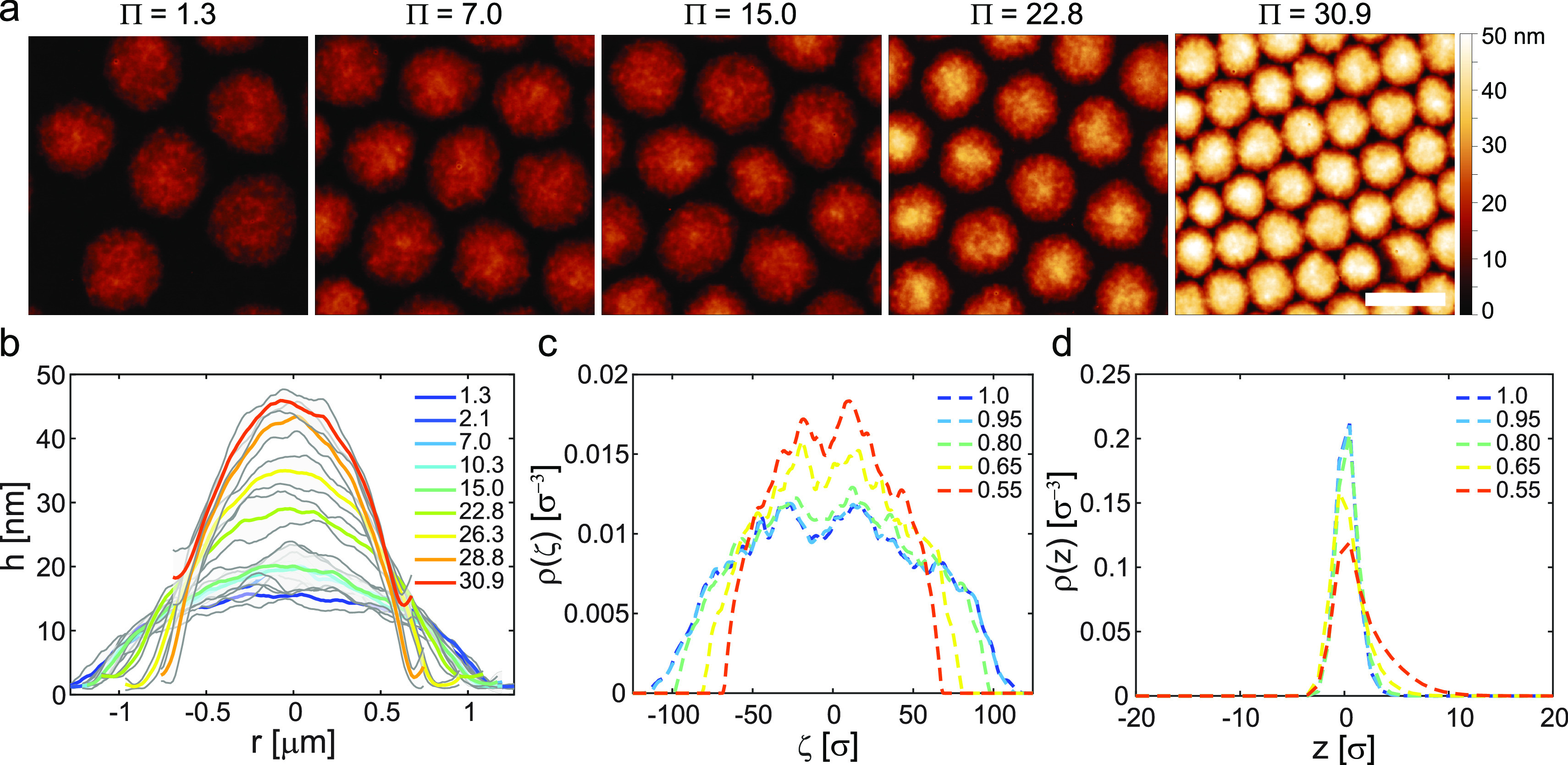
Compression of hollow microgels at the liquid interface. (a) AFM height images showing the monolayer microstructure at increasing surface pressure Π. Scale bar: 2 μm. (b) Microgel height profiles extracted from images as in (a) at increasing Π. The shaded regions correspond to the standard deviations of the height profiles calculated on around 6–10 particles. (c,d) Numerical density profiles within the plane of the interface ρ(ζ) (c) and across the interface ρ(z) (d) for different degrees of radial compression of the hollow microgels defined as D_i/D_i⁰, where D_i is the interfacial size of hollow particle without compression; for ρ(z), negative z corresponds to the oil phase.

Information on the macroscopic response of the microgel monolayer comes from the compression curve reported in Figure 5b, which displays the surface pressure as a function of the microgel–microgel interparticle distance d_cc. It can be noted that the curve presents three different slopes, depending on the range of d_cc analyzed. The first regime at very low and almost constant surface pressure (d_cc > 2.4 μm) corresponds to a dilute monolayer, where the distance between particles is higher than the size of a single isolated particle at the interface, and the result is a disordered arrangement (Figure 5a, Π = 1.3 mN·m^–1). Compressing such a dilute monolayer causes a progressive increase of the effective concentration of microgels at the interface until all particles in the assembly are in contact through their outer polymeric chains. This happens when the distance between microgels is approximately equal to their lateral size at the interface, marked in Figure 5b as D_i⁰. Correspondingly, the particles assemble into a hexagonal packing, as evidenced by the gradual increase in the hexagonal order parameter ψ₆, which reaches a maximum at around d_cc = 2.2 μm (inset in Figure 5b, corresponding AFM image in Figure 4a and Figure S10).

Upon increasing compression, the monolayer enters a second regime where the surface pressure rises while the particle morphology does not exhibit significant changes, as previously described. Correspondingly, the monolayer retains a high degree of hexagonal order, and ψ₆ substantially remains constant. We note that the slight decrease of ψ₆ is presumably due to both size and mechanical polydispersity, which becomes relevant when microgels are extensively compressed with respect to their initial conformation, as previously observed in ref (41) The effective mechanical behavior of the monolayer for small particle deformations is captured by assuming that the microgels interact via a generalized Hertzian potential (see Materials, Models, and Methods). From this description, we extract two important facts. First, the fit nicely describes the data only for values of d_cc for which the height profiles of the microgels do not exhibit significant deformation in the third dimension. Second, the fit gives a power-law exponent a = 1.7 ± 0.1, which is close to the one obtained for common core–corona microgels at the hexane–water interface (a = 1.8 ± 0.2).¹⁷ These two facts indicate that the macroscopic response of the monolayer in this compression range is similar, irrespective of the internal microgel structure. As a conclusion, we argue that only the outer pNIPAM chains determine the mechanical behavior upon compression in this surface pressure range..

Finally, we observe a third regime in the compression curve. For d_cc < 2 μm and Π > 20 mN·m^–1, the out-of-plane deformation of the microgels translates into a variation of the slope of the compression isotherm. In this regime, when microgels completely cover the fluid interface, a further increase in the surface pressure can be explained in terms of interfacial elasticity.⁴² At first sight, the slope change reminds one of similar trends that have been reported for batch-synthesized microgels.^41,43 However, in the latter case, for microgels of similar size, this is typically ascribed to an isostructural solid–solid phase transition which occurs when the outer microgel coronas collapse, enabling core–core contacts.⁴³ In the case of hollow microgels instead, the absence of polymer in the core allows the particles to shrink in the interfacial plane without affecting their hexagonal packing. On the macroscopic level, this results in a 2D assembly that maintains the same hexagonal order throughout the compression isotherm but with a continuously decreasing particle size and, correspondingly, lattice constant (Figure S11).

Conclusions

In this work, we coupled experiments and numerical simulations to provide a detailed description of the internal polymer distribution of core–shell microgels undergoing varying degrees of core degradation. In particular, by endowing the soft cores with chemically cleavable cross-linkers, we obtained particles with controlled internal structures, ranging from the as-synthesized core–shell case to hollow microgels with a thin shell (∼115 nm at 22 °C) and a large cavity (∼640 nm) after full degradation of the core. Such architectures, encompassing small ratios of polymer shell thickness versus size of the cavity, are not easily accessible by common synthetic strategies, where hollow particles are made by dissolving a hard inorganic core.^23,32 In the latter case, the core does not deform in aqueous suspension, and thicker shells are produced, causing the hollow microgels to behave similarly to their core–shell parent particles, with comparable swelling and deswelling properties.^29,34

We found that the internal structure of the particles, which we characterize in the bulk aqueous phase, is tightly linked to both the global mechanical response of microgel monolayers at a fluid interface and their microstructure upon isothermal compression. In particular, we rationalized the properties of the two-dimensional assemblies by characterizing the morphology of individual microgels at the fluid interface. Here, we evidenced that the monolayer response at low compression is similar for all microgel internal structures and appears to be solely governed by the rearrangements of the outer polymer chains constituting the microgel corona at the interface. Conversely, a greater degree of compression led to a different phase behavior of the hollow microgels compared to that of common batch-synthesized ones, with a continuous compaction of a hexagonally packed monolayer instead of the commonly occurring isostructural transition found for standard microgels of comparable size.⁴³ Similar continuous transitions have been already reported in the case of nanometer-sized microgels⁴¹ or for microgels with a low cross-linking density.^39,40 However, in these cases, the hexatic order usually drops upon increasing compression, leading to a disordered monolayer at high pressure. The absence of a core instead enables the hollow microgels to expand out of the interface plane, allowing the assembly to maintain a high degree of hexatic order throughout the compression isotherm. Incidentally, the behavior observed for bulk suspensions of hollow microgels is radically different from that described here at the interface, indicating a central role of the surface tension in determining their collective behavior. Indeed, a recent study has shown the absence of crystal formation in three dimensions in favor of deswelling, interpenetration, and faceting depending on the concentration regime under investigation.⁴⁴

Our findings provide a comprehensive understanding on the effect of the internal structure on the interfacial behavior of soft colloids. In particular, we remark the fact that the structural and mechanical behavior at the fluid interface under low compressions, i.e., corresponding to small overlaps between the particles, appears to be independent of the presence of an inner cavity. This presents us with new challenges and opportunities during synthesis. Indeed, most synthetic efforts are targeted to control the radial cross-linking density profiles of the microgels. However, the interfacial response is initially governed by the properties of a corona of loosely cross-linked or even un-cross-linked chains that surround the microgel within the interface plane. Based on these considerations, we expect that a bigger impact in the tailoring of the monolayer response can be achieved by engineering the properties of the coronas, rather than of the overall density profiles. Possible strategies encompass the controlled growth of shells of linear polymers of different length after completing the cross-linking reaction. At the same time, a closer inspection of the fate of the chains composing the corona during compression would certainly greatly add to our understanding. Nonetheless, the importance of the internal structure emerges at higher compression, delineating a large, and only partially explored, parameter space for the controlled designed of tailored two-dimensional assemblies of soft particles.

Materials, Models, and Methods

Synthesis of Core–Shell and Hollow Microgels

The hollow microgels used in this study were synthesized by a two-step free-radical precipitation polymerization following, with some modifications, a procedure previously reported by Nayak et al.(28)

Core Preparation

N-Isopropylacrylamide (NIPAM, 0.5 g), 5 mol % of methacrylic acid (MAA), and 10 mol % of N,N′-(1,2-dihydroxyethylene)bis(acrylamide) (DHEA) were dissolved in 50 mL of MQ water at room temperature. The reaction mixture was then immersed into an oil bath at 80 °C and purged with nitrogen for 1 h. The reaction was started by adding 6.5 mg of potassium persulfate (KPS) previously dissolved in 1 mL of MQ water and purged with nitrogen. The polymerization was carried out for 6 h in a sealed flask. Afterward, the colloidal suspension was cleaned by dialysis for 1 week and by eight centrifugation cycles and resuspension in pure water. The use of a lower amount of initiator and the absence of surfactants in the reaction mixture allowed us to produce microgels of bigger size in comparison to those in ref (28).

Shell Addition

In a reaction flask, 29 mg of the core microgels was dispersed in 10 mL of MQ water at 80 °C and purged with nitrogen for 1 h. In parallel, NIPAM (0.1 g), 5 mol % of MAA, and 5 mol % of N,N′-methylenebis(acrylamide) (BIS) were dissolved in 10 mL of MQ water at room temperature and purged with nitrogen for 1 h. In a third vial, 2 mg of KPS was dissolved in 1 mL of MQ water and purged with nitrogen. Still keeping the flask sealed, the temperature of the solution containing the core particles was increased to 80 °C prior to adding the initiator. Immediately afterward, we started the feeding of the monomer solution (at 166 μL/min) into the reaction flask. When the feeding was terminated, the reaction was quenched by opening the flask in air and placing it in an ice bath. The obtained colloidal suspension was cleaned by dialysis for 1 week and by eight centrifugation cycles and resuspension in pure water. A polymerization reaction by continuous monomer addition was chosen over the more common batch reaction in order to ensure a more controlled and homogeneous shell growth.^25,26 The final shell is therefore chemically grafted onto the surface of the polymeric cores. Additionally, the fact that the core microgels are collapsed during synthesis imposes that there is only limited diffusion of BIS molecules inside the polymeric core, leading to a small interfacial region where an interpenetrated network is formed.²⁸

Core Degradation

The controlled degradation of the particles’ cores was achieved by exposing core–shell particles to known amounts of sodium periodate (NaIO₄) over different times. In particular, the required amount of mols of sodium periodate with respect to DHEA molecules in solution was added to 500 μL of microgel suspension, and the total volume was increased to 1.5 mL. The amount of DHEA was estimated knowing the microgel concentration, the cores’ size, and assuming that the entire amount of DHEA added during the cores’ synthesis was incorporated in the particles. Three different exposure times were used: 20 h, 3 days, and 8 days. When the required time elapsed, the particle suspension was cleaned by centrifugation and supernatant exchanged once a day for 10 days in order to ensure complete removal of loose polymer chains from the interior of the particles.

Experimental Methods

DLS and SLS

Dynamic light scattering experiments were performed using a Zetasizer (Malvern, UK). The scattering vector for DLS experiments was q = 0.026 nm^–1. The samples were let to equilibrate for 15 min at the required temperature (22 or 40 °C) prior to performing six consecutive measurements. To record volume phase transition curves, the temperature was scanned from 20 to 50 °C with 2 °C steps. At each temperature, the sample was left to equilibrate for 10 min before four consecutive measurements were performed. For SLS, a CGS-3 compact goniometer (ALV, Germany) system was used, equipped with a Nd:YAG laser, λ = 532 nm, output power of 50 mW before optical isolator, with measuring angles from 30 to 150° with 2° steps.

Form Factor Fitting Procedure

Static scattering form factor analysis was performed using the FitIt! tool developed by Otto Virtanen for MATLAB.⁴⁵ The intensity distributions were fitted by assuming the following density profile:

This minimal model gives an excellent description of the experimental form factors of the hollow microgels (see Figure S1) with only two parameters: the size R and the rate of decay of the density from the outer surface toward the center of the microgel λ. The size of the microgels is assumed to be normally distributed.

To calculate the mass removed during the reaction with NaIO₄: ΔM = M₀ – M, we calculated the final mass as 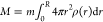and the initial mass as M₀ = 4/3πR³mρ₀, where m is the mass of a monomer unit. The relative mass loss 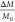is thus calculated as

3

We then estimated the relative mass loss of the core X as

where M_c and M_c0 are the final and the initial mass of the core, and R_c is the radius of the core. We do not expect the uncertainty in R and λ to affect the relative molar mass estimation. In fact, R depends on the distance between the minima in the scattering intensity or, in other words, on its periodicity. λ depends instead on the relative magnitude of the local maxima that is on the rate of decay of the signal. Since the size of the microgels in question is about 1 μm, we do not expect minima below q ≈ 0.01 nm^–1. Therefore, the low scattering vectors contain little (or even no) information about the magnitude of R, which is instead well-captured by the distance between the minima for q > 0.01 nm^–1. Analogously, λ mainly depends on the relative magnitude of the local maxima for q ≫ 0.01 nm^–1. Overall, the uncertainty in R and λ depends on the scattering vectors and intensity at the minima and maxima for q ≥ 0.01 nm^–1, which is the region covered by our measurements.

The 95% confidence intervals of X were estimated using the Monte Carlo method. In particular, the lower and upper bounds were constructed by calculating the 5th and the 95th percentile of the distribution of X obtained by propagating the uncertainty in R, R_c, and λ after 10000 trials. The values of X plotted in Figure 1 as symbols are the medians of such distributions.

Deposition of Isolated Microgels from a Hexane–Water Interface

Microgels were deposited from a hexane–water interface onto silicon wafers for atomic force microscopy imaging of isolated dried particles following an already reported procedure.⁴⁶ Silicon wafers were cut into pieces and cleaned by 15 min ultrasonication in toluene (Fluka Analytical, 99.7%), isopropyl alcohol (Fisher Chemical, 99.97%), acetone, ethanol, and MQ water. A piece of silicon wafer was placed inside a Teflon beaker on the arm of a linear motion driver and immersed in water. Successively, a liquid interface was created between MQ water and n-hexane (Sigma-Aldrich, HPLC grade 95%). Around 100 μL of the microgel suspension was injected at the interface after appropriate dilution in a 4:1 MQ water/isopropyl alcohol solution. After 10 min equilibration time, extraction of the substrate was conducted at a speed of 25 μm·s^–1 to collect the microgels by sweeping through the liquid interface.

Langmuir Trough Deposition

Microgels self-assembled at the hexane–water interface at controlled surface pressure (Π) values were deposited onto silicon wafers for visualization using a custom-made setup already reported in the literature.⁴³ We used a KSV5000 Langmuir trough equipped with a dipper arm immersed in water for holding a silicon substrate forming an angle of approximately 30° with the water surface. The silicon substrate was further cleaned in a UV–Ozone cleaner (UV/Ozone Procleaner Plus, Bioforce Nanosciences) for 15 min to ensure a hydrophilic surface prior to microgel deposition. After a hexane–water interface was formed, the substrate was lifted to pierce the liquid interface. Microgels were then injected on the liquid interface, while the surface pressure was simultaneously measured with a platinum Wilhelmy plate. When the required initial surface pressure was reached, the injection was stopped and the interface was left to equilibrate for 15 min. Successively, the dipper was activated to extract the substrate at a constant speed of 0.3 mm·min^–1, and after 2 min, the barriers started moving at a compression speed of 2.3 mm·min^–1. When the compression finished, the barriers were immediately opened while the substrate was still moving up in order to achieve a discontinuity in microgel concentration deposited on the silicon wafer.

The conformation of microgels at the interface and their 2D assembly as a function of the surface pressure was then inferred by analyzing the substrates using AFM. Images from the initial position of the three-phase contact line to the end of the substrate were recorded at a fixed distance of 500 μm. The discontinuity in microgel deposition ensures a correct assignment of the surface pressure value measured at the liquid interface during compression to the corresponding position on the silicon substrate. More specifically, the highest value of surface pressure measured during the experiment was assigned to the position on the substrate corresponding to the highest density of microgels. Consequently, knowing the dipper speed and the distance between AFM images of the substrate, we scanned the surface pressure curve backward, assigning to each AFM image its corresponding value of Π.

AFM Imaging and Analysis

Microgels deposited on silicon wafers were characterized by AFM (Bruker Icon Dimension), in tapping mode, using cantilevers with ∼300 kHz resonance frequency and a ∼26 N·m^–1 spring constant (OMCLAC160TS-R3, Olympus). Height and phase images were recorded at the same time. Images were first processed with Gwyddion and successively analyzed with custom MATLAB codes. The following procedure was used to obtain an average height profile: for each microgel, horizontal and vertical profiles passing through its center were measured from AFM height images. Successively, an average of over around 10 microgels was obtained by aligning each profile by its center value. For the height profiles of a single microgel inside 2D assemblies (Figure 4), the same procedure was used; the profiles were then cut on the x-axis to exclude neighboring microgels.

The average interparticle distance d_cc at different Π was estimated by extracting the positions of the microgels from AFM images taken at different locations on the substrates. For a given set of particles’ coordinates (x,y), d_cc was calculated as the average distance between neighboring particles. The neighbors’ list was constructed based on the Voronoi tessellation using the Freud open-source Python libraries.⁴⁷ Such a neighbors’ list was also used to calculate the average hexatic order parameter parameter ψ₆:

4

where N_j is the number of neighbors of the jth particle in the AFM image, θ_jk is the angle between the unit vector (1,0), and the vector r = r_k – r_j connecting particle j and its kth neighbor.

The compression isotherms (Π = f(d_cc)) were fitted by assuming the following: (i) the interparticle interactions between microgels adsorbed at the oil–water interface can be described by the generalized Hertzian potential^48,49 of the form

where ϵ is the energy scale, s is the diameter of an isolated microgel at the interface, Θ is the Heaviside step function, and a is a power-law exponent that defines the softness of the potential (a = 5/2 for the purely Hertzian case); (ii) the microgels assemble into a hexagonal lattice:¹⁷

5

The fitting was performed using the curve fitting tool of MATLAB. A good description of the experimental data was obtained by constraining the range of d_cc to 0.75–1 s. This is because for d_cc ≥ s the monolayers are not hexagonally packed, and for d_cc ≲ 0.75 s, Π displays a sudden change of slope that cannot be captured by the functional form of the generalized Hertzian potential.

Nanoindentation

Nanoindentation measurements were performed in MQ water using an Asylum Research MFP 3D AFM (Oxford Instruments, Santa Barbara, CA) on microgels deposited from the hexane–water interface onto silicon wafers. A silica microparticle (diameter = 2 μm, Microparticles GmbH) was glued with a two-component epoxy glue (UHU Plus endfest, UHU GmbH, Germany) to the end of a tipless cantilever using a home-built micromanipulator. The normal spring constant (0.14 N·m^–1) of the Au-coated cantilever (CSC-38, Mikromash, Bulgaria) was measured by the thermal-noise method.⁵⁰ Force versus distance curves were recorded using the force-mapping mode over an area of 10 × 10 μm². The applied force was kept smaller than 2 nN to reduce any substrate effect. Force versus distance curves recorded at the center of the microgels were then converted into force versus indentation curves (the indentation was measured by subtracting the cantilever deflection by the vertical piezodisplacement) and fitted using the Hertz model:

6

where F is the applied force and R is the radius of the colloid used. By knowing the silica probe elastic modulus and the sample Poisson’s ratio (ν), Young’s modulus E of the microgels was obtained by applying the Hertz fit function in the dedicated Asylum Research software (version AR13).

Numerical Models and Methods

In Silico Synthesis

The coarse-grained microgels used for the simulations are characterized by a fully bonded, disordered network, as previously described.^21,51 This is obtained starting from an ensemble of N two- and four-folded patchy particles, which mimic the connectivity of monomers and cross-linkers employed in the chemical synthesis. The spherical shape of the microgels is obtained by letting the patchy particles self-assemble in a spherical cavity of radius Z. For the numerical synthesis of hollow microgels, we also apply an inner spherical force field which does not allow patchy particles to enter a region of radius Z_in, with Z_in < Z. For standard microgels, we add a designing force on cross-linkers only in order to reproduce their inhomogeneous distribution between core and outer periphery as detailed in ref (21). For the hollow microgels investigated here, there are no major differences in applying or not the additional designing force (Figure S10). Each microgel is assembled with the OXDNA simulation package.⁵²

The assembly process is terminated once almost all possible bonds are formed (>99.9%). Subsequently, the topology of the microgel is fixed by means of the Kremer-Grest bead spring model,⁵³ according to which all particles experience a steric repulsion via the Weeks–Chandler–Anderson (WCA) potential,

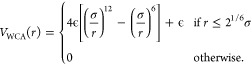7

As commonly defined in coarse-grained simulations, ϵ sets the energy scale, σ is the diameter of the particles, which also defines the unit of length, and r is the distance between two particles. Also, bonded beads interact via the finitely extensible nonlinear elastic (FENE) potential:

8

with k_F = 15, which determines the stiffness of the bond, and R₀ = 1.5 is the maximum bond distance. In this work, we study microgels with Z = 100σ and 75σ with a fraction of cross-linker c = 5%. The model for standard microgels employed in this work is the one described in ref (21), with an average internal density of monomers ρ ∼ 0.08σ^–3. For the hollow particles, we employ Z_in = 0.75Z and ρ = 0.035σ^–3; the consequences of varying these parameters are discussed in the Supporting Information, Figures S12–S15. In all cases, we assume that the low amount of charges present after the chemical synthesis does not affect the structural features and the swelling behavior of the in silico microgels.

The protocol just described does not allow one to reproduce all of the stages of the chemical synthesis procedure. Nonetheless, it allows generating standard and hollow microgels independently, ensuring that the structural features of the final particles resemble experimental results. For this reason, in order to assess the core degradation process, we also make use of a standard microgel with Z = 90σ, ρ = 0.08σ^–3, and c = 10% (corresponding to the DHEA-cross-linked microgel in the chemical synthesis), which is then inserted in the central cavity of a hollow microgel, mimicking a core–shell particle. By progressively removing the internal monomers and thus reducing the internal density, we reproduce the experimentally accessible core degradation stages (Figure S16).

Finally, in order to provide a qualitative comparison between the form factors extracted during this process and the experimental ones, we need to further consider the experimentally observed size increase as a function of X and, accordingly, rescale each numerical form factor to obtain a comparison in nm^–1.

Bulk Behavior

Microgels in bulk are investigated by means of molecular dynamics simulations with implicit solvent. Thermoresponsivity is mimicked by adding a solvophobic potential

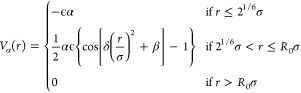9

with 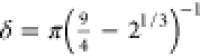and 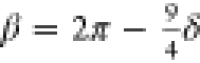.⁵⁴V_α effectively introduces an attraction among all monomers of the network, modulated by the parameter α: in the case where α = 0, the standard Kremer–Grest model is recovered, whereas higher values of α mimic an increase in the temperature of the dispersion, leading to a microgel in the collapsed state at α ≈ 1.1. Simulations in bulk are performed in the NVT ensemble, fixing the reduced temperature T* = k_BT/ϵ = 1 with a Nosé-Hoover thermostat.

Interfacial Behavior

Investigations at the liquid–liquid interface are carried out in the presence of explicit solvent particles in order to reproduce the effect of the surface tension between the two solvents. Solvent particles are modeled as soft beads within the dissipative particle dynamics (DPD) framework.^55,56 The total interaction force among beads is 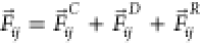, where

10

11

12

where 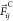is a conservative repulsive force, with w(r_ij) = 1 – r_ij/r_c for r_ij < r_c and 0 elsewhere, 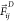and are a dissipative and a random contribution of the DPD, respectively; a_ij quantifies the repulsion between two particles, γ = 2.0 is a friction coefficient, θ is a Gaussian random variable with zero average and unit variance, and Δt = 0.002 is the integration time step. According to previous works,^18,24 in order to reproduce a hexane–water interface, we choose a_ww = a_hh = 8.8, a_hw = 31.1. Instead, for the monomer–solvent interactions, we choose a_mw = 4.5 and a_mh = 5.0. The cutoff radius is always set to be r_c = 1.9σ and the reduced solvent density ρ_DPD = 4.5. In this case, the reduced temperature T* is fixed to 1 via the DPD thermostat. At the interface, we limit the study to microgels with Z = 75σ because of the exceptional computational cost to carry out the simulations in the presence of explicit solvent. Under these conditions, more than 5 × 10⁶ solvent particles are inserted in the simulation box. Simulations are performed with the LAMMPS simulation package.⁵⁷

For microgels adsorbed at the interface, we perform compression tests by imposing an external force of cylindrical symmetry, with the main axis perpendicular to the plane of the interface, along the z-axis. In this way, microgel monomers experience a harmonic force F(r) = −k(r – R)² with F(r) = 0 if r > R, where r is the distance from the monomer to the center axis of the cylinder, R is the equilibrium radius of the cylinder, and k = 10 is the intensity of the force. Solvent particles are not subjected to F(r).

Measured Quantities

In order to compare simulations and experiments, we calculate the numerical form factors in bulk as

13

where r_ij is the distance between monomers i and j, while the angular brackets indicate an average over different configurations and over different orientations of the wavevector . From the rescaling factor between simulations and experiments, we get an effective size of the monomer bead, for which σ = 8.25 nm. Although larger microgel sizes would be required to achieve a bead size comparable to the Kuhn length,²¹ to date, they cannot be easily handled in simulations. In real space, we calculate the radial density profiles of the microgel as

14

with 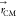being the distance from the microgel center of mass. At the interface, similarly to that in ref (24), we also determine ρ(z), which is the density profile obtained by dividing the simulation box along the z-axis (with z perpendicular to the interfacial plane) into three-dimensional bins that are parallel to the interface, and ρ(ζ), with ζ = x, y, for which bins are taken orthogonally to the interfacial plane. The latter is calculated at a distance ζ from the microgel center of mass and averaged over x and y.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.1c02486.

• Additional data at different temperatures obtained by DLS and SLS, including fittings of the form factors; additional AFM images of individual microgels and microgel assemblies; calculated dry mass of adsorbed microgels as a function of core removal; additional AFM nanointendation results; top-view simulation snapshot of a hollow microgel adsorbed at a oil–water interface; plot of the center-to-center distance as a function of the area per particle in interfacial assemblies (PDF)

Author Contributions

Author contributions are defined based on the CRediT (Contributor Roles Taxonomy) and listed alphabetically. Conceptualization: L.I. and E.Z. Formal analysis: F.C., F.G., and J.V. Funding acquisition: L.I., J.V., and E.Z. Investigation: F.C., F.G., L.I., S.N.R., J.V., and E.Z. Methodology: F.C., F.G., L.R., J.V., and E.Z. Project administration: L.I. and E.Z. Software: F.C., F.G., and L.R. Supervision: L.I and E.Z. Validation: F.C. and J.V. Visualization: F.C., F.G., L.I., J.V., and E.Z. Writing–original draft: F.C., F.G., L.I., J.V., and E.Z. Writing–review and editing: F.C., F.G., L.I., L.R. J.V., and E.Z.

The authors declare no competing financial interest.