Computational Models of Memory Search

Abstract

The capacity to search memory for events learned in a particular context stands as one of the most remarkable feats of the human brain. How is memory search accomplished? First, I review the central ideas investigated by theorists developing models of memory. Then, I review select benchmark findings concerning memory search and analyze two influential computational approaches to modeling memory search: dual-store theory and retrieved context theory. Finally, I discuss the key theoretical ideas that have emerged from these modeling studies and the open questions that need to be answered by future research.

1. INTRODUCTION

In their Annual Review of Psychology article, Tulving & Madigan (1970, p. 437) bemoaned the slow rate of progress in the study of human memory and learning, whimsically noting that “[o]nce man achieves the control over the erasure and transmission of memory by means of biological or chemical methods, psychologists armed with memory drums, F tables, and even on-line computers will have become superfluous in the same sense as philosophers became superfluous with the advancement of modern science; they will be permitted to talk, about memory, if they wish, but nobody will take them seriously.” I chuckled as I first read this passage in 1990, thinking that the idea of external modulation of memories was akin to the notion of time travel—not likely to be realized in any of our lifetimes, or perhaps ever. The present reader will recognize that neural modulation has become a major therapeutic approach in the treatment of neurological disease, and that the outrageous prospects raised by Tulving and Madigan now appear to be within arm’s reach. Yet, even as we control neural firing and behavior using optogenetic methods (in mice) or electrical stimulation (in humans and other animals), our core theoretical understanding of human memory is still firmly grounded in the list recall method pioneered by Ebbinghaus and Müller in the late nineteenth century.

2. MODELS FOR MEMORY

2.1. What Is a Memory Model?

Ever since the earliest recorded observations concerning memory, scholars have sought to interpret the phenomena of memory in relation to some type of model. Plato conceived of memory as a tablet of wax in which an experience could form stronger or weaker impressions. Contemporaneously, the Rabbis conceived of memories as being written on a papyrus sheet that could be either fresh or coarse (Avot 4:20). During the early eighteenth century, Robert Hooke created the first geometric representational model of memory, foreshadowing the earliest cognitive models (Hintzman 2003).

Associationism formed the dominant theoretical framework when Ebbinghaus carried out his early empirical studies of serial learning. The great continental philosopher Johannes Herbart (1834) saw associations as being formed not only among contiguous items, as suggested by Aristotle, but also among more distant items, with the strength of association falling off with increasing remoteness. James (1890) noted that the most important revelation to emerge from Ebbinghaus’s self-experimentation was that subjects indeed form such remote associations, which they subsequently utilize during recall (compare with Slamecka 1964).

In the decades following Ebbinghaus’s experiments, memory scholars amassed a huge corpus of data on the manner in which subjects learn and subsequently recall lists of items at varying delays and under varying interference manipulations. In this early research, much of the data and theorizing concerned the serial recall task in which subjects learned a series of items and subsequently recalled or relearned the series. At the dawn of the twentieth century, associative chaining and positional coding represented the two classic models used to account for data on serial learning (Ladd & Woodworth 1911).

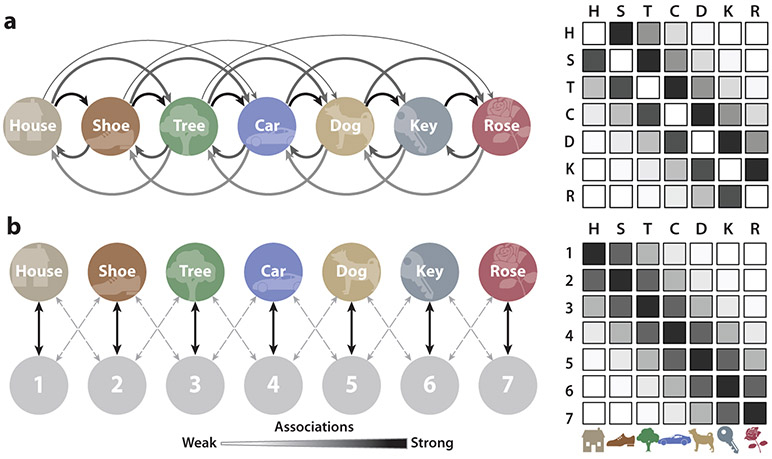
Associative chaining theory posits that the learner associates each list item and its neighbors, storing stronger forward- than backward-going associations. Furthermore, the strength of these associations falls off monotonically with the distance between item presentations (Figure 1a). Recall begins by cuing memory with the first list item, which in turn retrieves the second item, and so on. Positional coding theory posits that the learner associates each list item with a representation of the item’s position in the list. The first item is linked most strongly to the Position 1 marker, the second to the Position 2 marker, and so on (Figure 1b). During recall, items do not directly cue one another. Rather, positions cue items, and items retrieve positions. By sequentially cuing memory with each of the position markers, one can recall the items in either forward or backward order.

Figure 1.

Associative chaining and positional coding models of serial learning. Illustration of the associative structures formed according to (a) chaining and (b) positional coding theories. Darker and thicker arrows indicate stronger associations. Matrices with filled boxes illustrate the associative strengths among the items, or between items and positions (the letters in the right panels refer to the words in the left panels). Figure adapted with permission from Kahana (2012).

Although the above descriptions hint at the theoretical ideas developed by early scholars, they do not offer a sufficiently specific description to derive testable predictions from the models. Indeed, the primary value of a model is in making explicit predictions regarding data that we have not yet observed. These predictions show us where the model agrees with the data and where it falls short. To the extent that a model includes parameters representing unobserved aspects of memory (and most do), the model-fitting exercise produces parameter estimates that can aid in the interpretation of the data being fitted. By making the assumptions explicit, the modeler can avoid the pitfalls of trying to reason from vaguely cast verbal theories. By contrast, modeling has its own pitfalls, which can also lead to misinterpretations (Lewandowsky & Farrell 2011).

Like most complex concepts, memory eludes any simple definition. Try to think of a definition, and you will quickly find counterexamples, proving that your definition was either too narrow or too broad. But in writing down a model of memory, we usually begin with a set of facts obtained from a set of experiments and try to come up with the minimal set of assumptions needed to account for those facts. Usually, although not always, this leads to the identification of three components common to most memory models: representational formalism, storage equation(s), and retrieval equation(s).

2.2. Representational Assumptions

When we remember, we access stored information from experiences that are no longer in our conscious present. To model remembering, we must therefore define the representation that is being remembered. Plato conceived of these representations as images of the past being called back into the present, suggesting a rich but static multidimensional representation based in perceptual experience. Mathematically, we can represent a static image as a two-dimensional matrix, which can be stacked to form a vector. Memories can also unfold over time, as in remembering speech, music, or actions. Although one can model such memories as a vector function of time, theorists usually eschew this added complexity, adopting a unitization assumption that underlies nearly all modern memory models.

According to the unitization assumption, the continuous stream of sensory input is interpreted and analyzed in terms of meaningful units of information. These units, represented as vectors, form the atoms of memory and both the inputs and outputs of memory models. Scientists interested in memory study the encoding, storage, and retrieval of these units of memory.

Let ${\mathbf{f}}_i\in {\mathbb{R}}^N$ represent the memorial representation of item i. The elements of f_i, denoted f_i(1), f_i(2), … , f_i(n), may represent information in either a localist or a distributed manner. According to localist models, each item vector has a single, unique, nonzero element, with each element thus corresponding to a unique item in memory. We can define the localist representation of item i as a vector whose features are given by f_i(j) = 0 for all i ≠ j and f_i(j) = 1 for i = j (i.e., unit vectors). According to distributed models, the features representing an item distribute across many or all of the elements. Consider the case where f_i(j) = 1 with probability p and f_i(j) = 0 with probability 1 − p. The expected correlation between any two such random vectors will be zero, but the actual correlation will vary around zero. The same is true for the case of random vectors composed of Gaussian features, as is commonly assumed in distributed memory models (e.g., Kahana et al. 2005).

The abstract features representing an item must be somehow expressed in the electrical activity of neurons in the brain. Some of these neurons may be very active, exhibiting a high firing rate, whereas others may be quiet. Although the distributed representation model described above may exist at many levels of analysis, one could easily imagine such vectors representing the firing rate of populations of neurons coding for specific features.

The unitization assumption dovetails nicely with the classic list recall method in which the presentation of known items constitutes the miniexperiences to be stored and retrieved. But one can also create sequences out of unitary items, and by recalling and reactivating these sequences of items, one can model memories that include temporal dynamics.

2.3. Multitrace Theory

Encoding refers to the set of processes by which a learner records information into memory. By using the word “encoding” to describe these processes, we tacitly acknowledge that the learner is not simply recording a sensory image; rather, she is translating perceptual input into more abstracted codes, likely including both perceptual and conceptual features. Encoding processes not only create the multidimensional (vector) representation of items but also produce a lasting record of the vector representation of experience.

How does our brain record a lasting impression of an encoded item or experience? Consider the classic array or multitrace model described by Estes (1986). This model assumes that each item vector (memory) occupies its own “address,” much like memory stored on a computer is indexed by an address in the computer’s random-access memory. Repeating an item does not strengthen its existing entry but rather lays down a new memory trace (Hintzman 1976, Moscovitch et al. 2006).

Mathematically, the set of items in memory form an array, or matrix, where each row represents a feature or dimension and each column represents a distinct item occurrence. We can write down the matrix encoding item vectors f₁, f₂, … f_t as follows:

$$M=\left(\begin{array}{cccc}\hfill f_1(1)\hfill & \hfill f_2(1)\hfill & \hfill \dots \hfill & \hfill f_t(1)\hfill \\ \hfill f_1(2)\hfill & \hfill f_2(2)\hfill & \hfill \dots \hfill & \hfill f_t(2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill f_1(N)\hfill & \hfill f_2(N)\hfill & \hfill \dots \hfill & \hfill f_t(N)\hfill \end{array}\right).$$

The multitrace hypothesis implies that the number of traces can increase without bound. Although we do not yet know of any specific limit to the information storage capacity of the human brain, we can be certain that the capacity is finite. The presence of an upper bound need not pose a problem for the multitrace hypothesis as long as traces can be lost or erased, similar traces can merge together, or the upper bound is large relative to the scale of human experience (Gallistel & King 2009). Yet, without positing some form of data compression, the multitrace hypothesis creates a formidable problem for theories of memory search. A serial search process would take far too long to find any target memory, and a parallel search matching the target memory to all stored traces would place extraordinary demands on the nervous system.

2.4. Composite Memories

As contrasted with the view that each memory occupies its own separate storage location, Sir Frances Galton (1883) suggested that memories blend together in the same manner that pictures may be combined in the then-recently-developed technique of composite portraiture (the nondigital precursor to morphing faces). Mathematically, composite portraiture simply sums the vectors representing each image in memory. Averaging the sum of features produces a representation of the prototypical item, but it discards information about the individual exemplars (Metcalfe 1992). Murdock (1982) proposed a composite storage model to account for data on recognition memory. This model specifies the storage equation as

$${\mathbf{m}}_t=\alpha {\mathbf{m}}_{t-1}+{\mathbf{B}}_t{\mathbf{f}}_t,$$ 1.

where m is the memory vector and f_t represents the item studied at time t. The variable 0 < α < 1 is a forgetting parameter, and B_t is a diagonal matrix whose entries B_t (i, i) are independent Bernoulli random variables. The model parameter, p, determines the average proportion of features stored in memory when an item is studied (e.g., if p = 0.5, each feature has a 50% chance of being added to $\tilde{\mathbf{m}}$). If the same item is repeated, it is encoded again. Because some of the features sampled on the repetition were not previously sampled, repeated presentations will fill in the missing features, thereby differentiating memories and facilitating learning. Murdock assumed that the features of the studied items constitute independent and identically distributed normal random variables [i.e., $f(i)\sim \mathcal{N}(0,\sqrt{1∕N})$].

Rather than summing item vectors directly, which results in substantial loss of information, we can first expand an item’s representation into a matrix form, and then sum the resultant matrices. This operation forms the basis of many neural network models of human memory (Hertz et al. 1991). If a vector’s elements, f(i), represent the firing rates of neurons, then the vector outer product, ff^⊤, forms a matrix with elements M_ij = f(i)f(j). This matrix instantiates Hebbian learning, whereby the weight between two neurons increases or decreases as a function of the product of the neurons’ activations. Forming all pairwise products of the elements of a vector distributes the information in a manner that allows for pattern completion (see Section 2.6).

2.5. Summed Similarity

When encountering a previously experienced item, we often quickly recognize it as being familiar. This feeling of familiarity can arise rapidly and automatically, but it can also reflect the outcome of a deliberate retrieval attempt. Either way, to create this sense of familiarity, the brain must somehow compare the representation of the new experience with the contents of memory. To conduct this comparison, one could imagine serially comparing the target item to each and every stored memory until a match is found. Although such a search process may be plausible for a very short list of items (Sternberg 1966), it cannot account for the very rapid speed with which people recognize test items drawn from long study lists. Alternatively, one could envision a parallel search of memory, simultaneously comparing the target item with each of the items in memory. In carrying out such a parallel search, we would say “yes” if we found a perfect match between the test item and one of the stored memory vectors. However, if we required a perfect match, we may never say “yes,” because a given item is likely to be encoded in a slightly different manner on any two occasions. Thus, when an item is encoded at study and at test, the representations will be very similar, but not identical. Summed similarity models present a potential solution to this problem. Rather than requiring a perfect match, we compute the similarity for each comparison and sum these similarity values to determine the global match between the test probe and the contents of memory.

Perhaps the simplest summed-similarity model is the recognition theory first proposed by Anderson (1970) and elaborated by Murdock (1982, 1989) and Hockley & Murdock (1987). In Murdock’s TODAM (Theory of Distributed Associative Memory), subjects store a weighted sum of item vectors in memory (see Equation 1). They judge a test item as “old” when its dot product with the memory vector exceeds a threshold. Specifically, the model states that the probability of responding “yes” to a test item (g) is given by

$$P(\text{yes})=P(\mathbf{g}\cdot \mathbf{m}>k)=P\left(\mathbf{g}\cdot \left[\sum _{t=1}^L{\alpha }^{L-t}{\mathbf{B}}_t{\mathbf{f}}_t\right]>k\right).$$ 2.

Premultiplying each stored memory by a diagonal matrix of Bernoulli random variables implements a probabilistic encoding scheme, as in Equation 1.

The direct summation model of memory storage embodied in TODAM implies that memories form a prototype representation—each individual memory contributes to a weighted average vector whose similarity to a test item determines the recognition decision. However, studies of category learning indicate that models based on the summed similarity between the test cue and each individual stored memory provide a much better fit to the empirical data than do prototype models (Kahana & Bennett 1994).

Summed-exemplar similarity models offer an alternative to direct summation (Nosofsky 1992). These models often represent psychological similarity as an exponentially decaying function of a generalized distance measure. That is, they define the similarity between a test item, g, and a studied item, f_i, as

$$\text{similarity}(\mathbf{g},\mathbf{f})=\text{exp}(-\tau \Vert \mathbf{g}-\mathbf{f}{\Vert }_{\gamma })=\text{exp}\left(-\tau {\left[\sum _{j=1}^N[g(j)-f(j){]}^{\gamma }\right]}^{1∕\gamma }\right),$$ 3.

where N is the number of features, γ indicates the distance metric (γ = 2 corresponds to the Euclidean norm), and τ determines how quickly similarity decays with distance.

Following study of L items, we have the memory matrix M = (f₁ f₂ f₃ … f_L). Now, let g represent a test item, either a target (i.e., g = f_i for some value of i) or a lure (i.e., g ∉ M). Summing the similarities between g and each of the stored vectors in memory yields the following equation:

$$S=\sum _{i=1}^L\text{similarity}(\mathbf{g},{\mathbf{f}}_i).$$ 4.

The summed-similarity model generates a “yes” response when S exceeds a threshold, which is often set to maximize hits (correct “yes” responses to studied items) and minimize false alarms (incorrect “yes” responses to nonstudied items).

2.6. Pattern Completion

Whereas similarity-based calculations provide an elegant model for recognition memory, they are not terribly useful for pattern completion or cued recall. To simulate recall, we need a memory operation that takes a cue item and retrieves a previously associated target item or, analogously, an operation that takes a noisy or partial input pattern and retrieves the missing elements.

Consider a learner studying a list of L items. We can form a memory matrix by summing the outer products of the constituent item vectors:

$$M=\sum _{i=1}^L{\mathbf{f}}_i{\mathbf{f}}_i^{\mathsf{T}}.$$ 5.

Then, to retrieve an item given a noisy cue, ${\tilde{\mathbf{f}}}_i={\mathbf{f}}_i+ϵ$, we premultiply the cue by the memory matrix:

$$M{\tilde{\mathbf{f}}}_i=\sum _{j=1}^L{\mathbf{f}}_j{\mathbf{f}}_j^{\mathsf{T}}{\tilde{\mathbf{f}}}_i={\mathbf{f}}_i{\mathbf{f}}_i^{\mathsf{T}}{\tilde{\mathbf{f}}}_i+\sum _{j\ne i}{\mathbf{f}}_j{\mathbf{f}}_j^{\mathsf{T}}{\tilde{\mathbf{f}}}_i={\mathbf{f}}_i({\mathbf{f}}_i\cdot {\tilde{\mathbf{f}}}_i)+\sum _{j\ne i}{\mathbf{f}}_j({\mathbf{f}}_j\cdot {\tilde{\mathbf{f}}}_i)={\mathbf{f}}_i+\text{error}.$$

This matrix retrieval operation is closely related to the dynamical rule in an autoassociative neural network. For example, in a Hopfield network (Hopfield 1982), we would apply the same storage equation to binary vectors. The associative retrieval operation would involve a nonlinear transformation, such as the sign operator, that would assign values of +1 and −1 to positive and negative elements of the product $M{\tilde{\mathbf{f}}}_i$, respectively. By iteratively applying the matrix product and transforming the output to the closest vertex of a hypercube, the model can successfully deblur noisy patterns as long as the number of stored patterns is small relative to the dimensionality of the matrix. These matrix operations form the basis of many neural network models of associative memory (Hertz et al. 1991). An interesting special case, however, is the implementation of a localist coding scheme with orthogonal unit vectors. Here, the matrix operations reduce to simpler memory strength models, such as the Search of Associative Memory model (see Section 5.1).

2.7. Contextual Coding

Researchers have long recognized that associations are learned not only among items but also between items and their situational, temporal, and/or spatial context (Carr 1931, McGeoch 1932). Although this idea has deep roots, the hegemony of behavioristic psychology in the post–World War II era discouraged theorizing in terms of ill-defined, latent variables (McGeoch & Irion 1952). Whereas external manipulations of context could be regarded as forming part of a multicomponent stimulus, the notion of internal context did not align with the Zeitgeist of this period. Scholars with a behavioristic orientation feared the admission of an ever-increasing array of hypothesized and unmeasurable mental constructs into their scientific vocabulary (e.g., Slamecka 1987).

The idea of temporal coding, however, formed the centerpiece of Tulving & Madigan’s (1970) Annual Review of Psychology article. Although these authors distinguished temporal coding from contemporary interpretations of context, subsequent research brought these two views of context together. This was particularly the case in Bower’s (1972) temporal context model. According to Bower’s model, contextual representations constitute a multitude of fluctuating features, defining a vector that slowly drifts through a multidimensional context space. These contextual features form part of each memory, combining with other aspects of externally and internally generated experience. Because a unique context vector marks each remembered experience, and because context gradually drifts, the context vector conveys information about the time in which an event was experienced. Bower’s model, which drew heavily on the classic stimulus-sampling theory developed by Estes (1955), placed the ideas of temporal coding and internally generated context on a sound theoretical footing and provided the basis for more recent computational models (discussed in Section 5.2).

By allowing for a dynamic representation of temporal context, items within a given list will have more overlap in their contextual attributes than items studied on different lists or, indeed, items that were not part of an experiment (Bower 1972). If the contextual change between lists is sufficiently great, and if the context at time of test is similar to the context encoded at the time of study, then recognition-memory judgments should largely reflect the presence or absence of the probe (test) item within the most recent (target) list, rather than the presence or absence of the probe item on earlier lists. This enables a multitrace summed-attribute similarity model to account for many of the major findings concerning recognition memory and other types of memory judgments.

We can implement a simple model of contextual drift by defining a multidimensional context vector, c = [c(1), c(2), … , c(N)], and specifying a process for its temporal evolution. For example, we could specify a unique random set of context features for each list in a memory experiment, or for each experience encountered in a particular situational context. However, contextual attributes fluctuate as a result of many internal and external variables that vary at many different timescales. An elegant alternative (Murdock 1997) is to write down an autoregressive model for contextual drift, such as

$${\mathbf{c}}_i=\rho {\mathbf{c}}_{i-1}+\sqrt{1-{\rho }^2}ϵ,$$ 6.

where ϵ is a random vector whose elements are each drawn from a Gaussian distribution, and i indexes each item presentation. The variance of the Gaussian is defined such that the inner product, ϵ_i · ϵ_j, equals one for i = j and zero for i ≠ j. Accordingly, the similarity between the context vector at time steps i and j falls off exponentially with the separation: c_i · c_j = ρ^∣i−j∣. Thus, the change in context between the study of an item and its later test will increase with the number of items intervening between study and test, producing the classic forgetting curve.

To put context into memory, we can simply concatenate each item vector with the vector representation of context at the time of encoding (or retrieval) and store the associative matrices used to simulate recognition and recall in our earlier examples. Alternatively, we can directly associate context and item vectors in the same way that we would associate item vectors with one another (I discuss this class of context models in Section 5.2).

3. ASSOCIATIVE MODELS

3.1. Recognition and Recall

This section combines the representational assumptions and the encoding and retrieval operations discussed above to build a simple matrix, or network model of associative memory. This model is loosely based on ideas in the classic models presented by Murdock (1982, 1997), Metcalfe-Eich (1982), and Humphreys et al. (1989). I examine how this model simulates two classic memory paradigms: item recognition and cued recall.

Consider a study phase in which subjects learn a series of f_i−g_i pairs. During a subsequent test phase, subjects could make recognition judgments on individual items (e.g., answering the question, “Was g_i on the study list?”), or they could provide recall responses to the question, “What item was paired with f_i?” Rather than modeling each task independently, we can imagine an experiment in which subjects provide both recognition and recall responses for each studied pair. For the recognition test, subjects would say “yes” to items or pairs that appeared in the study phase and “no” to new pairs, or to rearranged pairs or previously studied words. In the recall task, they would simply recall the word that appeared alongside the retrieval cue.

Let the pair of vectors (f_i, g_i) represent the ith pair of studied items. The following equation represents the information stored in memory following study of a list of L pairs:

$$M=\sum _{i=1}^L({\mathbf{f}}_i+{\mathbf{g}}_i)({\mathbf{f}}_i+{\mathbf{g}}_i{)}^{\mathsf{T}}=\sum _{i=1}^L{\mathbf{f}}_i{\mathbf{f}}_i^{\mathsf{T}}+{\mathbf{f}}_i{\mathbf{g}}_i^{\mathsf{T}}+{\mathbf{g}}_i{\mathbf{f}}_i^{\mathsf{T}}+{\mathbf{g}}_i{\mathbf{g}}_i^{\mathsf{T}}.$$ 7.

The terms in this equation carry both item-specific information supporting recognition and associative or relational information supporting cued recall. To simulate cued recall, we premultiply the memory matrix, M, with the cue item, f_k. This yields an approximate representation of the studied pair, f_k + g_k, as given by the following equation:

$$\begin{gathered} M{\mathbf{f}}_k=\sum _{i=1}^L({\mathbf{f}}_i{\mathbf{f}}_i^{\mathsf{T}}+{\mathbf{f}}_i{\mathbf{g}}_i^{\mathsf{T}}+{\mathbf{g}}_i{\mathbf{f}}_i^{\mathsf{T}}+{\mathbf{g}}_i{\mathbf{g}}_i^{\mathsf{T}}){\mathbf{f}}_k, \\ =({\mathbf{f}}_k+{\mathbf{g}}_k)({\mathbf{f}}_k\cdot {\mathbf{f}}_k+{\mathbf{g}}_k\cdot {\mathbf{f}}_k)+\sum _{l\ne k}({\mathbf{f}}_l+{\mathbf{g}}_l)({\mathbf{f}}_l\cdot {\mathbf{f}}_k+{\mathbf{g}}_l\cdot {\mathbf{f}}_k)={\mathbf{f}}_k+{\mathbf{g}}_k+\text{error}. \end{gathered}$$

The match between the retrieved trace and the cue item, given by Mf_k · f_k, then determines the probability of successful cued recall. If the vectors are orthonormal, retrieval is error free. Because vector addition is commutative, this implementation of cued recall is inherently symmetrical. Even if the strengths of the f and g items are differentially weighted, the forward and backward heteroassociative terms would have the same strength. The symmetric nature of these linear models also applies to their nonlinear variants (Hopfield 1982). We could (and should) generalize the above equations to include contextual features, but for now we make the simplifying assumption that the list context defines the entire contents of memory, and we can thus omit an explicit representation of context from the model.

To simulate the recognition process, we first cue memory with g_i and retrieve its associated pattern, as in the cued recall model described above. We then compute the similarity between this retrieved vector and the cue. Using the dot product as our measure of similarity, as in TODAM, we obtain the following expression:

$$M{\mathbf{g}}_i\cdot {\mathbf{g}}_i=({\mathbf{f}}_i+{\mathbf{g}}_i)\cdot {\mathbf{g}}_i+\sum _{k\ne i}({\mathbf{f}}_k+{\mathbf{g}}_k)\cdot {\mathbf{g}}_i.$$

If the resulting similarity, given by the above expression, exceeds a threshold, the model will generate a “yes” response. Alternatively, we can use this expression as the input to a stochastic decision process, which would allow us to obtain predictions regarding response times to various cue types (Hockley & Murdock 1987).

Kahana et al. (2005) analyzed this class of models, along with three other variants, to determine which model provided the best account of data from successive recognition and recall tasks. They found that the local matching matrix model provided a good quantitative account for various aspects of the recognition and recall data so long as the model allowed for item–item similarity, output encoding, and variability in the goodness of encoding during study, as simulated using probabilistic encoding (Equation 1). Not only could this model account for data on repetition effects in both item recognition and cued recall, but also it could account for the pattern of correlations observed between successive recognition and recall tasks, and how those correlations varied under manipulations of encoding variability.

3.2. Serial Learning

In this section, I extend the basic matrix model to the problem of serial learning. In serial learning, subjects study a list of randomly arranged items and subsequently recall the list in forward order. In early work, researchers asked subjects to learn long lists of randomly arranged syllables over repeated study test trials (Young 1968). In more recent work, researchers asked subjects to immediately recall a short list after a single presentation (Farrell 2012). Given its historical importance, I use serial learning to illustrate the basic challenges of extending simple associative models to account for recall of entire lists.

The classic associative chaining theory of serial order memory assumes that each item vector directly associates with the immediately preceding and following items in a list. Although one can write down a chaining model using only direct forward associations, subjects perform nearly as well at backward serial recall (Madigan 1971), suggesting the existence of bidirectional forward and backward associations. Furthermore, some theories assume that subjects form remote associations, with associative strength falling off exponentially with item lag (Solway et al. 2012).

Figure 1 illustrates the associative structure hypothesized in chaining theory. Recall proceeds by cuing with the first list item, or a beginning-of-list contextual marker, and chaining forward through the list. Cuing with the first list item tends to retrieve the second list item because the associative strength between the first and second list items is greater than the associative strength between the first list item and any other item. We assume that the memory system strengthens the associations during both encoding and retrieval. Thus, when learning a list over multiple study-test trials, both the correct responses and the errors made on the previous trials become reinforced in memory.

We can generalize our matrix model (e.g., Equation 5) to simulate chained association. If we assume that the vector f_k denotes the kth list item, and that the representation of item k can be maintained until the presentation of item k + 1, the following equation represents bidirectional pairwise associations between contiguously presented items:

$$M=\sum _{k=1}^{N-1}{\gamma }_{\mathrm{F}}{\mathbf{f}}_{k+1}{\mathbf{f}}_k^{\mathsf{T}}+{\gamma }_{\mathrm{B}}{\mathbf{f}}_k{\mathbf{f}}_{k+1}^{\mathsf{T}}.$$

If we can (somehow) reinstate the vector corresponding to the first list item f₁, then applying the retrieval rule, Mf₁, retrieves f₂. If f₂ is successfully retrieved, reapplying the retrieval rule retrieves a mixture of f₁ and f₃, creating a target ambiguity problem (Kahana & Caplan 2002). In a neural network implementation, one can resolve this ambiguity by introducing a temporary suppression (or inhibition) mechanism for recalled items (Farrell & Lewandowsky 2012). By biasing the network away from retrieving already-recalled patterns, one can prevent the network from repeatedly cycling between already-recalled items. In contrast, such a mechanism will make it more difficult to recall lists with repeated items, as in the Ranschburg effect (Crowder & Melton 1965, Henson 1998).

Early researchers recognized that subjects could use other cues to help solve the problem of serial order memory. For example, some subjects would report using spatial strategies when learning serial lists, linking each item to a position in an array (Ladd & Woodworth 1911). The major early evidence in favor of this view came from Melton & Irwin’s (1940) observation that intrusions of items presented on prior lists tend to have been from positions near that of the correct response on the current list. These and other observations led to the development of positional coding models of serial order memory, which remain prominent among contemporary theorists (Hitch et al. 2005).

To construct a matrix implementation of positional coding, we need to specify a vector representation for positional codes. To do so, we could implement a dynamic representation of context that evolves gradually over the course of list presentation. Alternatively, we could simply define two random vectors—one vector representing the beginning of the list, p₁, and one representing the end of the list, p_L. We would then define each interior position p_j as the weighted average of these two vectors, with interior positions close to the start of the list weighted more heavily toward p₁ and interior positions close to the end of the list weighted more heavily toward p_L. Both of these approaches embody the notion of graded associations, with stronger associations to the correct position and weaker associations to positions of increasing distance.

To implement a positional coding neural network model, we can modify the matrix model of paired-associate memory to learn the associations between position vectors, p_j, and item vectors, f_i. At test, we would first cue the memory matrix with p₁ and retrieve the list item most strongly associated with that position (likely f₁). We would then successively cue memory with p_i for each position i. A key difference between associative chaining and positional coding models is that in the positional model one can easily continue cuing memory after a retrieval failure because one can always increment the positional cue. In contrast, in the associative chaining model, a failure to make a transition means that one must rely on the weak remote associations rather than the strong nearest-neighbor association for the next recall.

Lewandowsky & Murdock (1989) showed that a chaining model implemented using convolution and correlation as the associative operators accounts for many findings concerning serial recall and serial learning. Several phenomena, however, indicate that positional coding may be more important than chaining in immediate recall of short lists. Examples include protrusions and the pattern of recall errors in lists of alternating confusable and nonconfusable items (Henson et al. 1996). Both of these phenomena cannot be easily explained with associative chaining theory. Beyond the evidence for interitem and position-to-item associative processes, research on serial learning has shown that subjects likely form hierarchical structures, such as in the organization of linguistic material. Such evidence has led scholars to develop models in which groups of items form special associative structures called chunks. Farrell (2012) presents a particularly impressive formulation of this type of model, showing how it can account for numerous findings in both serial and free recall.

4. BENCHMARK RECALL PHENOMENA

Among the many paradigms researchers have used to study memory, the free and serial recall tasks have generated the richest data and have led to the most well-developed theories. Before discussing two major models of list recall, I review some of the benchmark phenomena that any successful recall model should be able to explain.

In list recall tasks, subjects study a series of sequentially presented items that they subsequently attempt to recall. In free recall, subjects may recall the items in any order; in serial recall, subjects must recall items in their order of presentation, beginning with the first item. Words serve as the stimuli of choice because they are abundant, subjects know and agree upon their meanings, and modern word-embedding algorithms provide vector representations for every word in semantic memory, or their lexicon. In free recall, the order in which subjects recall list items provides valuable clues to the process of memory search. Serial recall, in requiring that subjects report items in their order of presentation, provides valuable information about subjects’ memory for order information. Whereas most theorists have treated these two recall paradigms separately, recent research highlights the considerable similarities between the tasks (Klein et al. 2005, Ward et al. 2010).

4.1. Serial Position Effects

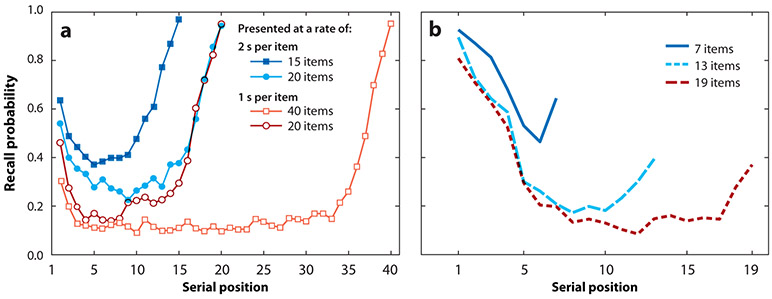
By virtue of presenting each list item individually, we can ask how the serial position of an item affects its likelihood of being recalled. This leads us to the classic serial position analysis, which illustrates the principles of primacy and recency—enhanced memory for the first few and last few items in a list. In immediate free recall (IFR), subjects exhibit a strong recency effect and a smaller, yet robust, primacy effect. In immediate serial recall, subjects exhibit a strong primacy effect but only a modest recency effect. Scoring free recall is very straightforward; one simply counts the number of correct recalls in each serial position and divides it by the number of possible correct recalls. For serial recall, either researchers adopt a strict procedure in which they score as correct only the items recalled in the their absolute position, or they adopt a more lenient procedure, giving credit for items recalled in their correct order relative to one or more prior items.

Figure 2 shows serial position curves in IFR and serial recall for lists of varying lengths. These figures illustrate primacy and recency effects, as well as a modest effect of list length, whereby subjects recall a smaller percentage of items with increasing list length. Whereas increasing list length reduced recall of early- and middle-list items, it did not reliably change recall of the last few items. Analogously, slowing the rate of item presentation increased recall of early- and middle-list items, but did not have any discernible effect on recall of final-list items (Murdock 1962). Serial position analyses have revealed many dissociations between recall of recency and prerecency items, including the effects of semantic similarity, which affects only prerecency items, and the effect of presentation modality, which affects primarily recency items. The recency effect, in particular, is highly vulnerable to any distracting activity performed between study and test, such as solving a few mental arithmetic problems or counting backward by threes. These dissociations between recency and prerecency items fueled models in which recall of recently experienced items results from a specialized short-term memory module that obeys principles very different from the memory processes that govern longer-term recall.

Figure 2.

Serial position effects. (a) Murdock’s (1962) classic study of the serial position effect in free recall. The four curves represent lists of 15 items (blue filled squares) and 20 items (light blue filled circles), both presented at a rate of 2 s per item, and lists of 20 items (red open circles) and 40 items (orange open squares), both presented at a rate of 1 s per item. (b) Serial position curves for immediate (forward) serial recall of 7-item, 13-item, and 19-item lists (Kahana et al. 2010). Figure adapted with permission from Kahana (2012).

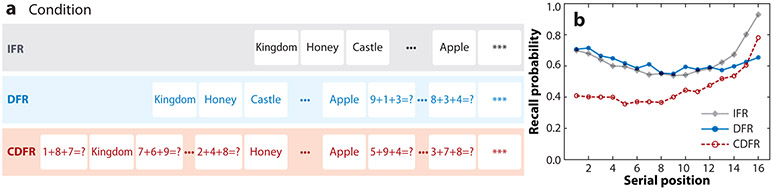
To the extent that recency in free recall arises from accessibility of items in short-term store (STS), one should see a marked reduction in recency in continual-distractor free recall (CDFR). The finding of long-term recency in CDFR (Figure 3b) has thus proven to be a major challenge to dual-store theories. Dual-store theorists have responded to this challenge by positing that separate mechanisms may give rise to immediate and long-term recency (Davelaar et al. 2005).

Figure 3.

The long-term recency effect. (a) Illustration of presentation schedules in IFR, DFR, and CDFR. Arithmetic problems fill the distractor intervals. (b) Recency appears in both IFR and CDFR but is sharply attenuated in DFR. Modest primacy is observed in both IFR and DFR but is attenuated in CDFR because the distractor task disrupts rehearsal. Abbreviations: CDFR, continual-distractor free recall; DFR, delayed free recall; IFR, immediate free recall. Figure adapted with permission from Kahana (2012).

The primacy effect evident in both IFR and delayed free recall (DFR) has also attracted the interest of memory theorists. The classic explanation for primacy is that subjects who are highly motivated to recall as many items as possible share rehearsal time between the currently presented item and items presented in earlier serial positions (Brodie & Murdock 1977, Tan & Ward 2000). Experimental manipulations that tend to promote rehearsal, such as providing subjects with longer interpresentation intervals, also enhance primacy. By contrast, conditions that discourage rehearsal, such as incidental encoding, fast presentation rates, or interitem distraction, reduce primacy effects (Kahana 2012).

4.2. Contiguity and Similarity Effects

Aristotle hypothesized that similar and contiguously experienced items tend to come to mind successively for the rememberer. In the free recall task, we can measure subjects’ tendency to cluster recalls on the basis of their temporal or semantic similarity. To quantify the temporal contiguity effect in free recall, Kahana (1996) computed the probability of transitioning from an item studied in serial position i to an item studied in serial position j, conditional on the availability of such a transition. Consistent with associationist ideas, this conditional response probability (CRP) decreased with increasing interitem lag = j − i. Figure 4a shows this measure, termed the lag-CRP, in both DFR and CDFR conditions. Subjects tend to make transitions among contiguous items, and do so with a forward bias, as shown by the higher probabilities for lag = +1 than for lag = −1 transitions.¹ The same pattern is observed in IFR, final free recall, and autobiographical memory tasks and under a wide range of experimental manipulations that would be expected to alter subjects’ encoding and/or retrieval strategies (Healey et al. 2019).

Figure 4.

Temporal and semantic organization in free recall. (a) The conditional response probability (CRP) as a function of lag exhibits a strong contiguity effect in both delayed free recall (DFR) and continual-distractor free recall (CDFR). Subjects performed a 16-s arithmetic distractor task immediately following the list (DFR) or between list items (CDFR). (b) Semantic-CRP curve for these conditions (Lohnas & Kahana 2014). Figure adapted with permission from Kahana (2012).

Comparing the lag-CRPs observed in DFR and CDFR (Figure 4) reveals the persistence of contiguity across timescales (Healey et al. 2019, Howard & Kahana 1999). Asking subjects to perform a demanding distractor task between items should disrupt their tendency to transition among neighboring items. Yet the data indicate that contiguity is preserved despite the disruption of the encoding process. The same 16 s of distractor activity were sufficient to sharply attenuate the recency effect in the same experiment (Figure 3b).

Applying the lag-CRP analysis to serial recall reveals that order errors are frequently items from list positions near that of the just-recalled item, regardless of that item’s serial position (Bhatarah et al. 2008, Solway et al. 2012). Analyzing transitions following the first-order error on each trial, Solway et al. (2012) observed that subjects often pick up with the item that followed the erroneous recall in the list, or fill in with the preceding item. Thus, subjects’ errors in serial recall tend to cluster around the position of the just-recalled item, even when that item was placed in the wrong position.

Just as the lag-CRP analysis reveals the contiguity effect, we can use a similar approach to measure the semantic organization of recall. Specifically, we can compute the conditional probability of recall transitions between items i and j as a function of their semantic similarity (Howard & Kahana 2002b). This semantic-CRP analysis reveals strong semantic organization effects even in studies using word lists that lack obvious semantic associates (Figure 4b). For these analyses, we used Google’s Word2Vec algorithm to model the semantic similarity of any two words in the lexicon.

Beyond temporal and semantic clustering, memories can exhibit many other forms of organization. Polyn et al. (2009) asked subjects to make size or animacy judgments on words during the study phase of a free recall experiment. They found that, in addition to temporal and semantic clustering, subjects clustered their recalls on the basis of encoding task—successively recalled words tended to belong to the same encoding task. Miller et al. (2013) found evidence for spatial organization in free recall. They asked subjects to deliver objects as they navigated a previously learned three-dimensionally rendered virtual town. On each trial, subjects delivered a series of 16 objects, each to a randomly chosen store. They then recalled the delivered objects without regard to order or location. Miller et al. (2013) observed that subjects clustered the delivered objects according to both their sequential order of presentation and their spatial location, despite the fact that these two variables were uncorrelated due to the random sequence of delivery locations. Long et al. (2015) asked whether emotional attributes of words elicit similar organizational tendencies in free recall. They found that subjects were more likely to transition among items that shared affective attributes merely on the basis of variation in valence across a random sample of common English words. Long et al. confirmed that subjects still exhibited affective clustering even after controlling for the finding that words with similar affective valence possess greater semantic similarity (Talmi & Moscovitch 2004).

4.3. Recall Errors

A detailed study of the dynamics of memory retrieval also offers a window into the processes that give rise to false memories. In free recall, false memory may be said to occur whenever a subject recalls an item that was not on the study list. When making such intrusions, subjects are sometimes highly confident that the item they incorrectly recalled was presented as part of the study list (Roediger & McDermott 1995). As noted by Schacter (1999), many of the same memory processes that give rise to correct recalls also give rise to errors. This idea can be seen by examining subjects’ tendency to commit prior-list intrusions (PLIs) as a function of list recency (Zaromb et al. 2006). Figure 5a shows that PLIs exhibit a striking recency effect, with most such intrusions coming from the last two lists.

Figure 5.

Recency, contiguity, and similarity influence recall errors. (a) Proportion of PLIs decreases with increasing list lag (analyses exclude the first 10 lists). (b) Successive PLIs that occur tend to come from neighboring serial positions on their original list (Zaromb et al. 2006). (c) Transitions from correct items to errors (PLIs and ELIs) have higher semantic relatedness values than transitions to other correct responses (Kahana 2012). Abbreviations: ELI, extralist intrusion; PLI, prior-list intrusion. Figure adapted with permission from Kahana (2012).

Further evidence for Schacter’s thesis comes from analyses of successively committed PLIs. Although such responses are relatively uncommon, when they do occur they exhibit a strong contiguity effect (Figure 5b). This finding demonstrates that when subjects recall an item associated with an incorrect context, they use that item as a cue for subsequent recalls, leading them to activate neighboring items from the incorrect prior list.

Assuming that prior-list items compete with current-list items for recall and that semantic information is an important retrieval cue, Schacter’s thesis about recall errors would predict that PLIs should have greater semantic relatedness to the just-recalled word than do correct recalls. Testing this hypothesis, Zaromb et al. (2006) found that subjects exhibit a strong tendency to commit PLIs whose recall-transition similarity values are, on average, higher than those for correct recall transitions (Figure 5c).

4.4. Interresponse Times

Interresponse times (IRTs) have long provided important data for theory construction. Murdock & Okada (1970) demonstrated that IRTs in free recall increase steadily throughout the recall period, growing as an exponential function of the number of items recalled. This increase in IRTs predicted recall termination—following IRTs longer than 10 s, people rarely recall additional items (Figure 6a). To the extent that IRTs reflect the associative strength between items, one would expect that other predictors of retrieval transitions will also influence IRTs. We find that transitions between neighboring items exhibit faster IRTs than transitions among more remote items (Figure 6b) and that transitions between semantically related items exhibit faster IRTs than transitions between less similar items (Figure 6c).

Figure 6.

Interresponse times (IRTs) in free recall. (a) IRTs increase as a joint function of output position and total number of recalled items. (b) One can observe a contiguity effect in the average IRTs for recall transitions between neighboring items. Here, IRTs for transitions between item i and i + lag are faster when lag is small. (c) Semantic similarity also influences IRTs as observed in faster transitions between semantically similar items, as measured by Google’s Word2Vec algorithm. Data in panel a are from Kahana et al. (2018). Figure adapted with permission from Kahana (2012).

In immediate serial recall, errorless trials reveal long initiation times followed by fast IRTs that generally exhibit an inverse serial position effect—faster responses at the beginning and end of the list (Kahana & Jacobs 2000). With repeated trials, and longer lists, errorless recall often exhibits grouping effects—fast IRTs for items within groups of three or four items, and slow IRTs between groups (Farrell 2012).

5. MODELS FOR MEMORY SEARCH

This section discusses two theoretical approaches to modeling memory search. I first consider dual-store models of memory search, best exemplified in the Search of Associative Memory (SAM) retrieval model. I then discuss retrieved context theory (RCT), which builds on the classic stimulus sampling theory presented by Estes (1955), but introduce a recursive dynamical formulation of context that accounts for recency and contiguity effects across timescales.

5.1. Dual-Store Theory

Much of our knowledge concerning the detailed aspects of list recall emerged during the cognitive revolution of the 1960s. Whereas earlier research had focused on the analysis of learning and forgetting of entire lists, and the critical role of interference in modulating retention, the late 1950s saw the rise of the item-level analysis of memory (Brown 1958, Murdock 1961), which was also known as the short-term memory paradigm. Soon, this research spawned a broad set of models embracing the distinction between two memory stores with different properties: short-term memory and long-term memory (Murdock 1972).

According to these dual-store models, items enter a limited-capacity STS during memory encoding. As new items are studied, they displace older items already in STS. While items reside together in STS, their associations become strengthened in a long-term store (LTS). At the time of test, items in STS are available for immediate report, leading to strong recency effects in IFR and the elimination of recency by an end-of-list distractor. Primacy emerges because the first few list items linger in STS, thus strengthening their LTS associations. The last few items spend the shortest time in STS, which accounts for the finding that subjects remember them less well on a postexperiment final free recall test (Craik 1970).

Atkinson & Shiffrin (1968) presented the most influential early dual-store model. Shiffrin and colleagues advanced this research in subsequent papers that developed the SAM model discussed below (e.g., Shiffrin & Raaijmakers 1992). Because SAM set the standard for future theories of memory search, and because it remains a benchmark model to this day, I provide an overview of the model’s mechanisms and discuss how it gives rise to many of the benchmark phenomena discussed above.

5.1.1. Encoding processes.

Figure 7a illustrates the encoding process as a list of words is studied for a subsequent recall test. As the word House is encoded, it enters the first of four positions in STS (the size of STS is a model parameter). When Shoe is encoded, it takes its place in the first position, pushing House into the second position. This process continues until STS is full, at which point new studied items displace older ones in STS. The matrices in Figure 7 illustrate how rehearsal in STS modifies the strengths of associations in LTS. SAM assumes that for each unit of time that an item, i, spends in STS, the strength of its association to context, S(i, context) increases. Rehearsal also increases the strength of the associations among items in STS; specifically, the model increments S(i, j) and S(j, i) (possibly by different values) for each time step that items i and j co-occupy STS. SAM also includes a parameter to increment the self-strength of an item. This parameter plays an important role in modeling recognition, but not recall data. Parameters that determine the learning rates for each type of association (item-to-item, item-to-context, and self-strength) can be estimated by fitting the model to behavioral data.

Figure 7.

The Search of Associative Memory model. (a) Schematic of the encoding process (from left to right). Each word enters short-term store (STS), which can hold up to four items. When STS is full, new words probabilistically knock out older ones. While words reside in STS, the associations among them strengthen in long-term store (LTS), as shown in the matrices with shaded boxes and rows and columns labeled by the first letter of each word. The shading of the cells represents the strength of a particular association: between list items (each denoted by its first letter), between list items and context, or between a list item and itself (darker shading indicates stronger associations). X denotes an item that was not in the study list. The row labeled “Ctxt” represents the associative strengths between each item and the list context. Across the four matrices, the strengths of the associations change as each item is encoded. The matrix labeled “Semantic memory” shows the strength of preexisting semantic associations that are presumed not to change over the course of item presentation. (b) Retrieval begins with recall of items in STS and continues with a search of LTS cued by context and previously recalled items. Recalling an item from LTS involves first probabilistically selecting candidate items for potential recall and then probabilistically determining whether the candidate item is recalled. Recall ends after a certain number of retrieval failures. Figure adapted with permission from Kahana (2012).

5.1.2. Retrieval processes.

In immediate recall, SAM first reports the contents of STS (Figure 7b). Next, SAM begins the search of LTS using context as a retrieval cue, with the probability of an item being sampled depending on the strength of the association between context and that item. One of the words that has not already been recalled from STS is sampled with a probability that is proportional to the strength of the items’ association with the list context. Sampling probabilistically is analogous to throwing a dart at a dartboard—the larger the area of a given target (corresponding to a candidate item in memory), the more likely you are to hit it. In this example, House and Tree have the highest probability of being sampled, followed by Dog, as determined by the amount of time these items occupied STS. Figure 7b also illustrates the function that relates cue-to-target strength to the probability that a sampled item will be subsequently recalled. Stronger cues lead to higher probabilities of recalling sampled items. The weight matrix in Figure 7b indicates that successful recall of Tree further strengthens its association with context in episodic LTS. After successfully recalling an item, the model assumes that the recalled item combines with context as a compound cue for subsequent sampling and recall, following a similar process as described above. Regardless of an item’s strength of association with context, with other retrieved items, or with both, SAM assumes that an item that was previously recalled cannot be recalled again within a given trial. When retrieval cues lead to successful recall, the strengths of the item’s associations with the retrieval cues are incremented in LTS. SAM assumes that recall terminates after a certain number of failed recall attempts.

5.1.3. Model extensions and evaluation.

SAM accounts for many recall phenomena, including serial position effects (Figure 2), dissociations between recall of recency and prerecency items (Figure 2), contiguity effects (Figure 4), and IRTs (Figure 6). Versions of SAM allow contextual associations to change gradually as items are studied or recalled (Mensink & Raaijmakers 1988) and add a separate semantic LTS that works together with the contextually based (i.e., episodic) LTS (Kimball et al. 2007, Sirotin et al. 2005). These additions enable SAM to account for category clustering, semantic organization of recall, intrusions, spacing effects, and false memory effects, among other phenomena. Because STS is responsible for both recency and contiguity effects, SAM predicts that both should be disrupted in CDFR, contrary to the finding that recency and contiguity persist across timescales (Figures 3 and 4). Indeed, both recency and contiguity persist across very long timescales, extending to memory for new stories and autobiographical events spanning many months and even years (Moreton & Ward 2010, Uitvlugt & Healey 2019). These findings challenge the view that recency and contiguity effects reflect short-term memory processes, such as rehearsal or persistence of representations in working memory.

The following subsection discusses RCTs of memory search. These theories emerged as a response to the challenges facing dual-store theories, such as SAM. Although RCT eschews the distinction between short-term and long-term memory processes, it nonetheless embodies several core ideas of the SAM retrieval model, most notably a dynamic cue-dependent retrieval process guided by multiple prior representations.

5.2. Retrieved Context Theory

Contextual drift formed the core idea of Estes’s (1955) stimulus sampling theory and Bower’s (1967, 1972) multiattribute theory of recognition memory. According to these early formulations, a randomly drifting representation of context (Equation 6) helped explain the phenomena of forgetting and spontaneous recovery of previously learned associations after a delay (Estes 1955). Glenberg & Swanson (1986) suggested that an evolving context representation could explain the phenomenon of long-term recency (Figure 3), and Mensink & Raaijmakers (1988) demonstrated how a variable context signal in the SAM model could account for the major results obtained in studies of associative interference. Whereas these earlier formulations saw context as a cue for items, they did not explicitly consider items as a cue for context. That is, drifting contextual representations changed the accessibility of items, but item retrieval did not systematically alter the state of context.

RCT (Howard & Kahana 1999, 2002a) introduced the idea that remembering an item calls back its encoding context, which in turn serves as a retrieval cue for subsequent recalls. At its most basic level, this theory proposes that items and context become reciprocally associated during study: Context retrieves items, and items retrieve context. But because context is drifting through a high-dimensional space, and because such a drift process is correlated with the passage of time, contextual retrieval embodies the essential feature of episodic memory, which is the ability to jump back in time to an earlier contextual state. This contextual retrieval process, in cuing subsequent recalls, can generate the contiguity effect illustrated in Figure 4. That is, retrieving the context associated with item i triggers memories of items studied in similar contexts, such as items i − 1 and i + 1.

5.2.1. Context evolution and the bidirectional associations between items and context.

RCT conceives of context as evolving due to the nature of experience itself, rather than as a result of a random input to a stochastic process. We thus begin by writing down a general expression for the evolution of context:

$${\mathbf{c}}_i={\rho }_i{\mathbf{c}}_{i-1}+\beta {\mathbf{c}}^{\text{IN}},$$ 8.

where c^IN is an as-yet-unspecified input to context and ρ_i is a constant ensuring that ∥c_i∥ = 1. As the learner encodes or retrieves an item, RCT assumes that new associations form, both between the item’s feature representation and the current state of context (stored in the matrix M^FC) and between the current state of context and the item’s feature representation (stored in the matrix M^CF). These associations follow a Hebbian outer-product learning rule, as in earlier models of associative memory. Specifically, we can write the evolution of these associative matrices as

$$\begin{gathered} M_t^{\text{FC}}=M_{t-1}^{\text{FC}}+{\gamma }_{\text{FC}}{\mathbf{c}}_{i-1}{\mathbf{f}}_i^{\mathsf{T}}, \\ {M}_t^{CF}=M_{t-1}^{\text{CF}}+{\gamma }_{\text{CF}}{\mathbf{f}}_i{\mathbf{c}}_{i-1}^{\mathsf{T}}, \end{gathered}$$ 9.

where the γ_FC and γ_CF parameters determine the learning rates for item-to-context and context-to-item associations, respectively. Through these associative matrices, presentation or recall of an item evokes its prior associated contexts, and cuing with context retrieves items experienced in overlapping contextual states.

In RCT, the currently active item, f, retrieves (a weighted sum of) its previous contextual states via the M^FC matrix, which in turn serves as the input to the context evolution equation: c^IN = M^FCf_i. Normalizing this input and replacing the expression in Equation 8 yield the recursion

$${\mathbf{c}}_i={\rho }_i{\mathbf{c}}_{i-1}+\beta \frac{M^{\text{FC}}{\mathbf{f}}_i}{\Vert M^{\text{FC}}{\mathbf{f}}_i\Vert },$$ 10.

where model parameter β governs the rate of contextual drift (a large value of β causes context states to decay quickly). During list recall, or when items are repeated, context recursively updates on the basis of the past contextual states associated with the recalled or repeated item.² Because context is always of unit length, it can be thought of as a point on a hypersphere, with β determining the distance it travels with the newly presented item and M^FCf_i determining the direction of travel.

In simulating list recall experiments, RCT initializes the context-to-item and item-to-context associative matrices with preexperimental semantic associations, as defined by a model of semantic memory. In this way, the context retrieved by a just-recalled item supports the subsequent retrieval of semantically related items. Polyn et al. (2009) introduced this initialization to model the effects of semantic organization on memory (Figures 4b, 5c, 6c). Lohnas et al. (2015) extended the Polyn et al. model by allowing the associative matrices and the context vector to accumulate across many lists, thereby allowing the model to simulate data on intrusions.

5.2.2. Retrieval processes.

RCT models free recall by using the current state of context as a cue to retrieve items, via associations stored in the M^CF matrix:

$${\mathbf{f}}_t^{\mathbf{IN}}=M^{\text{CF}}{\mathbf{c}}_t.$$ 11.

The resulting ${\mathbf{f}}_t^{\mathbf{IN}}$ gives the degree of support, or activation, for each item in the model’s lexicon. Different implementations of RCT have used different models to simulate the recall process. Several early papers (e.g., Howard & Kahana 1999) used a probabilistic choice rule similar to the sampling rule in SAM, but then one must propose a specific rule for recall termination. Sederberg et al. (2008) modeled the recall process as a competition among racing accumulators (one for each candidate recall) on the basis of the decision model proposed by Usher & McClelland (2001). In this model, the activation of each candidate item evolves according to a discrete Ornstein–Uhlenbeck process:

$${\mathbf{x}}_n=(1-\tau \kappa -\tau \lambda \mathbf{N}){\mathbf{x}}_{n-1}+\tau {\mathbf{f}}_t^{\mathbf{IN}}+ϵ,$$ 12.

where x_n is a vector with one element for each retrieval candidate. When the retrieval competition starts, all elements are set to zero (i.e., x₀ = 0), and the initial activation of each item is used as its starting point in the race to threshold. τ is a time constant, κ is a parameter that determines the decay rate for item activations, and λ is the lateral inhibition parameter, scaling the strength of an inhibitory matrix N that subtracts each item’s activations from all of the others except itself. ϵ is a random vector with elements drawn from a Gaussian distribution with μ = 0 and σ = η. The first word whose accumulator crosses its threshold, prior to the end of the recall period, wins the competition. Use of this leaky competitive accumulator model to simulate recall allowed RCT to generate realistic IRT data, matching several empirical phenomena (Polyn et al. 2009). However, it is possible that other competitive choice models, or nonlinear network models, could also enable RCT to account for IRT data.

5.2.2.1. Postretrieval editing.

Cuing memory with context generates the first response in a list recall experiment. The winner’s representation is reactivated on F, allowing the model to retrieve the contextual state associated with the item and update the current context. Before the item is actually output by the model, however, it undergoes a postretrieval editing phase, consistent with the observation that people often report thinking of items that they do not overtly recall during free recall experiments (Wixted & Rohrer 1994). Editing is accomplished by comparing the context representation retrieved by the candidate item with the currently active context representation (Dennis & Humphreys 2001):

$${\mathbf{c}}_{t+1}^{\text{IN}}\cdot {\mathbf{c}}_t.$$ 13.

Because associations are formed between items and the context that prevailed when they were originally presented, true list items will tend to retrieve a context that is similar to the context that prevails during retrieval. The match between retrieved context and the current context will depend on how much contextual drift has occurred between the original presentation and the recall event. Relatively little drift will have occurred for items that were actually presented on the current list, whereas considerable drift will have occurred for items that were presented on earlier lists. Thus, on average, accurate recalls will produce a higher value than either PLIs or extralist intrusions. If the comparison returns a value that is beneath a threshold parameter, the item is rejected. Once an item is either recalled or rejected, another recall competition begins. This series of competitions continues until the end of the recall period, at which point the next trial begins.

5.2.2.2. Repetition suppression.

When attempting to recall items learned in a given context, subjects very rarely repeat themselves, even though the items they have already recalled are presumably among the strongest in memory. Lohnas et al. (2015) addressed this observation by incorporating a repetition suppression mechanism into their implementation of RCT. Specifically, they dynamically set the retrieval threshold of each item as the recall period progresses to allow items that were recalled earlier in the period to participate in, but not dominate, current retrieval competitions. At the beginning of the recall period, each item i has a threshold of Θ_i = 1. If item i is retrieved, its threshold is incremented by a value ω and then gradually returns to one with subsequent recalls:

$${\Theta }_i=1+\omega {\alpha }^j,$$ 14.

where j is the number of subsequent retrievals and α is a parameter between zero and one. The larger the value of α is, the more intervening retrievals are needed before an already-recalled item is likely to be retrieved again.

5.2.3. Recency and primacy.

RCT naturally accounts for the classic recency effects observed in many recall tasks because the context at the time of test is most similar to the contexts associated with recently experienced or recalled items. This effect is not dependent on the number of previously studied items. In contrast, increasing list length makes it harder to recall items from early- and middle-list positions because of increased competition from other list items, consistent with data shown in Figure 2. In the accumulator model (Equation 12), the level of activation of a given item determines the degree to which it suppresses the activations of other items, thus increasing the level of competition in the model. However, the recent items are somewhat insulated from this competition because they are strongly activated by the time-of-test context cue in immediate recall. Items retrieved later in the recall sequence are relatively less well activated and thus feel the effects of competition more sharply. In delayed recall, the distractor task will have caused the representation of context to drift away from its state at the end of the studied list. As such, RCT predicts that the recency effect should be greatly diminished following a period of distracting mental activity. In CDFR, the distractors between item presentations will have reduced the overlap in the context representations among all of the list items. However, because recall is a competition based on the relative activations of all of the list items, time-of-test context will produce a large recency effect because all of the items will have been similarly affected by the distractors.

The context-similarity mechanism that gives rise to recency cannot, however, explain the enhanced recall of early-list items (i.e., the primacy effect). The two main sources of primacy effects in free recall are an increased tendency to rehearse items from early serial positions throughout the list presentation (Tan & Ward 2000) and increased attention or decreased competition during the study of early-list items giving rise to better encoding (Sederberg et al. 2006, Serruya et al. 2014). To account for primacy within a model of recall, one must model either the rehearsal process or the change in attention over the course of item presentations, or both. Whereas the SAM model characterizes the rehearsal process, RCT assumes that early-list items attract more attention due to their novelty (see also Burgess & Hitch 1999). This approach is supported by the observation that the major phenomena of free recall (other than primacy) do not appear to depend strongly on rehearsal. Specifically, Sederberg et al. (2006) introduced the scalar ϕ_i factor to describe the recall advantage for items in early serial positions (its value is determined by two manipulable parameters of the model). This factor starts at a value above one; as the list progresses, it decays to one, at which point it has no effect on the dynamics of the model:

$${\varphi }_i={\varphi }_s{e}^{-{\varphi }_d(i-1)}+1.$$ 15.

Here, ϕ_s scales the magnitude of the primacy effect and ϕ_d controls the rate at which this advantage decays with serial position (i).

5.2.4. Contiguity, asymmetry, and compound cuing.

Recalling item f_i retrieves its associated list context as well as its associated preexperimental context (i.e., the average of contexts experienced prior to the study list). The preexperimental context was the input to the context evolution equation when item f_i was studied. Following recall of item f_i, these two components combine with the current state of context to form the new state of context, which in turn cues the next response. Each of these three components will bias retrieval in a particular way. Insofar as the prior state of context contained items from the end of the list, that portion of the context vector will activate recent items. In contrast, the retrieved list context will tend to activate items studied contiguously to the just-recalled item. Because the list context is (approximately) equally similar to the items that preceded and followed it in the list, this component of context will facilitate transitions to neighboring items in a symmetrical manner. In contrast, the retrieved preexperimental context associated with item f_i was incorporated into the context vector only following the presentation of that item. As such, this component of context will provide a strongly asymmetric cue favoring transitions to subsequent-list items rather than prior-list items. The combined forward-asymmetric and bidirectional cue for subsequent recalls gives rise to the characteristic asymmetric contiguity effect.

In RCT, the contiguity effect arises because recall of an item activates the context that was associated with that item during list presentation, as well as (preexperimental) contexts associated with the item prior to the most recent study list. These retrieved contextual states combine with the current state of context to serve as the retrieval cue for the next response. Because the list context associated with an item overlaps with the encoding context of the item’s neighbors, a contiguity effect results. Because the preexperimental context associated with an item overlaps with the encoding context of the item’s successors in the list, there is a forward asymmetry in recall transitions. Finally, to the degree that the time-of-test context overlaps with the context of recently studied items, there will be a tendency to make transitions to end-of-list items.

In CDFR, the distractor activity interpolated between study items will diminish the degree to which the context associated with an item overlaps with the context associated with its neighbors. However, because recall is competitive, the overall reduction in the contextual overlap among items will not significantly diminish the contiguity effect. To the extent that the activations of neighboring-list items are greater than the activations of remote-list items, a contiguity effect is predicted. The absolute activations of the items are thus less important than their relative activations.

Due to the recursive definition of context, RCT predicts that multiple prior items serve as part of the cue for the next recalled item. Lohnas & Kahana (2014) tested this compound cuing prediction through a meta-analysis of free recall experiments. Consistent with this prediction, they found that following recall of two temporally clustered items, the next recalled item is more likely to also be temporally clustered.

5.2.5. Memory and aging.

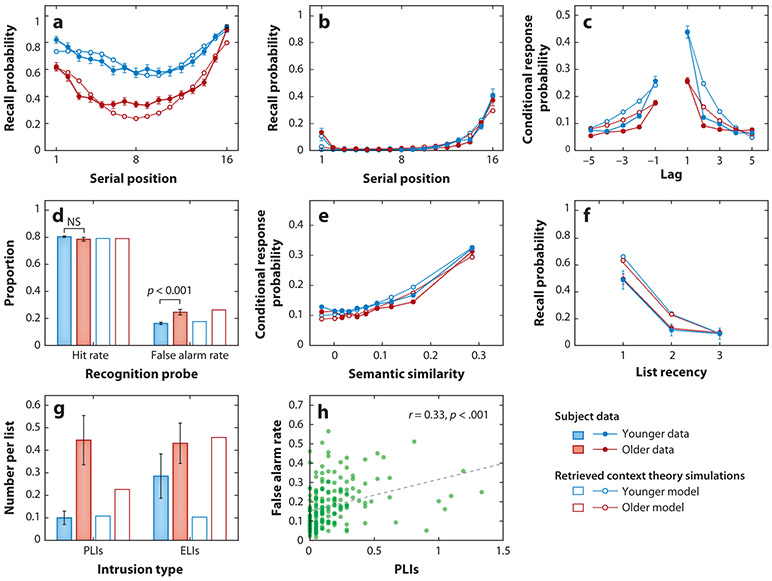
Healey & Kahana (2016) applied RCT to recall data from younger and older adults. They added a context-similarity model of recognition judgments based on the same mechanism used to filter intrusion errors. They first fitted RCT to data from younger adults, allowing all model parameters to vary; they then identified the smallest subset of parameter changes required to match the older adults’ data. This method identified four components of putative age-related impairment: (a) contextual retrieval, (b) sustained attention (related to the primacy gradient), (c) error monitoring (related to rejecting intrusions), and (d) decision noise. Figure 8a-g shows that the full model provided a reasonable account of younger adults’ recall dynamics and that adjusting the four components mentioned above enabled the model to account for age-related changes in serial position effects, semantic and temporal organization, intrusions, and recognition data.

Figure 8.

Age-related changes in recall and recognition. (a) Serial position. (b) Probability of first recall (i.e., the serial position curve for the very first recalled item). (c) Contiguity effects. (d) Recognition memory hits and false alarms. (e) Semantic organization. (f,g) Intrusion errors. (h) Correlation between intrusions and false alarms. Red lines and bars represent data from older adults, and blue lines represent data from younger adults. Solid lines with filled symbols or filled bars show subject data, and broken lines with open symbols or unfilled bars show retrieved context theory simulations (Healey & Kahana 2016). Abbreviations: ELI, extralist intrusion; NS, nonsignificant; PLI, prior-list intrusion. Figure adapted with permission from Kahana (2012).

RCT provides a natural mechanism for simulating recognition memory judgments. Specifically, a recognition test probe will retrieve its associated context state in exactly the same way that items retrieve their associated contexts during encoding and retrieval. Comparing this reinstated context with the current state of context provides a measure of the match between the current context and the encoding context of the item, which can then drive a recognition decision. Healey & Kahana (2016) introduced this mechanism, proposing that subjects judge an item as “old” when ${\mathbf{c}}_{t+1}^{\text{IN}}\cdot {\mathbf{c}}_t>c_{\text{recog}}$. If endorsed as “old,” the item’s associated context is integrated into the current state of context (see Equation 10). The authors assumed that context updating did not occur for “new” judgments.

Healey & Kahana (2016) demonstrated that this recognition model could account for the pattern of hits and false alarms observed for younger and older adults. Moreover, they suggested that the common modeling assumptions behind recognition and the rejection of intrusions should lead to a novel and testable prediction: specifically, that subjects who commit more intrusions in free recall should also commit more false alarms in item recognition. Confirming this prediction, they found a significant positive correlation between intrusion rates in free recall and false alarm rates in recognition (Figure 8h).

5.2.6. Recall in the list-before-last paradigm.

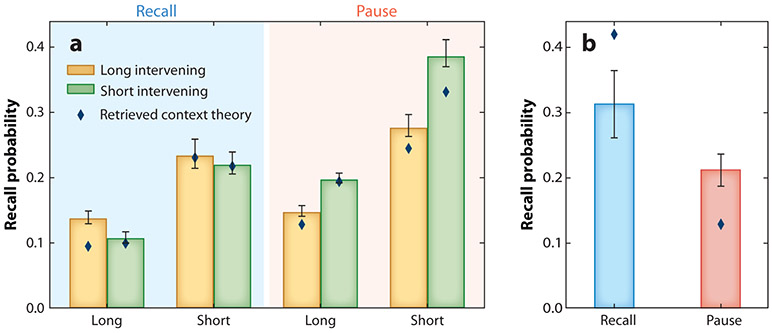
Unlike traditional free recall, where subjects search their memory for items on a just-presented list, a recall procedure introduced by Shiffrin (1970) probes memory for items learned in more remote contexts. On each trial, he asked subjects to recall the items from the list before last (LBL). In this method, subjects would study list n, then recall list n − 1, then study list n + 1, then recall list n, and so on. Although challenging, subjects are able to do this task, recalling many more items from the target list than from the intervening list. Because cuing memory with time-of-test context will retrieve items from the most recent (intervening) list, it is not clear whether RCT can accommodate subjects’ ability to recall items from the (target) LBL. Indeed, Usher et al. (2008) cited the lack of a directly retrievable list context as a shortcoming of RCT.

Lohnas et al. (2015) examined whether existing mechanisms in RCT could account for LBL recall. RCT’s postretrieval editing process (Equation 13) allows the model to filter out responses from the intervening list until an item associated with the target-list context is retrieved. When an item is retrieved, the context retrieved by that item is compared with the current state of context. The model can use the similarity between retrieved context and current context as a filter for rejecting items if they are deemed either too similar to have been in the LBL or too dissimilar to have been in the current experiment. Lohnas et al. assumed that LBL recall initiates with the first retrieved item whose context similarity falls in the appropriate range. Retrieval of this item’s context serves to cue the next recall, and subsequent recalls follow as in regular free recall.

Lohnas et al. applied this model to data from an LBL study reported by Jang & Huber (2008). On half of the lists in their experiment, subjects skipped the recall phase between lists, pausing rather than recalling the LBL. In all cases, subjects recalled a smaller fraction of items when the target list was long than when it was short. However, lengthening the intervening list reduced target recall only in the pause condition. RCT predicts the target-list length effect because long target lists have more items associated with a similar contextual cue than the short target lists. Thus, when target-list context is reinstated, target-list items have stronger activation values in the decision competition than items from other lists, and with longer target-list length there will be more such target-list items. A decision process including more items with strong activations is functionally equivalent to a decision process with more items competing, resulting in proportionally fewer target-list recalls in longer lists. However, in the recall (between successive lists) condition, increasing the length of the intervening list did not reliably reduce recall of target-list items. RCT accounts for this result because, during the post-target-list recall period, context states of target-list items (list n − 1) and earlier-list items (list n − 2) are retrieved, which serve to reduce the influence of the intervening-list items. So long as at least one item was retrieved during that prior recall period, irrespective of what list it came from, RCT yielded a null effect of intervening-list length. RCT predicts that the proportion of intervening-list intrusions (which is low overall) is greater with recall between lists (Figure 9b). With a pause between lists, RCT covertly retrieves more intervening-list intrusions prior to discovering the target list. These items are assigned a higher threshold for subsequent retrievals (Equation 14), reducing the set of recallable intervening items.

Figure 9.

Recalling the list before last. (a) Recall as a function of target- and intervening-list lengths in the recall and pause between list conditions. (b) Intervening-list intrusions in recall and pause conditions. Diamonds indicate retrieved context theory fits to the data (Lohnas et al. 2015). Figure adapted with permission from Kahana (2012).

6. CONCLUSIONS AND OPEN QUESTIONS

There has now been sufficient convergence among models that it is possible to identify the key modeling assumptions required to account for many recall phenomena. The cue-dependent nature of memory retrieval, which draws support from a wealth of experimental data, lies at the core of virtually every model of memory. Analyses of retrieval dynamics provide particularly strong evidence for cue-dependent retrieval: Following recall of a given item, subjects tend to recall items with similar temporal, semantic, source, spatial, or affective attributes. The retrieved context models and dual-store models discussed here, as well as other important classes of models, such as those based on chunking (Farrell 2012), all embody the principle of cue-dependent retrieval, and each of these models provides a good account of many benchmark findings on recall organization.

To characterize the cue-dependent nature of memory retrieval, we need to model the similarity relations among memories. Thus, I began the discussion of memory models with an analysis of the multidimensional nature of memories, often modeled as vectors of features. I then defined a similarity function based on the geometric distances among item vectors and examined how summed similarity models account for the basic features of recognition memory.

Students of memory have long embraced the distinction between content and context, recognizing that memories become associated with an ever-changing tapestry of background elements, and that forgetting often occurs when the context prevailing at time of test no longer matches the context in which an experience was encoded. In memory search paradigms such as free recall, context forms an important cue for retrieval (i.e., the list) and contextual cuing reduces associative interference caused by similar items that occurred in other lists. At this point, nearly all models of memory search have come to include an explicit representation of item or list context. Whereas a representation of list context can help focus retrieval on a target list (e.g., Davelaar et al. 2005), a dynamic representation of temporal context can also account for the persistence of recency and contiguity across multiple timescales (Sederberg et al. 2008).

Memory search does not go on indefinitely. At a certain point, people stop recalling, either because they run out of time or because they cannot easily recall additional items. Several models posit that memory search terminates after a certain number of retrieval failures (Farrell 2012, Raaijmakers & Shiffrin 1981, Sirotin et al. 2005). Models that generate IRTs terminate recall when the retrieval period ends (e.g., Healey & Kahana 2016, Lohnas et al. 2015, Sederberg et al. 2008). But retrieval failures also play a critical role in determining search times. This occurs not only because failed retrievals take time but also because they result in a poor cue for subsequent recalls, leading subjects to find themselves in a mental cul-de-sac, without any strong cues for the remaining recall candidates (Miller et al. 2012).

In recalling a list of words, subjects rarely repeat items that they have already recalled. Given that subjects are most likely to recall those items that possess strong retrieval cues (and which were encoded well), it is perhaps surprising that repetitions occur so infrequently. Without some way of suppressing retrieval of already-recalled items, many models would repeatedly sample the same items over and over again. Whereas many recall models have simply excluded repetitions as candidates for recall, some models (e.g., Healey & Kahana 2016, Lewandowsky & Farrell 2011, Lohnas et al. 2015) assume that recalling an item temporarily increases its recall threshold, making subjects less likely to recall that item for a period of time. This suppression effect gradually dissipates, allowing subjects to repeat a previously recalled item following the recall of several other nonrepeated items, as observed in the data. Alternatively, subjects may use a context-similarity mechanism, rather than response suppression, as a means of editing out repetitions. Although this idea has not been rigorously explored, it is analogous to the Lohnas et al. approach to modeling data from the LBL paradigm.

Data on recall transitions reveal a striking forward asymmetry (Figure 4a). In both chaining and dual-store recall models, researchers have employed a scaling factor to boost the strengths of forward associations (Sirotin et al. 2005, Solway et al. 2012). Chunking models naturally predict asymmetric retrieval because retrieval of a chunk is assumed to produce forward serial recall of the items within the chunk (Farrell 2012). According to RCT, the forward bias in contiguity arises because recall of an item retrieves both the context stored during list presentation (which is similar to both the prior- and subsequent-list items) and the preexperimental contextual states associated with the item. Because the preexperimental contextual state associated with an item is added to the context vector at the time of the item’s encoding, that part of the retrieved context is similar to the contextual states associated with subsequent-list items but not prior-list items. Thus, the context retrieved by an item includes a symmetric component (the contextual state associated during list presentation) and an asymmetrical component (the preexperimental contextual states), which combine to produce the forward asymmetry in the contiguity effect.

Perhaps the most widely debated theoretical mechanism in models of memory search is that of a phonological short-term memory buffer. The exact nature of such a buffer varies from model to model, but a common feature of buffer models is that they impose a specific timescale on both the recency and contiguity effects owing to the size of the buffer. These models are thus challenged by data on the persistence of both recency and contiguity across timescales. By contrast, these models can neatly account for experimental dissociations between recency and contiguity measured at different timescales. One can easily imagine a model in which recency and contiguity are partially accounted for by the operation of a phonological buffer. In such a hybrid model, contextual dynamics may produce both recency and contiguity to some extent, but phonologically based rehearsal processes may enhance one or both of these effects.

Another potential ingredient is linguistic organization, or other types of chunking or grouping processes. Subjects report using these strategies, and it would be odd if such strategic activities did not affect retrieval dynamics. Models that do not include these mechanisms provide a fairly comprehensive account of temporal clustering effects, but grouping effects do exist and call for additional mechanisms (Farrell 2012).

Finally, several recent models have advanced the idea that variability in memory encoding is not simply a result of stochastic variation in attention or learning parameters, but rather that the memory system uses prediction to control the learning of new information and the way in which memories are organized into specific events (e.g., Gershman et al. 2012). This research offers great promise in linking models of reinforcement learning and models of episodic memory and, moreover, extends the explanatory scope of memory search models far beyond the confines of laboratory list memory tasks. In particular, these models will allow theorists to make specific predictions about how subjects recall naturally occurring events, such as narratives and films, and we are beginning to see important progress in this regard (Franklin et al. 2019).

The foregoing list is far from complete. Memory search is a highly complex process, and it is likely that a successful model will include additional ingredients beyond those named above. Although it is beyond the scope of this review, neural measures taken during memory search tasks can provide vital evidence to help distinguish among theories as well as to suggest missing theoretical mechanisms. Whereas the analysis of behavior was relegated primarily to the motor output of the organism, and particularly speech, we now have tools for measuring internal mental states and their dynamics. It is likely that joint models of internal memory dynamics and overt behavior will give rise to key advances in our understanding of memory search in the coming years.

Associative chaining:

forming a chain of associations among contiguously presented items

Positional coding:

forming associations between items and their relative position in a temporal or spatial sequence

Memory vector:

an ordered set of numbers representing the features of a memory

Unitization:

parsing of the continuous stream of experience into individual memory vectors

Memory matrix:

an array of numbers in which each column is a memory vector, and the set of columns form a matrix that contains a large set of memories

Multitrace theory:

theory positing that new experiences, including repeated ones, add more columns to an ever-growing memory matrix

Bernoulli random variables:

variables that take the value of one with probability p and zero with probability 1 − p

Theory of Distributed Associative Memory (TODAM):

theory combining elements of Anderson’s (1970) matched filter model with holographic associative storage and retrieval

Probabilistic encoding:

each feature of a memory vector is encoded with probability p, and set to zero with probability 1 − p

Pattern completion:

a memory process wherein a partial or noisy input retrieves a more complete memory trace; also termed deblurring or redintegration

Successive testing paradigm:

two successively administered tests probing memory for the same learning episode; correlations between these tests can vary greatly depending on the nature of the retrieval cues given to subjects

Ranschburg effect:

spaced repetition of an item in a serial list usually leads to impaired recall, with subjects misplacing or omitting the second occurrence of the repeated item

Convolution–correlation models:

an alternative to matrix models; they use convolution and cross-correlation operations for associative storage and retrieval

Protrusion:

incorrect recall of an item studied in position p on a previous list in the same position on the present list

Continual-distractor free recall (CDFR):

a recall task requiring subjects to perform a demanding distractor task between item presentations and prior to recall