Solute Transport Dependence on 3D Geometry of Hydrogel Networks

Abstract

Hydrogels are used in drug delivery applications, chromatography, and tissue engineering to control the rate of solute transport based on solute size and hydrogel-solute affinity. Ongoing modeling efforts to quantify the relationship between hydrogel properties, solute properties, and solute transport contribute toward an increasingly efficient hydrogel design process and provide fundamental insight into the mechanisms relating hydrogel structure and function. However, here we clarify previous conclusions regarding the use of mesh size in hydrogel transport models. We use 3D geometry and hydrogel network visualizations to show that mesh size and junction functionality both contribute to the mesh radius, which determines whether a solute can diffuse within a hydrogel. Using mesh radius instead of mesh size to model solute transport in hydrogels will correct junction functionality-dependent modeling errors, improving hydrogel design predictions and clarifying mechanisms of solute transport in hydrogels.

Graphical Abstract

Frequently used 2D representations of hydrogel polymer networks lead to inaccurate mathematical models of solute transport within hydrogels. Here, 3D representations are introduced and compared with respect to universal structural parameters to define the term, mesh radius (r_m)and to show that two hydrogel formulations with equivalent mesh sizes (ξ) may have differing mesh radii. This fundamental analysis will improve solute transport characterization in hydrogels.

Introduction

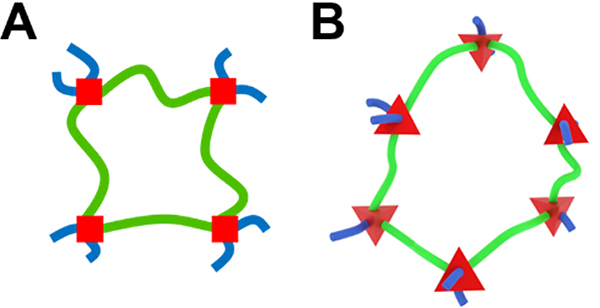
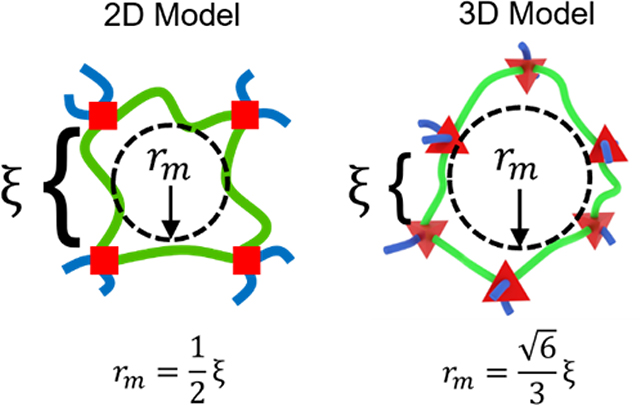
Schematic representations for swollen polymer networks, also known as hydrogels, frequently oversimplify the structure. The most commonly used and symbolic schematic for a swollen polymer network has four polymer chains in an overlapping hash pattern,^[1–4] implying that the network junctions are tetrafunctional and all chains are restricted to a 2D plane. In those representations, the network appears to form a square portal that a solute could pass through if its diameter were less than the length of one network chain between two junctions (Figure 1A). As a result, mesh size (ξ) is treated ambiguously,^[4] simultaneously used to describe the length of a network chain between junctions^{[5, 6]} and the maximum diameter of a solute that can pass through a hydrogel.^{[7, 8]} However, there are two conceptual limitations to this approach.

Figure 1.

Hydrogel mesh portals represented by a 2D model (A) and a 3D model (B). Red squares and tetrahedrons represent junctions. The green chains outline a complete network portal, and the blue chains represent connections to a larger network.

First, many hydrogel formulations do not have tetrafunctional junctions. Of course, it is true that four-arm poly(ethylene glycol) (PEG) macromers reacted with other four-arm PEG macromers form tetrafunctional networks, as do bifunctionally cross-linked hydrogels, such as glutaraldehyde-cross-linked poly(vinyl alcohol) (PVA) or radically polymerized/crosslinked poly(acrylic acid) with a small amount of a crosslinking agent such as bisacrylamide.^{[9, 10]}

Other networks, such as those formed by multi-arm PEGs with three arms or more than four arms, end-linked poly(ethylene glycol) diacrylate (PEGDA), gelatin methacrylamide (GELMA), and dendrimer- or nanoparticle-linked networks break the tetrafunctional junction assumption,^[10–13] resulting in a great variety of network geometries with either controlled, homogeneous junction functionalities (e.g., multi-arm PEGs) or kinetics-based heterogeneity in junction functionalities (e.g., PEGDA).

Second, network chains are not restricted to a 2D plane. Instead, they will favor the most entropically favorable geometries in 3D space. For example, tetrafunctional junctions will approximate a tetrahedron with each chain extending from a face of the polygon (Figure 1B).^[14] While these geometries are not easily represented in 2D space, they have significant implications for the mesh-restricted diffusion of large solutes within hydrogels. Specifically, the influence of mesh size on solute diffusivity must be considered in the context of junction functionality and 3D geometry of network openings.

Here, we used 3D modeling of swollen polymer networks to provide realistic representations of network geometry. We discuss four structural parameters that can be used to control physical properties in all swollen polymer networks and show how distinct network-forming reactions produce equivalent network structures. Finally, we make an argument based on 3D lattice structures for introducing mesh radius, which depends on both mesh size and junction functionality-based geometry, as the primary structural feature of hydrogels affecting large solute diffusivity. We anticipate that this conceptual contribution to hydrogel research will refine quantitative structure-function analysis and mitigate future misunderstandings regarding hydrogel structures.

Universal Structural Parameters

Four parameters collectively define the structure of a stable, single-macromolecule hydrogel. Each parameter can be independently manipulated prior to network synthesis and has a distinct effect on the resulting network structure.^{[10, 15]} The four parameters, represented in Figure 2, are as follows:

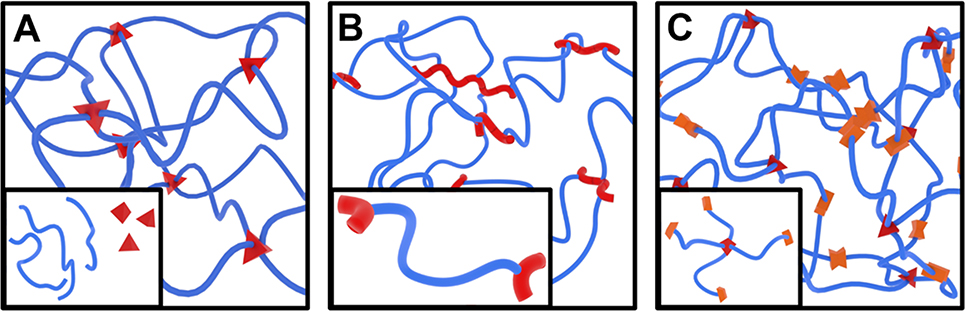
Figure 2.

Comparing the effects of changing network structures. The right half of each group represents an increase in (A) polymer volume fraction, (B) degree of polymerization between junctions, (C) junction functionality (from 4 to 8), or (D) frequency of chain-end defects, highlighted by green chains.

1. The Initial Polymer Volume Fraction (φ₀) describes the initial concentration of polymer in solution before network formation (Figure 2A).

2. The Degree of Polymerization Between Junctions (N_j) describes the number of repeating units in each chain between two junctions (Figure 2B).

3. The Junction Functionality (f) describes the number of chains that converge at each junction in the network (Figure 2C).

4. The Frequency of Chain-End Defects (γ) describes the fraction of chains that do not connect two network junctions (Figure 2D).

As we have recently validated,^[10] the synthesis-controlled initial polymer volume fraction matches the relaxed polymer volume fraction, which can be measured immediately following network formation. Swelling to equilibrium from the relaxed state with an excess of water results in the equilibrium-swollen polymer volume fraction (φ_s), which depends on both the initial polymer volume fraction and the degree of polymerization between junctions. At the limit of low initial polymer volume fraction (the de Gennes overlap threshold, c*; often estimated around 2–5% polymer volume fraction^[14]), there will not be enough overlap between polymer chains to form a network.^{[7, 9]} At excessively high concentrations (dependent on the network’s chemical properties such as hydrophobicity), polymer-polymer interactions will out-scale polymer-solvent interactions, disrupting expected thermodynamic relationships, and the entropic strain upon adding excess water may break chains and create macroscopic cracks in the network.

The degree of polymerization between junctions serves as a structural representation of the often-discussed number average molecular weight between cross-links (${\stackrel{-}{M}}_c$). Description of the length of chains in a network using the degree of polymerization between junctions assumes identical repeating units (so corrections would be needed for copolymer and protein-based networks) and monodisperse or at least a Gaussian distribution of chain lengths within the network.

Networks with low degrees of polymerization between junctions leave the regime in which the polymer chains act as entropic springs, potentially causing strain-induced macroscopic cracks during synthesis or swelling to equilibrium.^[5] On the other side, high degrees increase the chance of polymer-polymer entanglements. Both extremes lead to deviations from predictable thermodynamic behavior. In recent work,^[10] we identified deviations in swelling behavior of PVA hydrogels below a degree of polymerization of N_j=40. No swelling deviation was observed in the lowest degree of polymerization of PEGDA hydrogels tested, N_j=76, but variability greatly increased at the highest degree of N_j=589.^[10]

Treating junction functionality as a universal structural parameter overcomes the assumption of tetrafunctional junctions, but it still assumes that all network junctions have the same functionality. The four-parameter approach also implicitly assumes small, point-like junctions. Larger dendrimer- and nanoparticle-linked networks may significantly deviate from point-like junctions.^{[12, 16]} Radically polymerized junctions, such as those found in PEGDA networks, likely take the shape of a hydrophobic coiled chain that can uncoil under strain, breaking the point-like assumption (which treats all network junctions as infinitely small points), especially at high junction functionalities.^[17–19] Trifunctional junctions are the lower limit to form networks, but it is unclear if an upper limit exists for junction functionality, especially with the use of nanoparticles and dendrimers as network junctions.^{[12, 20]}

Fourth, the frequency of chain-end defects partially describes the imperfection of the network, focusing on chains that are not load-bearing. Using a single term for the frequency of chain-end defects requires that the defects distribute homogeneously within the network, as too many defects clustered in an area could result in a largely inactive section of the network or even a smaller secondary network encapsulated in—but not connected to—the larger network. Secondarily, the mechanically inactive dangling chains could still provide a hindrance to solute diffusion, depending on their length and concentration. The lower limit of the frequency of chain-end defects approaches zero for an ideal network, and the upper limit depends on the concentration of active chains needed to form a complete network.

Based on our work, we conclude that the four-parameter approach does not address low-order loop defects within the network, such as primary loops, multiple links between adjacent junctions, and trapped entanglements. While innovative approaches are being developed to quantify^[21–24] and control^{[14, 25]} low-order loop defects, a generally applicable synthesis-structure correlation for predictably manipulating loop defects comparable to the four universal structural parameters is not yet available. As loop defect control and analysis becomes more precise and generalizable, the four-parameter approach and swollen polymer network models will need to incorporate the effects of loop defects on hydrogel swelling, stiffness, and solute diffusivity.

As we show below, the four universal structural parameters provide a framework for quantitatively describing the structure of a broad variety of hydrogel formulations, enabling precise comparisons of different hydrogel formulations that use the same polymer as well as comparisons across hydrogels made with different polymers. Furthermore, the four-parameter approach quantitatively contributes to the swollen polymer network model, which fundamentally predicts hydrogel swelling behavior and stiffness as well as the solute diffusivity within a hydrogel.^[15] Specifically, all four parameters contribute to the estimation of swollen polymer volume fraction (φ_s; Eq. 1), which is then used alongside two of the structural parameters to estimate the mesh size (ξ; Eq. 2). The four universal structural parameters therefore enable a greater focus on the physical properties of hydrogels and their structural associations.

$${\phi }_s^{-\frac{1}{3}}\left[\ln \left(1-{\phi }_s\right)+{\phi }_s+\chi {\phi }_s^2\right]=-1*\left(1-\frac{2}{f}\right)\left(1-\gamma \right)\frac{V_1{\rho }_d}{M_r{N}_j}{\phi }_0^{\frac{2}{3}}$$ (1)

In Equation 1,χ is the Flory polymer-solvent interaction parameter, V₁ is the molar volume of the solvent, ρ_d is the dry density of the polymer, and M_r is the formula weight of the polymeric repeating unit.

$$\xi ={\phi }_s^{-\frac{1}{3}}{\left[\left(1-\frac{2}{f}\right){\stackrel{-}{l}}^2{C}_{\mathrm{\infty }}\lambda N_j\right]}^{\frac{1}{2}}$$ (2)

In Equation 2, $\stackrel{-}{l}$ is the weighted average of the bond lengths in the backbone of the repeating unit, C_∞ is the Flory characteristic ratio, and λ is the number of linear backbone bonds per repeating unit.

Comparing Network Structures Across Reaction Schemes

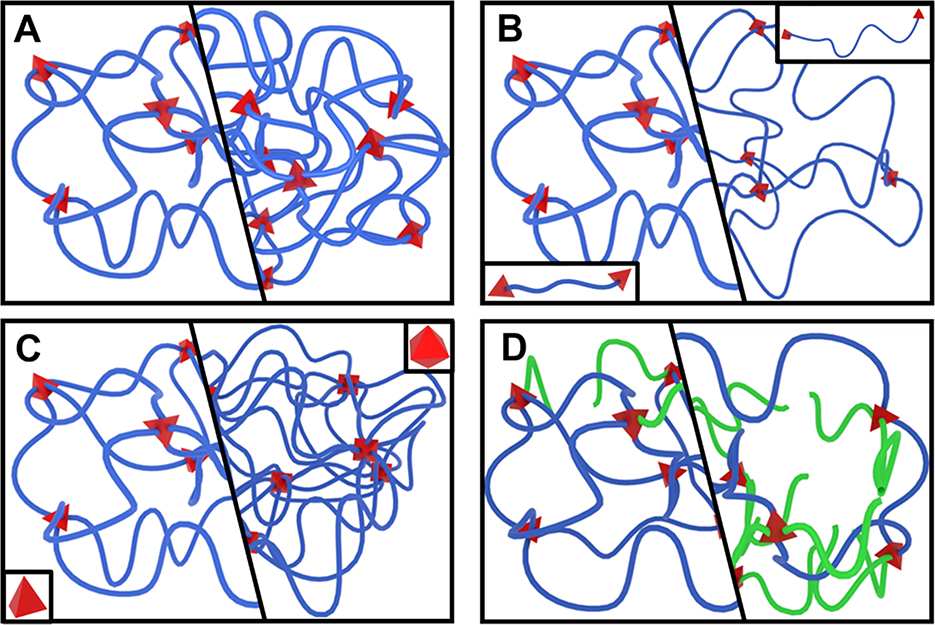
To demonstrate the cross-system utility of the four-parameter approach, we rendered network structures formed by standard cross-links (Figure 3A), end-links (Figure 3B), and mid-links (Figure 3C). In reference to real networks, these reaction schemes correspond to PVA, PEGDA, and multi-arm PEG hydrogels, respectively. For each network, the red components represent the junctions. For the cross-linked and mid-linked networks, the junctions have clearly defined and consistent junction functionalities, but the junction functionalities of the end-linked network vary from only one chain (a chain-end defect) up to many chains. For such networks, junction functionalities above 100 are viable,^[26] but the representative model was limited to functionalities of six for visual clarity. For the mid-linked network, the reaction points are highlighted with paired orange prisms. In this network, chain-end can be identified by unreacted chains terminating with one face of the orange mid-linking structure.

Figure 3.

Hydrogel network structures with tetrafunctional cross-links (A), radically polymerized end-links (B), and bifunctional (orange) mid-links (C) that represent the network formation schemes of PVA, PEGDA, and multi-arm PEG hydrogels, respectively. Insets represent associated network precursor molecules.

All three types of networks can be described quantitatively using the four hydrogel structure parameters shown in Figure 2. As a result, it is possible for the four structural parameters to be equivalent in two hydrogels with different polymers or different network formation reactions. Careful design and characterization of such structurally equivalent hydrogels will enable researchers to isolate the chemical influences of each polymer and network formation reaction on network properties.

Mesh Radius and Solute Diffusion in a Network

To explain the importance of junction functionality in solute transport through hydrogels, the use of mesh size to describe both the distance between adjacent connected junctions and the effective diameter of a mesh portal must be clarified. Here, we use mesh size to describe the distance between junctions. Average mesh sizes can be calculated from the equilibrium-swollen polymer volume fraction and the molecular weight between cross-links, as described by Canal and Peppas,^[6] with recent modifications to address phantom-like swelling deformation, variable junction functionality, and non-vinyl polymers (Eq. 2).^[15] We hereby suggest that the second definition of mesh size, the maximum size of a spherical solute that can pass through a mesh portal, should be converted to a new and distinct term, the mesh radius (r_m). We explain below how the mesh radius depends on both the mesh size and the junction functionality-dependent 3D geometry of the network.

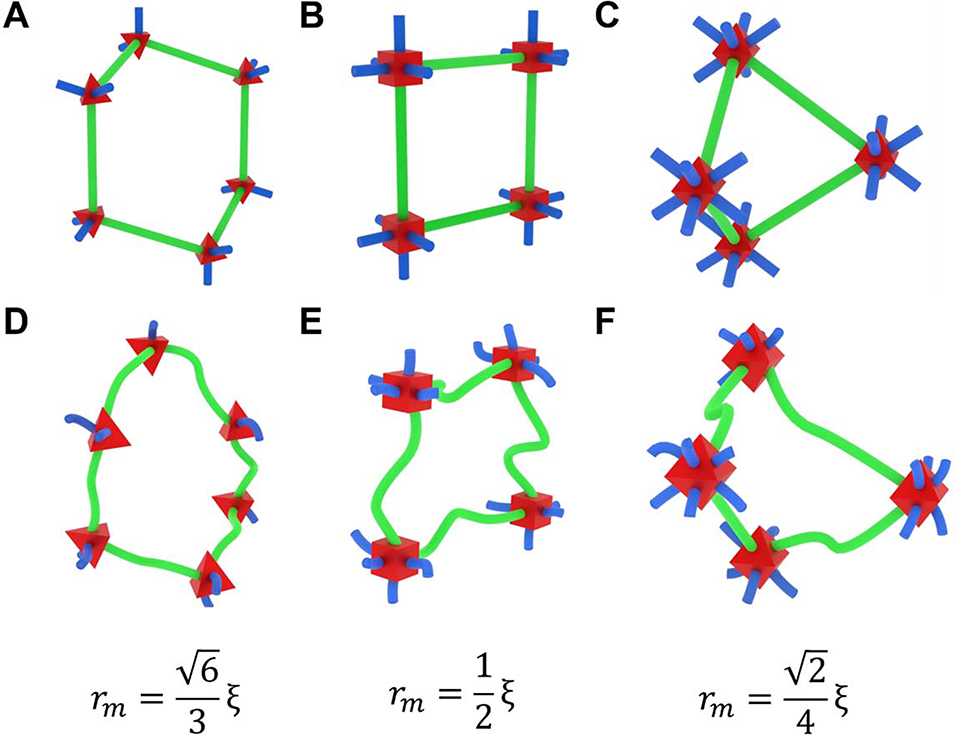
Three-dimensional network geometry and the dynamic, highly flexible nature of polymer chains confound analysis of solute diffusion in hydrogels, even when neglecting solute-polymer interactions. To reduce the complexity associated with chain dynamics, we used a crystal-like 3D lattice structure approach to estimate the relationship between a network’s mesh size and the size of a solute that can pass through the network. Specifically, we treated the chains as straight rods with a specific length (i.e., the mesh size) connected by junctions that optimally distribute the rods in 3D space based on the faces of a regular tetrahedron (f = 4), cube (f = 6), and octahedron (f = 8) (Figure 4A–C). From these crystal-like structures, we identified the plane that would create the largest mesh portal area for solutes to pass through and calculated the radius of a circle inscribed in that area.

Figure 4.

The effect of junction functionality on mesh radii using lattice-like (A-C) and realistic (D-F) chains with tetrafunctional (A, D), hexafunctional (B, E), and octafunctional (C, F) junctions. Mesh portals are highlighted with green chains. The estimated relationship between mesh size ($\xi$) and mesh radius ($r_m$) is provided for each junction functionality.

The tetrafunctional network formed a hexagonal portal (similar to a carbon ring chain conformation), the hexafunctional networks formed a square portal, and the octafunctional network formed a square-diamond portal. The in-plane mesh size (${\xi }_f^{\text{'}}$) was reduced compared to the actual mesh size for the tetrafunctional and octafunctional lattices, with ${\xi }_4^{\text{'}}=\frac{2\sqrt{2}}{3}\xi \approx 0.94\xi$ and ${\xi }_8^{\text{'}}=\frac{\sqrt{2}}{2}\xi \approx 0.71\xi$, respectively. Unlike the hexafunctional network portal, the tetrafunctional and octafunctional network portals have plane-normalized depths (denoted by ${\xi }^{”}$) of ${\xi }_4^{”}=\frac{1}{3}\xi \approx 0.33\xi$ and ${\xi }_8^{”}=\frac{\sqrt{2}}{2}\xi \approx 0.71\xi$. Resulting from the portal geometry and the in-plane mesh size reductions, the inscribed circle radii were $r_{m,4}=\frac{\sqrt{6}}{3}\xi \approx 0.82\xi$ for the tetrafunctional network, $r_{m,6}=\frac{1}{2}\xi =0.5\xi$ for the hexafunctional network, and $r_{m,8}=\frac{\sqrt{2}}{4}\xi \approx 0.35\xi$ for the octafunctional network. Further explanation of the geometric calculation process is provided in the supplementary materials. From these mesh size-normalized radii comparisons in lattice structures, it is evident that mesh size alone is insufficient when describing the size of a solute that can pass through a hydrogel network.

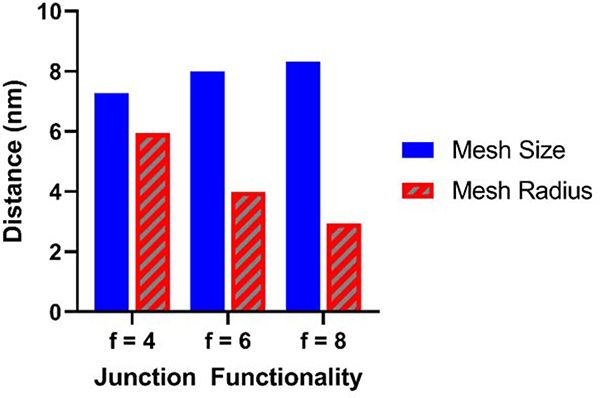
As junction functionality increases, the geometry of the network structure becomes more restrictive to solute transport, marked by the decreasing portal radius with respect to the mesh size. Indeed, the non-equivalence of mesh size and the size of solutes that can pass through a hydrogel corroborates prior evidence that solutes with larger diameters than the structurally estimated mesh size can pass through a network.^[27–31] Therefore, we recommend that quantitative models relating the diffusion coefficient of solutes within a network to mesh size, such as the multiscale diffusion model^[32] replace the mesh size term with the “mesh radius” as calculated above, incorporating the effect of both mesh size and junction functionality. This replacement mathematically changes the influence of junction functionality hydrogel solute transport models. As shown in Figure 5, multi-arm PEG hydrogels with identical initial polymer volume fractions, degrees of polymerization between junctions, and frequencies of chain-end defects but with junction functionalities increasing from four to eight are expected to slightly increase in mesh size but steeply drop in mesh radius, (calculations and additional parameter values provided in the supplementary materials) suggesting that increasing junction functionality would decrease solute diffusivity by creating more restrictive portal geometries.

Figure 5.

Mesh size and mesh radius predictions as a function of junction functionality for multi-arm PEG hydrogels with ${\phi }_0$ = 0.10, $N_j$ = 60, $\gamma$ = 0 based on Equations 1 & 2 (for $N_j=60,{\stackrel{-}{M}}_c\approx 2600g/mol$).

Notably, defining the optimally distributed crystal lattice structure and subsequent identification of the appropriate portal plane is non-trivial for junction functionalities other than 4, 6, and 8,^[33] but it is reasonable to assume that the mesh radius will decrease monotonically and asymptotically toward zero with increasing junction functionality as angles between adjacent chains decrease.

Despite the usefulness of the crystal lattice representation, it remains critical when modeling solute diffusion within hydrogel networks to recognize that almost all real hydrogel networks are imperfect, inhomogeneous, and dynamically fluctuating, meaning that the rods in the lattice model represent actively fluctuating and possibly incomplete chains.^[25] The lattices act as idealized references for the amorphous structure of the real networks with the same junction functionalities (Figure 4D–F). As a result, even the introduction of a well-defined mesh radius does not preclude a solute with a larger radius moving throughout the network. Similarly, a smaller solute could be blocked from transport by an unusually small portal or a polymer chain that has momentarily coiled into its path. However, accurately accounting for such nonstandard events first requires a realistic understanding of how both mesh size and junction functionality affect solute transport in hydrogel networks, described here for the first time.

Conclusions

Two-dimensional schematics of hydrogel networks have oversimplified structural considerations in hydrogel physical properties. Here, we presented 3D models of hydrogel networks to illustrate how four controllable parameters represent most hydrogel structures, independent of the reaction scheme used to form the network. We showed how assuming tetrafunctional junctions and ignoring 3D geometry led to misuse of mesh size in quantitative models that estimate solute diffusion within hydrogels. We anticipate that further consideration of real 3D geometry in hydrogel interactions will lead to more insight regarding physical properties of hydrogels. For example, the shape and orientation of solutes within the network should be studied and incorporated into predictive models, especially since many proteins used in biomaterial hydrogel applications are non-spherical. Development of precise modeling and model-driven experiments to broadly characterize structure-function relationships in hydrogels will lead to the systematic design of more advanced and nuanced biomaterials that will expand the possibilities for biosensors, human-machine interfaces, drug delivery devices, and tissue engineering scaffolds.

Experimental Note and Data Availability

No experiments were performed for this study. Figures 1–4 were developed using the free 3D modeling software Blender (blender.org) (Version 2.80). and the associated Blender modeling files are available online: https://doi.org/10.6084/m9.figshare.14700159.v1

Biography