Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jul 22;125(30):8325–8330. doi: 10.1021/acs.jpcb.1c01818

Dependence of Work on the Pulling Speed in Mechanical Ligand Unbinding

Hong An Pham †, Duc Toan Truong †, Mai Suan Li ‡,*
PMCID: PMC8389893  PMID: 34292743

Abstract

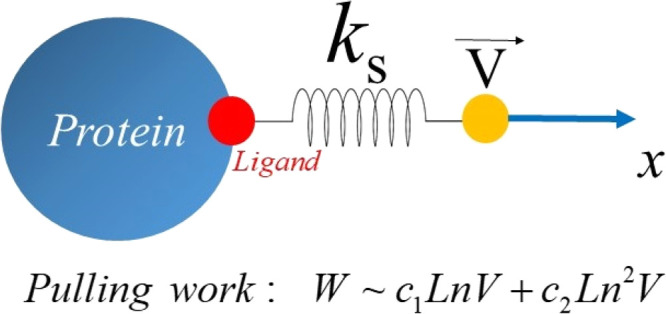
graphic file with name jp1c01818_0005.jpg

In single-molecule force spectroscopy, the rupture force Fmax required for mechanical unfolding of a biomolecule or for pulling a ligand out of a binding site depends on the pulling speed V and, in the linear Bell–Evans regime, Fmax ∼ ln(V). Recently, it has been found that non-equilibrium work W is better than Fmax in describing relative ligand binding affinity, but the dependence of W on V remains unknown. In this paper, we developed an analytical theory showing that in the linear regime, W ∼ c1 ln(V) + c2 ln2(V), where c1 and c2 are constants. This quadratic dependence was also confirmed by all-atom steered molecular dynamics simulations of protein–ligand complexes. Although our theory was developed for ligand unbinding, it is also applicable to other processes, such as mechanical unfolding of proteins and other biomolecules, due to its universality.

In recent decades, single-molecule force spectroscopy (AFM, laser optical tweezers, and magnetic tweezers) has been widely used to understand biomolecular processes such as protein, RNA, and DNA unfolding, ligand unbinding, and so forth. In experiments, where the external force is ramped up at a constant speed V, the force–displacement/time profile contains the maximum or rupture force Fmax that can be used to characterize mechanical stability of the biomolecule or binding affinity of the ligand.

The question of the dependence of the rupture force on the puling speed attracts the attention of many researchers because such a dependence can be used to extract the parameters characterizing the free energy landscape. In the linear or Bell–Evans regime,1,2 where V is small enough and it is assumed that the transition state is not shifted under an external force, Evans and Ritchie showed that2Fmax ∼ ln(V), and this dependence has been confirmed by numerous experimental and simulation works (see ref (3) and references therein). To go beyond the linear regime, different scenarios of the dependence of the rupture force on the pulling speed were proposed.4,5

From a computational point of view, the steered molecular dynamics (SMD)6−8 can be used to mimic the results obtained by using single-molecule force spectroscopy. In particular, several groups have shown9−14 that this method is effective in predicting the relative binding affinity of small ligands to proteins based on the fact that the greater the rupture force, the higher the binding affinity. SMD can provide results as accurate as other standard methods for estimation of the binding free energy like MM-PBSA but computationally much faster11 as it deals with a non-equilibrium process related with fast pulling. Therefore, the use of this method is becoming more and more popular in computer-aided drug design.9,11,13,15

It was shown16 that non-equilibrium work, defined as

graphic file with name jp1c01818_m001.jpg 1

where r is the ligand displacement, has a better correlation with the experiment on binding affinity than the rupture force because W is defined for the entire process, while Fmax is calculated in only one state. This result indicates that W can be used as a good score for the ligand binding affinity. Despite this important fact, the dependence of the non-equilibrium work on pulling speed has not been obtained. Moreover, knowledge of this dependence should be useful for a deeper understanding of the free energy landscape of biomolecular systems, especially ligand–receptor complexes. The dependence of the average dissipated work on the displacement in the DNA hairpin pulling experiment was obtained numerically, but the analytical formula was missing.17 This prompted us to develop a theory by exactly solving a one-dimensional problem, which shows that at sufficiently low pulling speeds, the dependence of W on V is determined using the quadratic function of ln(V). We also performed all-atom simulations of protein–ligand complexes in explicit water, which confirmed our theory.

One-Dimensional Model with Harmonic Potential

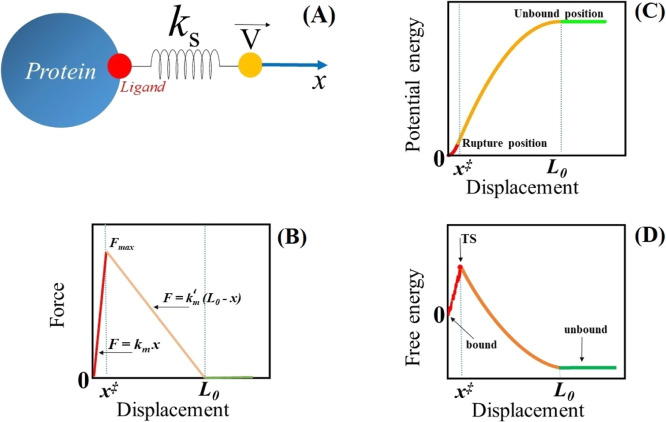
Following Hummer and Szabo,18 we consider a one-dimensional motion of a ligand interacting with the receptor through potential V0(x). In order to mimic the single-molecule force experiment, an external force is applied to a dummy atom which is connected with the ligand using a spring with a spring constant ks (Figure 1A). Assuming that the external force is increased at a constant speed V, the motion of ligand in the viscous environment is described by the following equation

graphic file with name jp1c01818_m002.jpg 2

here x ≡ x(t) is the time-dependent displacement, γ̅ is the Stokes friction coefficient, and ξ(t) is a Gaussian random force with ⟨ξ(t)⟩ = 0 and ⟨ξ(t)ξ(t′)⟩ = 2γ̅kBTδ(t – t′).

Figure 1.

Figure 1

Open in a new tab

(A) Schematic description of the SMD method and single-molecule experiment. (B) Force–displacement profile: F = kmx, k′m(L0 – x), and 0 for x ≤ x‡, x‡ < x ≤ L0, and x > L0, respectively. (C) Dependence of potential energy V0(x) given using eq 3 on position. For simplicity, the constant in eq 3 is set to 0. (D) Conceptual graph of free energy vs x. The TS, which appears at x‡, separates the bound state from the unbound one.

To choose an analytical expression for potential V0(x), we analyze a typical force–extension profile, obtained for a ligand pulled from the binding site of the protein by using all-atom SMD simulations in explicit water (Figure S1A in the Supporting Information). The ligand motion can be divided into three regimes: x ≤ x‡, x‡ < x ≤ L0, and x > L0, where x‡ corresponds to the position of the rupture force Fmax and it is the distance from the bound sate and transition state (TS).18,19 Note that x‡ corresponds to the TS because, as was clearly shown in our previous work,19 this is the maximum of the binding free energy (see also Figure S1B) obtained by using the Jarzynski’s identity.20,21 For x ≤ x‡ and x‡ < x ≤ L0, the dependence of the force experienced by the ligand on the displacement can be approximated using a linear function (Figure S1A), that is, F = kmx and F = k′m(L0 – x), respectively (Figure 1B), where km and k′m are spring constants. Above L0, the force and the receptor–ligand interaction disappear. Thus, V0(x) can be approximated using a harmonic potential as follows

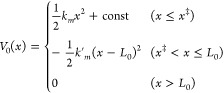graphic file with name jp1c01818_m003.jpg 3

The constant in eq 3 can be obtained from the condition that the potential must be continuous at the rupture point x‡. In general, the spring constants km and k′m differ from ks of the cantilever.18V0(x) given by eq 3 correctly describes the fact that in the first regime (x ≤ x‡), the force experienced by the ligand increases and then it decreases in the second regime (x‡ < x ≤ L0) before vanishing at x > L0 (Figure 1C). In addition, the dependence of V0(x) on x (Figure 1C) is similar to that obtained from the SMD simulations (Figure S1C), which implies that our choice of potential energy is reasonable as it is supported by all-atom simulations. Based on the SMD results (Figure S1B), we can schematically describe free energy as a function of displacement (Figure 1D), which shows that ligand binding/unbinding is a barrier-crossing process. Bound and unbound states are separated by the TS, which occurs at the rupture position x‡. Our free energy profile differs, for example, from Hummer and Szabo,18 who were interested in the behavior of the rupture force without caring about the second regime x‡ < x ≤ L0. By contrast, we must take this regime into account because it contributes to the work. As in the protein folding problem, x‡ depends on the external force, but in this work, we assume it to be constant, which means that we adopt the Bell–Evans approximation.

Equation 2 with the harmonic potential (eq 3) was solved exactly, and then, using eq 1, we can obtain W. Because in the third region (x > L0), the work is zero, W = W1 + W2, where W1 and W2 correspond to the first and second intervals, respectively.

Work in the First Region x ≤ x‡

In this region, the ligand is located in the binding site and the viscosity term in eq 2 is neglected as it is much smaller than the ligand–protein interaction term.18 Then, eq 2 is replaced by eq S1 in the Supporting Information with initial conditions x(0) = 0 and ẋ(0) = v0. This equation can be written as eq S2 using the Fourier transformations (eqs S3–S5) and has the exact solution for x(ω) (eq S6) and velocity v(ω) (eq S7).

The work in the first region, W1, was calculated using the definition given by eq 1 (see also eq S8 in the Supporting Information) and the expression for F (eq S9). After several steps (eqs S10 and S11), we obtained the work which depends on the random force (eq S12). Averaging over the random force (eqs S13–S14) and using rupture time tmax ≈ Fmax/ksV, we obtained W1 (eq S15) for one MD trajectory with a given Fmax.

Work in the Second Region x‡ ≤ x ≤ L0

In this region, we have to keep the viscosity term and solve full eq 2. Similar to the first case, the motion equation was exactly solved (eqs S16–S19). Details of derivation of the work in the second region, W2, are described in the Supporting Information (eqs S20–S22). After averaging over the random force, we obtained the expression for W2 (eq S24).

Dependence of the Average Total Work on the Pulling Speed

Using eqs S15 and S24, we obtain the total work

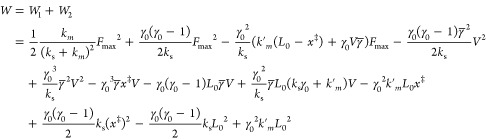graphic file with name jp1c01818_m004.jpg 4

where γ0 = ks/ks – k′m.

In order to obtain the experimentally measurable work, we have to average W over the distribution of Fmax, <W> = ∫P(Fmax)W(Fmax) dFmax, where in the Bell–Evans approximation, the distribution of the rupture force is given by the following expression18

graphic file with name jp1c01818_m005.jpg 5

where k0 is the intrinsic rate constant. Using the distribution given by eq 5, one can exactly calculate ⟨Fmax⟩ and ⟨Fmax2⟩18

graphic file with name jp1c01818_m006.jpg 6a
graphic file with name jp1c01818_m007.jpg 6b

with Euler constant γ = 0.577. Equation 6a describes the well-known dependence Fmax ∼ ln V2, which has been widely used in interpretation of results obtained by single-molecule force spectroscopy for protein unfolding under an external force.22,23 This relationship is also valid for the ligand unbinding from the receptor at low loading rates.3

Using eq 6a to calculate the average work eq 4 ,we obtain

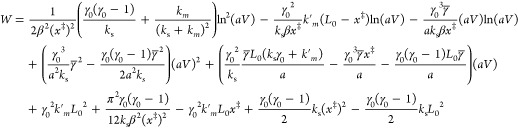graphic file with name jp1c01818_m008.jpg 7

where aV is the dimensionless speed with a = βksx‡/k0eγ.

In the Jarzynski identity exp(−ΔF/kBT) = <exp(−W/kBT)>,20 we must calculate the exponential average of work over all possible trajectories connecting the states A and B. The free energy difference ΔF = FB – FA, which is obtained in equilibrium, does not depend on the pulling speed, and the exponential average of work is also independent of V, despite the fact that work distribution depends on the pulling speed. This can be explained by the fact that trajectories with small W (rare events) make the largest contribution to the exponential average. Because the process with small W is very close to equilibrium, <exp(−W/kBT)> does not depend on the pulling speed. In our case, we calculated the linear average of work, <W>, where the contribution from trajectories with large W (far from equilibrium) is important, and therefore, the result depends on the pulling speed.

To estimate the contribution of each term in eq 7, we rewrite the mechanical work as follows

graphic file with name jp1c01818_m009.jpg 8

where a1, ..., and a6, which have a unit of energy, are shown in the Supporting Information (eq S25). To estimate these coefficients, we took the typical value of the spring constant of the cantilever in the AFM experiment ∼1 N m–1,24 the friction coefficient γ̅ ∼ 10–14 kg s–1,25 and rate constant k0 ≈ 107 s–1.26 The rupture position and rupture force depend on the system and pulling speed (see Figure S1B and ref (19)), but we can set x‡ ≈ 10–10 m and Fmax ≈ 1000 pN. Then, the spring constant km ≈ Fmax/x‡ ≈ 1000 pN/(10–10 m) ≈ 10 Nm–1. The spring constant k′m can be obtained from the condition that the first derivative of V0(x) with respect to x should be continuous at x‡, which implies that kmx‡ = k′m(L0 – x‡). Using L0 ≈ 2 nm (Figure S1A) and the values of km and x‡ given here, we obtain k′m ≈ 0.5 Nm–1. For clarity, all parameters which will be used for estimation of a1 – a6 are shown in eq S26 in the Supporting Information. Using eq S25 and these parameters, we obtained a1 ∼ 10–21, a2 ∼ 10–21, a3 ∼ 10–27, a4 ∼ 10–34, a5 ∼ 10–25, and a6 ∼ 10–18 J (Table S1). We tested a few different sets of parameters, but the results did not change qualitatively.

It can be shown that for low pulling speeds V < 102 nm/ns, the third, fourth, and fifth terms in eq 8 can be neglected, resulting in the following expression of the average work

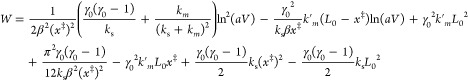graphic file with name jp1c01818_m010.jpg 9

Because the experiment is conducted at low V ∼ nm/s, this dependence must be valid for its interpretation. Thus, in the Bell–Evans approximation, contrary to the rupture force case, the dependence of work on the pulling speed contains not only the ln(V) term but also the quadratic term ln2(V). At high pulling speeds V > 102 nm/ns, the terms ∼V and V2 in eq 8 prevail over logarithmic terms, but this area is not interesting from an experimental point of view.

SMD Simulations

To support our analytical theory (eq 9), we performed all-atom SMD simulations with explicit water for two protein–ligand complexes: the SBX small compound bound with the FKBP12 protein (PDB ID: 1FKH) and ZB6 carboxylic acid, a small compound, in complex with the AmpC beta-lactamase protein(PDB ID: 4KZ6) (Figure S2). The FKBP12 protein, consisting of 107 amino acids,27 is a cytosolic protein that is abundantly expressed in all tissues. It binds to FK506 and rapamycin, mediating the immunosuppressive action of drugs.28 Beta-lactamase,29 a well-known enzyme produced by bacteria,30 is responsible for bacterial resistance to many beta-lactam antibiotics. For clarity, the two protein–ligand complexes will hereinafter be referred as 1FKH and 4KZ6 after their PDB code.

We used the CHARMM27 force field 3331 and the TIP3P32 water model for molecular modeling. SMD simulations were carried out for a pulling speed V in the range 0.025–54 nm/ns, where eq 9 is applicable. Simulations below this range are beyond our computational capabilities. The number of trajectories was from 10 to 200 depending on the system and V (Table S2 in the Supporting Information). To mimic the AFM experiment, we chose the typical spring constant ks = 600 kJ/(mol nm2) of the spring that connects the center of mass of the ligand to the dummy atom. To prevent the receptor from drifting under the influence of an external force, its Cα-atoms were restrained but the side chains were allowed to fluctuate. The details on SMD simulations are given in Supporting Information. The results obtained for Fmax and W of two complexes with various pulling speeds are shown in Table S3.

At low pulling speeds, the rupture force is linear with ln(V) (Figure 2) for both systems, but for 1FKH (the first nine points), the linear theory works over a wider range than 4KZ6 (the first seven points). The correlation level of the fit is high with R = 0.98 and 0.96 for 1FPK and 4KZ6, respectively. Dudko–Hummer–Szabo nonlinear theory with ν = 1/2 and 2/34 is applicable to the entire region (Figure 2).

Figure 2.

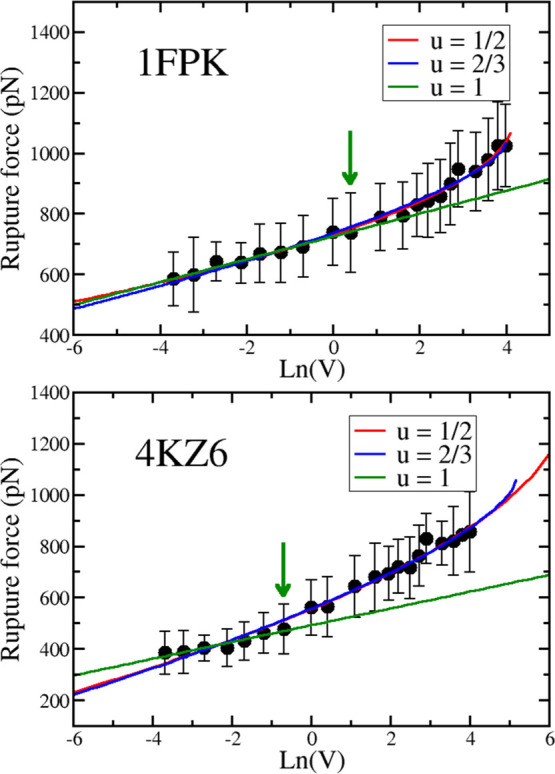
Figure 2

Open in a new tab

Dependence of the rupture force Fmax on the logarithm of the pulling speed for complexes 1FKH (top) and 4KZ6 (bottom). The blue line is a linear fit for the first nine data points of 1FPK (R = 0.983) and the first seven points of 4KZ6 (R = 0.955). The correlation level R is shown in parentheses. The arrow indicates the point below which the Bell–Evans theory applies. The red and green curves are nonlinear fits using Dudko–Hummer–Szabo theory with ν = 1/2 and 2/3 for the whole data set (ν = 1 corresponds to Bell–Evans theory). For 1FPK, R = 0.994 and 0.992 for ν = 1/2 and 2/3, respectively, and for 4KZ6, R = 0.991 for both values of ν.

Because our theory was developed in the Bell–Evans approximation, we first applied the quadratic fit (eq 9) to the region where the rupture force linearly depends on ln(V), confining ourselves to the data points on the left side of the arrow in Figure 3. This fit (green curve) works perfectly for 1FPK (R = 0.996) and 4KZ6 (R = 0.997), which fully supports our theory. The blue curve in Figure 3 is a quadratic fit for the entire data set. Because the fit is good with R = 0.983 and 0.988 for 1FPK and 4KZ6, respectively, within error bars, our theory works for a wider range than linear. This may be due to the fact that compared with the Bell–Evans theory, we have one more fitting parameter associated with the term ln2(V). Additional protein–ligand complexes should be studied to clarify this issue.

Figure 3.

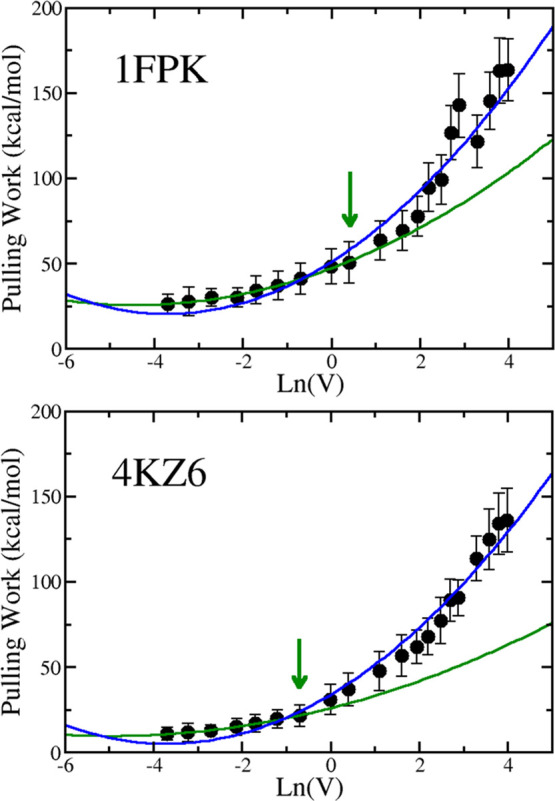
Figure 3

Open in a new tab

Dependence of W on ln(V) for 1FKH (top) and 4KZ6 (bottom).The arrow refers to the point below which the rupture Fmax is linear with ln(V). The green curve is a quadratic fit for the first nine data points of 1FPK (R = 0.996) and the first 7 points of 4KZ6 (R = 0.997), which is the area where Bell–Evans theory is valid. The correlation level is indicated in parentheses. The blue curve is also the quadratic fit but for the entire data set with R = 0.983 and 0.988 for 4FPK and 4KZ6, respectively.

Conclusions

We developed a theory for the dependence of the mechanical work performed by the ligand during the escape from the receptor binding site on the pulling speed. Our exactly solvable one-dimensional model was based on the results obtained using all-atom MD simulations with explicit water. Assuming that the position of the transition state does not depend on the external force and that the receptor–ligand interaction can be described using a harmonic potential, we obtained the exact expression of W as a quadratic function of ln(V) at low enough pulling speeds. It would be interesting to confirm our theory experimentally. Although our theory was developed for ligand unbinding, it should be applied to the mechanical unfolding of proteins, RNA, and DNA and, presumably, to other more complex processes in cells.33 In general, the quadratic dependence (eq 9) works for the case when the force–extension profile is similar to the one shown in Figure 1B, that is, unbinding/unfolding occurs without intermediates.

Agmon and Hopfield34 developed a two-dimensional model of CO binding to heme proteins, in which the conceptual protein coordinate is included in addition to the CO-iron distance. This model can be used35 to understand recent experiments on enzyme-catalyzed reduction of disulfide bonds in proteins using the mechanical force applied to the ends of the protein.36 Thus, it would be interesting to extend our theory to the case where the ligand binding reaction coordinate is coupled to the protein coordinate that is responsible for the disulfide bond cleavage.35 This problem is challenging due to the biphasic force dependence of the bond breaking rate.

Single-molecule force spectroscopy is an effective tool for studying the breaking and formation of non-covalent protein–protein bonds, which are critical for the functions of cell adhesion complexes. It is generally believed that the external force reduces the free energy barrier to break the bond and thus shortens the bond lifetime.2 In contrast, Dembo et al.(37,38) hypothesized that force can also increase the bond lifetime by transforming the adhesive complexes into a bound state.

These two different ways of responding to external force, known as slip and grip tricks.37,38 By developing a phenomenological theory, Barsegov and Thirumalai showed39 that the dependence of the rupture force on ln(V) is linear in the slip regime, while it becomes more complicated (almost linear but with two different slopes) in the catch bond regime. Because our theory was developed for the case when Fmax ∼ ln(V), it is applicable to the slip mode. Extension to the case, where catch–slip transition occurs, requires further investigation. Then, instead of one bound state in the energy landscape, one has to deal with two bound states or two pathways.39

In general, extension of our theory beyond the Bell–Evans approximation is of great interest. Work in this direction is in progress.

Acknowledgments

This work was supported by Narodowe Centrum Nauki in Poland (Grant 2019/35/B/ST4/02086), the Department of Science and Technology at Ho Chi Minh City (Grant 07/2019/HD̵-KHCNTT), the TASK Supercomputer Center in Gdansk, PLGrid Infrastructure, Poland, and the ICST Computer Center, Ho Chi Minh City, Vietnam.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.1c01818.

  • Typical force–displacement profiles, binding free energy and potential energy obtained by using all-atom SMD simulations at a pulling speed V = 5 nm/ns; derivation of the analytical expression for the pulling work; SMD simulations of 1FPK and 4KZ6 in complex with different ligands; number of trajectories used for various pulling speeds; and average rupture force and pulling work obtained by using SMD simulations for systems 1FPK and 4KZ6 (PDF)

Author Contributions

MSL designed the research. HAP and DTT conducted the experiment. HAP, DTT, and MSL analyzed the results. All authors wrote and reviewed the article.

The authors declare no competing financial interest.

Supplementary Material

jp1c01818_si_001.pdf (820.7KB, pdf)

References

  1. Bell G. Models for the specific adhesion of cells to cells. Science 1978, 200, 618–627. 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
  2. Evans E.; Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys. J. 1997, 72, 1541–1555. 10.1016/s0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Rico F.; Russek A.; González L.; Grubmüller H.; Scheuring S. Heterogeneous and rate-dependent streptavidin–biotin unbinding revealed by high-speed force spectroscopy and atomistic simulations. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 6594–6601. 10.1073/pnas.1816909116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Dudko O.; Hummer G.; Szabo A. Intrinsic rates and activation free energies from single-molecule pulling experiments. Phys. Rev. Lett. 2006, 96, 108101–108104. 10.1103/physrevlett.96.108101. [DOI] [PubMed] [Google Scholar]
  5. Friddle R. W.; Noy A.; De Yoreo J. J. Interpreting the widespread nonlinear force spectra of intermolecular bonds. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 13573–13578. 10.1073/pnas.1202946109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Grubmüller H.; Heymann B.; Tavan P. Ligand binding: molecular mechanics calculation of the streptavidin-biotin rupture force. Science 1996, 271, 997–999. 10.1126/science.271.5251.997. [DOI] [PubMed] [Google Scholar]
  7. Izrailev S.; Stepaniants S.; Balsera M.; Oono Y.; Schulten K. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 1997, 72, 1568–1581. 10.1016/s0006-3495(97)78804-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Isralewitz B.; Izrailev S.; Schulten K. Binding pathway of retinal to bacterio-opsin: a prediction by molecular dynamics simulations. Biophys. J. 1997, 73, 2972–2979. 10.1016/s0006-3495(97)78326-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Colizzi F.; Perozzo R.; Scapozza L.; Recanatini M.; Cavalli A. Single-molecule pulling simulations can discern active from inactive enzyme inhibitors. J. Am. Chem. Soc. 2010, 132, 7361–7371. 10.1021/ja100259r. [DOI] [PubMed] [Google Scholar]
  10. Mai B. K.; Viet M. H.; Li M. S. Top leads for swine influenza A/H1N1 virus revealed by steered molecular dynamics approach. J. Chem. Inf. Model. 2010, 50, 2236–2247. 10.1021/ci100346s. [DOI] [PubMed] [Google Scholar]
  11. Suan Li M.; Khanh Mai B. Steered molecular dynamics-a promising tool for drug design. Curr. Bioinf. 2012, 7, 342–351. 10.2174/157489312803901009. [DOI] [Google Scholar]
  12. Villarreal O. D.; Yu L.; Rodriguez R. A.; Chen L. Y. Computing the binding affinity of a ligand buried deep inside a protein with the hybrid steered molecular dynamics. Biochem. Biophys. Res. Commun. 2017, 483, 203–208. 10.1016/j.bbrc.2016.12.165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Chen L. Y. Hybrid Steered Molecular Dynamics Approach to Computing Absolute Binding Free Energy of Ligand-Protein Complexes: A Brute Force Approach That Is Fast and Accurate. J. Chem. Theory Comput. 2015, 11, 1928–1938. 10.1021/ct501162f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ytreberg F. M. Absolute FKBP binding affinities obtained via nonequilibrium unbinding simulations. J Chem Phys 2009, 130, 164906. 10.1063/1.3119261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ho K.; Truong D. T.; Li M. S. How Good is Jarzynski’s Equality for Computer-Aided Drug Design?. J. Phys. Chem. B 2020, 124, 5338–5349. 10.1021/acs.jpcb.0c02009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Vuong Q. V.; Nguyen T. T.; Li M. S. A new method for navigating optimal direction for pulling ligand from binding pocket: application to ranking binding affinity by steered molecular dynamics.. J. Chem. Inf. Model. 2015, 55, 2731–2738. 10.1021/acs.jcim.5b00386. [DOI] [PubMed] [Google Scholar]
  17. Monge A. M.; Manosas M.; Ritort F. Experimental test of ensemble inequivalence and the fluctuation theorem in the force ensemble in DNA pulling experiments. Phys. Rev. E 2018, 98, 032146. 10.1103/physreve.98.032146. [DOI] [Google Scholar]
  18. Hummer G.; Szabo A. Kinetics from nonequilibrium single-molecule pulling experiments. Biophys. J. 2003, 85, 5–15. 10.1016/s0006-3495(03)74449-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Truong D. T.; Li M. S. Probing the Binding Affinity by Jarzynski’s Nonequilibrium Binding Free Energy and Rupture Time. J. Phys. Chem. B 2018, 122, 4693–4699. 10.1021/acs.jpcb.8b02137. [DOI] [PubMed] [Google Scholar]
  20. Jarzynski C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. 10.1103/physrevlett.78.2690. [DOI] [Google Scholar]
  21. Hummer G.; Szabo A. Free energy reconstruction from nonequilibrium single-molecule pulling experiments. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 3658–3661. 10.1073/pnas.071034098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Williams P. M.; Fowler S. B.; Best R. B.; Luis Toca-Herrera J.; Scott K. A.; Steward A.; Clarke J. Hidden complexity in the mechanical properties of titin. Nature 2003, 422, 446–449. 10.1038/nature01517. [DOI] [PubMed] [Google Scholar]
  23. Kumar S.; Li M. S. Biomolecules under mechanical force. Phys. Rep. 2010, 486, 1–74. 10.1016/j.physrep.2009.11.001. [DOI] [Google Scholar]
  24. Binnig G.; Quate C. F.; Gerber C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. 10.1103/physrevlett.56.930. [DOI] [PubMed] [Google Scholar]
  25. Veitshans T.; Klimov D.; Thirumalai D. Protein folding kinetics: timescales, pathways and energy landscapes in terms of sequence-dependent properties. Folding Des. 1997, 2, 1–22. 10.1016/s1359-0278(97)00002-3. [DOI] [PubMed] [Google Scholar]
  26. Bruce N. J.; Ganotra G. K.; Kokh D. B.; Sadiq S. K.; Wade R. C. New approaches for computing ligand–receptor binding kinetics. Curr. Opin. Struct. Biol. 2018, 49, 1–10. 10.1016/j.sbi.2017.10.001. [DOI] [PubMed] [Google Scholar]
  27. Clackson T.; Yang W.; Rozamus L. W.; Hatada M.; Amara J. F.; Rollins C. T.; Stevenson L. F.; Magari S. R.; Wood S. A.; Courage N. L.; Lu X.; Cerasoli F.; Gilman M.; Holt D. A. Redesigning an FKBP–ligand interface to generate chemical dimerizers with novel specificity. Proc. Natl. Acad. Sci. U.S.A. 1998, 95, 10437–10442. 10.1073/pnas.95.18.10437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ivery M. T. G. Immunophilins: switched on protein binding domains?. Med. Res. Rev. 2000, 20, 452–484. . [DOI] [PubMed] [Google Scholar]
  29. Majiduddin F. K.; Materon I. C.; Palzkill T. G. Molecular analysis of beta-lactamase structure and function. IJMM Int. J. Med. Microbiol. 2002, 292, 127. 10.1078/1438-4221-00198. [DOI] [PubMed] [Google Scholar]
  30. Jameel N.-u.-A.; Ejaz H.; Zafar A.; Amin H. Multidrug resistant AmpC β-lactamase producing Escherichia coli isolated from a paediatric hospital. Pakistan J. Med. Sci. 2014, 30, 181. 10.12669/pjms.301.4045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. MacKerell A. D. Jr; Banavali N.; Foloppe N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers 2000, 56, 257–265. . [DOI] [PubMed] [Google Scholar]
  32. Sun Y.; Kollman P. A. Hydrophobic solvation of methane and nonbond parameters of the TIP3P water model. J. Comput. Chem. 1995, 16, 1164–1169. 10.1002/jcc.540160910. [DOI] [Google Scholar]
  33. Müller D. J.; Dumitru A. C.; Lo Giudice C.; Gaub H. E.; Hinterdorfer P.; Hummer G.; De Yoreo J. J.; Dufrêne Y. F.; Alsteens D. Atomic Force Microscopy-Based Force Spectroscopy and Multiparametric Imaging of Biomolecular and Cellular Systems. Chem Rev. 2020, 10.1021/acs.chemrev.0c00617. [DOI] [PubMed] [Google Scholar]
  34. Agmon N.; Hopfield J. J. CO binding to heme proteins: A model for barrier height distributions and slow conformational changes. J. Chem. Phys. 1983, 79, 2042–2053. 10.1063/1.445988. [DOI] [Google Scholar]
  35. Roy M.; Grazioli G.; Andricioaei I. Rate turnover in mechano-catalytic coupling: A model and its microscopic origin. J. Chem. Phys. 2015, 143, 045105. 10.1063/1.4926664. [DOI] [PubMed] [Google Scholar]
  36. Liang J.; Fernández J. M. Kinetic Measurements on Single-Molecule Disulfide Bond Cleavage. J. Am. Chem. Soc. 2011, 133, 3528–3534. 10.1021/ja109684q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Dembo M.; Torney D. C.; Saxman K.; Hammer D.; Murray J. D. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1988, 234, 55–83. 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
  38. Dembo M.Lectures on Mathematics in the Life Sciences. Some Mathematical Problems in Biology; American Mathematical Society: Providence, RI, 1994; Vol. 24, pp 51–77. [Google Scholar]
  39. Barsegov V.; Thirumalai D. Dynamics of unbinding of cell adhesion molecules: transition from catch to slip bonds.. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 1835–1839. 10.1073/pnas.0406938102. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c01818_si_001.pdf (820.7KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES