Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jul 12;125(28):7628–7637. doi: 10.1021/acs.jpcb.1c02322

Nanomechanical Stability of Aβ Tetramers and Fibril-like Structures: Molecular Dynamics Simulations

Adolfo B Poma †,%,*, Tran Thi Minh Thu ‡,§,⊥, Lam Tang Minh Tri §,⊥, Hoang Linh Nguyen ‡,∥,⊥, Mai Suan Li #,*
PMCID: PMC8389904  PMID: 34253022

Abstract

graphic file with name jp1c02322_0008.jpg

Alzheimer’s disease (AD) is a neurodegenerative disorder and one of the main causes of dementia. The disease is associated with amyloid beta (Aβ) peptide aggregation forming initial clusters and then fibril structure and plaques. Other neurodegenerative diseases such as type 2 diabetes, amyotrophic lateral sclerosis, and Parkinson’s disease follow a similar mechanism. Therefore, inhibition of Aβ aggregation is considered an effective way to prevent AD. Recent experiments have provided evidence that oligomers are more toxic agents than mature fibrils, prompting researchers to investigate various factors that may influence their properties. One of these factors is nanomechanical stability, which plays an important role in the self-assembly of Aβ and possibly other proteins. This stability is also likely to be related to cell toxicity. In this work, we compare the mechanical stability of Aβ-tetramers and fibrillar structures using a structure-based coarse-grained (CG) approach and all-atom molecular dynamics simulation. Our results support the evidence for an increase in mechanical stability during the Aβ fibrillization process, which is consistent with in vitro AFM characterization of Aβ42 oligomers. Namely, using a CG model, we showed that the Young modulus of tetramers is lower than that of fibrils and, as follows from the experiment, is about 1 GPa. Hydrogen bonds are the dominant contribution to the detachment of one chain from the Aβ fibril fragment. They tend to be more organized along the pulling direction, whereas in the Aβ tetramers no preference is observed.

Introduction

According to the amyloid cascade hypothesis,1 Alzheimer’s disease (AD) is caused by extracellular aggregation of amyloid beta (Aβ) peptides, leading to the formation of fibrils and plaques. This hypothesis may be true for other diseases such as Parkinson’s disease, type II diabetes, amyotrophic lateral sclerosis, and so on, but with the accumulation of other proteins.2 Initially, mature Aβ fibrils with a cross-β-sheet structure were considered to be neurotoxic argents, but later experiments showed that soluble oligomers of the 2–32 chains are more toxic.3−5 Aβ42 (peptide of 42 amino acids), but not Aβ40 (40 amino acids), oligomers have been found to form pores in lipid membranes, resulting in a loss of ionic homeostasis.6,7 This result is consistent with the observation that Aβ42 tetramer or larger oligomers transversal to the neuron membrane and calcium ions enter the cell, causing the neurotoxicity.8

Recently, Ruggeri et al.9 demonstrated the first in vitro experimental evidence of a difference in nanomechanical stability between the Aβ clusters, protofibrils, and extended fibril-like structures in Aβ42 systems. The range of the Young modulus reported varies between 1 and 3 GPa for Aβ clusters and mature fibrils.

In this study we shed light onto the mechanical stability of the Aβ clusters and ordered fibril-like structures under nonequilibrium forces. If we consider protein–protein interactions, for example, we know that the amount of mechanical force that a protein complex can resist before breakage can be decorrelated from its binding affinity which is dominated by thermodynamics. By use of biophysical tools such as the atomic force microscope (AFM), it is possible to study in vitro the mechanical responses of small molecular complexes that, when mechanically stressed, dissociate along energetic pathways that are inaccessible under purely thermal excitation. These properties lead to diverse mechano-responsive behaviors in biological systems, such as force-activated catch bonds,10 mechano-chemistry response in GPCR molecules,11 and enhanced cell adhesion of pathogens under Brownian motion.12 Typical nanoindentation is based on AFM in contact mode which allows to quantify the resistance of individual biomolecules (e.g., protein, polysaccharide, and nucleic acids) and their molecular complexes under loading forces in the range of piconewtons–nanonewtons. The aim is to understand how mechanical stability plays a role in adhesion of proteins and how they perform their intended functions at the molecular level. Through these experiments one can understand what makes protein interactions mechanically strong and characterize the system via the determination of the elastic constants (i.e., Young modulus).

Molecular simulation offers a reliable, reusable, and cost-effective way of investigating the mechanical stability of individual protein chains and protein complexes; furthermore, the molecular mechanism that triggers those responses can be elucidated. One common technique that characterizes the nanomechanics of protein complexes is steered molecular dynamics (SMD) simulation.13,14 The success of this approach comes from the characterization of a series of events needed to unfold a single or a protein complex at the atomistic resolution. The SMD can reproduce various structural characteristics of the unfolding events, and it has been used for the study of tensile deformation in β-amyloid fibrils,15,16 elucidating the mechanism of high stability in the nanonewtons range for cohesin–dockerin binding,17 and so on. In addition, a structure-based coarse-grained (CG) model based on one atom (Cα) per amino acid is more suitable to capture an essential picture of deformation for a very large system and longer time scales.18 They remove several degrees of freedom of the system, which enables one to reach the experimental time and length scales required to describe the relevant phenomena, while maintaining the description of the system under consideration at the molecular level. In particular, our CG model can be used to infer the elastic parameters in ideal conditions (solvent free). When it actually follows a theoretical model, the elastic modulus can be obtained from the linear response. Most importantly, the mechanism of deformation that gives rise to the linear response can be characterized in a CG simulation.

In this study we combined all-atom MD and structure-based CG to quantify the mechanical stability of the Aβ tetramers through SMD simulation and CG nanoindentation. Our results agree with AFM experiments9 and provide a quantitative description of the mechanical gain during the Aβ fibril growth.

Materials and Methods

Steered Molecular Dynamics (SMD) Simulation

The atomic structure of Aβ fibrils was obtained by various experimental techniques, including solid-state NMR and cryo-EM. However, the structure of small oligomers cannot be resolved experimentally due to their transient nature that comes from fast aggregation in solution. In this situation MD simulations were used to obtain their structures.2,19−21

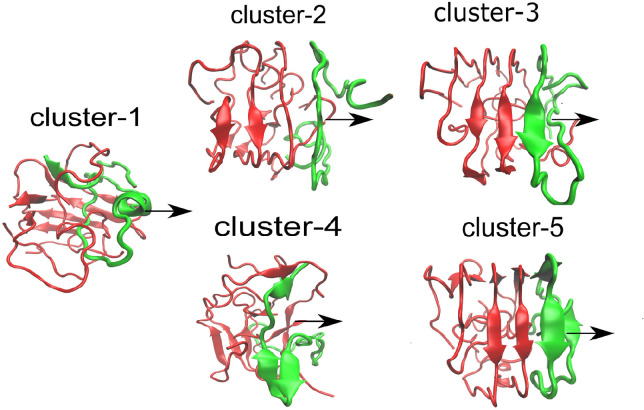
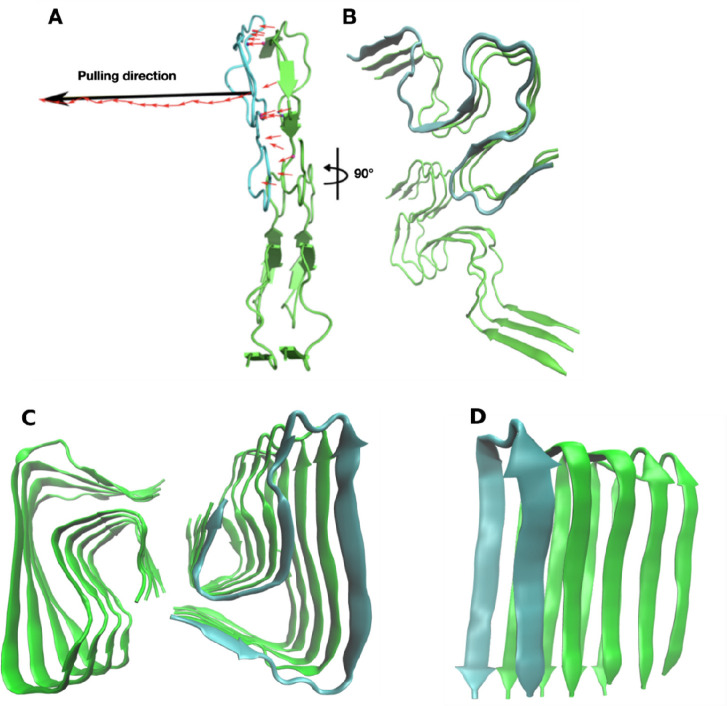
Here we used the initial structures of the Aβ tetramers (see Figure 1), which were obtained from our previously reported study19 by all-atom MD simulation with the OPLS-AA/L force field in explicit solvent with the TIP3P water model. The structures of Aβ42 protofibrils were retrieved from Protein Data Bank (PDB) with code 2NAO(22) (Figure 2A,B), 5OQV(23) (Figure 2C), and 2BEG(24) (Figure 2D). Because our simulation will be done at pH 7, but 50QV was obtained at pH 2, we must check its stability at pH 7. As can be seen from Figure S1 in the Supporting Information, the root-mean-square deviation (RMSD) of Cα atoms remains below 0.4 nm, which indicates that 5OQV is also stable at pH 7 and can be used in our simulations.

Figure 1.

Figure 1

Open in a new tab

Computational models of Aβ tetramers taken from Nguyen et al.19 The arrows indicate the pulling direction in SMD simulation.

Figure 2.

Figure 2

Open in a new tab

Aβ fibril fragment (PDB code 2NAO) has a 2-fold symmetry. Panel A shows the vector of interchain HBs at the interface (red) and the total vector (black). The pulling direction was chosen along this total vector. Panel B depicts the Aβ system rotated by 90°. Panels C and D represent the fibril structures with PDB code 5OQV and 2BEG, respectively.

To generate starting structures for SMD simulations, at the first stage of simulation, all systems were minimized by the steepest-descent method and equilibrated under a constant volume (NVT) ensemble in 1 ns and constant pressure (NPT) in 1 ns, maintaining an isotropic pressure at 1.0 bar. Initial random velocities were generated from the Maxwell distribution at 300 K. We used the v-rescale thermostat to keep the temperature close to 300 K.25 The pressure was kept fixed by the Parrinello–Rahman algorithms.26 A physiological salt concentration of 150 mM was used. The last structure obtained in the equilibration step was used as starting conformation for SMD simulations.

The choice of pulling direction in SMD simulation of a protein–protein complex is not unique, and one of the possible choices was described in Nguyen et al.27 On the basis of the fact that hydrogen bonds (HBs) between two subunits play a key role in the stability of the complex, we choose the pulling pathway in the direction of the total HB vector (see Figure 2A). In fact, this direction of pulling maximizes the response (HB breaking) of the system under load (a HB is considered to be present when the distance between donor atom and acceptor atom is less than 0.35 nm and the angle between acceptor-H-donor atom is larger than 135°). HB between two monomers was represented as a vector by using Pymol software. Each HB has two possible directions, and we choose the direction that maximizes the sum of all vectors (see Figure 2A). The pulling direction, obtained by our protocol for the tetramer models, is shown in Figure 1.

Proteins were placed in a rectangular box that is large enough to have space for pulling simulations and satisfy the minimum image convention condition. For Aβ tetramers, except the chain to which the external force was applied, all the remaining chains were restrained to prevent them from drifting due to pulling. Unlike tetramers, in the case of protofibrils, only the neighbor chain was used as an immobile reference for the pulling simulations. An external force was applied to one end of a spring that is attached to the center of mass (COM) of one of the monomers and pulled it along the arrow shown in Figures 1 and 2.

The spring constant (k) of a spring connecting a dummy atom and COM of the pulled chain was set equal to 239 kcal/(mol nm2) (or 1000 kJ/(mol nm2)) as in AFM experiments.27,28 Because of limited computational facilities, the pulling speed (v) in SMD simulation was chosen to be 1 nm/ns, which is much larger than its experimental reference value, but the qualitative results should not depend on v. The force experienced by the pulled peptide was calculated as F = k(vt – x), where x denotes its displacement from the initial position. If the interactions that stabilize the fibril structure are disrupted, the single chain detaches from the core of the performed template, resulting in a force drop as resistance disappears. Thus, similar to the stretching of a single protein chain, Fmax can characterize the mechanical stability of the entire fibril. To obtain a force–extension profile, for each time step, the resulting force was computed. For each case, we performed five trajectories and the maximum force and pulling work were calculated as the average value. From the force–time profile, we collected the rupture force Fmax, a force needed for the protein–protein dissociation. Moreover, Vuong et al.29 showed that the pulling work Wpull better describes experiment than the rupture force because it is a function of the entire process, while Fmax is determined only in a single state. Thus, we can use the pulling work as a score function for measuring the mechanical stability of the fibril. The pulling work is computed by the following equation:

graphic file with name jp1c02322_m001.jpg 1

All systems were simulated with the TIP3P water model and CHARMM36m force field,30 which was developed for intrinsically disordered proteins such as Aβ peptides. Indeed, this force field has been validated in previous studies of Aβ42 monomers19 and oligomers.20 The GROMACS package, ver. 5.1.2,31 was the molecular dynamics engine.

Nanomechanics of Proteins: A Coarse-Grained Model

We have employed the structure-based CG approach (i.e., Go̅-like model) that has been tuned by all-atom MD and experimental rupture forces.18,32 Our approach is based on a well-determined structure which serves to devise a contact map (CM) of native interactions. In general, one can take a deposited protein structure from the Protein Data Bank to obtain a CM or use MD simulation to construct a dynamical CM.33 Our approach has been validated in several applications from the reconstruction of protein sequences,34 stretching of biomolecules, and modeling of large conformational changes in protein complexes.35−37 This methodology has been successful to map those changes in protein assemblies under applied large forces inducing local deformations such as during nanoindentation. Thus, we performed a computational nanoindentation study which has been validated for single transmembrane proteins and biological filaments.18,38,39 In the case of nanomechanical indentation we consider a spherical object with the radius of curvature Rind that is in contact with the amyloid cluster and press against the direction of maximal hydrogen bond contribution with a speed of vind. Once the indenter travels inside the cluster the distance of h away from the undeformed situation, then the force of reaction generated by the cluster is F(h). This process is continued until the indenter reaches a penetration depth which typically is about 0.5–1 nm. The relationship that holds F and h is given by Hertz elastic model,40 which is equal to 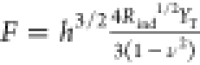Inline graphic, where ν denotes the Poisson ratio of the protein assembly. It is defined as the ratio of the transverse contraction strain to the axial strain in the direction of the stretching deformation. In this case we took it equal to 0.5.

The linear part of the F vs h3/2 profile provides a direct calculation of the Young modulus (YT). In experiments, the indenter has a finite stiffness, and the resulting compliance has to be subtracted from the full indentation depth. In simulations, we can eliminate the compliance of the indenter by making it sufficiently stiff. It should be commented that during the indentation process we went further than the reversible region, and we carry out several indentation tests (n = 100) to account for the standard deviation (SD) in the process.

Results and Discussion

All-Atom Steered Molecular Dynamics Simulation

Previous studies proved that the maximum force Fmax can be used as a measure of the mechanical stability of proteins.41−43 This concept has also been useful in identifying a possible relationship between mechanical stability and protein aggregation rate that the higher the aggregation rate, the more stable the fibrillar structure.44 This hypothesis is supported by the fact that Aβ42 aggregates faster than Aβ4045,46 because the rupture force of Aβ42 fibril is higher than Aβ40.44 Here both Fmax and Wpull will be used to characterize the nanostability of oligomers and mature fibrils. It is also interesting to note that Chakraborty et al.47 have shown that the difference in the rate of aggregation of Aβ42 and Aβ40 is associated with a higher population of the so-called fibril-prone state N* (N* is defined as the conformation of a monomer in a fibril state) of Aβ42 compared to Aβ40. This is consistent with the theory developed by Li et al.48,49 showing that the fibril formation time is controlled by the population of N*.

As mentioned above, Ruggeri et al.9 reported that Aβ42 fibrils are more stable than Aβ42 oligomers. To check this experimental result, we first performed SMD simulation for the Aβ42 tetramer with five representative models (Figure 1) and two fibril models 2NAO and 5OQV. To shed light on the effect of fibril morphology on mechanical stability, we also examined the 2BEG model24 of the truncated peptide Aβ17–42.

Mechanical Unfolding Pathways of the Tetramer Are More Complex than the Fibril

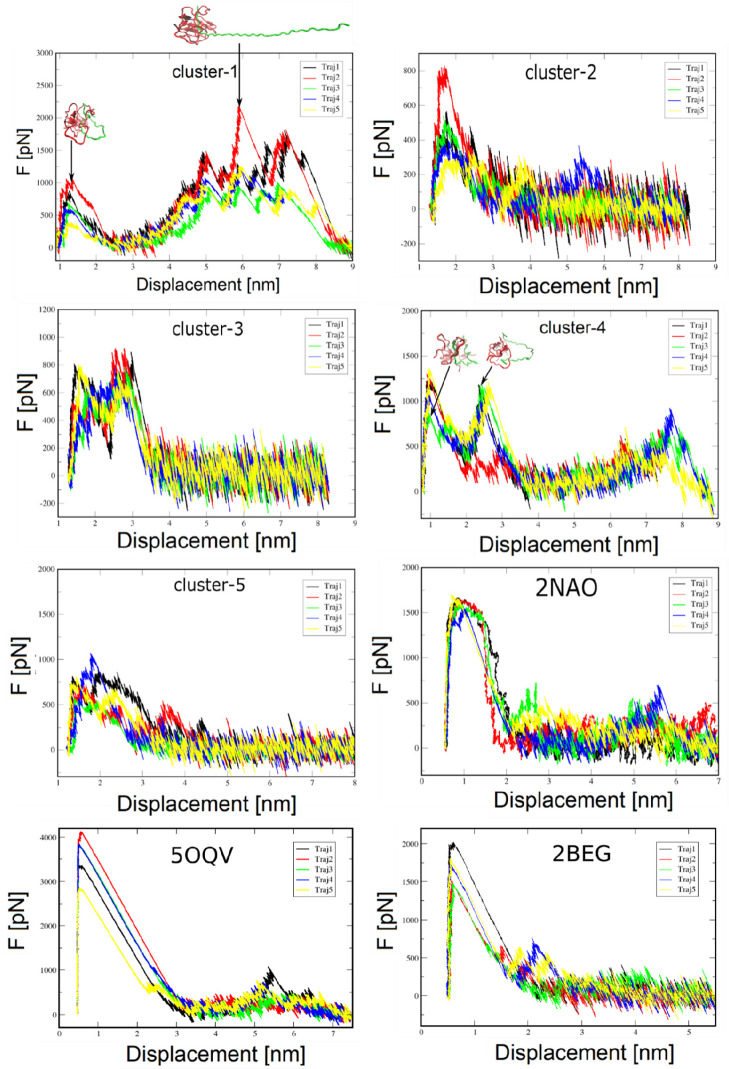
Figure 3 shows the snapshots of the Aβ42 tetramer during the pulling process and the time dependence of the pulling work in one SMD trajectory. Clearly, the oligomer remains compact after detachment of one chain, which may be associated with rapid pulling. In the case of the tetramer, the force exerted by a pulled chain versus displacement exhibits complex behavior depending on computational models (Figure 4). In particular, for clusters 1 and 4, several peaks are observed due to the entanglement of chains arising during unfolding. In trajectory 1 of model 1 (Figure 4) the pulled chain is still compact at the first peak. The system spends a lot of time on the second peak, when the pulled chain nearly unfolds because it is clinging to another chain. This clinging itself resulted in a great rupture force.

Figure 3.

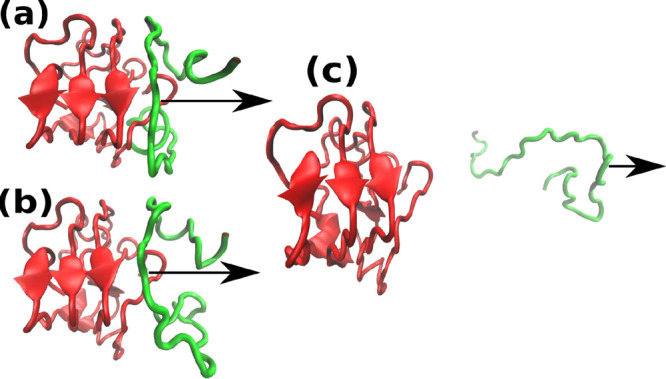
Figure 3

Open in a new tab

Snapshots of the Aβ tetramer at different displacement between COM of two chain along the pulling path (x-axis): (a) x = 1.30 nm (initial state, t = 0), (b) x = 1.75 nm (at the maximum force, t = 790 ps), and (c) x = 5.8 nm (the pulled chain is completely separated, t = 4500 ps).

Figure 4.

Figure 4

Open in a new tab

Force–displacement profile of SMD simulations. A chain is pulled out of the Aβ fibril fragment. Fmax measures mechanical stability. For Aβ tetramer clusters namely 1 and 4 are shown the structure of the chain at two instances of the pulling simulation. At the bottom we show the results for three fibrils 2NAO, 5OQV, and 2BEG.

Because the chains in the initial (PDB) structures 2NAO, 5OQV, and 2BEG are well separated, there is only one peak in the force–displacement profile (Figure 4), which implies that unfolding pathways of the mature fibril are less diverse than the tetramer. To better understand this problem, we built a contact map that shows only those “native” contacts that existed in the initial configuration but are broken at Fmax (Figure S2). Because the “native” contacts of the tetramer disappear in more different positions than the fibril, the detachment pathways in the first case are more complex than in the second. The number of hydrophobic–hydrophobic, hydrophobic–hydrophilic, and hydrophilic–hydrophilic contacts at the initial moment of time and rupture is indicated in Table S1, which suggests that the hydrophobic–hydrophilic interactions are less important than others.

Aβ Tetramers Are Mechanically Less Stable than Fibril-like Structures

The rupture forces obtained in all trajectories are reported in Table S2, and averaging over 20 runs we have Fmax = 2065, 703, 817, 1226, and 981 pN for clusters 1, 2, 3, 4, and 5, respectively. Averaging over five clusters gives Fmax = 1158 pN for the tetramer (Table 1). The average rupture force is 1534 and 4200 pN for 2NAO and 5OQV, respectively (Table 1), which is higher than that of the tetramer (1158 pN). Therefore, in agreement with Ruggeri et al.,9 mature fibrils are mechanically more stable than oligomers.

Table 1. Average Rupture Force Fmax and Pulling Work Wpull of Aβ Tetramer and Fibril-like Structuresa.

systems Fmax (pN) Wpull (kcal/mol)
tetramer 1158 ± 169 347 ± 51
2NAO 1534 ± 166 312 ± 29
5OQV 4200 ± 560 977 ± 169
2BEG 1416 ± 219 188 ± 42
Open in a new tab
a

The results were obtained by using 20 SMD trajectories and pulling speed v = 1 nm/ns.

Because there is no interaction between the pulled chain and the adjacent chain when they are completely separated, the pulling work was defined at the saturation stage (Figure 5). Wpull obtained for all the systems is shown in Table S3. For the tetramer, the average Wpull value is 347 kcal/mol, which is lower than 977 kcal/mol of 5OQV but higher than 312 kcal/mol of 2NAO (Table 1). This means that the oligomers are less stable than 5OQV but more stable than 2NAO. However, averaging over two fibril structures, we obtain Wpull = (977 + 312)/2 = 644.5 kcal/mol, which is higher than 347 kcal//mol of the tetramer. Thus, as in the Fmax case, our data on the pulling work also support the trend reported in experimental work9 that the fibril is more stable than oligomers. We do not compare the mechanical stability of the tetramer with 2BEG because this fibril structure was obtained for the truncated version of Aβ17–42, but not for the full-length peptide.

Figure 5.

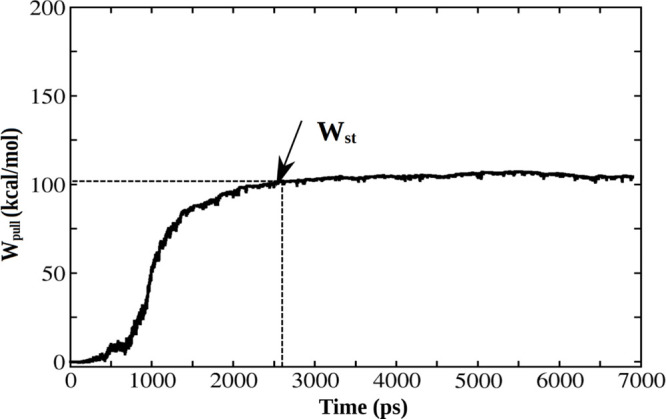
Figure 5

Open in a new tab

Time dependence of the pulling work with Wst at the saturation point.

Hydrogen Bonds Plays a Key Role in Stability of Aβ Aggregates

Experimentally, Ruggeri et al.9 found that hydrogen bonds (HBs) between β-sheets are the main factor determining the stability of Aβ aggregates. Moreover, during the aggregation process, oligomers possess partial β-sheet conformations.50 The number of HBs and β-content of all initial structures were calculated (Table 2). In terms of Fmax and Wpull (Table 1), the 5OQV fibril is much more stable compared to 2NAO, which is well correlated to the fact that 5OQV has 105 HBs vs 24 HBs of 2NAO. 5OQV also has the β-content (79.6%) higher than 2NAO (38.5%). Thus, in agreement with experiment, the more HBs and β-content, the more stable the fibrils.

Table 2. Number of Hydrogen Bonds and β-Content of Initial Structures of Tetramers and Fibrils.

Aβ system number of HBs β content (%)
cluster 1 22 16.7 ± 2.9
cluster 2 13 10.1 ± 2.3
cluster 3 15 16.1 ± 2.8
cluster 4 20 21.4 ± 3.2
cluster 5 16 28.0 ± 3.5
2NAO 24 38.5 ± 3.1
5OQV 105 79.6 ± 2.1
2BEG 57 77.7 ± 3.7
Open in a new tab

For tetramers, clusters 1 and 4 have more HBs than clusters 2, 3, and 5 (Table 2). On the other hand, the rupture force and pulling work of models 1 and 4 are larger (Tables 1) than the remaining models, which also confirms the importance of HBs in the stability of Aβ complexes.

Contribution of Interchain Electrostatic and van der Waals Interactions to Nanomechanical Stability Depends on the Aβ Structures

To understand the role of interchain electrostatic and van der Waals (vdW) interactions, we calculated them in initial structures (Table S4) and their time dependence in SMD simulations (Figure S3). Electrostatic interaction is more important than vdW for 5OQV and 2BEG, but vice versa in the case of 2NAO. In the case of a tetramer, the vdW interaction is more important than electrostatic for clusters 2, 3, and 5, but for clusters 1 and 4, the latter dominates. Because 5OQV is mechanically more stable than 2NAO, and models 1 and 4 have higher breaking force than models 2, 3, and 5 (Table S2), we would expect electrostatic interaction to dominate the vdW interaction in highly stable structures. It would be interesting to test this conclusion on other force fields and water models.

Mechanical Stability Depends on the Morphology of the Fibril

The 2NAO fibril has a S-bend topology, while 5OQV has a LS-shape (Figure 3), leading to different mechanical stability (Table 1). Thus, we hypothesize that mechanical stability depends on the fibril morphology. To further validate this hypothesis, we performed SMD simulations for 2BEG, which has a U-bend structure. Typical force–extension profiles are shown in Figure 4; Wpull and Fmax obtained for 10 trajectories are presented in Tables S2 and S3, respectively. The average rupture force (1416 pN) and pulling work (188 kcal/mol) (Table 1) are lower than those of 2NAO and 5OQV, which supports the hypothesis of the dependence of stability on the fibril structure.

Robustness of Results against Pulling Speeds

To show that our main conclusion about the higher stability of fibrils in comparison with oligomers does not depend on pulling speed, we simulated a tetramer and 2NAO fibril at v = 5 nm/ns. From Table S5, for the tetramer we obtained the average pulling work Wpull ≈ 681 kcal/mol, which is comparable with Wpull ≈ 691 kcal/mol of 2NAO. However, averaging the results obtained for five clusters of the tetramer (Table S6), we have Fmax ≈ 1624 pN, which is lower than Fmax ≈ 2271 pN of 2NAO. Thus, the lower stability of oligomers compared to that of fibrils does not depend on the pulling speed.

Coarse-Grained Simulation

Young Modulus of Aβ Tetramers Is Less than Fibril-like Structures

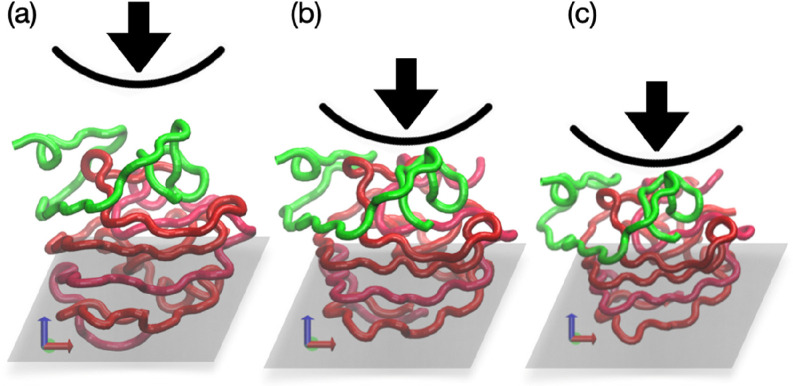
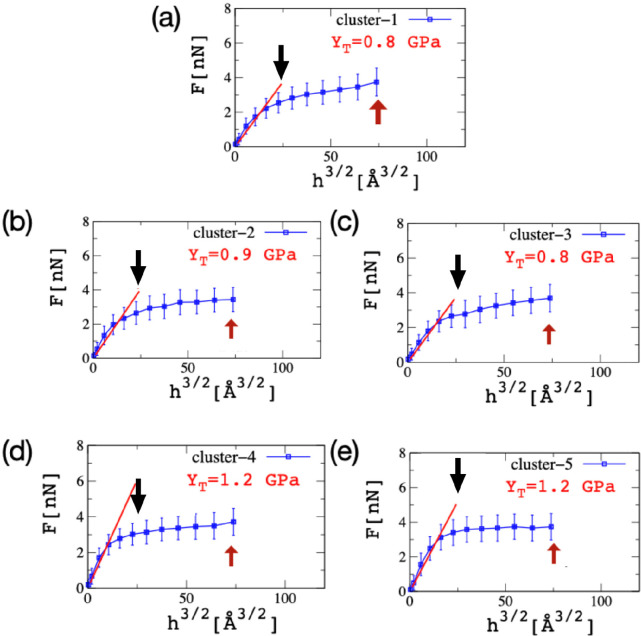
The computational nanoindentation of Aβ42 tetramers is described below. In vitro studies9 provide evidence of the relative difference in Young modulus (YT) between the fibril-like structure and the Aβ42 oligomers. Our results consider the size of the spherical indenter (Rind) equal to 10 nm and the expected force (F) to be between few nanonewtons when h is about 1 nm. We take vind of 5 × 10–7 nm/ps to match the experimental time scale. Figure 6 shows snapshots of the indentation process for an Aβ tetramer. The computational nanoindentation results are reported in Figure 7. Here we show the plot of F vs h3/2, and the linear fit that is used to determine YT. We find that the values of YT for Aβ tetramers vary in the range 0.8–1.2 GPa, which is in agreement with AFM studies.9 Our previous work39 showed a systematic comparison between in silico and in vitro experiments for the calculation of the YT modulus in Aβ42 and Aβ40 forming fibril structures. We reported for those systems a YT in the ranges 3–10 and 7–21 GPa for Aβ42 and Aβ40, respectively. Such a deviation in the Young modulus was associated with the type of amyloid symmetry and the high degree of crystal-like order retained in the CG model.

Figure 6.

Figure 6

Open in a new tab

CG nanoindentation of Aβ42 tetramers. Here we show the typical deformation process induced by a spherical indenter with Rind = 10 nm at different penetration depths (h) as follows: (a) h = 0 nm (no contact), (b) h = 1 nm (moderate deformation), and (c) h = 1.8 nm (large deformation). The top protein chain is highlighted in green color to indicate the first chain in the tetramer which is in contact with the indenter. The repulsive plane is also depicted for each snapshot.

Figure 7.

Figure 7

Open in a new tab

CG nanoindentation profiles of five Aβ tetramer clusters. The Young modulus is presented next to the linear fit and shows a deviation in the range 0.8–1.2 GPa. Vertical arrows show the position of the indenter at 1 and 1.8 nm as depicted in Figure 5.

This result was also validated by in vitro experiments for the related Aβ42 fibril, and it provides 3.3 GPa.9 The experimental value of the fibril-like Aβ40 has not yet been reported, but it is expected to fall in the range 2–4 GPa according to other amyloid systems (e.g., assembled from α-synuclein, heptapeptides, insulin, β-lactoglobulin, tau protein, lysozyme, ovalbumin, and bovine serum albumin).51,52 Those studies show how softer tends to be the oligomer state in comparison to the fibril-like state. According to our in silico studies here, we found that the YT drops by a factor of 10 in tetramers compared to the fibril system. This result indicates the loss of cooperative effect due to weak and unoriented native contacts in the Aβ tetramers state compared to fibril-like state. Overall, structure-based CG and SMD simulations provide similar results for the mechanical stability of Aβ aggregates.

Conclusions

Our work shows the important role of mechanical stability in Aβ systems, from the initial tetramer cluster formation to more stable fibril-like structures. Further studies can shed light onto the gain of the nanomechanical stability as a function of time in adhesion of proteins and their aggregation pathway. In addition, CG simulation based on the Cα backbone and the mapping all native interactions for each Aβ tetramer cluster show consistent results with all-atom MD. The indentation process was performed by a spherical hard object with a radius of curvature equal to 10 nm. Once it was in contact with the Aβ tetramer, the response of the system while pressing it against the direction of maximal HB deformation, a linear fitting was sufficient to show small variations in the Young modulus in the range 0.8–1.2 GPa. Such deviations are in agreement with experimental results.9

Recently, the MARTINI force field has drawn attention to the calculation of mechanical properties of biomolecules. Fontana and Gelain53 were able to assess the Young modulus from stretching simulations. So far, to our knowledge, the MARTINI force field has not been used to perform nanoindentation, so it would be interesting to use it to compare the stability of amyloid oligomers and fibrils.

Acknowledgments

We thank Ho Anh Kiet for his kind help in low-pH simulations. A.B.P. acknowledges financial support from the National Science Centre, Poland, under Grant 2017/26/D/ 504 NZ1/00466, the grant MAB PLUS/11/2019 from the Foundation for Polish Science, and also gratefully acknowledges the computing provided by the Jülich Supercomputing Centre on the supercomputer JURECA at Forschungszentrum Jülich. M.S.L. was supported by the National Science Centre in Poland (Grant 2019/35/B/ST4/02086). T.T.M.T., L.T.M.T., and H.L.N. acknowledge financial support from the Department of Science and Technology at Ho Chi Minh City (Grant 07/2019/HD-737 KHCNTT), Vietnam. N.H.L. was funded by Vingroup Joint Stock Company and supported by the Domestic Master/PhD Scholarship Programme of Vingroup Innovation Foundation (VINIF), Vingroup Big Data Institute (VINBIGDATA), code VINIF.2020.TS.92. Computer resources were supported by the PL-GRID infrastructure and the TASK supercomputer center in Gdansk, Poland.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.1c02322.

  • Figure S1: time dependence of the root-mean-square deviation (RMSD) of 5OQV at pH = 2 and pH = 7; Figure S2: contact map which shows only the contacts that have existed in the initial structure but are broken at the rupture force; Figure S3: time dependence of the interchain interaction energy, obtained in SMD simulation; Table S1: numbers of interchain contacts between the pulled chain and the other chains of the initial structures and structures at Fmax; Table S2: the rupture force Fmax of Aβ tetramer and fibril-like structures for 20 trajectories; Table S3: the pulling work of the Aβ tetramer and fibril-like structures for 20 trajectories; Table S4: interchain interaction energy of initial structures; Table S5: the pulling work of the Aβ tetramer and 2NAO was obtained for pulling speed v = 5 nm/ns and 10 trajectories; Table S6: Fmax of the Aβ tetramer and fibril-like structure 2NAO; results obtained for v = 5 nm/ns and SMD 10 trajectories (PDF)

Author Contributions

A.B.P. and T.T.M.T. contributed equally to this work.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Dave Thirumalai Festschrift”.

Supplementary Material

jp1c02322_si_001.pdf (1MB, pdf)

References

  1. Hardy J.; Selkoe D. J. The amyloid hypothesis of Alzheimer’s disease: progress and problems on the road to therapeutics. Science 2002, 297, 353–356. 10.1126/science.1072994. [DOI] [PubMed] [Google Scholar]
  2. Nguyen P. H.; Ramamoorthy A.; Sahoo B. R.; Zheng J.; Faller P.; Straub J. E.; Dominguez L.; Shea J.-E.; Dokholyan N. V.; De Simone A.; et al. Amyloid oligomers: A joint experimental/computational perspective on Alzheimer’s disease, Parkinson’s disease, Type II diabetes, and amyotrophic lateral sclerosis. Chem. Rev. 2021, 121, 2545–2647. 10.1021/acs.chemrev.0c01122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ciudad S.; Puig E.; Botzanowski T.; Meigooni M.; Arango A. S.; Do J.; Mayzel M.; Bayoumi M.; Chaignepain S.; Maglia G.; et al. Aβ (1–42) tetramer and octamer structures reveal edge conductivity pores as a mechanism for membrane damage. Nat. Commun. 2020, 11, 1–14. 10.1038/s41467-020-16566-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Baglioni S.; Casamenti F.; Bucciantini M.; Luheshi L. M.; Taddei N.; Chiti F.; Dobson C. M.; Stefani M. Prefibrillar amyloid aggregates could be generic toxins in higher organisms. J. Neurosci. 2006, 26, 8160–8167. 10.1523/JNEUROSCI.4809-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Haass C.; Selkoe D. J. Soluble protein oligomers in neurodegeneration: lessons from the Alzheimer’s amyloid β-peptide. Nat. Rev. Mol. Cell Biol. 2007, 8, 101–112. 10.1038/nrm2101. [DOI] [PubMed] [Google Scholar]
  6. Serra-Batiste M.; Ninot-Pedrosa M.; Bayoumi M.; Gairí M.; Maglia G.; Carulla N. Aβ42 assembles into specific β-barrel pore-forming oligomers in membrane-mimicking environments. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 10866–10871. 10.1073/pnas.1605104113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lee J.; Kim Y. H.; Arce F. T.; Gillman A. L.; Jang H.; Kagan B. L.; Nussinov R.; Yang J.; Lal R. Amyloid β ion channels in a membrane comprising brain total lipid extracts. ACS Chem. Neurosci. 2017, 8, 1348–1357. 10.1021/acschemneuro.7b00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Drews A.; Flint J.; Shivji N.; Jönsson P.; Wirthensohn D.; De Genst E.; Vincke C.; Muyldermans S.; Dobson C.; Klenerman D. Individual aggregates of amyloid beta induce temporary calcium influx through the cell membrane of neuronal cells. Sci. Rep. 2016, 6, 1–12. 10.1038/srep31910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ruggeri F. S.; Adamcik J.; Jeong J. S.; Lashuel H. A.; Mezzenga R.; Dietler G. Influence of the β-sheet content on the mechanical properties of aggregates during amyloid fibrillization. Angew. Chem. 2015, 127, 2492–2496. 10.1002/ange.201409050. [DOI] [PubMed] [Google Scholar]
  10. Schoeler C.; Malinowska K. H.; Bernardi R. C.; Milles L. F.; Jobst M. A.; Durner E.; Ott W.; Fried D. B.; Bayer E. A.; Schulten K.; Gaub H. E.; Nash M. A. Ultrastable cellulosome-adhesion complex tightens under load. Nat. Commun. 2014, 5, 1–8. 10.1038/ncomms6635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lo Giudice C.; Zhang H.; Wu B.; Alsteens D. Mechanochemical Activation of Class-B G-Protein-Coupled Receptor upon Peptide–Ligand Binding. Nano Lett. 2020, 20, 5575–5582. 10.1021/acs.nanolett.0c02333. [DOI] [PubMed] [Google Scholar]
  12. Yang J.; Petitjean S. J.; Koehler M.; Zhang Q.; Dumitru A. C.; Chen W.; Derclaye S.; Vincent S. P.; Soumillion P.; Alsteens D. Molecular interaction and inhibition of SARS-CoV-2 binding to the ACE2 receptor. Nat. Commun. 2020, 11, 1–10. 10.1038/s41467-020-18319-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Lu H.; Isralewitz B.; Krammer A.; Vogel V.; Schulten K. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 1998, 75, 662–671. 10.1016/S0006-3495(98)77556-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Baker J. L.; Biais N.; Tama F. Steered molecular dynamics simulations of a type IV pilus probe initial stages of a force-induced conformational transition. PLoS Comput. Biol. 2013, 9, e1003032. 10.1371/journal.pcbi.1003032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Xu Z.; Paparcone R.; Buehler M. J. Alzheimer’s abeta(1–40) amyloid fibrils feature size-dependent mechanical properties. Biophys. J. 2010, 98, 2053–2062. 10.1016/j.bpj.2009.12.4317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Paparcone R.; Keten S.; Buehler M. J. Atomistic simulation of nanomechanical properties of Alzheimer’s Abeta(1–40) amyloid fibrils under compressive and tensile loading. J. Biomech. 2010, 43, 1196–1201. 10.1016/j.jbiomech.2009.11.026. [DOI] [PubMed] [Google Scholar]
  17. Bernardi R. C.; Durner E.; Schoeler C.; Malinowska K. H.; Carvalho B. G.; Bayer E. A.; Luthey-Schulten Z.; Gaub H. E.; Nash M. A. Mechanisms of Nanonewton Mechanostability in a Protein Complex Revealed by Molecular Dynamics Simulations and Single-Molecule Force Spectroscopy. J. Am. Chem. Soc. 2019, 141, 14752–14763. 10.1021/jacs.9b06776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Senapati S.; Poma A. B.; Cieplak M.; Filipek S.; Park P. S. H. Differentiating between Inactive and Active States of Rhodopsin by Atomic Force Microscopy in Native Membranes. Anal. Chem. 2019, 91, 7226–7235. 10.1021/acs.analchem.9b00546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Nguyen H. L.; Krupa P.; Hai N. M.; Linh H. Q.; Li M. S. Structure and Physicochemical Properties of the Aβ42 Tetramer: Multiscale Molecular Dynamics Simulations. J. Phys. Chem. B 2019, 123, 7253–7269. 10.1021/acs.jpcb.9b04208. [DOI] [PubMed] [Google Scholar]
  20. Nguyen H. L.; Linh H. Q.; Matteini P.; La Penna G.; Li M. S. Emergence of Barrel Motif in Amyloid-β Trimer: A Computational Study. J. Phys. Chem. B 2020, 124, 10617–10631. 10.1021/acs.jpcb.0c05508. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Voelker M. J.; Barz B.; Urbanc B. Fully Atomistic Aβ40 and Aβ42 Oligomers in Water: Observation of Porelike Conformations. J. Chem. Theory Comput. 2017, 13, 4567–4583. 10.1021/acs.jctc.7b00495. [DOI] [PubMed] [Google Scholar]
  22. Wälti M. A.; Ravotti F.; Arai H.; Glabe C. G.; Wall J. S.; Böckmann A.; Güntert P.; Meier B. H.; Riek R. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, E4976–E4984. 10.1073/pnas.1600749113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Gremer L.; Schölzel D.; Schenk C.; Reinartz E.; Labahn J.; Ravelli R. B. G.; Tusche M.; Lopez-Iglesias C.; Hoyer W.; Heise H.; Willbold D.; Schröder G. F. Fibril structure of amyloid-β(1–42) by cryo–electron microscopy. Science 2017, 358, 116–119. 10.1126/science.aao2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lührs T.; Ritter C.; Adrian M.; Riek-Loher D.; Bohrmann B.; Döbeli H.; Schubert D.; Riek R. 3D structure of Alzheimer’s amyloid-β(1–42) fibrils. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 17342–17347. 10.1073/pnas.0506723102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  26. Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  27. Nguyen H. L.; Lan P. D.; Thai N. Q.; Nissley D. A.; O’Brien E. P.; Li M. S. Does SARS-CoV-2 Bind to Human ACE2More Strongly Than Does SARS-CoV?. J. Phys. Chem. B 2020, 124, 7336–7347. 10.1021/acs.jpcb.0c04511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Binnig G.; Quate C. F.; Gerber C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. 10.1103/PhysRevLett.56.930. [DOI] [PubMed] [Google Scholar]
  29. Vuong Q. V.; Nguyen T. T.; Li M. S. A New Method for Navigating Optimal Direction for Pulling Ligand from Binding Pocket: Application to Ranking Binding Affinity by Steered Molecular Dynamics. J. Chem. Inf. Model. 2015, 55, 2731–2738. 10.1021/acs.jcim.5b00386. [DOI] [PubMed] [Google Scholar]
  30. Huang J.; Rauscher S.; Nawrocki G.; Ran T.; Feig M.; de Groot B. L.; Grubmüller H.; MacKerell A. D. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  32. Poma A. B.; Chwastyk M.; Cieplak M. Polysaccharide–Protein Complexes in a Coarse-Grained Model. J. Phys. Chem. B 2015, 119, 12028–12041. 10.1021/acs.jpcb.5b06141. [DOI] [PubMed] [Google Scholar]
  33. Moreira R. A.; Guzman H. V.; Boopathi S.; Baker J. L.; Poma A. B. Characterization of Structural and Energetic Differences between Conformations of the SARS-CoV-2 Spike Protein. Materials 2020, 13, 5362. 10.3390/ma13235362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Chwastyk M.; Bernaola A. P.; Cieplak M. Statistical radii associated with amino acids to determine the contact map: fixing the structure of a type I cohesin domain in the Clostridium thermocellum cellulosome. Phys. Biol. 2015, 12, 046002. 10.1088/1478-3975/12/4/046002. [DOI] [PubMed] [Google Scholar]
  35. Poma A. B.; Cieplak M.; Theodorakis P. E. Combining the MARTINI and Structure-Based Coarse-Grained Approaches for the Molecular Dynamics Studies of Conformational Transitions in Proteins. J. Chem. Theory Comput. 2017, 13, 1366–1374. 10.1021/acs.jctc.6b00986. [DOI] [PubMed] [Google Scholar]
  36. Poma A. B.; Li M. S.; Theodorakis P. E. Generalization of the elastic network model for the study of large conformational changes in biomolecules. Phys. Chem. Chem. Phys. 2018, 20, 17020–17028. 10.1039/C8CP03086C. [DOI] [PubMed] [Google Scholar]
  37. Moreira R. A.; Chwastyk M.; Baker J. L.; Guzman H. V.; Poma A. B. Quantitative determination of mechanical stability in the novel coronavirus spike protein. Nanoscale 2020, 12, 16409–16413. 10.1039/D0NR03969A. [DOI] [PubMed] [Google Scholar]
  38. Poma A. B.; Chwastyk M.; Cieplak M. Elastic moduli of biological fibers in a coarse-grained model: crystalline cellulose and β-amyloids. Phys. Chem. Chem. Phys. 2017, 19, 28195–28206. 10.1039/C7CP05269C. [DOI] [PubMed] [Google Scholar]
  39. Poma A. B.; Guzman H. V.; Li M. S.; Theodorakis P. E. Mechanical and thermodynamic properties of Abeta42, Abeta40, and alpha-synuclein fibrils: a coarse-grained method to complement experimental studies. Beilstein J. Nanotechnol. 2019, 10, 500–513. 10.3762/bjnano.10.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Hertz H. Über die Berührung fester elastischer Körper. Journal für die reine und angewandte Mathematik 1882, 92, 22. [Google Scholar]
  41. Li M. S. Secondary Structure, Mechanical Stability, and Location of Transition State of Proteins. Biophys. J. 2007, 93, 2644–2654. 10.1529/biophysj.107.106138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Kumar S.; Li M. S. Biomolecules under mechanical force. Phys. Rep. 2010, 486, 1–74. 10.1016/j.physrep.2009.11.001. [DOI] [Google Scholar]
  43. Sułkowska J. I.; Cieplak M. Mechanical stretching of proteins—a theoretical survey of the Protein Data Bank. J. Phys.: Condens. Matter 2007, 19, 283201. 10.1088/0953-8984/19/28/283201. [DOI] [Google Scholar]
  44. Kouza M.; Co N. T.; Li M. S.; Kmiecik S.; Kolinski A.; Kloczkowski A.; Buhimschi I. A. Kinetics and mechanical stability of the fibril state control fibril formation time of polypeptide chains: A computational study. J. Chem. Phys. 2018, 148, 215106. 10.1063/1.5028575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Jarrett J. T.; Berger E. P.; Lansbury P. T. The carboxy terminus of the.beta. amyloid protein is critical for the seeding of amyloid formation: Implications for the pathogenesis of Alzheimer’s disease. Biochemistry 1993, 32, 4693–4697. 10.1021/bi00069a001. [DOI] [PubMed] [Google Scholar]
  46. Snyder S. W.; Ladror U. S.; Wade W. S.; Wang G. T.; Barrett L. W.; Matayoshi E. D.; Huffaker H. J.; Krafft G. A.; Holzman T. F. Amyloid-beta aggregation: selective inhibition of aggregation in mixtures of amyloid with different chain lengths. Biophys. J. 1994, 67, 1216–1228. 10.1016/S0006-3495(94)80591-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Chakraborty D.; Straub J. E.; Thirumalai D. Differences in the free energies between the excited states of Aβ40 and Aβ42 monomers encode their aggregation propensities. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 19926–19937. 10.1073/pnas.2002570117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Li M. S.; Co N. T.; Reddy G.; Hu C.-K.; Straub J. E.; Thirumalai D. Factors Governing Fibrillogenesis of Polypeptide Chains Revealed by Lattice Models. Phys. Rev. Lett. 2010, 105, 218101. 10.1103/PhysRevLett.105.218101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Nam H. B.; Kouza M.; Zung H.; Li M. S. Relationship between population of the fibril-prone conformation in the monomeric state and oligomer formation times of peptides: Insights from all-atom simulations. J. Chem. Phys. 2010, 132, 165104. 10.1063/1.3415372. [DOI] [PubMed] [Google Scholar]
  50. Hong D. P.; Han S.; Fink A. L.; Uversky V. N. Characterization of the non-fibrillar alpha-synuclein oligomers. Protein Pept. Lett. 2011, 18, 230–240. 10.2174/092986611794578332. [DOI] [PubMed] [Google Scholar]
  51. Adamcik J.; Lara C.; Usov I.; Jeong J. S.; Ruggeri F. S.; Dietler G.; Lashuel H. A.; Hamley I. W.; Mezzenga R. Measurement of intrinsic properties of amyloid fibrils by the peak force QNM method. Nanoscale 2012, 4, 4426–4429. 10.1039/c2nr30768e. [DOI] [PubMed] [Google Scholar]
  52. Knowles T. P. J.; Buehler M. J. Nanomechanics of functional and pathological amyloid materials. Nat. Nanotechnol. 2011, 6, 469–479. 10.1038/nnano.2011.102. [DOI] [PubMed] [Google Scholar]
  53. Fontana F.; Gelain F. Probing mechanical properties and failure mechanisms of fibrils of self-assembling peptides. Nanoscale Adv. 2020, 2, 190–198. 10.1039/C9NA00621D. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c02322_si_001.pdf (1MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES