Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jul 20;6(8):2800–2808. doi: 10.1021/acsenergylett.1c00972

Realistic Efficiency Limits for Singlet-Fission Silicon Solar Cells

Benjamin Daiber 1, Koen van den Hoven 1, Moritz H Futscher 1, Bruno Ehrler 1,*
PMCID: PMC8389984  PMID: 34476299

Abstract

graphic file with name nz1c00972_0006.jpg

Singlet fission is a carrier multiplication mechanism that could make silicon solar cells much more efficient. The singlet-fission process splits one high-energy spin-singlet exciton into two lower-energy spin-triplet excitons. We calculated the efficiency potential of three technologically relevant singlet-fission silicon solar cell implementations. We assume realistic but optimistic parameters for the singlet-fission material and investigate the effect of singlet energy and entropic gain. If the transfer of triplet excitons occurs via charge transfer, the maximum efficiency is 34.6% at a surprisingly small singlet energy of 1.85 eV. For the Dexter-type triplet energy transfer, the maximum efficiency is 32.9% at a singlet energy of 2.15 eV. For Förster resonance energy transfer (FRET), the triplet excitons are first transferred into a quantum dot, from which they then undergo FRET into silicon. For this transfer mechanism, the maximum efficiency is 28.% at a singlet energy of 2.33 eV. We show that the efficiency gain from singlet fission is larger the more efficient the silicon base cell is, which stands in contrast to tandem perovskite–silicon solar cells.

Solar cells are the most important cornerstone of transitioning the world’s energy production from a fossil-based system to a CO2-neutral future.1,2 The main solar cell technology in use today is based on silicon. Silicon solar cells have shown large improvements in efficiencies and cost, and the technology is mature and highly optimized. However, the record efficiency of silicon solar cells has improved only slightly from ∼24% to 26.7% in the past 20 years3 because it gets harder and harder to improve the already highly optimized cell structure and material quality. Including Auger recombination in the thermodynamic detailed-balance limit of solar cell efficiency leads to a theoretical maximum efficiency of silicon solar cells of 29.4%.4 The efficiency of the record silicon solar cell is 26.7%,5 which is a remarkable 91% of the theoretical maximum. New approaches are needed to improve the efficiency further. In this paper we calculate the realistic efficiency potential of singlet-fission silicon solar cells with three different geometries and transfer mechanisms, each with distinct advantages and challenges. These results can inform the practical application and search for new singlet-fission materials.

Silicon has a low bandgap energy of (1.12 eV), above which photons are absorbed. A large fraction of the photons of the solar spectrum have a higher energy and will lose their excess energy to thermalization losses. These high-energy photons can be converted into electricity more efficiently if they are split into multiple photons or excitations with an energy above the silicon bandgap. If such downconversion could be applied to silicon, we could build on the vast knowledge of silicon solar cells without the need for large changes in silicon solar cell architecture.

Singlet fission is an example of a downconversion process that can potentially increase the efficiency of silicon solar cells by using the solar spectrum more efficiently. High-energy photons are absorbed in the singlet-fission material and form a spin-singlet exciton. In certain organic materials like poly-acenes and perylene diimides (PDIs), this singlet exciton will split into two spin-triplet excitons of roughly half the energy of the singlet exciton.6 For an efficient implementation, this singlet-fission layer would be placed on top of a silicon solar cell, absorb all the high-energy light, convert each photon into two triplet excitons, and transfer their energy or charge into the silicon solar cell. Fortunately, the absorption coefficients of organic materials are high at the energies of the molecular transitions.7 Singlet fission can also be a very efficient process with efficiencies close to 200% in pentacene,8 meaning each singlet generates two triplet excitons. Therefore, the main bottleneck for the singlet-fission-sensitized silicon solar cells is the transfer of excitons from the absorber layer into silicon. Since triplet states are dark states that do not decay radiatively, the transfer of triplet excitons is not trivial.

Here we simulate how efficient a singlet-fission silicon solar cell could be given realistic materials and device parameters. We find that the absorption of typical singlet-fission materials needs to be improved, for example by sensitization schemes. The most efficient implementation based on a record-efficiency silicon solar cell would be the charge transfer from triplet excitons into silicon with the highest theoretically calculated efficiency of 34.6%. This efficiency maximum is reached at a surprisingly low singlet exciton energy of 1.85 eV with a realistic entropic gain of 100 meV. The simplest triplet-transfer implementation, Dexter transfer, could also achieve high efficiency (32.9%) but puts a stronger constraint on the singlet energy. FRET shows the lowest efficiency potential of 28.7% because of additional loss channels. Finally, we compare the singlet-fisson cells to the behavior of perovskite–silicon tandem solar cells and find that singlet fission shows the largest efficiency improvements for efficient silicon base cells, while tandem solar cells show a larger efficiency improvement for less efficient silicon base cells.

In order to calculate the solar efficiencies we have to model and discuss the absorption of the singlet-fission material. The absorption of any downshifting material should be large so that the maximum number of incoming photons can be absorbed and undergo the downshifting mechanism to multiply carriers and increase the photocurrent. Singlet fission takes place in organic molecules with a relatively large singlet–triplet exciton energy splitting, thus with a large exchange energy. Often these molecules are conjugated molecules. The absorption of these organic molecules is considered to be strong because the absorption coefficient is relatively high compared to other semiconductors.7 However, this is only the case at the absorption peaks at the specific energies of the π-orbital transitions, leading to a narrow absorption spectrum if compared to the band-to-band absorption of most inorganic semiconductors. Since the solar spectrum is broadband and reaches from energies of ca. 0.3 eV (4000 nm) to 4 eV (310 nm), the fraction of absorbed solar light of most singlet-fission materials is very low. To illustrate this point we show the absorbed solar irradiance in a thin pentacene layer of 300 nm (Figure 1a). Thicknesses below 300 nm are typical for films used in singlet-fission solar cells.9,10 This thickness is also in the order of the triplet exciton diffusion length in polycrystalline pentacene of 40–80 nm and single-crystal pentacene of 350–800 nm.11 If the thickness of the layer would be larger than the diffusion length not all excitons would reach the interface and would be lost. Figure 1a shows that only 32% of the power above the singlet energy is absorbed. 67% of the light above the singlet-exciton energy is transmitted and is lost to the singlet-fission process (see Supporting Information S1). Instead, the light is absorbed in the silicon solar cell below the singlet-fission absorber, where it adds current but does not benefit from carrier multiplication. Even for a film thickness of 1000 nm, around three times the single-crystal triplet diffusion length, we still lose 34% of the solar power above the pentacene singlet-exciton energy.

Figure 1.

Figure 1

Open in a new tab

(a) AM1.5 spectrum split into the light absorbed in a 300 nm thick pentacene layer and light that is transmitted through the pentacene layer to the bottom silicon solar cell. Even a thick 300 nm pentacene layer only absorbs 32% of the light with an energy above the singlet energy. (b) Detailed balance limit with the Auger recombination of silicon taken into account (dashed gray line) for an AM1.5 spectrum. The efficiency limit of a singlet-fission silicon cell based on this silicon base cell with tetracene and pentacene layers of different thicknesses, tetracene in red and pentacene in orange. Stars represent the case of infinite layer thickness. The singlet-energy/absorption onset is 1.7 eV for pentacene and 2.3 eV for tetracene. Triplet energies are 0.86 eV for pentacene and 1.25 eV for tetracene. The singlet-fission efficiency is set to 2 and no additional loss channels are assumed.

The limited absorption leads to a loss in photocurrent. We have calculated the theoretical maximum solar cell efficiency for a system that is ideal, where the only loss mechanism is incomplete absorption. We perform a detailed-balance-type calculation (see Supporting Information S2), with the tetracene and pentacene absorption spectra but otherwise 200% efficient singlet fission, no non-radiative recombination except Auger recombination in silicon, and no parasitic absorption. In case of pentacene, there is a voltage penalty since the triplet energy is smaller than the silicon bandgap. The recombination of charge carriers in the dark (J0) does not happen across the silicon bandgap but instead across a smaller gap equivalent to the triplet energy, since this is the smallest energy difference where recombination can occur. The larger recombination due to the smaller energy gap in turn leads to a reduced voltage. Figure 1b shows the efficiency of a tetracene–silicon and pentacene–silicon solar cell as a function of tetracene or pentacene thickness, including the limits for an ideal absorber with the respective absorption onsets. The dashed horizontal line shows the silicon-Auger limit, the solid lines represent the efficiency limits of tetracene and pentacene with different thicknesses on top of a silicon solar cell with the Auger-limited efficiency. The stars are the limits for large thicknesses. We use the energies at which tetracene and pentacene start to absorb as the absorption onset, which explains the discrepancies with the singlet-exciton energies. In this ideal case even a very thin tetracene layer increases the current, but the efficiency gain keeps rising for layer thicknesses well above the polycrystalline triplet diffusion length of ∼600 nm.12 A pentacene layer however would have to be at least 950 nm thick to improve on the silicon-Auger limit, which is many times the diffusion length of triplets in polycrystalline pentacene, 40–80 nm.11

Below we assess the influence of different loss factors on the efficiency potential of singlet-fission silicon solar cells. Because of the poor broadband absorption, we treat the absorption of our theoretical materials as ideal in the following, absorbing all light above the singlet energy. This broadband absorption could be achieved by using a sensitizing layer, as in a recent study where perovskite quantum dots were used as a broadband absorber, then the excitons are transferred into a singlet-fission material where they can undergo singlet fission.13 This additional layer makes use of the efficient band-to-band absorption, with the penalty of a certain transfer loss from the sensitizer to the singlet-fission material. Since this first sensitizing study already reports a singlet-exciton-transfer efficiency of 80% and additional gains are likely possible, we do not explicitly take this transfer loss into account in the calculations.

In the following we calculated the efficiency for three distinct transfer schemes: charge transfer, Dexter transfer, and FRET. We use the record silicon solar cell with an efficiency of 26.7%5 as a base cell into which additional current from singlet fission is injected. We explore the influence of different loss mechanisms and the difference between the transfer schemes, depicted in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Schematics and some SF material requirements of the four transfer schemes discussed in this paper. Charge transfer includes the dissociation of the triplet exciton at the interface and subsequent transfer of both electron and hole independently. Dexter transfer entails the transfer of the energy of the triplet exciton into silicon by concurrently transferring electron and hole. FRET transfer consists of the transfer of the triplet exciton energy into a quantum dot with subsequent transfer of the energy from quantum dot into silicon via FRET. The Photon Multiplier is very similar to the FRET case, however the transfer to silicon happens by emission and absorption of a photon.

Triplet excitons can be transferred into a silicon solar cell by charge transfer. In this transfer mechanism, the triplet exciton is dissociated into electron and hole at the interface between singlet-fission material and silicon. C60 and other fullerenes are often used as an electron acceptor for singlet-fission materials and can efficiently dissociate the triplet excitons.14,15 Here we assume that the electron is transferred into silicon and the hole has to travel through the singlet-fission material to an additional set of contacts on top of the singlet-fission layer. The holes from the photocurrent generated in silicon need to transfer through the singlet-fission material as well. The additional contacts and the long diffusion through the singlet-fission layer will lead to additional losses. A variation of this transfer scheme is to use metal top contacts on the silicon but below the singlet-fission layer. These buried contacts would accept the holes generated by the singlet-fission process and would be covered by electron blocking layers to prevent recombination. If the hole mobility of a singlet-fission material is high, this buried contact could eliminate the need for additional top contacts which would reduce parasitic absorption losses. In our model we assume a doubled series resistance, compared to the silicon cell alone and a 3% parasitic absorption loss from the additional top contacts. Further we assume 95% efficient triplet generation and a 95% efficient triplet dissociation, leading to an overall triplet yield of 1.805 per absorbed photon. We discuss the requirements for the hole mobilities in the singlet-fission material below.

An important element of modeling the charge transfer is the voltage penalty that applies if the triplet energy is smaller than the silicon bandgap. The radiative recombination will then occur between the smallest energy gap of the cell, which in this case is between the highest occupied molecular orbital (HOMO) of the singlet-fission material and the silicon conduction band.

For charge transfer the LUMO of the singlet-fission crystal needs to be aligned with the conduction band of silicon (or the HOMO with the valence band for hole transfer). Both the bands in silicon as well as the energy of the molecular orbitals can be tuned. Niederhausen et al.16 use a small fluorinated molecule to shift the energy-level alignment of silicon to tetracene by up to 0.55 eV, and Boucher et al.17 show that small organic molecules covalently attached to the silicon surface can shift the bands by up to 1 eV. The silicon surface was still passivated well, which is a crucial requirement for an efficient charge extraction from the silicon solar cell. However, the cell was measured in an aqueous environment, which might be different from the solid-state interface needed in our case. The organic molecules can be tuned by molecular design, for example it was calculated that electron-withdrawing groups can shift the HOMO and LUMO of tetracene by up to 0.4 eV.18 Experimental evidence for pentacene shows a similar tunability.19

If the triplet energy is smaller than the silicon bandgap, then the smaller effective bandgap increases the dark recombination current, which leads to a voltage penalty for triplet energies smaller than the silicon bandgap. In Figure 3 a we plot the solar cell efficiency of the charge-transfer singlet-fission silicon solar cell as a function of the singlet energy of the singlet-fission material in light red. The singlet energy is also the absorption onset of our ideal absorber. The triplet energy is half of the singlet energy, plus an entropic gain term. The entropic gain can dramatically increase the efficiency of a singlet-fission solar cell as shown by the dashed lines in Figure 3a. The details of the calculation can be found in the Supporting Information S3.1.

Figure 3.

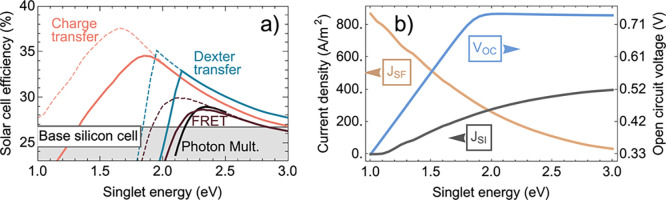
Figure 3

Open in a new tab

(a) Solar cell efficiency of charge transfer, Dexter energy transfer, and FRET as a function of the singlet energy of a theoretical singlet-fission material. The horizontal gray line is the record silicon solar cell that forms the bottom cell for the simulated singlet-fission solar cells with the different transfer schemes. The lines assume a 100 meV entropy gain, dashed lines assume an optimistic 300 meV entropy gain. We show the charge transfer (light red), Dexter transfer (blue), FRET (dark red), and Photon Multiplier (black) efficiencies. The photon multiplier results are taken from Futscher et al., 2018.20 The most efficient transfer mechanism is the charge transfer, which also shows the widest possible range of potential singlet-fission materials. (b) Different contributions to the charge-transfer solar cell efficiency for different singlet energies. We can see that the voltage penalty decreases the VOC below a singlet energy of 1.8 eV. JSF increases with lower singlet energy, since more absorbed photons can be converted by the singlet-fission process. The current generated in silicon decreases with lower singlet energy.

Naively, the maximum singlet-fission silicon solar cell efficiency could be expected at a singlet exciton energy of 2.2 eV, twice the silicon bandgap of 1.12 eV. However, this is not the case as seen in Figure 3a. The optimum singlet energy depends both on the transfer scheme and the entropic gain that is assumed. The charge-transfer model shows the maximum solar cell efficiency of 34.6% at a singlet exciton energy of 1.85 eV at 100 meV entropy gain, considerably lower than twice the silicon bandgap. To explain this behavior, we show the three most important quantities for the singlet-fission silicon solar cell efficiency: the short-circuit current from the singlet-fission layer (JSF), the silicon cell (JSi), and the solar cell open-circuit voltage (VOC), in Figure 3b with the same x-axis of singlet energy as in Figure 3a. JSF continuously increases with lower singlet energy thanks to an increased number of absorbed photons that can create two triplet excitons. At the same time JSi decreases, but not as quickly since every photon absorbed by the silicon cell generates at most one electron–hole pair. The voltage penalty, as seen in the decreasing VOC with decreasing singlet energy appears slightly below twice the silicon bandgap because of the entropic gain. Initially, the increase in photocurrent compensates the drop in voltage so that the efficiency optimum is in a regime where the solar cell suffers a small voltage penalty. The penalty only starts to reduce the efficiency below 1.85 eV. The fill factor also decreases with singlet energy, similarly to VOC, albeit not as strongly (see Figure S1 in the Supporting Information).

The entropic gain discussed earlier also leads to an increased efficiency and lower optimal singlet energy. Figure 3a shows the absolute efficiency gain plotted for 100 meV entropic gain and 300 meV entropic gain. Values of 200 and 220 meV have been observed in tetracene21 and perylene diimides (PDIs), respectively;22 see Supporting Information S4 for more details. These numbers only consider the entropic gain during the singlet-fission process in the singlet-fission material. Since there is also a certain density of states in silicon it is conceivable that an increased number of available states inside silicon could also lead to an additional entropy gain during the charge transfer. The change in entropy during the charge-transfer process will lead to a change in Gibbs free energy, G, via ΔG = −TΔS with the temperature T and the change in entropy ΔS. This formula for ΔG assumes that there is no change in enthalpy (ΔH = 0). The change in Gibbs free energy could therefore increase (ΔG < 0) or decrease (ΔG > 0) the transfer efficiency. The change in entropy can be calculated with the formula ΔS = kB(ln ΩS – ln ΩT) by counting the states in silicon ΩS and the available states of the free triplet exciton ΩT.

We will now perform a rough calculation for the additional entropy gain during the transfer between tetracene and silicon, assuming that the temperature stays constant. The number of states of a triplet excitons in tetracene has been calculated by Kolomeiskiy et al.21 by calculating the number of molecules within the Dexter radius of 10–20 Å. The number of molecules accessible for a triplet exciton is 19 for a Dexter radius of 10 Å, 37 for a radius of 15 Å, and 61 for a Dexter radius of 20 Å.

We can estimate the number of states in silicon by integrating square-root dependence of the density of states (units: Inline graphic) from the conduction band edge to 150 meV above the band edge. We use 150 meV since this is the difference in energy between the tetracene triplet exciton and silicon. Different effective masses for electrons and holes in silicon are taken into account, and the integral is split into two with integration boundaries for electron and hole from the band edge to 75 meV above. This calculation leads to a density of states of 0.12 nm–3. In silicon the exciton size is much larger than the Dexter radius since the dielectric constant is large (∼11) which leads to a large Wannier exciton of around 9 nm radius. This leads to a large number of states available within the sphere occupied by the Wannier exciton in silicon, namely 448. This change in the number of available states would lead to an additional entropy gain of 76 meV if the triplet state in tetracene has a Dexter radius of 10 Å, 59 meV for a Dexter radius of 15 Å, and 46 meV for a Dexter radius of 20 Å.

The additional entropy term could be beneficial to the transfer efficiency and potentially the solar cell efficiency. We calculated the entropy gain by using exciton radii which is presumably only realistic for a direct Dexter exciton transfer. Other transfer mechanisms might behave differently and our naive assumptions might not hold.

Also, the Coulomb barrier still needs to be overcome to dissociate the triplet excitons, and we can exchange entropic gain to overcome the barrier. In an organic solar cell, the band-like structure of the acceptor states in an organic PCBM crystal can supply up to 200 meV of entropic gain. However, in our case the triplet exciton is much smaller in size, which will lead to increased Coulombic binding energy and a weaker coupling between the triplet and the disassociated charges. The polarizability volume of triplet excitons is very small (10 times smaller than singlet excitons), which is an important metric for the charge separation efficiency.23 It is therefore important to consider the interplay of the two consequences of the localized nature of the triplet exciton: the increased Coulombic binding energy and the increased entropic gain during charge dissociation.

In Figure 3a we can see that a higher entropy term would extend the possible singlet-fission materials to lower singlet energies, as low as 1.65 eV at 300 meV entropy gain, where the efficiency is calculated to be 37.6%. We therefore conclude that it would be hugely beneficial to increase the entropy gain and thereby increase the singlet-fission silicon solar cell efficiency. Also, most synthetic efforts toward new singlet-fission molecules aim for singlet energies above 2 eV. However, our results show that singlet-fission materials with bandgaps below 2 eV are potentially even more interesting, since the peak of increased solar cell efficiency is very broad thanks to the trade-off between current gain and voltage loss in the charge transfer and the entropy gain.

Increasing the entropic gain will also lead to increased triplet diffusion lengths, since the singlet-mediated transport becomes more pronounced.24 The hole mobilities can be improved upon by chemically engineering the stacking of the molecules.25 Different side groups can influence the wavefunction overlap, orientation, and crystallinity, which can lead to greatly enhanced hole mobilities and increased stabilities.25

Since the charge-transfer scheme involves transport of holes from the singlet-fission material and silicon through tetracene, the low mobility of organic singlet-fission materials like tetracene will make charge extraction inefficient. This will be especially problematic since organic semiconductors have poor broadband absorption as described earlier, which necessitates thick singlet-fission absorber layers. To estimate the necessary hole mobilities and the resulting maximum thicknesses for any singlet-fission layer, we model the system using the Mott–Gurney law of space-charge-limited current. This model assumes that the contacts are not introducing any additional barriers, that the holes are not transported via traps and that the cell operates above the trap-filling voltage. The space-charge-limited current then becomes

graphic file with name nz1c00972_m002.jpg

with ε the singlet-fission material permittivity, μ the hole mobility, and L the layer thickness. We assume that we have to extract a typical current from the silicon cell at 1 sun of 40 mA/cm2 through the singlet-fission layer and that half of the silicon voltage drops over the singlet-fission layer, set to V = 0.36 V. With these assumptions we can solve for the thickness as a function of mobility as shown in Figure 4. We show three characteristic singlet-fission materials. A best-case scenario of single-crystal tetracene with a mobility of 2.4 cm2/(V·s)26 would allow for a maximum layer thickness of ∼1500 nm, which would lead to an ideal efficiency of 36% (Figure 1 b). The mobility in polyacenes is typically anisotropic,27 requiring aligned growth of the singlet-fission material for optimal performance. For pentacene the mobilities in two different crystal axes have a value of 0.45 cm2/(V·s) in the ab-plane and a 10 times lower mobility in the c-plane direction.27 In real devices, the transport would most likely occur in the low-mobility c-plane since that is the preferred growth direction on silicon,28,29 which would limit the singlet-fission layer thickness to 400 nm.

Figure 4.

Figure 4

Open in a new tab

Maximum singlet-fission layer thickness as a function of effective hole mobility. We assume a voltage drop of 0.36 eV and an extracted current of 40 mA/cm2.

Since there is a long history of research toward high-mobility organic materials for organic transistors30 that has yet to overcome mobilities above 20 cm2/(V·s) this is most likely a hard problem to solve with molecular engineering. However, if we use a sensitizer to efficiently absorb the light, we could design a much thinner singlet-fission layer combined with a thick absorber layer that also has a high mobility (e.g., a metal halide perovskite), which in turn puts lower requirements on the necessary hole mobility in the organic layer. Another strategy is the use of a bulk heterojunction, used in organic solar cells to overcome low mobilities by mixing the donor and acceptor phases resulting in much shorter transport distances, for example with a bulk heterojunction between the singlet-fission material and a hole extraction material such as PEDOT:PSS. Since there are already strategies to increase the solubility by functionalizing organic molecules with TIPS groups, such as TIPS-tetracene and TIPS-pentacene, a solution of singlet-fission material and hole extraction layer that could be spin-coated is feasible. Similarly, a very thin singlet-fission dye on a mesoporous substrate, as is used in dye-sensitized solar cells, could also overcome the absorption-length problem.

As mentioned above, another route would be to add buried contacts on top of silicon but below the singlet-fission layer that collects holes from both silicon and the singlet-fission material. If the lateral distance to a contact would be smaller than the film thickness, this geometry would also allow for shorter hole-transport distances. The lateral mobility in organic crystals can also be higher than the vertical mobility. However, the metal fingers used to collect charges on top of standard silicon solar cells would be unsuitable for this scheme since they are usually several millimeters apart. Metal grids with a pitch of 1 μm have been shown31 and could be combined with a singlet-fission charge-transfer solar cell. In case of a degraded singlet-fission layer, the direct collection of silicon holes at the silicon surface is also beneficial since the silicon solar cell might continue to be operational with an inactive, then transparent singlet-fission layer, as is the case for the anaerobic degradation of tetracene.32 Despite the attractive efficiency potential, charge transfer from triplet excitons into silicon has been attempted but not yet experimentally shown to occur with high transfer efficiencies.9

Dexter energy transfer directly transfers the whole triplet exciton energy at once, by concurrently transferring the electron and hole into the silicon. Since triplet excitons are dark states, FRET or photon emission cannot occur directly, and Dexter transfer is the only accessible energy-transfer mechanism. For efficient Dexter transfer, the wavefunction overlap between the triplet exited state on a singlet-fission molecule and the accepting material has to be large. In upconversion systems it has been shown that the triplet exciton states can be populated from electrons and holes occupying bands in inorganic semiconductors. A recent example is the sensitization of the rubrene triplet states by a lead halide perovskite film.33 These examples show the potential for large wavefunction overlap between the excitonic states and the band-like states.

The first demonstration of Dexter transfer from triplet excitons, generated by singlet fission, into an inorganic semiconductor was from tetracene into PbS quantum dots34 and from pentacene into PbSe quantum dots.35 After a long search, triplet transfer from tetracene into silicon has finally been demonstrated in a recent set of experimental studies,36,37 even though there is no conclusive evidence that the transfer mechanism was indeed Dexter transfer.

In our model we assume efficient transfer if the triplet energy is sufficient, meaning larger than the silicon bandgap. If the triplet energy is smaller than the silicon bandgap then we assume that the thermal energy can add to the total energy and allow the transfer. We implemented this by a population of triplets following the Maxwell–Boltzmann distribution. At room temperature, the energy of 25 meV is small compared to the exciton energy, so the efficiency for Dexter transfer falls dramatically if the triplet energy is too small, as can be seen in Figure 3 a by the steep decrease of efficiency at lower singlet energies. In practice, the Dexter-transfer solar cell would be very simple, just a single organic layer on top of a suitably prepared silicon solar cell. We assume no parasitic additional absorption since there are no additional extraction or dissociation layers, and as above, a quantum yield of 1.805 for the singlet-fission process, assuming an efficiency of 95% for both the triplet generation and triplet transfer. The details of the calculation can be found in the Supporting Information S3.2.

In comparison to charge transfer, Dexter transfer shows a higher efficiency for high singlet energies above 2.1 eV since the parasitic absorption is absent (Figure 3 a). The thick line in Figure 3 a is calculated with an entropic gain of 100 meV, the dashed line assumes a 300 meV entropic gain. The additional entropic gain extends the possible singlet energies down to lower values for potential singlet-fission materials, but shows the same abrupt decrease if the triplet energy is smaller than the silicon bandgap. We can see that the possible efficiencies are lower than in the charge-transfer case, with a maximum of 32.9% at 2.15 eV if 100 meV entropy gain is assumed and 35.2% at 1.95 eV for 300 meV entropy gain. This transfer scheme, however, might be easier to realize than the charge transfer or FRET (see below) since there is no need for an additional top contacts or quantum dot layer.

For the practical implementation one needs to consider the silicon passivation. Efficient silicon solar cells are typically covered with a layer of thick SiO2 or Si3N4 which acts both as a passivation layer and as an anti-reflection coating. For all transfer schemes the contact between the organic material and silicon needs to be close, thus one needs to remove the coating. While the low-index organic material would have some anti-reflection effect, the full performance would likely need to be restored by an additional anti-reflection layer on top of the organic layer. Also, the silicon layer would need to be passivated electronically. While some ultrathin layers have been developed (1.2 nm of SiO2,38 7 nm of Al2O3,39 15 nm of HfO240), they may still be too thick to transmit triplet excitons. In that case, ideally, the singlet-fission material would directly act as the passivation layer on silicon, for example by covalently attaching a singlet-fission molecule on the silicon surface.41

FRET is the dominating transfer for singlet excitons in organic semiconductors. However, since triplet exciton states are dark states, they cannot undergo FRET directly. It is, however, possible to transfer the excitons into an emissive material, for example quantum dots that have a large spin–orbit coupling so that triplet excitons can be converted into emissive excitons in these quantum dots. Then the exciton could be transferred into silicon via FRET. The main factor determining the efficiency of FRET between these quantum dots and the silicon acceptor is the very short Förster radius (distance at which transfer efficiency is 50%), which means that the quantum dots have to be very close (1 nm) to the silicon surface.42 The reason for the short Förster radius is the small overlap integral between the quantum dot emission at the silicon band-edge (1.12 eV) and the weak absorption cross section of silicon, an indirect-bandgap semiconductor. In an earlier work we have extended the FRET model that describes energy transfer between two dipoles to a more appropriate dipole–3D acceptor model, with a tunable bandgap PbS QD as the emitter and a slab of silicon as the acceptor. The distance dependence changes from a Inline graphic dependence of the dipole–dipole model to a Inline graphic dependence, making the transfer efficient for longer distances. The Förster radius in the 3D acceptor model for suitable quantum dots of 1.2 eV emission is 1.4 nm. In this work we simulate the dots directly at the interface, at a distance of 1 nm. The resulting transfer efficiency then depends on the wavelength of the emission since the overlap integral of the quantum dot PL and absorption changes. The PL emission wavelength is matched to the triplet energy of the singlet-fission material plus the entropic gain described earlier. Thus, we assume no energetic losses from the triplet energy transfer into the quantum dot. We assume no Stokes shift. The Stokes shift in PbS QDs originates in the polydispersity of the ensemble,43 in our case the QDs can be very dilute and presumably monodisperse, leading to a small or no Stokes shift. The details of the calculation can be found in the Supporting Information S3.3.

The triplet diffusion length has to be at least as long as the distance to a QD near the silicon surface. The transfer efficiency of triplets into the QDs is an additional loss channel and is assumed to be 90% efficient, a realistic number for small singlet-fission QD distances,34 leading to an overall quantum yield of 1.71. The parasitic absorption is assumed to be 5% due absorption in the QDs. In Figure 3a we show the efficiency as a function of singlet energy. The FRET curve follows the same general trend as the other transfer mechanisms, albeit with lower efficiency of 28.7% at a singlet energy of 2.33 eV in the 100 meV entropy gain case, because of additional parasitic absorption, additional transfer losses and quickly decreasing FRET efficiency at lower quantum dot emission energies. Additional entropy gains of 300 meV lead to a maximum efficiency of 30.0% at a singlet energy of 2.13 eV, extending the singlet exciton energies with an efficiency gain to lower energies, just as with the other two transfer mechanisms. In a realistic cell, this transfer scheme might be the easiest to manufacture, since it could be applied to any silicon solar cell with a thin passivation layer. However, for thick passivation layers that are currently the standard in silicon solar cells (for example a 80 nm Si3N4 passivation and antireflection layer) the FRET efficiency would effectively be zero and one would have to rely on the photon emission and absorption by the quantum dots, which necessitates new ways of directing the light downward toward silicon. We calculated the efficiency potential of such a “photon multiplier” scheme elsewhere,20 and include them in Figure 3 for completeness. The calculation uses the same record base cell and assumes a 100 meV entropy gain, a QD emission FWHM of 30 meV, a parasitic loss of 5%, and an 85% photon capture rate in the silicon cell. The maximum efficiency of 29.0% is achieved at a SF singlet energy of 2.34 eV. The photon multiplier results follow the FRET efficiencies, since they are closely related and differ only in the transfer efficiency of excitations from QD to silicon. In a real cell both transfer mechanisms will likely occur within the same structure, depending on the distance of the quantum dots to silicon.

The transfer efficiencies that have been discussed so far have been calculated with a record silicon solar cell of 26.7% efficiency.5 This is, however, not what is currently available commercially, so how does the performance change if the base cell is less efficient?

To explore the efficiency potential on a broad range of silicon base cells we used the same diode model as above but now with recombination constants and resistance values that fit the IV curves for these less efficient silicon solar cells. This approach is based on work of Futscher et al.20,44 The models for different silicon solar cells allow us to run the same calculations as before and observe the change with silicon cell efficiency. Figure 5 shows the results, with the optimal singlet energy for each transfer scheme and an entropy gain of 100 meV and other parameters as described above. As a comparison we have also included the results of an earlier calculation of an optimistic case for a perovskite–silicon two-terminal tandem solar cell.20 In this optimistic monolithic perovskite–silicon two-terminal tandem cell the perovskite top cell is as optimized in terms of non-radiative recombination and resistances as the current silicon record cell. We can see that the improvement in singlet-fission silicon solar cell efficiency is larger for more efficient base cells. This is in stark contrast to the behavior of the perovskite tandem cell, where the efficiency improvement decreases with more efficient base cells. The main reason for this difference is that we do not have to change the base cell at all for the singlet-fission case. The energetics and voltage matching stays the same, we simply inject additional current. The singlet-fission layer is connected optically in series, but electrically in parallel.45 Thus, to first order, the efficiency is increased by a certain percentage of the silicon efficiency, which leads to higher absolute efficiency gains for more efficient silicon cells. In the tandem solar cell, both cells have to be electrically connected and the electrical properties of the full cell are limited by each of the subcells, so it is easy to degrade the highly optimized record silicon solar cells. Therefore, the largest relative gains in efficiency with singlet fission can be found in already efficient base cells, where they are otherwise most difficult to achieve and most valuable.

Figure 5.

Figure 5

Open in a new tab

Calculated efficiency potential of singlet-fission silicon solar cells for charge transfer, Dexter transfer, and FRET, compared with the efficiency potential of perovskite–silicon tandem solar cells as a function of base silicon cell efficiency. Lines are a linear fit to the data points. The gray line is the base silicon solar cell. The efficiency gain grows for better silicon base cells in the case of singlet-fission cells, and vice versa for tandem solar cells.

Singlet fission can lead to large absolute efficiency gains for silicon solar cells. While the best silicon solar cells are now very difficult to improve, with sub-percent level improvements celebrated as great successes, singlet fission can potentially increase the efficiency of a record silicon solar cell from 26.7% to 37.6%. Such a huge efficiency improvement could be reached with charge transfer from the triplet state into silicon when all processes work well: the singlet-fission material absorbs all light above its bandgap, the efficiency of singlet fission is 95%, the triplet transfer is 95% efficient, the entropic gain during singlet fission is 300 meV, and the additional resistance and optical losses in the silicon cell are small (doubled series resistance and 3% parasitic absorption). With the exception of charge transfer from the triplet state into silicon, each of these quantities has been demonstrated individually, but the combination will still be a significant challenge to achieve. Yet, even somewhat less optimistic assumptions can lead to massive efficiency gains. We have shown that all transfer mechanisms can improve on the efficiency of silicon solar cells. Maybe most surprising is that the charge-transfer route of triplet dissociation and subsequent hole and electron collection is most efficient and most forgiving in terms of the viable singlet energies. The voltage penalty is partially offset by the larger portion of light absorbed in the organic material, such that the efficiency gain is less dramatically affected than naïvely assumed. Dexter energy transfer is simpler to implement, but the energetics of the process restricts the potential singlet-fission materials. FRET is also somewhat promising, but the additional transfer step has to be efficient and the parasitic absorption has to be low. The distance between quantum dots and silicon also has to be small since the Förster distance is small. All transfer schemes share the requirement of direct access to the silicon surface which will require the use of new passivation and anti-reflection coatings. A conventional 80 nm silicon nitride coating would not be compatible with these transfer schemes. A good surface passivation is also crucial, otherwise the additional gains from singlet fission are lost via recombination at the silicon surface, an especially important aspect in the case Dexter transfer and FRET, as most charge carriers in the silicon will be generated close to the surface. It is thus of great importance for these singlet-fission silicon solar cells to find thin (<1 nm) passivation layers that lead to very low surface recombination. Recent developments with metal oxides37 and molecular monolayers46 show promise. Alternatively, schemes where the singlet-fission material injects the triplet energy at point contacts and the remainder of the surface is well-passivated with a thick insulator could work with existing passivation materials. Our work shows that the search for new singlet-fission materials can be potentially less strict on the triplet energy requirements if charge-transfer schemes are adopted, but that the entropic gain is hugely important for the potential efficiency gain, and should hence get more attention in the design of the molecules and the crystal stacking thereof. A major benefit of singlet-fission silicon solar cells is that it will be easier to improve on already efficient silicon solar cells, which is most important for lowering the cost of solar energy. In that sense, singlet-fission silicon solar cells may form the next step after tandem solar cells have entered the market. They are potentially easier to fabricate and implement, and can possibly even be retrofitted, and benefit from highly efficient silicon base cells that are harder to improve in a tandem geometry.

Acknowledgments

The work is part of the Dutch Research Council (NWO) and was performed at the research institute AMOLF. The authors thank Juliane Borchert for commenting on the manuscript.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsenergylett.1c00972.

  • Methods and formulas describing the different transfer mechanisms (PDF)

The authors declare no competing financial interest.

Supplementary Material

nz1c00972_si_001.pdf (403.7KB, pdf)

References

  1. Bogdanov D.; Farfan J.; Sadovskaia K.; Aghahosseini A.; Child M.; Gulagi A.; Oyewo A. S.; Barbosa L. d. S. N. S.; Breyer C. Radical transformation pathway towards sustainable electricity via evolutionary steps. Nat. Commun. 2019, 10, 1077. 10.1038/s41467-019-08855-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Creutzig F.; Agoston P.; Goldschmidt J. C.; Luderer G.; Nemet G.; Pietzcker R. C. The underestimated potential of solar energy to mitigate climate change. Nature Energy 2017, 2, 17140. 10.1038/nenergy.2017.140. [DOI] [Google Scholar]
  3. NREL, Best Research-Cell Efficiency Chart, 2020; https://www.nrel.gov/pv/cell-efficiency.html (accessed Nov 4, 2020).
  4. Tiedje T.; Yablonovitch E.; Cody G. D.; Brooks B. G. Limiting Efficiency of Silicon Solar Cells. IEEE Trans. Electron Devices 1984, 31, 711–716. 10.1109/T-ED.1984.21594. [DOI] [Google Scholar]
  5. Green M. A.; Hishikawa Y.; Warta W.; Dunlop E. D.; Levi D. H.; Hohl-Ebinger J.; Ho-Baillie A. W. Solar Cell Efficiency Tables (Version 50). Prog. Photovoltaics 2017, 25, 668–676. 10.1002/pip.2909. [DOI] [Google Scholar]
  6. Smith M. B.; Michl J. Singlet fission. Chem. Rev. 2010, 110, 6891–6936. 10.1021/cr1002613. [DOI] [PubMed] [Google Scholar]
  7. Köhler A.; Bässler H. The Electronic Structure of Organic Semiconductors. Electronic Processes in Organic Semiconductors 2015, 307–388. 10.1002/9783527685172.ch4. [DOI] [Google Scholar]
  8. Wilson M. W.; Rao A.; Clark J.; Kumar R. S. S.; Brida D.; Cerullo G.; Friend R. H. Ultrafast Dynamics of Exciton Fission in Polycrystalline Pentacene. J. Am. Chem. Soc. 2011, 133, 11830–11833. 10.1021/ja201688h. [DOI] [PubMed] [Google Scholar]
  9. Macqueen R. W.; Liebhaber M.; Niederhausen J.; Mews M.; Gersmann C.; Jäckle S.; Jäger K.; Tayebjee M. J.; Schmidt T. W.; Rech B.; Lips K. Crystalline Silicon Solar Cells With Tetracene Interlayers: The Path to Silicon-Singlet Fission Heterojunction Devices. Mater. Horiz. 2018, 5, 1065–1075. 10.1039/C8MH00853A. [DOI] [Google Scholar]
  10. Ehrler B.; Wilson M. W.; Rao A.; Friend R. H.; Greenham N. C. Singlet Exciton Fission-Sensitized Infrared Quantum Dot Solar Cells. Nano Lett. 2012, 12, 1053–1057. 10.1021/nl204297u. [DOI] [PubMed] [Google Scholar]
  11. Poletayev A. D.; Clark J.; Wilson M. W.; Rao A.; Makino Y.; Hotta S.; Friend R. H. Triplet Dynamics in Pentacene Crystals: Applications to Fission-Sensitized Photovoltaics. Adv. Mater. 2014, 26, 919–924. 10.1002/adma.201302427. [DOI] [PubMed] [Google Scholar]
  12. Akselrod G. M.; Deotare P. B.; Thompson N. J.; Lee J.; Tisdale W. A.; Baldo M. A.; Menon V. M.; Bulovic V. Visualization of Exciton Transport in Ordered and Disordered Molecular Solids. Nat. Commun. 2014, 5, 3646. 10.1038/ncomms4646. [DOI] [PubMed] [Google Scholar]
  13. Lu H.; Chen X.; Anthony J. E.; Johnson J. C.; Beard M. C. Sensitizing Singlet Fission with Perovskite Nanocrystals. J. Am. Chem. Soc. 2019, 141, 4919–4927. 10.1021/jacs.8b13562. [DOI] [PubMed] [Google Scholar]
  14. Pazos-Outón L. M.; Lee J. M.; Futscher M. H.; Kirch A.; Tabachnyk M.; Friend R. H.; Ehrler B. A Silicon-Singlet Fission Tandem Solar Cell Exceeding 100% External Quantum Efficiency with High Spectral Stability. ACS Energy Letters 2017, 2, 476–480. 10.1021/acsenergylett.6b00678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Congreve D. N.; Lee J.; Thompson N. J.; Hontz E.; Yost S. R.; Reusswig P. D.; Bahlke M. E.; Reineke S.; Van Voorhis T.; Baldo M. A. External Quantum Efficiency Above 100% in a Singlet-Exciton-Fission–Based Organic Photovoltaic Cell. Science 2013, 340, 334–337. 10.1126/science.1232994. [DOI] [PubMed] [Google Scholar]
  16. Niederhausen J.; et al. Energy-Level Alignment Tuning at Tetracene/c-Si Interfaces. J. Phys. Chem. C 2020, 124, 27867–27881. 10.1021/acs.jpcc.0c08104. [DOI] [Google Scholar]
  17. Boucher D. G.; Kearney K.; Ertekin E.; Rose M. J. Tuning p-Si(111) Photovoltage via Molecule| Semiconductor Electronic Coupling. J. Am. Chem. Soc. 2021, 143, 2567–2580. 10.1021/jacs.0c12075. [DOI] [PubMed] [Google Scholar]
  18. Shen L.; Chen Y.; Li X.; Gao J. Effects of substituents on tetracene derivatives on their stabilities and singlet fission. J. Mol. Graphics Modell. 2014, 51, 86–96. 10.1016/j.jmgm.2014.04.017. [DOI] [PubMed] [Google Scholar]
  19. Kaur I.; Jia W.; Kopreski R. P.; Selvarasah S.; Dokmeci M. R.; Pramanik C.; McGruer N. E.; Miller G. P. Substituent Effects in Pentacenes: Gaining Control over HOMO LUMO Gaps and Photooxidative Resistances. J. Am. Chem. Soc. 2008, 130, 16274–16286. 10.1021/ja804515y. [DOI] [PubMed] [Google Scholar]
  20. Futscher M. H.; Rao A.; Ehrler B. The Potential of Singlet Fission Photon Multipliers as an Alternative to Silicon-Based Tandem Solar Cells. ACS Energy Letters 2018, 3, 2587–2592. 10.1021/acsenergylett.8b01322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kolomeisky A. B.; Feng X.; Krylov A. I. A Simple Kinetic Model for Singlet Fission: A Role of Electronic and Entropic Contributions to Macroscopic Rates. J. Phys. Chem. C 2014, 118, 5188–5195. 10.1021/jp4128176. [DOI] [Google Scholar]
  22. Eaton S. W.; Shoer L. E.; Karlen S. D.; Dyar S. M.; Margulies E. A.; Veldkamp B. S.; Ramanan C.; Hartzler D. A.; Savikhin S.; Marks T. J.; Wasielewski M. R. Singlet Exciton Fission in Polycrystalline Thin Films of a Slip-Stacked Perylenediimide. J. Am. Chem. Soc. 2013, 135, 14701–14712. 10.1021/ja4053174. [DOI] [PubMed] [Google Scholar]
  23. Pace N. A.; Clikeman T. T.; Strauss S. H.; Boltalina O. V.; Johnson J. C.; Rumbles G.; Reid O. G. Triplet Excitons in Pentacene Are Intrinsically Difficult to Dissociate via Charge Transfer. J. Phys. Chem. C 2020, 124, 26153–26164. 10.1021/acs.jpcc.0c08537. [DOI] [Google Scholar]
  24. Zhu T.; Wan Y.; Guo Z.; Johnson J.; Huang L. Two Birds with One Stone: Tailoring Singlet Fission for Both Triplet Yield and Exciton Diffusion Length. Adv. Mater. 2016, 28, 7539–7547. 10.1002/adma.201600968. [DOI] [PubMed] [Google Scholar]
  25. Petty A. J.; Ai Q.; Sorli J. C.; Haneef H. F.; Purdum G. E.; Boehm A.; Granger D. B.; Gu K.; Rubinger C. P. L.; Parkin S. R.; Graham K. R.; Jurchescu O. D.; Loo Y.-L.; Risko C.; Anthony J. E. Computationally aided design of a high-performance organic semiconductor: the development of a universal crystal engineering core. Chem. Sci. 2019, 10, 10543–10549. 10.1039/C9SC02930C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Reese C.; Chung W. J.; Ling M. M.; Roberts M.; Bao Z. High-Performance Microscale Single-Crystal Transistors by Lithography on an Elastomer Dielectric. Appl. Phys. Lett. 2006, 89, 202108. 10.1063/1.2388151. [DOI] [Google Scholar]
  27. Günther A. A.; Widmer J.; Kasemann D.; Leo K. Hole Mobility in Thermally Evaporated Pentacene: Morphological and Directional Dependence. Appl. Phys. Lett. 2015, 106, 233301. 10.1063/1.4922422. [DOI] [Google Scholar]
  28. Suzuki T.; Yagyu K.; Tochihara H. Initial Growth of Pentacene Thin Film on Si(001) Substrate. J. Phys. Chem. C 2019, 123, 2996–3003. 10.1021/acs.jpcc.8b11238. [DOI] [Google Scholar]
  29. Suzuki T.; Yagyu K.; Tochihara H. Initial Growth of Pentacene on a Si(111)- Surface. Phys. Chem. Chem. Phys. 2020, 22, 14748–14755. 10.1039/D0CP01582B. [DOI] [PubMed] [Google Scholar]
  30. Paterson A. F.; Singh S.; Fallon K. J.; Hodsden T.; Han Y.; Schroeder B. C.; Bronstein H.; Heeney M.; McCulloch I.; Anthopoulos T. D. Recent Progress in High-Mobility Organic Transistors: A Reality Check. Adv. Mater. 2018, 30, 1801079. 10.1002/adma.201801079. [DOI] [PubMed] [Google Scholar]
  31. Knight M. W.; van de Groep J.; Bronsveld P. C.; Sinke W. C.; Polman A. Soft Imprinted Ag Nanowire Hybrid Electrodes on Silicon Heterojunction Solar Cells. Nano Energy 2016, 30, 398–406. 10.1016/j.nanoen.2016.10.011. [DOI] [Google Scholar]
  32. Jiang Y.; Nielsen M. P.; Baldacchino A. J.; Green M. A.; McCamey D. R.; Tayebjee M. J. Y.; Schmidt T. W.; Ekins-Daukes N. J. Singlet Fission and Tandem Solar Cells Reduce Thermal Degradation and Enhance Lifespan. Prog. Photovoltaics 2021, 10.1002/pip.3405. [DOI] [Google Scholar]
  33. Nienhaus L.; Correa-Baena J. P.; Wieghold S.; Einzinger M.; Lin T. A.; Shulenberger K. E.; Klein N. D.; Wu M.; Bulović V.; Buonassisi T.; Baldo M. A.; Bawendi M. G. Triplet-Sensitization by Lead Halide Perovskite Thin Films for Near-infrared-to-Visible Upconversion. ACS Energy Letters 2019, 4, 888–895. 10.1021/acsenergylett.9b00283. [DOI] [Google Scholar]
  34. Thompson N. J.; Wilson M. W. B.; Congreve D. N.; Brown P. R.; Scherer J. M.; Bischof T. S.; Wu M.; Geva N.; Welborn M.; Voorhis T. V.; Bulović V.; Bawendi M. G.; Baldo M. A. Energy harvesting of non-emissive triplet excitons in tetracene by emissive PbS nanocrystals. Nat. Mater. 2014, 13, 1039–1043. 10.1038/nmat4097. [DOI] [PubMed] [Google Scholar]
  35. Tabachnyk M.; Ehrler B.; Gélinas S.; Böhm M. L.; Walker B. J.; Musselman K. P.; Greenham N. C.; Friend R. H.; Rao A. Resonant Energy Transfer of Triplet Excitons From Pentacene to Pbse Nanocrystals. Nat. Mater. 2014, 13, 1033–1038. 10.1038/nmat4093. [DOI] [PubMed] [Google Scholar]
  36. Daiber B.; Maiti S.; Ferro S. M.; Bodin J.; van den Boom A. F.; Luxembourg S. L.; Kinge S.; Pujari S. P.; Zuilhof H.; Siebbeles L. D.; Ehrler B. Change in Tetracene Polymorphism Facilitates Triplet Transfer in Singlet Fission-Sensitized Silicon Solar Cells. J. Phys. Chem. Lett. 2020, 11, 8703–8709. 10.1021/acs.jpclett.0c02163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Einzinger M.; Wu T.; Kompalla J. F.; Smith H. L.; Perkinson C. F.; Nienhaus L.; Wieghold S.; Congreve D. N.; Kahn A.; Bawendi M. G.; Baldo M. A. Sensitization of Silicon by Singlet Exciton Fission in Tetracene. Nature 2019, 571, 90–94. 10.1038/s41586-019-1339-4. [DOI] [PubMed] [Google Scholar]
  38. Glunz S. W.; Feldmann F. SiO2 Surface Passivation Layers – a Key Technology for Silicon Solar Cells. Sol. Energy Mater. Sol. Cells 2018, 185, 260–269. 10.1016/j.solmat.2018.04.029. [DOI] [Google Scholar]
  39. Hoex B.; Schmidt J.; Pohl P.; Van De Sanden M. C.; Kessels W. M. Silicon Surface Passivation by Atomic Layer Deposited Al2O3. J. Appl. Phys. 2008, 104, 044903. 10.1063/1.2963707. [DOI] [Google Scholar]
  40. Zhang X. Y.; Hsu C. H.; Lien S. Y.; Chen S. Y.; Huang W.; Yang C. H.; Kung C. Y.; Zhu W. Z.; Xiong F. B.; Meng X. G. Surface Passivation of Silicon Using HfO2 Thin Films Deposited by Remote Plasma Atomic Layer Deposition System. Nanoscale Res. Lett. 2017, 12, 324. 10.1186/s11671-017-2098-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Daiber B.; Pujari S. P.; Verboom S.; Luxembourg S. L.; Tabernig S. W.; Futscher M. H.; Lee J.; Zuilhof H.; Ehrler B. A Method to Detect Triplet Exciton Transfer From Singlet Fission Into Silicon Solar Cells: Comparing Different Surface Treatments. J. Chem. Phys. 2020, 152, 114201. 10.1063/1.5139486. [DOI] [PubMed] [Google Scholar]
  42. Tabernig S. W.; Daiber B.; Wang T.; Ehrler B. Enhancing Silicon Solar Cells With Singlet Fission: The Case for Förster Resonant Energy Transfer Using a Quantum Dot Intermediate. J. Photonics Energy 2018, 8, 1. 10.1117/1.JPE.8.022008. [DOI] [Google Scholar]
  43. Voznyy O.; Levina L.; Fan F.; Walters G.; Fan J. Z.; Kiani A.; Ip A. H.; Thon S. M.; Proppe A. H.; Liu M.; Sargent E. H. Origins of Stokes Shift in PbS Nanocrystals. Nano Lett. 2017, 17, 7191–7195. 10.1021/acs.nanolett.7b01843. [DOI] [PubMed] [Google Scholar]
  44. Futscher M. H.; Ehrler B. Efficiency Limit of Perovskite/Si Tandem Solar Cells. ACS Energy Letters 2016, 1, 863–868. 10.1021/acsenergylett.6b00405. [DOI] [Google Scholar]
  45. Hanna M. C.; Nozik A. J. Solar conversion efficiency of photovoltaic and photoelectrolysis cells with carrier multiplication absorbers. J. Appl. Phys. 2006, 100, 074510. 10.1063/1.2356795. [DOI] [Google Scholar]
  46. Veerbeek J.; Firet N. J.; Vijselaar W.; Elbersen R.; Gardeniers H.; Huskens J. Molecular Monolayers for Electrical Passivation and Functionalization of Silicon-Based Solar Energy Devices. ACS Appl. Mater. Interfaces 2017, 9, 413–421. 10.1021/acsami.6b12997. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nz1c00972_si_001.pdf (403.7KB, pdf)

Articles from ACS Energy Letters are provided here courtesy of American Chemical Society

RESOURCES