Abstract
Silk fibroin is the structural fiber of the silk filament and it is usually separated from the external protein, named sericine, by a chemical process called degumming. This process consists of an alkali bath in which the silk cocoons are boiled for a determined time. It is also known that the degumming process impacts the property of the outcoming silk fibroin fibers. In this work, we described the dataset obtained from a Design of Experiment (DoE) screening made on the alkali degumming. Four process factors were considered: the number of degumming baths, the process time, the process temperature, and the salt concentration. The data on the properties of the silk fibroin fibers were collected. In particular, the molecular weight was obtained by gel permeation chromatography (GPC), the mechanical data by tensile test and the secondary structure by Fourier Infrared Transform Spectroscopy (FTIR).
Keywords: Silk Fibroin, Fibers, Alkali Degumming, Design of Experiment
Specifications Table
| Subject | Biomaterials |
| Specific subject area | Silk Fibroin Fibers properties and their correlation with the degumming process. |
| Type of data | Table |
| How data were acquired | Analytic Balance, Kern ABS. Perkin Elmer Nano Drop UV spectrophotometer. Fourier-transform infrared - Attenuated Total Reflectance spectroscopy (FTIR-ATR), Perkin Elmer, Spectrum ONE equipped with a ZnSe crystal. Universal testing machine, Nanotensile machine Agilent T150. Gel permeation chromatography system (GPC): SB-806MHQ Shodex column (8.0 × 300 mm Exclusion limit [Pullulan] 4000E3) mounted on the pumping system (spectra system p4000 with a 20 µL loop and a vacuum membrane degasser thermo Electron SCM1000), UV detecting system Jasco UV-1570. |
| Data format | Dataset of the extrapolated data from the raw curve and dataset including the raw curves. |
| Parameters for data collection | The FTIR spectra were collected on each sample by mediating 16 scans in the 400–4000 cm−1 range with a resolution of 1 cm−1. The mechanical test of the fiber was done in controlled conditions of 20–21 °C and relative humidity 39–42%. The gel permeation chromatograms were collected by keeping the eluent at 27 °C throught a custom-built oven. |
| Description of data collection | The Weight loss (%) was obtained by weight difference. The Sericin removed (%) was obtained by UV-spectrophotometry. Ultimate Strength (MPa), Ultimate Strain (%), Young's modulus (MPa), Toughness modulus (MJ/m3) were obtained by analyzing the stress-strain curves. The fibers diameter were obtained by optical microscopy. The Relative amount of secondary structures (%) were obtained by FTIR-ATR. The Peak Molecular Weight (kDa), the Number average Molecular Weight (kDa), and Weight average Molecular Weight (kDa) were obtained by analyzing the chromatographs obtained by GPC. |
| Data source location | Institution: BIOTech Research Center, University of Trento City/Town/Region: Trento Country: Italy Latitude and longitude (and GPS coordinates, if possible) for collected samples/data: Latitude 46.0748° N, Longitude 11.1217° E |
| Data accessibility | Data is available in a public repository. Repository name: IEEE Dataport Data identification number: 10.21227/emar-9460 Direct URL to data: https://ieee-dataport.org/open-access/full-factorial-design-experiment-dataset-silk-fibroin-alkaly-degumming Instructions for accessing these data: Data is freely and openly available at the reported link. The use of the data is regulated by the creative commons. |
| Related research article | Alessio Bucciarelli, Gabriele Greco, Ilaria Corridori, Nicola M. Pugno, and Antonella Motta, A Design of Experiment Rational Optimization of the Degumming Process and Its Impact on the Silk Fibroin Properties, ACS Biomater. Sci. Eng. 2021, 7, 4, 1374–1393. 10.1021/acsbiomaterials.0c01657 |
Value of the Data
-
•
The data collected represents one of the first attempt to standardize a process on silk fibroin by the use of a statistical experimental design, opening new possibility in terms of the control of the material properties.
-
•
All the researchers on biomaterials and industries manufacturing silk can benefit the use of the collected data.
-
•
The data is in tidy format, ready to be used for further statistical analysis. Predictive models can easily be extrapolated from the analysis of the dataset.
1. Data Description
Silk is a natural fiber secreted by several arthropods with different purposes, from the prey capture in spiders [1] to the cocoons building in silk worms. Silk is known for several centuries and used to produce textiles. Also, the application of silk in biomedical fields is ancient: silk has been used as suture filament until the era of synthetic materials. The silk bave produced by Bombyx mori silkworm consists of two proteins in a core-shell structure in which two fibroin protein fibres (known as brin) are glued together by sericin, the external globular protein [2], [3], [4] (Fig. 1A). Fibroin is the structural protein and is responsible for the unique mechanical properties of silk, instead, sericin acts like a glue helping in the formation of the cocoon. Up to the typology of silk, sericin impacts 25–30% of the cocoon weight while the rest of the weight is due to fibroin [5].
Fig. 1.
(A) SEM of the progressive removal of sericin during the degumming process (scale bar 20 µm). The degumming starts from the outer shells were sericin is solubilized until the fibroin brins are completely clean. (B) Schematic structure of the silk bave and (C) the degumming process.
Nowadays, among other biopolymers, silk fibroin is widely used in tissue engineering for the development of films, porous and non-porous scaffolds, and other bio-related arichitectures [6] that exploit its usage in frontier applications, such as bio-eletronic [7] and bio-optic [8]. All this plethora of different materials starts from the extraction of the internal filaments of fibroin in a process called degumming. This process involves the use of a hot bath of Sodium Carbonate (Na2CO3) in which the cut cocoons are immersed for a determined amount of time. This allows the solubilization of the sericin, while the internal fibroin fibers remain intact [9] (SEM images of Fig. 1B). This process is schematically shown in Fig. 1C and involves 4 main factors: A-Number of baths, B-Process time, C-Process temperature, and D-Salt concentration. The process was studied in detail using a 24 Design of Experiment (DoE) [10] approach, which results are reported in our previous study [9]. This methodology allowed us to build predictive models of the properties of interest (called yield) based on the process parameters (called factors) [11,12] without any consideration about the underlining chemical and physical mechanisms that are usually taken into account in mechanistic approaches. The principle of DoE is schematically shown in Fig. 2A. The factor space explored is schematically summarized in Fig. 2B. For each factor, we choose 2 levels reported in Table 1. We explored all the possible levels combinations of the 4 studied factors for a total of 16 different degumming treatments described in our previus work [9].
Fig. 2.
(A) Scheme of how the data was collected, the process was considered as a black box, in which the controllable factors and the uncontrollable factors contributes to modify the material and its properties (yields). The effect of the uncontrollable factors has been mediated to zero by randomizing the trials. (B) The portion of the variables space studied. The space is split in two due to the presence of one discrete variable (the number of baths). The coordinates reports the time of the process in minutes, the temperature of the process in degrees Celsius and the salt concentration in grams over liter.
Table 1.
Factors and corresponding levels used to conduct the experiment. The 16 combinations of all the factors and all the levels can be easily recognized inside the dataset.
| Variable | Factor | Type | +1 Lv | -1 Lv |
|---|---|---|---|---|
| Number of baths | A | Discrete | 1 | 2 |
| Time (min) | B | Continuous | 90 | 20 |
| Temperature (°C) | C | Continuous | 98 | 70 |
| Salt Concentration (g/mL) | D | Continuous | 0.1 | 1.1 |
The results of the data analysis and the empirical models are available in our published work [9]. All the data collected has been organized into a dataset available in a public repository [13]. The data contained in the first sheet of the dataset is in tidy format (each row corresponds to an observation) and can be directly imported in R [14] and elaborated with the package Tidyverse. It should be noticed that the row with the standard order 49 corresponds to the reference degumming, while 50 corresponds to the test made on the bare silk fiber (not degummed). In this last case, neither the mass loss nor the secondary structures were determined. In fact, the examination of the secondary structure could not be done due to the sericin coating of the fiber. Each column is briefly described in the following list:
-
•
Column 1: Standard order of the run.
-
•
Column 2: Run order, the randomized order in which the samples were prepared.
-
•
Column 3: Factor A of the studied process, the number of baths. This is the only discrete factor of the process; it could assume only two values 1 or 2.
-
•
Column 4: Factor B of the process, the process time in minutes. This is a continuous factor. The levels choose were 20 min and 90 min.
-
•
Column 5: Factor C of the process, the process temperature in degrees Celsius. This is a continuous factor. The choose levels were 70 °C and 98 °C.
-
•
Column 6: Factor D of the process, the salt concentration of the bath in gram per litres. This is a continuous factor. The choose levels were 0.1 g/L and 1.1 g/L.
-
•
Column 7: Yield 1, Mean mass loss in the process in g calculated over 3 trials.
-
•
Column 8: Yield 2, Mean mass loss in the process in percentage.
-
•
Column 9: Yield 3, Mean mass in g of the sericin individuated by spectroscopic method inside the degumming bath correspondent to the removed sericin from the cocoons. This was calculated over 3 trials.
-
•
Column 10: Yield 4, The mean amount of removed sericin in % on the weight of the cocoons calculated on 3 trials.
-
•
Column 11: Yield 5, Hypothetical percentage of sericin still on the cocoons calculated on 3 trials considering the reference sample as completely degummed.
-
•
Column 12: Yield 6, Mean ultimate strength in MPa calculated as mean over at least 9 fibers per treatment (at least 3 for each replica). The value was evaluated as the strength reached when the fiber was broken.
-
•
Column 13: Yield 7, Standard deviation in MPa of the ultimate strength.
-
•
Column 14, Yield 8, Mean Young's modulus in GPa calculated as mean over at least 9 fibers per treatment (at least 3 for each replica). The value was evaluated as the angular coefficient of the stress-strain curve in the elastic part.
-
•
Column 15: Yield 9, Standard deviation in GPa of the Young's modulus.
-
•
Column 16: Yield 12, Mean ultimate strain in percentage as mean over at least 9 fibers per treatment (at least 3 for each replica). The value was evaluated as the strain reached when the fiber was broken.
-
•
Column 17: Yield 13, Standard deviation in percentage of the Strain at break.
-
•
Column 18: Yield 14, Mean toughness modulus in MJ/m3 calculated as mean over at least 9 fibers per treatment (at least 3 for each replica).
-
•
Column 19: Yield 15, Standard deviation of the toughness modulus.
-
•
Column 20: Yield 16, Mean fibers diameter in µm as mean over at least 9 fibers per treatment (at least 3 for each replica).
-
•
Column 21: Yield 17, Standard deviation of the mean fiber diameter.
-
•
Column 22: Yield 18, Estimation of the amount of Antiparallel β structures in percentage.
-
•
Column 23: Yield 19, Estimation of the amount of Native β structures in percentage.
-
•
Column 24: Yield 20, Estimation of the amount of Random coil structures in percentage.
-
•
Column 25: Yield 21, Estimation of the amount of β Turns structures in percentage.
-
•
Column 26: Yield 22, Estimation of the amount of Parallel β structures in percentage.
-
•
Column 27: Yield 23, Estimation of the amount of β structures (Native +antiparallel +parallel) in percentage.
The second sheet contains the information on the molecular weight of the tested samples. In this case, only one sample for each triplicate was tested. Both the standard order and the run order referred to the same samples of the first sheet. In the following list, each column is briefly described:
-
•
Column 1: Standard order of the run.
-
•
Column 2: Run order, the randomized order in which the samples were prepared.
-
•
Column 3: Peak molecular weight. The value in kDa of the peak in the GPC curve.
-
•
Column 4: Number average molecular mass in kDa, calculated from the GPC curve.
-
•
Column 5: Weight average molecular weight in kDa, calculated from the GPC curve.
-
•
Polydispersity index: Calculated from Columns 4 and 5.
In our raw data zip archive, two files are present, namely mechanical curve and molecular weight. The raw mechanical curves are reported in OriginLab format divided in datasheets numbered -as the sample from 1 to 48- with the additions of two datasheets, one for the reference curves (Ref) obtained from the Rockwood protocol [14] and the second from the raw cocoons (Raw). The single datasheets reports the stress and strain in the consecutive columns. The GPC data is reported in an excel file, the data is subdivided using the number of the tested sample (one sample for each treatment and one for the reference). For each sample we report the GPC signal, the logarithm of the molecular weight and the molecular weight calculated using Eqs. (8) and (9). The other two columns refer to the calculation of the numerator and denominator appearing in Eq. (10), from which the number average molecular weight (Mn), the weight average molecular weight (Mw) and the polydispersity index (D) have been calculated.
2. Experimental Design, Materials and Methods
2.1. Statistical analysis
A 24 full factorial design has been used to design the experiment and to collect the data. The process factors considered, and their respective levels are reported in Table 1. The complete empirical equation is reported in Eq. (1). The normality of the distributions of the data collected was tested to verify the basic assumption in the application of the design of experiment method. We studied some properties of interest (yield) and we built a predictive model based on the process factors. The considered yields are reported in Table 2, including the number of measurements conducted for each replica. It is important to notice that terms above the first order are not usually considered in methods that study the variation of one property vs. one factor. A Pareto plot and a half-normal plot were initially used to evaluate which terms need to be included in the model (terms which effect deviate from the normality). In the Pareto plot, the effects were listed in order of magnitude and only the effects higher than the critical t-value were chosen. The effects were also reported as second check in the half-normal plot and only the ones that resulted to be significantly out from the line (indicating the normality) were chosen. An analysis of variance (ANOVA) test was then performed to evaluate the significance of the selected terms and of the resulting model, consequently, the insignificant terms were eliminated. The terms were significant if their p value resulted to be <0.1 (90% of confidence interval), instead the model was considered significant only with p<0.05 (95% confidence interval). This discrepancy between the single terms and the model has been chosen to consider the intrinsic nature of silk fibroin, in which, as in any natural material, the property could vary from batch to batch. So, to detect the effect of the single factors (and eventually their combination) a larger confidence interval has been used. All the statistical tests were double tailed. The function of the considered yield (F(Y)) was selected to make the residuals normally distributed and without pattern. The entire process was then iterated again, considering the outcoming values of the function of the effects instead of the bare effects’ values.
| (1) |
Table 2.
Studied material properties, method of measurement and number of tests conducted for each replica. We performed only one measurement of the weight loss and the sericin removed per trial. We also performed only one measurement/replica for the FTIR and one measurement/treatment (only one measurement over the three replicas) in the case of the GPC because of the complexity of the technique. Instead, due to the variability of the tensile test, we perform it at least on 3 fibers per replica contemporary measuring the diameter by optical microscopy.
| Measured Properties | Method | n.measure/replica | Sheet | Mean | St. Deviation |
|---|---|---|---|---|---|
| Weight loss (%) | Weight difference | 1 | 1 | Column 7, 8 | - |
| Sericin removed (%) | UV-Spectrophotometry | 1 | 1 | Column 9-11 | - |
| Fibers Diameter (µm) | Optical Microscopy | 5 | 1 | Column 20 | Column 21 |
| Relative amount of secondary structures (%) | FTIR-ATR | 1 | 1 | Column 22-27 | - |
| Peak Molecular Weight (kDa) | GPC | 1 for each treatment | 2 | Column 3 | - |
| Number average Molecular Weight (kDa) | 2 | Column 4 | - | ||
| Weight average Molecular Weight (kDa) | 2 | Column 5 | - | ||
| Polydispersity | 2 | Column 6 | - | ||
| Ultimate Strength (MPa) | Tensile Test | At least 3 | 1 | Column 12 | Column 13 |
| Ultimate Strain (%) | 1 | Column 16 | Column 17 | ||
| Young's modulus (MPa) | 1 | Column 14 | Column 15 | ||
| Toughness modulus (MJ/m3) | 1 | Column 16 | Column 17 |
2.2. Silk fibroin degumming
Extraction and purification of silk fibroin were conducted using an adapted version of a well-known protocol [15]. For each performed trial, 3 g of Bombyx mori silk cocoons (Chul Thai Silk Co., Phetchabun, Thailand) were cut in small pieces and placed in 400 mL of sodium carbonate hot bath for a determined time and eventually a second bath was performed as graphically described in Fig. 1C. The 16 procedures described in our previous work [9] have been adopted here, 8 with a single bath and 8 with a double bath. Each process was conducted in triplicates for a total of 48 trials. The resultant degummed silk fibroin was progressively taken at room temperature, carefully rinsed for 3 times using ultrapure water and dried for 2 days under the hood. The fibers were kept in a desiccator until their use. Three replicates of a reference sample were prepared following the standard Rockwood protocol. Briefly, 5 g of cocoons were cut and degummed in a boiling bath of 2000 mL of a Na2CO3 solution (2.14 g/L) for 30 min. The resulting degummed silk was then carefully taken at room temperature and rinsed with distilled water for 3 times. Finally, the degummed silk fibroin was dried under the hood for 2 days. To avoid as much as possible the reduction of the solution volume due to the evaporation, the degumming baths were covered, and periodically some water was added to restore the initial volume. The order of preparation for the 51 trials (48+3) was randomized to mediate the effect of the environmental factors (humidity and temperature) to 0.
2.3. Weight loss and sericin amount
The weight loss is universally used as a measure of the effectiveness of the degumming. A degumming procedure is commonly considered complete with a weight loss between 25% and 30% accordingly with the specific typology of cocoon used. To evaluate the weight loss, for each performed trial (three for each of the 16 treatments), the weight was measured by the use of an analytic balance, before (mi) and after (mf) the degumming process. The mass loss was calculated as reported in Eq. (2). This equation remained valid both for the single bath process and for the double bath process. The calculated percentage of weight loss was reported in the first sheet of the dataset in column 8 (and in column 7 as absolute value in grams). To confirm the weight loss, we verified the amount of sericin present in the degumming bath by Spectroscopic analysis (NanoDrop 1000, Thermoscientific). 5µL from each degumming bath after the degumming procedure were collected and the protein absorption peak at 280 nm was used to evaluate the protein concentration. The concentration was estimated by comparing the absorption intensity results with a calibration curve obtained by a set of standard solutions (with a known sericin content) prepared starting from sericin powder (Sigma Aldrich) and ultrapure water. The equation of this curve is reported in Eq. (3). It was possible to calculate the concentration of sericine in mg/mL starting from the absorbance intensity at 280 nm after a dialysis of the bath solution performed to eliminate the Na2CO3 salt and repristinate a neutral pH. The calculated percentage of removed sericin was reported in Column 10 (Column 9 as absolute value in gram). Each value of Column 10 was subtracted to the value of percentage of removed sericin obtained from the reference (28.77) considered as completely degummed, to obtain the hypothetical quantity of sericine still attached to the fiber.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
2.4. Mechanical characterization
Silk samples were prepared following established protocols. In particular, the samples were glued, with double-sided tape on a paper support (square window 1 × 1 cm). The fiber diameter was measured by image analysis (ImageJ) on images obtained by an optical microscope (model Olympus BX61) with a 20x lens. The shape of the threads was approximated as a circular cylinder. The samples were mounted on a nanotensile machine Agilent T150 UTM and the standard testing speed was 0.10 mm/s [16]. The declared sensitivity of the machine in displacement is 1 nm. The machine takes measurement with a frequency of 20 Hz. The engineering strain was obtained by dividing the displacement for the gauge length and the engineering stress by dividing the force for the cross-sectional area (which was computed with the means of the diameters for each fiber). The Young's modulus was computed by the slope of the stress-strain curve in the initial linear elastic part. The slope was obtained with the support of Excel. The mean obtained among at least 3 fibers was then reported in column 14, and the standard deviation in column 15. The toughness modulus was obtained by calculating the area under the stress-strain curve (by integration with the rectangles rule). The mean value and the standard deviation were reported in Column 20 and 21, respectively. The strength and the ultimate strain were the final (and maximal) engineering stress before fracture and the corresponding strain (the mean values within their standard deviation are reported in Columns 12, 13, 16 and 17). At least 3 fibers, for each of the 48 prepared samples were tested. All samples were kept controlled conditions (20–21 °C and 39–42% RH) for two weeks and then tested in the very same conditions. This was done to stabilize the concentration of residual stresses and thus to minimize its effects on the mechanical properties.
2.5. Secondary structure
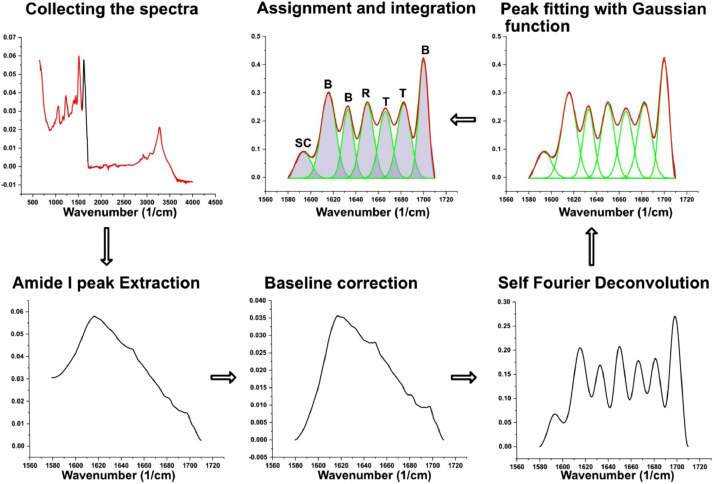
ATR-FTIR (Perkin Elmer, Spectrum ONE) equipped with a ZnSe crystal was used to evaluate the variations in the secondary structure on the fiber surface. The data analysis has been conducted by the use of OriginPro (Origin Lab Corporation, USA). The fibers to test were accurately selected based among all the fibers to be the one with less sericin present. Even in the case of not effective degummed procedure, we tried to avoid fibers coming from cut pieces of cocoons that resulted to be not degummed. This allowed us to avoid, as much as possible, the influence of the contribution of sericin to the FTIR signal. The secondary structures were quantified following the scheme reported in Fig. 3. The spectra were collected in the full range of the instrument (4000–400 cm−1) and then masked on the range of the primary amide peak (1580–1720 cm−1) to evaluate quantitatively the percentage amount of the secondary structure in the fibers. The I Amide peak was smoothed with a 5 points adjacent averaging function followed by a Fourier Self-Deconvolution (FSD, with a smoothing factor of 0.3 and gamma function of 30) to enhance the resolution and better shape the singular peaks. To identify the peaks position, the second derivative was applied to the deconvolved peak. The positions were then used to fit the gaussian functions by a fitting routine (OriginPro Peak Analysis) that was recursively applied until the variation of χ2 among during two successive cycles was under a certain amount (in our case 10−6). The assignment of the peaks has been done following our previous works. The total amount of area was calculated as the sum of the area of the peaks with the exclusion of the side chain peak that does not represent a secondary structure configuration. Then the ratio between each fitted peak area and the total area was calculated to determine the percentage of the specific structure assigned to the peak by the Eq. (7), where Ass is the area of the peak of the specific secondary structure and AT the total area. In Table 3, the assigned secondary structure for different bandwidths of the FTIR spectrum is reported, as well as the corresponded column of the dataset in which the percentage amount is presented.
| (7) |
Fig. 3.
Scheme describing the quantification of the secondary structure by FTIR. The spectra were collected over the entire range than the primary amide peak was extracted by masking and the baseline corrected. A Self-Fourier deconvolution was applied to enhance the single components separation then the peaks were fitted by a Gaussian function and integrated. The assignment was done by following the literature.
Table 3.
Peak assignment for the protein secondary structure and corresponding columns in which the calculated percentage amount has been reported inside the dataset.
| Assignment | Peak position cm−1 | Sheet | Column |
|---|---|---|---|
| Side chain | 1597–1609 | 1 | - |
| Antiparallel β – sheet | 1610–1625 | 1 | 22 |
| Native β – sheet | 1626–1636 | 1 | 23 |
| Random coil | 1637–1655 | 1 | 24 |
| α – helix | 1656–1662 | 1 | 25 |
| Β – turns | 1663–1696 | 1 | 26 |
| Parallel β – sheet | 1697–1703 | 1 | 27 |
2.6. Molecular weight
The molecular weight was evaluated by gel permeation chromatography (GPC) using a SB-806MHQ Shodex column (8.0 × 300 mm Exclusion limit [Pullulan] 4000E3) mounted on a pumping system (spectra system p4000 with a 20 µL loop and a vacuum membrane degasser thermo Electron SCM1000) and using a UV detecting system (Jasco UV-1570) set on 224 nm wavelength. The fibroin samples were dissolved in LiBr for 4 h at 60 °C, dialyzed in tube (Sigma Aldrich, cutting Mw 3500 Da) against ultra-pure water for 3 days and then double filtered (50 µm glass fibre filter) to eliminate impurities. Subsequently, the resulting regenerated fibroin solution was diluted with the eluent (PBS pH-7.4 Sigma P3813 plus 0.05 M Urea, filtered using a disposable filter with 0.22 µm pore size) until a concentration of 0.6 mg/mL was obtained. This specific concentration was chosen to be in the 0.5–0.8 mg/L range optimal to avoid the formation of protein aggregates due to the shear stress during the injection. The chromatography was operated with a flow rate of 1 ml/min and a column temperature of 27 °C set thought an oven. The specific temperature was set to compensate for the environmental temperature variation. A calibration curve was obtained with a Low/High Molecular Calibration Kit (Sigma Aldrich). Prior to the measurement, both standards and samples were centrifuged at 1200 rpm for 15 min and filtered with a 0.22 µm filter, to eliminate aggregates. The calibration curve was obtained using proteins with known molecular weight (Ribonuclease A Mw=13,700 Da, Carbonic anhydrase Mw=29,000 Da, Ovalbumin Mw=43,000 Da, Conalbumin Mw=75,000 Da, Aldolase Mw=158,000 Da, Ferritin Mw=440,000 Da, Blue Dextran Mw=2,000,000 Da) reporting the elution time against the logarithm of Mw and then fitting this trend with a straight line, the resulting law is reported in Eq. (8). The weight average molecular weight (Mw), the dispersion index (D), the number average molecular weight (Mn), and the molecular weight at the peak (Mp) were evaluated starting from the chromatogram as described in Fig. 4. The entire analysis has been conducted by OriginLab, the GPC curve was smoothed using a Fast Fourier Transform (FFT) filter with a window of 10 points and a cutoff frequency of 0.1, then the curve has been masked to only include the peak where the protein was present. The x axis has been then converted from the elution time (te) directly obtained from the GPC software to the Molecular weight by the use of Eq. (9). Mw, Mn and D where then calculated by Eqs. (10), (11) and (12), respectively, where the summation has to be considered on all the values of the peak and I is the intensity of the signal at the specific value of M. Mp has instead been evaluated as the M at which the signal reached its maximum, by using the peak analyzer in OriginLab. Fig. 4
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Fig. 4.
Scheme of GPC curve analysis. The curve was smoothed with an FFT filter and the peak was extracted by masking the curve. Throught the calibration the elution time was converted in the logarithm of the molecular weight and then on the molecular weight (M). The Intensity (I) have been normalized in the [0.100] range. Based on the M and the Normalized I the summatory have been calculated and subsequently the valued of the Weight average molecular weight (Mw), the number average molecular weight (Mn) and the disparity index (D) while the value of the molecular weight of the peak was directly determined by finding the M at which the maximum intensity was achieved.
CRediT Author Statement
Alessio Bucciarelli: conceived the idea, performed part of the experiments (degumming of the silk fibroin), analyzed the data to obtain the empirical models, and wrote the manuscript. Gabriele Greco and Ilaria Corridori: performed all the mechanical measurements and analyzed the mechanical curves. Nicola M. Pugno and Antonella Motta: edited the manuscript and supervised the work in all its stages, from the conceived idea to the experimental planning. All the authors contributed in the final editing of the manuscript prior to its submission.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships which have or could be perceived to have influenced the work reported in this article.
Acknowledgments
N.M.P. is supported by the European Commission under the FET Proactive (“Neurofibers”) Grant no. 732344, as well as by the Italian Ministry of Education, University and Research (MIUR) under the “Departments of Excellence” grant L. 232/2016, the ARS01- 01384-PROSCAN, and the PRIN-20177TTP3S grants. I. C. is supported by grant no. 732344.
The project leading this application has received founding for the European Union's Horizon 2020 Research and Innovation Staff Exchange Programme (RISE) under the Marie Sklodowska-Curie grant agreement MSCA-RISE 778078 (Remix project).
Footnotes
Supplementary material associated with this article can be found in the online version at doi:10.1016/j.dib.2021.107294.
Appendix. Supplementary materials
References
- 1.Greco G., Mastellari V., Holland C., Pugno N. Comparing modern and classical perspectives on spider silks and webs. Perspect. Sci. 2021;29:133–156. doi: 10.1162/posc_a_00363. [DOI] [Google Scholar]
- 2.Koh L.-D.D., Cheng Y., Teng C.-P.P., Khin Y.-W.W., Loh X.-J.J., Tee S.-Y.Y., Low M., Ye E., Yu H.-D.D., Zhang Y.-W.W., Han M.-Y.Y. Structures, mechanical properties and applications of silk fibroin materials. Prog. Polym. Sci. 2015;46:86–110. doi: 10.1016/j.progpolymsci.2015.02.001. [DOI] [Google Scholar]
- 3.Qi Y., Wang H., Wei K., Yang Y., Zheng R.Y., Kim I.S., Zhang K.Q. A review of structure construction of silk fibroin biomaterials from single structures to multi-level structures. Int. J. Mol. Sci. 2017 doi: 10.3390/ijms18030237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vepari C., Kaplan D.L. Silk as a biomaterial. Prog. Polym. Sci. 2007;32:991–1007. doi: 10.1016/j.progpolymsci.2007.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhou C.-Z., Confalonieri F., Jacquet M., Perasso R., Li Z.-G., Janin J. Silk fibroin: Structural implications of a remarkable amino acid sequence. Proteins Struct. Funct. Genet. 2001;44:119–122. doi: 10.1002/prot.1078. [DOI] [PubMed] [Google Scholar]
- 6.Kasoju N., Bora U. Silk fibroin in tissue engineering. Adv. Healthc. Mater. 2012;1:393–412. doi: 10.1002/adhm.201200097. [DOI] [PubMed] [Google Scholar]
- 7.Wang C., Xia K., Zhang Y., Kaplan D.L. Silk-based advanced materials for soft electronics. Acc. Chem. Res. 2019 doi: 10.1021/acs.accounts.9b00333. [DOI] [PubMed] [Google Scholar]
- 8.Boulet-Audet M., Buffeteau T., Boudreault S., Daugey N., Pézolet M. Quantitative determination of band distortions in diamond attenuated total reflectance infrared spectra. J. Phys. Chem. B. 2010;114:8255–8261. doi: 10.1021/jp101763y. [DOI] [PubMed] [Google Scholar]
- 9.Bucciarelli A., Greco G., Corridori I., Pugno N.M., Motta A. A design of experiment rational optimization of the degumming process and its impact on the silk fibroin properties. ACS Biomater. Sci. Eng. 2021 doi: 10.1021/acsbiomaterials.0c01657. [DOI] [PubMed] [Google Scholar]
- 10.D.C. Montgomery, Design and analysis of experiments eighth edition, 2012. doi: 10.1198/tech.2006.s372. [DOI]
- 11.Bucciarelli A., Reddy Chandraiahgari C., Adami A., Mulloni V., Lorenzelli L. Precise dot inkjet printing thought multifactorial statistical optimization of the piezoelectric actuator waveform. Flex. Print. Electron. 2020;5 doi: 10.1088/2058-8585/abbb7e. [DOI] [Google Scholar]
- 12.Bucciarelli A., Adami A., Chandaiahgari C.R., Lorenzelli L. Proceedings of the IEEE International Conference on Flexible, Printable Sensors and Systems. IEEE; 2020. Multivariable optimization of inkjet printing process of Ag nanoparticle ink on Kapton; pp. 1–4. [DOI] [Google Scholar]
- 13.Bucciarelli A., Greco G., Corridori I., Pugno N., Motta A. IEEE DataPort; 2021. Full Factorial Design of Experiment dataset of Silk Fibroin alkaly degumming. [DOI] [Google Scholar]
- 14.R.C. Team . R.C. Team; Vienna, Austria: 2019. R: A Language and Environment for Statistical Computing. [Google Scholar]
- 15.Rockwood D.N., Preda R.C., Yücel T., Wang X., Lovett M.L., Kaplan D.L. Materials fabrication from Bombyx mori silk fibroin. Nat. Protoc. 2011;6:1612–1631. doi: 10.1038/nprot.2011.379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Greco G., Pugno N.M. How spiders hunt heavy prey: the tangle web as a pulley and spider's lifting mechanics observed and quantified in the laboratory. J. R. Soc. Interface. 2021;18 doi: 10.1098/rsif.2020.0907. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.