Abstract
The endoplasmic reticulum (ER) is a vital organelle in mammalian cells with a complex morphology. Consisting of sheet-like cisternae in the cell center, the peripheral ER forms a vast tubular network on which a dispersed pattern of a few hundred specialized domains (ER exit sites (ERESs)) is maintained. Molecular details of cargo sorting and vesicle formation at individual ERESs, fueling the early secretory pathway, have been studied in some detail. The emergence of spatially extended ERES patterns, however, has remained poorly understood. Here, we show that these patterns are determined by the underlying ER morphology, suggesting ERESs to emerge from a demixing process that is quenched by the ER network topology. In particular, we observed fewer but larger ERESs when transforming the ER network to more sheet-like morphologies. In contrast, little to no changes with respect to native ERES patterns were observed when fragmenting the ER, indicating that hampering the diffusion-mediated coarse graining of domains is key for native ERES patterns. Model simulations support the notion of effective diffusion barriers impeding the coarse graining and maturation of ERES patterns. We speculate that tuning a simple demixing mechanism by the ER topology allows for a robust but flexible adaption of ERES patterns, ensuring a properly working early secretory pathway in a variety of conditions.
Significance
The endoplasmic reticulum (ER) is a central organelle in mammalian cells, consisting of sheet-like cisternae and a vast tubular network. On the ER network, a dispersed pattern of few hundred domains, called ER exit sites (ERESs), is observed. ERESs fuel the early secretory pathway, yet how their native pattern emerges has remained elusive. Here, we show that ERES patterns depend on ER morphology, indicating ER junctions to hamper domain coarse graining and pattern maturation. ERES patterns seem to emerge from a demixing process, akin to oil droplet growth in vinaigrettes, that is quenched by the ER network topology. Tuning a simple demixing mechanism by the ER topology presumably allows mammalian cells to flexibly adapt ERES patterns to varying demands.
Introduction
Compartmentalization and a concomitant spatial allocation of diverging tasks and functions is a ubiquitous phenomenon in living matter. This is most evident for eukaryotic cells in which distinct membrane-enveloped organelles host specific protein machineries to supply and maintain vital functions (1). In addition, dynamic nonequilibrium pattern formation but also condensation processes can create local activity hubs in eukaryotes and prokaryotes even without a confining envelope (see for example, (2)). Especially the dynamic emergence of compartments by condensation processes has recently received considerable attention, with a particular focus on liquid protein droplets and nucleic acid coacervates (3, 4, 5). In fact, different means of structuring the interior of cells are often intertwined, e.g., the formation of specialized membrane domains without specific boundaries is a frequent phenomenon on the envelopes of virtually all organelles (6). A prominent example is the endoplasmic reticulum (ER), which hosts different membrane domains, defined by solid-like lipid phases (7) or specialized protein assemblies (8,9).
The ER is a central organelle with manifold tasks ranging from lipid synthesis to quality control of membrane proteins (1). In contrast to many other organelles, it assumes a rather complex shape with sheet-like cisternae close to the nucleus, merged with a vast peripheral network of thin membrane tubules (10,11), whose junctions are stabilized by hairpin-like membrane proteins such as reticulons (12, 13, 14) and lunapark proteins (15, 16, 17). The ER network is highly dynamic, driven by its liaison with the cytoskeleton (11,18, 19, 20) and a vivid exchange with other organelles at specialized contact sites (21,22). On the ER’s complex network morphology, membrane domains with a distinct set of protein constituents, called ER exit sites (ERESs), are observed in mammals (8) but also in plants (23) and in some yeast species (24). ERESs typically assume a phenotype of a few hundred dispersed punctae (8), which fuel the early secretory pathway by shedding off COPII-coated vesicles that shuttle nascent protein cargo to the Golgi apparatus (9). So far, cargo sorting and adaptive transport carrier formation at the ERES have been studied in great molecular detail (see for example, (9,25,26), for reviews). Also, changes in the local turnover dynamics of ERES constituents upon depletion of cargo proteins (27), sterols (28), and dynein-motor components (29,30) or after starvation (31,32) have been quantified in this context. However, the emergence and maintenance of the ERES as a cell-wide punctuate pattern and the impact of the ER architecture on this pattern have remained poorly understood.
ERESs assume a fairly regular, crystalline-like configuration in untreated mammalian cells, which is consistent with a local depletion of free constituents because of a diffuse-and-capture process (33). Moreover, ERESs can be monitored over extended timescales, during which they maintain their average size with a diameter of some 100 nm (8). Although ERES positions appear stationary on large timescales, they show a distinct subdiffusional motion on short and intermediate timescales (34). In fact, their motion is distinct from that of ER junctions (20), i.e., ERESs appear to perform a one-dimensional random walk on shivering ER tubules that are shaken by the active cytoskeleton (19,20). These data also indicate that individual ERESs can make free excursions on ER tubules but eventually remain confined between adjacent ER junctions that seem to act as effective diffusion barriers and prevent ERES fusion events. In fact, observations in the small yeast Pichia pastoris revealed that freely moving ERESs can merge upon contact, whereas new ERESs can form de novo because of local concentration fluctuations of their constituent proteins (24). Subsequently, ERESs were seen to shrink or grow to the same preferential size. These observations suggest that ERES formation can be described as a two-dimensional and diffusion-driven demixing process of ERES constituents on ER membranes, potentially hindered or quenched in some stage by ER junctions. ER topology and/or geometry can therefore be expected to have a significant impact on ERES patterns.
To experimentally probe this hypothesis, we have combined chemical and biological treatments with quantitative imaging on mammalian culture cells. In particular, we have reshaped the native ER network morphology 1) to a more sheet-like configuration by depleting lunapark proteins via RNA interference (RNAi), and 2) to a dispersed set of disjoint vesicular structures by treating cells with filipin. Whereas disrupting the ER network into fragments via filipin had little to no effect on the observed ERES pattern, enforcing a more sheet-like ER morphology by RNAi resulted in a significant reduction of individual ERESs, with the remaining domains being significantly larger. Merely disrupting the microtubule cytoskeleton had little effect on ER morphology and ERES patterning, providing clear evidence that depletion of lunapark proteins, i.e., removing ER junctions, is key for the altered ERES pattern. Supplementary model simulations give support to the notion that diffusion barriers are key to obtain quenched ERES patterns in the native state, whereas maturated pattern of fewer but larger domains emerge in the absence of transport restrictions. Altogether, our data suggest that native ERES patterns are the result of a quenched, fluctuation-driven, two-dimensional demixing process.
Materials and methods
Cell culture and sample preparation
Human cervical cancer cells (HeLa, no. ACC-57; DSMZ, Brunswick, Germany) were cultured in Dulbecco’s Modified Eagle’s Medium with phenol red (Thermo Fisher Scientific, Dreieich, Germany) supplemented with 10% fetal calf serum (Biochrom, Holliston, MA), 1% L-glutamine, 1% sodium pyruvate, and 1% penicillin-streptomycin (all from Gibco, Dreieich, Germany) in T-25 flasks (Corning, Berlin, Germany) at 37°C and 5% CO2. Cells were split at 80% confluency every 3 days using prewarmed trypsin/EDTA with a maximum of 20 passages per cell batch. Cells were also periodically checked by PCR to be free of mycoplasma contaminations.
For fluorescence microscopy, cells were seeded in 700 μL culture medium on ibidi μ-slides (four wells, 30,000–50,000 cells each; ibidi, Martinsried, Germany). Transient transfections with DNA were performed 16–24 h before imaging using Lipofectamine 3000 (Thermo Fisher Scientific) according to the manufacturer’s protocol. In brief, 300–700 ng plasmid DNA per well were incubated for 15 min with 1 μL P3000 and 1.5 μL Lipofectamine 3000 reagent, diluted in 50 μL serum-free Opti-MEM (Gibco, Germany), and then added dropwise to the cells. For highlighting the ER and ERES, ssKDEL-RFP (a kind gift of J. Lippincott-Schwartz) (35) and Sec16-GFP (a kind gift of H. Farhan) (32) were used; for checking the integrity of the ER, GFP-tagged calnexin (CNX-GFP, a kind gift of G. Baldini) (36) and GFP-tagged calreticulin (CRT-GFP, plasmid no. 80978, deposited by P. Steyger; Addgene, Watertown, MA) (37) were also used. COPII-based staining of ERESs was done with EYFP-Sec23A and EYFP-Sec31A, as described before (27,30).
Transfection with small interfering RNA (siRNA) constructs was done 48 h before the experiment using Lipofectamine RNAiMAX (Thermo Fisher Scientific) according to the manufacturer’s protocol (1.5 μL Lipofectamine RNAiMAX reagent and 5 pmol siRNA diluted in 50 μL Opti-MEM, incubated for 5 min and then added dropwise to the cells; Thermo Fisher Scientific). To knock down lunapark, predesigned and validated siRNAs (AM16099 Ambion Silencer Select siRNA; Thermo Fisher Scientific) were used. For control of the uptake efficiency, the 5′ end of the siRNA was tagged with an Alexa Fluor 633. In addition, an adequate negative-control siRNA with the same labeling (4390820 Silencer Select Custom siRNA; Thermo Fisher Scientific) was used.
For checking the efficiency of protein reduction by siRNA treatment, protein size separation was done on a 0.75-mm 8% Bis-Tris-sodium-dodecyl-sulfate-polyacrylamide-gel-electrophoresis. The gel ran for 1 h at 150 V, after which proteins were transferred by wet Western blotting on Immun-Blot PVDF membrane (Bio-Rad Laboratories, Hercules, CA). The blot was blocked in 5% milk powder dissolved in TBST (tris-buffered saline and polysorbate 20). Primary antibodies (LNP PA5-53133; Thermo Fisher Scientific; and G8795; Sigma-Aldrich, Munich, Germany) were incubated overnight at 4°C in TBST and washed off three times with TBST for 5 min. Secondary antibodies were incubated for 1 h and washed off the same way. The protein signal was detected with chemiluminescence on a SuperSignal West Dura chemiluminescent substrate (Thermo Fisher Scientific) using a Fujifilm LAS-4000 Image Analyzer (Fujifilm, Tokyo, Japan) for 15 min. We found an average reduction of lunapark by 66% after 48 h (see Fig. S5).
Treatment of cells
To depolymerize microtubules, HeLa cells were treated with 10 μM nocodazole (Sigma-Aldrich) and transiently chilled on ice, as described and validated before (20,34). In brief, a 2-mM stock solution of nocodazole dissolved in dimethyl sulfoxide (both Sigma-Aldrich) was diluted to working concentration in Minimal Essential Medium without phenol red supplemented with 10% HEPES and 1% penicillin-streptomycin (all from Gibco). Nocodazole-treated cells were chilled on ice for 10 min before incubating at 37°C with 5% CO2 for 15 min. Subsequent imaging was performed in the presence of the drug using imaging medium (Minimal Essential Medium without phenol red supplemented with 10% HEPES and 1% penicillin-streptomycin).
Treatment with filipin was performed with a protocol adapted from (38) filipin III (from Streptomyces filipinensis, ≥85% HPLC; Sigma-Aldrich), diluted to a working concentration of 15 μg/mL in imaging medium, was applied 30 min before and during imaging, with the cells being exposed to room temperature. The resulting breakdown of the ER network, in agreement with previous reports (38), was confirmed by fluorescence imaging with CRT-GFP and KDEL-RFP.
Application of hypotonic stress was done as described in (39). Briefly cells were treated with hypotonic swelling medium (5% Dulbecco’s Modified Eagle’s Medium in water), incubated for 10 min at 37°C with 5% CO2, and then imaged for no longer than 30 min. In line with previous observations (39), we observed that ∼50% of all HeLa cells developed large intracellular vesicles (LICV) derived from ER membranes, as evidenced by simultaneously visualizing ER membrane (CNX-GFP) and ER lumen (KDEL-RFP) before and after hypotonic treatment. Cells were stable and viable during the experiments but died when returning to isotonic culture medium because of damaged mitochondria.
Microscopy
Before imaging, cells were washed twice in Dulbecco’s Phosphate Buffered Saline (D-PBS, Biochrom, Cambridge, UK) and subsequently supplemented with imaging medium. Three-dimensional imaging (i.e., acquisition of stacks of 25 individual images with a separation of 0.1 μm) was performed at 37°C with a customized spinning-disk confocal microscope consisting of a Leica DMI 6000 microscope body (Leica Microsystems, Wetzlar, Germany), a CSU-X1 (Yokogawa Electric, Tokyo, Japan) spinning-disk unit, and a custom-made incubator. Images were captured by a Hamamatsu ORCA-Flash 4V2.0 sCMOS camera (Hamamatsu Photonics, Hamamatsu City, Japan) with an exposure time of 500 ms per image, using an HC PL APO 63×/1.4 (Leica Microsystems) oil immersion objective. Illumination of the specimen at 490 and 561 nm was achieved by two solid-state lasers (Calypso and Jive; Cobolt, Stockholm, Sweden), the corresponding fluorescence was detected by bandpass filters (Semrock, Rochester, NY) in the range 500–550 and 575–625 nm, respectively. Transfection efficiency with siRNA constructs was checked by epi-fluorescence with standard filters for Alexa Fluor 633. The whole setup was controlled by custom-written LabView software (National Instruments, Austin, TX).
Image analysis and evaluation procedure
For image analysis, only the z-slice with the highest total fluorescence was considered. All of these slices from different cells and measurement conditions were merged by Fiji into a single stack and exported to ilastik, an interactive machine-learning tool for image analysis (40). To segment ERES fluorescence from background noise, ilastik’s interactive pixel classification was used, which invoked all pixel features with σ ≤ 3.5 (in total 25 features). It was sufficient to train the machine-learning algorithm on a single picture with ∼50 hand-drawn annotations for the ERES and background. The pixel prediction probabilities were exported and binarized with Fiji’s automated “minimal” thresholding. ER fragments after filipin treatment or hypotonic shock were segmented with ilastik in the same manner (15 cells, z-projection from 10 optical slices with displacement 0.2 μm). ER tubule networks were skeletonized, and positions of ER junctions were extracted as described before (20,34).
All subsequent image analyses were carried out with custom-written MATLAB scripts (The MathWorks, Natick, MA). To this end, binary images were imported, and detected objects assigned to the putative Golgi region were excluded. Therefore, the fluorescent haze in that region was masked by manually thresholding the maximal z-projection of the image stack, smoothed by a local Laplace filter (MATLAB routine locallapfilt; The MathWorks). Examples of the segmentation scheme are given in Fig. S2. For ER fragments, no Laplace filter was applied. To determine the fluorescence contribution of cytosolic Sec16-GFP, Fcyt, we combined all ERESs and the complete convex hull area of objects in the putative Golgi region, thickened the edges 10 times, and summed up the complement’s total fluorescence. All remaining fluorescence, i.e., basically the contribution of the aforementioned edges and the nonpatchy haze in the putative Golgi region, were included in Fnon, hence representing an estimate of Sec16-GFP on ER membranes outside the ERESs. See also the main text for additional information on evaluations and analyses.
Simulations
Particles with radius rc were allowed to attach to a two-dimensional surface (L × L) with rate kon from a pool of Nc unbound particles. Compensating this association, groups of np particles were allowed to dissociate with rate koff, leading to a steady-state fraction of Nm particles on the surface with N = ρL2 = Nc + Nm being the constant number of all particles in the system. Using monomer instead of group dissociation (with an updated koff) did not alter the results significantly. On the surface, particles were allowed to fuse instantly upon contact, forming circular domains for which the radius R = m1/2rc was set by the number of participating particles, m. Particles and domains were allowed to diffuse with a radius-dependent mobility set by an analytical approximation for the diffusion constant of a cylinder in a membrane (41,42) (membrane thickness: h = 4 nm; viscosity of membrane and cytosol: ηm = 100 and ηc = 0.5 Pas; see Fig. S7 A for visualization). Reflecting boundaries were imposed at the edges of the surface in the spirit of a blind-ant-algorithm, i.e., particles/domains that were assigned a diffusive step increment leading to an overlap of their area with these boundaries were not moved in this time step. For confined geometries, additional reflecting boundaries were imposed in the interior of the surface, leading to a periodic lattice of panels with dimensions λ × λ. In each of the panel boundaries, a gap of width 0 < g < λ was left open in the center for diffusional transport to next-neighbor panels; for g = λ, an unconfined scenario was recovered.
All simulations were performed with a custom-written code in GNU Fortran with parameters set to ρ = 103/μm2, λ = 1.5 μm, L = 6λ, rc = 28 nm, koff = 1/300 s, kon = koff/30, np = 4, and a time step Δt = 0.1 s. The value of the panel edge length λ was chosen to roughly match the membrane area of ER tubules (100 nm diameter at an average length of 1.1 μm (43)) and ER fragments (cf. Fig. 3 C) while still allowing for computational efficiency. At steady state, the kinetic rates led to 70–75 particles in each panel of edge length λ, which translates into a single domain of ∼0.18 μm2 (i.e., 500 nm diameter), roughly corresponding to the size of native ERESs. To match the experimentally observed mobility of ERESs on ER tubules (34), the size-dependent diffusional mobility after (41,42) was scaled by a prefactor so that a domain with m = 100 particles (radius 280 nm) featured a diffusion constant D = 1.4 × 10−3 μm2/s (cf. Fig. S7 A). After equilibration, positions and sizes of particles/domains were stored every 500 steps for subsequent analysis, yielding 100 independent data sets for each condition. Varying kon, koff, and/or D resulted basically only in a change of the average domain size in accordance with previous reports on the closely related model of raftlike domains under continuous recycling (44), i.e., only minor changes to the spatial arrangement of domains and the shape of the PDF of domain areas, p(A), was observed; see also below for further discussion.
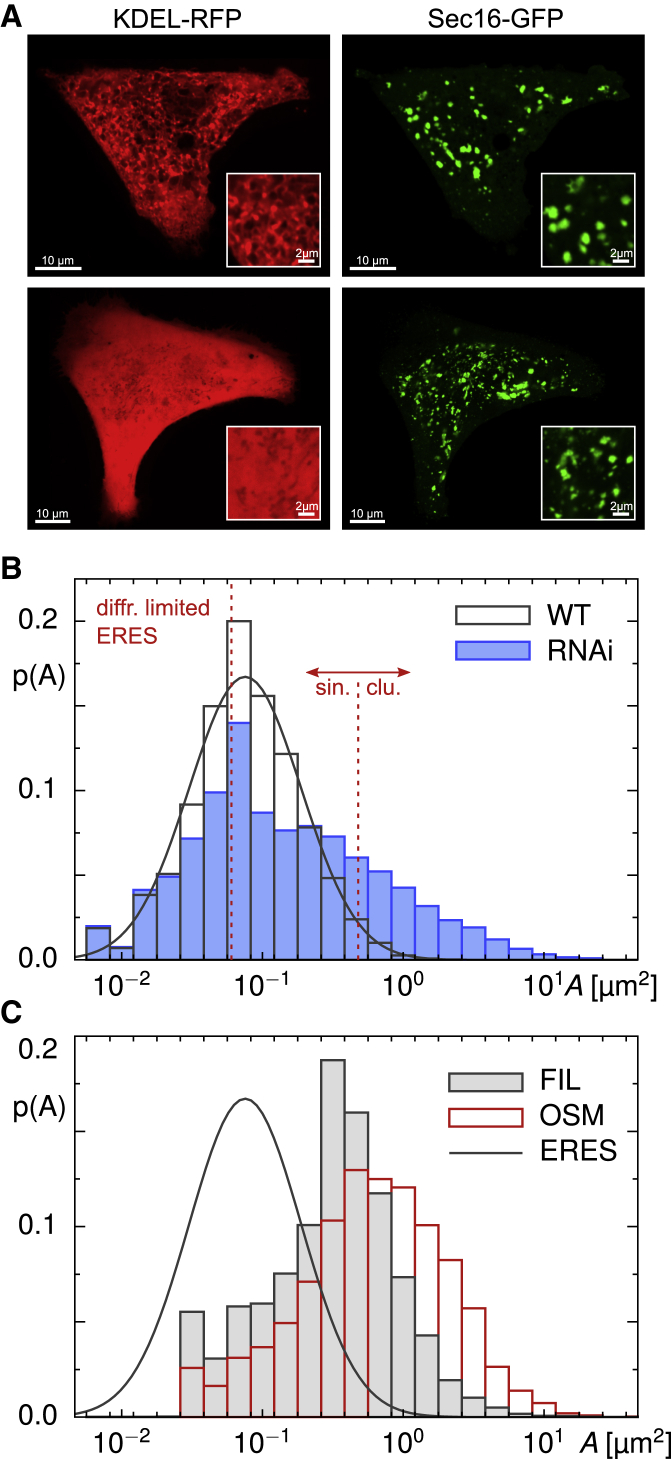
Figure 3.
(A) Representative images of the ER (left column, red) and the superimposed ERES pattern (right column, green) in cells in which lunapark proteins have been depleted by RNAi. Scale bars, 10 μm. Close-ups in the inset reveal that the ER has lost its network-like morphology, whereas superimposed ERESs have considerably grown in size. Scale bars, 2 μm. (B) The associated PDF of apparent ERES occupation areas, p(A), deviates strongly from the lognormal shape found for untreated cells (solid line), featuring a marked tail for large values of (A). Consequently, the number of clusters (ERESs with more than 150 pixels) is strongly enhanced (see also main text and Table 1). Displaying the same data in a double-logarithmic fashion (Document S1. Figs. S1–S7, Document S2. Article plus supporting materialD) further emphasizes the significant changes upon depleting lunapark proteins. (C) The PDF of apparent occupation areas of ER fragments after filipin treatment (gray histogram) or osmotic shock (red histogram) has a marked peak around 0.6 μm2, revealing that these host membranes are large enough to host ERESs without restricting their native size (solid black line indicates the lognormal PDF of native ERESs, as also included in Fig. 3B). To see this figure in color, go online.
Stored positions and sizes were transformed into binary images with pixel size (10 nm)2 to encode the surface occupation with particles. These images were subsequently subjected to Gaussian blurring (width 220 nm) in a custom-made MATLAB script (The MathWorks) to obtain similar properties as for experimental fluorescence images. Encoding these images as eight-bit TIF files, setting the apparent background (image values < 90) to 0, eroding, and dilating with a 3 × 3 unity matrix resulted in a binary mask that reflected the apparent area of visible spots well (for examples, see Fig. S7 B). This binary mask was then evaluated with the MATLAB routine bwconncomp (The MathWorks) to extract the number and areas of objects. The set of all areas from 100 images was used for producing the PDF p(A).
Results and discussion
Quantitative assessment of native ERES patterns
To probe the hypothesis that ER morphology impacts on ERES patterns in mammalian cells, we have used KDEL-RFP (35) as an established ER marker and Sec16-GFP as a well-characterized ERES constituent (32,45, 46, 47) (see Materials and methods for details). Sec16 is a peripheral membrane protein that is not only found on ERESs but also on the general ER and in the surrounding cytosol, i.e., the protein cycles between the ER/ERES and the surrounding cytosol with a typical timescale of 10–15 s (32). Recent reports have also uncovered that Sec16 closely interacts with the transmembrane protein TANGO1 (48), whose dephosphorylated form has been shown to be indispensable for ERES formation, i.e., ERESs were observed to disassemble upon phosphorylating TANGO1 (49).
Upon confocal imaging (see Materials and methods), the peripheral ER of untreated cells displayed the anticipated network structure to which several hundred spots of Sec16-GFP, i.e., putative functional ERESs, were superimposed (Fig. 1 A). ERES spots, as highlighted by Sec16-GFP, appeared significantly brighter than their surrounding (cf. line profile in Fig. 1 B), facilitating an extraction of ERESs via a recently introduced interactive machine-learning approach for bio-image analysis (ilastik) (40). Using this approach, we were able to segment and extract in all imaged cells the number and fluorescence of individual ERESs as well as their apparent occupation area (see Materials and methods). The latter was determined by the sum of pixel areas (56 × 56 nm2) in an ERES, as identified by the segmentation via ilastik. Based on these data, ERESs with less than 150 contributing pixels were classified as singletons, whereas larger ones were classified as clusters (see Fig. S2 for examples of this complementary assignment). The frequently observed fluorescence smudge near to the cell center is attributed to an increased density of ER tubules and sheets near to the juxtanuclear Golgi apparatus (29). Because of the finite resolution of light microscopy, ERESs in this region could not be resolved individually but rather appeared as a dense set of overlapping speckles, which were masked for the subsequent analysis of ERESs (see again Fig. S2 for examples on this assignment).
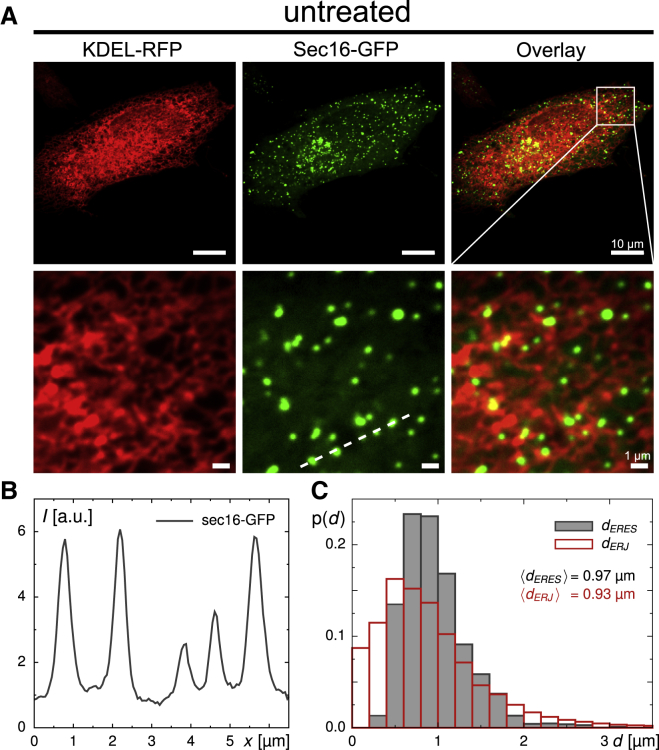
Figure 1.
(A) Representative images of the ER (left column, red), the superimposed ERES pattern (middle column, green), and their overlay (right column) in untreated cells. Close-ups in the lower panel reveal a network-like morphology of the peripheral ER to which ERESs are superimposed as dispersed spots. Scale bars represent 10 μm for the upper and 1 μm for the lower panel. (B) Taking a line profile of the Sec16-GFP fluorescence (dashed line in A) reveals that ERESs are, on average, about fivefold brighter than their surroundings. (C) The probability distribution of next-neighbor distances, p(d), of ERES punctae (black histogram) and ER junctions (red histogram) both feature a suppression of small distances, followed by a distinct peak around d = 1 μm. The average distance between neighboring ER junctions is in favorable agreement with previous findings on ER tubule lengths that were shown to vary around a mean value of 1.1 μm (43). To see this figure in color, go online.
Without any treatment, we found, on average, 0.45 ± 0.09 ERESs per μm2 of cell adhesion area (Table 1), amounting to an average of N ≈ 730 individual ERESs per cell. In agreement with earlier findings (33), the probability density function (PDF) of next-neighbor distances between individual ERESs, p(d), showed a marked suppression of small values with a peak around d = 1 μm (Fig. 1 C), i.e., dispersed ERESs keep the distance from each other. Skeletonizing the ER network (20) yielded a similar result for neighboring ER junctions (Fig. 1 C), hence confirming the previously reported typical ER tubule length of ∼1 μm (43) and suggesting that there is on average only one ERES per ER tubule.
Table 1.
Summary of central quantities obtained for ERESs in WT, after NOC, after RNAi against lunapark proteins, after using an NEG, and after applying FIL
| Cell ensemble size | ERES density (μm−2) | ERES cluster fraction Nc/(Ns + Nc) | 〈As〉 (μm2) | 〈Ac〉 (μm2) | |
|---|---|---|---|---|---|
| WT | n = 43 | 0.45 ± 0.09 | 2.33% (±1.61%) | 0.11 | 0.66 |
| NOC | n = 54 | 0.31 ± 0.07 | 2.37% (±1.84%) | 0.11 | 0.67 |
| RNAi | n = 48 | 0.20 ± 0.07 | 24.00% (±8.00%) | 0.13 | 2.19 |
| NEG | n = 43 | 0.48 ± 0.10 | 1.84% (±1.26%) | 0.11 | 0.61 |
| FIL | n = 49 | 0.35 ± 0.18 | 2.25 (±1.94%) | 0.11 | 0.67 |
See main text for details. FIL, filipin; NEG, negative-control siRNA; NOC, nocodazole treatment; WT, untreated cell.
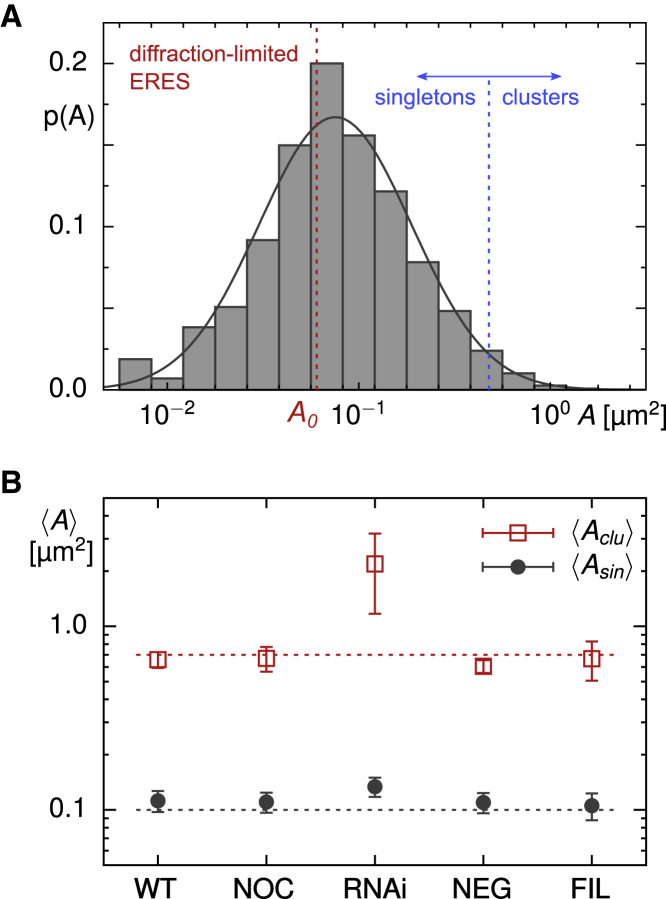
The combined set of singletons and clusters contributed ∼12% of the total fluorescence in a cell’s image, highlighting the large pool of Sec16-GFP proteins in the cytosol and on the ER membranes outside the ERES (cf. Fig. S3). Consistent with the visual perception, ERESs varied considerably in size when performing a quantitative analysis. In particular, the PDF of apparent occupation areas, p(A), assumed an almost lognormal shape with the vast majority of ERESs (∼98%) being classified as singletons (Fig. 2 A). Moreover, more than 60% of all ERESs featured occupation areas below 0.1 μm2. Because the segmentation process partially eroded or neglected contributing pixels at the rim of diffraction-limited spots, the apparent ERES occupation area could even assume values below the physical limit, A0 ≈ (λ/2)2 ≈ 0.06 μm2. Replacing these unphysical values by A0, the mean occupation area of singletons was 〈As〉 ≈ 0.11 μm2, whereas clusters (∼2% of all ERESs) featured a mean occupation area 〈Ac〉 ≈ 0.66 μm2 (Fig. 2 B; Table 1).
Figure 2.
(A) The probability density function (PDF) of apparent ERES occupation areas, p(A), obtained from an ensemble of n = 43 untreated cells, features an almost lognormal shape with parameters μ = 0.08 and σ = 0.398 (indicated by smooth solid line), yielding a marked peak near to 0.1 μm2. ERESs with less than 150 pixels (blue vertical line) were classified as singletons, larger ones as clusters. Apparent occupation areas below the diffraction-limited value A0 ≈ 0.06 μm2 (red dashed line) are due to an erosion of ERES edge pixels during the segmentation process; for all quantification purposes, they were treated as occupying the diffraction-limited area A0. (B) The average occupation areas of ERESs that were classified as clusters are around 〈Ac〉 ≈ 0.66 μm2 in untreated cells. Little to no change was observed when cells had been treated with nocodazole or filipin or had been transfected with negative-control siRNA (see Fig. S4). Upon transfection with siRNA against lunapark proteins, however, the mean shifted in a highly significant way to 〈Ac〉 ≈ 2.2 μm2 (p < 10−4 in a Kolmogorov-Smirnov test), whereas singletons retained an average occupancy area of 〈As〉 ≈ 0.13 μm2 in all cases. Horizontal dashed lines are included as a guide to the eye. To see this figure in color, go online.
Altered ER morphologies impact on ERES patterns
Because cytoskeletal elements, more precisely microtubules, are closely associated with the ER network and impact on the dynamics of both ER junctions and ERESs (20,34), we disrupted microtubules by nocodazole (see Materials and methods) as a first attempt to change the native ERES pattern. Imaging ERESs in an ensemble of cells within the first 2 h after breaking down microtubules hardly affected the cells’ overall morphology (see Fig. S1 B for representative images) and resulted overall only in mild changes with respect to untreated cells. Most prominent was the observation of a 30% lower density of ERESs (0.31 ± 0.07 ERESs per square micrometer of cell adhesion area; see Table 1), resulting in an average of only N ≈ 435 individual ERESs per cell. These fewer ERESs, however, showed an elevated brightness, so that the relative fluorescence share of all ERESs (singletons and clusters) remained almost unaltered with respect to untreated cells (Fig. S3). Presumably, the lack of an active rattling and reshaping by microtubules has led already after this short period to a local crumpling of the ER network, merging the fluorescence of closely neighboring ERESs to a single diffraction-limited spot. As a consequence, fewer but slightly brighter spots can be expected, consistent with our quantification. This reasoning is further supported by the frequently observed progressive collapse of the entire ER network after cells have been treated with nocodazole for several hours. Beyond this reduction of ERESs, however, disrupting the microtubule cytoskeleton had little effects on the ERES pattern: the PDF of apparent occupancy areas, p(A), was virtually unchanged with respect to its counterpart in untreated cells (see Fig. S4 A) and also, the area averages for singletons and clusters, 〈As〉 and 〈Ac〉, as well as the small fraction of clusters (2%), remained virtually unchanged (Fig. 2 B; Table 1). Thus, breaking down microtubules apparently did not result in gross changes of the ERES pattern, presumably because the ER network topology remained mostly unchanged despite its partial local crumpling.
Seeking a more effective means to change the ER network topology, we next tried to affect ER junctions. In particular, we focused on lunapark proteins that have been shown earlier to stabilize ER junctions (14, 15, 16). Upon depleting lunapark proteins with RNAi, a strong reduction of junctions and instead an enrichment of sheet-like morphologies has been reported (14). After this approach, we transfected cells for 48 h with siRNA constructs against lunapark proteins (see Materials and methods for details) and subsequently imaged ER structure and ERES patterns as before. As expected, siRNA-treated cells displayed a significant reduction in lunapark proteins (see Fig. S5), and the reticular ER structure was not observable anymore (Fig. 3 A). Even more striking, however, the ERES pattern was strongly altered, assuming a more coarse-grained and patchier phenotype (Fig. 3 A; Fig. S1 C). In contrast, transfection with a negative-control siRNA did not alter either the ER or the ERES phenotype (Document S1. Figs. S1–S7, Document S2. Article plus supporting material D).
Going beyond visual inspection, quantitative image analysis revealed a significantly reduced density of only 0.20 ± 0.07 ERESs per square micrometer in cells transfected with siRNA against lunapark proteins (Table 1), yielding an average of N ≈ 292 individual ERESs per cell. Unlike for nocodazole-treated cells, ERES structures had a larger share on the total cell fluorescence with no unresolvable masked region (Figs. S2 and S3). In addition to the decreased number of ERESs, also, the PDF of apparent occupancy areas, p(A), was significantly altered with respect to its counterpart in untreated cells (Fig. 3 B), featuring a large fraction of substantially bigger ERESs. A double-logarithmic plot style further emphasizes this marked change (Document S1. Figs. S1–S7, Document S2. Article plus supporting material D). In total, the fraction of clusters increased from only 2% in untreated cells to ∼22% after knocking down lunapark proteins (Table 1). Although the average occupation area of singletons, 〈As〉, remained almost unchanged, the value for clusters increased significantly to 〈Ac〉 ≈ 2.2 μm2 (Fig. 2 B; Table 1). In contrast, transfections with a negative-control siRNA yielded 0.48 ± 0.10 ERESs per square micrometer (Table 1), i.e., N ≈ 717 ERESs per cell, in favorable agreement with untreated cells. Also, the PDF of occupancy areas, p(A), did not show significant deviations from that of untreated cells (Fig. S4 B), and the average occupancy areas of singletons and clusters, 〈As〉 and 〈Ac〉, both agreed with untreated cells (Fig. 2 B; Table 1), with the fraction of clusters being as low as in untreated cells (Table 1).
At this point, it is worth emphasizing that the strongly changed ERES pattern upon knocking down lunapark proteins was not particular to the chosen marker protein, Sec16-GFP. Qualitatively similar results were seen when using COPII proteins as alternative ERES constituents (see Fig. S6). Thus, changing the ER topology from a network to a more sheet-like structure by knocking down lunapark proteins had a significant impact on the ERES pattern.
To further examine how ER morphology affects the ERES patterns, we sought for possibilities to convert the ER into a set of disjoint fragments. As a first means, we applied filipin to otherwise untreated cells (see Materials and methods), which led to a disintegration of the ER as previously described (38,50). As a result of the treatment, each cell displayed, on average, ∼700 ER fragments with a typical apparent area in the range of 0.6 μm2, i.e., they were on average markedly larger than ERESs in untreated cells (Fig. 3 C). The majority of ER fragments hosted ERESs (Fig. S1 E), and the observed phenotype did not change over time, i.e., we did not observe retubuluation of ER fragments toward a network. The area density of the ERESs was similar to untreated cells (0.35 ± 0.18 per μm2; cf. Table 1), and the relative share of ERESs on the cellular fluorescence was also similar (Fig. S3). Also, the PDF of area occupancies, p(A), was basically unchanged (Fig. S4 C) as well as 〈As〉, 〈Ac〉, and the fraction of clusters (see Fig. 2 B; Table 1). We therefore conclude that fragmenting the ER with filipin has little to no effect on the emergence of the punctuate ERES pattern.
To further explore the effects on ERES patterns when fragmenting the ER network, we also applied an osmotic shock to cells. In line with previous observations (39), a hypotonic treatment led to fragmentation into ∼300 mostly spherical ER vesicles per cell that were able to host ERESs (see Fig S1 F). Similar to filipin-treated cells, ER-derived vesicles had again an apparent area around 0.6 μm2 (Fig. 3 C), i.e., the vesicles’ size was on average markedly larger than native ERESs. Again, a retubulation of the ER was not observed, and the ERES patterns did not change during the experiments. Albeit the ERES pattern was qualitatively similar to filipin-treated cells, osmotically shocked cells also showed additional features: In contrast to filipin-treated cells, Sec16 was mostly released into the cytoplasm, and ERES punctae were only observable in ∼20% of the cell population. This indicates that not only the size of ER fragments determines the ERES pattern but also altered biochemical interactions of key molecular players need to be considered here to fully understand the observed phenotype.
Rationalizing ERES patterns with a demixing model
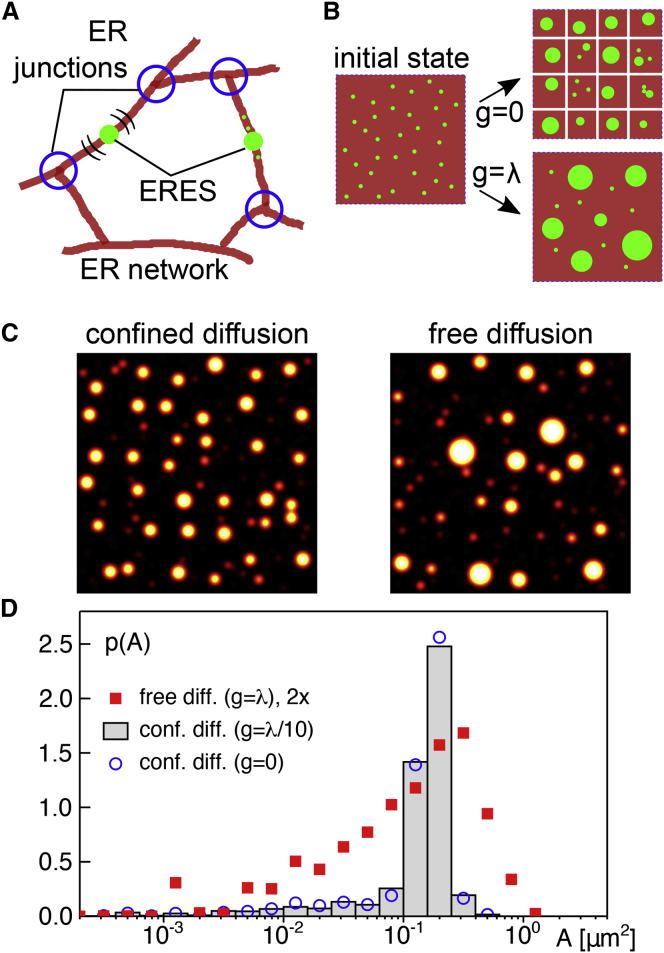
Integrating our experimental results with the restricted mobility of ERESs between ER junctions (34) and their lattice-like arrangement (33), and bearing in mind that ERESs have been seen to fuse and form de novo in the yeast P. pastoris (24), we hypothesized that ERES formation in mammalian cells can be described on mesoscopic scales as a quenched two-dimensional demixing process: dispersed ERES constituents undergo a fluctuation-driven segregation into small and premature domains on ER membranes, subsequently coarse graining by diffusion, collision, and local fusion events on the same ER tubule. This demixing process into constituent-rich and constituent-poor phases can be captured by a single interaction energy χ (also known as Flory-Huggins parameter) that integrates all attractive molecular interactions between different molecular players on smaller length scales (see also discussion below). The roundish shape of ERESs indicates χ to be much larger than thermal energy (χ ≫ kBT). In later stages, ER junctions act as diffusion barriers for sufficiently large domains, hence impeding long-range motion and subsequent fusion events of premature ERESs (Fig. 4 A). As a result, further coarse graining by fusion events is precluded and a quenched pattern of ERESs punctae with similar sizes and an almost lattice-like arrangement emerges in line with experimental observations on native ERES patterns. In the absence of diffusion barriers (=ER junctions), a continued coarse graining toward a pattern with fewer but larger domains can be expected, in line with our observations on ERES patterns when transforming the ER to a more sheet-like morphology via RNAi.
Figure 4.
(A) Schematic representation of the likely processes during ERES formation on the ER network. Starting from initially dispersed constituents, ERESs (green dots) self-assemble by demixing as protein-rich domains on individual ER tubules (red lines). ERESs are free to move on their host tubule but are eventually confined in their long-range motion by ER junctions (blue circles), prohibiting the fusion of domains on neighboring tubules. (B) Schematic representation of the model simulations (see also main text and Materials and methods for details). Starting from dispersed ERES constituents (green dots) on a square surface (edge length L), domains of different sizes form because of demixing. For confined diffusion, i.e., if the surface is dissected into panels of size λ × λ with diffusion-based material exchange being allowed only via gaps of size g < λ in panel boundaries, a lattice-like arrangement of spots with fairly uniform size emerges. Removing all diffusion barriers (g = λ), the spatial arrangement is more random, and domain sizes become less uniform. (C) Representative microscopy-like images of simulation results for both cases illustrate the obtained patterns (L = 6 and λ = 9 μm with g = λ/10 and g = λ for confined and free diffusion, respectively). (D) The PDF of spot areas, p(A), as determined from microscopy-like images of simulation data show a fairly narrow peak when diffusional exchange between panels is constrained (g = λ/10, gray histogram). Almost no changes are observed when diffusional exchange is totally abolished (g = 0, blue circles). Upon lifting all diffusion barriers, i.e., for g = λ, the PDF is broadened (red squares), featuring a marked tail for large spot areas (for better visibility, values of p(A) have been scaled up by a factor of 2). Albeit a quantitative comparison with experimental data is not meaningful because of the reduced complexity of the simulation model, these results are in very good qualitative agreement with experimental observations on ERES patterns (cf. Figs. 2 and 3). To see this figure in color, go online.
To probe more quantitatively whether this hypothesis is consistent with experimental observations on ERESs, we turned to a simulation model with reduced complexity (see Materials and methods for details). In particular, we considered only one effective ERES constituent that can slowly associate to and dissociate from a square surface with edge length L. This effective particle species may represent individual molecules or protein combinations (involving Sec16, TANGO1, and/or COPII proteins), with the association and dissociation rates encoding a generic cycling between ER membranes and another basin, e.g., the cytosol or the Golgi apparatus; see below for further discussion. While on the surface, particles were allowed to diffuse and irreversibly fuse to larger domains from which particles could escape by dissociation. This setting is similar to a previously analyzed kinetic model for raftlike domains under continuous recycling (44). Assuming a strong segregation between constituents and the surrounding membrane (χ ≫ kBT), domains were assumed to have a circular shape. Going beyond the related model of recycling raftlike domains (44), the random motion of particles and domains was based on physically plausible size-dependent diffusion constants (41,42). In addition to the surface’s outer boundary, internal repelling boundary conditions, mimicking the action of diffusion barriers, were also introduced. To this end, the interior of the total surface was divided into a periodic lattice of square panels (edge length λ) with each panel being surrounded by reflecting boundaries (see Fig. 4 B). Each of these boundaries had a gap of width 0 < g < λ in the center that was left open for diffusional exchange with next-neighbor panels. For mimicking untreated cells, in which ER junctions act as diffusion barriers, gaps in the range g/λ ∼ 0.1 were used to achieve a confined diffusion, whereas g = λ was used for an unconfined scenario, corresponding to experiments in which the ER had been transformed into a sheet-like structure.
Simulation parameters were chosen in accordance with the following considerations: given that TANGO1, a major constituent of the ERESs, is a transmembrane protein that can only leave and re-enter the ER via transport intermediates that travel along the secretory pathway, we assumed our effective particles to exchange with fairly low kinetic rates, i.e., with typical timescales in the range of several minutes. Hence, these rates may not represent the more rapid cycling of individual Sec16 and COPII proteins between cytosol and ER membranes (27,30,32), but rather may encode an exchange between the ER and more downstream membranes, e.g., early cisternae in the Golgi apparatus. To match the experimentally observed mobility of ERESs on ER tubules (34), we have scaled down all diffusion constants by a common prefactor, i.e., domains with the size of a typical ERES were assigned a diffusion constant in the range D ∼ 10−3 μm2/s (see Fig. S7 A; Materials and methods). Given that ER tubules have a diameter of ∼100 nm with typical lengths of ∼1.1 μm (43), hence providing similarly sized membrane areas as ER fragments after filipin treatment or osmotic shock (Fig. 3 C), panel dimensions of λ ∼ 1.0 μm appear plausible. Balancing this estimate with the associated computational demand, we have chosen λ = 1.5 μm. For brevity, we will focus on the chosen, prototypical set of parameters (see Materials and methods and legend of Fig. 4), indicating alongside how changes will affect the observed phenotypes. To allow for a fair comparison of our simulations with experimentally obtained fluorescence images, particle/domain positions and sizes from simulations were transferred to microscopy-like images by Gaussian blurring (see Materials and methods), and the PDF p(A) was obtained by subsequently evaluating these images (cf. Fig. S7 B).
Running simulations without any diffusion barriers (i.e., g = λ) yielded the following results: for sufficiently large system sizes (e.g., L = 9 μm), the PDF of domain areas, obtained without a transformation into microscopy-like images, showed a generic power law p(A) ∼ 1/A3/2 for small domains (Fig. S7 C), in agreement with the closely related model of recycling raftlike domains (44). When applying a Gaussian blur to transfer positions and sizes to microscopy-like images (see Fig. 4 C for an example), small domains were smudged to a more or less homogenous background, leading to a suppression of this generic power law and resulting in a PDF that is reminiscent of a slightly skewed lognormal distribution (Fig. 4 D; Fig. S7 C). Reducing the system size L eventually yields a well-mixed system in which diffusion is not limiting anymore, and hence, all particles merge in a single domain. The onset of this scenario can be estimated by comparing the system size with the mean-square displacement of a typical ERES within a period given by the inverse dissociation rate, i.e., 4D/koff = L yields L ≈ 1 μm for D = 10−3 μm2/s and 1/koff = 300 s. This estimate is in good agreement with the observation that a dominant peak in p(A) emerges when decreasing the system size (Fig. S7 C). For L = 1.5 μm, for example, the parameters used in the simulation predict a steady-state amount of ρL2kon/(kon + koff) = 70–75 particles, merged into a single domain of area A = 0.18 μm2 in very good agreement with the pronounced peak observed in p(A) for this system size. Reducing the system size even more, without altering rates and diffusivities, leaves the system in a well-mixed state with a single domain for which the area decreases with L2.
Fixing now the system size to L = 9 μm but confining domain diffusion by internal boundaries (panels of edge length λ with gaps of size g ≪ λ in the boundaries, Fig. 4 B) resulted in a lattice-like arrangement of fairly homogenously sized spots in marked contrast to the phenotype without diffusion barriers (see Fig. 4 C). Extracting the PDF of spot areas from these images confirmed the visual impression: in the presence of diffusion barriers (g = λ/10, L = 6λ = 9 μm), a fairly narrow PDF p(A) was obtained (Fig. 4 D) that was virtually identical to the case of completely isolated panels (g = 0) in which a well-mixed scenario with only a single domain per panel is expected (cf. discussion in the previous paragraph). Little to no changes of this result were observed when using gap sizes in the range g < λ/3. In contrast, removing all diffusion barriers (g = λ), i.e., free diffusion, led to a markedly broader distribution (Fig. 4 D). As stated before, because of the blurring procedure, the generic power law for small areas was masked (see also Fig. S7, C and D). The transition between the extremes (free versus fully confined diffusion) can be predicted to happen roughly at g/λ ≈ 0.35, when the single domain within an isolated panel (diameter ∼500 nm) is able to easily pass through the gap to merge with domains in neighboring panels. Above this gap size, panels become strongly coupled by diffusional exchange, leading to a PDF of domain areas that resembles the one found for free diffusion on an unconfined surface. Simulations with varying gap sizes confirm this reasoning (Document S1. Figs. S1–S7, Document S2. Article plus supporting material D).
Images and area distributions obtained by these simulations very much resemble the experimentally observed phenotypes, i.e., a lattice-like arrangement of fairly homogenously sized spots when diffusional exchange was restricted (corresponding to native ERES patterns, in which ER junctions hamper diffusion (34)), whereas removing diffusion barriers (like in siRNA-treated cells) led to fewer and, on average, larger spots with a broadened PDF of apparent areas. Despite the reduced complexity of our simulations, this favorable agreement supports the interpretation that ERES patterns emerge via a demixing scenario that is fine-tuned or quenched by diffusion barriers.
Similar to the related model of recycling raftlike domains (44), these findings can be extrapolated to other parameter choices in a straightforward fashion by considering the dominant timescales in the system (1/koff and λ2/D, with λ = L for an unconstrained system): by changing the ratio kon/koff, the number of particles can certainly be tuned at will, which will determine, for example, the domain size in the well-mixed limit. Maintaining the ratio and only speeding up the exchange, the balance will shift toward smaller domains if diffusion constants are left unaltered because dissociation outcompetes the slower diffusion-driven fusion events. Consequently, the well-mixed state will only be reached for smaller panel sizes. Compensating the more rapid cycling by elevated diffusion coefficients essentially leads to the same phenotype observed for the initial set of parameters. Similarly, one can tune the system by only varying diffusion constants and leaving the kinetic rates unchanged.
It is worth emphasizing, however, that PDFs found in our simulations can only show a qualitative agreement with our experimental data because of the strongly reduced complexity: 1) native ERES patterns in cells emerge on ER tubules with varying lengths, coupled by three-way junctions to a vast network structure (43). Therefore, the experimentally found p(A) will include varying panel sizes and geometries, and diffusion barriers will most likely not be simple walls with gaps but rather will rely on more complex energy landscapes that arise from elastic membrane deformations when the ERESs pass the junction. 2) siRNA-treated cells may still feature more complex ER geometries than a simple plane surface, e.g., tubular assemblies below the diffraction limit (11). Therefore, remnant barriers and complex membrane morphologies may still enter the experimentally determined p(A). And 3) ERES formation does not only invoke a single particle species but relies on the interaction of at least TANGO1 and Sec16 (48,49), with a phosphorylation of TANGO1 leading to the rapid disassembly of the ERESs (49). Moreover, COPII proteins are known to interact with Sec16 (32) and TANGO1 (26). In particular, it has been found that TANGO1 proteins form an engulfing ring around COPII-enriched membrane patches while wrapping large cargo molecules like collagen (26,51), and the concomitant bud formation has been investigated via continuum elasticity models (52). Thus, formulating a refined model, as compared with the one we have introduced here, will not only require considerably more details on membrane geometries and curvature energies but also demands a large set of additional parameters that reflect the mutual interactions and stoichiometry of all involved proteins and lipids.
However, it is worth emphasizing at this point that our mesoscopic model captures the main features of the ERES self-assembly irrespective of the molecular details on smaller length scales: constituents can associate to, dissociate from, and diffuse on the membrane, and their net attractive interaction is considered via fusion to larger domains upon contact. Domain fission, including the loss of individual particles toward the surrounding membrane, may be incorporated but will hardly change the gross phenomena observed in the easier scheme (see also discussion in (44)). Long-scale diffusion hindrance for large domains can certainly be modeled with refined repulsive potentials rather than considering simple gaps in an internal boundary, yet it is highly likely that the observed phenomena remain mostly unaltered because the major ingredient is the waiting time (or Kramers time) to escape to neighboring panels or tubules. Thinking about alternative models of ERES assembly that do not rely on a diffusion-driven fusion and growth of domains will essentially require localized seeds on the membrane to which ERES constituents can bind to directly from the cytosol. In such an approach, however, it remains unclear how such seeds are organized in the first place. Moreover, although we cannot rule out that the altered phenotype after RNAi treatment may also be explained by altered biochemical reaction rates rather than by lifting diffusion hindrance, the biochemistry behind ERES formation appears to be so robust that it even works in filipin-treated or osmotically shocked cells for extended timescales (hours). Altogether, it is therefore very plausible that the ERES formation is well described on a mesoscopic scale by a quenched demixing process that can be tuned by the ER morphology.
Adopting this view also provides a consistent explanation for the disassembly of ERESs during cell division. Identifying the cell-cycle-dependent phosphorylation of TANGO1 (starting upon entering mitosis) with a reduction of the Flory-Huggins parameter to χ ≪ kBT predicts ERES disintegration due to a lacking driving force for demixing, in line with the experimental observations of vanishing ERESs (49). Dephosphorylation of TANGO1 at the end of mitosis (49) then corresponds to a switch back to χ ≫ kBT, which drives demixing and, hence, restores the ERES patterns. Furthermore, annular ERES patterns in muscle cells (53) may also rely on a demixing process with the spatial arrangement being determined by the underlying ER morphology, e.g., by concentrating ER membranes in sheets around the nucleus. It is therefore tempting to speculate that ERES patterns always emerge by a switchable two-dimensional demixing scenario with the underlying ER morphology dictating the final spatial arrangement of domains, i.e., the degree of quenching. The combination of a robust physico-chemical pattern formation mechanism for the ERESs, fine-tuned by the ER morphology, may allow for a flexible adaption of vital cellular tasks even in changing environments, contributing to the robustness of living entities.
Conclusion
In conclusion, we have shown here by quantitative image analysis that ERES patterns depend on the morphology of the hosting ER membrane. To this end, we have exploited chemical and genetic tools to perturb the ER structure from a native network to a contiguous sheet-like geometry or to a set of isolated fragments. Bearing in mind the limitations of these tools and acknowledging the complexity and diversity of living cells, the observed quantitative reproducibility of ERES patterns under different conditions and especially the striking change upon deleting lunapark proteins is remarkable. Complementary model simulations suggest that native ERES patterns can be understood to emerge, on a mesoscopic level, from a demixing process that is quenched by the ER’s network topology. We speculate that employing a fairly simple and robust demixing mechanism allows eukaryotic cells to dynamically adapt their ERES pattern to their specific needs without having to change or re-invent the underlying protein constituents. Depending on size, nutrition state, environmental challenges, etc., cells can tune their ERES arrangement, and hence the source of the early secretory pathway, by altering the ER morphology within a modest period. Presumably, this is yet another example of how living matter aims at staying in a dynamic state that can quickly respond and adapt to fluctuating environments.
Acknowledgments
We thank Philipp Braaker for assistance with Western blotting.
Financial support by the VolkswagenStiftung (Az. 92738) and by the Elite Network of Bavaria (Study Program Biological Physics) are gratefully acknowledged.
Editor: Roland Winter.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.04.023.
Author contributions
K.S. carried out all experiments and analyses. L.S. drafted the siRNA approach and made initial experiments. M.W. designed the study, supervised the analyses, conceptualized the demixing model, and carried out all simulations. All authors contributed to writing of the manuscript.
Supporting material
References
- 1.Alberts B. Garland Science; New York: 2015. Molecular Biology of the Cell. [Google Scholar]
- 2.Schweisguth F., Corson F. Self-organization in pattern formation. Dev. Cell. 2019;49:659–677. doi: 10.1016/j.devcel.2019.05.019. [DOI] [PubMed] [Google Scholar]
- 3.Brangwynne C.P. Phase transitions and size scaling of membrane-less organelles. J. Cell Biol. 2013;203:875–881. doi: 10.1083/jcb.201308087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shin Y., Brangwynne C.P. Liquid phase condensation in cell physiology and disease. Science. 2017;357:eaaf4382. doi: 10.1126/science.aaf4382. [DOI] [PubMed] [Google Scholar]
- 5.Wheeler R.J., Hyman A.A. Controlling compartmentalization by non-membrane-bound organelles. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2018;373:20170193. doi: 10.1098/rstb.2017.0193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sezgin E., Levental I., Eggeling C. The mystery of membrane organization: composition, regulation and roles of lipid rafts. Nat. Rev. Mol. Cell Biol. 2017;18:361–374. doi: 10.1038/nrm.2017.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shen Y., Zhao Z., Min W. Metabolic activity induces membrane phase separation in endoplasmic reticulum. Proc. Natl. Acad. Sci. USA. 2017;114:13394–13399. doi: 10.1073/pnas.1712555114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Budnik A., Stephens D.J. ER exit sites--localization and control of COPII vesicle formation. FEBS Lett. 2009;583:3796–3803. doi: 10.1016/j.febslet.2009.10.038. [DOI] [PubMed] [Google Scholar]
- 9.Borgese N. Getting membrane proteins on and off the shuttle bus between the endoplasmic reticulum and the Golgi complex. J. Cell Sci. 2016;129:1537–1545. doi: 10.1242/jcs.183335. [DOI] [PubMed] [Google Scholar]
- 10.Terasaki M., Shemesh T., Kozlov M.M. Stacked endoplasmic reticulum sheets are connected by helicoidal membrane motifs. Cell. 2013;154:285–296. doi: 10.1016/j.cell.2013.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nixon-Abell J., Obara C.J., Lippincott-Schwartz J. Increased spatiotemporal resolution reveals highly dynamic dense tubular matrices in the peripheral ER. Science. 2016;354:aaf3928. doi: 10.1126/science.aaf3928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hu J., Shibata Y., Prinz W.A. Membrane proteins of the endoplasmic reticulum induce high-curvature tubules. Science. 2008;319:1247–1250. doi: 10.1126/science.1153634. [DOI] [PubMed] [Google Scholar]
- 13.Shibata Y., Shemesh T., Rapoport T.A. Mechanisms determining the morphology of the peripheral ER. Cell. 2010;143:774–788. doi: 10.1016/j.cell.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shemesh T., Klemm R.W., Rapoport T.A. A model for the generation and interconversion of ER morphologies. Proc. Natl. Acad. Sci. USA. 2014;111:E5243–E5251. doi: 10.1073/pnas.1419997111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen S., Novick P., Ferro-Novick S. ER network formation requires a balance of the dynamin-like GTPase Sey1p and the Lunapark family member Lnp1p. Nat. Cell Biol. 2012;14:707–716. doi: 10.1038/ncb2523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen S., Desai T., Ferro-Novick S. Lunapark stabilizes nascent three-way junctions in the endoplasmic reticulum. Proc. Natl. Acad. Sci. USA. 2015;112:418–423. doi: 10.1073/pnas.1423026112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang S., Tukachinsky H., Rapoport T.A. Cooperation of the ER-shaping proteins atlastin, lunapark, and reticulons to generate a tubular membrane network. eLife. 2016;5:e18605. doi: 10.7554/eLife.18605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Woźniak M.J., Bola B., Allan V.J. Role of kinesin-1 and cytoplasmic dynein in endoplasmic reticulum movement in VERO cells. J. Cell Sci. 2009;122:1979–1989. doi: 10.1242/jcs.041962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Georgiades P., Allan V.J., Waigh T.A. The flexibility and dynamics of the tubules in the endoplasmic reticulum. Sci. Rep. 2017;7:16474. doi: 10.1038/s41598-017-16570-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Speckner K., Stadler L., Weiss M. Anomalous dynamics of the endoplasmic reticulum network. Phys. Rev. E. 2018;98:012406. doi: 10.1103/PhysRevE.98.012406. [DOI] [PubMed] [Google Scholar]
- 21.Guo Y., Li D., Li D. Visualizing intracellular organelle and cytoskeletal interactions at nanoscale resolution on millisecond timescales. Cell. 2018;175:1430–1442.e17. doi: 10.1016/j.cell.2018.09.057. [DOI] [PubMed] [Google Scholar]
- 22.Lee J.E., Cathey P.I., Voeltz G.K. Endoplasmic reticulum contact sites regulate the dynamics of membraneless organelles. Science. 2020;367:eaay7108. doi: 10.1126/science.aay7108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ito Y., Uemura T., Nakano A. cis-Golgi proteins accumulate near the ER exit sites and act as the scaffold for Golgi regeneration after brefeldin A treatment in tobacco BY-2 cells. Mol. Biol. Cell. 2012;23:3203–3214. doi: 10.1091/mbc.E12-01-0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bevis B.J., Hammond A.T., Glick B.S. De novo formation of transitional ER sites and Golgi structures in Pichia pastoris. Nat. Cell Biol. 2002;4:750–756. doi: 10.1038/ncb852. [DOI] [PubMed] [Google Scholar]
- 25.Malhotra V., Erlmann P. Protein export at the ER: loading big collagens into COPII carriers. EMBO J. 2011;30:3475–3480. doi: 10.1038/emboj.2011.255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Raote I., Malhotra V. Tunnels for protein export from the endoplasmic reticulum. Annu. Rev. Biochem. 2021 doi: 10.1146/annurev-biochem-080120-022017. Published online January 27, 2021. [DOI] [PubMed] [Google Scholar]
- 27.Forster R., Weiss M., Pepperkok R. Secretory cargo regulates the turnover of COPII subunits at single ER exit sites. Curr. Biol. 2006;16:173–179. doi: 10.1016/j.cub.2005.11.076. [DOI] [PubMed] [Google Scholar]
- 28.Runz H., Miura K., Pepperkok R. Sterols regulate ER-export dynamics of secretory cargo protein ts-O45-G. EMBO J. 2006;25:2953–2965. doi: 10.1038/sj.emboj.7601205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Watson P., Forster R., Stephens D.J. Coupling of ER exit to microtubules through direct interaction of COPII with dynactin. Nat. Cell Biol. 2005;7:48–55. doi: 10.1038/ncb1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Verissimo F., Halavatyi A., Weiss M. A microtubule-independent role of p150glued in secretory cargo concentration at endoplasmic reticulum exit sites. J. Cell Sci. 2015;128:4160–4170. doi: 10.1242/jcs.172395. [DOI] [PubMed] [Google Scholar]
- 31.Zacharogianni M., Kondylis V., Rabouille C. ERK7 is a negative regulator of protein secretion in response to amino-acid starvation by modulating Sec16 membrane association. EMBO J. 2011;30:3684–3700. doi: 10.1038/emboj.2011.253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tillmann K.D., Reiterer V., Farhan H. Regulation of Sec16 levels and dynamics links proliferation and secretion. J. Cell Sci. 2015;128:670–682. doi: 10.1242/jcs.157115. [DOI] [PubMed] [Google Scholar]
- 33.Heinzer S., Wörz S., Weiss M. A model for the self-organization of exit sites in the endoplasmic reticulum. J. Cell Sci. 2008;121:55–64. doi: 10.1242/jcs.013383. [DOI] [PubMed] [Google Scholar]
- 34.Stadler L., Speckner K., Weiss M. Diffusion of exit sites on the endoplasmic reticulum: a random walk on a shivering backbone. Biophys. J. 2018;115:1552–1560. doi: 10.1016/j.bpj.2018.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Altan-Bonnet N., Sougrat R., Lippincott-Schwartz J. Golgi inheritance in mammalian cells is mediated through endoplasmic reticulum export activities. Mol. Biol. Cell. 2006;17:990–1005. doi: 10.1091/mbc.E05-02-0155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Granell S., Baldini G., Baldini G. Sequestration of mutated alpha1-antitrypsin into inclusion bodies is a cell-protective mechanism to maintain endoplasmic reticulum function. Mol. Biol. Cell. 2008;19:572–586. doi: 10.1091/mbc.E07-06-0587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Karasawa T., Wang Q., Steyger P.S. Calreticulin binds to gentamicin and reduces drug-induced ototoxicity. Toxicol. Sci. 2011;124:378–387. doi: 10.1093/toxsci/kfr196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Axelsson M.A., Warren G. Rapid, endoplasmic reticulum-independent diffusion of the mitotic Golgi haze. Mol. Biol. Cell. 2004;15:1843–1852. doi: 10.1091/mbc.E03-07-0459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.King C., Sengupta P., Lippincott-Schwartz J. ER membranes exhibit phase behavior at sites of organelle contact. Proc. Natl. Acad. Sci. USA. 2020;117:7225–7235. doi: 10.1073/pnas.1910854117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Berg S., Kutra D., Kreshuk A. ilastik: interactive machine learning for (bio)image analysis. Nat. Methods. 2019;16:1226–1232. doi: 10.1038/s41592-019-0582-9. [DOI] [PubMed] [Google Scholar]
- 41.Hughes B.D., Pailthorpe B.A., White L.R. The translational and rotational drag on a cylinder moving in a membrane. J. Fluid Mech. 1981;110:349–372. [Google Scholar]
- 42.Petrov E.P., Schwille P. Translational diffusion in lipid membranes beyond the Saffman-Delbruck approximation. Biophys. J. 2008;94:L41–L43. doi: 10.1529/biophysj.107.126565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ferencz C.-M., Guigas G., Weiss M. Shaping the endoplasmic reticulum in vitro. Biochim. Biophys. Acta. 2016;1858:2035–2040. doi: 10.1016/j.bbamem.2016.06.004. [DOI] [PubMed] [Google Scholar]
- 44.Turner M.S., Sens P., Socci N.D. Nonequilibrium raftlike membrane domains under continuous recycling. Phys. Rev. Lett. 2005;95:168301. doi: 10.1103/PhysRevLett.95.168301. [DOI] [PubMed] [Google Scholar]
- 45.Watson P., Townley A.K., Stephens D.J. Sec16 defines endoplasmic reticulum exit sites and is required for secretory cargo export in mammalian cells. Traffic. 2006;7:1678–1687. doi: 10.1111/j.1600-0854.2006.00493.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hughes H., Budnik A., Stephens D.J. Organisation of human ER-exit sites: requirements for the localisation of Sec16 to transitional ER. J. Cell Sci. 2009;122:2924–2934. doi: 10.1242/jcs.044032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kung L.F., Pagant S., Miller E.A. Sec24p and Sec16p cooperate to regulate the GTP cycle of the COPII coat. EMBO J. 2012;31:1014–1027. doi: 10.1038/emboj.2011.444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Maeda M., Katada T., Saito K. TANGO1 recruits Sec16 to coordinately organize ER exit sites for efficient secretion. J. Cell Biol. 2017;216:1731–1743. doi: 10.1083/jcb.201703084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Maeda M., Komatsu Y., Saito K. Mitotic ER exit site disassembly and reassembly are regulated by the phosphorylation status of TANGO1. Dev. Cell. 2020;55:237–250.e5. doi: 10.1016/j.devcel.2020.07.017. [DOI] [PubMed] [Google Scholar]
- 50.McEwen B.F., Telford J.N., Arion W.J. A critical evaluation of the use of filipin-permeabilized rat hepatocytes to study functions of the endoplasmic reticulum in situ. Cell Biochem. Funct. 1987;5:263–272. doi: 10.1002/cbf.290050405. [DOI] [PubMed] [Google Scholar]
- 51.Raote I., Ernst A.M., Malhotra V. TANGO1 membrane helices create a lipid diffusion barrier at curved membranes. eLife. 2020;9:e57822. doi: 10.7554/eLife.57822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Raote I., Chabanon M., Campelo F. A physical mechanism of TANGO1-mediated bulky cargo export. eLife. 2020;9:e59426. doi: 10.7554/eLife.59426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lu Z., Joseph D., Ralston E. Golgi complex reorganization during muscle differentiation: visualization in living cells and mechanism. Mol. Biol. Cell. 2001;12:795–808. doi: 10.1091/mbc.12.4.795. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.