Chromatin investigation in the nucleus using a phasor approach to structured illumination microscopy

Abstract

Chromatin in the nucleus is organized in functional sites at variable level of compaction. Structured illumination microscopy (SIM) can be used to generate three-dimensional super-resolution (SR) imaging of chromatin by changing in phase and in orientation a periodic line illumination pattern. The spatial frequency domain is the natural choice to process SIM raw data and to reconstruct an SR image. Using an alternative approach, we demonstrate that the additional spatial information encoded in the knowledge of the position of the illumination pattern can be efficiently decoded using a generalized version of separation of photon by lifetime tuning (SPLIT) that does not require lifetime measurements. In the resulting SPLIT-SIM, the SR image is obtained by isolating a fraction of the intensity corresponding to the center of the diffraction-limited point spread function. This extends the use of the SPLIT approach from stimulated emission depletion microscopy to SIM. The SPLIT-SIM algorithm is based only on phasor analysis and does not require deconvolution. We show that SPLIT-SIM can be used to generate SR images of chromatin organizational motifs with tunable resolution and can be a valuable tool for the imaging of functional sites in the nucleus.

Significance

Structured illumination microscopy is a popular super-resolution technique that finds application in the imaging of chromatin. We show that separation of photon by lifetime tuning can be used to reconstruct structured illumination microscopy super-resolved images via phasor analysis. This is the first demonstration, to our knowledge, that separation of photon by lifetime tuning is not limited to stimulated emission depletion microscopy but can be applied to other types of super-resolution techniques.

Introduction

The two main approaches to super-resolution (SR) microscopy are represented by the so-called stochastic switching techniques (e.g., photoactivatable localization microscopy—PALM (1,2) and stochastic optical reconstruction microscopy—STORM (3)) and targeted switching techniques (e.g., stimulated emission depletion microscopy—STED (4) and reversible saturable optical fluorescence transitions—RESOLFT (5)). An alternative strategy is the use of an additional channel of the microscope encoding subdiffraction spatial information (6,7). In gated STED (8,9) and separation of photons by lifetime tuning (SPLIT) (10, 11, 12), this additional channel is represented by the nanosecond fluorescence lifetime. The doughnut-shaped depletion beam causes a shortening of the fluorescence lifetime in the periphery of the point spread function (PSF), but it does not affect the fluorescence lifetime in the center of the PSF. This gradient of lifetime is used to isolate the fluorescence stemming from the center of the PSF and improve the effective resolution of the STED microscope without increasing the peak intensity of the STED beam. More specifically, in SPLIT, the fluorescence originating from the center of the PSF is extracted, at each pixel, by analyzing the profile of the intensity along the additional channel. The SPLIT computational approach allows us to mitigate the signal/noise-background reduction introduced by the time-gated detection hardware approach. Powerfully, SPLIT is not limited to the analysis of fluorescence lifetime but has a more general application in STED microscopy. Recently, we demonstrated that SPLIT can be applied to a series of STED images acquired with tunable depletion power (13,14). The results of this work have shown that SPLIT could be applied to any type of STED multidimensional image containing an additional channel or dimension able to encode spatial information. This suggests a more general application of SPLIT to other SR techniques. However, the application of SPLIT beyond STED has not been demonstrated yet.

Structured illumination microscopy (SIM) is one of the most implemented SR techniques (15,16). Compared with diffraction-unlimited SR techniques which can theoretically achieve unlimited spatial resolution, SIM enhances spatial resolution by a factor of two. Despite the modest twofold resolution improvement, linear SIM stands out as a more “gentle,” multicolor SR technique that can readily be applied to samples that are prepared for standard fluorescence microscopy (17). SIM relies on the use of a two-dimensional (2D) or three-dimensional (3D) structured illumination pattern, generated from the interference of two or three laser beams, respectively, to excite the sample. To achieve a uniform excitation of the sample, this pattern is sequentially shifted laterally (pattern translation steps) and tilted at different angles (pattern orientations). The images acquired at different pattern translation steps and angles are then processed to reconstruct an SR image (18). Thus, the image formation in SIM requires mathematical postprocessing of the raw data, which can easily lead to multiple artifacts during the reconstruction process (15,17,19). Several algorithms have been proposed for the reconstruction of SIM images (15,20, 21, 22, 23, 24, 25). The image formation algorithm is an important step in SIM, as it allows us to extend the effective optical transfer function of the microscope beyond its cutoff spatial frequency.

Here, we present a novel, to our knowledge, point of view in the reconstruction of SIM data using the concept of SPLIT (10). We look at SIM as a multidimensional SR technique, in which additional spatial information is encoded within the different illumination pattern translation steps and angles. We show that the profile of the intensity as a function of the pattern translation steps is a fingerprint of the position of the fluorophores within the PSF of the microscope. In other words, in SIM, the pattern position represents the additional encoding channel required for the application of SPLIT. The intensity profile along this channel can be visualized and analyzed in the phasor plot, which contains the Fourier transform (FT) of the profile at each pixel of an image (26, 27, 28). In SIM, we find that the center and the periphery of the PSF have different fingerprints in the phasor plot. This difference can be used to calculate the fraction of the total signal (i.e., the sum of all the images acquired at different translation steps and angles) corresponding to the center of the PSF and reconstruct a final SIM image with higher spatial resolution. The combination of SPLIT and SIM (SPLIT-SIM) is a powerful technique because it can reconstruct artifact-free images and because the phasor plot provides a visual, intuitive, and direct evaluation of the acquired data to nonskilled users as well. We show that the resolution in the focal plane can be tuned up to a factor of ∼2 by changing the value of a single parameter and without the use of deconvolution. As a benchmark for biological applications, we apply our method to the imaging of chromatin. Chromatin organization plays a key role in the regulation of genome-related processes and SR microscopy has become fundamental to understand how chromatin 3D structure influences genome function. We quantify the colocalization of functional nuclear sites at two different spatial scales by dual-color SPLIT-SIM. This work demonstrates for the first time, to our knowledge, that SPLIT is not limited to STED microscopy but has a more general application in the context of SR techniques and opens new perspectives in the context of SIM microscopy and related optical methods.

Materials and methods

Simulations

SIM images of point-like fluorophores were simulated using MATLAB (The MathWorks, Natick, MA). The object consisted of a variable number of point-like sources randomly distributed in an image of 128 × 128 pixels with a pixel size of 50 nm. The Siemens star object was simulated in MATLAB using the function im_radial_stripe (29).

A periodic illumination pattern I_αi(x, y, k) was simulated as

$$I_j\left(x,y,k\right)=1-m{\text{sin}}^2\left[h\pi \left(\frac{x\text{cos}{\alpha }_j-y\text{sin}{\alpha }_j}{T}+\frac{k}{N_{steps}}+p_{j,h}\right)\right],$$ (1)

where m is a constant between 0 and 1 (with 1 representing the maximal contrast), α_j is the orientation of the pattern (j = 1, …, N_angles with N_angles = 3), T is the period, p_j,h is the offset of the pattern at the orientation α_j, h is a constant indicating the first (h = 1) or second (h = 2) order of the pattern. For the simulations shown in Fig. 2 and Fig. S4, h was set to 1. The contrast of the pattern C_P is defined as the amplitude divided by the average, and its relation to the parameter m is given by C_P = (m/2)/(1 − m/2). The orientation of the pattern was set to the values α₁ = 2.895 rad, α₂ = α₁ + π/3, and α₃ = α₁ + 2π/3. The period was set to T = 450 nm unless specified otherwise. The position of the pattern was translated by varying the value of k between 1 and N_steps with N_steps = 5. For each image of the stack, the object image was multiplied by the excitation pattern I_αj(x, y, k) and then convolved with a Gaussian detection PSF of waist w_WF = 4.5 pixels = 225 nm. The maximal collectable number of photons in a single pixel from a point-like source, for each frame of the stack, was set to the value S. Finally, the images were corrupted by a Poisson noise realization whose average values are given by the number of counts at each pixel using the MATLAB function imnoise.

Figure 2.

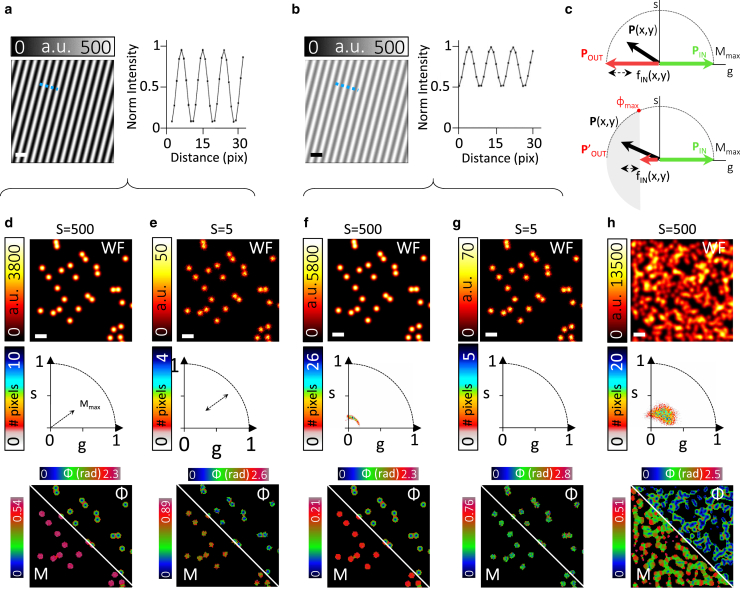
SPLIT-SIM on simulated SIM images of point-like sources. (a) Simulated image of a periodic illumination pattern with maximal contrast (C_p = 1) and corresponding line intensity profile along the dashed line. (b) Simulated image of a periodic illumination pattern with lower contrast (C_p = 0.33) and corresponding line intensity profile along the dashed line. (c) Schematic showing the possible setting of the phasors P_in and P_out. (d–g) SPLIT-SIM of simulated SIM images of sparse point-like sources with maximal (d and e) and low (f and g) pattern contrast and different noise levels, as determined by the intensity level S. Shown are, from top to bottom, the widefield image obtained by summing all the images of the stack (WF), the phasor plot, the modulation (M), and the phase (ϕ) image. (h) Same as in (d) but simulating a crowded object. Scale bars, 700 nm. To see this figure in color, go online.

SPLIT-SIM algorithm

The SPLIT-SIM algorithm was implemented in MATLAB. The algorithm operates on SIM image stacks F_j(x, y, k) consisting of N_angles orientations and N_steps pattern translation steps. For each orientation α_j, the phasor P_FL,j(x, y) is calculated via an FT according to Eq. 3. The phase ϕ_FL,j(x, y) and modulation M_FL,j(x, y) are then calculated as the phase and the modulus of P_FL,j(x, y).

For each harmonic, a periodic pattern I_j(x, y, k) is simulated according to Eq. 1 by setting the period to T = T_est, the orientation angle to α_j = α_j,est, and the pattern offset to p_j,h = p_j,h,est. The values T_est, α_j,est, and p_j,h,est represent the best estimation of the parameters describing the experimental illumination pattern. The phasor of the excitation intensity P_exc,j(x, y) is calculated as

$${\mathit{P}}_{exc,\text{j}}\left(x,y\right)=\sum _k{I}_{\text{j}}\left(\text{x},\text{y},\text{k}\right)e^{i\left[2\pi h(k-1)/N_{steps}\right]}/\sum _k{I}_{\text{j}}\left(\text{x},\text{y},\text{k}\right)$$ (2)

The phase ϕ_exc,j(x, y) is then calculated as the phase of P_exc,j(x, y). The corrected phasor P_j(x, y) is calculated according to Eq. 4. This procedure is repeated for j = 1, …, N_angles. The average phasor P(x, y) (average of the N_angles orientations) is calculated using Eq. 5.

The phase image ϕ(x, y), calculated as the phase of P(x, y), is used to estimate the illumination pattern parameters. The values T_est (pattern period), α_j,est (orientation angles), and p_j,1,est (first-order offsets) are first estimated as the values that minimize the average value of the first harmonic phase in an image, ϕ_AV = <ϕ(x, y)>, where the brackets denote averaging over all nonbackground pixels. The offset of the second order, p_j,2,est, can be expressed as p_j,2,est = p_j,1,est + Δp_j,2,est, where Δp_j,2,est is dependent on the shape of the pattern. The values Δp_j,2,est are estimated as the value that minimizes the average value of the second-order phase in an image, ϕ^{(h = 2)}_AV = <ϕ^{(h = 2)}(x, y)>. To speed up processing, the values of T_est, α_j,est, and Δp_j,2,est are calibrated (using a sample of 100-nm fluorescent spheres) and stored in a file. In this way, for any given sample, we must estimate only the parameters p_j,1,est.

Phasor plots were built as 2D histograms of the values g(x, y) = M(x, y)cosϕ_plot(x, y) and s(x, y) = M(x, y)sinϕ_plot(x, y) where ϕ_plot(x, y) = |ϕ(x, y)| and M(x, y) and ϕ(x, y) are the modulation and phase of the phasor P(x, y).

For each pixel, the fraction of photons corresponding to the center of the PSF f_IN(x, y) was calculated using Eqs. 6, 7, and 8 (experimental data) or only Eq. 6 (simulations). For the experimental data, the parameter M_max, which depends on the contrast of the experimental pattern, was determined by imaging a sample of sparse 100-nm fluorescent spheres. The parameter ϕ_max was set as specified. To force values of fraction to fall between 0 and 1, the values of f_IN(x, y) were filtered through a logistic function: f = 1/(1 + exp(−k_L(f − 1/2))) with k_L = 4. The super-resolved SPLIT-SIM image was calculated using Eq. 9. The residual fraction of photons corresponding to the periphery of the PSF was calculated as f_OUT(x, y) = 1 − f_IN(x, y), and the corresponding image was calculated as I_OUT(x, y) = f_OUT(x, y)I_WF(x, y), where I_WF(x, y) is the sum of all the images of the stack, I_WF(x, y) = Σ_j,kF_j(x, y , k).

A user-friendly version of the algorithm is available at https://github.com/llanzano/SPLITSIM.

Data analysis

Image correlation spectroscopy (ICS) and image cross-correlation spectroscopy (ICCS) analyses were performed in MATLAB using the algorithm described in Oneto et al. (30) and available at https://github.com/llanzano/ICCS. ICS was used to quantify the spatial resolution of the images. Spatial autocorrelation functions (ACFs) were fitted to a Gaussian model to extract the average width of the effective PSF expressed as full width at half maximum (FWHM) (31). ICCS was used to quantify the colocalization of nuclear sites from dual-color SPLIT-SIM images and to extract characteristic correlation distances.

Samples

A sample of 100-nm fluorescent spheres (yellow-green FluoSpheres Carboxylate-Modified Microspheres, F8803; Invitrogen, Carlsbad, CA) was prepared as follows. Glass coverslips were treated with poly-L-lysine (P8920; Sigma-Aldrich, St. Louis, MO) for 20 min at room temperature (RT), and the spheres, diluted in Milli-Q water by 1:10,000 v/v, were added onto the coverslips. After 10 min, the coverslips were washed with Milli-Q water, dried under nitrogen flow, and mounted overnight with Invitrogen ProLong Diamond Antifade Mounting Medium (P36965).

HeLa cells and MCF7 cells were grown in Dulbecco’s modified Eagle’s medium (Sigma-Aldrich) supplemented with 1% penicillin/streptomycin, and 10% fetal bovine serum (ECS0180L; Euroclone, Pero, Italy). Cells were grown in their flasks and then transferred to 14-mm glass coverslips, 1.5 high precision for imaging. HeLa cells were fixed for 10 min with 100% ethanol at −20°C, then washed three times in phosphate-buffered saline (PBS) and twice in 3% BSA for 5 min. Next, they were incubated for 1 h RT in Sigma-Aldrich normal goat serum (NS02L) with 0.2% Sigma-Aldrich Triton 100× in PBS. Immunostaining of H2B histone was performed with Abcam rabbit anti-histone H2B antibody, ChIP Grade (ab1790; Abcam, Cambridge, UK), 1:500 diluted, in 5% normal goat serum for 2 h. Upon incubation, the sample was washed for 15 min in 5% normal goat serum with 0.2% Triton, then twice for 15 min in 0.6% normal goat serum with 0.05% Triton 100× in PBS. The secondary antibodies, goat anti-mouse IgG H&L (Chromeo 488) (ab60314), 1/200 diluted, were incubated for 1 h at RT in 5% normal goat serum. Then, the sample was washed for 15 min in 5% normal goat serum with 0.2% Triton and twice for 15 min in 0.6% normal goat serum with 0.05% Triton 100×.

To label replication sites, nascent DNA was detected in MCF7 by incubation with 5-ethynyl-2′-deoxyuridine (EdU) at 37°C for 25 min with 10 μM EdU (Thermo Fisher Scientific, Waltham, MA; Invitrogen). Later on, cells were fixed with 4% paraformaldehyde (w/v) for 10 min at RT, then washed twice with BSA 3% and permeabilized with 0.5% Triton 100× for 20 min. EdU detection was performed using the Click-iT EdU imaging kit (Thermo Fisher Scientific) according to the manufacturer’s instructions, using Alexa azide 488. After 1 h blocking buffer (BB) (3% Sigma-Aldrich bovine serum albumin (BSA) and 0.5% Triton 100×) incubation at RT, immunostaining of the proliferating cell nuclear antigen (PCNA) was performed overnight at 4°C with the primary antibody Chromotek rat anti-PCNA (16D10; Planegg-Martinsried, Germany) in BB (1/2000 dilution), and then the sample was washed once in BB and twice in washing buffer (WB) (0.2% BSA and 0.05% Triton 100×). Next, cells were incubated with the secondary antibody anti-rat ATTO 594 in BB for 1 h at RT and then washed once in BB, twice in WB, and thrice in PBS.

As a negative control, we stained elongating RNA polymerases (RNApol2) and a marker of packed DNA, histone H3K9me2. Cells were treated for 1 h RT in BB, then incubated overnight with Abcam rabbit anti-RNApol2ser2 (ab5095), in BB (1/500 dilution), and Abcam mouse anti-H3K9me2 (ab1220). Upon incubation, cells were washed as previously. Next, cells were incubated 1 h RT with secondary antibodies anti-rabbit ATTO 594 in BB (1/500 dilution) and anti-mouse Alexa 488 (1/1000 dilution) and then washed once in BB, twice in WB, and thrice in PBS.

All samples were mounted overnight with Invitrogen ProLong Diamond Antifade Mounting Medium (P36965).

Experiments

All the measurements were performed on a Nikon N-SIM Super-Resolution microscope equipped with a 1.49 NA 100× objective (CFI Apo TIRF 100×c Oil; Nikon, Tokyo, Japan) and with the grating block suitable for our experiments, 3D EX V-R 100×/1.49. Excitation was provided by a standard four laser unit (405, 488, 561, 640 nm). Alexa 488 and Chromeo 488 excitation was performed at 488 nm and the emission was collected between 515 and 545 nm. ATTO 594 was excited at 561, and its emission was detected at 590–640 nm.

Data availability

The data that support the findings of this study are available on request from the corresponding author.

Results

The SPLIT method in structured illumination microscopy

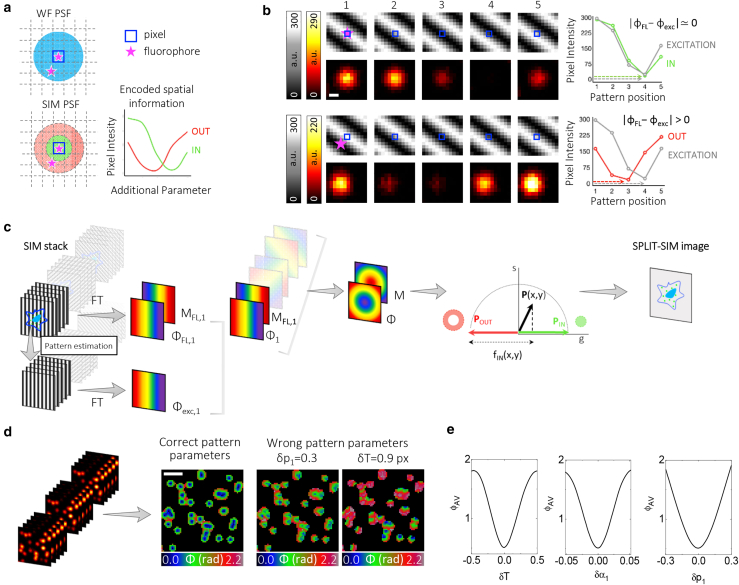
To apply SPLIT, we must demonstrate that SIM is a multidimensional, SR technique with additional spatial information encoded into an additional channel. In a conventional widefield (WF) microscope, two fluorophores that are closer than the diffraction limit cannot be distinguished. In other words, in WF, the intensity at any given pixel is always given by a mixed contribution of fluorophores centered with the pixel position (center of the PSF) and fluorophores that are located far from the pixel position but within the PSF (periphery of the PSF) (Fig. 1 a). In SIM, the sample is excited sequentially with a varying illumination pattern. This varying illumination pattern encodes additional spatial information on the position of the fluorophores within the diffraction-limited PSF. We can show that a fluorophore located in the center of the PSF has a different fingerprint than a fluorophore located at the periphery of the PSF when the intensity is plotted as a function of a parameter that defines a variation of the illumination pattern (Fig. 1 a).

Figure 1.

Description of the SPLIT-SIM method. (a) Schematic comparison between the widefield (WF) diffraction-limited point spread function (PSF) and the SIM PSF, which contains subdiffraction spatial information encoded into an additional channel. (b) Simulated SIM images for a point-like fluorophore (pink star) centered with the central pixel (top) and far from the central pixel (bottom). Shown are the images of the illumination pattern shifting in one direction (grayscale) and the corresponding fluorescence image (red heat scale). The intensity of the central pixel as a function of the position of the pattern is shown in the far right: when the fluorophore is centered with the central pixel, the fluorescence intensity (IN) is similar to the intensity of the illumination (EXCITATION) whereas when the fluorophore is far from the central pixel, the fluorescence intensity (OUT) shows a different behavior in respect to the illumination intensity. Scale bars, 200 nm. (c) Schematic workflow of the SPLIT-SIM algorithm, from the SIM image acquisition stack to the formation of the SPLIT-SIM image: calculation of a modulation and phase image for each orientation of a SIM stack, pattern parameter estimation, calculation of the average phase and modulation images, decomposition in the phasor plot, and reconstruction of the super-resolved image. (d) Simulated SIM image stack and corresponding phase images calculated with the correct pattern parameters, with a wrong value of the offset of the first angle (δp₁ = 0.3) and with a wrong value of the period (δT = 0.9 px), respectively. Scale bars, 1 μm. (e) Representations of the average phase value (ϕ_AV) as a function of the period (T), the first orientation angle (α₁), and the offset of the first angle (p₁). The setting of “correct” pattern parameters minimizes the average value of the phase (ϕ_AV). To see this figure in color, go online.

This point is made clearer with the simulation shown in Fig. 1 b. A typical SIM illumination pattern is simulated as a sinusoidal pattern shifting its peak position along one direction with five translation steps. The moving pattern generates, at each pixel, a sinusoidal excitation intensity as a function of the pattern position. At a given pixel, this excitation profile is a sine wave characterized by a phase ϕ_exc. The profile of the fluorescence intensity from the same pixel, as a function of the pattern position, is very different depending on whether the fluorophore is centered with that pixel (IN) or is shifted along the direction of the pattern (OUT) (Fig. 1 b, right). In the first case, the fluorescence intensity profile has a phase ϕ_FL similar to the phase ϕ_exc of the excitation profile (ϕ = |ϕ_FL−ϕ_exc| ≃ 0). In the second case, the fluorescence intensity profile has a phase ϕ_FL which is different from that of the excitation profile ϕ_exc ((ϕ = |ϕ_FL−ϕ_exc| > 0). Thus, the profile of the intensity as a function of the pattern position is a fingerprint of the location of the fluorophores within the PSF of the microscope.

The workflow of the SPLIT-SIM algorithm is depicted schematically in Fig. 1 c. The starting point is a SIM stack consisting of a total number of images N_images = N_steps × N_angles, corresponding to N_angles orientations of the illumination pattern and N_steps pattern translation steps for each orientation. For each orientation, α_j (i = 1, …, N_angles), we have a substack F_j(x, y, k) consisting of N_steps images. The algorithm performs an FT on this substack along the third dimension to obtain the phasor P_FL,j:

$${\mathit{P}}_{FL,\text{j}}\left(x,y\right)=\sum _k{F}_j\left(\text{x},\text{y},\text{k}\right)e^{i\left[2\pi h\left(k-1\right)/N_{steps}\right]}/\sum _k{F}_j\left(\text{x},\text{y},\text{k}\right),$$ (3)

where h represents the harmonic frequency number. The phasor P_FL,j(x, y) has phase ϕ_FL,j(x, y) and modulation M_FL,j(x, y). The excitation profile has a phase ϕ_exc,j(x, y) that depends on the pixel position and on the specific illumination pattern parameters. As explained in Fig. 1 b, we need to calculate ϕ_j = ϕ_FL,j − ϕ_exc,j. The algorithm finds the unknown ϕ_exc,j(x, y) via an iterative procedure, which, for the sake of clarity, is described in the Materials and methods. Thus, for the each orientation, we get the modulation M_FL,j(x, y) and the corrected phase ϕ_j(x, y). The corrected phasor is defined as

$${\mathit{P}}_{\text{j}}\left(x,y\right)={\mathit{P}}_{FL,\text{j}}\left(x,y\right)e^{-i{\varphi }_{\text{exc},\text{j}}(x,y)}$$ (4)

This calculation is performed on each of the substacks corresponding to the N_angles orientations.

The average phasor is then calculated as

$$\text{P}\left(\text{x,y}\right)=\sum _j\text{ Pj}\left(\text{x,y}\right)/\text{Nangles}$$ (5)

The phasor P(x, y) can be used to generate a super-resolved image. This is done by decomposing the phasor into a component corresponding to the center of the PSF, P_IN, and a component corresponding to the periphery of the PSF, P_OUT. For each pixel, the fraction of the total intensity corresponding to the center of the PSF is given by

$${\text{f}}_{\text{in}}^{\left(\text{h}=1\right)}\left(\text{x,y}\right)=\left({\mathbf{P}}_{\text{out}}-\mathbf{P}\left(\text{x,y}\right)\right)·\left({\mathbf{P}}_{\text{out}}-{\mathbf{P}}_{\text{in}}\right)/{\left|{\mathbf{P}}_{\text{out}}-{\mathbf{P}}_{\text{in}}\right|}^2$$ (6)

The value of f_in is proportional to the distance between the phasor P and the phasor P_out along the line connecting P_in and P_out. To understand this formula, consider first the phasors associated to single fluorophores located at a different distance from the center of the PSF (Fig. S1). If the fluorophore is in the center, the phasor has phase ϕ = 0 and thus f_in ∼1. If the fluorophore is at a distance d = T/2, where T is the period of the illumination pattern, the phasor has phase ϕ = π, and thus, f_in ∼0. Note that if the fluorophore is at a distance d = +d₀ or d = −d₀ from the center, the formula yields the same value. This is guaranteed by the choice of P_IN (ϕ = 0) and P_OUT (ϕ = π), parallel to the horizontal axis. Note that with P_IN and P_OUT being linearly dependent, it is not possible in SPLIT-SIM to isolate a third background component as in the lifetime-based SPLIT-STED approach (10). In general, the PSF will contain multiple fluorophores, and the resulting phasor will be the linear combination of the phasors of the single fluorophores (Fig. S2).

Spatial information related to the second order of the illumination pattern is contained in the phasor P^{(h = 2)}(x, y) calculated at harmonic number h = 2 (Eq. 3). This phasor is used to extract a fraction f_in^{(h = 2)}(x, y) using

$${\text{f}}_{\text{in}}^{\left(\text{h}=2\right)}\left(\text{x,y}\right)=\left({\mathbf{P}}_{\text{out}}-{\mathbf{P}}^{\left(\text{h}=2\right)}\left(\text{x,y}\right)\right)\text{·}\left({\mathbf{P}}_{\text{out}}-{\mathbf{P}}_{\text{in}}\right)/{\left|{\mathbf{P}}_{\text{out}}-{\mathbf{P}}_{\text{in}}\right|}^2$$ (7)

The information from both harmonics is then combined using the following formula:

$${\text{f}}_{\text{in}}\left(\text{x,y}\right)={\text{f}}_{\text{in}}^{\left(\text{h}=1\right)}\left(\text{x,y}\right){\text{f}}_{\text{in}}^{\left(\text{h}=2\right)}\left(\text{x,y}\right)$$ (8)

To understand this formula, consider the schematic reported in Fig. S3. For the harmonic h = 2, the period of the pattern is T₂ = T/2. Thus, the phasor P_OUT corresponds now to a distance from the center T₂/2 = T/4. In other words, the second harmonic phasor provides spatial information on a finer scale. Using Eq. 6, we calculate the fraction of the signal corresponding to the center of the PSF. Using Eq. 8, we calculate the fraction of this fraction corresponding to a more central region.

The final super-resolved image is obtained as

$${\text{I}}_{\text{IN}}\left(\text{x,y}\right)={\text{f}}_{\text{IN}}\left(\text{x,y}\right){\text{I}}_{\text{WF}}\left(\text{x,y}\right),$$ (9)

where I_WF(x, y) is the sum of the intensity of all the images of the stack.

In summary, the additional spatial information encoded in the phasor P(x, y) is used to improve the spatial resolution of the SIM system. It is worth noting that the phase ϕ(x, y) is dependent on a proper estimation of the pattern parameters. Fig. 1 d shows a simulation of SIM data with a known sinusoidal illumination pattern. The pattern is fully characterized by a period T, three orientation angles α_k, and three values for the offset of the initial position p_k. The use of “wrong” pattern parameters can be revealed by the calculated phase image ϕ(x, y) (Fig. 1 d). We find that the “correct” pattern minimizes the average value of the phase of an image, ϕ_AV (Fig. 1 e). Thus, the minimization of the value ϕ_AV can be used to estimate the parameters of an unknown illumination pattern.

Phasor plot representation of SIM data

We tested our SPLIT-SIM algorithm on simulated 2D SIM data (Fig. 2). SIM image stacks were generated using a sinusoidal illumination pattern (Fig. 2, a and b) with N_angles = 3 orientations and N_steps = 5 translation steps. Images of sparse particles were generated under different conditions of illumination contrast and level of photon counts (Fig. 2, d–g). The first image (Fig. 2 d) is obtained with a maximal contrast of the illumination pattern (C_P = 1) and a very high level of photon counts (S = 500). The resulting phasor plot, i.e., the 2D histogram of the values g = Mcosϕ and s = Msinϕ of all the pixels of the image, is approximated by an arc that spans the first quadrant. Note that for the purpose of visualization, phasors are only shown with positive phase values (0 < ϕ_plot < π) by setting ϕ_plot = |ϕ|. The points with ϕ = 0 correspond to the center of the PSF, whereas the points with larger values of ϕ correspond to the periphery of the PSF. The modulation M is roughly constant across the PSF and equal to the value M_max = 0.5. This value depends on the contrast of the illumination pattern C_P. In fact, if the contrast is reduced to C_P = 0.33, the modulation is reduced to the value M_max = 0.16 (Fig. 2 f). Thus, the radius of the arc formed by the phasor, in the case of sparse structures, is a measure of the contrast of the illumination pattern. For images simulated with lower photon counts (S = 5), the arc formed by the phasor spreads because of the presence of a higher level of Poisson noise, which casts uncertainty on the values of M and ϕ (Fig. 2, e and g). The effect of noise is also visible in the corresponding phase and modulation images. For crowded samples, the value of modulation is generally lower than the value M_max and we cannot detect the characteristic arc-shaped phasor (Fig. 2 h).

The determination of M_max is important for setting the positions of P_in and P_out. We can set the position of the phasor corresponding to the center of the PSF as P_in = M_maxexp(iϕ_in), with ϕ_in = 0, and the position of the phasor corresponding to the periphery of the PSF as P_out = M_maxexp(iϕ_out), with ϕ_out = π (Fig. 2 c, top). Because all phasors have M ≤ M_max, this choice only yields values of the fraction f_IN between 0 and 1 (Fig. 2 c, top). Instead, if we set P′_out = M′exp(iϕ_out), with ϕ_out = π and M′ = M_maxcos(−ϕ_max), where ϕ_max is a tunable parameter, Eq. 6 can now yield also negative values of the fraction f_IN (Fig. 2 c, bottom). In this case, we force the values of the fraction to fall between 0 and 1 through a nonlinear filter (see Materials and methods). This second choice provides a better improvement of spatial resolution but can potentially introduce artifacts in the reconstructed SPLIT-SIM image. We evaluated the effects of using different values of ϕ_max on a simulated Siemens star pattern (Fig. S4). We see that the appearance of artifacts is evident for values ϕ_max < 0.5π. Thus, we set the value 0.5π as a lower limit for the parameter ϕ_max.

SPLIT-SIM provides SR without deconvolution

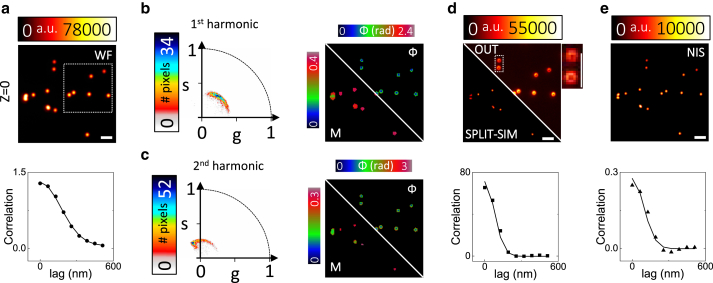
We then tested our SPLIT-SIM algorithm on 3D SIM images of fluorescent spheres acquired on a Nikon N-SIM microscope. Fig. 3 a shows a representative image of a sample of 100-nm fluorescent beads, at the plane z = 0 nm. The beads are sparse enough to show the characteristic phasor arc (Fig. 3, b and c). We show the two phasor plots corresponding to the first and second harmonic frequencies of the FT, respectively. The values of M_max in the two harmonics are M_max = 0.39 and M_max = 0.27, respectively, corresponding to a different contrast of the first and second order of the pattern. The phasor “arc” of the second harmonic spans a wider angle, in keeping with the fact that it contains spatial information at a higher frequency, also visible in the corresponding phase image (Fig. 3 c). We performed SPLIT by using information from both harmonics, by setting ϕ_max = 0.5π (Fig. 3 d). We estimated the resolution of the SPLIT-SIM image by ICS (30). The ACFs of the SPLIT and WF images yield a resolution given by FWHM_SPLIT = 130 nm and FWHM_WF = 282 nm, corresponding to a ∼2−fold improvement of spatial resolution of SPLIT with respect to WF.

Figure 3.

SPLIT-SIM on fluorescent spheres. (a) Widefield image of a sample of 100-nm yellow-green fluorescent spheres and corresponding autocorrelation function (ACF) calculated in the dashed box. (b) Phasor plot of the first harmonic and corresponding phase and modulation images. (c) Phasor plot of the second harmonic and corresponding phase and modulation images. (d) SPLIT-SIM image obtained with ϕ_max = 0.5π, image of the residual component corresponding to the periphery of the PSF (OUT), and ACF of the SPLIT-SIM image. For the OUT image, shown is also the zoom of a region containing two beads. (e) NIS Elements reconstruction and corresponding ACF. Scale bars, 1 μm. To see this figure in color, go online.

The SPLIT-SIM image is compared with a reconstruction processed with the manufacturer’s software (NIS image) (Fig. 3 e). For the NIS image, we obtain FWHM_NIS = 156 nm. It is worth noting that our result is obtained without any deconvolution step. However, we note that the twofold improvement is obtained only by setting ϕ_max = 0.5π. Indeed, if we set ϕ_max = π, we obtain for the SPLIT image FWHM_SPLIT = 210 nm, corresponding to only a modest ∼1.3-fold improvement of spatial resolution (data not shown).

We also note that the phasor decomposition provides optical sectioning. Fig. S5 shows an image of the same sample of fluorescent spheres at the plane z = 300 nm. In this case, the beads are out of focus, i.e., are at the periphery of the PSF along the z axis. The out-of-focus signal has lower modulation and phase shifted by about π. The algorithm removes the out-of-focus signal; namely, it assigns this signal to the “OUT” component. We observe efficient optical sectioning for both ϕ_max = 0.5π and ϕ_max = π (Fig. S5).

Application of SPLIT-SIM to biological imaging

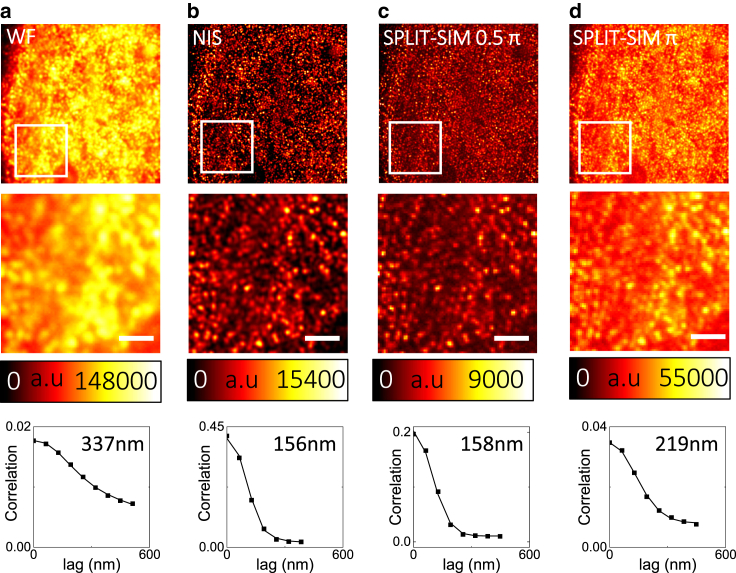
The SPLIT-SIM algorithm generates an improvement of resolution that depends on the value of the parameter ϕ_max. Decreasing values of ϕ_max yield a larger improvement of resolution in the focal plane. Setting ϕ_max = π provides optical sectioning but only a modest increase in spatial resolution. Setting ϕ_max = 0.5π provides optical sectioning and an ∼2-fold increase in spatial resolution. Fig. 4 shows the analysis of a 3D-SIM image of the histone H2B in HeLa cells. The SPLIT images obtained setting ϕ_max = 0.5π (Fig. 4 c) and ϕ_max = π (Fig. 4 d) are compared with the WF image (Fig. 4 a) and with a SIM reconstruction obtained with the NIS software (Fig. 4 b). We find by ICS that the apparent size of the structures formed by H2B is FWHM_WF = 337 nm in the WF image, FWHM_NIS = 156 nm in the NIS image, and FWHM_SPLIT,0.5π = 158 nm in the SPLIT image. If we set ϕ_max = π, we get confocal-like images, as this setting produces mainly an optical sectioning effect (Fig. 4 d). The apparent size of H2B, estimated by ICS, is in this case FWHM_SPLIT,π = 219 nm.

Figure 4.

SPLIT-SIM imaging of the chromatin histone H2B. Widefield image (a), NIS reconstruction (b), and SPLIT-SIM image reconstructed with ϕ_max = 0.5π (c) or ϕ_max = π (d) of a sample of histone H2B in fixed HeLa cells. Also shown are the ACFs calculated on the white box region along with the corresponding Gaussian fit. Scale bars, 1 μm. To see this figure in color, go online.

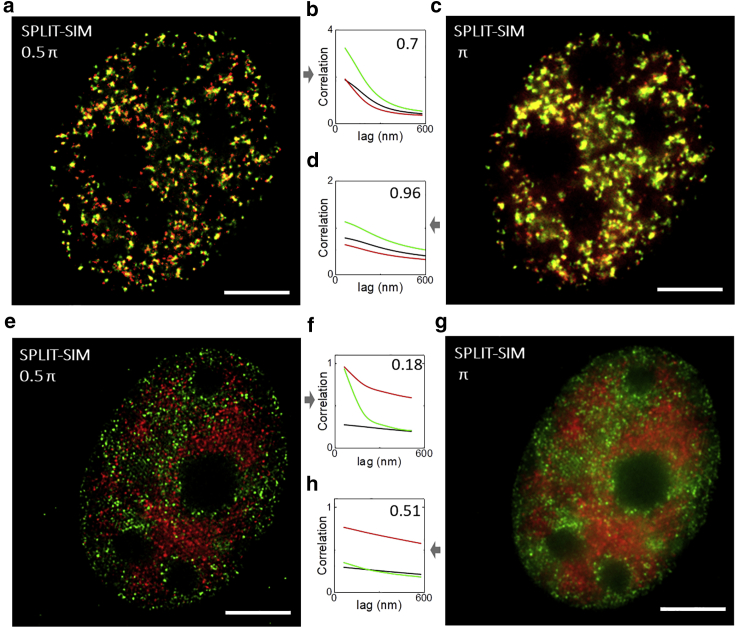
In Fig. 5, we applied SPLIT-SIM to quantify the colocalization between functional sites in the nucleus of MCF7 cells. In particular, we compared the nanoscale spatial distribution of two samples: 1) nascent DNA replication foci (labeled through incorporation of the nucleotide analog EdU) versus PCNA, a protein involved in the DNA replication process (32) that we expect closely associated in the nucleus; and 2) RNApol2 versus the transcriptionally repressive histone marker (H3K9me3), which we expect to be spatially segregated in the nucleus. The colocalization analysis was performed using a novel, to our knowledge, approach validated on dual-color STED images of nuclear foci (30) and recently extended to dual-color SIM images (33). This approach is largely based on the principles of ICCS (34). The amplitude of the cross-correlation function (CCF) of a dual-color super-resolved image is compared with the amplitudes of the ACFs of the single channels to extract the colocalized fraction. In addition, the width of the CCF is compared with the width of the ACFs to get an average correlation distance, in the case of colocalized samples (30,33). Fig. 5 a shows a dual-color SPLIT-SIM image (ϕ_max = 0.5π) of PCNA and EdU in MCF7 cells. The positive amplitude of the CCF demonstrates colocalization between PCNA and EdU (Fig. 5 b), with a colocalized fraction f = 0.70 (Fig. 5 c). The average correlation distance is d_ICCS = 99 nm. If the ICCS analysis is performed on the same SPLIT-SIM image processed with ϕ_max = π, the colocalized fraction raises up to f = 0.96 (Fig. 5 c) whereas the average correlation distance is d_ICCS = 92 nm. The different value of colocalized fraction in the two reconstructions is due to the different level of spatial resolution. At the resolution provided by ϕ_max = π (R = 210 nm), most of the PCNA and EdU sites appear overlapped (f = 0.96). In contrast, at the resolution provided by ϕ_max = 0.5π (R = 130 nm), some PCNA and EdU sites appear less overlapped, resulting in a lower value of colocalized fraction (f = 0.70). Fig. 5 e shows a dual-color SPLIT-SIM image (ϕ_max = 0.5π) of RNApol2 and H3K9me3. In this case, the lower amplitude of the CCF indicates the absence of colocalization between RNApol2 and H3K9me3 (f = 0.18), at a resolution of 130 nm, as expected (Fig. 5 f). The same ICCS analysis performed on the SPLIT-SIM images of the same cell, processed with ϕ_max = π, yields a larger value of the colocalized fraction (f = 0.5, Fig. 5 h).

Figure 5.

Quantitative analysis of the nanoscale distribution of nuclear sites. (a–d) ICCS analysis of PCNA (red) and EdU (green) in MCF7 cells imaged by SPLIT-SIM with ϕ_max = 0.5π (a and b) or ϕ_max = π (c and d). (e–h) ICCS analysis of RNApol2 (red) and histone H3K9me2 (green) in MCF7 cells imaged by SPLIT-SIM with ϕ_max = 0.5π (e and f) or ϕ_max = π (g and h). Shown are the image CCF (black) and ACF of the PCNA (red) and EdU (green) channels. Numbers indicate the measured value of colocalized fraction. Scale bars, 5 μm. To see this figure in color, go online.

Discussion

In this work, we have shown that the additional spatial information encoded within SIM data can be decoded by the SPLIT method. The SPLIT-SIM approach is different, in concept, from most SIM reconstruction algorithms. In these algorithms, each image of a SIM data set, obtained with a given position of the illumination pattern, is transformed into the Fourier space (the space of the image spatial frequencies) and combined with information from the other images (15). In contrast, SPLIT exploits the information encoded into an additional channel of the microscope to extract, at each pixel, a fraction of the intensity corresponding to the center of the PSF. In SPLIT-SIM, this additional channel is represented by the varying position of the illumination pattern, which induces variations of the intensity at each pixel. We have shown that fluorophores in the center and at the periphery of the PSF have different fingerprints on this channel. For this reason, it is possible to decompose the intensity at each pixel into two components and to generate a super-resolved image. Clearly, the use of the word “lifetime” in the SPLIT acronym is improper in the context of SIM. However, the entire method is fully inspired to the very same original SPLIT concept, with the main difference that the lifetime dimension is substituted by the dimension of the illumination pattern phase. SPLIT-SIM is based on phasor analysis and does not require deconvolution.

One potential application of the SPLIT-SIM method is the imaging of chromatin in the nucleus. Attractive features of SIM are the moderate levels of illumination power and the compatibility with multicolor imaging. For this reason, SIM is a widely used technique to investigate the spatial organization of chromatin at a spatial scale of ∼100 nm (35, 36, 37). In this respect, we have shown that SPLIT-SIM is a simple tool to generate super-resolved images of chromatin and other functional sites in the nucleus. We have also demonstrated that SPLIT-SIM, in combination with ICS and ICCS, can be used to extract quantitative parameters such as the resolution of the images, the colocalization fraction, and the distance between functional nuclear sites. It will be of interest to extend this robust SIM-ICCS analysis to data acquired with faster SIM setups (38,39) and study the organization of chromatin, dynamically, in living cells. Information on the organization of chromatin functional motifs at a scale of ∼100 nm, extracted by SIM-ICCS, would be complementary to other live-cell methods, such as Förster resonance energy transfer, that provide spatial information on a scale below ∼10 nm (40,41).

Thus far, the SPLIT method has been applied only in the context of STED microscopy (10, 11, 12, 13, 14). This work is the first demonstration, to our knowledge, that SPLIT can be applied to other types of SR imaging techniques. We envision that the SPLIT algorithm can find applications in other SR approaches, such as image-scanning microscopy (42,43) or the recent combination of SIM with single-molecule localization (e.g., SIMFLUX (44) and SIMPLE (45)).

Editor: Jochen Mueller.