Local actin dynamics couple speed and persistence in a cellular Potts model of cell migration

Abstract

Cell migration is astoundingly diverse. Molecular signatures, cell-cell interactions, and environmental structures each play their part in shaping cell motion, yielding numerous morphologies and migration modes. Nevertheless, in recent years, a simple unifying law was found to describe cell migration across many different cell types and contexts: faster cells turn less frequently. This universal coupling between speed and persistence (UCSP) was explained by retrograde actin flow from front to back, but it remains unclear how this mechanism generalizes to cells with complex shapes and cells migrating in structured environments, which may not have a well-defined front-to-back orientation. Here, we present an in-depth characterization of an existing cellular Potts model, in which cells polarize dynamically from a combination of local actin dynamics (stimulating protrusions) and global membrane tension along the perimeter (inhibiting protrusions). We first show that the UCSP emerges spontaneously in this model through a cross talk of intracellular mechanisms, cell shape, and environmental constraints, resembling the dynamic nature of cell migration in vivo. Importantly, we find that local protrusion dynamics suffice to reproduce the UCSP—even in cases in which no clear global, front-to-back polarity exists. We then harness the spatial nature of the cellular Potts model to show how cell shape dynamics limit both the speed and persistence a cell can reach and how a rigid environment such as the skin can restrict cell motility even further. Our results broaden the range of potential mechanisms underlying the speed-persistence coupling that has emerged as a fundamental property of migrating cells.

Significance

The universal coupling between speed and persistence (UCSP) is the first general, quantitative law describing motility patterns across the versatile spectrum of migrating cells. Here, we find that the UCSP emerges spontaneously in an existing, highly popular model of cell migration, generalizing its mechanism to cells with a more fluid definition of “polarity.” Importantly, this model now allows us to examine this migration law in many more complex geometries and environments. Studying the UCSP in different model frameworks and environments can help uncover how intracellular dynamics, cell shape, and environment interact to produce the diverse motility patterns found in migrating cells.

Introduction

Imagine a T cell moving in the outer layer of the skin. Tasked with patrolling the epidermis, it scans for early signs of reinvasion by pathogens known from earlier attacks. Its movement is rapid yet undirected; with narrow protrusions almost resembling dendrites, it probes its surroundings before choosing where to go next. Its decision made, it squeezes its way through the tight junctions between the skin’s keratinocytes, moving its attention to unexplored areas (1). Suddenly, the scene changes as a cut disrupts the tissue layer. The released damage signals attract neutrophils, which rapidly crawl toward the wound with a motion far more directed than that of the T cell patrolling this site earlier. Upon arrival, they stimulate the movement of yet another cell population; the epithelial sheet adopts a directed, slow-but-steady collective motion that (combined with proliferation) eventually closes the wound. Homeostasis is restored (2,3).

The earlier described scenario illustrates just a few of the many movement patterns and phenotypes found among migrating cells. Although all mammalian cells share the same basic mechanism of actomyosin-driven cell motion, differences in their molecular signatures—as well as in the structure of the environment they move in—nevertheless produce a rich spectrum of different migration modes (4). Movement can be fast or slow, in a persistent or frequently changing direction, across a two-dimensional (2D) surface or inside a three-dimensional (3D) matrix. Cells can be round or elongated, forming narrow or broad protrusions that do or do not rely on focal adhesions. Cells can move as isolated individuals or collectively as a cohesive sheet or stream.

Interestingly, despite these highly diverse migratory behaviors observed in different cell types and contexts, one universal law seems to describe motion patterns across many migrating cells in various controlled experimental settings: faster cells move more persistently (5, 6, 7). Maiuri et al. (7) proposed that this universal coupling between speed and persistence (UCSP) arises from a positive feedback on cell polarity mediated by the actin cytoskeleton. Because specialized clutch molecules provide friction between the actin filaments and the cell’s surroundings, these actin filaments move backward in the reference frame of the moving cell. This “actin retrograde flow” depends linearly on cell speed. A theoretical model revealed how actin retrograde flow can also stabilize cell polarity (and thus persistence) if it transports polarity cues toward the cell’s rear end. The resulting polarity cue gradient in turn stabilizes actin retrograde flow in a positive feedback loop; higher speeds yield higher persistence by stabilizing cell polarity through the actin retrograde flow. As actin retrograde flow is a highly conserved feature of cell migration, the UCSP holds for cells with very different migration modes.

Maiuri et al. (7) proposed this theoretical model to explain how the UCSP arises from the actin-based advection mechanism described earlier. Their one-dimensional (1D) model represented the cell as a nondeformable line that always has a well-defined “front” and “back.” By contrast, a real cell’s motion is linked closely to its shape (8), which dynamically responds to both the cell’s inner machinery and the environment, yielding a more promiscuous definition of the “front” and “back” of the polarized cell. It currently remains unclear how the UCSP mechanism generalizes to this case of deformable cells with complex shapes and environments; when multiple, competing protrusions can form along the cell perimeter (9,10), the direction of “polarity” becomes much less clear-cut. Indeed, exactly how migrating cells dynamically coordinate local protrusions and actin dynamics into a global polarized state under different conditions remains an open question in the field (11).

Here, we therefore examine a model in which speed and persistence emerge from a migration machinery that interacts with the cell’s shape and environment. We focus on the cellular Potts model (CPM), a popular framework for modeling cell migration that naturally captures complex cell shapes and cell-environment interactions (1,12,13). Rather than developing a new model, we explore an existing model inspired by actin dynamics that is known to reproduce cell migration with realistic cell shapes: the “Act-CPM” (12). Importantly, cell polarity in the Act-CPM emerges from local protrusion dynamics alone, without ever defining a global, cell-scale polarity direction. This allowed us to ask the following question: can the UCSP arise in a cell where no global front-to-back polarity direction is explicitly defined? Moreover, the polarity and motion of real cells also dynamically responds to surrounding obstacles. As the original experimental data mostly established the UCSP in simple, obstacle-free geometries (straight 1D adhesive lines or a free 2D surface) (5, 6, 7), the question remains whether this seemingly fundamental law is equally universal across the more diverse environments cells face in vivo. The spatial nature of the CPM allowed us to examine how the UCSP translates to more complex tissue environments.

Interestingly, we find that the UCSP emerges spontaneously in the Act-CPM in various environments through a mechanism relying only on the local polarity defined at the cell’s protrusions, without requiring one single, front-to-back polarity direction at the global cell scale. This also has consequences for the UCSP; in the Act-CPM, cell shape dynamics and the UCSP interact to define the patterns in which cells can migrate. Consequently, the UCSP may not be universal throughout all environments; our simulations predict that a strongly restrictive tissue may overrule speed-persistence coupling in T cells patrolling the epidermis.

Materials and methods

Model

CPM

Our model is an extension of the CPM (14,15), which represents a space as a discrete collection of pixels on a 2D or 3D grid. Each pixel p is assigned a cell identity σ_p = {0, 1, 2, …, n}, indicating which cell it currently belongs to (by convention, we use σ = 0 for the empty background and a unique integer σ > 0 for each of the n cells on the grid). Each pixel p locally “contacts” its Moore neighborhood, N(p), including diagonal neighbors (yielding eight neighbors in 2D and 26 in 3D).

Temporal dynamics arise because cells stochastically try to add or remove pixels at their borders in copy attempts (Fig. 1 A), where a source pixel p_s tries to “conquer” a target pixel p_t of another cell; if it succeeds, its identity is copied into p_t $\left({\sigma }_{p_t}\to {\sigma }_{p_s}\right)$. Any such changes are local because we only consider attempts in which p_s and p_t are neighbors: p_t ∈ N(p_s). Time is then measured in Monte Carlo steps (MCS), for which every MCS, we perform as many copy attempts as there are pixels on the grid.

Figure 1.

In silico simulation of shape-driven cell migration within complex environments. (A) A CPM represents a tissue as a collection of pixels on a grid, each belonging to a specific cell or the extracellular space. Pixels randomly try to copy their cell identity into pixels of neighbor cells, with a success probability P_copy depending on how that change would affect the “physical” properties of the involved cells (cell-cell adhesion and deviation from target volume and/or perimeter, dashed lines). The weighted sum of these energetic effects (ΔH) is negative for energetically favorable copy attempts. (B) Example track for a cell with only adhesion, volume, and perimeter constraints, resulting in Brownian, diffusion-like motion. Inset: distribution of instantaneous speeds, which remain very small throughout the track. (C) In the Act-CPM (12), each pixel’s “activity” represents the time elapsed since its most recent successful protrusion. Copy attempts into less active pixels are stimulated (negative ΔH_act), and copy attempts into more active pixels are punished (positive ΔH_act). (D) Act cells alternate between persistent motion and “stops” in which they change direction (intermittent random walk, “I-RW”). Plot shows example tracks of five Act cells with overlaying starting point (black dot, t = 0). Inset: distribution of instantaneous speeds during the I-RW, “stop-and-go” motion, with peaks at zero (the “stops” in the track) and at high speeds (“go” intervals). (E) Displacement plot of CPM cells. Brownian motion (without the Act extension, gray line) results in a linear curve. Act cell movement appears as Brownian motion on large time scales (linear part of red line) but is persistent on smaller time scales (nonlinear start of red line). To see this figure in color, go online.

These dynamics are regulated by the Hamiltonian H, the global energy of the system. Rather than letting each copy attempt succeed, the success rate P_copy of an attempt depends on the energetic “cost” ΔH of changing ${\sigma }_{p_t}\to {\sigma }_{p_s}$:

$$P_{\text{copy}}\left(p_s\to p_t\right)=\{\begin{array}{ll}{e}^{-\text{Δ}H/T}\hfill & \text{Δ}H>0\hfill \\ 1\hfill & \text{Δ}H\le 0\hfill \end{array}.$$ (1)

Thus, copy attempts tend to lower H because attempts with ΔH < 0 always succeed. The success rate of energetically unfavorable attempts instead decays exponentially with their cost depending on the temperature T (higher temperatures are more permissive for unfavorable attempts; see also the online “Simulation 1” at https://ingewortel.github.io/artistoo-supplements/ (16,17) to explore these dynamics interactively).

H itself is a function defined by the modeler. It may vary between CPM models, but typically contains terms to let cells maintain their shape and contacts with neighbor cells (Fig. 1 A). Here, we use three such terms to control cell-cell adhesion (14), cell volume (14), and the cell’s perimeter (18). The adhesion term in H assigns an energetic penalty to each pair of neighboring pixels belonging to different cells σ:

$$H_{\text{adhesion}}=\sum _{\text{pixels }\mathit{p}}\sum _{q\in N\left(p\right)}\{\begin{array}{cc}0& {\sigma }_q={\sigma }_p\\ J\left({\sigma }_p,{\sigma }_q\right)& {\sigma }_q\ne {\sigma }_p\end{array}.$$ (2)

The contact energy J is a model parameter that depends on the types of cells contacting each other; for example, contacts between two cells (nonbackground, σ > 0) can have a different energy than contacts between a cell and the background (σ = 0); see Table S1. At J > 0, this term stimulates pixels of the same cell to group together to minimize the number of contacts (within-cell contacts with σ_p = σ_q are “free” in Eq. 2, so there is no self-adhesion energy).

The volume and perimeter terms further control cell shape by assigning each cell a penalty for stretching or compressing beyond some specified target size V_target or perimeter P_target:

$$H_{\text{volume}}=\sum _{\text{cells}\sigma >0}{\lambda }_{\text{V}}\left(\sigma \right){\left[V\left(\sigma \right)-V_{\text{target}}\left(\sigma \right)\right]}^2$$ (3)

and

$$H_{\text{perimeter}}=\sum _{\text{cells}\sigma >0}{\lambda }_{\text{P}}\left(\sigma \right){\left[P\left(\sigma \right)-P_{\text{target}}\left(\sigma \right)\right]}^2.$$ (4)

Here, the parameters λ_V/λ_P scale the weight of each energy term. The volume V(σ) of cell σ is simply the number of pixels for which σ_p = σ. Its perimeter P(σ) sums, for each pixel p in the cell, the number of neighbors q belonging to other cells (analogous to Eq. 2):

$$P\left(\sigma \right)=\sum _{\text{pixels}p}\sum _{q\in N\left(p\right)}\{\begin{array}{cc}1& {\sigma }_p=\sigma ,{\sigma }_q\ne \sigma \\ 0& \text{otherwise}\end{array}.$$ (5)

The total cost ΔH of a copy attempt then depends on how each of these energy terms would change by setting ${\sigma }_{p_t}\to {\sigma }_{p_s}$:

$$\text{Δ}H=\text{Δ}{H}_{\text{adhesion}}+\text{Δ}{H}_{\text{volume}}+\text{Δ}{H}_{\text{perimeter}}+\dots ,\text{where}\text{Δ}{H}_X=H_{X,\text{after}}-H_{X,\text{before}}.$$ (6)

This general framework has two key properties: 1) because pixels can only have one identity σ at a time, “volume exclusion” naturally arises in the model; and 2) because all cells contribute to ΔH, P_copy depends on the shape of both the cell trying to move and the cell it tries to displace. These properties allow the CPM to reproduce realistic, dynamic cell shapes using only a few simple rules and parameters, making it a powerful tool for modeling cell interactions in complex environments. However, the energy described so far is based solely on adhesion and cell shape. Fluctuations at the cell border can cause the cell’s center of mass to move slowly over time, but because there is no energetic benefit for consistent motion in any direction, this is a Brownian, diffusion-like motion rather than actual migration (Fig. 1 B; speeds are positive but very low).

Act-CPM extension

We therefore use an extension of the CPM that does allow for active migration (12) (see also the online interactive explanation at https://ingewortel.github.io/artistoo-supplements/, “Simulation 2” (16,17). In this “Act-CPM,” a pixel p newly added to a cell at t = t^∗ remembers its recent protrusive “activity” A for a time of max_act MCS (with max_act a model parameter):

$$A\left(p,t\right)=\{\begin{array}{ll}1& t=t^{\text{∗}}\\ A\left(p,t-1\right)-\frac{1}{{\max }_{\text{act}}}& t-t^{\text{∗}}\le {\text{max}}_{\text{act}}\\ 0& \text{otherwise}\end{array}.$$ (7)

Copy attempts from active into less active pixels are rewarded via a negative energy contribution ΔH_act to the overall energy cost ΔH, stimulating copy attempts from source pixel p_s in an “active” region into a less active target pixel p_t:

$$\text{Δ}{H}_{\text{act}}\left(p_s\to p_t\right)=-{\lambda }_{\text{act}}\left({\text{GM}}_{\text{act}}\left(p_s\right)-{\text{GM}}_{\text{act}}\left(p_t\right)\right),$$ (8)

where GM_act(p) of pixel p is the geometric mean of the activities A of all pixels q in N(p) that belong to the same cell (σ_q = σ_p). Thus, max_act controls the steepness and temporal stability of the activity gradient, whereas the Lagrange multiplier λ_act determines its weight in the total cost ΔH of the copy attempt. ΔH_act is negative whenever GM_act(p_s) > GM_act(p_t). Note that rather than defining an energy H_act for the entire grid, we now consider the derivative ΔH for a specific copy attempt directly; thus, it can be interpreted as a force rather than an energy (15).

This term adds to the CPM a positive feedback loop in which recently added pixels are more likely to protrude again (Fig. 1 C). Consequently, local groups of active pixels form stable protrusions that drag the cell in a certain direction; at any given time, cells can have one protrusion, several protrusions, or no protrusion. As a result, cells typically alternate between intervals of persistent movement (often coinciding with a single active protrusion) and “stops” (coinciding with the disappearance of the active protrusion or appearance of competing protrusions) where they can switch direction (Fig. 1 D). This motion pattern is known as an “intermittent random walk” (I-RW) (7). On larger timescales, movement resembles Brownian motion (new protrusions form in random directions). Persistence is only evident on the smaller timescales on which the cell has a stable protrusion and maintains its direction (Fig. 1 E). This I-RW behavior qualitatively resembles the characteristic “stop-and-go” motility of T cells searching for antigen in the lymph node (19,20), as well as the motility of other cell types (7).

Parameter choices

The parameters used throughout the study were chosen to be in the “motile-but-stable” regime of the model. Far outside this regime, the model does not describe robust motile cells or allows cells to rupture.

Selecting parameters for a CPM can be difficult because parameters are interdependent. For example, the J and various λ parameters balance the terms in ΔH; when too low, the corresponding term effectively vanishes from ΔH (causing artifacts because cells are no longer affected by the adhesion/volume/perimeter constraints). If the λ parameter of a term is too high, that term can instead overshadow the other terms in ΔH. Thus, the λ and J parameters must be balanced such that each term contributes to the final behavior. Choosing a temperature T > 0 is then equivalent to scaling all J and λ parameters by a factor 1/T.

Here, parameters were selected to yield cells with realistic shapes and behavior as follows. The (2D) volume V_target of 500 pixels (Table S1) was chosen to resolve the cell shape and protrusions in some detail; changing it simply scales lengths in the model. Then, P_target must be large enough relative to V_target so that cell borders can fluctuate while membrane tension still keeps the cell intact: some deformation is required for cell migration, but too large a perimeter can cause cells to rupture. P_target also depends on the environment, as microchannel simulations required a larger perimeter to account for the elongated cell shape in microchannels. Contact energies J, λ parameters λ_V/λ_P, and the temperature T were then balanced empirically such that cells were deformable but stayed intact (as formally defined by a “connectedness” ≥95% for ≥95% of the time; see Supporting materials and methods). For the microchannels, J_{cell, channel} is not too important as long as it is within the same range as J_{cell, background}; very low J_{cell, channel} → 0 makes cells stick to the channel walls, whereas very high J_{cell, channel} makes them stretch out to avoid any contact with the channel walls. For skin simulations, the J_{keratinocyte, keratinocyte} and λ_{P, keratinocyte} parameters were chosen (again empirically) depending on the tissue type, with a higher λ_{P, keratinocyte} for a stiffer (less deformable) tissue, as well as a higher J_{keratinocyte, keratinocyte} so that cells can still squeeze through the keratinocytes. Most parameters were equal in 1D and 2D (except for P_target, as mentioned earlier); for 3D simulations, we had to select other parameters to account for changes in surface/volume ratio and the thus-altered relative contributions of the different terms to the total ΔH (especially important are the lower λ_P and J to account for the much larger perimeters).

Max_act “actin lifetime” values were chosen to obtain a realistic range of protrusion sizes (Table S2). Although max_act can in principle be infinitely large, this would yield a cell where each of the cell’s border pixels has the same (infinitely large) activity; no protrusion can form because there is no symmetry breaking to polarize the cell. Because we are interested in the motile parameter regime in which cells can break symmetry, we instead selected a range of max_act values for which protrusion sizes varied from small, local blebs to large protrusions occupying a substantial fraction, but not all, of the cell volume (see Analysis later; again, this means that max_act is chosen relative to the target volume V_target). For each max_act, a range of λ_act scaling factors was then chosen to let cells go from completely Brownian motion (persistence time ~5 MCS, the time between subsequent measurements of cell location) to maximally persistent motion (persistence time ~10,000 MCS). Persistence times higher than 10,000 MCS were not considered, as such high persistences will likely be underestimated because of the finite total simulation time (50,000 MCS). For skin simulations, T cells were modeled with max_act = 30 or 100 and variable λ_act in two different types of tissues (Table S3).

Analysis

All simulations were built using Artistoo (RRID:SCR_020983 (16)). For details on initial setup, see Supporting materials and methods; all simulation and analysis code is available at https://github.com/ingewortel/2020-ucsp (21). Every five MCS, we recorded both the position of the cell’s centroid (to compute speed and persistence time) and several other cell properties (to keep track of the cell’s shape and degree of polarization).

Quality control: shape and polarization

In the CPM, the pixels belonging to a single cell are held together mostly via the adhesion term in the Hamiltonian (Eq. 2). However, the adhesive force can become negligible relative to the other ΔH terms; for example, when ΔH_act is large because of a high λ_act. Thus, especially in 3D, cells may break apart at high values of λ_act, despite the unfavorable changes in adhesion energy associated with this break.

As frequent cell breaking causes artifacts in the tracking data that may bias the measurement of speed and persistence, it is important to use parameter ranges that prevent such an unbalanced contribution of the different ΔH terms. To estimate the frequency of cell breaking, we therefore recorded the connectedness (C) of the cell every five MCS of each simulation. This number is 1 for an intact cell and approaches 0 for a collection of unconnected pixels (see Supporting materials and methods for details). For all simulations reported in this manuscript, we checked that a connectedness below 0.95 did not occur in more than 5% of the measured values, ensuring that cells were intact for the majority of the simulation.

Additionally, to measure the total active protrusion area(s) of a cell, we counted which percentage of each cell’s pixels had an activity A > 0. Ranges of max_act and λ_act were chosen such that protrusions made up >0% but <100% of the cell’s volume.

Track analysis: speed and persistence time

Cell centroids were recorded at regular time intervals (five MCS) to reconstruct cell trajectories or “tracks.” All simulated tracks were analyzed in R (RRID:SCR_001905, version 3.6.1) using the celltrackR package (version 0.3.1) (22) to compute speed and persistence time. Speeds were computed from instantaneous “step” speeds along the track, and persistence time was defined as the half-life of the autocovariance curve. Analyses were performed in a step-based manner (combining steps from independent tracks for robustness), using separate groups of five tracks each to estimate variation. See Supporting materials and methods for details.

Results

Local polarity gradients in the Act-CPM reproduce the UCSP observed in migrating cells

We first tested whether the Act-CPM could reproduce the UCSP as observed in experimental data. Like in the UCSP model (7), migration in the Act-CPM arises from a positive feedback on cell polarity; persistent motion results in activity gradients, which in turn stabilize the direction of motion. But even though this feedback conceptually resembles the polarity stabilization driving the UCSP, the Act-CPM differs from the Maiuri model in a crucial way: activity gradients are local and arise dynamically from a combination of protrusion and cell shape dynamics. Cells are not 1D lines with a clearly defined “front” and “back,” but deformable objects that lack any single, cell-scale polarity direction (see, for example, Fig. S1 A and Interactive simulation S1 at https://ingewortel.github.io/2020-ucsp/; all black pixels are equivalent in terms of polarity). This means that polarity is fluid and can turn slightly within an existing protrusion as the cell deforms. Polarity is also less absolute in the sense that protrusions can split and merge dynamically and competing protrusions can form elsewhere along the perimeter (although the global negative feedback from membrane tension prevents this from happening too often). So, although the protrusive feedback should intuitively lead to some speed-persistence coupling in the Act-CPM, it is by no means certain that this relationship should be of the same (exponential) form as that reported by Maiuri et al. (7) or that it should hold when the cell is free to deform.

This more emergent nature of polarity also means that the effects of the main migration parameters λ_act and max_act on speed and persistence are impossible to derive from simple scaling arguments alone. Still, some qualitative relations can be established. By scaling the strength of the protrusive force ΔH_act relative to other, opposing terms (adhesion, volume, perimeter), higher λ_act values yield larger and more stable protrusions, as restoring forces like membrane tension are easier to overcome (Fig. S1, A and B); this should intuitively increase both speed and persistence. The second parameter, max_act, determines how long pixels remember their activity and can loosely be interpreted as a “lifetime” of polymerized actin. It limits the protrusion width (i.e., how much it can extend into the cell interior). Higher max_act values stabilize protrusions even at small λ_act (Fig. S1 B). However, the quantitative effect of these parameters on speed and persistence are far less trivial because they strongly depend on the dynamics of the cell boundary. The shapes of CPM cells interact with their cell-intrinsic motility and environment through an intricate interplay of local energies ΔH—in fact, it is this emergent nature of cell-cell interactions that makes the CPM such a popular framework (15). Thus, a more empirical approach is needed to assess whether the UCSP holds in our CPM model of local actin dynamics.

We therefore used the Act-CPM to simulate the experiments in which the UCSP was originally discovered. Maiuri et al. (5,7) mostly considered cells moving along adhesive tracks or within microchannels. To mimic this quasi-1D setup in silico, we constrained Act cells between two parallel walls, leaving a space of 10 pixels within the channel (Fig. 2 A). The resulting cell elongation was comparable to that observed for cells moving on 1D adhesive tracks (compare Fig. 2 A to Fig. 1 B in (7)). Act cells moving in these microchannels reproduce I-RW behavior, migrating persistently in one direction until they lose their active protrusion, at which point they wait for a new protrusion to form and can stochastically switch direction (Fig. S1 A; Video S1; Interactive simulation S1 at https://ingewortel.github.io/2020-ucsp/).

Figure 2.

The Act-CPM reproduces the UCSP observed in experimental data. (A) Simulation setup for “1D” migration in microchannels. Color gradients indicate active protrusions. Microchannels consist of two parallel walls with 10 pixels between them. (B) “Exponential” speed-persistence coupling arises in the Act-CPM (i.e., there is a range in which speed is proportional to the log persistence time; ρ = Spearman correlation coefficient). Red line and shaded area represent a loess fit ± 95% confidence interval. Both max_act and λ_act were varied; see Tables S1 and S2 for parameters used and (C) for the relationship at fixed max_act. (C) Speed-persistence coupling is stronger for cells with the same max_act. Plot shows mean ± standard deviation (SD) of persistence time plotted against speed, for two values of max_act; numbers in the plot indicate the corresponding value of λ_act. Shaded gray areas in the background indicate regions where the persistence time is lower than the time it takes for the cell to move 10% of its length. (D) Phase diagram of migration modes in microchannels for different max_act and λ_act (left), as based on the displacement distributions (right). Cells were classified as NM if they hardly moved (displacement distribution with a single peak centered at 0). Cells were classified as P-RW if the displacement distribution had two clear peaks (for motion to the left and right, respectively) and as I-RW if it had three peaks (with an extra peak at zero for the “stops”); see Supporting materials and methods for details. This classification yielded fairly consistent “phases” in the parameter space, although it was harder to distinguish peaks for cells that were barely moving (e.g., point 3). Some λ_act and max_act combinations in the CPM are not viable because the protrusion tear the cell apart; these were classified as “broken.” In the diagram, colors represent migration mode, and the intensity of the color represents agreement of the classification between different independent estimates (see Supporting materials and methods). To see this figure in color, go online.

Video S1. Act cells in microchannels have variable motility depending on their protrusion size

The movie first shows an Act cell with a small protrusion – giving rise to typical "stop-and-go" motility, followed by an Act cell with a more stable protrusion – yielding more continuous movement.

To examine whether the less strict polarization of deformable Act cells still gave rise to the UCSP, we assessed speed and persistence time in cell tracks for Act cells with various λ_act and max_act values. (Here, the “persistence time” is the average time over which the direction of motion changes, computed from the speed autocorrelation function as described in the Supporting materials and methods.) This analysis revealed a weak exponential coupling between speed and persistence (Fig. 2 B). Although weak in the heterogeneous data set of Act cells with highly different λ_act and max_act parameters, this correlation became markedly stronger when we stratified cells by max_act value (Fig. 2 C). There, we found the same exponential speed-persistence coupling as was observed in experimental data (7). Although the values of both speed and persistence are somewhat sensitive to other control parameters in the CPM (such as λ_V, λ_P, and J), we note that the shape of their correlation is not; for example, varying λ_P did not change the shape of the speed-persistence curve as long as values were chosen in a regime that allowed for cell migration without letting the cell fall apart (Fig. S1, C and D). Likewise, this finding was independent of the choice of max_act; curves were similar for both values of max_act (Fig. 2 C).

Even though changes in max_act did not affect speed-persistence coupling, they were associated with a change in migration mode. Whereas cells with lower max_act values switched from a nonmigratory (NM) phenotype to I-RW “stop-and-go” motion as λ_act increased, cells with higher max_act values instead went from nonmigratory to a “persistent random walk” (P-RW) mode with hardly any stops. To illustrate this difference, we computed a “phase diagram” of migration behavior with varying max_act and λ_act, using the distribution of displacements to determine migration modes (Fig. 2 D). This phase diagram strongly resembled that obtained by Maiuri et al. using the original UCSP model (7) (see Appendix A in the Supporting materials and methods for a more extensive comparison between the two models).

In summary, the Act-CPM exhibits an exponential speed-persistence relationship mediated by the λ_act parameter; whereas speed increases linearly with λ_act (Fig. S2 A), persistence time increases exponentially at higher λ_act values (Fig. S2 B). Indeed, the linear relationship between the Lagrange multiplier λ and cell speed has previously been explained for a similar CPM migration model based on a chemotactic, rather than cell-intrinsic, force (15). We find that the exponential relationship between λ_act and persistence follows directly from CPM kinetics and the size of the “energy barrier” cells need to cross to lose an active protrusion (Appendix B in the Supporting materials and methods). Thus, λ_act exponentially couples speed and persistence in the Act-CPM, demonstrating that local, actin-based protrusion dynamics suffice to explain both the UCSP and migration modes observed in migrating cells, even when there is no explicit global polarity direction.

Speed-persistence coupling in the Act-CPM spans a range of migration modes

We then exploited the spatial nature of the Act-CPM to examine the UCSP in environments other than a microchannel, giving cells even more freedom to deform into complex shapes (Fig. 3). Do local activity gradients still suffice to reproduce the UCSP when cells can form protrusions in any direction along their perimeter?

Figure 3.

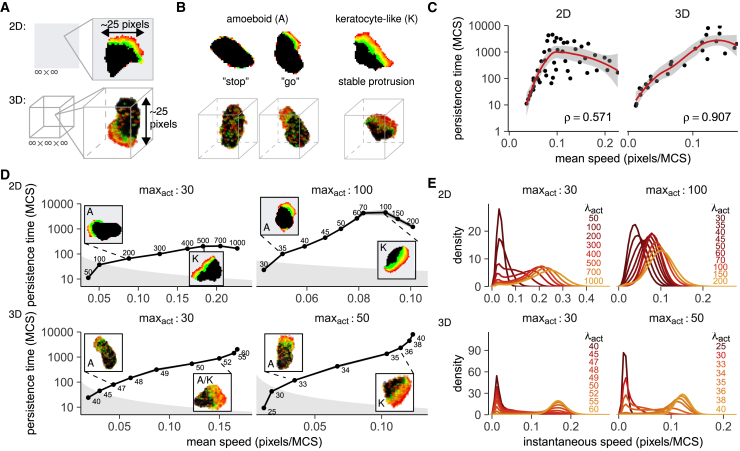
Speed-persistence coupling in 2D and 3D spans a range of migration modes. (A) 2D and 3D simulations were performed in an empty grid. (B) Migration modes in the Act-CPM; see also (12). Amoeboid cells form small, narrow protrusions that decay quickly, yielding stop-and-go motion. Keratocyte-like cells have broader, more stable protrusions. (C) Exponential speed-persistence coupling for various (λ_act, max_act). ρ = Spearman’s correlation. See Tables S1 and S2 for exact parameters. Red line and shaded area represent a loess fit ± 95% confidence interval. (D) The UCSP is stronger among cells with the same max_act and spans a transition from amoeboid to keratocyte-like motion. Plots show mean ± SD persistence time versus speed with representative cell shapes as insets (note the competing protrusion in one of the amoeboid cells); in the gray area, persistence times are below the time needed to move 0.1 cell length. See also Fig. S3A. (E) Instantaneous speed distributions of 2D and 3D Act cells. Cells transit from not moving (single peak at ~0 pixels/MCS), via “stop-and-go” motility (bimodal distributions), to near-continuous motion (single peak at high speed). See also Fig. S3B. To see this figure in color, go online.

In addition to discovering the UCSP in cells navigating “1D” adhesive tracks, Maiuri et al. (7) also confirmed this coupling in cells migrating on surfaces (“2D”) and within 3D environments. We mimicked these experiments by simulating Act cell migration in large, unconfined 2D and 3D spaces (Fig. 3 A). Like in the microchannel data (Fig. 2, B and C), we again found a weak exponential correlation between speed and persistence (Fig. 3 C) that became stronger when we stratified cells by max_act value (Figs. 3 D and S3 A). In fact, the exponential increase in persistence was now accompanied by a transition in cell shapes (insets in Fig. 3 D).

In contrast to the uniform, elongated shape observed in channels, Act cells moving in 2D and 3D can form different types of protrusions (Fig. 3, A, B, and D; Video S2; Interactive simulations S2 and S3 at https://ingewortel.github.io/2020-ucsp/; (12)). Low values of λ_act and max_act promote the formation of small and narrow protrusions that form and decay dynamically, giving rise to an amoeboid (“stop and go,” I-RW) migration mode (Fig. 3, B, left, and D; Video S2). By contrast, large values of λ_act and/or max_act favor the formation of broad, stable protrusions, yielding a more persistent “keratocyte-like” (P-RW) migration mode (Fig. 3, B, right, and D; Video S2). This transition occurred in both the 2D and the 3D model, although we note that the “amoeboid” behavior in 3D was slightly different in 3D than in 2D. In 3D, the “stops” tended to be longer, and many protrusions were too unstable to make the cell move far from its place. The “go” intervals were less frequent and required the cell to take on a somewhat broadened shape, although not as broad as in the “keratocyte-like” motion (Video S2; Interactive simulations S2 and S3 at https://ingewortel.github.io/2020-ucsp/).

Video S2. Act cells in 2D and 3D have both different shapes and migration patterns

The movie shows examples of typical migration patterns in 2D and 3D. At low max_act values, small, unstable protrusions form and decay dynamically – giving rise to amoeboid "stop-and-go" migration. At higher max_act values, the cell becomes broader and forms a large, stable protrusion perpendicular to its direction of movement – yielding a movement pattern similar to that observed in fish keratocytes ("keratocyte-like").

This shift in migration mode is most clearly visible in the instantaneous speed distributions from our simulated cell tracks (Figs. 3 E and S3 B). The bimodal shape of this distribution—especially at low values of max_act—reflects the “stop-and-go” I-RW behavior of migrating Act cells; cells in “stops” move at very low instantaneous speeds of ~0 pixels/MCS, whereas the “go” intervals yield peaks at higher speeds (similar to the displacement distributions in Fig. 2 D, except now we have more dimensions and an infinite number of directions rather than just two. We therefore look only at the magnitude of the displacement or velocity vector, so the separate peaks for “left” and “right” motion become one). At very low λ_act, the cell barely moves at all, as indicated by a single peak at instantaneous speeds near zero (Fig. 3 E). This corresponds to an NM cell without protrusions, spending most of its time in “stops.” As λ_act increases, the cell enters the “stop-and-go” (I-RW) amoeboid migration regime (bimodal distributions). Higher λ_act values not only increase migration speed (shifting this second peak upward) but also reduce the amount of time a cell spends in “stops” (decreasing the size of the first peak). As stops allow the cell to change its direction (Fig. 3 B), the reduced “stopping time” at high λ_act values explains why Act cells with high λ_act values migrate not only faster but also more persistently. Finally, at the highest max_act and λ_act values, the cell takes on a keratocyte-like shape and almost never stops moving (P-RW).

Together, these results demonstrate that the exponential speed-persistence coupling holds in 2D and 3D and spans different “regimes” of migration. Importantly, we find that the Act-CPM activity gradients remain sufficient to reproduce the UCSP in these settings, even when cells no longer have a clear “front” or “back.”

Both Act cell speed and persistence saturate in a cell shape-dependent manner

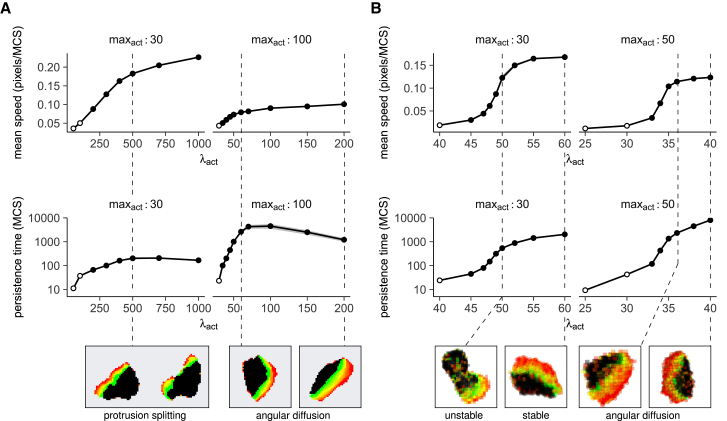
Interestingly, our data also show the saturation of the persistence at higher cell speeds that was reported in the experimental data (compare the 2D figures in Fig. 3 D to the data in (7)). In fact, this saturation was not limited to persistence. Whereas speed initially increased linearly with λ_act, it plateaued at higher λ_act values (Figs. 4, A and B and S3 C). The maximal speed reached depended on the protrusion shape-parameter max_act (Fig. S3, D and E), and in all cases, the initial linear part of the graph spanned the entire transition from amoeboid to a keratocyte-like shape. This finding suggests that having to maintain a broad protrusion limits the speed a cell can reach. In line with this idea, we did not observe this saturation in microchannels, which prevent the cell from acquiring the broad protrusions observed in 2D and 3D (Fig. S2 A).

Figure 4.

Cell shape dynamics limit both the speed and persistence of migrating cells. Mean ± SD of speed and persistence time of (A) 2D and (B) 3D Act cells, plotted against λ_act for different values of max_act. Open circles indicate points where the persistence time is lower than the time it takes the cell to move 10% of its length (corresponding to the points in the gray background in Fig. 3B). Insets show cell shapes at the indicated parameter values. To see this figure in color, go online.

Similarly, the cell shape changes observed in 2D and 3D seem to put an upper bound on persistence that disappears when the cell is constrained by a microchannel (Figs. 4, A and B, S2 B, and S3, C–E). The initial exponential increase in persistence again spanned the entire transition from amoeboid to keratocyte protrusion shapes before eventually saturating at a max_act-dependent value. Again, this phenomenon appears to be linked to protrusion shapes. Whereas cells with low max_act do tend to form keratocyte-like protrusions at high λ_act values, these protrusions do not extend far into the cell and are prone to splitting, forcing the cell to turn toward one of the (competing) protrusion halves (Fig. 4 A; Video S3). Although higher max_act values allow for larger persistence times by letting broad protrusions extend farther into the cell and preventing them from splitting (Fig. 4, A and B), persistence still saturates eventually because of slight, stochastic turning of the stable protrusion around the cell perimeter (“angular diffusion,” Fig. 4, A and B; Video S3; (7)).

Video S3. Different processes put an upper bound on persistence depending on the cell shape

For cells with an unstable protrusion (low max_act), active protrusions can split into two parts whenever the cell tries to form protrusions that are too broad to maintain. This forces the cell to turn in the direction of one of the protrusion halves, limiting persistence. The movie shows examples of such "protrusion splitting" (indicated by pauses and arrows). By contrast, for cells with a stable protrusion (high max_act), broad protrusions do not split or decay – but the most active part of the protrusion can still shift away from the protrusion center, causing the cell to turn ("angular diffusion"). The movie indicates this type of stochastic turning by showing in red the movement of the cell’s center of mass.

By showing how local protrusion dynamics and cell shape place a natural upper bound on both the speed and the persistence a cell can reach, these results explain the saturation of persistence observed by Maiuri et al. (7). However, there was a striking effect of dimensionality on this process; although we observed shape-driven saturation in both 2D and 3D, the shape of the speed-persistence curve was different for 2D and 3D simulations (Figs. 3 B and 4). In both settings, speed and persistence saturated at high λ_act after an initial increase (which was linear for speed and exponential for persistence). Yet, whereas persistence saturated before speed in 2D (Fig. 4 A), 3D Act cells showed a much stronger saturation of speed that preceded the saturation of persistence (Fig. 4 B). Thus, when both speed and persistence have a natural upper bound, the dominant saturation effect can be context dependent, altering the shape of the speed-persistence curve.

Environmental constraints break the UCSP for T-cell migration in the epidermis

So far, our models mimicked the environments in which the UCSP was initially discovered, where cells can migrate rather easily. But many cell types also need to move in crowded or stiff environments that strongly constrain cell shape. To investigate how such constraints would impact speed-persistence coupling, we modeled T-cell migration in the epidermal layer of the skin. As one of the key entry points through which pathogens can enter the body, healthy skin contains substantial numbers of T cells (23). T cells attracted to the epidermis during an infection can remain there for a long time; even a year after the resolution of an infection, specific T cells still persist in the same region of the epidermis (24, 25, 26, 27). Whereas subtle chemotaxis guides T cells toward infected cells during the effector phase (28), these remaining T cells actively patrol the epidermis without such chemotactic guidance (1), migrating in patterns shaped by a combination of cell-intrinsic factors and environmental constraints. Importantly, even though the tight contacts between keratinocytes make the epidermis one of the most rigid environments T cells encounter in vivo, T cells in the epidermis are nevertheless highly motile (1).

We therefore focused on this extreme example to examine how environmental structure can affect the UCSP. To this end, we simulated T-cell migration in the skin as reported previously (12), placing an Act cell in a grid covered completely with keratinocytes (Fig. 5 A). In this setting, Act T cells move by squeezing in between the keratinocytes (Video S4), but because of the opposing forces from the surrounding keratinocytes, cells now required higher λ_act forces to counter this resistance and start moving (Fig. S4). At sufficiently high λ_act values, they once again showed the characteristic “stop-and-go” motility before eventually switching to near-constant motion with hardly any stops (Figs. 5 B and S4; Video S4; Interactive simulation S4 at https://ingewortel.github.io/2020-ucsp/).

Figure 5.

Environmental constraints limit T-cell persistence in a model of the epidermis. (A) An Act T cell (black) moving in between keratinocytes (gray) in the epidermis. Simulations were performed in a 150 × 150 pixel grid with linked borders (for example, a cell moving off the grid toward the red region on the right re-enters the grid at the equivalent red region on the left). (B) Shapes of Act T cells constrained between keratinocytes. At lower λ_act/max_act values, T cells show typical amoeboid “stop-and-go” behavior. At higher λ_act and/or max_act values, cells do not obtain a broad, keratocyte-like shape like they normally would (Fig. 3) but stay elongated because of environmental constraints. At junctions between keratinocytes, however, protrusions tend to split. (C) Whereas formation of broad protrusions is mostly prevented in “stiff” skin tissue, Act cells in a more deformable tissue can form broad protrusions by pushing apart surrounding cells. (D) Mean persistence time plotted against speed for different combinations of λ_act and max_act, tissues with different stiffness. Shaded gray background indicates regions where the persistence time is lower than the time it takes for a cell to move 10% of its length. To see this figure in color, go online.

Video S4. Act T cells in the epidermis move by squeezing in between keratinocytes

At low λ_act and max_act, they follow the typical "stop-and-go" motion of an amoeboid cell. At high max_act and/or λ_act, they keep their elongated form in between the keratinocytes, rather than taking on the broad keratocyte-like shape that free Act cells would. However, they stop less frequently than cells with low max_act and λ_act, and actively probe their environment by letting parts of their active protrusion extend into the space between keratinocytes.

Unlike Act cells in an unconstrained environment, these Act T cells could not fully switch from amoeboid to keratocyte-like cell shapes as λ_act and/or max_act increased (Video S4). Even though cells at high λ_act and/or max_act became somewhat broader, they still mostly maintained their amoeboid shape, probing their surroundings with narrow protrusions and migrating in the direction of their longest axis. However, when these cells approached a “T-junction,” they sometimes formed a broad protrusion in the space between the keratinocytes that eventually split up into two separate protrusions going in opposite directions (Fig. 5 B). This protrusion splitting caused the cell to slow down until one of the two active regions gained the upper hand (Video S4).

In this setup, increases in λ_act were once again associated with a higher speed that gradually saturated at high λ_act values (Fig. S5 A), but persistence times now saturated much earlier, reaching a plateau at ~90 MCS for max_act = 30 and 140 MCS for max_act = 100 (Fig. S5 B). With cell speeds around ~0.12 and ~0.07 pixels/MCS, respectively, this corresponds to persistent movement over distances in the range of ~10–12 pixels—just under the distance the T cell can travel before arriving at another junction (Figs. 5 A and S5 C).

Thus, the structure of the environment appears to be a limiting factor for T-cell persistence in this scenario. Indeed, when we placed cells in a grid covered with more deformable cells, cells with a high max_act of 100 could once again form their preferred broad protrusions and move in straighter lines by pushing the surrounding cells apart (Fig. 5 C; Video S5). This in turn resulted in a higher persistence (Fig. S5 B) and a slighly increased speed (Fig. S5 A). By contrast, cells with a low max_act of 30—which cannot stably form broad protrusions even when unconstrained by tissue (Fig. 4 A)—had similar speed and persistence in the limit of high λ_act values, regardless of tissue stiffness (Fig. S5, A and B). These results demonstrate how interactions between the environment and cell shape determine how strongly the tissue affects motility patterns.

Video S5. Tissue stiffness affects Act T-cell migration mode

Cells with high max_act are mostly prevented from broad protrusions in a stiff tissue. Their protrusions only broaden in the space between keratinocytes before rapidly splitting in two. By contrast, the same cells can form and maintain broad protrusions in a more deformable tissue by pushing apart the cells surrounding them.

The observed rapid saturation of persistence eclipsed the UCSP for T cells migrating in the skin, removing the speed-persistence correlation (Fig. 5 D). This result was independent of the rigidity of the surrounding keratinocytes; although a reduction in tissue stiffness slightly increased the maximal persistence time for cells with high max_act (Fig. S5 B), this did not rescue speed-persistence coupling (Fig. 5 D). Thus, although the UCSP appears to be valid for all migrating cells, cell-intrinsic speed-persistence coupling may be obscured when environmental factors place additional, more stringent constraints on persistence.

Discussion

The rich interplay between cell-intrinsic and environmental factors has made cell migration a popular topic of study among biophysicists and computational biologists, raising questions such as how do single cells coordinate their motion to start moving collectively? How does each cell’s molecular machinery interact with its shape during motion? How do constraints on cell shape posed by a crowded tissue environment alter the (immune) cell migration patterns we see? And what migratory pattern should immune cells adopt to find their targets most efficiently? Over the years, many studies have shed light on these questions by studying the motion of single cells and collectives using both experimental and modeling approaches (13,29, 30, 31, 32). The models used are diverse, ranging from relatively simple particle models to detailed physical models linking intracellular signaling and cell shape (8,32). Here, we take a cell-intrinsic law of cell motion derived from a detailed but 1D mathematical model (7), the UCSP, and examine its behavior in different environments using the CPM. Although the CPM describes intracellular dynamics in less detail, it excels at predicting how single cells with dynamic cell shapes interact in complex environments (13,15). We show here that our model’s more local and dynamic definition of polarity 1) still captures the UCSP, and 2) opens up new opportunities to study the UCSP in more diverse and realistic environments.

Migration in the Act-CPM arises through a combination of local activation (the ΔH_act force allowing protrusion) and global inhibition (the “membrane tension” that makes the cell retract its rear after the protruding front has stretched its perimeter beyond the target value). This less strict polarity mechanism apparently suffices to reproduce the speed-persistence coupling observed in migrating cells (7), even though it only encodes local polarity gradients rather than imposing a global polarity with an explicit “front” and “back.” But although the UCSP holds in this more general case of deformable cells, it is not wholly unaffected; the more fluid nature of polarity couples the UCSP to cell shape dynamics. The increase in speed and persistence coincided with a transition between cell shapes and migration modes. Indeed, membrane tension dynamically links cell shape to motion in the CPM. Similar to shape-motility interactions observed in real cells (8), Act cell shapes are closely linked to both motility characteristics underlying the UCSP: speed and turning behavior.

The observed link between cell shape and speed is consistent with several other studies (30,33, 34, 35, 36). In T cells, this coupling arose from the same actin retrograde flow that also underlies the UCSP (7,37). Lavi et al. (36) recently extended the original UCSP model to a 2D free boundary model with dynamic cell shapes, in which higher speeds again correlated with broader cells, resembling the broadening of Act cells with increasing λ_act (Fig. 4). Likewise, cell shape is intricately linked to turning behavior. Fish keratocytes have a broad protrusion (“lamellipodium”) that normally allows them to migrate persistently. Yet, the stability of the lamellipodium partly depends on its shape, and deformation of the cell may destabilize the lamellipodium or reinforce symmetry breaking within an existing protrusion, disrupting persistent motion (38, 39, 40). Similar examples of protrusion splitting and/or competition have been observed in Dictyostelium cells, a popular model of amoeboid cell migration (9,10). Here, we again find an effect of cell shape on protrusion stability and persistence, in which existing protrusions may either become unstable (“splitting”) or break symmetry (“angular diffusion”) at certain parameter values (Fig. 4).

Given this interplay between cell shape, speed, and turning behavior, our model demonstrates how cell shape limits both migratory speed and persistence; both saturated at high λ_act levels at which cells had broader, more keratocyte-like shapes (Fig. 4). A similar saturation was found in fish keratocytes (30). These observations clearly show that not only persistence but also cell speed has a natural upper bound determined at least partially by cell shape dynamics.

Our results suggest a role for dimensionality in this process, as speed and persistence saturated differently in 2D versus 3D. However, we note that our cells behaved slightly differently in 3D; they had a harder time forming stable protrusions, but when they did, they almost always took on a broad, keratocyte-like shape (at least temporarily). This seemingly contradicts in vivo videos of T cells moving in a 3D environment such as the lymph node (19,41), where cells do seem to be able to move in an elongated shape for prolonged periods of time. However, it should be noted that whereas cells may move freely on the empty surface of a 2D petri dish, there is no such thing as “free” migration in 3D; in reality, cells migrating in 3D always encounter environmental barriers (be it the fibers of an extracellular matrix or surrounding cells). It is unclear whether the slightly altered behavior in 3D is an artifact of the model, of the free environment, or both; comparing speed and persistence saturation in different 3D models (42,43) may clarify this issue in the future. Nevertheless, these effects of dimensionality and environment do further stress the intricate link between changes in cell shape and the resulting motility patterns.

Together, these results shed new, to our knowledge, light on the shape of the experimental UCSP curves: whereas persistence saturated before speed in all experimental settings tested (7), our model suggests that depending on the cell’s shape, scenarios in which speed saturates earlier could likewise exist. These findings generalize the mechanism behind the UCSP to settings where cells can take on more complex shapes and lack a globally defined polarity. Importantly, they suggest that the UCSP may likewise emerge in other existing models of cell migration, especially those in which cell shape, speed, and persistence emerge from a protrusion mechanism combined with membrane tension (10,44, 45, 46, 47, 48, 49). In addition, several variations of the original UCSP model have now been developed (36,50,51). Studying the similarities and differences between these models may further clarify how cell shape and motility interactions can alter the shape of the speed-persistence curve.

The spatial nature of the CPM also allowed us to explore the UCSP in a more natural environment. It is increasingly recognized that environmental structure plays a crucial part in shaping cell migration, which has led to an ever-growing number of dedicated in vitro systems mimicking various environmental geometries (52), as well as studies examining how the cell’s inner machinery interacts with environmental signals (11). The (Act-)CPM offers another approach to probing migration and the UCSP in diverse geometries that constrain the shape and direction of cellular protrusions. For example, in our in silico model of T-cell migration in the epidermis, constraints posed by the dense keratinocyte layer restricted persistent movement and obscured the UCSP (Fig. 5), showing that environmental constraints can overrule the UCSP in at least some of the environments cells face in vivo. We therefore predict that speed-persistence coupling may not be visible in in vivo imaging data of T cells patrolling the epidermis; in such an environment, both speed and persistence likely reflect the maximum of what is feasible given the environmental constraints, rather than an intrinsic coupling. In complex, highly restrictive environments, cells may choose the path of least resistance (53), with a lesser role for their intrinsic polarity mechanism.

Still, compared with most other tissues, the epidermis is an extreme example of a confining environment, and the UCSP could have a larger influence on persistence when constraints on cell movement are less stringent. For example, Sadjadi et al. (54) recently detected speed-persistence correlations among T cells migrating in 3D collagen matrices, after Read et al. (55) had found a similar link between speed and turning behavior among T cells migrating in an inflamed lymph node. Although the latter study did not explicitly link this to the UCSP, random walk models incorporating this correlation captured the data better than those that did not, suggesting the UCSP poses an essential constraint on in vivo motility in at least some settings.

The universality of the UCSP has implications for computational models of cell migration used in different fields. For example, in the last decade, several studies have investigated the functional consequences of T-cell motility patterns: how should T cells move to find their targets most efficiently? Using mathematical or agent-based variations of random walk models, these studies compare different migratory strategies in terms of “search efficiency” (31,56, 57, 58, 59). However, selecting and fitting these models is difficult; multiple models can often fit the same experimental data depending on the metrics used to quantify migration (55,59,60), and even slight differences in the model used can have large consequences for the area exploration predicted on timescales beyond that of the experiment (61). Moreover, these models treat speed and persistence as input parameters that can be independently tuned when they are in fact linked through the UCSP. This may yield models that seemingly fit the data but in truth reflect motility patterns impossible for a real cell to adopt. Indeed, two recent studies showed how the UCSP can alter cell motion patterns and space exploration (62,63), although this may also depend on the environment. Incorporating the UCSP into our models or using models like the CPM in which it arises naturally depending on the structure of the environment may be crucial to focus our research on those migration patterns that are actually attainable by real cells.

Conclusions

The UCSP is a simple yet highly general quantitative law of cell motion, which holds across a broad spectrum of migrating cells. Given the incredible diversity of the mechanisms driving cell migration, it is remarkable that such a general law exists at all. Nevertheless, after the UCSP’s initial discovery (5), Wu et al. (6) later also found a robust speed-persistence coupling in an independent study. Maiuri et al. (7) explained it by showing that actin retrograde flow can mechanistically couple cell polarity to migration speed, and Yolland et al. (64) further strengthened this explanation by demonstrating that the actin flow field controls stable cell directionality. Here, we confirm this seemingly fundamental law of cell migration in a completely different but popular modeling framework (the CPM). We find that local protrusion dynamics at the front are sufficient to reproduce the UCSP, even in the absence of a global front-to-back polarity gradient, and show how cell shape dynamics and environmental constraints alter the shape of the speed-persistence curve. Models like the Act-CPM now allow us to probe these interactions in many more environments and geometries.

Author contributions

I.M.N.W., I.N., N.S.G., R.J.d.B., and J.T. designed the research. I.M.N.W., I.N., and P.M.K. performed simulations and analyzed the data. I.M.N.W., N.S.G., and J.T. wrote the manuscript. P.M.K. and R.J.d.B. critically revised the manuscript.

Editor: Lisa Manning.

Supporting citations

References (65, 66, 67) appear in the Supporting material.