Low-frequency component of photoplethysmogram reflects the autonomic control of blood pressure

Abstract

The question of how much information the photoplethysmogram (PPG) signal contains on the autonomic regulation of blood pressure (BP) remains unsolved. This study aims to compare the low-frequency (LF) and high-frequency components of PPG and BP and assess their correlation with oscillations in interbeat (RR) intervals at similar frequencies. The PPG signal from the distal phalanx of the right index finger recorded using a reflective PPG sensor at green light, the BP signal from the left hand recorded using a Finometer, and RR intervals were analyzed. These signals were simultaneously recorded within 15 min in a supine resting condition in 17 healthy subjects (12 males and 5 females) aged 33 ± 9 years (mean ± SD). The study revealed the high coherence of LF components of PPG and BP with the LF component of RR intervals. The high-frequency components of these signals had low coherence. The analysis of the signal instantaneous phases revealed the presence of high-phase coherence between the LF components of PPG and BP. It is shown that the LF component of PPG is determined not only by local myogenic activity but also reflects the processes of autonomic control of BP.

Significance

We report that the low-frequency component of photoplethysmogram variability is determined not only by local myogenic activity but also reflects the processes of autonomic control of blood pressure.

Introduction

A photoplethysmogram (PPG) signal detects blood volume changes in the microvascular bed of tissue (1,2). Common PPG sensors with one light-emitting diode (LED) and one photodetector (photodiode or phototransistor) allow detecting fluctuations in blood volume (3, 4, 5). The use of two LEDs in the PPG sensor (for example, red and infrared) allows additional detection of oxygen saturation (6). The use of a matrix of photodetectors and LEDs with different wavelengths is used in near-infrared spectroscopy (7). There are known methods for noninvasive assessment of systolic blood pressure (BP) (SBP) and diastolic BP (DBP) by PPG signal, which, however, require preliminary individual calibration (8,9). In PPG sensors measuring a reflected light intensity, LED and photodetector are located at the same side of a tissue that allows them to record signals from forehead or wrist, although signal acquisition from places such as finger or earlobe is more typical. Such widely used reflective sensors often use green or yellow light (10). In this case, they register signals from small diameter vessels at a depth of ∼1 mm (3). Even a simple reflective sensor with one LED provides important information about the heart rate (HR) and autonomic regulation of the circulatory system (1).

It is believed that PPG contains information about blood filling and blood flow in the distal vascular bed (small arteries, arterioles, capillaries, venules, and small veins) (1,2,11, 12, 13). Therefore, PPG analysis is important for studying the physiology of blood circulation (11,14) and solving applied problems of medical diagnostics (6,8,15,16). PPG is a reflection of the underlying circulation but modified by various optical, biomechanical, and physiological processes. Overall, the PPG provides a wealth of circulatory information, but its complex origin may be a limitation in some novel applications (1). In particular, understanding the nature of the spectral components of PPG is essential.

Usually, the activity in the high-frequency (HF) band (0.15–0.4 Hz) of the PPG power spectrum is related to the mechanical consequence of respiration (12,17,18), whereas the activity in the low-frequency (LF) band (0.05–0.15 Hz) is associated with the regulation of peripheral vascular tone (12,16). Taking into account that LF components of BP are also associated with the processes of peripheral vascular resistance (19, 20, 21) and HF components of BP are caused by the influence of respiration (22), one may expect the similarity of PPG and BP power spectra. However, Gonzalez et al. (23) concluded that oscillations in PPG and BP are not identical. Therefore, the question of how much information the PPG signal contains on the autonomic regulation of BP remains unsolved.

Another controversial question is what specific mechanisms of regulation of peripheral vascular tone are reflected in the LF components of PPG. Some researchers consider the contribution of relatively large arteries to the formation of the PPG signal to be significant (24,25) and associate the frequency components in the LF band of the PPG spectrum with the mechanisms of autonomic regulation of BP (1,26,27). Other researchers consider that LF components of PPG are determined predominantly by local myogenic mechanisms (28, 29, 30). For example, Krupatkin (30) in the experimental studies did not reveal changes in the power spectra of PPG signals within the LF band in patients with sympathetic denervation, whereas the other authors reported a significant correlation between the LF components of laser Doppler flowmetry and PPG signal (31). Nevertheless, in our previous experimental studies, we revealed significant phase synchronization between the LF components of PPG and interbeat (RR) intervals (32). Also, we showed a significant correlation between the degree of such synchronization and the health status of subjects (14) as well as between the degree of synchronization and various physiological states (33). The involvement of mechanisms of autonomic control can explain such interactions, given that the mechanisms leading to the occurrence of LF oscillations in PPG are independent of the mechanisms causing LF oscillations in RR intervals (34). In particular, LF oscillations in RR intervals are due to the activity of the centers of autonomic control of the HR (35,36), whereas the LF fluctuations in PPG are primarily due to the modulation of peripheral vascular tone caused by the autonomic control or local processes (1,26, 27, 28, 29, 30).

Thus, the purpose of this study is to compare the LF and HF components of PPG and BP in healthy subjects and to study their correlations with oscillations in RR intervals at similar frequencies.

Materials and methods

Ethical approval

The Ethics Committee of Saratov State Medical University in Saratov, Russia approved the study (protocol number (No.) 1; February 5, 2019), and written informed consent was obtained from all participants. All procedures involving human participants were performed by the ethical standards of the institutional research committee and the Declaration of Helsinki and its later amendments. The entire subjects gave voluntary informed consent to participate in research.

Subjects

Our study included 17 healthy subjects (12 males and 5 females) aged 33 ± 9 years (mean ± SD). The experimental studies were carried out at the Institute of Biomedical Problems of the Russian Academy of Sciences. All subjects in our experimental sample had no signs of pathology of the cardiovascular system. To exclude the diagnosis of hypertension, we used current clinical guidelines (37).

Signal recording

We analyzed 17 records from 17 different patients. All subjects underwent simultaneous recordings of electrocardiogram (ECG), BP, and PPG signals. Measurements started after 10 min of rest, and the duration of each recording was 15 min. The signals were recorded in the horizontal position of the body approximately 2 h after a meal in the morning.

BP signal was measured using a Finometer (Finapres Medical Systems, Enschede, the Netherlands) with simultaneous recording of ECG signal (PneumoCard; Medical Computer Systems, Moscow, Russia) and PPG signal. Finometer uses the volume clamp method of Penaz (38, 39, 40) for BP measurements. This method allows us to exclude the influence of invasive interventions on the experimental results, which are inevitable with direct measurement of BP using catheterization. At the same time, some researchers indicate that the Finometer signal with high accuracy reproduces the waveform and properties of the BP signal recorded in direct invasive studies with catheterization of large arteries (41, 42, 43). Hence, we assume that the conclusions obtained from the analysis of Finometer signal are also true for BP measured by a direct invasive method.

Although Finometer uses an optical measuring channel in its sensors, the principle of operation of the device is qualitatively different from photoplethysmography. The method is based on the development of the dynamic pulsatile unloading of the finger arterial walls using an inflatable finger cuff (39). A fast pneumatic servo system with a controlled feedback and a dynamic servo setpoint adjuster assure arterial unloading (40) at 0 transmural pressure and consequent full transmission of arterial BP to cuff air pressure.

The optical channel in the Finometer is used as an auxiliary element. Finometer uses a transmitted light plethysmograph in which an infrared LED and a photodetector are placed on opposite sides of the finger. The cuff with a plethysmograph is located on the proximal phalanx. Therefore, a significant contribution to this signal is made by fluctuations in the blood volume of the large digital arteries.

To study volumetric fluctuations in the blood flow of the microvasculature, we recorded a PPG signal using a reflective green light sensor (wavelength 560 nm). Such a PPG sensor register signals from small diameter vessels at a depth of ∼1 mm (3). The sensor was located on the distal phalanx of the finger, where there are no large arteries.

During 10 min of rest, mean arterial pressure was calculated as an average of the automated sphygmomanometer BP values obtained three times: during the beginning, middle, and the end of resting period. We used a DYNAMAP DPC100X-RU sphygmomanometer (GE Medical Systems Information Technologies, Boston, MA). Finometer waveforms were calibrated once to the average of these systolic, diastolic, and mean arterial pressure measurements. This ensured that BP measurements derived from the Finometer matched the absolute value of BP obtained from the sphygmomanometer. A similar calibration procedure was carried out, for example, in the work of Young et al. (44).

The signals from Finometer and PneumoCard were digitized at 1 kHz using E14–140 analog-to-digital converter (L-Card, Moscow, Russia) and POWER GRAPH software (DiSoft, St. Petersburg, Russia), whereas the signal from REHACOR-T (Medicom-MTD, Taganrog, Russia) was digitized at 250 Hz.

The band pass of all recorded signals was 0.003–100 Hz. The signal bandwidth during recording was limited by second-order Butterworth analog filters. The registration of ECG, BP, and PPG signals was synchronized in time.

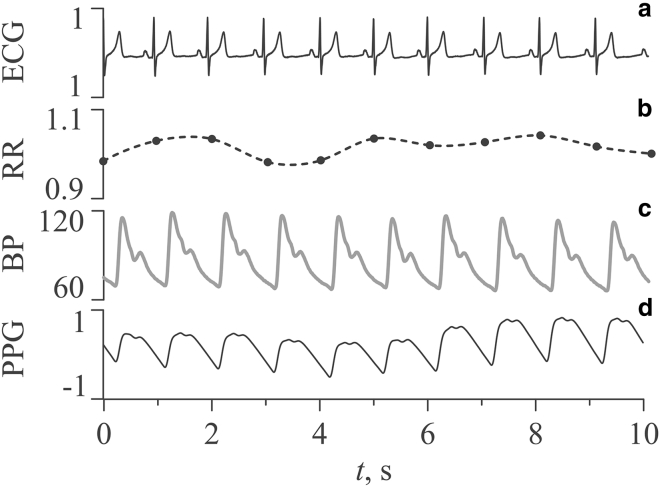
Fig. 1 shows the fragments of experimental signals of subject No. 4. The ECG signal (Fig. 1 a) was recorded in the standard lead I, according to Einthoven. Fig. 1 b shows RR intervals extracted from the ECG. The BP signal (Fig. 1 c) was recorded from the subject’s left hand. The PPG signal is shown in Fig. 1 d. The signals in Fig. 1 are typical for an experimental sample. The shape of the waveforms is typical for healthy subjects. HR for subject No. 4 was calculated during the analysis of RR intervals of the ECG signal and was 58 ± 2 bpm (mean ± SD). SBP and DBP were calculated from a sequence of beat-to-beat BP signal values over a 15-min recording period. SBP was 111 ± 4 mmHg, and DBP was 65 ± 2 mmHg (mean ± SD).

Figure 1.

Fragments of experimental signals of subject No. 4: (a) ECG, (b) RR intervals (nonequidistant sequence is shown by dots, and interpolated equidistant time series is shown by solid line), (c) BP, and (d) PPG. The ECG signal is shown in mV, RR intervals are in seconds, BP signal is in mm of mercury, and PPG signal is in arbitrary units.

Signal processing and analysis

SBP, DBP, mean BP, and HR for each subject were calculated as the average value of beat-to-beat indices over the registration period (15 min), as in (44). To assess the variability of SBP, DBP, and HR in the experimental sample, the mean and SD were calculated.

HR variability information was obtained from the ECG signal following the recommendations in (45). First, a sequence of RR intervals, i.e., a series of time intervals between the two successive R-peaks in ECG signal, was extracted. Then, to obtain equidistant time series from nonequidistant sequence of RR intervals, we interpolated it with cubic splines and resampled with a frequency of 5 Hz (Fig. 1 b). Thus, an equidistant RR interval time series was obtained. The information about the PPG variability (PPGV) and BP variability (BPV) was obtained directly from the analysis of the PPG and BP signals.

The coherence function C(f) was estimated in pairs between the PPG, BP, and RR intervals (46,47). After the estimation of cross-spectrum R_xy(f):

$$R_{\text{xy}}\left(f\right)=S_x\left(f\right)S_y^{\ast }\left(f\right),$$ (1)

where S_x(f) and S_y(f) are the Fourier transform of the experimental time series, ^∗ means complex conjugation, and f is the frequency. The coherence function was calculated as follows:

$$С\left(f\right)=\frac{\left|⟨R_{\text{xy}}\left(f\right)⟩\right|}{\sqrt{⟨R_{xx}\left(f\right)⟩}\sqrt{⟨R_{yy}\left(f\right)⟩}},$$ (2)

where angular brackets denote average over time. The coherence function takes the values between 0 and unity and characterizes the phase coherence between oscillations for the frequency f. The function Eq. 2 was estimated in 120-s windows moving along the time realization with a shift of 60 s. Thus, averaging was performed over 14 windows for each estimate of the coherence function. We calculated also the maximal C_max = max(C(f)) in the LF band.

To analyze the correlation and phase coherence between the LF components of PPG, BP, and RR intervals, we filtered these signals by finite impulse response filter with a 1000 taps and linear phase–frequency response in the 0.05–0.15 Hz band. Cross correlation g(l) was calculated in pairs between the signals PPG_LF, BP_LF, and RR_LF obtained as a result of such filtering (48). The lag l was varied over the range of ±10 s (about two characteristic periods of the analyzed LF components), and the maximal g_max = max(g(l)) was found.

Instantaneous phase contains important information about the signal oscillations (49, 50, 51). To analyze the phase coherence of LF components of the experimental signals, we defined the instantaneous phases of the signals. First, the analytic signal $\varsigma \left(t\right)$ for the signal x(t) obtained as a result of band pass filtration was constructed. The signal $\varsigma \left(t\right)$ is a complex function of time defined as:

$$\varsigma \left(t\right)=x\left(t\right)+i\tilde{x}\left(t\right)=A\left(t\right)e^{i\phi \left(t\right)},$$ (3)

where A(t) and $\phi \left(t\right)$ are, respectively, the amplitude and the phase of the analytic signal, and function $\tilde{x}\left(t\right)$ is the Hilbert transform (52) of x(t):

$$\tilde{x}\left(t\right)=\frac{1}{\pi }\text{P.V.}\underset{-\infty }{\overset{+\infty }{\int }}\frac{x\left(\tau \right)}{t-\tau }d\tau ,$$ (4)

where P.V. means that the integral is taken in the sense of the Cauchy principal value. Phase $\phi \left(t\right)$was defined from Eq. 3 as:

$$\phi \left(t\right)=\text{arctan}\frac{\tilde{x}\left(t\right)}{x\left(t\right)}$$ (5)

We used index S as a quantitative indicator of the coherence of instantaneous phases of analyzed signals. This index is calculated as the sum of the duration of the epochs of coherent phase behavior divided by the duration of the entire record (32). The epochs of coherent phase behavior were defined as the regions, where the phase difference of analyzed signals was close to a constant value. Earlier, index S was successfully applied for the analysis of nonstationary signals of biological nature (14,32, 33, 34).

We estimated the statistical significance of all analyzed indices by generating an ensemble of surrogate data using the amplitude-adjusted Fourier transform method (53). This method allows one to test the statistical hypothesis of uncoupled systems. The amplitude-adjusted Fourier transform method preserves the periodograms of analyzed signals but destroys the correlations between the signal phases. The results of our analysis were considered statistically significant if the p-value did not exceed 0.05.

Results

We calculated SBP, DBP, mean BP, and HR for all subjects in the sample. They took the following values: 117 ± 8, 70 ± 6, 94 ± 6, and 65 ± 10 (mean ± SD), respectively. These values are close to those obtained for samples of healthy people in works (44,54,55).

The results of spectral analysis of the experimental signals for subject No. 1 are presented in Fig. 2. The PPG, BP, and RR intervals power spectra exhibit characteristic peaks in the LF band (the basic frequency is usually ∼0.1 Hz) and peaks with the frequencies of ∼0.25 Hz in the HF band. Fig. 2 illustrates a typical situation in which the highest relative power in the HF band is observed for RR intervals. This power is determined mainly by a parasympathetic innervation that modulates the HR (56). The peaks in the HF band of PPG and BP power spectra are usually less pronounced and, as is known, are only the result of the mechanical effect of respiration (57).

Figure 2.

Fourier power spectra of PPG (thin line), BP (thick line), and RR intervals (dotted line) of subject No. 1. The spectra are normalized to the power of the maximal component in the LF band. Vertical lines mark the boundaries of the LF and HF bands.

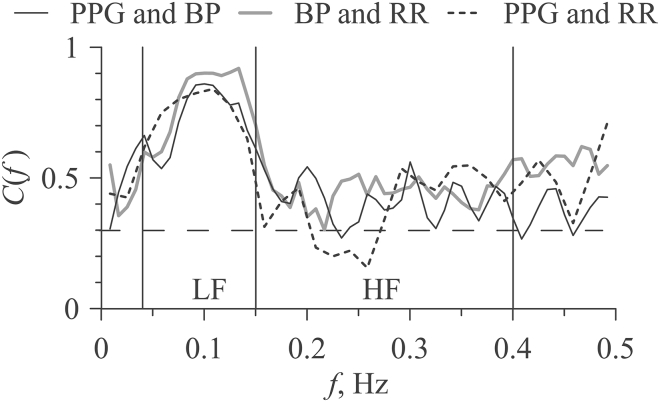
Fig. 3 depicts typical coherence functions for the analyzed pairs of signals for subject No. 1. As can be seen from Fig. 3, all experimental signals demonstrate statistically significant high coherence with each other in the LF band. The values of the C_max indices were 0.88 for PPG_LF and BP_LF, 0.92 for BP_LF and RR_LF, and 0.84 for PPG_LF and RR_LF. In the LF band, the coherence functions exhibit pronounced peaks, indicating that the signals interact or have common components in this range. The coherence functions do not show an increase in HF range, despite the presence of peaks in the power spectra in this range (Fig. 2).

Figure 3.

Coherence functions between PPG and BP (thin line), between RR intervals and BP (thick line), and between RR intervals and PPG (dotted line) calculated of subject No. 1. The horizontal dashed line indicates the critical level of statistical significance (p = 0.05). Vertical lines mark the boundaries of the LF and HF bands.

The pairwise differences of instantaneous phases of LF components of analyzed signals for subject No. 1 are presented in Fig. 4. The plots of all three phase differences show long (hundreds of seconds) epochs in which Δϕ is almost constant, which corresponds to high coherence between the phases of the signals. These plateaus of Δϕ alternate with the intervals of Δϕ variation, which correspond to the incoherent behavior of phases arising from the nonstationarity of the analyzed signals and the influence of stochastic fluctuations of various nature. The index S in the analysis of PPG_LF and BP_LF signals takes the value of 0.67. It means that in 67% of the observation time, the signal phases were coherent. The index takes the value 0.68 for BP_LF and RR_LF and 0.52 for PPG_LF and RR_LF. The index takes the value 0.68 for BP_LF and RR_LF and 0.52 for PPG_LF and RR_LF. In most subjects, the phase differences between the PPG_LF and RR_LF signals and between the BP_LF and RR_LF signals are observed at the same time intervals.

Figure 4.

Differences of instantaneous phases of PPG_LF and BP_LF (thin line), RR_LF intervals and BP_LF (thick line), and RR_LF intervals and PPG_LF (dotted line) for subject No. 1.

Comparison of the signal components related to the LF band was carried out separately for their instantaneous amplitudes and phases. Fig. 5 shows typical time series of the LF components of the experimental signals that were extracted using a filter with band pass 0.05–0.15 Hz for subject No. 1. As seen from Fig. 5, the analyzed signals exhibit phase coherence at certain time intervals.

Figure 5.

Time series of PPG_LF (thin line), BP_LF (thick line), and RR_LF intervals (dotted line) for subject No. 1. The signals are normalized to the maximal amplitude.

The results of calculating the earlier-mentioned indices C_max, g_max, and S for each subject are presented in Table 1. C_max and g_max indices were found to be statistically significant for all subjects (p < 0.05). The statistically significant (p < 0.05) values of the S index are marked with a footnote symbol in Table 1. Table 1 also shows the values of SBP, DBP, and HR averaged over beat-to-beat waveforms. The SBP and DBP values in Table 1 were calculated from the BP signal, whereas the HR values were calculated from the ECG signal. Indices averaged over the significant values of ensemble are shown in the last row of Table 1 and in Fig. 6.

Table 1.

Results of the analysis of the signals of PPG, BP, and RR intervals filtered in the LF band as well as the SBP, DBP and HR values for each of the subjects

Subject No.	Cmax			gmax			S			SBP (mmHg)	DBP (mmHg)	HR (bpm)
	PPGLF and BPLF	BPLF and RRLF	PPGLF and RRLF	PPGLF and BPLF	BPLF and RRLF	PPGLF and RRLF	PPGLF and BPLF	BPLF and RRLF	PPGLF and RRLF
1	0.88	0.92	0.84	0.70	0.65	0.61	0.67a	0.68a	0.52a	120 ± 19	77 ± 9	68 ± 14
2	0.85	0.82	0.59	0.31	0.54	0.45	0.35a	0.47a	0.21	121 ± 11	63 ± 5	48 ± 4
3	0.75	0.95	0.69	0.11	0.78	0.08	0.24	0.68a	0.21	118 ± 5	68 ± 4	57 ± 6
4	0.70	0.86	0.65	0.35	0.57	0.37	0.39	0.28a	0.16	111 ± 4	65 ± 2	58 ± 2
5	0.76	0.79	0.62	0.24	0.60	0.43	0.48a	0.34a	0.25	122 ± 7	74 ± 4	74 ± 4
6	0.80	0.86	0.62	0.48	0.59	0.42	0.52a	0.32a	0.08	120 ± 7	68 ± 5	67 ± 6
7	0.88	0.77	0.63	0.59	0.60	0.49	0.49a	0.44a	0.30	127 ± 6	73 ± 4	62 ± 3
8	0.93	0.97	0.80	0.58	0.80	0.47	0.48a	0.61a	0.24	118 ± 11	80 ± 7	75 ± 10
9	0.82	0.89	0.65	0.46	0.64	0.28	0.53a	0.65a	0.33a	105 ± 4	60 ± 3	71 ± 2
10	0.79	0.92	0.71	0.41	0.77	0.47	0.26	0.59a	0.17	111 ± 6	65 ± 3	63 ± 4
11	0.89	0.76	0.65	0.50	0.47	0.37	0.45a	0.26a	0.15	111 ± 5	76 ± 4	71 ± 4
12	0.77	0.85	0.78	0.46	0.58	0.37	0.26	0.30a	0.21a	123 ± 7	69 ± 5	49 ± 6
13	0.90	0.87	0.80	0.40	0.44	0.44	0.20	0.42a	0.21a	122 ± 7	76 ± 5	57 ± 4
14	0.80	0.80	0.70	0.43	0.59	0.50	0.47a	0.39a	0.26	101 ± 15	69 ± 8	69 ± 14
15	0.85	0.89	0.75	0.45	0.70	0.45	0.17	0.47	0.28	134 ± 7	71 ± 3	88 ± 4
16	0.97	0.91	0.91	0.79	0.80	0.63	0.67a	0.58a	0.39a	118 ± 18	78 ± 8	69 ± 12
17	0.78	0.79	0.80	0.45	0.52	0.33	0.33a	0.38a	0.19	108 ± 4	66 ± 3	62 ± 4
Ensemble average	0.83 ± 0.02	0.86 ± 0.02	0.72 ± 0.02	0.45 ± 0.04	0.63 ± 0.03	0.42 ± 0.03	0.49 ± 0.03a	0.46 ± 0.04a	0.33 ± 0.05a	117 ± 8	70 ± 6	65 ± 10

In the last three columns, the data are presented as mean ± SD. In the last line, the values of the indices averaged over the ensemble are presented as mean ± SE.

^aStatistically significant values of S index.

Figure 6.

Averaged over the ensemble indices C_max (a), g_max (b), and S (c) calculated between the signals PPG_LF and BP_LF (I), BP_LF and RR_LF intervals (II), and PPG_LF and RR_LF intervals (III). Indices are shown with its SEs.

The indices C_max and g_max characterizing the maximal values of coherence function and cross correlation, respectively, show the largest values for the pair of signals BP_LF and RR_LF (Fig. 6, a and b). The results presented in Fig. 6 and Table 1 demonstrate that similarity between the BP_LF and RR_LF signals is greater than between the PPG_LF and BP_LF and between the PPG_LF and RR_LF. However, the index S takes the highest values for the pair of signals PPG_LF and BP_LF (Fig. 6 c). It means that the coherence of instantaneous phases of these signals is greater than for the two other pairs of signals. Note that all three indices show the minimal values for the pair of signals PPG_LF and RR_LF.

Discussion

A PPG signal recorded using a reflective PPG sensor at green light carries mainly information about the signals of microcirculatory bed: arterioles, capillaries, and venules (5).

As for the HF component of PPG and BP, there is a consolidated opinion that it is mostly related to the mechanical consequence of respiration on venous return and stroke volume (12,57,58). In our study, we did not reveal any noticeable interaction of the HF components in all three studied signals. This result is likely due to different mechanisms that are involved in respiratory influences on PPGV and BPV. For PPGV, this influence is carried out mainly through the venous bed, and for BPV, it is carried out through the stroke volume of the heart. The main attention was paid in our study to the analysis of LF oscillations. We compared the LF components of PPG and BP, taking into account that the LF component of BP is associated mainly with autonomic modulation (21,59).

The nature of LF oscillations in the PPG signal remains a controversial question. Several researchers assume that these LF oscillations are mainly associated with local myogenic mechanisms (30,31) and are not associated with central regulatory processes, whereas the other authors assume that the LF component of PPG is mainly due to autonomic regulation processes (1,26,27). It is possible to draw a conclusion about the nature of the LF components of the PPG signal by directly comparing these oscillations with the components of the BP signal and RR intervals in the same frequency band.

Our first important result is that LF components of PPG and BP show statistically significant high coherence with the LF component of RR intervals (see Fig. 6). This indicates the presence of common components in all three signals in the LF frequency band. LF oscillations in the RR intervals are uniquely associated with autonomic control processes. Thus, the influence of autonomic control processes on LF PPG oscillations can be considered a confirmed fact.

This result confirms our earlier conclusions about the importance of interaction between the LF cardiovascular rhythms for the normal functioning of the cardiovascular system in humans (14,60,61). The reliability of the obtained result is confirmed not only by the tests for statistical significance (53) but also by the nature of the RR intervals. Its LF component reflects the process of frequency modulation of the HR by the autonomic nervous system. The main effect of baroreflexes to the modulation of cardiac autonomic outflows is known (62). The LF oscillations appear in the ECG power spectrum in the form of satellites near the main frequency of HR (i.e., at ∼0.9 and 0.11 Hz). This excludes the linear mixing of LF oscillations in RR intervals with those in PPG and BP and indicates the presence of interaction between the investigated LF oscillating processes.

As follows from Fig. 6, the LF components of PPG and BP show high coherence in healthy subjects. Thus, the second important result is that oscillations in the microvasculature bed are close to BP oscillations in the LF frequency band. Given the known differences in the mechanisms of the regulation of blood circulation in large arteries and microcirculatory vessels, this conclusion is not trivial. The result obtained is consistent with previous studies by other authors (63). BP oscillations are transmitted from large arteries, manifesting themselves in the PPG signals of the microcirculatory bed in accordance with the hydrodynamic laws and because of reorientation and/or packing of erythrocytes (7,64,65).

It is important to note that the C_max and g_max indices, based more on the analysis of signal amplitudes, reveal the highest coherence between the BP_LF and RR_LF intervals and not between the PPG_LF and BP_LF signals, as we a priori expected (Fig. 6, a and b). However, the S index, based on the analysis of instantaneous oscillation phases, demonstrates the highest coherence between PPG_LF and BP_LF (Fig. 6 c). Apparently, this result is due to the fact that PPG is influenced by local regulation processes, which affect the amplitudes more than the phases of the signals. Thus, when studying the processes of autonomic control according to PPG or BP signals, it is possible to recommend the use of methods based on the analysis of instantaneous phases of oscillations.

Interaction between the LF oscillations in RR intervals and PPG (Fig. 6) is a sign of functional integrity of whole cardiovascular autonomic control (14). In our previous work in patients during cardiac surgery under cardiopulmonary bypass (on-pump cardiac surgery), we showed that the coupling from the LF oscillations in PPG to those in RR intervals has probably a neurogenic nature, whereas the coupling in the opposite direction has a hemodynamic nature (because of cardiac output) (34).

The use of a noninvasive BP signal from Finometer for the analysis of phase coherence of its LF component with the processes of HR regulation seems to be promising for solving the problems of medical diagnostics of various circulatory pathologies. However, PPG recording is much more common and easier to use in practice than the BP measurement using Finometer or invasive methods. It represents a convenient and low-cost technology that can be applied to various aspects of cardiovascular monitoring, including the analysis of the processes of autonomic control of blood circulation and local regulatory mechanisms.

Conclusion

To answer the question of how much information the PPG signal contains on the autonomic regulation of BP, a direct comparison of PPG (reflective green light sensor on the distal phalanx of the finger), BP (noninvasively recorded using a Finometer device), and RR intervals was carried out. Coherence and correlation were assessed using the records of healthy subjects.

No correlations in the HF frequency band were found between the studied signals. This is explained by the different mechanisms of conducting the effect of respiration on BP and PPG in the HF band.

We have shown that in the LF band, BP and PPG signals have the same frequency components as the sequence of RR intervals. Because LF oscillations in RR intervals are uniquely associated with the autonomic control processes, LF oscillations in PPG, along with local regulation mechanisms, reflect the processes of autonomic control of blood circulation.

The high coherence of BP and PPG signals in the LF band indicates that the PPG signal can be used instead of BP in the studies of autonomic regulation of BP.

Author contributions

A.S.K., A.S.B., and A.R.K. designed research. A.S.K., E.I.B., and E.A.O. performed research. E.I.B., V.I.P., V.I.G., and B.P.B. contributed analytic tools. A.S.K., E.I.B., and M.A.S. analyzed data. A.S.K., A.S.B., M.D.P., and A.R.K. wrote the article. A.R.K., M.A.S., and V.I.G. conducted experimental research.

Editor: Mark Alber.