Depletion of HP1α alters the mechanical properties of MCF7 nuclei

Abstract

Within the nucleus of the eukaryotic cell, DNA is partitioned into domains of highly condensed, transcriptionally silent heterochromatin and less condensed, transcriptionally active euchromatin. Heterochromatin protein 1α (HP1α) is an architectural protein that establishes and maintains heterochromatin, ensuring genome fidelity and nuclear integrity. Although the mechanical effects of changes in the relative amount of euchromatin and heterochromatin brought about by inhibiting chromatin-modifying enzymes have been studied previously, here we measure how the material properties of the nuclei are modified after the knockdown of HP1α. These studies were inspired by the observation that poorly invasive MCF7 breast cancer cells become more invasive after knockdown of HP1α expression and that, indeed, in many solid tumors the loss of HP1α correlates with the onset of tumor cell invasion. Atomic force microscopy (AFM), optical tweezers (OT), and techniques based on micropipette aspiration (MA) were each used to characterize the mechanical properties of nuclei extracted from HP1α knockdown or matched control MCF7 cells. Using AFM or OT to locally indent nuclei, those extracted from MCF7 HP1α knockdown cells were found to have apparent Young’s moduli that were significantly lower than nuclei from MCF7 control cells, consistent with previous studies that assert heterochromatin plays a major role in governing the mechanical response in such experiments. In contrast, results from pipette-based techniques in the spirit of MA, in which the whole nuclei were deformed and aspirated into a conical pipette, showed considerably less variation between HP1α knockdown and control, consistent with previous studies reporting that it is predominantly the lamins in the nuclear envelope that determine the mechanical response to large whole-cell deformations. The differences in chromatin organization observed by various microscopy techniques between the MCF7 control and HP1α knockdown nuclei correlate well with the results of our measured mechanical responses and our hypotheses regarding their origin.

Significance

Heterochromatin protein 1α (HP1α) is an important architectural protein that functionally organizes the genome by compacting domains of chromatin. Its loss has been shown to increase the invasive potential of malignant cells. This work explores whether depletion of HP1α alters the mechanical properties of nuclei and thus of malignant cells. Probing nuclear mechanics with atomic force microscopy, optical tweezers, and microaspiration of MCF7 breast cancer cells with knockdown of HP1α expression demonstrated quantitative changes in the mechanical properties of the nuclear periphery that correlated with changes in heterochromatin and lamina morphology of these nuclei, as observed with microscopy and biochemical assays.

Introduction

The eukaryotic nucleus is defined by an envelope composed of the outer and inner nuclear membranes. Lining the inner nuclear membrane is the lamina, a proteinaceous layer comprising separate but interconnected intermediate filament networks of A-type lamin (A and C) and B-type lamin (B1 and B2) proteins (1, 2, 3, 4). This barrier houses the genome, in which DNA is wrapped around histone proteins to form chromatin fibers that undergo further levels of folding to create domains of highly condensed, transcriptionally silent heterochromatin and domains of less compact transcriptionally active euchromatin (5,6). This compartmentalization of the genome determines patterns of gene expression and thus cell identity. Heterochromatin protein 1α (HP1α) is an architectural protein that forms and maintains compact domains of heterochromatin by forming multivalent interactions with the chromatin fiber, including the interaction of its chromodomain with di- and trimethylated lysine 9 of histone H3 (H3K9me2/3) (7, 8, 9). HP1α also contributes to the sequestration of heterochromatin at the nuclear periphery through its interactions with proteins embedded in the lamina and nuclear membrane (7,10, 11, 12). This network of interactions between the nuclear envelope, the underlying lamina, and the adjacent heterochromatin ensures both nuclear and genomic integrity (13, 14, 15, 16).

As the largest cellular organelle, the nucleus is also a major physical entity in which the lamina and heterochromatin are key mechanical components (17). An A-type lamin network provides stiffness to the nucleus, whereas B-type lamins have been shown to contribute to nuclear elasticity (18,19). Depletion of lamin A results in a loss of nuclear rigidity (20,21), a reduction of chromatin-lamina attachments, and the loss of peripheral heterochromatin (22,23). In differentiated cells, it is found that the retention of heterochromatin at the nuclear periphery renders the nucleus less malleable, whereas a more diffuse pattern of stem-cell-like heterochromatin increases nuclear plasticity (24,25). Micromanipulation and atomic force microscope studies have increased the understanding of the contribution heterochromatin makes to the mechanical properties of the nucleus. In particular, these previous studies showed that the mechanical properties of the nucleus were influenced by the compaction state of chromatin, and how it dominates local small-strain responses (20,21,26, 27, 28, 29).

The modulation of HP1α expression in malignant breast cell lines indicates that HP1α can suppress the invasive potential of cells (30). Indeed, in the poorly invasive MCF7 breast cancer cell line, constitutive knockdown (KD) of HP1α has been shown to increase the ability of cells to move through a three-dimensional extracellular matrix without affecting cell growth (30). Conversely, introduction of HP1α into the highly invasive MDA-MB-231 breast cancer cell line, with low endogenous levels of HP1α, suppresses their invasive potential in vitro (30). These findings are supported by the correlation of reduced HP1α expression with highly invasive cell lines and the onset of malignant cell invasion in many solid tumors, including those of the thyroid and breast (31, 32, 33). Given the role of HP1α in heterochromatin organization, this raises the possibility that reduction of HP1α aids malignant cell invasion, not only by disrupting gene silencing but also by altering the mechanical properties of the nucleus. We therefore sought to measure these properties in nuclei extracted from MCF7 cells with HP1α KD against a matched control cell line.

Various techniques (34) have been used to characterize the mechanical properties of nuclei in many different cell types, including atomic force microscopy (AFM) indentation (24,35, 36, 37) and micropipette aspiration (MA) (24,25,38, 39, 40). The elastic modulus measured using these techniques typically ranges from 1 to 15 kPa. In this study, we have used a combination of AFM and MA-based micropipette techniques to characterize the mechanical properties of nuclei isolated from MCF7 control and HP1α KD cells, but we have also performed additional experiments using optical tweezers (OT). These OT experiments are indentation experiments carried out in the spirit of AFM, but they are considerably more sensitive and can probe the response of the very outer region of the nuclei, whose response is usually masked by the thermal fluctuations of the AFM cantilever. In addition, in the OT studies, longitudinal indentation (into the top of the surface-bound nucleus) was able to be complemented by a lateral indentation (into the side) of MCF7 nuclei, probing potential anisotropy. Given the small strain exerted in these local indentation experiments the response is expected to be dominated by the underlying peripheral heterochromatin, with the lamina not mechanically engaged (20,21,26, 27, 28, 29). We demonstrate using AFM and OT techniques that HP1α KD decreases the elasticity, at least of the periphery of the nuclei probed by these local, nonaffine deformations, by an order of magnitude as compared with nuclei from MCF7 control cells. In HP1α KD cells, the decrease in elasticity is associated with observed changes to the peripheral heterochromatin and the Lamin A/C network. In contrast, the mechanical properties assessed by micropipettes showed little difference in the deformation of the whole nuclei between HP1α KD and control, implying that reduced HP1α expression does not contribute to a decrease in the overall integrity of the nucleus and that, consistent with previous findings, it is the lamina and not the heterochromatin that dominates the large strain response (26,27,29,41).

Materials and methods

Creation and maintenance of the HP1α knockdown cell line

MCF7 (RRID: CVCL_0031) cells (ATCC, USA) with constitutive KD of HP1α were created using Qiagen SureSilencing shRNA plasmids. Briefly, MCF7 cells were transfected with linearized scrambled or HP1α KD shRNA (shRNA 1–4) plasmids using X-tremeGENE 9 DNA Transfection Reagent (Roche, USA). Transformed cells were selected with 200 μg/mL hygromycin B to obtain a polyclonal population of cells to minimize insertional variation. After determining the level of HP1α KD compared with both MCF7 cells and the scrambled shRNA MCF7 control line, the MCF7 HP1α KD line established with shRNA4 (HP1α KD) was used for this study along with the scrambled shRNA MCF7 control line. The MCF7 HP1α KD and matched control line were maintained in DMEM (Gibco, ThermoFisher Scientific, USA) supplemented with 35 μg/mL hygromycin B (Gibco), 10 μg/mL insulin (Sigma-Aldrich, USA), 1$\text{\%}$ penicillin/streptomycin (Gibco), and 10$\text{\%}$ fetal bovine serum (Gibco) at ${37}^{\circ }\text{C}$ with 5$\text{\%}$ ${\text{CO}}_2$ in a humidified atmosphere.

Antibodies

The primary antibodies used for this study were HP1α (2616; Cell Signaling Technology, USA), histone H3K9me2 (ab1220; Abcam, UK), histone H3K9me3 (ab8898; Abcam), Lamin A/C (ab108595; Abcam), phospho-Lamin A/C Ser22 (PA5-17113; Invitrogen, ThermoFisher Scientific, USA), Lamin B1 (702972; Invitrogen), Lamin B receptor (PA5-66473; Invitrogen), PRR14 (ab174532; Abcam), and α-tubulin (ab4074; Abcam). Secondary antibodies were anti-mouse Alexa 555 (ab150114; Abcam), anti-rabbit Alexa 647 (ab150079; Abcam), HRP-linked anti-mouse (NA931; GE Healthcare, USA), and HRP-linked anti-rabbit (NA934; GE Healthcare).

Immunofluorescence

Asynchronously growing cells adhered to lysine-coated coverslips were washed twice with phosphate-buffered saline (PBS) containing MgCl₂ and CaCl₂, fixed in 4$\text{\%}$ paraformaldehyde/PBS for 15 min at room temperature (RT), and then washed with PBS. Cells were permeabilized (0.5$\text{\%}$Triton X-100, PBS) for 5 min at RT and washed again with PBS before incubation in blocking buffer (PBS, 5$\text{\%}$ bovine serum albumin, 0.5$\text{\%}$ Tween-20) for 30 min at RT. The appropriate primary antibodies (diluted in blocking buffer) were then added to the cells for 16 h at 4°C. After washing (0.1$\text{\%}$ Triton X-100, PBS), cells were incubated with the appropriate Alexa-fluorophore-conjugated secondary antibody, washed again, and stained with DAPI before imaging on either a Leica SP5 DM6000B or Zeiss LSM 900 Scanning Confocal Microscope using an oil-immersion 63× objective lens (NA 1.4). Laser excitation wavelengths and collection ranges appropriate to the fluorophores of each sample were used to detect the emission spectra of the specific combination of DAPI (ex 405 nm, em 410–530 nm) and the secondary antibody Alexa fluorophores; 555 (ex 555 nm, em 565–600 nm) or 647 (ex 647, em 670–720 nm). The z-stacks were collected with a 0.35-μm vertical offset and projected with maximal intensity. All images were digitally processed for presentation and quantification with ImageJ (42). Quantification of fluorescence intensity was performed by plotting the profile of gray color values along a line through a medial optical slice.

Cell fractionation and immunoblot analyses

Adapted from Kapoor et al. (43), cells at 90$\text{\%}$ confluence were harvested, washed in PBS, and resuspended in buffer A (20 mM Tris-HCl pH 7.5, 75 mM KCl, 30 mM ${\text{MgCl}}_2$, 1 mM DTT, 0.5 mM EDTA, 0.5$\text{\%}$ NP40, cOmplete EDTA-free protease inhibitor, Roche) to a concentration of $0.5\text{×}{10}^6$ cells/100 μL and incubated on ice for 10 min with intermittent mixing. An aliquot was removed and retained as the whole-cell lysate fraction. The remaining sample was centrifuged at 7000 × g for 10 min at 4°C, and the supernatant was collected as the cytoplasmic fraction. The remaining pellet was resuspended in buffer A to provide the nuclear fraction. For immunoblot analysis, samples were resolved by 10$\text{\%}$ SDS-PAGE and then transferred to nitrocellulose. The blots were processed as previously described by Tretiakova et al. (31) and visualized using an Azure c600 imaging system (Azure Biosystems, USA).

Scanning electron microscopy

Isolated nuclei adhered to lysine-coated coverslips were fixed in modified Karnovsky’s fixative (3$\text{\%}$ gluteraldehyde (Merck, USA) (v/v), 2$\text{\%}$ formaldehyde (w/v) in 0.1 M phosphate buffer, pH 7.2) for at least 8 h. After rinsing three times in 0.1 M phosphate buffer (pH 7.2), the coverslips were dehydrated in a graded series of aqueous ethanol solutions (25, 50, 75, 95$\text{\%}$) for 15 min each and then in 100$\text{\%}$ ethanol for 1 h. Samples were critical-point-dried using liquid ${\text{CO}}_2$ as the CP fluid and 100$\text{\%}$ ethanol as the intermediary (Polaron E3000 series II critical point drying apparatus). Once dried, samples were mounted on an aluminum stub, sputter-coated with ∼100 nm of gold (BAL-TEC SCD 005 sputter coater) and viewed in a FEI Quanta 200 scanning electron microscope at an accelerating voltage of 20 kV.

Transmission electron microscopy

Cells were harvested at confluence and pelleted at 200 × g for 5 min. The pellet was resuspended in molten low-melting-point agarose and centrifuged at 8000 × g for 1 min to form a cell pellet suspended in agarose. The cells were fixed in modified Karnovsky’s fixative for at least 8 h and washed three times in 0.1 M phosphate buffer (pH 7.2) for 10 min, followed by postfixing in 1$\text{\%}$ osmium tetroxide in 0.1 M phosphate buffer for 1 h. The sample was then washed as described earlier, dehydrated in a series of graded aqueous acetone mixtures (25, 50, 75, 95, 100$\text{\%}$), and infiltrated in an equal mixture of resin and acetone overnight before embedding in 100$\text{\%}$ epoxy resin (Procure 812; ProSciTech, Australia). The resin was replaced another three times for 8 h or overnight before the epoxy resin was cured at 60°C for 48 h. The embedded samples were cut to 100 nm using a diamond knife (Diatome, Switzerland) on a Leica EM UC7 ultra-microtome (Leica Biosystems, Germany). These cuts were then stretched with chloroform vapor and mounted on grids using a Quick Coat G pen (Daido Sangyo, Japan). The grids were stained with saturated uranyl acetate in 50$\text{\%}$ and lead citrate. Samples were then examined with an FEI Technai G2 Spirit BioTWIN transmission electron microscope (Czech Republic).

Isolation of nuclei for biophysical analyses

Asynchronously growing MCF7 cells were harvested at confluence, washed twice with PBS, and then resuspended in ice-cold nuclei extraction buffer (320 mM sucrose, 10 mM HEPES, 5 mM ${\text{MgCl}}_2$, 1$\text{\%}$ Triton X-100, pH 7.4) at a concentration of $1\text{×}{10}^6$ cells/mL and vortexed gently for 10 s. The cells were incubated on ice for 15 min, vortexed briefly every 5 min, and then centrifuged at 2000 × g for 5 min at 4°C. The nuclear pellet was resuspended in nuclear wash buffer (320 mM sucrose, 10 mM HEPES, 5 mM ${\text{MgCl}}_2$, pH 7.4), and the nuclei were then processed further as required.

Biophysical techniques

AFM, OT, and micropipetting-based experiments were used to quantify the material properties of nuclei isolated from MCF7 control and HP1αKD cells. The material properties of these nuclei were compared using the two-sample t-test, and the p-values used to determine the statistical significance of differences are reported in the figure captions or elsewhere in the article. Wilcoxon signed-rank tests (applied for unequal variances) were also used for OT and AFM data sets; however, the p-values were similar to those obtained using a two-sample t-test.

AFM setup

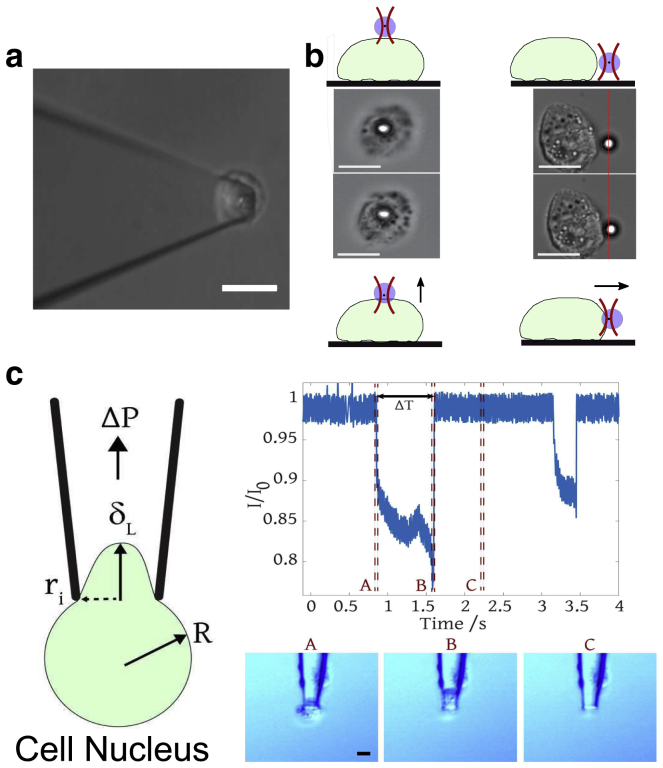
AFM measurements were performed using a JPK Nanowizard II (JPK Instruments, Bruker) mounted on an inverted fluorescent optical microscope (LSM 710; Zeiss). The microscope was equipped with a double illumination optical setup, which enables illumination of the top and bottom of the sample at the same time. This allows observation of nuclei in a high-contrast mode under top illumination while being able to observe the nuclei and the colloidal probe hidden under the cantilever from the bottom (44,45), enabling accurate positioning of the colloidal probe above the center of the nucleus (Fig. 1 a). Indentation measurements were performed using PNP-TR-TL 200-μm-long cantilevers ($f_0$ $\sim$ 17 kHz) (NanoWorld) with ${\text{SiO}}_2$ spheres of 2 μm in diameter (Polysciences AG) mounted using a two component epoxy glue (UHU Schnellfest, UHU). A spherical bead was used here instead of a sharp tip to average over a larger surface area with a well-defined contact geometry. The sample was placed in a petri dish with the culture media and mounted on the temperature-controlled AFM stage. The cantilever was first positioned above the cell surface using a mechanical XY stage, and then the position was further adjusted using an XY piezo stage operated using a manipulation control option in the contact mode. Once positioned, illumination was switched off to minimize temperature fluctuations. The force measurements were performed at three values of force set point, 300, 500, and 1000 pN, and the cantilever travel speed was 0.5 μm/s operated in the closed loop mode to minimize hydrodynamic contributions (46). The cantilever spring constant was calibrated using the thermal fluctuation method (47). The typical values of spring constant were 0.04 N/m. The force data were preprocessed using JPK software to perform baseline subtraction. Indentation force (F) and depth (D) data were then exported and fitted using MATLAB (R2016) (The MathWorks, Natick, MA) to obtain an apparent Young’s modulus (E). The Young’s modulus was determined using the classical Hertz contact model (48).

$$F=\frac{4}{3}\frac{E}{\left(1-{\nu }^2\right)}\sqrt{R{D}^3},$$ (1)

where R is the radius of the spherical bead, v is the Poisson ratio (v = 0.4) (49), and E is the apparent Young’s modulus. This model, which describes indentation of elastic solid objects by a spherical indentor, has been widely used to determine elasticity in cell mechanics studies (49, 50, 51).

Figure 1.

Techniques used to probe nuclei. (a) AFM indentation: cantilever with a bead attached at the tip for probing the nuclei is shown. Scale bars, 10 μm. (b) OT setup: a nucleus is either moved toward the trapped bead longitudinally (from the top) or laterally (from the side), producing an indentation on the nuclei. The schematic of the experimental procedure shows the bead deflection. Scale bars, 5 μm. (c) Microaspiration experiments and analysis are shown. (Left image) Schematic of the deformation parameters used for the solid elastic model is shown (see text for definitions). (Right image) Example of an experimental current trace showing two aspiration events, and (bottom right) the corresponding video frames for the first event where frame A is the first frame of aspiration, frame B is the last frame of aspiration, and frame C is when no aspiration is occurring. Scale bars, 5 μm. To see this figure in color, go online.

OT setup

Indentation experiments were carried out using an inverted microscope (Nikon Eclipse TE2000-U) with a 60× 1.2 NA (Nikon, Plan Apo VC 60× WI) water immersion objective lens and a CCD camera (Andor Neo) to image and track beads. An Nd:Yag Laser (Spectra Physics) of power 1 W at the laser head and a wavelength of 1064 nm was used to trap beads. A 2.5-mW probe laser (S1-FC-675; Thorlabs), which is placed along the same beam path and focused at a quadrant photodiode (QPD) using the back focal plane of the condenser was used to detect the translations of a bead in a trap via a change in the interference pattern on the QPD. A piezo electric stage (PI P-517.3CD) was used to control precise stage displacement $\left(SD\right)$. Measurements were conducted at an ambient RT of T = 20°C. A sample chamber consisting of a polylysine-coated coverslip and a welled microscope slide was prepared and filled with the loading medium and 2-μm-diameter polystyrene beads (Poly Sciences Polystyrene 2.6$\text{\%}$ Solids latex, 0.001$\text{\%}$ suspension).

MCF7 nuclei were allowed to settle on the polylysine-coated coverslip, which was subsequently mounted on the piezo stage. Nuclei were laterally and longitudinally moved toward, and then into, an optically trapped bead, as shown in the Videos S1 and S2. As the nucleus is indented, the bead becomes displaced away from its equilibrium position within the optical trap (Fig. 1 b). This bead displacement $\left(BD\right)$ is recorded using a probe laser and QPD and using an image analysis methodology simultaneously. For the QPD data, bead displacement is indicated by a shift of an interference pattern generated by a probe laser passing through the bead on the QPD. This effect is registered as varying voltages from each quadrant of the photodiode. The displacement is also tracked using changes on the standard deviation of the pixel intensity values from images in the region of interest around the particle. The conversion from standard deviation values to displacement was obtained by imaging a bead that was bound to a coverslip and moving the bead in the z-direction through the probe laser with a 4-μm sinusoidal wave (Fig. S1) via a piezo stage and monitoring the standard deviation of the image. The QPD was also used to detect displacements perpendicular to the surface. However, as the probe laser passes through the nuclei in this arrangement, the interference pattern on the QPD can be unduly affected by the presence of nuclei. Although in this arrangement the QPD signal was nosier than that obtained from image analysis, as a consequence of this, the absolute bead deflection measured was similar in both cases. The total displacement of the bead when indenting nuclei from the top is a combination of both longitudinal (perpendicular to the surface) and lateral (parallel to the surface) components of displacement. Hence, monitoring both the components gives the total force exerted on the bead by the nuclei, which gives more accurate force measurements (Fig. S2).

Video S1

Longitudinalindentation, from the top

The trap stiffness was calibrated in situ by recording the power spectrum of the diffusion of a bead within the trap and then applying the equipartition theorem. The laser power was fixed to 1 W at the source. The longitudinal spring constant obtained for this laser power was 28 pN/μm, whereas the lateral spring constant (the trap strength resisting motion parallel to the surface, perpendicular to the direction of the propagation of the laser) was found to be 48 pN/μm for the same laser power, similar to that found in previous measurements (52).

The apparent Young’s modulus (E) was obtained from $F-D$ measurements by using the Hertz contact model, as in the AFM experiments. However, owing to the considerably lower magnitude and range of forces applied in the OT experiment, which limits the exploration of the control variable space, fitting to the full functional form was not carried out in this case. Instead, an analysis procedure inspired by the work of Guz et al. (50) and Bacabac et al. (53) was used. In this methodology, the indentation depth is written as a constant common indentation depth $\left(D_o\right)$ plus a small varying indentation, and Eq. 1 is expanded as a Taylor series around $D_o$. Retaining only the first order term yields

$$E=\frac{3\left(1-{\nu }^2\right)}{4\sqrt{D_{o}R}}S.$$ (2)

In this work, the bead radius was $R=1$ μm; the Poisson ratio, ν, was 0.4 (49); and $D_o$ was pragmatically set to 50 nm for each case (corresponding to a difference between the applied stage movement and indentor response of $\ge$ 10 nm, as shown in Fig. 7 a), allowing the comparison of the moduli from different samples. $S=\frac{dF}{dD}$ can be extracted from a simple linear fit to the selected region of the experimental $F-D$ curve. It is worth noting that this chosen interval remained within the region of the linear relation between $SD$ and D. Analyses were performed using MATLAB (R2016).

Figure 7.

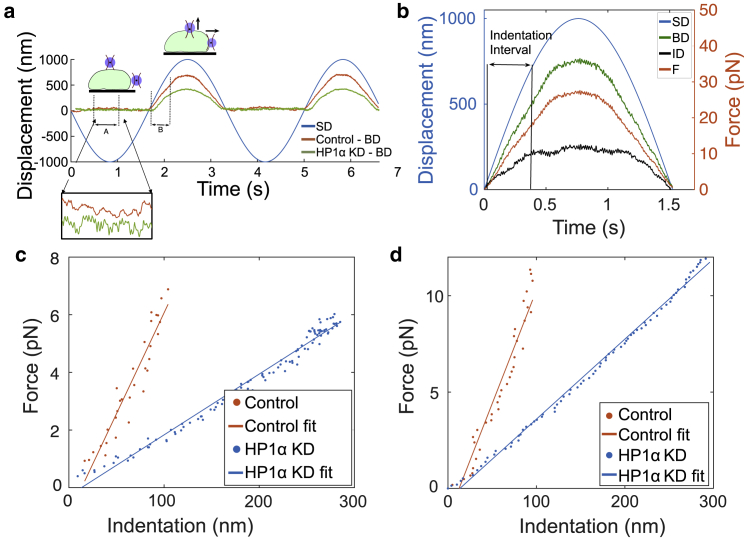
OT Indentation experiments. (a) Stage and bead displacements: $SD$ is represented by the blue curve. MCF7 control and HP1α KD nuclei $BD$ are represented by red and green curves, respectively. Trap stiffness is calculated from interval A, in which the bead is freely diffusing in the optical trap. The indentation D on the nuclei is extracted from interval B. (b) This figure represents the measured $BD$ (green), calculated F (red), and D (black) during the indentation interval, when the bead interacts with MCF7 control and HP1αKD nuclei, respectively. (c) $F-D$ curves extracted from the indentation interval for longitudinal indentation (from the top). (d) $F-D$ curves extracted from the indentation interval for lateral Indentation (from the side). To see this figure in color, go online.

Micropipetting experiments

Micropipettes were fabricated from borosilicate glass capillaries (QF-100-50-7.5; Sutter Instruments) using a ${\text{CO}}_2$ laser pipette puller (P-2000; Sutter Instruments). The micropipettes had an inner diameter of (6.5 $\pm$ 0.5) μm. To reduce adhesion, each pipette was immersed in a silanizing agent (Sigmacote; Sigma-Aldrich) for 1–2 s and left to air dry overnight to form a uniform surface coating at the tip.

The micropipetting instrumentation, shown in Fig. 1 c, has been previously described in (54,55). During an experiment, a micropipette was backfilled (56) and immersed in an electrolyte bath filled with 3 mL 1$\times$ PBS. Once the pipette was affixed in place, 50 μL of a solution containing nuclei isolated from MCF7 cells was transferred to the electrolyte bath near the pipette tip. To begin each experiment, a potential of 0.1 V and suction pressure $\left(\text{Δ}P\right)$ of 25–200 mbar (2.5–20 kPa) was applied using the electrometer and pressure pump, respectively. An electrical current between the electrodes (I) was recorded simultaneously with an optical microscopy video focused on the pipette tip (Fig. 1 c (top-right image)). In this study, aspiration events differed from conventional MA experiments because each event consisted of a MCF7 cell nucleus being deformed and additionally completely drawn through the pipette tip. Each experiment was run for 60–90 s, during which multiple events were captured. The micropipette was replaced between experimental runs when it became obstructed or clogged. It was of interest to measure the duration of each aspiration event. The electrical data were used for this because electrical signals were sampled at 300 Hz, whereas optical microscopy videos were captured at 24 frames per second. The electrical current decreases as a nucleus enters the tip and recovers when the nucleus traverses the tip, clearing the ionic transport pathway. Aspiration event times (T) were typically 0.5–2 s.

Two models based on previous analyses carried out in more conventional MA experiments were adopted to quantify cell nucleus mechanics. In both cases, we refer to derived mechanical properties as “effective” due to the modeling assumptions applied. The first assumes that the deformed particle is an incompressible, elastic solid (57,58). This modified model has been detailed in (55) and relies solely on optical microscopy. When a nucleus starts to be aspirated, it undergoes an initial elastic deformation, as shown in Fig. 1 c (left image). Here, R is the radius of the cell nucleus outside of the pipette, $r_i$ is the pipette opening radius, ${\delta }_L$ is the initial aspirated length, and $\text{Δ}P$ is the pressure applied. ${\delta }_L$ is measured from optical microscopy using the first video frame in which the nucleus is aspirated into the micropipette tip (e.g., Fig. 1 c (bottom-right image)). The effective elastic modulus $\left(E^{\prime }\right)$ deduced using this model is

$$E^{\prime }=\frac{r_i\text{Δ}P}{{\delta }_L}.$$ (3)

The second model is based on those developed for viscoelastic particles (58), but data analysis is customized for full aspiration of particles into a conical pipette, as described previously (54). Although conventional MA often uses optical microscopy data to analyze the total aspirated length (L) as a function of time, here only the event duration ($\text{Δ}$T) is used. This is obtained from the electrical signal (Fig. 1 c (top-right image)), which has better resolution than optical data (Fig. S3). At the start of an experiment a baseline current $\left(I_0\right)$ is established and measured. $\text{Δ}T$ is defined as the time it takes for the nucleus to pass through the pipette tip constriction, measured as the time during which $I<0.95I_0$. Using the geometry of the pipette tip and the cell nucleus, a velocity for aspiration (u) can be estimated. The critical pressure required for aspiration to start, related to the surface tension of the cell nucleus, is assumed negligible compared with $\text{Δ}P$, and friction is also neglected in this analysis. The effective viscosity $\left({\eta }^{\prime }\right)$ of the nucleus is

$${\eta }^{\prime }=\frac{r_i\text{Δ}P}{3\pi u}.$$ (4)

The viscous and elastic regimes are separated by a constant stress relaxation time (τ), and an effective elastic modulus $\left(E^{\prime }\right)$ obtained using this second model is

$$E^{\prime }=\frac{3\pi \eta }{\tau }.$$ (5)

The value $\tau =0.3$ s was used for MCF7 nuclei, assumed to be the same as for MCF7 cells (59). For this model, the corresponding video frames (Fig. 1 c (bottom-right image)) are used to verify the timing of each aspiration event. Analyses were performed using MATLAB (R2016).

Results and discussion

HP1α knockdown alters heterochromatin organization

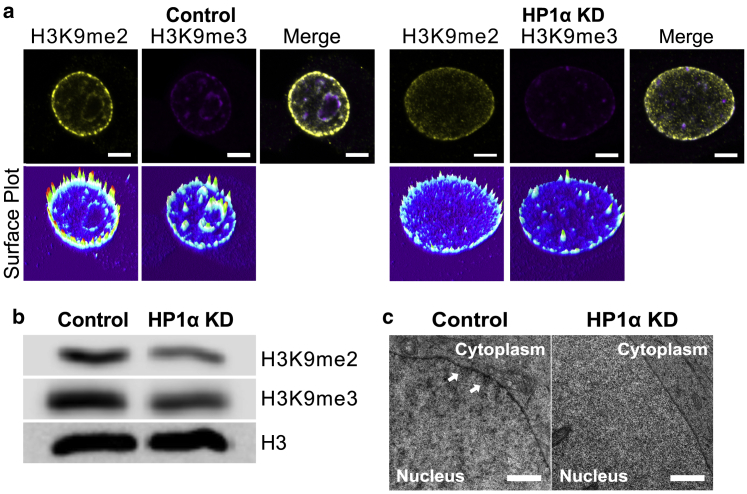
To explore whether the reduction of HP1α alters the biophysical and biological properties of nuclei, MCF7 cells with constitutive KD of HP1α and a matched MCF7 control line were established. The reduction in HP1α expression in the MCF7 cells was confirmed by immunoblotting and immunofluorescence microscopy using an antibody directed against HP1α. Fig. 2 a shows a reduction in the level of protein expression compared with the control cells, which have distinct HP1α foci that are not present in the nuclei of the HP1α KD cells (Fig. 2 b). Interestingly, when these cells are growing in two-dimensional culture, the shape of their nuclei differs. The nuclei, represented by DAPI-stained genomic DNA, appear to be rounder in the MCF7 control cells and flatter in the HP1α KD cells, although there was no significant difference in the volumes of these nuclei (Fig. S4).

Figure 2.

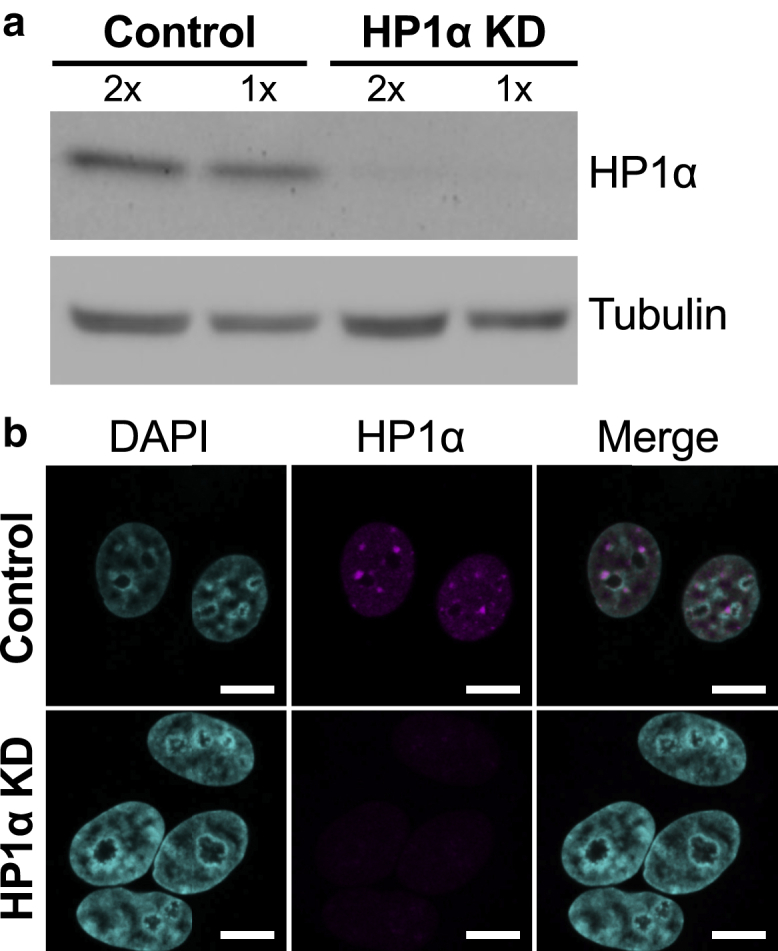
Level of HP1α protein in MCF7 cells with constitutive HP1α KD. (a) Immunoblot showing HP1α expression in MCF7 cells that constitutively express either an HP1α shRNA or the matched scrambled shRNA control. Increasing amounts of total cell lysates, (1×) 25 μg and (2×) 50 μg, are loaded. The immunoblot was stained with antibodies against HP1α and α-tubulin as a loading control. (b) Immunofluorescence confocal microscopy images of MCF7 control (top panel) and MCF7 HP1α KD (bottom panel) cells stained with DAPI to detect DNA (cyan) and an antibody directed against HP1α (magenta) are shown. Scale bars, 20 μm. To see this figure in color, go online.

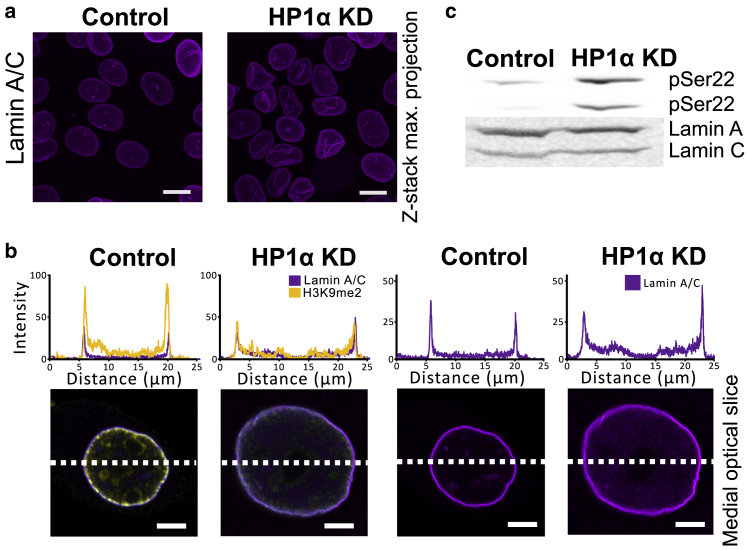
Because heterochromatin domains are marked by H3K9me2 and H3K9me3, to determine whether the reduction of HP1α disrupts heterochromatin organization, the level and localization of these heterochromatin marked domains was analyzed by confocal immunofluorescence microscopy. Medial optical slices through the nuclei show a general reduction in both H3K9me2- and H3K9me3-marked heterochromatin, including the lamina-associated domains enriched in H3K9me2 (6,60), in nuclei lacking HP1α (Fig. 3 a), which agrees with the observed global reduction in the level of H3K9me2 and H3K9me3 in these cells compared with the control cells (Fig. 3 b). These differences are also reflected in electron micrographs that show MCF7 control cells have characteristic electron-dense regions of heterochromatin and lighter regions of euchromatin, whereas the pattern of chromatin appears more homogeneous in the HP1α KD cells (Fig. 3 c). To determine whether the reduction of H3K9me2-enriched lamina-associated heterochromatin upon HP1α KD interferes with the integrity of the nuclear lamina, the individual lamin networks were visualized by immunofluorescence confocal microscopy. The morphology of the Lamin A/C network generally appears more crumpled in the HP1α KD cells compared with those of the MCF7 control cells (Fig. 4 a). Medial optical slices through the nucleus show the Lamin A/C layer overlaps the H3K9me2-enriched domains at the nuclear periphery in the control cells as demonstrated by the line plots (Fig. 4 b). Interestingly, more Lamin A/C appears to be located within the interior of the nuclei MCF7 cells with HP1α KD (Fig. 4 b), indicating an increase in the soluble pool of Lamin A/C within the nucleus of these cells. This is supported by the demonstration that the level of Lamin A/C phosphorylated on serine 22, which is associated with nucleoplasm localized Lamin A/C during interphase (61), is higher in cell lysates prepared from HP1α KD cells than control cells (Fig. 4 c).

Figure 3.

Knockdown of HP1α disrupts heterochromatin organization in MCF7 cells. (a) Representative immunofluorescence confocal microscopy images of MCF7 control (left panel) and MCF7 HP1α KD cells (right panel) stained with antibodies against markers of heterochromatin, dimethylation of lysine 9 on histone H3 (H3K9me2) (yellow), and trimethylation of lysine 9 on histone H3 (H3K9me3) (magenta) are shown. Fluorescence surface plots of the medial slices through the nuclei (above) demonstrate the intensity of antibody staining. Scale bars, 5 μm. Additional images of cells are presented in Fig. S5. (b) Immunoblot analysis of extracted histones from MCF7 control and HP1α KD cells probed with antibodies against H3K9me2 and H3K9me3. An antibody against histone H3 is used as a loading control. (c) Representative electron micrographs showing regions of compact heterochromatin at the nuclear periphery in MCF7 control cells (white arrows), whereas the nuclei of MCF7 HP1αKD cells have a more diffuse chromatin patterning. Scale bars, 500 nm. To see this figure in color, go online.

Figure 4.

Knockdown of HP1α alters the lamin A/C network. (a) Representative confocal microscopy images of z-stack maximal intensity projections of MCF7 control and MCF7 HP1α KD cells probed with an antibody against Lamin A/C are shown. Scale bars, 20 μm. (b) Representative confocal microscopy medial sections of individual nuclei from MCF7 control and MCF7 HP1α KD cells stained with antibodies against Lamin A/C and H3K9me2 are shown. Top panel: medial slice showing Lamin A/C (magenta) alone. Bottom panel: Lamin A/C (magenta) overlaid with H3K9me2 (yellow) is shown. Above each medial slice are line plot profiles of fluorescent intensity (percentage of gray value saturation). Scale bars, 5 μm. Additional images of cells are presented in Figs. S6 and S7. (c) Whole-cell lysates from an equal number of MCF7 control or HP1α KD cells were analyzed by immunoblotting with an antibody against Lamin A/C phosphorylated on serine 22 (top panel) and Lamin A/C (bottom panel). To see this figure in color, go online.

In contrast to the Lamin A/C layer, the distribution of Lamin B1 appears to be comparable between the MCF7 cells and HP1α KD (Fig. 5 a), with minimal disruption to the morphology of the Lamin B1 layer (Fig. 5 b). To determine whether lamin expression is altered in cells with reduced HP1α, cell fractions were prepared from MCF7 control and HP1α KD cells. Fig. 5 c shows there is no change in the expression of Lamin A/C or B1 with HP1α KD, nor is there a difference in the amount of each lamin present in the nuclear fraction. However, there is an increase in the expression of the Lamin B receptor, which is embedded in the nuclear lamina/inner nuclear membrane and interacts with HP1α and the adjacent chromatin (Fig. S9). Expression of PRR14, another embedded protein known to interact with HP1α, is relatively unchanged, suggesting there may be subtle changes to the composition proteins embedded in the lamina/inner nuclear membrane with HP1α KD (10, 11, 12,23).

Figure 5.

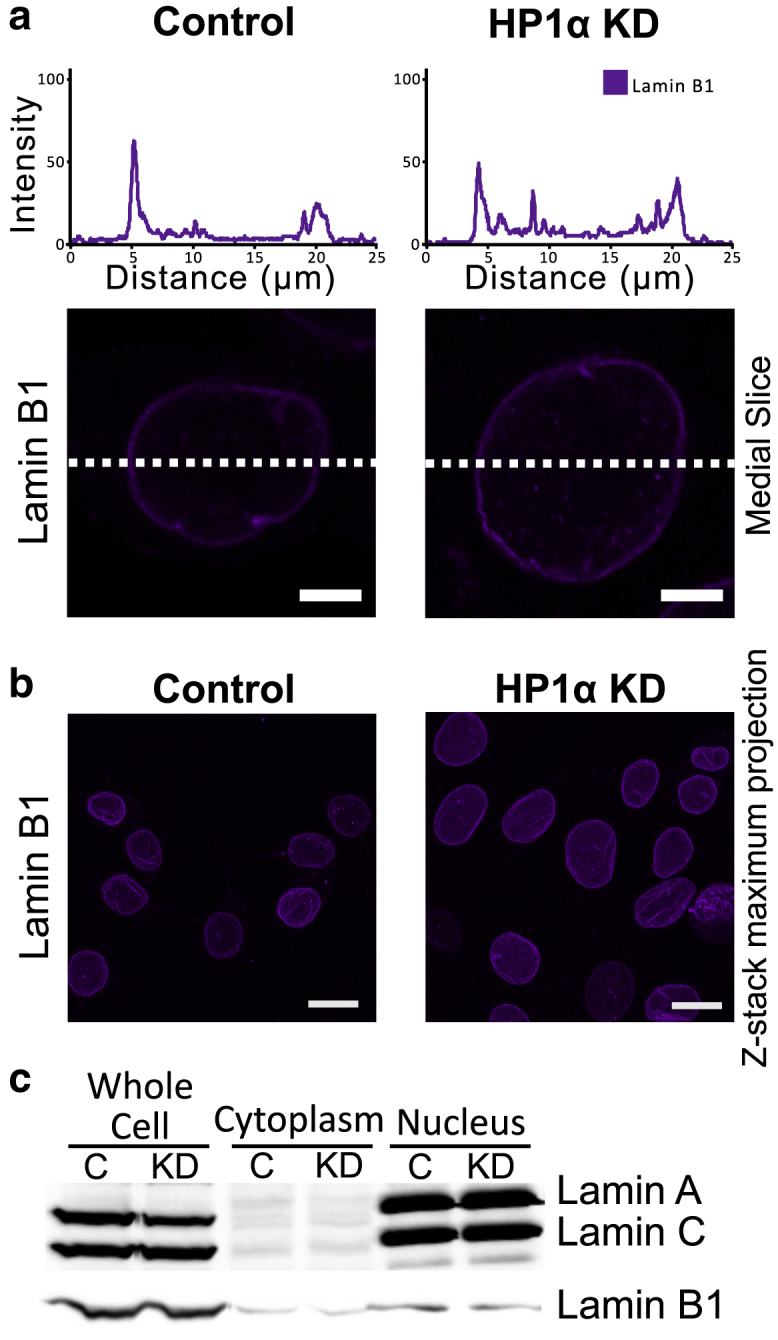
The Lamin B1 network is not disrupted by knockdown of HP1α. (a) Representative medial slice from confocal microscopy images of MCF7 control and MCF7 HP1α KD cells probed with an antibody against Lamin B1 is shown. Above each medial slice are line plot profiles of fluorescent intensity (percentage of gray value saturation). Scale bars, 5 μm. Additional images of cells are presented in Fig. S8. (b) Representative confocal microscopy images of z-stack maximal intensity projection from MCF7 control and MCF7 HP1α KD cells probed with an antibody against Lamin B1 are shown. Scale bars, 20 μm. (c) Whole and fractionated cell lysates from an equal number of MCF7 control or HP1α KD cells were analyzed by immunoblotting with an antibody against Lamin A/C (top panel) and Lamin B1 (bottom panel). To see this figure in color, go online.

In summary, reduction of HP1α alters heterochromatin organization. The apparent changes to the lamin-associated heterochromatin marked by H3K9me2 likely reflect a decrease in the tethering of heterochromatin to the nuclear envelope/lamina due to loss of the interaction of HP1α with Lamin B receptor and PRR14 (10, 11, 12,23). Interestingly, a disruption to the nuclear lamina was not observed in previous studies when the overall level of heterochromatin was reduced through the expression of HMGN5 or treatment with HDAC inhibitors (20,26), whereas loss of HP1α does appear to be influencing the integrity of the Lamin A/C layer. Although lamin expression is unchanged, reduction of HP1α, given its role in gene silencing, could be disrupting the lamina by altering the activity of pathways that regulate Lamin A/C dynamics, which is suggested by the increase in phosphorylated Lamin A/C. However, reduced tethering of peripheral heterochromatin to the nuclear lamina could also be contributing by distorting the postmitotic assembly of the lamina and nuclear envelope (62,63).

HP1α knockdown results in softer nuclei as determined by AFM force measurements

To determine whether these changes in the HP1α KD cells alter the malleability of the nuclear periphery, nuclei were isolated from the MCF7 cell lines for the mechanical measurements. The integrity of the isolated nuclei was confirmed using SEM, as shown in Fig. 6 a; the extraction procedure resulted in nuclei with little associated debris.

Figure 6.

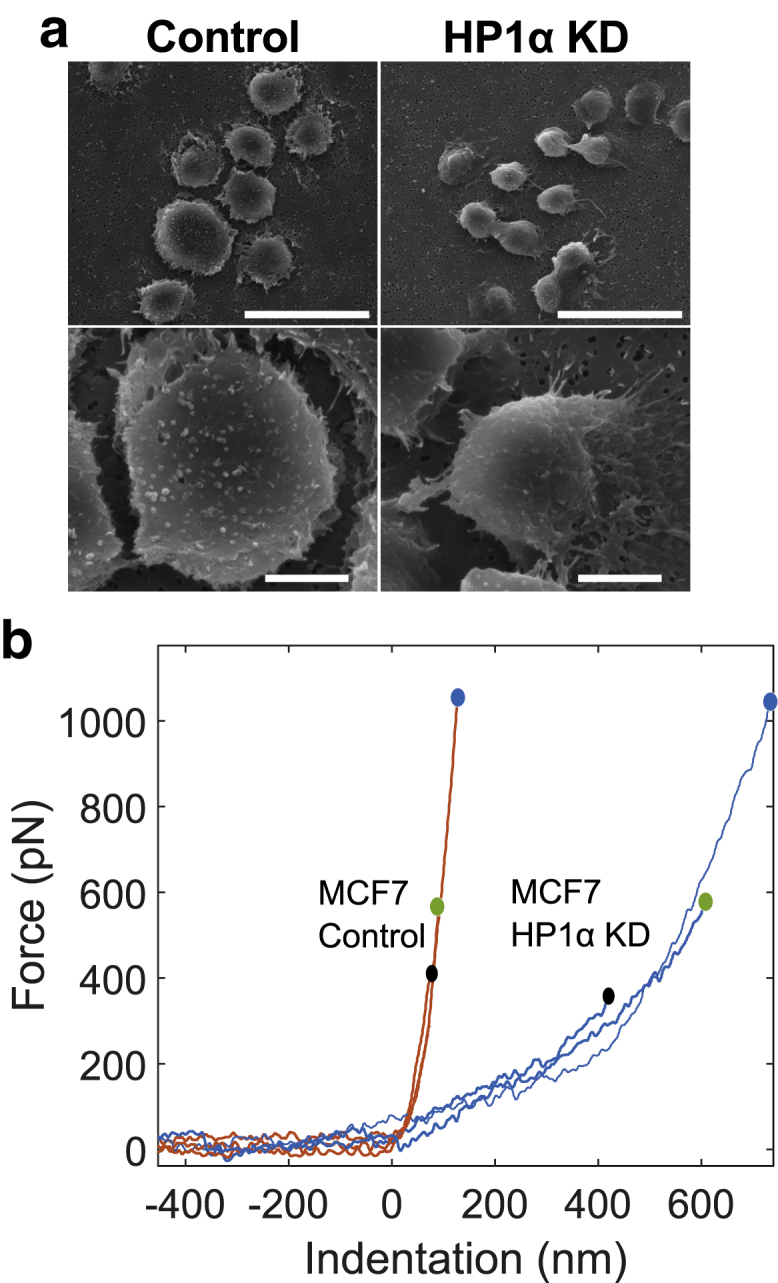
(a) Representative scanning electron micrographs of nuclei isolated from MCF7 control and MCF7 HP1α KD cells are shown. Scale bars, (top panel) 30 μm and (bottom panel) 5 μm. (b) AFM indentation: three sweeps were applied between zero and maximal forces of 300 pN (black circle), 500 pN (green circle), and 1000 pN (blue circle) on MCF7 control and HP1α KD nuclei. The Hertzian fit to the $F-D$ curves is shown in Fig. S10. To see this figure in color, go online.

Fig. 6b shows results obtained using AFM. Nuclei were indented at a constant rate of 0.5 μm/s, and three sweeps were performed between zero and maximal forces of 300 pN (black circle), 500 pN (green circle), and 1 nN (blue circle). The indentation and the retraction curves were similar, suggesting that the response was highly reversible and hence can be considered to be consistent with largely elastic behavior. A clear difference can be observed in the $F-D$ curve recorded for the control and for the HP1α KD nuclei. The magnitude of the indentation for HP1α KD nuclei is about an order of magnitude higher than for control nuclei, signifying that the HP1α KD nuclei are comparatively softer in response to this type of local deformation.

Indentations performed by higher nanonewton-scale forces are likely to induce damage and may have an effect on the measured modulus and were not pursued. Measuring forces below ∼$30$ pN was not possible in these AFM experiments because of the thermal fluctuations of the AFM cantilever in liquid setting a limit below which applied forces could not be measured and the absolute indentation becomes impossible to assess. To have an absolute estimate of indentation and modulus at forces below 30 pN, OT were implemented.

HP1α knockdown results in softer nuclei as determined by OT

To measure deformations at low forces, OT were used to perform indentation by laterally (from the side, parallel to the surface) and longitudinally (from the top, perpendicular to the surface, as in an AFM experiment) moving the MCF7 nuclei against optically trapped microbeads and measuring the $BD$ as shown in Fig. 7 a. When the trapped bead is pushed into the nuclei, the apparent Young’s modulus can be estimated using the Hertzian contact model as described in Materials and methods. The same size bead (2-μm diameter) and the same deformation rate (0.5 μm/s) as applied in the AFM measurements were used in order for the experiments to be as comparable as possible. It should be noted however that, owing to the extreme sensitivity of the OT, experimental data will be obtained in a regime in which the AFM experiment would be unable to determine whether contact has yet been made and, owing to this a large offset, is expected in the putative zero displacement point in the two experiments.

Fig. 7a shows the sweeping, sinusoidal movement of the stage during experiments. The trap stiffness is measured in situ during the first half of the sinusoidal period, when the nucleus is far away from the optically trapped particle and the bead is diffusing in the trap. This is shown in the inset for the interval A in Fig. 7 a. The interaction between a single nucleus and a bead is observed in the second half of each sinusoid, whereupon the nucleus is driven into the optically trapped bead. $BD$ is measured as described in the Materials and methods. Once the trap stiffness (k) and $BD$ are known, Hooke’s law is used to estimate the restoring force (F) generated $\left(F=-kBD\right)$. When the nucleus comes into contact with the bead and begins to push it, $BD$ increases in the same direction as $SD$. The difference between the displacement of the stage (and thus nucleus) and the resultant displacement of the trapped bead gives the indentation depth $\left(D=SD-BD\right)$. Region B in Fig. 7 a represents D, where the linear region is used to estimate the elastic modulus as described in Materials and methods.

To investigate potential anisotropy in the mechanical properties of the nuclear periphery, nuclei were indented both laterally and longitudinally in relation to the surface. Nuclei having a semispherical shape (as opposed to being substantially spread on the surface to which they are attached) are able to be indented laterally, as shown in Fig. 1 b. This lateral indentation avoids potential laser-induced local heating that is present for longitudinal indentation, when the laser passes through the nuclei (64).

From the temporal sequences for the indentation intervals shown in Fig. 7 b (control nuclei—longitudinal indentation), $F-D$ curves similar to AFM were obtained (compare Fig. 7, c and d, with Fig. 6 b). Fig. S11 shows the temporal sequences for the indentation intervals for longitudinal (from the top) (HP1αKD nuclei) and lateral (from the side) (control and HP1αKD nuclei) indentations. Consistent with the AFM experiments, the MCF7 nuclei with HP1α KD have greater indentation compared with the control nuclei for the same applied force. The slope of the $F-D$ plot is used to estimate Young’s modulus using Eq. 2. Using the OT method, we can clearly distinguish forces as low as 1 pN, which allows a more accurate estimate of mechanical properties in the range from 1 to 10 pN in comparison with AFM experiments. Table 1 gives the maximal indentation for both types of nucleus, obtained using lateral and longitudinal indentation methods (uncertainty indicates standard deviations). The average indentation for the two indentation methods is similar, giving confidence in both methods and showing that there is probably little effect of any anisotropy in this setting. The periphery of the MCF7 control nuclei have smaller indentations compared with HP1α KD nuclei, suggesting that reduced expression of HP1α makes the nuclei softer to local low-strain indentations.

Table 1.

Maximal indentation

Method of indentation	Control nuclei	HP1α KD
Longitudinal (nm)	105 $\pm$ 31	359 $\pm$ 137
Lateral (nm)	123 $\pm$ 61	351 $\pm$ 79

Whole-cell results reflect those obtained on isolated nuclei

Along with probing isolated MCF7 nuclei, mechanical measurements of whole MCF7 cells were carried out using OT for both control and HP1α KD. The apparent Young’s modulus distributions, as shown in Fig. S13, confirm that the whole cells are affected by the KD in a similar way to the isolated nuclei. As expected, the whole HP1α KD cells show a slightly higher modulus ((64 $\pm$ 3) Pa) as compared with those of isolated nuclei (longitudinal (54 $\pm$ 5) Pa, lateral (40 $\pm$ 3) Pa), most likely owing to the properties of the cytoskeleton (Fig. S4 b (top)) above the nucleus in both control and HP1α KD cells. Here, uncertainties indicate standard errors in the mean. A lateral view projection of z-stack images of the cell obtained from confocal microscopy (Fig. S4 b (bottom)) show that although nuclei (cyan) are by far the largest organelle in MCF7 cells, there is indeed a small layer of cytoskeleton between the nuclei and cell membrane.

Comparison of elastic modulus using OT and AFM

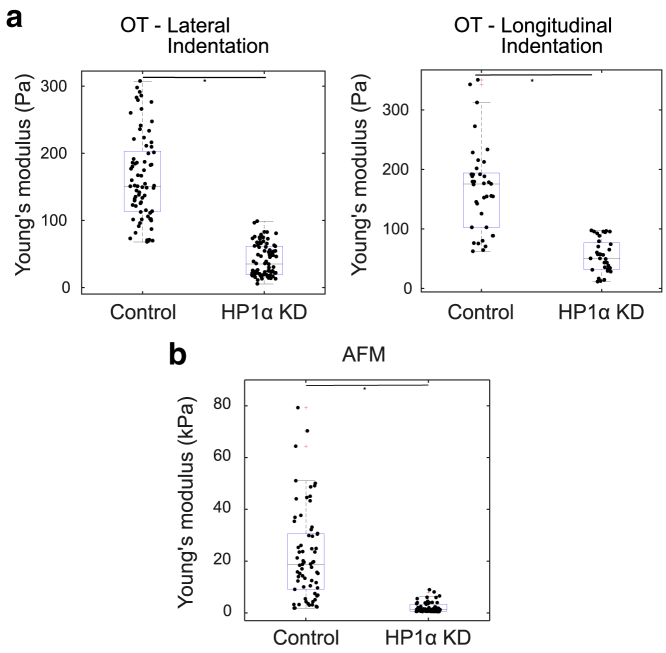
The distributions of repeated elastic modulus measurements for the MCF7 control and HP1α KD nuclei obtained using AFM and OT are shown in Fig. 8 in box plot distributions. For OT (lateral indentation), experiments were carried out on 22 nuclei (control) and 19 nuclei (HP1α KD) (Fig. 8 a (left image)). For OT (longitudinal indentation), experiments were carried out on 12 nuclei (control) and 10 nuclei (HP1α KD) (Fig. 8 a (right image)). For AFM, experiments were conducted on 17 nuclei from both MCF7 control and HP1α KD nuclei. Three to four $F-D$ curves per nuclei were collected (total number of $F-D$ curves denoted by n in Fig. 8). A difference in the elastic modulus of the nuclear periphery between control and HP1α KD can be observed using either AFM or OT (p < 0.0001). Fig. 8 b shows the Young’s modulus obtained for a maximal force of 0.5 nN. Similar AFM experiments were carried out for a maximal force of 0.3 and 1 nN (Fig. S12). These results are consistent with previous studies on differences of nuclei mechanics extracted from benign (MCF-10A) and malignant (MCF-7) cells (36).

Figure 8.

Comparison of elastic modulus using OT and AFM. Box plot representation of Young’s modulus values measured using OT and AFM (^∗p < 0.0001, two-sample t-test and Wilcoxon signed-rank test (a) Young’s modulus obtained for lateral (from the side) and longitudinal (from the top) indentation using OT (n = 73 (control - lateral indentation), 64 (HP1α KD - lateral indentation), 38 (control - longitudinal indentation), 32 (HP1α KD - longitudinal indentation)) is shown. (b) Young’s modulus obtained using AFM data for a maximal force of 0.5 nN [n = 67 (control), 64 (HP1α KD)] is shown. The n indicates total number of indentations (3–4 curves per nuclei) in each condition pooled from multiple cell passages. To see this figure in color, go online.

The apparent Young’s moduli measured for the control nuclei have a larger spread of values, signifying that the structure of the MCF7 control nuclei are more mechanically heterogeneous in nature compared with the HP1α KD. For the same loading rate (0.5 μm/s), the apparent elastic moduli determined using OT ((164 $\pm$ 8) Pa (lateral) and (168 $\pm$ 12) Pa (longitudinal) for the control, (40 $\pm$ 3) Pa (lateral) and (54 $\pm$ 5) Pa (longitudinal) for the HP1αKD) are much smaller than AFM values ((22.23 $\pm$ 2.12) kPa for the control, (2.13 $\pm$ 0.24) kPa for the HP1αKD). Here, uncertainties indicate standard errors in the mean. A similar difference in modulus measured by AFM and OT has been reported for MC3T3-E1 osteoblasts and MLO-Y4 osteocytes cells isolated from fetal chicken calvariae (49,53) and for breast cancer cell lines (37). The difference is mainly due to the vast difference in the magnitude of forces applied, as shown in Fig. S14. AFM provides insight into the mechanical properties of the nuclei at larger forces (∼1 nN) than used for OT. However, OT gives better measurements of the absolute indentation for lower forces (∼10 pN) at which AFM measurements are limited by the thermal noise of the cantilever in liquid. In Fig. S14, it can be seen that the cantilever noise is around (50 $\pm$ 30) pN (uncertainty indicates standard deviation), which is roughly the maximal force exerted in our OT setup. The OT are capable of measuring an apparent modulus at an indentation length for which AFM is unable to conclusively report that contact has been made (Fig. 10 b).

Figure 10.

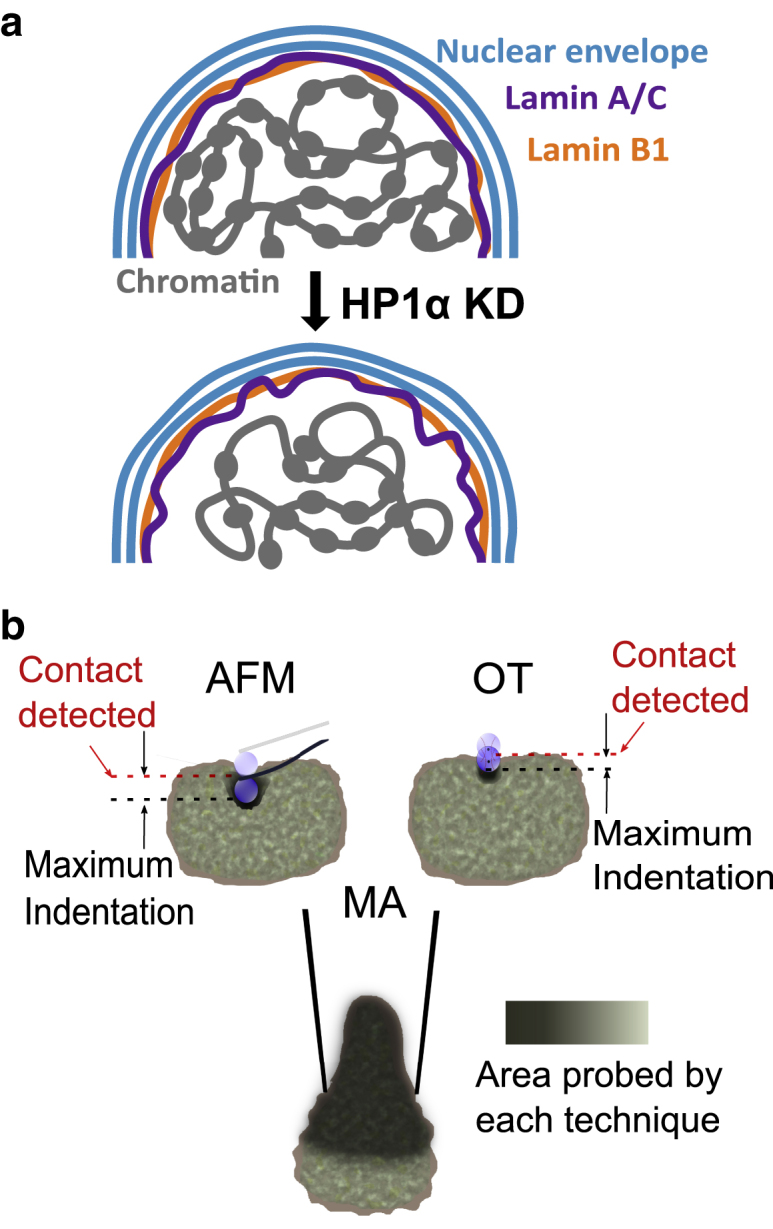
(a) Schematic diagram showing the disruption to the nuclear periphery when HP1α expression is reduced. Loss of HP1α disturbs the organization of heterochromatin, disrupting its tethering to the nuclear lamina and causing a change in the dynamics of the lamina. These changes result in a nucleus with a more malleable shell. (b) Schematic showing the difference in contact point using AFM and OT (local deformation) and larger area probed using MA (global deformation). To see this figure in color, go online.

Nuclei from HP1α knockdown and control cells have similar bulk properties as determined by micropipette experiments

Micropipette measurements are different in nature from OT and AFM because the test involves deformation of the whole nucleus as opposed to the local deformations of the outer regions of the nuclei that are imposed by OT and AFM. Much greater forces and strains are applied, and the applied deformation includes both the bulk of the chromatin interior and response of lamins. In contrast, only a small area of the outer region of the nuclei is locally deformed when using a micron-sized indentor bead, so that the results obtained for effective Young’s modulus from micropipette (Fig. 9) are not expected to be directly comparable to OT and AFM data. The values obtained in Fig. 9 can be seen to lie between those obtained using OT and AFM in Fig. 8. The apparent Young’s moduli obtained using the solid model are similar $\left((1.56\pm 0.10\right)$ kPa for the control and $\left(1.95\pm 0.10\right)$ kPa for the HP1α KD) but slightly larger (p < 0.05) for the nuclei extracted from the HP1α KD cells. Similarly, results from the viscoelastic model indicate that the control nuclei are less stiff $\left((220\pm 90\right)$ Pa compared with $\left(690\pm 180\right)$ Pa) with lower effective viscosity $\left((7\pm 3\right)$ Pa s compared with $\left(22\pm 6\right)$ Pa s) than the HP1α KD nuclei (Fig. S15)). Here, uncertainties indicate standard errors in the mean.

Figure 9.

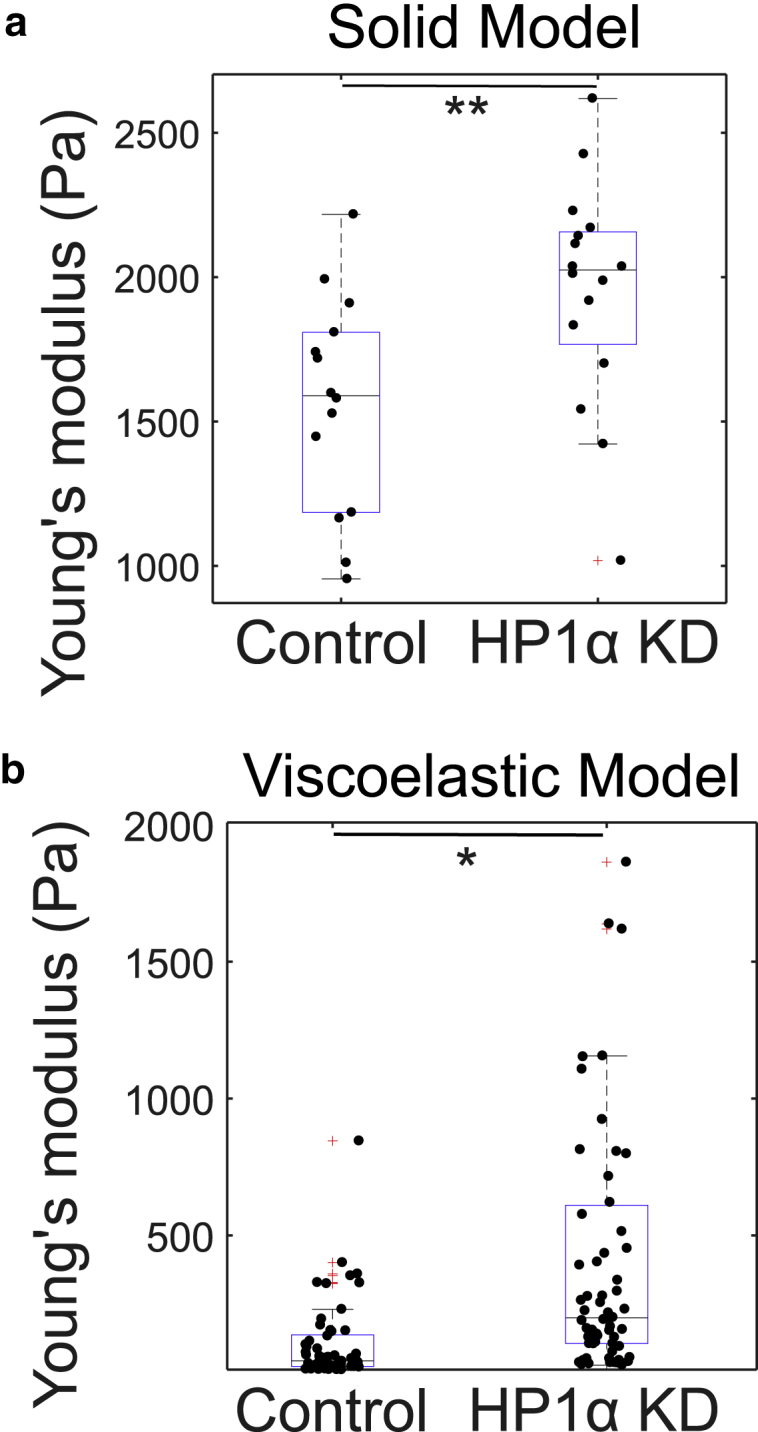
Effective Young’s modulus from microaspiration experiments. (a) Values obtained using the solid model (Eq. 3, ^∗∗p > 0.01) (n = 14 (control), 16 (HP1αKD)) are shown. (b) Values obtained using the viscoelastic model (Eq. 5, ^∗p < 0.05) (n = 61 (control), 67 (HP1αKD)) are shown. Here, n represents the total number of nuclei aspirated in each condition pooled from multiple cell passages. To see this figure in color, go online.

A likely explanation for this difference involves deformation of the bulk, and it is possible that the bulk mechanical properties of HP1α KD nuclei are a little higher than those for control nuclei (in contrast to the results for the local indentation of the outer regions). It is also likely that lamins are playing a role in these high-strain experiments (21). Indeed, previous work concluded that although chromatin affects the mechanical response of nuclei at short extensions (<3 μm, or 30% strain), lamina have significant affects at larger extensions.

It is worth revisiting the two models used to obtain the data shown in Fig. 9 for the micropipette experiments, both of which give values that are intermediate between the AFM and OT results. Data obtained using the solid model are greater and are closer to the AFM values. This may be because the solid model only analyzes small initial deformations that may be less affected by the bulk properties of the nuclei. In contrast, the viscoelastic model uses the entire duration of the deformation and incorporates stress relaxation. Additionally, the prediction of the solid model may be slightly high because of geometric factors in 3, as explained by Aoki et al. (65). The differences in the extracted parameters (both between the two models and with the other techniques) demonstrate that attention must be paid to the details of the analysis method, and not just the experimental technique, when comparing absolute measurements of bioparticles. It is therefore appropriate to designate the data presented in Fig. 9 as “effective” parameters. Nevertheless, the comparison between particle types is not so reliant on modeling assumptions.

Conclusions

In this work, we have studied the mechanical properties of nuclei isolated from MCF7 cells with constitutive KD of HP1α expression using three mechanical measurement techniques that deform the nuclei in very different ways. They probe the outer regions of the nuclei (∼100 nm) with forces on scales of 10 pN (OT) or 1 nN (AFM) and the bulk properties with whole-of-nuclei deformations (micropipette). Although OT and AFM both locally probe the nuclear periphery, AFM experiments were carried out at higher forces compared with OT, and care must be taken when interpreting the absolute indentation (53). Absolute values of Young’s modulus obtained using these three techniques are not in close agreement, as might be expected (66). This highlights that mechanical measurements carried out on nuclei are difficult because they are viscoelastic and heterogeneous.

Despite the inherent approximations of the analysis, data from indentation techniques (AFM and OT) demonstrate that there is a significant decrease in the apparent Young’s modulus of the MCF7 HP1α KD cells as compared with control nuclei, reflecting the altered organization of the peripheral heterochromatin and changes to Lamin A/C dynamics observed in these nuclei. The reduced variation in the spread of mechanical values for these nuclei is consistent with the observed homogeneous chromatin organization and altered peripheral heterochromatin in HP1α KD nuclei (Fig. 10 a). In contrast, the bulk moduli obtained by micropipette experiments show little difference, with the nuclear interior and stretched lamin networks potentially playing a larger role.

More specifically, the observed changes to the heterochromatin upon HP1α KD correlates with the reduced elastic modulus of the periphery of the HP1α KD nuclei. Considering the higher magnitude of forces applied by AFM compared with OT, it is likely that the higher apparent magnitude of the moduli originates from engaging more of the adjacent lamina shell in the more extreme local deformation. In contrast, OT is mostly probing the extremity of the nucleus (Fig. 10 b) and is capable of reporting absolute indentations at much lower forces (Fig. S14).

Author contributions

Experimental work and data analyses were carried out by S.P. (OT, AFM, MA), R.S. and T.K.H. (cell maintenance, nuclei extraction, microscopy, and biochemical assays), A.G. (MA), and G.E.Y.(AFM). All authors contributed to the planning of the work, the interpretation, and the writing of the manuscript.

Editor: Tom Misteli.