Spatiotemporal dynamics of growth and death within spherical bacterial colonies

Abstract

Bacterial growth within colonies and biofilms is heterogeneous. Local reduction of growth rates has been associated with tolerance against various antibiotics. However, spatial gradients of growth rates are poorly characterized in three-dimensional bacterial colonies. Here, we report two spatially resolved methods for measuring growth rates in bacterial colonies. As bacteria grow and divide, they generate a velocity field that is directly related to the growth rates. We derive profiles of growth rates from the velocity field and show that they are consistent with the profiles obtained by single-cell-counting. Using these methods, we reveal that even small colonies initiated with a few thousand cells of the human pathogen Neisseria gonorrhoeae develop a steep gradient of growth rates within two generations. Furthermore, we show that stringent response decelerates growth inhibition at the colony center. Based on our results, we suggest that aggregation-related growth inhibition can protect gonococci from external stresses even at early biofilm stages.

Significance

Many bacterial species cluster together to form three-dimensional colonies. Growth arrest within these clusters has been associated with stress tolerance, yet it has proven difficult to characterize growth at spatial resolution. Here, we show that the velocity field generated by growing bacteria can be used for measuring growth rates within spherical colonies with spatiotemporal resolution. Independently, we track lineages and demonstrate that combining both approaches provides a robust method for determining growth rates. The human pathogen Neisseria gonorrhoeae rapidly develops characteristic growth profiles that depend on a response to starvation. We envision that our method will be suitable for characterizing the growth dynamics within bacterial colonies formed by a variety of different species, relating growth inhibition to stress tolerance.

Introduction

As part of their lifestyle, many if not most bacterial species cluster together and form colonies and biofilms. At the surface of biofilms, bacteria have maximal access to environmental nutrients and space for cell growth and division. At the center of the biofilm, access to nutrients and space is limited. Therefore, we expect that growth and death dynamics depend on position and time (1, 2, 3, 4, 5, 6). However, to determine growth rates with spatial resolution, it is necessary to track the offspring of a single cell in space and time. This task is technically demanding within three-dimensional (3D) biofilms, and there are only few reports that systematically characterize growth rates of biofilm-associated bacteria with spatiotemporal resolution (7). Measuring generation times in space and time is crucial for understanding the mechanisms of biofilm development and the development of antibiotic tolerance at the center of biofilms (8, 9, 10, 11).

Bacterial growth has been investigated at the colony level by analyzing the colony radius R as a function of time t (3,12,13). In young colonies, the colony radius grows exponentially as expected if all cells grow at the same rate. In older colonies, the function R(t) deviates from exponential growth and tends to become linear. Simulations indicate that this behavior is caused by a gradient of growth rates within the colony. Using reporter strains for distinguishing between growing and nongrowing cells, it was shown that growth was arrested at the center of mature biofilms (14, 15, 16). However, the corresponding growth rates have not been measured.

Lineage tracking allows for the determination of generation times or growth rates with spatial resolution. Within two-dimensional colonies, individual cell division events are detectable by means of bright-field or fluorescence microscopy, and therefore, lineages arising from a single cell can be tracked (17,18). In 3D colonies, confocal microscopy or light sheet microscopy enable single-cell detection within colonies (19, 20, 21). Advanced image analysis techniques have been developed for characterizing local order, gene expression, and stress responses with spatial and temporal resolution (22, 23, 24). Growth dynamics of Vibrio cholerae has been characterized recently. As a consequence of their rod-like shape, V. cholerae shows liquid crystalline order, and this structure gives rise to collective, fountain-like motion of bacteria growing in colonies (20). To our knowledge, little work has focused on the measurement of spatiotemporal growth dynamics within 3D colonies. Given that the size of the bacterial cell body exceeds the limit of optical resolution only ∼2–3-fold, lineage tracking is technically difficult. A recent study reported growth rates in colonies formed by V. cholerae (7). Interestingly, the growth rate was constant throughout the colonies, and no spatial gradient was observed.

In this study, we investigate collective motion and growth dynamics of spherical bacteria (cocci) within spherical colonies. We show that growth generates radial motion and demonstrate that the spatial profile of growth rates can be inferred from the resulting velocity field (VF). In a complementary approach, we determine the growth rate with spatial resolution by counting the offspring of bacteria within the colony. Combining both techniques, we characterize the growth profile within bacterial colonies during biofilm development. At the edge of the colony, the growth rate remains constant for several hours. Within the colony, a gradient of growth rates develops, and growth ceases close to the colony center. We show that inhibition of stringent response (a response to limitation of various nutrients) accelerates growth inhibition at the colony center. We conclude that spatial gradients develop rapidly even in relatively small colonies containing several thousands of bacteria.

Results

Colony growth indicates a transition from homogeneous growth to heterogeneous growth

In the first step, we characterized the growth of 3D gonococcal (GC) colonies. Colonies were formed in liquid and subsequently introduced into a flow chamber where growth was monitored for many hours under constant nutrient flow. The shape of gonococcal colonies is spherical (24, 25, 26), and therefore, characterization of the colony radius R is sufficient for determining the number of cells within the colony. The radii R of the growing colonies were measured as a function of time. Assuming constant cell density, we derived the number of cells within the colony relative to the number of cells at the start of the experiment: t = 0, N_col(t)/N_col(0) = (R(t)/R(0))³. For wt∗ Neisseria gonorrhoeae, the number of cells increased exponentially during the initial 2 h (Fig. 1; Fig. S1). Using an exponential fit, N_col(t)/N_col(0) = exp(λ_colonyt), we found that the growth rate was λ_colony = (0.56 ± 0.01)h⁻¹. After 2 h, N_col(t)/N_col(0) deviated from an exponential behavior (Fig. S1). In the next step, sfgfp-expressing bacteria (wt^∗ green) will be used for determining the growth rate at spatial resolution. sfgfp was expressed under the strong pilE promoter to ensure detectability of all fluorescent cells. We assessed whether expression and illumination of the fluorescent marker caused a growth defect by quantifying growth of wt^∗ green colonies and found a transition from exponential growth to subexponential growth at the same colony age as for wt^∗ colonies (Fig. 1). The growth rate was ${\lambda }_{colony}^{green}$ = (0.42 ± 0.01)h⁻¹. This difference must be considered in the single-cell-counting (CC) analysis discussed later.

Figure 1.

Expression of sfgfp slightly reduces growth rate. Mean number of cells within colony N_col(t) normalized by the number of cells in the colony at t = 0, N_col(0) for wt^∗ (Ng150, black) and wt^∗ green (Ng194, gray). Full lines indicate exponential fits with N_col(t)/N_col(0) = exp(λ_colonyt) with λ_{colony, wt^∗} = (0.56 ± 0.01)h⁻¹ and λ_{colony, wt^∗ green} = (0.42 ± 0.01)h⁻¹. (Given is mean ± standard error, >40 colonies for each data point.)

Based on the growth analysis at the colony level, we predict that the profile of growth rates is homogeneous during the initial 2 h of growth and spatial heterogeneity develops after 2 h.

Lineage tracking within 3D colonies

We developed a lineage tracking method for measuring growth rates of N. gonorrhoeae (gonococcus) within colonies. Recently, the growth rate of rod-shaped cells was measured by quantifying temporal changes in cell length along the major axis of the rod (7). In cocci, this method is hampered by the fact that the change in aspect ratio before cell division is small, and additionally, the division plane switches every generation (27). Instead, we track lineages within colonies. N. gonorrhoeae form spherical colonies (24,25). Tracking of all cells individually over multiple generations is prohibited by three factors. Firstly, gonococci are very densely packed (24), and secondly, type-4-pilus-mediated interactions between the cells cause them to move actively (28). As a consequence, high time resolution would be necessary to allow for single-cell tracking, and the associated photodamage would prohibit growth rate analysis. Furthermore, background fluorescence in colonies consisting exclusively of fluorescent cells would prohibit single-cell detection.

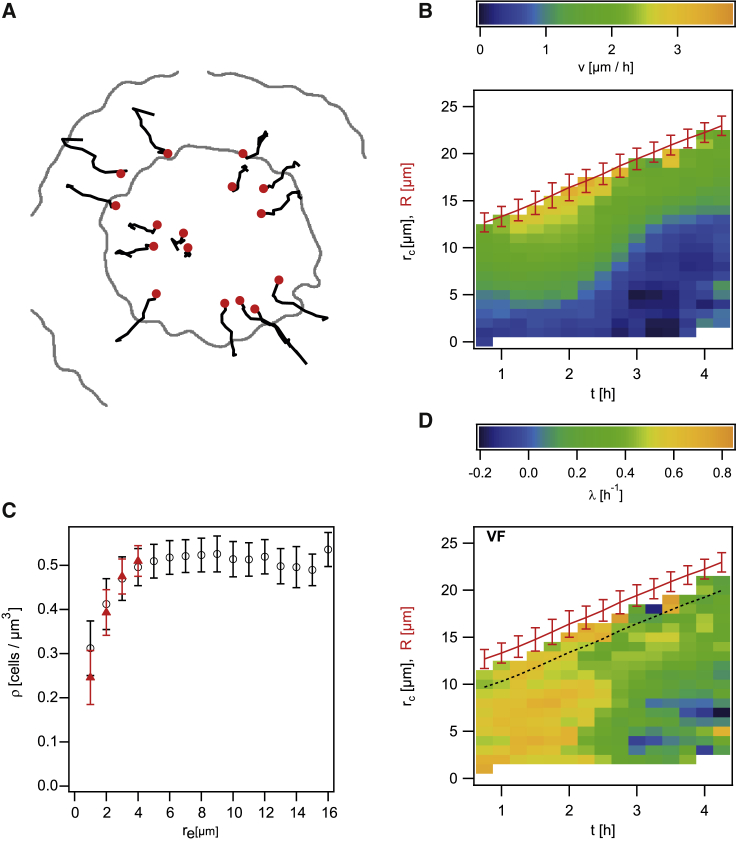
To avoid these problems, we tracked the offspring of single or few fluorescent cells. A small fraction of sfgfp-expressing cells (wt green) was mixed with nonfluorescent wt^∗ cells. This mixture was inoculated into a flow chamber. Medium was continuously flushed through the chamber, providing constant nutrient and oxygen supply for multiple hours. The medium contained propidium iodide (PI), a fluorescent dye that stains dead cells. The fluorescence signals of growing colonies were detected using confocal microscopy (Fig. 2 A). Individual fluorescent cells were identified, and their positions within the colonies were determined (Fig. 2 B; Video S1). The circumference of the colony was determined using the bright-field images (Fig. 2 C; Video S2).

Figure 2.

Lineage tracking in gonococcal colonies. Shown is wt^∗ (Ng150) mixed with wt^∗ green (Ng194). (A) Typical confocal plane (h = 3 μm) through a colony at different time points. Shown is the overlay between bright field (gray), sfGFP fluorescence (green), and PI fluorescence (red). (B) 3D reconstruction of positions of fluorescent cells. The blue frame denotes the plane shown in (A). The gray circles denote the edge of the colony, whereby Δh between gray circles: 1 μm. (C) Cluster dynamics in growing colony. Green circles represent positions of wt green gonococci. 3D projections of all wt green cells are shown. Black circle represents the circumference of one single cluster. Blue lines represent the trajectory of the center of mass of this cluster. White lines represent the edges of the colony. Red circles depict the radii of the colony. Scale bars, 10 μm. To see this figure in color, go online.

A cluster was defined as an assembly of wt^∗ green cells residing in close proximity (Video S3). Given that only few fluorescent (1% at the beginning of the experiment) cells were immersed within the colony initially, wt^∗ green cells can be associated with specific clusters. The cells within the cluster are the offspring of a single or few cells contained within the cluster at time t = 0. In the following two paragraphs, we will describe how the analysis of these clusters allows us to measure the growth rate with spatial resolution. First, we counted the number of cells, N, within the cluster, reflecting the growth rate of wt^∗ green cells within the cluster. Second, we analyzed the cluster velocity which is influenced by the growth of all cells (mostly wt^∗ cells) residing closer to the colony center than the cluster and pushing the cluster toward the edge of the colony.

CC method: single-CC reveals that local growth rates decline rapidly at the center of growing colonies

The spatially resolved growth rate was measured by counting the number of wt^∗ green cells within a cluster, N, as a function of time. One example of a cluster arising from a single cell is shown in Fig. 3, A and B and Videos S2 and S3. In this example, the first three cell division events occur nearly simultaneously for all cells belonging to the cluster with a generation time of ∼90 min.

Figure 3.

Spatiotemporal dynamics of growth of wt^∗ green (Ng194) mixed with wt^∗ (Ng150). (A) Example of single growing cluster highlighted in Fig. 2. (B) Number of cells N(t) within the cluster shown in (A). (C) Growth rate λ (color coded) as a function of distance from center of colony (r_c) and time t. (λ is the mean growth rate of 10–200 clusters for each data point.) (D) Fraction of dead cells f_dead (color coded) as a function of distance from center of colony (r_c) and time t. Red represents the mean colony radius (±standard deviation, >40 colonies for each data point) as a function of time. To see this figure in color, go online.

We determined the effective local growth rate λ by fitting N(t + τ)/N(t) = exp(λτ) with τ = (0 − 1.5)h as described in the Materials and methods. The growth rate was λ ≈ 0.45 h⁻¹ close to the edge of the colony (Fig. 3 C; Fig. S3). This growth rate corresponds to a generation time of T ≈ 1.5 h. Although the growth rate at the edge of the colony remained close to λ ≈ 0.45 h⁻¹ up to 4.5 h after inoculation, the growth rate decreased as a function of the penetration depth into the colony. The spatial profile of growth rates was shallow for young colonies. At t > 2 h, growth rates dropped severely, and growth ceased near the centers of the colonies. The development of heterogeneous growth after 2 h is consistent with the transition from exponential to subexponential growth of the colony radius at 2 h (Fig. 1).

The effective growth rate λ depends on cell duplications and on cell death. Therefore, we determined the fractions of dead cells f_dead = N_dead/N_total with spatial and temporal resolution (Fig. 3 D). To this end, we added PI to the medium. PI stains cells with permeable membranes, indicating cell death. Please note that for determination of N_total, we assumed that the density ρ of cells is constant throughout the colony. Within r_e ≤ 3 μm, the cell density is lower compared with the remainder of the colony (Fig. 4 C), and therefore, the fraction of dead cells is overestimated in this regime. Most importantly, the fractions of dead cells were f_dead < 5% for all positions and time points. Therefore, the influence of cell death on the changes in N(t) is negligible, and the effective growth rate λ determined in our experiment is very close to the real growth rate, and the term “effective” will be discarded in the following. In older colonies, the fraction of dead cells at the centers of the colonies increased the strongest.

Figure 4.

Growth rates inferred from VF of wt^∗ green (Ng194) mixed with wt^∗ (Ng150). (A) Trajectories of individual clusters moving within one colony acquired over 3 h. Shown are clusters residing at different heights within the colonyandprojected into one plane. Red circles represent the start of a trajectory, black lines represent the trajectories, and gray lines the colony outlines at 0 and 3 h, respectively. (B) Radial components of cluster velocities v as a function of distance from center of colony (r_c) and time t. (λ is the mean growth rate of 10–200 clusters for each data point.) Red represents the mean colony radius (±standard deviation) as a function of time. (C) Cell density ρ profile through colonies. Black circles represent densities in cylindric coordinates, and red triangles represent densities in spherical coordinates. (D) Growth rates λ (color coded) inferred from VF as a function of distance from center of colony (r_c) and time t. (λ is the mean growth rate of 10–200 clusters for each data point.) Red line represents the mean colony radii (±standard deviation, >40 colonies for each data point) as a function of time. The black dotted line denotes the area in which reduced cell density introduces a systematic error to λ. To see this figure in color, go online.

In summary, after a short initial period of exponential growth, complex spatiotemporal growth profiles developed within gonococcal colonies with severely reduced growth at the colony centers.

VF method: the generation time can be determined from the radial flow of clusters

Cell growth and division generate collective cellular movement directed from the center of the colony toward its periphery (Fig. 4 A). In one- and two-dimensional systems, analysis of this cellular movement has been employed to infer concentration profiles of nutrients and nutrient uptake functions bacterial populations (29). Here, we show that the VF can be used for determining the growth rate with spatial resolution in spherical colonies. The velocity of cluster movement $\stackrel{\rightharpoonup }{v}\left(r_c\right)$ was determined by analyzing the trajectories of the centers of mass of individual clusters (Fig. 4 A). Because of the spherical symmetry of the colony, the radial velocity associated with growth is $v\left(r_c\right)=\stackrel{\rightharpoonup }{v}{\stackrel{\rightharpoonup }{e}}_r$, i.e., the velocity vector was projected onto the unit vector ${\stackrel{\rightharpoonup }{e}}_r$ pointing from the colony center toward its edge, yielding the radial component of the cluster velocity v(r_c). v(r_c) was close to 0 at the center of the colony at r_c ≈ 0 (Fig. 4, A and B). With increasing distance from the center, r_c, the velocity of clusters increased. At a colony age of less than 2 h, the speed increased linearly as a function of r_c with v(r_c) = (0.17 ± 0.01)h⁻¹ × r_c (Fig. S4). In older colonies, the speed decreased, and v(r_c) became nonlinear consistent with heterogeneous growth.

By analyzing the flow field v(r_c, t), we can infer the growth rate λ(r_c, t). To this end, we formulate the continuity equation with a growth term λρ, which breaks mass conservation

$$\dot{\rho }=-\overrightarrow{\nabla }\cdot \left(\stackrel{\rightharpoonup }{v}\rho \right)+\lambda \rho .$$ (1)

Here, $\rho \left(\overrightarrow{r},t\right)$ is the spatially and temporally varying number density of cells in the colony. We find that the cell density is constant within the colony, but the density decreases at r_e ≤ 3 μm (Fig. 4 C) in agreement with theoretical predictions (26). In the following, we disregard the low-density area at the colony edge. We note that type 4 pili generate bacterial movement within colonies as pili belonging to neighboring cells bind to each other and retract (28). The pilus-mediated motility has been described as diffusive (21,26,30). Thus, the mean velocity of pilus-driven movement is 0 and does not contribute to the radial velocity analyzed in this study. As an additional test, we determined the azimuthal components of the velocity vectors (Fig. S5). Although growth affects only the radial component, pilus-mediated motility affects both components. Consistent with isotropic movement, we find that the mean azimuthal velocity component is close to 0.

First, we consider colonies with an age t < 2 h. During this period of time, the growth rate is nearly constant in space and time. In this regime, Eq. 1 simplifies to λ = 3v_cluster/r. The linear fit shown in Fig. S4 a provides λ = (0.51 ± 0.01)h⁻¹. This value is slightly higher than the growth rate determined by the CC method (Fig. 3).

Next, we consider older colonies with an age t > 2 h. In these colonies, the growth rate depends on position. By numerically solving Eq. 1 and assuming constant ρ, i.e., ∂_r(r²v_r) = r²λ, we calculate the growth rate λ(r_e, t) (Fig. 4 D). Importantly, we find the same qualitative profiles as by the CC method (Fig. 3 C; Fig. S4). At t < 2 h, the growth rates are spatially homogeneous. In older colonies, the growth rate decreases as a function of distance from the edge of the colony. The total growth rates in Fig. 4 D are slightly but significantly higher compared with the rates shown in Fig. 3 C. The reason for this small quantitative discrepancy can be explained as follows. The velocity of the cluster formed by wt^∗ green cells is determined by all cells residing at a position $r_c<r_c^{cluster}$. Given that only 1% of the cells within the colony was fluorescent, the cluster velocity is determined by the growth of wt^∗. By contrast, the CC method used for Fig. 3 relies exclusively on wt^∗ green cells, which have a lower growth rate (Fig. 1).

In conclusion, bacteria move radially from the center toward the periphery of the colony as a consequence of cell growth, and the VF allows determining the growth rate. This method confirms that a characteristic growth profile develops after only two generations of growth within the colony.

External nutrient supply is nearly saturating

Unexpectedly, the growth rate decreased even within small colonies continuously supplied with rich medium. We hypothesized that either a metabolite or oxygen were depleted at the centers of the colonies. To assess this hypothesis, we increased the flow rate of the medium fivefold. Indeed, the growth rate increased slightly (Figs. S6 and S7). However, the colony radius grew exponentially only for 2 h, indicating that growth became heterogeneous. Reminiscent of the experiments run under standard flow rates, after 2 h of growth, the growth rate decreased strongly as a function of penetration depth (Fig. S6). This behavior was observed consistently with the CC method and with the VF method. We conclude, therefore, that limitation of external supply with nutrients or oxygen is not the main cause for the growth inhibition in gonococcal colonies.

Lack of stringent response influences the spatiotemporal growth dynamics

Limitation of nutrients at the center of colonies is one potential explanation for decreased growth rate. The stringent response is involved in adaptation to nutrient limitation including amino acid, carbon, and fatty acid starvation (31,32). RelA and SpoT adjust the level of (p)ppGpp, the accumulation of which triggers stringent response (33). Deletion of relA suppresses (p)ppGpp production in gonococci, and deletion of spoT reverses the growth defect caused by relA deletion alone (34). We addressed the question whether stringent response affected growth and death in our system. To this end, we mixed ΔrelA ΔspoT green cells with ΔrelA ΔspoT cells and characterized the spatiotemporal dynamics of growth and death in these mixed colonies (Fig. 5).

Figure 5.

Stringent response affects growth and death dynamics. ΔrelA ΔspoT green (Ng224) cells were mixed with ΔrelA ΔspoT (Ng198) cells. (A) Growth rate λ (color coded) as a function of distance from center of colony (r_c) and time t (CC method). (λ is the mean growth rate of 10–150 clusters for each data point.) (B) Radial components of cluster velocities v as a function of distance from center of colony (r_c) and time t. (The v-value is the mean growth rate of 10–150 clusters for each data point.) (C) Growth rates λ (color coded) as functions of distance from center of colony (r_c) and time t. Black dotted line denotes the area in which reduced cell density introduces a systematic error to λ (VF method). (λ is the mean growth rate of 10–150 clusters for each data point.) (D) Fraction of dead cells f_dead (color coded) as a function of distance from center of colony (r_c) and time t. Red lines represent the mean colony radii (±standard deviation, >40 colonies for each data point) as functions of time. To see this figure in color, go online.

We found that at early time points, the growth rates of the ΔrelA ΔspoT colonies were higher compared with the rates in wt^∗ colonies (Fig. 5; Figs. S7 and S8). However, the growth rates dropped even in young colonies after t > 1 h at the colony center (Fig. 5; Figs. S7 and S8). This behavior was found both by the CC method (Fig. 5 A), by the VF method (Fig. 5, B and C), and by analyzing the total number of cells within colonies (Fig. S8). The fraction of dead cells close to the colony center was higher by a factor of ∼2 in the ΔrelA ΔspoT compared with the fractions in wt^∗ colonies (Fig. 5 D).

Taken together, we found that inhibition of stringent response affects growth and death within the colony. Specifically, growth arrest in stringent-response-deficient colonies occurs prematurely.

Discussion

Potentials and limitations of different methods for determining growth rates

Measuring growth rates is tricky and prone to various errors. The classic method for determining growth rates, i.e., the determination of optical density (OD600) as a function of time during bacterial growth, yields the growth rate, i.e., Malthusian parameter. Although this method is well accepted, it is prone to various errors often ignored in the literature. For example, adhesion between bacteria and between the bacteria and surface reduces the OD600, mimicking reduced growth rates (35). Furthermore, the OD600 can be susceptible to changes in gene expression or changes in cell size, affecting the optical properties of the bacteria. One of the most accurate methods for determining relative changes in growth rates through mutations is the competition assay (36,37). But even this method is error prone; for example, cellular interactions like toxin secretion can falsify the growth rates determined by this method.

The methods introduced here are based on single-cell visualization and, therefore, do not suffer from the problems described above. We developed two different methods allowing the determination of growth rates at spatial resolution. As discussed in the following, both methods implicate complementary advantages and disadvantages. We propose combining both methods to robustly characterize the growth profile within bacterial colonies. First, by counting the number of offspring of one or few fluorescent cells over short periods of time, the growth rates were determined (CC method). Most importantly, this method allows characterizing rates with spatial and temporal resolution. It relies on detection of single cells within a large 3D structure, and therefore, a sufficiently strong fluorescence signal of individual cells is essential. To achieve a high signal/noise ratio, sfgfp was expressed under the control of the strong pilE promoter, causing a reduction of growth rate (Fig. 1). Second, we inferred the growth rates from the VF caused by cell growth (VF method). This method does not suffer from effects related to sfgfp expression or cell damage by laser light because the fraction of wt^∗ green cells was only 1%, and the VF is dominated by wt^∗ cells. However, the method is susceptible to changes in cell density. Under the conditions studied, cell density was constant within the bulk of the colony but decreased considerably at the edge of the colony. Therefore, the growth rate could not be determined in this region with the second method. Some external stresses cause swelling of cells (21). Swelling would cause the colony to expand and would introduce errors to the determination of growth rates. Although both methods have complementary problems, they yield comparable growth profiles. Quantitatively, the VF method tends to provide slightly higher growth rates consistent with the values determined for the total numbers of cells within a colony derived from the colony radii.

Growth of gonococci was considerably more efficient on agar plates. In earlier work, we characterized gonococcal growth in fluorescent colonies on agar plates by quantifying the fluorescence intensity as a function of time (38,39). Exponential colony growth proceeded for many hours, and the growth rates were considerably higher. In the agar plate assay, bacteria grew into flat colonies for many generations, and we hypothesize that this geometric difference together with different concentrations of O₂ and CO₂ is responsible for the discrepancy.

Within few generations, growth rates become spatially heterogeneous, and stringent response retards development of heterogeneity

Rather unexpectedly we found that a characteristic growth profile develops within small gonococcal colonies after no more than two generations under continuous supply of medium optimized for gonococcal growth. The growth rate is constant as a function of time within a 3-μm ring at the periphery of the colony. Remarkably, this is the low-density area. Within the colony, the growth rate decreases continuously as a function of penetration depth, and growth stops at a depth of ∼10 μm, corresponding to ∼10 bacteria. Interestingly, this gradient develops even faster when stringent response is inhibited. This result suggests that stringent response drives the cells to reallocate their resources more efficiently to maintain growth within colonies, and we conclude that stringent response plays a role in adaptation to life in colonies as shown for biofilms formed by other species (9).

What inhibits growth at the center of gonococcal colonies? Depletion of nutrients or O₂ might be responsible for growth inhibition. Cells residing at the colony edge are likely to deplete nutrients, generating a gradient of nutrient-O₂ concentration (29). Increasing the flow rate did not delay the onset of growth arrest, suggesting that external supply of nutrients was not growth limiting. Strongly reduced diffusion of nutrients into or waste out of the colonies would explain growth arrest. Mechanical constraints may be another factor that inhibits growth (40, 41, 42). Gonococci are tightly packed within colonies with an estimated volume fraction of Φ ≈ 0.5. We have shown that freshly assembled colonies rearrange with a relaxation time of ∼1 min (24), suggesting that mechanical constraints should not limit proliferation in young colonies. In older colonies, the matrix has matured and likely inhibits cellular rearrangements. As a consequence, mechanical stress would build up as cells grow, potentially inhibiting cellular proliferation (6). Future studies need to address different mechanisms of growth inhibition.

To our knowledge, growth rates have been determined with spatial resolution only for V. cholerae colonies so far (7). There, growth rates were constant even at a penetration depth of 30 μm. Different bacterial densities and cell shapes may explain the different growth profiles. The volume fraction Φ of V. cholerae of Φ ≈ 0.2 (43) was considerably lower compared with N. gonorrhoeae. Moreover, rod-shaped V. cholerae orient vertically and move collectively as the colony grows and expands (20). For spherical gonococci, however, we find a radial flow at early times, the speed of which declines as the colony ages.

Materials and methods

Growth conditions

GC base agar was made from 10 g/L dehydrated agar (BD Biosciences, Bedford, MA), 5 g/L NaCl (Roth, Darmstadt, Germany), 4 g/L K₂HPO₄ (Roth), 1 g/L KH₂PO₄ (Roth), 15 g/L Proteose Peptone No. 3 (BD Biosciences), 0.5 g/L soluble starch (Sigma-Aldrich, St. Louis, MO), and supplemented with 1% IsoVitaleX (IVX): 1 g/L D-glucose (Roth), 0.1 g/L L-glutamine (Roth), 0.289 g/L l-cysteine-HCL × H₂O (Roth), 1 mg/L thiamine pyrophosphate (Sigma-Aldrich), 0.2 mg/L Fe(NO₃)₃ (Sigma-Aldrich), 0.03 mg/L thiamine HCl (Roth), 0.13 mg/L 4-aminobenzoic acid (Sigma-Aldrich), 2.5 mg/L β-nicotinamide adenine dinucleotide (Roth), and 0.1 mg/L vitamin B12 (Sigma-Aldrich). GC medium is identical to the base agar composition but lacks agar and starch.

Bacterial strains

All strains used in this study (Table S1) are based on wt^∗ (4). In this strain, we deleted the G4 motif responsible for pilin antigenic variation. If this motif were present, the primary structure of the major pilin PilE would vary, and this variation may affect T4P-T4P interactions and colony dynamics (44).

For construction of wt^∗ green, the pilE promotor region (P_pilE) was amplified from genomic DNA of strain NG150 (ΔG4) using primers TC22 (5′-AGTTCTTCACCTTTGCTAACCATAAAATTACTCCTAATT GAAAGGGGAAATG-3′) and NB065 (5′-TTTTAATTAATTCCGACCCAA TCAACACACCC-3′). The sfgfp gene sequence was amplified from plasmid pET28a-sfgfp (plasmid #85492; Addgene, Watertown, MA) with primers TC21 (5′-CATTTCCCCTTTCAATTAGGAG TAATTTTATGGTTAGCAAAGGTGAAGAACT-3′) and NB066 (5′-TTGGCCGGCCTTATTTATACAGTTCATCCATACCGTG-3′). Both fragments were subsequently merged in a fusion-PCR: fragments were mixed in a 1:1 ratio, and a PCR was performed for 20 cycles without the addition of primers. Afterward, primers NB065 and NB066 were added to the reaction, and the PCR was continued for another 20 cycles. The obtained fusion product PpilE-sfgfp was subsequently subcloned into the vector pLAS (39) via FseI and PacI (New England Biolabs, Ipswich, MA) digest. The generated plasmid pLAS-sfgfp was transformed into Escherichia coli DH5α, and transformants were selected on Luria broth agar plates containing kanamycin. The correct sequence of the vector insert was verified by sequencing with primers TC19 (5′-CCTTAATTAAGGTTATTTATACAGTTCATCCATACCGTG-3′) and TC20 (5′-TCTGGCCGGCCTTCCGACCCAATCAACACACC-3′). Finally, the plasmid was transformed into strain NG150 (ΔG4) to insert the PpilE-sfgfp gene between the lctP and aspC loci. Transformants were selected on GC agar plates containing spectinomycin. Expression of sfgfp was confirmed via fluorescence microscopy.

Strain ΔrelA ΔspoT (Ng198) was constructed as follows. Regions upstream and downstream of relA gene were amplified from isolated genomic DNA of strain ΔG4 (Ng150). PCRs were performed using primers GS_043 (5′-TATGCTGACCGGGGTTTTGG-3′) and GS_044 (3′-TTAAACCAGTTCCT CTCATCATTTACGGTGCATAGGCGGG-5′) for amplification of relA 5′ untranslated region (UTR), whereas GS_047 (5′-TGTCTCATTCCGCTTCCGTA GGATAACGCTTCAGACGGCA-3′) and GS_048 (3′-GCG GTCGTTAA AACTCCCGAA-5′) were applied for relA 3′ UTR. kanR was amplified from kanamycin-resistant strain Ng050 using primers GS_045 (5′-GAT GAGAGGAACTGGTTTAAATATCGTCGCAAGATGCGGT-3′) and GS_046 (3′-TACGGAAG CGGAATGAGACA GTCCCGTCAAGTCAGCGTAA-5′). The resulting three single fragments were linked by fusion-PCR and transformed into strain Ng150. Transformants (Ng197) were selected on GC agar plates containing kanamycin. Deletion of relA was confirmed by sequencing with primers GS_043 (5′-TAT GCTGACCGGGGTTTTGG-3′), GS_045 (5′-GATGAGAGGAACTGGTTTAAATATCG TCGCAAGATG CGGT-3′), and GS_046 (3′-TACGGAAGCGGAATGAGACAGTCCCGTCAAGTCAGC GTAA-5′).

Deletion of spoT was achieved by amplifying spoT 5′ UTR from genomic DNA of ΔG4 strain (Ng150) with primers GS_037 (5′-TGCGCCGGCAAGTATGAATAC-3′) and GS_038 (3′-TAATAAGTAAAG CAGGTAAAACGGGTTGC-5′). For amplification of spoT 3′ UTR, primers GS_041 (5′-CACGAGCT CCTTCAGACGGCTTTCGGGATG-3′) and GS_042 (3′-GGTTGGAAAATATACAGGTAAAAAATATG TCC-5′) were used. Isolated plasmid DNA of ermR-pIGA served as a template for amplification of ermC with primers GS_039 (5′-TTTACCTGCTTTACTTATTAAATAATTTATAGCTATTGAAAAG-3′) and GS_040 (3′-GCCGTCTGAAGGAGCTCGTGCTATAATTATAC-5′). PCR products were merged by fusion-PCR, transformed strain Ng197 and selected on GC plates containing erythromycin, resulting in strain ΔrelA ΔspoT (Ng198). Replacement of spoT by ermC was verified via sequencing using primers GS_037 (5′-TGC GCCGGCAAGTATGAATAC-3′), GS_ 049 (5′-ATTGCCGAACCCGCCGTTCT-3′), GS_050 (5′-GCA AACCCGTATTCCACGAT-3′), and GS_51 (5′-CGGTCGGTTTGTTATTGCGG-3′).

Gene sfgfp is expressed under the control of the pilE promoter with high expression levels. We investigated whether sfgfp expression affects the growth rate of gonococci in our assay by comparing the number of cells per colonies N_col(t) as a function of time (Fig. 1). We found that the growth rate of wt^∗ green cells expressing sfgfp is 14% lower compared with wt^∗ cells that do not express fluorescent proteins. Illumination reduces the growth rate further, resulting in a difference of 25% (Fig. 1). Therefore, the growth rate determined by counting the number of wt^∗ green cells per cluster, N(t), is expected to be lower compared with the growth rate determined from colony growth during the exponential phase in agreement with Fig. 3 A. The VF method, on the other hand, does not suffer from reduced growth rates of the sfgfp-expressing strain because the latter are used as fluorescent objects probing the VF.

Confocal microscopy

The wt^∗ and wt^∗ green cells were grown for 14 h on GC + IVX plates at 37°C, 5% CO₂, and resuspended in 5 mL GC + IVX medium at an OD 0.1. The ratio of nonfluorescent wt^∗ and fluorescent wt^∗ green cells was set to 100:1. Supplementation of 100 μL Mili-Q water (MilliporeSigma, Burlington, MA) dissolves existing bacterial colonies, and shaking at 37°C, 5% CO₂ for 30 min allows for colony reassembly. From this suspension, 250 μL are injected into a microfluidic flow chamber (Ibidi Luer 0.8 mm channel height + Ibitreat; ibidi, Planegg, Germany) connected to a peristaltic pump (model 205U; Watson Marlow, Falmouth, UK) for constant nutrient supply of 1 rpm (standard flow rate) or 5 rpm (fivefold flow rate) (GC + IVX + 0.004% PI). Prior usage, all flow chambers were coated with Poly-L-Lysine (cat. no. P4832, 50 μg/mL; Sigma-Aldrich).

Images were acquired using an inverted microscope (Ti-E; Nikon, Tokyo, Japan) equipped with a spinning disk confocal unit (CSU-X1; Yokogawa, Tokyo, Japan) and a 100×, 1.49 NA, oil immersion objective lens. The excitation wave lengths were 488 and 561 nm. The sfGFP signal of the cells and a bright-field image were recorded for 5 h every 15 min. Starting from the surface of the glass cover slide, 40 μm × 40 μm × 25 μm large image stacks with a voxel size of 0.08 μm × 0.08 μm × 0.4 μm were acquired.

Detection of single-cell positions and cluster analysis

Bright-field images were used to determine the colonies’ centers of mass and radius. For this purpose, a circle was fitted to the colony contour, which is determined by a threshold applied on the filtered bright-field images. The height of the center of mass of the colony was estimated with 0.85 × colony radius.

From the confocal image stacks, single-cell positions of wt^∗ green cells were determined. All confocal images were registered using the center of mass of the colony and stretched by a factor of three in z-direction to obtain spherical intensity profiles of all particles. Every image voxel was taken to the power of three to increase the image contrast. The mean intensity profile of several different monococci inside bacterial colonies were used to generate a symmetrical 3D kernel for convolution of all images. Spheroidal features were found using the MATLAB feature3d function (The MathWorks, Natick, MA) written by Yongxiang Gao and Maria Kilfoil (45) based on Interactive Data Language code written by John C. Crocker and David G. Grier (46). Clusters are defined by spheroidal features, which are less than 2 μm apart from each other. Because the number of clusters is much smaller compared with the number of features, clusters can be tracked by the MATLAB trackmem function (The MathWorks) written by Maria Kilfoil, again based on Interactive Data Language code written by John C. Crocker. We applied the tracking algorithm to cluster positions located in time intervals [t, t + 1.5 h] with tϵ[0 h:0.25 h:3 h]. Only trajectories with a length of 1.5 h were used for further analysis.

We derived the mean growth rate as a function of the distance r_e from the edge of the colony by fitting <N^∗(r_e, t + τ) >= exp(λτ), where N^∗ is the normalized and averaged data of individual clusters within position intervals [r_e, r_e + 2 μm] within 1.5-h time intervals. The mean distance to the colony edge was defined for each cluster by averaging every distance to the colony edge within the 1.5-h time intervals. The velocity of each cluster depends on the distance to the center of mass of the colony. Hence, we sorted the data relative to the colony center of mass in the intervals [r_c, r_c + 2 μm]. In general, we did not select for a specific colony size. However, it was necessary for the heatmaps illustrations. Hence, we determined the mean colony radius R and its standard deviation at every time point. Colonies, which were larger or smaller than a standard deviation from the mean colony radius, were discarded. Growth rates were plotted relative to the mean colony radius, and velocities were plotted relative to the center of mass of the colonies.

To assess the robustness of our algorithm with respect to the order of data averaging and exponential fitting, we fitted the N(t) data of individual clusters as follows. To obtain Fig. S2, we derived growth rates of single clusters by fitting an exponential function $\frac{N\left(t+\tau \right)}{N_0\left(t\right)}=\exp \left(\lambda \tau \right)$ to the number of cells, N, inside a cluster within the time interval indicated. The medians of the distributions in Fig. S2 agree well with the data shown in Fig. 3 C. We note, however, that there are pronounced peaks at λ_single = 0, indicating that some clusters do not start replicating.

Determination of growth rate from VFs

The growth rate λ was calculated by λ = div(v) = 2 ×$\frac{v}{r_c}+\frac{dv}{d{r}_c}$ using spherical coordinates. Given the velocities shown in the heatmaps, the previous equation simplifies to λ(r) = 2 × $\frac{v\left(r\right)}{r_c\left(r\right)}+\frac{v\left(r-1\mu m\right)-v\left(r+1\mu m\right)}{2\mu m}$. Thus, the growth rates were directly calculated from the velocities given in the heatmaps.

Determination of fraction of dead cells

The medium (GC + IVX), which was continuously supplied to the flow chamber, was supplemented with 0.004% PI to stain dead cells during image acquisition. Spheroidal features (dead cells) were detected using the same method as described in the previous paragraph for detecting living cells. The number of dead cells, δ, was normalized: δ^∗(r) = $\frac{\delta \left(r\right)}{\rho \left(r\right)V\left(r\right)}$, where the cell density ρ(r) is set to be constant (19). Because of a lower cell density up to 2 μm away from the colony edge, the fraction of dead cells is underestimated there. The volume of interest V(r_e) is determined as a function of the distance from the colony edge r_e within [r_e, r_e + 2 μm]. For better comparison between the heatmaps, the fractions of dead cells were averaged within 1.5-h time intervals.

Conclusions

The rapid growth arrest at the centers of the gonococcal colonies suggests that aggregation can rapidly cause tolerance against antibiotics acting on growing bacteria. This is consistent with previous reports showing that gonococcal aggregation enhances their survivability under ceftriaxone treatment with the fraction of dead cells being highest at the colony edge (21,47). Our methods are applicable to all spherical colonies, and it will be interesting to compare the growth profiles between different species.

Author contributions

A.W., M.H., and B.M. designed research. A.W., M.H., N.B., T.C., and G.S. performed research. A.W. and M.H. analyzed data. B.M. wrote the manuscript.

Editor: Alex Mogilner.