Free energy and kinetics of cAMP permeation through connexin26 via applied voltage and milestoning

Abstract

The connexin family is a diverse group of highly regulated wide-pore channels permeable to biological signaling molecules. Despite the critical roles of connexins in mediating selective molecular signaling in health and disease, the basis of molecular permeation through these pores remains unclear. Here, we report the thermodynamics and kinetics of binding and transport of a second messenger, adenosine-3′,5′-cyclophosphate (cAMP), through a connexin26 hemichannel (Cx26). First, inward and outward fluxes of cAMP molecules solvated in KCl solution were obtained from 4 μs of ± 200 mV simulations. These fluxes data yielded a single-channel permeability of cAMP and cAMP/K⁺ permeability ratio consistent with experimentally measured values. The results from voltage simulations were then compared with the potential of mean force (PMF) and the mean first passage times (MFPTs) of a single cAMP without voltage, obtained from a total of 16.5 μs of Voronoi-tessellated Markovian milestoning simulations. Both the voltage simulations and the milestoning simulations revealed two cAMP-binding sites, for which the binding constants K_D and dissociation rates k_off were computed from PMF and MFPTs. The protein dipole inside the pore produces an asymmetric PMF, reflected in unequal cAMP MFPTs in each direction once within the pore. The free energy profiles under opposite voltages were derived from the milestoning PMF and revealed the interplay between voltage and channel polarity on the total free energy. In addition, we show how these factors influence the cAMP dipole vector during permeation, and how cAMP affects the local and nonlocal pore diameter in a position-dependent manner.

Significance

Connexins are wide-pore channels permeable to cellular signaling molecules. They mediate molecular signaling crucial in physiology, pathology, and development; mutations in connexins cause human pathologies. However, the fundamental structural, thermodynamic, and kinetic determinants of molecular permeability properties are unknown. Using multiple molecular dynamics simulation techniques, we report an in-depth investigation of the free energy and the directional transition rates of an important biological signaling molecule, adenosine-3′,5′-cyclophosphate, through a connexin channel. We reveal the energetics and binding sites that determine the adenosine-3′,5′-cyclophosphate flux, and the effects of mobile ions and external electrical field on the process. The results provide a basis for understanding the unique features of molecular flux through connexins and other wide-pore channels.

Introduction

Many protein channels are known to have pores sufficiently wide enough to mediate the permeation of small molecules, here defined as having molecular mass between 100 and 1000 Da, in addition to atomic ions. Wide-pore channels fall into two structural categories: channels in which the basic pore structure is formed by curved and closed β-sheet (β-barrel channels) and channels in which the pore is formed by transmembrane α-helical domains roughly normal to the plane of the membrane. The former are found in prokaryotes and in the prokaryotic-derived organelles (chloroplasts and mitochondria) of eukaryotes. Well-known examples include VDAC (voltage-dependent anion channel) and the extensive bacterial porin family (1). Non-β-barrel wide channels are found in eukaryotic and some bacterial plasma membranes. In eukaryotes, they include connexins, pannexins, innexins, calcium homeostasis modulator and volume-regulated anion channel (2,3). The fundamental backbone structures of the two classes of pores differ greatly, which likely has consequences for the dynamics and mechanisms of molecular permeation and selectivity. Although biological signaling molecules are known to permeate the eukaryotic wide pores, the mechanism of permeation has not been explored computationally to date.

Connexin proteins can function as plasma membrane channels (“hemichannels”) or as intercellular channels (“gap junction channels”), which allow direct transfer of small cytoplasmic molecules between cells. The intercellular channels are formed by end-to-end docking of two hemichannels across the extracellular gap between adjacent cells. The pores are permeable to atomic ions and small molecules in the size-range of key cellular signaling molecules including cAMP, cGMP, ATP, IP₃, and glutathione. Each of the 21 human connexin isoforms are composed of channels with distinct permeability and regulatory properties (4,5). With the exception of electrical signaling in excitable tissues, the primary biological function of connexin channels is to mediate movement of small cytoplasmic signaling molecules and metabolites between cells and/or to release them into the extracellular environment in a highly regulated manner. Mutations in connexins that alter channel function or expression produce human pathologies (6,7). These mutations ultimately exert their pathological effects by disrupting the proper molecular permeability of junctional and/or plasma membranes.

A large literature documents that channels formed by the different connexin isoforms have dramatically different permeability properties. Their unitary conductances range from 10 to 300 pS, their cation/anion permeability ratios (P_K+/P_Cl-) range from 8.0 to 0.8, and their permeabilities to fluorescent tracers are highly disparate. Strikingly, none of these parameters correlate with each other (e.g., the connexin channel with the largest unitary conductance is among the most size-restrictive). Quantitative measurements of permeability to biological signaling molecules are difficult to obtain as the molecules are not fluorescent and do not carry significant current in the presence of physiological saline. Nevertheless, it is clear that among the different connexin channels, permeabilities to biological signaling molecules are quite distinct. Furthermore, for a given type of connexin channel, there are remarkable degrees of selectivity and relative permeability among biological permeants. These connexin-specific and permeant-specific permeability properties are not reasonably inferred from differences in permeabilities to fluorescent tracers (8).

Molecular dynamics (MD) simulation has been used to study the permeation of various small molecules through channels. Most studies have focused on β-barrel channels, including ATP transport through VDAC (9,10), various substrates transported through Omp (11, 12, 13, 14, 15), and DNA and peptide translocation through α-hemolysin (16, 17, 18, 19). Permeation of molecules with mass less than 100 Da, such as urea, glycerol, and acetate, through highly selective and relatively narrow non-β-barrel pores have also been computationally studied (e.g., aquaporins (20, 21, 22, 23, 24), acetate channels (25), and urea channels (26,27)). To our knowledge, this is the first computational study of a biological relevant molecule crossing a non-β-barrel wide-pore channel.

Previous work refined the open state connexin26 (Cx26) crystal structure using all-atom MD simulation and reproduced the experimental single-channel conductance to atomic ions with Grand Canonical Monte Carlo Brownian dynamics simulations (28). Using this model, we have explored the free energy profiles of uncharged permeant and nonpermeant tracer molecules (∼500 Da) with Hamiltonian replica-exchange umbrella sampling (29). That study indicated that the determinants of molecular permeation differ from those that dominate the permeation of atomic ions, emphasizing the unique aspects of small molecules with conformational and orientational degrees of freedom in a wide pore. However, although validating the atomistic system and overall free energy profiles, quantitative kinetic information of the permeation process is still missing. Furthermore, the results using uncharged tracer molecules do not characterize the biomedically crucial process of permeation by biological signaling molecules, which typically are charged. This study explores the binding and transport kinetics of a negatively charged second messenger, adenosine-3′,5′-cyclophosphate (cAMP), as it permeates a connexin pore. Not only is cAMP an important signaling molecule known to permeate connexin channels (8,30,31), its experimentally assessed transit time from two independent groups is in the range of low microseconds (32,33), making it suitable for investigation by atomistic simulation. In addition, the size of cAMP is similar to the sugar permeant we previously simulated in Cx26 but differs in molecular charge (29).

All-atom MD simulation of a single permeation event with a timescale of submicrosecond to microseconds is within reach of today’s computational power. However, a large number of transition events are required to obtain meaningful statistics, for which simulations orders of magnitude longer than the mean transition time are required. For a charged molecule such as cAMP, permeation can be accelerated by imposing a voltage or concentration gradient. Theoretically, if the system reaches a steady state, a mean flux rate and a steady-state density profile can be obtained from the ensemble of nonequilibrium processes using a sufficient number of permeation events. However, the effect of an unphysiologically large voltage or electrochemical gradient on channel property is likely system dependent and difficult to predict over a long simulation time.

Because a permeation process is a mix of small barrier crossing (diffusive) process and large barrier crossing (binding/unbinding) processes, the overall rate is often dominated by the free energy profile or potential of mean force (PMF) along the channel axis. Various methods have been developed to estimate the transition rate from PMF, such as the Smoluchowski diffusion model or a reactive flux model. Previously we estimated the relative transition rates of two sugar molecules through Cx26 using transition state theory based on PMF profiles (29). However, transition state theory requires assumptions such as a single dominant transition state and no recrossing at the barriers, which are often difficult to satisfy even for a simple ion pair dissociation (34). Alternatively, a class of rare-event sampling techniques have been developed, such as Markov state models (MSM) (35), milestoning (36), weighted ensemble path sampling (37, 38, 39). Those techniques allow extraction of kinetic quantities directly from short MD simulations, without assumptions on single-barrier crossing or computing the position-dependent diffusion coefficient. A notable application of MSM in a wide-pore channel is ATP permeation through VDAC (10).

Voronoi-tessellated Markovian milestoning is a version of milestoning that allows reconstruction of the long-time dynamics of a system from independent simulations confined within a set of cells spanning the space of the reaction coordinates (40). Compared with conventional MSM, milestoning does not require the definition of a lag time. In addition, the Markovian assumption in Markovian milestoning refers to transitions between hypersurfaces of the phase space (milestones), which makes it easier to be satisfied or approximated than in MSM, in which transitions between regions of space are considered (41). Indeed, it was shown that Markovian milestoning yields exact mean first passage times (MFPTs) if the milestones are chosen such that successive transitions between them are statistically independent (40,41). This method has successfully captured the rates of CO entry/exit in myoglobin (42) and protein-ligand binding kinetics (43).

Here, we make use of the “soft-walls” Voronoi-tessellated Markovian milestoning (referred to as “milestoning” hereafter), which confines the sampling within the Voronoi cells using flat-bottom harmonic restraining potentials (44). This approach is easy to implement, allowing us to take advantage of CUDA-accelerated MD engine, and has been shown to yield the same results as the original “hard-walls” version, which instead inverts atomic velocities at the cell boundaries. The “soft-walls” version has been used to study nucleation of an ionic liquid (45) and ion permeation across a paracellular channel (46) and a nicotinic acetylcholine receptor (47). In this study, we use milestoning to reconstruct the kinetics of a single cAMP molecule permeation through an open Cx26 hemichannel. Using both nonequilibrium and rare-event sampling approaches, our results revealed that the steady-state distribution of cAMP inside the channel captures similar energetic barrier and binding sites as from milestoning, though opposite voltages exert different perturbation on the cAMP permeation kinetics because of the intrinsic protein dipole.

Materials and methods

Force field and cAMP parameterization

CHARMM36 force field was used for protein (48,49), 1-palmitoyl-2-oleoylphosphatidylcoline (POPC) lipids (50), KCl, and TIP3P water (51). Mg²⁺ parameters were from Yoo and Aksimentiev (52), in which the van der Waals (vdW) interaction parameters were fine-tuned to reproduce experimental osmotic pressure. For cAMP, force field parameters were first generated from CHARMM CGenFF (53). Additional dihedral fitting between imidazole and pyran groups in the cAMP structure was performed in VMD ffTK plugin (54). The final optimized cAMP parameters are provided in Table S1 and available at https://github.com/LynaLuo-Lab/Connexin-cAMP-milestoning.

System setup and equilibrium protocol

The atomistic model of Cx26 hemichannel was taken from our previous work (29). The system of Cx26 embedded in a solvated POPC bilayer with ions and TIP3P water molecules was built and equilibrated following the step-by-step protocol used in Membrane Builder on CHARMM-GUI website (55,56). The terminal amino acid of each segment was capped using acetylated N-terminus and methylated C-terminus. Three disulfide bonds were added between the residue pairs of C53 and C180, C64 and C169, and C60 and C174, respectively, per protomer, so the entire channel contained a total of 18 disulfide bonds, consistent with the original crystal structure of the Cx26 junctional channel (Protein Data Bank: 2ZW3). Recent cryo-EM of purified Cx26 hemichannels in nanodiscs confirms that the hemichannel structure is essentially the same as that in junctional channels (57). Two systems containing a single cAMP for milestoning simulations and 27 cAMP molecules for nonequilibrium simulations were constructed. K⁺ and Cl⁻ ions were added to mimic physiological salt concentration and also to neutralize the protein charge. In addition, Mg²⁺ ions were added in 1:1 ratio with cAMP to explore whether copermeation of Mg²⁺ and cAMP exists (see Table S2 for system details). The system was energy minimized and serially equilibrated in NVT and NPT ensembles with positional restraints using AMBER18 (58). Temperature was maintained at 310.15 K using Langevin thermostat (59,60) and 1 atm was maintained by Monte Carlo barostat pressure control (61,62). The time step was 2 fs. Cutoff for calculating vdW interactions and short-range electrostatic interactions was set at 12 Å and force-switched at 10 Å. Long-range electrostatic interactions were calculated using the particle mesh Ewald algorithm (63).

Voltage simulation protocol

After 35 ns of equilibrium simulation using AMBER18, the system was run on Anton2 supercomputer with 2.0 fs timestep. Lennard-Jones interactions were truncated at 11–13 Å, and long-range electrostatics were evaluated using the k-Gaussian Split Ewald method (64). Pressure regulation was accomplished via the Martyna-Tobias-Klein barostat, to maintain one bar of pressure, with a τ-parameter of 0.0416667 ps and reference temperature of 310.15 K. The barostat period was set to the default value of 480 ps per timestep. Temperature control was accomplished via the Nosé-Hoover thermostat with the same τ-parameter. The mts parameter was set to four timesteps for the barostat control and one timestep for the temperature control. The thermostat interval was set to the default value of 24 ps per timestep. A 600 ns equilibrium simulation was finished before applying voltage. Constant electric fields of −200 or +200 mV, respectively, were added for 2 μs of simulation time with trajectories saved every 200 ps.

Markovian milestoning

For a molecular permeation event through a channel, it is reasonable to consider the progression of the permeant along the pore axis as the reaction coordinate. This allowed us to define a set of Voronoi cells along the axis coordinate, and to identify the milestones as the boundaries between the cells. We then ran many local simulations confined in the cells and collected kinetics of transitions between milestones. In detail, we introduced a set of M Voronoi cells B_i, i = 1,…,M. If k_i→j is the rate of attempted escape from cells B_i to B_j, because at statistical equilibrium the total flux in and out of each cell is zero, the equilibrium probability π_i for the permeant to be in cell B_i satisfies a balance equation:

$$\sum _{j=1,j\ne i}{\pi }_j{k}_{j\to i}=\sum _{j=1,j\ne i}{\pi }_i{k}_{i\to j,}\sum _{i=1}{\pi }_i=1.$$ (1)

The free energy of each cell can be obtained from the solution of Eq. 1 as -k_BTln(π_i). By defining a milestone S_ij as the boundary between two adjacent Voronoi cells B_i and B_j, the dynamics of the system is reduced to that of a Markov chain in the state space of the milestone indices (40). The MFPT between any pair of milestones S_ij and S_ik can hence be calculated from the rate matrix whose elements q_ij,ik, the rate of moving from milestone S_ij to S_ik, are given by Eq. 2:

$$q_{ij,ik}=\frac{{\pi }_i{n}_{ij,ik}^i}{{\pi }_i{r}_{ij}^i+{\pi }_j{r}_{ij}^j},$$ (2)

where $n_{ij,ik}^i$ is the number of transitions from S_ij to S_ik, normalized by the time spent in cell B_i, and $r_{ij}^i$ is the time passed in cell B_i after having hit S_ij before hitting any other milestone, normalized by the total time spent in cell B_i. The inward and outward MFPT profiles were obtained by reversing the milestone indices when constructing the rate matrix.

Milestoning MD simulation setup

A total of 53 Voronoi cells were evenly distributed 2 Å apart along the z axis. The AMBER18 CUDA version currently does not support Cartesian coordinates as a collective variable. Thus, we pinned two water molecules using high Cartesian restraint of 6000 kcal mol⁻¹ Å⁻² force constant in the top and bottom bulk regions (20 Å away from the intracellular entrance and 35 Å away from the extracellular entrance of the channel). We then used the projected distance on the z vector between the nearest pinned water oxygen and center of mass of cAMP to define the Voronoi cells along the z axis. A cylindrical restraint with a radius of 30 Å and force constant 1 kcal mol⁻¹ Å⁻² was applied to cAMP to confine the sampling in the bulk region. To prevent protein drifting, a harmonic distance restraint with force constant 2000 kcal mol⁻¹ Å⁻² along x, y, and z axes between the fixed water oxygen in intracellular bulk and the center of mass of the protein was added. The simulation protocol, nonbonded cutoff, and PME are the same as the AMBER18 protocol described above, except all milestoning simulations were run in NVT ensemble. A Langevin thermostat at 310.15 K and a friction coefficient of 1.0 ps⁻¹ was used (65). To avoid missing transition events, which would over-estimate the MFPT, all the milestoning trajectories were saved every 1 ps (timestep 0.2 fs). Confinement within the Voronoi cells was obtained using flat-harmonic restraint with force constant of 100 kcal mol⁻¹ Å⁻².

Decorrelation time versus wait time between transitions

Markovian milestoning yields exact MFPTs if the milestones are chosen such that successive transitions between them are statistically independent (41). To check this assumption for transitions between two neighboring milestones, in each cell, the velocity autocorrelation function and position autocorrelation function were computed for cAMP (Fig. S1, a and b) and compared with the average wait time of transition event between two milestones (Fig. S1 c). For all pairs of milestones, the z velocity decorrelation time is within few tens of fs and the z position decorrelation time is between 5 and 348 ps. In contrast, the average wait time for transition between milestones ranges from 1.5 to 233 ns, except for cell 19, which has a wait time of 470 ns, corresponding to the major cAMP-binding site (see Results). Therefore, in our milestoning setup, the decorrelation time is much smaller than the wait time of transition between two milestones.

Convergence of PMF and MFPT from milestoning

Running independent simulations in the many Voronoi cells allows focused sampling on the cells with slow convergence. For PMF, the convergence of π_i (Eq. 1) was monitored on the fly by plotting the accumulated rate of attempted escape on both sides of the cell B_i, called k_i→j and k_i→k, as well as the retention rate inside each cell B_i over time (Fig. S2 a). The convergence of MFPT can be monitored directly from the accumulated $n_{ij,ik}^i$ and $r_{ij}^i$ (Fig. S2 b). The final 10 ns windowed relative root mean-square deviation (RMSD) (given at the top of each panel) can serve as a measure of the degree of convergence for the corresponding rate matrix entry components. RMSD within 5% (averaged over all replicas) was used as convergence criteria for all Voronoi cells (in most cases, RMSD is below 2% of the mean value). The convergence plots of all 53 cells are available on Github https://github.com/LynaLuo-Lab/Connexin-cAMP-milestoning. By monitoring the convergence plots on the fly, our code allows users to employ trajectories of arbitrary length and number of replicas within milestoning cells to improve sampling. Based on our convergence criteria, the sampling time in each cell ranges from 20 ns to 2 $\mu \text{s}$ (Fig. S2 c), which yields a total 16.5 μs of multireplica milestoning. The confidence intervals of the PMF and MFPTs were computed by sampling k_ij, $n_{ij,ik}^i$ and $r_{ij}^i$ using Markov chain Monte Carlo procedure (43,66).

Results

cAMP flux and single-channel permeability from voltage simulations

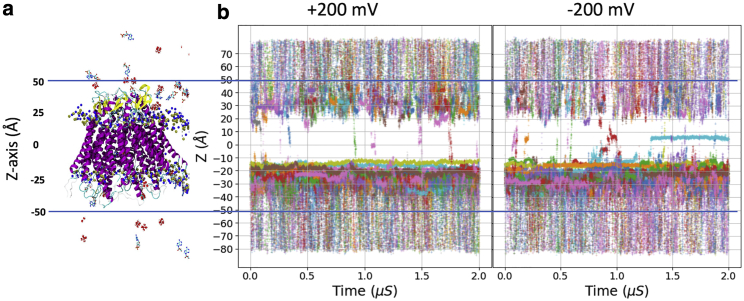
The single-channel permeability for cAMP was computed from inward/outward flux rates under voltages and symmetric cAMP concentrations using a previously validated open pore of Cx26 hemichannel model (28,29). To obtain a sufficient number of transition events and ensure unidirectional flux, we applied ±200 mV transmembrane potentials. Based on the number of water molecules in the simulated system, one cAMP corresponds to ∼1 mM concentration (physiological concentration is in low $\mu$M range). To increase the probability of cAMP diffusing to the pore, 27 cAMP molecules were included in the system, corresponding to 26.5 mM (Table S2). Using z < |50| Å as boundaries of the hemichannel (center of mass of protein is at z = 0 Å), nine single-molecule transitions were observed at +200 mV and 12 transitions at −200 mV during each 2 μs simulation (Fig. 1; Table 1; raw data in Table S3). All transitions were in the same direction at each voltage. The confidence interval for the average transition time (<t>) of cAMP was obtained by fitting the transition times to an exponential distribution. Based on maximum likelihood estimation, <t> is 448 ns at +200 mV with 95% confidence interval (CI₉₅) of 204–1646 ns, and 510 ns (CI₉₅, 249–1571 ns) at −200 mV. The average time between consecutive transition events (τ = length of simulation ÷ number of transits) is 222 ns at +200 mV and 166 ns at −200 mV. Given the confidence intervals, there is no significant difference in the flux in each direction. The ratio <t>/τ is 2.0 and 3.1, for +200 and −200 mV, respectively, which indicates there are on average two to three cAMP molecules in the channel at any given time at each voltage. Inspection of the trajectories shows that this is only due exclusively to the binding of multiple cAMP molecules at the intracellular entrance (Figs. 2 and 3).

Figure 1.

Simulations of cAMP permeation through Cx26 hemichannel at ±200 mV membrane potential. (a) Snapshot of the simulated system. Protein backbone is shown in cartoon mode and colored by the secondary structure (helix in magenta, β-sheet in yellow, loop in cyan). cAMP molecules are shown in licorice with atom color code (red, oxygen; cyan, carbon; blue, nitrogen; yellow, phosphorus). Lipids, ions, and water molecules are not shown. (b) The z coordinates of all 27 cAMP molecules during the simulations are shown in different colors. Note that the flux of cAMP is in the direction opposite to the field; thus, cAMP flux is inward (down in this figure) under +200 mV and outward under −200 mV. Data are summarized in Table 1. To see this figure in color, go online.

Table 1.

Transition time of cAMP through Cx26 hemichannel under voltage

	+200 mV	−200 mV
cAMP flux direction	Inward	outward
Transition events in 2 μs	9	12
Events per μs	4.5	6.0
Time between transition events	222 ns	166 ns
Mean transition time (CI95)a	448 ns (204–1646)	510 ns (249–1571)
Mean dwell time (CI95)	305 ns (149–940)	398 ns (205–1086)
Mean barrier crossing time (CI95)	143 ns (79–330)	106 ns (54–290)

^aSample mean and CI₉₅ values are based on maximum likelihood estimate by fitting the exponential distributions (see Code availability).

Figure 2.

Charge density and cAMP mass density profiles from voltage simulations. (a) Charge density of protein, lipids, total ions, and individual charged groups (K⁺, Cl⁻, cAMP, Mg²⁺) along the channel z axis from the −200 mV simulation. (b) Volumetric mass density of cAMP from −200 mV simulation. Density higher than bulk is shown (green to red color representing low to high). (c) Boltzmann inversion of the cAMP 2D-density (log-density) along the channel z axis and radial distance $R=\sqrt{{\left(x_{cAMP}\right)}^2+{\left(y_{cAMP}\right)}^2}$ from channel center axis (x,y = 0,0). (d) 1D log-density of the cAMP within the pore along z axis. Arrows indicate the direction of cAMP flux at each voltage. Note that a log-density profile is not a PMF (see PMFs under voltage in Fig. 5). To see this figure in color, go online.

Figure 3.

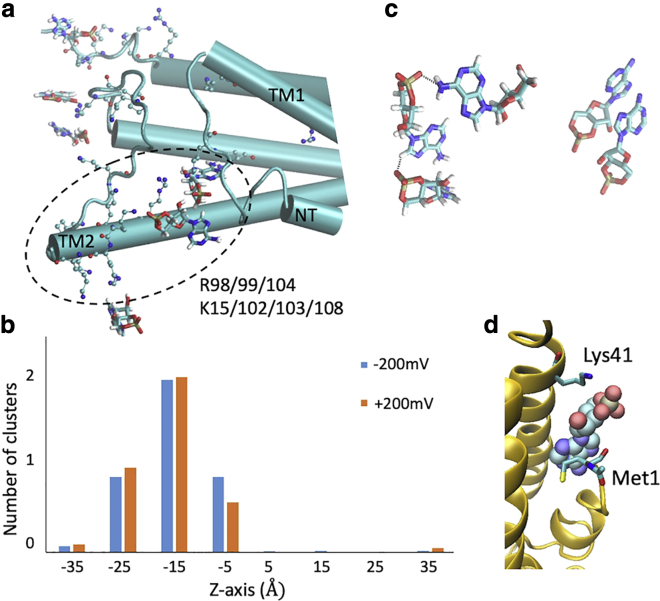
cAMP-cAMP interactions and cAMP-channel interactions. (a) Snapshot showing cAMP molecules (in licorice mode) near positively charged residues (in CPK mode) at the intracellular entrance, corresponding to the high density in Fig. 2b. Protein is in cartoon mode. (b) Number of cAMP clusters in each 10 Å window along the channel z axis during ±200 mV simulations. A cluster is defined as at least two cAMP molecules with centers of mass within 20 Å at any time during the simulations. (c) Snapshots of two cAMPs clustered via π-stacking and three cAMPs clustered via hydrogen bonds. (d) Snapshot showing one cAMP trapped between Lys41 and Met1 under −200 mV simulation, corresponding to the blue trace in Fig. 1b. To see this figure in color, go online.

Quantitative experimental measurements of the flux of cAMP through Cx26 channels in cells are very complex and subject to a variety of potential confounding factors (8). Although there is no transition rate reported for hemichannels, two studies, which used different indirect strategies to report cAMP flux through junctional channels in the absence of junctional voltage, yielded estimates of cAMP permeability of 6.2 × 10⁻³ and 47 × 10⁻³ μm³ s⁻¹, respectively (32,33). Under symmetric concentration and voltage, the current $\left(I\right)$ and the permeability $\left(P\right)$ can be related by the Goldman-Hodgkin-Katz current equation, $I=P{z}^2\frac{V_m{F}^2}{RT}\left[c\right],$ where $z$ is the charge of cAMP (−1e), $V_m$ is the voltage, F is the Faraday constant, R is the gas constant, T is the absolute temperature, and $\left[c\right]$ is the concentration of cAMP. If we use the average of inward and outward transition times (479 ns) under ±200 mV, the current is 3.3 × 10⁻¹³ C s⁻¹. Thus, the single-channel permeability (P) of cAMP crossing an open Cx26 junctional channel at 310.15 K obtained from our voltage simulations is 16.58 × 10⁻³ μm³ s⁻¹, which is in between the two experimentally measured values.

An experimental cAMP/K⁺ permeability ratio of 0.027 was previously reported using simultaneous measurements of Cx26 junctional conductance and reporter-based intercellular transfer of cAMP (33). We calculated K⁺ transition time in presence of 27 cAMP is 13.1±13.0 ns at +200 mV and 6.8$\pm$7.8 ns at −200 mV. If we approximate the time needed to cross the junctional channel (two hemichannels docked at the extracellular ends) is the sum of the transition time in two opposite directions, we obtain a cAMP/K⁺ ratio of 0.021, reasonably close to the experimental ratio of 0.027.

Pore cAMP density and binding sites from voltage simulations

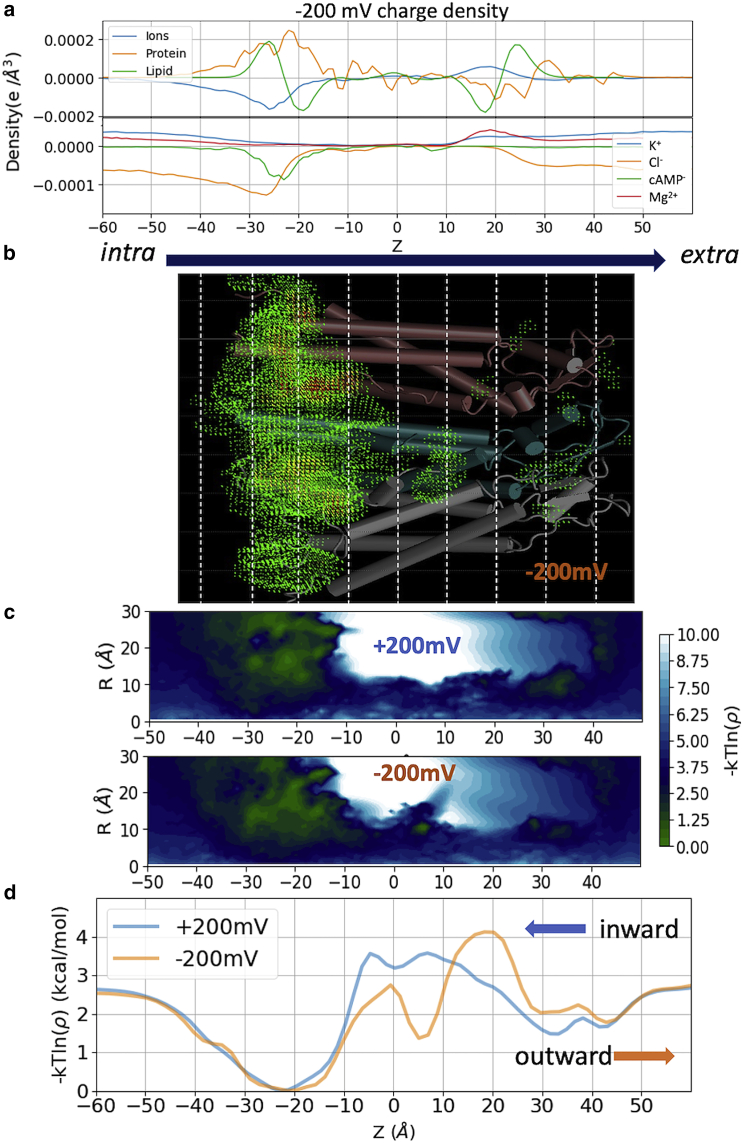
Once the accumulated cAMP density along the channel from voltage simulations reaches the steady state, it can provide an estimate of the locations of energetic barriers and binding sites. We first plotted the charge densities of protein, lipids, total ions, and individual ions (K⁺, Cl⁻, cAMP, Mg²⁺) along the channel z axis (Fig. 2 a). It can be seen that the channel is largely positive at intracellular entrance where the highest density of Cl⁻ and cAMP anions are located. The increased density of cAMP at the intracellular entrance can be seen in Fig. 1 and in the three-dimensional (3D) density of cAMP inside the channel in Fig. 2 b. A smooth indicator of cAMP distribution is shown using Boltzmann inversion $\left(-kTln\left(\rho \right)\right)$ of the cAMP density; we will call these log-density plots. Fig. 2 c shows the two-dimensional (2D) cAMP log-density along the z axis and the lateral distance from center of channel lumen (R). Fig. 2 d is the one-dimensional (1D) cAMP log-density along the z axis. Note that these log-density profiles are acquired from nonequilibrium simulations under the influence of voltage, hence do not represent equilibrium free energy profiles. The symmetric cAMP density in the bulk regions on each side of the channel is the result of the periodic boundary condition used for MD simulations. We will derive the PMFs under voltages using the equilibrium PMF from the milestoning simulation (Fig. 5).

Figure 5.

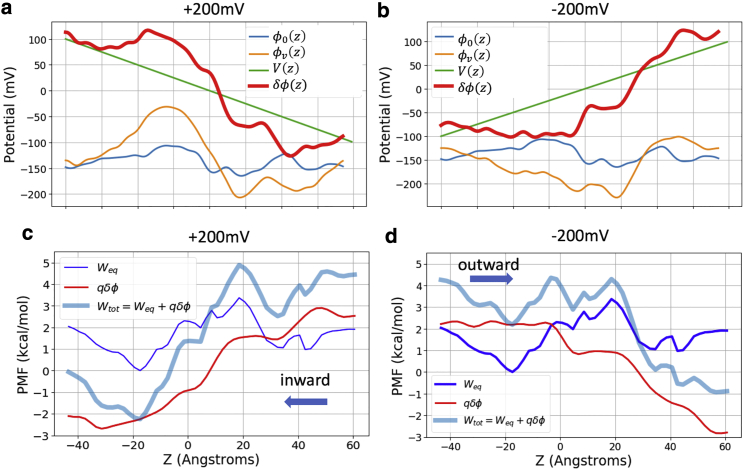
Electrostatic potentials and PMFs under voltages. (a and b) Applied potential in green (±200 mV) and the electrostatic potential under voltage φ_v(z) in orange, and without voltage φ₀(z) in blue. The sum of applied potential and reaction potential (see Eq. 4) in shown in red. (c and d) Total PMF under a constant electric field (thick blue line) computed using Eq. 4. The intrinsic PMF in absence of an electric field (thin blue line) is obtained from milestoning, and the additional electrostatic potential energy introduced by the applied field (red line) is computed from (a and b). To see this figure in color, go online.

The 1D cAMP log-density profiles (Fig. 2 d) have a broad minimum at the intracellular entrance of the channel and a major peak in the middle of the channel. The shapes of the global minimal region are essentially identical under both voltages. There is a second well in the −200 mV density that appears to bisect the central peak (discussed below). The dwell times of cAMP (Table 1) at the broad minimum (−50 < z < 10 Å) are quite large under both voltages: 305 ns at +200 mV, and 398 ns at −200 mV (Table 1). In contrast, the rest of the channel region (−10 < z < 50 Å), which contains the major barriers, was crossed by cAMP more rapidly: 143 ns for inward flux (at +200 mV), and 106 ns for outward flux (at −200 mV).

The cAMP-binding site (−50 < z < −10 Å) present at both voltages is located in the C-terminal regions of the second transmembrane helix (TM2) and the N-terminal helix (NTH). Contact frequency analysis between cAMPs and protein sidechains indicates that cAMP bind to R99/104 and K103 on TM2 over 70% of the simulated time, and bind to K102 and R98 on TM2, and K15 on NTH over 30% of the time (Fig. 3 a). Further investigation reveals that the cAMP forms clusters between −30 < z < 0 Å, but almost no clusters are found in the rest of the channel (Fig. 3 b). Most of the clusters contain 2 cAMPs, which interact through π-stacking of adenosine rings. Clusters of three cAMPs forming hydrogen bonds with each other also exist (Fig. 3 c). These clusters are not seen in the bulk. It appears that the positively charged residues at the intracellular entrance of the pore facilitate cAMP clustering by reducing the translational and rotational entropy of the molecules.

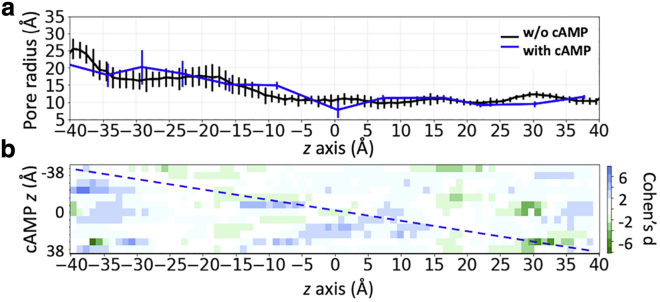
To check whether this cAMP clustering produces a “crowding” effect at the entrance of the pore, we compared the radius of the unoccupied lumen with and without cAMP molecules (Fig. S3 a). The minimal radius between −35 < z < −15 Å suggests that the presence of multiple cAMPs blocks the pore very transiently, so has little effect on the average and standard deviation values of the available cross-sectional area at the pore entrance (radius > 8 Å). In addition, the peaks in the two log-density profiles (Fig. 2 d) do not closely correlate with the narrow regions of the pore (see Figs. 8 a and Document S1. Figs. S1–S5 and Tables S1–S3, Document S2. Article plus supporting material a for radius measurements using two different methods), indicating that steric hindrance is not a major contributor to the cAMP transition barrier. This is also consistent with the number of water molecules in the cAMP solvation shell decreasing slightly only at the intracellular binding site but remains intact throughout the narrow pore region (Fig. S3 b).

Figure 8.

Local and nonlocal effect of cAMP on Cx26 pore radius. (a) The mean and standard deviation of Cx26 pore radius as a function of the pore axis (z) during simulations. Black line is the pore radius without cAMP and the blue line is the radius at the position of the cAMP. (b) Cohen d-scores of pore radius distributions (see Eq. 5). The y axis indicates the z position of the cAMP, and x axis is the full-length pore axis. The dashed diagonal line indicates changes in pore radius at the position of the cAMP, whereas off-diagonal colors indicate cAMP’s nonlocal effect on the pore radius. Blue color indicates cAMP increase the pore radius, and green color indicates cAMP decrease the pore radius. To see this figure in color, go online.

During one of the 12 permeation events at −200 mV simulation, one cAMP was trapped between Met1 in the NTH and Lys41 on the first transmembrane helix (TM1) (Figs. 1 b and 3 d). This was reflected in the log-density profile as a large dip in the bisected peak at z = 5 Å (Fig. 2 d). Both NTH and Lys41 have been suggested to be involved in voltage-sensing in Cx26 (67,68). This raised the question of whether the single instance of a long residency of a cAMP molecule at this position at −200 mV, but not at +200 or 0 mV (from milestoning PMF below) is a consequence of voltage-driven repositioning of these charged moieties. To evaluate their responses to the electric field, we plotted the orientation angles between the z axis and the principal vector of Lys41 or NTH (residues 1–11) on each channel subunit (Fig. S4, a and b). Except for a reduction in Lys41 fluctuation in subunit 5, where the cAMP was trapped, there is no clear preference in the orientation of the Lys41 or NTH in response to the two opposite voltages. Of course, this result does not indicate that the NTH and Lys41 are uninvolved in voltage-sensing, only that they did not respond to ±200 mV within the 2-μs simulations. Below we show that this binding site (z = 5 Å) occured under negative voltage is not due to protein conformational change in response to voltage, but the result of the PMF under voltage (Fig. 5).

Free energy profiles of cAMP permeation using Markovian milestoning

The two voltage simulations above resulted in similar cAMP density profiles and similar ranges of flux rates. However, the small number of stochastic events (21 in total) led to the large uncertainty in the transition rate. In contrast to a long trajectory exploring the whole channel, multiple MD simulations confined in intervals partitioning the space can offer sufficient statistics within a shorter running time. Here, Voronoi-tessellated Markovian milestoning on a tessellation along the z coordinate of the center of mass of a single cAMP is used to estimate the PMF and the MFPT of permeation through the channel at zero membrane voltage (see Materials and methods and Code availability).

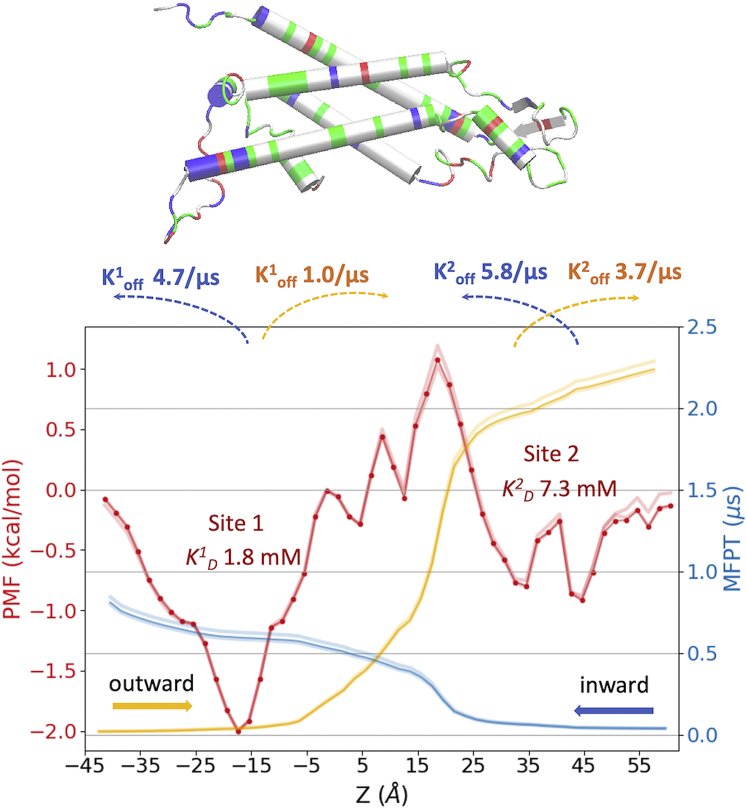
Fig. 4 shows the 1D PMF (in red) obtained from the equilibrium probability of finding cAMP in each milestoning cell. This PMF of a single cAMP permeating without applied voltage shares key common features with the log-density plots from the voltage simulations (an intracellular binding site and a free energy barrier spans between −20 < z < 30 Å). The height of the barrier relative to bulk (1.2 kcal/mol) is between those seen at −200 mV (1.8 kcal/mol) and +200 mV (0.8 kcal/mol). However, the binding wells (z ≈ −20 Å) from voltage simulations are wider and deeper (−2.8 kcal/mol) than the well in the PMF (−2 kcal/mol), likely due to the cAMP clustering that is absent in the single cAMP milestoning.

Figure 4.

Free energy and kinetics of a single cAMP permeation through Cx26 hemichannel from milestoning simulation (V = 0 mV). PMF in red, inward MFPTs in blue, and outward MFPTs in orange. The CI₉₅ confidence intervals are represented by shaded colors (see Materials and methods). Binding constants and dissociation rates derived from PMF and MFPT profiles are indicated. The graphic at the top shows the backbone of one Cx26 subunit with z positions aligned with the plot below (basic residues in blue, acidic in red, polar in green, and nonpolar in white). To see this figure in color, go online.

Like the voltage simulations, milestoning simulation without voltage reveals two binding sites for cAMP, a major one (site 1) near the intracellular entrance between NT and TM2 and a (bisected) much smaller one (site 2) at the extracellular loop (E1) region (Fig. 4). The single cAMP dissociation constant, K_D, can be estimated from the single cAMP equilibrium PMF using Eq. 3 (69):

$$1/K_D=\pi R^2\underset{z_1}{\overset{z_2}{\int }}dz{e}^{-W\left(z\right)/k_{B}T}.$$ (3)

W(z) is the PMF with bulk as reference. R is the radius of a cylindrical restraint (30 Å). Integrals over individual energy wells indicate that cAMP binds to the intracellular site (binding site 1: −43.4 < z < 18.6 Å) with K_D of 1.8 mM and to the extracellular site (binding site 2: 18.6 < z < 60.6 Å) with K_D of 7.3 mM (Fig. 4). The integral over the entire PMF yields a total K_D of 1.4 mM for the entire channel. Thus, at the bulk cAMP concentration of the voltage simulations (26.5 mM), both binding sites are likely highly occupied, whereas at the concentration equivalent to the single cAMP used in milestoning (1 mM), none of the binding sites would be occupied more than 50%.

Kinetics of cAMP permeation and binding using Markovian milestoning

The inward and outward MFPT profiles inside the channel (Fig. 4, blue and orange) suggest that it takes ∼0.81 μs (CI₉₅, 0.80–0.82 μs) for the inward transition and 2.23 μs (CI₉₅, 2.22–2.25 μs) for the outward transition. The faster inward than outward transition time inside the channel is consistent with the asymmetric PMF, which shows a maximum of 3.2 kcal/mol barrier for outward flux, which takes 1.0 μs to cross, whereas the two smaller barriers of 2.0 kcal/mol for inward flux only take 212 ns (site 1) and 145 ns (site 2) to cross. It should be noted that the MFPT profiles obtained here only describe the kinetics of diffusion, binding/unbinding and barrier crossing of a single cAMP inside the pore and a limited solvent region close to the entrances, hence do not include the exchange rate with bulk. The full kinetics and flux at finite bulk concentrations of the permeant also depend on bulk diffusivity and concentration, and the diameters of the entrance at each end of the pore. For instance, diffusion current to a disk-like adsorber is I = 4DRC, where C is the permeant concentration in the infinite bulk, D is bulk diffusion constant, and R is the radius of the disk-shaped absorber (70). For Cx26 hemichannel, the intracellular entrance (radius R = 25 Å) is larger than the extracellular entrance (R = 10 Å) (see pore radius in Fig. 8 a). Considering the effective radius of cAMP as r = 3.75 Å (calculated from the maximal solvation shell distance minus the effective radius of water, see Fig. S3 b), the effective pore radii are 21.25 and 6.25 Å for the intracellular and extracellular pore entrances, respectively, indicating that it is ∼3.4-fold more likely for cAMP to reach the pore by random diffusion from bulk to the intracellular than the extracellular side. This consideration, along with the calculated MFPTs, yields approximately equal fluxes in each direction in the absence of a cAMP concentration gradient.

Based on the locations of the binding sites identified by the PMF, we can use MFPT profiles to estimate the time needed for a single cAMP to exit each binding site (i.e., dissociation rate k_off). For outward transition, k_off¹ for binding site 1 is 1.0 μs⁻¹ (−17.4 < z < 18.6) and k_off² for binding site 2 is 3.7 μs⁻¹ (32.6 < z < 60.6). For inward permeation, k_off¹ is 4.7 μs⁻¹ (−41.4 < z < −17.4) and k_off² is 5.8 μs⁻¹ (18.6 < z < 42.6) (Fig. 4). Together with the equilibrium constant K_D from the PMF, one can estimate the association rate k_on¹ of 0.6 μs⁻¹ mM⁻¹ and k_on² of 0.5 μs⁻¹ mM⁻¹ for outward permeation, and k_on¹ of 2.6 μs⁻¹ mM⁻¹ and k_on² of 0.8 μs⁻¹ mM⁻¹ for inward permeation.

The relation between single-channel permeability (P) and MFPT has been derived as $P=\frac{{\int }_{z_1}^{z_2}dz{e}^{-W\left(z\right)/k_{B}T}}{2\times MFPT}$ (71). If we take the average MFPT (1.5 μs) inside the hemichannel from both directions, and the average effective pore radius 13.75 Å, the permeability of cAMP is 75.5 × 10⁻³ μm³ s⁻¹. Although the bulk exchange rate is not included, the permeability estimated from PMF and MFPT is within an order of magnitude of the values computed from nonequilibrium simulation and the experiments. Note that the PMF and MFPT obtained for a hemichannel cannot be presumed to exactly correspond to those for each hemichannel within a junctional channel. An adjacent hemichannel will have an impact upon the electrostatics and fluid dynamics at the extracellular junctional point. However, our hemichannel PMF and MFPT indicate that the rate-limiting region is the major binding site at the intracellular end of the pore, thus the impact of the junctional point on the binding/unbinding kinetics of cAMP inside the junctional Cx26 channel may be minimal.

Voltage effect on asymmetric permeation free energy

The 1D log-density plots in Fig. 2 d are not the true PMFs of cAMP under two voltages. They were obtained from the steady-state density during voltage simulations. The symmetric density in the bulk regions on each side of the channel is the result of the periodic boundary condition used for MD simulations. However, the total PMF under voltage should not be symmetric. It has been shown previously that the total PMF under voltage $W_{tot}\left(z\right)$ can be computed as the sum of the intrinsic PMF in the absence of external field $W_{eq}\left(z\right)$ (in this case the equilibrium PMF derived from milestoning), and the additional potential introduced by the external field $q\delta \phi \left(z\right)$ (Eq. 4; (72, 73, 74)). This additional potential has two components. One is the constant electric field throughout the entire simulated periodic cell E = $V\left(z\right)$/L_Z, where $V\left(z\right)$ is the voltage linear to L_Z, the length of the box in the z direction. The other component is the reaction potential due to the voltage-induced changes of the spatial distribution and orientation of the water dipole and mobile ions, as well as flexible and charged atoms in the protein and membrane (75). This approach presumes that the channel and the permeant do not undergo substantial conformational changes due to the external field within the time of simulation (2 μs in this case). This assumption is supported by our results from ±200 mV simulations showing highly similar cAMP density distribution (Fig. 2) and pore radius profile (Fig. S3 a).

$$W_{tot}\left(z\right)=W_{eq}\left(z\right)+q\delta \phi \left(z\right)=W_{eq}\left(z\right)+q\left(V\left(z\right)+{\phi }_v\left(z\right)-{\phi }_0\left(z\right)\right).$$ (4)

The reaction potential introduced by external field may be approximated by the difference in electrostatic potential in presence and absence of the external potential, ${\phi }_v\left(z\right)-{\phi }_0\left(z\right)$. To calculate this difference in electrostatic potential, three additional 100 ns simulations at −200, 0, and +200 mV were carried out for the same system but without cAMP. Fig. 5, a and b show the 1D potential along the central pore z axis without voltage (in blue) and under ±200 mV (in orange).

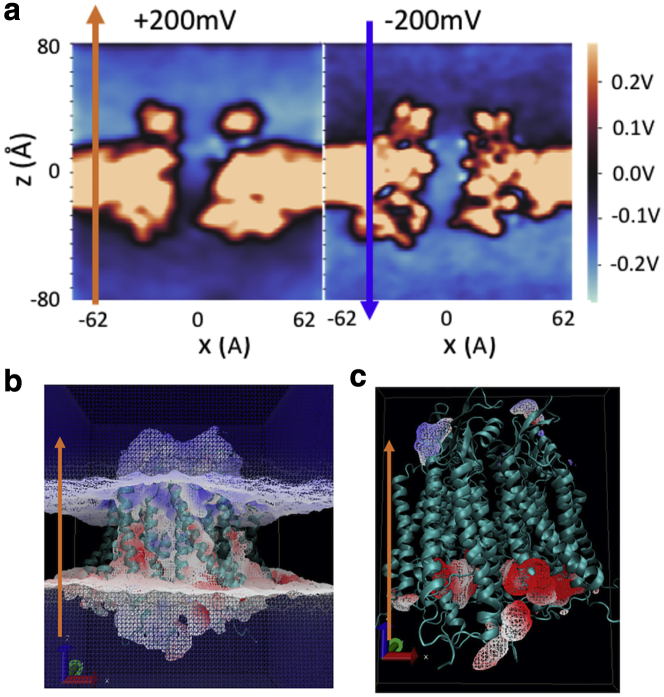
Cx26 is largely positive in the intracellular side (−40 < z < 0 Å), negative near the extracellular side (15 < z < 25 Å), and slightly positive near extracellular entrance (25 < z < 35 Å) (Fig. 2 a and reflected in Fig. 5, a and b, blue lines); thus, it has an overall dipole vector pointing toward the negative z direction. Consequently, within the protein-membrane region, positive voltage produces a potential ${\phi }_v\left(z\right)$ that enhances the protein dipole, whereas the one from negative voltage counters the protein dipole (Fig. 5, a and b, orange lines). In the bulk region and lipid headgroup region (z > |15| Å), the ${\phi }_v\left(z\right)$ nearly cancels out the external field $V\left(z\right)$. The sharp drop of the ${\phi }_v\left(z\right)$ under +200 mV can be visualized on 2D-electrostatic potential maps of the whole system (Fig. 6 a), and the 3D-electrostatic potential overlaid onto the solvent mass density isosurface (Fig. 6 b) or onto the cAMP density isosurface (Fig. 6 c).

Figure 6.

Electrostatic potential at ±200 mV membrane potential. (a) 2D-electrostatic potential maps (vector 1,0,1 in Cartesian space). (b) The 3D-electrostatic potential at +200 mV overlaid onto the solvent mass density isosurface. The color scale is −12.11 to 32.95 kT/e (−323 to +880 mV) from blue to red. Only the electrostatic potential at +200 mV is shown here as the color change in −200 mV is much less prominent (because of the opposite orientation of the intrinsic dipole as described in the text). (c) Electrostatic potential overlaid onto the cAMP density isosurface at +200 mV. The color scale is −267 to +267 mV. The isosurface contour cutoff is 0.1 amu/ų for (b and c). All data in this figure are calculated from the 3D electrostatic potential map (r) based on all charged atoms in the simulated system by solving Poisson equation on a 1-Å resolution grid using the VMD PMEPot plugin (76). PMEPot approximate point charge by a spherical Gaussian with an Ewald factor of 0.25. (r) is reported as the average of 1000 snapshots from the last 200 ns. To see this figure in color, go online.

Fig. 5, c and d shows the total PMF under each voltage $W_{tot}\left(z\right)$ obtained from Eq. 4. Clearly, +200 mV facilitates the inward flux of the negatively charged cAMP by increasing the free energy on the extracellular side of the protein (z > 0) and decreasing the free energy on the intracellular side (z < 0). The two inward flux energy barriers remain similar to those of the intrinsic PMF (∼2.3 kcal/mol). However, the outward $W_{tot}\left(z\right)$ at −200 mV significantly reduced the outward barrier from 3.2 kcal/mol of the intrinsic PMF to 2.3 kcal/mol. This is consistent with the shorter barrier crossing time under −200 mV (106 ns) than under +200 mV (143 ns) observed above, despite the large confidence interval (Table 1). In addition, due to the interplay between the external voltage and intrinsic PMF, the binding site around z = 5 Å shows up in the −200 mV PMF but is entirely absent in the +200 mV PMF, consistent with the difference in the cAMP density profiles obtained from voltage simualtions above.

Rotating cAMP dipole during permeation with or without voltage

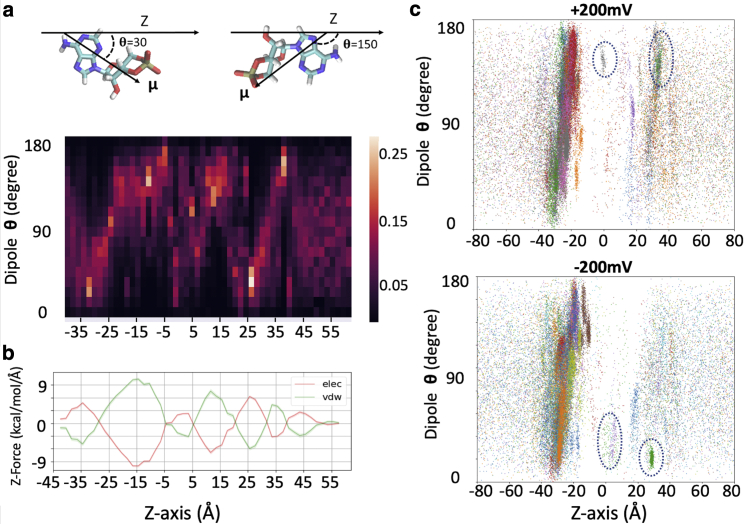
cAMP is a fairly rigid molecule with a shape of an irregular prolate spheroid and a dipole moment of 37.1 Debye. Fig. 7 a shows the probability distribution of the angle between the cAMP dipole vector and the z axis from milestoning simulations. Strikingly, the cAMP molecule rotates nearly 180° five times on its way through the pore (−40 to −20, −20 to 0, 0–10, 10–20, and 20–40 Å along the z axis, also see Video S1). To understand this, the z components of the force vector acting on the cAMP from the rest of the system (protein, water, ions, lipids) are decomposed into electrostatics and vdW terms and plotted for each milestoning cell (Fig. 7 b). The reciprocal forces of electrostatics and vdW terms along the channel indicate that cAMP has close interaction with the walls of the pore lumen. The positive forces push cAMP in the positive z direction, thus facilitating outward permeation, whereas the negative force facilitates inward permeation toward the negative z direction. Fig. 7, a and b demonstrated a clear correlation between cAMP dipole orientation and the electrostatic force vector acting on the cAMP (i.e., cAMP dipole rotates when the electrostatic force vector switches the sign). Thus, milestoning simulations captured the correct orientations of cAMP dipole induced by the local electric field along the pore lumen.

Figure 7.

Dipole moment distribution and force decomposition for cAMP molecules along z axis (Å). (a) cAMP dipole angles are shown as a probability distribution for each milestoning simulation cell along the z axis. Color bar shows the probability scale, lighter color represents higher probability. Representative dipole angles are illustrated on the cAMP molecule above. (b) Mean electrostatic and vdW forces along z axis on cAMP. Lines represent the running average of three milestoning cells and shaded areas represent standard error of mean within each milestoning cell. (c) Dipole angle scatterplot of permeating cAMP at −200 and +200 mV voltage simulations, respectively. To see this figure in color, go online.

What is the cAMP dipole orientation during the voltage-induced transition? Fig. 7 c shows scatter plots of dipole vectors of permeating cAMP molecules from the two voltage simulations. Between the intracellular entrance and the major binding site (−40 to −15 Å), dipole angles show orientation under both voltages similar to those at zero voltage, likely because of the large magnitude of the channel local field. Although the sampling is scarce in the barrier crossing region (−20 < z < 20 Å), cAMP shows a clear preference in orientation at z ≈ 0 and at z ≈ 25–30 Å, adopting the opposite orientation under the two voltages. Thus, these position-dependent dipole orientations of the permeant during our voltage simulations were the results of a competition between channel’s internal field and external voltage.

Position-dependent influence of cAMP on pore radius

The presence of cAMP at different locations inside the pore may have local or nonlocal effect of the pore radius. To investigate the local effect, we first compared the mean and standard deviations of the pore radius along the length of the pore, without cAMP (Fig. 8 a, black), and the radius at the position of the cAMP (Fig. 8 a, blue). Notice that these pore radii, obtained using grid-based cavity search program trj_cavity (77) ranged between 10 and 15 Å, larger than the 7.5–10.5 Å radius obtained using the Hole program (Fig. S3). This is because the Hole algorithm uses a spherical probe of increasing radius, which underestimates the space within an irregularly shaped pore. Fig. 8 a shows that the influence on pore radius depends on where cAMP resides. For instance, the radius increases when cAMP is around z = −10 Å but decreases when it is around z = 30 Å, near the extracellular entrance of the pore.

To investigate the nonlocal effect of cAMP on pore radius, we used Cohen d score of pore radius distributions to compare the mean radius with and without cAMP. Fig. 8 b is a heat map of Cohen d score, which depicts the changes in pore diameter along its length (x axis of Fig. 8 b) caused by the presence of cAMP at each z position (y axis of Fig. 8 b). Cohen d score was calculated using Eq. 5:

$$\text{Cohen}d\left(z\right)=\frac{⟨r^{\prime }\left(z\right)⟩-⟨r\left(z\right)⟩}{S{D}_{pooled}},$$ (5)

where $⟨r\left(z\right)⟩$ is the average pore radius without cAMP (Fig. 8 a, black) and $⟨r^{\prime }\left(z\right)⟩$ is the average pore radius with cAMP at various locations of the pore, obtained from milestoning simulation trajectories. $S{D}_{pooled}$ is the pooled standard deviation of $r^{\prime }\left(z\right)$ and $r\left(z\right)$. For instance, a d score of 6 (blue) means the presence of cAMP increased the mean pore radius by 6$S{D}_{pooled}$, and a score of −6 (green) means the presence of cAMP decreased the mean pore radius by 6$S{D}_{pooled}$.

On the heatmap, the d score colors along the diagonal line represent changes in pore radius at the position of the cAMP, corresponding to the Fig. 8 a blue profile. The off-diagonal colors represent nonlocal changes in pore radius away from where the cAMP is in the pore. It is evident that the presence of cAMP can have effects on lumen radius distant from the position of cAMP itself. Most interestingly, the scores on the upper off diagonal are more populated by green color and lower off diagonal shows more blue color. This trend suggests that when cAMP permeates through the pore, it tends to enlarge the radius on the left side (toward intracellular) and narrow the radius on the right side (toward extracellular).

Discussion

In this work, we use both long timescale MD simulations and Voronoi-tessellated Markovian milestoning to explore how a charged biological signaling molecule, cAMP, permeates a connexin open pore. We first obtained the steady-state density profile and the inward/outward cAMP flux under ±200 mV voltages from two 2 μs MD simulations in the presence of multiple cAMPs. These results were compared with the PMF and MFPT of a single cAMP at zero voltage obtained from a total 16.5 μs of multireplica milestoning simulations. Those two computational approaches—long timescale under voltage (nonequilibrium) and milestoning without voltage (equilibrium)—provided crossvalidation and complementary information that allowed detailed analysis of the kinetics of cAMP transit in the absence and presence of voltage, and in absence and presence of multiple cAMP molecules. Both ±200 mV simulations in 26.5 mM cAMP and single cAMP milestoning simulation featured a prominent intrapore-binding site, characterized by a high density of positive charge in a wide entrance region of the pore. The single-channel permeabilities estimated from both approaches are in qualitative agreement with known experimental data. The PMF and MFPT from milestoning further allow us to estimate the K_D, k_on, and k_off of cAMP inside the channel. Both the channel geometry and dipole contributed to the asymmetric permeation free energy and kinetics in the pore. The relation between voltage simulations and milestoning simulations was further investigated by deriving the PMF under voltage from the intrinsic PMF. We show that positive voltage increases the free energy barrier by enhancing the protein dipole, whereas negative voltage reduces the free energy barrier by reducing protein dipole. In addition, unbiased simulations within each milestoning cell allowed us to examine the dipole orientation of cAMP through the pore and the short-range and long-range effects of cAMP on pore width.

Although our voltage simulations show that more than one cAMP can be within the pore, this multiple occupancy only occurs at the wide intracellular entrance, and that there is single cAMP occupancy in the rest of the pore. Thus, we do not anticipate for cAMP the types of multioccupancy effects seen in many ion channels that involve interactions between sequential single-occupancy binding sites in the permeation path. The self-interactions among the cAMP molecules at the pore entrance (and not in bulk) is likely because of the 26.5 mM concentration of cAMP used to obtain a measurable number of transits during the voltage simulation, which was greatly increased at the pore entrance. The cAMP self-interactions are unlikely to occur at any physiological cAMP concentrations. However, this finding does point out a caution when a high concentration of ligands is used in computations to speed up the sampling.

In current study, we included 1:1 ratio of Mg²⁺ and cAMP in all simulations. Modeling magnesium-phosphate interaction is an active area of force field development (78,79). The Mg(H₂O)₆²⁺ model used here was previously developed to reproduce the osmotic pressure of Mg²⁺-anion solutions (52). Based on the nature of the model, we do not expect direct contact ion pairs to form between Mg²⁺-cAMP or Mg²⁺-protein. We did observe one solvent-separated ion pair between Mg²⁺ and the calcium-binding site (D50, D46, E47) on one subunit during +200 mV simulations with dwell time ∼1.5 μs (Fig. S5). However, we did not observe solvent-separated ion pairs between Mg²⁺-cAMP during cAMP permeation or binding, nor does cAMP permeation displace Mg²⁺. We note that when a Mg²⁺ was coordinated at the above site, there was no effect on pore width, which was wide enough to allow passage of fully hydrated cAMP. This absence of effect on pore width is consistent with the cryo-EM data of Ca²⁺ bound to this site (80). It should be noted that copermeation of Mg²⁺ with ATP will be more likely as one Mg²⁺ can be coordinated by two or three phosphate groups (79).

The analysis methods and code presented in this study can be applied to understand the molecular permeation through a large pore in general. The primary impact of this work will be to establish a way to generate meaningful hypotheses/understanding about the basis of molecular selectivity of connexin channels and to understand how mutations of connexin proteins alter the selectivity and thereby cause human pathologies.

Code availability

Input files and raw data used to generate each figure, as well as python3 scripts for multireplica milestoning analysis and convergence check are publicly available at https://github.com/LynaLuo-Lab/Connexin-cAMP-milestoning. Long timescale MD trajectories are publicly available on Anton2 supercomputer.

Author contributions

W.J. prepared the system, reparameterized cAMP force field, and performed nonequilibrium simulations. Y.-C.L. performed milestoning simulations. W.J. and Y.-C.L. analyzed both simulation results. W.B.-S. prepared milestoning analysis scripts in python3 and performed convergence analysis. Y.L.L., W.B.-S., and L.M. supervised milestoning simulation. Y.L.L., A.L.H., L.M., and J.C. designed the project and wrote the article with input from all authors.

Editor: Michael Grabe.