Ab Initio Machine Learning in Chemical Compound Space

Abstract

Chemical compound space (CCS), the set of all theoretically conceivable combinations of chemical elements and (meta-)stable geometries that make up matter, is colossal. The first-principles based virtual sampling of this space, for example, in search of novel molecules or materials which exhibit desirable properties, is therefore prohibitive for all but the smallest subsets and simplest properties. We review studies aimed at tackling this challenge using modern machine learning techniques based on (i) synthetic data, typically generated using quantum mechanics based methods, and (ii) model architectures inspired by quantum mechanics. Such Quantum mechanics based Machine Learning (QML) approaches combine the numerical efficiency of statistical surrogate models with an ab initio view on matter. They rigorously reflect the underlying physics in order to reach universality and transferability across CCS. While state-of-the-art approximations to quantum problems impose severe computational bottlenecks, recent QML based developments indicate the possibility of substantial acceleration without sacrificing the predictive power of quantum mechanics.

1. Introduction

Promising applications of machine learning techniques have been rapidly gaining momentum throughout the chemical sciences. Apart from this present special issue in Chemical Reviews, a number of special issues in common theoretical chemistry community journals have appeared, including International Journal of Quantum Chemistry (2015),¹Journal of Chemical Physics (2018),²Journal of Physical Chemistry (2018),³Journal of Physical Chemistry Letters (2020),⁴ and Nature Communications (2020).⁵ Books, essays, reviews, and opinion pieces have also been contributed by practitioners in the field.⁶⁻²³ Such growth of interest prompted a general discussion in Angewandte Chemie within a trilogy of essays by Hoffmann and Malrieu on the seemingly conflicting nature of simulation and understanding in quantum chemistry.²⁴⁻²⁶ The overall enthusiasm in the hard sciences for machine learning has even led to the introduction of novel journals, such as Springer’s Nature Machine Intelligence, IOP’s Machine Learning: Science and Technology,²⁷ or Wiley’s Applied Artificial Intelligence Letters.²⁸

In this review, we attempt to provide a comprehensive overview on recent progress made regarding the problem of using machine learning models to train and predict quantum properties throughout chemical compound space (CCS) (Figure 1). In contrast to the current trend of machine learning in quantum computing, we here refer to the application of statistical learning to quantum properties as “quantum machine learning” (QML). This notation follows a common convention in atomistic simulation, where the quantum nature of the object to be studied corresponds to a prefix, while the actual algorithms are rather classical in nature. Examples include Quantum Monte Carlo or Quantum Molecular Dynamics (also known as ab initio or “first-principles” molecular dynamics).

Figure 1.

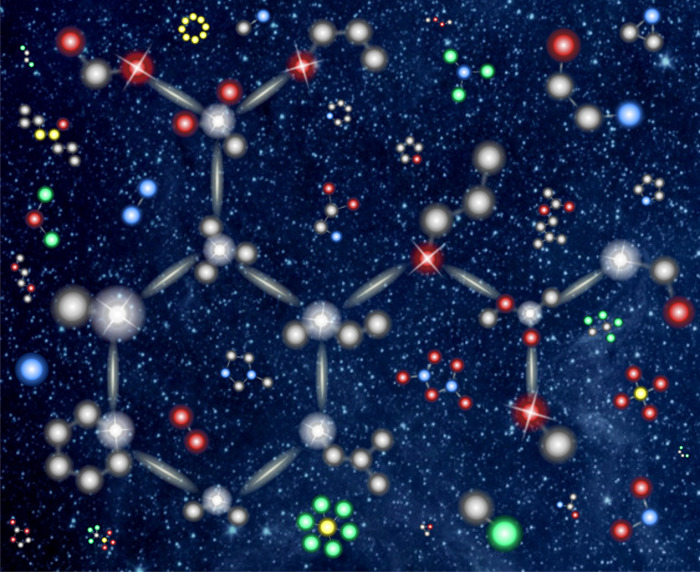
A cartoon of similarities among atoms across chemical compound space, not in conflict with quantum mechanics. The exemplary molecule aspirin is highlighted by bonds, and each of its atoms is superimposed with a similar atom in another molecule (hydrogens omitted for clarity). Green, yellow, gray, red, and blue refer to sulfur, phosphor, carbon, oxygen, and nitrogen, respectively. Reproduced with permission from ref (15). Copyright 2020 Springer Nature.

Within this introductory section, we will begin by first providing a qualitative description of chemical compound space (CCS) in terms of fundamental variables, which is consistent with the quantum mechanical picture within the Born–Oppenheimer approximation and neglecting nuclear quantum and relativistic effects. Thereafter, we briefly review related but complementary and system specific QML models which predominantly are not used throughout CCS but rather for training and predicting potential energies and forces in terms of conformational degrees of freedom, e.g., using molecular dynamics. Quantum mechanics based explorations for the purpose of materials design are mentioned subsequently, followed by a short subsection on studies which establish the quantitative and rigorous quantum chemistry based view on CCS.

1.1. Multiscale Nature of CCS

Figuratively speaking, CCS refers to the virtual set of all the theoretically (meta-)stable compounds one could possibly realize in this universe. To paraphrase Buckingham and Utting, a compound “...is a group of atoms...with a binding energy which is large in comparison with the thermal energy kT”.²⁹ In other words, with respect to all its spatial degrees of freedom, it is that locally averaged atomic configuration, for which the free energy is in a local minimum surrounded by barriers sufficiently high to prevent spontaneous reactions within some observable lifetime. As such, CCS depends on external conditions. It loses all meaning, for example, when conditions are such that bonding spontaneously emerges and vanishes (e.g., aggregation state of plasma).

The mathematical number of compounds grows explosively with the number of constituting atoms due to the mutual enhancement of combinatorial scaling at three rather distinct but well established energetic scales: First, the number of possible stoichiometries for any given system size (in terms of electrons and total proton number) represents an integer partitioning problem which grows combinatorially, see ref (30), for example. The energetic variance among compounds that differ in stoichiometry is on the scale of chemical bonding due to having different number and different types of atoms. Second, the number of possible connectivity patterns, i.e., incomplete labeled undirected weighted graphs distinguishing constitutional isomers/allotropes (commonly drawn as Lewis structures) is mathematically known to grow combinatorially with number of atoms.³¹⁻³³ The energetic variance among constitutional isomers is on the scale of differences in chemical bonding. Third, the number of possible conformational degrees of freedom grows combinatorially with number of atoms in a molecular graph (cf. Levinthal’s paradoxon for polymers), and one could even consider different atomic configurations of disconnected graphs, i.e., macromolecular or molecular condensed systems, to fall into this category of isomers. As such, the energetic variance among conformational isomers is on the scale of noncovalent intra- as well as intermolecular interactions. We note that stereoisomerism typically occurs among constitutional and conformational isomers. Its extension to compositional chirality has been proposed only recently.³⁴ Given such size and diversity, highly universal, and efficient methods are in dire need in order to meaningfully explore CCS in search of deepened chemical insight and intuition and of new compounds and materials which exhibit desirable properties. While quantum mechanics and statistical mechanics offer the appropriate physical framework for dealing with CCS in an unbiased and universal manner, the computational complexity of the equations involved has hampered their widespread use.

We note that our ab initio definition of CCS implies that only those compounds are part of CCS that should, at least in principle, be experimentally accessible as long as sufficiently sophisticated synthetic chemical procedures and reservoirs of the necessary chemical elements are available. While any such synthetic procedure would have to follow the corresponding relevant free energy paths, by navigating the virtual analogue of CCS we do enjoy more design freedom and can, namely for any property that is a state function, also exploit unrealistic fictitious transformations in line with Hess’ law, i.e., without the need for direct correspondence to experimental realization (cf. “alchemical” transmutations).

We conclude this section by noting that our definition generalizes the more commonly made reference to CCS, which typically excludes conformational isomers, reactive intermediates, or minima in electronically excited states. For example, first steps toward an ab initio based representative exploration of the latter were also proposed in 2013 for drug-like compounds by Beratan and co-workers.³⁵ However, for this review, we do not assume the most general view on CCS which would still be consistent with quantum mechanics, namely, that CCS comprises any chemical system, i.e., compounds with any chemical composition and any atomic configuration (being close to some state’s energy minimum or not). Such an encompassing definition would sacrifice the minimal free energy requirement mentioned above, and it would trivially correspond to the entire domain of CCS. Therefore, it would forego the useful link to observable lifetimes of systems as well as the appealing complementarity (not to be confused with orthogonality) to the well established problem of sampling potential energy hyper surfaces to study free energies or competing elementary reaction steps.

1.2. Machine Learning the Potential Energy Surface

While QM based studies of CCS are mostly concerned with (meta-)stable compounds, from inspection of the electronic Hamiltonian, it is quite clear that the effect of nuclear charges and nuclear coordinates are intimately linked. The well-known cusp condition due to Kato’s theorem³⁶ explicitly links these two variables through the electron density observable. As such, ab initio studies of the PES aimed at calculating geometric distortion, transition states, or statistical mechanical averages are closely related to the topic of this review. More specifically, early attempts of QML have focused on the PES of homonuclear system (e.g., diamond³⁷ or Si_n cluster³⁸) due to its relative simplicity (cf. compositional degree of freedom), for which many QML methods developed are also applicable to CCS. The distinction between CCS and the PES is somewhat arbitrary. For example, some molecular quantities of significant interest, such as libraries of ensemble properties of protein–ligand binding free energies, require accurate potentials as well as representative sampling of CCS. Also, instead of considering (meta-)stable constitutional or conformational isomers as distinct compounds, they can also equally well be viewed as local minima of the global PES hypersurface.

As mentioned above, within studies of the PES, the focus (at least currently) is typically placed on a single system and on computing energies and forces from scratch, i.e., ab initio. As such, one does not exploit correlations, constraints, and relationships, which only emerge through relationships observed among constitutional and compositional isomers, i.e., throughout all dimensions of CCS. The most common use-case of quantum methods for atomistic simulations deals with the problem of sampling the configurational degrees of freedom of the atoms of a given system. To develop a better informed understanding of the field, we now also briefly discuss relevant and select machine learning studies which touch upon the quantum based understanding of CCS but which primarily are concerned with the PES.

The question of how to best model a PES using some (physical or surrogate) function approximator and based on scarce and expensive potential energy surface data sets of specific systems, i.e., not through CCS, obtained from computationally demanding calculations, is long-standing. Potential energy hypersurfaces were traditionally studied for the purpose of molecular spectroscopy or for molecular dynamics applications of a given system. The development of empirical interatomic potentials, particularly the reactive force-field (ReaxFF) approach developed by van Duin and co-workers since 2001,^39,40 amounts essentially to a traditional multidimensional regression problem for fixed functional basis functions and constitutes one of the mainstream efforts in this active field. Unlike traditional force field approaches, ReaxFF requires no predefined connectivity between atoms (topology) and casts the empirical interatomic potential within a formalism of bond order, which depends on the interatomic distances only. This improved adaptation of an atom to its environment allows for accurate descriptions of bond breaking and bond formation and has been applied extensively to model reactive chemistry at heterogeneous interfaces, involving typically very large systems,⁴⁰ made up of millions of atoms.

The force-field approach, despite its efficiency, its chemical motivation, and its broad applicability and potential accuracy, suffers from the fixed functional forms imposed when relying on empirical interatomic potentials, implying that the model is hard to improve by adding more training data and could even fail catastrophically in certain regimes and classes. This limitation motivates interest in more flexible data-driven models. For example, already in 1994, Ischtwan and Collins improved the Shepard interpolation scheme for PES approximations.⁴¹ This paper illustrates the close relationship to QML: The authors utilized a formalism very similar to the modern kernel ridge regression, one of the workhorses of QML. The authors also already discussed one of the frequent challenges coming along with any new ML model project: How to best down-select optimal configurations for minimal data acquisition and training costs, and how to obtain systematic model improvements with increasing training set size.⁴¹ Early awareness of the trade-off between accuracy and training cost was also already addressed more than a decade earlier in the 1981 paper by Wagner, Schatz, and Bowman: Given a finite compute budget, data for which training instances should be acquired in order to obtain the most accurate model of the potential energy hypersurface?⁴² When facing the exploration of CCS with QML models, analogous questions must be addressed. For references to similar studies related to the problem of potential fitting and preceding 1989, we refer the reader to the comprehensive review by Schatz.⁴³

Most of the data-driven models in the 1990s favored the neural network regressors for PES fitting. More specifically, in 1992, Sumpter and Noid published a neural network model for macromolecules.⁴⁴ Additional neural network potentials were published by Blank et al. in 1995⁴⁵ for the CO/Ni(111) system, and Brown et al. in 1996⁴⁶ for the study of ground-state vibrational properties of two weakly bound molecular complexes: (FH)₂ and FH–ClH. Neural networks were revisited for systems with increased size in the same year by Lorenz, Gross, and Scheffler⁴⁷ for H2/K(2×2)/Pd(100) (with substrate fixed), followed by their application to represent high-dimensional potential energy surfaces for H₂O₂ by Manzhos and Carrington in 2006.⁴⁸ Even larger systems, i.e., water clusters (up to 6 units), were dealt with by Handley and Popelier from 2009 onward,⁴⁹ accounting for important electrostatic properties through learning of the atomic multipoles. These early developments used Cartesian/internal coordinates directly as the input of NN models, which is justified for modeling small to medium-sized systems; for large systems, however, this setup proves to be too inefficient. In 2007, Behler and Parinello published much improved deep neural network-based potentials,⁵⁰ encoding molecular geometry effectively in terms of rotation, translation, and permutation invariant atom-centered symmetry function (ACSF), followed by molecular dynamics applications using metadynamics to identify Si phases under high pressure.⁵¹ A detailed overview of various neural network-based advances since 2010 was given in 2017.⁵² Starting in the same year, multiple, more universal, neural network models were introduced. In particular, Smith et al. advanced the idea of Behler’s symmetry functions in neural networks with the aforementioned normal mode displacements in order to generate a powerful neural network trained on millions of configurations of tens of thousands of organic molecules, called ANI.⁵³ An accurate and transferable neural network exploiting an “on-the-fly” equilibration of atomic charges was introduced that same year by Faraji et al.,⁵⁴ and soon thereafter, equally universal neural nets SchNet⁵⁵ and PhysNet⁵⁶ were published. An extensive review on neural network potentials for modeling the potential energy surfaces of small molecules and reaction is also part of the present issue in Chemical Reviews.⁵⁷

Kernel models started to play a noticeable role for PES fitting in the late 1990s. In 1996, Ho and Rabitz presented kernel-based models for the fitting of potential energies⁵⁸ for three small systems, He–He, He–CO, and H₃⁺. Similar to early PES fitting works within NN framework, these early kernel-based models also utilized simple Cartesian/internal coordinates as input, and therefore applicability was limited. While the mathematics of kernel-based surrogate models was firmly established many decades ago, only from 2010 and onward, kernel-based models began to flourish, building on the seminal work contributed by Csanyi, Bartok, and co-workers within their “Gaussian-Approximated Potential” (GAP) method, relying on Gaussian process regression (GPR) and an atom index invariant bispectrum representation.⁵⁹ In 2012, Henkelmann and co-workers introduced an interesting application of support vector machines (SVM) toward the identification of transition states.⁶⁰ One year later, the first flavor of the smooth overlap of atomic positions (SOAP) representation for GPR based potentials was published.³⁸ The SNAP⁶¹ method popularized the GAP idea using linear kernels in 2015, and other GPR applications with automatically improving forces were published the same year.^62,63 Around the same time, a first stepping stone toward a universal force field, trained on atomic forces throughout the chemical space of molecules displaced along their normal modes, was established.⁶⁴ Reproducing kernels were also shown in 2015 to be applicable toward dynamic processes in biomolecular simulations,⁶⁵ and ever more accurate GPR based potentials were introduced in 2016⁶⁶ and in 2017.^67,68 GPR was also applied to challenging processes in ferromagnetic iron⁶⁹ and to the problem of the on-the-fly prediction of parameters in intermolecular force fields.⁷⁰ Amorphous carbon was studied using SOAP based GPR/KRR models,^71,72 and GDML, another series of highly robust and accurate GPR/KRR based molecular force fields, was introduced in refs (67 and 73−75) starting in 2017.

GPR and NN are currently the two most popular regressors for PES fitting, and each exhibits advantages and disadvantages. Seemingly very different in design, they do resemble each other to some extent in the sense that they take the role of basis functions (to be elaborated in section “Regressor”), although the similarity may be blurred within the framework of deep NN. Numerical comparison of the performance of these two methods is interesting. Most notably, such a comparison was made for modeling the potential energy surface of formaldehyde in 2018 by Manzhos and co-workers.⁷⁶ A similar yet independent study on the same system was performed in 2020 by Meuwly and co-workers.⁷⁷ Both studies confirm that kernel based QML models reach higher predictive power than neural network based models for same training set sizes. A highly related comparative study on modeling vibrations in formaldehyde was contributed by Käser et al.,⁷⁷ also in 2020.

As for the active learning of interatomic potentials, most of the related studies relied on the kernel framework, some of them also detailed below in the section “Training Set Selection”. As early as in 2004, De Vita and co-workers proposed updating potential parameters to ab initio results during molecular dynamics runs (“learning-on-the-fly”),⁷⁸ for a very large system, i.e., silicon systems composed of up to ∼200 000 atoms, although the reference level of theory is quite approximate. Podryabinkin and Shapeev proposed the so-called D-optimality criterion for selecting the most representative atomistic configurations for training on-the-fly as early as 2017.⁷⁹ Using kernel ridge regression (KRR, a variant of GPR), Hammer and co-workers revisited the on-the-fly learning idea for structural relaxation in 2018,⁸⁰ and investigated the exploration vs exploitation trade-off.⁸¹ In 2019, Weinan, Car, and co-workers contributed another active learning procedure for accurate potentials of Al–Mg alloys,⁸² and Westermayr et al. extended the use of neural networks for molecular dynamics in the electronic ground state toward photodynamics.⁸³ Among the many purposes (also challenges) of QML for PES, one particular one is to scale to an extremely large (thus more realistic) system. Numerous efforts have pushed us closer to this goal, and most notably, Weinan, Car, and co-workers made full use of the Summit supercomputer to simulate 100 million atoms with ab initio accuracy using convolutional neural networks,⁸⁴ for which they subsequently were awarded the Gordon Bell prize 2020 by the Association for Computing Machinery.

1.3. Navigating CCS from First Principles

The scientific research question of how properties trend across CCS lies at the core of the chemical sciences. Because of ever-improving hardware performance, improved approximations to Schrödinger’s equation, most notably within density functional theory and localized coupled cluster theory, QM data sets of considerable size have emerged, enabling the use of statistical learning to train surrogate QML models which can provide accurate and rapid quantum property estimates for new compounds within their applicability domain.

While quantum mechanics based computational materials design efforts had been undertaken as early as the 1990s⁸⁵⁻⁸⁸ with important progress made in the 1980s,^89,90 the first-principles based computational high-throughput design has by now become an important success story.⁹¹ First attempts to employ machine learning and quantum predictions to discover new ternary materials databases date back to seminal work by Hautier and Ceder in 2010.^92,93

As a promising alternative to ab initio high-throughput computations (or solving Schrodinger equation in general), one often assumes locality of atoms in molecules when constructing the mapping from molecular distance/similarity to difference in properties within QML, and the final predictive performance depends on how similar two local (and thus global) entities are, i.e., nuclear types covered by a test set are required to be retained in the training set. The capability of QML to treat species made up of elements not seen in training set is, however, very limited. There exists the so-called “alchemical” methods, being quite different in philosophy, allowing for effective and efficient treatment of the change of nuclear types, with or without the constraint that the number of electron number (N_e) being fixed (i.e., isoelectronic). We note in passing that alchemy is typically established within the density functional theory framework, as it would be tremendously simpler to expand molecular property (mostly energy) as a function of four variables (x, y, z, and Z) than 4N_I ones in the case of wave function-based formulation.

Previous methodological works tackling chemical compound space from first-principles through variable (“alchemical”) nuclear charges were contributed by various pioneers, including Wilson’s formal four-dimensional density functional theory⁹⁴ in 1962, which expresses the exact nonrelativistic ground-state energy of an electronic system as a functional of the electron density, which per se is a function of the spatial coordinates, and nuclear charges. Following Wilson’s idea, Politzer and Parr⁹⁵ in 1972 made one step further toward practical computation by transforming Wilson’s formula into a functional of the total electrostatic potential V(r, Z) and derived some useful semiempirical formulas for the total energy of atoms and molecules, through the use of thermodynamic integration.⁹⁵ Later in the 1980s, Mezey made some interesting discoveries^96,97 about the global electronic energy bounds for a variety of isoelectronic polyatomic systems, which may be found useful for quantum-chemical synthesis planning, using multidimensional potential surfaces.

The theoretical alchemical research was resurrected in the new millennium. Among the numerous contributions, notable ones include a variational particle number (variable proton and electron number) approach for rational compound design⁹⁰ proposed by one of the authors and collaborators, followed by a more detailed description of the underlying theories, in the name of molecular grand-canonical ensembles (GCE).⁹⁸ In the same year, a reformulation of GCE in terms of linear combinations of atomic potentials (LCAP)⁹⁹ (instead of Z and N_e as in GCE) was proposed by Wang et al., but for the optimization of molecular electronic polarizability and hyper-polarizability, with the optimal molecule determined analytically in the space of electron–nuclei attraction potentials. For the isoelectronic case, related works include the development of ab initio methods for the computation of higher-order alchemical derivatives¹⁰⁰ by Lesiuk et al. in 2012, as well as the assessment of the predictability of alchemical derivatives¹⁰¹ by Munoz et al. in 2017. More recently, alchemical normal modes in CCS,¹⁰² alchemical perturbation density functional theory,¹⁰³ and even a quantum computing algorithm for alchemical materials optimization¹⁰⁴ were proposed, further enriching the field.

Starting in 1996 with stability of solid solutions,¹⁰⁵ multiple promising applications, based on quantum alchemical changes, have been published over recent years, including thermodynamic integrations,¹⁰⁶ mixtures in metal clusters,^107,108 optimization of hyperpolarizabilities,¹⁰⁹ reactivity estimates,¹¹⁰ chemical space exploration,¹¹¹ covalent binding,¹¹² water adsorption on BN-doped graphene,¹¹³ the nearsightedness of electronic matter,¹¹⁴ BN-doping in fullerenes,¹¹⁵ energy and density decompositioning,¹¹⁶ catalyst design,^117−119 and protonation energy predictions^120,121 Symmetry relations among perturbing Hamiltonians have also enabled the introduction of “alchemical chirality”.³⁴

An extension of computational alchemy toward descriptions which go beyond the Born–Oppenheimer approximation has been introduced within path-integral molecular dynamics, enabling the calculation of kinetic isotope effects, already in 2011,¹²² and subsequently by Ceriotti and Markland.¹²³

However, also varying the electron number is a long-standing concept within conceptual DFT.^124,125 Actual variations have only more recently been considered, e.g., to estimate redox potentials,^98,126 higher-order derivatives,^100−102 or for the development of improved exchange-correlation potentials.¹²⁷

2. Heuristic Approaches

Modern systematic attempts to establish quantitative structure–property relationships (QSPRs) have led to computationally advanced bio-, chem-, and materials-informatics methodologies. Unfortunately, conventional approaches in QSPR predominantly rely on heuristic assumptions about the nature of the forward problem, and are thus inherently limited to certain applicability domains. The implicit bias, often due to lacking basis in the underlying physics is known, as discussed, e.g. in a 2010 review by G. Schneider,¹²⁸ and many improvements have been contributed more recently.²⁰

While heuristic in nature, QSPR can still provide useful qualitative trends and insights for relevant applications, and sometimes yield accurate predictions for specific property subdomains and systems. Albeit not directly relying on the laws of quantum mechanics, these early developments are still valuable, in the sense that some just correspond to special variants of the more complicated models, for instance, a linear model can be mapped onto the framework of kernel method, by choosing a linear kernel, instead of say Gaussian kernel for Gaussian process regression (GPR). Other heuristic approaches, exhibiting more quantitative characteristics can be considered important precursors for modern QML. Such examples include Collin’s improved Shepard interpolation scheme⁴¹ for accurate representation of molecular potential energy surfaces, which resembles the form of kernel methods except that the weights are determined in a heuristic way, instead of being regressed as in GPR. One may also argue that Collins’ scheme could be recast into the kernel framework, except that a specific kernel is chosen such that the Shepard interpolation weights in Collins’ scheme are exactly reproduced (with the constraint that these weights sum up to 1). Another highly related concept is Ramon Carbo-Dorca’s quantum similarity (for a comprehensive review, see ref (129)), derived based on density matrix, or molecular orbitals, or other related quantum quantitites, it is also closely linked to kernel based methods and may be used directly as parameter-free kernel matrix elements (unlike in GPR, kernel matrix element characterizing similarity is typically hyper-parameter dependent).

In the sections below, we focus on relevant literature regarding three distinct perspectives which largely follow chronological order: (i) low-dimensional correlations or simple models from the early days of chemistry, (ii) coarse representations of molecules and derived quantities, mostly providing an overview of QSPR, and (iii) molecular representations based on properties.

2.1. Low-dimensional Correlations

Early practices of fundamental chemical research dealt with spotting correlations between inherent properties of the system and systematic changes of observed quantities. Possibly the most famous example for such work is Mendeleev’s discovery of the periodic table.¹³⁰ Other important examples correspond to Pauling’s electronegativity concept and covalent bond postulate,¹³¹ or Pettifor’s Mendeleev numbering scheme.^132,133 Work along such lines has been continued, and recent contributions include revisiting Pettifor scales,^134,135 use of variational autoencoders to “rediscover” the ordering of elements in the periodic table,¹³⁶ or the chemplitude model which extends Pauling’s concept,¹³⁷ among many others. Free-energy relationships are the subject of yet another broad category of early research which is still active today. Relating logarithms of reaction constants (free energy difference) across CCS for related series of reactions¹³⁸ has led to the famous Hammett equation, a 2D projection of all degrees freedom onto composition and reaction conditions.^139−141 Similarly low-dimensional effective degrees of freedom have been identified within Hammond’s postulate,¹⁴² or Bell–Evans–Polanyi principle.^143,144

Most of the aforementioned concepts were proposed to gain a better (or more useful) understanding of molecular behavior in the first place. For extended systems such as metallic surfaces, complexities arise and many of the simplified molecular models are no longer applicable. With the advent of density functional theory (DFT),^145−149 alternative descriptors have been proposed during the past decades, playing an increasingly important role. Notable contributions include the d-band center model by Hammer et al.,^150,151 the generalized coordination number,^152,153 and the Fermi softness.¹⁵⁴ Free-energy relationships are more robust against subtle changes in the electronic structure and are being widely applied in analyzing surface elementary reaction steps.¹⁵⁵ Scaling relations between the energetics of adsorbed species on surfaces¹⁵⁶ also enjoy extensive attention and have been proven useful for catalyst design regardless of the surface not being metallic.^157−159 Many of the empirical chemical concepts such as electronegativity, softness/hardness, and electrophilicity/nucleophilicity can be rationalized and quantified within what is known as “conceptual” DFT.^160,161 This specific field, as pioneered by Fukui or Parr and Yang,¹⁶⁰ has been championed and furthered by many including Geerlings, De Proft, Ayers, Cardenas, and co-workers.^161,162

We note that simple models, involving one or a few variables in general, represent effective coarse-grained schemes applicable to specific subdomains of chemistry. While they lack the desired transferability of quantum mechanics, they often do encode well tempered approximations and therefore are capable of capturing much of the essential physics. As such, they have much to offer, and they could, for example, serve the design of robust and general representations enabling the training and application of improved QML models (see below or refs (6 and 163)). Alas, this idea, to connect low-dimensional model, based on well established heuristics, with more recently developed generic ML models, is still largely unexplored, despite the fact that the latter often bear (magic) black box characteristics allowing for little qualitative insights. Unifying modern ML with low-dimensional model could therefore also help resolve open challenges in QML. For instance, how can we properly represent different electronic (spin-) states of molecules in the molecular representation or different oxidation states? Conceptual DFT derived linear or quadratic energy relationships suggest treating the number of electrons (N_e) and/or its powers as independent features might be a reasonable starting point. Another thus-inspired direction of research is to utilize conceptual DFT-based local indicators as properties of composing atoms/bonds/fragments of a target molecule as a starting point (much like the fundamental variables such as Z and R) for building representations. This might be necessary in order to address hard and outstanding problems such as building QML models of intensive properties or to account for multireference character in the electronic structure.

2.2. Stoichiometry

Given a fixed pattern of structure, stoichiometry alone can be used as a unique representation of the system under study. This idea has been demonstrated for an exhaustive QML based scan of the elpasolite (ABC₂D₆ stoichiometry) subspace of CCS, predicting cohesive energies of all the 2 million crystals made up from main-group elements.¹⁶⁴ Elpasolites are the most abundant quaternary crystal form found in the Inorganic Crystal Structure Database. Comparison of the QML results to known competing ternary and binary phases enabled favorable stability predictions for nearly 90 crystals (convex hull) which subsequently have been added to the Materials Project database.¹⁶⁵ A compact stoichiometry based representation in terms of period and group entry for elements A, B, C, and D was shown to reach the accuracy of explicit geometry based many-body potential representations at larger training set size, indicating the dominance of the former in large training data regimes.¹⁶⁶ Similar work was subsequently done by Ye et al.¹⁶⁷ as well as Marques et al. for perovskites on crystal stability,¹⁶⁸ as well as by Legrain et al.,¹⁶⁹ for predicting vibrational free energies and entropies for compounds, drawn from the Inorganic Crystal Structure Database.

A naive but useful derived concept is the so-called “dressed atom” concept,¹⁷⁰ which characterizes the atom in a molecule of a fixed stoichiometry. When using this approach together with a linear regression model to approximate the total energy (or atomization energy), the accuracy turns out to be surprisingly reasonable,¹⁷¹ at least for common data sets of organic molecules with small variance among constitutional isomers. For instance, the corresponding mean absolute error (MAE) for QM7 data set is only 15.1 kcal/mol.¹⁷⁰ Using bond counting, the MAE could be improved further to less than 10.0 kcal/mol, within reach of a conventional DFT GGA functionals.¹⁷² Therefore, it seems advisible to always use the dressed atom approach for centering the data for any fixed stoichiometry (i.e., averaging out constitutional and conformational isomers) before proceeding to the next level of QML training on the complete set of degrees of freedom. This normalization step can also be seen as data preprocessing, enabling the QML model to focus on “minor” deviations from the mean.^164,173

2.3. Connectivity Graph

When the systems under study do not share some common structural skeleton, stoichiometry alone is not enough, and the covalent bonding connectivity between atoms, as well as conformations, may have to be also examined.

It is worth pointing out that chemists often assume a one-to-one relationship between the molecular graph and its associated global conformational minima (or the second lowest energy minima, or the third, etc.), and therefore it should be possible to build a QML model to predict relevant quantum properties of such ordered minima from graph-input only. In fact, the remarkable performance of extended Hückel theory for some systems could be explained in this way.

Because of the intuitive accessibility and applicability of (incomplete) graph based representations, such as Lewis structures and their extensions, for a wide range of molecular systems, associated ML methods have received broad attention and wide applications in many fields such as cheminformatics or bioinformatics. Examples of such representations include various fingerprint representations,¹⁷⁴ such as the signature methodology.^175−177 Another notable example corresponds to the so-called extended circular fingerprint (ECFP).¹⁷⁸ ECFP and similar representations have been used for drug design^179,180 and qualitative exploration of CCS.^181,182 ECFP has also been used in KRR models for prediction of quantum properties of QM9 molecules. Numerical results for ECFP based QML models indicate a substantially worse performance compared to more complete, geometry derived representations.¹⁸³

Modern molecular graphs, typically in SMILES format, based neural networks models, have gained considerable momentum during the past decade. A vast amount of related literature deal with chemical synthesis and retrosynthesis in such representation spaces (mainly in organic chemistry),^184,185 typically favoring different deep learning architectures, chemical reaction network,¹⁸⁶ as well as molecular design using variational autoencoder (VAE, which maps a molecule represented by SMILES string to some latent space¹⁸⁷). The absence or presence of relationships between functional groups and binding affinity was also recently explored through use of random matrix theory in drug design.¹⁸⁸ The incorporation of new and improved formats, such as SELFIES,¹⁸⁹ might still lead to further improvements for such research.

In the context of a first-principles view on CCS, we note however that molecular graphs only encode a (biased) statistical average of the many conformational configurations for a molecule near some local minima in the potential energy surface. As such, they are naturally disposed for use of QML models of ensemble properties. Work along such lines still awaits being explored in the future. Albeit popular and justified for certain problems, graph-based approaches are inherently limited when it comes to noncovalent problems, such as supramolecular assembly processes governed by van der Waals interactions, metal cluster/bulk/surface adsorption involving “multivalent” (transition) metal elements controlled by weaker metallic bond (cf., covalent bond), or chemical reactions requiring the transformation of graphs from one into the other. In such situations, the intuitive concept of a graph is ill-defined, and the necessary corrections are not always obvious.

2.4. Coarse-grained

As the system size grows, the cost in training and prediction of QML models increases accordingly, although with more favorable scaling than typical quantum chemistry methods. Therefore, it may become very demanding or even impossible to deal with system sizes which cross certain thresholds. In such scenarios, one typically represents the systems in a coarse-grained fashion, meaning “superatoms” (groups of atoms in close proximity, or beads) in a molecule are being considered. Coarse-grained approaches can drastically reduce the number of degrees of freedom and are therefore the only feasible way to model systems at macroscopic scale. More importantly, they enable a significant collapse of the size of chemical space due to the transferability of beads by design.¹⁹⁰

Current practices of coarse-grained ideas comprise mostly coarse-grained force fields (CGFF) for simulation of large systems such as macromolecular systems and soft matter. With the emerging need for systematic control of the accuracy of models of such systems, coarse-grained representation based QML models (CGQML) may be a rather promising alternative to CGFF, much the same as how QML models based on full-atom representation remedy the deficiencies of classical force field approaches for small to medium-sized molecules.¹⁹ Such comparison between QML and FF makes sense, as the most modern implementations of ML hold promise to approach the computational efficiency of FFs. Some of the first studies on coarse-grained representation used together with QML include John and Csányi’s free energy surface modeling of molecular liquids in 2017.¹⁹¹ Later, efforts to tackle complicated biosystems were reported by Bereau and co-workers in 2019,¹⁹⁰ as well as by Clementi and co-workers.¹⁹² Compared to CGFF, CGQML could be significantly more accurate once the system information is properly encoded in the coarse-grained representation, as the QML part can recover what is missing in the CG part by careful selection of training data (vide infra).

2.5. Property Based

There exists another type of representation, typically referred to as descriptor and the least “ab initio” in spirit, in which the basic idea is to simply select a set of pertinent atomic/molecular properties as underlying degrees of freedom. The properties can stem from calculation and/or experiment and have to be relatively easy to obtain and are typically supposed to somehow “describe” the property of interest, and hence the name “descriptor”. This representation is often utilized in combination with some nonlinear regressor like a neural network, as the relationship between the chosen properties is commonly highly nonlinear. Although this approach could be universally applicable, no matter the size or composition of target systems, its predictive power is limited by construction due to its potential lack of uniqueness.^30,163 Most of the studies following this direction can be traced back to the early applications of ML in chemistry and related fields, one example being Karthikeyan et al.’s work¹⁹³ on melting and boiling points prediction of molecular crystals using the properties of standalone molecules as a feature vector. A more recent and systematic study of this idea has applied optimization algorithms toward the down-selection of descriptor candidates in order to build predictive ML models of formation energies of binary solids.¹⁹⁴ From a first-principles point of view, however, such representations are questionable because relationships between different observables (or other arbitrary mathematical properties), obtained as expectation values of independent operators, are not necessarily well-defined.

3. QML Methodology

The fundamental idea to employ machine learning models in order to infer solutions to Schrödinger’s equation throughout CCS, rather than solving them numerically, was first introduced in 2011.¹⁹⁵ The authors stated that ”....the external potential...uniquely determines the HamiltonianHof any system, and thereby the ground state’s potential energy by optimizing Ψ”, and they show that one can use QML instead (encoding the number of electrons implicitly by imposing charge neutrality). As such, the problem of predicting quantum properties throughout CCS belongs to what is commonly known as “supervised learning”. One typically distinguishes between unsupervised (compound data only) and supervised (data records including compounds and associated properties) learning. In this review, we focus on the latter, i.e., on the question how, given sufficient exemplary structure–property pairs, properties can be inferred for new, out-of-sample compounds.

The generic procedure for supervised learning requires first defining the model architecture, i.e., the mathematical expression for the statistical surrogate model f, which estimates some quantum property p as a function of any query compound M, p^QML(M) ≈ f((M)|{M_i},{p_i^ref};{c_i}), wherefcorresponds to the regressor, and regression coefficients and hyper parameters {c_i} are obtained via minimization of training loss-function quantifying the deviation of p^QML from {p_i} for all training compounds {M_i}. In other words, f is parametric in regression coefficients and hyperparameter which, in return, are nonlinear functions in the training data. The origin (calculated or measured) as well as the actual existence (some properties, such as energies of atoms in molecules,¹¹⁶ are not observables but can still be inferred) of p^ref is secondary. Noise in the data (due to experimental or numerical uncertainty, or due to minor inconsistencies) can be accommodated to a certain degree through well-established regularization procedures. Converged cross-validation protocols help to avoid overfitting and to enable the optimization of hyper-parameters as well as meaningful estimates for any interpolative query. For introductory texts on kernel based regressors, the reader is referred to the book by Rasmussen et al.;¹⁹⁷ as for representation and training sets, several reviews have recently been published.^7,10,19,198

3.1. Regressor

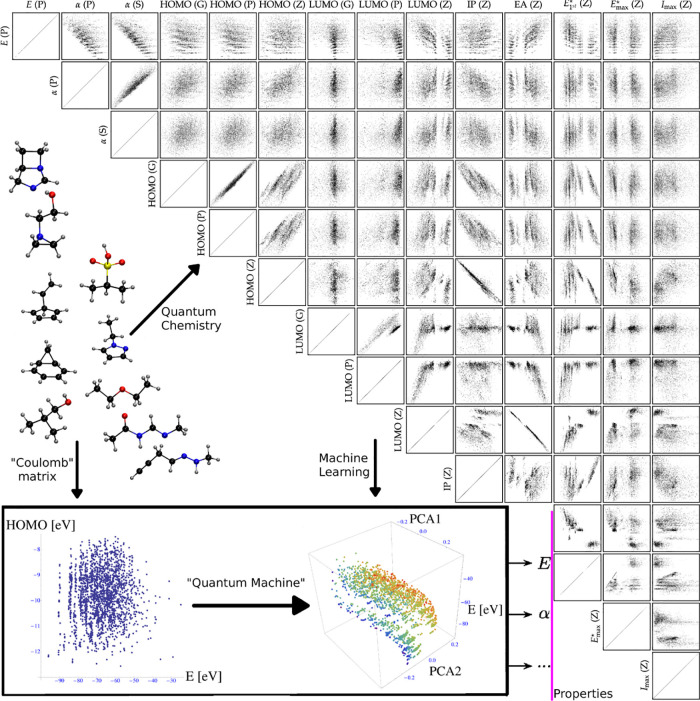
When considering the problem of fitting a generic set of basis functions to precalculated data, some of the most commonly made choices in the field of atomistic simulation include support vector machines (kernel ridge regression), tantamount to Gaussian process regression in their specific model form, neural networks, random forests, or permutationally invariant polynomials (PIPs).^197,199,200 While agnostic about the training labels by construction, the choice of these basis set expansions constitutes a crucial step. Most evidently for support vector machines, nonlinear kernel functions (based on feature representations vide infra) map any nonlinear high-dimensional regression problem into a low-dimensional kernel space within which the regression problem becomes linear and therefore straightforward to solve through a closed-form expression (“kernel-trick”). How kernel space relates to CCS is also quite intuitive to grasp when thinking about it as a graph of compounds. As displayed in Figure 2, each compound, being representable by a molecular graph (or derived matrix such as a Coulomb matrix or Cartesian coordinate and nuclear charge vector) is projected into higher-dimensional feature space (shown are only three principal dimensions from the infinite number of dimensions defined within the framework of KRR/GPR). The complete connection between all compounds in the new space form another type of graph, with each vertex corresponding to a compound and each edge corresponding to a similarity measure of compounds (edge length may indicates a metric distance between two compounds). Inferring the property of a new compound (labeled as pink “X” in Figure 2) may be conceptualized as summing up distance scaled property weights. Within this picture, it becomes intuitively obvious that the interpolating accuracy must improve with increasing compound density.

Figure 2.

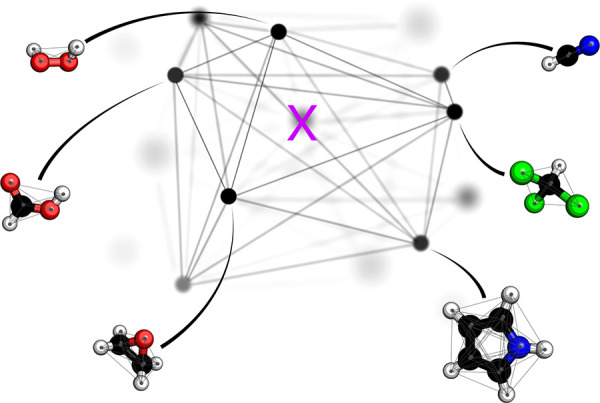
3D projection of high-dimensional kernel representation of chemical compound space. Within kernel ridge regression, chemical compound space corresponds to a complete graph where every compound is represented by a black vertex and black lines correspond to the edges which quantify similarities. Each compound, in return, can be represented by a molecular complete graph (e.g., the Coulomb matrix (CM)¹⁹⁵) recording the elemental type of each atom and its distances to all other atoms. Given known training data for all compounds shown, a property prediction can be made for any query compound as illustrated by X. Choice of kernel-function, metric, and representation will strongly impact the specific shape of this space and thereby the learning efficiency of the resulting QML model.

While deep neural network models are very powerful and possess significant black-box character, their training requires data sets of very large size as well as a substantial calculation effort in order to optimize the regression coefficients and hyper-parameters (no closed-form solution is known). In this sense, kernel methods are rather lightweight and preferable in scarce data scenarios, as they enjoy the potential benefits of being more intuitive and faster to train. The specific architecture of the neural network will affect its performance and data efficiency dramatically. Deep, recurrent, convolutional, message passing, generative, adversarial, geometric neural networks, and other flavors, as well as choices of activation function, number of layers, and neurons, have all shown significant impact on the cost of training and on the predictive power in atomistic simulation.

In the case of GPR/KRR, the architecture is much simpler and hence of a lesser concern (GPR/KRR can be seen as a single-layer neural network model in the limit of infinite width²⁰¹), but the specific kernel space does not only depend on the choice of kernel function but also on the choice of metric. While it is clear that one should avoid similarity measures which do not meet the mathematical criteria of how a metric is defined (identity, symmetry, triangle inequality), the impact of the specific metric choice has not yet been studied much in the field of atomistic simulation. Euclidean, Manhattan, or Frobenius norms are commonly used. Only most recently, the use of the Wasserstein norm has been proposed to gain permutational atom-index invariance while using index-dependent matrix representations.²⁰² From inspection of Figure 2, it should be obvious that any nonlinear change in metric will strongly affect the shape of the kernel regression space and thereby the overall performance.

3.2. Learning Curves

Correct implementations of ML algorithms applied to noise-free data sets afford interpolating ML models, which avoid overfitting and enable statistically meaningful predictions of properties of out-of-sample compounds,¹⁹⁹ after proper regularization and hyper-parametrization through converged cross-validation protocols, as discussed in great detail in the literature, for example, in refs (203 and 204).

On the basis of statistical learning theory, the leading order term of the out-of-sample prediction error (E) was shown to decay inversely with training set size N, i.e., E ∝ a/N^b, for GPR/KRR as well as for neural network models.^205,206 This is not surprising, considering the great similarities shared between NN models and GPR/KRR model, as also mentioned in the preceding subsection. This asymptotic behavior for QML models has been confirmed numerically within numerous and independent studies, many of which are referenced herein. As illustrated in Figure 3, learning curves (LC), i.e., prediction error E vs training set size N, plotted on log–log scales assume linear form (log E = log a – b log N) and serve as a useful standard, facilitating systematic comparison and quality control of the efficiency of differing ML models. For maximal consistency, the QML models should be trained and tested on the exact same cross-validation splits stemming from the exact same data set. When the data contains noise, or when relevant degrees of freedom are neglected (e.g., through use of a nonunique representation, such as the bag of bond (BoB) representation,¹⁷⁰ see section 4.1 for more details), the learning will cease eventually for some training-set size, manifesting itself visually through learning curves which level off, cf. solid-black line in Figure 3. For noise-free data and complete representations, however, a linear correlation between log(E) and log(N) is to be expected (see the dotted and dashed lines in Figure 3), with some slope b typically more or less a constant for different unique representations and related to the effective dimensionality of the problem, and some offset log a, which typically reflects the capability of the representation to capture the most relevant feature variations in kernel space. More specifically, the offset measures the degree to which the representation encodes the right physics. An illustrative example for this statement can be given by comparison of the learning curves obtained for the CM representation versus derived matrices with off-diagonal entries dependent on alternative interatomic power-laws.¹⁶³ For interatomic off-diagonal elements approaching London’s R^–6 law, the representation achieved lower offsets than for off-diagonal elements decaying according to Coulomb’s law. Correspondingly, representation matrices with off-diagonal elements linearly or quadratically growing with the interatomic distances resulted in LCs with dramatically increased offsets.¹⁶³ At first glance, it might seem that the slope of LC (aka, “learning rate” of QML model) barely changes, when switching from one unique representation to another. It is therefore natural to ask if it is impossible to further speed up the learning process as indicated by the dotted-dashed learning curve in Figure 3, exhibiting a much steeper slope. Through an expert-informed reduction of effective dimensionality (through a priori removal of irrelevant information stored in randomly selected training data), it was shown that this is indeed possible. Such strategies for a more rational sampling of training data will be discussed in section 6. Note that in contrast to conventional curve fitting, training errors for properly trained machine learning models applied to synthetic data are typically orders of magnitude smaller than the variance of the signal. As such, they are negligible and carry little meaning because noise levels are typically close to zero or at least many orders of magnitude smaller than label variance. Consequences of model construction, i.e., choice of regressor, metric, optimizer, loss-function, representation, or computational efficiency, become immediately apparent in the characteristic shape of learning curves. When training a small parametric regressor, e.g., a shallow neural network with few neurons, to estimate a complex and high-dimensional target function, the learning curve will rapidly “saturate” and converge toward a finite optimal residual prediction error that can no longer be lowered by mere increase of training set size. As such, it should come as no surprise that learning curves have emerged as a crucial tool for development, validation, comparison, and demonstration purposes of QML models in the field.

Figure 3.

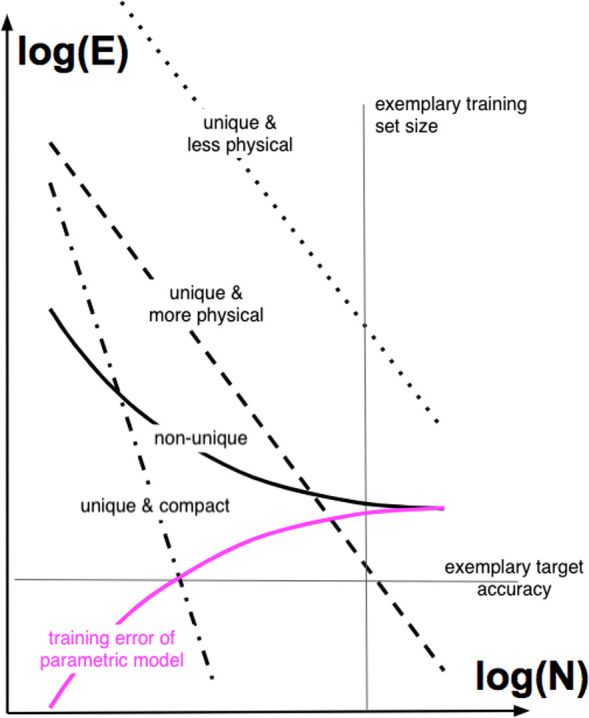
Illustration of learning curves: Errors (E) versus training set size (N). Horizontal and vertical thin lines illustrate exemplary target accuracy and available training set size, respectively. For functional ML models, training errors are close to zero (not shown), and prediction errors must decay linearly with N on log–log scales. Black-solid, dotted, dashed and dotted-dashed lines exemplify prediction errors of ML models with incomplete information (ceases to learn for large N due to being parametric, using nonunique representations, or training on noisy data), unique and less physical representation, unique and more physical representation, and explicit account of lowered effective dimensionality (i.e., “compact”), respectively. The solid-pink line corresponds to the training error for a parametric model. Training errors for ML models are negligible for noise-free data.

3.3. Loss Functions

Imposing differential relationships during training amounts to adaptation of the loss function to better reflect the problem at hand. In particular, inclusion of derivative information (gradients and Hessian) has led to dramatic improvements when tackling the problem of potential energy surface fitting.^66,67,73,74 A generalization of this idea to adapt the loss function for response properties of any QM observable was established for KRR in 2018^207−209 (exemplified for forces, Hessians, dipolemoments, and IR spectra) and for deep neural nets in 2020 (FieldSchNet exemplified moreover also for solvent effects and magnetic effects).²¹⁰

While conventional machine learning assumes that train and test loss function are identical, for atomistic simulation (or other application domains for that matter), a mathematically, more “gready” alternative might exist. In particular, the role of gradients in loss functions differing for training and testing has been studied in ref (211), with results suggesting that for predicting atomization energies throughout a CCS of distorted structures, inclusion of gradients in training improves learning curves negligibly while surely inflating the number of necessary kernel basis functions. However, when it comes to predicting the potential energy surface of a given system, they do improve the energy predictions in the above referenced studies. Conversely, when predicting gradients throughout CCS, the use of energies alone in training offers no advantage over using forces, suggesting that the inclusion of forces (if computationally less demanding than energies) should always be beneficial.

4. Representations

One could consider the choice of functional form of the representation M to be part of the machine learning methodology. However, this is a much studied question which is at the heart of how one views CCS. More specifically, what are the truly defining aspects in a compound? And how does one measure similarity? These are old questions which have already been answered for an impressive array of applications and instruct much of the basic and fundamental textbook knowledge. For example, Hammett’s σ-parameter provides a low-dimensional quantitative data-driven measure of similarity between distinct functional groups in terms of their impact on reaction rates or yields.^212,213 Within QML, physically more motivated representations are sought after for subsequent use within high-dimensional nonlinear interpolators which are more universal and transferable. As illustrated for KRR in Figure 2, also the specific form of the representation (as well as the metric used) can dramatically affect the way CCS is represented within the regressor. It should therefore not come as a surprise that the data efficiency of QML models was found to depend dramatically on the specifics of the representation used. Because the importance of the choice of the distance measures has already been mentioned above, in this section, we will focus on research that was done to find improved representations.

The choice of this particular compound representation, aka descriptor or feature, plays a particularly crucial role. Correspondingly, substantial research on the design of descriptors has already been made in the fields of chem-, bio-, or materials informatics where scarce data is typical.^174,214 Often, a large set of prospective features is hypothesized and subsequently reduced within iterative procedures in order to distill the most relevant variables and low-dimensional projections pertinent to the problem at hand (see above). While it is certainly possible to also pursue this approach within a quantum mechanical description of CCS,¹⁹⁴ its heuristic and speculative character remains as unsatisfactory as its lack of universality and transferability. Fortunately, the quantum nature of CCS allows us to follow more systematic and rigorous procedures in order to address this question.

For example, it is a necessary condition for any successful ML model to rely on uniqueness (or completeness) in the representation, as pointed out, proven and discussed several years ago in refs (215 and 216) and more recently in refs (217 and 218), Uniqueness is essential in order to avoid the introduction of spurious noise due to uncontrolled “coarsening” of that subset of degrees of freedom which is neglected. Molecular graphs based on covalent bond connectivity only, for example, do not account for conformational degrees of freedom. Consequently, their use as a representation will make it impossible to quench prediction errors below the variance of the target property’s conformational distribution, no matter how large the training set.

Other characteristics, desirable for representations to display, include compactness, computational efficiency, symmetries, invariances, and meaning. Representations, in conjunction with the regressor’s functional form, define the basis functions in which properties are being expanded and strongly affect the shape of the learning curves, e.g., accounting for a target property’s invariances through the representation typically leads to an immediate decrease of the learning curve’s offset.

While it is possible to model all QM properties using the same representation and kernel,²¹⁹ as also demonstrated for neural nets with multiple outputs already in 2013,²²⁰ it should be stressed, however, that this is a distinct feature of QML which stands in stark contrast to conventional QSAR or QSPR, where the ML model is typically strongly dependent on the target property. If regressor, metric, and representation M are independent of the label, i.e., the quantum property, there is a strict analogy to quantum mechanics in the sense of the Hamiltonian (or the wave function) of a system not depending on the operator for which the expectation value of any given observable is calculated.⁸ This becomes obvious by considering the training of a KRR model where the regression coefficients are obtained through inversion of the kernel matrix, α = (K + λ I)⁻¹p^ref, where for synthetic calculated data with signals being orders of magnitude smaller than noise, the regularization λ (also known as noise level) is typically close to zero. Using property independent representations, metrics, and kernel functions, it is therefore obvious that the regression coefficients adapt to each property only because of the reference property vector p^ref. In ref (219), this has been illustrated numerically by generating learning curves for various properties using always the same inverted kernel matrix for any fixed training set size.

The predictive accuracy for specific properties varies wildly as a function of representation and regressor choice.¹⁸³ The historic development over years 2012–2018 for a selection of ever-improved machine learning models (due to improved representations and/or regressor architectures) can be exemplified for the prediction errors of atomization energies stored in the QM9 data set¹⁷¹ and has also recently been summarized in the context of the “QM9-IPAM-challenge” in refs (15, 16, and 18).

The inclusion of increasingly more (less) “physics” in the representation has been demonstrated to systematically improve (worsen) learning curves¹⁶³ and has been followed by a series of developments which have all been benchmarked on the same set of atomization energies of small organic molecules in the QM9 data set¹⁷¹ and which demonstrate the progress made. While binding energies of “frozen” geometries still constitute an application somewhat remote from most real-world applications in chemistry, from a basic physics point of view they do represent a crucial intermediate step before tackling more complex properties. In other words, if machine learning models failed to predict binding energies, one should not expect them to work for free energies. But also from a practical point of view, the computational cost of single-point energy calculations typically dominates all quantum chemistry compute campaigns and therefore represents one of the most worthwhile targets for surrogate models used for the navigation of CCS.

We note that with the emergence of deep neural networks, the problem of also “learning” the representation can be mitigated to be incorporated in the overall learning problem.^55,221 While many intriguing and sophisticated representations, such as Fourier-series expansions,²¹⁶ wavelets,²²² multitensors,²²³ or molecular orbitals²²⁴ have been proposed, most representations can be categorized to either correspond to discrete adjacency matrices or to continuous many-body expansions through distribution functions. We therefore limit ourselves to discuss in the following, both predominantly in the context of KRR based QML models. A comprehensive overview on representations for KRR based QML models has also recently been contributed by Rupp and co-workers.²²⁵

4.1. Discrete

Coordinate-free, bonding neighbors (covalently bonded atom pairs) based graphs, as well as their systematic extensions to arbitrary number of neighboring shells, have formed an important research direction in cheminformatics for many years.^{32,174,176,178,214} In 2011, supervised learning was proposed as an alternative to solving Schrödinger’s equation throughout a chemical compound space relying as a representation on a complete undirected labeled graph that encodes the simplex spanned by all atoms.¹⁹⁵ More specifically, this graph was represented by the “Coulomb matrix” (CM), an atom by atom matrix with the nuclear Coulomb repulsion on off-diagonal elements and with approximate energy estimates of free atoms (E_I ≈ 0.5Z_I^2.4226) as diagonal elements. Formal requirements such as uniqueness, translational and rotational invariance, as well as basic symmetry relations (symmetric atoms will share the same matrix elements in their respective rows or columns) are all met by the CM. Atom index invariance can be achieved through use of its eigenvalues (thereby sacrificing uniqueness^215,227), sets of randomly permuted CMs,²²⁰ or sorting by norms of rows,²⁰³ thereby losing differentiability due to sudden switches in ranks.²⁰² We reiterate once more that the atom indexing dependence can be mitigated through using more sophisticated distance measures such as the Wasserstein metric.²⁰²

Similarly encouraging findings of KRR based QML models applicable throughout CCS were quickly reproduced for other materials classes such as polymers²²⁸ or crystalline solids.²²⁹ While off-diagonal elements with a London dispersion power law (r^–6) have subsequently been found to be preferable for QML models of atomization energies,¹⁶³ other representations (vide infra) offer lower learning curve offsets. In particular, the bag of bonds representation (BoB) is worthwhile mentioning.¹⁷⁰ Introduced in 2015, BoB groups the entries of the CM in separate sets for each combination of atomic element pairs within which all entries have been sorted. When calculating the similarity between two molecules, only Coulomb repulsions between atoms with the same nuclear charge are being compared, rendering thereby the similarity measurement more balanced and effectively lowering the learning curve offset. While even more compact than the CM, BoB lacks uniqueness due to being strictly a two-body representation which can not distinguish between homometric configurations.²¹⁶ The generalization of BoB toward the explicit incorporation of covalent bond information, angles, as well as dihedrals in terms of a systematic expansion in Bond, Angle, and higher-order interactions (i.e., BAML representation) was accomplished in 2016¹⁶³ by using functional forms and parameters from the universal force-field.²³⁰ A similar, but more elaborate, parameter-free, many-body dispersion (MBD) based representation involving two and three body terms²³¹ was proposed later in 2018.

The CM has been essential as a baseline for the interpretation, analysis, and further development of subsequent QML models. It has also been adapted successfully to account for periodicity in the condensed phase, as evinced by learning curves for formation energies of solids.²³² For other properties, such as forces, electronic eigenvalues, or excited states, the CM (or its inverse distance analogues for QML applications with fixed chemical composition) is still competitive with state of the art representations.^{67,73−75,83,233−236} Furthermore, because of its uniqueness, compactness, and obvious meaning, the CM (or its variants) are conveniently used to overcome frequent data analysis problems in atomistic simulations, such as removal of duplicates, quantification of noise levels, and simple learning tests.

Regarding the interatomic distance dependent decay rate of off-diagonal elements, it is also worthwhile to mention exponential functions, rather than 1/r. In particular, the overlap matrix between atomic basis functions of all atoms has been proposed²³⁷ and used with great success for QML models of basis-set effects²³⁸ and excited-state surfaces.²³⁹ The overlap matrix was also included within a recent sensitivity assessment of various state-of-the art representations and performed in impressive ways.²¹⁸ A constant-size descriptor based on a combination of the CM with more common molecular graph fingerprints was also proposed in 2018.²⁴⁰

Viewing BoB and CM as first and second rank tensors, to the best of our knowledge, use of a third rank tensor (explicitly encoding the surface of all possible triangles in a compound) has not yet been tested.

4.2. Continuous

Aforementioned discrete and global representations such as BoB enjoy fast computation. One important requirement for this kind of representation to work, however, is to introduce atom indexing invariance by sorting atoms according to the magnitude of entries belonging to each bond or other many-body types. This is artificial and may introduce derivative discontinuities with unfavorable consequences in related applications such as force predictions.

The sorting and associated problems can be naturally overcome by selecting continuous or distribution based representations, which, in essence, integrate out atom index dependent terms such as distance (w/wo angle and dihedral angle) and/or nuclear charge (i.e., alchemically¹⁶⁶) through use of smeared out projections (a Gaussian is commonly placed on each degree of freedom). Distribution based representations, also closely related to many-body or cluster expansion,²⁴¹ have gained much popularity also within QML models building on Behler’s seminal work on atom-centered symmetry functions for training neural networks on potential energy surfaces,²⁴² or through the subsequent introduction of smooth overlap of atomic potentials (SOAP) for use in GPR by Bartok et al. in 2013.³⁸ The first variant of linearly independent distribution based representations for QML models, applicable throughout CCS, a Fourier series expansion of nuclear charge weighted radial distribution functions, was also contributed already in 2013,²¹⁶ albeit published in its final version only in 2015. Radial distributions were also used for representing crystals in solids in 2014.²²⁹ The atomic spectrum of London Axilrod–Teller–Muto (aSLATM) terms was first presented in 2017 within the “AMON” approach by Huang et al.²⁴³ (vide infra), yielding unprecedentedly low offsets in learning curves for atomization energies in the QM9 data set.¹⁷¹ In that same year, SOAP based QML models were generalized and shown to be also applicable throughout CCS.²⁴⁴

The generic histogram of distances, angles, and dihedrals (HDAD),²³⁴ a continuous but simplified version of BAML, both including many-body terms up to torsions, was contributed in 2017. In the following year, Faber et al. conceived the idea of adding alchemical degrees of freedom in a structural distribution based many-body representation, dubbed FCHL18¹⁶⁶ (FCHL indicating the first letters of the last names of the authors and 18 in the year 2018). The FCHL family of representations encodes a systematic interatomic many-body expansion in terms of Gaussians weighted by power laws due to the insights gained in ref (163). Power law exponents and Gaussian widths were optimized as hyper-parameters through nested cross-validation during training. FCHL18 consists of three parts: The one-body term corresponds to a two-dimensional Gaussian encoding the chemical identity of the atom in terms of groups and periods of the periodic table; the two-body term encodes the interatomic distance distribution scaled down by r^–4, and the three-body term encodes all angular distributions and is scaled down by r^–2. The impact of four-body terms has been tested on QM9 but was found to have negligible impact on learning curves.¹⁶⁶ Most importantly within the context of CCS, FCHL18 based QML models have been demonstrated to be capable of accurately inferring property estimates of systems containing chemical elements which were not part of training. More specifically, consider the family of molecules of formula H_nY ∼ X, where Y corresponds to an element from group IV (either C, Si, or Ge), where “∼” represents single, double, or triple bond depending on chemical element X being from groups VII, VI, or V, respectively, and where n is the number of H atoms that saturates the total valences. Semiquantitative covalent bond potential binding curves have been predicted for any X/Y/bond-order combination using QML models after training on corresponding DFT curves for all other molecules that neither contain X nor Y.(see the top- and left-most subplot in Figure 4 for an illustration). For example, the ML binding curve of HC#N was obtained after training on binding curves of all other molecules that neither contained N nor C, i.e., when predicting the blue curve in the upper left panel of Figure 4, the red and green curves of that panel were not part of training nor were any other blue curve from the other panels. FCHL19, a recent revision, has been shown to provide a substantial speed-up in training and testing while imposing only a small reduction in predictive accuracy.²⁰⁹

Figure 4.

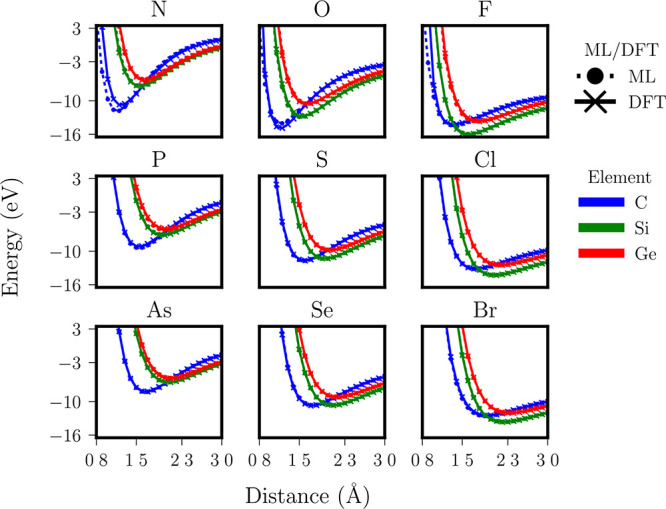
QML models infer properties for new chemical compositions. DFT and QML (FCHL+KRR) based predictions of covalent triple, double, and single bonding between groups IV and V (left column), VI (mid column), and VII (right column) elements, respectively. Open valencies in the group IV elements have been saturated with hydrogens. QML models were trained on the DFT results for all of those chemical elements that are not present in the query molecule. Reproduced with permission from ref (166). Copyright 2018 licensed under a Creative Commons Attribution (CC BY) license.

We note in passing also the related moment tensor model (MTM) by Shapeev and co-workers, introduced in 2018,²⁴⁵ as well as the unifying interpretation of many of the popular distribution based representations by Ceriotti and co-workers.²⁴⁶

5. Regressor

Depending on how regression parameters are being obtained, the incorporation of legacy methods in QML models applicable throughout CCS is typically done either within neural networks or within Gaussian process regression (GPR) (or kernel ridge regression, KRR for short). Here, we mostly focus on kernel methods, mentioning only shortly the idea of transfer learning in neural network models,²⁴⁷ which is also applicable to QML models as shown in 2018 by Smith et al.²⁴⁸

More specifically, five categories of QML models can easily be distinguished, each of which accounting for legacy information in its own way: QML models of parameters of existing models, QML models of corrections to existing models (Δ-ML), multifidelity ML (MF-ML), multilevel-grid-combination (MLGC), and transfer learning techniques. We briefly review each of these in the following.

5.1. ML Models of Parameters

Existing force-field models can capture nicely the essential physics of a wide range of chemical systems, the main drawback being that force-field parameters (e.g., atom charges, harmonic force constants, etc.) are often rigid and unable to adapt to different atomic environments. Therefore, it would be natural to make these parameters flexible and predicted by ML models. This idea dates back to the 1990s, and the first piece of related works was done by Hobday et al.,²⁴⁹ where they proposed a neural network model to predict parameters of the Tersoff potential for C–H systems. In 2009, Handley and Popelier proposed to use machine learning models for multipole moments.⁴⁹ This idea was revisited in 2015, when learning curves for atomic QML models of electrostatic properties, such as atomic charges, dipole moments, or atomic polarizabilities were presented.²⁵⁰ Their use for the construction of universal noncovalent potentials was established in 2018.⁷⁰ Neural-network based equilibrated atomic charges were also proposed in 2015 by Goedecker and co-workers^54,251 and in 2018 by Roitberg, Tretiak, Isayev, and co-workers.^252,253

Similar strategy could also be applied to semiempirical quantum chemistry methods relying on parameters typically fitted by computational/experimental data. In 2015, QML models of nuclear screening parameters were contributed by Pavlo and co-workers.²⁵⁴ In 2018, unsupervised learning for improved repulsion in tight-binding DFT was introduced by Elstner et al.,²⁵⁵ followed by substantial further improvements in 2020.²⁵⁶ Extended Hückel theory was revisited in 2019 by Tretiak and co-workers.²⁵⁷

5.2. Δ-ML

The idea to present QML models of label corrections applicable throughout CCS and which systematically improve with training data size was first established in 2015 in terms of Δ-machine learning. Numerical results provided overwhelming evidence for the success of this idea as demonstrated for modeling energy and geometry differences between various levels of theory, including PM7, PBE, BLYP, B3LYP, PBE0, G2MP4, HF, MP2, CCSD, and CCSD(T) for QM9¹⁷¹ and subsets thereof.²⁵⁸

Δ-ML also works for correcting complex and subtle properties, such as van der Waals interactions in extremely data-scarce limits, as illustrated for DFT corrections based on training sets with less than 100 training instances,²⁵⁹ or to model higher-order corrections to alchemical perturbation density functional theory based estimates of heterogeneous catalyst activity.²⁶⁰ Among many other applications, Δ-ML has enabled corrections to electron densities,²⁶¹ electron correlation based on electronic structure representations within Hartree–Fock or MP2 level of theory,²⁶² or DFT and CCSD(T) based potential energy surface estimates.²⁶³

For noise-free data and functional QML models (unique representations), numerical results for learning curves indicate a constant lowering of offset, no matter which training set size. Such nonvanishing improvement appears to turn into vanishing improvement when employing Δ-ML in order to correct low-quality or coarse-grained baselines, such as a semiempirical PM7²⁵⁸ or Hammett’s relation.²¹³

5.3. Multifidelity

The success of Δ-ML is encouraging, enabling a significant reduction in high-accuracy reference quantum chemical data necessary for training, to reach the same level of predictive accuracy as traditional QML models. However, it still consumes a considerable amount of data calculated at some high level of theory, as its structure in design is too simple to fully exploit the underlying correlation between varied quality of properties. In fact, well-established quantum chemical methods abound in literature, exploiting effectively the underlying correlation, in the name of the so-called composite methods, for example, the famous Gn series.^264−266 In essence, these methods approximate some specific part of correlation energy (e.g., energy lowering due to inclusion of diffuse orbital in basis set) from a high level of theory (for instance CCSD(T)) by the same quantity calculated from a relatively low level of theory (say MP2). Because of error cancellation, composite methods have been proven to be extremely effective toward reaching an accuracy of experimental quality and are widely used for calculations of high-quality thermochemical data.^264−266

To do interpolation and meanwhile exploit error cancellation effectively, multifidelity ML (MF-ML) comes into play. The core idea of MF-ML is hereafter demonstrated by total energy (E) prediction. For brevity, we deal with two levels of theory (the low and high level are denoted by 0 and 1, respectively) and focus on one flavor of MF-ML, i.e., recursive KRR (r-KRR for short, or MF-KRR),²⁶⁷ which is similar to its counterpart, recursive GPR (r-GPR, or MF-GPR),^268,269 and differs to MF-GPR to some extent, in analogy to the difference between KRR and GPR. Unlike Δ-ML, MF-ML comprises multiple machines with different labels to learn (two for our exemplified case). The first one is just a traditional QML model trained on a set of data (denoted as S₀) associated with the low level of theory, i.e., E_j⁰ = Σ_i∈S0c_ik_(i,j), where j ∈ S₀ denotes the molecular representation vector and c⁰ is the regression coefficient associated with the low level of theory. This machine is also called the baseline model. Then we build a second machine with training set S₁ satisfying S₁ ⊂ S₀ and energy delta, i.e., E¹ – E⁰, as label, the same as a Δ-ML model. In math, ΔE_n^0→1 = E_n – E_n⁰ = Σ_m∈S1c_mk_(m,n), where n ∈ S₁. Once trained separately for each machine, all c^l’s are obtained and MF-KRR predicts the property of any query q out-of-sample at the high level of theory by E_q¹= E_q + ΔE_q^0→1.

Extending r-KRR to more than two levels of theory is straightforward: except the baseline model for the lowest level, one needs to build one machine for every two adjacent levels of theory, and the final test energy is just the summation of the inferred energies by all machines, i.e., E_q^L = E_q + Σ_l = 0^L–1 ΔE_q, where l is the level indicator (starts from 0, the lowest level) and L corresponds to the largest l, or the target level. Bear in mind that S₀ ⊂ S₁ ⊂··· ⊂ S_L.

We note in passing that MF-GPR has a rather different formulation compared to MF-KRR and benefits from the stochastic nature of GP, i.e., it is capable of providing the variance estimate of prediction. Like GPR, data at each level of theory in MF-GPR is modeled as a GP,^268,269 and every two adjacent levels are connected by a linear transformation, i.e., E^l+1 = γE^l + ϵ, where γ is a scaling factor and ϵ is a correction term respectively and both of which may depend on the two involved levels of theory (i.e., l and l + 1). Nevertheless, both MF-KRR and MF-GPR could end up with the same set of working equations under certain conditions. For detailed derivation of the equations of MF-GPR, the reader is referred to an early review on QML.¹⁰ Last but not least, one should note that MF-KRR converges toward the conventional KRR model associated with the highest level as the difference between training sets for each machine vanishes.

Albeit well-founded in mathematics decades ago, the power of MF-ML has not been harvested until recently. Applications include quantum collision for the Ar–C₆H₆ system by Cui et al.,²⁷⁰ bandgap prediction of solids done by Pilania et al.,²⁷¹ dopant formation energy prediction in hafnia by Batra et al.,²⁷² high-accuracy potential energy surface prediction for small molecules by Wiens et al.,²⁷³ and the recently performed molecular crystal structure prediction study by Egorova et al.²⁷⁴

5.4. Multilevel Grid Combination

In spite of the drastic improvement over Δ-ML, MF-ML has its own limitations. For one, the computational cost of the baseline evaluation for every query compound can still be considerable. Furthermore, it must be strictly satisfied that the increasingly more expensive training sets form a nested structure, implying that possible and beneficial correlations between non-nested reference data calculated at different level of theory are not being exploited. To overcome this drawback, Zaspel et al.²⁶⁷ proposed a multilevel model in 2018, combining successfully ML with sparse grid (SG),²⁷⁵ a numerical technique widely used to integrate/interpolate high dimensional functions.

The genuine SG approach assumes (quasi-)uniform grids along each dimension, which serves as basis functions (more precisely, centers of basis functions, such as triangular function) and based on tensor products of which any multidimensional function could be represented/expanded.²⁷⁵ The expansion weight for each tensor product is dependent on only the indices of associated grid and spacing along each dimension and determined by multivariant Boolean algorithm.²⁷⁶

Replacing such a grid by abstract variable (or combinations of which) such as electron correlation level (x_C), basis set (x_B) and expressing system property as a function of these abstract variables represents an appealingly rigorous alternative. For example, the total energy of a system could be expressed as E = E(x_C, x_B). Given some sparse grids comprising small x_C combined with all x_B’s, and small x_B combined with all x_C’s, and intermediate x_B’s combined with intermediate x_C’s, we are able to interpolate/extrapolate the E at some different combination of x_C and x_B. Of particular interest is extrapolation to regions unsampled, i.e., regions with large x_C and x_B. However, one major issue with such extension is the elusive nature of distance between two abstract variables, which is essential in determining the weight associated with each grid, as mentioned above. More specifically, it is unknown how to quantitatively characterize how distant HF and MP2 are along the dimension C, although qualitatively it is certain that HF lies closer to MP2 compared to CCSD(T). The B subspace, is understood much better, as the magnitude of x_B could be at least characterized by the largest angular channel, or more straightforwardly, although less rigorously, by the number of basis functions. This ill definition of these abstract variables is absent in genuine SG, as grids there reside typically in Euclidean space and therefore distance is well-defined. To rise to this problem, a workaround is to assume uniformality of grids along each dimension (i.e., equidistant) and grids along each dimension is represented simply by indices starting from 0 (now weights depend solely on the indices of grids). This, however, should always be done with great care. In the original MLGC paper,²⁶⁷ electron correlation levels are reasonably chosen as HF, MP2, and CCSD(T), together with three basis sets, i.e., STO-3G, 6-31G, and cc-pVDZ (the number of basis functions increases by a factor of ∼2).

Note that the aforementioned SG approach deals with typically one system at a time. To incorporate it within ML framework, one extra variable has to be introduced, i.e., training set (x_N), the size of which indicates the magnitude of x_N.²⁶⁷ Accordingly, E = E(x_C, x_B, x_N). Unlike subspace C or B, x_N is well-defined with explicit value. Nevertheless, it has to be treated in a similar fashion as for x_C/x_B, i.e., given the minimal x_N (aka. N₀) and a ratio (s) between any two adjacent x_N’s, training sets are to be assigned an array of indices starting from 0 (for N₀) and an increment of 1. This assignment is necessary so as to comply to what has been done for subspaces C and B. Now each grid in this abstract space is a combination of three variables: (x_C, x_B, x_N), with x_I ∈{0, 1, . . ., I_max}, I ∈{C, B, N}. For each such combination, an associated ML model is trained (with N training instances of course). Given a query system, its energy is predicted as a weighted summation of test energies from all ML models, with weights derived from Boolean algorithm.^267,276 Note that in practice, to reduce the cost of generation of reference quantum data, a large x_N is associated with a low level of correlation and/or small basis set, while only few(er) labeled data are needed for high(er) correlation level and/or large(r) basis set.

With the above setting, Zaspel et al. were able to show²⁶⁷ that MLGC enables ∼10-fold reduction (cf. traditional single level ML model) in the costly highest level quantum data (i.e., CCSD(T)/cc-pVDZ) to reach chemical accuracy in predicting atomization energy of out-of-sample QM7b molecules. Last but not least, it is worth pointing out that MLGC reduces to MF-ML if only one dimension is being considered.

5.5. Transfer Learning

While multilevel methods are most naturally combined with kernel methods, they may have even more far-reaching effects for neural network (NN) models, as training a NN model, deep NN (DNN) in particular, is a nontrivial problem. Furthermore, current ad hoc DNN models are typically specialized, meaning a (D)NN model may need to be retrained for a slightly different task.

Transfer learning (TL)²⁷⁷ is one popular approach employing multiple levels in machine learning that can greatly alleviate the aforementioned problems, which reuses the knowledge gained through solving one task (base task) as a starting point for a second task (target task), different but highly related. For instance, knowledge obtained from learning to infer DFT energies could be applied to infer CCSD(T) energies.²⁷⁸ A successful transfer of knowledge can improve the performance of the target DNN model significantly. Speaking the language of learning curve, TL could offer²⁷⁷ (i) smaller offset as the transferred model per se provides a decent starting point and (ii) steeper learning curve due to the transferred model usually accounting for a parameter space rather close to the optimal one.

On the basis of the type of traditional ML algorithms involved, TL could be categorized into several variants. Here we focus on a variant named inductive transfer learning, in which the labeled source and target domains are the same, yet the source and target tasks are different from each other.

In TL, there are two essential ingredients: (i) a pretrained model, obtained by either training a network from scratch on some data set and a specific task, or simply from published models, and (ii) target network, to be trained on a target data set and task, but utilizing the learned features from (i). This process is likely to work only if the features are general (i.e., generic features) to both base and target tasks, as would be captured by the initial layers of NN models. When retraining the target model, one may choose to either freeze the initial layers in the base network to use them as feature extractors for the target model or fine-tune the last several layers further for improved performance. A rule of thumb is to freeze when target labels are scarce (to avoid overfitting), while fine-tune otherwise.

To develop a successful TL model, it is vital to choose the proper base model and associated training data set. However, it remains largely an open question how to make the choice. This may require profuse intuition developed via experience. Furthermore, there exists one major potential risk of using TL, i.e., negative transfer, which refers to scenarios where the reuse of base-task knowledge degrades the overall performance of the target task. To avoid negative transfer, one may have to resort to approaches that explicitly model relationships between tasks and include this information in the transfer method.²⁷⁹

Applications of TL covers mainly computer sciences, such as image recognition and natural language processing. For chemistry-related problems, TL is emerging as a promising approach. Examples include Smith et al.’s work on predicting CCSD(T)/CBS energies based on transferred knowledge gained through training on DFT energies²⁷⁸ for the ANI-1x data set (see section 8.1), Iovanac et al.’s work on property prediction of QM9 molecules,²⁸⁰ as well as Cai et al.’s recent work on drug discovery.²⁸¹

6. Training Set Selection

Among all factors determining the performance of a QML model, training set selection plays another fundamentally important role in the sense that all knowledge essential for making confident predictions are implicitly encoded in the training data.

Several pertinent fundamental and distinct questions have remained open:

• Q1How to extract the most representative and least redundant general subset from a given data set?
• Q2How to quantitatively define the suitability of a given training set for a specific query at hand?
• Q3How to systematically select the most relevant training set for a specific system?

Because of their highly nonlinear impact of training instances on model parameters, these questions are challenging and have not been studied much. Of course, the problem of training set selection is not a problem unique to chemistry, and it is relevant to most supervised learning problems in other fields. Currently, the aforementioned issues are mostly addressed through random selection. Although universally applicable, random selection suffer inevitably from selection bias inherent in the data itself. More specifically, in the randomly selected training set, many instances can be ignored and their inclusion in training does not improve predictive performance of the QML model (due to redundancy) or could even degrade it (due to being irrelevant for a given query test or due to noise).

Bias could become a very serious issue as the systems under study are increasingly more complicated. The origins of the bias issue could be divided into two components: (i) Curse of dimensionality. This is mainly related to the size of the systems and plagued further by compositional diversity. More specifically, as the system size and/or the encompassing number of types of elements grow, the size of the thus-spanned CCS grows combinatorially (see above). (ii) the inhomogeneity of CCS. The energetics in chemistry typically favors one kind of bonding over another. For instance, hydrogen atom favors a single σ bond with other atoms, while carbon atom can exhibit several different bonding patterns such as sp³, sp², and sp. Consequently, random sampling will introduce more subsampling of hydrogen environments, but proportionally fewer C–sp local environments leading to worse model estimates of properties for C than for H.

To tackle the bias issue, previous and ongoing research has been trying to almost exclusively tackle Q1, assuming a pre-existing data set (or a data set that is straightforward to generate, e.g., in molecular dynamics). Examples include the use of genetic algorithms (requiring labeled data to gradually expand the optimal training set),^80,282 or “active learning” approaches,^79,223 which selects the most representative subset “on-the-fly” from a given set of unlabeled configurations, i.e., no quantum chemical data is needed for making decisions about whether or not a query configuration is redundant. The AMONs concept proposed by the authors²⁴³ partially resolves question Q3 (cf. Q1 and Q2), at the same time allowing for significant dimension reduction of CCS as well as the effective removal of statistical redundancy of training sets (see below for details). Other related work shifts the attention to training set reduction instead, primarily in molecular dynamics simulations, for instance, Li et al.⁶² proposed a “learning-and-remembering” scheme, in which the decision to recompute QM data for a new configuration was taken every n steps. Another relevant contribution to active learning in CCS was made in 2018 by Smith et al.,²⁸³ relying on “query by committee”, i.e. ensemble information obtained through use of multiple neural networks (of the ANI kind⁵³). Potentially promising alternative directions could possibly be inspired by recent developments in computer science, among many others notably the idea of artificial “soft” labels, curated through carefully blending features of training instances.^284,285 In the original paper, this idea was tested on the MNIST data set (a database of handwritten digits) and similar performance was achieved with much fewer but soft labels, as compared to training on almost the entire data set. This idea should in principle also be applicable to CCS requiring the design of some fictitious averaged training molecules, interestingly probable to violate common rules of chemical bonding. In the following, we review the three most promising approaches toward training set selection: genetic algorithm, active learning, and the AMONs approach.

6.1. Genetic Algorithm

Genetic algorithms (GA) have been widely used in (global) optimization problems in quantum chemistry, such as first-principles based global structure optimization²⁸⁶ (for compounds with desired physio-chemical property), a key topic in the inverse-design problem.²⁸⁷ To the best of our knowledge, the first piece of work about using GA for training set selection within QML was done by Browning et al.²⁸² for molecules, followed by Jacobsen’s work⁸⁰ on SnO₂(110) surface reconstruction.

In the following, we discuss the central idea of GA for the selection of the most representative set of QM9 molecules as done in ref (282). For applications to other properties and systems such as chemisorption systems,²⁸⁸ only technical details will differ. Given a set (S₀) of N molecules, GA carries out three consecutive steps for optimization: (a) Generate M random sets of size N₁. This forms a starting population of training sets (aka. the parent population), labeled as Ŝ⁽¹⁾ = {S_i}, where i ∈ {1, 2, . . ., M}. Note that the initial size needs to be balanced against the diversity of the molecules for optimal performance. (b) Train a QML model on each set in Ŝ⁽¹⁾ and then test on some joint preselected out-of-sample molecules (i.e., not part of Ŝ⁽¹⁾), the resulting test error ϵ_i (measured by for instance mean absolute error) serves as a “fitness” indicator, characterizing how fit s_i is as a training set (smaller ϵ_i means better fitness). (c) Evolution of Ŝ⁽¹⁾ takes place through three consecutive steps: selection, crossover, and mutation. In the selection step, decisions have to be made on which S_i ∈ Ŝ⁽¹⁾ should be kept in the population to produce a temporary refined smaller set t̂⁽¹⁾, and a set with larger fitness value means higher probability to be kept in t̂⁽¹⁾. The crossover step involves the update on Ŝ⁽¹⁾ from t̂⁽¹⁾, and the resulting new population is relabeled as Ŝ⁽²⁾, each of which is obtained by mixing molecules from two subsets of t̂⁽¹⁾. The last step mutation randomly modifies molecules in some subset of Ŝ⁽²⁾ to promote diversity, e.g., replace −NH₂ group by −CH₃. To avoid introduction of chemical environments alien to the whole data set, the replacements in mutation have to be constrained locally in S₀. (d) Go back to step (b) and repeat b–d until there is no improvement in the population and the fitness value has no significant improvements for over n iterations. The final converged set corresponds to a “optimal” training set and is labeled as Ŝ.

It is not a surprise that selected Ŝ should be able to represent all the typical atomic environments in S₀, and therefore a QML model trained on Ŝ warrants significantly improved test results in comparison to randomly drawn training sets. As the fitness value decreases during the GA iterations, the QML models “tried” out the sensitivity with respect to inclusion of certain training instances, and this can serve their systematic inclusion/exclusion. The usefulness of the optimized set Ŝ has to be assessed by the generalizability of the QML model trained on Ŝ to new molecules absent in S₀. Indeed, improved generalizability is observed for PubChem molecules compared to random sampling, as was reported in ref (282).

In spite of its power for solving hard optimization problems, such as finding the optimal training set composition, the drawback of most GA implementations is also obvious: It typically relies on the availability of labeled data to evaluate the fitness in each iteration. As such, it only offers computational cost savings in terms of QML model efficiency and not in terms of reducing the total need for available training data. Possible solution to circumvent this is to introduce heuristics in feature space, e.g., accounting for the fitness by some distance metric instead, meanwhile avoiding the costly training-test procedure in each iteration.²⁸⁹

6.2. Active Learning

Active learning (AL) is more interesting than GA for training set selection, as it can use directly unlabeled data, i.e., before the acquisition of costly labels. Intuitively, it makes sense that this should be possible as the quantum properties of any compound are implicit functions of its composition and geometry, which is the only input required for calculating rigorous representations. Among the many categories of AL algorithms used for determining which unlabeled data points should be labeled, below we mainly focus on the variance reduction query strategy, which labels only those points that would minimize output variance (uncertainty in prediction). Note that the task of variance estimation is fundamentally different from mean error estimation, and the variance based selection method differs significantly from the mean error based selection method (such as GA mentioned above) accordingly. Relevant works on active learning include the D-optimality approach^79,223 and methods based on variance estimators using Gaussian process regression (GPR),^290−292 as well as neural network (NN) models.

Rooted in linear algebra, the D-optimality approach^79,223 takes advantage of (i) the dimension of features could in principle be significantly lower than the number of degrees of freedom spanned by the molecules (in particular for molecules that are in or close to their equilibrium states) and (ii) linearly parametrized local atomistic potential. Given a set of K molecules, the total energy of the qth molecule could be approximated as E^(q) = Σ_i = 1^NV(x_i) = Σ_i = 1^N Σ_j = 1θ_jb_j(x_i^(q)) = Σ_j = 1θ_jB_j(x^(q)) (in matrix form, E = θB), where B_j(x^(q)) = Σ_i = 1^Nb_j(x_i) serves as the effective basis function of dimension m and b_j(x_i^(q)) is some function dependent only on the local representation x_i of the ith atom in q, N is the number of atoms of q. Then deriving the D-optimality criteria boils down to finding the “best” submatrix (of size m × m) from the overdetermined matrix A^K×m (where K > m and A_kl = B_k(x^(l))) such that the absolute value of det A reaches its maximum. Well-established algorithms exist to achieve the D-optimality criteria, e.g., the maxvol algorithm.²⁹³ To obtain an optimal set, one typically has to iterate the procedure, one new query per time. If the corresponding magnitude of det A increases, it would be selected (query strategy) and discarded otherwise. Numerical results⁷⁹ have shown much improved performance for long-time MD simulation compared to classical on-the-fly learning.⁶² However, the downside of D-optimality approach is also noticeable, that is, the model has to be updated at each iteration and application of the model could be prohibitive for a data set bearing a large feature space. Furthermore, the linear potential B_j depends on the proposed representation and the potential form, the latter of which in particular may suffer from lack of expressive power for some systems, i.e., the potential form may lack general applicability for a wide range of molecular systems. And last but not least, this approach relies on the choice of ratio (of det A values of two consecutive iterations) threshold manually chosen, which has to be tailored for a specific data set and may not be applicable to other data sets that only differ ever so slightly.

We note in passing that an alternative view⁷⁹ of D-optimality criteria is to assume that the energy has a Gaussian random noise and the best submatrix A corresponds to the minimal variance in the solution of E = θB. Besides, consideration of other properties such as forces could be naturally incorporated into this framework by simply taking derivatives of B_j with respect to Cartesian coordinates, expanding the feature matrix B.⁷⁹

Another variance-based approach relies on the GPR directly. That is, once trained, the model can estimate the variance directly, without referring to other criteria (as in the D-optimality approach). The estimated variance serves as a natural indicator, telling if any newly added data point would improve the model (if the variance is large with respect to a user-defined tolerance) or not (if the variance is very small). A small variance typically also means that the newly added data lie within or close to the current training space, distant otherwise. Methods like Gaussian process regression (GPR) are stochastic in nature and inherently capable of calculating the variance of prediction. More specifically, GPR aims to estimate the predictive distribution for any test data (unlike the kernel ridge regression model). Related works include that of Snyder et al.’s,²⁹⁰ in which the Bayesian predictive variance is shown to correlate with the actual error, and recently Reiher’s group^291,292 used GPR to select optimal training sets in an automated fashion to explore chemical reaction network²⁹¹ and subsequently adjust for systematic errors in D3-type dispersion corrections, with one (sequential scheme) or multiple systems (batchwise variance-based sampling, BVS) selected each time.

Neural network (NN) based methods also offer a quite distinct perspective on the confidence of predictions. The general finding is that for NN methods estimates tend to be overconfident,²⁹⁴ possibly due to the lack of principled uncertainty estimates²⁹⁵ (i.e., NN model typically produces one single value for an input instead of a preditive distribution like GPR) and/or that the tools for mean estimation perhaps do not generalize.²⁹⁵ In spite of the lack of native variance estimate, variance can still be modeled in practice through consideration of multiple parallel NN models. In analogy to GPR, uncertainty in NN models can be understood by taking a Bayesian view of the uncertainty of weight with some distribution assumed a priori and then updated by training data. There exists several variants of such NN models, including the ensemble neural network models,^{283,296−298} where NN models share the same architecture but varied parameters (typically, ensembles are generated by NN submodels training on distinct subsets of data), and the dropout regularized neural network,²⁹⁹ a lower cost framework for deriving uncertainty estimates (randomly dropout some nodes each time). These NN models are highly dependent on the training data, and therefore the predicted variance may not be reliable if the test data is distinct from training data, as is commonly expected for CCS exploration. Another type of NN model based uncertainty metrics, widely adopted, may alleviate this deficiency, which employs distances in feature space (or some latent space) of the test data point to the current training data to provide an estimate of similarity measure and thus model applicability.³⁰⁰ This kind of approach enjoys several other advantages, such as easy interpretation, model independence, as well as potentially fast computation, but suffer from high dependence on the representation.³⁰⁰

6.3. AMON Based QML

Having a closer look at all the selection methods presented above, one notices that there is always some footprint of random sampling, i.e., one prerequisite for all those methods is a pre-existing starting training data, usually randomly selected, and reaching convergence of training data through iterative addition of new feature inputs may be slow if the starting points barely represent the space spanned by test data. The AMONs approach²⁴³ attempts to mitigate these shortcomings through selection of the “optimal” training set on-the-fly, i.e., only after having been provided a given specific query test feature input. In essence, AMON based QML exploits the locality of an atom in molecule which allows to reconstruct extensive properties, such as the ground-state energy, in some analogy to the nearsightedness of electronic systems.^301,302 For the sake of a succinct discussion, we turn our attention to valence saturated system only and we neglect hydrogens. However, extension to other systems (e.g., system involving radicals, charges, conformational changes, vibrations, reactions, or noncovalent interactions) are also possible^207,243). Note that throughout the whole process, we are only concerned with heavy atoms.

The AMONs selection procedure²⁴³ can be divided into four major steps: (i) The connectivity graph G of a query molecule is constructed using its 3D geometry. (ii) Next, all subgraphs are enumerated (the ith subgraph is labeled as G_i) of G with increasing number of heavy atoms (denoted as N_I). For a given G_i, one performs a series of checks to see if it is a representative subgraph: (a) Is it a connected subgraph? (b) does subgraph isomorphism hold true? (c) Are all atoms valency-saturated after rationalization of the subgraph? And (d), is ring structure retained when all associated nodes are present in the current subgraph? If all of these criteria are met, then G_i is ready for further filtering and discarded otherwise. Criteria b is concise yet informative: subgraph isomorphism ensures that hybridization states of all atoms in the subgraph are retained, implying that bonds in query graph with bond order larger or equal to 2 are not allowed to break for fragmentation. (iii) Perform geometry relaxation for the corresponding fragment (now with valencies saturated with hydrogen atoms) using, for example, Universal Force Field (UFF)³⁰³ or other force-field optimizer with dihedral angles fixed to match the local geometry of the query molecule (to avoid conformational changes in local environments). This step is followed by geometry relaxation using some quantum chemistry program. At this stage, it may happen that the subgraph candidate dissociates (turning into a disconnected graph) or is transformed into a molecule with different connectivity. In the former case, the fragment should be discarded, while in the latter case, the subgraph isomorphism has to be rechecked. (iv) One proceeds if the subgraph candidate has experienced no change in connectivity or if subgraph isomorphism is retained despite there being change in connectivity. The resulting fragment is selected for the AMON database.

As the number of atoms in the subgraph increases, one continues looping through {G_i} until the set has been exhausted. The resulting set of AMONs is considered the query-specific “optimal” set which is representative of all local chemistries in the query molecule.

Figure 5 shows all AMONs for an exemplified QM9 molecule named 2-(furan-2-yl)propan-2-ol with AMON size (N_I) being at most 7 by applying the above algorithm. Not surprisingly, there exist only two molecules possessing N_I = 1, i.e., CH₄ and H₂O. For N_I = 2, a C=C double bond is allowed to be cleaved from the 5-membered ring, forming a valid AMON H₂C=CH₂, as the resulting AMON retains its original coordination number for C’s, meanwhile keeping their valence saturated (i.e., meeting octet rule). While a fragment such as H₂C–OH, also extracted from the ring, is not a valid AMON as the valence of C atom is not saturated. Repeating similar arguments for increasingly larger N_I’s, we end up with only 30 AMONs, but which as a whole represent the complete set of local atomic environments present in the target and has the potential to extrapolate accurately the properties of the exemplified target QM9 molecule, as well as infinitely many other molecules that share the same set of AMONs after fragmentation.

Figure 5.

All AMONs sizes 1–7 for training system specific QML models of exemplary query molecule 2-(furan-2-yl)propan-2-ol (top right).

AMON based QML models exhibit improved slopes and offsets in learning curves, as evinced for thousands of molecules after reaching respective training set sizes of only ∼50 on average. By contrast, 20 times larger training set sizes are required using random sampling.²⁴³ One should note that graph based AMONs are not omnipotent. They are best suited for sampling chemical spaces of large systems. To extend AMONs to also handle configurational spaces is possible in principle, but not trivial as it faces challenges similar to modeling large systems without explicit graphs, such as metals, metal surfaces, or molecular crystals or liquids.

7. Properties

As we focus on supervised learning throughout this text, properties (or labels) of molecules have to be always paired with some molecular representation. Starting from regression of experimental properties, e.g., atomization energies, dipole moment, boiling point, in the early practises of machine learning, by now the scope of properties has been expanded significantly.

Because of its determining role for stability and dynamics, energy is among the most important properties, and it is also the primary target property of most studies. As early as in 2011,³⁰⁴ reorganization energies in a subspace of CCS consisting of polyaromatic hydrocarbons relevant to photovoltaic applications were already predicted using ML models. While the pioneering work on demonstrating the applicability of QML models for navigating CCS was published in 2012 for atomization energies only,¹⁹⁵ a multiproperty neural network was published shortly after,²²⁰ covering not only atomization energies but also polarizabilities, molecular orbital eigenvalues, ionization potentials, electron affinities, and excited-states properties at various levels of theory. The correlations among these properties have confirmed some of the well-established physical principles as well as shown some interesting patterns. As illustrated in Figure 6, the ionization potential (IP) is well correlated with the HOMO energies, as expected from Koopman’s theorem; the polarizability is linked to the stability, as often implied by the hard–soft acid–base principle. Properties calculated at different levels of theory are strongly correlated, suggesting the possibility to exploit implicit correlations for the training of QML models with superior data efficiency. What is more interesting is that, for properties such as HOMO and atomization energies displaying little correlation, after training the neural network encodes some of the underlying and hidden correlations among these properties (box in Figure 6), indicating already in 2013 that neural network based QML models are amenable to “explainable AI”, as also illustrated subsequently in 2017 for effective atomic chemical potentials.³⁰⁵

Figure 6.

Property vs property matrix for ∼7k organic molecules at various levels of theory. A multiproperty neural net trained in CCS encodes underlying correlations as evinced by the first principal components of the last layer for 2k molecules not part of training. Reproduced with permission from ref (220). Copyritht 2013 licensed under a Creative Commons Attribution 3.0 license.

While QML commonly deals with properties which correspond to observables, other well-defined but more arbitrary labels can also be modeled. Examples include atomic charges or energies which do not have a unique definition. A more exotic application consists of successfully trained QML models of “time-to-solution” in terms of estimates of the number of iterations necessary to reach convergence for given initial conditions: In 2020, QML models of the computational cost of common quantum chemistry calculations have been demonstrated to enable optimal load-balancing and scheduling in ensemble calculations of high-throughput compute campaigns through CCS.³⁰⁶

To provide a more comprehensive perspective on the interesting subject of property, below we divide all properties into three main categories depending on the number of atoms/species involved: atomic property (atom/bond/functional group in a molecule), molecular property (the entire molecule), and intermolecular property (at least two molecular species). And within each section, we briefly review models of important properties in a rough chronological order. Note that the boundary between different categories is not clear-cut. For instance, the highest vibrational frequency of a molecule may be attributed to certain functional group but only in an approximate way, the exact value of which may still depend on all the other atoms in the molecule. For this and similar cases, we prefer to classify the relevant properties into atomic rather than molecular properties.

7.1. Atomic

Generally speaking, atomic properties are relatively easy to learn as they typically benefit the most from the general assumption of locality of an atom in a molecule. On the basis of the QM9 database, QML models were introduced for atomic properties, such as core level excitations, forces (see previous section), or NMR-shielding constants.⁶⁴ Atomic QML models of electrostatic properties, such as atomic charges, dipole moments, or atomic polarizabilities, were introduced in 2015,²⁵⁰ and their use for the construction of universal noncovalent potentials was established in 2018.⁷⁰ Deep neural networks for similar properties were also contributed in 2018 and 2019 by Unke and Meuwly.^56,307 Information from topological atoms has also been used to build dynamic electron correlation QML models in 2017.³⁰⁸ In 2017 and 2018, atomic energies and potentials were also discussed in refs (166, 173, 309, and 310). QML models of polarizabilities based on tensorial learning were presented in 2020,³¹¹ and most recently, Gastegger and co-workers introduced external field effects within neural networks and demonstrated interesting performance for predictions of IR, Raman, and NMR spectra, as well as for continuum solvent effects on chemical reactions.²¹⁰ Multiscale models of atomic properties have also been proposed.³¹²

QML models of NMR shifts in molecules were first studied in 2015⁶⁴ and 2017,²⁴³ followed by shifts in solids in 2018,^313,314 and NMR shifts in solvated proteins, coupling, a kaggle challenge, and an in-depth revisit of shifts in molecules were all contributed in 2020.^315−318

In 2017, self-correcting KRR based models of potential energy surfaces and vibrational states were presented in ref (319) as well as neural network based molecular dynamics for the calculation of infrared spectra.³²⁰ Out of all QML models for properties studied in the 2017 overview study on the CCS of QM9,²³⁴ it was only for the highest vibrational (fundamental) frequency that random forests performed better than KRR or neural networks, the likely reason being that the QML model’s task consisted “only” of detecting if an O–H or N–H bond present on top of the C–H bonds, and to assign the typical corresponding bond-frequency, and that typically random forests work well for such classification tasks. Other 2018 studies dealing with infrared spectra include refs (207, 252, and 253).

7.2. Molecular

At the molecular level, properties are greatly diversified, ranging from properties for ground state to excited ones, from static to dynamic ones, as well as from single molecule in vacuum to condensed phase.

QML models of electronic properties, such as excited states, quantum transport, or correlation, have remained rather sparse over the years. Examples include QML models for electron transmission coefficients for transport across molecular bridges of varying composition,³²¹ and Anderson impurity models³²² in 2014, and dynamical mean field theory³²³ and excitation energies²³³ in 2015. Only recently QML has been extended to also study nonadiabatic excited states dynamics for given systems (conformational sampling) by Dral, Barbatti, and Thiel³²⁴ or Westermayr and Marquetand.^83,325 And the recent introduction of SchNarc,³²⁶ a combination of the deep neural net architecture SchNet⁵⁵ and the surface hopping ab initio molecular dynamics code SHARC,³²⁷ has led to promising first results for CCS studies involving small sets of small molecules.³²⁸ For more details we refer to the recently published reviews on this field.^329−331

QML models of electron affinities and ionization potentials with deep neural networks have also recently been proposed.³³² Symmetry conserving neural networks for efficient calculations of electronic and vibrational spectra have been presented in 2020.³³³

7.3. Intermolecular

As the system becomes more complicated, the associated properties also tend to show more interesting, and sometimes surprising patterns. Hereafter, we will focus on energetic properties, unless otherwise stated. Depending on whether or not the system has experienced significant reconstruction in the relative orientation between atoms, intermolecular energetics could be further divided into intermolecular binding energy or reaction energy/barriers. Below, we summarize relevant contributions for each of these two subcategories.

In terms of binding energies within assemblies of atoms, ever since the publication of ref (195) in 2012, a large variety of systems has been addressed, reaching from formation energy predictions of diverse inorganic materials,^164,166,334 over models of chemical bonds in molecules,³³⁵ to models of electronic properties of transition metal complexes.³³⁶ GPR/KRR based QML models represent a unified approach, as demonstrated for applications to surface reconstructions, organic molecules, as well as protein ligands.²⁴⁴ Symmetry adapted learning of tensorial properties was introduced in 2018,³³⁷ as well as neural networks for atomic energies,³¹⁰ on-the-fly learning for structural relaxation,⁸⁰ crystal graph convolution networks for materials properties,³³⁸ solvation and acidity in complex mixtures,³³⁹ and a machine learning based understanding of the chemical diversity in metal–organic-frameworks.³⁴⁰ An extensive review of big data in metal–organic frameworks was also published in 2020.³⁴¹

Accurate QML prediction of reaction related properties, the reaction barrier in particular, is a difficult task, as typically off-equilibrium configurations are involved, and the training space is undersampled.

The use of QML models to investigate properties relevant for catalysis represents another major domain of research. A GPR model was used in 2016 to estimate free energies of possible adsorbate coverage for surfaces in order to accelerate the construction of Pourbaix diagrams.³⁴² In 2017, Ulissi et al. introduced a neural network based exhaustive search enabling the identification of active site motifs for CO₂ reduction,³⁴³ as well as a GPR based estimator of adsorption energies for identifying the most import reaction step.³⁴⁴ QML models of reaction barriers of elementary reactions (using 236 dehydrogenation, 38 N₂ dissociation, and 41 O₂ dissociation examples) on surfaces were proposed by Singh et al. in 2019.³⁴⁵ Quantum machine learning based design of homogeneous catalyst candidates was presented in 2018.³⁴⁶ In 2020, QML models of competing reaction barriers and transition state geometries corresponding to S_N2 and E2 reactions in the gas phase were successfully trained and applied throughout a CCS covering thousands of reactants,³⁴⁷ relying on the QMrxn data set.³⁴⁸ That same year, Bligaard and co-workers employed active learning to identify stable iridium oxide polymorphs and study their usefulness for the acidic oxygen evolution reaction,³⁴⁹ introduced a Bayesian framework for adsorption energies of bimetallic alloy catalyst candidates,³⁵⁰ and proposed a bond information based GPR as a means to speed up structural relaxation across different types of atomic systems.³⁵¹ In 2020, neural networks have been proposed for the prediction of overpotentials relevant for heterogeneous catalyst candidates,³⁵² as well as a higher-order correction scheme in alchemical perturbation density functional theory applications to catalytic activity.²⁶⁰ An overview on machine learning for computational heterogeneous catalysis was also contributed in 2019.³⁵³

8. Data Sets

As implied already in previous sections, the availability of training sets is vital for any machine learning. Admittedly, it would be ideal to generate training set only when necessary, i.e., to minimize the number of QM computations throughout CCS, or for converging the sampling using molecular dynamics. However, for general applications of QML, a pre-existing data set is indispensable, for instance, to tackle the inverse design problem to identify some compound with unknown composition and exhibiting specified and desirable ground-state physiochemical properties. Currently, this is only feasible with a given labeled data set being as representative as possible for the local chemistries that we know to affect the properties of interest.

Alongside the increasing popularity of QML in chemistry and related sciences, many data sets have emerged in recent years. By now, there are a multitude, built for various purposes. Here we detail all those data sets we know of that encode quantum information throughout CCS, with a coarsened and incomplete overview given in Table 1.

Table 1. Overview: Synthetic Quantum Data Sets in Three Data Families of Chemical Compound Space: Generated Data Base (GDB^33,354,361), Transition Metal Complexes (TMC), and Periodic Systems (Crystalline Solids or Surfaces)^a.

family	data set	composition	size	method	properties	year	notes
GDB	QM7386	C, O, N, S	7165	PBE0	E	2012
	QM7b359	C, O, N, S, Cl	7211	PBE0, ZINDO, GW	E, ε, α, E*, etc.	2013
	QM9171	C, O, N, F	134k	B3LYP/6-31G(2df,p)	E, μ, α, ε, Pthermo, etc.	2014
	QM8364	C, H, O, N, F	20k	TDDFT, CC2/def2-TZVP	E*, f1, f2	2015	excited state
	ANI-1367	C, O, N, F	20M	w97x/6-31G(D)	E	2017	off-equilibrium
	QM7bMl267	C, O, N, S, Cl	7211	{HF,MP2,CCSD(T)}/ {sto-3g, 6-31g, cc-pVDZ}	E	2018	multifidelity QML
	Alchemy363	C, N, O, F, S, Cl	119k	B3LYP/6-31G(2df,p)	E, μ, α, ε, Pthermo, etc.	2019
	QM7-X360	C, H, O, N, S, Cl	4.2M	PBE0+MBD	E, f, ε, μ, α, qA, C6, etc.	2020	off-equilibrium
	ANI-1x368	C, O, N, F	5M	w97x/def2-TZVPP and CCSD(T)/CBS	E, f, μ, qA, etc.	2020	off-equilibrium
	AGZ7366	B, C, N, O, F, Si, P, S, Cl, Br, Sn, I	140k	B3LYP/cc-pVTZ	E, μ, α, ε, Pthermo, etc.	2020
TMC	tmQM383	3d, 4d and 5d transition metals, B, Si, N, P, As, O, S, Se, halogens	86k	TPSSh-D3BJ/def2-SVP	E, μ, qA, ε, etc.	2020	GFN2-xTB geometry
	(MIT)384,387	Cr, Fe, Mn, Co, Ni, C, N, O, S, Cl	>2M	B3LYP/LANL2DZ (6-31g*)	E, ΔEH–L, redox potential	2017, 2020
periodic	Materials Project165	across periodic table	>600k	PBE	E, electronic and response properties	2011
	AFlow388	across periodic table	3M	PBE	E, electronic and response properties	2012
	OQMD389	across periodic table	300k	PBE	E, electronic and response properties	2013
	OC20390	across periodic table	>1M	RPBE	E, Eads	2020

^aProperties covered include E (total energy (or atomization energy)), f (atomic forces), q_A (atomic charges), μ (dipole moments), α (polarizability), ε (eigenvalues), E* (excitation energy), f_i: oscillation strength for transition from ground state to the ith excited state (i = 1 or 2), ΔE_H–L (high- and low-spin energy difference), C₆ (London dispersion coefficients), P_thermo (thermochemical properties such as internal energies, enthalpy, free energy, and heat capacity); E_ads (chemisorption energy).

8.1. GDB

The synthetic GDB (generated database) data sets created by Reymond and co-workers for the main purpose of exploring the CCS of organic drug-like molecules comprise the probably largest list of systematically generated molecular graphs (constitutional and compositional isomers only) of small to medium sized organic molecules of biochemical relevance.^{182,354−356} To date, GDB17^182,356 represents the single largest set of molecules, which contains more than 166 billion molecules made up of H, C, N, O, S, and halogens (up to 17 non-hydrogen atoms), obeying certain chemical rules for stability and synthesizability. GDB17 has two main subsets, GDB11 (26M)^354,357 and GDB13 (970M),³⁵⁵ together with a variety of smaller subsets featuring specificity of organic chemistry. Because of its systematic enumeration, interesting new structures have been identified and subsequently been synthesized, as exemplified by the synthesis of trinorbornane.³⁵⁸

Other than the implicit information that any compound listed corresponds to a stable constitutional isomer, the original GDB data sets are unlabeled in the sense that only molecular composition and connectivity information are detailed, without calculated quantum properties. The first extension of the GDB data set to also include quantum data, QM7¹⁹⁵ consists of 7165 ground-state geometries and energies of molecules with up to 23 atoms (with up to 7 heavy atoms C, N, O, or S) calculated at the PBE0 level. QM7 is also the first quantum benchmark data set covering the organic subspace CCS for QML. Some extensions exists, such as QM7b,³⁵⁹ QM7b multilevel data set²⁶⁷ (QM7bMl for short), and QM7-X.³⁶⁰

QM7b³⁵⁹ extends QM7 by including chlorine-containing molecules (expanding the set size to 7211), and reporting 13 additional calculated electronic properties (e.g., polarizability, HOMO/LUMO energies, excitation energies). QM7bMl²⁶⁷ was designed for studying QML combinations with legacy quantum chemistry methods such as multilevel, multifidelity, or transfer learning. Starting from the original coordinates at PBE level, geometries of QM7b molecules were refined at the level of B3LYP/6-31G(D), and subsequently single-point energies were calculated at nine levels of theory, corresponding to all possible combinations of electron correlation treatment {HF, MP2, CCSD(T)} and basis sets {STO-3G, 6-31G, cc-pVDZ}). QM7-X, the largest extension of QM7, is a comprehensive data set comprising ∼4.2 M equilibrium and nonequilibrium structures of QM7b molecules, accompanied by 42 physicochemical properties computed at the PBE0+MBD level, covering global (molecular) and local (atom-in-a-molecule) properties ranging from ground-state quantities (such as atomization energies and dipole moments) to response quantities (such as polarizability tensors and dispersion coefficients).

Because of the limited molecular size, QM7 and its variants are scarcely scattered across CCS and barely begin to represent its full diversity and complexity. Targeting “big data” Ramakrishnan et al. released the QM9¹⁷¹ data set in 2014, derived from molecular graphs drawn from GDB17,³⁶¹ totalling ∼134k organic molecules made up of C, H, O, N, or F, and up to nine non-hydrogen atoms. Except for equilibrium geometries and electronic ground-state properties, QM9 also records a series of thermochemical properties at 298 K and 1 atm pressure estimated based on harmonic frequencies, namely enthalpies, and free energies of atomization at the level of B3LYP/6-31G(2df,p). Alongside, additional QM data is reported for the subset of all of QM9’s 6k constitutional isomers with sum formula C₇H₁₀O₂, i.e., thermochemical properties computed at the G4MP2 level. In 2020, QM9 was augmented by more accurate energies, calculated at multiple levels of theory, including M06-2X, wb97xd, and G4MP2.³⁶² Another similar data set, dubbed alchemy³⁶³ (sized 119 487) expands the volume and diversity of QMx series and is made up of 9–14 C, N, O, F, S and Cl atoms, sampled from the GDB MedChem subset of GDB17.³⁵⁶

The only data set that deals with excited-state properties across CCS is QM8,³⁶⁴ totalling ∼20k structures subsampled from QM9 and comprising up to eight heavy atoms C, O, N, or F. Ground-state energies (S₀) and the lowest two vertical electronic singlet–singlet excitation energies (S₁ and S₂) are included, calculated at two TDDFT levels employing the density functional theory/basis-set combination PBE0/def2-SVP or CAM-B3LYP/def2-TZVP, as well as post-Hartree–Fock level CC2/def2-TZVP. Corresponding oscillator strengths (f₁) for each transition from S₀ to S₁ have also been recorded.

As also evinced for GDB17, when increasing the number of atoms per molecule, the data set quickly grows out of control, and it becomes prohibitive to conduct QM calculations for comprehensive subsets of CCS. The Amon based dictionary of building blocks designed to cover GDB³⁶¹ and Zinc³⁶⁵ and containing no more than seven heavy atoms (AGZ7) has been introduced to alleviate this curse of dimensionality.³⁶⁶ It was obtained by systematically fragmenting all larger molecules (from GDB17 and zinc³⁶⁵) into smaller entities containing no more than seven non-hydrogen atoms (i.e., atom-in-molecule based fragements, aka, AMONs²⁴³). To date, AGZ7 is the most compact yet most diverse data set relevant for organic/biochemistry, totalling only 140k molecules but covering up to 13 elements (H, B, C, N, O, F, Si, P, S, Cl, Br, Sn, and I). It also includes a similar set of properties as in QM9 but relying on a slightly different level of theory (B3LYP/cc-pVTZ as well as pseudopotentials for Sn and I).

Apart from QM7-X,³⁶⁰ all data sets mentioned so far deal with equilibrium geometries only, representing the typical constraint for what defines a stable molecule. To enable the QML based study of dynamics and reactivity of nonequilibrium geometries throughout CCS, however, configurational sampling involving nonstationary geometries has to also be accounted for through the data sets. Similar to QM7-X, ANI-1³⁶⁷ also explores nonequilibrium geometries but for relatively larger systems drawn from GDB11.^354,357 It consists of more than 20 M off-equilibrium structures (sampling both chemical and conformational degrees of freedom) and wB97x/6-31G(d) energies for 57 462 small organic molecules containing up to 11 CONF atoms. Two follow-up data sets expand ANI-1 considerably, i.e., ANI-1x and ANI-1ccx.³⁶⁸ The former contains multiple QM properties (density-derived properties and forces) from 5 M DFT calculations (wB97x/6-31G* and wB97x/def2-TZVPP), while the latter contains 500k CCSD(T) energies for estimated CBS limits.

For MD simulations, two main data sets are being frequently benchmarked. One is ISO17,^55,309 containing MD trajectories of 129 molecules randomly drawn from the aforementioned 6k C₇O₂H₁₀ isomers, each comprising 5000 conformational geometries with total energies and atomic forces calculated at PBE level plus van der Waals correction.³⁶⁹ The other is MD-17,^73,370 which records energies and forces from ab initio molecular dynamics trajectories (133k to 993k frames) at the DFT/PBE+vdW-TS level of theory at 500 K for eight organic molecules: benzene, uracil, naphthalene, aspirin, salicylic acid, malonaldehyde, ethanol, and toluene. More accurate CCSD(T) energies and forces are also available but only for ethanol (with basis cc-pVTZ), toluene and malonaldehyde (cc-pVDZ), and CCSD/cc-pVDZ for aspirin. Recently, a revised MD-17 data set was published,²¹¹ with a lower noise floor in DFT forces thanks to tighter SCF convergence criteria and denser integration grids. In 2020, G4MP2 benchmarks of organic molecules with up to 14 non-hydrogen atoms were contributed by Dandu et al.,³⁷¹ and resulting QML models were compared and discussed.

8.2. PubChem amd ZINC

While the GDB family currently dominates QML campaigns, GDB compounds resulted from virtual exhaustive graph enumeration campaigns and mostly correspond to molecules for which neither thermodynamics stability nor synthesizability has been established. Within practical applications, such aspects matter for the experimental design and fabrication of new chemical compounds. With respect to QML, some theoretically possible local chemical environments may not be viable within the entire molecular framework, and ruling out such possibilities when training could help to further improve data efficiency and transferability. PubChem³⁷² is an ever-growing open chemistry database hosted at the National Institutes of Health (NIH). As of October 2020, there were over 111 million unique chemical structures records listed together with many a experimental property, as contributed by hundreds of data sources. To harvest the richness and popularity of this database, Maho Nakata, and co-workers lauched the so-called PubChemQC project,³⁷³ consisting of ground-state geometries and properties (at B3LYP/6-31G* level), as well as low-lying excited states of approximately four million molecules via time-dependent DFT at the level of B3LYP/6-31+G*. A PubChemQC derived subset, called pc9,³⁷⁴ covering over 99k molecules made up of CHONF was published afterward and encoded the same set of properties as QM9. The full potential of PubChemQC remains yet to be generally explored.

ZINC,³⁶⁵ yet another large database, focuses more on biochemistry, in particular drug design. Quantum calculations on this database per se have not taken place, except for its associated fragment set. That is, AZ7, a subset of AGZ7,³⁶⁶ contains all ZINC AMONs of up to seven non-hydrogen atoms (with optimized geometries and electronic properties, as for AGZ7 described above). AGZ7 could be considered as an effective set covering all local chemistries of ZINC and may serve as a scaffold for building larger drugs through a theoretical approach.

Beside PubChem and ZINC, there are several other public big databases being exploited within QML. One of them is the Cambridge Structural Database (CSD),³⁷⁵ on the basis of which Stuke et al.³⁷⁶ reported a diverse benchmark spectroscopy data set of 61 489 molecules, denoted OE62. Using geometries optimized by PBE plus vdW correction, OE62 provides total energies and orbital eigenvalues at PBE and PBE0 levels for all molecules in vacuum and at the PBE0 level for a subset of 30 876 molecules in (implicit) water. Also based on CSD, Schober et al.³⁷⁷ extracted 95 445 molecular crystals thereof and carried out computations on electronic couplings (at the level BLYP and fragment molecular orbital-based DFT) and intramolecular reorganization energies (by QM/MM with an ONIOM-scheme) as two main descriptors for charge mobility, hoping to facilitate the theoretical design and discovery of high mobility organic semiconductors.

8.3. Barriers and Spin

Quantum data sets on chemical reaction profiles are rather scarce. The QMrxn³⁴⁸ reports calculated quantum properties for S_N2 and E2 reactions amounting to 4466 transition state and 143 200 reactant complex geometries and energies at MP2/6-311G(d) and single-point DF-LCCSD/cc-pVTZ level of theory, respectively. QMrxn covers the subset of CCS that is spanned by the substituents −NO₂, −CN, −CH₃, −NH₂, and with −H,−F, −Cl, and −Br as nucleophiles and leaving groups. A different data set featuring elementary reactions comes from Grambow et al.,³⁷⁸ totalling 12k organic reactions that involve H, C, N, and O atoms, calculated at the wB97X-D3/def2-TZVP level, with optimized geometries and thermochemical properties for reactants, products, and transition states.

Going beyond mostly singlet-state chemistry, Schwilk et al. introduced QMspin,³⁷⁹ consisting of ∼5k (∼8k) singlet (triplet) state carbenes derived from 4k randomly selected QM9 molecules. QMspin also contains optimized geometries (B3LYP/def2-TZVP for triplet state and CASSCF(2e,2o)/cc-pVDZ-F12 for singlet state), as well as the singlet–triplet vertical spin gap computed at MRCISD+Q-F12/cc-pVDZ-F12 level of theory.

For the QML models of the computational cost of typical quantum chemistry computations (measured by the CPU wall time), Heinen et al. reported the QMt data set,³⁸⁰ consisting of timings of various tasks (single point energy, geometry optimization, and transition state search) for thousands of QM9 molecules at several levels of theory including B3LYP/def2-TZVP, MP2/6-311G(d), LCCSD(T)/VTZ-F12, CASSCF/VDZ-F12, and MRCISD+Q-F12/VDZ-F12.

Treating noncovalent interaction (NCI) within QML is an interesting and important research subject, with relevant large data sets emerging only as of recently. Most notably, several collections of NCI data sets have by now become publicly available,³⁸¹ covering 3700 distinct types of interacting molecule pairs: (i) DES370 K, contains interaction energies for more than 370k dimer geometries with NCI energy calculated at the level of CCSD(T)/CBS (MP2(aVTZ, aVQZ) correlation energy is used for extrapolation, and (ii) DES5M, comprising NCI energies calculated using SNS-MP2, for nearly 5 M dimer geometries. The monomers involved include typical organic species, made up of common p-block elements as well as alkali metal ions, most of which containing no more than seven heavy atoms.

Data sets including artificial molecules which violate basic principles of chemical bonding may also of great interest for QML, i.e., they may serve the use of “soft” labels, where relatively few compounds might more effectively represent CCS than selected many. MB08-165,³⁸² proposed by Grimme, exemplifies that idea, relying on systematic constraints rather than uncontrolled chemical biases. Originally, this data set was designed for benchmarking DFT methods. The potential of such “unbiased” artificial molecules as soft labels (training set) in QML has yet to be unraveled.

8.4. Transition Metals

Transition metal complexes (d-block atom/ion center plus ligands, TMC for short) are pervasive in chemistry and have been widely used and studied. Because of their complicated electronic structure and the resulting higher computational cost (in comparison to typical organic molecules), the effective exploration of the chemical space spanned by TMCs remains a challenge and current efforts into this subspace are constrained to relatively low level of theory, primarily DFTB or DFT method with some small basis. Examples include tmQM³⁸³ and the TMC data sets^289,336,384 from Kulik and co-workers, as described below.

tmQM³⁸³ contains geometries and common electronic properties (as for QM9) of 86 665 mononuclear complexes extracted from the Cambridge Structural Database (CSD). tmQM includes Werner, bioinorganic and organometallic complexes based on a large variety of organic ligands and 30 transition metals. On the basis of the DFTB(GFN2-xTB) geometry, common quantum electronic properties (orbital energies, dipole meoment and atomic charges) were computed at the TPSSh-D3BJ/def2-SVP level.

The largest and most comprehensive TMC data sets are from Kulik’s group at MIT and have been contributed across multiple publications.^289,336,384 Overall, they correspond to combinations of several metal centers (Cr, Mn, Fe, or Co, Ni) and a wide range of ligands, ranging from weak-field chloride (Cl^–) to strong-field carbonyl (CO) along with representative intermediate-field ligands and connecting atoms, including S (SCN^–), N (e.g., NH₃), and O (e.g., acetylacetonate). Calculated properties are primarily energetic, including total energy, high and low spin-state energy difference (ΔE_H–L), and redox potential and solubility in candidate M(II)/M(III) redox couples, at the level of theory B3LYP/LANL2DZ (6-31G* for ligands) with or without polarizable continuum model (PCM) for solvents. The total size could reach up to several millions.

Recently introduced metal–organic frameworks (MOF) data set by Rosen and co-workers,³⁸⁵ called Quantum MOF (QMOF), represent another broad category of metal complexes. QMOF consists of computed properties (energy, band gap, charge density, and density of states) at the PBE-D3(BJ) level of theory, for more than 14 000 experimentally synthesized MOFs, which are made up chemical elements that span nearly the entire periodic table.

8.5. Solid and Solid Surface

Compared to TMCs, solid and solid surfaces present a challenge on their own due to the diversity in composition and spatial arrangements, as well as the resulting complexity of electronic structure. Typically DFT based methods are used for generating large-scale (or high-throughput) data sets for these systems. The most frequently used method is GGA (PBE) or GGA+U with PAW (projected augmented wave) potentials. On the basis of relaxed geometry, associated calculated properties fall into either electronic properties, e.g., cohesive energy, band structure (and derived properties including density of states and band gap), or response properties such as elastic tensor, bulk modulus, and thermodynamic properties (vibrational spectra, free energy, specific heat, and entropy) within harmonic approximations.

Relevant well-known solid databases and compute platforms include (i) AFlow,³⁸⁸ an open data set of more than 3 M material compounds (including alloys, intermetallics, and inorganic compounds) with over 596 M calculated properties. (ii) The Open Quantum Materials database³⁸⁹ (OQMD), a high-throughput database currently consisting of nearly 300k total energy calculations of compounds from the Inorganic Crystal Structure Database (ICSD). (iii) The Materials Project¹⁶⁵ (www.materialsproject.org) covers the properties of almost all known inorganic materials, currently containing over 131k inorganic compounds and more than 530k nonporous materials. (iv) The Materials Cloud (www.materialscloud.org),³⁹¹ a platform designed to enable open and seamless sharing of resources for computational science, driven by applications in materials modeling. (v) The Novel Materials Discovery (NoMaD, http://nomad-repository.eu), led by Scheffler, Draxl et al. (vi) The Open Materials Database (http://openmaterialsdb.se, currently under development) spearheaded by Armiento. The latter both are public archives for hosting, sharing, and reusing material data in their raw form. Apart from comprehensive public repositories for solid data sets, there are also select contributions for select materials classes, including the aforementioned data set of ∼10k AB₂C₂ elpasolites covering all main-group elements up to Bi from Faber et al.¹⁶⁴

Regarding solid surfaces, the new Open Catalyst Project³⁹⁰ aims to help discover and design new catalysts for renewable energy storage using ML (https://opencatalystproject.org), currently including mainly the OC20 data set,³⁹⁰ consisting of >1 M relaxations (over 26 M single point evaluations) at RPBE level for a wide range of adsorbates (C-, N- and O-containing species) and surfaces.

9. Software Packages

To perform and supplement the aforementioned studies with methods and data sets, numerous software packages have been developed over recent years. We briefly mention the available codes and categorize them into three main types, the first of which being those related to the acceleration of legacy quantum codes, such as ab initio molecular dynamics (MD) runs in VASP,³⁹² Gaussian process based geometry optimization in ASE,³⁹³ machine learning adaptive basis sets within CP2K,²³⁸ as well as SNAP³⁹⁴ in LAMMPS, a machine-learning interatomic potential using bispectrum components to characterize the local neighborhood of each atom of the system.

Codes which fall into the second category are standalone packages, some of which having also been interfaced to other atomistic simulation software. QMLcode^209,395 which is an open-source python-based package featuring the Coulomb-matrix,¹⁹⁵ BoB,¹⁷⁰ SLATM/aSLATM,²⁴³ FCHL18, and FCHL19^166,209 and other representations. AQML code³⁹⁶ is a variant of QMLcode featuring the BAML¹⁶³ representation, and on-the-fly selection of AMONs for training.²⁴³ PLUMED³⁹⁷ is an open-source, community-developed library that provides a wide range of methods including enhanced-sampling algorithms, free-energy methods, and MD data analysis capabilities. It also interfaces with some of the most popular MD engines. TensorMol³⁹⁸ is a package of neural networks for chemistry, capable of running many common tasks in quantum chemistry such as geometry optimizations, molecular dynamics, Monte Carlo, nudged elastic band calculations, etc. It can also take into account screened long-range electrostatic and van der Waals interactions. TorchANI³⁹⁹ is a PyTorch implementation of ANI. It can compute molecular energies, gradients, Hessian and derived properties from the 3D coordinates of molecules. It also include tools to work with ANI data sets (e.g., ANI-1, ANI-1x, etc.).

The third category of software packages deals predominantly with data set construction, management and analysis. In particular, specific platforms include AFlow³⁸⁸ which has been mentioned above in section 8.5, and AiiDA,⁴⁰⁰ an open-source infrastructure for automation, management, sharing and reproduction of the workflows associated with big data in computational sciences.

10. Compound Discovery

The computational design and discovery of new compounds can be generally conducted following either one of two distinct approaches. The Edisonian and more basic one is straightforward, within a brute-force high-throughput screening, through solving Schrödinger equations sequentially or in parallel for potential materials candidates one by one, followed by subsequent ranking and selection. Given sufficient coverage and having used the data for training, the ab initio solver could successively be replaced by QML models, capable of making faster and equally accurate predictions of target properties of interest. It is obvious that such an approach suffers from limited domains of compounds conceived in the first place, no matter what solver is used for computation of properties. Also, as the intended search domain expands in CCS, the number of possible potential candidates will grow combinatorially. Therefore, when adopting this strategy, one should refrain from generally expanding the search domain and rather focus on a constrained subdomain of compounds, sharing one or more common features, e.g., the same stoichiometry and space group, as was exemplified for the elpasolite family ABC₂D₆ by Faber et al.,¹⁶⁴ where compounds with exotic atomic oxidation states were identified.

The second more sophisticated approach attempts to solve the problem in an inverse fashion; more specifically, given a specific (range of) value(s) for the target property, how to best locate the corresponding optimal (set of) compound(s) from CCS. One particularly promising variant is the gradient-based inverse design,¹⁴ which can be reformulated as a global optimization problem and has the potential to search chemical subspace for substantial domains, due to its analytical nature. Strictly speaking, almost all current ML-guided studies (mostly neural network based) on gradient-based inverse design (e.g., ref (187), for a review, see ref (287)) fall into the QSPR regime, as the input is seldomly 3D geometry, but rather SMILES or other molecular graph derived features (therefore, the mapping from representation to property is not unique). This strategy is however the only attainable way by now, as otherwise (i) the search subspace (when optimizing for the “optimal” compound) would become overwhelmingly large due to the explosion of conformational degrees of freedom (Levinthal’s paradox). (ii) There exists, to the best of our knowledge, no 3D geometry-based representation that is compact enough for decoding, i.e., restoring the original geometry from its representation vector/matrix/tensor (or simply x), even with the help of a neural network model like variational encoder (VAE), as the entries in x are highly intertwined (significantly more so than the SMILES string). The fact that many representations are still being haunted by the uniqueness issue, further plagues these efforts, as often only two- and three-body terms are included in distribution-based representation. While inclusion of four-body terms are mandatory for reconstructing geometry, as evinced by the Z-matrix representation of geometry, the resulting x would become very expensive for generation, and more importantly, this could further perplex the feature vector decoder. However, representing a molecule in its most native form in terms of nuclear charges and coordinates,{Z; R}, i.e., by the variables employed in the electronic Hamiltonian, or some transformed form, such as an external potential, one is free from such problems. This strategy would be consistent with the aforementioned GCE and LCAP approach detailed in section 1.3.

11. Outlook and Conclusion

While QML is still in its infancy, very encouraging progress has already been achieved. It is still a long way, however, before we will reach the goal of routinely designing and discovering novel molecules and materials on a computer. Some of the most fundamental problems, also among the most common tasks in quantum chemistry calculations, such as correctly predicting ground-state energy and forces of novel molecules or materials with high efficiency and accuracy, still remain unresolved at large. Such seemingly simple tasks are particularly challenging when it comes to systems that are highly distorted, charged, or multireference in nature or that involve long-range nonbonded interactions. Successful QML models could easily demonstrate their applicability by energy ranking of competing structures of real materials. We believe that such tasks will be crucial for subsequent more challenging QML applications.

Another interesting path to pursue might be the integration of alchemical perturbation theory into QML. Because the alchemical problem could be essentially reformulated as a ML problem that involves both energy and energy gradient with respect to nuclear charges. A corresponding extension would exploit similarities between alchemical interpolations in pseudopotential parameter space and compositional representations that explicitly account for group and period in the periodic table, on top of all the structural degrees of freedom. Within the FCHL representation,¹⁶⁶ preliminary results for inferring properties of chemical elements absent in training have already been obtained (see Figure 4).

Besides the curse of dimensionality, imposed by the compositional, constitutional, and conformational diversity of CCS, the lack of a more theoretical underpinning of the genesis of data sets is maybe among the most severe shortcomings. Little, if nothing, is known about fundamental questions such as: (i) Are there any basic quantities characterizing the completenes of a molecular data set, for instance in terms of diversity and/or sparsity? (ii) On the basis of the inherent properties of the data set, representation and regressor, can we infer the performance of a model without actual training/test runs, as translated into the slope and offset of resulting learning curve. (iii) What, if any, characterizes the “correct” distribution in CCS. Answering such questions rigorously, i.e., based on the laws of physical chemistry, is not only of conceptual importance but would also benefit the practical design of more efficient/accurate QML models.

Other unresolved issues include (i) the lack of appropriate QML models that deal with intensive properties such as HOMO/LUMO energy, or dipole moments, which may require careful consideration of both local and long-ranged features of a molecule. (ii) The lack of high-accuracy data sets at the level of experimental quality (e.g., CCSD(T)-F12/CVQZ-F12 or multireference) for medium-sized molecules: published data sets of such quality are still limited to very few or small molecules, containing typically no more than three heavy atoms.

As the field has been growing massively and rapidly,¹⁶ we can unfortunately not guarantee completeness of our outlook. Furthermore, several related important new research directions, i.e., going beyond the mere supervised learning problem of the electronic Schrödinger equation, possibly being out of the scope of “conventional” QML, have not been mentioned. They include, for example, variational autoencoders which can be used to help solving the inverse design challenge in CCS (e.g., applied to the design of improved molecular electronics⁴⁰¹), the reconstruction of quantum states,⁴⁰² or the generation of molecular structures.⁴⁰³ Other intriguing efforts deal with tackling the problem of reaction planning,^404−409 phase diagrams,^410−415 studying the electronic structure in more depth and detail,^{261,416−419} or the systematic incorporation of experimental information in order to improve experimental design.⁴²⁰

To recap, we have provided succinct explanations and pointers to three major ingredients of QML: representation, regressor, and training set. We have briefly discussed select relevant studies which deal with the development and use of surrogate machine learning models of quantum properties throughout CCS. One of the primary goals of QML, i.e., rational computational discovery and design of compounds with desired properties, however, has not yet been achieved in general, and most of the relevant studies are either conducted in a high-throughput fashion, merely accelerated by QML, or rely on coarsening the problem through neglect of relevant degrees of freedom. We have pointed out several open questions and challenges that must be overcome to reach this general goal, as well as potential solutions, and suggestions about interesting new research directions. Given the overall rapid growth and the multiple success cases already achieved in this young field, we are optimistic about its future and strongly believe that QML will develop into a helpful component for solving some of the long-standing problems in the atomistic sciences.

Biographies

Bing Huang (Hubei, China, 1987) was initially trained in physical chemistry under the supervision of Prof. Lin Zhuang in Wuhan University and completed his Ph.D. there in 2015, investigating and developing reactivity theory concerning solid surface. Afterwards, he moved to Basel, Switzerland, to work as a postdoc with Anatole von Lilienfeld at the Department of Chemistry, University of Basel, shifting research interests to the development of machine learning models and methods in quantum chemistry to explore chemical compound space. As of 2020, he has relocated to Vienna, Austria, to continue his postdoctoral research with Anatole von Lilienfeld at the Faculty of Physics, University of Vienna. His research interests include electronic structure theory, chemical reactivity theory, theoretical surface science and quantum machine learning.

O. Anatole von Lilienfeld (Rochester, Minnesota, USA, 1976) is a full university professor of computational materials discovery at the Faculty of Physics at the University of Vienna. Research in his laboratory deals with the development of improved methods for a first principles based understanding of chemical compound space using perturbation theory, machine learning, and high-performance computing. Previously, he was an associate and assistant professor at the University of Basel, Switzerland, and at the Free University of Brussels, Belgium. From 2007 to 2013, he worked for Argonne and Sandia National Laboratories after postdoctoral studies with Mark Tuckerman at New York University and at the Institute for Pure and Applied Mathematics at the University of California Los Angeles. In 2005, he was awarded a Ph.D. in computational chemistry from EPF Lausanne under the guidance of Ursula Röthlisberger. His diploma thesis work was done at ETH Zürich with Martin Quack and the University of Cambridge with Nicholas Handy. He studied chemistry at ETH Zürich, the Ecole de Chimie Polymers et Materiaux in Strasbourg, and the University of Leipzig. He serves as Editor-in-chief of the IOP journal Machine Learning: Science and Technology and on the editorial board of Science Advances. He has been on the editorial board of Nature’s Scientific Data from 2014 to 2019. He was the chair of the long IPAM UCLA program “Navigating Chemical Compound Space for Materials and Bio Design”, which took place in 2011. He is the recipient of multiple awards, including a Swiss National Science Foundation postdoctoral grant (2005), a Harry S. Truman postdoctoral fellowship (2007), a Thomas Kuhn Paradigm Shift award (2013), a Swiss National Science professor fellowship (2013), the Odysseus grant from the Flemish Science Foundation (2016), an ERC consolidator grant (2017), and the Feynman Prize in Nanotechnology (2018).

The authors declare no competing financial interest.