Machine Learning for Electronically Excited States of Molecules

Abstract

Electronically excited states of molecules are at the heart of photochemistry, photophysics, as well as photobiology and also play a role in material science. Their theoretical description requires highly accurate quantum chemical calculations, which are computationally expensive. In this review, we focus on not only how machine learning is employed to speed up such excited-state simulations but also how this branch of artificial intelligence can be used to advance this exciting research field in all its aspects. Discussed applications of machine learning for excited states include excited-state dynamics simulations, static calculations of absorption spectra, as well as many others. In order to put these studies into context, we discuss the promises and pitfalls of the involved machine learning techniques. Since the latter are mostly based on quantum chemistry calculations, we also provide a short introduction into excited-state electronic structure methods and approaches for nonadiabatic dynamics simulations and describe tricks and problems when using them in machine learning for excited states of molecules.

1. Introduction

1.1. From Foundations to Applications

In recent years, machine learning (ML) has become a pioneering field of research and has an increasing influence on our daily lives. Today, it is a component of almost all applications we use. For example, when we talk to Siri or Alexa, we interact with a voice assistant and make use of natural language processing,^1,2 which was used to perform quantum chemistry calculations recently.³ ML is applied for example for refugee integration,⁴ for playing board games,⁵ in medicine,⁶ for image recognition⁷ or for autonomous driving.⁸ A short historical overview over general ML is provided in ref (9).

Recently, ML has also gained increasing interest in the field of quantum chemistry.^10,11 The power of (big) data-driven science is even seen as the “fourth paradigm of science”,¹² which has the potential to accelerate and enable quantum chemical simulations that were considered unfeasible just a few years ago.¹³ The reason is, at least in theory, that ML models can learn any input–output relation and offer interpolations thereof at almost no cost while retaining the accuracy of the underlying reference data. With regard to quantum chemical applications, it allows decoupling of the expenses of quantum chemistry calculations from the application, such as dynamics simulations or the computation of different types of spectra. In general, the field of ML in quantum chemistry is progressing faster and faster. In this review, we focus on an emerging part of this field, namely, ML for electronically excited states. In doing so, we concentrate on singlet and triplet states of molecular systems since almost all existing approaches of ML for the excited states focus on singlet states and only a few studies consider triplet states.¹⁴⁻¹⁷ We note that electron detachment or uptake further leads to doublet and quartet states, and even higher spin multiplicities, such as quintets, sextets, etc. are common in transition metal complexes, where an important task is to identify which multiplicity yields the lowest energy and is thus the ground state;¹⁷ see, e.g., refs (18−21).

The theoretical study of the excited states of molecules is crucial to complement experiments and to shed light on many fundamental processes of life and nature.²²⁻²⁴ For example, photosynthesis,^25,26 human vision,^27,28 photovoltaics,²⁹⁻³² or photodamage of biologically relevant molecules are a result of light-induced reactions.³³⁻³⁵ Experimental techniques such as UV/visible spectroscopy or photoionization spectroscopy³⁶⁻⁴³ lack the ability to directly describe the exact electronic mechanisms of photoinduced reactions. The theoretical simulation of the corresponding experiments can go hand-in-hand with experimental results and can provide the missing details of photodamage and -stability of molecules.^42,44−68 However, the computation of the excited states is highly complex and costly, and often necessitates expert knowledge.⁶⁹ As ML models have only recently been applied in the field of photochemistry, keeping track of the approaches is still possible, and this field is still in its initial stage.

Because of the multifaceted photochemistry of molecular systems, ML models can target this research field in many different ways, which are summarized in Figure 1. For example, the choice of relevant molecular orbitals for active space selections can be assisted with ML.⁷¹ The fundamentals of quantum chemistry, e.g., to obtain an optimal solution to the Schrödinger equation or density functional theory, can be central ML applications. For the ground state, ML approximations to the molecular wave function⁷²⁻⁸⁰ or the density (functional) of a system exist.^70,80−89 Obtaining a molecular wave function from ML can be seen as the most powerful approach in many perspectives, as any property we wish to know could be derived from it. Unfortunately, such models for the excited states are lacking and have yet been investigated only for a one-dimensional system,⁹⁰ leaving much room for improvement.

Figure 1.

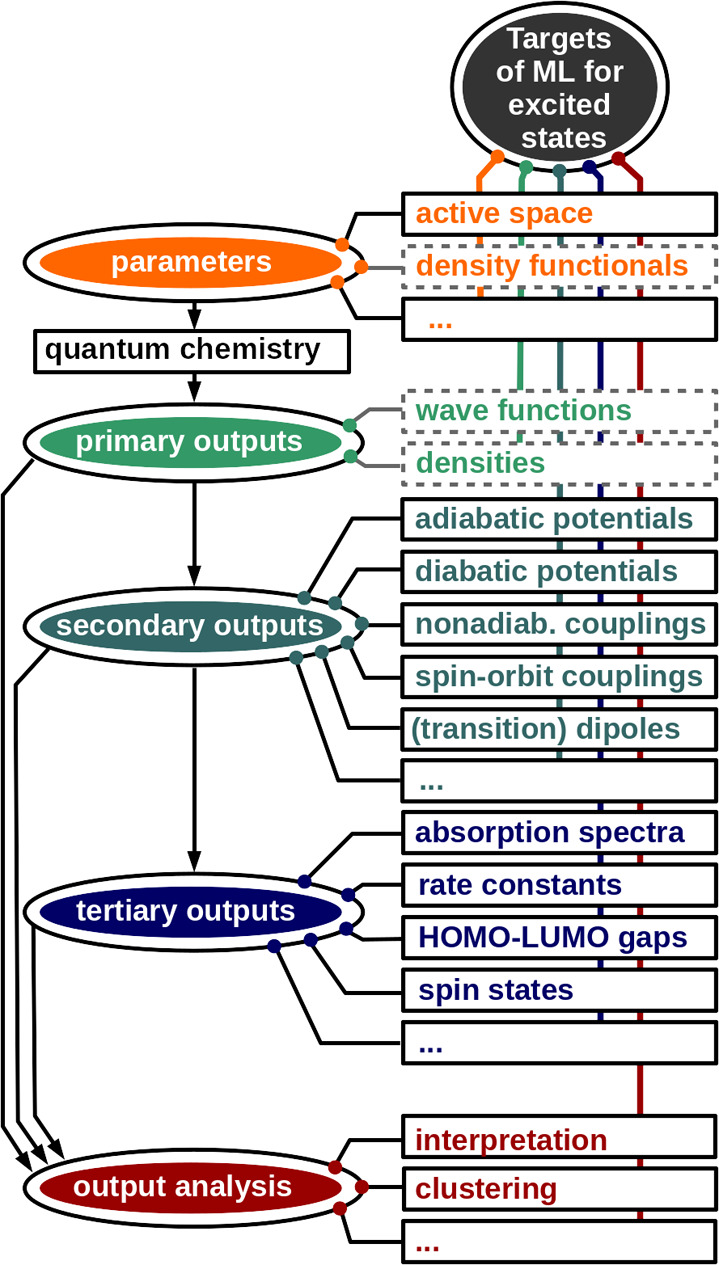
Targets of ML for the excited states of molecules (dashed: not yet achieved). All areas of excited-state quantum chemistry (QC) calculations can be enhanced with ML, ranging from input to primary outputs that are used in the computation of secondary outputs, which in turn are employed to calculate tertiary outputs. Analysis can be carried out at all stages. The classification is inspired by the one in ref (70).

Most ML studies instead focus on predicting the output of a quantum chemical calculation, the so-called “secondary-output”.⁷⁰ Hence, they fit a manifold of energetic states of different spin multiplicities, their derivatives, and properties thereof. With respect to different spin states of molecular systems, only a few studies exist, which predict spins of transition metal complexes^17,91 or singlet and triplet energies of carbenes¹⁴ of different composition or focus on the conformational changes within one molecular system^15,92,93 for the sake of improving molecular dynamics (MD) simulations. The energies of a system in combination with its properties, i.e., the derivatives, the coupling values between them, and the permanent and transition dipole moments,^{15,16,92−99} can be used for MD simulations to study the temporal evolution of a system in the ground-state^100−137 and in the excited states.^{15,16,92−94,132,138−145,145−149,149−151}

With energies and different properties, tertiary outputs can be computed, such as absorption, ionization or X-ray spectra,^152−155 gaps between highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), or vertical excitation energies.^156−159

In addition, quantum chemical outputs can also be analyzed or fitted in a direct way, e.g., reaction kinetics, as results of dynamics simulations can be mapped to a set of molecular geometries and can be predicted with ML models.¹⁶⁰ Excitation energy transfer properties can be learned,^161,162 and structure–property correlations can be explored to design materials with specific properties.^{18,31,32,77,133,154,163−170}

1.2. Scope and Philosophy of this Review

ML has entered the research field of excited states relatively late, and it might seem that this research field is developing at a slower pace than the exploding field of ML for the electronic ground state.^{169,171−174} Important reasons are in our opinion the complexity and high expenses of the underlying reference calculations and the associated complexity of the corresponding ML models, which might make it more suitable to say that ML for the excited states is developing at a similar pace, but toward a much more complex target. Simulation techniques to understand the excited-state processes are not yet viable for many applications at an acceptable cost and accuracy. Therefore, within this review, we also want to highlight the existing problems of quantum chemical approaches that might be solvable with ML and put emphasis on identifying challenges and limitations that hamper the application of ML for the excited states. The young age of this research field leaves much room for improvement and new methods.

This review is structured as follows:

• (1)After a general introduction,
• (2)we will start by discussing the differences between the ground-state potential energy hypersurfaces (PESs) and the excited-state PESs and will also emphasize the difference in their properties in section 2.
• (3)We provide an overview of the theoretical methods that can be used to describe the excited states of molecules. In the forthcoming discussion, we will describe different reference methods with a view to their application in time-dependent simulations, namely, MD simulations.^59,172 It is worth mentioning that, unlike for the ground state, where a lot of different methods can provide reliable reference computations for training, choosing a proper quantum chemistry method for the treatment of excited states is a challenge on its own.^175−177 Many methods require expert knowledge, prohibiting their use further.^178,179 In addition, not any method can provide the necessary properties for any type of application. Subsequently, we aim to review the different flavors of excited-state MD simulations with a focus on nonadiabatic methods that have been enhanced with ML models lately.
• (4)After having provided the basic theoretical background on electronic structure theory and quantum chemical simulation techniques, we go on and summarize the basic ML models applied in studies with a focus on the excited states of molecules. The different types of ML models will help the reader to identify a proper model for a specific purpose. Advantages and disadvantages of certain regressor and descriptors are discussed.
• (5)The theoretical background on electronic structure theory and ML is followed by a discussion on how to generate a comprehensive yet compact training set for the excited states from the quantum chemistry data. We will summarize the existing approaches that are applied to create a full-fledged training set and put emphasis on the bottlenecks of existing methods that can limit also the application of ML. This will provide the reader with the knowledge about starting points for future research questions and clarify where method development is needed. It further provides the basis for the discussion of ML models for the excited states of molecular systems.
• (6)A summary of state-of-the-art ML methods for photochemistry follows. We will differentiate between single-state and multistate ML models and single-property and multiproperty ML models.⁹⁵ As mentioned before, ML models can tackle a quantum chemical calculation in many different ways; see Figure 1. The different ML models will be classified in the ways they enhance quantum chemical simulations. Most approaches aim at providing an ML-based force field for the excited states, so we put particular emphasis on this topic. Lastly, the prospects of ML models to revolutionize this field of research and future avenues for ML will be highlighted.

Noteworthy, we focus on the excited states of molecules, as the excited electronic states in the condensed phase are challenging to fit and are thus often not explicitly considered in conventional approaches.^180−185 In solid state physics for example, the electronic states are usually treated as continua. The density of states at the Fermi level,¹⁸⁶ band gaps,^187−189 and electronic friction tensors^125,190,191 have been described with ML models to date, and especially the electronic friction tensor is useful to study the indirect effects of electronic excitations in materials.^192−197 Electron transfer processes as a result of electron–hole-pair excitations can be further investigated along with multiquantum vibrational transitions by discretizing the continuum of electronic states and fitting them (often manually) to reproduce experimental or quantum chemical data in a model Hamiltonian.^{183,198−203} Yet, to the best of our knowledge, the excited electronic states in the condensed phase have not been fitted with ML. A recent review on reactive and inelastic scattering processes and the use of ML for quantum dynamics reactions in the gas phase and at a gas-phase interface can be found in ref (204).

Besides the electronic excitations that take place in molecules after light excitation, ML models have successfully entered research fields, which focus on other types of excitations as well. Those are, for example, vibrational or rotational excitations giving rise to Raman spectra or infrared spectra,^{41,111,205−209} nuclear magnetic resonance,²¹⁰ or magnetism,^211,212 which we will not consider in this review.

2. General Background: From the Ground State to the Excited States

The chemistry we are interested in is not static, but rather depends to a large extent on the changes that matter undergoes. In this regard, it is more intuitive to study the temporal evolution of a system. Much effort has been devoted to develop methods to study the temporal evolution of matter in the ground state potential. As an example, physical functions can be obtained with conventional force fields, such as AMBER,²¹³ CHARMM,²¹⁴ or GROMOS.^215,216 The first ones already date back to the 1940s to 1950s. Such force fields enable the study of large and complex systems, protein dynamics or binding-free energies on time scales up to a couple of nanoseconds.^{180,217−225} However, their applicability is restricted by the limited accuracy and inability to describe bond formation and breaking. Novel approaches, such as reactive force fields exist, but still face the problem of generally low accuracy.²²⁶

The accuracy of ab initio methods can be combined with the efficiency of conventional force fields with ML models. The latter have shown to advance simulations in the ground state considerably and allow for the fitting of almost any input–output relation.^{100−134,137,172,227} Accurate and reactive PESs of molecules in the ground state can be obtained with a comprehensive reference data set, which contains the energies, forces, and ground-state properties of a system under investigation. Proper training of an ML model then guarantees that the accuracy of the reference method is retained, while inferences can be made much faster. In this way, they allow for a description of reactions and can overcome the limitations of existing force fields.^{135,171,228−232}

Regarding the excited states, processes become much more complex, and the computation of excited state PESs is far more difficult than the computation of the ground state PESs. Figure 2 gives an overview of the excited state processes that will be discussed within this review. As can be seen, several excited states of different spin multiplicity in addition to the ground state have to be accounted for, which feature different local minima, transition states, or saddle points and crossing points. Especially, the latter make a separate treatment of each electronically excited state inaccurate and lead to further challenges that prohibit the straightforward and large-scale use of many existing quantum chemical methods and consequently also existing ML models for the ground state.

Figure 2.

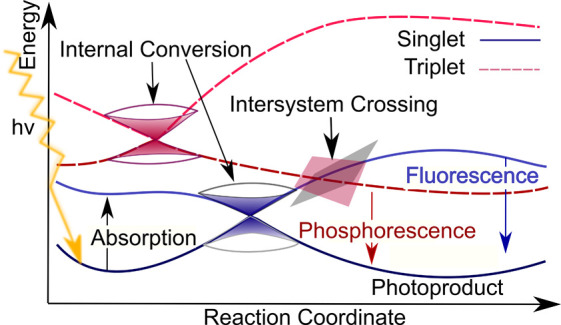
Excited-state processes that can take place after excitation of a molecule by light. Absorption of light can make the molecule enter a higher electronic singlet state. Internal conversion to another state of same spin-multiplicity and/or intersystem crossing to a triplet state can take place. Radiative emission, i.e., fluorescence and phosphorescence, are possible reactions from an excited singlet and triplet state, respectively.

As it is visible, processes usually start from a minimum in the electronic ground state (dark-blue line). When light hits a molecule and the incident light coincides with the energy gap between two electronic states, it can be absorbed, and higher electronic states can be reached when dipoles are allowed (here the second excited singlet state in light blue). Internal conversion between states of the same spin multiplicity and/or intersystem crossing between states of different spin multiplicity (here a transition to triplet states indicated as dashed red curves) can prevent the molecule from photodamage. Nonradiative transitions usually take place on a sub-picosecond time scale. With respect to intersystem crossing, it was long believed that it happens on a longer time scale and is only possible if heavy atoms are part of the molecule.^233,234 However, this belief has been disproved, and today many examples of small molecules or transition metal complexes are known, which show ultrafast intersystem crossing.^{178,235−237} In the case of nonradiative transitions, the energy is lost due to molecular vibrations, and the molecule relaxes back to the original starting point in the ground state. However, also photodamage can occur via such nonradiative transitions, where photoproducts can be formed, e.g., by bond breaking and bond formation. When nonadiabatic transitions are not taking place, radiative emission, i.e., fluorescence and phosphorescence, can happen on a much slower time scale, i.e., in the range of nano- to milliseconds.

For small system sizes, such as SO₂, highly accurate ab initio methods can be applied to describe the excited states, while more crude approximations have to be used for larger systems. The unfavorable scaling of many quantum chemical methods with the size of system under investigation requires this compromise between accuracy and system size. Crude approximations for systems that are larger than several hundreds of atoms become inevitable.^44,178,238

Additionally, computations of the excited states suffer from being generally less efficient. To name only one central problem: The larger the system becomes, the closer the electronic states lie in energy, and the more excited-state processes can usually take place. The necessary consideration of an increasing number of excited states increases the already substantial computational expenses even more and restricts the use of accurate methods to systems containing only a few dozens of atoms in a reasonable amount of time with current computers. This increasing complexity makes not only the reference computations, but also the application of ML models for the excited states more complicated than for the ground state. At the same time, the application of ML models for the excited states might also be more promising, because higher speed-up can be achieved.

For the excited states, methods similar to force fields, like the linear vibronic coupling (LVC) approach,^239,240 are usually limited to small regions of conformational space and restricted to a single molecule. General force fields that are valid for different molecules in the excited states do not exist. Also the ML analogue, so-called transferable ML models, to fit the excited state PESs of molecules throughout chemical compound space are unavailable to date. Only recently, we have provided a first hint at transferability of the excited states by training an ML model on two isoelectronic molecules.²⁴¹ It is clear that an ML model, which is capable of describing the photochemistry of several different molecular systems, e.g., different amino acids or DNA bases of different sizes, is highly desirable. A lot remains to be done in order to achieve this goal, and yet, to the best of our knowledge, no more than a maximum of about 20 atoms and 3 electronic states with a distinct multiplicity have been fitted accurately with ML models (refs (15, 16, 92−94, 96, 132, 138−145, 146−149, 149−151, and 241)).

Whether or not the excited states of a molecular system become populated depends on the ability of a molecule to absorb energy in the form of light, or more generally, electromagnetic radiation of a given wavelength. Usually, the so-called resonance condition has to be fulfilled; i.e., the energy gap between two electronic states has to be equivalent to the photon energy of the incident light. Note however that also multiphoton processes can occur, where several photons have to be absorbed at once to bridge the energy difference between two electronic states.^242−244 Further, the absorption of light not only provides access to one, but most often to a manifold of energetically close-lying states. The number of states that can be excited is related to the range of photon energies that is contained in the electromagnetic radiation. This energy range is inversely proportional to the duration of the electric field, e.g., of a laser pulse, due to the Fourier relation of energy and time.²⁴⁵ However, the energy range of the photons and the energy difference between the electronic states are not the only factors influencing the absorption of light, which gives rise to questions like: Is the molecule able to absorb light of a considered wavelength? Which of the excited states is populated with the highest probability?

An answer to these questions can be obtained from an analysis of the oscillator strengths for different transitions. In order to make an electronic transition possible, an oscillating dipole must be induced as a result of the interaction of the molecule with light. The oscillator strength, f_ij^osc, between two electronic states, i and j, is proportional in atomic units (a.u.) to the respective transition dipole moment, μ_ij, and the respective energy difference, ΔE_ij:²⁴⁶

1

If the transition dipole moment between two states is zero, no transition is allowed. The reasons can be that a change of the electronic spin would be required, and the transition is thus spin forbidden. Another reason can be the molecular symmetry, leading to symmetry forbidden transitions. The latter are common in molecules that carry an inversion center, and transitions that conserve parity are forbidden.²⁴⁷ An energetic state is called dark if the transition dipole moment is very small or zero. In contrast, a state is called bright if the transition dipole moment is large. Most often, studies that target the photochemistry of molecules focus on excitation to the lowest brightest singlet state, i.e., the state that absorbs most of the incident energy. The same is true for emission processes. While fluorescence is an allowed transition, phosphorescence is a spin forbidden process, i.e., a triplet-singlet emission in many cases.²⁴⁸

After an excitation process, the molecule is considered to move on the excited-state PESs and is expected to undergo further conversions. The excess of energy a molecule carries—as a result of the initial absorption of energy—is most often converted into heat, light, such as fluorescence or phosphorescence, or chemical energy. If the molecule returns to its original state, then the molecule is photostable. Otherwise, either photodamage, such as decomposition, or useful photochemical reactions including bond breaking/formation occur. In all cases, heat or light can be emitted, which can also be harnessed in light-emission applications.^59,249−251 With respect to photostability, ultrafast transitions, in the range of femto- to picoseconds (10^–15–10^–12 seconds) take place and lead the molecule back to the ground state. This means that the electronic energy is converted into vibrations of the molecule, and the molecule is termed hot. This heat is usually dissipated into the environment, a process that is often neglected in excited-state simulations due to the cost of describing surrounding molecules.

Radiationless transitions from one electronic state to another take place in so-called critical regions of the PESs. As the name already suggests, critical regions are crucial for the dynamics of a molecule, but are also challenging to model accurately. The critical points, where transitions are most likely to occur, are called conical intersections and are illustrated in Figure 2. At these crossing points, PESs computed with quantum chemistry can show discontinuities. These discontinuities can occur also in other excited-state properties and pose an additional challenge for an ML model when fitting excited-state quantities.

In addition to the aforementioned complications of treating a manifold of excited states, also the probability of a radiationless transition between them has to be computed somehow. This probability is usually determined by couplings between two approaching PESs. Between states of the same spin multiplicity, nonadiabatic couplings (NACs) arise, and spin–orbit couplings (SOCs) give rise to the transition probability between states of different spin multiplicities. These couplings are intimately linked to the excited-state PESs and therefore should also be considered with ML. However, only a handful of publications describe couplings with ML,^{15,92,94−96,140,145,146,149,252} which highlights the difficulty of providing the necessary reference data as well as the challenges of accurately fitting them. New methods are constantly needed to further enhance this exciting research field.

3. Quantum Chemical Theory and Methods

In this section, we present some key aspects of quantum theory for excited states, which is the basis of any study focusing on ML for excited states of molecules. We do so because (i) the outcome of the corresponding calculations serve as training data for ML, leaving quantum chemistry and ML thus inseparably connected in many cases and (ii) to clarify the employed nomenclature. We will discuss electronic structure theory (section 3.1), the different bases (section 3.2), i.e., the diabatic, adiabatic, and diagonal bases, the computation of excited-state molecular dynamics simulations (section 3.3) with different flavors of quantum nuclear dynamics and mixed quantum-classical methods, along with the computation of dipole moments and spectra. Experts on these topics may skip directly to section 4, which focuses on ML methods.

In the following, we provide a description of the differences of excited-state computations to calculations for the electronic ground state and the challenges that arise due to the treatment of a manifold of excited states. These challenges also point to issues that are problematic for ML. These explanations will provide the groundwork to evaluate different quantum chemical methods for their use to generate a training set for ML and to use it for different types of applications, such as excited-state MD simulations. Naturally, we can only provide a general idea of this field and refer the interested reader to pertinent textbooks and reviews, such as refs (178, 253−264).

In order to follow a consistent notation within this review, we try to explain all basic concepts with notations that are frequently used in the literature. Currently, a zoo of different notations for the same property can be found. For example, the NACs, or derivative couplings, are sometimes referred to as so-called interstate couplings, i.e., couplings between two states multiplied with the corresponding energy gap between those two states,¹⁴⁴ while in other works interstate couplings refer to off-diagonal elements of the Hamiltonian in another basis, where the potential energies are no eigenvalues of the electronic Schrödinger equation. We want to avoid a confusion of different notations and thus provide a consistent definition below. For the excited states, a number of different electronic states are required. Throughout this review, we adopt the following labeling convention for different electronic states: The lower case Latin letters, i, j, etc. will be used to denote different electronic states. The abbreviations N_S, N_M, and N_A will indicate the number of states, molecules, and atoms, respectively.

The foundation for the following sections is a separation of electronic and nuclear degrees of freedom, which is based on the work of Born and Oppenheimer.²⁶⁵ However, the famous Born–Oppenheimer approximation is later (partly) lifted, and the coupling between electrons and nuclei is taken into account in nonadiabatic dynamics simulations.

3.1. Electronic Structure Theory for Excited States

The main goal when carrying out an electronic structure calculation is usually to compute the potential energy and other physicochemical properties of a compound. We distinguish between two overarching theories to achieve this goal: wave function theory (WFT) and density functional theory (DFT) as outlined, e.g., by Kohn in his Nobel lecture.²⁶⁶

The basis of WFT, as for any electronic structure calculation, is the electronic Schrödinger equation^267,268 with the electronic Hamilton operator, Ĥ_el, and the N-electron wave function Ψ_i(R, r) of electronic state i, which is dependent on the electronic coordinates r and parametrically dependent on the nuclear coordinates, R:

2

From the wave function, i.e., the eigenvector of this eigenvalue equation, any property of the system under investigation can be derived. How to solve the electronic Schrödinger equation exactly to obtain the potential energy of an electronic state i, E_i, is known in theory. However, from a practical point of view, the computation is infeasible for molecules that are more complex than for example H₂, He₂⁺, and similar systems.²⁶⁹ In order to make the computation of larger and more complex systems viable, approximated wave functions are introduced.

In contrast to WFT, DFT reformulates the energy of a system in terms of the ground state electron density rather than the N-electron wave function, and the energy is expressed as a functional thereof. The advantage of DFT is a rather high accuracy at a rather low computational cost. If DFT is applied properly, it is considered as one of the most efficient ways to obtain reliable and reasonably accurate results of molecules up to hundreds of atoms. In solid state physics, DFT is even the workhorse of most studies aiming to describe ground state properties.²⁷⁰ However, the problem is that the equations to be solved are unknown. The missing piece is the exact exchange-correlation functional of a system. To date, researchers have come up with many different approximations to this functional that can be used to treat specific problems, but a universal functional capable of describing different problems equally accurately has not yet been found. Moreover, there is no systematic way to improve a density functional. The results obtained with DFT therefore critically depend on the choice of the functional.^269,271

In the following sections, we will describe both theories and focus on the excited states of molecules. We will start to cover ab initio methods, which means that they are derived from first-principles without parametrization. We mention the basic underlying concepts here because we believe them to be essential in order to generate training data and carry out ML for excited states. Furthermore, these methods present starting points for an ML approximation to the excited-state wave function or density, which is still lacking, to the best of our knowledge. Nevertheless, such an ML model would be extremely powerful and could provide a solution to many existing quantum chemical problems.

3.1.1. Wave Function Theory

The basis of all discussed ab initio methods is the Hartree–Fock method. The N-electron wave function is represented by a single Slater determinant, ϕ₀, which makes N coupled one-electron problems out of the N-body problem. This Slater determinant is the antisymmetric product of one-electron wave functions, the spin orbitals, which can be atomic, molecular, or crystal orbitals, depending on the system. In the case of molecular (or also crystal) orbitals, they are usually expanded as a linear combination of atomic orbitals, where the expansion coefficients are optimized during the calculation. In order to do so efficiently, the atomic orbitals are themselves expanded with the help of a basis set. The N-electron wave function is therefore obtained as a double expansion. Two approximations are applied, which is the use of a finite basis set to represent the atomic orbitals and in turn also the molecular orbitals on the one hand and the use of a single Slater determinant on the other hand. This usually gives a poor description of a system under investigation, due to a lack of electronic correlation.

Electronic correlation describes how much the motion of an electron is influenced by all other electrons. Since the Hartree–Fock method can be seen as a mean-field theory, where an electron “feels” only the average of the other electrons, correlation is quantified by the correlation energy, which is the difference between the Hartree–Fock energy and the exact energy of a system.

Unsurprisingly, all further discussed quantum chemical methods aim at improving the Hartree–Fock method. They can be seen as different flavors of the same solution to the problem: They all include more determinants in one way or another. Accordingly, the wave function is expanded as a linear combination of determinants, where a determinant consists of molecular orbitals, which are expanded in atomic orbitals. This ansatz contains two types of coefficients that can be optimized, the ones for the determinants and the ones yielding the molecular orbitals. If the latter are kept the same for different determinants, we speak of a single-reference wave function. If both types of coefficients are adapted, we speak of a multireference wave function. Similarly, the electron correlation is also divided into two parts, termed dynamic correlation and static correlation. Single-reference methods improve on the dynamic correlation, while a multireference wave function allows for static correlation. However, the separation is not so strict, as can be seen by the following fact: Both the aforementioned single-reference variant and the multireference variant become equivalent when including an infinite number of terms and deliver the exact solution to the Schrödinger equation if also an infinite basis set is used.

Configuration Interaction

In the case of single-reference methods, the orbitals obtained from the reference calculation (usually Hartree–Fock) are kept fixed. Since usually more orbitals than the number of electrons in the system are calculated, the possibility of constructing different Slater determinants from these orbitals exist, which can be used for expanding the actual wave function:^272,273

3

Each Slater determinant is weighted by a coefficient, c_iI. These coefficients can be obtained variationally by minimizing the total energy under the constraint of fixed orbitals, ending up in the configuration interaction (CI) methods. ϕ₀ is the reference, Hartree–Fock, wave function. In principle, the exact solution can be obtained by considering all possible Slater determinants in combination with a complete basis set. The use of all possible configurations is called full-CI and represents the case when all electrons are arranged in all possible ways. Practicable methods require truncation; e.g., CIS (CI singles) or CISD (CIS and doubles) are frequently used, where only single excitations or additionally double excitations are accounted for, respectively. Figure 3 gives a schematic overview of the improvements of CI that one can apply. A huge advantage of these methods is that how to obtain the exact solution is known and that they are systematically improvable. However, truncated CI does not scale correctly with the system size and is therefore not size-extensive and also not size-consistent (i.e., the energy of two fragments A and B at large distance computed together, E(A + B), is not equal to the sum of the energies of the fragments from separate calculations, ≠ E(A) + E(B)).²⁷⁴

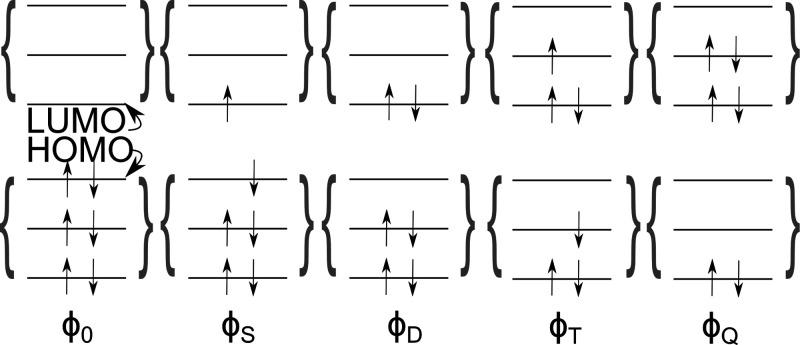
Figure 3.

Different arrangements of electrons in molecular orbitals giving rise to the configuration interaction (CI) method. Inclusion of excited configurations in addition to the ground-state, reference determinant, ϕ₀, allows one to go beyond the Hartree–Fock method. Electrons are excited into higher electronic orbitals, and Slater determinants are indicated using the letters S, D, T, and Q, which refer to single, double, triplet, and quadruple excitations.

The CI scheme can be employed to improve the ground-state wave function by mixing the Hartree–Fock determinant and determinants of different electron configurations. In the same way, also wave functions of excited states can be computed. Then, the coefficients, c_iI, are optimized for higher eigenvalues of the electronic Hamiltonian instead of the first one. Beginners in the field then often get confused by terms such as single excitation in comparison to the first excited state. A single excitation determinant (see Figure 3) can be part of the wave function for the first excited state but can also be a part of the ground-state wave function.

Electron Propagator Methods

Another class of methods that we shortly want to mention here are electron propagator methods that are based on one electron Green’s function and are a variant of perturbation theory schemes. One popular method that is based on Green’s function one electron propagator approach is the algebraic diagrammatic construction scheme to second-order perturbation theory (ADC(2)).²⁷⁵ ADC(2) is a single-reference method and can be used to efficiently compute excited states of molecules. It offers a good compromise between computational efficiency and accuracy, while being systematically improvable (higher order variants such as ADC(2)-x or ADC(3) exist). The time evolution of a systems polarizability is obtained by applying the polarization propagation, which contains information on a system’s excited states.^{272,276−279} The ground-state energy of ADC(2) is based on Møller–Plesset perturbation theory of second order,^280,281 MP2, where the latter can formally be shown to include double excitations for the improvement of Hartree–Fock; see ref (272). The dependence of ADC(2) on MP2 gives rise to instabilities in regions, where excited states come close to the ground state, or homolytic dissociation takes place. The excited states of bound molecules are described with reasonable accuracy. Compared to multireference CI methods (see below), the black box behavior of ADC(2) is a clear advantage.²⁷⁵

Coupled Cluster

The current gold standard of ab initio methods for the ground state is the family of coupled cluster (CC) methods. CC is often referred to as the size-extensive and size-consistent version of CI. The different electronic configurations accounting for single or double excitations (such as in CIS and CISD for example) are obtained by applying an excitation operator, T̂:²⁸²

4

Similarly to CI, this operator can be truncated. If T̂ = T̂₁+T̂₂, single and double excitations are accounted for. When using the same number of determinants, CC usually converges faster than CI.

Excited states can be computed in a single-reference approach by equation-of-motion-CC (EOM-CC), where the excited-state wave function is written as an excitation operator times the ground-state wave function. For further details, see, e.g. refs (283) or (284).

CASSCF

The problem of missing static correlation in the Hartree–Fock approach is tackled by a multireference ansatz for the wave function. Not only coefficients, but also orbitals are optimized.²⁷¹ This treatment is important for many excited-state problems, but also some transition metal complexes in their ground state, transition states, or homolytic bond-breaking with the dissociation of the N₂ molecule being a notoriously difficult example.^285,286 An accurate ML training set for many chemical problems in the excited states often calls for such methods.

The multiconfigurational self-consistent field (MCSCF) method can be seen as the multireference counterpart to the Hartree–Fock method.²⁸⁷ One of the most popular variants of MCSCF methods is the Complete Active Space SCF (CASSCF),^288,289 where important atomic orbitals and electrons are selected giving rise to an active space. An example is shown in Figure 4. According to this scheme, the orbitals are split into an inactive, doubly occupied part, an active part, and an inactive, empty part. Within the active space, a full CI (FCI) computation is carried out. The active space has to be chosen manually by selecting a number of active electrons and active orbitals. CASSCF is no black box method, and a meaningful active space selection is the full responsibility of the user. As an advantage, CASSCF can describe static correlation well, which is necessary in systems with nearly degenerated configurations with respect to the reference Slater determinant. For completeness, state-averaging (i.e., SA-CASSCF) is most often applied, where states belonging to the same symmetry are averaged. Another variant of MCSCF methods is restricted active space SCF (RASSCF), which is very similar to CASSCF, but within RASSCF the active space is restricted and no FCI computation is carried out.²⁷²

Figure 4.

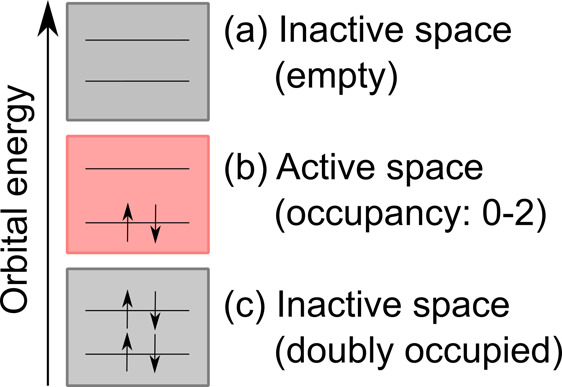
Electrons and orbitals of an arbitrary system to exemplify the active space needed for many multireference methods. (a) The highest, not considered, molecular orbitals are inactive and always empty. (c) The lowest, not considered, molecular orbitals are always doubly occupied. (b) The active space is shown with two active electrons in two active orbitals.

DMRG

As an alternative to deal with large active spaces, the density matrix renormalization group (DMRG) can be used.²⁹⁰ A DMRG-SCF calculation is similar to a CASSCF calculation, but instead of a FCI solution of the active space, an approximated solution with DMRG is obtained to avoid the exponential scaling of the computational costs with the number of active orbitals.^291−296 Very recently, transcorrelated DMRG (tcDMRG) was introduced for strongly correlated systems.²⁹⁷

MR-CI

Even higher accuracy can be obtained with multireference CI methods,^253,298,299 such as MR-CISD, that additionally add single and double excitations out of the active space and are therefore based on CASSCF wave functions. With this approach, electronic correlation, i.e., static and dynamic correlation, can be treated.

CASPT2

Alternatively, complete-active-space perturbation theory of second order, CASPT2,^300−302 can correct electronic correlation effects via treating multireference problems with perturbation theory. This variant of multireference perturbation theory methods uses the CASSCF wave function as the zeroth order wave function. CASPT2 can be applied to each state separately (single-state (SS)-CASPT2) or correlated states can be mixed at second order resulting in a multistate perturbation treatment (MS-CASPT2).^300−302 Other perturbation approaches for multireference problems exist, like the n-electron valence state perturbation theory (NEVPT2).^303−305

MRCC

In addition to multireference methods based on CI, multireference variants of CC approaches exist. A relatively efficient implementation is for example the Mk-MRCC approach of Mukherjee and co-workers³⁰⁶ or the Brillouin-Wigner approach,³⁰⁷ which is however not size extensive. Noticeably, the development of multireference CC approaches is a rather young research field compared to other excited-state methods, and the computation of properties and forces is not well explored. Many studies therefore focus on the simulation of energies of low-lying states with MRCC methods. Additionally, such methods suffer from algebraic complexity and numerical instabilities. Interested readers who seek for a more extensive summary of existing MRCC methods are referred to refs (253, 308, and 309).

Challenges

The probably biggest drawback of the aforementioned multireference methods is that their protocols are very demanding. Finding a proper active space is a tedious task that often requires expert knowledge. Too small active spaces can lead to inaccurate energies, and problems with so-called intruder states are common. Those are electronic states that are high in energy at a reference molecular geometry, but become very low in energy at another molecular geometry, that is visited along a reaction coordinate. The active space then changes along this path. This behavior can result in inconsistent potential energies. In the case of CASPT2, the configurations of intruder states can lead to large contributions in the second-order energy, making the assumption of small perturbations invalid. Especially for describing molecular systems with many energetically close-lying states and for the generation of a training set for ML, such inconsistencies are problematic. Figure 5 shows an example of potential energy curves of three singlet states and four triplet states of tyrosine computed with (a) CASSCF(12,11) and (b) CASPT2(12,11), where 12 refers to the number of active electrons and 11 to the number of active orbitals. We used OpenMolcas³¹⁰ to compute an unrelaxed scan along the reaction coordinate, which is a stretching of the O–H bond located at the phenyl-ring of tyrosine.

Figure 5.

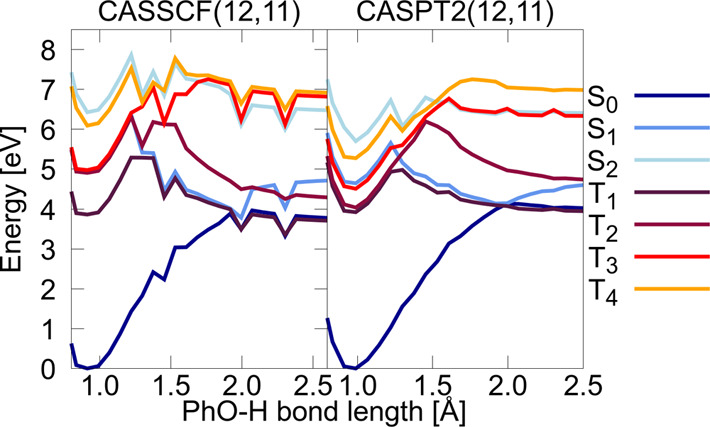
Potential energy curves of the three lowest singlet (S₀–S₂) and the four lowest triplet state (T₁–T₄) of the amino acid tyrosine along the O–H bond length of the hydroxy group located at the phenyl ring (Ph–OH) computed with CASSCF(12,11)/ano-rcc-pVDZ and CASPT2(12,11)/ano-rcc-pVDZ.³¹¹

Intruder states are no exception. Actually, they are quite common in small- to medium-sized organic molecules. A large enough reference space can mitigate this problem, but makes computations almost infeasible. The computational costs increase exponentially with the number of active orbitals. In many cases, the improved accuracy due to a larger active space cannot justify the considerably higher expenses. At its best and with massively parallel simulations, an active space of about 20 electrons in 20 orbitals can be treated,³¹² which is impracticable for many applications, such as dynamics simulations. For medium-sized molecules, the active space that would be required for a given simulation might even be way too large to be feasible for calculations in a static picture. With respect to ML, a model that can detect such regions along reaction coordinates would be very helpful. Indeed, the dipole moment or nonadiabatic couplings are commonly used to identify a change in a character of a state. Monitoring of these properties along reaction coordinates could potentially help to identify such regions. To the best of our knowledge, such a model does not yet exist. What is known so far is that ML can provide a smooth interpolation of such cusps in energy potentials as long as the density of electronic states is not too high.^94,171

Worth mentioning at this point are also Rydberg states, which often need to be considered in small- to medium-sized molecules. Rydberg states can be strongly interlaced with valence excited states. In such cases, the active space needs to be large enough to treat both the valence and Rydberg molecular orbitals. Additionally, the one electron basis set should be flexible enough to describe both types of orbitals. This increases the computational costs additionally. More details on the inclusion of Rydberg states in simulations can be found in refs (313−316). Especially in such cases, an ML representation of the electronic wave function to reduce the computational time would be highly beneficial.

A promising tool to eliminate the complex choice of active orbitals is autoCAS.^317−319 It provides a measure of the entanglement of molecular orbitals that is based on DMRG. In principle, there is no prerequisite for the active space selection. If possible, the reference space should be the full valence in order to identify the relevant orbitals and electrons. If the full valence space is too large for a DMRG-CI calculation, one or several smaller chemically sensible reference active spaces should be selected to be able to analyze the importance of all orbitals.^317−319 As an alternative, ML can be used to determine an active space.⁷¹

3.1.2. Density Functional Theory

A complementary view on how to obtain the energy of a system is provided by DFT. DFT dates back to 1964, when it was formulated by Hohenberg and Kohn³²⁰ entirely in terms of the electron density, η(r⃗). A one-to-one correspondence between this density and an external potential, v(r⃗) exists and the potential acts on the electron density. The energy can be formulated in terms of a universal functional, F[η(r⃗)], of the electron density, which is independent of the external potential. In this way, the energy of a system’s ground state can be computed with the following equation:

5

The most widely used implementations of DFT rely on the Kohn–Sham approach.³²¹ In fact, Kohn–Sham DFT is so successful that it is often simply referred to as DFT. In this approach, an auxiliary wave function in the form of a Slater determinant is employed. Since a single Slater determinant is the exact solution for a system of noninteracting electrons, this DFT approach can be seen as describing a system of noninteracting electrons that are forced to behave as if they were interacting. The latter effect can be achieved only by an unknown modification of the Hamiltonian or rather of the aforementioned functional. In other words, a Slater determinant as wave function ansatz is exact, but the Hamiltonian can only be approximated, in contrast to Hartree–Fock, where the true electronic Hamiltonian is used, but the Slater determinant is only an approximate wave function.

The functional F[η(r⃗)] can be separated into Coulombic interactions and a non-Coulombic part. The latter can further be divided into two terms: the kinetic energy of the noninteracting electrons and the exchange-correlation part, which describes the interaction of electrons and thus also corrects the kinetic energy by the difference of the real kinetic energy and the kinetic energy of the fictitious system of noninteracting electrons. The exchange-correlation functional is the part of DFT that is unknown, and finding the exchange-correlation functional remains the Holy grail of DFT.

In principle, if the exact functional was known, the exact ground-state energy of a system could be computed. Unfortunately, it is not known, and the success of a DFT calculation critically depends on the approximation that is used to the unknown exchange-correlation functional.

Excited States

As explained above, the electron density is computed from a single reference Kohn–Sham wave function, i.e., the one of noninteracting electrons with the density of the real system. This single-reference wave function makes DFT a single-reference method. In fact, most failures of DFT are a consequence of an improper description of static correlation.²⁷¹ In order to describe excited states, the time-dependent (TD) version of DFT, namely, TDDFT, can be used. The foundation of this theory was laid in the 1980s with the Runge-Gross theorems,³²² which can be regarded as analogies to the Hohenberg–Kohn theorems. They are based on the assumption that a one-to-one correspondence exists also between a time-dependent potential and a time-dependent electron density in this potential. A system can therefore be completely described by its time-dependent density. Also in the time-dependent case, the variational principle for the density is proposed.

The most widely used approach of TDDFT is linear response TDDFT (LR-TDDFT). Again, often TDDFT is used as a synonym for LR-TDDFT due to its extensive use. Within this theory and the KS approximation, no time dependent density is necessary to compute excitation energies and excited state properties. Linear response theory can be directly applied to the ground state density.^323,324 Casida’s formulation of this theory is the most popular one and gives rise to random-phase approximation pseudoeigenvalue equations, which are also known as the Casida equations. Within the adiabatic approximation, they are implemented efficiently in many existing electronic structure programs. The Tamm-Dancoff approximation^325,326 further simplifies the equations to an eigenvalue problem, resulting in the counterpart to CIS.³²⁷ Especially in cases when the time evolution of a system is studied, the Tamm-Dancoff approximation is beneficial since it leads to more stable computations close to critical regions of the PESs.^269,328

Advantages and Disadvantages

The advantage of LR-TDDFT is its computational efficiency. The reasonable accuracy if a proper functional is chosen makes this approach often the method of choice to study the photochemistry of medium-sized to large and complex systems, which are not feasible to treat with costly multireference WFT based methods.^253,329,330 Shortcomings of LR-TDDFT are the incorrect dimensionality of conical intersections, which are, however, one of the most important regions during nonadiabatic MD simulations.^331−336 The incorrect dimensionality of conical intersections with standard TDDFT implementations leads to a qualitatively incorrect description of such critical regions. The missing couplings can be corrected for example with the CI-corrected Tamm-Dancoff approximation³³⁷ or the hole–hole Tamm-Dancoff approximation,³³⁸ which can recover the missing couplings and provide correct dimensionality at conical intersections. Alternatively, an incorporation of the spin-restricted ensemble-referenced Kohn–Sham method into the tight-binding TDDFT approach³³⁹ can be used to describe conical intersections with reasonable accuracy.

In addition, one should be aware that by definition, double excitations cannot be accounted for with LR-TDDFT. The computation of double excitations can be achieved by using a frequency dependent exchange kernel, which is known as dressed TDDFT.^340,341 Alternatively, spin-flip TDDFT^342−344 can be used, where a triplet state is taken as a reference state, and single excitations are treated with a flip in the electron’s spin. However, spin-contamination is quite common within these methods. In general, the description of double excitations from a multireference state would be more favorable, although spin-flip TDDFT is often considered to be a multireference method. In order to compute specific orbital occupations and consequently excitations and charge-transfer states, an alternative approximation exists, which is known as the Δ-SCF approach. In this theory, the electrons are forced into specific KS orbitals. The SCF is applied to converge the energy with respect to this configuration.^345−347 Other multireference variants of TDDFT exist too. However, their description is beyond the scope of this review, and we refer the reader to recent reviews covering this topic in much more detail.^253,348 The accuracy of (TD)DFT simulations for the ground state³⁴⁹ or excitation energies and absorption spectra of organic molecules could be improved by ML corrections, which were obtained from the genetic algorithm and NN approach (GANN),³⁵⁰ support vector machines,³⁵¹ or AdaBoost ensemble correction models³⁵² for example.

Last but not least, we briefly want to discuss the most critical part of a DFT calculation, which is the proper choice of the exchange-correlation functional. In the case of excited states, the treatment of valence excitations, Rydberg states and long-range charge transfer excitations on the same footing are highly problematic. While hybrid (meta-) generalized gradient approximation (GGA) or range-separated hybrid functionals³⁵³ are for example well suited for vertical excitations and the latter also for Rydberg states, global hybrid meta GGA or range-separated hybrid GGA functionals are better to describe charge transfer.^269,354 Most often, functionals are accurate for one specific problem, but they fail to describe others. Although much effort has been devoted to develop functionals, finding a universal functional for DFT is still far from being achieved.^{180,253,269,328} ML could be particularly powerful to advance DFT and TDDFT in this regard. For example, models exist to predict the energy of a system based on self-consistent charge densities or external potentials. Kohn–Sham DFT can be circumvented, and density functionals can be constructed from ML models. Besides the density-potential, energy-density maps, and whole functionals can be learned.^82,355−357

In summary, it should be stressed that, in general, there is not only one single solution to a particular problem, but that many possible ways can be considered, which lead to an equivalent description of a particular problem. Considering the excited states of molecules, it should be mentioned that it is of utmost importance to think carefully about the photochemical processes that may occur in order to find the most appropriate method for most of the assumed reactions. It often happens that within the same molecular system, one method can describe a certain photochemical reaction quite well, while another reaction can be described better with another method. However, the mixing of methods is not practicable for standard applications. Recently, studies on ML models have emerged that combine the different strengths of several methods, e.g. Δ-learning techniques^358,359 or transfer learning.³⁶⁰ These methods could be well-suited solutions for many future applications to overcome the current limitations of existing quantum mechanical methods for the excited states. Even more than for ground state properties, the quality of the excited states depends critically on the ability of a method to describe the different possible reaction—as a consequence of the larger accessible configuration space of a molecular system. Even for medium-sized systems, it should be clear that a suitable method may already be computationally impracticable, and a balance between accuracy and computational effort has to be found.

3.2. Bases

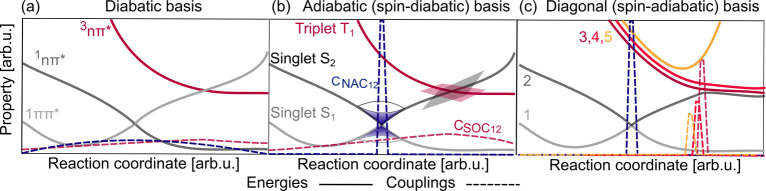
The potentials computed with the aforementioned methods for different nuclear geometries can be represented in different bases, which are connected by unitary transformations. An example of five states in different bases is given in Figure 6. Note that often a system in a certain basis is also referred to as being in a certain picture or representation; here we will not use the term representation in order to not confuse the reader with molecular representations used in ML. As it is visible in the figure, we focus on three types of bases: (a) the diabatic basis, (b) the adiabatic (spin-diabatic) basis, i.e., the direct output of standard electronic structure programs, (c) the diagonalized version of (a) and (b), i.e., the spin-adiabatic basis. Throughout the literature, different names are given to these bases, which are summarized in Table 1. They stem from a partition of the total wave function into a sum of electronic and nuclear contributions, which can be written for all bases as

6

Figure 6.

(a) Example of three potential energy curves ordered by their character along with respective potential couplings between different states shown by dashed lines. (b) Two singlets (E_i and E_j) and one triplet state (E_k) including coupling values (with vectorial properties, , shown by their norm) in the adiabatic basis, in which the triplet state crosses singlet states. (c) The diagonal, or spin-adiabatic, basis, in which all states are ordered by their energy and are spin-mixed. Kinetic couplings are shown by their norm. Note that the ground state is not shown. Potential energy curves are represented using solid lines and couplings using dashed lines.

Table 1. Commonly Used Names of Bases for the Excited-State Potential Energy Surfaces^a.

a	b	c
diabatic	adiabatic	diagonal
crude adiabatic	spin-diabatic	spin-adiabatic
spectroscopic	MCH	field-adiabatic
quasi-diabatic	field-free	field-dressed

^aBased on refs (239, 256, and 362−365). The labels a, b, and c are consistent with Figure 6.

In principle, the total wave function can be expanded in infinitely many different bases. The electronic part ψ_i^basis(r,R) corresponds to the eigenfunctions of the electronic Hamiltonian only for one of the bases (namely, the one from column B of Table 1). Associated with these functions are the corresponding potentials, depicted for a model system in Figure 6. Note that a different approach is taken in the exact factorization method,³⁶¹ where the total wave function is expanded only in a single product, i.e., without the sum in eq 6, giving rise to only one (time-dependent) potential.

3.2.1. Adiabatic (Spin-Diabatic) Basis

The direct output of an electronic structure calculation usually provides the eigenenergies and eigenfunctions of the electronic Hamiltonian. In many cases, only one spin multiplicity is calculated. If this procedure is repeated along a nuclear coordinate, potential curves result that are termed adiabatic. Adiabatic means ”not going through” (from greek a = not, dia = through, batos = passable), and, indeed, the potentials never cross when considering one multiplicity. This situation is schematically illustrated in Figure 6b for singlet S_i and singlet S_j.

Within one multiplicity, 3N_A-dimensional adiabatic PESs are obtained that are strictly ordered by energy. Hence, the states are usually denominated with the first letter of the multiplicity and a number as subscript, e.g., S₀, S₁, etc. For states of the same multiplicity, critical points and seams exist. These regions of the PESs are referred to as conical intersection (seams), in which the corresponding states become degenerate. Such features make adiabatic PESs nonsmooth functions of the atomic coordinates, which make them difficult to predict with the intrinsically smooth regressors of ML. At a conical intersection, the approaching potential energy curves form a cone, and the NACs, denoted as 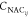, between them show singularities as a result of the inverse proportionality to the vanishing energy gap:^298,366

7

Second-order derivatives are neglected here, as is done in many quantum chemistry programs that compute NAC vectors. The blue dashed curve in Figure 6a illustrates the norm of the NAC vector,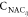, that couples the states S_i and S_j. At the avoided crossing points of the states, the NAC norm shows a sharp spike, but is almost vanishing elsewhere. If more than one multiplicity is considered, the term adiabatic is not adequate anymore, because potentials of different multiplicity might cross through each other. This situation is then called diabatic with respect to the spin multiplicities, or spin-diabatic in short. For example, singlets are adiabatic among each other, triplets are adiabatic among each other, but singlets are diabatic with respect to triplets. However, also the diabatic basis (see Figure 6a and also below) qualifies as spin-diabatic. Because of this nomenclature issue, which even gets experts confused sometimes, we refer to this basis as “Molecular Coulomb Hamiltonian” (MCH) because it is obtained from the eigenfunctions and eigenvalues of the nonrelativistic electronic Hamiltonian, where only Coulomb interactions are considered.

As an example, a crossing of a singlet state and a triplet state is shown in Figure 6b. As it is visible, the triplet components, which are defined by different magnetic quantum numbers, are degenerate. The states are coupled by SOCs (denoted as 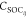), which are usually obtained as smooth potential couplings with standard quantum chemistry programs:^256,365,367

8

These couplings are single real-valued or complex-valued properties.^368,369 Whether they are complex or not depends on the electronic structure program employed, but they can be converted into each other.^{256,257,368,370} It is important to know in which way the SOCs are presented by an electronic structure program in order to find the best possible solution for ML approximations.¹⁵

Ĥ^SO in eq 8 is the spin–orbit Hamilton operator, which describes the relativistic effect due to interactions of the electron-spin with the orbital angular momentum, allowing states of different spin-multiplicities to couple.^370−372 Note that also SOCs between different states of the same multiplicity exist except for singlets. No exact expression on how to include relativistic effects into the many-body equations has been found yet. Among the most popular approximations used is the Breit equation,³⁷³ applying an adapted Hamiltonian instead of the electronic Hamiltonian, which comprises, among other terms, a relativistic part. This additional part of the Hamiltonian accounts for spin–orbit effects and is proportional to the atomic charge,^{257,368,370,372,373} leading to the belief that SOCs would only be relevant in systems with heavy atoms.^233,234 Today, it is known that spin–orbit effects also play a crucial role in many other molecular systems and are important for intersystem crossing between states of different spin multiplicities.^{178,235−237}

The states in the MCH basis can also be coupled via external electric-magnetic fields, e.g., by sunlight or a laser. The corresponding couplings stem from the transition dipole moments multiplied with the electric field. Since the effect of the field is not included in the potentials but as off-diagonal potential couplings, the MCH basis is also called field-free.^{362−364,374} However, also the diabatic basis qualifies as field-free.

3.2.2. Diabatic Basis

In the diabatic basis, the electronic wave function is not parametrically dependent on the nuclear coordinates. Diabatic potentials usually need to be determined from adiabatic potentials and are not unique; i.e., they rely on the method and the reference point, which is chosen in the adiabatic basis to fit diabatic potentials.^239,256 The advantage of diabatic potentials is that singularities in NACs are removed together with nondifferentiable points of the PESs. Note that such a strictly diabatic basis for polyatomic systems does not exist in practice, and only approximated, so-called, quasi-diabatic, PESs can be fit, where NACs are almost removed, but not completely. In the literature, quasi-diabatic PESs are most often referred to as diabatic ones, so we will also use this notation here.

An example of a system in the diabatic basis is given in Figure 6a, and commonly used notations can be found in Table 1 in the first column. In regions where an avoided crossing is present in the adiabatic basis, the coupled diabatic potential energy curves cross. Since the electronic wave function of a state is ideally independent of the nuclear coordinates, its character is conserved. Consequently, the states are labeled according to their character and multiplicity, e.g., as ¹ππ* or according to symmetry labels. Similar to the character, also spectroscopically important quantities like the dipole moment are mostly conserved or vary smoothly along the nuclear coordinates. Therefore, spectroscopic experiments can easily be interpreted when using the diabatic basis, which is thus sometimes also called spectroscopic basis. Note that sometimes labels like S₁, etc. are used also when referring to the diabatic basis, especially in experimental papers when an identification of the wave function’s character has not been carried out and only one geometry is considered. However, at a different geometry, the energetic order of the states might have changed such that a state previously labeled as S₂ might now be lower in energy than a state previously labeled as S₁. Furthermore, this labeling scheme in the diabatic basis can lead to confusion with the labels from the MCH basis, and we suggest to reserve it only for the MCH basis.

Because of the mostly conserved characters and the crossing of states, diabatic potentials are smooth functions of the nuclear coordinates, in contrast to adiabatic potentials. A diabatic PES is thus highly favorable for several numerical applications including ML.

The MCH and diabatic bases can be interconverted by a unitary transformation

9

with a unitary matrix, U, that is determined up to an arbitrary sign (as a result of the arbitrary sign of the wave function, which will be discussed in detail in section 5.3). In the case of two states, U, is a rotation matrix:

10

and is dependent on the rotation angle, θ. Accordingly, the peaky NACs, which are obtained as derivative couplings (also called kinetic couplings) in the MCH basis, are converted to smooth potential couplings in the diabatic basis. The smooth SOCs from the MCH basis become even smoother (ideally constant) in the diabatic basis.

While one can straightforwardly apply diagonalization to convert diabatic PESs to adiabatic PESs (and similarly adiabatic PESs to diagonal PESs), a dilemma arises when one wants to take the inverse way to obtain diabatic PESs from adiabatic ones (and similarly adiabatic PESs from diagonal ones). In fact, finding diabatic PESs is highly complex and most often requires expert knowledge. To date, only small molecules could be represented with accurate diabatic potentials, and developing a method to automatically generate diabatic PESs remains an active field of research. Existing methods to obtain diabatic potentials require human input and are mostly applicable to small systems and certain reaction coordinates. Early pioneering works can be found in refs (239 and 375). Today, a lot more variants exist. Examples are diabatization using explicit derivative couplings,^376,377 the propagation diabatization procedure,³⁷⁸ diabatization by localization,³⁷⁹ Procrustes diabatization,²⁵² or diabatization by ansatz.^142,380,381 Further, methods can be based on couplings or other properties,^382−385 configuration uniformity,³⁸⁶ block-diagonalization,^387,388 a hybrid diagonalization combining block-diagonalization and diabatization by ansatz,^389,390 CI vectors,³⁹¹ whereas some procedures are carried out at least partly using ML.^{142,143,380,390,392}

3.2.3. Diagonal Basis

As the name indicates, the diagonal basis can be obtained by a diagonalization from the MCH or diabatic bases. In this case, a strictly adiabatic picture is obtained, where states never cross.²⁵⁶ Accordingly, the concept of multiplicity for a single state is lost because the state might be of singlet character in one region and of triplet character in another region. Therefore, the basis is also called spin-mixed or spin-adiabatic.^257,369,393 The states are strictly ordered by energy and can be labeled simply with numbers (see Figure 6c). The resulting wave functions are eigenfunctions of the relativistic electronic Hamiltonian.^236,256,257 These eigenfunctions as well as the eigenenergies can be also obtained directly with, e.g., relativistic two-component or four-component calculations,³⁹⁴ instead of via diagonalization.

In this basis, the effect of the SOCs is incorporated into the PESs to a large extent. What remains are localized kinetic couplings, which are similar in nature to the NACs in the MCH basis. An example is given in Figure 6c. The parts of the potentials that correspond to the different triplet components in the MCH basis are split energetically in the diagonal basis. In the case of small SOCs, the diagonal potentials look similar to the MCH potentials. However, if the SOCs are strong, potentials that are degenerate in the MCH basis can be easily shifted apart by 1 eV in the diagonal basis. Such splittings are then also experimentally observable, and the diagonal basis yields a more intuitive interpretation of these experiments.^43,395,396

As mentioned above, the states in the MCH basis can also be coupled via electromagnetic fields. A diagonalization of the potential matrix then yields so-called field-dressed states or light-induced potentials, which can also be termed field-adiabatic.^{362,374,397−399} Since the fields are usually time-dependent, the most important axis along which the potentials in this field-dressed basis need to be plotted is time.³⁷⁴

In principle, all these bases are equivalent but only if an infinite number of terms is considered in eq 6. In practice, potentials represented in different bases have different advantages for dynamics simulations, especially in combination with different approximations made in the different dynamics methods as outlined below.

3.3. Excited-State Dynamics Simulations

In order to investigate the temporal evolution of an isolated molecular system in the excited states, the time-dependent Schrödinger equation has to be solved:²⁵⁴

11

From a technical point of view, a sequence of time steps is computed, where in every step the electronic problem is solved to yield potentials, which determine the forces acting on the nuclei such that the nuclear equations of motion can be solved for the current time step.

Ideally, the nuclei are treated quantum mechanically. In this case, the PESs are usually computed in advance and either interpolated or stored on a grid for later use. The hope is that ML can improve the interpolation of potentials drastically. Such global PESs are needed because a wave function is employed for the nuclei, which extends over a range of nuclear coordinates at the same time (see Figure 7a). An overview over corresponding dynamics methods is given in section 3.3.1.

Figure 7.

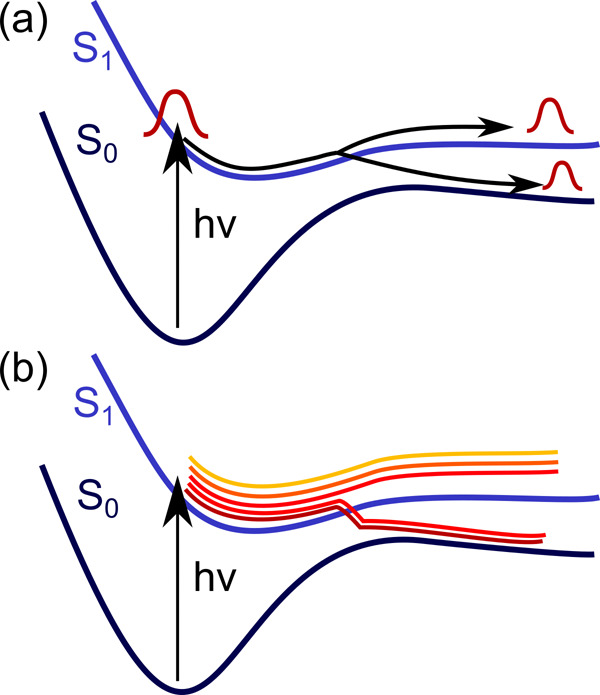
Excited-state dynamics can be treated with (a) quantum approaches, where wave functions are used for the nuclei, or (b) classical approaches, based on trajectories.

The nuclear dynamics can also be approximated classically while quantum potentials are used; i.e., mixed quantum classical dynamics (MQCD) simulations are carried out. Such methods is discussed in section 3.3.2. Since the classical nuclear trajectories are defined only at one nuclear geometry at a time (see Figure 7b), on-the-fly calculations of the potential energies are possible. An on-the-fly scheme is computationally advantageous if the number of visited geometries during the dynamics is smaller than the number of points needed to represent the conformational space on a grid or via interpolation.^{236,256,258,331,332,367,400} No fitting of PESs is necessary in an on-the-fly approach, but fitted PESs can still be used as an alternative. Since ML approaches provide such interpolated potentials, the amount of training points generated with quantum chemistry must be less than the number of points needed in an on-the-fly approach in order to be advantageous. This demand is satisfied, e.g., for long time scales or if many trajectories are necessary.

In the following, we will shortly discuss the different types of describing nuclear motion and the opportunities of ML models to enhance the respective dynamics simulations.

3.3.1. Quantum Nuclear Dynamics

The computational cost of an exact nuclear dynamics simulation scales exponentially with the nuclear degrees of freedom. Hence, simulations are limited to small systems, typically containing less than five atoms.^{59,368,401,402} Still, the calculation of the PESs of the molecule can be a rather expensive part of the whole scheme, and the use of ML algorithms is advisable even for such small systems.

To treat larger systems, approximations have to be invoked.⁴⁰² A prominent approach that can be converged to the exact solution is the multiconfigurational time-dependent Hartree (MCTDH) approach.^48,403−405 Its high efficiency stems from the use of time-dependent basis functions to represent the nuclear wave functions. Nonetheless, the computations are computationally costly, and the nuclear degrees of freedom are often reduced to only a few important key coordinates,^239,406 where classical simulations can help identify the latter.⁴⁰⁷ Whether quantum dynamics of such reduced-dimensionality models are better than using classical dynamics of a full-dimensional system is still under debate and probably depends on the system. In the case of quantum dynamics, the potentials need to be presented to the algorithm in the diabatic basis, mostly due to numerical stability (e.g., smooth couplings are easier to integrate than singular ones). For more than 20 years, the (modified) Shepard interpolation has been used to fit diabatic potentials.^{151,408−411} Notably, the grow algorithm¹⁵¹ can be used to efficiently generate the database of points upon which the interpolation is based. However, it is clearly desirable to treat larger systems, and ML models like neural networks (NNs) promise higher performance or more flexibility in such cases.^{143,146,147,149,378,392,412−414}

More recently, on-the-fly methods addressing quantum dynamics have been developed.^{145,415−417} They mostly rely on a combination of Gaussians to represent the nuclear wave function.²⁵⁸ For example, the variational multiconfiguration Gaussian method (dd-vMCG)⁴¹⁸ offers a variational and thus accurate solution for the equations of motion. Also full multiple spawning^45,401,419 can be regarded as fully quantum mechanically by describing the wave function with a number of time-dependent Gaussian functions that follow classical trajectories with quantum mechanically determined time-dependent coefficients. In its more affordable ab initio multiple spawning variant, more approximations are introduced such that the results sometimes draw near the classical solutions.^420,421 Further related methods exist, like the ab initio multiple cloning method,⁴²² or the thawed Gaussian approximation.⁴²³

Another class of dynamics methods are semiclassical approaches, which allow the inclusion of quantum effects in the classical dynamics of nuclei, such as quantum mechanical tunnelling or coherence.⁴²⁴ Note that these methods, where the nuclear dynamics is treated semiclassically, should not be confused with the MQCD approaches (see below) that are also often termed semiclassical (because the nuclei are treated classically and the electrons quantum-mechanically). The semiclassical dynamics methods range from the initial value representation,^425,426 adapted with the Zhu–Nakamura approach leading to the Zhu–Nakamura–Herman–Kluk initial value representation,⁴²⁷ to path integral approaches.⁴²⁸

The path integral formalism is especially interesting when the quantum and classical degrees of freedom should be coupled in a dynamically consistent manner. By using so-called ring-polymers, i.e., replica of the original classical system, a deviation of the nuclear dynamics from the classical path can be obtained, and the time evolution of a system including nuclear quantum effects can be investigated. However, ring-polymer dynamics suffer from high computational efforts as a consequence of the large number of replica required. Accelerated formalisms exist, which are for example implemented in the Python wrapper i-PI,^429,430 which allow interfacing path-integral methods with programs that provide PESs, but are mostly dedicated to the electronic ground state. To date, only a few implementations of semiclassical methods in atomistic simulation software are available. Compared to classical mechanics, the computational costs increase by a factor of about 10–100.^424,431,432

3.3.2. Mixed Quantum-Classical Molecular Dynamics

While semiclassical methods are promising to simulate the dynamics of molecular systems containing up to tens of atoms highly accurately, the study of larger systems is still dominated by computationally cheaper MQCD methods, where the nuclear motion is treated fully classically.^59,431−433 In contrast to quantum dynamics, the motion of the nuclei can be computed very fast using classical mechanics, and the computation of the PESs, on which the nuclei are assumed to move, remains the time limiting step. In this sense, ML models have a huge potential to enhance MQCD simulations by providing the electronic PESs and enabling the investigation of reactions that are not feasible with conventional approaches.^{15,175,434,435} In fact, most studies to date that describe photochemistry with ML aim to replace the quantum chemical calculation of the PESs in MQCD approaches.

The most popular MQCD method is trajectory surface hopping,^436−438 schematically represented in Figure 7b. A manifold of independent trajectories is required to obtain statistically relevant results and to mimic the extended nuclear wave functions. For a single trajectory, the nuclei move classically on one of the quantum potentials, and hence only one state is considered to be active, but transitions between different states are allowed.⁴³⁹

Different approaches exist to determine the probability of such a transition, also called hop or jump in surface hopping methods. To this aim, different quantities are needed that are commonly provided in the MCH basis, as it is the direct outcome of a quantum chemical simulation. One of the first implementations to compute the hopping probability is based on the Landau–Zener formalism.^440,441 On the basis of the Landau–Zener formula, the potential energy differences are used to determine the hopping probability. No information about couplings is required, which implies that the approach must fail for states that do not couple but lie close in energy. Very similar to this approach is the Zhu–Nakamura theory.^442−445 Also here, the computation of couplings is omitted, and only information about PESs is used. Among the mostly used hopping algorithm is Tully’s fewest switches algorithm,⁴³⁶ which is valid for many cases and based on the NACs between different PESs. An extension to other couplings is provided, e.g., in the surface hopping including arbitrary couplings (SHARC) method.²³⁶ When couplings are considered, an internal transformation from the MCH basis to the diagonal basis is most advantageous because the localized couplings of the diagonal picture precisely indicate where the few switches of the fewest switches approach should take place. In cases where the PESs are fit in advance, either with ML models or other types of analytical functions, the use of a diabatic basis is favorable (because of the Berry phase, see below), but should be transformed to the diagonal picture for the calculation of hopping probabilities. Other flavors to account for transitions exist. However, they have not been applied in simulations with ML algorithms yet. Interested readers are therefore referred to refs (47, 236, 256, 257, 332, 436, 443, and 446−450) for further information.

The bottleneck of approaches that require NACs is that the computation of the couplings remains one of the most expensive parts of a quantum chemical calculation. The computational effort to compute a NAC vector is comparable to that of a force calculation. However, more NACs are present than there are forces, i.e., N_S × (N_S – 1)/2 NACs need to be computed, whereas N_S forces are needed (respectively with entries for the Cartesian coordinates of each nucleus). Note that in the case of fitted PESs with ML, all of these vectors have to be computed for each data point. Conventional approaches with an ab initio on-the-fly evaluation of the PESs can make use of the fact that only one active state needs to be considered at a certain time step. Many MD programs therefore only require a computation of the forces of the active state and the respective couplings arising from this state.

Note that despite the benefits of MQCD simulations, they obey microreversibility only approximately,⁴⁵¹ and effects due to coherences or tunneling necessitate additional considerations as a consequence of the classical treatment of nuclear motion.⁴⁵²

A more approximate approach is the Ehrenfest dynamics method, also referred to as mean-field trajectory method. It is often used for large systems and also frequently in material science.^183,194 The Ehrenfest method is based on the approximation that nuclei move classically on an average potential, rather than switching from one specific state to another.^332,453,454 Because of the treatment of each electronic state separately, surface hopping methods allow the accurate bifurcation into different reaction channels, while such effects are neglected in a mean-field treatment of PESs.

The main limitation of MQCD approaches is the expensive evaluation of ab initio potentials, which allows dynamics simulations only for up to a couple of picoseconds. In addition, rare reaction channels are hardly explored as a result of usually bad statistics.^257,455,456 In this sense, MQCD simulations offer a perfect place for ML to enter this field of research and advance it significantly. The fast evaluation of the ML PESs can help to explore different reaction channels and to obtain accurate reaction kinetics. Observables and macroscopic properties can be computed directly or with postprocessing as well as analysis runs and offer another fulcrum for ML. The computed observables should then be directly compared to experiments.

3.4. Dipole Moments and Spectra

An important property for comparing experiment and theory is the dipole moment. The permanent dipole moment of the ground state is a frequent target of studies with ML.^{111,172,457−467} The permanent dipole moment, μ_i (or μ_ii), of a state i can be obtained via the dipole moment operator (see eq 13 below) or as the sum of partial charges, q_a,i of atom a in state i, and the vector that describes the distance of the position of atom a to the center of mass of the molecule, r_a^CM:

12

It can be used for the computation of infrared spectra with MD simulations. The spectrum is then obtained as the Fourier transform of the time autocorrelation function of the time derivative of the dipole moment.⁴⁶⁸

In contrast to the ground state, excited-state simulations often make use of the transition dipole moments, which are computed from the dipole moment operator within many quantum chemistry programs:

13

The ground state dipole moment can differ strongly from those in the excited states, due to a frequency shift and altered electron distribution upon light-excitation.⁴⁶⁹

Transition and permanent dipole moments are the target of some very recent studies, see refs (16, 94, 95, 97, and 241). Worth mentioning is the charge model of ref (111) originally proposed for the ground state and adapted by us for an arbitrary number of excited states,²⁴¹ where point charges are never learned directly, but instead are inferred as latent variables by an NN dipole model making use of r_α^CM.¹⁷² In this way, the rotational covariance can be preserved.

Noticeably, the computation of absolute values of permanent and transition dipole moments is very challenging even when highly accurate quantum chemistry methods are employed and experimental values are hardly reproduced.^95,470 However, also experimental studies provide absolute values only in a few cases. Most computational studies therefore do not aim to reproduce the absolute values of transition dipole moments but rather use relative values to obtain reasonably accurate absorption spectra, which can be compared to experiments.^{55,254,256,471−473} Since many molecules absorb in the UV, the terms UV spectra and absorption spectra are often used interchangeably. However, absorption can take place in many regions of the electromagnetic spectrum, including, e.g., X-rays, where rather core electrons than valence electrons are excited.⁴⁷⁴

As already mentioned shortly, absorption spectra can be obtained from a calculation of excited-state energies and oscillator strengths, which are proportional to the squared transition dipole moments. Noticeably, the transition dipole moment is only defined up to an arbitrary sign as a result of the arbitrary phase of the wave function (see section 5.3).^16,94 To circumvent this ill-definition, oscillator strengths or the lengths of dipole vectors can be fitted with ML. However, this workaround can be problematic if explicit field–dipole interactions should be considered with ML models, as the relative orientation of the field vector and the dipole vector can be important in this case. In theory, when computing UV/visible absorption spectra, the absorption related to a type of transition of one molecular geometry results in a delta function. However, in experiments lines are usually broadened due to the experimental technique and instrument used and because the molecules vibrate and collide with each other. Therefore, the computation of spectra requires the evaluation of transition properties of not only one conformation, but of many thousands. Wigner sampling⁴⁷⁵ or sampling via MD can help to achieve better agreement with experiment in the case of absorption spectra, but the line shapes due to different vibrational lifetimes can usually not be described. Therefore, the lines are broadened using Gaussian, Lorentzian, or Voigt functions, which can approximate effects due to Doppler broadening, broadening due to the uncertainty of the lifetimes of excited states, or a combination of these effects, respectively.^246,476

4. ML Models

Besides the reference method to compute the training set, which defines the highest possible accuracy an ML model can attain, the type of regressor and the descriptor to represent a molecule to the ML model also play important roles.⁴⁷⁷ Improper choices of regressors and descriptors can result in inaccurate ML models.

4.1. ML Models: Type of Regressor

Given the vast number of ML algorithms applied in the field of computational chemistry, one might ask which one to use or adapt for photochemistry. As recent studies applying ML for quantum chemistry have shown, many possible choices of ML approaches exist, and there is no single solution. Nevertheless, a trend can be observed: Many studies that use ML in the research field of quantum chemistry employ labeled data sets, i.e., supervised learning techniques. Within supervised learning, one can distinguish between regression and classification. Classification aims at finding patterns and at grouping data into certain clusters.⁴⁷⁸ Those types of ML models are often used, e.g., in spam filters, in medicine to diagnose diseases,^479,480 or in food research, e.g., to guarantee a certain wine quality or origin.⁴⁸¹ Examples of applied classification models in the field of computational chemistry are for example support vector machines, random forests, or decision trees used, e.g., to classify enzymes⁴⁸² or for the selection of an active space.^71,483

More often than classification models, regression models are applied to assist the search for a solution of a quantum chemical problem. Regression is used to fit functions that can relate a molecular input, X, to a quantum chemical output, Y. The simplest relation that can be assumed is linear. However, most quantum chemical problems cannot be accurately described with a linear function as given in eq 14. Linear regression is not seen as a universal approximator, while this quality has been proven, e.g., for NNs.^484,485 This is why we do not consider linear regression as an ML method in this review. Note that seemingly accurate fits can be achieved with linear regression when using more inputs (descriptors, features) than data points, but such an agreement rather resembles spurious correlation than real learning. Nonetheless, linear models are the foundation of many ML approaches and can serve as a baseline model to evaluate the minimum accuracy that an ML model should obtain.⁹⁴ In the linear relation,

14

the regression coefficients, also known as weights, w, and biases, b, are tailored for a given problem under investigation. Here, ordinary least-squares minimization can be applied to find these coefficients. The process of finding the optimal relation between X and Y is termed training. The coefficients are optimized by minimizing a so-called loss function, L, which monitors the error between the original property, Y^QC, and the predicted property by the ML model, Y^ML, with respect to the training instances. Most often, the L₁ loss or the L₂ loss is used as an indicator for the training convergence. The L₁ monitors the MAE and the L₂ loss the mean squared error (MSE) of predictions:

15

The Greek letter β runs over all molecules, N_M, inside the training set. In principle, any error estimate can be used to train an ML model and find suitable regression coefficients.

An example specifically developed for excited-state problems is the aforementioned phase-less loss (see section 5.3.2).¹⁵ Such adapted loss functions and also conventional ones are employed in different types of ML models. In the following, we focus on the two most widely used models for the description of the excited states: Kernel methods and NNs.

4.1.1. Kernel Methods

Kernel methods⁴⁸⁶ are based on a similarity measure between data points. Examples are KRR or GPR, which go beyond linear regression by applying the kernel trick and ridge regression. Ridge regression is used to find the weights, which differs from linear regression by a regularization term, λ:

16

Y^QC refers to the training data and K to the kernel matrix.

The kernel trick makes it possible to apply ridge regression to nonlinearly separable data by mapping them into a higher-dimensional feature space, in which the data points are linearly separable. Therefore, a kernel function, k, e.g., a Gaussian or Laplacian, is placed on each compound to measure the distance to all of the other compounds in the training set. The kernel function defines the nonlinearity of the model. A property of a query compound, α, can be obtained as the weighted sum of regression coefficients and kernel instances:

17

The size of the kernel matrix is dependent on the number of training points, and hence the depth of the model is inherently linked to the size of the training set, which is why they are called “nonparametric”.^478,487

An advantage of kernel methods is that they mainly contain two hyperparameters, i.e., internal model parameters, which need to be optimized for proper training. Most important are the width of the nonlinear kernel function, σ, and the regularization. The latter is used to prevent the model from overfitting—the case when the model fits training data including noise almost exactly and fails to accurately predict data points not included in the training set but stemming from an interpolative regime. As quantum chemical data are most often noise-free, the regularization term is usually small.

Especially for excited-state data, there are, however, systematic errors that can be seen as noise: Inconsistencies in potential energy curves along certain reaction coordinates are quite common and NACs are singular at crossing points of two PESs.¹⁷¹ In these cases, care should be taken in order to avoid overfitting. A powerful way to mitigate the problem of overfitting, e.g., for kernel methods, is, for instance, k-fold cross-validation.^478,488 Although kernel methods are generally said to be resistant to overfitting,^95,489 we shortly want to discuss k-fold cross validation here. By applying k-fold cross-validation, the whole data set is split into a training and test set. The test set is held back until the optimal hyperparameters are found and the remaining training set is split into k parts, which is most often 5 or 10. The kernel method is trained on k–1 parts of the training set, while the hyperparameters are optimized in order to minimize the error the model makes on the last part of the training set, i.e., the validation data in this case. The procedure is carried out k-times, and each time the validation data consist of another part of the training set. This procedure allows the optimization of hyperparameters without being biased by the error on the test set. In case data are sparse and expensive, k-fold cross-validation is a powerful technique to find optimal hyperparameters of an ML model without the need to compute massive amounts of additional data for validation and testing. The accuracy of the final ML model is then assessed by computing the error on the test set. This procedure is similarly valid for NNs, whereas overfitting is most often mitigated by applying an early stopping mechanism, which will be discussed in the context of NNs in the next paragraph.

As the optimization of hyperparameters is often a tedious task, kernel methods with their few hyperparameters are easier to use than, e.g., NNs with many hyperparameters. Nonetheless, kernel methods can provide almost exact solutions of problems under investigation.¹²⁷ A drawback is, however, that the inversion of the kernel matrix can become expensive and even be rendered infeasible on current computers due to increasing memory requirements with increasing training set size.⁹⁵

Further, kernel methods are usually defined to only map an input to a single output. Therefore, they can treat only one electronic state at a time in standard implementations and, thus, can be referred to as single-state models. A single-state treatment requires a separate ML model for each electronic state or for each property resulting of a pair of states, whereas a multistate ML model describes all electronic states and properties resulting from different pairs of states at once.^95,175 Hence, in their standard implementation, the treatment of several excited states necessitates the use of several kernel models, which is commonly done in the research field of quantum chemistry.^{139,140,149,490,491} The description of forces is possible for the ground state or a single excited state and is implemented, e.g., in the QML toolkit using KRR and the Faber–Christensen–Huang–Lilienfeld (FCHL) representation,⁴⁶⁶ in the symmetric gradient domain ML (sGDML)^122,122 method, with smooth overlaps of atomic positions (SOAP)⁴⁹² for GPR,¹²¹ or GAP¹⁰¹ originally developed for materials, but recently also applied for molecules, e.g., fluid methane.⁴⁹³

4.1.2. Neural Networks

Another prominent approach in ML is the use of NNs as highly flexible parametric functions, which can fit huge amounts of data and can map a molecular input to many quantum chemical outputs.⁹⁵ The simplest form of NNs is the multilayer feed-forward NNs, which are schematically represented in Figure 8.

Figure 8.

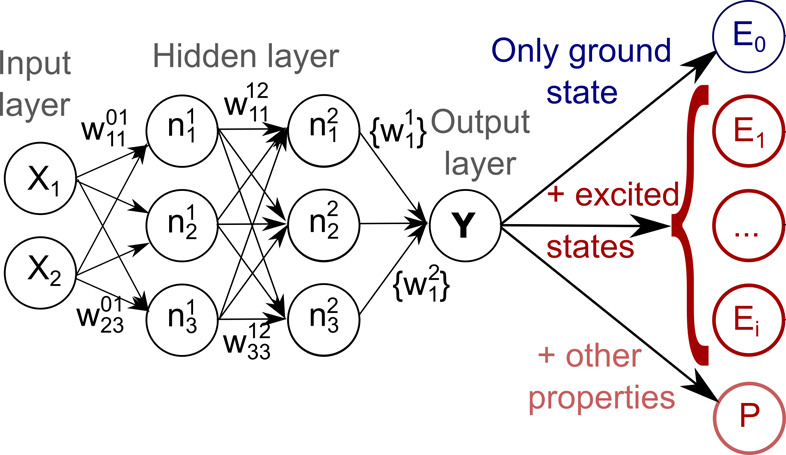
Schematic representation of a multilayer feed-forward NN with inputs, X, nodes, n, and outputs, Y. In the usual implementation for the fitting of PESs, the NN maps a molecular geometry to the ground state, which could be similarly done for any other single state. In the case a manifold of excited states is described, one molecular input can also be mapped to a vector of different excited states, and additionally, other properties can be included. The forces are treated as derivatives of the NN potentials with respect to Cartesian coordinates.

As it is visible in Figure 8, the width of the model is dependent on the number of nodes, n_r^t, which are connected to each other using weights, w_rs. The indices refer to a connection between node r and node s from layer t and layer u, respectively. The number of nodes and hidden layers can be chosen independently of the training set size.

Because of the highly flexible functional form of NNs, highly complex relationships can be fit, but an analytical solution to find the weights is not available (in contrast to KRR). A numerical solution can be obtained with stochastic gradient algorithms, which are frequently applied to obtain a stepwise update of the weights:

18

The gradient of the loss function as given in eq 15 with respect to the weights is multiplied with a so-called learning rate, l_r. This hyperparameter is deemed one of the most important hyperparameters used for training.^10,494 In order to obtain an optimal solution, the learning rate needs to be chosen properly. Algorithms such as AdaGrad⁴⁹⁵ or Adam⁴⁹⁶ can automatically adapt the learning rate during training. Further, the second-order derivatives can be included into algorithms, which is for instance done in the global extended Kalman filter,⁴⁹⁷ in its parallel variant,⁴⁹⁸ or the element-decoupled variant.¹⁰⁵ The loss function can be adapted so that more than only one property can be trained at once. This is often done to include the forces in the training process.

In general, NNs possess various hyperparameters like the learning rate, regularizers, number of nodes, etc. As a consequence, an extensive hyperparameter search complicates the use of NNs and makes them more complex to apply than kernel methods. One common hyperparameter optimization procedure is random grid search.^10,494 Therefore, the hyperparameters of the model are randomly shuffled, and ML models are trained using these parameters. After training, the errors on a validation set are compared to each other, and the hyperparameter space, which has to be explored, can be narrowed. This procedure is beneficial if it is repeated several times while narrowing the space of hyperparameters every time. As hyperparameter optimization is an optimization problem, algorithms, such as Bayesian optimization^499−502 have been designed for this task and are frequently applied for deep ML models and kernel methods. Because of the tedious procedure of manually tuning hyperparameters or the expert knowledge, which is required in most cases to find optimal hyperparameters, ML models have been designed which automatically learn optimal hyperparameters and only require little human intervention, see, e.g., refs (15,77, 461, 465, 503−508).

In addition, NNs are prone to overfitting. Therefore, during training, it can be beneficial to split the training data into two parts, typically in a ratio of 9:1, with the first part being directly used for training (i.e., adjusting the weights) and the second only for validation. In every training epoch, the error of the ML model on the training and validation data is compared. As soon as the error on the validation data increases, the training is stopped. This process is known as early stopping and is, besides drop-out or the comparison with less complex ML architectures, a powerful tool to prevent an NN from overfitting.^10,478

Besides simple multilayer feed-forward NNs, high-dimensional variants exist. These networks comprise several atomic NNs, which represent atoms in their chemical and structural environment and are thus also called atomistic NNs. Each local atomic contribution, E_a, can be summed up to provide the energy of the whole system, E, which is well-known to work for the ground-state PESs:

19

and was originally implemented by Behler to construct high-dimensional NN potentials.⁵⁰⁹ Embedded-atom NNs⁵⁰⁸ are similar to high-dimensional NNs in their way of constructing the energy of a system. They differ in the underlying descriptors to the ones of Behler. Atomic contributions to the energy are dependent on the embedded density of atoms and are summed up according to eq 19. These embedded density-like descriptors are approximated from atomic orbitals.

Independent of a simple or an atomistic architecture, the model can be used to fit a single output or a vector of many outputs at the same time. For ground state problems, a single-state model is usually used, which maps an input to a single output, e.g., the PES of the ground state. Oftentimes, this single-state fashion is adapted to fit different excited states with different NN models.^{16,141,204,510} However, it has been shown that including more excited-states in one model can be advantageous,⁹⁵ as the excited-states are inherently linked to each other and so are the excited-state properties.¹⁷⁸ Treating many excited states can be referred to as multistate model, and the inclusion of more properties can result in a multiproperty model.^{77,95,97,175,191} The different properties can be weighted with respect to their magnitudes or importance for a given chemical problem under investigation, such that the best possible accuracy can be obtained.¹⁵

Convolutional NNs represent another class of networks and are most often applied in image or speech recognition,^511−513 but can also be adapted to process a molecular input and identify an optimal molecular descriptor. This type of network can be combined in an end-to-end fashion with an architecture, which fits this generated molecular representation to a query output.^{461,465,503,507,514}

An important ingredient of all these ML models is the descriptor, which is mapped to the output. In most studies, the descriptor is one of many different possibilities to represent a molecule, which will be discussed in the next section.

4.2. Descriptors and Features

Electronic structure methods can process and uniquely identify molecules using, e.g., Cartesian coordinates. In contrast, such types of inputs are not optimal for ML models as the same molecular geometry, but translated or rotated, could only be mapped to the same output with great effort and unnecessary computational cost. Hence, a molecular descriptor should fulfill the following requirements: It should be translationally, rotationally, and permutationally invariant as well as differentiable.¹⁰⁴ It should also be unique with respect to the relative spatial arrangement of atoms, universally applicable for any kind of system, and computationally efficient.⁴⁷⁷ However, a descriptor can be more than that; it can already include a part of the mapping, e.g., from a molecular structure to an energy. It can thus ease the task of the regressor and help to attain the best possible accuracy for a given training set.

The ways to represent a molecule to an ML model can be classified roughly into two categories: molecule-wise descriptors, which represent the molecule as a whole to the ML model, and atom-wise descriptors, which represent atoms in their chemical and structural environment and build up a property using local contributions.^104,515 Both ways in describing a molecular system have their merits and pitfalls and will be discussed along with their applications in recent studies for the excited states in the following.

4.2.1. Molecule-wise Descriptors

The distance matrix is one of the simplest descriptors that preserves rotational and translational invariance. Most often it is used in its inverse form with distances between atoms a and b,

20

giving rise to the symmetric inverse distance matrix, D. Because of the ill-definition of diagonal elements, which are not differentiable, the diagonal elements are excluded, and only the upper or lower triangular matrix is used to represent a molecule to an ML model.⁴⁹¹ Since the Hamiltonian contains distances rather in the denominator, it makes sense to also use the matrix of inverse distances.⁹⁴ The matrix of inverse distances is very similar to the Coulomb Matrix, C:¹⁰²

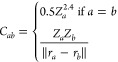21

but the Coulomb matrix additionally considers fixed point charges, Z, as employed in classic force fields. These types of descriptors are frequently used in ML studies for the excited states. For example, MLMD simulations in the excited states could be advanced using these simple descriptors^{94,95,139,140} and were also accurate enough to fit NNs and KRR models for excited-state properties.^{94,95,162,358,490,510} Distance based descriptors are further implemented in several program packages that have been used for photodynamics simulations with KRR. For example, MLAtom⁵¹⁶ contains the Coulomb Matrix and a representation that includes all nuclear pairs in form of normalized inverted internuclear distances.⁵¹⁷ The QML toolkit⁵¹⁸ includes the Coulomb matrix in addition to other representations, such as bag of bonds.⁵¹⁹ Another variant is polynomials formed from inverse distances.⁹⁴

These molecule-wise descriptors have the advantage of being easy to use and implement. Especially for small molecular systems and with regard to the training of an ML model, they are cheap. However, they might miss some important information based on angular distributions. Currently, it is also investigated whether representations based on two-body or three-body terms are accurate enough to uniquely identify a molecule.⁵²⁰

A problematic issue of the aforementioned types of distance-based molecular descriptors is that they are not permutationally invariant.^{104,175,514,515} This problem can be mitigated by data augmentation, i.e., randomly permutation of atoms by mixing of matrix rows, which results in more data points for the same molecular input. The additional amount of data increases rapidly with the system size and could lead to long training times.^514,515 Alternatively, another metric than the commonly used L₁ or L₂ norms can be employed, the so-called Wasserstein metric, which was tested with the Coulomb matrix.⁵²¹

Permutation invariant polynomials (PIPs), introduced by Bowman and co-workers,^522−524 are frequently applied in a PIP-NN approach by Yarkony, Guo, and co-workers to investigate ground state^412−414 and photochemical problems.^{143,144,147,392} The advantage of these polynomials is that they are invariant to permutation of atoms and inversion.¹⁴⁷ They comprise single-valued functions, p_ab, such as logarithmic or Morse-like functions, which incorporate internuclear distances, r_ab. The PIP vector, G, is obtained applying a symmetrization operator, Ŝ, accounting for possible permutation operations:

22

with an example of p_ab:

23

Evidently, additional hyperparameters such as c have to be optimized, and the choice of PIPs is generally not unique.^413,525 It is worth mentioning that the internuclear distances are redundant for molecules with more than four atoms, but this redundancy does not affect the description of the PES.

Some studies suggest that molecule-wise descriptors might be superior to atom-wise descriptors as the bonds are possibly better represented by internuclear distances.^95,158,175 A negative aspect of molecule-wise descriptors is, however, that they can only treat one molecular system, because the input size is fixed. The input dimension could, in principle, be defined according to the largest system included in the training set, but this would lead to unnecessarily large input vectors for smaller systems, which would then contain many zero values.^509,514 The training of more ML models, each for one specific system size, is one possible solution,¹⁶² but obviously necessitates the training and evaluation of more than one ML model.

Atom-wise Descriptors

In contrast, atom-wise representations allow for a fitting of molecules of arbitrary size and composition. Such descriptors are state-of-the-art for ground-state problems. The main principle for the design of atom-wise descriptors is to fit a reference property as the sum of atomic contributions, as given in eq 19 for the molecular energy of a system. The molecule is thus split into atoms, which are represented in their chemical and structural local environment. Usually, these types of descriptors rely on a cutoff function, which defines the sphere around an atom, which is deemed to be important and is therefore considered when modeling the atomic local environment. Commonly used examples are the SOAP,⁴⁹² atom-centered symmetry functions (ACSF),⁵⁰⁹ weighted ACSFs,^526,527 embedded-atom density-like descriptors,⁵⁰⁸ moment tensor potentials,⁵²⁸ spectral neighbor analysis potentials (SNAPs),⁵²⁹ or the FCHL representation.^127,530 Interatomic distance between atoms is considered very important for the design of the descriptor and is most often included in representations in the form of radial distribution functions, so-called two-body terms. They are often used together with angular distribution functions, i.e., three-body terms. It is further beneficial to include one-body terms, i.e., the element types of atoms and hence the stoichiometry.^{127,461,526,527} Most often, higher order terms than three-body terms are not included due to increasing costs and little improvements in accuracy.⁵¹⁴ Lately, some models have emerged, which take the embedded electron density⁵⁰⁸ or interactions of pairs of atoms^77,80 into account. To allow a scalable and accurate representation of larger molecules, geometric moments could further serve the construction of descriptors. They have been formulated using pairwise distance vectors.⁵³¹

Much effort is further devoted to reduce the costs of the descriptors. For instance, weighted ACSFs,^526,527 embedded-atom density-like,⁵⁰⁸ moment tensor,⁵²⁸ and descriptors used for SNAPs⁵²⁹ reduce the amount of many-body terms. Especially tantalizing is the reduction of the sum over many-body terms into a product of two-body terms in the last three mentioned descriptors. Very recently, Zhang and Jiang propose so-called piecewise switching function based descriptors⁵³² for embedded-atom NNs, which scale linearly with the number of neighboring atoms.

The description of PESs from atomic contributions is beneficial in order to treat systems of arbitrary sizes and to use systematic molecular fragmentation methods.¹⁰⁹ Admittedly, the validity of this approach is not so clear for the excited-states, and consequently, such representations are less frequently used in ML studies targeting the excited states. To date, only small molecules have been fitted with atom-wise representations, which are too small to prove the validity of excited-state PESs, which are constructed from local atomic contributions. To the best of our knowledge, the largest molecule fitted with atom-wise descriptors contained 12 atoms and was N-methylacetamide.⁹⁷ Other molecules were CH₂NH₂⁺,^15,95 CH₂NH,¹⁴¹ SO₂,¹⁵ or CSH₂.¹⁵ Further studies are needed to demonstrate whether an atom-wise construction of excited-state properties and PESs is possible or not. Nevertheless, this approach is most powerful for studies that aim to describe large and complex systems, which could potentially be described from smaller building blocks. For instance, the construction of a DNA double strand or a peptide could be, at least in principle, constructed from ML models that are trained on their smaller subsystems, i.e., DNA bases and amino acids, respectively. Unfortunately, we are far away from having achieved a description of large molecular systems for the excited states, let alone the construction of accurate PESs of medium-sized molecular systems, such as DNA bases or amino acids.

Other Types of Descriptors

Besides the benefits that high-dimensional ML models offer for the fitting of PESs of molecules, descriptors are not restricted to the aforementioned examples. In general, any type of descriptor might be suitable for a given problem. Applied descriptors range from topological and binary features generated from SMILES strings⁵³³ to normal modes, which are often used as a coordinate system and descriptors to fit diabatic PESs (refs (16, 99, 136, 143, 145, 145−147, 149, 392, 534)). Other types of molecular features besides structure-based ones, e.g., electronegativity, bond-order, oxidation states, ...,^17,71 are also used.

Automatically Generated Descriptors

The selection of an optimal descriptor and the optimization of the related parameters for this descriptor are not trivial tasks and require expert knowledge in many cases.⁵¹⁴ A way to circumvent an extensive parameter search is offered by the aforementioned message passing NNs,⁵⁰³ which include the descriptor parameters in the network architecture. In this way, they automatically fit the optimal parameters of a descriptor for a given problem, i.e., training set under investigation. Such tailored descriptors can guarantee highly accurate solutions if the NN model is trained properly. PhysNet,⁵⁰⁴ HIP-NN,⁵⁰⁵ DeepMD,⁵⁰⁶ or Deep Tensor NN (DTNN),⁵⁰⁷ which forms the basis of the deep learning model SchNet,^461,465 which in turn is used within the SchNarc approach for excited states,¹⁵ are examples of such NNs.

5. Data Sets for Excited States

The basis of any successful ML model is a comprehensive and accurate training set that can describe the required conformational space of a molecule comprehensively and accurately with as little noise as possible.⁵³⁵ While electronic structure theory for ground state problems is almost free of noise, the same cannot be said so easily for problems in the excited states. “Bad points with abrupt changes”¹⁶ within ab initio calculations for the excited states are frequently observed, which can occur even far away from any critical point of the PESs and are difficult to detect.^15,16,94 The amount of noise in the reference data depends not only on the chosen method (and in the case of multireference methods on the selected active space), but also on the number of electronic states considered and the photochemistry of the molecule under investigation.

5.1. Choosing the Right Reference Method for Excited-State Data

Many existing training sets for ML in quantum chemistry are based on DFT.^{103,105,112,526,536−538} The ease of use and low computational costs of DFT-based methods make them suitable to treat large systems with acceptable accuracy. In fact, DFT is the workhorse of many studies solving ground-state problems. In contrast, TDDFT has not yet managed to equal DFT for the treatment of excited-state problems. Consequently, training sets for the excited states are less frequently computed with TDDFT^{93,97,98,162,358,539} and rely most often on multireference methods. Examples of applied methods are CASSCF^{15,139−141,145,146,149,160} or MR-CI schemes,^{14−16,92,94−96,142,144,540−545} where the latter method is more expensive than the former and therefore limited to describe small systems.

In general, the computation of excited-state PESs is much more expensive than the computation of the ground state potential of the same molecule. Not only highly accurate ab initio methods have to be applied for many systems, but also forces and couplings are required for the considered states. A high density of electronic states present in a molecular system can thus increase the costs of a calculation considerably. In this regard, an active, efficient, and meaningful training set generation is indispensable, especially when photodynamics simulations are the target of a study.

Keeping in mind that the quality of the reference data confines the quality of an ML model, several key questions can be identified when designing a study based on ML potentials. We believe the following questions to be important for the selection of a suitable reference method:

• (1)What is the goal of an ML model, and what properties must it predict in order to benefit from the advantages that ML can offer? Are only energy gaps of different electronic states to the electronic ground state necessary, or are gaps between other states and couplings between them also relevant? Especially, the description of couplings requires further consideration, as they cannot be calculated with all quantum chemistry methods and additionally face the problem of random sign jumps along different reaction coordinates.^92,94,546
• (2)How many excited states are relevant, and which method is computationally affordable to treat the amount of states required? A comparison with experiment and the computation of vertical excitation spectra with reference methods can help to obtain an answer to this question.
• (3)How large is the system under investigation, and how complex are the excited state processes that are considered to be important? This question is important in order to identify whether single reference methods such as LR-TDDFT or ADC(2) make sense for certain reactions that might occur. While large and flexible molecules with a lot of energetically close-lying states can give rise to a multifaceted photochemistry including dissociation, homolytic bond-breaking, and bond-formation, the dynamics of rigid molecules might only be dominated by one main reaction channel and lose the additional energy in the form of molecular vibrations. The complexity of the excited-state processes can help to estimate the number of necessary data points to describe the relevant configurational space of the molecule.

In case multireference methods are necessary to describe many different excited-state processes of a molecule, the training set generation can become unfeasible. For example, 356 data points were computed for the 15-atom cyclopentoxy molecule with MR-CISD(5,3)/cc-pVD(T)Z.⁹⁶ Respective calculations comprised 19,302,445 configuration state functions, and one reaction coordinate could be fitted in the diabatic basis. We also ran into a similar problem when fitting the excited states of the amino acid tyrosine containing 24 atoms, which also requires a multireference treatment. The size of the active space and the number of states needed for an accurate description made multireference methods such as CASSCF or CASPT2 computationally too expensive; see Figure 5. In these cases, the computation of an ample training set is far too expensive with multireference methods, and the quantum chemistry calculations remain the bottleneck even when using ML.

In addition to the aforementioned intricacies to build up a meaningful, yet accurate training set for the excited states, the process is further complicated by the arbitrary phase of the wave function. As a consequence, excited-state properties resulting from two different electronic states, such as transition dipole moments or couplings between different electronic states,^{15,16,92,94,95,546} are not uniquely defined and cannot simply be fitted with conventional ML models. Either an additional data preprocessing, termed phase correction, or an adaption of the learning algorithm has to be incorporated to render data learnable with ML models. Details on how to correct these data in advance or during training will be discussed in section 5.3. The subsequent discussion will be dedicated to the training set generation and common training sets applied to date.

5.2. Training Set Generation

The requirements and desirable specifications for a training set can vary strongly, dependent on the type of application: When the focus of a study is the investigation of the huge chemical space and the search for certain patterns thereof or the design of new molecules with targeted properties, usually the training set should be as large as possible to cover as many molecules as possible. In the best case, the data points are computed with high accuracy, and this reference method is accurate for the excited states of many different types of systems. In terms of accuracy and general applicability, ab initio methods are more suitable, as they do not require the selection of a density functional, which might be accurate for some cases, but fail for others. However, the costs and complexity of highly accurate multireference ab initio methods limit their applicability, so that TDDFT remains the method of choice when making predictions throughout the chemical compound space.^152,358,547

The problems of TDDFT have been discussed very recently by Thawani et al.⁵⁴⁸ The authors developed a data set for relevant photoswitches, which are useful, e.g., for medical applications or renewable energy technologies. To this aim, photochemical properties of azobenzenes and associated derivatives were manually extracted from experimental papers. The ππ* and nπ* transitions turned out to be key to accurately describe a molecule with photoswitching activity. Different ML models were subsequently trained using different types of descriptors to fingerprint these compounds. Comparable accuracy to TDDFT could be achieved as well as superior performance to human chemists in predicting these transitions. This work highlights very well how data sets can be generated from experiments and provides a practical, useful tool for chemists not versed in TDDFT.

Besides this data set based on experimental data, the most widely applied approach to generate a training set for screening purposes or for the exploration of chemical compound space is to start from an existing (ground-state) database that already covers a large chemical space of certain types of molecules. In this way, not much effort has to be devoted into the exploration of chemical space and structure optimizations to get the most stable conformations of different molecules.

For the purpose of ML-based excited-state dynamics simulations, things look quite different. Note that for photodynamics simulations, only molecule-specific ML models exist until now, which can potentially develop into a universal excited-state force field, but much remains to be done to achieve this goal. Indeed, the generalization of the excited state PESs and corresponding couplings is expected to be a highly complex task, especially due to the problematic generalization of excited states.⁹⁴ A comparison of the isoelectronic molecules CH₂NH₂⁺ and C₂H₄ can serve as an example. Their conical intersection between the first excited singlet state and the ground state is accompanied by a rotation along the dihedral angle, which could lead to very similar photoinitiated processes. However, higher-lying excited states are ordered completely different in both molecules and excitation leads to completely different photodynamics.^{28,94,549−558} Particularly promising in order to achieve the goal of an excited-state ML force field is the construction of excited-state potentials from atom-wise contributions, i.e., an ML model which learns the surrounding of an atom rather than the molecule as its whole. Promising models are multilayer energy-based fragment methods similar to ref (536) in combination with high-dimensional NNs⁵⁰⁹ and density-like descriptors,⁵⁰⁸ or automatically learned descriptors based on geometric information.^461,528,529 Especially, ML for wave functions like the SchNOrb model^77,80 could be helpful in this regard and are further interesting for dynamics simulations to compute wave function overlaps from ML. Further, it is important to encode the charge of the molecule in order to treat molecules of same composition, but different electronic charges. However, as it stands, existing ML models for photodynamics simulations are developed to investigate the photoinitiated processes of one specific molecule, which is why we focus on this goal in the following discussion.

Overall, we arrive at the following wish list for the training set, which has been identified also for MD in the ground state:^{103,117,515,559} (1) The training set should be as small as possible to keep the number of reference calculations at a minimum. (2) At the same time, the relevant conformational space of the molecule that is required for the reaction under investigation should be sampled comprehensively.^{94,117,359,515,535}

Keeping this in mind, an efficient procedure to obtain relevant molecular structures has to be applied. A large number of schemes to achieve this goal have been proposed, which are mainly based on two different strategies: One approach is to simulate MD in the ground and excited states with the reference method and putting much effort into covering critical regions of the PESs comprehensively.^139−141 Structure-based sampling or subsequent clustering is beneficial in this case.^{139,140,517,560,561} The other strategy is to use an active learning approach, which decreases the number of necessary reference calculations considerably, but is usually more time-consuming.⁵¹⁵ Noticeable, within ML for quantum chemistry, active learning often refers to an approach, where an initial training set is used to fit an ML model, and this previously learned information is applied to expand the training set.⁴³⁵ The latter approach is often carried out with the help of MD simulations. Simulation of many trajectories on-the-fly and estimation of the reliability of the ML-fitted PESs at each time step are powerful to identify under-sampled or unknown regions of the PESs. Retraining of the ML models as a data point is added to the training set is required, which makes such a procedure generally expensive. Recently, this active learning procedure has also been adapted in a trajectory-free way,^435,562 which can reduce the costs for the training set generation considerably. The different strategies to generate an ample training set for the excited states will be discussed in the following.

5.2.1. Basic Sampling Techniques and Existing Databases

To find patterns within certain groups of molecules, to explore chemical space, and to develop new methods that can fit for example different properties of molecules, such as the valence density used in DFT,⁸² or large molecules from small building blocks,¹⁰⁹ a good starting point is often considered to be an already existing database. Prominent examples are the QM databases, namely, QM7, QM7b, QM8, and QM9,⁴⁵⁷ which have been used in a large number of publications to date and provide a benchmark for many ML studies.^{14,152,461,466,467,526,530,563−565} Especially the QM9⁴⁵⁷ data set containing more than 133k small organic molecular structures and corresponding DFT energies, enthalpies, harmonic frequencies, and dipole moments (to name only a few properties) is very popular among the scientific community and has also been used in challenges on kaggle, where researchers and laypersons all over the world can compete against each other to find the most suitable solution to a given task. Prices up to several thousand dollars are quite common.⁵⁶⁶ In a similar spirit, the QM9 IPAM ML 2016 challenge requires predicting the energies of QM9 from only 100 training points within chemical accuracy (error of ∼0.05 eV).⁵⁶⁷

All aforementioned databases originate from GDB databases^568−570 and are often a subset thereof. The chemical universe GDB databases have been designed using molecular graphs to sample a comprehensive space of molecular structures for the search of new lead compounds in drug design.⁵⁷⁰

One of the first databases available for the scientific community to treat the excited states of molecules is most probably the QM7b⁵⁷¹ data set, which contains the excitation energies computed with TDDFT for a total amount of >14k molecules with atoms C, N, O, H, S, and Cl. This data set is based on the molecular geometries of the QM7^102,570 data set plus an additional amount of 7211 molecules containing a chlorine atom. The excitation energies of the first singlet state and other properties were recomputed for each optimized molecular geometry. Very similar, the QM8³⁵⁸ database was developed, based on the GDB-17 database.⁵⁷² This data set can be used for the computation of vertical excitation spectra. It hence includes not only the vertical excitation energies of the first excited singlet state, but also the corresponding oscillator strengths. Oscillator strengths are also reported in an autogenerated data set for optoelectronic materials with DFT.⁵⁴⁷ Note that the oscillator strength is computed from the squared transition dipole moment, and hence an arbitrary phase factor cancels out and the data does not have to be preprocessed. In addition to the TDDFT energies, CCSD energies are reported, having enabled the development of the so-called Δ-learning approach—a powerful way to obtain the accuracy of highly accurate ab initio methods with only a small amount of respective reference calculations. Two ML models are trained in this approach, one on a less accurate method and another one on the difference between the less accurate and higher sophisticated method.⁵⁷³ This scheme can also be applied multiple times to achieve increasing accuracy with little additional computational effort³⁵⁹ and has been adapted for spectroscopy in the condensed phase as well.¹⁵³

The QM9 data set has further been the basis of a very recently constructed data set for singlet and triplet states of >13k carbene structures, termed QMspin.¹⁴ A total of 4000 geometries from the QM9 data set were randomly selected, hydrogen atoms were subtracted, and singlet and triplet states were optimized using CASSCF(2,2)/cc-pVDZ-F12 and open-shell restricted KS-DFT with the B3LYP^574,575 functional, respectively. The MR-CI method was subsequently used to compute the electronic energies of singlet and triplet states. This data set has been used to investigate structural and electronic relationships in carbenes, which are important intermediates in many organic reaction networks.¹⁴

The OE62⁵⁷⁶ database, a benchmark data set applicable for spectroscopy, is another descent of several existing data sets, such as the QM8 and QM9 data sets. It consists of >61k organic molecules able to form crystals including up to 174 non-hydrogen atoms. Reported are the orbital energies of molecules computed with DFT/PBE.⁵⁷⁷

Another database, which also contains excited state data, is the PubChemQC database.⁵⁷⁸ It contains over three million molecules, whose structures are reported along with the energies at DFT/B3LYP/6-31G* level of theory. In addition, the excitation energies of at least three million structures are reported for the 10 energetically lowest-lying singlet states at TDDFT/B3LYP/6-31G* level of theory.

A simple strategy was carried out by Kolb et al.,⁵⁷⁹ who used an existing analytical PES to create an ML potential: They randomly sampled data points, trained an ML model, and added more points in regions with deviations from the original PES. Other strategies have been carried out mainly for the fitting of ground state potentials and for materials which are however also relevant to consider for the excited states. One novel, suitable strategy is for example “de novo exploration” of PESs using a similarity measure provided by ML models.⁵⁸⁰ At least for material discovery, this method can be used to omit any additional active learning procedure to converge PESs. Similar strategies are ab initio random structure searching (AIRSS),⁵⁸¹ particle swarm optimization with the CALYPSO method,⁵⁸² or USPEX, an evolutionary algorithm.⁵⁸³ The latter methods are used in the condensed phase and for inorganic systems mainly, but can be adapted for the search of molecular structure, and the desire to compute as few reference data points as possible is also relevant in this case.

A different approach to build a training set is to employ molecule-generating ML models,^165,584,585 such as the recently developed Gschnet.⁵⁸⁶ Alternatively, MD simulations with the reference method can provide a good starting point for training.^122,507,563 For example, Ye et al.⁵¹⁰ sampled 70k conformations for N-methylacetamide via MD simulations with the OPLS force field⁵⁸⁷ within GROMACS⁵⁸⁸ for subsequent UV spectra calculations. We have applied a similar scheme to generate a training set of SO₂ based on an LVC model.²⁴⁰ Surface hopping MD simulations with the SHARC method^236,256,589 were carried out with the reference method LVC(MR-CISD) ending up with >200k data points of different conformations of SO₂.¹⁵ Because of the crude sampling and low cost of the reference method, no emphasis was put on clustering the training set into a smaller, still comprehensive set.

A total of 90k data points were required in an ML-based surface hopping study of CH₂NH with the Zhu-Nakamura method. Reference data for the ground and first excited singlet state, S₀ and S₁, were generated with CASSCF(2,2)/6-31G via ground-state and surface hopping MD simulations. The latter method was applied to sample the regions around conical intersections between the S₀ and S₁ state.¹⁴¹

Similarly, Hu et al.¹³⁹ sampled 200k data points of 6-aminopyrimidine using ground-state and surface hopping MD with CASSCF(10,8)/6-31G*. State-averaging over three singlet states was applied. In addition, structures that led to hops between different states were used as starting points to find minimum energy conical intersections, and clustering was carried out to reduce the amount of data for training.

One way to select data points more efficiently is a structure-based sampling scheme, as proposed for instance by Ceriotti et al. with sketch map,^560,590,591 an algorithm for dimensionality reduction of atomistic MD simulations or enhanced sampling simulations. Likewise, Dral et al.¹⁴⁰ applied a grid-based sampling method to construct PESs of a model spin-boson Hamiltonian to execute surface hopping MD with KRR. The energetically low-lying regions of the PESs were first sampled via an inexpensive method, and subsequently the distances between the molecular structures were computed. In this way, 10 000 data points were obtained.^140,517 ML models trained on only 1000 data points were accurate enough to reproduce reference dynamics. This approach was compared with random sampling for the methyl chloride molecule and was shown to reduce the amount of training data needed up to 90% for static calculations.^517,561

Another technique to explore PESs, which is frequently applied for the electronic ground state, is geometry optimization. In the past few years, effort has been devoted toward acceleration of the optimization with ML; see e.g. refs.^592−597 Most often, single-state ML models, which are mainly based on GPR, are employed to optimize minima, transition states, minimum energy paths, and many more. Very recently, Raggi et al.⁵⁹⁷ used internal coordinates and variance-restriction instead of commonly applied Cartesian coordinates in combination with a step restriction. The use of internal coordinates removes transitional and rotational variance and allows for different length scales. The variance measure can be directly obtained from GPR models to restrict the step in the geometry optimization process. The latter enables an exploration of large geometry displacements in some cases, i.e., dependent on the acceptable variance.

5.2.2. Active Learning

As shown in the previous section, training sets with the respective equilibrium structure of a large number of molecules are very powerful for investigating the huge chemical space or for the design of new molecules. However, the usefulness of such training sets for photodynamics is rather questionable. The reason for this deficiency is that, especially in MD simulations in the excited states, the excess of energy carried by a molecule very quickly leads to conformations that are far beyond the equilibrium structure and most likely far away from originally sampled structures. The formation and breaking of bonds is quite common in photodynamics simulations and is usually only accessible from an excited, dissociative state. The use of photodynamics simulations with the reference method could solve this problem, but is not feasible if specific reactions occur on a rather slow time scale or if many different processes take place.^{59,171,175,178,257,367} As previous studies have shown, inefficient sampling techniques lead to a huge amount of data, which still does not guarantee that the training set is comprehensive enough for excited-state MLMD simulations. In fact, ML models fail dramatically in undersampled and extrapolative regions of the PESs. A smarter sampling technique is advantageous in these cases in order to efficiently identify such undersampled regions and build trustworthy ML models.

Active learning, where ML “asks” for its training data, is one solution to create a data set more efficiently. An example from chemistry is the adaption of an initially generated training set due to an uncertainty measure for ML models trained on this initial training set. This concept has already been introduced in 1992 as query by committee⁵⁹⁸ and has been adapted for quantum chemistry quite fast due to the required fitting and interpolation of PESs for grid-based quantum dynamics simulations. Pioneering works by Collins and co-workers^{150,151,408,599} applied modified Shepard interpolation to fit PESs and iteratively adapt them in out-of-confidence regions using the GROW algorithm.^599,600 The first version similar to query by committee for the fitting of NNs was proposed by Artrith and Behler.⁶⁰¹ Since then, several sampling techniques have been developed that are based on MD and an extension of databases using interpolation moving least-squares,^602,603 permutation invariant polynomial fitting,^522,524 and different ML models for the ground state^{101,103,111,508,515,559,604−616} and also excited states.^15,94,140

As active learning starts from already trained ML models, an initial training set has to be provided. Some strategies to provide this initial reference data set will be discussed, following strategies applied to adapt this initial training set. Note that all previously discussed methods can be similarly applied to generate an initial training set. Although we cannot give a general guide on how large a training set should be, in our cases, it was beneficial to cover approximately one-fourth of the training set with data obtained from initial sampling and the rest with data obtained from active learning techniques. About 300–400 data points per degree of freedom of a molecule turned out to be sufficient at least for small molecules.

Initial Training Set

In general, an initial training set can be obtained in many different ways. As photoinitiated MD simulations usually start from vertical excitation of the ground state equilibrium geometry, this structure is commonly used as the starting point and reference geometry for the training set generation. In principle, any technique can be applied to then add conformations to obtain a preliminary training set. A good starting guess is to use normal modes of a molecule, as they are generally important for dynamics. In two recent works, we carried out scans along different normal modes and combinations thereof to sample conformations of small molecules.^15,94 Normal modes were also sampled for generating ANI-1 NN PESs.¹¹⁵ For the excited states, it is generally favorable to include critical regions of the molecule in the initial training set by carrying out optimization of these geometries and including the calculations into the training set.^94,139

When small molecules are targeted, this initial training set can already be comprehensive to start the training of ML models and adapt the training set based on an uncertainty measure provided by the ML models.⁹⁴ In case more flexible and larger molecules are studied that give rise to a complex photochemistry and a high density of states including different spin multiplicities, a small initial training set might not be sufficient, and a larger conformational space of the molecule needs to be sampled. This can be done for example via Wigner sampling⁴⁷⁵ and also with MD simulations in the ground state.^617,618 Suitable methods are for example umbrella sampling,⁶¹⁹ trajectory-guided sampling,⁶²⁰ enhanced sampling,⁶²¹ or metadynamics⁶²² in combination with a cheap electronic structure method such as the semiempirical tight-binding based quantum chemistry method GFN2-xTB⁶²³ or existing ground-state force fields. A large amount of different geometries can be created very fast and inexpensively, which then can be clustered to exclude similar conformations of the molecule to keep the number of reference simulations at a minimum. The selected data points for the training set can then be computed with the chosen reference method, whose accuracy is targeted with ML. Additionally, if certain reaction coordinates have been shown to be important in experiments or previous studies, then it is favorable to include data from scans along these reaction coordinates.^96,175

As soon as meaningful ML models can be obtained from the initial training set, active learning techniques can be applied to enlarge the set. What number of data points turns out to be sufficient for the initial training set is dependent on a lot of different factors, such as the size and flexibility of the molecule under investigation, the number of excited electronic states described, and the ML model and descriptor applied.^94,95 In order to give a ballpark figure, we note that we used approximately 1000 data points as initial training set for small molecules in recent studies using deep multilayer feed-forward NNs.^15,94

Strategies for Actively Expanding the Training Set

The next step in active learning is to expand the initial training set by adding points from out-of-confidence regions. The detection of these undersampled regions can be done in many different ways, whereby most approaches rely on MD simulations.

Among the most popular strategies is the iterative sampling scheme of Behler,⁵¹⁵ originally developed for fitting ground-state PESs. Today, it is widely used, see for example refs,^103,559,624 and has been modified as a so-called adaptive sampling approach.¹¹¹ The latter has been adapted by us for the generation of a training set for the excited state PESs of molecules including couplings.⁹⁴ The basis of almost any iterative or adaptive sampling scheme is a similarity measure to judge whether a molecular geometry can be predicted reliably with ML models or not. While kernel methods intrinsically provide a measure of similarity for each molecular geometry, NNs do not. Therefore, adaptive sampling with NNs requires at least two ML models. In the case of KRR or GPR, two ML models can be used as well, but are not necessarily needed. Indeed, the statistical uncertainty estimate of the predictions remains a huge advantage of GPR models.^525,535,625 As a remark, from a materials’ perspective, Gaussian approximation potentials (GAPs) can be used as a similarly useful tool to provide such an uncertainty measure.^121,626

The adaptive sampling scheme for the excited states is illustrated in Figure 9 and exemplified with two ML models. The whole process starts with an initial training set, which is used to train the two (or more) preliminary ML models. These models differ in their initial weights or model parameters. The resulting dissimilar ML architectures guarantee that the ML models do not predict the exact same number for a given molecular input. The hypothesis underlying this scheme is that inferences of different ML models trained on the same training set will be similar to each other as long as an interpolative regime is given. The inferences of the ML models are inaccurate and should differ from each other to a much larger extent if a molecular input lies in an unknown or undersampled region of the PESs.

Figure 9.

Adaptive sampling scheme illustrated using two ML models (blue and red blocks). The active learning procedure starts from an initial, preliminary training set (yellow), which is used to train ML models. A sampling step, e.g., a time step of an MD simulation, is executed: The ML models take the molecular geometry of the sampling step as an input and predict the energies of the considered excited states, their derivatives, and additional required photochemical properties. In case the predictions of the ML models are deemed to be different, quantum chemical reference calculations are carried out, ML models are retrained, and the serial steps are carried out again. This procedure is executed until the desired quality of the ML PESs is attained in order to sufficiently describe the chemical problem under investigation.

In order to find such regions, sampling steps are carried out, e.g., by running (excited-state) MD simulations based on the mean of the inferences made by the different ML models for energies, E̅^ML, forces, F̅^ML, and if required also couplings, . In each sampling step, the variances for each predicted property are computed. In the present example, energies and forces are treated together as σ_E + F^ML (but can also be used separately), separately from variance of the couplings σ_C. If a variance exceeds a predefined threshold, the ML models diverge, and the predictions are deemed untrustworthy. N_ML refers to the number of different ML models, ζ, used for adaptive sampling:

24

25

Note that the variance is averaged over all states for energies and forces and over all pairs of states for couplings, that are described with the ML models. As a variant, each state could also be treated separately. However, as the different electronic states are not independent of each other, a mean-treatment is assumed to be advantageous.⁹⁵

Each data point that is predicted with a variance larger than the predefined threshold for a given property, is recomputed with the reference quantum chemistry method and added to the training set. In this way, under-sampled or generally unknown regions of the PESs are identified. Whenever the variance of each property is within the range that is thought to be reliable, the mean of the inferences is forwarded to the MD program to propagate the nuclei and continue MLMD simulations. The name adaptive sampling is based on the recommendation to choose a rather large threshold in the beginning of the adaptive sampling procedure and to adapt this threshold to smaller values as the ML models become more accurate and robust.¹¹¹ A first estimate for the initial value of a threshold can be obtained from the mean absolute error (MAE) of the corresponding ML model on the initial training set.

In principle, adaptive sampling can be carried out for every property, that should be represented with ML potentials, and is not restricted to energies, forces, and couplings. Similarly, it does not need to be executed with excited-state dynamics, but could also be done with ground-state MD or any sampling method that is considered to be suitable.

As a negative side effect, this procedure is generally more time-consuming than many other sampling techniques because ML models have to be trained each time a new data point is added to the training set. To apply adaptive sampling in a more efficient way, it is advantageous to execute not only one ML trajectory, but many hundred trajectories in parallel, as it is usually done in MD simulations. The ML models should then only be retrained, when all ML-based trajectories have reached an undersampled conformational region.^94,111,515 Despite the higher complexity of adaptive sampling compared to random sampling, it can reduce the number of required data points for MLMD simulations substantially. In this regard, also the computational costs for the training set generation can be kept at a minimum.

Adaptive sampling was carried out successfully to generate a training set of 4000 data points of CH₂NH₂⁺ containing three singlet states and couplings. ML-based surface hopping MD simulation could be carried out on long time scales using the average of two deep NNs. The concept of iterative sampling also proved beneficial for the long MD simulation to guarantee accurate ML potentials throughout the production run. Here, the threshold was not adapted anymore, and the MD was continued from the current geometry after a training cycle was completed.⁹⁴ In addition, the average of more NNs turned out to be more accurate than the prediction of only one NN, which was also shown in ref (111).

Another quality control besides the property-based one proposed by Behler can be obtained by comparing the molecular structures at each time step as done by Dral et al.^140,517 and Ceriotti et al.⁵⁶⁰ A combination of a structure-based and property-based detection of sparsely sampled regions of the PESs has been done by Zhang et al. and Guo et al.^{392,607,627−629} Very recently, an alternative approach has been applied with NNs by Lin et al.⁴³⁵ that does not require MD simulations. It is based on the finding that the negative of the squared difference surface obtained from NNs approaches zero in regions, where no data points are available.⁶⁰³ Therefore, new points can be computed at the minima of the negative squared difference surfaces of at least two NNs (or, equivalently, at local maxima of the squared difference surface). This method is supposed to be very efficient in cases, where different conformations are separated by large energy barriers or strongly stabilized local minima are common. MD simulations would take a long time to overcome the potential barriers and reach the region of unknown molecular structures.⁴³⁵

The idea behind this technique is similar to previous works with GPR. A measure of confidence can be provided with GPR models, which enables the search of regions with large variance in the ML predictions. In these regions, data points can be added to build up a training set.^{562,630−632} Similarly, Bayesian Optimisation Structure Search (BOSS) has been proposed for constructing energy landscapes of organic and inorganic interfaces.⁶³³ A combination of different approaches has also been applied by Häse et al.,¹⁶² who fitted TDDFT excited-state energies of a light-harvesting system. Given a large enough, error-free, and comprehensive data set, ML has the potential to determine known and unknown (un)physical laws within the data.⁶³⁴

5.3. Phase of the Wave Function

In contrast to ground state properties, excited-state properties such as transition dipole moments, NACs, or SOCs arise from two different electronic states. As a consequence of the arbitrary phase of the wave function of each electronic state, properties resulting from two different states carry an arbitrary sign, which makes them generally double-valued. In the case of vectorial properties, such as dipole moments or coupling vectors, the whole vector can be multiplied by +1 or −1 and is still a valid solution. Similarly, single valued properties, such as SOCs obtained from electronic structure programs, can be multiplied by +1 or −1 and are equally correct. This additional complexity prohibits that conventional ML algorithms learn such raw data of quantum chemistry and hampers the training process to find a proper relation between a molecular geometry and the excited-state property.^94,546

A one-dimensional example of this problem is illustrated for the NAC (exemplified using one single value along the reaction coordinate) that couples an excited singlet state, S_i, and a second excited singlet state, S_j, in Figure 10. A positively signed function of atomic coordinates is shown by dashed blue lines with a cusp at the point at which the two singlet states are degenerate. Such a smooth function (besides the sharp spike at the conical intersection) is highly desirable when fitting with ML models is aimed for. It is worth mentioning that a consistent negative sign (light-blue dashed line) along this reaction coordinate is equally correct and that it is desirable to seek for one global sign. However, the direct output of a quantum chemistry program along this reaction coordinate looks more similar to the dashed magenta line in-between the blue curves. As one can imagine, no proper training can be guaranteed with these inconsistent data. Note that existing MD programs for the excited states usually track such phase jumps within electronic wave functions in order to account for nonadiabatic transitions correctly.²⁵⁶

Figure 10.

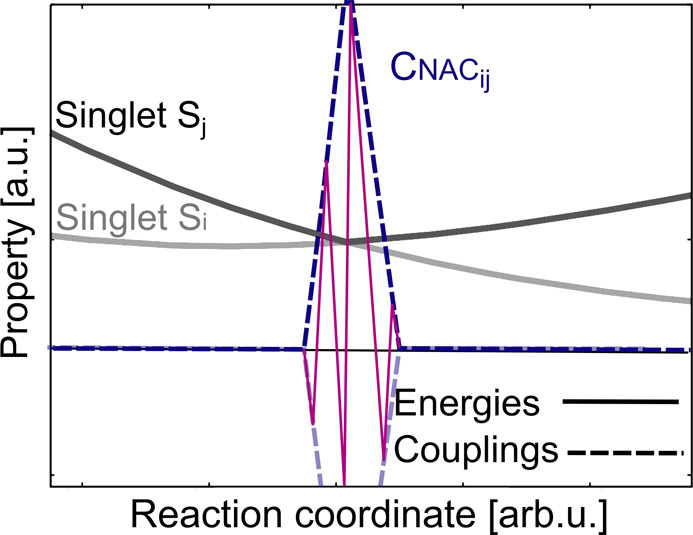
NAC value between singlet state S_i and S_j in the MCH basis. A consistent sign along the reaction path of couplings is shown by blue dashed lines. The direct output of a quantum chemical calculation is shown by a magenta line.

The idea of phase tracking can also be applied in ML in order to thwart the problems due to the arbitrariness within coupling or dipole elements. Some algorithms have been developed to remove the arbitrary sign jumps and provide smooth functions of atomic coordinates.^15,16,94,635 Noticeably, the properties obtained after a transformation to the diabatic basis are already smoothly varying functions of atomic coordinates.³⁶⁹ However, the challenges arising due to the arbitrary phase of the wave function still persist, because the inconsistencies within adiabatic properties have to be removed in order to make the diabatization process feasible.^16,92

It is worth mentioning at this point that also another kind of phase exists that cannot be eliminated in the aforementioned way. It is called the Berry phase or geometric phase. After a loop was performed in space around a conical intersection and returning to the original point, a change in the phase of the wave function of π can be observed; i.e., the same point is only reached after two loops around the conical intersection. Neglecting this effect can lead to false transition probabilities, depending on the dynamics method and the system. While in most cases in MQCD the Berry phase can be safely neglected, this is not possible in quantum dynamics simulations. A diabatic basis is advantageous in this case because the Berry phase is absent in this picture. However, the Berry phase still has to be kept in mind, when fitting diabatic potentials from adiabatic ones.^636−641

5.3.1. Phase Correction of Adiabatic Data

First ML studies on dynamics in the adiabatic basis omitted a preprocessing and were unable to reproduce reference results based on ML alone,¹⁴⁰ or avoided the phase problem by using the Zhu–Nakamura method.^139,141 Evidently, potentials and forces can be learned with conventional ML approaches, but adaptations or a preprocessing of data is necessary to learn coupling elements or transition dipole moments. Independent of the purpose, the fitting of adiabatic quantities^94,546 or the diabatization of adiabatic data with property-dependent diabatization schemes,¹⁶ adiabatic data have to be corrected to remove the arbitrary sign jumps that are due to the arbitrary phase of the wave function. Several ways for these corrections exist, which have been shown to work well for different excited-state problems.

One possibility is to preprocess data according to the wave function overlap—between the wave functions from a geometry of interest and a reference geometry—for each electronic state. This process is termed phase correction^256,546 and has been applied by us in order to generate a training set for three singlet states of CH₂NH₂⁺⁹⁴ and two singlet and two triplet states of CSH₂. SOCs,¹⁵ NACs,^15,94,95 and transition dipole moments^94,95 could be fitted in the adiabatic basis with deep NNs and kernel ridge regression (KRR).^15,94,95 Very recently, Zhang et al.⁹⁷ applied this procedure to describe transition dipole moments of N-methylacetamide.

The wave function overlap matrix, S, with size N_S × N_S, is computed between two molecular geometries α and β:⁶⁴²

26

In many cases along a given reaction path, the off-diagonal elements of the overlap matrix are very close to zero, and the diagonal elements are very close to +1 or −1, indicating whether the phase of a state has changed along this path or not. Whenever a new state enters along the reaction path or adiabatic states switch their character, which is common after passing through a conical intersection for example, the off-diagonal elements provide the relevant phase information instead of the diagonal elements. Taking all these effects into account, a phase vector, p, can be derived for each given molecular geometry. A property resulting from electronic state i and j has to be multiplied by the corresponding phase factors of these states.⁹⁴

An advantage of this algorithm is that it does not require any manual fitting of data. However, this procedure has to be carried out for every data point included in the training set with respect to one predefined reference wave function. This reference wave function can be for example the wave function of the ground-state equilibrium structure of the molecule and needs to be identified to guarantee an almost globally consistent sign of elements. During a photoinitiated simulation, it is common that geometries quickly start to differ from the reference geometry. The wave function overlap then tends to zero and cannot provide information about the correct sign of a certain electronic state. In this case, the phase must be propagated from the reference geometry on with n interpolation steps. The phase vector applicable for the correction of the data point to be included in the training set is then obtained by multiplication with all previously obtained phase vectors, p₀ to p_n–1:

27

Intruder states prohibit a proper tracking because their wave function is absent at the earlier geometries. Hence, a phase correction may be rendered infeasible for systems with a high density of states.

In order to obtain the correct phase, more states can be included in the simulations, which however increases the computational cost. A solution is to take many electronic states into account only close to the reference geometry. The amount of states can then be reduced along a given reaction coordinate, and relevant states can be disentangled from irrelevant ones. Further, it makes sense to save the already phase-corrected wave functions of several geometries in addition to the reference geometry. Whenever a new data point should be included into the training set, the distance to each saved data point can be computed in order to find the closest available structure and reduce the amount of interpolation steps.^94,175

This problem has also been recognized by Robertson et al.³⁹¹ for a diabatization process, where a sufficiently large vector space of the CAS wave function is required for proper diabatization. The overlaps of electronic states can be maximized by rotation of CI vectors of CAS wave function states. A similar version to use the information on CI vectors for diabatization was applied by Williams et al.,¹⁴² who used NNs to assist the diabatization process of adiabatic NO₃ potentials.

Another way to correct the sign of data points was carried out by Guan et al.,¹⁶ who fitted diabatic 1,2¹A PESs and dipole moment surfaces of NH₃ from MR-CISD/aug-cc-pVTZ data with NNs. The diabatic PESs were taken from a previous study and obtained with the Zhu–Yarkony diabatization procedure.^377,643,644 By diagonalization, the rotation matrix defined in eq 10 could be obtained, which connects the diabatic and the adiabatic basis (see eq 9). The adiabatic dipole moments, μ^MCH, could then be transformed into the diabatic basis using the unitary matrix, U:

28

As the unitary matrix U is only defined up to an arbitrary sign, the signs of the diabatic dipole moments have to be corrected in order to provide a consistent diabatic dipole moment surface. This correction has been done with a so-called cluster growing algorithm.⁶³⁵

The cluster growing algorithm requires an initial set of phase corrected data points. In this work, 347 data points were adjusted manually for this purpose. Subsequently, a Gaussian process regression (GPR) model⁶⁴⁵ was fitted to these data points. The signs of the rest of the data points to be corrected were then adjusted with the GPR model. Several iterations were carried out, where each iteration aims for the inclusion of close-lying points to the cluster, leading to the name “cluster growing” algorithm.¹⁴⁸

The singularities in regions close to conical intersections can make this algorithm fail. Therefore, data points in such regions have been removed by setting a threshold. Data points with energy gaps lower than this threshold were excluded from the cluster. The regions around conical intersections could not be fitted as comprehensively as other regions of the PESs. As another drawback, the authors note that the initial manual fitting of the signs is a tedious task, especially when larger systems and more dimensions are described.

Two of the authors also fitted diabatic PESs of two singlet states and one triplet state as well as the SOCs between singlets and triplets of formaldehyde, CH₂O, with NNs.⁹² The electronic structure reference method was MR-CISD/cc-pVTZ. The diabatic potentials were obtained using an adapted version of the Boys localization.³⁸² The energy differences between two states were incorporated in the equations in order to remove earlier identified diabolic singularities.¹⁴⁸ The range of π, which the rotation angle for the diabatization covers, guarantees a proper treatment of the Berry phase. The diabatization procedure further requires consistent transition dipole moments, which were adjusted manually for this purpose. The diabatic SOCs were then obtained as a linear combination of the adiabatic SOCs by applying the same rotation matrix as for the energies. One separate NN function was used to fit each coupling value and electronic state separately.

It becomes clear that only a small number of works on this topic exist. At the moment, many problems remain unsolved for generating a training set that properly accounts for both types of phases, the arbitrary phase and the Berry phase, and is applicable for large systems with many states. An automatic phase correction procedure without the need of manual input would be very advantageous, especially when larger and more flexible systems are treated. Further developments are needed.

5.3.2. ML-Based Internal Phase Correction

One step toward a routine application of ML for photochemical studies and an easier training set generation with quantum chemistry is an ML-based internal phase correction, which has been implemented by us into the SchNarc approach for photodynamics simulations.¹⁵ In contrast to the phase correction algorithm to correct the training data, this procedure renders the learning of inconsistent quantum chemical data possible. A modification of the training process, termed phase-free training, is required for this purpose.¹⁵ We implemented this training algorithm in a combination of the deep continuous-filter convolutional-layer NN SchNet,^461,465 adapted for excited states, and the MD program SHARC.^236,256,589

Similar to standard training algorithms, parameters of an ML model are optimized in order to minimize a cost function. Most frequently, the L₁ or L₂ loss functions are applied, which take the mean absolute error or mean squared error between predicted and reference data into account. The phase-free training algorithm uses a phase-less loss function, which includes all trained properties at once and additionally removes the influence of the random phase switches. In this way, the computational costs for the training set generation can be reduced.

Compared to the previously reported ML models for photochemistry, where each state was fitted independently,^16,92,141 SchNarc is capable of describing all PESs at once, including the elements resulting from different pairs of states. This results in an overall loss function with several terms, where each term is weighted with a different trade-off value, t, that can be defined manually:

29

If only energies (E) and forces (F) are fitted, then the loss function is equal to a linear combination of L₂ loss functions for energies and forces.^15,111 The parts of the SOCs and NACs are

30

and

31

respectively. The error for SOCs and NACs that enters the loss function is the minimum error that can be achieved when trying out all possible combinations of phases for each pair of states, i.e., possible solutions. The algorithm takes into account that the signs of SOCs and NACs coupling different pairs of states depend on each other.

The error function containing all possible solutions for SOCs, ε_SOC^κ, and NACs, ε_NAC, can be obtained as follows:

32

33

This phase-less loss procedure does not require any preprocessing of training data. Quantum chemistry calculations can be directly fitted with this adaption of the loss function. The power of this approach is that, once a given phase vector for a data point has been found, it can be directly applied to correct the arbitrary signs of other properties, such as transition dipole moments. If other properties are targeted, the loss function applied for NACs can be similarly used for other vectorial properties, and the loss function applied for SOCs can be used for any other single- or complex-valued element of arbitrary sign.¹⁵ However, as a consequence of the higher complexity of the loss function, the training process is generally more expensive. The computational effort required for training can be reduced if only one type of coupling is treated within MD simulations. In these cases, a simpler adaption of the phase-free loss is also applicable.¹⁵

6. Application of ML for Excited States

In this section, we review ML studies of excited states and their properties. We aim to show how they have been employed to improve static and dynamics calculations and focus on the used type of regressor, descriptor, training set, and property. We will classify the approaches according to Figure 1.

6.1. Parameters for Quantum Chemistry

Traditionally, the user decides whether a multireference method is needed or a single-reference method is sufficient to describe a chemical problem. Recently, Kulik and co-workers¹⁷⁶ have presented an NN model based on a semisupervised virtual adversarial training approach and a diagnostic inputs training set¹⁷⁷ to learn the multireference character of molecular systems. The authors developed a decision engine to detect strongly correlated systems, which can be applied in a high-throughput screening fashion. Their work can potentially pave the way toward automatic selection of a proper reference method—a tool that is urgently needed, especially in the research field of ML for excited states.

Besides this seminal work, ML can help to select an active space for multireference methods. Jeong et. al⁷¹ developed an ML protocol for classification based on XGBoost⁴⁸³ to allow for a “black box” use of many multireference methods by automatically selecting the relevant active space for molecular systems. The tedious selection of active orbitals and active electrons can thus be avoided. The accuracy of this approach was demonstrated for diatomic molecules in the dissociation limit, and the molecules were represented via the molecular orbital bond order and the average electronegativity of the system.

6.2. ML of Primary Outputs

To the best of our knowledge, no ML models for providing primary outputs of quantum chemistry exist for excited states (see Figure 1). Targeting the primary output of a quantum chemistry simulation, i.e., the N-electron wave function, or providing ML density (functionals) is far from trivial even for ground-state problems.^{72−80,82,90,355,646−649} However, such an approach for excited states could solve many problems and allow for wave function analysis, providing additional insights like the excited state characters.⁶⁵⁰ Therefore, we expect such models to appear in the near future.

6.3. ML of Secondary Outputs

In the following, we summarize the contributions of ML models that fit the secondary output of quantum chemical calculations, i.e., PESs, SOCs, NACs, and transition as well as permanent dipole moments in the adiabatic and diabatic basis (Figure 1). The prediction of the manifold quantities (see Figure 2) can be done in two ways, i.e., in a single-state fashion and in a multistate fashion.⁹⁵ The applicability of such ML models to the simulation of photodynamics will be discussed.

6.3.1. ML in the Diabatic Basis

Diabatic PESs have been fitted with ML and related methods for more than 25 years.^151,408 An advantage of diabatic PESs is their smoothness, which is perfectly matched by ML models built upon smooth functions. However, the tedious procedure to generate diabatic PESs remains. Some effort is therefore devoted to develop ML-assisted diabatization procedures and eliminate this limiting step.

Diabatization

Williams et. al¹⁴² incorporated NNs into diabatization by ansatz and fit diabatic NO₃ PESs. The ground state vibrational energy levels were computed, and subsequently, the authors used the diabatic potentials for quantum dynamics simulations in five dimensions.³⁸¹ The diabatization procedure was further modified to properly account for complete nuclear permutation inversion (CNPI) invariance.³⁹⁰ To this aim, the molecular input was replaced by CNPI invariant coordinates. Recently, Shen and Yarkony⁹⁶ fit two diabatic potentials of the cyclopentoxy radical, C₅H₉O, and one state of cyclopentoxide, C₅H₉O^–, with 356 data points sampled from scans along different reaction coordinates. The diabatization was assisted with NNs. Because of the high dimensionality of the system, the authors resort to application of regularization in the fitting algorithm and an adapted loss function to obtain an accurate representation of two-state diabatic PESs with NNs. This novel strategy is envisioned for the computation of the photoelectron spectrum of cyclopentoxide.⁹⁶ Fitting 39 degrees of freedom in the diabatic basis is a huge improvement in this research field. The authors further note that a comprehensive sampling of the full relevant PESs in such high dimensional space is problematic. PIP-NNs were used to introduce a new diabatization procedure recently.⁶⁵¹ The ground and first excited state of ammonia served as a test molecule. Four separate NNs were trained to fit the parts of the diabatic Hamiltonian, while the loss function was formulated in the adiabatic basis and adiabatic energies, forces, and adapted derivative couplings obtained from the diabatic fitted Hamiltonian after diagonalization were mapped to the adiabatic reference data.

Recently, Shu et al.⁶⁵² proposed a new, semiautomatic diabatization approach based on two training sets—one is formed from adiabatic energies, and one contains a selected number of diabatic potential energy matrix elements, which are assumed to be known at some molecular conformations, e.g., dissociated geometries or the equilibrium structure. The authors further demonstrate that results from diabatization in lower dimensions can be used for higher-dimensional diabatization. The diabatization scheme was tested using a two-state analytical model and two states of thiophenol with adiabatic data obtained from Extended Multi-Configuration Quasi-Degenerate Perturbation Theory (XMC-QDPT).⁶⁵³

Because of the aforementioned problems, a description of medium-sized to large molecules with diabatic potentials is often done with more crude approximations.^142,407 An example is the LVC model,²³⁹ with its one-shot variant,²⁴⁰ or the exciton model.^182,654 For more details on this topic, the reader is referred to refs (64, 239, 331, and 655−657). The Frenkel exciton Hamiltonian can be used to describe light-harvesting systems.^182,654 Such a Hamiltonian was constructed for the investigation of the excited state energies of bacteriochlorophylls of the Fenna–Matthews–Olson complex. Multilayer feed-forward NNs with the Coulomb matrix as a molecular descriptor could accelerate the construction of such Hamiltonians for the prediction of excited-state energies.¹⁶² The effective Hamiltonian of the whole complex was subsequently used to predict excitation energy transfer times and efficiencies. Therefore, Häse et al. used exciton Hamiltonians as an input to NNs, which were trained to reproduce excitation transfer times and efficiencies of pigments in the complex. The excitation energy transfer properties for the training set were computed via hierarchical equation of motion technique,⁶⁵⁸ which is costly and thus limited due to the large number of pigments that need to be computed. By using ML to learn the relation between a Frenkel Hamiltonian and excitation energy transfer properties, large-scale screening studies are enabled and an efficient design and search of novel excitonic devices becomes possible.⁶⁴ The hyperparameters of the ML model were optimized by applying a Bayesian optimization algorithm. Overall, the accuracy of the model was in excellent agreement to reference data, and out-of-sample Hamiltonians could be computed reasonably well for geometries close to those inside of the training set.¹⁶¹ Recently, Krämer et al. have used DFT Tight Binding data to train a KRR model to simulate the exciton transfer properties of anthracene. Although the semiempirical reference method is computationally efficient compared to ab initio methods, an acceleration was achieved that is concluded to be even more pronounced in larger systems. A perspective on ML for the prediction of phenomena related to light-harvesting systems is provided in ref (659).

Fitting Diabatic Potentials and Properties

Given diabatic PESs, ML models can be used to fit them. KRR models are often employed for this task, due to their ease of use and ability to provide accurate predictions, as mentioned above. Recent studies by Habershon and co-workers focus on interpolation of diabatic PESs and their use for grid-based quantum dynamics methods, i.e., variational Gaussian wavepackets and MCTDH. The butatriene cation has been investigated in two dimensions comprising two electronic states.¹⁴⁹ The description of this molecule has been recently advanced with a new diabatization scheme, namely, Procrustes diabatization. The method was evaluated with two-state direct-dynamics MCTDH (DD-MCTDH) simulations of LiF and applied to four electronic states of butatriene.²⁵² Some of the authors also carried out DD-MCTDH 4-mode/2-state¹⁴⁵ and subsequently 12-mode/2-state dynamics of pyrazine.¹⁴⁶ The investigation of the higher-dimensional space of pyrazine could be achieved by systematic tensor decomposition of KRR and advances conventional MCTDH simulations considerably with respect to accuracy and computational efficiency. Further, the method was applied to investigate the ultrafast photodynamics of mycosporine-like amino acids, which are suitable as ingredients in sunscreens due to their photochemical properties and photostability.⁶⁶⁰ However, the reduced 6-dimensional and 14-dimensional DD-MCTDH simulations with KRR interpolated PESs were unable to reproduce the expected ultrafast photodynamics, which had been observed in previously performed surface hopping calculations and is typical for sunscreen ingredients. The authors note that the inclusion of more adiabatic states for the diabatization procedure and the consideration of additional relevant modes can lead to more accurate results. All of the reference simulations were carried out at the CASSCF level of theory with KRR fitted diabatic PESs.

In addition to KRR models, NNs were also used to describe diabatic PESs. Seminal works include PIP-based NNs by Guo, Yarkony, and co-workers. Absorption spectra and the dynamics of excited states of NH₃ and H₂O could be studied by fitting potential energy matrix elements.^{143,147,392,412−414,525} Subsequently, some of the authors fit the dipole moments corresponding to the diabatic 1,2¹A surface of NH₃.¹⁶ SOCs of formaldehyde were learned with NNs in the diabatic picture.⁹² A total of 341 data points were used for training of SOCs. A singlet and a triplet state in the adiabatic basis were transformed to diabatic states using Boys localization.³⁸² Since this diabatization is based on transition dipole moments, the respective properties of the excited states had to be phase corrected. The authors proved the accuracy of their fitted PESs and emphasized the usability of the ML models to describe full-dimensional quantum dynamics.^16,92,525 Very recently, they investigated the OH + H₂ reaction, i.e., the nonadiabatic quenching of the hydroxyl radical colliding with molecular hydrogen. Four diabatic potentials including forces and couplings were fitted using a least-squares fitting procedure. A total of 1345 data points of 1,2,3 ²A adiabatic PESs were computed with MR-CISD.⁵²⁵

The aforementioned ML models are single-state models. Each energetic state and each coupling or dipole moment value resulting from different pairs of states are fitted with a separate ML model. While this yields justifiable accuracy for energies and diabatic coupling values,⁹⁵ dipole moments are vectorial properties and need to preserve rotational covariance.^97,241

As the aforementioned studies show, ML models are generally powerful to advance quantum dynamics simulations for the excited states and can also assist the construction of effective Hamiltonians. However, currently, diabatic PESs cannot simply be fit for systems with arbitrary size and arbitrary complexity. The diabatization remains a methodological bottleneck, where additional developments are needed.

The investigation of medium-sized to larger molecular systems, especially the investigation of their temporal evolution, is more often carried out in the adiabatic basis using on-the-fly simulations. An increasing number of recent studies focus on fitting such adiabatic PESs. The inconsistencies in adiabatic properties make such quantities generally more challenging to fit, which is why this field of research gained a lot of attention relatively late, i.e., only in the last 3 years—after early examples dating back already to 1999.⁶⁶¹

6.3.2. ML in the Adiabatic Basis

Surface Hopping MD

The first NN models for MQCD calculations probably date back to the year 2008.⁹⁸ Nonadiabatic MD simulations were carried out with NN-interpolated PESs to investigate O₂ scattered from Al(111). Symmetry functions were used as descriptors.⁶⁶² A spin-unpolarized singlet and a spin-polarized triplet state at DFT level of theory were fitted with 3768 data points.^662,663 This two-state spin-diabatic problem allowed for evaluation of coupling values and singlet–triplet transitions with the fewest switches surface hopping approach.^436,437 In a later study, another adiabatic spin-polarized PES was included, and coupling values were computed between singlets and triplets⁶⁶⁴ and evaluated from constructed Hamiltonian matrices.⁹³ MD simulations were executed using a manifold of ML-fitted PESs according to different spin-configurations.^93,98 The studies showed that singlet–triplet transitions are highly probable during the scattering event of O₂ on Al(111). As it has been shown later by embedded correlated wave function computations,⁶⁶⁵ the activation barrier of O₂ on Al(111) is rather due to charge transfer than spin-flip as described above. The description of the activation barrier has been improved later⁶⁶⁶ using six-dimensional PESs parametrized using the London–Eyring–Polanyi–Sato function.⁶⁶⁷

After the two studies by Carbogno et al., the interest in advancing ML-based MQCD simulations for the excited states in the adiabatic basis increased mainly in the last three years. One of the first works during this time was conducted by Hu et. al,¹³⁹ who investigated the nonadiabatic dynamics of 6-aminopyrimidine with KRR and the Coulomb matrix. Because of the many degrees of freedom of the molecule and including three singlet states, a large amount of training data was required (>65k data points). Coupling values were not fitted, but, instead, the Zhu-Nakamura approach was used to compute hopping probabilities.

Later, Dral et al.¹⁴⁰ applied KRR models to accurately fit a two-state spin-Boson Hamiltonian and reproduce reference dynamics using 1000 and 10 000 data points. NAC vectors were fit in a single-state fashion. During dynamics simulations, conformations close to critical regions were computed with the reference method instead of the ML model in order to allow for accurate transitions.

In another study, Chen et al.¹⁴¹ used two separate deep NNs to fit the energies and forces of two adiabatic singlet states of CH₂NH. About 90k data points were used to generate these single-state models. Using the Zhu-Nakamura approach to account for hopping probabilities, the reference dynamics could be reproduced, and quantum chemical calculations were replaced completely during the dynamics.

Cui and co-workers⁶⁶⁸ further developed a multilayer energy-based fragmentation method to study the excited-state dynamics and photochemistry of larger systems. This scheme composes a molecular system into a photochemically active (inner) region and a photochemically inert (outer) region. In the original scheme, the active region and the interactions with the outer region are described with the multireference method CASSCF, whereas the outer region is treated with DFT. This decomposition of the total energy of a system allows one to treat larger systems, which cannot be described fully with CASSCF. Compared to quantum mechanics/molecular mechanics (QM/MM) schemes, the energy-based fragmentation method can be rigorously derived from a many-body energy expansion. Different truncation levels and methods can be used for each intralayer and interlayer interactions, so that its accuracy and efficiency can be controlled according to the need. The authors simulated two-state photodynamics of CH₃N=NCH₃ (inner region) including five water molecules (outer region) without the use of ML. The Zhu–Nakamura approximation to model hopping probabilities in nonadiabatic MD simulations was applied.⁶⁶⁸ In order to make the simulations more efficient, the authors replaced the DFT calculations with deep multilayer feed-forward NNs using a distance-based descriptor;^125,506 hence, they describe the ground state energies and forces of the photochemically inert region with ML and describe the S₁ and S₀ state of the inner region with CASSCF. The hybrid ML multilayer energy-based fragmentation method can reproduce the photodynamics of the system.⁵³⁶ Subsequently, the deep NNs were replaced with embedded-atom NNs,⁵⁰⁸ and accurate second derivatives could be computed efficiently.⁵³⁷

Recently, we sought to fit NACs and transition and permanent dipole moments in addition to energies and forces of three singlet states of the methylenimmonium cation, CH₂NH₂⁺, using deep NNs and the matrix of inverse distances as a molecular descriptor.⁹⁴ We were able to perform ML-enhanced excited-state MD simulations with hopping probabilities based on ML-fitted NACs. NNs replaced the reference method MR-CISD completely during the dynamics, which is one of the key factors behind a successful MLMD study as it allows one to completely decouple the costs of the expensive reference method from the dynamics simulations. The accuracy of the ML-approximated PESs and couplings was further assessed by comparing the populations in the different excited states of the reference dynamics, of the ML models, and of the same quantum chemical reference method, namely, MR-CISD, but with a slightly different basis set. This comparison helped to estimate the meaning of “good agreement” for population dynamics. Root mean squared deviations of the nuclear geometries tracked over a short time scale also helped in assessing the success of the MLMD model in reproducing dynamics before using it for, e.g., simulation of longer time scales and better statistics. Such long time scale photodynamics simulations for 1 ns were achieved using the mean of two NN models in approximately two months, whereas the reference method would have taken an estimated 19 years to compute the dynamics for 1 ns on the same computer. This study demonstrated the possibility of MLMD simulations to go beyond time scales of conventional methods. As another benefit of the ML models, it was shown that a large ensemble of trajectories could be calculated, still at a lower cost than a few trajectories with the reference method.⁹⁴

Recently, Li et al.⁶⁶⁹ built on these recently developed techniques and developed the MD program PyRAI²MD (Python Rapid Artificial Intelligence Ab Initio MD). NNs were trained on the S₁ and S₀ states of of CF₃–CH=CH–CF₃ (hexafluoro-2-butene) at the CASSCF(2,2)/cc-pVDZ level of theory in order to enable 10 ns photodynamcis simulations. Generation of an initial training set via Wigner sampling, optimizations of critical regions, and short time-scale trajectories in addition to adaptive sampling resulted in a training set of 6232 data points. The descriptor was generated from inverse distances and (dihedral) angles, and a phase-less loss function¹⁵ was applied to render NACs learnable.

The performance of KRR in comparison to NNs was assessed by us together with von Lilienfeld and co-workers.⁹⁵ The operator formalism⁶⁷⁰ and the FCHL representation^127,530 were used to fit the three singlet states of CH₂NH₂⁺ using the previously generated training set of 4000 data points. A single-state treatment and a multistate treatment for predicting energies were compared. To this aim, a multistate KRR approach as developed with an additional kernel that encodes the quantum energy levels. The accuracy of KRR models could be improved using this extended approach.⁹⁵ The KRR models were further compared to deep NN models regarding their ability to predict dipole moments and NACs. While NNs yielded a slightly higher accuracy at the largest available training set size, KRR models exhibited a steeper learning curve, and hence more efficient learning. The multireference quantum chemical potential energy curves could be faithfully reproduced with KRR models and NN models for the three singlet energies of CH₂NH₂⁺ at first sight. Interestingly, the small differences lead to correctly predicted dynamics with the NNs, while the KRR model was unable to reproduce the reference dynamics. Hence, small differences between the reference method and ML models, especially in critical regions of the PESs, can lead to completely wrong photodynamics simulations.⁹⁵ The different performance of NNs and KRR models was proposed to be a result of the parametric dependence of the depth of NNs and the nonparametric dependence of the depth of KRR models.

Further, it was shown that inconsistencies along QC PESs, which are common especially close to conical intersections, were not reproduced by ML models.^94,171 The problematic fitting of nonsmooth functions representing NACs, i.e., their singularities at conical intersections, was circumvented by employing so-called smooth couplings. To arrive at the latter, the NACs were multiplied with the respective energy gaps. Hence, accurately trained energies were also required in this approach. For prediction, the smooth fitted couplings were subsequently divided by the inferred energy gaps of the ML model. In this way, the training process became more robust.⁹⁵ For some quantum chemical reference methods and some chemical problems, it might be beneficial to remove data points from conformations very close to a conical intersection. Although these regions need to be represented well, such a procedure can reduce the amount of data points with cusps in energy potentials and thus problematic data points in the training set.^15,148

In order to omit the extensive hyperparameter search of the descriptor and regressor, we further developed the SchNarc approach for photodynamics,¹⁵ which is based on SchNet.^461,465 SchNarc allows for (1) a description of SOCs, (2) an NAC approximation based on ML-fitted PESs, their first and second derivatives with respect to Cartesian coordinates, and (3) a phase-free training algorithm to enable a training of raw quantum chemical data. The SchNarc approach is based on the message passing NN SchNet,^461,465 which was adapted by us for the treatment of a manifold of excited electronic states. Additionally, this model can describe dipole moments using the charge model of ref (111), also adapted for excited-states. All excited-state properties can be described in one ML model in a multistate fashion. The performance of SchNarc was evaluated with surface hopping dynamics: Three singlet and three triplet states of SO₂ were computed with ML models for 700 fs, and the underlying PESs were based on an “one-shot” LVC(MR-CISD) model.²⁴⁰ CSH₂ was investigated using two singlets and two triplet states for 3 ps at the CASSCF level of theory representing slow population transfer, and the performance of SchNarc to reproduce ultrafast transitions during dynamics was assessed using CH₂NH₂⁺ with the aforementioned training set. The hopping probabilities were computed according to ML-fitted SOCs and NACs—the latter being fitted in a rotationally covariant way as derivatives of virtual ML properties and approximated from ML PESs. In all cases, excellent agreement with the reference method could be achieved. Noticeably, all the aforementioned photodynamics studies with ML models^{15,94,95,139−141} make use of Tully’s fewest switches surface hopping approach with hopping probabilities based on coupling values or approximated schemes.^436,437

It is further worth mentioning that ML models, which provide energies and derivatives, can be used to optimize reaction coordinates to find, e.g., local minima or minimum energy conical intersections.^94,171,241 In general, a successful MLMD study should make it possible to investigate reactions at longer time or larger length scales than complementary studies with quantum chemical reference methods or should enable large scale screenings, which would not be feasible with the reference method. With respect to different ML models, kernel methods are usually faster during training, but take longer for predictions. In contrast, deep NNs require longer training times and more complex hyperparameter optimization, but once trained, they can predict properties and derivatives thereof extremely fast.^175,671 In the following paragraphs, we compare the timings of some electronic structure methods with predictions made by the deep NN model SchNarc.

Exemplary Timings of Single Point Calculations

The speed-up of simulations is one of the main arguments employed for promoting ML in quantum chemistry. In order to get an idea about the computational time used in different calculations, we provide an example here. In order to get a better feeling of the speed-up one can achieve for excited-state energies and derivatives of medium-sized molecules, the topic will be discussed here. In the next paragraph, timings for dynamics simulations of smaller molecules, which have been achieved up to date, will be provided. Different electronic structure methods and the SchNarc model are used to compute energies and derivatives of 5 singlet and 8 triplets states of tyrosine (24 atoms) on a 2x Intel Xeon E5-2650 v3 CPU and GeForce GTX 1080 Ti GPU. The training of the SchNarc model on the same GPU took about 7 days. One advantage of ML in this case is that it provides access to properties, which are not available with any electronic structure theory, such as NACs, approximated from first and second derivatives of ML PESs.¹⁵ As it becomes visible from the examples shown in Table 2, the most time-consuming parts are the derivatives with second derivatives being far more expensive than first derivatives. These simulations can be accelerated a lot by ML models. Further, a NAC computation is comparable to a gradient computation. However, there are not only N_S NAC calculations to carry out, but N_S × (N_S – 1) calculations.

Table 2. Comparison of the Timings to Compute Different Excited-State Properties of the Molecule Tyrosine with Different Electronic Structure Methods and SchNarc^15a.

method	processor	time [s]
Energies (13 States)
ADC(2)	CPU	2,160
TDDFT	CPU	724
CASSCF	CPU	5,719
CASPT2	CPU	7,972
SchNarc	CPU	1.5
SchNarc	GPU	0.03
Energies + Gradients (13 states)
ADC(2)	CPU	9,280
TDDFT	CPU	5,938
CASPT2	CPU	129,389
SchNarc	CPU	2
SchNarc	GPU	0.1
Hessian (1 State, Frequency)
ADC(2)	CPU	11,760
SchNarc	CPU	97
SchNarc	GPU	15
Approximated NACs (All States) (Not Implemented for QC Methods)
SchNarc	CPU	1,260
SchNarc	GPU	186

^a2x Intel Xeon E5-2650 v3 CPUs and GeForce GTX 1080 Ti GPUs are used for computations. In order to keep the notation short ADC(2) refers to ADC(2)/def2-SVP, CASSCF to CASSCF(10,9)/ano-rcc-vDZP, CASPT2 to MS-CASPT2(10,9)/ano-rcc-vDZP, and TDDFT to TDDFT/B3LYP/def2-SVP. The programs Turbomole⁶⁷² (for ADC(2)), openMolcas³¹⁰ (for CASSCF and CASPT2), and ORCA⁶⁷³ (for TDDFT) were used.

Exemplary Timings for MLMD, LVC Dynamics, and MQCD

The timings of surface hopping MD with analytical PESs (from LVC), quantum chemical PESs, and ML-fitted PESs based on fitted and approximated NACs from Hessians can be found for three exemplary molecules in Table 3.

Table 3. Comparison of the Timings to Compute 100 fs with the Surface Hopping Including Arbitrary Couplings (SHARC)^236,256,589 method^a.

	100 fs dynamics [s/CPU]
	MLMD1	MLMD2	reference
SO2	10	12	2–3
CH2NH2+	24	250	74,224
CSH2	14	16	104

^aFor SO₂ and CH₂NH₂⁺, three singlet states are described and for CSH₂ two singlet and two triplet states. The molecule SO₂ is approximated using a highly efficient LVC model,²⁴⁰ while the underlying reference method to describe the excited states of CH₂NH₂⁺ is MR-CISD/aug-cc-pVDZ and of CSH₂ is CASSCF(6,5)/def2-SVP. SchNarc is used for the MLMD simulations. Once energies, forces, and NACs are trained and predicted (MLMD1), and once NACs are approximated from first- and second-order derivatives of ML PESs (MLMD2). 2x Intel Xeon E5-2650 v3 CPUs are used.¹⁵

Obviously, crude excited-state force fields like the LVC model are faster than ML models, e.g., for SO₂. We note that even such force field implementations can probably still be streamlined for speed but will always be more expensive than ground-state MD simulations, where it would take approximately 0.005 s to simulate 100 fs for the gas-phase methylenimmonium cation, CH₂NH₂⁺, using a state-of-the-art program like Amber.²¹³

However, dynamics based on highly accurate quantum chemical calculations can be accelerated significantly with ML-fitted PESs, e.g., SchNarc models for CH₂NH₂⁺ based on MR-CISD/aug-cc-pVDZ.¹⁵ The speedup is higher if NACs are learned directly (MLMD1) compared to when they are approximated from Hessians (MLMD2). A lot of Hessian evaluations are required in this example because ultrafast transitions occur in CH₂NH₂⁺. The second-order derivatives reduce the efficiency by a factor of about 10. Nevertheless, Hessian calculations of ML-PESs can be accelerated by a factor of about 5–10 using a GPU (dependent on the molecule and GPU used).

Table 3 further shows that a cheaper underlying reference method, such as CASSCF(6,5)/def2-SVP used for CSH₂, does not allow for such a significant speedup. In this example, however, the difference between simulations with learned NACs and approximated NACs is small because the dynamics of CSH₂ is characterized by slow population transfer. Hence, less Hessian evaluations are required to estimate the hopping probabilities.

The time required to train a SchNarc model on a GeForce GTX 1080 Ti GPU is approximately 11 h for energies and forces of 3 singlet states with 3000 data points of CH₂NH₂⁺, about 13 h for energies, forces, and SOCs of 2 singlet and 2 triplet states using 4000 data points of CSH₂ and about 4 h for energies and forces of 3 singlet states of SO₂ using 5000 data points.

Dipole Moments and Atomic Charges

In addition to the investigation of the temporal evolution of some systems in the excited states, permanent and transition dipole moments have been computed with ML models. As mentioned before, in our earlier approaches, we fitted permanent and transition dipole moments as single values with NNs and KRR—strictly speaking, we were neglecting the rotational covariance of the vectors (since rotations were negligible in these simulations).^94,95 The NN and KRR models for dipole moments have been evaluated and compared to quantum chemical reference dipole moments using learning curves and MAEs. Their potential to compute UV spectra was emphasized.

The use of dipole moments to actually simulate UV spectra was demonstrated by Jiang, Mukamel, and co-workers using N-methylacetamide, a model system to investigate peptide bonds.^97,510 They evaluated the ability of ML to describe transition dipole moments at TDDFT level of theory. In a first attempt,⁵¹⁰ the authors predicted dipole vectors as independent values. Fourteen internal coordinates in combination with multilayer feed-forward NNs were used to predict transition energies of N-methylacetamide. XYZ representations served as an input for fitting ground state dipole moments. The Coulomb matrix was employed to fit transition dipole moments for the nπ* and ππ* transitions, but did not lead to sufficiently accurate results. Higher accuracy was obtained by replacing the atomic charges in the Coulomb matrix (eq 21) with charges from natural population analysis. The choice of descriptors was justified by screening different types of descriptors for prediction of different properties. In a later work, some of the authors used embedded-atom NNs to predict transition dipole moments from atomic contributions in a rotationally covariant way. The dipole moment vector between two states i and j was obtained as a linear combination of three contributions:

34

μ_Tⁱ and μ_T were modeled using the charge model of ref (111). A third contribution, μ_T³, was obtained as the cross product of μ_T and μ_T^j:

35

μ_Tⁱ, μ_T, and q_a³ were outputs of the same embedded-atom NN.

Recently, we extended the SchNarc model to describe permanent and transition dipole moments of an arbitrary number of electronic states and pairs of states as vectorial properties in a single ML model in addition to the excited-state energies, forces, and couplings.²⁴¹ Also this model is based on the charge model of ref (111) and allows one to predict latent partial charges for excited states. This charge model relying on atom-wise descriptors thus preserves the correct direction of the permanent and transition dipole moments.

6.4. ML of Tertiary Outputs

The secondary outputs, such as dipole moments or excited state energies, can be used to calculate oscillator strengths (eq 1) and energy gaps (Figure 1d). These properties can serve for the modeling of UV absorption spectra. UV spectra were computed in the previously described studies of N-methylacetamid with the ML fitted transition dipole moments. Jiang, Mukamel, and co-workers⁵¹⁰ applied the transition dipole moment and additionally fitted nπ* and ππ* excitation energies to compute UV spectra of this molecule with NNs. Subsequently, some of the authors⁹⁷ used these excitation energies and the transition dipole moments to model a Frenkel exciton Hamiltonian for proteins using amino acid residues and peptide bonds. This effective Hamiltonian could further be used to approximate UV spectra of proteins. The interaction between amino acid residues and peptides was neglected, so only the isolated peptide excitation energies, i.e., those of N-methylacetamid, and the respective transition dipole moments were needed to construct the Hamiltonian. The authors made use of the dipole–dipole approximation⁶⁷⁴ and applied embedded-atom NNs. High transferability and predictive power were obtained.

In addition, the transition dipole moments of SchNarc²⁴¹ have been used to predict UV/visible spectra of the methylenimmonium cation and ethylene. Both molecules were trained simultaneously. Although they differ in their photochemistry, i.e., the first excited singlet state is bright in the case of ethylene, whereas it is dark in the case of the methylenimmonium cation, with an opposite behavior observed for the second excited singlet state, ML models trained on both molecules were slightly superior to ML models trained on single molecules. In contrast to the previous models, where each property and electronic state or transition energy is fitted separately in one model, the SchNarc model can treat excited-state energies, forces, permanent dipole moments, and transition dipole moments in one model simultaneously, while being able to fit any predefined number of electronic states of different spin multiplicities. According to eq 12, dipole moments are obtained as the sum of atomic contributions, which are obtained from latent partial charges inferred by the ML model multiplied with the vector of an atom with respect to the center of mass. In this way, direct access to the atomic charges is provided, which should, in principle, also be possible with the embedded-atom NN used in ref (97), but has not been evaluated. As the charge distribution in a molecule is highly dependent on the underlying partitioning scheme, a comparison of the different schemes is not straightforward. The Hirshfeld charges⁶⁷⁵ are often considered more accurate than, e.g., Mulliken charges.⁶⁷⁶ Hirshfeld charges were compared to the latent partial charges of the ML model and found to agree well.^172,241 The ML charges further were used to compute electrostatic potentials and charge redistribution after light excitation.²⁴¹

Because of the excellent agreement of the ML predictions and the reference data, the transferability of SchNarc for the excited state energies and dipole moments was evaluated. Therefore, electrostatic potentials and UV/visible spectra of aminomethylene (CHNH₂) and methylenimine (CH₂NH) were computed with SchNarc, and qualitatively correct results could be obtained. This result left us to conclude that at least similar structured molecules can be predicted with ML models even though they are not included in the training set. The high costs and complexity of the underlying multireference quantum chemical method hampered the exploration of more molecules and the transferability of SchNarc toward a larger chemical space.²⁴¹

Ramakrishnan et. al³⁵⁸ predicted excitation energies of the lowest-lying two excited singlet states, S₁ and S₂, as well as corresponding oscillator strengths obtained from TDDFT calculations with KRR. The QM8⁵⁷² database was used consisting of 20k organic molecules. With the Δ-learning approach, CC2 accuracy could be obtained. Very recently, Xue et al.⁴⁹⁰ assessed the performance of KRR models with the normalized inverse distances as a molecular descriptor to predict absorption spectra of benzene and a derivative of acridine containing 38 atoms. Therefore, the authors learned the excited-state energy gaps of several states and the corresponding oscillator strengths in a single-state fashion. Applying a nuclear ensemble approach, the absorption cross sections could be computed at TDDFT accuracy using a fraction of ensemble points.

Pronobis et al.¹⁵⁸ compared two-body, three-body, and automatically designed descriptors to learn TDDFT HOMO–LUMO gaps as well as first and second vertical excitation energies. More than 20k molecules of the QM9 database^457,572 were selected for this purpose, and learning curves were used to evaluate the learning behavior of different ML models. While atom-wise descriptors worked well for HOMO–LUMO gaps, the authors concluded that the accuracy of predicted transition energies is not sufficiently accurate and suggested that advanced nonlocal descriptors might be necessary to achieve higher accuracy. They further proposed the idea of encoding information about the electronic state in the ML model.¹⁵⁸ Indeed, our recent study, in which we compared the performance of KRR and NN models with atom-wise and molecule-wise descriptors demonstrated that encoding of the energy level is advantageous.⁹⁵

Recently, Kang et. al⁵³³ used 500 000 molecules of the PubChemQC⁵⁷⁸ database to train a random forest model on the excitation energy and the oscillator strength corresponding to the electronic state with the highest oscillator strength. Ten singlet states, as available in the PubChemQC database, were evaluated for that purpose. The authors used simplified molecular-input line-entry system (SMILES) strings and converted them into descriptors. The descriptors comprised several topological⁶⁷⁷ and binary⁶⁷⁸ fingerprints, which were calculated with the help of the RDkit library.⁶⁷⁹ The authors compared the prediction accuracy to the aforementioned models and stated that their model outperformed previous ML models in the task of predicting accurate oscillator strengths and excitation energies for the most probable transition in organic molecules. Analysis of important features led the authors identify that nitrogen-containing heterocycles are important for high oscillator strengths in molecules. The authors concluded that their study could serve the design of new fluorophores with high oscillator strengths.⁵³³

Ghosh et. al¹⁵² used multilayer feed-forward NNs, convolutional NNs and DTNNs to fit the 16 highest occupied orbital energies from DFT, where the respective eigenvalues are broadened by Gaussians with a full width at half-maximum of 0.5 eV. The resulting spectra are probably comparable to ionization potentials in line with Koopmans’ theorem. Geometries from the QM7b^570,571 and QM9^457,572 database were used for training, and predictions were tested using 10k additional diastereomers, which were also used by Ramakrishnan et al.³⁵⁸ to evaluate the Δ-learning approach. The convolutional NNs with the Coulomb matrix and DTNNs with an automatically generated representation outperformed the simpler NNs. Overall, good agreement to reference DFT calculations could be achieved.¹⁵²

Markland and co-workers⁵³⁹ trained NNs with atom-centered Chebyshev polynomial descriptors¹¹⁰ on the TDDFT/CAM-B3LYP/6-31+G* S₀–S₁ energy gap of the deprotonated trans-thiophenyl-p-coumarate (chromophore of yellow protein) in water and Nile red chromophore in water and benzene. Farthest point sampling¹²³ was used to select about 2000 data points from a larger set of 36 000 data points and was compared to random sampling. The authors assessed the performance of three different ML approaches to compute absorption spectra, spectral densities, and two-dimensional electronic spectra. One model (hidden solvation) completely ignored any environmental effects and only described the chromophore, another model (indirect solvation) incorporated environmental effects within a 5 Å cutoff of the atomistic descriptor for the chromophore, and a third model (direct solvation) treated the whole system, i.e., the chromophore and the atoms of the solvent, explicitly. As expected, the hidden solvation model turned out to be insufficiently accurate for systems with strong solvent–chromophore interactions, but was comparable to the hidden solvation model when describing Nile red chromophore in benzene. The indirect solvation and direct solvation models were comparable to each other, but with respect to the computational efficiency, the indirect solvation model was beneficial. This model could reproduce reference linear absorption spectra, spectral densities, and could capture spectral diffusion of two-dimensional electronic spectra of all treated chromophores.⁵³⁹

Penfold and co-workers¹⁵⁵ applied deep multilayer feed-forward NNs to prove the ability of ML to predict X-ray absorption spectra (XAS), which provide a wealth of information on the geometry and electronic structure of chemical systems, especially in the near-edge structure region. Note that X-ray free-electron laser spectroscopy can further be used to generate ultrashort X-ray pulses to investigate photodynamics simulations in real-time. The training set for the prediction of Fe K-edge X-ray near-edge structure spectra contained 9040 data points. The inputs for NNs were generated using local radial distributions around the Fe absorption site of arbitrary systems taken from the Materials Project Database.⁶⁸⁰ Qualitatively accurate peak positions and intensities could be obtained computationally efficient, and the structural refinement of nitrosylmyoglobin and [Fe(bpy)₃]²⁺ was assessed with NNs. The authors noted that future development is needed to accurately capture structures far from equilibrium as well as irregularities in the bulk. The spectral shapes and other properties of X-ray laser pulsed from free-electron laser facilities could be predicted by Sánchez-González et. al⁶⁸¹ with NNs and support vector regression.

Another study was executed by Aarva et al.,⁶⁸² who focused on XAS and X-ray photoelectron spectra of functionalized amorphous carbonaceous materials. By clustering of DFT data with unsupervised ML techniques average fingerprint spectra of distinct functionalized surfaces could be obtained. The authors use GPR. Similarly to the aforementioned state encoding,⁹⁵ the authors encoded the electronic structure, i.e., the Δ-Kohn–Sham values (core–electron binding energies), in a Gaussian kernel. This kernel was then linearly combined with a structure-based kernel based on the SOAP³⁰ descriptor. The spectra computed from the different clusters were used to fit experimental spectra allowing for an approximation to the composition of experimental samples on a semiquantitative level. The so-called fingerprint spectra, which enabled the differentiation of the spectral signatures, were assessed in a previous study using different models for amorphous carbon,⁶⁸³ among them an ML fitted PES using GPR.^112,684

Kulik and co-workers¹⁷ used deep NNs to predict the spin-state ordering in transition metal complexes to determine the spin of the lowest lying energetic state in open-shell systems. The determination of spin states is important to evaluate catalytic and material properties of metal complexes. Descriptors based on a selection of empirical features were used to capture the bonding in inorganic molecular systems. The performance of descriptors including different features was assessed for a set of octahedral complexes with first-row transition metals. The most important features were identified to be the atom, which connects the ligand to the metal, its environment and its electronegativity, the metal identity and its oxidation state, as well as the formal charge and denticity of the ligand.⁶⁸⁵ The ML models were tested on spin-crossover complexes and could assign the correct spin in most cases. Additionally, ML models were applied for the discovery of inorganic complexes^686−689 Similarly, Behler and co-workers⁹¹ applied high-dimensional NNs to predict spin states of transition metal oxides, which are for instance important for lithium ion batteries. In addition, the atomic oxidation state could be predicted.

The inverse design of molecules with specific properties was further targeted by Schütt et. al,⁷⁷ who developed SchNOrb, a deep NN model based on SchNet. The automatically generated descriptor was extended with a description of atom pairs in their chemical and structural environment. An analytic representation of the electronic structure of a molecular system was obtained in a local atomic orbital representation. The analytic derivatives of the electronic structure allowed for optimization of electronic properties. This was demonstrated by minimizing and maximizing the HOMO–LUMO gap of malonaldehyde.⁵⁶³ Besides, the ML method was used to predict the lowest 20 molecular orbitals of ethanol at the DFT level of theory, to investigate proton transfer in malonaldehyde using ground-state dynamics and to analyze bond order and partial charges of uracil.

Bayesian NN models were applied by Häse et al.¹⁶⁰ to relate molecular geometries to the outcome of nonadiabatic MD simulations obtained with CASSCF. Normal modes with and without velocities of initial conditions served as an input for NN models. Velocities in addition to normal modes as descriptors improved the accuracy of ML models slightly, pointing out that normal modes contain already enough information for the sake of their study. The dissociation times of 1,2-dioxetane obtained from nonadiabatic MD simulations was the targeted output. The NNs could faithfully reproduce dissociation times and further provided a measure of uncertainty. The authors noted that their method could be particularly interesting for analysis of MLMD simulations.

Lately, regression and ML models have emerged to assist the prediction of the quantum yield, which is a property targeted in studies for the design of photoactive materials, such as organic light emitting diodes (OLEDs), molecules useful in phototherapy, solar cells, or biomedical labeling. The yield of fluorescence and phosphorescence can be targeted. It can be determined from the ratio of the rate of nonradiative emission and the rate of radiative emission. As radiative emission usually takes place on time scales in the range of nano- to milliseconds, theoretical methods to determine their rates, i.e., dynamics simulations, are limited. Approximations can be made using static calculations, such as it has been done by Kohn et al.,⁶⁹⁰ who developed a semiempirical method to compute the fluorescence quantum yield of chromophores of molecules using TDDFT. The coefficients, which could not be determined from theory, were fit to experimental data. Qiu et al.⁶⁹¹ studied aggregation induced emission of triphenylamine compounds using a support vector machine (SVM). The charge of three carbon atoms adjacent to a central nitrogen atom served as an input to the classifier. Inactive and active materials could be identified and in combination with DFT leading to aggregation induced emission were investigated. Different types of ML models, such as KRR and NNs, were further compared to predict emission and absorption wavelengths and luminescence quantum yields of organic dyes that show fluorescence after excitation. Different fingerprints were compared generated from an external software and data was obtained from experiments.⁶⁹² The tested model emphasized the possibility to combine experimental data with ML algorithms to enable large scale screening and the design of novel materials and compounds.

6.5. ML-Assisted Analysis

The aforementioned studies have shown that ML enables the simulation of MD simulations and spectra predictions at low computational costs. The computational efficiency allows for enhanced statistics, i.e., in the case of MD simulations a huge number of trajectories and the simulations on long time scales.^15,94 Therefore, subsequent analyses of production runs can become a time limiting step of studies. This problem was identified in the aforementioned study on the dissociation times of 1,2-dioxetane by Häse et al.¹⁶⁰ Therefore, the authors further used their method to interpret the outcomes of nonadiabatic MD simulations. 1,2-Dioxetane is the target of their study as it is the smallest molecule known to show chemiluminescence after nonadiabatic transitions from the ground state to an excited state. The chemiluminescent properties of this compound were related to its decomposition rate into two formaldehyde molecules, which was also identified to be relevant in an earlier work of some of the authors.⁶⁹³ By analysis of the ML models that fit the dissociation times, correlations could be observed between the normal modes and the dissociation times. For example, the modes corresponding to the symmetric C–O bond stretchings, and simultaneous planarization of the two formaldehyde moieties were found to be relevant for the accurate prediction of dissociation times. It was further emphasized by the authors that although the findings of NNs were expected and obey physical laws, ML models were helpful to extract relevant information of large amount of data and could potentially serve as an inspiration to humans.

Recently, some of the authors used classification algorithms to further analyze the different types of geometries identified in the ab initio MD simulations of the decomposition reaction of dioxetane,⁶⁹⁴ which can lead to successful dissociation or frustrated dissociation. Both in this study and in previous work,⁶⁹⁵ it was found that the planarization of the two formaldehyde moieties is key for dissociation of dioxetane.⁶⁹⁴

Time-resolved experimental photoluminescence spectra could be analyzed with the LumiML software developed by Đord̵ević et al.,⁶⁹⁶ who applied linear regression models to learn from computer-generated photoluminescence data. The software was employed to predict decay rate distributions⁶⁹⁷ of perovskite nanocrystals from data generated with femtosecond broadband fluorescence upconversion spectroscopy.⁶⁹⁸ The authors highlighted the applicability of their method to enhance studies on the optimization and design of optical devices and further noted that their approach can also be used to analyze transient absorption spectra. Aspuru-Guzik and co-workers¹⁵⁴ applied Bayesian NNs to find correlations of nanoaggregates with electronic coupling in semiconducting materials using absorption spectra. In general, the analysis of experimental spectra and the inverse design of compounds is most frequently applied in the research field of material science. Their description goes beyond the scope of this review, and the reader is referred to refs (164−168, and 170).

6.6. Open Questions and General Remarks on a Successful ML Method

The most important open questions in this field are in our opinion the following: what is generally necessary to go to larger length scales, and which reference method can be used in order to describe the excited-state energies and properties accurately for large systems? While multireference methods suffer from high costs and varying active spaces for different molecules, single-reference methods cannot describe reactions and the formation and breaking of bonds accurately. While it could be shown that long time scale photodynamics simulations in the range of nanoseconds are possible at high accuracy with ML, it is not clear how to go to time scales of seconds or minutes, which might be even more relevant. What is necessary to combine both long time scales and large length scales? How many data points are needed in order to describe the excited states of large molecules with ML on long time scales? How can we construct transition properties, such as couplings, from atomic contributions in a universal way that is valid not only for one molecule? As all of the above-mentioned questions are not answered yet, and it is not clear how to develop a universal ML force field for the excited states, we can only conclude by trying to summarize the key factors for a meaningful ML study, which focuses on one molecular system in the case of dynamics simulations and on many molecules in case of static simulations:

• (1)As a first step, the relevant processes that are assumed to happen after light excitation in a molecule should be evaluated, and the reference method should be decided based on these findings. In general, it might be easier—for the practitioner as well as for the ML model learning the excited states of a molecule—to use a single-reference method with a black box character, which is additionally less expensive compared to multireference methods. However, multireference methods cannot be circumvented in many cases.
• (2)As soon as the reference method has been identified, an initial training set should be computed, which samples the region around the equilibrium configuration comprehensively in the case of dynamics simulations. In case different molecules are treated, an existing database could be used, and molecular conformations could be extracted and relevant properties recomputed. Whenever transition properties are needed, it is important to either apply a phase correction in advance or adapt the loss function of the ML model.
• (3)The choice of the ML model is dependent on the type of study: If different molecules are treated, it is beneficial to use atom-wise descriptors. Whenever only one molecule is used, it cannot be said in advance what type of descriptor is better suited. The same accounts for kernel methods and neural networks—both have their merits and pitfalls. Hyperparameters should be tuned for the given problem under investigation.
• (4)As soon as the model is trained, the accuracy should be checked, usually by computing the error on a separate test set. It should be further assessed whether the model is overfitting or not. If so, a less complex model might be more suitable.
• (5)The success of an ML study can be evaluated whenever a speed-up can be obtained by applying ML instead of the reference method, e.g., longer time scales can be reached or more molecules can be scanned to design new molecules with targeted functions. A single prediction made by an ML model should be much less expensive than the reference method, but should maintain its accuracy.

7. Conclusion and Future Perspectives

In the past few years, machine learning (ML) has started to slowly enter the research field of photochemistry, especially the photochemistry of molecular systems. Although this field of research is rather young compared to ML for the electronic ground-state, some groundbreaking works have already shown the potential of ML models to significantly accelerate and improve existing simulation techniques. So far, most studies provide a proof of concept using small molecular systems or model systems. Different applications are targeted and will also be aimed at in the future, ranging from dynamics with excited-state ML potentials via absorption spectra to the interpretation of data, see Figure 1.

Analyzing the different studies reviewed here, some trends in the choice of reference methods, ML models, and descriptors can be observed. These trends are illustrated in Figure 11.

Figure 11.

Pie diagrams summarizing the reference methods used for the training set generation, the chosen ML models, and the type of descriptors for the description of the excited states with ML. Analysis is based on 45 studies of ML for the excited states.

The pie chart in Figure 11a shows the used reference methods for the computation of a training set to describe the excited states or excited-state properties of molecules. As can be seen, about half of the training sets are computed with multireference methods (refs (14−16, 71, 92, 94−96, 139, 141−147, 149, 160, 252, 392, 412, 413, and 660)). The employed single-reference approaches are exclusively based on DFT (refs (17,77, 93, 97, 98, 152, 158, 358, 510, 533, 539, 547, and 683)). Analytical methods or experimental data are also applied.^{140,154,161,162,696}

When restricting the analysis to studies targeting dynamics, the fraction that employs multireference methods even increases. About 72% of all dynamics studies use multireference methods to compute the training data for ML models. A total of 14% of the studies use single-reference methods, and an equally large portion apply model Hamiltonians or analytical potentials. This shows that most chemical problems for the investigation of the excited states of molecules require multireference accuracy.

Recent studies of ML-based photodynamics simulations have shown that many thousands of data points are necessary to describe a few excited-state potentials of small molecular systems. To the best of our knowledge, the dynamics in the excited states with ML for molecules with more than 12 atoms in full dimensions has not yet been investigated.^139,145,146 Especially, the huge number of data points is concerning in this case, as larger molecules with more energetic states and a complex photochemistry could require many more data points. A meaningful training set generation, which can be achieved with active learning, adaptive sampling, and structure-based sampling techniques, is thus essential for dynamics simulations.^{94,111,515,559} Clustering of molecular geometries obtained from dynamics simulations with a cheap method further is beneficial for selecting important reference geometries.^{139,140,517,560,561} Still, the high costs and the complexity of multireference methods to compute an ample training set for ML also hamper the application of ML models to fit the excited states of larger polyatomic systems, whose accurate photochemical description is often additionally complicated by a high density of electronic states.

Single reference methods, such as time-dependent DFT, are advantageous with respect to the computational costs of the training set, but suffer from qualitatively incorrect PESs in some conformational regions of molecules, such as dissociative regions. In principle, these conformational regions could be excluded from the training set, and the remaining conformational space could be interpolated using ML, but the training set would then remain incomplete and so would the dynamics. Schemes like the Δ-learning approach³⁵⁸ or transfer learning³⁶⁰ could be helpful in this regard. These approaches might be useful to let ML models learn from single-reference data and adjust their accuracy according to multireference methods. The direct use of approximated methods, such as time-dependent DFT-based tight binding, is most likely not suitable for photodynamics on long time scales, because such approaches might easily be quantitatively incorrect. Of particular concern is then the accumulation of quantitatively tiny errors in the underlying potentials toward wrong dynamics trends. At the current stage of research, it is not clear whether such approximate potentials can provide qualitatively correct trends for reaction dynamics.¹⁷⁵

In addition to the aforementioned problems, the training set generation is complicated by the arbitrariness of the signs of coupling values and properties resulting from two different electronic states.^{15,16,92,94,95,97} This arbitrariness has to be removed in order to make data learnable with conventional methods. Such a correction scheme is termed phase correction and has been applied to correct coupling values and dipole moments.^{16,92,94,97,546} An alternative phase correction training algorithm has been shown to be beneficial with respect to the costs of the training set generation and has enabled the learning of raw quantum chemical data.¹⁵

Figure 11b shows which ML models are applied in the discussed studies. About two-thirds rely on NNs, whereby simple multilayer feed-forward NNs are most often employed. Several research fields were advanced with NN-fitted functions: photodynamics simulations (refs (15, 93−95, 98, 140, 141, 143, 144, 147, 392, 412, and 413)), spectra predictions and analysis,^{97,152,155,241,490,510,539} excited-state properties,^{15−17,92,95,97,510} diabatization procedures,^96,142 interpretation of reaction outcomes,^160,696 and the prediction of HOMO–LUMO gaps or gaps between energetic states.^77,152,158 In these studies, between one and seven hidden layers with varying numbers of nodes were used. KRR methods were mainly applied to interpolate diabatic potentials^{145,146,149,252,660} and in studies focusing on more than one molecular systems.³⁵⁸ In general, only a few studies focused on extrapolation throughout chemical compound space in the excited states. Yet, only the energies, HOMO–LUMO gaps, or spectra based on fitted oscillator strengths could be predicted using a single ML model for different molecules.^{17,155,158,358} Decision trees were used to select an active space for diatomic molecules⁷¹ and semisupervised classification was applied to assess whether a molecule require multireference or single-reference treatment.¹⁷⁶

One drawback of recently developed ML models is that they are molecule-specific and thus not universal. In part, this issue is related to the used molecular descriptors. As can be seen in Figure 11c, most studies apply descriptors that capture molecules as a whole. The few studies, which describe PESs and properties of molecular systems from atomic contributions, either treat small molecular systems^15,95,97 or predict properties related to the ground-state equilibrium structure of a molecular system or to electronic ground state calculations, e.g., the HOMO–LUMO gaps.^77,152,158 Because of the limited transferability of existing ML models to predict the excited state PESs and properties of different molecular systems, an extrapolation throughout chemical compound space is hindered in many cases. Nevertheless, in order to preserve rotational covariance especially in transition properties, such as transition dipole moments or NAC values, atom-wise descriptors have proven to be more successful.^97,241

In order to fully exploit the advantages that ML models offer and to achieve the aforementioned goal of a transferable ML model for the excited states, a highly versatile descriptor is required, which can describe atoms in their chemical and structural environment and enable an ML model to treat molecules of arbitrary size and composition. It would be highly desirable if an ML model could then describe the photochemistry of large systems, which are too expensive to compute with precise multireference methods, using only small building blocks, i.e., small enough ones to describe their electronic structure accurately. For example, the excited states of proteins or DNA strands could potentially be predicted from contributions of amino acids or DNA bases, respectively, which is most often done using effective model Hamiltonians to date.⁵⁵ A local description of the excited-state PESs and their properties derived from the ML-fitted PESs could further provide a way toward excited-state ML/MM simulations alike QM/MM techniques.^175,536,668 Unfortunately, it is not yet known whether the excited-state PESs and properties can be constructed from atomic contributions or not.¹⁷⁵

In studies comparing different ML models, it was even suggested that nonlocal descriptors might be needed or that the electronic state has to be encoded explicitly in the molecular representation to enable a transferable description of the excited states with ML.^95,158

To conclude, the reviewed studies focus on almost all aspects of excited-state quantum chemistry and improve them successfully: ML models can help to choose a proper active space for multireference methods, and they predict secondary and tertiary outputs of quantum chemical calculations and help in the interpretation of theoretical studies. ML models push the boundaries of computed time scales⁹⁴ and are used to investigate and analyze the huge amount of data we produce every day in experiments or with high-performance computers.^160,696

It should be emphasized once more that the recent studies show that the goal of ML is not to replace existing methods completely, but to provide a way to improve them. In fact, ML models for the excited states at their current stage are far from replacing existing quantum chemical methods, and they are also far from being routine. Without human intervention, ML cannot solve existing problems, and much remains to be done to describe systems beyond single, isolated molecules.

To the best of our knowledge, what is still missing is the proof that ML can provide an approximation to the multireference wave function of a molecular system. Such an achievement would be a great advancement in the research field of photochemistry, as any property we wish to know could possibly be derived from the ML wave function. An ML representation of the electronic structure would further be beneficial to allow for an inverse design of molecules with specific properties, which has been shown to be feasible for the ground state of a molecular system.⁷⁷ The optimization of photochemical properties with respect to molecular geometries would be useful for many exciting research fields, e.g., photocatalysis,¹⁶⁶ photosensitive drug design,⁶⁹⁹ or photovoltaics.^29,30

The multifaceted photochemistry offers a perfect playground for ML models. It may be important to highlight that, despite the negative image ML has suffered in some research communities, it cannot be denied that it opens up many new ways and possibilities to improve simulations and make studies feasible that were considered unattainable only a few years, if not only months ago.⁵³⁵ The computational efficiency and high flexibility of deep learning models can lead this research field toward simulations of long time and large length scales. The possibilities ML models offer are far from being exhausted. The enormous chemical space, estimated to consist of more than 10⁶⁰ molecules,⁷⁰⁰ and the desire to develop methods, which could develop into a universal approximator, make ML models perfectly suited to advance this research field. The possibility of deep ML models to process a huge amount of data can even assist the interpretation and analysis^160,696 of many photochemical studies and can help to explore unknown physical relations and be a source of potential human inspiration.

Biographies

Julia Westermayr works as a postdoctoral research fellow at the University of Warwick (United Kingdom) in the research group of Assoc.-Prof. Dr. Reinhard Maurer. She studied Chemistry at the University of Vienna (Austria) and received her Ph.D. degree in 2020 in theoretical chemistry under the supervision of Priv.-Doz. Dr. Philipp Marquetand and Univ.-Prof. Dr. Dr. h.c. Leticia González, for which she was awarded the uni:docs fellowship of the University of Vienna. Her research interests include the photochemistry of molecules and materials and the development of machine learning models to accelerate nonadiabatic molecular dynamics simulations.

Philipp Marquetand studied chemistry at the University of Heidelberg and the University of Würzburg, where he completed his Ph.D. under the supervision of Prof. Dr. Volker Engel in 2007. He did a postdoctoral stay at the École Normale Supérieure in Paris with Prof. James T. Hynes until 2010. Afterwards, he pursued his habilitation mentored by Univ.-Prof. Dr. Dr. h.c. Leticia González at the University of Jena and the University of Vienna. Since 2017, he has been a senior scientist and university teacher (Privatdozent) at the University of Vienna. His research interests comprise machine learning with a focus on electronically excited states, computational photochemistry, and excited-state ab initio molecular dynamics. He is a developer of the SHARC program package for nonadiabatic dynamics. Furthermore, he is interested in interactions of matter with strong fields including multiphoton ionization and quantum dynamics.

The authors declare no competing financial interest.