MitoWave: Spatiotemporal analysis of mitochondrial membrane potential fluctuations during I/R

Abstract

Mitochondria exhibit unstable inner membrane potentials (ΔΨ_m) when subjected to stress, such as during ischemia/reperfusion (I/R). Understanding the mechanism of ΔΨ_m instability involves characterizing and quantifying this phenomenon in an unbiased and reproducible manner. Here, we describe a simple analytical workflow called “MitoWave” that combines wavelet transform methods and image segmentation to unravel dynamic ΔΨ_m changes in the cardiac mitochondrial network during I/R. In vitro ischemia was affected by placing a glass coverslip on a monolayer of neonatal mouse ventricular myocytes for 1 h and removing the coverslip to allow for reperfusion, revealing complex oscillatory ΔΨ_m. MitoWave analysis was then used to identify individual mitochondrial clusters within the cells and track their intrinsic oscillation frequencies over the course of reperfusion. Responses segregated into five typical behaviors were quantified by MitoWave that were corroborated by visual inspection of the time series. Statistical analysis of the distribution of oscillating mitochondrial clusters during reperfusion showed significant differences between the five different outcomes. Features such as the time point of ΔΨ_m depolarization during I/R, area of mitochondrial clusters, and time-resolved frequency components during reperfusion were determined per cell and per mitochondrial cluster. Mitochondria from neonatal mouse ventricular myocytes subjected to I/R oscillate in the frequency range of 8.6–45 mHz, with a mean of 8.73 ± 4.35 mHz. Oscillating clusters had smaller areas ranging from 49.8 ± 1.2 μm², whereas nonoscillating clusters had larger areas 66 ± 1.5 μm². A negative correlation between frequency and mitochondrial cluster area was observed. We also observed that late ΔΨ_m loss during ischemia correlated with early ΔΨ_m stabilization after oscillation on reperfusion. Thus, MitoWave analysis provides a semiautomated method to quantify complex time-resolved mitochondrial behavior in an easy-to-follow workflow, enabling unbiased, reproducible quantitation of complex nonstationary cellular phenomena.

Significance

Understanding mitochondrial instability in ischemia/reperfusion (I/R) injury is the key to determining the efficacy of interventions. MitoWave analysis is a powerful yet simple tool that enables even nonexpert users to analyze nonlinear oscillatory behavior of physiological variables from time series microscopy data. Although we used it to detect inner membrane potentials changes during I/R, it can be adapted to detect any such spatiotemporal changes. It standardizes the quantitative analysis of complex biological signals and opens the door to in-depth screening of the genes, proteins, and mechanisms underlying metabolic recovery after I/R.

Introduction

Spatiotemporal oscillations (electrical and contractile) are fundamental to normal cardiac function but are also a potential source of pathological instability and chaos (1). A stable supply of energy is required to prevent maladaptive emergent phenomena, and mitochondria are well suited to dynamically adapt to the varying workloads of the organism. Nevertheless, both under physiological conditions (2) or after metabolic stress, mitochondrial oscillations (3), flickers (4,5), transients (6), or fluctuations (7,8) have been observed when parameters such as ΔΨ_m, flavin, or NADH redox potential, pH, or reactive oxygen species (ROS) have been measured. For example, inner membrane potentials (ΔΨ_m), ROS, and NADH were shown to oscillate in a self-sustaining manner in adult cardiomyocytes subjected to substrate deprivation (9) or oxidative stress (10) in a frequency range spanning from ∼1 to 40 mHz (11). Similarly, local mitochondrial superoxide oscillations (“mitoflashes”) in cardiomyocytes had a frequency of ∼40 mHz (12). As we have previously reported, ΔΨ_m oscillation also reproducibly occurs upon reperfusion after ischemia in neonatal rat ventricular myocyte monolayers (13). Importantly, interventions that suppress mitochondrial ΔΨ_m instability on reperfusion also abrogate cardiac arrhythmias, both in neonatal myocytes (13) and isolated perfused hearts (14,15). Hence, understanding the mechanism of mitochondrial destabilization during oxidative stress or ischemia/reperfusion (I/R) injury is essential to developing novel therapeutic strategies to prevent cardiac arrhythmias and contractile dysfunction associated with metabolic stress.

Determining the efficacy of interventions targeting spatiotemporal changes in mitochondria requires a robust, unbiased analytical approach, yet there are few reports describing methods for the automated analysis of nonstationary fluctuations observed in image time series. We have previously employed wavelet transform as a tool to describe the frequency components and clustering of emergent mitochondrial ΔΨ_m oscillations after a localized laser flash using a hand-drawn grid to define individual mitochondria in the highly ordered mitochondrial network of the adult cardiac myocyte (10,11,16,17). Here, we describe a new analytical workflow for characterizing spatially distributed ΔΨ_m loss and oscillation during I/R in less well-ordered mitochondrial networks, such as neonatal cardiac myocytes. We analyze the time-resolved frequency components, area of mitochondrial clusters, and times of reversible (ischemia) or irreversible (reperfusion) ΔΨ_m loss by applying discrete or continuous wavelet transform methods, followed by feature extraction, to analyze reperfusion-induced unsynchronized ΔΨ_m oscillations in neonatal ventricular myocytes. The method accurately identifies key transitions in mitochondrial behavior during I/R and quantifies the principal frequency components of mitochondrial instability and how they evolve over time. Moreover, the method is generalizable to the analysis of spatiotemporal variation of any parameter recorded during image time series, providing a way to automate microscopy analysis that allows for unbiased, reproducible quantitation of complex nonstationary cellular phenomena.

Materials and methods

Neonatal cardiomyocyte isolation and cell culture

Animal experimentation conforms to the Guide for the Care and Use of Laboratory Animals published by the National Institutes of Health (National Institutes of Health publication #85-23, revised 1996) and was approved by the Johns Hopkins Animal Care and Use Committee. Neonatal mouse cardiac myocytes were isolated using the MACS cell separation kit (catalog #130-100-825 and #130-098-373; Miltenyi Biotec, Bergisch Gladbach, Germany). Briefly, hearts from 0- to 2-day-old mice were excised, chopped into small pieces, and digested using reagents supplied by the kit. A cardiomyocyte-rich cell suspension was obtained by separation of magnetically labeled noncardiac cells from total cell suspension upon application of a magnetic field. 1 × 10⁶ neonatal mouse cardiac myocytes were plated on fibronectin-coated (10 μg/mL) 35-mm (D = 20 mm) glass coverslip dishes (catalog #801001; NEST, Jiangsu, China) in Medium-199 supplemented with 25 mM HEPES, 2 μg/mL vitamin B12, 50 U/mL penicillin-streptomycin, 1× nonessential 286 amino acids. and 10% fetal bovine serum. The next day, the medium was changed to 2% fetal bovine serum medium. I/R experiments and imaging were performed on the fifth to sixth day of culture.

Inducing ischemia and reperfusion and ΔΨ_m imaging

To monitor mitochondrial inner membrane potential (ΔΨ_m), 50 nM tetramethylrhodamine methylester (TMRM) was loaded for 30 min at 37°C before the start of the experiment, and the media was then replaced with fresh Tyrode’s buffer (130 mM NaCl, 5 mM KCl, 1 mM MgCl₂, 10 mM NaHEPES, 1 mM CaCl₂, and 5 mM glucose). The experiment was performed at 37°C. A typical protocol included a baseline reading for 10 min followed by 60 min of regional ischemia induced by placing a glass coverslip and followed by 60 min of reperfusion upon removal of the coverslip, as previously described in neonatal rat ventricular myocytes (13,18). During this 130-min period, images were obtained every 15 s on a laser-scanning confocal microscope (FV3000RS; Olympus, Tokyo, Japan). TMRM fluorescence was imaged using a 40× silicone-immersion objective (UPLSAPO40XS; Olympus) with 561 nm excitation/570–620 nm emission. Cells were imaged in Galvano scanning mode without averaging. Each image was 16-bit with a size of 318.2 × 318.2 microns (512 × 512 pixels). At the 15-s image acquisition interval, only frequencies below 66.67 mHz are resolvable based on Nyquist-Shannon sampling theorem (19). To minimize laser-induced damage during the long protocol, a neutral density filter of 10% was applied in the excitation path, and the laser intensity was set by the software to 0.06% power (source: 20 mW, 561 nm light-emitting diode laser). We detected no laser-induced oscillations, photo damage, or bleaching of TMRM in control imaging experiments of equal duration (130 min), confirming that the observed oscillatory phenomena were the result of ischemia-reperfusion rather than a direct effect of laser-induced oxidative stress (see Fig. S1; Video S1).

Image analysis

Image series of the time course of I/R experiments were analyzed using the open-source software Fiji (https://imagej.net/Fiji/Downloads), a customized distribution of ImageJ. A custom-built segmentation-analysis macro was generated to track each cell’s ΔΨ_m during the in vitro I/R injury. ΔΨ_m response to I/R was analyzed at the cellular level by segmentation analysis. Steps for segmentation analysis included a preprocessing step to align the images in the stack using a “StackReg” plugin (20). Segmentation of each cell was done by applying a median filter (radius = 2) to the first image of the stack and then applying an auto local threshold (Niblack). All particles above the radius of 60 were included in the analysis. TMRM fluorescence intensity for each cell over ischemia and reperfusion were obtained (see Supporting materials and methods for macros).

Results

Discrete and continuous wavelet transform

Limited information can be obtained through the use of frequency domain methods such as Fourier transform when analyzing complex biological signals that are nonstationary and time varying. Wavelet transform methods, on the other hand, permit resolution of the time of event occurrences and changes in the frequency relationship over time. Signal processing by a selected wavelet transform function called the “mother wavelet” is scaled and shifted along the source signal with “daughter wavelets.” This generates coefficients that represent the best fit of the wavelet transform function to the source signal (21). There are two kinds of wavelet transforms, discrete and continuous wavelet transforms (CWT). With discrete wavelet transform, the signal is decomposed into discrete frequency bands, without overlap of the time-frequency windows of the wavelet function. To detect major transitions that may be hidden in the noise of a physiological signal, the maximal overlap discrete wavelet transform (MODWT) (21) can be employed. MODWT decomposes the signal into finer and finer frequency levels. As the level increases, large-scale approximations of the signal are obtained, and lower-frequency components of the signal are well resolved. MODWT of a signal allows for multiresolution analysis (MRA) that reconstructs the decomposed time series as a sum of several new series that are aligned in time with the original signal. MODWT-MRA effects a zero-phase filtering of the signal. Features are time aligned, unlike MODWT alone. CWT involves transformation of the signal by continuously changing the scaling and shifting factors. Although this introduces some information redundancy, it presents a more detailed, high-resolution view of the characteristics of the signal. Coefficients generated by CWT are represented by a scalogram that is a visual representation of the frequency components of the signal as they change over time.

In our experiments on cardiomyocytes loaded with the potentiometric fluorophore TMRM and subjected to an in vitro I/R protocol, we used MODWT-MRA to identify the timing of the major ΔΨ_m depolarization during ischemia for each cell. CWT was utilized to analyze the more complex time-varying frequency components of the ΔΨ_m oscillations observed in individual “clusters” of mitochondria during reperfusion. Mitochondrial clusters refer to contiguous regions of interest (ROIs) within the cell where the TMRM signal changes repeatedly (oscillates) on reperfusion, as defined by image segmentation of the differential image stack (described below). The clusters represent mitochondria-displaying coupled ΔΨ_m behavior. In this study, we used the symlet wavelet (4,8). Symlet wavelet was chosen over others as the “mother wavelet” because it closely matched the TMRM signal from the mitochondria. The image processing and wavelet transform workflow, along with feature extraction from the images and scalograms obtained, allowed us to precisely determine the following: 1) the time point of ΔΨ_m loss for each cell during ischemia, 2) the incidence of ΔΨ_m oscillation for each mitochondrial cluster and its frequency throughout the reperfusion period, 3) whether ΔΨ_m stabilized or irreversibly collapsed during reperfusion, and 4) the size distribution of the oscillating mitochondrial clusters.

Identification of transition time points of inner mitochondrial membrane potentials during ischemia

To analyze a time series of the mitochondrial inner membrane potential, we used MODWT-MRA to identify time-localized changes in the TMRM signal employing the wavelet toolbox of MATLAB (The MathWorks, Natick, MA https://www.mathworks.com/products/wavelet.html). The TMRM signal from each cell during the ischemic period was transformed with a sym4 wavelet with four levels of decomposition. Lower-level decompositions involve higher frequencies, and higher-level decompositions involve slower frequencies. For example, Fig. 1 shows a raw TMRM signal from a single cell (Fig. 1 A) decomposed into four levels using a sym4 wavelet transform (Fig. 1 B). Level 1 has the frequency components between 33.4 and 16.7 mHz, level 2 has 17.3–8.05 mHz, level 3 has 8.62–4.02 mHz, and level 4 has 4.3–2.1 mHz. All levels of decompositions have associated relative energies. For our purpose of estimating the ΔΨ_m depolarization time, we removed all higher-frequency components with lower relative energy and reconstructed the signal by retaining the highest relative energy (of more than 99%) (Fig. 1 C). We essentially filter out the “noise” by this process. With this time-aligned reconstructed signal, we used the MATLAB function “findchangepoints” to obtain the time point at which the reconstructed signal changed significantly (Fig. 1 C). The time point of ischemic depolarization can thus be automatically determined for several cells (Fig. 1 E).

Figure 1.

Identification of ischemic depolarization time. Raw TMRM signals during ischemic period (A) are decomposed using MODWT (B) and reconstructed by retaining the signal with the highest relative energy (C). MATLAB’s “findchangepoints” function identifies the time point at which the signal changed significantly during ischemia. Here, it is at 43 min. (D) Example of a cell with the first image at baseline and subsequent images in the last phases of depolarization. Images are 15 s apart. TMRM intensity is abruptly diminished at the 43rd min. (E) Example of I/R experiment with >100 cells in which the black dots represent ischemic depolarization time points.

Obtaining features and frequency components of ΔΨ_m oscillations during reperfusion

Mitochondria exhibited nonstationary oscillatory behavior throughout reperfusion (Fig. 2). We categorized ΔΨ_m oscillatory behavior based on our visual observations of 10 experiments. There were five outcomes that were observed based on the oscillatory state of ΔΨ_m throughout the reperfusion time period, i.e., 1) ΔΨ_m oscillations persisting throughout; 2) no or very few ΔΨ_m oscillations; 3) ΔΨ_m oscillations that stabilized after oscillating initially; 4) ΔΨ_m oscillations that occurred, but there was early ΔΨ_m loss; and 5) no ΔΨ_m oscillations occurred, and there was early ΔΨ_m loss (Fig. 2). We used CWT (sym8, MATLAB) to process the TMRM signal and observed that the signal processing tool readily detected transitions and frequencies depicting the behavior of mitochondrial ΔΨ_m changes. Fig. 2 (right panel) shows the scalograms obtained after performing a wavelet transform of the TMRM signal. We observed that an oscillating cluster has high coefficients concentrated in the scale of ∼1–10, corresponding to a frequency of 4.3–45 mHz (Fig. 2, red brackets), which does not exist in the scalogram of the nonoscillating cluster or during ischemia. Periodic features in the scalogram, indicated by the red brackets, illustrate the high-frequency features appearing in the scalogram when ΔΨ_m is oscillating, at least for some period, during reperfusion. These features are absent in nonoscillating clusters. The wavelet transform function generates 64 × 241 coefficients per mitochondrial cluster, and the coefficient scale ranges from 4000 to −2000. To reduce this large data set, we used autothresholding from Fiji to help reduce the data. Autothresholding is a histogram-based thresholding method that uses the same critical value across the whole image. Because of differences in TMRM intensity between different mitochondria, the CWT coefficients generated by different mitochondria are slightly different. Therefore, a single critical value is not set for all mitochondria across all experiments. We allowed the autothresholding algorithm to automatically select a critical value above which coefficients were further considered. We consider high scalogram coefficients as those that exceed the automated thresholding routine used to further quantify and statistically analyze the scalogram components, as shown in Fig. 3 H.

Figure 2.

Mitochondria exhibit different ΔΨm oscillatory behaviors upon reperfusion. ΔΨm signals (TMRM fluorescence) for representative mitochondrial clusters during ischemia and reperfusion are shown in the left panels, and corresponding CWTs are shown in the right panels as scalograms. Frequencies and corresponding transition time points can be extracted from the scalograms. Mean TMRM fluorescence intensities of an oscillating cluster (A), a nonoscillating cluster (B), an oscillating cluster exhibiting ΔΨm loss (C), a cluster that oscillates before stabilizing (D), and a nonoscillating cluster exhibiting ΔΨm loss (E). If a cluster oscillates as in (A), (C), and (D), they exhibit high coefficients concentrated in the scale of ~1–10, corresponding to a frequency of 4.3–45 mHz (indicated by a red bracket), which is absent in the scalogram of a nonoscillating cluster or during ischemia. To see this figure in color, go online.

Figure 3.

Schematic of MitoWave analysis for ΔΨm feature extraction. It involves the following steps: (A) image acquisition with a confocal microscope using TMRM monitors ΔΨm changes, (B and C) cellular segmentation using custom-made Fiji macros separates each cell, (D) differential stack z-projection image for each cell is used to identify mitochondrial clusters that oscillate (MATLAB/Fiji Routine), (E and F) TMRM fluorescence time course for each cluster is obtained, (G) scalograms are generated by CWT of the TMRM signal, (H) features and frequency components are extracted from the scalograms, and (I) mitochondrial oscillators are classified into high/low frequency bands to obtain patterns of oscillatory behavior as a function of reperfusion time.

This wavelet tool was then applied to detect transitions, frequencies, and times associated with these changes automatically for a large number of cells (>100 per experiment) and mitochondrial clusters (>400 per experiment). The MATLAB/Fiji platform was used to perform feature extraction for ΔΨ_m changes throughout the reperfusion time period (Fig. 3). The procedure involved the following steps: image acquisition with a confocal microscope using TMRM to monitor ΔΨ_m changes (Fig. 3 A); cellular segmentation using custom-made Fiji macros to define each cell (Fig. 3 B); autothresholding, in which each frame of the image sequence was thresholded using the same criteria, and each cell was separated into its own image series (Fig. 3 C); and creation of an image differential stack of the reperfusion phase of the image series by subtracting the nth image from the (n−1)th image (Fig. 3 D). The sum of differentials in this stack was then used to highlight the mitochondrial clusters that oscillated during the reperfusion period: thresholding the z-projection of this differential image stack to obtain ROIs outlining oscillating mitochondrial clusters (Fig. 3 E); application of the ROIs to the reperfusion phase to obtain TMRM signals for each cluster through this time period (Fig. 3 F); and CWT of the TMRM signal (with a sym8 wavelet) to generate a coefficient matrix, visualized as a scalogram (Fig. 3 G). The regions on the scalogram with large coefficients indicate where the mother wavelet fits the signal well. The x axis represents the scaled time points, and the y axis represents the scale (scale α 1/frequency). Usually, an oscillating mitochondrion shows high-coefficient peaks corresponding to the scale range from 3 to 10. ΔΨ_m can also undergo larger transitions throughout reperfusion, and these changes are reflected in the scalograms as high coefficient peaks: importation of the resulting coefficient matrix as a scalogram image and extraction of predominant frequency features as a function of reperfusion time (Fig. 3 H). The x and y coordinates of the outlined maximal coefficients were obtained. The x axis of the scalogram represents the time, and the y axis represents the scale (scale α 1/frequency); mitochondrial oscillators associated with time were then classified into high/low frequency bands (Fig. 3 I). If a mitochondrial cluster oscillated in different frequency bands at multiple times during the reperfusion phase, then its average frequency at each time was plotted. Thus, patterns of oscillatory behavior were obtained. We will henceforth refer to this routine as the MitoWave analysis.

See Supporting materials and methods for ImageJ macros and MATLAB codes or on GitHub https://github.com/dashok1/MitoWave/releases/tag/v1.0.2.

Defining oscillatory behavior patterns during reperfusion

The behavior of each mitochondrial cluster was plotted into its corresponding frequency band, which varied over the reperfusion time period, as represented in violin plots (Fig. 4). Frequencies were categorized as high frequency ranging from 45 to 4.3 mHz (∼22–230 s), moderately fast frequencies ranging from 4.3 to 2.2 mHz (∼230–450 s), slow frequencies ranging from 2.2 to 1.8 mHz (∼450–550 s), and below 1.8 mHz. Mitochondrial oscillators typically were present in the 45–4.3 mHz band. We also plotted the time at which there was complete ΔΨ_m loss during the reperfusion period. Applying MitoWave Analysis on 10 in vitro I/R experiments, we verified that our visual observations matched the quantitative analysis. In experiments in which the mitochondrial oscillations persisted throughout the reperfusion period, high-frequency oscillators appeared at all time periods in the violin plots (Fig. 4 A), and when mitochondria had few or no oscillations (Fig. 4 B), the plot was dominated by clusters appearing in the lowest frequency band (below 1.8 mHz), with the few high-frequency oscillators disappearing by 20 min of reperfusion. Another pattern consisted of mitochondrial oscillations that occurred at the beginning of reperfusion and then underwent ΔΨ_m depolarization at mid-to-late reperfusion; this appeared as a tapering off of the high-frequency oscillations and an increased density in the lowest band denoting complete ΔΨ_m depolarization (Fig. 4 C). In other experiments, mitochondria exhibited high-frequency oscillations during early reperfusion and then transitioned to a stable polarized state (below 1.8 mHz) after 20 min reperfusion (Fig. 4 D). Finally, in some experiments, we observed that ΔΨ_m could remain stable for the first 30–40 min of reperfusion but then depolarize over the next 30 min, appearing as a shift in the population from the “below 1.8 mHz” band into the ΔΨ_m loss band (Fig. 4 E). We classified these reperfusion behaviors into five different categories: oscillating (Fig. 4 A; Video S2), nonoscillating (Fig. 4 B; Video S3), oscillating with early ΔΨ_m loss (Fig. 4 C; Video S4), oscillating with early ΔΨ_m stabilization (Fig. 4 D; Video S5), and nonoscillating with early ΔΨ_m loss (Fig. 4 E; Video S6).

Figure 4.

Defining ΔΨm oscillatory patterns during reperfusion qualitatively and quantitatively. Visual observations of the I/R image stack can qualitatively classify oscillatory behavior patterns of mitochondrial clusters during reperfusion. We classified oscillatory patterns from 10 experiments into five groups: oscillating, not oscillating, oscillating with early ΔΨm loss, oscillating with ΔΨm stabilization, and nonoscillating clusters with early ΔΨm loss (Table 2). By subjecting the TMRM signal from each mitochondrial cluster to MitoWave analysis, we characterize oscillatory behavior quantitatively with violin plots (A–E). Each dot represents a mitochondrial cluster oscillating at a certain frequency corresponding to a certain time point. Visual observations (Table 2) are corroborated by results from the quantitative MitoWave analysis routine (A–E). We see that a mitochondrial cluster can change its oscillatory pattern throughout the reperfusion period, i.e., its frequency may change from one frequency band to another. The y axis shows six frequency bands as well as the time at which a mitochondrial cluster completely loses ΔΨm during reperfusion. The x axis represents the time of reperfusion. To see this figure in color, go online.

Predominant frequencies of mitochondrial clusters

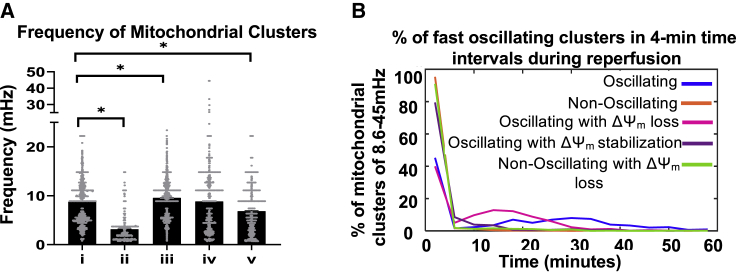
We obtained the predominant frequencies of mitochondrial clusters by considering the first, fast frequency band (8.6–45 mHz). If the mitochondrial cluster did not have a frequency in that band, the next frequency band was considered and so on till the slowest frequency band. This way, we could extract the frequencies that most closely represented mitochondrial oscillating frequencies. An average or a weighted average could not be used because most mitochondrial clusters also have slow frequency components but not all mitochondria have fast frequency components. Oscillating clusters have a frequency of 8.73 ± 4.35 mHz (1081 clusters; mean ± SD), nonoscillating clusters have 3.13 ± 2.61 mHz (732 clusters), oscillating clusters with early ΔΨ loss have 9.56 ± 3.66 mHz (1402 clusters), oscillating clusters with ΔΨ_m stabilization have 8.81 ± 6.03 mHz (1009 clusters), and nonoscillating clusters with early ΔΨ_m loss have 6.82 ± 4.63 mHz (880 clusters) (Fig. 5 A).

Figure 5.

Predominant frequencies exhibited by mitochondrial clusters during reperfusion. The predominant frequencies exhibited by mitochondrial clusters fell within the 8.6–45 mHz band. (A) The mean predominant frequency ±SD for (i) oscillating clusters, 8.73 ± 4.35 mHz (1081 clusters); (ii) nonoscillating clusters, 3.13 ± 2.61 mHz (732 clusters); (iii) oscillating cluster with early ΔΨm loss, 9.56 ± 3.66 mHz (1402 clusters); (iv) oscillating cluster with ΔΨm stabilization, 8.81 ± 6.03 mHz (1009 clusters); and (v) nonoscillating clusters with 15 early ΔΨm loss, 6.82 ± 4.63 mHz (880 clusters). One-way ANOVA was performed to determine statistical significance; ^∗p < 0.0001. (B) Percentage of mitochondrial clusters oscillating in the 8.6–45 mHz frequency band binned at 4-min intervals during the reperfusion period. To see this figure in color, go online.

Further, we analyzed the distribution of high-frequency oscillators (in the 8.6–45 mHz frequency band) to see how they vary throughout reperfusion time among the different categories. Clusters that did not have a frequency in this band (of 8.6–45 mHz) were given a value of zero. We plotted the percentage of the different categories of oscillating clusters against time (Fig. 5 B). We observed that among the oscillating category (blue line), 8–12% of mitochondria exhibited this high-frequency oscillation from 15 to 40 min of reperfusion. This was absent in the nonoscillating (orange line), in the oscillating with early ΔΨ_m stabilization (violet line), and the nonoscillating with ΔΨ_m loss (green line) categories. The oscillating with early ΔΨ_m loss (pink line) shows that ∼7–15% of mitochondria exhibit high frequency only in the early reperfusion phase, until ∼25 min, after which they do not. Further, we also statistically analyzed the distribution of these high-frequency oscillators. A Kolmogorov-Smirnov nonparametric two-sample test (kstest2 on MATLAB) was performed to test the null hypothesis that distribution of various oscillation behaviors was not different during the reperfusion time period. Kolmogorov-Smirnov test shows significant differences between the different categories, comparing oscillating and nonoscillating clusters, oscillating and oscillating with early ΔΨ_m loss, oscillating and ΔΨ_m stabilizing clusters, and oscillating and nonoscillating with early ΔΨm loss (p < 0.0001). Thus, we quantitatively confirm our visual observations that the distribution of oscillating mitochondrial clusters that change dynamically over time are different between different categories of oscillating experiments.

Frequency and mitochondrial cluster size are negatively correlated

We observed that in experiments in which there were no/few oscillations, mitochondrial clusters appeared larger than in experiments in which mitochondria had persistent oscillations. Previous reports in adult cardiac myocytes also showed that larger clusters have slower oscillations (11). Therefore, we wanted to check if this was true in neonatal cardiac myocytes as well. MitoWave analysis of neonatal mouse ventricular myocytes (NMVMs) subjected to I/R agreed with our visual observations. Oscillating mitochondria had the smallest area of 49.8 μm² vs. a larger area of 66 μm² for nonoscillating mitochondria (Fig. 6 A). We performed nonparametric correlation coefficient analysis to understand the relationship between the size of mitochondrial clusters and its frequency. We found that there is a negative correlation between oscillating frequency and the size of the mitochondrial cluster, with a correlation coefficient of r = −0.58 (Fig. 6 B). Mitochondrial cluster size decreased by ∼4.6 μm² for every millihertz increase. This suggests that if mitochondria are organized in larger clusters, they undergo slower oscillations and may eventually stabilize ΔΨ_m and be protected against ΔΨ_m loss during reperfusion after ischemia.

Figure 6.

(A) Mitochondrial cluster size and frequency relationship. Areas of mitochondrial clusters were compared for clusters exhibiting different oscillatory behaviors (across several experiments). (i) Oscillating clusters had an area of 49.8 ± 1.2 μm² (1081 clusters); (ii) nonoscillating clusters, 66 ± 1.5 μm² (732 clusters); (iii) oscillating cluster with early ΔΨ loss, 49.7 ± 0.9 μm² (1402 clusters); (iv) oscillating cluster with ΔΨm stabilization, 53.2 ± 1.2 μm² (1009 clusters), and (v) nonoscillating clusters with early ΔΨm loss, 67.9 ± 1.7 μm² (880 clusters). One-way ANOVA was performed to determine statistical significance; ^∗p < 0.0001. Area mean ± SE are indicated. (B) Frequency and cluster size show an inverse relationship. In oscillating clusters, the area of the cluster decreases by ~4.6 μm² for every millihertz increase. 95% confidence intervals are plotted (red) with linear regression line (black). To see this figure in color, go online.

Correlation between ischemic depolarization time point and ΔΨ_m oscillation frequency

Next, we examined whether early irreversible ΔΨ_m loss on reperfusion was correlated with mitochondrial behavior during the preceding ischemia. We quantified the time to ΔΨ_m loss during ischemia per cell (Fig. 7 A) and also the time to ΔΨ_m loss per mitochondrion during reperfusion (Fig. 7 B) for the different reperfusion outcome categories. We found that the two categories showing early irreversible ΔΨ_m loss on reperfusion (oscillating early ΔΨ_m loss, iii, and nonoscillating early ΔΨ_m loss, v) had shorter average times to depolarization during ischemia. Thus, the history of the behavior during ischemia was a more important determinant of mitochondrial recovery than whether or not a mitochondrial cluster oscillated or not upon reperfusion. This is also evident in the empirical cumulative distribution functions to visualize the time to ΔΨ_m loss during ischemia, in which later ΔΨ_m loss during ischemia correlated with mitochondrial ΔΨ_m stabilization during reperfusion, regardless of whether the mitochondria were oscillating or not (orange and violet plots in Fig. 8, A and B).

Figure 7.

Time taken for ΔΨm loss during ischemia and reperfusion. (A) Time taken for ΔΨm loss during ischemia versus the ensuing oscillatory behavior on reperfusion. (i) Oscillating clusters maintained ΔΨm until 43.52 ± 5.87 min; (ii) nonoscillating clusters, 46.36 ± 9.17 min; (iii) oscillating with early ΔΨm loss, 35.62 ± 9.25 min; (iv) oscillating with early ΔΨm stabilization, 52.84 ± 11.17 min; and (v) nonoscillating clusters with early ΔΨm loss, 30.46 ± 7.81 min (mean and SD are indicated). (B) Percentage of mitochondrial clusters exhibiting irreversible ΔΨm loss during reperfusion. Oscillating clusters lost ΔΨm on average at 58.71 ± 6.3 min of reperfusion, nonoscillating clusters maintained stable ΔΨm to the end of 60.25 min of reperfusion, oscillating clusters with early ΔΨm loss depolarized at 45.8 ± 11.05 min, oscillating clusters with ΔΨm stabilization lasted 60.1 ± 2 min, and nonoscillating clusters with early ΔΨm loss depolarized at 53.38 ± 10.99 min (mean and SD are indicated). To see this figure in color, go online.

Figure 8.

Relationship between ischemic ΔΨm depolarization time and oscillatory behavior during reperfusion. (A) Empirical cumulative distribution functions showing the probability of depolarization as a function of time during ischemia. Note that mitochondria displaying early ΔΨm loss on reperfusion (regardless of whether or not they oscillated) correlated with earlier loss of ΔΨm during ischemia. (B) Empirical cumulative distribution functions showing the probability of depolarization as a function of time during reperfusion. Mitochondria that stabilized and resisted depolarization during reperfusion correlated with a history of later ΔΨm loss during ischemia (purple lines in A and B). To see this figure in color, go online.

Discussion

Over the course of ischemia-reperfusion, the mitochondrial networks of cultured neonatal mouse cardiomyocytes displayed complex spatiotemporal patterns, including bistability and time-varying oscillatory behavior, presenting significant challenges to analysis. This work combined image segmentation with the versatility of wavelet transforms to quantify key transitions associated with the pathophysiology of I/R injury in an unbiased manner. Essential information could be captured in a semiautomated workflow, including the time to mitochondrial depolarization during ischemia, frequency of ΔΨ_m oscillation of individual mitochondrial clusters upon reperfusion, and time to catastrophic loss of ΔΨ_m with prolonged reperfusion. Subsequent data reduction permits one to make statistical comparisons between different experiments to determine if a given treatment or intervention has a significant effect on mitochondrial function.

Much of the current information on mitochondrial dynamic network properties were obtained from adult cardiac myocytes, with well-developed mitochondrial network and sarcomeric proteins. We have previously reported that adult cardiomyocytes subjected to metabolic or oxidative stress undergo spontaneous oscillations in ΔΨ_m that occur either in small clusters or are synchronized across the whole cell (11). Cell-wide ΔΨ_m synchronization is observed after a critical number of mitochondria in the network show oxidative stress, a phenomenon we termed “mitochondrial criticality” (22). Synchronization of mitochondria in the organized array of the adult myocyte depends on ROS-dependent neighbor-neighbor interactions between organelles, with long-range cluster interactions following the behavior of a percolation lattice (23). However, in neonatal myocytes, the mitochondrial network is less ordered, and reperfusion-induced oscillations are less likely to be synchronized throughout the entire network (13). This is consistent with a short effective diffusion distance for ROS-induced ROS release (10). In contrast, when the system is forced by a uniform environmental stress, such as ischemia, mitochondrial network depolarization occurs on a cell-by-cell basis, likely determined by the anaerobic ATP-generating capacity and glycogen store of the individual cells.

Previous studies in our lab induced whole cell mitochondrial oscillations in adult guinea pig cardiomyocytes using either substrate deprivation, antioxidant depletion, or a localized laser flash as the initiating stress. In this study, we focused on observing and quantifying mitochondrial oscillatory behavior during the pathophysiologically relevant condition of ischemia-reperfusion. In our prior work (11,16,17,24), we used wavelet transform methods to uncover frequencies of oscillating mitochondria, with a manually drawn grid to identify individual mitochondria. This was feasible because of the regular lattice-like organization of the adult myocyte mitochondrial network but would have been intractable for this study of oscillating clusters in the less ordered network of NMVMs, in which an a priori assumption about how to define an individual mitochondrion is impossible. Hence, a key advance is the two-step process of automated segmentation followed by wavelet transform analysis. Moreover, the wavelet transform was used not just to uncover frequencies but also to identify transition time points, such as the times to ischemic depolarization or terminal ΔΨ_m depolarization during reperfusion. Wavelet transform was used to effectively “de-noise” the TMRM signal by frequency component decomposition, revealing a clear major transition in polarization.

In a less ordered system such as neonatal cardiomyocytes, it was important to establish a method to quantify ΔΨ_m oscillatory behavior in an unbiased manner. We observed that individual mitochondrial clusters could exhibit different kinds of oscillatory behavior during reperfusion (Fig. 2, left panel). Subjecting the TMRM signal from individual mitochondrial clusters to wavelet transform allowed for extraction of different features of ΔΨ_m behavior. The first step to begin automating the process of feature extraction was to define the oscillating mitochondrial clusters. The image stack subtraction method to generate a differential stack was a novel and powerful way to capture the behavior of distinct oscillating mitochondrial clusters during reperfusion. After outlining individual mitochondrial clusters, we obtained the TMRM signal from each mitochondrial cluster throughout the reperfusion phase. Thus, we could automate the method of obtaining ΔΨ_m signals from >400 mitochondrial clusters and >100 cells from multiple experiments.

Another advantage of the wavelet approach over other methods is that fast Fourier transform and power spectral analysis are limited to short duration signals of ∼7 min (25), whereas the wavelet transform method, with its ability to scale and shift to fit the original signal, can be used for long time periods.

Biological implications of analyzing ΔΨ_m instability

Synchronization of a network of dynamically coupled oscillators spanning a broad frequency range to a single dominant frequency is common to physical, chemical, and biological systems. The lack of synchronization in NMVMs and the broader frequency distribution (Fig. 5) may be the result of the more disorganized arrangement of mitochondria in neonatal myocytes or weaker coupling between mitochondria in the immature cells. These findings show that in NMVMs subjected to I/R, ΔΨ_m oscillation frequency is inversely correlated with cluster size (Fig. 6). This is in agreement with the negative correlation obtained by wavelet transform analysis of adult myocytes under oxidative stress, with large mitochondrial clusters showing slow ΔΨ_m oscillations that could span the entire cell with a stereotypical frequency of 1–10 mHz (11).

The average time to ischemic ΔΨ_m depolarization for a given coverslip was compared to the oscillatory behavior of mitochondrial clusters on reperfusion (Figs. 7 and 8). Interestingly, early ΔΨ_m loss during ischemia correlated with early ΔΨ_m loss during reperfusion; however, this was equally true for both oscillating and nonoscillating clusters, suggesting that there is no specific protective advantage of the oscillatory behavior. In fact, there was a trend toward earlier depolarization during reperfusion for oscillating versus nonoscillating mitochondrial clusters. At least concerning mitochondrial recovery after reperfusion, these findings argue against the idea that oscillations in metabolism might preserve a higher average ATP/ADP ratio while decreasing free energy dissipation compared with steady-state operation (26). Instead, mitochondrial ΔΨ_m oscillation could simply be an inevitable consequence of the nonlinear control properties of the nonlinear bioenergetic system. In addition, late ΔΨ_m loss during ischemia correlated with ΔΨ_m stabilization after oscillation on reperfusion. Together, these data indicate that mitochondrial energetic recovery strongly depends on resistance to initial ischemic depolarization, consistent with data from intact perfused hearts (27). Thus, information about the frequency, cluster size, and sensitivity to oscillation can provide clues to the myocyte’s susceptibility to death.

The method described here provides a way to uncover and quantify different mitochondrial responses to I/R stress that might otherwise be overlooked if one were to only examine the average behavior of a monolayer, of individual cells, or at single time points during a protocol (e.g., measuring lactate dehydrogenase release as an index of damage after reperfusion). A current limitation of the method is that it would be affected by significant movement of the objects being analyzed in the optical field, which was minimal in our experiments. In the future, it might be possible to further develop the approach by incorporating object tracking methods. Nevertheless, the approach is applicable to any spatially distributed system of time-varying oscillatory signals. Unlike Fourier transform analysis, the underlying oscillator frequencies and phases do not have to be time invariant, and the method is largely immune to changes in signal offset (such as photobleaching) or background artifacts. This novel approach, which standardizes the quantitative analysis of complex biological signals, opens the door to in-depth screening of the genes, proteins, and mechanisms underlying metabolic recovery after ischemia-reperfusion.

Author contributions

D.A. performed experiments, performed analysis, wrote codes for analysis, and wrote the article. B.O. conceived the idea and wrote the article.

Editor: Anne Kenworthy.

Supporting material

Document S1. Supporting materials and methods

Fig. S1. Control imaging experiment with no I/R