Determinants of conductance of a bacterial voltage-gated sodium channel

Abstract

Through molecular dynamics (MD) and free energy simulations in electric fields, we examine the factors influencing conductance of bacterial voltage-gated sodium channel Na_vMs. The channel utilizes four glutamic acid residues in the selectivity filter (SF). Previously, we have shown, through constant pH and free energy calculations of pKa values, that fully deprotonated, singly protonated, and doubly protonated states are all feasible at physiological pH, depending on how many ions are bound in the SF. With 173 MD simulations of 450 or 500 ns and additional free energy simulations, we determine that the conductance is highest for the deprotonated state and decreases with each additional proton bound. We also determine that the pKa value of the four glutamic residues for the transition between deprotonated and singly protonated states is close to the physiological pH and that there is a small voltage dependence. The pKa value and conductance trends are in agreement with experimental work on bacterial Na_v channels, which show a decrease in maximal conductance with lowering of pH, with pKa in the physiological range. We examine binding sites for Na⁺ in the SF, compare with previous work, and note a dependence on starting structures. We find that narrowing of the gate backbone to values lower than the crystal structure's backbone radius reduces the conductance, whereas increasing the gate radius further does not affect the conductance. Simulations with some amount of negatively charged lipids as opposed to purely neutral lipids increases the conductance, as do simulations at higher voltages.

Significance

Conduction of sodium ions through voltage-gated sodium channels is an essential biological process and has been shown experimentally to be pH dependent. However, the molecular mechanism of this dependence is unclear. Here, we show that channel conductance decreases with each proton bound to the glutamic acid residues in the selectivity filter (SF). Proton binding changes the electrostatic environment around the SF and induces conformational transitions of the SF, both of which increase the free energy barrier for the sodium ions around the SF. The conductance and barrier are shown to relate to each other through the Arrhenius equation, which suggests that the conduction is a simple process. We also show that the conduction is influenced by the lipid composition of the membrane.

Introduction

Voltage-gated sodium (Na_v) channels allow passage of sodium ions into cells. The transition from the closed, nonconducting state to an open, conducting state occurs in response to an initial depolarization of the transmembrane potential. After activation and entry into the open state, Na⁺ channels transition into one or more nonconducting inactivated states and eventually the closed state. As Na_v channels contribute to the rising phase of the action potential in excitable cells, their mutations can cause various diseases of the heart and the nervous system, such as cardiac arrhythmia, epilepsy, and chronic pain (1, 2, 3). Therefore, Na_v channels are appealing targets in drug development.

Prokaryotic and eukaryotic Na_v channels are homotetramers and pseudotetramers respectively. Each of the four domains of the tetramer contains six segments, named S1–S6. S1–S4 form the voltage-sensing domain (VSD) (Fig. 1), and S5 and S6 form the pore domain. The P-loops between S5 and S6 construct the selectivity filter (SF), the narrowest part of the pore and the region responsible for selection of sodium ions. The SF sequence is highly conserved, i.e., it is EEEE for prokaryotic channels and DEKA for eukaryotic channels. Deeper into the pore is the central cavity, then followed by the activation gate facing the intracellular side. The C-terminal domain starts at the end of S6 helices and includes a nonhelical region and a coiled-coil bundle. Prokaryotic Na_v channels are of interest, not only because of similarity to eukaryotic Na_v channels but also because the signature ring of carboxyl groups is widely shared among various channels, such as calcium channels, cyclic nucleotide-gated channels, and many transient receptor potential channels, which contain either the EEEE or DDDD motif in the SF. Unlike for prokaryotic Na_v channels, the open-channel structures of most of these channels have not been resolved, so examinations into open prokaryotic Na_v channels may contribute toward understanding of the mechanisms of other channels’ functions.

Figure 1.

Crystal structure of Na_vMs (PDB: 5HVX). Central cavity is denoted by “CC” and activation gate by “AG” in figures. For clarity, only two segments have their voltage-sensing domains shown, and the other two segments have their pore domains and C-terminal domains shown. The side chain atoms of two Glu residues in the SF are shown as spheres. To see this figure in color, go online.

Many crystallographic structures of Na_v channels have been resolved within the last decade, paving the way for computational studies of the mechanisms. However, because structures of eukaryotic Na_v channels (Na_v1.2, Na_v1.4, and Na_v1.7) (4, 5, 6, 7, 8, 9, 10) have been available only since 2017, the bacterial channels have served for many years as models for study of voltage-gated Na_v channels. The majority of the crystal structures of bacterial Na_v channels are with closed gates (11, 12, 13, 14, 15); however, several open conformations were also resolved (15, 16, 17, 18), Most of the open-channel structures lack the VSD and/or the C-terminal domain (15, 16, 17), but recently a full-length crystal structure of a bacterial Na_v channel from Magnetococcus sp. (Na_vMs) was resolved with a high resolution of 2.45 Å (18). We have employed this most recent structure in this work.

Computational studies have provided much information about the conduction mechanisms (19), including the average number of ions in the channel, the ways ions interact with each other and protein residues around it, the flexibility of glutamic acid residues in the SF, etc. Most computational studies of the conduction mechanism have reported the “knock-on” mechanism (20, 21, 22, 23, 24, 25, 26), in which an incoming Na⁺ ion knocks on the lower ions to push them down, although the ions’ movement may not be concerted. In addition to this mechanism, some studies have reported the “pass-by” mechanism (27, 28, 29, 30), in which the incoming ion passes by an ion bound in the SF, and a single study has reported Na⁺ ions moving through the channel in a single-ion process (31).

Some differences in observed properties can be attributed to starting structures. For example, structures in which ion channels are closed did not exhibit electron density assigned to Na⁺; however, three binding sites were proposed by analysis of the SF radius and electron density of water molecules (11). In contrast, the open-form crystal structures exhibited electron density in the SF that was, with high likelihood, attributed to Na⁺ ions. These new open-form binding sites (15, 16, 17, 18) did not completely coincide with the closed-form hypothesized sites (11). Furthermore, the radius of the SF between the open and closed channels in crystal structures exhibits noticeable differences. Simulations starting with closed and open structures also exhibited differences; whereas simulations with the closed structures suggested three major binding sites (20,24,25,29), simulations with open channels (25,31) suggested additional and different sites. In this work, we will address this discrepancy with additional molecular dynamics (MD) simulations of an open conformation.

Single-channel conductance of several bacterial sodium channel homologs has been measured either experimentally or computationally (25,31, 32, 33, 34, 35). The computational inward conductance measurements ranged from 24 to 34 pS for Na_vMs (25,31,34,35), in agreement with the electrophysiological result (∼33 pS) (31), whereas the simulations were done with different choices of voltages, channel models, restraints, and other details. In one work employing unrestrained simulations of the full-length wild-type model (35), a nonconducting state was observed because of the so-called “hydrophobic gating” (36,37) (dewetting in a narrow hydrophobic pore). Conductance was restored by applying suitable mutations to residues at the gate (35) to make the gate wider. In all of the above simulations of conductance, the four Glu residues in the SF were modeled as deprotonated, although their protonation states in nature are not evident and would affect channels’ conduction as discussed below.

Different protonation states of the four Glu residues in SF were studied by simulations in closed Na_vAb channels. The fully deprotonated state and singly protonated state were believed to be conducting (28), based on the potential of mean force (PMF). Yet, by protonating one Glu residue, the Na⁺ occupancy in the SF was decreased (20,28), and sodium ion conduction was anticipated to be impeded as suggested by the free energy profile (21). Protonation of more Glu residues (two, three, or four) further reduced the binding affinity of Na⁺ ions in the SF and ceased the passage of Na⁺ ions into the SF (20,21,28). No study of conduction of different protonation states in the open Na_v channel has been reported until now, to our knowledge.

The pH dependence of conductance for sodium channels has been explored in experiments. Eukaryotic Na_v channels exhibit decreased conductance when pH is lowered, with an associated pKa of 5–6 (38, 39, 40, 41, 42). Decreased conductance with lower pH was reported for bacterial Na_v channels NaChBac as well, with a pKa value for conductance estimated to be ∼7.6 (43). This macroscopic pH dependence may be explained by protonation and deprotonation of the four Glu residues at SF, as suggested by the structurally similar calcium channels; eukaryotic voltage-gated calcium channels (Ca_v), which contain the same EEEE signature sequence as bacterial Na_v channels (44), also show a pH dependence, with a pKa estimated to be greater than 7 (45). Ca_v channels exhibit two conductive states, a high-conductance state and a low-conductance state. Whereas the former one was assigned to the fully deprotonated state, the latter one was believed to be the singly protonated state (with one protonated Glu residue in the SF). A mutation of the SF Glu to Gln abolishes the high-conductance state (46), suggesting that it is indeed protonation of the Glu in SF that gives rise to the low-conductance state.

Determining the pKa values computationally can be a challenge, especially for ionizable groups found in protein interiors, because such groups can exhibit conformation transitions coupled with protonation or deprotonation (47, 48, 49, 50, 51, 52). Methods based on static structures, such as those based on solutions of the Poisson-Boltzmann equation, can fail to accurately predict pKa values because they do not take into account this structural reorganization. In that respect, methods based on MD simulations such as constant pH simulations (53) are appropriate, as they allow for simultaneous description of protonation state changes and conformational changes. One of the biggest challenges in constant pH methods is conformational sampling. To enhance the conformational sampling, pH replica exchange (54, 55, 56, 57) can be incorporated into the constant pH method, which also improves the sampling of protonation state transitions. There are also several other methods that can be coupled to the constant pH method and thus enhance the sampling, e.g., the temperature replica exchange method (58,59), accelerated MD (60), umbrella sampling (61,62), and coarse-grained methods (63). A reservoir pH replica exchange method (64) can further enhance the sampling by periodic injection of structures from reservoirs generated from MD simulations (standard or enhanced) into the constant pH replicas. In a previous work on Na_vMs (65), we performed pKa calculations through a constant pH method, the enveloping distribution sampling with Hamiltonian replica exchange (55,66), and the free energy perturbation (FEP) methodology. We showed that the protonation state of the SF is modulated by ions and the fully deprotonated and singly and doubly protonated states are all feasible at physiological pH (65). In this work, we examine the conduction behavior of the protonation states determined as feasible in our previous work.

The composition of membrane lipids is important for proper functioning of ion channels (67, 68, 69, 70, 71, 72, 73, 74, 75), especially the charged phospholipids (71,76,77). In potassium channels (KcsA and K_v), several binding sites for negatively charged lipids have been identified (78). In K_v channels, interaction between lipid phosphate groups and the basic residues in ion channels’ S4 segments is essential for stabilizing the channel and modulating gating by coordinating the transition of S4 during activation and inactivation (78,79). Eukaryotic Na_v channels are also affected by membrane lipid composition: in cardiac Na_v channels, increase in cholesterol significantly reduces sodium current density and alters inactivation (80); in Na_v1.4, regulation by cholesterol was believed to take effect through changes in bilayer elasticity, where a less-stiff lipids bilayer shifts half-maximal inactivation voltage to be more hyperpolarized (81). Bacterial Na_v channels—Na_vSp, Na_vMs, and NaChBac—all prefer negatively charged lipids in terms of cumulative Na⁺ uptake into proteoliposomes (82). Moreover, pore-domain-only constructs are much less sensitive to lipid composition than the full-length ones, demonstrating that the lipid specificity mainly originates from interaction between the VSD and lipids. Most of the computational works on Na_v channels performed so far only considered neutral and single-lipid species. To investigate the lipid dependence of conductance in an open-state Na_v channel, here we utilize both pure 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) membrane patch (neutral) and the membrane with a mix of neutral and negatively charged lipids corresponding to the lipid composition in human embryonic kidney 293T cells in which the conductance of Na_vMs was experimentally measured (31,83).

Materials and methods

Simulated systems and system setups

The wild-type full-length crystal structure of Na_vMs from Magnetococcus marinus MC-1 in a fully open conformation (Protein Data Bank (PDB): 5HVX) (18) was used as the starting model for all the simulations (Fig. 1). Table 1 shows the systems employed in the calculations and their simulation conditions. Following Furini and Domene’s work (34), four mutations per chain at the activation gate (L211A, F214A, I215A, and I218A) were applied for all systems. This shortens the side chains of those residues and helps with preventing the hydrophobic gating that we initially observed. We used Chemistry at Harvard Macromolecular Mechanics Graphical User Interface (CHARMM-GUI) membrane builder (84, 85, 86, 87, 88, 89, 90) to prepare the systems, including modeling missing residues (residues 92–99), modeling protonation states, adding mutations in some cases, embedding the protein in lipids, placing ions and water, and generating equilibration scripts. The input structure of each system for CHARMM-GUI was either the raw crystal structure (“no” in the column “Gate modeled?” in Table 1) or a gate-modeled structure (“yes” in that column) in which several gate residues (T207, V210, L211, F214, I215, I218, and V219) have conformations from chain B of another Na_vMs structure (PDB: 4F4L). We introduced the gate-modeled structure because we observed that it exhibits a wider gate where side chains of pore-aligned gate residues point more away from the central axis. The four Glu residues at the SF (E178) were initially set to be protonated, so that each of them contained a proton on one of the carboxyl oxygen atoms. These protons were introduced so they could be turned into dummy protons and/or turned back for switching between protonation states. H237 residues were also set to be protonated in all systems, according to their pKa value calculated by PROPKA (91). For all the other titratable residues, the default protonation states in water at physiological pH 7.4 were used. An additional mutation, V219D, was included in systems NR_V219D and GR_V219D. One of the following two lipid compositions was used: pure neutral with 368 POPC lipids or mixed charged consisting of neutral lipids (148 POPC, 80 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE), and 48 oleoyl sphingomyelin (OSM)) and negatively charged lipids (8 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoglycerol (POPG), 88 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoserine (POPS), and 32 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoinositol (POPI)). The choice and percentage of each lipid species in mixed lipids matches the experimental value (83). The systems using neutral lipids are labeled as “POPC” in the column “Lipids” in Table 1, and the systems using mixed lipids are labeled as “mix.” The column “[Na⁺]” in Table 1 indicates the concentration of NaCl, 150 or 120 mM, set in CHARMM-GUI. The transferable intermolecular potential with 3 points (TIP3P) water model was used. Additional water molecules were added to fill the channel pore that was not hydrated during CHARMM-GUI preparation. The sizes of systems are ∼130 Å in the x, y, and z dimensions, with small differences for different systems.

Table 1.

Simulation conditions

Systema	Gate modeled?	Lipids	[Na+] (mM)	Restraints	Temperature (K)	Time step (fs)
NR	yes	mix	150	no	303	2
NR_1fs	yes	mix	150	no	303	1
NR_POPC	yes	POPC	150	no	303	1
NR_310K	yes	mix	150	no	310.15	1
NR_V219D	yes	mix	150	no	303	2
GR	no	mix	150	gate	310.15	2
GR_POPC	no	POPC	150	gate	310.15	2
GR_120mM	no	mix	120	gate	310.15	2
GR_V219D	no	mix	150	gate	310.15	2

^aNR stands for no restraints; GR stands for gate restraints.

Five protonation states were studied: deprotonated state S₀ (no E178 was protonated); singly protonated state S₁ (only E178 on chain C was protonated); and doubly protonated states S_2-AB (two opposite E178s were protonated: E178s on chains A and B were deprotonated, E178s on chains C and D were protonated), S_2-AD (two adjacent E178s were protonated: E178s on chains A and D were deprotonated, E178s on chains B and C were protonated), and S_2-BD (two adjacent E178s were protonated: E178s on chains B and D were deprotonated, E178s on chains A and C were protonated). While the protonated state of E178 is standard for protonated Glu, the deprotonated state of E178 has a dummy proton (with 0 charge and 0 Van der Waals (vdW) radius), and the charges and vdW terms on other atoms are of the deprotonated state. Every protonation state described above is different from the status output from CHARMM-GUI in which the four E178 residues were all protonated, and the ions were added to neutralize this charge state. Changing the protonation states as described above would change the total charge and make it deviate from zero. To keep the systems electrically neutral, we treated the S₀ state as the default state and added four more Na⁺ ions to neutralize the S₀ state. For each protonation of E178 with respect to the default state S₀, we changed one water molecule to hydroxide (OH⁻) by altering the charges and vdW terms of water atoms and having a dummy proton.

Minimization and equilibration protocols

The systems with no restraints and those with gate restraints were minimized and equilibrated via different protocols. In some testing systems without gate restraints, we observed that equilibrating with Na⁺ ions in the SF could delay the closing of the gate, though this collapse happened eventually within a longer timescale even when started with three Na⁺ ions in the SF. Here, the no-restraint and gate-restrained systems were equilibrated with zero and three Na⁺ ions in the SF, respectively. While being in the deprotonated state S₀, the no-restraint systems were minimized, heated up with a step of 10 K, and equilibrated through CHARMM-GUI’s default equilibration protocol during which the restraints on protein and lipids were gradually released. After being switched to other protonation states (or continuing with S₀), the no-restraint systems were equilibrated for another 50 ns with constant pressure before production runs with an external electric field that is only supported in the NVT (constant number, volume, and temperature) ensemble by Amber. In contrast, in gate-restrained systems, different protonation states were separated since minimization. They were minimized and then equilibrated through an 11-step protocol described in Table S1. During the equilibration, the restraints on lipids and protein are gradually released until there is no restraint for lipids but only the distance restraints on the protein. These distance restraints in the last step of equilibration were applied on α carbon atoms of six gate residues per chain (residue ID: 214–219) restricting only inward movements with reference to the PDB structure and with a force constant of 0.5 kcal/mol/Ų. As listed in the column “Restraints” in Table 1, no-restraint systems are labeled as “no,” which means no restraint was applied in production simulations, and gate-restrained systems are labeled as “gate,” referring to the distance restraints on gate used in their production, which were the same as the restraints in the last step of equilibration.

MD simulations

In each system, simulations were carried out at multiple voltages and with one or multiple protonation states (Table S2). For each system, voltage, and protonation state, three independent copies were simulated starting from different initial velocities, except that 20 copies were done for the system NR at ∼−100 mV with protonation state S₀. The columns “Temperature” and “Time step” in Table 1 show the temperature kept in production and the time step used, respectively. All simulations were performed using the Amber (version 18) software (92), with the CHARMM36m force field (93) including nonbonded fix (NBFIX) corrections for Na⁺ ions and the pair-specific NBFIX corrections for NaCl and Na-carboxylate (94,95). Bonds to hydrogens were constrained by SHAKE. The particle mesh Ewald method was adopted to calculate electrostatic interactions with the real space interaction cutoff of 12 Å. Temperature was kept using Langevin dynamics with a collision frequency of 5 ps⁻¹. During the constant pressure equilibration, pressure was maintained at 1 bar by a Monte Carlo barostat with relaxation time of 1 ps. We performed 450 ns of production for the no-restraint systems and 500 ns for the gate-restrained systems. In the following figures for MD simulations, all data shown are averaged over a 450 ns timescale for no-restraint systems and 500 ns for gate-restrained systems.

Membrane voltage was calculated as a product of electric field and the box size in the z dimension (96). To achieve target voltages, the values of electric field were specified in the Amber input scripts. Because of the small differences in systems’ box sizes, individual voltages vary slightly. Accurate voltages and their standard deviations (SDs) are shown in Table S3. For measuring the conductance, sodium ions were traced. A whole conduction event was counted when the ion entered through the SF from the extracellular side, passed the gate, and went into the intracellular side. A half event was counted when the ion entered via SF and stayed in central cavity till the end of the simulation or the ion started in the central cavity and left through the gate during the simulation. Pore inner radius measurements were done with program HOLE (97). The free energy profile was constructed from the distribution of Na⁺ ions within a central cylinder with a radius of 10 Å via Eq. S1 and was calibrated so that the average free energy in bulk water was zero. The electrostatic potential was calculated by volmap command in Visual Molecular Dynamics (VMD) (98) and then averaged over a horizontal square with a side length of 2 Å at the center of channel for each value of z. An Na⁺ ion is defined to be in the pore when its radius is less than 10 Å and its z coordinate is greater than −25 Å and less than 6 Å. Figures depicting protein structures were generated with VMD (98).

Free energy calculations

FEP methodology with Bennett’s acceptance ratio method was used to calculate transition free energy and predict microscopic pKa for E178 residues. To achieve better convergence, the Hamiltonian replica exchange method was coupled to FEP, and 12 replicas were generated. To attain adequate overlap in phase space between two adjacent replicas, which is required for convergence, charges of atoms in E178 were scaled linearly between charges of the two states, and the vdW terms of Hamiltonian were changed approximately linearly by finely tuning the Lennard-Jones (LJ) parameters of atoms OE2 and HE2 and those of pairs OE1-SOD and OE2-SOD (details in Table S4), with the overall Hamiltonians ranging between those of the deprotonated state and the protonated state. With NBFIX correction, the LJ parameters for interaction between sodium ions and carboxylate oxygens are different from those calculated by the simple Lorentz-Berthelot combining rules. As a result, the LJ parameters for the above two pairs were modified for each replica manually and explicitly, instead of having the Amber program calculate them automatically based on the Lorentz-Berthelot rules.

The S₀-S₁ transition was examined, and the corresponding pKa value was calculated. We performed two sets of free energy calculations, one set with neutral lipids and the other with mixed lipids, which started from snapshots from MD simulations of two protonation states (S₀ or S₁) of system NR_POPC and system GR, respectively (see Table 1). FEP simulations were carried out at two voltages, 0 and −170 mV for the neutral lipids set and 0 and −100 mV for the mixed lipids set (Table S5). For every specific combination of voltage and protonation state during MD simulations, there were two copies starting from two independent structures, resulting in 16 FEP simulations in total. Twelve simulations completed 300 ns, and four simulations had time lengths of 173–193.5 ns. Trajectories were analyzed to obtain the microscopic pKa of E178. Considering the symmetry correction for proton-binding constants, the macroscopic pKa values were calculated through Eq. 1 (65).

$${\mathrm{pKa}}_{\mathrm{mac}.}={\mathrm{pKa}}_{\mathrm{mic}.}+\log \left(4\right)$$ (1)

Results

Correlation between conductance and pore radius

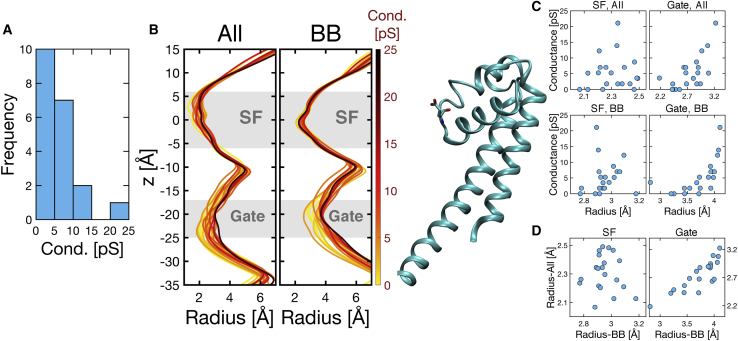
In this study, 173 MD simulations were performed for investigating conduction through the open Na_vMs channel. Initially, we performed three independent simulations with the system NR and with protonation state S₀ at ∼−100 mV. We observed a large difference in conductance between these three copies (copies 1–3, conductance: 1.8, 1.8, and 21.1 pS). To investigate the origin of this difference, 17 additional copies were simulated with this condition. Fig. 2 A shows the histogram of observed conductance values in the 20 simulations we performed, and Fig. 2 C shows individual conductance values, indeed confirming the large difference in conductance between individual copies, ranging from 0 to 21.1 pS. The individual observed conductance values are shown in Table S6.

Figure 2.

Conductance of the system NR. (A) Distribution of conductance values. (B) Pore radius along the z axis, “all atoms” radius on the left (denoted by “All” in figures) and backbone radius on the right (denoted by “BB” in figures), with a representative structure aside (only the pore domain of one segment is shown for clarity). The color scale bar indicates the mapping of conductance value into color. (C) Conductance versus pore radius of the SF (left) or gate (right), and for “all atoms” (top) or backbone (bottom). (D) “All atoms” radius versus backbone radius, for the SF (left) or gate (right). To see this figure in color, go online.

To rationalize this large difference in conductance, we show the radius of the pore for the 20 copies, colored based on conductance value (Fig. 2 B). The left plot of Fig. 2 B shows the radii considering all atoms of the protein, and the right plot considers only backbone atoms. The trajectories were centered to the center of mass of N, C, O, and Cα atoms of residues 176–179, which form the SF in all four segments. Consequently, the 0 value of z roughly corresponds to the carbonyl oxygen atoms of L177 residues. In both plots of Fig. 2 B, the larger the radius is, the darker the color is, especially in the region of the activation gate, which demonstrates a positive correlation between pore radius and channel conductance. Fig. 2 C shows the correlation between conductance and averaged radius for the 20 copies (each dot represents one copy), in which the radius is averaged over two regions, the SF (z from −6 to 6 Å) and gate (z from −17 to −25 Å), respectively. There seems to be no obvious dependence of conductance on the “all atoms” radius of the SF. However, the conductance does correlate linearly with the backbone radius of the SF for most copies. The three observed outliers have gate radii being either very large or very small, which might be the reason why they depart from the more linear relation obeyed by the others. As for the gate, both “all atoms” and backbone radius show a good correlation with conductance. In Fig. 2 D, “all atoms” radii are plotted against backbone radii for the SF and gate. The SF’s “all atoms” radius does not correlate with its backbone radius, reflecting the large conformational space explored by side chains of SF residues. In contrast, the “all atoms” and backbone radii of the gate well correlate with each other, which may be due to the fact that the residues at the gate are all hydrophobic and likely do not exhibit large conformational fluctuations in water.

Simulations with gate restraints

Simulations with no restraints yield conductances that are smaller than the experimentally observed conductance of 33 pS; Fig. 3 A is showing conductance averaged over different copies at different voltages and two different temperatures (303 and 310 K) for the system with no restraints. Table 2 is showing the individual conductance values. Our analysis described in previous paragraph showed that the conductance correlated with gate radius. Fig. S1 is comparing the average backbone radius in our simulations with no restraints to backbone radius in the PDB structure. It shows that the gate backbone collapsed with respect to the PDB structure.

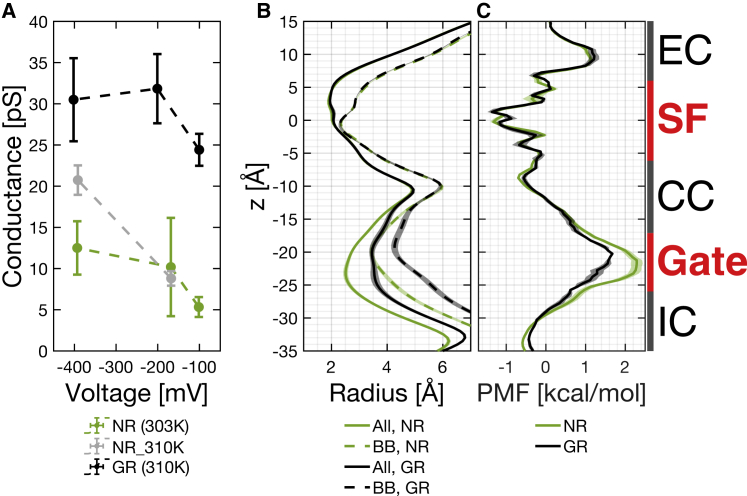
Figure 3.

Effect of gate restraints. (A) Calculated conductance of different simulated systems. Error bars represent standard errors. (B) Radius of the pore along the z axis, showing “all atoms” (solid) and backbone (dashed) radii of systems NR (green) and GR (black). (C) Free energy profiles, using the same color coding as (B). Shaded areas in (B) and (C) represent standard errors. Bars on the right side indicate the extracellular (denoted by “EC” in figures), SF, central cavity (denoted by “CC” in figures), gate and intracellular (denoted by “IC” in figures) regions. To see this figure in color, go online.

Table 2.

Conductance values for simulations with protonation state S₀and systems NR, NR_310K, and GR

System	Voltage (mV)a	Individual conductance (pS)			Average conductance (pS)
		Copy 1	Copy 2	Copy 3
NR	−170	4.2	4.2	22.1	10 ± 6
	−400	9.5	9.0	19.0	13 ± 3
NR_310K	−170	7.4	8.5	10.5	8.8 ± 0.9
	−400	19.6	24.2	18.4	20.7 ± 1.8
GR	−100	25.4	20.7	27.2	24.4 ± 1.9
	−200	25.4	39.7	30.3	32 ± 4
	−400	39.7	29.4	22.4	30 ± 5

^aVoltage numbers shown are target voltages.

To prevent the collapse, distance restraints were applied to the gate backbone atoms to maintain the backbone conformation of the PDB structure (details are in Materials and methods). In Fig. 3, we compare the system GR and systems without restraints (NR and NR_310 K). All three systems were simulated with protonation state S₀ and had three copies for each condition, except for the system NR at ∼−100 mV, which had 20 copies. All data points shown in Fig. 3 were averages over different copies. Fig. 3 A and Tables 2 and S6 show the conductance measurements for the three systems, with color coding in the figure in which the system NR is colored green, GR black, and NR_310K gray. The conductance values of runs with gate restraints (in system GR) are much higher than those without restraints (in systems NR and NR_310K), proving that preventing the gate radius from collapse with respect to the PDB structure accelerates conduction and yields conductance values comparable to experimental values.

Fig. 3, B and C show the radius of pore and the free energy profiles, respectively, for systems NR and GR (using the same color coding) at ∼−100 mV. They clearly show that the two systems mainly differ at the gate in both the pore size and the free energy. The wider gate of the gate-restrained system lowered the free energy barrier at the gate, which in turn increased the conductance.

Ion binding sites

Fig. 4 shows the distribution of Na⁺ ions along the channel’s primary axis (z) at ∼−100 mV for state S₀ (black dashed lines, labeled as “All”) and its decomposition according to the ion’s binding patterns (colored solid lines). The Na⁺ ions were considered to bind to a residue if the coordinating atoms of the residue showed up in the first solvation shells of Na⁺ ions (within 3.18 Å). As indicated in Fig. 4, there are five binding sites of Na⁺ ions, Site0 through Site4, with similar locations and probability densities between the systems NR and GR. The two systems also have the same residues with which Na⁺ ions interact at each site. For both systems, Site0 is close to the average position of the γ oxygen atoms of S179 residues, Site1 and Site2 are both supported by carboxylates of E178 residues, Site3 is where Na⁺ ions bind to either only L177 or both L177 and E178, and Site4 is at the height of carbonyl oxygen atoms of T176 residues. Notice that at Site2, the brown peaks for “Other” were probably stabilized by L177 and E178, though with an Na-O distance greater than 3.18 Å, because they are between the involved oxygen atoms from these two residues. Na⁺ ions are partially dehydrated at Site1 or Site3 and may maintain full hydration shells at the other three sites. It is worth noting that there are three well-separated sites (Site1, Site2, and Site3) at which Na⁺ ions could be directly coordinated by E178 carboxylates.

Figure 4.

Na⁺ ions binding patterns, for systems NR (left) and GR (right). Four binding patterns are shown: “E” when Na⁺ interacts solely with carboxylate oxygen atoms of E178 residues (red lines), “L” when Na⁺ interacts solely with carbonyl oxygen atoms of L177 residues (blue lines), “EL” when Na⁺ interacts with both E178 and L177 at the same time (green lines), and “Other” for any other binding condition (brown lines). A representative structure aside shows the coordinating residues, accompanied by the number density along z of involved oxygen atoms for both systems (NR, gray; GR, black). The first peak from the top corresponds to S179 hydroxyl oxygen atoms, the second to E178 carboxylate oxygen atoms, the third to L177 carbonyl oxygen atoms, and the fourth to T176 carbonyl oxygen atoms. To see this figure in color, go online.

The similarity of the binding profile between the two systems with and without gate restraints, together with the similarity of SF’s pore width and the free energy profile at SF (Fig. 3), indicates that the gate of the channel is decoupled from the SF. This will allow us to draw conclusions about the effects of protonation states in the SF on conductance by using a system with gate restraints.

Fig. 5 shows the distribution of the “all atoms” radius of the SF for the 20 copies in system NR with protonation state S₀ at ∼−100 mV. Interestingly, although the four SF residues all exhibited a single peak in their positional distribution along z, two conformational states of the SF were observed, as strongly implied by the appearance of two distinct peaks in the distribution of the SF radius. In the wider SF state, we observe that the Na⁺ ions sit between E178 carboxylates and L177 carbonyls before they get knocked down by an incoming ion. By contrast, in the narrower SF state, the ions stay slightly lower, on the plane of L177 carbonyls. Conformational transitions between the two SF states have been observed on a timescale of hundreds of nanoseconds.

Figure 5.

Distribution of SF radius of individual copies (top) and the average (bottom), for the 20 copies in system NR with protonation state S₀ at ~−100 mV. The copies are colored based on their conductance values. The color scale bar indicates the mapping of conductance value into color. Shaded area in the bottom plot represents standard errors. To see this figure in color, go online.

Conductance of different protonation states

Our previous work has demonstrated that the protonation states S₀, S₁, S_2-AB, S_2-AD, and S_2-BD are all accessible at physiological pH. Here, these five protonation states were simulated in the system GR at three different membrane voltages (∼−100, ∼−200, and ∼−400 mV). Three copies were performed at each of the conditions, over which the data shown in Fig. 6 were averaged. Fig. 6 A and Tables 2 and 3 show the conductance measurements for the five protonation states. At physiological voltage −100 mV, the conductance of S₀ is ∼24.4 pS, which is not too far from the experimental value of 33 pS. The ratio of conductance of S₀ to that of S₁ is roughly 5 for −100 and −200 mV and is ∼1.7 for −400 mV. The conductance values of the three doubly protonated states are lower than those of state S₀ and S₁, ranging from −0.3 to 6.2 pS. This decaying trend of conductance along with protonation is also observed in a no-restraints system (Fig. S2 A).

Figure 6.

Effect of protonation states. (A) Calculated conductance values. Error bars represent standard errors. (B) Pore radius along the z axis. (C) Free energy profiles. (D) Conductance versus $e^{-E_{barrier}/RT}$, fitted to a linear function. To see this figure in color, go online.

Table 3.

Conductance values for simulations with system GR and four protonated states

Protonation state	Voltage (mV)a	Individual conductance (pS)			Average conductance (pS)
		Copy 1	Copy 2	Copy 3
S1	−100	3.2	4.8	6.4	4.8 ± 0.9
	−200	8.0	3.2	6.4	5.9 ± 1.4
	−400	27.4	13.9	13.6	18 ± 5
S2-AB	−100	0.0	0.0	0.0	0 ± 0
	−200	1.6	0.0	0.0	0.5 ± 0.5
	−400	0.0	3.2	0.8	1.3 ± 1.0
S2-AD	−100	0.0	0.0	3.2	1.1 ± 1.1
	−200	2.4	0.8	7.3	3.5 ± 1.9
	−400	9.6	2.4	6.5	6 ± 2
S2-BD	−100	0.0	4.8	1.6	2.1 ± 1.4
	−200	0.8	−0.8	−0.8	−0.3 ± 0.5
	−400	2.0	2.4	0.8	1.7 ± 0.5

^aVoltage numbers shown are target voltages.

Fig. 6, B and C show the radius of pore and free energy profile, respectively, for the five protonation states at ∼−100 mV. Protonated states possess narrower SFs than state S₀ because of the protonated side chains of E178 pointing toward the central cavity. This narrowing of SF leads to a decrease in the number of coordinating waters (Fig. S3 A, region z = −2 Å to z = −6 Å) by about one water molecule. The protonated states’ higher free energy barriers at the SF could originate from either the loss of negative charge at the SF or the smaller SF size, which impacts hydration of the ion. Fig. 6 D displays conductance against the exponential of −E_barrier/RT for the five protonation states at ∼−100 mV and the fitting of data to a linear function, where E_barrier is defined to be the highest peak between z = −6 Å and z = 15 Å (in the shown extracellular and SF regions), R is the universal gas constant and T is the absolute temperature. The values of maximal barriers are shown in Table S7. The good linear relationship (R² = 0.9978) between conductance and $e^{-{\mathrm{E}}_{\mathrm{barrier}}/\mathrm{RT}}$ (e: Euler's number) suggests that conduction rates could be well predicted by the Arrhenius equation (Eq. S2) (99) when we interpret the conduction through the pore as a reaction and the highest free energy barrier as the activation energy of the reaction. The slope of the fitted line is 161 ± 4 pS and corresponds to a pre-exponential factor of 1.0e8 s⁻¹ in the Arrhenius equation (detailed calculations in Supporting materials and methods). The pre-exponential factor is related to the molecular collision frequency in a chemical reaction and might be related to the frequency of Na⁺ ions colliding with the mouth of the channel pore.

Table S8 shows the frequency of collisions between incoming Na⁺ ions and the channel for the five protonation states at ∼−100 mV. Three choices of collision interface were used: 20, 16, and 13 Å. The plane z = 20 Å is where the PMF starts to deviate from 0 and where the ions start to interact with the channel (Fig. S4, left). The plane z = 16 Å is where the PMFs of different protonation states start to diverge and where the ions start to interact differently with the channel (Fig. S4, left). The plane z = 13 Å is where the electrostatic potentials start to deviate from 0 and below where the ions are within the screening length from the channel (Fig. S4, right). Table S8 clearly demonstrates that as the defined interface approaches the channel, collision frequency decreases and the difference among protonation states increases. These are consistent with the increasing and diverging PMFs.

Effects of lipid composition on conductance

It was shown that bacterial sodium channels exhibited larger cumulative Na⁺ uptake into proteoliposomes composed of POPE and some negatively charged lipids, as opposed to neutral lipids (82), but most of previous simulation works used neutral lipids. Here, we investigate how charged lipids affect channel conductance by comparing a system with neutral lipids (GR_POPC) and a system with a mix of neutral and negatively charged lipids (GR_120mM), which we refer to as “Neutral” (red) and “Charged” (blue), respectively, in Fig. 7. Negative charges in the lipid headgroups of the charged system, −64e (e: elementary charge) in both upper and lower leaflets, dramatically influence the distribution of sodium ions near the lipid-water interfaces and thus affect the equilibrated bulk concentration of sodium. As a result, whereas the neutral system’s preset sodium concentration was 150 mM, the charged system was set to 120 mM to achieve a final bulk sodium concentration similar to that of the neutral system (Table S9). Both systems were simulated with protonation state S₀, under three membrane voltages (∼−100, ∼−200, and ∼−400 mV) and had three copies for each condition. Data shown in Fig. 7 were averaged over the copies. Fig. 7 A and Table 4 show the conductance of the two systems at three voltages. The conductance of the charged system is higher than that of the neutral system by 7.3 pS (28%) at ∼−400 mV, whereas the differences between the two systems are insignificant at ∼−100 and ∼−200 mV, as suggested by the error bars overlapping. It is worth mentioning that the systems GR (preset 150 mM of Na⁺) and GR_120mM (preset 120 mM of Na⁺) exhibit quite similar conductance values (Fig. S5), indicating that the difference of 30 mM in the preset sodium concentration is too small to create observable effect in the conduction rates.

Figure 7.

Effect of lipid composition. The neutral-lipid system is colored red and the charged-lipid system blue. (A) Calculated conductance values. Error bars represent standard errors. (B) Pore radius along the z axis. (C) Linear density of charge from lipids and ions along the z axis. The difference of this charge density between the two systems is shown as a black dashed-dotted line, together with its decomposition into the difference caused by lipids (gray dotted line) and ions (gray dashed line). (D) Electrostatic potential energy profiles. The difference between the two systems is shown as a black dashed-dotted line. Gray dashed-dotted line is the difference of electrostatic potential energy excluding the contribution from Na⁺ ions in a central cylinder with a radius of 10 Å. (E) Number probability density of Na⁺ ions within a central cylinder with a radius of 10 Å along the z axis. Shaded areas in (B) to (E) represent standard errors. To see this figure in color, go online.

Table 4.

Conductance values for simulations with protonation state S₀ and systems GR_POPC and GR_120mM

System	Voltage (mV)a	Individual conductance (pS)			Average conductance (pS)
		Copy 1	Copy 2	Copy 3
GR_POPC (neutral)	−100	20.5	30.2	11.1	21 ± 6
	−200	30.7	19.0	26.9	26 ± 3
	−400	23.2	27.8	26.9	26.0 ± 1.4
GR_120mM (charged)	−100	17.5	20.5	38.5	26 ± 7
	−200	31.1	26.8	17.7	25 ± 4
	−400	37.8	38.3	23.7	33 ± 5

^aVoltage numbers shown are target voltages.

Fig. 7B shows the radius of pore for the neutral and charged systems at ∼−100 mV and demonstrates a similar pore width profile between the two systems. This suggests only a small conformational change of protein in the pore area. Fig. 7, C–E show the charge density of lipids and ions, the electrostatic potential energy, and the probability density of Na⁺ ions in the pore of the two systems at ∼−100 mV, respectively. The differences in Fig. 7, C and D are calculated by subtracting the neutral-system value from the charged-system value. The electrostatic energy difference shown in Fig. 7 D between extracellular side (z = 15 Å) and intracellular side (z = −35 Å) is 2.3 kcal/mol, corresponding to the membrane potential of −100 mV. Although there is no difference at the gate in Na⁺ ions distribution of the two systems (Fig. 7 E), the difference is observed mainly at the SF, resulting from the negative charges of lipid headgroups sitting around z ∼9 Å (see the gray dotted line in Fig. 7 C) and ion redistribution (gray dashed line in Fig. 7 C).

The gray dashed-dotted line in Fig. 7 D shows the difference between the two systems in the electrostatic energy, excluding the portion generated by the Na⁺ ions in a central cylinder with radius 10 Å. This difference allows us to see the electrostatic effect caused by the charged lipids and the accompanied redistribution of ions outside of the central cylinder. This lipid-and-outside-ion electrostatic effect is negative above z = 4 Å, which might be caused by the net accumulation of negative charge in this region (black line in Fig. 7 C). This negative shift of lipid-and-outside-ion electrostatic attracts more Na⁺ ions to this region, which is also the entrance into the SF, and the increase in the local concentration of Na⁺ there (Fig. 7 E) makes it more possible to initiate a conduction event. Also, these additional Na⁺ ions positively shift the inside-ion electrostatic and result in a positive change of total electrostatic potential (black line in Fig. 7 D). In contrast, in the region between z = 0 Å and z = 4 Å (shaded in Fig. 7, C–E), the net change of charge is positive (black line in Fig. 7 C). Considering that the change of charge in the pore in this region is negative on average (Fig. 7 E), the change of charge caused by lipids and outside ions must thus be even more positive. This outside positive charge accumulation might give rise to the positive shift of the lipid-and-outside-ion electrostatic (gray line in Fig. 7 D). This positive shift could exclude Na⁺ ions there, which is indeed seen in Fig. 7 E, and consequently decrease the inside-ion electrostatic. As a result, the total change of electrostatic is negative between z = 0 and 4 Å (black line in Fig. 7 D). Also, the exclusion of Na⁺ ions in this region might lead to the small downward shift of the Na⁺ probability peak around z = 0 Å.

Table S10 shows the sodium ion collision frequency for the neutral and charged lipids systems at ∼−100 mV. Three definitions of collision interface were used, as discussed and used above. The lipid composition clearly affects the collision frequency, and the difference between two lipid compositions is more pronounced near the channel, which is consistent with the more diverged PMF (Fig. S6).

Dependence of conductance on voltage

As shown above (Figs. 3 A, 6 A, and 7 A; Tables 2, 3, and 4), conductance is voltage dependent, even at two low voltages −100 and −200 mV. Here, we propose a possible mechanism of this voltage dependence. Fig. 8 shows the correlation between conductance and SF radius considering all atoms among different voltages for both no-restraints and gate-restrained systems with protonation state S₀, and data were averaged over copies. Different voltages are colored differently: black for ∼−100 mV, green for ∼−170 mV, blue for ∼−200 mV, red for ∼−400 mV, and purple for ∼−620 mV. The quantities plotted on the y and x axes, conductance and “all atoms” SF radius, are well correlated. Also, high-voltage dots appear to occupy the upper right corner and low-voltage ones the lower left corner. This indicates a correlation between conductance, SF radius, and membrane voltage. Table 5 shows the R²-values and slopes of the linear fits for conductance-radius and conductance-voltage data for each of the eight systems. The R²-values are close to 1 in most cases, which demonstrates a good correlation between the three quantities. Higher voltage runs tend to possess wider SFs, which could be responsible for higher conduction rates. In other words, high voltage could induce conformational changes in the SF, whose structure is crucial for conduction, and consequently make an impact on conductance. Another explanation could be that the relationship between current and voltage is nonlinear (non-Ohmic) because the PMF in the channel is not constant (100).

Figure 8.

Voltage dependence of conductance and SF radius. Four no-restraints systems are shown on the left (A) and four gate-restrained systems on the right (B). Voltage numbers shown are target voltages. Error bars represent standard errors. To see this figure in color, go online.

Table 5.

The coefficient of determination R² and slopes of linear fits for conductance SF radius and conductance voltage

System	Conductance versus SF radius		Conductance versus voltage
	R2	Slope (pS/Å)	R2	Slope (pS/V)
NR	0.89	151	0.93	−30
NR_1fs	1.00	55	0.99	−38
NR_310K	1.00	50	1.00	−53
NR_V219D	1.00	37	1.00	−24
GR	0.78	55	0.40	−16
GR_POPC	0.86	99	0.64	−16
GR_120mM	0.94	57	0.87	−28
GR_V219D	0.77	82	0.98	−46

For system GR, we tested whether the conduction is a Poisson process by plotting the Eq. 12 in Pohorille and coworkers (2014) (100) and assessing whether the plots are straight lines (Fig. S7 A, left). The data could be fitted with linear equations with high coefficient of determination (R² = 0.98 for all three lines). Thus, the conduction we are simulating is a Poisson process, which means that at fixed voltage, the channel does not undergo large conformational changes after it has been equilibrated (100). However, different voltages could lead to different equilibrated “stationary” conformations, and the possibility of voltage-induced conformational changes is not ruled out because conduction is a Poisson process.

Fig. S7A (right) also indicates that the probability of having two conduction events within 10 ns is low at ∼−100 and ∼−200 mV. Specifically, at ∼−100 mV, no events occurred within 10 ns of each other. For low voltages, our data are consistent with a recovery time. If there is a recovery, that recovery time is ∼10 ns. This is also supported by another long (1.8 μs) similar simulation from our unpublished work (A.Y.C., B.R.B., and A.D., unpublished data) (Fig. S7 B). With more data points, although we observe 11 points between 5 and 10 ns, the probability of interval time being less than 5 ns is still very low with only two points (Fig. S7 B, right), suggesting that the recovery time might be as short as 5 ns. At higher voltage (∼−400 mV), we did not observe a recovery time (Fig. S7 A, right, red line). The shortest time we observed between two conduction events is 0.7 ns. So, if there is a recovery at −400 mV, the recovery time is less than 1 ns. The recovery time might arise from necessary relocation of ions in the channel and local rearrangement of SF side chains.

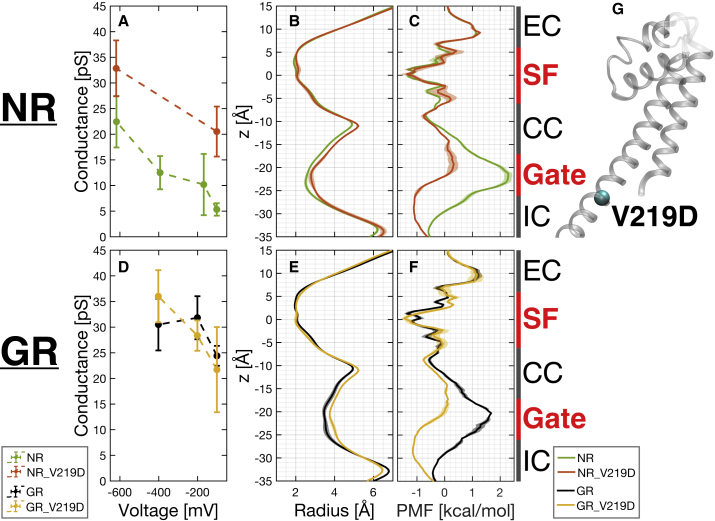
Effects of mutation V219D on conductance

A mutation, V219D (Fig. 9 G), was introduced to systems NR_V219D and GR_V219D, aiming at reducing free energy barrier at the gate and hence boosting the conduction rate. In Fig. 9, two mutated systems are compared to their corresponding unmutated systems NR and GR, respectively, with protonation state S₀. All data points for the four systems were averaged over three copies, except for those for the system NR at −100 mV, which were averages of the 20 copies. Fig. 9 A shows conductance of the two no-restraint systems and Fig. 9 D that of the two gate-restrained systems (data also shown in Tables 2, 6, and S6). In no-restraint systems, the mutation V219D enhanced the channel’s conductance by 15.2 pS (285%) at ∼−100 mV and 10.4 pS (46%) at ∼619 mV. However, in gate-restraint systems, the effect of the V219D mutation is neither consistent nor considerable. Fig. 9, B and E and C and F show the radius of the pore and free energy profiles, respectively. The mutation V219D made gates wider by a similar amount and decreased free energy barriers around gate in both no-restraint and gate-restraint runs. However, the wider gates make a difference in conductance only in the no-restraint systems. That is to say, the correlation between gate width and conductance, as discussed in section Correlation between conductance and pore radius of Results, seems to only hold true when gate radii are in a lower region (no-restraint cases). When gates are already sufficiently wide (gate-restraint cases), there is no gain of conduction from a further wider gate caused by the mutation V219D. One explanation for this is that in the case of a wide enough gate (gate-restraint cases), no dehydration occurs, so the gate widening via V219D does not change the number of coordinating water molecules. This is indeed the case; as shown in Fig. S3 B, right panel, the number of coordinating water molecules around gate is ∼5.5 in both cases. However, in the case of a relatively narrow gate (no-restraint cases), dehydration of the ion is larger, and V219D mutation results in ∼0.5 additional water molecules being bound to the ion and thus smaller dehydration in the region of z = −24 Å to z = −28 Å (Fig. S3 B, left) and gain of conduction. This effect has also been observed in a potassium channel (101), where the incomplete or full coordination of the ion was shown to be the major regulatory factor. Also, in a calcium channel, the conductance was found to be governed by pore hydration (102).

Figure 9.

Effect of mutation V219D. (A and D) Calculated conductance values. Error bars represent standard errors. (B and E) Pore radius along the z axis. (C and F) Free energy profiles. Shaded areas in (B, C, E and F) represent standard errors. (G) A representative structure showing the location of the backbone atoms of the residue 219. To see this figure in color, go online.

Table 6.

Conductance values for simulations with protonation state S₀ and systems NR, NR_V219D, and GR_V219D

System	Voltage (mV)a	Individual conductance (pS)			Average conductance (pS)
		Copy 1	Copy 2	Copy 3
NR	−620	21.4	14.3	31.6	22 ± 5
NR_V219D	−100	15.8	30.3	15.5	21 ± 5
	−620	43.0	31.2	24.3	33 ± 5
GR_V219D	−100	23.9	34.9	6.4	22 ± 8
	−200	34.2	26.2	24.7	28 ± 3
	−400	28.2	45.6	34.2	36 ± 5

^aVoltage numbers shown are target voltages.

pKa value of E178

We performed free energy calculations simulating the transition between protonation state S₀ and state S₁, titrating a single E178 residue on chain C, to yield microscopic pKa values of E178. The macroscopic pKa values were then calculated via Eq. 1 in Materials and methods. The free energy simulations were done for a system with neutral lipids (system NR_POPC) and a system with mixed charged lipids (system GR), starting from structures equilibrated with either protonation state S₀ or state S₁, running at two different voltages for each of the systems and having two copies for every condition started from two independently equilibrated structures, respectively. These simulations are 300 ns long. As shown above, conformational changes of SF are decoupled from those of the gate. Therefore, though the two systems have different conditions of gate restraints, we do not expect this difference to affect the pKa values of the E178 residues in the SF. Fig. 10 shows how the macroscopic pKa values evolve with time. Data points are averages over the two independent copies and over a time period of 0.5 ns (thin gray lines) or 10 ns (thick colored lines). As time goes by, simulations started from S₀ equilibrated structures (solid lines) exhibited higher pKa values and those from S₁ (dashed lines) lower pKa values. Meanwhile, the pKa values of the two sets became closer to each other. Although there was still hysteresis for three pairs of starting protonation states S₀ and S₁, the hysteresis between S₀ and S₁ simulations, which were run at 0 mV, and for the system with charged lipids disappeared at around 80 ns. The 10 ns averaged pKa values appear to be higher, especially after some initial relaxation, when the simulations were performed with external membrane voltages (red lines) compared to the runs without voltages (blue lines), with one exception that was started from state S₀ in the charged-lipid system.

Figure 10.

The pKa value as a function of time for the systems with neutral lipids (A) and charged lipids (B). To see this figure in color, go online.

Table 7 shows the averages over the two independent copies and over the last 50 ns of simulations for pKa value, SF radius, and number of Na⁺ ions in the pore (criteria used are described in the Materials and methods), together with the associated SDs. The SF radius and the ion number were also averaged over the 12 Hamiltonian replica exchange method replicas. The rows labeled with “average” were further averaged over the two starting protonation states. Table 7 clearly shows that, along with applying external electric field, the pKa values increase, and so do the SF radii. However, these increases are less than their corresponding deviations. That is to say, the voltage dependence of pKa values, though seems true according to averages, might be unreal considering the deviations. Also, the increases in average SF radii might affect pKa averages; however, these changes are smaller than their deviations and also much smaller than the changes seen in the MD simulations, so we cannot draw conclusions about the correlation between pKa changes and SF radius changes. It is also noticed that the number of Na⁺ ions in the pore remains stable across different voltages, and the composition of lipids does not appear to influence the three listed quantities.

Table 7.

The pKa value, SF radius, and number of Na⁺ ions in the pore for the free energy simulations

		Neutral		Charged
		0 mV	−170 mV	0 mV	−100 mV
pKa	S0	5.5 ± 0.7	7.0 ± 1.3	6.5 ± 0.7	6.9 ± 1.3
	S1	7.3 ± 1.5	8.3 ± 0.7	6.9 ± 0.7	8.0 ± 1.1
	average	6.4 ± 1.6	7.6 ± 1.2	6.7 ± 0.6	7.5 ± 1.2
SF radius (Å)	average	2.16 ± 0.11	2.21 ± 0.10	2.15 ± 0.08	2.23 ± 0.09
Number of Na+	average	1.9 ± 0.2	1.81 ± 0.19	1.96 ± 0.11	1.82 ± 0.19

Voltage numbers shown are target voltages.

Discussion

Our results show that protonation of E178 side chains decreases the channel conductance. In simulations with gate restraints (system GR), S₀ state exhibits an average conductance of 24.4 pS at ∼−100 mV. By protonating one E178 side chain (with S₁ state) at the same voltage, the conductance is reduced to 4.8 pS, roughly one-fifth of that of S₀ state. The conductance values of the three S₂ states are further decreased, ranging from 0.0 to 2.1 pS for ∼−100 mV. Similar decreased trend of conductance is also seen at the other two voltages (−200 and −400 mV) and in simulations with no restraints (Fig. S2 A). The relationship between channel conductance and the largest free energy barrier above the central cavity is well described by the Arrhenius equation, which suggests a simple conduction process.

It is expected from experiments that the channel conductance is influenced by protonation states of SF. A eukaryotic Ca²⁺ channel, which also has the EEEE ring in SF, shows pH dependence of channel conductance, with a pKa greater than 7 (45). The Ca²⁺ channel displays a high-conductance state (140 pS) and a low-conductance state (45 pS), which are believed to belong to protonation states S₀ and S₁, respectively (46). The high-conductance state can be abolished by mutating a single Glu in the SF to Gln (46). This would be consistent with our result that state S₀ is more conductive than state S₁. The experimental pH dependence of a bacterial voltage-gated sodium-selective ion channel NaChBac was also reported. This channel has a similar structure to Na_vMs. For NaChBac, the whole-cell normalized currents were measured against voltages at multiple pH values (43). The normalized conductance can be extracted from the slope of the data points in the linear region where all ion channels are activated. The conductance, in fact the slope, was shown to decrease with lowering pH value, which again coincides with our result. In addition, based on the normalized conductance at different pH, we can estimate the pKa value for conductance, which is 7.6 ± 1.0. This estimated pKa agrees well with our pKa results determined via free energy calculations.

With protonation state S₀, the distribution of Na⁺ ions along the z axis presented here is very similar to that reported in another MD work (35) that uses the same crystal structure (PDB: 5HVX). When peaks in the central cavity are aligned, the distribution in this work shows an order of peaks as Site2 > Site3 > Site4 > Site1 ∼Site0 (see Fig. 4 for distribution of sites), and Ke et al. (35) show the same order, except that the numbering of sites is shifted by 1 and there is no corresponding site for Site0. This distribution and the binding pattern shown in Fig. 4 appear to be unique to the PDB: 5HVX structure and different from those obtained with other crystal structures of open Na_vMs (25,31,34,65) or with closed Na_vAb structures (27). Differences in the pore radii of these structures are shown in Fig. S8. Although two MD works using PDB: 4F4L of open Na_vMs (25,31) also have distributions with five major peaks near SF, their highest peaks are at Site1 (designated as “HFS” (high field strength) in (25) and as “S1” in (31)) and much higher than the peaks at Site2 (designated as “BAR”(barrier) in (25) and as “S2” in (31)), whereas this work’s highest peak is at Site2 and much higher than the peak at Site1. In one of the two works (31), although the sites’ locations and coordinating groups of each site generally agree with ours, there is only one site (Site1) at which the Na⁺ ions have a partial hydration shell, unlike in this work, in which an additional site, Site3, is noticed to be partially dehydrated. These two MD works, though simulating the same channel Na_vMs as ours but using another crystal structure (PDB: 5HVX versus PDB: 4F4L), show difference in Na⁺ distribution from ours, which indicates the influence of the starting point of simulations, i.e., the crystal structure. Another MD study (27), simulating a closed Na_vAb channel, shows a very different binding pattern from that of this work, in which there are only three sites coordinated by E178 carboxylates, both E178 carboxylates and L177 carbonyls, and T176 carbonyls, respectively. The differences in binding patterns between this work and the study for closed Na_vAb may be due to the different initial SF conformations of the two homologs (Na_vMs and Na_vAb), which are discussed below.

The protonated states (S₁ and S₂) of this work possess new, to our knowledge, features in Na⁺ distributions as well. Although our previous work (65) simulating Na_vMs reported several Na⁺ binding sites for protonation state S₁ between z = −5 Å and z = 2 Å, this work reveals a new, to our knowledge, site in both no-restraints and gate-restrained systems around z = 7 Å (without external voltage, Fig. S2 B) and z = 6.5 Å (at ∼−100 mV, Fig. 6 C), respectively. Meanwhile, unlike the previous work in which Na⁺ ions do not populate below z = −5 Å in S₂ states, in this work, the continuous free energy profiles of S₂ states (Figs. 6 C and S2 B) demonstrate passage of Na⁺ ions through the whole pore domain. The above discrepancies might be due to the differences in crystal structures used (PDB: 4F4L versus PDB: 5HVX). Another possible reason could be that in the previous work, the channel gate closed during the course of simulations. Considering this, simulating open channels is necessary and vital to provide accurate information on ion conduction. A comparison between the protonated states in this work and those of a closed Na_vAb channel (PDB: 3RVY) (21,28) shows that the highest free energy barriers of S₂ states are all in the extracellular region in Na_vAb simulations, and within the SF in this work. This disagreement about free energy profiles might be caused by the differences between the two sodium channel homologs, a closed Na_vAb and an open Na_vMs. The open Na_vMs structure (PDB: 5HVX) has pore radii smaller than those of the closed Na_vAb (PDB: 3RVY) everywhere in the SF except near the carboxyl groups of glutamic acids of the SF, where the two structures’ radii are similar (Fig. S8 A). Especially, the open Na_vMs structure (PDB: 5HVX) is narrower than the closed Na_vAb one (PDB: 3RVY) by ∼1 Å on the plane of carbonyl oxygen atoms of L177, which form the Site3 and play a crucial role in coordinating Na⁺ ions during conduction processes. With these in mind, findings based on Na_vAb structures may not be generalized to the Na_vMs channel.

Systems without and with gate restraints exhibited very similar average numbers of Na⁺ ions in the pore (Table S11) when there is no voltage and ∼−100 mV, respectively: 2.3 vs. 2.1 for the S₀ state, 1.2 vs. 1.3 for the S₁ state, and 0.9 vs. 0.9 for the S₂ states. These numbers are also similar to but slightly larger than the numbers from our previous work simulating Na_vMs but using PDB: 4F4L (65). We compare the no-voltage runs to the previous work also performed without voltage: 2.3 vs. 1.8 for the S₀ state, 1.2 vs. 1.0 for the S₁ state, and 0.9 vs. 0.2 for the S₂ states. This increase may be, again, due to the difference in the two crystal structures. In addition, these numbers are also similar to, but slightly smaller than, those from previous MD studies simulating closed Na_vAb (28): 2.3 vs. 2.3 for the S₀ state, 1.2 vs. 2.0 for the S₁ state, and 0.9 vs. 1.2 for the S₂ states. This decrease could possibly be explained by the narrower SF of open Na_vMs compared to the closed Na_vAb’s SF.

The fact that we needed to apply mutations to the gate, as well as apply distance restraints, to observe conduction raises the question of whether the PDB structure (PDB: 5HVX) used here is an open state. We note that similar gate closing is observed for simulations with PDB: 4F4L and PDB: 3ZJZ structures in the absence of either mutations or restraints (31,34,65). This uncertainty in the functional representation of the structure could be a limitation of all computational work (including this) performed on these structures.

The comparison between the system with neutral lipids and that with mixed negatively charged lipids (Fig. 7) shows that negatively charged lipids enhance Na⁺ ion conduction in bacterial Na_v channels, which agrees with experiments (82). Those experiments suggest that the preference for negatively charged lipids is a result of the interaction between lipids and VSD. However, here we observe that the electrostatic changes in SF caused by charged lipids, without any considerable conformational changes, could also contribute to that preference.

The conductance measurements (Figs. 3 A, 6 A, 7 A, and 9, A and D) show that the channel conductance depends on membrane voltage, regardless of protonation states or systems (no restraint or gate restraint, neutral or charged lipids, etc.). More specifically, conductance almost always increases as the magnitude of membrane voltage increases, with only three exceptions. Indeed, as Fig. 8 shows, higher voltage is likely to induce an increment in SF radius, and the voltage-dependent SF radius positively correlates with channel conductance. So, this voltage dependence of conductance may arise from changes in SF conformation caused by membrane voltages. Care is needed when employing high voltages that may induce unrealistic SF conformational changes and could possibly alter the conduction mechanism. Owing to the positive dependence of conductance on voltage magnitude, if conductance is calculated from the slope of the linear fit of the current-voltage data, then the conductance could be overestimated because the high-voltage data points increase the slope.

MD simulations of the 20 copies with no restraints show positive correlations between channel conductance and the radius of the gate. Given the correlations and the fact that the gate radius shrunk in unrestrained simulations, we conducted simulations by restraining the gate backbone atoms with the PDB structure as reference. The comparison between no-restraint and gate-restraint simulations confirms that a wider gate gives rise to significantly higher conductance, as shown in Fig. 3, whereas these gate restraints do not distort SF (Fig. 4). A wider gate could also be achieved by the mutation V219D. In no-restraint simulations in which the gate is relatively narrow, the mutation-induced gate widening is capable of raising conductance. However, in gate-restrained simulations, the conductance is not raised, suggesting that when the gate is wide enough, additional widening of the gate does not raise conductance.

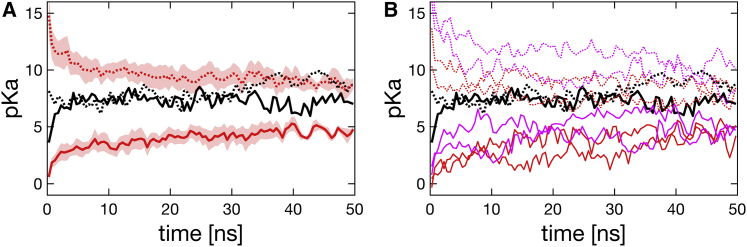
Although the lipid composition does not appear to affect the pKa of E178 residues, the free energy calculations for both neutral-lipid and charged-lipid systems show that applying negative external electric fields is likely to cause increases in average pKa values, accompanied by widening of the SF opening on average. However, these changes are within their corresponding SDs, the correlations between membrane voltage, the pKa value of E178, and the SF radius are therefore not guaranteed. The pKa values from the last 50 ns are close to the physiological pH 7.4, which proves that both states S₀ and S₁ are accessible at the physiological pH and justify considering the protonated state S₁. In fact, our previous work (65) has shown that states S₀, S₁, and S₂ are all feasible at the physiological pH. Our previous work demonstrated the modulation of SF protonation states by Na⁺ ions and showed that pKa values decayed with increasing number of ions. The previous work was performed with neutral lipids and without membrane voltages, so here we compare this work’s pKa values from the neutral-lipid system with 0 mV to the numbers from the previous work (Fig. 11). Among the previous runs, we chose and plotted the set with an average number of ions of 2.0 because the mentioned runs from this work possessed a similar number of ions, 1.9, on average. Fig. 11 shows that the pKa values calculated from simulations started from S₁-equilibrated structures (Fig. 11 A, red dashed line) appear to converge to the previous pKa values (Fig. 11 A, black lines), whereas the simulations started with S₀-equilibrated starting structures exhibited lower but increasing pKa values (Fig. 11 A, red solid line). To rule out statistical fluctuations as a source of error, Fig. 11 includes four additional 50 ns simulations (Fig. 11 B, magenta lines) from this work’s neutral-lipid system with 0 mV. Fig. 11 B shows that indeed there are statistical fluctuations in pKa values among independent simulations. However, for S₀ equilibrated simulations, the difference is statistically significant between the previous work’s pKa values and the values averaged over four simulations from this work (Fig. 11 A, solid lines). This means that the pKa difference around 50 ns is likely not due to a statistical fluctuation, but rather systematic reasons, which could be the difference between the PDB structures PDB: 5HVX and PDB: 4F4L (Fig. S8 B) or the fact that in previous simulations, the channel gate was closed. It is worth mentioning that although the pKa values from the two works did not converge within 50 ns, the S₀-started pKa values were clearly still increasing after 50 ns, as observed in long (300 ns) simulations (Fig. 10 A, blue solid line), and are more converged to the previous values with longer time. Systems in this work might just need more time to achieve convergence, and this is consistent with a larger initial pKa difference between S₀-started and S₁-started simulations.

Figure 11.

Comparison of pKa values. Comparison of the averaged (A) or individual (B) pKa values between our previous work (65) (black) and the neutral-lipid system at 0 mV from this work (red or magenta) is shown. Simulations started from S₀-equilibrated structures are plotted as solid lines and S₁ as dashed lines. In (B), red lines represent part of the long (300 ns) simulations shown in Fig. 10, and magenta lines represent additional short (50 ns) simulations. Shaded areas in (A) represent standard errors. To see this figure in color, go online.

Conclusions

Through 173 MD simulations of 450 or 500 ns, we examined multiple factors influencing conductance of Na_vMs, namely protonation state, voltage, width of gate, lipid composition, and, through comparison with previous work, starting PDB structures. Large variation of conductance was observed between independent copies started with different initial velocities, suggesting the importance of performing multiple independent simulations. We determined the conductance of five protonation states that are accessible at physiological pH and show that the deprotonated state is most conductive, with conductance further decreasing with each additional proton bound. This decaying trend of conductance agrees with an experimental work on NaChBac (43), which showed a decrease in normalized maximal conductance with lowering of pH. Moreover, the relationship between the conductance and free energy barriers of the five protonation states meets the Arrhenius equation. We observed the decrease of the gate radius compared to the PDB radius. This decrease reduces the channel conductance. We further performed gate-restrained simulations that maintained PDB backbone radius, and these simulations show higher conductance while maintaining the properties of the SF. The mutation V219D increases the gate radius in both no-restraints and gate-restrained systems. This gate widening increases conductance only in no-restraints simulations and does not affect the conductance in gate-restrained ones. This suggests that although widening the gate toward the PDB structure increases the conductance, the further increase of gate width beyond the PDB value does not affect the conductance. We show that negatively charged lipids help enhance the conduction as opposed to purely neutral lipids. This is likely achieved, as shown by the change in the electrostatic potential, by attracting more Na⁺ ions to the SF entrance. We also show that the conductance increases with voltage magnitude and a widening of the SF happens concurrently. A good correlation was noticed between the conductance and radius of the SF. So, the voltage-induced change of the SF radius might contribute to the voltage dependence of conductance. The conduction process is shown to be a Poisson process, but possibly with a recovery time at low voltages. We examined the Na⁺ ions distribution in the SF for different protonation states and compared with previous works utilizing PDB structures PDB: 4F4L (for Na_vMs) and PDB: 3RVY (for Na_vAb). These two PDB structures both have a wider SF than that of PDB: 5HVX on average. Their simulations show different binding patterns and/or free energy profiles. This suggests a unique Na⁺ ion distribution pattern for PDB: 5HVX and a dependence on starting structures. We also observed two SF conformations and transitions between them. With hundreds-of-nanoseconds-long free energy simulations, we also determined the pKa values of E178 residues for the transition between deprotonated and singly protonated state with and without external voltage in systems with neutral lipids or charged lipids. The pKa values are close to the physiological pH and in agreement with the experimental work on NaChBac (43). That means that the singly protonated state is accessible at physiological pH, agreeing with our previous study (65). The pKa values exhibit small voltage dependence and likely no dependence on lipid composition.

Author contributions

All authors designed research. A.Y.C. performed research and drafted the manuscript. A.D. and B.R.B. edited the manuscript. All authors approved the final manuscript.

Editor: Christopher Ahern.