Orientation of neurites influences severity of mechanically induced tau pathology

Abstract

Chronic traumatic encephalopathy is a neurodegenerative disease associated with repeated traumatic brain injury (TBI). Chronic traumatic encephalopathy is a tauopathy, in which cognitive decline is accompanied by the accumulation of neurofibrillary tangles of the protein tau in patients’ brains. We recently found that mechanical force alone can induce tau mislocalization to dendritic spines and loss of synaptic function in in vitro neuronal cultures with random cell organization. However, in the brain, neurons are highly aligned, so here we aimed to determine how neuronal organization influences early-stage tauopathy caused by mechanical injury. Using microfabricated cell culture constructs to control the growth of neurites and an in vitro simulated TBI device to apply controlled mechanical deformation, we found that neuronal orientation with respect to the direction of a uniaxial high-strain-rate stretch injury influences the degree of tau pathology in injured neurons. We found that a mechanical stretch applied parallel to the neurite alignment induces greater mislocalization of tau proteins to dendritic spines than does a stretch with the same strain applied perpendicular to the neurites. Synaptic function, characterized by the amplitude of miniature excitatory postsynaptic currents, was similarly decreased in neurons with neurites aligned parallel to stretch, whereas in neurons aligned perpendicular to stretch, it had little to no functional loss. Experimental injury parameters (strain, strain rate, direction of stretch) were combined with a standard viscoelastic solid model to show that in our in vitro model, neurite work density during stretch correlates with tau mislocalization. These findings suggest that in a TBI, the magnitude of brain deformation is not wholly predictive of neurodegenerative consequences of TBI but that deformation relative to local neuronal architecture and the neurite mechanical energy during injury are better metrics for predicting trauma-induced tauopathy.

Significance

Soldiers and athletes exposed to frequent traumatic brain injuries have increased likelihood of developing neurodegenerative diseases such as chronic traumatic encephalopathy. Chronic traumatic encephalopathy is characterized by cognitive decline and dense deposits of aggregated tau protein in the brain. This study provides experimental evidence demonstrating that functional and tauopathic consequences of a high-strain-rate injury are impacted by the orientation of injured neurons with respect to the direction of mechanical injury. This study combines neuroscience techniques (electrophysiology, transfection, fluorescent imaging) with theoretical mathematical models to elucidate a previously unknown relationship between mechanical injury and biological consequences at the cellular scale.

Introduction

Traumatic brain injury (TBI) is a serious public health concern because of its association with long-term neurological degeneration and cognitive decline (1,2). TBIs are typically caused by falls, automobile crashes, sports-related impacts, and military-related injuries. Recent epidemiological studies in the United States indicate that there are ~2.8 million TBI-related emergency department visits, hospitalizations, and deaths per year. Additionally, an estimated 5.3 million Americans are living with a disability that stems from a TBI (3, 4, 5). However, these statistics likely underestimate the true impact of TBI, as mild TBIs frequently go unreported, especially in instances of violence (6,7). Much of the current attention being paid to TBIs is due to the observation of long-term neurological deficits in those who have sustained multiple mild TBIs in their lives (notably in former professional athletes and military veterans), associated with chronic traumatic encephalopathy (CTE). CTE is a neurodegenerative disease whose clinical symptoms include behavioral changes, memory deficits, and other symptoms of cognitive decline (8, 9, 10, 11, 12). CTE is one of several neurodegenerative diseases characterized by the dysfunction of the tau protein in neurons, called tauopathies, and is currently only confirmable via autopsy diagnosis.

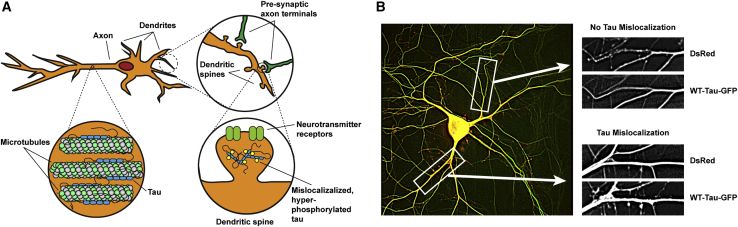
Tau is a microtubule-associated protein that normally acts to stabilize microtubules and is involved in axonal transport in central nervous system neurons (13, 14, 15). Dense clusters of hyperphosphorylated tau, called neurofibrillary tangles (NFTs), are used to diagnose CTE and other tauopathies (16,17). In CTE, the NFTs tend to be most concentrated in the brain’s sulcal depths and in perivascular regions immediately surrounding blood vessels (11,12,17, 18, 19, 20). Computational models of TBI suggest that the strain experienced by these regions of the brain is amplified because of the geometry of the sulcus and the relative rigidity of blood vessels compared to brain tissue (21,22). Studies of mechanical injury to axons suggest that strain is a primary determinant of neuronal damage and that different regions of the brain are disparately affected by strain (23, 24, 25, 26). However, the combination of strain rate, strain, and direction can be a valuable predictor of the severity and consequences of injury at the cellular scale (27,28). In vitro models of tauopathy (29, 30, 31, 32, 33) and TBI (22) have shown that tau becomes hyperphosphorylated and mislocalizes from axons to dendritic spines, where tau is not normally found. This mislocalization of tau leads to postsynaptic deficits due in part to α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA)-receptor internalization in the afflicted dendritic spine (22,29, 30, 31, 32, 33). We have previously shown that cell-scale tau pathology and synaptic deficits can be elicited by a high-strain-rate mechanical injury (22).

In situ, neurons are highly organized into various gray- and white-matter tracts. In vivo imaging of human brains during noninjurious head impacts has shown that distinct strain patterns emerge during impact that are dependent on these anisotropic architectural differences (34). Computational models of axonal injury have yielded similar results, concluding that strain in the direction of neuronal orientation is one of the most significant predictors of traumatic or diffuse axonal injury (35,36) and that the inclusion of neuronal tract architecture improves finite-element models of brain deformation (37, 38, 39, 40, 41). In vitro studies have indicated that nerve bundle geometry affects neuron functionality after mechanical trauma (42, 43, 44). Taken together, these data suggest that the relative orientation of neuronal alignment and brain deformation during injury is an important mediator of injury outcome.

Here, using cultured hippocampal rat neurons, we report an in vitro tauopathy model of TBI that relates neuronal architecture and high-strain-rate mechanical deformations to tau pathology and functional synaptic deficits. We find that neurons whose neurites are aligned parallel to stretch orientation showed significantly greater tau mislocalization than those aligned perpendicular to stretch or with no alignment when exposed to high-strain-rate strains. Loss of neuronal function, identified by miniature excitatory postsynaptic current (mEPSC) characteristics, was similarly greater in parallel aligned neurons. By combining TBI-simulation injury parameters (strain, strain rate, direction) with a standard viscoelastic solid material model and an image-based quantification of neuronal orientation, we calculated the work density during TBI-like stretching and found that total work density correlates with tau mislocalization, suggesting that tau mislocalization is mediated by mechanical energy during stretch. Taken together, these studies are an important step toward understanding the role of mechanical forces in tauopathy and the early stages of CTE.

Materials and methods

Cell culture construct preparation

Standard photolithography techniques were used to created polydimethylsiloxane (PDMS) stamps patterned with a linear array of 5 μm raised features (45, 46, 47, 48). 15 μm raised features were separated by 100 μm gaps, creating an array of linear channels. PDMS stamps were then placed into a vacuum desiccator with a petri dish that contained ~400 μL of trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma-Aldrich, St. Louis, MO) and left overnight to create a self-assembled monolayer of silane, which allows for easier release of the stamps from cured PDMS (49). The high-velocity stretching constructs were prepared for neuronal culture by first spin coating a 10-μm-thick layer of 1:1 Sylgard 527 PDMS (Ellsworth Adhesives, Germantown, WI) onto 2 × 3 inch rectangles of 0.010-inch-thick silicone sheeting (SMI, Saginaw, MI). To emboss linear channels into membranes, the silanized PDMS stamps were delicately placed into the uncured PDMS layer and allowed to cure in an 80°C oven for at least 2 h. After curing, the PDMS stamps were carefully removed, and the membranes were suspended in tension between two custom-designed stainless-steel brackets (Oakdale Precision, Saint Paul, MN). A 1:10 Sylgard 184 PDMS (Ellsworth Adhesives) ring was then adhered to the membrane to contain culture media upon seeding of neurons. The assembled constructs were treated with a UVO-Cleaner (Jelight, Irvine, CA) for 8 min and then incubated in a solution of 100 μg/mL poly-D-lysine and 4 μg/mL laminin (Sigma-Aldrich) overnight to promote cellular adhesion.

Cell isolation and culture

Primary hippocampal neurons were harvested from neonatal Hsd:Sprague Dawley rat pups as previously described (Envigo, Indianapolis, IN) (50). The hippocampal sections were isolated and pooled together into Earl’s Balanced Medium with 1 mM D-glucose that was chilled on ice. Tissues were then digested, and the resulting cells were seeded onto the stretching constructs at a density of ~10⁶ cells per construct in plating media (minimal essential media with Earle’s salts, 10 mM HEPES, 10 mM sodium pyruvate, 0.5 mM glutamine, 12.5 μM glutamate, 10% fetal bovine serum, and 0.6% glucose; Thermo Fisher Scientific, Waltham, MA). The day of harvest and plating was denoted as day-in-vitro 1 or DIV1. 4 h after plating, the media was replaced with fresh plating media to remove debris and nonadherent or dead cells. 24 h after plating (DIV2), the media was replaced with NbActive1 neuron culture media (BrainBits, Springfield, IL). Cells were kept in a 37°C, 5% CO₂ incubation environment for the duration of experiments. 50% of the media was removed and replaced with fresh NbActiv1 media on a weekly basis.

High-speed stretching of neurons

A linear motor (PS01-23×80F/100×160-HP-R; LinMot USA, Elkhorn, WI) was used to perform mechanical deformations of cultured hippocampal neurons seeded on our custom-designed cell culture constructs. The motor applied a high-strain-rate uniaxial injury to neurons by displacing one of the stretchable cell culture construct brackets. Finite control over strain (ϵ) and strain rate $\left(\dot{\epsilon }\right)$ allowed us to perform a variety of injury simulations. Single stretches were performed with ϵ = 0–20% and $\dot{\epsilon }$ = 10/s. This setup was used to deform all neurons in the study, including neurons aligned parallel to the stretch or perpendicular to the stretch and neurons that were unaligned.

Transfection constructs

The DsRed construct used was expressed in the pRK5 vector and driven by a cytomegalovirus promoter. The human-tau construct used in this study was expressed in the pRK5 vector, tagged with enhanced GFP on the N-terminus, and driven by a cytomegalovirus promoter (Clontech, Mountain View, CA). This wild-type (WT)-Tau-GFP construct encoded for human 4R tau lacking the N-terminal sequences (4R0N) and contained exons 1, 4–5, 7, and 9–13; intron 13; and exon 14.

Transfection and cellular imaging

Neurons were transfected with DsRed and WT-Tau-GFP using a standard calcium phosphate transfection method at DIV7 (51). Neurons were transfected at a 2:1 ratio of DsRed/WT-Tau-GFP. DsRed was used to visualize the morphology of the neurons, including the dendritic spines, and WT-Tau-GFP was used to track the localization of tau within the neuron. Transfected cells were allowed to mature for 3 weeks before experimentation. On DIV30, 24 h after a stretch was applied, the neuron-containing constructs were mounted on a custom-designed platform above a Nikon inverted epifluorescent microscope (Nikon, Tokyo, Japan). Images were collected using a 40× water immersion objective lens. 15-image stacks with a 0.5 μm step in the z-direction were acquired using a computerized focus motor and MetaMorph Imaging System (Universal Imaging, Bedford Hills, NY). After acquisition, stacks were processed using MetaMorph’s two-dimensional nearest-neighbors deconvolution method before out-of-focus slices were removed. The remaining slices of the stack were then averaged into a single image. DsRed and WT-Tau-GFP imaged were overlaid and colorized using Adobe Photoshop (Adobe, San Jose, CA) to count dendritic spines and dendritic spines that contained tau. Each spine was treated as a data point with a binary outcome (tau present or no tau present), and the total sample population of dendritic spines was used for statistical analysis. A maximum of two cells per dish were imaged for tau mislocalization imaging experiments.

Electrophysiology

mEPSCs were recorded from hippocampal neurons at DIV30 using 5 MΩ glass pipettes. Whole-cell recording was performed with a holding potential of −55 mV (30). Recordings lasted up to 5 min and were done using an Axopatch 200B amplifier and pClamp 11 (Molecular Devices, San Jose, CA). For each second recorded, a sweep of 200 ms was sampled. Recordings were filtered at 1 kHz, and the gain was set to α = 1. Before recording, neurons were rinsed three times with artificial cerebrospinal fluid (ACSF) at room temperature. 2 mL of ACSF was left in each construct during recording. ACSF was comprised of 119 mM NaCl, 2.5 mM KCl, 5.0 mM CaCl₂, 2.5 mM MgCl₂, 26.2 mM NaHCO₃, 1 mM NaH₂PO₄, and 11 mM glucose. Additionally, ACSF was supplemented with 100 μM (2R)-amino-5-phosphonovaleric acid (an NMDAR antagonist), 1 μM tetrodotoxin (TTX) (a sodium channel blocker), and 100 μM picrotoxin (GABAa receptor antagonist) and bubbled with 95% O₂-5% CO₂ for 20 min before experiments. The glass patch pipette was filled with an internal solution comprised of 100 mM cesium gluconate, 0.2 mM EGTA, 0.5 mM MgCl₂, 2 mM ATP, 0.3 mM GTP, and 40 mM HEPES (pH 7.2 with CsOH) (Sigma-Aldrich). Each individual mEPSC was manually identified using MiniAnalysis software (Synaptosoft, Fort Lee, NJ) based on a threshold amplitude of 3 pA, a characteristic fast-rising phase, and a slow decaying phase indicative of mEPSCs. The average amplitude of mEPSCs and the overall frequency of mEPSCs for each neuron were calculated and treated as a single data point. A maximum of one cell per dish was patched for all electrophysiology experiments.

Viscoelastic model of neurite deformation

Mechanical energy added to the dendritic spine during injury was determined by calculating the work density (work per unit volume) done on the cell during stretching, as described in our previous manuscript (22). Local neurite orientation angle (θ) relative to stretch orientation throughout the neuron was determined using DsRed images of individual neurons and a custom MATLAB (The MathWorks, Natick, MA) code (52, 53, 54, 55). The local strain (ϵ) parallel to neurite alignment was taken as a function of applied strain (ϵ_applied) such that

$$\epsilon ={\epsilon }_{applied}{\cos }^2\theta .$$ (1)

Neurons act as viscoelastic Kelvin solids (56), but neurites become more fluidic with increasing stress (57). To capture both of these observations, we modeled the neurite as a standard viscoelastic solid with two springs and one dashpot and described by the equation

$$\frac{\dot{\sigma }}{E_1}+\frac{\sigma }{{\eta }_1}=\frac{E_1+E_2}{E_1}\dot{\epsilon }+\frac{E_2}{{\eta }_1}\epsilon ,$$ (2)

where σ is the stress; ϵ is the strain; $\dot{\sigma }$ and $\dot{\epsilon }$ are the stress and strain rates, respectively; E₁ and E₂ are the moduli of the springs; and η₁ is the viscosity of the dashpot. E₁, E₂, and η₁ were determined by simulating a creep test previously reported by Grevesse et al. (57), and fitting the parameters to their results using least-squares fitting (22). This method yielded E₁ = 11.33 MPa, E₂ = 1.13 kPa, and η₁ = 8.88 kPa s.

To model neurite stretching, we let ϵ and $\dot{\epsilon }$ match those applied experimentally and calculated σ using Eq. 2 and finite differences. The work density (w) was taken as

$$w=\int \sigma d\epsilon ,$$ (3)

over the period from the initiation of stretch to the time at which ϵ is at its peak value. Whole-neuron mean work density is reported. A parameter study was performed to determine how the values of E₁, E₂, and η₁ influence the results by setting E₁ = βE₂ and repeating the solution above for a given β.

Statistical analyses

To quantify tau mislocalization, the total number of dendritic spines and the number of dendritic spines containing an observable tau presence were recorded (spines and spines with tau were summed from all recorded images in each treatment group). The fraction of dendritic spines containing tau was calculated from these two numbers. A χ² test for multiple proportions was used to assess for statistical differences between treatment groups, followed by two-proportion pooled z-tests to determine pairwise statistically significant differences between each of the treatment groups. For electrophysiology data (mEPSC amplitude and frequency) and mean work density versus strain data, one-way ANOVA was used to test for variance between all groups, followed thereafter by a Tukey post hoc test for pairwise comparisons. For cumulative frequency distributions, Kolmogorov-Smirnov (K-S) tests were used to compare mEPSC amplitude and period distributions between unstretched cells and stretched groups (unaligned, parallel, and perpendicular). The ratio of the K-S test statistic (D) to the statistical critical value (D_crit) is reported in the figure captions. All tests had statistical significance set for α = 0.05. χ² tests, two-proportion pooled z-tests, analysis of variance, and Tukey tests were performed using SigmaPlot 11.0 (Systat Software, San Jose, CA). K-S tests were performed using Microsoft Excel (Microsoft, Seattle, WA).

Animal usage

The breeding, handling, and usage of rats and mice have been approved by the Institutional Animal Care and Use Committee at the University of Minnesota (Protocol #1809-36344A). Rat pups (<1 week old) were decapitated to harvest brain tissues strictly following the Institutional Animal Care and Use Committee guidelines.

Results

Substrate patterning influences neurite architecture in vitro

We previously developed an in vitro device to impart strains onto rat primary hippocampal neurons cultured on elastic membranes (Fig. 1, A and B) (22). In our prior studies, the cells formed a monolayer with no discernable organization (Fig. 2 A). Here, we aimed to direct neuronal organization to better mimic in vivo neural tracts by micropatterning ridges into PDMS-coated elastic membranes (Fig. 2 B). Neurites of neurons seeded on the ridged substrates primarily aligned parallel to the ridges, resulting in cellular architecture that was distinct from neurons seeded on nonpatterned substrates (Fig. 2, C–E).

Figure 1.

In vitro TBI simulations are performed on elastic cell culture constructs. (A) A neuron-containing elastic substrate was deformed at high speeds by a linear motor. (B) The elastic substrate upon which neurons were cultured was composed of an elastic membrane layer spin coated with Sylgard 527 PDMS and surface coated with poly-D-lysine and laminin. To see this figure in color, go online.

Figure 2.

Embossing PDMS ridges onto cell culture constructs allows for preferential alignment of neuron growth along a chosen axis. (A) Without alignment, neurons form an unorganized monolayer on cell culture constructs. (B) Method for embossing ridges onto elastic membranes using a PDMS stamp. (C) Neurons aligned parallel to the axis of stretch. (D) Neurons aligned perpendicular to the axis of stretch. (E) Fluorescent images of neurons in the three alignment states (left) with accompanying neurite angle histograms (right), demonstrating the utility of this method. Histograms represent the neurite angle distribution of the representative cell immediately to the left. To see this figure in color, go online.

Neuronal alignment in vitro influences tau pathology caused by high-strain-rate stretching

To investigate the effect of neuronal architecture on tau pathology, we used our custom-designed cell stretcher to simulate a TBI in vitro by applying high-strain-rate deformations to primary hippocampal neurons. Neurons were patterned so that neurites aligned parallel to or perpendicular to stretch, or they were left unpatterned so that neurite alignment was random (Fig. 2 E). We co-transfected neurons with DsRed and WT-Tau-GFP plasmids to track the localization of tau within the neuron after a mechanical injury, allowing observation of tau mislocalization to dendritic spines (Fig. 3, A and B). Neurons were exposed to a single stretch with a strain rate $\left(\dot{\epsilon }\right)$ of 10/s at a magnitude of 5, 10, or 20% strain (ϵ). Unstretched neurons showed a minimal amount of mislocalization in both patterned and unpatterned cells (Fig. 4 A). Consistent with our previous results, neurons with no preferred alignment showed increased tau mislocalization with increased strain magnitude. Neurons aligned parallel to stretch showed a similar relationship between tau and stretch, but the overall levels of tau mislocalization were higher for each prescribed injury level. Conversely, neurons aligned perpendicular to the stretch showed low levels of tau mislocalization in the control, 5% strain, and 10% strain conditions and only showed a substantial increase in mislocalization at 20% strain (albeit still lower than the unaligned and parallel neurons) (Fig. 4, B–E). These data suggest that neuronal injury, as characterized by tau mislocalization, is dependent on cellular architecture and correlated with the magnitude of the strain along the long axis of the neurites.

Figure 3.

Tau mislocalizes to dendritic spines and ultimately aggregates into NFTs in tauopathies. (A) Postsynaptic neuron with tau bound to its axonal microtubules (bottom left magnification). Synapses with presynaptic neurons occur at the dendritic spines (top right magnification). Hyperphosphorylated tau that has mislocalized to and aggregated within a dendritic spine, where it interferes with AMPA-receptor trafficking (bottom right magnification), is shown. (B) A representative neuron transfected to express DsRed and WT-Tau-GFP fluorescent proteins (left). A dendrite without significant tau mislocalization to dendritic spines (top right) and a dendrite with tau mislocalization to dendritic spines (bottom right) are shown. To see this figure in color, go online.

Figure 4.

Tau mislocalization driven by mechanical injury is dependent on cellular architecture and injury severity. (A–D) Representative images of cultured rat hippocampal neurons transfected with DsRed (left) or WT-Tau-GFP (center). Images were overlaid to assess tau mislocalization (right). Alignment configurations are relative to the axis of stretch: perpendicular (top), unaligned (middle), and parallel (bottom). (A) Unstretched neurons. (B) Neurons stretched to 5% strain at 10/s. (C) Neurons stretched to 10% strain at 10/s. (D) Neurons stretched to 20% strain at 10/s. (E) Quantification of tau mislocalization, measured as fraction of spines with tau present (mean ± standard deviation (SD)). Spines/images: 0-perpendicular = 412/10, 0-unaligned = 273/13, 0-parallel = 413/10, 5-perpendicular = 352/10, 5-unaligned = 1134/18, 5-parallel = 428/12, 10-perpendicular = 216/10, 10-unaligned = 219/10, 10-parallel = 205/10, 20-perpendicular = 951/17, 20-unaligned = 319/11, 20-parallel = 507/16. # indicates statistical difference from other alignments within a strain group, ^∗ indicates statistical difference between unstretched cells in a given alignment, p < 0.05. Note: 0-perpendicular and 0-parallel are the same data point, as cells are simply aligned without a stretch. Additionally, all images were cropped and rotated for efficiency. A perfect left-to-right stretch from the shown perspective only occurred in the parallel configurations of (B)–(D). To see this figure in color, go online.

Loss of synaptic function after high-velocity stretch is dependent on neuron architecture

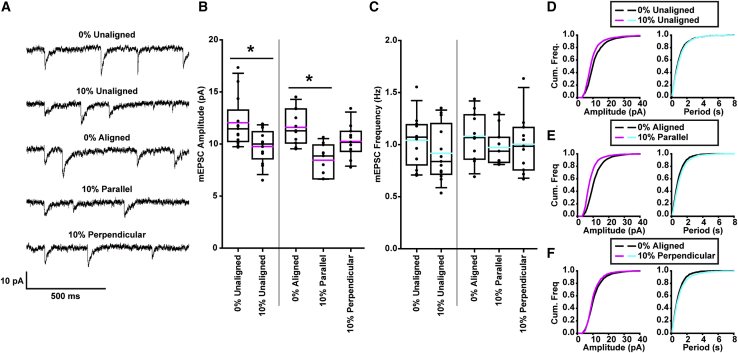
In vitro models of Alzheimer’s disease (AD) (29, 30, 31,33) and our previous in vitro model of TBI (22) showed that tau mislocalization in neurons, induced by either a familial AD mutation or mechanical injury, was associated with synaptic deficits. Thus, we aimed to assess the impact of neuronal architecture-associated differences in mislocalization on these synaptic impairments after simulated TBI. Using whole-cell patch clamp, we recorded mEPSCs, which can be used as a proxy for synaptic functionality and health (Fig. 5 A). We applied an intermediate stretch (ε = 10%, $\dot{\epsilon }$ = 10/s), at which our tau mislocalization experiments showed differential degrees of tau pathology between alignment groups. Consistent with our previous results, 24 h after injury, we observed a statistically significant decrease in mEPSC amplitude, indicative of postsynaptic dysfunction, between unstretched-unaligned neurons and stretched-unaligned neurons. In aligned neurons, we observed a significant decrease in mEPSC amplitude between unstretched neurons and neurons stretched parallel to neurite alignment, but not in those stretched perpendicular to neurite alignment (Fig. 5, B and D–F). mEPSC frequency, which is indicative of presynaptic function, was not significantly affected by stretch (Fig. 5, C–F). These data suggest that architecture-dependent tau mislocalization results in architecture-dependent postsynaptic deficit after mechanical injury.

Figure 5.

Neuron synaptic function after exposure to a stretch injury is dependent on architectural alignment. (A) Representative mEPSCs from each of the five stretch and alignment combinations (all stretches were 10% strain, 10/s). (B) Quantification of mEPSC amplitudes (black line: median, pink line: mean, box: 25–75%, whisker: 10–90%). (C) Quantification of mEPSC frequency (black line: median, blue: mean, box: 25–75%, whisker: 10–90%). (D) Cumulative frequency distribution of mEPSC amplitudes (left) and peak-to-peak periods (right) of unstretched-unaligned neurons versus stretched-unaligned neurons. (E) Cumulative frequency distribution of mEPSC amplitudes (left) and peak-to-peak periods (right) of unstretched-aligned neurons versus stretched-parallel neurons. (F) Cumulative frequency distribution of mEPSC amplitudes (left) and peak-to-peak periods (right) of unstretched-aligned neurons versus stretched-perpendicular neurons. Cells/mEPSCs: unstretched-unaligned = 13/2581, stretched-unaligned = 13/2231, unstretched-aligned = 11/2153, stretched-parallel = 11/1907, stretched-perpendicular = 11/1782. All plots: ^∗p < 0.05. To see this figure in color, go online.

Tau mislocalization is associated with mechanical energy during stretching

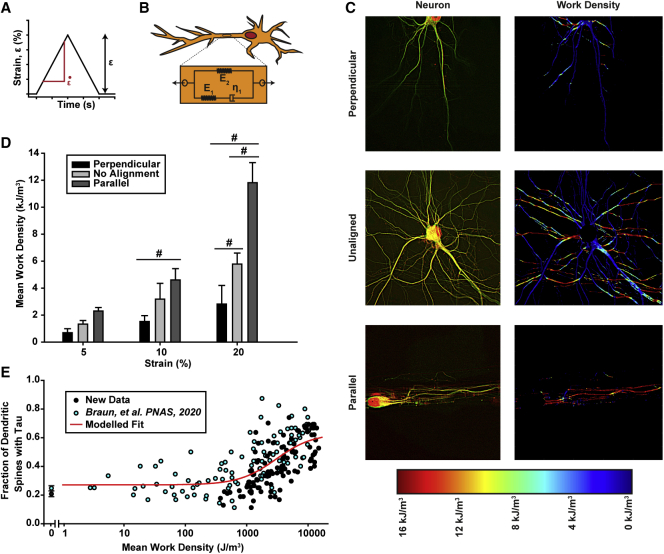
In our previous study, we found that tau mislocalization is both strain magnitude and strain rate dependent (22) (Fig. S1). This finding is consistent with other studies showing that neurites exhibit viscoelastic behavior (56, 57, 58, 59, 60). To capture both the impact of strain and strain rate on tau mislocalization, we modeled the neurite as a standard one-dimensional viscoelastic solid oriented parallel to the primary alignment of the neurite and determined the work density done on all neurites during stretching (Fig. 6, A and B). In this model, neurites aligned parallel to stretch underwent substantially higher work than those aligned perpendicular to stretch (Fig. 6 C), so, as expected, neurons patterned to align parallel to stretch underwent higher mean work than unpatterned and perpendicularly patterned neurons (Fig. 6 D). When neurons from our previous study were included (all unpatterned, but stretched with differing strains and strain rates), a distinct relationship between neurite work density and tau mislocalization was observed (Fig. 6 E). Work density proved to be a better predictor of tau mislocalization than average strain or average stress in a neuron at the maximal applied strain during injury (Fig. S2). Further, a parameter study found that the observed relationship between work density and tau mislocalization was qualitatively conserved over a wide range of model parameter values (Fig. S3). These data suggest that the tau mislocalization observed after stretch is mediated by the mechanical energy added to the neurons during deformation.

Figure 6.

Viscoelastic model of stretched neurons demonstrates that mechanical work during injury causes tau mislocalization. (A) Example injury protocol for simulating TBI on neurons with strain (ε) and strain rate $\left(\dot{\epsilon }\right)$. (B) Standard linear solid model of viscoelasticity used to model neuron mechanical behavior. (C) Fluorescent images of neurons in the three alignment states (left) and heat maps showing work density done on the neuron from an ε = 20%, $\dot{\epsilon }$ = 10/s stretch (right). (D) Quantification of mean work density, measured by averaging the mean work density of each imaged in an experimental group (mean ± SD). Images: 5-perpendicular = 10, 5-unaligned = 18, 5-parallel = 12, 10-perpendicular = 10, 10-unaligned = 10, 10-parallel = 10, 20-perpendicular = 17, 20-unaligned = 11, 20-parallel = 16. # indicates statistical difference from other alignments within a strain group, p < 0.05. (E) Experimentally derived tau mislocalization versus mean work density done on a neuron during injury. Black points are new data from this study. Blue points are images from Braun et al. (22) that were reanalyzed using this study’s methods. The two points with a mean work density of 0 represent the average (± SD) tau mislocalization of all unstretched control neurons from both studies (n = 585 spines from this study, n = 1559 spines from Braun et al. (22)). Modeled fit is based on a Hill equation (dose-response curve) and does not include the unstretched cells from each study (points with mean work density of 0). Note: cell somas were removed from images in (C) so that their rounded morphology would not affect calculations involving neurite architecture or alignment.

Discussion

During TBI, neural tissues undergo high-strain-rate deformation throughout the brain that causes damage to neurons and glia (61, 62, 63, 64, 65). Brain injuries are not uniform, however, because of the anisotropic nature of the brain at both the tissue and cellular scale (23,34,39). Neurons and brain tissue behave viscoelastically, and brain injury is a function of both strain and strain rate of the tissue (56, 57, 58, 59, 60). Computational models of brain deformation during TBI suggest that strains are greatest in the sulcal depths and perivasculature regions, where geometric qualities or material differences between brain and vascular tissue contribute to heightened strain, respectively (21,22). These same regions of the brain exhibit the heightened presence of NFTs in CTE patient autopsies, suggesting that mechanical strain is the primary driver of NFT accumulation in TBI. Notably, neurons in the sulcal depths (and the cortex as a whole) are highly aligned into columnar architectures that are arranged perpendicular to the cortical surface (66, 67, 68). Within this columnar architecture, the axons of neurons (of greatest interest, as tau typically resides in axons) are oriented in parallel with the larger scale-columnar axis, whereas dendrites are arranged in a more diffuse manner that is not necessarily in the basal-apical direction (69). Here, we demonstrated that this cellular architecture may play an important role in determining the degree of mechanically induced tauopathy caused by TBI.

Cellular architecture plays an important role in a wide range of cellular functions, including migration (70), cytoskeletal force generation (52,53), and action potential propagation (71). Here, by stretching aligned neurons cultured on elastic substrates, we quantified the degree to which cellular architecture affects the tauopathic and synaptic consequences of TBI. In our previous study (22), regardless of neurite orientation, tau mislocalization to dendritic spines was observed in neurons exposed to large (ε = 20%) strains with large strain rates ($\dot{\epsilon }$ = 10/s). Here, at lower strains (ε = 10%), however, the degree of tauopathy was notably dependent on alignment of the neurites with stretch. These data suggest that the consequences of head injury depend not only on magnitude of the blow but on the orientation of the force.

Our studies reaffirmed and extended previous results indicating that tau mislocalization is associated with functional synaptic deficits in affected neurons. We have reported previously in models of AD (31), Parkinson’s disease (72), frontotemporal dementia with parkinsonism-17 (30), and TBI (22) that tau mislocalization to dendritic spines is associated with postsynaptic deficits. Here, a similar effect was observed, as decreased mEPSC amplitudes coincided with higher levels of tau mislocalization, suggesting that mechanically driven tau mislocalization decreases the number of AMPA receptors present on a dendritic spine (32,73). mEPSC amplitude decreases were also apparent in neurons aligned parallel to stretch. But, in neurons aligned perpendicular to stretch, the decreases were not significant. Interestingly, unlike at high strain (ε = 20%), which we have previously studied (22), mechanical stretching at a lower strain (ε = 10%) caused minimal impairment in presynaptic function (mESPC frequency), suggesting that postsynaptic functions are more vulnerable to some consequences of mechanical stretching than presynaptic functions. We saw a uniform (nonsignificant) decrease in frequency in all groups exposed to stretch, which did not correlate with the nonuniform tau mislocalization.

The mechanisms by which mechanical injury leads to CTE are not well understood. In healthy neurons, tau is located on axonal microtubules, but in chronic neurodegenerative tauopathies like AD, tau becomes hyperphosphorylated and mislocalizes to dendritic spines (29, 30, 31, 32, 33). Our results suggest that mechanical injury accelerates the mislocalization process, leaving the injured neurons phenotypically similar to those in chronic tauopathies. Prior in vitro and in silico studies have suggested that mechanical forces can induce microtubule rupture, resulting in neurite collapse characterized by focal swelling (26,74, 75, 76). Although we did not observe focal swelling, our model suggests a similar mechanism, wherein cytoskeletal damage occurs when mechanical energy exceeds a threshold value, which results in tau release from microtubules. Our model, however, is not mechanistic and could be representing the stretching of cytoskeletal elements or stretch relative to the positioning of neuronal adhesion sites. Further study is needed to better elucidate this pathway.

Finally, these results have potential clinically translatable importance. A number of studies have been performed correlating the whole-head acceleration during impact with brain deformation and clinical outcomes (77, 78, 79, 80). Our results suggest that neural architectures and mechanical energy added to a neuron during deformation are key factors mediating tauopathy after TBI at the cellular level. Although our in vitro cellular system may not capture all neurodevelopmental milestones, dendritic spines are stable and mature at DIV21 in cultures and 1 month in live animals with similar developmental patterns (81, 82, 83). We believe that this cellular injury model, combined with comprehensive mapping of brain geometry and neuronal architecture within the brain, may prove useful as a component of an injury prediction model for victims of TBI in its various forms (84,85). Understanding how the basic cellular subunits of the brain are affected by high-strain deformations is crucial in creating a biomechanical framework for computational TBI models and developing future clinical interventions.

Conclusions

This study provides direct cellular evidence that the direction of mechanical stretching in relation to the orientation of neurites is an important determinant in the mechanical-injury-induced tau mislocalization to dendritic spines, which is a common mechanism in the pathogenesis of multiple neurodegenerative diseases (32). Moreover, the subsequent synaptic deficits caused by mislocalized tau also depend upon the alignment of the neurites with mechanical stretching. Our in-depth cellular and biophysical analyses will help us better understand the pathophysiology of TBI and develop novel strategies to combat its symptoms and long-term effects.

Author contributions

N.J.B., D.L., and P.W.A. all participated in the design and performance of the experiments and in the writing and revising of the manuscript.

Editor: Valentin Nagerl.