CRISPRclassify: Repeat-Based Classification of CRISPR Loci

Abstract

Detection and classification of CRISPR-Cas systems in metagenomic data have become increasingly prevalent in recent years due to their potential for diverse applications in genome editing. Traditionally, CRISPR-Cas systems are classified through reference-based identification of proximate cas genes. Here, we present a machine learning approach for the detection and classification of CRISPR loci using repeat sequences in a cas-independent context, enabling identification of unclassified loci missed by traditional cas-based approaches. Using biological attributes of the CRISPR repeat, the core element in CRISPR arrays, and leveraging methods from natural language processing, we developed a machine learning model capable of accurate classification of CRISPR loci in an extensive set of metagenomes, resulting in an F1 measure of 0.82 across all predictions and an F1 measure of 0.97 when limiting to classifications with probabilities >0.85. Furthermore, assessing performance on novel repeats yielded an F1 measure of 0.96. Although the performance of cas-based identification will exceed that of a repeat-based approach in many cases, CRISPRclassify provides an efficient approach to classification of CRISPR loci for cases in which cas gene information is unavailable, such as metagenomes and fragmented genome assemblies.

Introduction

CRISPR and CRISPR-associated proteins (Cas) constitute the prokaryotic adaptive immune system.^1–6 CRISPR-Cas systems enable precise cleavage of nucleic acid targets from invading bacteriophages and other predatory mobile genetic elements through the guidance of DNA-encoded targeting sequences, termed “spacers.”^7–9 The ability to discern and cleave targets in a nucleotide-specific manner has proven an invaluable tool to the field of biotechnology and has been exploited for a myriad of applications in genome editing across a wide array of industries, including agriculture, medicine, bioprocessing, and biotechnology.^10–15 CRISPR-Cas systems are currently organized into 2 classes, 6 types, and 33 subtypes based on characteristics of the effector complex, the presence of signature and accessory cas genes, and the architecture of the CRISPR-Cas locus.¹⁶ Different CRISPR-Cas types vary in their molecular mode of action, with variability observed across effector complex composition, target nucleic acid types, and cleavage outcomes, affording a diversity of genetic applications.

Recent major advances in sequencing technology have substantially increased the throughput, in combination with decreasing costs, and thus have dramatically accelerated metagenomic sampling and sequencing, generating vast amounts of public metagenomic data. Because CRISPR-Cas systems are found in ∼40% of bacteria and ∼90% of archaea, metagenomes, which typically contain diverse populations of microbes, are ideal candidates for the discovery of novel CRISPR-Cas variants.^17,18 Due to the natural complexity of these data, numerous assembly algorithms, typically based on de Bruijn graphs, have been employed to assemble contiguous metagenomic sequences (contigs) accurately.^19–23 A major hindrance to these algorithms is the processing of repetitive sequences, which increase the computational complexity of the assembly and often result in partially assembled CRISPR loci at the contig extremities, separating CRISPR arrays from their corresponding cas genes. Although several methods have been developed with the explicit goal of improving the assembly of CRISPR-Cas sequences in metagenomes, most of these algorithms operate through reference-based assembly, thus limiting the results based on pre-existing knowledge of the data set or on matches to known reference sequences in current databases.^24–27 Because CRISPR-Cas systems are typically first identified by the defining and core feature of the CRISPR array—namely, the repeat—and are then classified based on the adjacent cas genes, the true biotechnological novelty of the metagenome can be diminished. Beyond the practical applications, measuring diversity of CRISPR-Cas systems in large metagenomic data sets is crucial to gain ecological insights into complex microbial communities, as well as to improve our understanding of the distribution and evolution of CRISPR-Cas systems across varied environments.

The CRISPR repeat is central to each of the three phases of adaptive immunity: adaptation, expression, and interference. The repeat serves as the template for integration of newly acquired spacer sequences, enables crRNA maturation by providing the substrate for processing, and is critical for the appropriate binding of mature crRNA to Cas effector proteins, leading to cleavage of nucleic acid targets.^6,28–32 Thus, we investigated the feasibility of a repeat-based approach to CRISPR-Cas classification, as opposed to the canonical cas-centric approach, and demonstrate here that the application of this technique leads to an increased number of classified CRISPR loci in assembled metagenomic data. Repeat-based analysis not only allows for classification of CRISPR arrays that have been separated from their associated cas genes but has the advantage of being less computationally intensive than traditional cas identification methods, which are based on exhaustive BLAST or Hidden Markov Model (HMM) searches against protein sequence databases.¹⁶ Decreased dependence on computational resources could simplify and expedite analyses of data sets with large memory footprints, which could prove prohibitive to users without access to high-performance hardware or servers.

Several previous studies have explored evolutionary conservation and classification of CRISPR repeats through sequence alignment, clustering, and analysis of secondary structures. However, the primary objective of these studies was first to identify and categorize repeats into families and only then to examine the associations with CRISPR subtypes across the identified repeat families.^33,34 An important first step in approaching cas-independent classification was recently pioneered by CRISPRCasTyper,³⁵ with an implementation of an extreme gradient boosted tree (XGBoost) model trained on repeat sequence data. The XGBoost model is a decision-tree-based ensemble algorithm widely used in classification problems, where each tree is generated sequentially, learning from errors made by previous trees.³⁶ Here, we validate and expand this technique through the exploration of new model input features and detailed analysis of the contributions of the underlying features that enable successful recognition of each subtype.

Multiple modeling approaches were explored. However, given the high dimensionality of the k-mer-based feature set and the complex interaction among both biological and k-mer-based features, an XGBoost model was employed for repeat classification. While biological features (GC content, repeat length, and palindromicity) are generally among the highest impact features across subtypes, k-mer features are largely unique to a subtype.

The performance of CRISPRclassify was evaluated against a large publicly available set of metagenome-assembled genomes (MAGs), referred to as the test set.³⁷ We found that the predictive performance of the CRISPRclassify model on the training and validation sets largely translated to this previously unseen test set. Although it is unlikely that a repeat-based approach will outperform the traditional cas-based approach directly, this methodology can provide complementary biological context in cases where the data on adjacent cas genes are inadequate and identifies key features of the repeats that are central to the accurate subtype assignment.

Methods

Data sources

Genomes with previously classified CRISPR loci¹⁶ were downloaded from the National Center for Biotechnology Information (https://www.ncbi.nlm.nih.gov/). Repeats were extracted via MinCED (github.com/ctSkennerton/minced), a tool derived from CRT with default options.³⁸ All detectable repeat sequences were retained. Repeats and associated strain information were subsequently stored in a Postgres database, resulting in 7,808 CRISPR loci and 15,669 repeat sequences across 30 subtypes, shown in Supplementary Table S1. Stratified random split was used to divide the data into an 80% derivation cohort (training set) and 20% validation cohort. Representation of all available subtypes in the training set was verified prior to the model training procedure. The derivation cohort for the resource probability model consisted of 12,534 repeats across 30 subtypes, and the validation cohort contained 3,135 repeats across 30 subtypes.

Feature selection

For each repeat, a set of biological features, as well as k-mer-based features comprised of nucleotide “words” of k length, were extracted to form the feature set used in the classification model. Biological features include: (1) length—the count of the characters in the repeat sequence; (2) GC content—the frequency of G and C nucleotides over the length of the repeat sequence; and (3) palindromic index—the fraction of matching nucleotides between the repeat sequence and its reverse complement at the same index position. In addition to the biological features, repeat sequences were tokenized to extract all contiguous, overlapping k-mers at varying k-mer lengths.³⁹ Given the unknown cardinality of the repeat sequence, the reverse complement of each sequence was also tokenized. The k-mer feature set for a given repeat sequence is therefore comprised of the occurrence frequency of each distinct k-mer from both the repeat sequence and its reverse complement.

Model

Given the overlapping k-mers, an assumption of conditional independence of the feature set could not be made. A nonlinear approach that accounts for the complex interaction between both biological and k-mer-based features was necessary, leading to the implementation of an extreme gradient boosted tree model (XGBoost).³⁶ While XGBoost can be employed as a multiclass classifier, the CRISPRclassify model was implemented using a one-vs-all (OVA) binarization strategy where a separate model stratum is trained for each subtype, with the subtype itself being extracted as the binary response variable.⁴⁰ The probability, P_i,k, of subtype k for repeat i conditional on a set of biological features $Bi{o}_i$ and a set of k-mer word tokens $Kme{r}_i$ is calculated using equation (1):

$$P_{i,k}\left(Subtypek|Bi{o}_i,Kme{r}_i\right)=XG{B}_k\left(Bi{o}_i,Kme{r}_i\right)foralli,k$$ (1)

The highest probability subtype, j*(i), for repeat i is found using equation (2):

$$ŷ={argmax}_{k\in \left\{1\dots K\right\}}{P}_{i,k}$$ (2)

The highest probability subtype (i.e., argmax) across model strata is assigned to each repeat using equation (2). In order to identify the optimal k-mer length, the OVA XGBoost model was applied to feature sets derived from k-mer lengths from three to seven. The final deployed model uses a feature set with a k-mer length of five, coupled with the three aforementioned biological features. Hyper-parameter optimization resulted in final max depth of 15, a learning rate of 0.3, with early stopping at 10 rounds and an upper limit of 50 rounds. While all subtypes were included in the derivation and validation data, some subtype model strata were excluded due to low volume (n < 11). These included subtypes: IV-C, V-B2, III-E, V-U1, VI-D, III-F, V-U2, VI-C, and V-B1. Due to their exclusion from the derivation data set, these subtypes were not considered for classification and were not predicted by CRISPRclassify. Analysis was conducted using the XGBoost package with R v3.6.2. (https://www.R-project.org/, https://CRAN.R-project.org/package=xgboost). Determination of the optimal probability cutoff was made by comparing receiver operating characteristic (ROC) curves using the pROC package for R.⁴¹

Exploratory stratified logistic regression and multiclass XGBoost models were trained using the same training and validation datasets as the final OVA XGBoost model. All models were optimized using a grid search pattern where an exhaustive combination of a predetermined list of hyperparameter values was used to train the models.

CRISPRclassify development

The CRISPRclassify application was developed in R (https://www.R-project.org/). Repeats were identified and extracted using MinCED with default options and a custom Bash script derived from CRISPR Visualizer.⁴² To control the false-positive rate of CRISPR locus detection using MinCED, previously described filtering methods were employed.^35,43 Putative false CRISPR arrays were identified and excluded from further classification if the repeats exhibited overall sequence identity <0.7, spacers displayed overall sequence identity >0.6, or if one or more spacers were 70% shorter than the average spacer length across the entire locus. The biological and k-mer-based repeat features were generated directly from the repeat sequence using the tidyverse package (https://www.tidyverse.org/). To maximize the support for various levels of end users, CRISPRclassify was developed as a Shiny application with a web-interface (https://shiny.rstudio.com/) that is deployed on a user's local machine via the command line. Additionally, CRISPRclassify can be executed directly on the command line without invoking the user interface for improved pipeline integration.

Benchmarking through cas-based classification

To enable benchmarking of CRISPRclassify against a test metagenome, a custom cas-based pipeline was developed in Bash and Python. The test set, comprised of more than 10,000 metagenome samples, contains a total of 52,515 MAGs. These data were obtained from the Joint Genome Institute Genome Portal (https://genome.jgi.doe.gov/portal/GEMs/GEMs.home.html).³⁷ The cas identification pipeline identified repeats in the metagenome using MinCED and extracted 20 kb flanking regions upstream and downstream of the CRISPR locus. The flanking regions were queried against a reference BLAST database aggregated from previously described cas sequences.^16,18,44,45 BLASTx searches were carried out with an E-value threshold of 1e-6 and a minimum cas identity of 60%. CRISPR loci were then classified by subtype based on the presence of signature cas genes, and these results were subsequently compared against predictions made by the CRISPRclassify model. For loci that could not be classified through the cas-based approach (i.e., no flanking identifiable cas genes), no comparison could be made, and those loci were omitted from the analysis. To ensure accurate benchmarking, loci with multiple signature cas genes located in their flanking regions were also omitted from the analysis. Only repeats classified by CRISPRclassify with probabilities >0.85 were evaluated. Benchmarking performance was evaluated based on the F1 score: (2 × Precision × Recall)/(Precision + Recall).

Results

Model performance on validation data

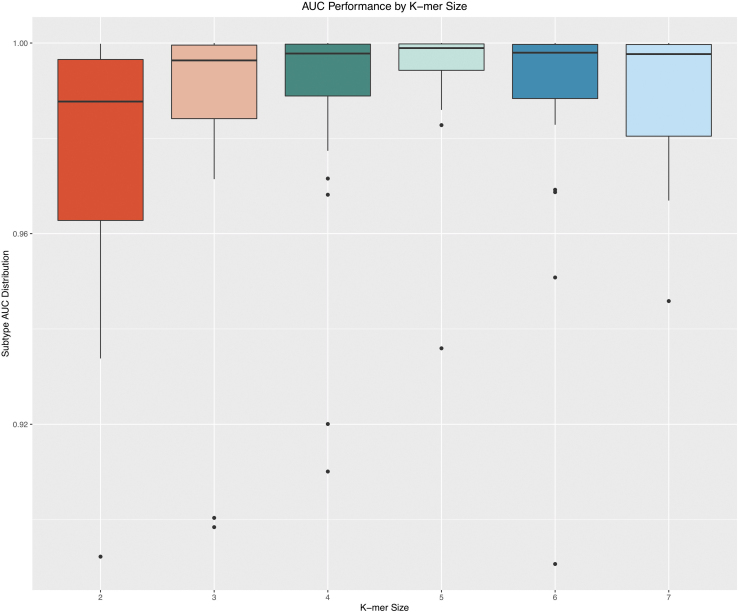
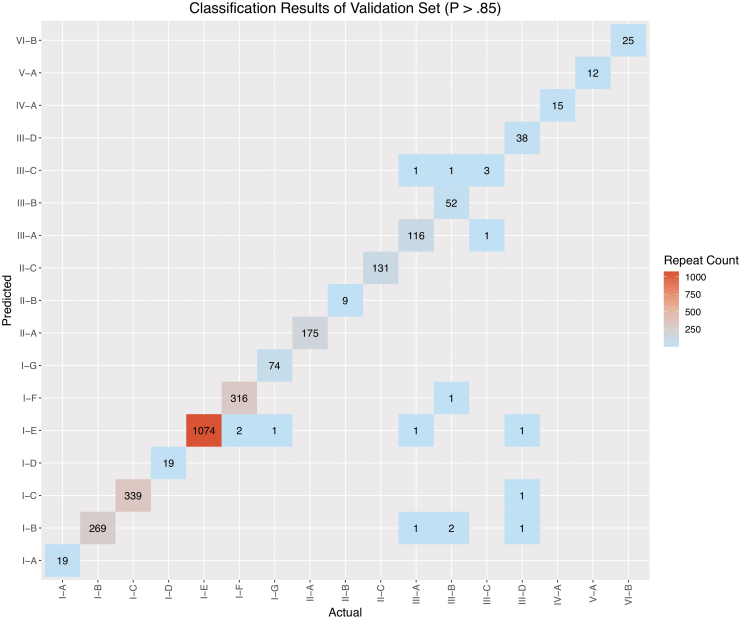
In the exploration phase of this study, three model schemes were evaluated. The first model was a multivariate logistic regression stratified by subtype. Despite the appeal of the feature interpretability provided by a linear model, the predictive performance was suboptimal relative to the nonlinear XGBoost model. The mean area under the curve (AUC) of the stratified logistic regression was 0.9062 (95% confidence interval [CI] 0.8477–0.9651). The second model scheme was a multiclass implementation of XGBoost, resulting in a mean AUC of 0.9937 (95% CI 0.989–0.998). The third model that was ultimately selected for CRISPRclassify employs an OVA scheme. With this approach, a separate XGBoost model was created for each subtype, with the subtype itself being a binary response variable. The AUC performance of the OVA XGBoost model across subtype strata for k-mer lengths 3–7 is illustrated in Figure 1. The AUC results are based on the validation cohort. The k-mer length of 5 (five-gram) produced the highest mean AUC of 0.993, with the least degree of variance (95% CI 0.983–1; Supplementary Table S2). To account for predictions with greater uncertainty, Youden's J statistic was used to determine an optimal probability cutoff value of 0.85.^46,47 To suppress uncertain predictions, this cutoff was applied to the argmax results of the validation set, leading to a considerable reduction in inaccurate predictions (Fig. 2). AUC values for each subtype can be found in Supplementary Table S1.

FIG. 1.

Area under the curve (AUC) performance by k-mer size. Model performance varied based on the k-mer length selected during training. A length of 5 provided optimal performance, with a mean AUC of 0.993. K-mer lengths of 4 and 6 also performed well, both with mean AUCs of 0.988. AUC performance with a k-mer length of 2 had the lowest performance of 0.966.

FIG. 2.

Prediction matrix of one-vs-all (OVA) XGBoost results on validation set. Application of the 0.85 probability threshold leaves only 14 total repeats incorrectly classified. The bottom-right quadrant of the graph displays the few examples from subtypes III-A, III-B, and III-D that were misclassified in the validation set.

Feature importance

Feature importance was evaluated across a range of k-mer length models within each subtype stratum. As is customary for XGBoost models, feature importance was calculated as a measure of “gain.” The gain metric measures the degree to which a feature reduces entropy, or disorder, within the underlying decision trees used within the XGBoost model. The top five highest-gain features by subtype are listed in Table 1, and a full list of all features by subtype can be found in Supplementary Table S3. A common underlying signal for k-mer features was identified regardless of the k-mer length. As a representative example, Table 2 lists the 20 highest-gain k-mers across all k-mer length models for the I-A subtype stratum. The highest-gain k-mer comes from the five-gram model, and the top k-mers from the three and four-gram models are primarily derivatives of the AATTG pentamer, which itself is fully contained in (“AGAATTG “) or overlaps with (“AATTCT”) in the high-gain k-mers of the six- and seven-gram models.

Table 1.

High-Gain Features by Subtype

Subtype	Feature	Gain	Cover	Frequency	Subtype	Feature	Gain	Cover	Frequency
I-A	length	0.16	0.18	0.11	III-F	AAACA	0.16	0.62	0.21
I-A	AATTG	0.15	0.12	0.02	III-F	ACAAG	0.14	0.02	0.13
I-A	gc	0.07	0.01	0.10	III-F	CTTCC	0.15	0.01	0.12
I-A	AGAAT	0.05	0.00	0.01	III-F	CTGGA	0.17	0.00	0.13
I-A	CGATA	0.03	0.00	0.01	III-F	CCAGC	0.13	0.00	0.04
I-B	gc	0.19	0.12	0.08	IV-A	CCCCC	0.20	0.15	0.05
I-B	length	0.31	0.07	0.08	IV-A	GGTTA	0.06	0.09	0.04
I-B	CATCA	0.03	0.04	0.01	IV-A	CGATA	0.18	0.08	0.03
I-B	GGTAC	0.02	0.04	0.00	IV-A	length	0.05	0.00	0.08
I-B	AGGCG	0.02	0.01	0.00	IV-A	gc	0.06	0.00	0.09
I-C	GCGAC	0.36	0.09	0.01	IV-C	CTAGA	0.07	0.29	0.10
I-C	length	0.12	0.08	0.11	IV-C	TTGCA	0.23	0.13	0.14
I-C	GTGGA	0.06	0.04	0.01	IV-C	CCTAG	0.06	0.08	0.05
I-C	ATCCA	0.05	0.03	0.01	IV-C	TGCAA	0.41	0.07	0.33
I-C	gc	0.06	0.02	0.10	IV-C	palIdx	0.16	0.03	0.19
I-D	length	0.12	0.11	0.07	V-A	GTAGA	0.57	0.30	0.14
I-D	AATCC	0.06	0.08	0.02	V-A	GTCTA	0.04	0.21	0.07
I-D	CGGGA	0.03	0.02	0.01	V-A	AAATT	0.16	0.01	0.12
I-D	gc	0.06	0.01	0.07	V-A	CTAAG	0.05	0.00	0.06
I-D	ATCCC	0.06	0.01	0.02	V-A	TTAAA	0.02	0.00	0.07
I-E	length	0.24	0.09	0.09	V-B1	AAGCT	0.18	0.34	0.11
I-E	TCCCC	0.51	0.08	0.01	V-B1	AAAGC	0.10	0.26	0.06
I-E	CGGAG	0.04	0.07	0.01	V-B1	TGCCA	0.10	0.02	0.06
I-E	gc	0.03	0.07	0.08	V-B1	AACGG	0.11	0.01	0.07
I-E	CCCGC	0.04	0.05	0.02	V-B1	gc	0.09	0.00	0.12
I-F	CTGCC	0.58	0.15	0.03	V-B2	CAACC	0.12	0.88	0.26
I-F	TCATC	0.05	0.09	0.01	V-B2	AACCC	0.11	0.05	0.10
I-F	CCATC	0.03	0.08	0.00	V-B2	GCGAA	0.08	0.01	0.05
I-F	length	0.14	0.08	0.10	V-B2	CGCGA	0.26	0.00	0.18
I-F	TCTAA	0.03	0.01	0.01	V-B2	GCACA	0.06	0.00	0.03
I-G	CAATG	0.24	0.10	0.02	V-F	gc	0.21	0.12	0.13
I-G	length	0.08	0.09	0.08	V-F	GTTAA	0.06	0.06	0.04
I-G	gc	0.05	0.01	0.09	V-F	length	0.08	0.01	0.08
I-G	CTTCA	0.15	0.01	0.02	V-F	palIdx	0.08	0.00	0.13
I-G	CCTCA	0.06	0.00	0.02	V-F	CATTC	0.07	0.00	0.02
II-A	AAAAC	0.29	0.11	0.04	V-K	GTTGA	0.22	0.22	0.07
II-A	length	0.12	0.07	0.05	V-K	length	0.09	0.04	0.07
II-A	TCTAA	0.06	0.04	0.02	V-K	CTTTC	0.10	0.01	0.08
II-A	gc	0.06	0.04	0.08	V-K	CCTCC	0.09	0.01	0.06
II-A	ACTCT	0.05	0.03	0.01	V-K	gc	0.06	0.00	0.11
II-B	ATAAT	0.08	0.35	0.06	V-U1	ATGAG	0.23	0.71	0.26
II-B	ACTGA	0.12	0.16	0.05	V-U1	GGTTA	0.13	0.01	0.08
II-B	length	0.11	0.09	0.10	V-U1	CATTA	0.13	0.01	0.08
II-B	CCCTC	0.11	0.01	0.02	V-U1	AGCAG	0.13	0.00	0.08
II-B	AATAA	0.09	0.00	0.03	V-U1	ATTAA	0.13	0.00	0.16
II-C	length	0.39	0.24	0.06	V-U2	AAGCT	0.06	0.10	0.09
II-C	TAAAA	0.06	0.05	0.02	V-U2	TCGAA	0.07	0.05	0.08
II-C	CTACA	0.04	0.04	0.01	V-U2	CCAAG	0.13	0.03	0.08
II-C	AAATG	0.02	0.02	0.01	V-U2	GAATC	0.27	0.03	0.13
II-C	AAAAT	0.02	0.01	0.02	V-U2	palIdx	0.05	0.00	0.06
III-A	AGGGG	0.06	0.08	0.02	V-U4	CGGAC	0.11	0.28	0.07
III-A	gc	0.08	0.08	0.07	V-U4	CGGTC	0.12	0.16	0.12
III-A	CCGTC	0.12	0.05	0.01	V-U4	palIdx	0.05	0.01	0.06
III-A	CGAGA	0.03	0.00	0.00	V-U4	gc	0.19	0.00	0.15
III-A	CGGAA	0.05	0.00	0.00	V-U4	length	0.06	0.00	0.05
III-B	gc	0.08	0.08	0.07	VI-A	ACCTC	0.04	0.18	0.06
III-B	GGCCA	0.04	0.07	0.01	VI-A	AGTCC	0.05	0.03	0.05
III-B	TCCGA	0.05	0.05	0.01	VI-A	ATAAT	0.04	0.01	0.04
III-B	length	0.05	0.04	0.05	VI-A	GGATA	0.32	0.01	0.05
III-B	ATTAA	0.04	0.03	0.01	VI-A	GATAA	0.04	0.00	0.02
III-C	AGGAT	0.07	0.08	0.03	VI-B	GGGTA	0.13	0.25	0.05
III-C	gc	0.07	0.01	0.10	VI-B	TGCAA	0.10	0.12	0.02
III-C	palIdx	0.09	0.01	0.11	VI-B	CCAAC	0.07	0.03	0.05
III-C	CAAGG	0.09	0.01	0.02	VI-B	CTTCA	0.06	0.00	0.04
III-C	AGATA	0.04	0.00	0.01	VI-B	AGAGC	0.09	0.00	0.02
III-D	length	0.11	0.11	0.05	VI-C	TCCAA	0.39	0.70	0.34
III-D	GCACC	0.03	0.04	0.00	VI-C	AAACG	0.07	0.12	0.09
III-D	gc	0.06	0.02	0.09	VI-C	GACTA	0.14	0.10	0.14
III-D	palIdx	0.02	0.01	0.06	VI-C	CCCTC	0.07	0.00	0.02
III-D	ATTGA	0.01	0.00	0.01	VI-C	CCTCG	0.09	0.00	0.05
III-E	CTAGA	0.15	0.08	0.16	VI-D	ACTAG	0.35	1.00	0.50
III-E	CTAGC	0.10	0.03	0.09	VI-D	gc	0.32	0.00	0.21
III-E	CAATC	0.21	0.00	0.13	VI-D	GTCTA	0.14	0.00	0.13
III-E	ATGCC	0.10	0.00	0.06	VI-D	CTAAA	0.13	0.00	0.08
III-E	GCGGA	0.10	0.00	0.06	VI-D	palIdx	0.03	0.00	0.04

The five highest-gain features are provided for each subtype. The three highest-gain features identified were “CTGCC” for I-F, with a gain of 0.58, “GTAGA” for V-A, with a gain of 0.57, and “TCCCC” for I-E, with a gain of 0.51.

Table 2.

High-Gain k-mers for Subtype I-A

k-mer	Reverse compliment k-mer	Gain	k-mer length model
AATTG	CAATT	0.225	5
AAT	ATT	0.205	3
AATT	AATT	0.195	4
AGAATTG	CAATTCT	0.118	7
AAG	CTT	0.072	3
AATTCT	AGAATT	0.071	6
AATA	TATT	0.050	4
AAC	GTT	0.048	3
CTTTA	TAAAG	0.039	5
AAAG	CTTT	0.034	4
TAA	TTA	0.034	3
AAA	TTT	0.032	3
CAATTC	GAATTG	0.032	6
ATA	TAT	0.031	3
AATAAT	ATTATT	0.028	6
ACTGAA	TTCAGT	0.027	6
CTAAAG	CTTTAG	0.026	6
AGA	TCT	0.026	3
ATTC	GAAT	0.026	4

The gain for each k-mer feature is dependent on the k-mer length of the model. The “AATTG” k-mer displays the highest gain across all length k-mer models, with a gain of 0.225 for a k-mer length of 5.

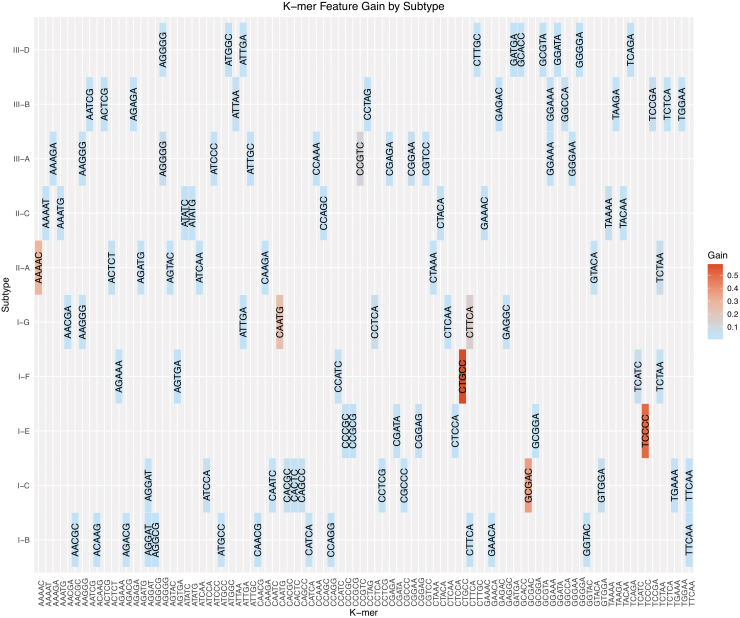
The k-mers that make major contributions to subtype classification are heterogeneous across subtypes. Figure 3 illustrates the relationship of high-gain k-mers across subtype models. High-gain k-mers were identified as having 90% CI (z > 1.645) based on the natural log of the gain value. Seven of the 74 high-gain five-gram features are represented in two subtype strata, and none are represented in three or more strata. Such heterogeneity indicates that k-mer markers are largely unique to a subtype and that the XGBoost model relies mostly on a limited set of unique k-mers. This observation indicates mutually exclusive associations between specific k-mer sequences and the subtypes.

FIG. 3.

K-mer feature gain by subtype. Subtypes that demonstrated the highest-gain k-mer features were I-C (“GCGAC”), I-E (“TCCCC”), I-F (“CTGCC”), I-G (“CAATG”), II-A (“AAAAC”), and III-A (“CCGTC”). High-gain k-mers are distinct to individual subtypes. Only subtypes with >50 validation examples are listed for clarity.

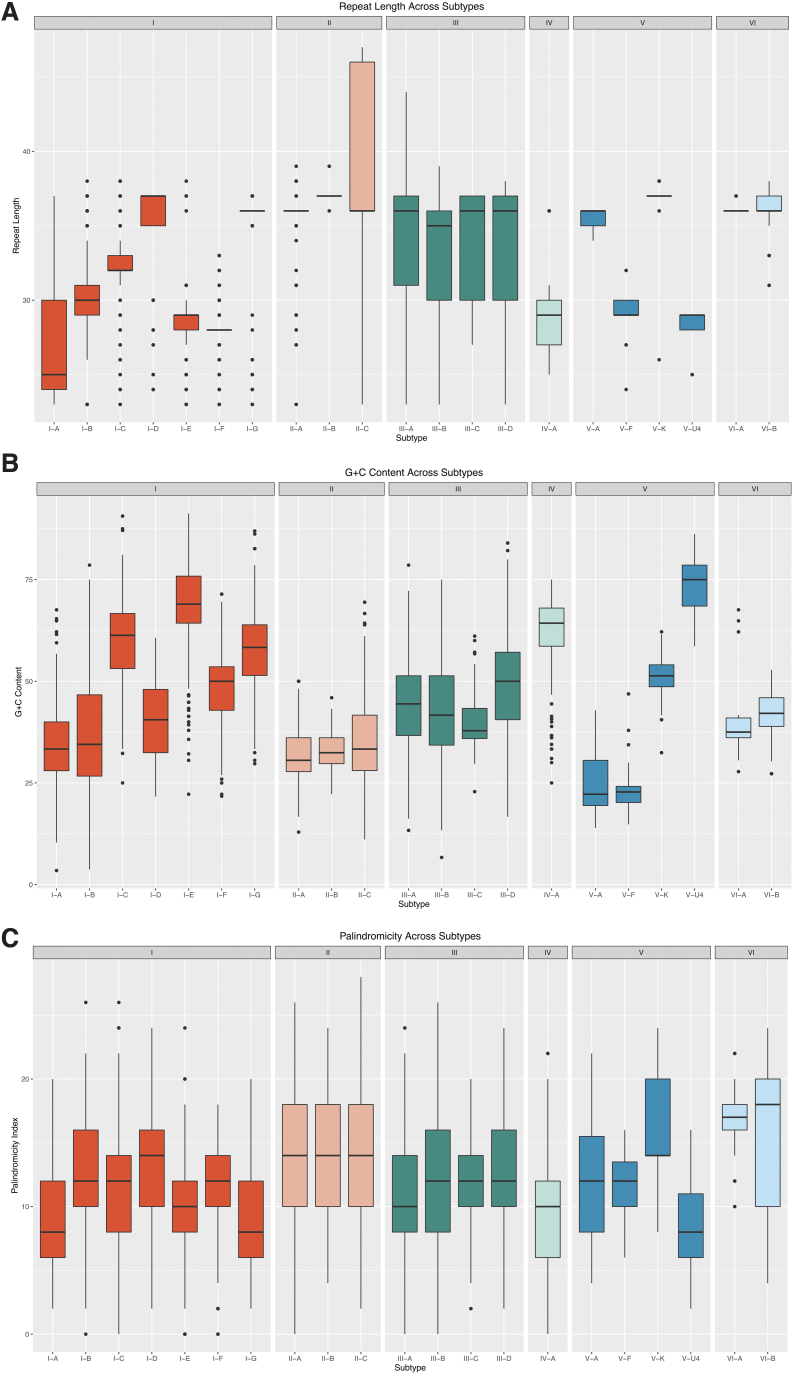
In addition to k-mer-based features, biological features also proved impactful in the prediction of subtypes. Figure 4 presents a visual summary of the distribution of derived biological features for subtypes with >20 training examples. Repeat length varies widely across type I, but subtypes I-F and I-G contain repeats of conserved lengths of 28 and 36 bp, respectively. Subtypes II-A and II-B also exhibit conserved repeat lengths of 36 and 37 bp, respectively. Although the repeat length across type III is not as tightly concentrated around the median as those for some of the type I and type II subtypes, the interquartile range distribution across type III is similar, with a median of either 35 or 36 bp. The length of type V repeats are broadly variable, with median lengths from 29 bp (V-U4) to 37 bp (V-K). Like the length distribution of the type I repeats, their GC content shows a wide range of values across the type I subtypes. In contrast to the high similarity across type II repeats, type V repeats demonstrate notable variability, with median values as low as 22% (V-A) and as high as 75% (V-U4). Across all analyzed repeats, the palindromicity index shows much less variation between subtypes.

FIG. 4.

Distribution of biological features by subtype. Box plots of repeat length (A), GC content (B), and palindromicity index (C) are shown for repeats in the training set. Repeat length, GC content, and palindromicity index display the widest variability across type I and type V repeats, while the median of these features is more conserved within type II and type III repeats.

The relative importance of features varied by subtype, but generally, biological features exhibited higher gain across subtypes than k-mer-based features. Repeat length was the most impactful feature, with a mean gain of 0.159 (95% CI 0.086–0.232), followed by the GC content, with a mean gain of 0.067 (95% CI 0.031–0.0960). The palindromic index was found to be a less predictive biological feature, with a mean gain of 0.012 (95% CI 0.006–0.018). Repeat length was particularly important for subtypes II-C, I-B, and I-E, with gain values of 0.39, 0.31, and 0.24, respectively. GC content disproportionately impacted the prediction of subtype I-B, with a gain of 0.19, followed only by III-A, with a gain of 0.08. Palindromicity was relatively important for subtypes III-B, III-C, and III-D, with gain values of 0.03, 0.02, and 0.02, respectively.

CRISPRclassify tool overview

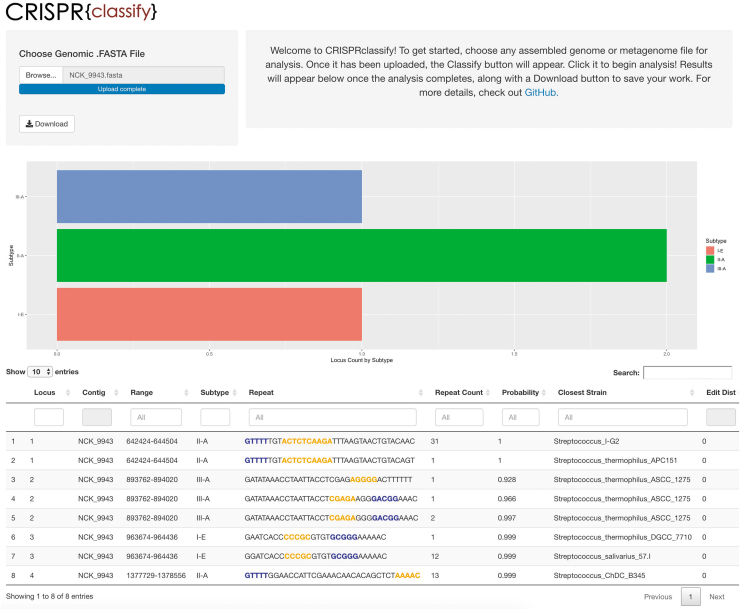
The CRISPRclassify pipeline consists of three distinct processes: identification of CRISPR arrays, feature extraction, and classification with the stratified model described above. Repeats and spacers were identified using a string searching algorithm implemented in MinCED. Putative false CRISPR arrays were then filtered out if repeat sequences were non-uniform, spacer sequences were highly similar, or if any irregular spacer lengths were detected. Biological features and overlapping k-mer features were then generated for each repeat in the data set and passed to the model for classification. The web interface allows simple upload of assembled genomic files (.fasta, .fna, etc.) and provides classified repeats in a downloadable .csv format. Results are provided in both plot and table formats. The plot displays counts of CRISPR loci by subtype, whereas the table lists each distinct repeat, its location in the source file, the predicted subtype with its corresponding computed probability, the organism in the training data with the most similar matching repeat sequence, as well as the number of single nucleotide polymorphisms present in the most similar matching repeat sequence, termed the “edit distance” (Fig. 5). This analysis can also be executed entirely on the command line without the web interface, resulting in the same .csv file generated by the user interface. It is also possible to classify repeats that have been previously identified and extracted using other CRISPR detection tools such as CRISPRDetect, CRISPRCasFinder, or CRISPRidentify.^43,48,49 Note that in order to identify CRISPR loci using the primary pipeline, this tool requires assembled genomes or metagenomes and will not process raw reads.

FIG. 5.

Overview of the web interface of CRISPRclassify. Locus counts are displayed by subtype, and distinct repeats are listed by locus, along with predicted subtype and corresponding probability. High-gain k-mers are highlighted in the repeat sequence either in blue, indicating forward orientation, or in yellow, indicating the reverse complement. The strain with the closest matching repeat from the training data set is calculated and listed as “Closest Strain,” along with the corresponding number of single nucleotide polymorphisms between the repeats (Edit Dist).

Benchmarking CRISPRclassify

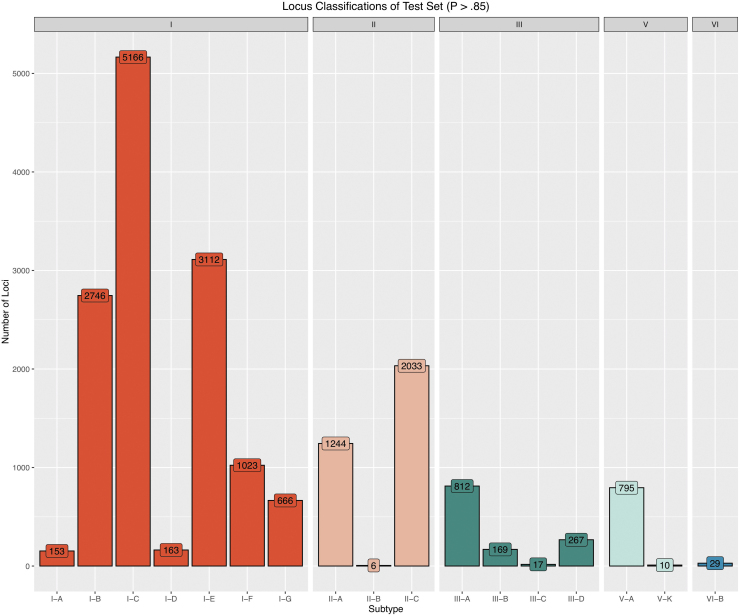
To validate the model performance, results from CRISPR classify were benchmarked against cas-based predictions of a diverse test set not seen by the model during training. After filtering out putative false loci, CRISPRclassify detected 28,438 CRISPR loci in the 52,515 genomes in the test set. For proper classification, unique repeats were grouped by locus: the same repeat sequences in two different loci were considered unique. When grouping by locus, we identified 75,513 unique repeats. After limiting this set to only classifications with probabilities >0.85, 18,504 loci remained, ultimately resulting in high-confidence classifications for 65.1% of detected CRISPR loci. Grouping the high-confidence repeats by locus yielded 42,700 distinct repeats for subsequent benchmarking. The outputs of all further analyses were obtained with the high-confidence probability threshold of 0.85 unless otherwise stated. The resulting distribution of predictions by locus subtype is shown in Figure 6. Subtype I-C dominated the predicted subtypes, representing 28.1% of all classified loci. Notably, although type III has been previously reported to be more abundant than type II in most major bacterial and archaeal phyla,^16,18 predictions of type II loci outnumbered those of type III, making up 17.8% of all classified loci versus 6.9% represented by type III.

FIG. 6.

Overview of CRISPRclassify results on an unseen test set. The number of high confidence loci (p > 0.85) grouped by subtype shows types I and II comprise a majority of the test data, while types III, V, and VI have more limited representation. A total of 28,438 CRISPR loci were detected in the test set.

Investigation into the relationship between predicted subtype probabilities and edit distance yielded a trend that as subtype probability increases, edit distance decreases (Supplementary Fig. S1). The mean edit distance across all detected repeats was 5.3. Repeats with predictions above the 0.85 probability threshold had a mean edit distance of 3.2 compared to the mean edit distance of 7.0 for repeats that fell beneath the 0.85 threshold. This indicates that in general, the model generates higher confidence predictions when classifying repeats that are more similar to what it was exposed to during training, although some high-confidence predictions were made on repeats with large edit distances, and vice versa, some low probability predictions were made for repeats with small edit distances.

The cas-based pipeline, using a conservative 60% cas identity threshold, successfully assigned a subtype to 3,625 out of the total 28,438 loci detected, resulting in 9,938 classified repeats out of the total 75,513 repeats detected. Of the total 28,438 loci considered for benchmarking, 13,085 (46%) had at least one detectable flanking cas gene. However, only 3,635 of these also contained the signature cas gene required for subtype classification, typically due to contig truncation. The remaining 15,353 (54%) unclassified loci are “orphan” CRISPR arrays that have been separated from any associated cas genes or are not associated with cas genes at all, and therefore could not be classified.⁵⁰

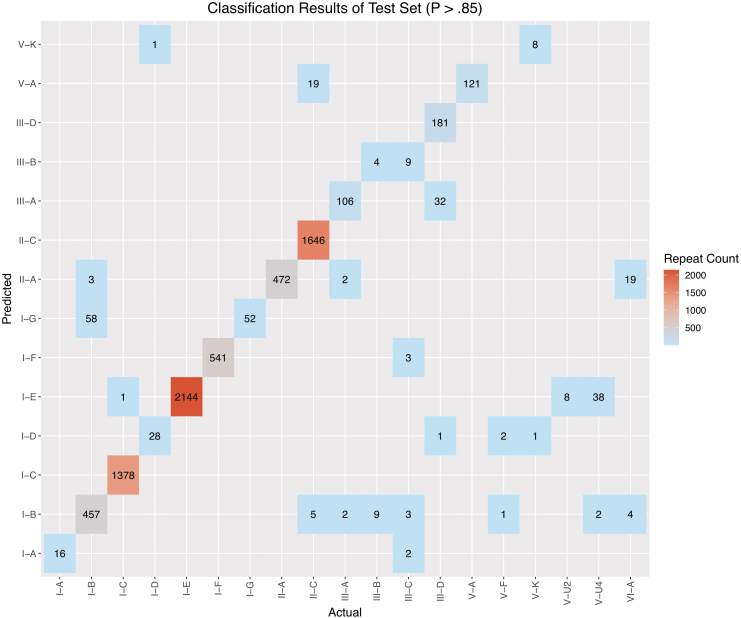
These cas-based predictions were compared against the high-confidence predictions generated with CRISPRclassify, yielding an overlapping set of classified repeats for benchmarking, comprised of 7,410 repeats in total. The overall counts of the benchmarking comparison are depicted in Figure 7, with performance measures listed in Table 3. The confusion matrix values used to calculate performance measures can be found in Supplementary Table S4. The overall model had an F1 score of 0.97, with 13/20 subtypes having an F1 score >0.8. The subtypes with low representation (n < 30 training examples)—namely, III-C, V-F, V-U2, V-U4, and VI-A—demonstrated poor performance, as anticipated. Notably, however, although subtypes V-A, V-K, and VI-B had low representation in the training set, with 58, 33, and 113 examples, respectively, they showed high performance. Subtype I-G had an F1 score of 0.64, which was much lower than expected, considering the number of training examples. The recall for I-G was perfect, with a value of 1, but the precision was low at 0.47. Upon further examination, 57/58 false-positives found for I-G were duplicate instances of the same I-B CRISPR locus encoded on the Thermus thermophilus HB8 plasmid pTT27. When accounting for this duplication of false-positives from a single source locus, the performance dramatically improved for both I-G and I-B, in the latter case due to the reduction of false-negatives.

FIG. 7.

Benchmarking result counts for the test set. Cas-based locus classification results (Actual) are plotted against CRISPRclassify predictions (Predicted). Subtypes with the most misclassified loci were I-B (61 false-negatives), V-U4 (40 false-negatives), II-C (24 false-negatives), and VI-A (23 false-negatives). The overall F1 score for the high confidence predictions (p > 0.85) of the test set is 0.97.

Table 3.

Benchmarking Performance Results

Subtype	Precision	Recall	F1	Repeats detected in test set	Training examples
I-A	0.89	1.00	0.94	16	147
I-B	0.95	0.88	0.91	518	1,429
I-C	1.00	1.00	1.00	1,379	1,448
I-D	0.88	0.97	0.92	29	164
I-E	0.98	1.00	0.99	2,144	4,388
I-F	0.99	1.00	1.00	541	1,314
I-G	0.47	1.00	0.64	52	356
II-A	0.95	1.00	0.98	472	803
II-C	1.00	0.99	0.99	1,670	637
III-A	0.77	0.96	0.85	110	697
III-B	0.31	0.31	0.31	13	268
III-C	0.00	0.00	0.00	17	19
III-D	1.00	0.85	0.92	214	408
V-A	0.86	1.00	0.93	121	58
V-F	0.00	0.00	0.00	3	17
V-K	0.89	0.89	0.89	9	33
V-U2	0.00	0.00	0.00	8	6
V-U4	0.00	0.00	0.00	40	18
VI-A	0.00	0.00	0.00	23	20
VI-B	1.00	1.00	1.00	31	113

Performance metrics listed per subtype show high precision, recall, and F1 scores for subtypes with >30 training examples, with the exception of subtype III-B, which had 268 training examples but a low F1 score of 0.31.

Subtype III-B had the low F1 score of 0.31, with four true positives, nine false-negatives that were falsely classified as subtype I-B, and nine false-positive predictions (Supplementary Table S4). The loci of the true positive predictions harbor both cas1 and cas2 (cas1/2) genes, whereas the loci containing the nine false-negatives contained no cas1/2 genes. Repeats of the nine false-positive predictions all belonged to bona fide III-C loci. Predictions of the III-C subtype were poor as well, missing each of the 17 loci predicted via cas gene identification. To identify the sources of these discrepancies, we examined the III-B and III-C training data in greater detail. The III-C training data consisted of 20 bacterial and archaeal strains. All but three of these strains possessed III-C loci that co-occur with at least one other type I system. In total, 13/20 strains contained III-C loci that lacked adjacent cas1/2 genes. This pattern of co-occurrence and lack of cas1/2 genes was observed across the III-B training examples as well, albeit to a lesser extent. Generally, among the strains that contained a type III-B or III-C (III-B/C) locus lacking cas1/2 genes and also possessed a type I system, the repeats of the type III locus were almost identical in sequence to the repeats of the co-occurring type I locus. This is expected because, in such cases, the type I Cas1–Cas2 adaptation complex recognizes the type III repeats.^51–53 When cas1/2 genes were present at the type III-B/C locus, the repeat sequences between the type III and type I loci in the same genome shared substantially less identity (Supplementary Fig. S2). In summary, repeats from type III-B/C loci lacking cas1/2 genes will be falsely classified as type I due to their high sequence similarity.

It is worth noting that the cas-based analysis of the test set (138 GB) that involved identification of the CRISPR loci, extraction of the flanking genomic regions, and the search for signature cas genes took 46 h to complete. The analysis of the same data set with CRISPRclassify on the same hardware produced the results in <5 h. Both analyses were carried out on an iMac Pro with 64 GB of RAM and a 3 GHz processor.

To complement the cas-based benchmarking analysis, we performed another round of benchmarking against the results of a popular alternate classification tool, CRISPRCasFinder.⁴⁹ Although several tools were considered for generating an alternate benchmarking comparison such as CRISPRDetect and CRISPRCasTyper,^35,48 CRISPRCasFinder was ultimately selected due to its rapid execution speed and easily parsable output. This analysis resulted in an overall F1 measure of 0.93 (Supplementary Table S5). Again, we saw poor performance when classifying subtypes III-B and III-C. However, 10/13 classified subtypes exhibited an F1 measure >0.7, while the F1 measures of subtypes I-C, I-E, I-F, I-G, II-A, II-C, and V-A were ≥0.95.

In order to approximate CRISPRclassify's potential for identification and discovery of novel loci, we investigated performance on repeats with an edit distance >6, which are dissimilar to repeats seen by the model during training. Overall, benchmarking these repeats resulted in an F1 measure of 0.96 (Supplementary Table S6). These data broadly mimic the larger set of benchmarking performance results, with 11/17 detected subtypes scoring an F1 measure >0.8. As expected, subtypes with low training representation—III-C, V-F, V-U4, and VI-A—demonstrated low F1 measures.

To evaluate differences in model performance that can be attributed to the inclusion of biological input features in combination with the five-gram pattern, we compared benchmarked results from CRISPRclassify and CRISPRCasTyper's repeat-based prediction function, which also uses XGBoost (Supplementary Table S7). To make an equitable comparison, no cutoff probability values were used for either model, and all predictions were considered. Running CRISPRCasTyper with default options (k-mer length of 4) resulted in an overall F1 score of 0.73. The same analysis carried out with CRISPRclassify yielded an F1 score of 0.82, producing a mean increase in F1 score by 0.09.

Discussion

In this work, we developed an efficient method for the classification of CRISPR systems by analysis of repeat sequences alone using a machine learning approach based on an XGBoost model. Such models have received increased recognition in recent years, as they have proven to outperform alternative nonlinear approaches regularly, including deep learning-based methods.³⁶ Because XGBoost models train quickly relative to competing models, they effectively mitigate the risk of overfitting with proper hyper-parameter tuning and offer substantially improved interpretability over deep learning approaches. For these reasons, XGBoost was implemented as the primary approach over a variety of potential deep learning architectures. Furthermore, OVA scheme models often lead to improved performance over multiclass classifiers as individual binary models can better discriminate within a two-class subset. However, the OVA XGBoost model produced results comparable to the multiclass model in this case. Although the multiclass model is executed more efficiently, only invoking a single model per classification, the OVA scheme model provides valuable gain data per subtype, which is not possible for a multiclass model lacking stratification.

In terms of feature importance, biological features contributed the most gain per subtype, with repeat length being the highest-gain feature, on average. These findings validate and support a previous study that reports the conservation of repeat length within subtypes.⁵⁴ When varying the k-mer length used by the model, we detected considerable variability in discrimination between subtypes. The consistency in high-gain k-mer features observed across the models of various k-mer lengths reflects unique biological signatures of each subtype. The five-gram models that significantly contributed to subtype classification showed minimal overlap across subtypes, with 67/74 present in a single stratum. Although a k-mer length of five resulted in the best overall performance, some subtypes were better predicted using different k-mer lengths.

Due to the nature of multinomial classifiers, a prediction must be made for each input provided, typically, without consideration for uncertainty. To account for this, Youden's J statistic was used to distinguish informed predictions from those with higher uncertainty. Aside from suppressing uncertain predictions, low probabilities represent one metric to aid in the identification of potentially novel and thus biologically interesting repeats. Although low probability predictions are not a direct indicator of novelty, they reveal nucleotide patterns and biological features with minimal representation in the training data and could be used to flag loci for further investigation.

In order to evaluate the model performance thoroughly, we benchmarked against a comprehensive collection of metagenomes, representing a diversity of organisms and environments that encompass 135 phyla. In general, benchmarking against this test set yielded highly accurate results for subtypes with more than 30 training examples, demonstrating that the XGBoost approach, in combination with both biological and k-mer-based features, is sufficient for accurate classification of an unknown data set. Accurate prediction of classes with sparse representation was and will remain challenging until sufficient numbers of training examples can be gathered. Notably, however, features of subtypes V-A, V-K, and VI-B provided enough distinction that these loci could be accurately predicted even with low class representation in the training set. Furthermore, by comparing the classifications from CRISPRCasTyper and CRISPRclassify against cas-based predictions of the test set, we confirmed that extending a k-mer-based model with biological input features in combination with five-gram sequence features led to an overall performance improvement, most notably for subtypes I-A, I-B, I-D, II-A, and III-D.

Despite high F1 scores for the relatively abundant subtypes, accurate prediction of subtypes III-B and III-C proved problematic. It is well known that III-B/C systems often lack their own adaptation machinery and extend their CRISPR arrays by co-opting the required Cas proteins from CRISPR-Cas systems encoded in other genomic locations.⁵⁵ In accordance with this trend, we observed that the presence of cas1 and cas2 genes in a III-B or III-C locus determines whether the repeats in the respective CRISPR array conform to the nucleotide sequence of the endogenous type I locus or carry a sequence signature that can be leveraged for subtype prediction. This being the case, we found that most predictions for the III-B/C subtypes actually classified the co-occurring type I systems rather than the type III system itself. This observation illustrates the complex co-evolutionary dynamics between CRISPR arrays and cas genes—the two distinct modules of a single system that must operate in coordination to acquire and maintain adaptive immunity. Classification of CRISPR-Cas loci can be further complicated by the shuffling of CRISPR-Cas components due to recombination between closely related adaptation modules.¹⁶

Ultimately, of the 28,438 CRISPR loci detected in the test set, CRISPRclassify confidently identified 18,504 (65.1%). In contrast, the cas-based pipeline generated classifications for only 3,625 (12.8%). Clearly, one major contributing factor to the low detection rate of the cas-based pipeline is the conservative 60% identity threshold that was required for cas identification. This high threshold was empirically selected to minimize spurious cas matches which convoluted the subsequent benchmarking results with incorrect locus classifications. For example, when 30% was used as the minimum identity cas threshold, 10,401 loci were classified, but the false-positive rate significantly increased because many signature type V genes (cas12) were falsely identified due to their homology to transposon-encoded tnpB genes, which are extremely abundant across bacteria and archaea.⁵⁶ Even at the relatively permissive 30% minimum identity cutoff, the cas-based approach leaves 18,698 loci unclassified compared to the 9,934 from CRISPRclassify. Utilization of repeat-based classification enabled improved coverage of metagenomes in less time than the traditional cas-based approach, and successfully classified CRISPR loci where adjacent cas genes were missing or fell below the minimum alignment threshold against reference data. Highly sensitive identification of cas genes using Cas protein family profiles as queries for sequence searches is feasible, but it is challenging to implement in automatic pipelines without compromising specificity.¹⁶ Additionally, the demonstrated high performance on dissimilar repeat sequences from those seen in training indicates that use of this model could extend beyond classification of familiar repeats to support identification and discovery of novel loci in metagenomes.

Conclusion

We report here that due to the dependence of traditional CRISPR-Cas identification approaches on BLAST and HMM alignments to known Cas protein sequences, a substantial proportion of CRISPR loci in metagenomes remain unclassified, highlighting the need for supplemental tools to maximize the efficiency of CRISPR analysis, especially in metagenomic data. This analysis validates the feasibility of repeat-based classification and, furthermore, elucidates the salient features of CRISPR repeats that are crucial for subtype level classification. As metagenome samples and sequencing data continue to accumulate at a spectacular pace, the approaches developed in this work could provide guidance into the development and application of additional machine learning models to facilitate identification and characterization of CRISPR-Cas loci.

Author Disclosure Statement

The authors declare no potential conflict of interest.

Funding Information

The authors acknowledge support from NC State University and the NC Ag Foundation.

Supplementary Material

Supplementary Figure S1

Supplementary Figure S2

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3

Supplementary Table S4

Supplementary Table S5

Supplementary Table S6

Supplementary Table S7