Abstract

The β decay of 241Pu to 241Am results in a significant ingrowth of Am during the interim storage of PuO2. Consequently, the safe storage of the large stockpiles of separated Pu requires an understanding of how this ingrowth affects the chemistry of PuO2. This work combines density functional theory (DFT) defect energies and empirical potential calculations of vibrational entropies to create a point defect model to predict how the defect chemistry of PuO2 evolves due to the incorporation of Am. The model predicts that Am occupies Pu sites in (Pu,Am)O2±x in either the +III or +IV oxidation state. High temperatures, low oxygen-to-metal (O/M) ratios, or low Am concentrations favor Am in the +III oxidation state. Am (+III) exists in (Pu,Am)O2±x as the negatively charged (AmPu1–) defect, requiring charge compensation from holes in the valence band, thereby increasing the conductivity of the material compared to Am-free PuO2. Oxygen vacancies take over as the charge compensation mechanism at low O/M ratios. In (Pu,Am)O2±x, hypo- and (negligible) hyperstoichiometry is found to be provided by the doubly charged oxygen vacancy (VO) and singly charged oxygen interstitial (Oi1–), respectively.
Introduction
The management of the large stockpiles of Pu, separated from spent nuclear fuel or nuclear weapons programs, pose a series of technical challenges associated with its potential storage, disposal, and reuse. In particular, oxidation of the material during interim storage and the formation of hyperstoichiometric PuO2+x may initiate chemical reactions that cause potential pressurization of PuO2 storage canisters.1 Previous theoretical investigations of the defect chemistry of PuO2 suggest that pure PuO2 is very reluctant to form hyperstoichiometric PuO2+x.2 However, under storage conditions, aged PuO2 contains significant ingrowth of Am produced by 241Pu decaying into 241Am. Am builds up relatively quickly due to the short half-life of 241Pu (14.4 years), with Am concentrations peaking after approximately 70 years, at which point, it too begins to decay faster than it is produced.3 Incorporation of Am is predicted to alter the defect chemistry of PuO2; in a density functional theory (DFT) investigation on Pu–Am mixed oxide surfaces, Chen et al.4 report that the presence of Am promotes the formation of O vacancies that increase the favorability of molecular adsorption of water on PuO2 surfaces while reducing the favorability of dissociative water adsorption. The consequence of this could be an increased likelihood of chemical reactions including the aforementioned pressurization.4
Pu–Am mixed oxides have also been investigated as a fuel candidate in the design of the fourth generation (GEN-IV) of nuclear reactors. The oxygen-to-metal O/M ratio is an important parameter of the fuel and influences multiple thermophysical properties, including the oxygen potential. Osaka et al.5 experimentally determined the oxygen potential of (Pu0.91Am0.09)O2–x as a function of the O/M ratio, as well as measuring the deviation x from stoichiometry as a function of oxygen partial pressure. Matsumoto et al.6 experimentally studied the oxygen potential of (Pu0.928Am0.072)O2–x at high temperatures as a function of the O/M ratio and constructed point defect equations to describe the deviation x from stoichiometry. A doubly charged vacancy is predicted as the source of all hypostoichiometry.6 Using X-ray absorption spectroscopy, Belin et al.7 were able to quantitatively determine Pu and Am valences in the reduction process of (Pu,Am)O2–x, validating an earlier prediction made by Osaka et al.5 that all Am (+IV) will reduce to Am (+III) prior to any reduction in Pu (+IV) occurring.
Globally, significant amounts of Pu exist in the environment, a proportion of which is the form of PuO2.8 The subsurface mobility of the material is very complex and is likely impacted by the accumulation of Am, which has a different environmental mobility.8,9238PuO2 is also the most commonly used isotope in radioisotope thermoelectric generators and heating units for space applications.10 A better understanding of how PuO2 continues to evolve and accommodates Am growth is, therefore, of widespread interest. In particular, the oxidation state that Am adopts in PuO2 is of importance as it will alter, to some degree, the materials surface reactivity, thermophysical properties, and environmental mobility. Here, we construct a point defect model from DFT to investigate the mode of Am incorporation within PuO2 and the impact its presence has on the defect chemistry. Using the model, we are able to predict how the stoichiometry in (Pu1–yAmy)O2±x changes in response to Am ingrowth under a range of environmental conditions (oxygen partial pressure and temperature).
As with other actinide oxides, the application of DFT to study plutonium oxides must be approached with care. Use of conventional semilocal functionals results in the self-interaction error that causes PuO2 to be described as conducting as opposed to its correct classification as a charge-transfer insulator.11 This is caused by an over delocalization of the 5f electrons.11 Multiple approaches exist to overcome this shortcoming, two of these are the use of hybrid functionals and the DFT + U method. Using hybrid functionals, good reproduction of the experimental properties of PuO2 has been achieved.12,13 Hybrid functionals blend a portion of the Hartree–Fock (HF) exchange into a part of a density functional; they are known to offer significantly improved descriptions of band gaps, especially in small- to medium-gap systems (<5 eV).14 The DFT + U method has been applied more extensively due to its lower computational cost in comparison to hybrid functionals. DFT + U models require the selection of U and J as input parameters and are usually obtained by fitting to the structural and electronic properties of PuO2.12,15−19 The determination of appropriate values for U and J is made difficult by the variation in experimental properties reported in the literature, in particular the value of the electronic band gap. McNeilly et al.20 reported a value for the band gap of 1.8 eV, while more recently, Mark McCleskey et al.21 reported a higher value of 2.8 eV. Consequently, a wide variety of U and J values have been used in previous DFT simulations of PuO2.
Methodology
Computational Procedure
DFT simulations were performed using the Vienna Ab initio Simulation Package (VASP)22−25 employing the projector augmented wave (PAW)26,27 method implemented with the frozen-core approximation. The plutonium and americium 6s, 6p, 5f, 6d, and 7s, and oxygen 1s, 2s, and 2p electrons are treated as valence. Following convergence testing, the cutoff energy for the plane-wave basis set was selected to be 500 eV and a 2 × 2 × 2 Monkhorst–Pack k-point mesh28 was used for the 96-atom PuO2 supercells. The noncollinear relativistic computational study of the PuO2 magnetic structure by Pegg et al.12 finds a longitudinal 3k antiferromagnetic (AFM) magnetic ground state for PuO2, which was adopted in this study. Spin–orbit interaction (SOI)29 is considered as not including it resulted in a different magnetic ground state being obtained.12
For the calculation of defect energies in PuO2 supercells, we apply the DFT + U method using the Liechtenstein approach.30 DFT + U calculations are performed with the generalized gradient approximation (GGA) formulation of Perdew–Burke–Ernzerhof functional revised for solids (PBEsol + U).31,32 The energy threshold for electronic convergence is set as 1 × 10–6 eV with structural convergence deemed complete when the forces on all atoms did not exceed 2 × 10–2 eV Å–1. The U parameter of the PBEsol + U approximation was set at 7.0 eV, selected to reproduce the band gap obtained from the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional.33−36 The HSE06 functional achieves good reproduction of experimental structural properties of PuO2 and predicts an electronic band gap of 3.04 eV.12 The J parameter was fixed at a value of 0.0 eV throughout this study, as any introduction of J was shown to detrimentally affect the reproduction of the band gap for PuO2.15 The decision and justification for the selection of our U and J parameters are discussed in detail in our previous work, which also reports the equilibrium properties the HSE06 and PBEsol + U (U = 7.0 eV) functionals attain simulating PuO2.2 In summary, it was chosen to reproduce the HSE06 band gap to set U as the experimental data shows a large variation, and this functional has been proven to replicate experimental band gaps.37 In the Supporting Information, we present a comparison of the projected densities of states (DOS) obtained using the PBEsol + U and HSE06 functionals as well as evidence that while the choice of U impacts the DOS, the impact to the DFT formation energy of a defect is minimal.
The defects considered in this study are presented in Table 1. For the defects studied here, only one unique site exists in the supercell, due to the symmetry of the PuO2Fm3̅m lattice. By adding or removing electrons from the supercell, variation in the charges of the defects can be studied. Defect-containing supercells were relaxed under constant volume, using the lattice constants obtained from defect-free simulations.
Table 1. Defects Studied in This Investigation, Represented with Kröger–Vink Notation,38 Modified to Display Charge as an Integer Value (No Charge Indicated by ×).
| defect | charge states | |
|---|---|---|
| oxygen | interstitials | Oi×, Oi, Oi2– |
| vacancies | VO×, VO, VO2+ | |
| plutonium | interstitials | Pui×, Pui, Pui2+, Pui, Pui4+ |
| vacancies | VPu×, VPu, VPu2–, VPu, VPu4– | |
| americium | interstitials | Ami×, Ami, Ami2+, Ami, Ami4+ |
| Pu substitutions | AmPu4–, AmPu, AmPu2–, AmPu, AmPu×, AmPu, AmPu2+, AmPu, AmPu4+, AmPu | |
| O substitutions | AmO×, AmO, AmO2+, AmO, AmO4+, AmO, AmO6+ | |
To provide reference for the Am oxidation state and to assess the thermodynamical stability of (Pu,Am)O2±x, AmO2 and Am2O3 were simulated with DFT. The PBEsol + U functional is used with U set to 4 eV, SOI considered, and a 5 × 5 × 5 k-point mesh applied. For AmO2, transverse 3k AFM order is applied,15 while we simulate A-type Am2O3 with longitudinal 1k AFM order.39 The bulk properties produced with these simulation parameters are reasonable compared to experiment (see the Supporting Information).
Vibrational Entropies
Following Cooper et al.40 and Soulié et al.,41 when calculating the defects formation energy, we consider the difference in vibrational entropy between defective and perfect supercells (ΔSvib). Vibrational entropies are obtained using empirical potentials as the required phonon calculations become very expensive in defect-containing supercells. The General Utility Lattice Program (GULP)42 together with the Cooper, Rushton, and Grimes (CRG)43,44 potential is adopted. The CRG potential is a many-body potential model used to describe actinide oxide systems that achieves good reproduction of thermodynamic and mechanical properties. Previous work demonstrated that the phonon DOS for PuO2 produced using the CRG potential compares reasonably well to the experimental data of Manley et al.2,45 The calculation of vibrational entropies, Svib, closely follows the approach described in refs (40, 46, 47), where using eq 1, defect entropies are calculated from the normal vibrational frequencies, vn, which are themselves calculated by diagonalizing the dynamical matrix of the system
| 1 |
In this formula, h is Planck’s constant, N is the number of atoms in the crystal, T is the temperature, and kB is the Boltzmann constant. In this study, the system to calculate vibrational entropies is a 4 × 4 × 4 expansion of the PuO2 unit cell. Defective supercells are created by adding or removing atoms and are relaxed under constant volume. Defect vibrational entropies are found by calculating the difference in vibrational entropies between the defective and perfect supercell (ΔSvib). The ΔSvib values calculated for the Am extrinsic defects are presented in Table 2, and the ΔSvib values for the intrinsic defects remain the same as in ref (2). As the charges assigned to the ions in an empirical simulation are fixed, the same value of ΔSvib is given to all charge states of a given defect.
Table 2. Difference in Vibrational Entropy of PuO2 due to the Addition of Am Extrinsic Defects, Calculated Using the CRG Potential.
| defect
entropy (ΔSvib/kB) |
|||
|---|---|---|---|
| T (K) | Ami | AmPu | AmO |
| 400 | 6.835 | –0.081 | 5.268 |
| 600 | 7.322 | –0.081 | 4.711 |
| 800 | 7.810 | –0.081 | 4.479 |
| 1000 | 8.332 | –0.081 | 4.363 |
| 1200 | 8.796 | –0.081 | 4.305 |
| 1400 | 9.307 | –0.081 | 4.259 |
| 1600 | 9.667 | –0.070 | 4.236 |
| 1800 | 9.922 | –0.070 | 4.224 |
| 2000 | 10.305 | –0.081 | 4.201 |
Charge Corrections
As discussed extensively in ref (48), the introduction of charged defects into the small simulation supercells accessible using DFT introduces a number of finite size effects. These include Coulombic interactions between the defect and its periodic image as well as with the neutralizing background charge. The result is that defect formation energies exhibit a strong dependence on the size of the supercell used, and this must be corrected for when calculating a defect’s formation energy. Several correction methods exist; it was previously found that the scheme developed by Kumagai and Oba49 was very successful at accounting for finite size effects exhibited in PuO2, and therefore it is applied in this work.2 The scheme of Kumagai and Oba is an extension of that developed by Freysoldt et al.50 and uses the atomic site electronic potentials of supercells with (Vdefect,q) and without (Vbulk) defects to calculate the correction. The energy correction, Ecorr, for a defect with charge q is summarized following ref (49) as
| 2 |
| 3 |
| 4 |
where ΔVPC,q/b is the potential difference between the defect induced potential Vq/b and the point charge (PC) potential VPC,q.50 ΔVPC,q/b|far is ΔVPC,q/b at a position far from the defect site but still within the supercell. For a cubic system, such as PuO2, the PC correction energy (EPC) can be expressed as51
| 5 |
where α = 2.837 is the lattice-type-dependent Madelung constant, L is the supercell lattice constant, and ε is the static dielectric constant. The static dielectric constant of PuO2 was calculated using density functional perturbation theory (DFPT)52,53 as implemented in VASP giving a value of 19.66.2
Defect Formalism
The defect formation energy, ΔGfi, for a defect, i, is given by eq 6
| 6 |
where Edef and Eperf are the DFT total energies of the defective and perfect supercells, nα is the number of atoms of species, α, added to or removed from the system to make defect i, μα is the chemical potential of species α, and μe is the electron chemical potential. Using Boltzmann statistics, the concentration of defect i, ci, can be calculated using the formation energy of defect i and its multiplicity, mi
| 7 |
The electron chemical potential, μe = EVBM + εF, is expressed as the sum of the energy of the valence band maximum (VBM), EVBM, and the electron chemical potential above the VBM, εF. As overall charge neutrality of the system must be maintained, the concentrations of ionic and electronic defects must be such that at any given temperature and oxygen partial pressure, the following criterion is met54
| 8 |
The first term is the sum of the charges of the point defects. The second and third terms are determined by applying Fermi–Dirac statistics to the electronic DOS to obtain the concentrations of electrons (e–) in the conduction band and concentration of holes (p+) in the valence band, respectively. Within these two integrals are gv(E) and gc(E), the density of electronic states in the valence band and conduction band per formula unit of PuO2, respectively. For calculation of the electron population, ECBM is the energy of the conduction band minimum. The Defect Analysis Package55 employs linear bisection to find the value of εF that ensures charge neutrality for any given oxygen partial pressure and temperature. This enables plotting of the concentration of a defect as a function of the oxygen partial pressure or temperature. Additionally, the calculated defect concentrations are used to calculate the deviation in stoichiometry, x in (Pu,Am)O2±x. Using the concentration of a defect summed over all charge states, w, y, and z in Pu1+wAmyO2+z are given by
| 9 |
| 10 |
| 11 |
x in (Pu1–yAmy)O2+x or −x in (Pu1–yAmy)O2–x can be defined as
| 12 |
| 13 |
Chemical Potentials
The chemical potentials of plutonium, μPu(PO2,T), and oxygen, μO2(PO2,T) are defined using the chemical potential of solid PuO2 (μPuO2(s))
| 14 |
For a solid μ(PO2°,T°) ≈ μ(0,0), therefore, the temperature and pressure dependencies have been dropped. Under equilibrium conditions, the chemical potential of Pu cannot exceed that of solid Pu, otherwise a Pu precipitate would form. This upper bound is the Gibbs free energy of Pu in its natural state. It can therefore be said that under Pu-rich conditions
| 15 |
To find μPu(s), we simulate the α phase of Pu with DFT using PBEsol + U. We use the recommendation of the review by Söderlind et al.56 to use small U and J values, setting U and J parameters at 2.2 and 0.58 eV, respectively. The atomic volume obtained with these values (18.27 Å3) matched closely the atomic volume obtained by Söderlind et al.56 when using PBE + U. To determine the chemical potential of oxygen, the approach of Finnis et al.57 is adopted. This method uses the known experimental formation energy of the oxide (ΔHfPuO2 (PO2°,T°) = −10.94 eV58) to obtain the chemical potential of oxygen at standard temperature and pressure, i.e.,
| 16 |
Unlike the solid species in eq 16, the temperature and pressure dependence of the oxygen chemical potential cannot be neglected and is extrapolated from μO2(PO2°,T°) using formulas derived by Johnston et al.59
| 17 |
where the temperature-dependent Gibbs free energy per mole is fitted to a polynomial derived from experimental data (coefficients listed in Table 3)59
| 18 |
While the chemical potential of americium (μAm(PO2,T)) can be determined from DFT, here, the chemical potential is fitted to reproduce the desired concentration of Am, allowing for a comparison with experiment. μAm(PO2,T) is determined using a linear bisection in the Defect Analysis Package.55
Table 3. Coefficients for Gibbs Free Energy Expression in Eq 18(59).
| A | 29.659 × 10–3 kJ mol–1 K–1 |
| B | 6.137261 × 10–6 kJ mol–1 K–2 |
| C | –1.186521 × 10–9 kJ mol–1 K–3 |
| D | 0.095780 × 10–12 kJ mol–1 K–4 |
| E | –0.219663 × 103 kJ mol–1 K |
| F | –9.861391 kJ mol–1 |
| G | 237.948 × 10–3 kJ mol–1 K–1 |
Results and Discussion
The formation energies of the Am-based extrinsic defects are plotted as a function of the Fermi level at 1000 K and an oxygen partial pressure of 0.10 atm in Figure 1. Figure 1 displays the charge state of each defect that corresponds to the lowest formation energy at a given position in the band gap. A similar plot for the intrinsic defects is given in previous work.2 It is clear from Figure 1 that the AmPu defects have significantly lower formation energies than AmO and Ami defects across the whole band gap. This result is found to be consistent at both high and low oxygen partial pressures and Am concentrations. This shows that in (Pu,Am)O2, Am is preferentially accommodated as a substitutional defect on the Pu site. The most energetically stable charge state of AmPu is seen to vary across the band gap, with four states in total dominant at one time. However, it is the AmPu1– and AmPu charge states that dominate across the majority of the band gap, suggesting that it is these two defects that accommodate americium under most equilibrium conditions. By studying the electron occupation of the Am atom in the simulated defect-containing supercells, it was possible to infer an oxidation state for americium of +III and +IV in AmPu1– and AmPu, respectively. The results of a Bader charge analysis60 (Table 4) helps us to confirm this result, using AmO2 and Am2O3 as reference oxides for the Am (IV) and Am (III) charge states, respectively. Pu remains in the +IV oxidation state, regardless of defect. AmPu defects do not cause significant distortion of the PuO2 lattice; only a small distortion of the eight nearest oxygen atoms is observed, as shown in Figure 2. In cells containing the AmPu1– defect, the O–Am bond length is just 0.05 Å higher than the O–Pu bond length of 2.34 Å in Am-free PuO2; this increase is lower in cells containing the AmPu defect. This is explained and supported by the reported crystallography: Am (+IV) and Am (+III) with eightfold coordination have ionic radii of 0.95 and 1.09 Å, respectively.61 Pu (+IV) with eightfold coordination has an ionic radius of 0.96 Å.61
Figure 1.

Defect formation energies for AmPu, AmO, and Ami defects in (Pu1–yAmy)O2±x (y = 0.001) as a function of Fermi energy. Calculated at 1000 K and an oxygen partial pressure of 0.10 atm. Only the charge state with the lowest formation energy for a given Fermi level is shown for each defect, represented with numeric label.
Table 4. Bader Charge of Am in AmPu Defects and Am Oxides.
| AmPu× | 2.44 |
| AmPu1– | 2.02 |
| AmO2 (Am (IV)) | 2.38 |
| Am2O3 (Am (III)) | 1.96 |
Figure 2.

Final relaxed structure for the AmPu1– defect in PuO2. Plutonium, americium, and oxygen are represented with gray, blue, and red spheres, respectively.
The Brouwer diagrams in Figure 3 show the defect concentrations in (Pu1–yAmy)O2±x as a function of oxygen partial pressure at 1000 K with comparison made for y values of 0.0 and 0.001. At all values of oxygen partial pressure tested, Am is seen to be accommodated as substitutional defects on Pu sites, with concentrations of Am interstitials and O substitutions negligible to such an extent they are not shown on the Brouwer diagrams. The Brouwer diagram shows that as the O/M ratio in (Pu1–yAmy)O2±x (y = 0.001) decreases, the dominant extrinsic defect transitions from AmPu× to AmPu. As previously discussed, this transition corresponds to a reduction in the oxidation state for Am of +IV to +III. This supports the experimental work of Belin et al.7 as well as the model of Osaka et al.5 that find and predict all Am is reduced prior to Pu reduction when the O/M ratio decreases from stoichiometry. Charge compensation for the AmPu1– defect is provided by holes in the valence band at high oxygen partial pressures, before VO defects compensate when their concentration becomes sufficiently high. Figure 3 shows that when Am (+IV) is the dominant oxidation state, the concentration of Am (III) ions remains elevated and stable: Am (III) contributes ∼17% to the total Am concentration in the region of stability in Figure 3. Consequently, the concentrations of holes also remain high to provide charge compensation, with concentrations several magnitudes higher than Am-free PuO2. It can therefore be said that Am behaves as a p-type dopant, acting to make PuO2 more conductive.
Figure 3.
Brouwer diagrams showing the defect concentrations and value of x in (Pu1–yAmy)O2±x as a function of oxygen partial pressure at a temperature of 1000 K and y value of 0.0 (left) and 0.001 (right). At partial pressures to the left of the vertical dashed line, (Pu,Am)O2±x is predicted to be thermodynamically unstable with respect to Am2O3.
By comparing the two Brouwer diagrams in Figure 3, we observe that Am incorporation also impacts the intrinsic defect chemistry. The defect responsible for hypostoichiometry remains oxygen vacancies, however, the presence of Am is observed to alter the favored oxygen vacancy charge state; the Brouwer diagrams show that the doubly charged VO2+ defect dominates. In contrast, in PuO2–x, the neutral oxygen vacancy was preferred. Increased Am concentration promotes positively charged oxygen vacancies, as higher concentrations are required to charge-compensate (AmPu). Hyperstoichiometry remains very low and accommodated by oxygen interstitials. In pure PuO2+x, the Oi2– interstitial is dominant. However, the dominant charge state is seen to be altered with the addition of Am: the Oi interstitial is now dominant. Prodan et al.13 have previously reported that Oi1– is the most energetically favorable charge state for the oxygen interstitial. Acting as a p-type dopant, increasing the Am concentration lowers the Fermi level of the system to such a degree that Oi becomes the interstitial with the lowest formation energy and VO2+ is the vacancy with the lowest formation energy.
To assess the reliability of the point defect model, the results are compared to the experimental studies of Osaka et al.5 and Matsumoto et al.6 who studied the O/M ratio in (Pu,Am)O2–x. By matching the temperature and Am concentrations of the experiments, it was possible to determine how x in (Pu,Am)O2–x changes with oxygen partial pressure. The results are compared to these previous experimental works in Figure 4. It is seen that both the trends and absolute values of x are very well replicated by the model.
Figure 4.
Values of x in (Pu1–yAmy)O2–x as a function of oxygen partial pressure at y values of (a) 0.09 and (b) 0.072, with comparison to the experimental results of Osaka et al.5 and Matsumoto et al.6
From Figures 3 and 4, we see an evolving dependence of [VO2+] and x on the oxygen partial pressure. At near-stoichiometry, our model shows that the presence of Am results in [e–] ≪ [h+], in contrast to Am-free PuO2, where [e–] = [h+] at near-stoichiometry. Therefore, to construct equations describing the defect chemistry of (Pu,Am)O2–x, we cannot say that [e–] = [h+] as suggested by Matsumoto et al.6 Instead, we propose that at low concentrations of VO and near-stoichiometry, the formation of VO2+ is charge-compensated by the removal of holes, which exist at concentrations many orders of magnitude greater than VO at near-stoichiometry. The defect reaction and the corresponding equilibrium constant (k1) are written as
| 19 |
| 20 |
We see in Figure 3 that at near-stoichiometry, the concentration
of holes can be considered fixed. We can therefore show that [VO2+] (and x in (Pu,Am)O2 – x) is proportional to 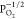
| 21 |
Figure 3 shows that when oxygen partial pressures are low enough to cause sufficiently high concentrations of VO2+, reduction of Am begins. The defect reaction and corresponding equilibrium constant (k2) becomes
| 22 |
| 23 |
In the reducing region, [AmPu1–] = 2[VO]. Eq 23 can be rearranged to show that [VO2+] (and x in (Pu,Am)O2 – x) is proportional to both 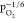 and [AmPu]2/3 (see eq 24). This explains the curve we see
in Figures 3 and 4: as Am (+IV) is reduced, the rate of VO2+ formation decreases
and when reduction is complete, [VO] remains constant.
and [AmPu]2/3 (see eq 24). This explains the curve we see
in Figures 3 and 4: as Am (+IV) is reduced, the rate of VO2+ formation decreases
and when reduction is complete, [VO] remains constant.
| 24 |
As oxygen partial pressure is reduced further, the value of x in (Pu,Am)O2–x will continue to evolve. The start of reduction in Pu is predicted to result in the formation of defect clusters;6 however, both cluster formation and the higher defect concentrations at low O/M ratios are beyond the capabilities of the point defect model.
Figure 5 shows the impact of varying temperature on the defect chemistry of (Pu1–yAmy)O2±x where y = 0.0 or 0.001. Am (+III) concentration increases with temperature, becoming the dominant oxidation state at high temperatures. The Am (+IV)/Am (+III) ratio increases with decreasing temperature, and at low temperatures, the Am in (Pu1–yAmy)O2±x is composed entirely of Am (+IV). This is supported by the recent finding of Emerson et al.8 who measured the Am L3-edge X-ray absorption near-edge structure (XANES) spectrum of aged PuO2 samples finding a spectrum characteristic of Am4+O2.
Figure 5.
Defect concentrations in (Pu1–yAmy)O2±x as a function of temperature at an oxygen partial pressure of 0.1 atm and y value of 0.0 (left) and 0.001 (right). At temperatures to the left of the vertical dashed lines (a) and (b), (Pu,Am)O2±x is predicted to be thermodynamically unstable with respect to Am2O3 and AmO2, respectively.
The impact of varying the concentration of Am (y in (Pu1–yAmy)O2±x) is shown in Figure 6. Regardless of its concentration, Am is always accommodated in either the +IV or +III oxidation state, with the ratio of the two oxidation states varying quite significantly depending on the concentration of Am present. At very low concentrations, Am (+III) is the dominant oxidation state, whereas accumulation of Am in PuO2 results in the promotion of the +IV oxidation state. Although the Am (+IV) concentration increases more rapidly, the Am (+III) concentration also continues to increase as Am accumulates accompanied by a concomitant increase in conductivity of the material. Increasing Am concentration can be seen to create a more reducing environment; oxygen vacancy concentrations increase with increasing Am, and oxygen interstitial concentrations decrease. Therefore, under any condition, the O/M ratio is lower if Am concentration in PuO2±x is increased. This is a similar result to that found in (U,Am)O2±x where increased Am content is seen to hinder oxidation.62 PuO2 is much more resistant to oxidation than UO2, and we see here that adding Am further increases this resistance.
Figure 6.

Defect concentrations in (Pu1–yAmy)O2±x as a function of the concentration of Am at an oxygen partial pressure of 0.1 atm and temperature of 1000 K. At Am concentrations to the right of the vertical dashed line, (Pu,Am)O2±x is predicted to be thermodynamically unstable with respect to AmO2.
In Figures 3–6, the dashed vertical lines highlight the point at which the model predicts (Pu,Am)O2±x is thermodynamically unstable and will decompose into a combination of two tested Am oxides: AmO2 and A-type Am2O3. The model predicts that at low oxygen partial pressures, low temperatures, or high Am concentrations, (Pu,Am)O2±x becomes unstable. To precipitate out of the material, the Am oxides would require significant energy to overcome barriers to migration within (Pu,Am)O2±x. As it is found that at high temperatures (Pu,Am)O2±x is stable, it is unlikely that under the conditions of instability predicted (Pu,Am)O2±x would have the energy to decompose into the Am oxides, despite being thermodynamically favorable. Improvement may also be required in the DFT model for AmO2 and Am2O3. Specifically, the best approach to modeling with the DFT + U approach remains uncertain. Caution is therefore attached to the results regarding thermodynamic stability.
Conclusions
The mode of Am incorporation within PuO2 and the impact Am makes to the defect chemistry of the host have been investigated using DFT and a point defect model. Under all conditions and Am concentrations investigated, Am is found to be accommodated on Pu vacancies, with Am existing in a combination of the (+IV) and (+III) oxidation states. Reduction in the O/M ratio of (Pu,Am)O2±x is seen to change the dominant extrinsic defect from AmPu× to AmPu corresponding to the reduction of Am (+IV) to Am (+III). Am (+IV) is promoted by low temperatures and high Am concentrations. The addition of Am results in the concentration of holes in the valence band increasing by multiple orders of magnitude compared to Am-free PuO2, to provide charge compensation to Am (+III). It is, therefore, anticipated that the presence of Am increases the electrical activity of PuO2.
Acknowledgments
This work was completed using the High End Computing facility at Lancaster University. The visualization of crystal structures was performed with VESTA,63 and finite size corrections were calculated using pymatgen.64 This project was funded as part of EPSRCs TRANSCEND project (EP/S01019X/1).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.1c03274.
The evolving defect chemistry of (Pu,Am)O2±x: Appendix A: The impact of the U parameter in PBEsol + U on the density of states and DFT formation energies of defects in PuO2. Appendix B: Structural and electronic properties obtained in DFT simulation of Am oxides (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bailey G.; Bluhm E.; Lyman J.; Mason R.; Paffett M.; Polansky G.; Roberson G. D.; Sherman M.; Veirs K.; Worl L.. Gas Generation from Actinide Oxide Materials, No. LA-13781-MS; Los Alamos National Laboratory: NM (US), 2000; 72.
- Neilson W. D.; Pegg J. T.; Steele H.; Murphy S. T. The defect chemistry of non-stoichiometric PuO2±x. Phys. Chem. Chem. Phys. 2021, 23, 4544–4554. 10.1039/D0CP06497A. [DOI] [PubMed] [Google Scholar]
- Peterson V.Reference Computations of Public Dose and Cancer Risk from Airborne Releases of Plutonium. Nuclear Safety Technical Report, 1993.
- Chen J. L.; Kaltsoyannis N. Computational Study of Plutonium-Americium Mixed Oxides (Pu0.92Am0.08O2 – x); Water Adsorption on {111}, {110}, and {100} Surfaces. J. Phys. Chem. C 2020, 124, 6646–6658. 10.1021/acs.jpcc.9b11601. [DOI] [Google Scholar]
- Osaka M.; Kurosaki K.; Yamanaka S. Oxygen potential of (Pu0.91Am0.09)O2–x. J. Nucl. Mater. 2006, 357, 69–76. 10.1016/j.jnucmat.2006.05.044. [DOI] [Google Scholar]
- Matsumoto T.; Arima T.; Inagaki Y.; Idemitsu K.; Kato M.; Morimoto K.; Sunaoshi T. Oxygen potential measurement of (Pu0.928Am0.072)O2–x at high temperatures. J. Nucl. Sci. Technol. 2015, 52, 1296–1302. 10.1080/00223131.2014.986243. [DOI] [Google Scholar]
- Belin R. C.; Martin P. M.; Lechelle J.; Reynaud M.; Scheinost A. C. Role of cation interactions in the reduction process in plutonium-americium mixed oxides. Inorg. Chem. 2013, 52, 2966–2972. 10.1021/ic3023776. [DOI] [PubMed] [Google Scholar]
- Emerson H. P.; Pearce C. I.; Delegard C. H.; Cantrell K. J.; Snyder M. M. V.; Thomas M.-L.; Gartman B. N.; Miller M. D.; Resch C. T.; Heald S. M.; et al. Influences on Subsurface Plutonium and Americium Migration. ACS Earth Space Chem. 2021, 5, 279–294. 10.1021/acsearthspacechem.0c00277. [DOI] [Google Scholar]
- Cantrell K. J.; Felmy A. R.. Plutonium and Americium Geochemistry at Hanford: A Site Wide Review. No. PNNL-21651; Pacific Northwest National Laboratory (PNNL): Richland, WA (United States), 2012.
- O’Brien R. C.; Ambrosi R. M.; Bannister N. P.; Howe S. D.; Atkinson H. V. Safe radioisotope thermoelectric generators and heat sources for space applications. J. Nucl. Mater. 2008, 377, 506–521. 10.1016/j.jnucmat.2008.04.009. [DOI] [Google Scholar]
- Wen X. D.; Martin R. L.; Henderson T. M.; Scuseria G. E. Density functional theory studies of the electronic structure of solid state actinide oxides. Chem. Rev. 2013, 113, 1063–1096. 10.1021/cr300374y. [DOI] [PubMed] [Google Scholar]
- Pegg J. T.; Shields A. E.; Storr M. T.; Wills A. S.; Scanlon D. O.; De Leeuw N. H. Hidden magnetic order in plutonium dioxide nuclear fuel. Phys. Chem. Chem. Phys. 2018, 20, 20943–20951. 10.1039/C8CP03583K. [DOI] [PubMed] [Google Scholar]
- Prodan I. D.; Scuseria G. E.; Sordo J. A.; Kudin K. N.; Martin R. L. Lattice defects and magnetic ordering in plutonium oxides: A hybrid density-functional-theory study of strongly correlated materials. J. Chem. Phys. 2005, 123, 014703 10.1063/1.1953427. [DOI] [PubMed] [Google Scholar]
- Marsman M.; Paier J.; Stroppa A.; Kresse G. Hybrid functionals applied to extended systems. J. Phys. Condens. Matter 2008, 20, 064201. 10.1088/0953-8984/20/6/064201. [DOI] [PubMed] [Google Scholar]
- Pegg J. T.; Aparicio-Anglès X.; Storr M.; de Leeuw N. H. DFT+U study of the structures and properties of the actinide dioxides. J. Nucl. Mater. 2017, 492, 269–278. 10.1016/j.jnucmat.2017.05.025. [DOI] [Google Scholar]
- Ghosh P. S.; Arya A. First-principles study of phase stability, electronic and mechanical properties of plutonium sub-oxides. Phys. Chem. Chem. Phys. 2019, 21, 16818–16829. 10.1039/C9CP01858A. [DOI] [PubMed] [Google Scholar]
- Nakamura H.; Machida M.; Kato M. LDA+U Study on Plutonium Dioxide with Spin-Orbit Couplings. Prog. Nucl. Sci. Technol. 2011, 2, 16–19. 10.15669/pnst.2.16. [DOI] [Google Scholar]
- Zhang P.; Wang B. T.; Zhao X. G. Ground-state properties and high-pressure behavior of plutonium dioxide: Density functional theory calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 144110 10.1103/PhysRevB.82.144110. [DOI] [Google Scholar]
- Sun B.; Zhang P.; Zhao X. G. First-principles local density approximation+U and generalized gradient approximation+U study of plutonium oxides. J. Chem. Phys. 2008, 128, 084705 10.1063/1.2833553. [DOI] [PubMed] [Google Scholar]
- McNeilly C. E. The electrical properties of plutonium oxides. J. Nucl. Mater. 1964, 11, 53–58. 10.1016/0022-3115(64)90120-5. [DOI] [Google Scholar]
- Mark McCleskey T.; Bauer E.; Jia Q.; Burrell A. K.; Scott B. L.; Conradson S. D.; Mueller A.; Roy L.; Wen X.; Scuseria G. E.; et al. Optical band gap of NpO2 and PuO2 from optical absorbance of epitaxial films. J. Appl. Phys. 2013, 113, 013515 10.1063/1.4772595. [DOI] [Google Scholar]
- Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Steiner S.; Khmelevskyi S.; Marsmann M.; Kresse G. Calculation of the magnetic anisotropy with projected-augmented-wave methodology and the case study of disordered Fe1 – xCox alloys. Phys. Rev. B 2016, 93, 224425 10.1103/PhysRevB.93.224425. [DOI] [Google Scholar]
- Liechtenstein A. I.; Anisimov V. I.; Zaanen J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467–R5470. 10.1103/PhysRevB.52.R5467. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
- Csonka G. I.; Perdew J. P.; Ruzsinszky A.; Philipsen P. H. T.; Lebègue S.; Paier J.; Vydrov O. A.; Ángyán J. G. Assessing the performance of recent density functionals for bulk solids. Phys. Rev. B 2009, 79, 155107 10.1103/PhysRevB.79.155107. [DOI] [Google Scholar]
- Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
- Heyd J.; Scuseria G. E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. 10.1063/1.1760074. [DOI] [PubMed] [Google Scholar]
- Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
- Krukau A. V.; Vydrov O. A.; Izmaylov A. F.; Scuseria G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106 10.1063/1.2404663. [DOI] [PubMed] [Google Scholar]
- Garza A. J.; Scuseria G. E. Predicting Band Gaps with Hybrid Density Functionals. J. Phys. Chem. Lett. 2016, 7, 4165–4170. 10.1021/acs.jpclett.6b01807. [DOI] [PubMed] [Google Scholar]
- Kröger F. A.; Vink H. J. In Relations between the Concentrations of Imperfections in Crystalline Solids, Seitz F.; Turnbull D., Eds.; Solid State Physics; Academic Press, 1956; Vol. 3, pp 307–435. [Google Scholar]
- Talla Noutack M. S.; Geneste G.; Jomard G.; Freyss M. First-principles investigation of the bulk properties of americium dioxide and sesquioxides. Phys. Rev. Mater. 2019, 3, 35001 10.1103/PhysRevMaterials.3.035001. [DOI] [Google Scholar]
- Cooper M. W.; Murphy S. T.; Andersson D. A. The defect chemistry of UO2 ± x from atomistic simulations. J. Nucl. Mater. 2018, 504, 251–260. 10.1016/j.jnucmat.2018.02.034. [DOI] [Google Scholar]
- Soulié A.; Bruneval F.; Marinica M.-C.; Murphy S.; Crocombette J.-P. Influence of vibrational entropy on the concentrations of oxygen interstitial clusters and uranium vacancies in nonstoichiometric UO2. Phys. Rev. Mater. 2018, 2, 083607 10.1103/PhysRevMaterials.2.083607. [DOI] [Google Scholar]
- Gale J. D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. 10.1039/a606455h. [DOI] [Google Scholar]
- Cooper M. W. D.; Rushton M. J. D.; Grimes R. W. A many-body potential approach to modelling the thermomechanical properties of actinide oxides. J. Phys. Condens. Matter 2014, 26, 105401 10.1088/0953-8984/26/10/105401. [DOI] [PubMed] [Google Scholar]
- Cooper M. W. D.; Murphy S. T.; Rushton M. J. D.; Grimes R. W. Thermophysical properties and oxygen transport in the (Ux,Pu1 – x)O2 lattice. J. Nucl. Mater. 2015, 461, 206–214. 10.1016/j.jnucmat.2015.03.024. [DOI] [Google Scholar]
- Manley M. E.; Jeffries J. R.; Said A. H.; Marianetti C. A.; Cynn H.; Leu B. M.; Wall M. A. Measurement of the phonon density of states of PuO2 (+2% Ga): A critical test of theory. Phys. Rev. B 2012, 85, 132301 10.1103/PhysRevB.85.132301. [DOI] [Google Scholar]
- Mishin Y.; Sørensen M. R.; Voter A. F. Calculation of point-defect entropy in metals. Philos. Mag. A 2001, 81, 2591–2612. 10.1080/01418610108216657. [DOI] [Google Scholar]
- Andersson D. A.; Garcia P.; Liu X.-Y.; Pastore G.; Tonks M.; Millett P.; Dorado B.; Gaston D. R.; Andrs D.; Williamson R. L.; et al. Atomistic modeling of intrinsic and radiation-enhanced fission gas (Xe) diffusion in UO2 ± x: Implications for nuclear fuel performance modeling. J. Nucl. Mater. 2014, 451, 225–242. 10.1016/j.jnucmat.2014.03.041. [DOI] [Google Scholar]
- Durrant T. R.; Murphy S. T.; Watkins M. B.; Shluger A. L. Relation between image charge and potential alignment corrections for charged defects in periodic boundary conditions. J. Chem. Phys. 2018, 149, 024103 10.1063/1.5029818. [DOI] [PubMed] [Google Scholar]
- Kumagai Y.; Oba F. Electrostatics-based finite-size corrections for first-principles point defect calculations. Phys. Rev. B 2014, 89, 195205 10.1103/PhysRevB.89.195205. [DOI] [Google Scholar]
- Freysoldt C.; Neugebauer J.; Van de Walle C. G. Fully Ab Initio Finite-Size Corrections for Charged-Defect Supercell Calculations. Phys. Rev. Lett. 2009, 102, 016402 10.1103/PhysRevLett.102.016402. [DOI] [PubMed] [Google Scholar]
- Leslie M.; Gillan N. J. The energy and elastic dipole tensor of defects in ionic crystals calculated by the supercell method. J. Phys. C: Solid State Phys. 1985, 18, 973–982. 10.1088/0022-3719/18/5/005. [DOI] [Google Scholar]
- Baroni S.; Resta R. Ab initio calculation of the macroscopic dielectric constant in silicon. Phys. Rev. B 1986, 33, 7017–7021. 10.1103/PhysRevB.33.7017. [DOI] [PubMed] [Google Scholar]
- Gajdoš M.; Hummer K.; Kresse G.; Furthmüller J.; Bechstedt F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112 10.1103/PhysRevB.73.045112. [DOI] [Google Scholar]
- Youssef M.; Yildiz B. Intrinsic point-defect equilibria in tetragonal ZrO2: Density functional theory analysis with finite-temperature effects. Phys. Rev. B 2012, 86, 144109 10.1103/PhysRevB.86.144109. [DOI] [Google Scholar]
- Murphy S. T.; Hine N. D. M. Point Defects and Non-stoichiometry in Li2TiO3. Chem. Mater. 2014, 26, 1629–1638. 10.1021/cm4038473. [DOI] [Google Scholar]
- Söderlind P.; Landa A.; Sadigh B. Density-functional theory for plutonium. Adv. Phys. 2019, 68, 1–47. 10.1080/00018732.2019.1599554. [DOI] [Google Scholar]
- Finnis M. W.; Lozovoi A. Y.; Alavi A. The Oxidation Of NiAl: What Can We Learn from Ab Initio Calculations?. Annu. Rev. Mater. Res. 2005, 35, 167–207. 10.1146/annurev.matsci.35.101503.091652. [DOI] [Google Scholar]
- Johnson G. K.; Van Deventer E. H.; Kruger O. L.; Hubbard W. N. The enthalpies of formation of plutonium dioxide and plutonium mononitride. J. Chem. Thermodyn. 1969, 1, 89–98. 10.1016/0021-9614(69)90039-1. [DOI] [Google Scholar]
- Johnston K.; Castell M. R.; Paxton A. T.; Finnis M. W. SrTiO3 (001) (2 × 1) reconstructions: First-principles calculations of surface energy and atomic structure compared with scanning tunneling microscopy images. Phys. Rev. B 2004, 70, 085415 10.1103/PhysRevB.70.085415. [DOI] [Google Scholar]
- Henkelman G.; Arnaldsson A.; Jónsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. 10.1016/j.commatsci.2005.04.010. [DOI] [Google Scholar]
- Shannon R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
- Epifano E.; Prieur D.; Martin P. M.; Guéneau C.; Dardenne K.; Rothe J.; Vitova T.; Dieste O.; Wiss T.; Konings R. J. M.; et al. Melting behaviour of uranium-americium mixed oxides under different atmospheres. J. Chem. Thermodyn. 2020, 140, 105896. 10.1016/j.jct.2019.105896. [DOI] [Google Scholar]
- Momma K.; Izumi F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
- Ong S. P.; Richards W. D.; Jain A.; Hautier G.; Kocher M.; Cholia S.; Gunter D.; Chevrier V. L.; Persson K. A.; Ceder G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





