Three States Involving Vibronic Resonance is a Key to Enhancing Reverse Intersystem Crossing Dynamics of an Organoboron-Based Ultrapure Blue Emitter

Abstract

The recently developed narrow-band blue-emitting organoboron chromophores based on the multiple-resonance (MR) effect have now become one of the most important components for constructing efficient organic light emitting diodes (OLEDs). While they basically emit through fluorescence, they are also known for showing substantial thermally activated delayed fluorescence (TADF) even with a relatively large singlet–triplet gap (ΔE_ST). Indeed, understanding the reverse intersystem crossing (RISC) dynamics behind this peculiar TADF will allow judicious molecular designs toward achieving better performing OLEDs. Explaining the underlying nonadiabatic spin-flip mechanism, however, has often been equivocal, and how the sufficiently fast RISC takes place even with the sizable ΔE_ST and vanishingly small spin–orbit coupling is not well understood. Here, we show that a vibronic resonance, namely the frequency matching condition between the vibration and the electronic energy gap, orchestrates three electronic states together and this effect plays a major role in enhancing RISC in a typical organoboron emitter. Interestingly, the mediating upper electronic state is quite high in energy to an extent that its thermal population is vanishingly small. Through semiclassical quantum dynamics simulations, we further show that the geometry dependent non-Condon coupling to the upper triplet state that oscillates with the frequency ΔE_ST/ℏ is the main driving force behind the peculiar resonance enhancement. The existence of an array of vibrational modes with strong vibronic rate enhancements provides the ability to sustain efficient RISC over a range of ΔE_ST in defiance of the energy gap law, which can render the MR-emitters peculiar in comparison with more conventional donor–acceptor type emitters. Our investigation may provide a new guide for future blue emitting molecule developments.

Introduction

Thermally activated delayed fluorescence (TADF) has recently emerged as a promising and pragmatic alternative to more traditional phosphorescence in the fabrication of efficient organic light emitting diodes (OLEDs).¹⁻⁴ Via triplet-to-singlet upconversion, so-called reverse intersystem crossing (RISC), TADF permits singlet emission of nearly 100% internal quantum efficiency (IQE) in OLEDs. 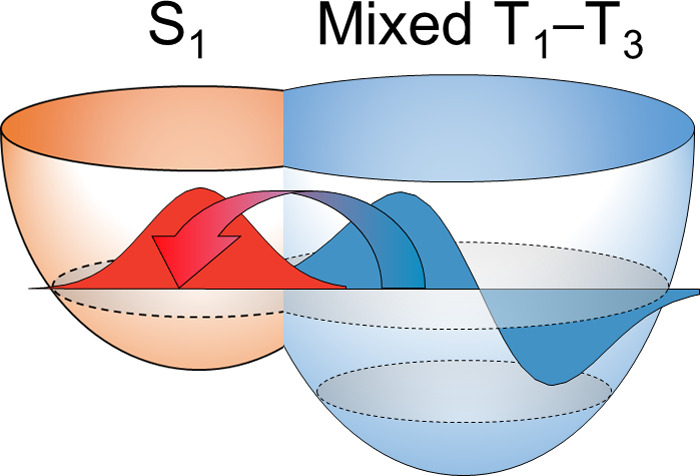Due to considerably weak spin–orbit couplings (SOCs) in purely organic emitters, an important parameter for TADF performance has been the energy gap between the singlet and the triplet excited states (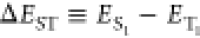), which is related to the exchange interaction K between electrons in the frontier orbitals with ΔE_ST ≃ 2K.⁵ In this regard, conventional TADF emitters often adopt the donor–acceptor (DA) structure for spatial separation of the frontier orbitals, thereby reducing K and ΔE_ST. However, such DA-type emitters have inherently a dominant charge transfer character in the S₁ state. Therefore, they entail broad emission features, typically with a full-width-at-half-maximum (fwhm) > 50 nm,⁶ resulting in low color purity. This aspect has indeed been one of the major hurdles to overcome for commercialization. For instance, the fwhm of the blue emission spectrum from the latest OLED display is ∼30 nm,⁷ and meeting this specification will require to implement a narrow-band color filter. This will inescapably compromise the efficiency and damage the enhanced performance via TADF. Of course, this drawback will be especially serious for battery powered displays.

With regard to achieving high color purity in the blue region, the molecular design concept that arose recently by utilizing the multiple-resonance (MR) effect is indeed revolutionary and has already attracted significant attention.⁸⁻¹¹ It is realized by placing electron-donating nitrogen atoms at para-positions to a central electron-accepting boron atom in a π-conjugation scaffold as in 5,9-diphenyl-5,9-diaza-13b-boranaphtho[3,2,1-de]anthracene (DABNA, Figure 1).⁸ Hence, the distributions of the highest-occupied molecular orbital (HOMO) and the lowest-unoccupied molecular orbital (LUMO) alternate within the same rigid molecular unit. As a result, a relatively fast emission (>10⁷ s^–1) with an ultrapure blue spectrum (fwhm < 30 nm) results, owing to the local-excitation character and the structural rigidity of the S₁ state.

Figure 1.

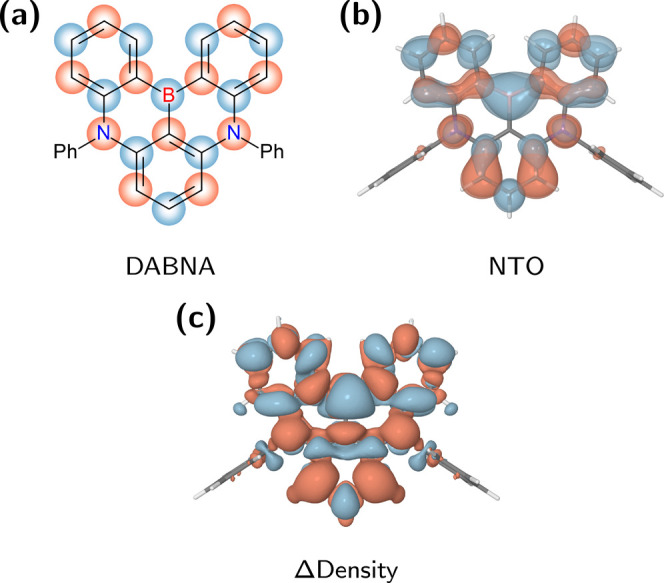
Narrow-band blue TADF emitter, DABNA. (a) Chemical structure with an illustration of the multiple-resonance effect (HOMO/LUMO in red/blue). (b) Hole/particle wave functions shown in red/blue, as represented by the natural transition orbitals from ω*B97X calculations. (c) Difference density plot upon S₀–S₁ excitation calculated at the SCS-ADC(2) level where the decreased/increased electron density is shown in red/blue. Notice that the transition densities include correlation effects from double excitation terms and appear somewhat differently from b.

Interestingly, in MR-type emitters, although the spin–orbit coupling (SOC) between the S₁ and the T₁ states is insignificantly small and ΔE_ST is non-negligibly large, it is known that the RISC process also participates in generating the S₁ state during electroluminescence. While the ensuing delayed fluorescence is not remarkably swift (e.g., ∼10⁴ s^–1 for DABNA⁸), the existence of this noticeable amount of TADF is important in many respects. Indeed, the RISC process not only improves the light emitting efficiency but suppresses exciton quenching (e.g., triplet–triplet annihilation and triplet–polaron quenching), while also helping the emitters remain chemically intact during the shortened T₁ state lifetime.¹² From this perspective, understanding the molecular factors behind RISC of MR-TADF emitters is of central importance to ultimately improve their excited state behaviors. However, RISC processes are generally nonradiative and nonadiabatic in nature, and accordingly, experimental and computational assessments tend to be notoriously difficult. Even greater complications are added to already-difficult computations when vibronic contributions to RISC dynamics in the form of spin–vibronic coupling are considered,¹³⁻¹⁵ requiring a model that can handle this complex state mixing.^16,17 Recently, researchers have been actually tackling this difficult but important system theoretically.^15,18,19 For example, Northey and Penfold¹⁵ employed the multiconfiguration time-dependent Hartree (MCTDH) quantum dynamics simulation method with a model Hamiltonian derived from the time-dependent density functional theory (TDDFT) to highlight the importance of the spin–vibronic mechanism in the ISC process from S₁ to T₁ and T₂, facilitated by nonadiabatic coupling within the singlet manifold. However, they could not observe S₁–T₁ ISC even with a sizable SOC between the two states, likely due to the overestimation of ΔE_ST from TDDFT (∼0.6 eV) and an accidental quasi-degeneracy between S₁ and T₂. Although some spatial separation of the frontier orbitals occurs due to the alternating HOMO/LUMO distribution, the relatively small ΔE_ST of an MR-type emitter (<0.2 eV) is induced mainly by higher-order electron correlations.¹⁹⁻²¹ Pershin et al.¹⁹ employed a high level ab initio method to correctly investigate the theoretical origin of the reduced ΔE_ST in DABNA by explicitly considering the electron correlation effects that renders the local density rearrangement in spatially alternating HOMO–LUMO regions. In fact, achieving a correct energy gap structure is important not just for estimating the S₁–T₁ gap. If the T₁ energy is underestimated or the S₁ energy is overestimated, the close-by T₂ state¹⁵ or even T₃ state¹⁸ may mistakenly get into energetic resonance with S₁, rendering the T₂–S₁ or T₃–S₁ intersystem crossing (ISC) estimated to be unphysically too fast. Such artifacts will of course distort the prediction on the interconversion kinetics among all involved electronic states. Therefore, one can easily imagine that combining high level ab initio methods and kinetics and/or dynamics simulation tools will be important in unraveling the processes that are happening in DABNA.

In this work, with such purposes in our mind, we unravel the RISC dynamics of DABNA as a prototype of an ultrapure blue MR-emitter with TADF. Based on high-level quantum chemical calculations, we first evaluate the RISC rate constant (k_RISC) through Fermi’s golden rule between T₁ and S₁ by perturbatively expanding the two involved states within the full singlet and triplet spin manifolds. We also perform semiclassical quantum dynamics simulations to investigate a superexchange behavior in its RISC. Then, by comparing with DA emitters, we discuss distinctive characteristics in the RISC of DABNA, where the spin crossover in a range of ΔE_ST is effectively mediated by successive and overlapping appearances of the spin–vibronic enhancements provided by an array of vibrational modes. This characterization leads to a new design rule for the development of efficient MR-TADF emitters.

Results and Discussion

Reverse Intersystem Crossing Rate

We reiterate that low-cost correlated excited state methods such as linear response TDDFT do not predict ΔE_ST well for DABNA, as electron correlations in the form of double excitations tend to reduce the gap.²¹ We therefore employed a relatively higher level of theory, SCS-CC2/TZVPP//SCS-ADC(2)/SVP. Its spin-component scaling can also improve the accuracy of the excited state potential energy surface²² and, therefore, aids the normal-mode analyses toward obtaining mode-mixing rotations and displacements between pairs of excited states.²³ In addition, reliably calculating the energy gaps between excited states improves the quality of perturbation expansions.

We estimated the RISC upconversion kinetics with the golden rule formula, as it can provide a quantitative basis for understanding physical characteristics governed by thermally populated vibrational states of the initial T₁ state. Presuming an instantaneous thermalization among the substates of T₁ with M = 0 and ±1, the rate constant of RISC is given by²⁴

1

where the δ-function imposes energy conservation with the T₁ and the S₁ vibrational energies E_ν and E_ν′. The thermal population at temperature T is described by Boltzmann distribution P_ν. The nonadiabatic interaction between the two electronic states is represented by 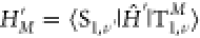originating from the spin–orbit (SO) and the non-Born–Oppenheimer (nBO) couplings, 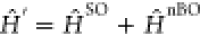. After perturbatively expanding both T₁ and S₁ state vectors with respect to 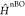within their respective spin manifolds T′ and S′, one can show that the coupling matrix element can be expressed as a sum-over-state expansion:^25,26

2

The first term represents first-order direct spin–orbit (DSO) coupling driven by the electronic characters of S₁ and T₁, while the second and the third terms serve as second-order spin–vibronic (SV) coupling, where intermediary states in the triplet and the singlet manifolds assist the spin–orbit coupling. See also Supporting Information (SI) Text 1 for the derivation details on the coupling matrix elements of the full second-order SV terms.

The rate constant k_RISC can be analytically solved from a correlation function formalism combined with a path-integral expression²⁷⁻³⁰ as briefly summarized in SI Text 1. Because k_RISC involves 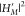, it includes pure DSO and SV contributions from the squares of the corresponding terms in eq 2. We will respectively refer to them as k_DSO and k_SV. Of course, an SV–DSO cross term will also arise, but it vanishes due to time-reversal symmetry.³⁰ The calculated rate constants are listed in Table 1 together with other related photophysical properties obtained by quantum chemical calculations. One can see that our computed k_RISC of 1.05 × 10⁴ s^–1 agrees quite well with the experimental value of 0.99 × 10⁴ s^–1 measured in a thin film condition.⁸ Of course, care must be taken in assessing the degree of agreement as both theory and experiment will surely have limitations when estimating rate constants.

Table 1. Calculated Photophysical Properties of DABNA and its Related Molecules^a.

					SOC (cm–1)e		NAC (bohr–1)f
molecule	kRISCb (104 s–1)	kSV contribution (%)	ΔESTc (eV)	S1d (eV)	S1/T1	S1/T3	T1/T3
DABNA	1.05	99.1	0.144 (0.15g)	3.04 (2.71g)	0.035	0.804	8.56
TBN-TPA	0.94	95.4	0.137 (0.14h)	3.03 (2.64h)	0.040	0.698	9.06
TABNA	0.16	99.9	0.161 (0.21i)	3.36 (3.11i)	0.005	0.439	14.23

^aExperimental values in parentheses are from refs (8), (38), and (39).

^bAverage rate in a small range around ΔE_ST as explained in the text.

^cAdiabatic singlet–triplet energy difference.

^dVertical emission energy calculated at the S₁ geometry.

^eTriplet substate-averaged spin–orbit coupling.

^fNorm of the derivative coupling vector, .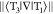

^gMeasured in ethanol,

^hPMMA/1 wt % thin film, or in

ⁱtoluene.

Direct Spin–Orbit Coupling versus Second–Order Spin–Vibronic Coupling

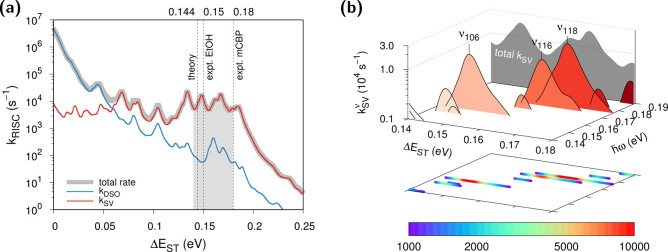
In fact, what is much more important than observing a numerical agreement is analyzing the driving force for the spin crossover. The spin–orbit coupling between the T₁ and the S₁ states of DABNA is merely ∼0.04 cm^–1, which is clearly insufficient to incur any meaningful RISC unless it is matched with an unphysically very small ΔE_ST (<0.05 eV). From Table 1, one can see that k_SV affected by intermediary spin states actually dominates k_RISC. To gain further insights, we parametrically varied ΔE_ST in the golden rule estimation and subsequently recalculated k_RISC. Figure 2a displays the RISC rate constants thus obtained. The single ΔE_ST value as obtained with the adopted SCS-CC2 method is marked with a vertical line, together with experimental ΔE_ST values measured under two different conditions.⁸ Surprisingly, unlike typical organic molecules, the trend of the rate constants deviates substantially from the conventional energy gap law, which would manifest as a linearly decaying line in our log-scaled plot. Based on a deconvolution into k_DSO and k_SV portions also shown in Figure 2a, this unusual kinetic behavior can be attributed mainly to the latter spin–vibronic part.

Figure 2.

Vibronic enhancement of RISC. (a) Total RISC rate as a function of ΔE_ST and its decomposition into DSO and SV contributions. Some notable ΔE_ST values are marked as vertical lines: the computational (SCS-CC2) result at 0.144 eV; the experimentally observed gaps in ethanol solvent and in 3,3′-di(9H-carbazol-9-yl)-1,1′-biphenyl (mCBP) host at 0.15 and 0.18 eV. (b) Deconvolution of the SV component into each normal mode contribution in the ΔE_ST range of 0.14–0.18 eV. Rate contributions greater than 1000 s^–1 are shown. The vertical scale is visually supplemented by the coloring scheme shown at the bottom. The contribution sum is depicted by the gray projection. The vibrational frequencies are represented along the axis denoted with ℏω.

Not only is RISC dynamics completely governed by SV coupling, but k_SV also remains nearly constant within an order of magnitude when ΔE_ST is in 0.14–0.18 eV. This range actually covers all ΔE_ST values predicted by both theory and experiment and was used for calculating average rates reported in Table 1. Beyond this range, k_SV decays in a monotonous manner following the energy gap law. We have further broken down the rate components associated with each vibrational normal mode as 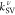(Figure 2b). We immediately see that, in this range, multiple modes can contribute quite significantly to enhancing the RISC rate in a successive and overlapping manner as long as their frequencies match ΔE_ST closely. For instance, if ΔE_ST is 0.148 eV (close to both theoretical and experimental values), the calculated total rate of 1.95 × 10⁴ s^–1 is mainly governed by a single vibrational mode “ν₁₀₆” at 1279 cm^–1. Without the SV contribution, k_RISC would have been as small as k_DSO = 56 s^–1. Similar analyses were also performed for other gaps and are shown in Table S1.

At first sight, as accelerations in exciton transfers by gap-matching vibrations have been continuously reported,³¹⁻³⁴ this RISC enhancement may appear trivial: spin crossover via a resonance between S_1,ν′=0 and T_1,ν=1. In the present case, however, T₁–S₁ SOC is very small, and k_DSO is still small even in the existence of a resonant vibration. Indeed, from Figure 2a, one can see that RISC by only DSO would have been 2 orders of magnitude slower even with the vibronic resonance. RISC becomes sufficiently fast only when the process is mediated by another electronic state, and the mediation is somehow strongly influenced by the vibrational frequency. Thus, we now turn our attention to which intermediary state plays the most important role in enhancing RISC rate in DABNA.

Contributions by Individual Electronic States

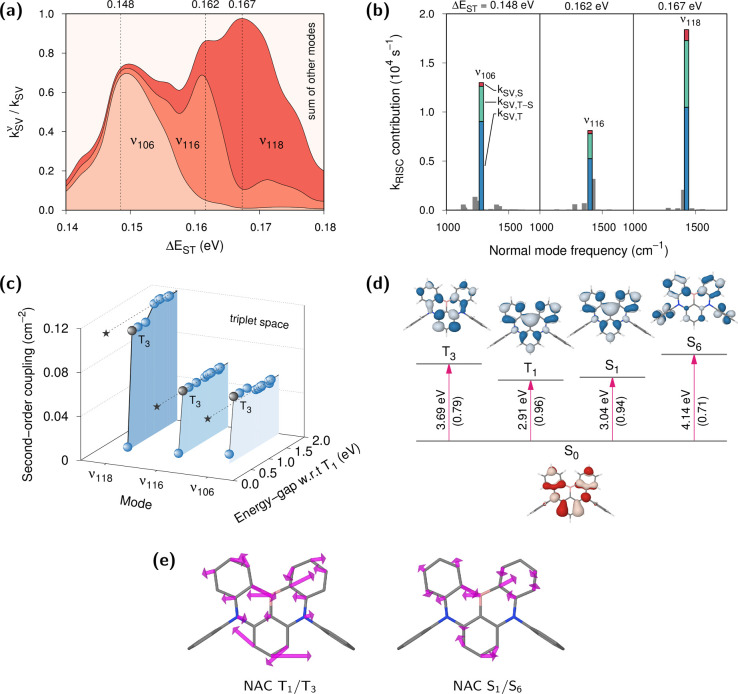
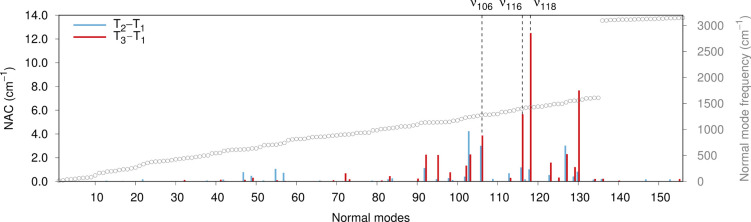
The successive vibronic enhancements by an array of vibrational modes serve to sustain the RISC rate for a plausibly expected range of ΔE_ST in DABNA. When we focus on three normal modes, ν₁₀₆, ν₁₁₆, and ν₁₁₈, which preeminently contribute to the total k_RISC as shown in Figure 3a, SV coupling through the triplet manifold originating from the second term in eq 2 is dominant as denoted by k_SV,T in Figure 3b. On the other hand, the contribution from the singlet manifold, k_SV,S, is the least significant. Interestingly, the singlet manifold contributes more substantially via the cross-product of the second and the third terms, shown with k_SV,T-S in Figure 3b. To identify important upper excited states that vibronically mediate T₁ and S₁, Figures 3c and S1 show the convergence profiles of the sum-over-states expansions in eq 2 again with respect to ν₁₀₆, ν₁₁₆, and ν₁₁₈. In the triplet manifold, which often acts as an important route toward spin–vibronic mixing, the nonadiabatic coupling effect between the T₁–T₃ pair is the most noticeable. For example, the nonadiabatic coupling between these states caused by a displacement corresponding to the normalized ν₁₁₈ mode vector amounts to 12.5 cm^–1 (Figure 4). This is enormously larger than the conventional SOC size in organic molecules. In addition, SOC between S₁ and T₃ is approximately 23 times larger than that between S₁ and T₁ (Table 1). This confirms that it is the T₃ state, which strongly mixes with the T₁ state via the “ΔE_ST-matching” vibrational mode, that enhances k_SV.

Figure 3.

Analysis of k_RISC in DABNA. (a) Contributions by vibrational modes with strong resonance enhancements, namely ν₁₀₆, ν₁₁₆, and ν₁₁₈. The ΔE_ST values at which 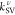become maxima are marked as vertical lines. (b) Contributions by each vibrational mode to k_SV at the vertically marked energies in a. The contribution is further partitioned into spin-manifold components according to eq 4. (c) Convergence profiles of the sum-over-electronic-states expansion for each mode in the triplet manifold. Similar profiles in the singlet manifold are provided in Figure S1. Here, the excited state with a dominant contribution (T₃) can be easily identified as marked with gray spheres. Convergence was reached with 20 excited states as denoted with dashed lines and stars. The T₁ energy was used as the zero energy reference. (d) Natural transition orbital pairs from the ω*B97X calculations at the S₁ geometry. Hole (red) and particle (blue) wave functions are represented by frontier orbitals with the largest weights, shown in parentheses. The S₁ and the T₁ energies are from the SCS-CC2 level calculations. (e) Nonadiabatic T₁–T₃ and S₁–S₆ coupling vectors responsible for RISC.

Figure 4.

Mode–projected nonadiabatic couplings between T₂ and T₁ (blue) and between T₃ and T₁ (red). Projections were carried out onto each mode vector, normalized in the atomic unit (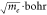). Each mode is supplemented with its vibrational frequency (gray). Modes at 3000 cm^–1 and above are stretches involving terminal hydrogen atoms.

It is noteworthy that the T₂ state, on the other hand, even with a reduced energy gap, has relatively insignificant contribution to the total coupling due to little nonadiabatic component along the same ΔE_ST-matching vibrational mode. This might be surprising when one considers that the T₂–T₁ nBO coupling is slightly larger than the T₃–T₁ coupling at least along a few vibrational modes (Figure 4). At this point however, we emphasize that, from the perturbative expansion in eq 2, the total coupling responsible for RISC is determined by the product of nBO coupling and SOC terms between vibronic states. This combined coupling will undoubtedly be the decisive factor and revealing the important electronic state should be judged based on that combined factor. Given that T₂–S₁ SOC is only ∼1/3 of T₃–S₁ SOC (Figure S2), T₂ will not be able to outcompete T₃ with slight advantages that are only occasionally found in Figure 4. Namely, the combination of nBO coupling and SOC renders T₂ not as important toward promoting resonantly enhanced vibronic RISC. Even the mode ν₁₀₃, along which the T₂–T₁ coupling has the largest component in Figure 4, afforded at best 12.5% of the k_RISC at ΔE_ST = 0.146 eV, where the spin crossover was mostly steered by the T₃–T₁ coupling along the ν₁₀₆ direction (Figure 3a).

To reason why the T₃–T₁ nBO coupling dominates, we may resort to the relationship between the spatial motions of three gap-matching vibrational modes and the nature of the electronic transitions. The atomic motions of the modes are in general along in-plane ring distortions (Figure S3) and will match well with the changes in conjugation patterns. The electronic change characterized by the switch from the T₁ particle wave function to the T₃ one shown in Figure 3d indeed shares a similar character. However, care must be taken with this reasoning. In the case of the T₂–T₁ pair, because the two states share almost the same particle wave functions (Figure S4), the electronic change may be characterized by the switch from the T₁ hole wave function to the T₂ one. In fact, this change is also with a conjugation switch. This aspect also cautions us against overusing the natural transition orbitals in reasoning for three-state-involving transition properties. As the nature of electronic transitions is determined by the involved many-electron wave functions, reasoning by visualizing one electron orbitals may become oversimplifications at times. Though computationally demanding, verifying with numerical data as presented here can form the clearest evidence.

The fact that T₂ contributes little is in line with an earlier report with MCTDH simulations,¹⁵ where no appreciable T₂–T₁ internal conversions were found. In fact, if we had considered only T₁ and T₂ as in that report, we would have observed that the singlet manifold would contribute more than the triplet one by inferring from, for instance, a largish singlet coupling for ν₁₁₈ (Figure S1) that is bigger than the T₂-coupling (Figure 3c). In addition, we believe that the cross-product term k_SV,T-S is particularly enhanced because there is an electronic state that strongly resembles T₃ in the singlet manifold. Namely, the electronic character of S₆ is very similar (Figure 3d), and accordingly, the directionality of the nonadiabatic coupling vectors between the S₁–S₆ and the T₁–T₃ pairs will also be similar (Figure 3e). As a result, the second-order spin–vibronic transition paths between the T₁ and the S₁ states that involve the two intermediary states will likely cooperate.

Resonance Enhancement that Involves Three States

Now that we identified T₃ as the most important intermediary state for DABNA, we can infer that there is a strong and peculiar resonance enhancement in k_SV from a vibration (1) because it oscillates at a frequency that matches ΔE_ST and (2) because it induces strong T₁–T₃ coupling. This vibronic resonance is peculiar and is different from earlier observations³¹⁻³⁴ in that it involves more than two electronic states. We also stress that this superexchange process involving T₃ should be distinguished from a stepwise conversion including the “reverse internal conversion” (RIC) from T₁ to T₃. The calculated gap between the two electronic states is much larger than the thermal energy with 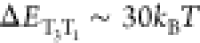(Table S2), and as a result the equilibrium constant between T₁ and T₃ will be diminutive. Furthermore, S₁ and T₃ are not isoenergetic with 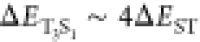, which will also significantly prohibit the spin conversion between these states. Should the RISC process take place via the spin crossover as T₃ → S₁ after a pre-equilibrium involving RIC as T₁ ⇌ T₃, the overall rate will be too slow. One may also wonder about the role of T₃ hot excitons that can form transiently during electroluminescence. For DABNA, a direct hot exciton transfer from T₃ to S₁ is appraised as an unlikely event, because with the strong vibronic coupling between the two triplets, the T₃ → T₁ transition will prevail and lead to an almost complete and instant population transfer to the lowest triplet.

To further substantiate the peculiar resonance, we have also employed a semiclassical quantum dynamics simulation approach, Poisson bracket mapping equation (PBME-nH).^35,36 Based on the observations described in the above, we have chosen {S₁, T₁, T₃} as our electronic state space. These states and one underdamped vibration corresponding to ν₁₀₆ form our minimal model for exhibiting the resonance. The underdamped mode actually vibronically couples T₁ and T₃, and the coupling strength changes in proportion to the normal mode displacement (see Computational Methods). To further probe the resonant behavior by ν₁₀₆, we scanned its frequency around its physical value. Figure 5 displays how k_RISC changes as a function of this frequency and we can indeed directly observe a resonant behavior again near the physical frequency, 1279 cm^–1 (= 0.159 eV). As is shown in the same figure, when we fortuitously set the T₁–T₃ coupling as constant in time with the ν₁₀₆ mode still preserved in the system, the S₁ population did not grow any faster than what was allowed by the small SOC between T₁ and S₁, even when the constant T₁–T₃ coupling was rather strong and the ν₁₀₆ frequency matched ΔE_ST. Thus, the fluctuating nature of the T₁–T₃ coupling is the key to the RISC enhancement, which is maximized when the fluctuating frequency is in a near-resonant condition with ΔE_ST.

Figure 5.

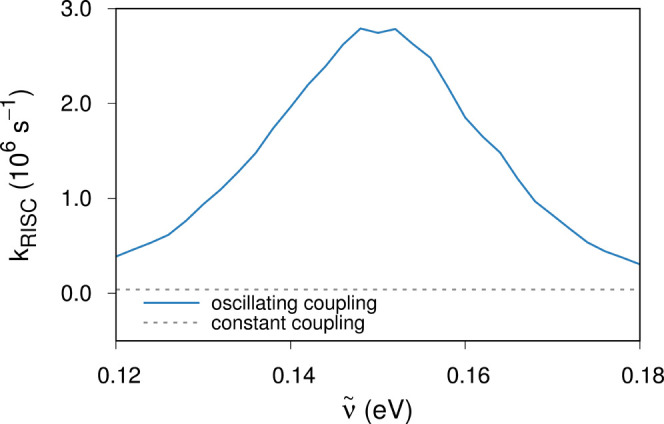
Resonance enhancement of RISC by a coupled vibration. The blue line denotes the rate estimated with PBME-nH quantum dynamics simulations with an underdamped emitter vibration with a frequency 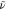that induces T₁–T₃ coupling in a non-Condon manner. The gray line shows the rate with a strong constant coupling but without this non-Condon effect, 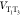= 500 cm^–1.

It is intriguing to observe that the vibrational resonance involves three electronic states, with the frequency matching both the energy gap for the T₁–S₁ pair and the coupling oscillation for the T₁–T₃ pair. Thus, RISC enhancement through SV coupling bears a strong superexchange character.³⁷ When this peculiar resonance condition is met, the RISC process can take place even when ΔE_ST is rather substantial as was already noted with Figure 2a. This interesting behavior can be explained in the following manner. The oscillating non-Condon T₁–T₃ coupling (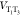) forces the electronic characters of a triplet state to alternate in time. Namely, a state initially at T₁ will become a superposition of T₁ and T₃, whose composition will vary with the vibrational motion. Because the T₃–S₁ SOC is relatively large (Table 1), the new superposition state can transfer the population to S₁ with a much larger probability than the pure T₁. In addition, because 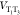oscillates in time, the T₃ composition will keep fluctuating and sustain the transfer until all triplet population is consumed. Surprisingly, if 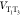is constant in time, i.e., Condon coupling, the electronic character of the triplet state quickly settles to a steady state, from which the RISC process is not as effective. In fact, the constant coupling adopted with Figure 5 was twice larger than the root-mean-squared average of the oscillating coupling. The fact that the two RISC kinetics shown in the figure are drastically different evidently exhibits the importance of the oscillating nature of the vibronic coupling, with the matching resonance condition with ΔE_ST. Perhaps, the resonantly fluctuating coupling is taking a role of replenishing the fragile coherence³¹ between T₁ and T₃. We note that the time scale of state transitions in OLED materials is often much longer than that of light harvesting systems, and it is striking that there can still be a process with commonly shared characters³¹ between the two different groups.

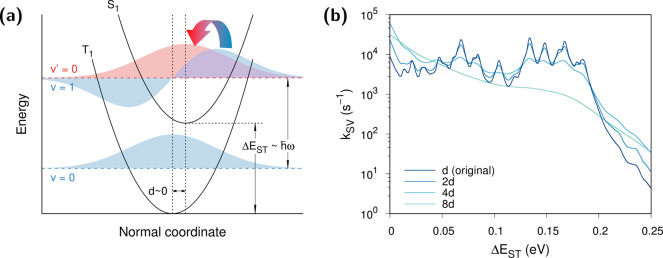
The physical foundation of the spin–vibronically enhanced RISC at substantial ΔE_ST can be additionally explained with Figure 6a, where molecular factors affecting k_SV are schematically displayed. Because both the S₁ and the T₁ states share the identical local excitation character, the potential energy surfaces are quite similar in shape to each other. In addition, structural rigidity stemming from extensive conjugation in combination with planarity resembling nanographene restricts the T₁–S₁ geometric distortion as 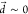(Figure S5). These aspects combine to produce only slightly shifted vibrational frequencies and a diagonal-dominant Duschinsky matrix from T₁ to S₁ (Figure S6), resulting in no normal mode mixing upon state switching. RISC dynamics can therefore be reduced to independent mode-by-mode dynamics (Figure 6a). When ΔE_ST ≠ 0, the δ-function in eq 1 and hence k_RISC will reach a maximum as ΔE_ST approaches the vibrational gap ℏω. In addition, as discussed above, the spin crossover process is undertaken through the state mixing with T₃ especially when 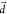is along the T₁–T₃ coupling direction. Therefore, for an optimal k_RISC, 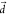along ν₁₀₆ must remain small to maximize the Franck–Condon factor and the derivative integral between the v = 0 and the v′ = 1 vibrational wave functions (SI Text 1). The effect of the displacement can be easily verified numerically by increasing the quantum chemically obtained 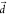into fortuitously larger 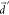. Indeed, the vibronic enhancement in k_SV almost disappears at large 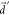in the golden rule rate estimation (Figure 6b), and a similar behavior is also observed from PBME-nH simulations (Figure S7). We also note that at larger ΔE_ST, increasing 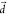will lead to a slower decay of k_DSO (Figure S8). The temperature effect was also investigated (Figure S9), affirming that k_SV becomes more prominent at higher temperature because the transition originates from a thermal population at v = 1.

Figure 6.

Mechanism of vibrational enhancement of RISC. (a) Schematic representation of the vibronic spin-flip transition. The vibrational wave functions are illustrated with filled curves (T₁, blue; S₁, red). (b) Displacement dependence of the second-order (spin–vibronic) RISC rates at varying ΔE_ST as measured by fortuitously increasing the original displacement vector 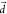by some integers, 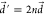. See SI Text 1 for the mathematical formulation of .

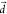Behaviors of DABNA Variants

We further applied the same golden-rule rate analysis to a few more emitting molecules related to DABNA (Table 1 and Figure S5). First, TBN-TPA with a carbazole group in a para-position to boron and six additional tert-butyl groups on peripheral phenyl rings was investigated. As shown in the table, the added carbazole moiety only slightly reduces ΔE_ST by ∼0.01 eV. At this energy gap, predominance of the SV contribution was retained (Figure S10a). If we assume that we can tune the energy gap by changing the doping conditions, our calculations indicate that it will be possible to obtain a maximum k_RISC at 1.07 × 10⁴ s^–1 appearing at ΔE_ST ≃ 0.15 eV. The average rate over a small range (±0.1 eV) of ΔE_ST is estimated as 0.94 × 10⁴ s^–1. This is comparable to DABNA, allowing us to speculate that the reported higher PLQY (98%) from an earlier experiment³⁸ is due to the bulky tert-butyl groups that physically hinder external quenching factors. TABNA with an added phenylamino group onto the DABNA core was also considered, even though its emission is excessively blue-shifted with λ_max = 399 nm.³⁹ In this case, while k_SV still governed the RISC dynamics because T₁–S₁ SOC was almost negligible, the absolute value of k_SV was smaller by an order of magnitude, resulting in no vibrational resonance peaks (Figure S10b). This is mainly due to a much larger geometric difference between T₁ and S₁ states, corresponding to a reorganization energy of λ = 434 cm^–1 by the emitter itself. This reaffirms that a small geometric change is needed to observe vibrational enhancement of k_SV (Figure 6).

Finally, we note that the energy gap between the vibronically coupled triplet pair (the T₁–T₃ gap for DABNA) will also be important for efficient and practical RISC. This is easily discernible both with the golden rule and PBME formalisms. When the gap is too large, the contribution of T₃ in the perturbation expansion for T₁ diminishes. Likewise, T₁–T₃ mixing in PBME weakens under the same condition and the effect of superexchange becomes unimportant. Therefore, reducing this gap should also be a tactic of consideration if one attempts to optimize k_RISC through k_SV. Of course, achieving this without disturbing electronic structure properties, such as the MR effect, will be important, as breaking it can return the emitter properties to conventional DA-type behaviors.⁴⁰ Indeed, we have already seen that TABNA does not exhibit a resonantly enhanced RISC rate even with the reduced T₁–T₃ gap (Table S3) and subsequently increased nonadiabatic coupling (Table 1). This is because the electronic structure consistency between S₁ and T₁ is broken with the added modification from DABNA.

Donor–Acceptor Type versus Multiple–Resonance Type Emitters

Due to conflicting preferences for the exchange energy K,⁴¹ DA-emitters tend to have different natures in their lowest excited states: charge-transfer (CT) S₁ vs locally excited (LE) T₁ states.^42,43 This entails relatively large geometric differences (Table S4) and, subsequently, large reorganization energies during ISC between them. While a small displacement can be expected for DA type emitters when both the S₁ and the T₁ states correspond to the same CT character, the displacement will likely be still larger than in DABNA. This is because there should be another LE triplet state whose energy is close to the T₁ energy to facilitate the RISC process. With the neighboring LE state, due to inevitable electronic mixing, T₁ will still have a non-negligible amount of LE character, which will subsequently induce a noticeable size of displacement from the S₁ geometry. As we observed in Figure 6b, the vibrational rate enhancement in k_SV disappears when 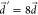. The reorganization energy of 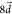amounts to 2128 cm^–1 (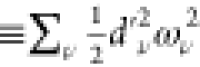), which is close to the reorganization energies of DA-TADF emitters. Thus, it explains why a drastic vibrational enhancement in k_SV was not observed in more flexible DA-TADF emitters in an earlier study.³⁰ In addition, El-Sayed-allowed DSO between a charge transfer S₁ state and a locally excited T₁ state provides the primary pathway to RISC, with reducing ΔE_ST working as the widely accepted design principle.^4,42,43 Hence, for DA-TADF emitters, the DSO portion will play a major role with a minor enhancement from SV coupling.³⁰ We should, however, note that by exploiting the disparate responses of CT and LE states to the surrounding polarity, the ¹CT–³CT pair can be (quasi-)degenerate or be even more stable than the ³LE state in a polar medium. In such cases, the SV coupling can be elevated for DA-TADF emitters at the expense of a redshift in the emission wavelength.¹³

Owing to the similarity between the electronic structures of T₁ and S₁, ΔE_ST of DABNA, albeit being reduced by electron correlations, remains relatively large. In addition, the DSO coupling between T₁ and S₁ is suppressed by the El-Sayed rule.⁴⁴ However, such an electronic structure similarity gives rise to a small geometric displacement in the spin crossover. If there is a vibrational mode that energetically matches ΔE_ST and effectively induces the coupling between the lowest excited state and higher-lying intermediary state, then such a SV coupling can speed up the RISC process dramatically. It is evident that, from the existence of multiple modes with such properties, the vibronic enhancement can be contiguous over extended ΔE_ST values. These aspects will defy the energy gap law that essentially governs the RISC processes in DA-TADF molecules.

With the above comparisons, it will be interesting to further consider how the present case differs from the recently discussed spin–vibronic mechanism with a third mediating state in a DA-TADF system DPTZ-DPTO2.^13,14 As a matter of fact, the spin–vibronic mechanism of state switching involving two different spin multiplicities has been known for quite some time (for instance, ref (25)), and there can be many different possibilities through which the mechanism can manifest itself. In the case of DPTZ-DPTO2, the energy resonance condition between the involved electronic states was discussed to be crucial, and the “Type II” case with ¹CT, ³CT, and ³LE states gathered together at near-degeneracy was suggested as an ideal system for TADF. When that condition is met, because the spin–orbit coupling is much larger for the ³LE–¹CT pair than for ³CT–¹CT, and because ³LE is thermally quite accessible, RISC via ³LE–¹CT will play a dominant role either through a direct transfer or through mediation involving ³CT. In this case, a vibration plays only a nonadiabatic coupling role for the ³LE–³CT pair but not for the energy resonance. Our results with the MR-TADF system, whose S₁/T₁/T₃ states play the somewhat analogous roles of ¹CT/³CT/³LE of the DA-TADF system, show different behaviors in a few crucial ways.

• 1.The T₁ energy is noticeably lower than the S₁ energy in MR-TADF. Thus, a vibration should be combined to satisfy the energy resonance condition to facilitate the T₁–S₁ conversion. Indeed, we have verified the associated RISC rate enhancement as shown in Figures 2 and 5. Again, the vibrational frequency resonance is a key to MR-TADF but not for DA-TADF. Also, there are multiple vibrations that can resonantly enhance the state switching rate.
• 2.The mediating T₃ state in DABNA is quite high in energy and is thermally inaccessible for hopping or reverse internal conversion. On the other hand, in DA-TADF systems, the mediating ³LE state tends to lie below the ³CT level especially when ΔE_ST is large and a significant spin–vibronic effect is expected. This difference induces many different aspects: for example, the extraordinarily large non-Condon effect, which appears important for the RISC rate enhancement with DABNA.
• 3.The geometric distortion associated with the T₁ → S₁ switch is quite small with DABNA, whereas the equivalent distortion with a DA-TADF molecule tends to be large when T₁ is ³LE, with different characters from ¹CT as S₁ (Table S4). Indeed, we found that a large distortion will simply erase the resonant vibronic RISC enhancement (Figure 6b), and the vibrational rate enhancement as in DABNA will not be observed in DA-TADF systems.

This leads us to an important alternative of designing effective MR-TADF emitters: the optimal SV coupling through vibronic resonance. For certain molecules like DABNA, lowering ΔE_ST can often be challenging. Sometimes, peripheral substitutions for improving other functionalities such as intermolecular interactions and charge transport behaviors should often be conducted even at the cost of increasing ΔE_ST. In such cases, it will be ideal if the increase in ΔE_ST can be compensated by the vibrational resonance effect. One may be concerned that the resonance would be too fragile as the gap energy can be easily changed by the emitter environment and matching the frequency might be too restrictive. We believe this will not be too serious as there may be multiple vibrations that can play the enhancing role. With DABNA, indeed, three modes with enough overlaps with the T₁–T₃ derivative coupling (Figure S3) can take their turns when ΔE_ST was varied (Figure 2). In addition, the resonance peaks are actually quite broad (Figures 2 and 5), and strictly matching the frequency is not a necessity.³⁴

Conclusion

We have applied a spin–vibronic model and a semiclassical quantum dynamics simulation tool to elucidate the RISC dynamics of MR-TADF organoboron emitters with superior color purity. We found that it is highly driven by a spin–vibronic effect, which emerges as a second-order process with the golden rule description and as a superexchange event from the semiclassical treatment. More importantly, we observed a peculiar three-state involving resonance with which the RISC rate is enhanced significantly when the frequency of a vibration that induces a non-Born–Oppenheimer coupling between the T₁–T₃ pair matches the gap energy between the T₁–S₁ pair. We also showed that multiple vibrational modes exist so that they can resonantly enhance exciton transfers over a wide enough range of ΔE_ST.

The fact that the spin–vibronic effect plays a major role in the considered MR-TADF emitters is in stark contrast to the aspect observed with more conventional DA-TADF emitters, where the dynamics could be explained largely by the first-order direct spin–orbit coupling.³⁰ Perhaps, the widely accepted design principle for achieving superior TADF emitters by minimizing ΔE_ST may not be the only path to consider at least for the emitters with rigid core structures, and maximizing the spin–vibronic coupling through vibronic resonance can be additionally sought for. Nonetheless, predicting in an a priori fashion whether a vibration will participate to resonantly enhance RISC will not be a simple task as it requires comprehensively computing the emitter properties with the rather complicated network of excited states, as attempted in our present work. Even still, we conclude that treating spin–vibronic coupling is of utmost importance and should be included in a regular basis, as well-defined design principles based on second-order effects will surely benefit the development of efficient emitters. As is often the case with any excited state tuning, predicting the relationships between multiple modification aspects will be a complicated undertaking, but a viable solution can still be reached by adopting advanced tools as screening measures. We hope that our approaches described here can serve such a purpose in future molecular designs.

Computational Methods

Electronic Structure Calculations

Electronic structure calculations were performed with the TURBOMOLE 7.3⁴⁵ and Q-Chem 5.1⁴⁶ program packages. With the original spin-component scaling parameters,⁴⁷ the excited state geometries were optimized by the strict variant of the second-order algebraic diagrammatic construction (SCS-ADC(2)) method.⁴⁸ This was followed by the approximate coupled-cluster singles and doubles (SCS-CC2) method⁴⁹ for the energy evaluations. The resolution-of-the-identity approximation for the electron repulsion integrals were used in treating correlations. For normal mode calculations, numerical Hessians were employed with a frequency scaling factor of 0.9631.⁵⁰ The optimized geometries and the corresponding vibrational frequencies are provided in Tables S5 and S6. Because the nonadiabatic and spin–orbit couplings were not available at the ADC(2) or CC2 level, single-point time-dependent DFT calculations under the Tamm–Dancoff approximation was adopted instead, with the gap-tuned long-range corrected ω*B97X functional.⁵¹ Because the nuclear screening two-electron term is often small and is less important in the context of spin–vibronic model with the more contributing vibronic coupling, we have employed the one-electron Breit–Pauli spin–orbit Hamiltonian.⁵² Solvent effects were treated with the polarizable continuum model in the integral equation formalism (IEF-PCM).⁵³ The amorphous molecular solid film condition was imitated by the parameters of ϵ = 2.84 and n = 1.7, derived from an archetypal blue host material 1,3-bis(N-carbazolyl)benzene (mCP). Natural transition orbital (NTO) analyses were postprocessed by TheoDORE 2.0 package.⁵⁴ The def2-SVP basis set was used for all calculations. A number of progressively larger basis sets were tested in order to evaluate the basis set effect on ΔE_ST and only slight shifts were observed. See SI Text 2 for other details.

Golden Rule Rates

Fermi’s golden rule rate calculations with the time-correlation function formalism³⁰ were carried out through the discrete Fourier transform with the FFTW 3.3.6 library.⁵⁵ The time integration was performed in the domain of [−6553.6:6553.6] fs and the time correlation functions were discretized in steps of 12.5 ps, which corresponded to 2¹⁹ points in the positive time direction. Of course, the rate expression is obtained with the square modulus of eq 2. Because the rate in eq 1 includes infinity from the δ-function, damping is often introduced to avoid divergence in k_RISC.^56,57 Physically, the damping time scale is related to the dephasing time of the involved excited state and is often difficult to deduce, which leads to a certain degree of ambiguity in the calculated rate. In our case with DABNA, there was no ambiguity because the rate change was quite insignificant for any damping time chosen in a wide range of 1 ps ≤ γ ≤ 100 ns. See SI Text 3 for more details.

Because the cross-product of the DSO and the SV terms vanishes due to the time-reversal symmetry,³⁰ the total RISC rate can be neatly partitioned into individual components:

3

Because there are two SV terms in eq 2, the spin cross-product from the second and the third terms in that equation does not vanish and contributes to k_SV. Still, we can separately compare and contrast the contributions by the spin manifolds to gain insights into the details of the process:

4

as displayed in Figure 3b. This decomposition is feasible because, in the nonrelativistic regime, the singlet and the triplet excited states are computed independently from each other.

PBME-nH Simulations

The electronic subsystem Hamiltonian was defined by the two gap energies (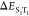 = ΔE_ST and 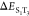) and two SOC elements ( 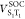and 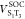). One harmonic underdamped mode (ν₁₀₆) was set to induce the nonadiabatic coupling between T₁ and T₃. Parameters for forming this Hamiltonian elements were taken from the quantum chemical data as listed in Tables 1, S3, S6, and S7. As the nonadiabatic coupling is dictated by the derivative coupling ⟨T₁|∇|T₃⟩ and fluctuates with geometric distortions by the ν₁₀₆ normal mode motion, it is intrinsically non-Condon. The diagonal energy coupling by the normal vibrations of the emitter were included by considering the mode-specific reorganization energies as specified in Table S8. A thermal bath representing the emitter environment was also added as a Debye spectral density with a reorganization energy λ_ph = 20 cm^–1. Starting with 100% population at T₁ initially, multiple trajectory simulations were performed for 1 ps durations and k_RISC was obtained by monitoring the S₁ population growth in an extrapolating manner. More details about the quantum dynamics simulations can be found in SI Text 4.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00179.

• Details about the adopted computational methods and the proof of the finiteness of k_RISC; Tables with normal mode specific analyses, quantum chemical data, S₁–T₁ geometric differences of MR and DA type emitters, and k_RISC dependence on the damping time parameter; Figures analyzing various nonadiabatic coupling, spin–crossover rates, and the related data based on normal modes and natural transition orbitals (PDF)

The authors declare no competing financial interest.