Skip to main content
PMC home page
JACS Au logoLink to JACS Au
. 2021 May 26;1(7):945–954. doi: 10.1021/jacsau.1c00132

Key of Suppressed Triplet Nonradiative Transition-Dependent Chemical Backbone for Spatial Self-Tunable Afterglow

Indranil Bhattacharjee 1, Kikuya Hayashi 1, Shuzo Hirata 1,*
PMCID: PMC8395709  PMID: 34467341

Abstract

graphic file with name au1c00132_0007.jpg

Highly efficient persistent (lifetime > 0.1 s) room-temperature phosphorescence (pRTP) chromophores are important for futuristic high-resolution afterglow imaging for state-of-the-art security, analytical, and bioimaging applications. Suppression of the radiationless transition from the lowest triplet excited state (T1) of the chromophores is a critical factor to access the high RTP yield and RTP lifetime for desirable pRTP. Logical explanations for factor suppression based on chemical structures have not been reported. Here we clarify a strategy to reduce the radiationless transition from T1 based on chemical backbones and yield a simultaneous high RTP yield and high RTP lifetime. Yellow phosphorescence chromophores that contain a coronene backbone were synthesized and compared with yellow phosphorescent naphthalene. One of the designed coronene derivatives reached a RTP yield of 35%, which is the best value for chromophores with a RTP lifetime of 2 s. The optically measured rate constant of a radiationless transition from T1 was correlated precisely with a multiplication of vibrational spin–orbit coupling (SOC) at a T1 geometry and with the Franck–Condon chromophore factor. The agreement between the experimental and theoretical results confirmed that the extended two-dimensional fused structure in the coronene backbone contributes to a decrease in vibrational SOC and Franck–Condon factor between T1 and the ground state to decrease the radiationless transition. A resolution-tunable afterglow that depends on excitation intensity for anticounterfeit technology was demonstrated, and the resultant chromophores with a high RTP yield and high RTP lifetime were ideal for largely changing the resolution using weak excitation light.

Keywords: persistent room temperature phosphorescence, vibrational spin−orbit-coupling, Frank−Condon factor, high-order excited state, emission microscopy

Introduction

Research interest in the field of room-temperature phosphorescence (RTP) has increased significantly in the past decade because of the versatile application of RTP in the fields of lighting,1−3 display technology,4−7 and bioimaging.8,9 RTP materials with a phosphorescence lifetime at room temperature (RT) of more than 100 ms are termed persistent RTP (pRTP). pRTP materials can detect emissions after excitation ceases by using small-scale and low-cost photodetectors with a slow response time and that are independent of fluorescence from impurities.10−13 These characteristics allow for high-contrast contactless imaging for state-of-the-art security14−16 and bioimaging applications.8,17,18 From a materials perspective, such advantages can be achieved by using cost-effective long-persistent emitting particles that have been commercialized for a long time.19−22 A futuristic application for pRTP materials is that long-persistent luminescence emitters have not achieved high-resolution afterglow imaging because they are more suitable for achieving an afterglow brightness.12 To obtain a desirable pRTP, the enhancement of phosphorescence yield at RT [Φp(RT)] and the phosphorescence lifetime at RT [τp(RT)] are critical for the materials.

Φp(RT) and τp(RT) are controlled mainly by several physical parameters: the yield of an intersystem crossing (ISC) from the lowest singlet excited state (S1) to triplet states at RT [Φisc(RT)], the radiative rate constant of phosphorescence (kp), the rate constant of intramolecular vibration-based nonradiative transition from the lowest triplet excited state (T1) to the ground state (S0) at RT [knr(RT)], and the quenching rate of T1 that is triggered by intermolecular processes at RT [kq(RT)]. kp acceleration with a minimization of knr(RT) and kq(RT) is critical to achieve a higher Φp(RT). Strong triplet confinement is required to minimize kq(RT).11,23 Long conjugated substituents that are related to the high-order singlet state (Sn) enhance kp,12 and rigid amorphous host materials with a higher T1 energy level can be used to suppress kq(RT).11 For knr(RT), a decrease by using the isotope effect has been reported.11 However, no clear strategy exists to reduce knr(RT) as a function of chemical structure beyond the isotope effect.

We provide an effective design strategy for heavy-atom free chromophores with an efficient pRTP emission by decreasing knr(RT) based on a conjugated backbone. Yellow phosphorescent polycyclic aromatic carbons (PACs) that were substituted with a secondary amino long conjugation were synthesized. One of the synthesized chromophores had a Φp(RT) of 35% with a τp(RT) = 2.2 s when deuterated and used in an appropriate host. A two-dimensional fused extension of the PACs with long conjugated substituents accelerated kp and suppressed knr(RT), which led to a simultaneous large Φp(RT) and large τp(RT). The optically measured knr(RT) correlated well with the multiplication of vibrational spin–orbit coupling (SOC) at RT and the Franck–Condon factor between T1 and S0. Analyses of the correlation clarified that the two-dimensional fused extension of PACs decreases the vibrational SOC at RT and the Franck–Condon factor that suppresses the knr(RT) for an efficient and extended RTP. Self-spatial modulation of the high-resolution afterglow depends on the excitation intensity, which allows for advanced state-of-the-art anticounterfeiting, and was demonstrated by using the chromophore. Chromophores with a large Φp(RT) and large τp(RT) were found to be suitable for largely changing the resolution using weak excitation.

Results and Discussion

Design Strategy and Molecular Structures

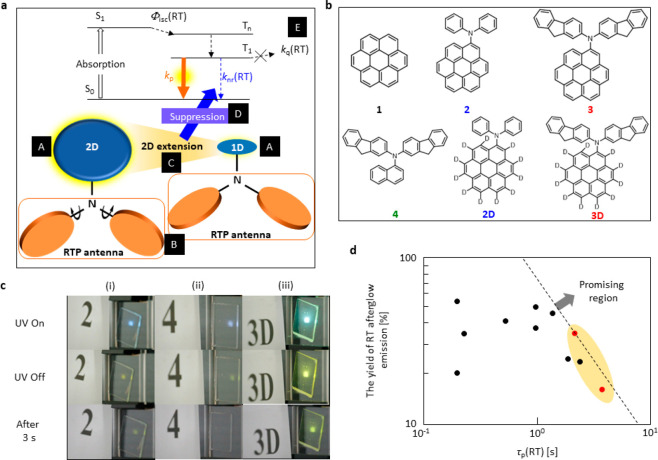
An effective chromophore design is one of the most important prerequisites to extract the maximum efficiency from the chromophores. Our designed strategy was based on two main elements: PAC determines the pRTP emission color, which is termed the RTP center (A in Figure 1a), and the twisted long π-conjugated secondary amine substituent is termed the RTP antenna (B in Figure 1a). The effect of the RTP antenna to enhance Φisc(RT) and kp has been discussed in our previous report.12,24 In this work, we show that a two-dimensional delocalization of the RTP center (C in Figure 1a), substituted with the RTP antenna, decreased knr(RT) (D in Figure 1a) for a simultaneous large Φp(RT) and τp(RT).

Figure 1.

Figure 1

Open in a new tab

Molecular design, chemical structure and efficient pRTP. (a) Molecular design of the dopant chromophores for large Φp(RT) and τp(RT). (b) Chemical structures of the chromophores used in this study. (c) Photographs of 2 (i), 4 (ii), and 3D (iii) under (top), soon after ceasing (middle), and 3 s after ceasing (bottom) the UV excitation at 360 nm (3.94 mW cm–2) when the white room light intensity was 0.05 mW cm–2. (d) Relationship between Φp(RT) and τp(RT) of the reported chromophores and chromophores studied in this report. Red dots in the shaded area indicate the chromophores in this report, and black dots are the reported chromophores.

We used coronene as the RTP center and substituted a secondary amine to determine the effect of this substitution. In Figure 1b, 1–3 were used to establish the role of substitution on the RTP center and the effect of the extended conjugation length of the RTP antenna. 4 (Figure 1b) was used to monitor the effect of the RTP center, which changed to naphthalene to keep the RTP antenna the same as 3, on the photophysical parameters between 3 and 4. The chromophores were prepared by the method in the Supporting Information (see section S1 and Figures S1–S6).

Optical Properties

We used 2, 4, and 3D as dopant chromophores to demonstrate the pRTP efficiency in bright room light. The emission intensities in bright room light (power density 0.05 mW cm–2) are shown in Figure 1c. β-Estradiol was used as a host for all chromophores (0.3 wt %) to suppress kq(RT), as the host has a higher T1 energy level and intrinsic rigid nature (E in Figure 1a).11,12,24 The doped materials were sandwiched in the amorphous state between two glass substrates, and the film absorbance at 360 nm was 0.40. When the films were excited using ultraviolet (UV) light at 360 nm (power density 3.94 mW cm–2), chromophores 2 and 4 showed similar emission intensities during the UV excitation, whereas 3D showed a brighter emission compared with that of the earlier two (top photos of (i)–(iii) in Figure 1c). Immediately after ceasing the UV excitation, a yellow pRTP emission was detected for 2 and 4 (middle photos of (i) and (ii) in Figure 1c), but a bright-yellow pRTP emission from 3D was detected easily by the naked eye (middle photo of (iii) in Figure 1c) under bright-white room light. The existence of a yellow pRTP emission of 2 and 4 disappeared rapidly within a few seconds because of the low brightness and longevity of the pRTP emission (bottom photos of (i) and (ii) in Figure 1c), and for 3D the yellow pRTP emission remained (bottom photo of (iii) in Figure 1c and Movies S1–S3). Because the sample absorbance was the same at 360 nm (Figure S7), the difference in pRTP brightness and endurance occurred only because of the large difference in Φp(RT) and τp(RT). In Figure 1d, to the best of our knowledge, we have shown that the reported chromophores had a Φp(RT) ≥ 20% with τp(RT) ≥ 0.1 s.12,25−30 This example fulfills the given criteria, even though a combination of Φp(RT) ≥ 20% with τp(RT) ≥ 1.0 s shortens the window. In this work, we have shown that the chromophores have a τp(RT) greater than 2 s with a Φp(RT) of 35%, which is at the highest level for Φp(RT) and τp(RT). A Φp(RT) of 35% is the highest for materials with τp(RT) ≥ 2 s.

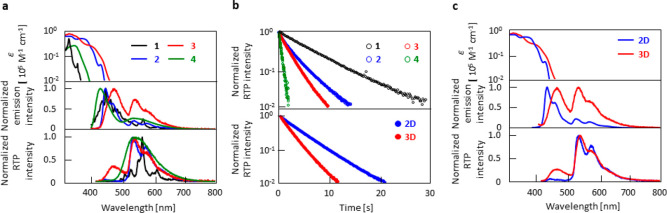
Chromophores 1–4 (0.3 wt %) in the amorphous β-estradiol show a large, structured absorption band below 400 nm, which can be assigned to a π–π* transition. A broad absorption band was visible at ∼380–440 nm for 2–4 because of charge transfer (CT) from the RTP antenna to the RTP center (top graph of Figure 2a). Chromophores 1–4 showed emission spectra from 410 to 750 nm under UV-light excitation (middle graph of Figure 2a). The origin of the emission peak from 410 to 500 nm resulted because of the fluorescence, as the lifetime of these emissions was in the nanosecond range (Figure S8). The fluorescence quantum yields at RT (Φf(RT)), fluorescence lifetimes (τf(RT)), rate constant of fluorescence (kf), quantum yield of the intersystem crossing from S1 to the triplet states at RT (Φisc(RT)), and the rate constant of intersystem crossing from S1 to the triplet states at RT (kisc(RT)) of the 0.3 wt % doped 1–4 in β-estradiol are summarized in Table 1 (Figures S9–S11 and Table S1). For 1, the small kf can be explained by a symmetric forbidden transition (Figure S12).31 For 2–4, the enhancement of kf was observed because the allowed CT transition nature appears with fluorescence by an introduction of the RTP antenna (Figure S12). Introduction of the RTP antenna enhanced kf and increased kisc(RT), as also observed in the calculations (see section S3 and Figures S13–S16). A comparison of the extent of enhancement between kf and kisc(RT) shows that the increase in kisc(RT) dominates and results in a large Φisc(RT) for 2–4 (Table 1).

Figure 2.

Figure 2

Open in a new tab

Optical properties. (a) Absorption spectra (top graph), emission spectra under excitation (middle graph), and emission spectra soon after ceasing excitation (bottom graph) of 0.3 wt % 1–4 doped in amorphous β-estradiol. (b) RTP decay characteristics of 0.3 wt % 1–4 doped in amorphous β-estradiol (top graph) and 0.3 wt % 2D and 3D doped in amorphous β-estradiol (bottom graph). (c) Absorption spectra (top graph), emission spectra under excitation (middle graph), and emission spectra soon after ceasing excitation (bottom graph) of 0.3 wt % 2D and 3D doped in amorphous β-estradiol.

Table 1. Photophysical Parameters of 1–4, 2D, and 3D Related to Fluorescence and ISC from S1.

chromophore Φf(RT) [%]a τf(RT) [10–9 s]a kf [107 s–1]b λf [nm]c Φisc(RT) [%]d kisc(RT) [107 s–1]g
1 25 238 0.1 445 (42 ± 11f)e 0.2
2 24 17.3 1.4 445 76 (88 ± 22)e 4.4
3 20 7.03 2.8 472 80 (84 ± 21)e 11
4 22 2.78 8.1 425 78 (89 ± 22f)e 28
2D 26 18.3 1.4 445 74 (82 ± 21)e 4.1
3D 19 7.14 2.7 472 81(86 ± 22)e 11
Open in a new tab
a

Values using 0.3 wt % chromophore doped in β-estradiol.

b

Calculated kf = Φf(RT)/τf(RT).

c

Peak wavelength of fluorescence.

d

Φisc(RT) = 1 – Φf(RT), and parentheses indicate values measured using transient absorption method in ref (32).

e

The data of Φisc(RT) by transient absorption generally has errors of ±25% of the values as reported in ref (33).

f

Values reported in Table 1 in ref (24).

g

kisc(RT) = Φisc(RT)/τf(RT).

After ceasing the excitation, chromophores 1–4 show emission spectra from ∼500 to 750 nm for a few seconds (bottom graph of Figure 2a). The decay characteristics approach a single-exponential decay of this persistent emission (top graph of Figure 2b), which indicates that this emission results because of the pRTP characteristics of the chromophores. The τp(RT) of 0.3 wt % doped 1–4 in β-estradiol was 6.0, 3.1, 1.8, and 0.45 s, respectively (top graph of Figure 2b, Table 2). Φp(RT) of 0.3 wt % doped 1–4 in β-estradiol was separated by using time-dependent emission spectral analysis (see section S4 and Figure S17) and quantified as 3.4%, 11%, 19%, and 10%, respectively (Table 2). Comparable excitation spectra of pRTP with absorption spectra indicate that the observed pRTP was not caused by impurities (Figure S18). In 3, the afterglow RT emission yield was 23%, which included the contribution of afterglow thermally activated delayed fluorescence (TADF) (Table 2). The afterglow RT emission yield above 20% is the top level of molecular solids with an afterglow lifetime of approximately 2 s.25,29,34 Because the large Φp(RT) and τp(RT) are based on a chemical backbone of 3, clarification of more logical points that led to the result is useful for the design of chromophores with larger Φp(RT) and longer τp(RT). Deuteration of 2 and 3 was performed to improve Φp(RT) and τp(RT). Chromophores 2D and 3D showed identical absorption spectra compared with that of 2 and 3 (top graph of Figure 2c). In the steady-state emission spectra, a significant enhancement of yellow pRTP emission occurred (middle graph of Figure 2c), with a similar pRTP emission spectral shape compared with that of 2 and 3 (bottom graph of Figure 2c). An enhancement of τp(RT) was also observed (bottom graph of Figure 2b). Although Φf(RT) and τf(RT) of 2D and 3D hardly changed compared with undeuterated chromophores (Table 1), Φp(RT) of 2D and 3D was 16% and 35%, respectively, whereas the τp(RT) of 2D and 3D was 3.8 and 2.2 s, respectively, when doped into β-estradiol (Table 2). 3D in β-estradiol presented an afterglow TADF with a 6% yield and a lifetime of 1.4 s (Table 2) because the spectral signal could be observed soon after excitation (bottom of Figure 2c). Therefore, an afterglow RT emission yield of 3D reached 41%. Because 2D and 3D had a comparable Φisc(RT) to that of 2 and 3 (Table 1), respectively, the enhancement of Φp(RT) and τp(RT) resulted mainly because the suppression of knr(RT) was caused by a general isotope effect (Table 2).11,12,35−37 Although an increase in the τp(RT) from the decrease in knr(RT) by the isotope effect has been reported, Φp(RT) was often 10%–20% for chromophores with a τp(RT) greater than 2 s.11 However, this combination of isotope effect and decrease in knr(RT) owing to the appropriate chemical backbone increased Φp(RT) to 35%.

Table 2. Photophysical Parameters of 1–4, 2D, and 3D Related to pRTP.

chromophore Φp(RT) [%]a τp(RT) [10° s]a λp [nm]b kp [s–1]c knr(RT) [s–1]d kq(RT) [s–1]e
1 3.4 6.0 567 0.01 0.12 0.04
2 11 3.1 540 0.05 0.23 0.04
3 19 (4)f 1.8 (1.1)f 545 0.13 0.27 0.15
4 10 0.45 550 0.30 1.8 0.12
2D 16 3.8 540 0.06 0.16 0.05
3D 35 (6)f 2.2 (1.4)f 545 0.20 0.16 0.10
Open in a new tab
a

Values using 0.3 wt % chromophore doped in β-estradiol.

b

Peak wavelength of phosphorescence.

c

Values determined by substituting experimentally observed Φp(RT), τp(RT), and Φisc(RT) = 1 – Φf(RT) into kp = Φp(RT)Φisc(RT)−1τp(RT)−1.

d

Values determined using fitting lines of knr(T).

e

Values determined by subtracting knr(RT), which is determined using the fitting lines of knr(T), from experimentally observed knr(T) + kq(T).

f

Parentheses indicates TADF values.

Temperature-Dependent Analysis

Because the effect of deuteration to suppress the knr(RT) between 2 and 2D or 3 and 3D is a well-known and established science,11,12,35−37 we considered the reason for the significant difference in photophysical properties depending on the chemical structures of 1–4. To assess the reason for this behavior, we need to establish the related physical parameters. Φp(RT) and τp(RT) are generally expressed as11,23

graphic file with name au1c00132_m001.jpg 1
graphic file with name au1c00132_m002.jpg 2

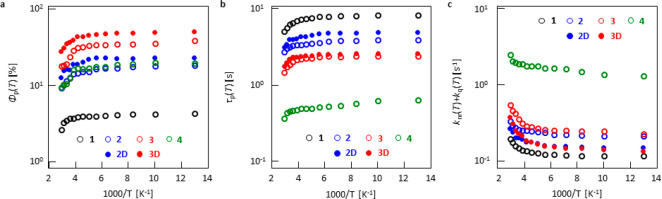
Equations 1 and 2 indicate that a large Φisc(RT), large kp, and small knr(RT) + kq(RT) are essential for the large Φp(RT) and τp(RT). Because Φisc(RT) was comparable and large for 2–4, the different Φp(RT) was caused by the difference of kp, knr(RT), and kq(RT). To investigate these three factors, first we estimated kp of 1–4 by substituting Φisc(RT), Φp(RT), and τp(RT) into eq 1 (Table 1). Next, a temperature-dependent analysis of Φp(T) and τp(T) was performed to establish the knr(RT) and kq(RT) of 1–4. The temperature-dependent analysis shows that Φp(T) decreased slightly from 77 K to RT (Figures 3a and S19) and a similar tendency was also observed for the τp(T) for all chromophores (Figures 3b and S20). A substitution of kp and the dependence of τp(T) into eq 2 yielded the temperature-dependent knr(T) + kq(T) (Figure 3c). The plot could be fitted into a sum of two exponential equations (Figure S21). In a previous report, it was confirmed that a large increase of knr(T) + kq(T) in a higher-temperature region is caused by kq(T)11,38 and the lower temperature component is caused by knr(T), which depends on the vibrational SOC and Franck–Condon factor between T1 and S0 of the chromophores.24,39

Figure 3.

Figure 3

Open in a new tab

Temperature-dependent analysis of 1–4, 2D, and 3D. (a) Φp(T), (b) τp(T), and (c) knr(T) + kq(T). Φp(T) and τp(T) were measured under vacuum conditions, whereas Φp(RT) and τp(RT) did not show any change between vacuum and ambient conditions.

After the temperature-dependent estimation of knr(T) of 1–4, the estimated values of knr(RT) for 1–4 were 1.2 × 10–1, 2.3 × 10–1, 2.7 × 10–1, and 1.8 × 10° s–1, respectively. The quantified kp and knr(RT) of 1–4 are summarized in Table 2.

An incorporation of the substituent (comparison of 1 and 2) to coronene, which acted as a RTP center, was responsible for the enhancement of kp and knr(RT). Because the enhancement of kp was larger than that of knr(RT), the substituents led to an increase of Φp(RT) from 3.4% for 1 to 11% for 2. A similar tendency was observed, depending on the change from 2 to 3 when the conjugation length of the RTP antenna increased. The enhancement of kp was greater compared with that of knr(RT). As a result, Φp(RT) increased from 11% for 2 to 19% for 3. We have already reported that the enhancement of kp using RTP antenna can be explained by the increase of the Sn–S0 transition dipole moment caused by an extension of the RTP antenna.12 The tendency was observed as well in the comparison between 1–3 (see section S5 and Figure S22). However, a different tendency with the increase of kp being much less than that of knr(RT) was observed when the RTP center changed from the coronene for 3 to the naphthalene for 4.

Effect of RTP Center for knr(RT) Suppression

The origin of the suppression of knr(RT) of 3 compared with that of 4 needs to be understood for a comprehensive molecular level understanding. Without any consideration of molecular coordination change that is caused by vibrations, knr(RT) is often expressed based on a nonadiabatic SOC between T1 and S0 (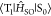Inline graphic) as40

graphic file with name au1c00132_m004.jpg 3

where FC is the Frank–Condon factor. The calculated 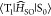Inline graphic2 for 1–4 were 3.4 × 10–7, 4.2 × 10°, 3.9 × 10–1, and 6.3 × 10–1 cm–2, respectively (Table 3). A poor correlation resulted when these values were plotted against the experimental knr(RT) (Figure 4a). We have reported a calculation method to predict knr(RT) of a variety of undeuterated chromophores with free vibrations allowed by energy corresponding room-temperature.24 The calculation was based on an approximation that knr(RT) is an approximate multiplication of the vibrational SOC term of the equation that considers the Herzberg–Teller SOC and FC. In theory, knr(RT) is approximately expressed as

graphic file with name au1c00132_m006.jpg 4

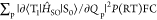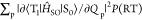where QP is the mass-weighted normal coordinate that corresponds to the pth vibrational mode at T1 and P(RT) is the vibrational factor at RT. The calculated Inline graphic for 1–4 are 4.7 × 10–5, 9.9 × 10–5, 1.2 × 10–4, and 5.9 × 10–4 au, respectively (Table 3). This result has an excellent correlation with the optically measured knr(RT) (Figure 4b) and a strong correlation was observed in a variety of chromophores with different RTP colors (Figures S23, S24 and Table S2–S7). Therefore, the correlation allows for a deeper analysis of the relationship between knr(RT) and the molecular structure. 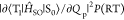Because eq 4 is constructed mainly from two factors; Inline graphic, where Inline graphic is abbreviated as VSOC(RT) for easier reading, and FC, we first analyzed ΣpVSOC(RT) of 1–4 in the following paragraph.

Table 3. Calculated Photophysical Parameters Related to Triplet States of 1–4.

chromophore ⟨T1|ĤSO|S0⟩2 [cm–2]a ΣPVSOC(RT)FC [au]a ΣPVSOC(RT) [au]a η (ET1–S0 – E0)/η [103 cm–1]b FC [10–5 au]c
1 3.4 × 10–7 4.7 × 10–5 5.8 × 100 0.333 40.9 0.81
2 4.2 × 100 9.9 × 10–5 8.7 × 100 0.368 39.4 1.14
3 3.9 × 10–1 1.2 × 10–4 1.0 × 101 0.367 39.1 1.23
4 6.3 × 10–1 5.9 × 10–4 1.7 × 101 0.410 34.6 3.42
Open in a new tab
a

Calculated values using the PBE0 functional and TZP basis sets using optimized structure at T1 by DFT (Gaussian09/B3LYP/6-31G(d)).

b

Data of λp in Table 2 used to determine ET1–S0.

c

Data determined by substituting (ET1–S0 – E0)/η into log FC ≈ [10–4(ET1–S0 – E0)/η]−1 – 1, which is summarized in Figure 7 in ref (36).

Figure 4.

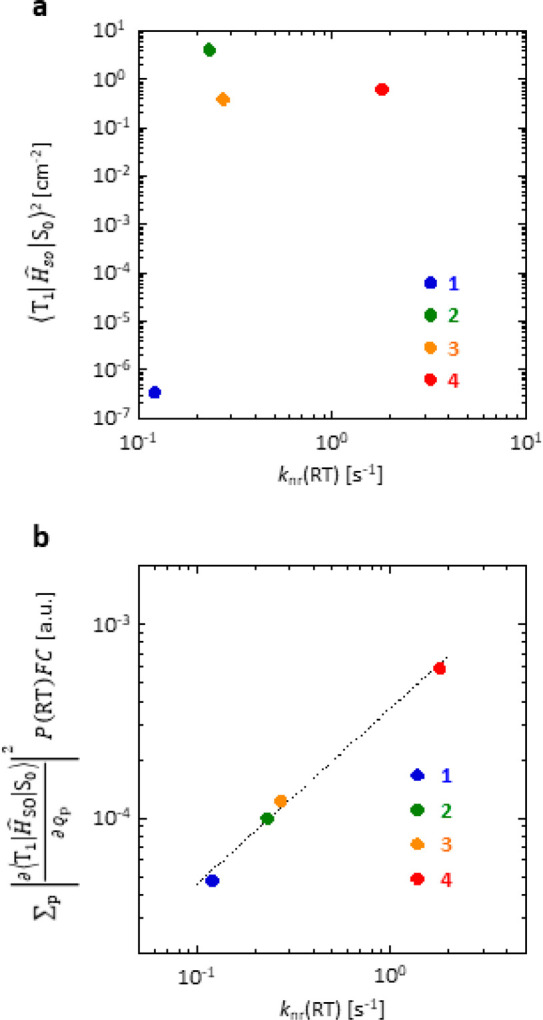
Figure 4

Open in a new tab

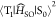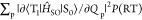Relationship between knr(RT) and nonadiabatic SOC and SOC considering vibrations allowed at RT. (a) Relationship between Inline graphic and knr(RT) for 1–4. (b) Relationship between Inline graphicand knr(RT) for 1–4. The slope of the dashed fitting line based on the least-squares method is 0.91.

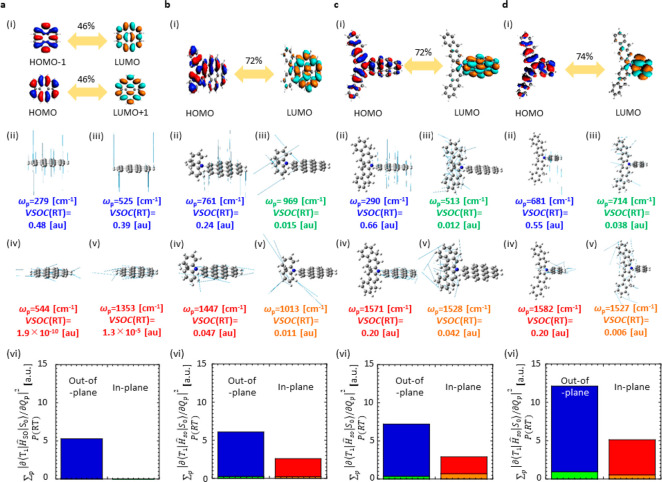
The difference of ΣpVSOC(RT) among 1–3 is explained depending on the different nature of the T1–S0 transition, whereas that between 3 and 4 was caused by the different sizes of fused rings of the RTP center. For 1–3 as chromophores with coronene as a RTP center, ΣpVSOC(RT) increased slightly by introducing RTP antennas as substituents and an extension of the antenna. For 1, out-of-plane modes of coronene (RTP center) were predominantly responsible for the knr(RT) and the overall VSOC(RT) was 5.8 × 10° au. (Table 3). 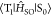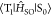Because Inline graphicdiffers depending on the out-of-plane vibrations, the out-of-plane vibrations have a large VSOC(RT) ((ii) and (iii) in Figure 5a). Because Inline graphichardly changes depending on the in-plane vibrations, the in-plane vibrations have a small VSOC(RT) ((iv) and (v) in Figure 5a). The tendency was confirmed by checking that the integration of VSOC(RT) for all out-of-plane vibrations (blue shaded area in (vi) of Figure 5a) was larger than that of the in-plane vibrations (red shaded area in (vi) of Figure 5a). For 2 and 3, however, the in-plane vibrations of the coronene moiety ((iv) in Figure 5b and c) and the out-of-plane vibrations of the coronene unit ((ii) of Figure 5b and c) enhanced the knr(RT) (blue and red shaded area in (vi) of Figure 5b and c). The overlapping density of the two molecular orbitals (MOs) is related to the T1–S0 transition located at the coronene part and at the slightly conjugated substituents ((i) in Figure 5b and c). Because the in-plane vibrations of coronene were not parallel to the conjugated plane of the conjugated substituents, the vibrations allow for spin flipping for the electron at the substituents. Therefore, in- and out-of-plane vibrations of the coronene part contribute to an increase in ΣpVSOC(RT). However, vibrations of the substituents hardly increase ΣpVSOC(RT) (green and orange shaded area in (vi) of Figure 5b and c). Consequently, the overall calculated values of ΣpVSOC(RT) for 2 and 3 are 8.7 × 10° and 1.0 × 101 au, respectively, which increase slightly compared with that of 1 (Table 3). The slight increase from 1 to 2 and 3 may be explained by the increase in the CT nature for the T1–S0 transition. Because ΣpVSOC(RT) increases largely when the T1–S0 transition has a strong CT nature, such as for benzophenone,24 a slight increase of the CT nature that is caused by the substituents for 2 and 3 ((i) in Figure 5a) compared with 1 ((i) in Figure 5b and c) explains the increase in ΣpVSOC(RT). A larger difference of ΣpVSOC(RT) that is independent of the nature of the T1–S0 transition was observed between 3 and 4. The contribution of the HOMO–LUMO transition to the T1–S0 transition is comparable between 3 ((i) in Figure 5c) and 4 ((i) in Figure 5d). However, the ΣpVSOC(RT) of 4 is 1.7 times larger than that of 3 (Table 3). Compared with 3 (blue and red shaded areas in (vi) of Figure 5c), the contribution of out-of-plane and in-plane vibrations of 4 (blue and red shaded areas in (vi) of Figure 5d) to increase ΣpVSOC(RT) is large. A comparison of 3 and 4 shows that the extension of the two-dimensional fused ring contributes to a decrease in ΣpVSOC(RT) for smaller knr(RT).

Figure 5.

Figure 5

Open in a new tab

Nature of transition and analysis of knr(RT) depending on VSOC(RT) of 1–4. (a) 1, (b) 2, (c) 3, and (d) 4. In (a)–(d), the mode of transition at the T1 geometry (i), VSOC(RT) in the representative vibration modes (ii)–(v), total magnitude of VSOC(RT) considering all possible out-of-plane vibration modes of RTP center (blue shaded are), all possible in-plane vibration modes of RTP center (red shaded area), all possible out-of-plane vibration modes of RTP antenna (green shaded area), and all possible in-plane vibration modes of RTP antenna (orange shaded area) (vi).

Because FC is related to knr(RT) based on eq 4, a careful check of the contribution to knr(RT) is necessary. Although all chromophores showed a comparable yellow pRTP, which indicates a comparable energy difference between T1 and S0 (ET1–S0) (bottom of Figure 2a and Table 2), it was noted that FC depends on ET1–S0 and on the relative number of hydrogen atoms in the molecule (η), which is defined as C1−ηHη.36 As the number of nitrogen atoms in 2–4 is small compared with the total number of atoms, η of 1–4 is determined as shown in Table 3. The values of FC were determined by substituting ET1–S0 and η into log FC ≈ [10–4(ET1–S0 – E0)/η]−1 – 1, where E0 = 4000 cm–1 is the empirical parameter by Siebrand (Figure S25).36,41,42 The FC of 1–4 is summarized in Table 3. For 1–3, FC is comparable, but for 4 it increases significantly (Table 3). The large decrease in FC from 4 to 3 is explained because of the decrease in η when log FC ≈ [10–4(ET1–S0 – E0)/η]−1 – 1 is considered. The decrease in the number of hydrogen atoms compared with other atoms because a two-dimensional fused extension of the RTP center corresponds to a decrease in η and FC could be reduced by the two-dimensional fused extension of the RTP center. The overall calculation result for ΣpVSOC(RT) and FC indicates that a two-dimensional fused extension of the RTP center tends to decrease ΣpVSOC(RT) and FC to allow a large decrease in knr(RT) to improve Φp(RT) and τp(RT).

Self-Spatial Modulated High-Resolution Afterglow

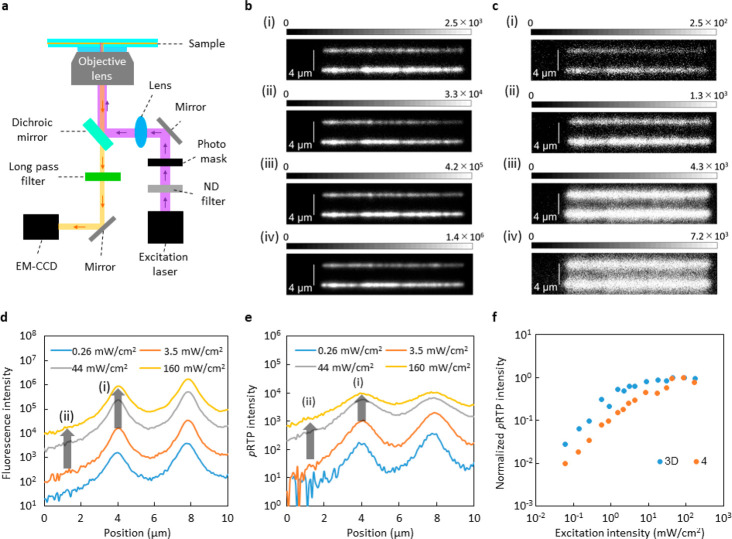
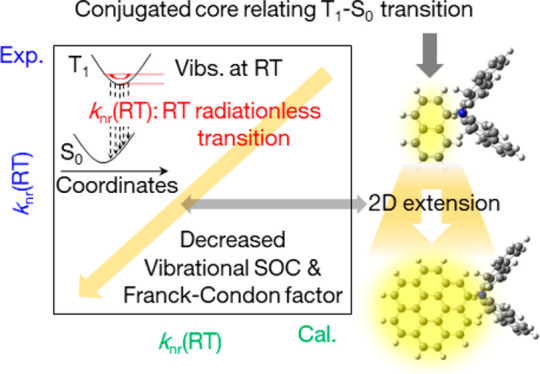
A change in photopatterned spatial information requires a mechanical change of optics, including photomasks. If the materials automatically change emission spatial information independent of the mechanical changes, they reach a point that has not been obtained by other materials and technologies. For example, a 445 nm high-resolution light through a photomask and objective lens was irradiated on a poly[(9,9-di-n-octylfluorenyl-2,7-diyl)-alt-(benzo[2,1,3]thiadiazol-4,8-diyl)] (F8BT) film on a glass substrate (sample F8BT) and 3 wt % 3D doped amorphous β-estradiol film between two glass substrates (sample 3D). Figure 6a provides a schematic illustration of the high-resolution imaging technique that was used in this demonstration. For sample F8BT, two lined high-resolution yellow fluorescence patterns according to the photomask appeared under a weak excitation at 2.6 × 10–1 mW/cm2 (Figure 6b; (i)). The line widths did not change when the excitation power density increased gradually to 1.6 × 102 mW/cm2 (Figure 6b; (ii)–(iv)). For sample 3D, yellow afterglow phosphorescence patterns of sample 3D soon after ceasing the 445 nm excitation light are shown in Figure 6c. Although a similar high resolution of the afterglow lines was observed when the excitation power density was weak (2.6 × 10–1 mW/cm2) (Figure 6c; (i)), a distinct broadening of only high-resolution lines were observed with an increase in excitation intensity to 1.6 × 102 mW/cm2 (Figure 6c; (ii)–(iv)). A broadening of emission lines was not observed for steady-state emission under strong excitation because fluorescence without strong annihilation became extremely dominant in the strong excitation (Figure S26).

Figure 6.

Figure 6

Open in a new tab

Self-spatial modulation of high-resolution afterglow. (a) Optical setup for demonstration. (b) Fluorescence images of sample F8BT under 445 nm excitation with difference in irradiance. (c) Afterglow images of sample 3D integrated for 0.1 s after ceasing 445 nm excitation with difference in irradiance. In (b) and (c), (i) 2.6 × 10–1 mW/cm2, (ii) 3.5 × 100 mW/cm2, (iii) 4.4 × 101 mW/cm2, and (iv) 1.6 × 102 mW/cm2. (d) Intensity profiles of fluorescence line width of sample F8BT at difference excitation intensity of 445 nm. (e) Intensity profiles of persistent RTP line width of sample 3D integrated for 0.1 s after ceasing 445 nm excitation with difference in irradiance. (f) Difference of pRTP intensity depending on excitation intensity at 355 nm for sample 3D and sample 4. The saturated intensity was normalized to 1.

The large broadening is related largely to a saturation of pRTP intensity, which depends on excitation intensity. It has been reported that saturation occurs because of annihilation that is caused mainly by a singlet–triplet resonance energy transfer and a triplet–triplet resonance energy transfer because of a concentrated accumulation of triplet excitons in the materials.43,44 In epifluorescent imaging with a resolution that approaches the diffraction limit, the excitation profile of the line width does not have a top-hat shape. Therefore, the emission profile has a center ((i) in Figure 6d) and tail parts ((ii) in Figure 6d). For sample F8BT, the fluorescence intensity at the center and tail approximately increases 50 times when the excitation intensity increases from 3.5 to 160 mW/cm2 ((i) and (ii) in Figure 6d). Therefore, the shape of the fluorescence profile is independent of the power (Figure 6d). For sample 3D, the afterglow intensity at the center part ((i) in Figure 6e) increased only 9 times, whereas that at the tail ((ii) in Figure 6e) increased approximately 50 times when the excitation intensity increased from 3.5 to 160 mW/cm2. Because of the much larger increase in afterglow intensity at the tail part compared with that at the center, a large broadening of the afterglow emitting lines was observed with an increase in excitation intensity.

The simultaneous large Φp(RT) and τp(RT), such as those for 3D, are suitable for the self-spatial modulation of a high-resolution afterglow. To determine the extent of saturation, we measured the power-dependent pRTP intensity. Chromophore 4, 3 wt % doped in amorphous β-estradiol film between two glass substrates (sample 4), was used as a reference sample. The absorbance of samples 3D and 4 were comparable (Figure S27). Compared with sample 4, the pRTP of sample 3D was saturated in a weaker excitation intensity (Figure 6f). Because the triplet accumulation to induce the saturation depends theoretically on a multiplication of Φisc(RT) and τp(RT)31 and 3D and 4 have a comparable Φisc(RT) (Table 1 and Table 2), the much larger τp(RT) of 3D compared with 4 allows for a self-spatial modulation in weaker excitation light. A high-power light source is required for epi-emission imaging compared with confocal imaging for two-dimensional homogeneous excitation. Therefore, a decrease in excitation intensity in the light source is recommended for mobile applications. The decrease in Φp(RT) is not accepted when materials show a longer τp(RT) because the brightness of the afterglow decreases and causes no signal in the high-resolution imaging because the brightness became less than the dark noises of the two-dimensional photodetectors. Because two-dimensional photodetectors that are used in mobile applications do not tend to have cooling and a significant amplifier, a large Φp(RT) is required to allow for a high-resolution afterglow and to decrease the error for a readout of a high-resolution afterglow. A large τp(RT) is needed for the large self-spatial modulation of the high-resolution afterglow. Therefore, a chemical approach to suppress knr(RT) without a large decrease in kp for chromophores is critical to achieve materials with a large Φp(RT) and large τp(RT) and contributes to a safer advanced society. The change in the afterglow emission pattern using the waveguide mode was demonstrated.45 However, the function may depend on the material shape, and spatial information on the low-resolution information could be obtained by using materials with different pRTP decay lifetimes in different positions. The demonstrated self-spatial tunable afterglow in this work was based on excitonic interactions that allow for a high-resolution approach to a diffraction limit level. The self-spatial tunable resolution that uses high-resolution information approaches the diffraction limit and provides a state-of-art secret quality that previous materials and technologies have not achieved.

Conclusions

The structure–property relationship in the field of pRTP science is one of the most obvious aspects, as it provides an opportunity to improve the properties of designed chromophores. The fused two-dimensional poly aromatic carbon, coronene, acts as an RTP center, and it was substituted with a long π-conjugated RTP antenna. One of the chromophores had a Φp(RT) = 35% and τp(RT) = 2.2 s in an amorphous short conjugated rigid host at ambient conditions. A comparison of the two synthesized coronene derivatives showed that the RTP antenna enhanced kp more than 10 times whereas the increase in knr(RT) remained approximately double. A comparison of coronene and naphthalene, as the RTP center with the same RTP antenna, indicated that knr(RT) decreased using a two-dimensional fused extension without a considerable decrease in kp. For the chromophores, the optically measured knr(RT) correlated precisely with a multiplication of the computationally calculated vibrational SOC and FC between T1 and S0. The correlation allowed for clarification that the two-dimensional fused extension decreased the vibrational SOC and FC. A guideline to the decrease in knr(RT) independent of kp is critical for large τp(RT) and large Φp(RT) from a variety of chromophores. A saturation behavior of bright pRTP characteristics owing to materials with a large τp(RT) and large Φp(RT) allowed for a tunable high-resolution afterglow depending on a weaker excitation intensity. The self-spatial modulation of a high-resolution afterglow yields difficulties for fake production, and detection using a low-cost and mobile optical setup is a promising way to increase anticounterfeit quality in secret media significantly.

Experimental Procedures

Materials

Chromophore 1 (Tokyokasei Chemical Industries (TCI), Tokyo, Japan) and β-estradiol (TCI) are commercially available. Chromophore 1 was purified via vacuum sublimation before preparing the sample for optical measurement. Chromophores 2, 3, 2D, and 3D were synthesized and their structure was identified via 1H NMR, 13C NMR, high-resolution mass spectroscopy, and elementary analysis. Details are provided in the Supporting Information (see section S1). The synthesis and characterization of 4 is reported in the Supporting Information of a previous report.12 All chromophores were used as dopant, with a 0.3% mass fraction dissolved in melted β-estradiol at 200 °C, and the mixture was spread between two quartz or glass substrates heated at 200 °C. The transparent film was obtained by gradual cooling of the substrate to RT.

Fundamental Photophysical Characteristics

Absorption spectra of all samples were measured using an absorption spectrometer (V-630, JASCO, Tokyo, Japan). The fluorescence spectra, RTP spectra, and RTP lifetime at RT were measured using a photonic multichannel analyzer (PMA-12, Hamamatsu Photonics, Shizuoka, Japan) and monochromatic light from the excitation unit of a fluorimeter (FP-8300, JASCO) as the excitation source. Temperature-dependent measurements were achieved by using a cryostat (Optistat DN-V, Oxford Instruments, Abingdon-on-Thames, UK). The emission yield, including Φf(T) and Φp(T), was measured by the method described in the Supporting Information of a previous report by using an absolute luminescence quantum yield measurement system (C9920-02G, Hamamatsu Photonics) (see section S4 in this article).11 Φisc(RT) in benzene was determined by using the previously reported method with a subnanosecond transient absorption spectrophotometer (picoTAS, Unisoku, Osaka, Japan) and a 355 nm Q-switched microchip laser (PNV-M02510-1×X0, Teem Photonics, Meylan, France) (see section S2 in this article).

High-Resolution Microscopy Measurements

An inverted optical microscope (Olympus, IX73, Japan) with an oil immersion objective lens (Olympus, UPlan FLN ×100/1.3 NA, oil) was used to achieve high-resolution excitation through a photomask. A laser at 355 nm (PNV-M02510-1×0, Teem Photonics, France) and a laser diode with a wavelength of 445 nm (TC20-4450-4.5, Neoark, Tokyo, Japan) were used as excitation. The emission images were collected using an electron multiplying (EM) CCD camera (iXon Ultra/life 897, Andor Technology, UK). A dichroic mirror (FF470-Di01, Semrock, USA) and a long-pass filter (LP02-473RU, Semrock, USA) were used to excite the sample and collect only the sample emission. For the conditions of the CCD and amplifier, appropriate values of gain and setting temperature were selected depending on the purpose. The excitation power was measured using a photodiode power sensor (S130VC, Thorlabs, Germany). All measurements were performed in air at RT.

Calculations

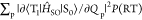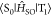S0 and T1 geometries were calculated by using Gaussian09 based on density functional theory (DFT), and the S1 geometry was determined by using Gaussian09 based on time-dependent DFT. The B3LYP functional and 6-31G(d) basis sets were used to calculate the molecular orbitals and oscillator strength related to the S1–S0 transition at the S1 geometry. To calculate Inline graphic, vibrations at the T1 geometry were calculated using Gaussian09 with the B3LYP functional and 6-31G(d) basis sets to determine Qp. 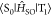Inline graphic that depends on the Qp from Qp = −1.0 to Qp = +1.0 was calculated by using the Amsterdam Density Functional 2017 package. 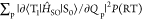The parameter Inline graphic was treated as a perturbation based on scalar relativistic orbitals with the PBE0 functional and TZP basis sets. Scalar relativistic–time dependent DFT calculations included 1 singlet + 1 triplet excitations, which were used as a basis for the perturbative expansions in the calculations. Detailed procedures have been reported in the literature,24 and the same procedure and functional and basis sets were used to determine Inline graphic. The T1 geometry was used to analyze the relationship between kp and MOs that relate the T1–S0 transition (see section S5). A detailed procedure has been reported in the literature,12,24,39 and the same procedure and functional and basis sets were used to analyze kp.

Acknowledgments

This work was supported by JST FOREST Program (Grant Number JPMJFR201T, Japan) and JSPS KAKENHI (Grant Numbers JP18H02046, JP18H04507, JP20H04664, and JPH02011).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00132.

  • NMR and mass spectra of chromophores, supporting optical spectra, data to determine Φisc(RT), supporting molecular orbitals and calculation data (PDF)

  • Video of pRTP emission from 2 under room light (AVI)

  • Video of pRTP emission from 4 under room light (AVI)

  • Video of pRTP emission from 3D under room light (AVI)

The authors declare no competing financial interest.

Supplementary Material

au1c00132_si_001.pdf (1.9MB, pdf)
au1c00132_si_002.avi (2.7MB, avi)
au1c00132_si_003.avi (1.8MB, avi)
au1c00132_si_004.avi (3.8MB, avi)

References

  1. Reineke S.; Lindner F.; Schwartz G.; Seidler N.; Walzer K.; Lüssem B.; Leo K. White Organic Light-Emitting Diodes with Fluorescent Tube Efficiency. Nature 2009, 459, 234–238. 10.1038/nature08003. [DOI] [PubMed] [Google Scholar]
  2. D’Andrade B. W.; Forrest S. R. White Organic Light-Emitting Devices for Solid-State Lighting. Adv. Mater. 2004, 16, 1585–1595. 10.1002/adma.200400684. [DOI] [Google Scholar]
  3. Sasabe H.; Kido J. Development of High Performance OLEDs for General Lighting. J. Mater. Chem. C 2013, 1, 1699–1707. 10.1039/c2tc00584k. [DOI] [Google Scholar]
  4. Baldo M. A.; O’Brien D. F.; You Y.; Shoustikov A.; Sibley S.; Thompson M. E.; Forrest S. R. Highly Efficient Phosphorescent Emission from Organic Electroluminescent Devices. Nature 1998, 395, 151–154. 10.1038/25954. [DOI] [Google Scholar]
  5. Adachi C.; Baldo M. A.; Thompson M. E.; Forrest S. R. Nearly 100% Internal Phosphorescence Efficiency in an Organic Light Emitting Device. J. Appl. Phys. 2001, 90, 5048–5051. 10.1063/1.1409582. [DOI] [Google Scholar]
  6. Lee J.; Chen H. F.; Batagoda T.; Coburn C.; Djurovich P. I.; Thompson M. E.; Forrest S. R. Deep Blue Phosphorescent Organic Light-Emitting Diodes with Very High Brightness and Efficiency. Nat. Mater. 2016, 15, 92–98. 10.1038/nmat4446. [DOI] [PubMed] [Google Scholar]
  7. Park H. Y.; Maheshwaran A.; Moon C. K.; Lee H.; Reddy S. S.; Sree V. G.; Yoon J.; Kim J. W.; Kwon J. H.; Kim J. J.; Jin S. H. External Quantum Efficiency Exceeding 24% with CIEy Value of 0.08 using a Novel Carbene-Based Iridium Complex in Deep-Blue Phosphorescent Organic Light-Emitting Diodes. Adv. Mater. 2020, 32, 2002120. 10.1002/adma.202002120. [DOI] [PubMed] [Google Scholar]
  8. Zhen X.; Tao Y.; An Z.; Chen P.; Xu C.; Chen R.; Huang W.; Pu K. Ultralong Phosphorescence of Water-Soluble Organic Nanoparticles for in vivo Afterglow Imaging. Adv. Mater. 2017, 29, 1606665. 10.1002/adma.201606665. [DOI] [PubMed] [Google Scholar]
  9. Nicol A.; Kwok R. T.; Chen C.; Zhao W.; Chen M.; Qu J.; Tang B. Z. Ultrafast Delivery of Aggregation-Induced Emission Nanoparticles and Pure Organic Phosphorescent Nanocrystals by Saponin Encapsulation. J. Am. Chem. Soc. 2017, 139, 14792–14799. 10.1021/jacs.7b08710. [DOI] [PubMed] [Google Scholar]
  10. Zhang G.; Chen J.; Payne S. J.; Kooi S. E.; Demas J. N.; Fraser C. L. Multi-Emissive Difluoroboron Dibenzoylmethane Polylactide Exhibiting Intense Fluorescence and Oxygen-Sensitive Room-Temperature Phosphorescence. J. Am. Chem. Soc. 2007, 129, 8942–8943. 10.1021/ja0720255. [DOI] [PubMed] [Google Scholar]
  11. Hirata S.; Totani K.; Zhang J.; Yamashita T.; Kaji H.; Marder S. R.; Watanabe T.; Adachi C. Efficient Persistent Room Temperature Phosphorescence in Organic Amorphous Materials Under Ambient Conditions. Adv. Funct. Mater. 2013, 23, 3386–3397. 10.1002/adfm.201203706. [DOI] [Google Scholar]
  12. Bhattacharjee I.; Hirata S. Highly Efficient Persistent Room-Temperature Phosphorescence from Heavy Atom-Free Molecules Triggered by Hidden Long Phosphorescent Antenna. Adv. Mater. 2020, 32, 2001348. 10.1002/adma.202001348. [DOI] [PubMed] [Google Scholar]
  13. Mathew A. S.; DeRosa C. A.; Demas J. N.; Fraser C. L. Difluoroboron β-diketonate Materials with Long-Lived Phosphorescence Enable Lifetime Based Oxygen Imaging with a Portable Cost Effective Camera. Anal. Methods 2016, 8, 3109–3114. 10.1039/C5AY02959G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Deng Y.; Zhao D.; Chen X.; Wang F.; Song H.; Shen D. Long Lifetime Pure Organic Phosphorescence Based on Water Soluble Carbon Dots. Chem. Commun. 2013, 49, 5751–5753. 10.1039/c3cc42600a. [DOI] [PubMed] [Google Scholar]
  15. Long P.; Feng Y.; Cao C.; Li Y.; Han J.; Li S.; Peng C.; Li Z.; Feng W. Self-Protective Room-Temperature Phosphorescence of Fluorine and Nitrogen Codoped Carbon Dots. Adv. Funct. Mater. 2018, 28, 1800791. 10.1002/adfm.201800791. [DOI] [Google Scholar]
  16. Louis M.; Thomas H.; Gmelch M.; Haft A.; Fries F.; Reineke S. Blue-Light-Absorbing Thin Films Showing Ultralong Room-Temperature Phosphorescence. Adv. Mater. 2019, 31, 1807887. 10.1002/adma.201807887. [DOI] [PubMed] [Google Scholar]
  17. Fateminia S. M. A.; Mao Z.; Xu S.; Yang Z.; Chi Z.; Liu B. Organic Nanocrystals with Bright Red Persistent Room-Temperature Phosphorescence for Biological Applications. Angew. Chem., Int. Ed. 2017, 56, 12160–12164. 10.1002/anie.201705945. [DOI] [PubMed] [Google Scholar]
  18. Yang J.; Zhen X.; Wang B.; Gao X.; Ren Z.; Wang J.; Xie Y.; Li J.; Peng Q.; Pu K.; Li Z. The Influence of the Molecular Packing on the Room Temperature Phosphorescence of Purely Organic Luminogens. Nat. Commun. 2018, 9, 840. 10.1038/s41467-018-03236-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Abdukayum A.; Chen J. T.; Zhao Q.; Yan X. P. Functional Near Infrared-Emitting Cr3+/Pr3+ Co-Doped Zinc Gallogermanate Persistent Luminescent Nanoparticles with Superlong Afterglow for in vivo Targeted Bioimaging. J. Am. Chem. Soc. 2013, 135, 14125–14133. 10.1021/ja404243v. [DOI] [PubMed] [Google Scholar]
  20. Sun S. K.; Wang H. F.; Yan X. P. Engineering Persistent Luminescence Nanoparticles for Biological Applications: from Biosensing/Bioimaging to Theranostics. Acc. Chem. Res. 2018, 51, 1131–1143. 10.1021/acs.accounts.7b00619. [DOI] [PubMed] [Google Scholar]
  21. Pan Z.; Lu Y. Y.; Liu F. Sunlight-Activated Long-Persistent Luminescence in the Near-Infrared from Cr3+-Doped Zinc Gallogermanates. Nat. Mater. 2012, 11, 58–63. 10.1038/nmat3173. [DOI] [PubMed] [Google Scholar]
  22. Yan S.; Liu F.; Zhang J.; Wang X. J.; Liu Y. Persistent Emission of Narrowband Ultraviolet-B Light upon Blue-Light Illumination. Phys. Rev. Appl. 2020, 13, 044051. 10.1103/PhysRevApplied.13.044051. [DOI] [Google Scholar]
  23. Hirata S. Recent Advances in Materials with Room-Temperature Phosphorescence: Photophysics for Triplet Exciton Stabilization. Adv. Opt. Mater. 2017, 5, 1700116. 10.1002/adom.201700116. [DOI] [Google Scholar]
  24. Hirata S.; Bhattacharjee I. Vibrational Radiationless Transition from Triplet States of Chromophores at Room Temperature. J. Phys. Chem. A 2021, 125, 885–894. 10.1021/acs.jpca.0c09410. [DOI] [PubMed] [Google Scholar]
  25. Kuila S.; George S. J. Phosphorescence Energy Transfer: Ambient Afterglow Fluorescence from Water-Processable and Purely Organic Dyes via Delayed Sensitization. Angew. Chem., Int. Ed. 2020, 59, 9393–9397. 10.1002/ange.202002555. [DOI] [PubMed] [Google Scholar]
  26. Zhao W.; Cheung T. S.; Jiang N.; Huang W.; Lam J. W.; Zhang X.; He Z.; Tang B. Z. Boosting the Efficiency of Organic Persistent Room-Temperature Phosphorescence by Intramolecular Triplet-Triplet Energy Transfer. Nat. Commun. 2019, 10, 1595. 10.1038/s41467-019-09561-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Demangeat C.; Dou Y.; Hu B.; Bretonnière Y.; Andraud C.; D’Aléo A.; Wu J. W.; Kim E.; Le Bahers T.; Attias A. J. σ-Conjugation and H-Bond-Directed Supramolecular Self-Assembly: Key Features for Efficient Long-Lived Room Temperature Phosphorescent Organic Molecular Crystals. Angew. Chem. 2021, 133, 2476–2484. 10.1002/ange.202011770. [DOI] [PubMed] [Google Scholar]
  28. Gu L.; Wu H.; Ma H.; Ye W.; Jia W.; Wang H.; Chen H.; Zhang N.; Wang D.; Qian C.; et al. Color-Tunable Ultralong Organic Room Temperature Phosphorescence from a Multicomponent Copolymer. Nat. Commun. 2020, 11, 944. 10.1038/s41467-020-14792-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Bian L.; Shi H.; Wang X.; Ling K.; Ma H.; Li M.; Cheng Z.; Ma C.; Cai S.; Wu Q.; et al. Simultaneously Enhancing Efficiency and Lifetime of Ultralong Organic Phosphorescence Materials by Molecular Self-Assembly. J. Am. Chem. Soc. 2018, 140, 10734–10739. 10.1021/jacs.8b03867. [DOI] [PubMed] [Google Scholar]
  30. Zhao W.; He Z.; Lam J. W.; Peng Q.; Ma H.; Shuai Z.; Bai G.; Hao J.; Tang B. Z. Rational Molecular Design for Achieving Persistent and Efficient Pure Organic Room-Temperature Phosphorescence. Chem. 2016, 1, 592–602. 10.1016/j.chempr.2016.08.010. [DOI] [Google Scholar]
  31. Kamatsuki T.; Bhattacharjee I.; Hirata S. The Substituent-Induced Symmetry-Forbidden Electronic Transition Allows Significant Optical Limiting under Weak Sky-Blue Irradiance. J. Phys. Chem. Lett. 2020, 11, 8675–8681. 10.1021/acs.jpclett.0c02694. [DOI] [PubMed] [Google Scholar]
  32. Huang R.; Avó J.; Northey T.; Chaning-Pearce E.; dos Santos P. L.; Ward J. S.; Data P.; Etherington M. K.; Fox M. A.; Penfold T. J.; et al. The Contributions of Molecular Vibrations and Higher Triplet Levels to the Intersystem Crossing Mechanism in Metal-Free Organic Emitters. J. Mater. Chem. C 2017, 5, 6269–6280. 10.1039/C7TC01958K. [DOI] [Google Scholar]
  33. Burrows H.; Fernandes M.; de Melo J.; Monkman A.; Navaratnam S. Characterization of the Triplet State of Tris(8-hydroxyquinoline)aluminium(III) in Benzene Solution. J. Am. Chem. Soc. 2003, 125, 15310–15311. 10.1021/ja037254f. [DOI] [PubMed] [Google Scholar]
  34. Gu L.; Shi H.; Bian L.; Gu M.; Ling K.; Wang X.; Ma H.; Cai S.; Ning W.; Fu L.; et al. Colour-Tunable Ultra-Long Organic Phosphorescence of a Single-Component Molecular Crystal. Nat. Photonics 2019, 13, 406–411. 10.1038/s41566-019-0408-4. [DOI] [Google Scholar]
  35. Robinson G. W.; Frosch R. P. Electronic Excitation Transfer and Relaxation. J. Chem. Phys. 1963, 38, 1187–1203. 10.1063/1.1733823. [DOI] [Google Scholar]
  36. Schlag E. W.; Schneider S.; Fischer S. F. Lifetimes in Excited States. Annu. Rev. Phys. Chem. 1971, 22, 465–526. 10.1146/annurev.pc.22.100171.002341. [DOI] [Google Scholar]
  37. Kropp J. L.; Dawson W. R. Radiationless Deactivation of Triplet Coronene in Plastics. J. Phys. Chem. 1967, 71, 4499–4506. 10.1021/j100872a054. [DOI] [Google Scholar]
  38. Kwon M. S.; Yu Y.; Coburn C.; Phillips A. W.; Chung K.; Shanker A.; Jung J.; Kim G.; Pipe K.; Forrest S. R.; et al. Suppressing Molecular Motions for Enhanced Room-Temperature Phosphorescence of Metal-Free Organic Materials. Nat. Commun. 2015, 6, 8947. 10.1038/ncomms9947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Hirata S. Intrinsic Analysis of Radiative and Room-Temperature Nonradiative Processes Based on Triplet State Intramolecular Vibrations of Heavy Atom-Free Conjugated Molecules Toward Efficient Persistent Room-Temperature Phosphorescence. J. Phys. Chem. Lett. 2018, 9, 4251–4259. 10.1021/acs.jpclett.8b01711. [DOI] [PubMed] [Google Scholar]
  40. Metz F.; Friedrich S.; Hohlneicher G. What is the Mechanism for the Nonradiative Decay of the Lowest Triplet State of Aromatic Hydrocarbons?. Chem. Phys. Lett. 1972, 16, 353–358. 10.1016/0009-2614(72)80291-4. [DOI] [Google Scholar]
  41. Siebrand W. Mechanism of Radiationless Triplet Decay in Aromatic Hydrocarbons and the Magnitude of the Franck—Condon Factors. J. Chem. Phys. 1966, 44, 4055–4057. 10.1063/1.1726576. [DOI] [Google Scholar]
  42. Siebrand W.; Williams D. F. Isotope Rule for Radiationless Transitions with an Application to Triplet Decay in Aromatic Hydrocarbons. J. Chem. Phys. 1967, 46, 403–404. 10.1063/1.1840415. [DOI] [Google Scholar]
  43. Hirata S.; Totani K.; Yamashita T.; Adachi C.; Vacha M. Large Reverse Saturable Absorption under Weak Continuous Incoherent Light. Nat. Mater. 2014, 13, 938–946. 10.1038/nmat4081. [DOI] [PubMed] [Google Scholar]
  44. Hirata S.; Vacha M. Large Transmittance Change Induced by Exciton Accumulation under Weak Continuous Photoexcitation. Adv. Opt. Mater. 2016, 4, 297–305. 10.1002/adom.201500378. [DOI] [Google Scholar]
  45. Zhou B.; Yan D. Simultaneous Long-Persistent Blue Luminescence and High Quantum Yield within 2D Organic–Metal Halide Perovskite Micro/Nanosheets. Angew. Chem., Int. Ed. 2019, 58, 15128–15135. 10.1002/anie.201909760. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au1c00132_si_001.pdf (1.9MB, pdf)
au1c00132_si_002.avi (2.7MB, avi)
au1c00132_si_003.avi (1.8MB, avi)
au1c00132_si_004.avi (3.8MB, avi)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES