Towards a computational phenomenology of mental action: modelling meta-awareness and attentional control with deep parametric active inference

Abstract

Meta-awareness refers to the capacity to explicitly notice the current content of consciousness and has been identified as a key component for the successful control of cognitive states, such as the deliberate direction of attention. This paper proposes a formal model of meta-awareness and attentional control using hierarchical active inference. To do so, we cast mental action as policy selection over higher-level cognitive states and add a further hierarchical level to model meta-awareness states that modulate the expected confidence (precision) in the mapping between observations and hidden cognitive states. We simulate the example of mind-wandering and its regulation during a task involving sustained selective attention on a perceptual object. This provides a computational case study for an inferential architecture that is apt to enable the emergence of these central components of human phenomenology, namely, the ability to access and control cognitive states. We propose that this approach can be generalized to other cognitive states, and hence, this paper provides the first steps towards the development of a computational phenomenology of mental action and more broadly of our ability to monitor and control our own cognitive states. Future steps of this work will focus on fitting the model with qualitative, behavioural, and neural data.

Introduction

Towards a scientific study of mental action

The control of cognitive states through mental action is a hallmark of human phenomenology. The underlying mechanisms, effects, and (dys)functions of cognitive control are highly relevant to cognitive, clinical, and theoretical neurosciences. The control of attentional states, for instance, is thought to be at the heart of several psychiatric conditions. Even beyond the obvious relevance to attention-deficit disorders, recent work suggests that attentional control plays an important role in the aetiology of schizophrenia (Brown et al. 2013) and the associated phenomenon of depersonalization disorder (Ciaunica et al. 2021), as well as in depression (Rock et al. 2014) and across the autism spectrum (Van de Cruys et al. 2014; Kiverstein et al. 2020). These involve specific and subtle dysfunctions that affect perception, thought, and mood, which stem from the atypical inference about one’s higher-order states and faulty control over the associated processes. These are of higher order in that they govern the attribution of confidence to one’s own perceptions (Palmer et al. 2017; Lysaker et al. 2020).

We define meta-awareness in this context as the ability to ‘explicitly’ notice the current content of a conscious episode. [The definition of meta-awareness is a topic of ongoing discussion in metacognition and mindfulness research. For instance, Dunne et al. (2019) recently argued that meta-awareness can be non-propositional and continuous. This model has the capacity to account for such nuances. For our purposes, as discussed in the text, we define states of meta-awareness as those (third-order) states of the system that are about, and enable the opacity of, (second-order) attentional states. They thus function analogously to attentional states, which enable the opacity of, (first-order) perceptual states. As such, this computational definition does not currently require a propositional self-reflection of the form ‘I am paying attention to reading this text’.] A canonical example of meta-awareness is to become aware of an episode of mind-wandering (Schooler et al. 2011). Generally speaking, the capacity of meta-awareness provides the agent knowledge about the objects of experience and experience itself, which can be used to increase control over mental processes or to revise beliefs. Mental action, in turn, refers to goal-directed internal behaviour, without necessarily having a direct consequence on the external environment (e.g. as through muscular action). A paradigmatic example of mental action is covert attention. Mental actions are categorized by their phenomenology of ownership, goal directedness, a subjective sense of effort, and the perceived sense of agency and mental self-control (Metzinger and Wiese 2017).

The aims of this paper are 3-fold: (i) to explicitly model meta-awareness, (ii) to account for the computational consequences of meta-awareness on cognitive control, and (III) to provide a computational account of mental (covert) action. Formally speaking, the crucial thing to note about these cognitive processes is that they are ‘about’ other such processes. The deployment and control of attentional states and processes, for instance, are quintessentially a higher-level ability: such states and processes monitor and modulate other, typically lower-level, perceptual states. Third-order, higher-level processes, in turn, oversee these attentional processes: we can be aware of our attention being grabbed and make a deliberate decision to focus our attention elsewhere. It would seem, then, that effective self-regulation of attention depends on the ability to access, evaluate, and control the quality of these attentional processes themselves—in the same way that attentional processes are necessary to consciously access, assess, and control lower-level perceptual states.

In computational terms, the central place of confidence and reliability in effective self-regulation speaks to the key role of the ‘precision’ (or inverse variance) of implicit beliefs (i.e. probabilistic or posterior Bayesian beliefs that describe a probability distribution over some latent quantity; these beliefs are subpersonal; however, the argument pursued in this work is that Bayesian beliefs about Bayesian beliefs can, in certain situations, become propositional) and the way they are estimated, optimized, and controlled (Hesp et al. 2020, 2021). Precisions, in a nutshell, quantify our confidence in our beliefs; say, how confident we are about what we know about states of the world, about their relation to our sensory observations, or about how these states change over time. By analogy with physical action, a ‘mental’ (or ‘covert’) action consists in deploying and adjusting these key quantities, without there necessarily being an explicit behavioural counterpart to these covert actions (Limanowski and Friston 2018, 2020). The nascent field of computational psychiatry is largely about deciphering these precision-related processes, shedding light on their physiological implementation (Lecaignard et al. 2020) and establishing their causal link with specific clinical traits (Friston et al. 2017a).

Covert or mental actions, as just defined, also speak to other fields of neuroscience. In some traditions, such as mindfulness meditation, an objective of training is to make cognitive processes accessible and hence controllable. The field of meditation research, sometimes referred to as contemplative neuroscience, has grown rapidly since the early 2000s (Eberth and Sedlmeier 2012; Sedlmeier et al. 2012; Tang et al. 2015; Fox et al. 2016). This literature has increased our understanding of the relationship between meta-awareness and cognitive control, especially with regard to attentional processes. Mechanistic models of these processes are beginning to appear (Farb et al. 2015; Jamieson 2016; Manjaly and Iglesias 2020; Lutz et al. 2019; Pagnoni 2019; Laukkonen and Slagter 2021). Complementary to this work, the contribution of this paper is a formal and computational architecture of these processes derived from first (Bayesian or variational) principles, which explicitly disambiguates the relationship between meta-awareness and attention.

Several conceptual frameworks exist in phenomenology, clinical psychology, and cognitive sciences to describe this relationship. For the purpose of this work, we focus on ‘regulatory’ cognitive control strategies, in which an agent seeks to control their mental states by becoming aware of the state as a cognitive process (as opposed to regulation strategies where one remains engrossed in the contents of the state). This style of regulation is central in mindfulness-related intervention, where patients learn to change their relation to thoughts and emotions, rather than change the thoughts and emotions themselves. As such, this regulation accounts for the positive effect of mindfulness meditation on mood disorders (Wetherell et al. 2017; Segal and Teasdale 2018). The ensuing meta-perspective on mental states has been labelled as phenomenological reduction (Varela 1996), decentering (Bernstein et al. 2015), cognitive defusion (Fletcher and Hayes 2005), mindful attention (Papies et al. 2012), dereification (Lutz et al. 2015), or opacification (Metzinger 2003). In contrast to this stance, being self-immersed in the contents of one’s mind has been called cognitive fusion (Fletcher and Hayes 2005), reification (Lutz et al. 2015), absorption (Tellegen and Atkinson 1974), experiential fusion (Dahl et al. 2015), subjective realism (Lebois et al. 2015), or transparency (Metzinger 2003).

To operationalize this aspect of meta-awareness, we will follow the distinction found in the self-model theory of subjectivity (Metzinger 2004), as it has already been used in previous treatments that directly influence the present work (Limanowski and Friston 2018), namely, the distinction between opacity and transparency.

Target phenomenology: opacity and transparency

The capacity of a system to access some subset of its own states has been theorized under the rubric of ‘opacity’ versus ‘transparency’ (Metzinger 2003). According to this framework, the mental states of human beings can be broken down into two kinds: those that are accessible to the system per se, which are labelled as ‘opaque’ (in the sense of being perceptible), and those that are not, which are labelled as ‘transparent’ (in the sense of being imperceptible). Some mental processes function only to make aspects of the world perceivable. We are not aware of them ‘as such’, but rather, we are aware of the content that they make available: these cognitive processes are ‘transparent’, like a glass window that allows us to see what is outside. Other processes, however, make these cognitive constructive processes accessible per se. This second set of processes are about other states of the mind, to which they provide access, as a new source of data now made available for further processing. These processes are akin to the scroll wheel on a pair of binoculars, which has a position state that its user can control and which enables one to apprehend and to control the precision of sensory inputs.

Transparent states and processes are thought to be by far the more common kind, which we share with most other animals. They mediate the agent’s access to the latent causes of their sensory states, to things appearing ‘out there’ in the world. The basic idea, then, is that we are not conscious of many of our mental states (the transparent ones) ‘as being’ mental states, i.e. grasping them explicitly as being the results of constructive cognitive processes. Rather, such processes allow us to access some content, which is not experienced as constructed or mental. Accordingly, Metzinger argues that a state is transparent just in case the processes that construct it or constitute it are ‘not available’ to the system through ‘introspective attention’ (Metzinger 2003). For example, the process of dreaming is a transparent state until the dreamer becomes lucid, i.e. aware of the fact they are dreaming, at which point the dreaming process becomes opaque (i.e. perceptible as a process that can be controlled) (Konkoly et al. 2021).

Generalizing from the concept as it figures in the self-model theory of subjectivity, we can say that some set of states and processes is partially ‘opaque’ when the cognitive agent (i) usually employs them transparently, to interact with things, events, and places appearing subjectively real in the world or the mind but (ii) is also able to represent these states to itself or ‘access’ them as well, as data for further inference. They are fully ‘transparent’ when condition (ii) does not hold. Certain cognitive processes, especially attentional ones, are related to the hallmark intentional features of opacity, in that they render other states opaque. (Note that these states themselves are not ‘necessarily’ opaque; as we will see below, to make them accessible requires a further set of processes.) Attentional states, for instance, are ‘about’ perceptual states—they are second-order states, just as precisions are second-order parameters pertaining to first-order parameters (their mean values). In other words, they are about the results of an inferential process (Parr and Friston 2017b). Or again, consider emotional states and processes, which are about interoceptive and exteroceptive states (Clark et al. 2018; Allen et al. 2019; Hesp et al. 2021). In all these cases, the states and processes at play in attention and emotion not only guide behaviour implicitly but they can be grasped as such, as when we introspectively reflect and leverage meta-awareness. This architecture of cognitive opacity is thought to be that which underwrites human cognitive capacities in general.

This paper takes steps towards the development of a formal, computational account of cognitive control as defined above in terms of cognitive opacity (i.e. meta-awareness) and mental action (e.g. the control of attention). This will take the form of a ‘computational (neuro)phenomenology’ of processes in question. Neurophenomenology is an influential approach to the naturalistic study of conscious experience (Varela 1997; Lutz 2002; Ramstead 2015). Computational phenomenology (Ramstead et al. 2021) aims to leverage advances in computational modelling to formalize the aspects of lived experience that are revealed by phenomenological description—e.g. classical phenomenological accounts of the lived experience of moving about as an embodied agent (Merleau-Ponty 1945) or having an inner consciousness of time (Husserl 1927)—by providing a model of the inferential processes that would have to be in play for an agent to have that kind of experience, allowing for the target phenomenology to be experienced as such (e.g. for such an account of inner time consciousness, see Varela 1997; Grush 2005; Wiese 2017).

Computational modelling of mental action

We build on recent advances in computational modelling that are shedding light on the inferential processes underpinning the perception and behaviour of embodied organisms. These technical advances make it possible to implement self-reflective, hierarchically structured inferences and simulate behavioural dynamics that can be formally linked to cognitive opacity and the execution of covert (mental) actions, such as attentional control.

At the root of these advances is a biologically plausible, neurocognitive and behavioural modelling framework called ‘active inference’ (Friston et al. 2016; Friston 2019). Active inference provides us with a Bayesian mechanics, that is, a mechanics of knowledge-driven action and active perception, which explains from first principles how autonomous agents can thrive within their ever-changing environments. Active inference descends from, and is closely related to, older and more familiar Bayesian theories of the brain, such as the Bayesian brain hypothesis (Knill and Pouget 2004) and predictive coding (Rao and Ballard 1999; Friston 2005, 2008; Bastos et al. 2012). It casts perception, learning, and action as essentially being in the same game—that of gathering evidence for the model that underwrites the existence of the agent (Friston 2013; Ramstead et al. 2018, 2019a). In this sense, active inference casts living and cognitive processes as self-fulfilling prophecies, which gather evidence for an implicit (generative) model that the agent embodies and enacts (Ramstead et al. 2019b).

Formal approaches to the study of the capacities for meta-awareness have recently been developed that leverage ‘parametrically deep active inference’ (Hesp et al. 2021). Parametric depth is a property of cognitive architectures, such that this architecture comprises nested belief or knowledge structures, that is, beliefs about beliefs and inferential processes that operate on (or take as their input) the results of other inferential processes, as data for further processing. By construction, such cognitive architectures are capable of a rudimentary form of access to self-states and meta-awareness. This is because having an internal structure (a generative model) that evinces parametric depth endows the agent with higher-level states that renders the results of lower-level inference (e.g. posterior state and precision estimates) available as data for further self-inference. This enables the agent to access and control crucial aspects of themselves (Limanowski and Friston 2018).

Parametrically deep active inference as it is currently formulated is limited to ‘implicit’ higher-order forms of cognitive access and control; e.g. it is able to model the deployment of attentional and emotional ‘processes’ that direct the flow of perceptual inference and action (Parr and Friston 2017b) but cannot yet model the agent’s access to, and evaluation and control of, its own attentional ‘states’. Here, we propose an extension of active inference that overcomes this limitation. To do this, this paper extends the parametrically deep active inference framework to account for the agent’s capacity for ‘explicit’ meta-awareness and mental action. This extension endows the agent’s generative model with a deep, tertiary, hierarchical architecture (see the ‘Methods’ section): policy selection (i.e. the formation of self-fulfilling beliefs about action) can then be formulated hierarchically, allowing us to construct an active inference model of an agent’s meta-awareness of, and control over, aspects of their own generative model (i.e. higher-level policies that drive transitions in cognitive states which condition precisions at the lower level).

This approach differs from existing work in active inference modelling of attentional control (Berk et al. 2016, 2019) or awareness of internal states (Smith et al. 2019a,b) in a few key ways. Crucially, the ‘depth’ evoked here is not a result of a decision of the experimenter to model temporal depth (Friston et al. 2017c; Pezzulo et al. 2018; Parr et al. 2020) or conceptual depth (Smith et al. 2019b; Heins et al. 2020) or even to model the desired phenomenology of attention and meta-awareness. Instead, the hierarchical structure comes from the decision to endow the model with ‘parametric depth’, i.e. precision-dependent state inference.

Attentional states (and meta-awareness states) then arise naturally as higher-level state factors, which condition the precision of observations at the level below (see the ‘Methods’ section). This is in contrast to positing attentional states as another state factor on the same level (Berk et al. 2016) or as a goal-dependent precision modulation (Berk et al. 2019). The focus here is on the interaction between meta-awareness and attentional control, and we do not explicitly treat the question of the role of selective attention in epistemic foraging.

Finally, a novel development here is the hierarchical formulation of policy selection applied to states that parametrize lower levels. This is similar to the two-level model presented by (Whyte and Smith 2020), with the distinctions that, here, the levels are purely parametric (i.e. higher-level state factors are only those that condition precisions of the level below) and that we extend this scheme to a third, meta-awareness level. This allows for the formulation of distinct categories of policies that condition transitions on a particular parametric level (e.g. attentional shift via mental action). This builds on previous work on attention as likelihood precision (Parr and Friston 2017a,b; Parr et al. 2018) and attentional control as precision deployment (Feldman and Friston 2010; Brown et al. 2011; Kanai et al. 2015) by providing a generalizable computational scaffolding for policies that condition precision beliefs.

In the example treated here of sustained attentional control, it becomes crucial to be aware of where one’s attention is focused and to recognize shifts in attention (i.e. distractions) quickly, to then recalibrate attentional processes accordingly. We demonstrate that, during a focused attention task, agents possessing a parametrically deep generative model exhibit the phenomenological cycles of focus and mind-wandering that have long been associated with focused attention and mindfulness meditation practices (Lutz et al. 2008). Furthermore, this deep architecture enables such agents to report on their higher-order observations, such as the extent to which they are aware of where their attention is focused. This extension to the active inference framework makes it possible to plausibly simulate the processes at play in meta-awareness and cognitive control. More generally, it provides a biologically plausible understanding, derived from first principles, of the computational architecture required for the emergence of central aspects of human phenomenology, namely, meta-awareness of cognitive states and explicit control of attention.

In summary, in this paper, we argue (i) that conscious mental action is predicated on a higher-level access to cognitive states, (ii) that the distinction between partially opaque and fully transparent states and processes can be formalized under deep active inference via a formal treatment of meta-awareness and its implications, and (iii) that understanding this inferential architecture constitutes a first step towards a formal, computational neurophenomenological account of cognitive control in general. The remainder of this paper is structured as follows. After reviewing the active inference framework, which forms the methodological and theoretical backbone of our proposal, we turn to numerical proofs of principle. We close by discussing the implications of our model for the study of consciousness, attention, and mental action generally under active inference.

Methods

The methodology we employ rests on a generative model that captures the inferential architecture required for the phenomenon of interest; in this case, the opacity-versus-transparency distinction and ensuing forms of monitoring and control. Having specified this model, in the following section, we implement this model in computational simulations that reproduce the target behaviour. We illustrate meta-awareness and cognitive control by examining the emergent dynamics of focused attention and mind-wandering. We will see that simulated agents endowed with this form of inferential architecture organically reproduce the relevant phenomenology.

Introduction to the active inference formulation

The key technical innovation presented in this paper is an extension of the active inference framework derived from the work of Hesp et al. (2021). It builds on previous work suggesting that to deliberately attend to a set of states, and thereby render them opaque, corresponds to the top-down deployment of second-order inference, i.e. inference about confidence or precision (Limanowski and Friston 2018, 2020).

Active inference models cast perception, learning, and behaviour as governed by a single imperative—to minimize variational free energy (Ramstead et al. 2018; Friston 2019). This variational free energy is an information theoretic construct that, in general, quantifies the divergence between observed and expected data, under a probabilistic model of the process that generated this data (the generative model). In a nutshell, it scores the probability of each model of how the data was generated by quantifying (technically, by providing an upper bound on, or approximation of) how much evidence for the model is provided by the data. This measure or score is the complement of variational free energy, and inference based on finding the model associated with the least free energy is known as variational inference. To minimize variational free energy, then, is equivalent to maximizing Bayesian model evidence (Friston et al. 2010; Friston 2019) or self-evidencing (Hohwy 2016).

Variational inference was originally developed in statistical mechanics to convert intractable inference problems into easier optimization problems, where the difficult problems associated with inferring the latent causes of data are converted into an easier optimization problem, namely, selecting the model associated with the least free energy (Feynman 1972). In the current context, we treat the brain as an empirical scientist that is trying to make sense of their world, through careful sampling of sensory data (e.g. visual palpation) and then selecting the perceptual hypotheses that have the greatest evidence (Gregory, 1980).

Generative models

In this context, variational free energy quantifies the discrepancy between observed outcomes (i.e. the sensory states of an organism) and the outcomes that would be predicted under a statistical (generative) model of how their sensory data were produced, which are thought to be implemented in the networks of the brain.

Generative models are so-called because they are models of the ‘generative process’ ‘out there in the world’ that cause (or generate) our sensory data (Friston et al. 2016). The generative process is typically specified using equations of motion that capture the dynamics of how the environment generates observations. The active inference agents themselves, of course, do not have access to the generative process and must deploy inference and action to guesstimate its structure, but in practice, when simulating these dynamics, we usually write down the ‘true’ process, as we will below. The generative models considered here are called Markov decision processes, a commonly used scheme that applies to discrete state-spaces.

The most basic generative model, written to account for perception, is depicted in Fig. 1. This elementary generative model quantifies the relation between observations (denoted o) and the latent or hidden states (s) that caused them. Here, this relation is captured by a likelihood mapping, denoted A, which encodes beliefs about how states of the world are related to the observations that they generate (i.e. ‘assuming that some hidden state s is the case, what is the probability of observing o?’). Technically, this likelihood mapping is implemented as a matrix (A) specifying the probability of a particular observation, given a hidden state; formally, this is denoted P(o| s). The initial state vector, D, in turn, specifies beliefs about the most likely state of the world independently of any observation, formally, P(s): these are known as prior (Bayesian) beliefs.

Figure 1.

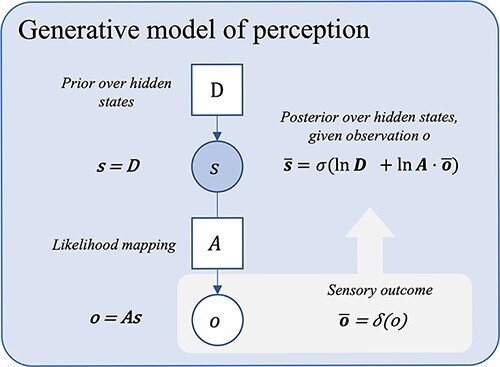
A probabilistic graphical model showing a basic generative model for moment-to-moment perception. This figure depicts a simple generative model for perception. Inference here inverts the likelihood mapping from causes to their outcomes, P(o | s), using prior beliefs about states (D) and sensory data (o), to obtain (or approximate) the most probable state P(s | o). Here, Bayesian beliefs are noted in bold, bar notation represents posterior beliefs, σ is the softmax function (returning a normalized probability distribution), and δ is the Kronecker delta function (returning 1 for the observed outcome, zeros for all non-observed outcomes). o is used to denote the predictive posterior over observations, and represents the actual observation. For the derivation of the latent state belief update equations shown, see Friston et al. (2016, Supplementary Appendix A). [Please note that, by convention in the active inference literature, the ‘dot’ notation is used to represent a backwards matrix multiplication and renormalization when applied to a matrix A of shape (m, n) and a set x of n probabilities, i.e. A· x = y, where y is a normalized set of m probabilities such that Ay = x. See Friston et al.(2017c)]. The graphical presentation was adapted from a template given in Figure 1a in the study by Hesp et al. (2021).

In this context, variational inference moves from the quantities that the system can access—i.e. its observations, o, its prior beliefs, P(s), and its beliefs about how its observations are caused by states of the world, P(o| s)—to the quantity that it is trying to infer, namely, the most probable cause of its sensations, P(s| o).

We can always associate some level of confidence to each of the parameters described above. As discussed, precision is defined as the ‘inverse variance’ of some distribution. Precision is also known as confidence and captures the degree to which the information encoded in the associated parameter is reliable. Of note is that precision already introduces some degree of parametric depth into the generative model because it is a second-order statistic: it is a belief about some other beliefs, namely, about how reliable they are.

In active inference, ‘attentional processes’ have been formulated in terms of the precision (here denoted γ_A) of—or confidence in—the likelihood mapping (the A matrix; Parr and Friston 2017b). Since they operate on the basis of second-order statistics (i.e. ‘precision’), attentional processes are seen as implicitly realizing a form of cognitive control in this framework. Intuitively, we can see why precision-modulation over A corresponds with attentional processes: the precision on A represents the extent to which the agent believes their observations ‘accurately map onto’ hidden states. Attending to some stimuli increases the relative weight or gain on inferences made on the basis of that particular data or observation. For example, by paying closer attention to an ambiguous sound, the agent has greater confidence in determining the location of its origin than when the sound was first heard without being heeded. The process of combining available data with estimations of that data’s reliability—in order to arbitrate its effect (relative to prior beliefs) on the overall inferential process—is known as ‘precision weighting or precision control’. Under active inference, this is the candidate mechanism for attentional modulation of perception (see Fig. 2).

Figure 2.

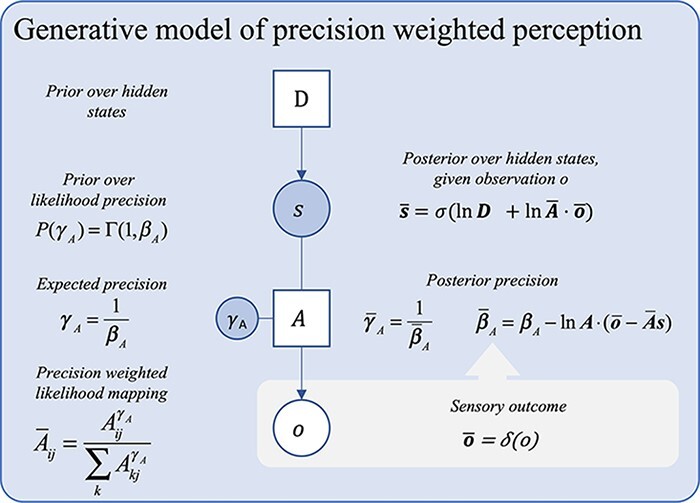
A Bayes graph showing a basic generative model of perception with precision. The precision term, γ_A, over the likelihood mapping A is sampled from a gamma distribution with inverse temperature parameter β_A. The precision weighted likelihood mapping, Ā, is obtained by exponentiating each element in the ith row and jth column of the A by γ_A and normalizing (see Parr et al. 2018). For the derivation of the precision belief update equation shown, see Friston and Parr (2017, Supplementary Appendix A.2). The graphical presentation was adapted from a template given in Figure 1a in the study by Hesp et al. (2021).

This basic generative model can only do posterior state estimation (i.e. perception) on a moment-to-moment basis: it does not encode knowledge that would allow its user to make predictions about the future. Active inference models, however, are not confined to processes unfolding from moment to moment. Indeed, these models have been extended to account for knowledge of temporal dynamics of states by inducing ‘beliefs about state transitions’, denoted B. These encode the probability of being in some state s₂ at some time step τ + 1, given that the system was in state s₁ at time step τ, formally, P(s₂ | s₁). Equipped with such Markovian models, an agent can effectively make inferences about future states of affairs.

Equipping a model with beliefs about state transitions opens up a whole new domain of inference, namely, controlling observations through the selection of actions. As such, active inference is a game of ‘policy selection’. A policy, denoted π, is defined as a set of beliefs about which actions one is currently undertaking. Policies are necessary because, in active inference, the agent must actively infer what course of action they are pursuing, on the assumption that what they are doing is likely to minimize variational free energy (Friston et al. 2016). Policy selection is implemented through the updating of beliefs about state transitions, now informed by the consequences of action. Intuitively, this implicit view of action is due to the fact that the agent does not have unmitigated or direct access to the actions that they undertake. Rather, they can only access the sensory consequences of those actions, and so, they must infer what they are doing, given their action prior and their sensory data. A policy, then, is just a series of state transitions (B matrices)—and policy selection means selecting the sequence of B matrices that is associated with the least expected free energy (G). Thus, as the name suggests, active inference casts action as a form of (variational) inference, as a self-fulfilling prophecy (Friston 2011).

Two additional parameters of note are the prior preference mapping (or C matrix), which specifies prior beliefs about sensory outcomes, and the prior over policies (E). Both these beliefs affect policy selection directly. The E matrix encodes beliefs about what the agent would do, independent of the expected free energy in the current context. The expected free energy scores the posterior probability of different allowable policies in terms of outcomes. Selecting a policy that minimizes expected free energy, G, minimizes ‘ambiguity’ and ‘risk’ (see Fig. 3). Here, risk is the difference between predicted and preferred outcomes under each policy. Preferred outcomes are parameterized by a C matrix that feeds into the calculation of the expected free energy for every policy: in short, prior beliefs implement a bias in the agent’s action model towards policies that realize preferred outcomes. We refer readers to Smith et al. (2021) for an in-depth introductory tutorial to active inference.

Figure 3.

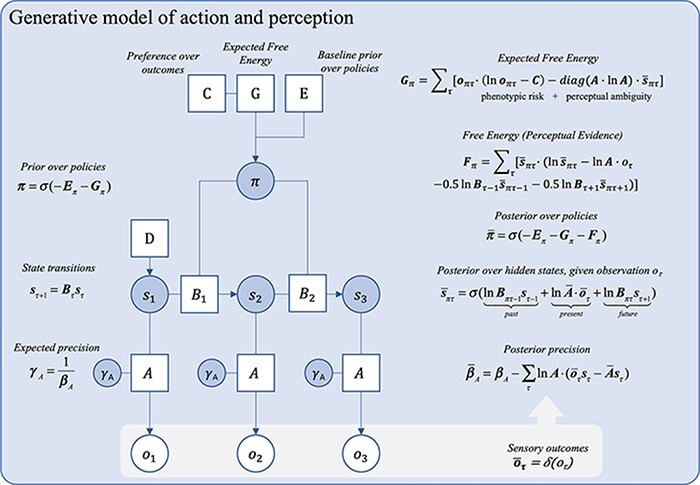
A Bayes graph showing a deep generative model for policy selection. This model is equipped with beliefs about state transitions. Posterior state beliefs at each time step now depend on beliefs about the previous and subsequent states, mediated by the state transition matrix B. Adapted from a template given in Figure 2 in the study by Hesp et al. (2021).

Formalizing meta-awareness, attention, and cognitive control under active inference

Finally, ‘attentional states’ and ‘states of meta-awareness’ can also be defined in terms of active inference (Hesp et al. 2021). In such a scheme, a further hierarchical level of states and corresponding processes of posterior state and precision estimation are introduced into the model. In this paper, we define two levels in addition to the first outlined above. The second level comprises ‘attentional states’ that entrain likelihood mapping precisions at the first level. The third level comprises what one might call ‘meta-awareness states’ (i.e. a state representing the degree to which one is aware of their own attentional state) that entrain likelihood mapping precisions at the second level. There is nothing special about these states, other than they generate outcomes at lower levels that speak—not to which state the world is in but—to the precision of beliefs about which state the world is in Fig. 4.

Figure 4.

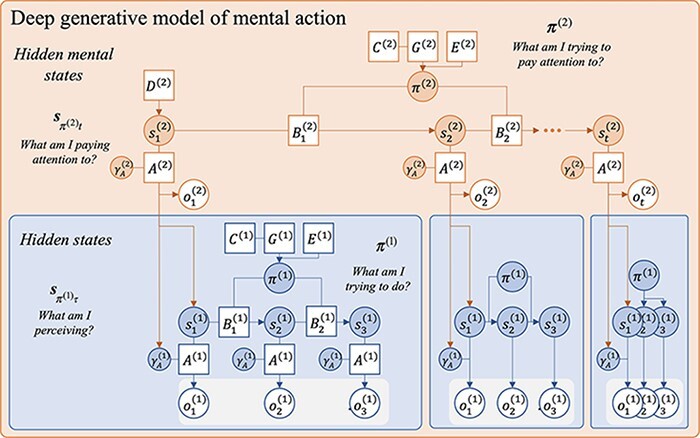
A probabilistic graphical model showing a deep generative model with second-order, attentional states. This deep generative model includes a new level of states, denoted s⁽²⁾, which conditions the precision on the first-order likelihood mapping A⁽¹⁾. Attentional policies, π⁽²⁾, represent mental (covert) actions that condition transitions between attentional states. Adapted from a template given in Figure 4 in the study by Hesp et al. (2021).

As we noted above, attentional processes always already involve some opacity, in the sense that they take as their input, and operate on, lower-level (perceptual) states. Deep active inference models add new hierarchical levels of state inference to exploit the parametric depth induced by the lower-level state and (especially) precision estimation. In the parlance of the self-model theory of subjectivity (Metzinger 2003, 2004), the use of precision and state estimation at lower levels as data or observations by higher layers of the model effectively renders the lower levels opaque. This in turn results in modulation of the precisions at the first level dependent on ‘attentional control states' at the second level. Having defined attentional states, and having connected them appropriately to the precisions they control at the first level, we can treat them the exact same way that we treat other states, namely, by estimating their posterior expectation through (variational) inference. In effect, this means that our active inference agent has to infer in what attentional state they find themselves.

The next, crucial step is to define a transition matrix B⁽²⁾ at the second level, which specifies beliefs about ‘transitions between attentional states’. Since attentional states are just ordinary states—defined at the higher level—we can equip the model with state transitions at that level as well.

Given this set-up, we can define ‘mental (covert) policy selection’. Attentional states transition one into the other as well, and we have defined the B⁽²⁾ matrix at the second level to capture the agent’s beliefs about those transitions. This set-up means ‘attentional control’ becomes ‘top-down state-dependent precision deployment’. Having defined mental state transitions, a mental policy can now be defined in the usual way—as a policy that conditions hidden state transitions at the second level, i.e. affecting the elements of B⁽²⁾. The key difference is that these hidden mental states themselves condition precisions at the lower level. This provides a formal treatment of mental action as the deployment of precision as proposed by Limanowski and Friston (2018), by defining an appropriate generative model showing that covert action arises naturally from the formal definition of attention.

Finally, we can define a further level of state inference, which we can associate with the meta-awareness of being in a given attentional state. These might be called ‘meta-awareness states’, which take as input the posterior state and precision estimates at the second (attentional) level. Recall that, to enable the agent to control the perceptual opacity on the first level, we defined a second level of the generative model, which observes state and precision estimates at the first level. The same reasoning now applies to attentional states. In order to capture the phenomenology of deliberate, sustained meta-awareness, as found in meditation practices (Lutz et al. 2015), we define a third layer of hidden states, which represents latent meta-awareness states of the agent. Transitions between states at this level represent shifts in the level of meta-awareness that the agent has of where their attention is focused. The resulting three-level model of meta-awareness and control is presented in Fig. 5.

Figure 5.

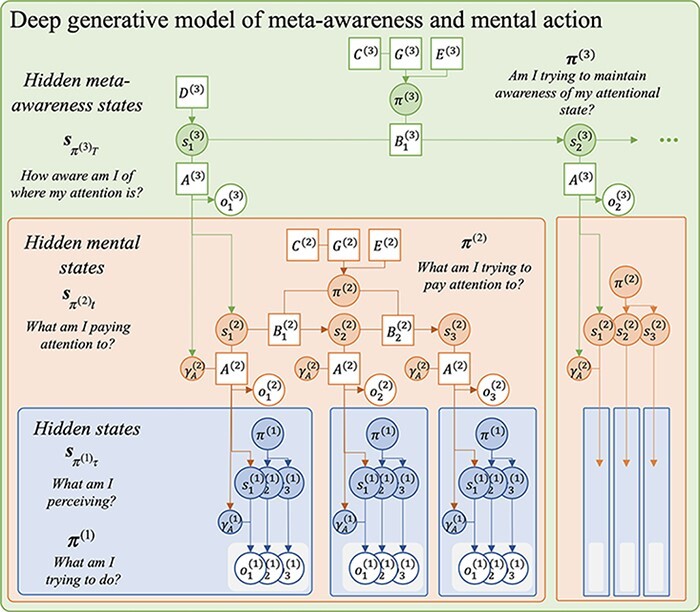
A probabilistic graphical model showing a deep generative model with three hierarchical levels of state inference. Higher-level states condition the likelihood mapping precision at the level below. Attentional states, s⁽²⁾, modulate the confidence in sensory observations, and meta-awareness states, s⁽³⁾, modulate the confidence in higher-order observations.

One might wonder whether such a level is necessary to model meta-awareness and attentional opacity, since a precise (opaque) attentional likelihood mapping A⁽²⁾ can be defined without the need for the third level. However, this level is required because it is necessary for the ‘explicit control of meta-awareness’. Attentional states are hallmark control states, but for some traditions, such as mindfulness meditation, the question is less about the mechanisms that selectively enhance or suppress some aspects of experience and more about accessing and assessing the quality of these attentional states and processes themselves. To deliberately control their attentional state, after all, the agent must be explicitly aware of it. This is to say that attentional states at the second level must also be made as opaque as possible, which is the work done by state inference and control at the meta-awareness level.

Mathematically, the attentional and meta-awareness state inference is calculated based on three sources of evidence: prior beliefs, direct perceptual evidence (e.g. the metacognitive observation of one’s attentional state), and ascending evidence based on the precision beliefs of the level below. For the ascending messages from the ‘continuous’ expected precision to the ‘discrete’ states, we use Bayesian model reduction (Friston et al. 2017b) (for the derivation, see Friston et al. 2018) to evaluate the marginal likelihood under the priors associated with each higher-level state. This gives, in the case of the attentional evidence for example,

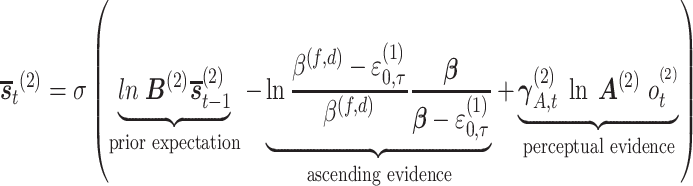(1)

where ε is the updating term for the inverse precision at the first level [see Friston and Parr (2017) for the derivation], β^(f,d) is the value of the inverse precision associated with each attentional state we simulate (see the ‘Results’ section), β^(f) = 0.5, and β^(d) = 2.0. This corresponds to a high precision ‘focused’ state (γ^(f) = 2.0) and a low precision ‘distracted’ state (γ^(d) = 0.5). These effectively set the upper and lower bounds for the likelihood precision.

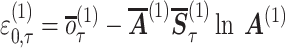(2)

This approach is analogous to that taken by Hesp and colleagues in their treatment of higher-level affective states (Hesp et al. 2021), here applied to the likelihood precision, γ_A, rather than model precision, γ_G.

Another key difference here is the inclusion of the perceptual evidence afforded by the direct observations caused by these higher-level latent states, e.g. o⁽²⁾. Note that this evidence is only available when the higher-level likelihood precision (e.g. 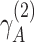) is non-zero, i.e. when the state is opaque to some degree. As a result, the transparency–opacity distinction can be directly related to the evidence calculation. For example, with zero precision, the cognitive state is not consciously observed; however, it can still be inferred implicitly (and therefore experienced transparently) from the evidence ascending from the level below. The transition from transparent to opaque is therefore related to the accumulation of perceptual evidence afforded by a non-zero, higher-level likelihood precision.

To summarize, this paper makes three novel contributions to parametrically deep active inference models of cognitive control. The first contribution is to stipulatively define attentional and meta-awareness ‘states’ as the mechanism of opacity control at different hierarchical levels. The second is to provide a formal definition of attentional and meta-awareness ‘control’ via an account of the higher-level policy selection. The third is to formally demonstrate the relationship between meta-awareness states and the capacity for deliberate attentional control. The resulting model is presented in Fig. 5. In what follows, we simulate belief updating during an attentional task using the above inference architectures to illustrate the emergence of meta-awareness-modulated cycles of focus and mind-wandering.

Results

This section provides numerical (simulation) results to show how the model described in the previous section engenders opacity–transparency phenomenology. This provides a formal account of meta-awareness and also a model for attentional control—formalized as state-dependent, precision control. We will present simulation results of an agent endowed with this deep three-layer generative model during a perceptual task. The following subsections will provide commentary on the results, beginning at the perceptual level and building up to the cross-level dynamics of the full deep model.

Level 1: attention, opacity, and awareness

With the above architecture in place, we can begin to examine how the process of sustained attentional control unfolds. Beginning at the first hierarchical level, we can simulate the effect of equipping a generative model with attentional states by examining numerically how varying precision on A⁽¹⁾ impacts the dynamics of perceptual posterior state estimation.

In the simulation below, depicted in Fig. 7, an active inference agent is shown in a ‘passive’ visual oddball paradigm, i.e. only perception without action is modelled. In such a paradigm, the agent is shown a repetitive visual cue, the ‘standard’ stimulus. This repeating cue is occasionally disrupted by the presentation of a different cue, the ‘deviant’ stimulus (or so-called oddball). Here, the standard and deviant stimuli are simulated by a perceptual state factor, s⁽¹⁾, with two levels representing the two possible states of the ‘visual’ cue shown to the agent. The generative process of this state is predetermined, with a deviant stimulus shown every 20th time step. This is meant to reproduce changes in the content of perception during phases of attention and distraction. Sensory habituation is not modelled here. At each time step, the agent infers the latent cause of their observations, i.e. the actual stimuli that were presented. To demonstrate the impact of a changing attentional state, the agent is held artificially in the ‘focused’ state for the first half of the trial. This endows them with a high level of sensory precision (high precision γ_A over the likelihood mapping A⁽¹⁾) and provides a simple illustration of the perceptual belief updating of a participant who is ‘paying attention’. In the second half of the trial, on the other hand, the attentional state is set to ‘distracted’ resulting in a lower precision over A⁽¹⁾. Mathematically speaking, changing the expected precision γ_A can have the same effect as updates in individual elements of A⁽¹⁾ in response to incoming evidence, which can render the likelihood mapping more or less informative. The core difference is that the expected precision applies to all the elements of the likelihood mapping, thereby providing empirical constraints on the mapping and a different kind of statistical structure to the generative model. If this structure is apt to describe the high-order statistics of the sensorium at hand, it will promote free energy minimization.

Figure 7.

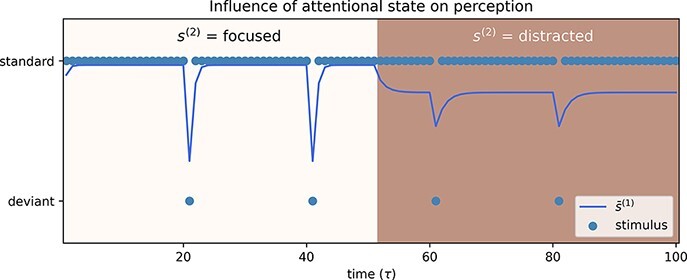
Simulation of an active inference agent attending an oddball paradigm. The agent is equipped with higher-level attentional states, s⁽²⁾, which modulate the precision of the likelihood mapping A⁽¹⁾. In the first half of the trial, the agent is in the ‘focused’ state, which confers a higher precision, i.e. the agent is generally more confident about how their observations map onto states. In the second half of the trial, the precision drops as the agent moves into the ‘distracted’ state. As a result, their beliefs about latent states are updated more slowly.

When ‘focused’, the agent is able to update their beliefs about what they are seeing immediately upon presentation of the deviant stimulus. When ‘distracted’, they do not have enough confidence in their observations to update their beliefs as quickly, and as a result, their beliefs about hidden states are not fully adjusted when the deviant is presented. This illustrates a ubiquitous aspect of precision control and attentional gain, namely, precision plays the role of a ‘rate constant’ in evidence accumulation and consequent belief updating. In other words, when attending to a particular stream of information, you will converge on posterior beliefs more quickly because certain aspects of sensory information are afforded more precision and have a greater influence on belief updating, at higher levels of hierarchical inference.

Level 2: simulating inference of hidden attentional states: the cycle of focused attention and distraction

We now introduce a version of the oddball paradigm described above, which implements a form of mental action. In this modified oddball paradigm, the agent’s task is to move their attentional focus to the stimuli (the repeating uniform stimulus) and to maintain focus on this object, thereby remaining in a specific attentional state (‘focused’).

Extant work on the phenomenological dynamics of focused attention tasks has shown that, in general, an individual will cycle back and forth between two states: remaining focused and becoming distracted (Lutz et al. 2008; Hasenkamp et al. 2012). This cycle goes through four distinct phases. To begin with, individuals are focused on a particular task or stimulus and successfully maintain their attention on a focal point or object. We label this attentional state ‘focused’. At some point, they will inevitably become distracted, transitioning to an attentional state that we label as ‘distracted’. Crucially, this state transition is, at least initially, unknown to individuals for a short period of time. This period is known as ‘mind-wandering’, a state of being distracted while also unaware of being distracted. Eventually, individuals realize they are no longer focused and become aware of having become distracted, a moment we label ‘aware of distraction’, which then prompts them to redirect their focus to the task at hand (i.e. returning to attentional state ‘focused’) (see Fig. 8).

Figure 8.

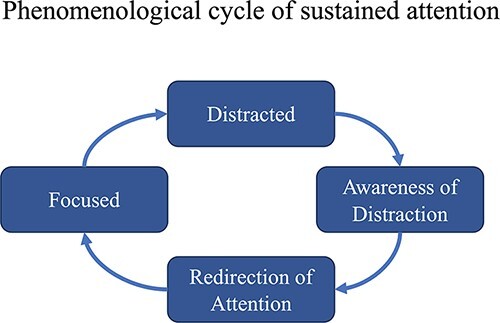
Diagram of the phenomenological cycle that occurs during sustained attention tasks. The process cycles through being focused, becoming distracted, becoming aware of the distraction, and then refocusing.

Asking participants to remain focused on a particular stimulus is equivalent, in this scheme, to asking them to maintain a higher-order attentional state (‘focused’). In order to remain focused and notice whether they have become distracted, the agent must continuously infer which attentional state they are in. By defining attentional states as controllable higher-order latent states (i.e. as states that can be selected through policy selection at the second level), we effectively allow the agent to control what they are attending to.

We can test whether this architecture gives rise to the attentional dynamics of attention and distraction we might expect. This well-documented phenomenological cycle of focused attention, described above, emerges organically from simulations when we cast attentional states as a higher-level latent states that the agent must infer.

In the simulation reported below, an active inference agent infers which attentional state they are currently in. We have built in a preference for the agent to observe itself in the ‘focused’ state (this is built into the prior preference or C⁽²⁾ matrix), which encodes the task instruction to focus on the stimuli. Thus, the agent expects to be in the ‘focused’ state and will engage in active inference such that this expectation or preference is fulfilled: if the agent infers that they have become ‘distracted’, they will enact a policy to return them to the ‘focused’ state. Second, we have programmed a ‘generative process’ that regulates the ‘true’ state transitions that the agent undergoes. Under this generative process, there is a policy-dependent probability that the agent will transition from one attentional state to the other (see Fig. 6).

Figure 6.

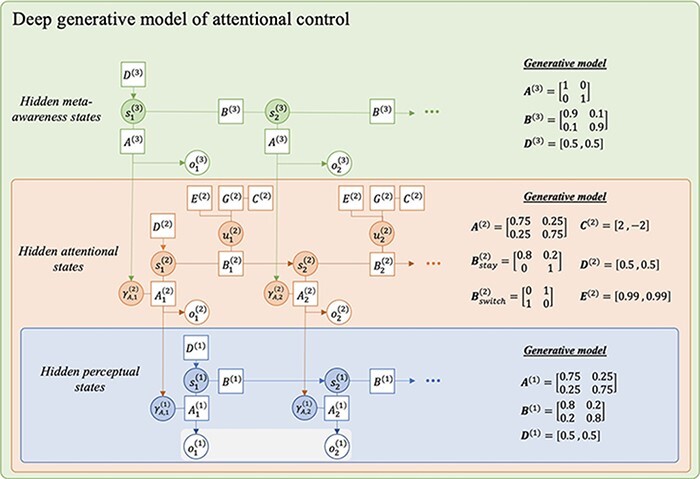
The probabilistic graphical model used to simulate an agent capable of attentional control during a focused-attention perceptual task. Hidden states at each level have a single factor with two levels, the perceptual state can be either ‘standard’ or ‘deviant’, the attentional state can be ‘focused’ or ‘distracted’, and the meta-awareness state can be ‘high’ or ‘low’. Higher-level states determine the likelihood precision at the level below. The agent is given the instruction to pay attention to a visual oddball stimulus; this is modelled as a preference in C⁽²⁾ to observe the ‘focused’ outcome at the second level. Action here is only defined on the second level, with two possible actions u⁽²⁾, ‘stay’ and ‘switch’, which condition the attentional transition matrix B⁽²⁾ as shown.

The results are shown in Fig. 10. Here, the agent becomes distracted several times during the trial. Since the agent must ‘infer’ their attentional state, however, this fact is not immediately inferred. Observations of the agent’sattentional state result in a prediction error that causes the agent to revise their beliefs after a few observations, with increasing confidence.

Figure 10.

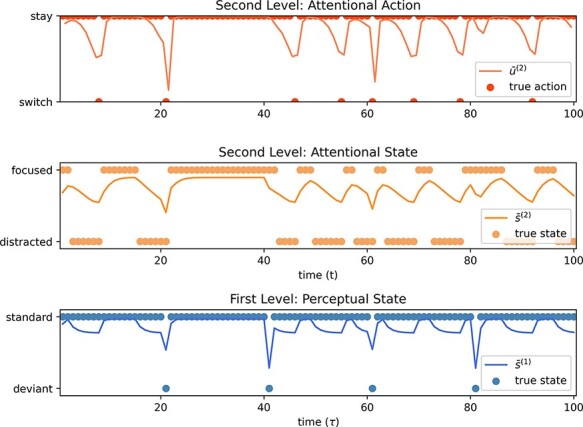
Simulation of the attentional cycle of an agent during an oddball perceptual task. Numerical demonstration of the cycle of distraction, meta-awareness of distraction, and redirecting focus. The active inference agent is inferring their own perceptual and attentional states at each time step. The state posterior lines are bounded by 100% confidence in either state. In this example, the agent is never fully confident in inferring the deviant perceptual posterior since it is only presented for a single time step, not long enough for more evidence to accumulate. At the beginning of the task, the agent is ‘focused’. At some time t, they become distracted. After a few moments, the agent infers a higher probability of being ‘distracted’ than ‘focused’ and given that they would prefer to observe the outcome associated with the ‘focused’ state selects a mental action, u⁽²⁾, to ‘switch’ their attentional state.

Here, the focused stage is the period during which the agent’s beliefs align with the true (‘focused’) attentional state. The mind-wandering stage is well captured by the numerical results, as the moments when the true attentional state has transitioned to ‘distracted’, while the agent’s beliefs have not yet been updated (the agent still believes they are ‘focused’). The agent is effectively unaware of their distracted state: their ‘mind’ has wandered. Over the following time steps, the agent collects enough evidence (i.e. higher-order observations of their attentional state and ascending precision evidence) to update their beliefs and to ‘realize’ that their attentional state has shifted (to ‘distracted’). Finally, now aware of their being distracted, the agent performs a mental action at the second level, to transition the attentional state back to the ‘focused’ state (see Fig. 9). This occurs once the agent infers a higher probability of being ‘distracted’ than ‘focused’. Note that the agent updates their attentional beliefs rapidly when the oddball is presented. The prediction error caused by the change in perception provides stronger ascending evidence arising from the change in first-level precision beliefs. This result is in line with empirical work, which shows that mind-wandering is increased when perceptual demands are low (Lin et al. 2016).

Figure 9.

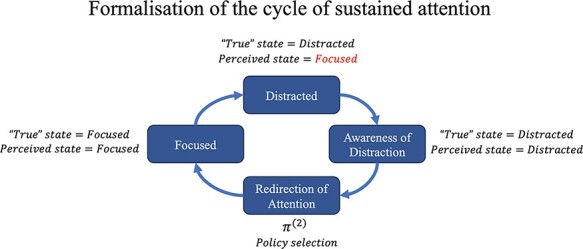
Illustration of the computational conditions associated with each phenomenological stage of sustained attention. This figure depicts schematically the main phases of the cycle of focused attention and distraction. Here, being distracted (i.e. mind-wandering) is characterized as the period following the shift in the true latent attentional state from ‘focused’ to ‘distracted’, but before the agent has updated their beliefs to align with the true latent attentional state, i.e. the period in which the agent believes that they are ‘focused’ while they are actually ‘distracted’.

Level 3: simulating the impact of changes in meta-awareness states on attentional control

As discussed above, the ability to maintain attentional focus and to quickly become aware of distractions has been associated with the level of meta-awareness of the individual (Mrazek et al. 2013). We now examine the impact of changing meta-awareness states on attentional state inference dynamics. We demonstrate that meta-awareness-dependent attentional control arises naturally from casting meta-awareness states as third-order states that modulate the likelihood precision of second-order attentional states, much like attentional states modulate the precision of first-order perceptual states.

In Fig. 11, a simulated agent performs the same focused attention task as just described, with one notable change: we introduce the third level meta-awareness states. As in Fig. 7, for the sake of a clear demonstration, we have defined the generative process at this level such that the agent is in a high meta-awareness state for the first half of the trial and low for the second half. It should be noted that we could have let the generative model roam its meta-awareness states freely. However, the effects emergent from these recursive interactions—however interesting for future research—would make simulation results hard to interpret for the reader. Therefore, we have opted for a clear meta-awareness manipulation for clarity.

Figure 11.

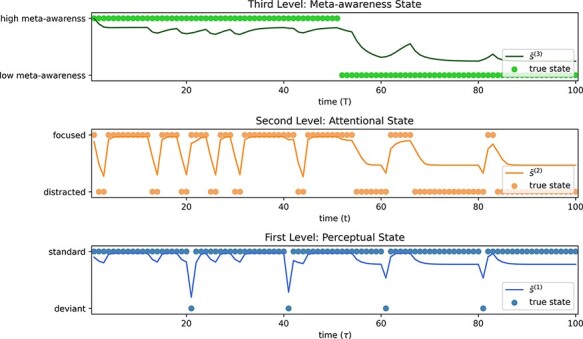
Simulation of an agent with changing levels of meta-awareness during an oddball perceptual task. This figure depicts an active inference agent that shifts from a state of high meta-awareness (i.e. high precision on A⁽²⁾) to a state of low meta-awareness halfway through the trial. Note that the period of state evidence accumulation is increased (i.e. longer mind-wandering) when the agent is in a low meta-awareness state.

We report that the decreased precision of A⁽²⁾ due to low meta-awareness (i.e. reduced opacity of the attentional states) results in an extended period of mind-wandering before the agent accumulates enough evidence to realize they have become distracted. In fact, in this example, the agent does not realize their mind has wandered until the contents of their perception changes (i.e. the oddball is presented), which provides further evidence that they have lost focus, prompting them to switch their attentional state. The reduction of the duration of mind-wandering, due to stronger meta-awareness modulation and increased precision afforded to attentional states, is an established relationship in attentional phenomenology, particularly in relation to focused attention meditation practices (Mrazek et al. 2013). This relationship is illustrated here as an organic dynamic that emerges naturally from the hierarchical architecture of higher-level states encoding precisions at lower levels. This completes our numerical analysis.

Discussion and directions for future research

Expanding the model to other parameters

The model presented makes it possible to simulate, under a single framework, both physical (overt) actions and mental (covert) actions—in effect providing a single model of perceptual inference and behaviour that can provide a computational bridge between mental and embodied life. This work provides a principled approach to modelling complex behaviours in tasks that require both motor action selection (e.g. saccadic movements) and the deliberate deployment of attentional resources (e.g. paying attention to a particular stimulus to the exclusion of another). Our model also provides insights into the form of cognitive architectures, which may be required to support the emergence of cognitive monitoring (i.e. phenomenological opacity of mental states) and control.

We have focused on attentional processes that implicate the likelihood mapping or A matrix. The natural next step is to consider the implications of generalizing this treatment, to model the access to—and control of—the precision of other parts of the generative model: e.g. the precision of beliefs about state transitions (B), preferences over outcomes (C), prior beliefs over states (D), prior beliefs about policies (E), and the expected variational free energy itself (G; as in Hesp et al. 2021). Mathematically, it is perfectly valid to condition the prior precisions associated with any part of the generative model on a higher-level state. Figure 12 depicts the structure of a generative model that might enable this.

Figure 12.

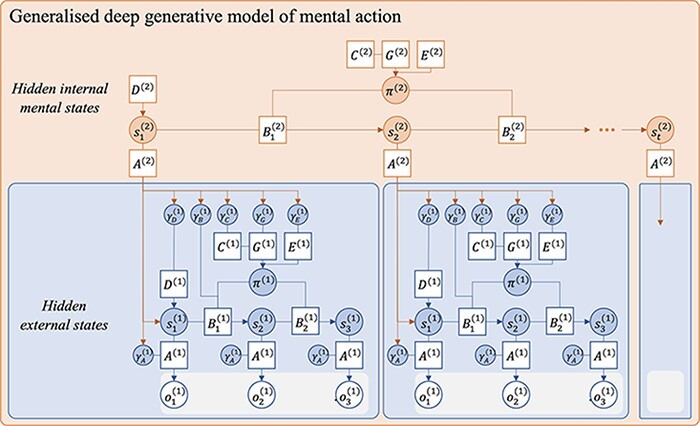
A Bayes graph of a deep generative model of mental action generalized over all precision parameters. With this architecture, higher-level states s⁽²⁾ contain multiple factors modulating all lower-level precisions. This structure provides a direction towards the formalization of a wide phenomenology of mental states and policies (π⁽²⁾). Adapted from a template given in Figure 4 in the study by Hesp et al. (2021).

The result of this innovation is a diversification of the mental actions available to the agent. Thus, higher-level states s⁽²⁾ stand for hidden mental states generally and are not restricted to modelling attentional states. Mapping the precision of the other parts of the generative model onto dimensions of phenomenological experience is beyond the scope of this paper. We anticipate that this strategy could provide a general framework to conceptualize different styles of higher-order regulations and mental actions. It could, for instance, provide a computational scaffold for examining how different cultural and social settings shape cognitive styles in different ways (Proust and Fortier 2018), with implications for our understanding of the development of meta-awareness and cross-cultural variability in psychiatric symptomatology. An exciting avenue will be to use this approach to refine and extend the modelling of various psychiatric conditions such as mood disorders (Kiverstein et al. 2020).

This modelling strategy, we emphasize, is completely general—and is not restricted to modelling attentional processes. It shares a commitment to understanding perception in terms of inference (Von Helmholtz 1924; Gregory 1968, 1980; Fleming 2020) and, in particular, the high-order aspects of perceptual inference. In terms of enactive perception (Wurtz et al. 2011), active inference provides a principled description of how actions are deployed to reduce variational free energy; in this generic scheme, there is no fundamental difference between a simple reflex, a series of complex movements, and a mental action—c.f., the premotor theory of attention (Rizzolatti et al. 1987). We model mental action as a generic hidden process that is at the root of many aspects of human mental life. Other such aspects, such as emotional self-awareness and control, would be implemented in the same way (i.e. through the deployment of precision). For example, in the work by Hesp et al. (2021), expected precision of the action model itself (G) has been associated with valenced responses. Our model is generic and adaptable, but it is not currently implemented to cover other kinds of mental action. We intend to explore such directions in future work.

The distinction between—on the one hand—accessing or perceiving one’s own mental states and—on the other hand—controlling them is crucial here. It is the control aspect that is novel in our approach in the computational modelling tradition. Indeed, computationally speaking, one could argue that hierarchical generative models (e.g. empirical Bayes) have been around for a long time and that they are useful in allowing us to implement perception and learning as inference in a way that enables to infer the (deep) causal structure of the environment. This part is not exactly novel. Such a hierarchical structure underlies mainstream approaches in machine learning via deep neural networks (e.g. convolutional neural network and recurrent neural networks, which build up a hierarchical model with hidden layers pertaining to different features at different scales). What is novel about our model is the coupling of this deep inferential architecture with ‘action and its control’, that is, we do not speak merely of deep or hierarchical inference but of deep ‘active’ inference. Our modelling strategy offers us a means of controlling previously uncontrolled parameters through the top-down deployment of precisions.

Towards a computational phenomenology

Another future possible application of the present framework is to provide a formal tool to explore, theoretically and experimentally, the ‘naturalization of phenomenology’ as proposed by the proponents of neurophenomenology (Varela 1996, 1997; Roy et al. 1999; Petitot 1999; Lutz 2002; Lutz and Thompson 2003). Naturalizing phenomenology is a scientific research programme that aims to characterize the mind–brain system on its own terms, as it were—the way that it appears to itself for itself, as a subject of experience, rather than only focusing on it as a mere thing (Roy et al. 1999; Ramstead 2015). What is at stake here is how best to characterize the relation between first-person data obtained from phenomenological accounts of lived experience to third-person cognitive and neuroscientific accounts. For instance, how might one relate the direct lived experience of watching a beautiful sunset to its physiological manifestation?

Because the proponents of neurophenomenology believe that first-person experience opens onto a field of phenomena that is irreducible to any other, they typically acknowledge the epistemological importance of bridging the kind of knowledge gleaned from first-person (phenomenological) and third-person (ordinary) data (Petitot 1999). Neurophenomenology has been described as the search for ‘generative passages’ between the neurobiological, phenomenological, and mathematical levels of description, going beyond the description of mere isomorphisms between these levels, towards mutual epistemological and methodological accountability and cross-fertilization (Varela 1997; Petitot 1999; Lutz 2002). Neurophenomenology aims to bridge the gap between these kinds of data via the formal, metaphysically neutral levels of the description provided by mathematics and computational work. The strategy of neurophenomenology (Varela 1996) then is to build and validate an integrative model of conscious experience based on ‘mutual constraints’ between the domain of phenomena revealed by experience, the domain of neurophysiological states that are measured by cognitive neurosciences, and the domain circumscribed by formal models (Varela 1996, 1997).

The pioneers of neurophenomenology had sought to bridge this gap using formal models and analytical tools from dynamical systems theory. From our point of view, these can be seen as anticipating, without the same degree of formal precision, several core principles of the active inference framework. The formalism available at the time was not yet well enough equipped to model explicitly those subtle phenomenological constructs such as transparency, opacity, meta-awareness, and mental action. In this view, the present model could extend and complement this earlier endeavour.

‘Computational phenomenology’ formalizes the aspects of lived experience that are made accessible by the phenomenological description and models of the inferential processes that enable the emergence of target phenomenologies (Ramstead et al. 2021). From the point of view of computational phenomenology, deep active inference models can act as maps of the processes and factors at play in the emergence and dynamics of lived or conscious experience. Indeed, the model presented here first started from the phenomenology of focused attention and emerged as a model of the architecture of beliefs and inferences that would make such a phenomenology possible and interpretable as such an experience. The degree of complexity of the model was commanded and constrained by the target phenomenology; in this case, we needed three hierarchical levels. The general form of this kind of investigation—using active inference directly as a means of formalizing the basic requirements that can explain the structure of lived experience—may point towards an interesting path for computational neurophenomenology.

Conclusion

The aim of this paper was to begin moving towards a computational phenomenology of mental action, meta-awareness, and attentional control based on deep active inference. Understanding these processes of cognitive awareness and control is critical to the study of human beings, since it is perhaps the most characteristic facet of the human experience. We used the modelling and mathematical tools of the active inference framework to construct an inferential architecture (a generative model) for meta-awareness of, and control of, attentional states. This model consists of three nested levels, which afforded, respectively, (i) perception of the external environment, (ii) perception of internal attentional states, and (iii) perception of meta-awareness states. This architecture enables the modelling of higher-level, mental (covert) action, granting the agent some control of their own attentional processes. We replicated in silico some of the more crucial features of meta-awareness, including some features of its phenomenology and relationship to attentional control.

Supplementary data

Supplementary data is available at NCONSC Journal online.

Data availability

Code and data available to view at https://colab.research.google.com/drive/1IiMWXRF3tGbVh9Ywm0LuD_Lmurvta04Q?usp=sharing.

Funding

This research was supported by a Research Talent Grant of the Netherlands Organisation for Scientific Research (no. 406.18.535) (C.H.), the LABEX CORTEX of Université de Lyon (ANR-11-LABX-0042) within the ‘Investissements d’Avenir’ program (ANR-11-IDEX-0007) (L.S.S., A.L., and JM), by a European Research Council grant (ERC-Consolidator 617739-BRAINandMINDFULNESS) (A.L.), by a grant from the French National Research Agency (‘MindMadeClear,’ ANR-17-CE40-0005-02) (A.L. and J.M.), by a Wellcome Trust Principal Research Fellowship (Ref: 088130/Z/09/Z) (K.J.F.), and by the Social Sciences and Humanities Research Council of Canada (M.J.D.R.).

Conflict of interest statement

None declared.