No ordinary proteins: Adsorption and molecular orientation of monoclonal antibodies

Antibodies adsorbing to the interface are shown to dynamically reorient and unfold to define a quasi-equilibrium state.

Abstract

The interaction of monoclonal antibodies (mAbs) with air/water interfaces plays a crucial role in their overall stability in solution. We aim to understand this behavior using pendant bubble measurements to track the dynamic tension reduction and x-ray reflectivity to obtain the electron density profiles (EDPs) at the surface. Native immunoglobulin G mAb is a rigid molecule with a flat, “Y” shape, and simulated EDPs are obtained by rotating a homology construct at the surface. Comparing simulations with experimental EDPs, we obtain surface orientation probability maps showing mAbs transition from flat-on Y-shape configurations to side-on or end-on configurations with increasing concentration. The modeling also shows the presence of β sheets at the surface. Overall, the experiments and the homology modeling elucidate the orientational phase space during different stages of adsorption of mAbs at the air/water interface. These finding will help define new strategies for the manufacture and storage of antibody-based therapeutics.

INTRODUCTION

The adsorption of proteins from aqueous solution onto fluid (air/solution or oil/solution) interfaces displays a phenomenology that differs substantially from the well-known adsorption properties of low–molecular weight amphiphiles (e.g., lipids and fatty acids) (1, 2). As with simple amphiphiles, protein adsorption is driven by hydrophobicity. The adsorption of proteins to fluid interfaces can reduce the interfacial tension. However, unlike simple amphiphiles, which adsorb to form reversible monomolecular layers, adsorbed proteins tend to reconfigure, bringing buried hydrophobic residues to the surface. This unfolding (denaturation) can result in irreversible adsorption, surface aggregation and networking, and multilayer formation, leading to a cohesive, thick surface film of high elasticity and viscosity not usually observed with simple amphiphiles (3, 4).

Early interest in protein adsorption at fluid interfaces targeted applications in the food industry. These protein systems are used to stabilize multiphase fluid systems by reducing the interface tension and forming cohesive surface films to facilitate highly stable dispersions (5, 6). These proteins include several food-compatible “protein hydrocolloids” such as lysozyme (LYZ), bovine serum albumin, α- and β-lactoglobulin, ovalbumin, myoglobin, and β-casein that can be used in foam or emulsion-based edible preparations, as well as creams and lotions for the topical delivery of drugs through the skin, and in skin, hair care, and cosmetic products (7). Protein-based multiphase fluid systems can also be used to stabilize foam scaffolds for cell transplantation and tissue growth (8), as well as being central to many human physiological processes, e.g., the functioning of the human lung (9).

Recent attention on the adsorption of proteins to fluid interfaces has targeted monoclonal antibodies (mAbs); as the fastest growing biologics in the pharmaceutical industry, mAbs have emerged as a leading treatment for human cancers, autoimmune disorders, and infectious diseases (10, 11). The focus of this study is the adsorption of mAbs to the air/aqueous solution interface. This adsorption occurs during the filling, storage, and administration of mAbs in vials, syringes, or intravenous bags, where the proteins adsorb to the air/aqueous solution interface at the head space (12, 13) or on entrained bubbles. In this context, the study of the adsorption is important because it can result in a substantial amount of the biologic residing on the interfaces in a native (active) or unfolded (inactive) form, inducing aggregation and subsequent risk of triggering an immune response in patients. These adsorption layers, when subject to further changes in interfacial area due to flow or agitation, have been observed to form and shed aggregates into solution, limiting the mAb dosage and decreasing shelf life (11, 14).

The dynamics of antibodies as they adsorb from bulk solution to a clean air/water interface has only recently begun to be understood, while, for protein hydrocolloids, the understanding is more complete because of the longstanding food science interest. Initial studies used radiotracer labeling and ellipsometry to measure the surface adsorption and dynamic tension measurements to correlate the adsorption with the tension reduction [e.g., (15, 16)]. The structural details of the adsorbed protein, on a molecular scale, have been more recently examined by optical fluorescence microscopy to demarcate phase behavior, neutron (NR) (17), and x-ray reflectivity (XRR) measurements (18) to determine orientation and layer thickness and infrared reflection adsorption spectroscopy (IRRAS), circular dichroism (CD), and sum frequency vibrational spectroscopy (19) to detail changes in the secondary and tertiary structure.

The general characteristics of the adsorption obtained from these techniques can be summarized in four observables. First, the initial adsorption of proteins to a bare surface is known to have an “induction” period where proteins adsorb into a low-density “gaseous” state in which the molecules are separated from one another and the surface tension negligibly changes from that of a clean interface [e.g., for LYZ (20) and β-casein (21)]. Fluorescence evidence (22, 23) indicates the presence of a denser phase coexisting with the gaseous state during the induction, which explains why the surface maintains the clean tension value. As adsorption proceeds, the denser state grows until it occupies the entire surface at which point additional adsorption creates an increasing surface pressure that terminates the induction period. Second, at longer times, a quasi-equilibrium is achieved where the tension slowly decreases with time. As the bulk concentration increases, these quasi-equilibrium tensions continue to decrease up to a critical concentration for which the tension plateaus through a range of bulk concentrations (16, 20). The plateau demarcates a condensation of the layer as the surface concentration is typically found to increase and is interpreted as a reorientation or a condensation of the adsorbed molecules to accommodate a higher density without lowering the surface tension. For both LYZ and bovine serum albumin, as well as other hydrocolloids, multilayers are observed to form for high concentrations beyond the condensation region. Third, the adsorbed protein can lower its free energy by “unfolding” and exposing buried hydrophobic residues to the air side of the interface. The extent of this structural rearrangement is proportional to the rate at which the protein unfolds relative to the prevailing adsorption rate (24). Protein arriving at an interface can begin to unfold at any time after their adsorption, but unfolding is energetically most favorable for protein molecules adsorbed during the early induction period because the large area per molecule (19, 25–27). Fourth, the observed formation of multilayers, secondary and tertiary structural rearrangement (at low bulk concentrations), and lack of a plateau in tension relaxation for long times provides strong evidence that the adsorption of the hydrocolloids is generally “irreversible” (28).

Relative to the protein hydrocolloids, the mAb we study here, immunoglobulin G (IgG), has a distinctly different molecular architecture that can influence how the protein adsorbs to an air/aqueous interface. IgG antibodies are multidomain proteins structured in a “Y” shape and are composed of two identical heavy polypeptide chains (≈50 kDa) and two identical light chains (≈25 kDa) linked together by interchain disulfide bonds (see Fig. 1A). The heavy chains consist of variable and constant domains with a connecting “flexible” hinge region. Each light chain consists of a variable and a constant region. The light chains are joined to the heavy chains by disulfide linkages to form the Fab arm (antigen-binding fragment) on one side of the hinge, and the heavy domains on the other side of the hinge form the Fc fragment (crystalline fragment) with disulfide linkages binding the heavy chains at the hinge region (see Fig. 1). The dimensions of the mAb used in this study, as obtained from homology modeling (see Materials and Methods and the Supplementary Materials), are shown in Fig. 1A and are typical of the IgG class. They illustrate that the Y shape is flat with overall dimensions of 150 by 125 Å and with a thickness of 40 Å (Fab) and 55 Å (Fc). This contrasts with many of the protein hydrocolloids, which have three-dimensional (3D) structures that are more spherical (e.g., β-lactoglobulin) or adopt a prolate spheroidal form with a major and minor axis (e.g., LYZ, ovalbumin, and bovine serum albumin) (29). This flat configuration suggests that at low adsorption densities, the molecules can orientate flat on the surface to maximize hydrophilic interactions with the water subphase, while at high surface concentrations, end-on or side-on configurations are feasible (Fig. 1B) with efficient stacking of their flat planes, as has been observed for adsorption from aqueous solution to hydrophobic solid surfaces (30–32).

Fig. 1. IgG mAb structure and orientations at the air/water interface.

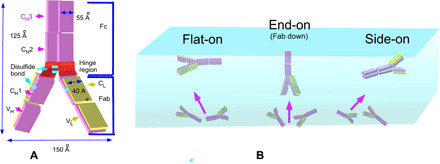
(A) Structure of an IgG mAb showing the variable and constant domains of the light and heavy chains and the interconnecting disulfide linkages. The dimensions of mAb shown in the figure are not up to the scale. (B) Possible orientations at an air/aqueous interface, including flat-on, side-on, and end-on configurations.

As with all proteins, surface activity derives from hydrophobic residues exposed to the solvent-accessible surface. Chennamsetty et al. (33) map the residues that expose themselves to the solvent face over a fixed period of molecular simulation and assign a spatial aggregation propensity (SAP) score based on the hydrophobicities of the residues. Proteins with larger SAP values are often prone to bulk aggregation and surface adsorption. A number of recent efforts have examined the adsorption dynamics of IgG antibodies adsorbing onto an air/aqueous interface, including the tension relaxation, the quasi-equilibrium surface tension as a function of bulk concentration (34–37), the surface concentrations of adsorbed antibodies and their orientation using XRR and NR (31, 37–39), the unfolding following adsorption using fluorescence and IRRAS (36, 40, 41), and the surface dilatational properties (42, 43) to understand conditions for the aggregate shedding. The measurements of the dynamic tension reduction demonstrated the presence of an induction period (14, 35, 37) and a condensation in the quasi-equilibrium–adsorbed layer for a range of high bulk concentrations (36) as was observed with the protein hydrocolloids. However, these studies did not characterize the orientation of the adsorbed antibodies during the induction period or whether a change in orientation occurred during the condensation. The NR (31, 38, 39) and XRR (37) studies have measured adsorbed layer thicknesses and surface concentrations but did not examine in detail reorientation as the bulk concentration increased. Unfolding of IgGs adsorbed to an interface is not well understood: IRRAS studies (36) demonstrated minor unfolding of IgG structure, while the fluorescence studies (41) demonstrated an increase in surface hydrophobicity with adsorption possibly linked to protein unfolding. The aim of this study is to provide, using in-tandem dynamic tension and XRR measurements, a more complete measurements of surface concentrations and protein orientation during the induction period and the condensation and higher concentration regions and to develop a more complete understanding of unfolding.

We first present pendant bubble dynamic tension measurements for the adsorption of our IgG mAb to the air/aqueous interface, and we demonstrate the presence of an induction period at early adsorption times and low bulk concentrations. To examine orientation, we use XRR measurements on layers adsorbed from solution to the planar air/aqueous interface in a trough for various times (surface ages) from the beginning of the adsorption process, using the pendant bubble measurements to infer the surface tension for the surface age of the XRR measurements. XRR measurements provide the adsorbed layer thicknesses and surface concentrations through the measured electron density profiles (EDPs). In addition, using the EDP information, we can infer the orientation via simulation. To provide more detailed information, we use a static (homology) model of the mAb to predict the EDP as a function of the angles (θ and ϕ) specifying the orientation of the mAb relative to the flat interface. Maps of the relative error between the computed and measured EDPs along the 2D landscape of θ and ϕ allow one to deduce the probable mAb orientations as a function of surface tension and surface age and provide insight into unfolding. The XRR measurement of the EDP, and its use in this way to determine orientation, represents a notable advantage of the XRR technique relative to ellipsometry. While both techniques measure the thickness and surface concentration of the adsorbed species, ellipsometry infers orientation by comparing these measurements in a more qualitative, geometric manner based on the size and shape of the molecule.

RESULTS AND DISCUSSION

Dynamic surface tension measurements

The IgG mAb used in this study is dissolved in histidine buffer at pH 5.8 for a range of bulk concentrations c_o (see Materials and Methods). The relaxations in the dynamic surface tension for this IgG mAb, adsorbing from solution onto the clean air/water interface of a pendant bubble, are obtained using a pendant bubble/drop tensiometer (see Materials and Methods). The relaxations are shown in Fig. 2A for bulk concentrations c_o in the range of 7.0 × 10⁻⁵ to 5.0 × 10⁻¹ mg/ml. The lower mAb concentration is chosen to uniquely define different orientations of mAb molecules at the surface. The highest concentration of mAb used in the study reflects the concentration of therapeutic proteins for intravenous administration. The relaxations at each of these concentrations are monitored from 1.0 to 1.0 × 10⁴ s. The relaxation curves show three distinct features. First, as the bulk concentration increases, the relaxations accelerate. This follows from the fact that the transport of the mAb to the air/water interface from bulk solution is a process of bulk diffusion and kinetic adsorption. As each of these processes is accelerated by an increase in the bulk concentration, the surface populates more rapidly with mAb molecules, and the tension correspondingly decreases more rapidly with c_o. The second feature is that, for each c_o, the tensions do not, in time, asymptote to a constant plateau value as is observed with low–molecular weight surfactants. The dynamic surface tension appears to reach quasi-equilibrium for each c_o. The absence of a plateau is a common characteristic of food hydrocolloids and IgGs indicating irreversible adsorption and is indicative of slow surface unfolding or rearrangement of the already adsorbed protein molecules at the air/water interface. The extended relaxation at the highest bulk concentrations (5.0 × 10⁻¹ mg/ml) may reflect the longer time it takes to unfold at the correspondingly high surface concentrations due to the packing constraints imposed by its neighbors.

Fig. 2. Pendant bubble tensiometer surface tension relaxation profiles of mAb.

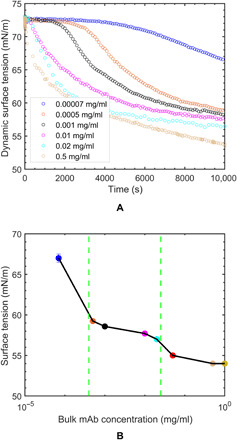
(A) Dynamic surface tension measured as a function of time at different mAb bulk concentrations and (B) quasi-equilibrium surface tension isotherm based on the long-time pendant bubble surface tension measurements and identification of condensation region from plateau behavior in tension. The surface tension values at 5 × 10⁻² mg/ml (red) and 1.0 mg/ml (yellow) are based on the interpolated and extrapolated values from the dynamic tension reduction as measured by the pendant bubble tensiometer. Error bars are based on two experimental results. For higher mAb concentration, the error bars are smaller than the marker size. The vertical dashed lines in green demarcate the start and end of the condensation region.

The third feature is that the relaxations show the presence of an induction period in the tension relaxation for low bulk concentrations of 7.0 × 10⁻⁵ to 1.0 ×10⁻³ mg/ml, where the tension remains nearly constant at the “clean” (i.e., buffer only) interface value before relaxing sharply. The pendant bubble volume remains constant throughout the duration of tension measurement (see Materials and Methods). However, the surface area of the bubble remains constant during the induction period, but the surface area increases during the process of lowering the tension due to the relaxation in shape (fig. S1 and the Supplementary Materials). For solutions of buffer alone, a tension of 72.5 mN/m is obtained, which is constant in time and corresponds to the tension of pure water at 20°C. The adsorbed proteins adsorb initially in a low-density (gaseous) state; as time progresses, the surface density increases, and a second, denser phase emerges. The two phases coexist—explaining the constant tension—with the denser phase occupying, in time, more space on the surface relative to the gaseous phase as adsorption proceeds. At the critical time (t_c), the dense phase completely occupies the surface, further adsorption in time increases the surface pressure, and the tension drops rapidly as the adsorbed molecules are packed more tightly. Note that the critical time t_c demarcates when the surface is covered with the denser phase. The critical time (t_c) decreases with an increase in the bulk concentration as the transport of proteins to the surfaces increases with c_o, and, hence, the surface more rapidly fills with the denser state. For bulk concentrations larger than 1.0 ×10⁻³ mg/ml, the induction periods are so short that they are not evident in the dynamic tension relaxations that, here, are restricted to a time resolution of 1 s.

Figure 2B plots the quasi-equilibrium tensions obtained from the dynamic relaxations as a function of bulk concentration (i.e., a surface tension isotherm) for this IgG mAb. The data show three regions in the concentration space, which are demarcated by the two vertical lines. For mAb concentrations beginning with a histidine buffer solution and extending to 5.0 ×10⁻⁴ mg/ml, a significant reduction in tension is observed (the tension of the histidine buffer, 72.5 mN/m, is not shown). Note that from Fig. 2A, the mAb concentrations in this region of sharp decrease in quasi-equilibrium tension are concentrations that clearly show the induction period, but the quasi-equilibrium measurements extend beyond the induction to lower tensions than the clean (buffer only) surface value. The second region in the concentration of 5.0 ×10⁻⁴ to 2.0 ×10⁻² mg/ml shows a tension plateau in which the tension decreases by a few percent. This is followed by a third region (c_o≥ 2.0 ×10⁻² mg/ml) in which the tension again decreases although not as rapidly as in the first region. Note that for the concentrations in the second region, the induction period becomes increasingly shorter with c_o until it is not observable in the last region. A few studies have constructed the quasi-equilibrium tension/bulk concentration isotherms for IgGs: Mahler et al. (34) demonstrated a sharp decrease in tension for low c_o but did not extend the measurements to larger concentrations and did not observe a plateau behavior, while Koepf et al. (36) measured the low c_o sharp decrease, and plateau at higher c_o, but did not observe the decrease in tension past the plateau at higher bulk concentrations (36).

The intermediate plateau region in Fig. 2B is distinctive. The increase in bulk concentration would be expected to increase the quasi-equilibrium surface concentration monotonically due to the fact that the increase in c_o raises the chemical potential in the bulk and the surface attempts to equilibrate by increasing the surface concentration (and hence decreasing the tension) to obtain an equilibrium. As noted earlier, the plateau is observed for food hydrocolloids (16, 20) and has been attributed to a condensation of the monolayer; the surface concentration does increase, but the monolayer readjusts extensively by realignment or condensation so a decrease in tension is not observed. The third region has usually been interpreted in terms of either a further increase in surface concentration in the readjusted adsorbed layer that increases the surface pressure or a formation of adsorbed layers underneath the surface. The surface concentration of the adsorbed mAb molecules and details of their molecular structure and orientation in this condensation region will be presented in the following XRR measurements and Simulated EDPs using a rigid homology model construct for the mAb subsections.

XRR measurements

To obtain quantitative information about the surface concentrations and thicknesses of the layers of IgG mAb adsorbed at the air/aqueous interface and determine the molecular orientations, XRR measurements at the interface are undertaken. XRR probes the variation in the electron density, along the dimension perpendicular to the interface (Z), averaged over the in-plane dimension parallel to the interface (X-Y plane), ρ(Z), or the EDP. From this profile, the thickness of the adsorbed layer can be obtained, and the surface concentrations can be determined by integration in the Z direction. Given the known structure of the mAb used in this study (Fig. 1A), the surface concentrations obtained from the EDP provide some information about the orientation (Fig. 1B). Subsequently, the EDP can be used to provide more precise information about orientation by comparing the EDP to homology modeling predictions from assumed orientations of the mAb.

For the XRR experiments (see Materials and Methods), a buffered solution of IgG mAb at a given bulk concentration is gently poured into a custom-fabricated miniature rectangular trough, and an adsorbed film forms by adsorption from the bulk to the interface. An incident x-ray beam from a synchrotron source (λ = 1.24 Å) is directed at an incident angle α to the interface (measured relative to the plane of the interface), and the specularly reflected radiation is measured with a detector. For a given scan, α is varied through a range such that the momentum transfer vector Q_z = (4π/λ) sin (α) covers the range 0.016 < Q_z<0.6 Å⁻¹. The reflectivity measurements as a function of the momentum transfer vector Q_z [i.e, R(Q_z)] are reported as the normalized reflectivity R/R_F as a function of Q_z, where R_F(Q_z) is the Fresnel reflectivity from an ideally smooth surface of pure water with a step function–based EDP. The measured reflectivity data are fit using the Parratt method (44, 45), where the electron density of the adsorbed layer is divided into multiple slabs and electron densities to calculate the reflectivity profile are compared with the measured profile. After the fit, the EDP as a function of interfacial depth Z is generated (for more details on the fitting procedure, see the Supplementary Materials).

Each reflectivity measurement requires a minimum of 40 min to cover the wave vector transform up to 0.6 Å⁻¹, and hence, an instantaneous XRR measurement is not possible. Including the time required for scan preparation, the surface ages from formation of the interface to the end of each scan are 1, 2, and 3 hours. The tension reported during each scan is taken as the value of the tension at the end of the scan. The tension at that time is obtained by first noting the time elapsed from the moment the solution was poured into the trough and the time at the end of the individual scan (the surface age). The surface tension corresponding to this surface age is then interpolated from the dynamic tension reductions as measured by the pendant bubble tensiometer (Fig. 2A).

Figure 3A reports the normalized reflectivity R/R_F as a function of Q_z for a range of bulk concentrations (7.0 × 10⁻⁵ to 1.0 mg/ml) in which the dynamic tensions are measured (Fig. 2A). The tensions at the end of each individual scan are also reported in Fig. 3A. For the mAb solution (1.0 mg/ml), the dynamic tension was not obtained, and the reported value is extrapolated from Fig. 2A. The general shapes of the reflectivity curves provide the first insight into the accumulation of mAb and reorientation at the surface. Thus, the reflectivity profile at bulk concentration (7.0 × 10⁻⁵ mg/ml) corresponding to the surface tension value of 72.5 mN/m (Fig. 3A), which lies in the induction period, shows a broad maximum at a relatively low Q_z value. A shift in the reflectivity profile to lower Q_z indicates a general increase in the layer thickness. As the bulk concentration of the antibody is increased and as the surface tension decreases further, another peak emerges from the broad maximum in the spectrum. For concentrations of 0.02 and 0.05 mg/ml (55 to 60 mN/m), reflectivity measurements show an additional peak for Q_z ≈ 0.08 Å⁻¹. Similarly, for the 0.5 mg/ml (54 mN/m) and 1.0 mg/ml (<54 mN/m), a third distinct peak emerges for Q_z ≈ 0.05 Å⁻¹. The appearance of these multiple peaks (at the lower tensions corresponding to higher bulk concentrations) can be attributed to a more vertical orientation of the adsorbed mAb as this orientation displays a more extended electron density distribution of the protein (Fig. 3B).

Fig. 3. XRR measurements from adsorbed layers at the air/water interface derived from adsorption from bulk solutions of mAb.

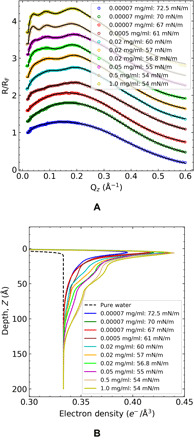
(A) Normalizing XRR, R/R_F symbols as a function of the wave function Q_z and slab model fits calculated by Parratt method (solid line) for mAb concentration along the function of time or surface tension value. The upper nine XR curves are shifted for clarity, although R/R_F → 1 as Q_z → 0 for all measurements. (B) Corresponding electron density determined by the fits for mAb layers as a function of interfacial depth. The black dashed line is the theoretical EDP curve from the pure water surface.

The Parratt fits of the normalized reflectivity curves are shown in Fig. 3A, and the corresponding EDPs from these fits are given in Fig. 3B. In the EDPs, Z = 0 represents the idealized interface (the position of the first slab), and positions Z > 0 correspond to regions deeper into the liquid phase. For each experimental XRR scan, the point on the Z axis at which the EDP merges with the electron density of water represents the thickness d of the adsorbed protein layer at the interface and defines the interfacial zone for the purpose of Gibbs constructions of surface excesses. The integrated area under the EDP curves between the curves and the water electron density asymptote represents the total number of electrons per unit surface area due to the mAbs in the adsorbed layer and excess water molecules in the interfacial zone and, hence, shows (along with the thickness d) the expected trend that the surface concentration of the adsorbed mAbs increases with either an increase in surface age (reduction in tension) at a fixed bulk concentration or an increase in concentration at the same surface age.

The EDP curves (Fig. 3B) show a characteristic behavior in which all the profiles exhibit a sharp first peak at approximately 5 Å (immediately underneath the surface), followed by a monotonic decrease in density, with the curves becoming more articulated with local changes in curvature as the thicknesses (surface concentration) increases. This same behavior in the EDP was also observed in the EDPs obtained from XRR data by Yano et al. (2, 25, 26) in the studies of LYZ, bovine serum albumin, and myoglobin including a sharp first peak in the electron density, just underneath the surface at ≈5 Å. The features of the EDP curves reflect the structure and orientation of the mAb at the interface and are best interpreted by comparison to constructs of EDPs derived from structural models of the protein at the interface (see the Simulated EDPs using a rigid homology model construct for the mAb section).

From the measured thickness of the interfacial zone, d, and the integration of the EDP through the zone, the surface concentration of protein, Γ, and water can be computed using the molar densities of water and the mAb, as detailed in the Supplementary Materials. The computed mAb surface concentrations [Γ, or equivalently the area per molecule 𝒜 = 1/(Γ)] and thicknesses d as a function of the bulk concentration and tension are given in Table 1. The error bars are calculated on the basis of one SD from the best fit value. In the following subsections, these data are used to provide information about the orientation of the mAbs during and after the induction period, as well as to construct a relation between the tension and the surface concentration and an adsorption isotherm.

Table 1. XRR mAb surface concentrations.

mAb concentration (mg/ml)	Time (×103 s)	γ (mN/m)	d±5 (Å̊)	Γ (mg/m2)	$\mathcal{A}$ (Å̊2 per molecule)
0.00007	3.6	72.5	70	0.98 ± 0.03	24,582 ± 656
0.00007	7.2	70	70	1.12 ± 0.05	21,589 ± 1030
0.00007	10.8	67	70	1.23 ± 0.04	19,508 ± 661
0.0005	7.2	61	110	1.63 ± 0.02	14,817 ± 157
0.02	3.6	60	120	1.79 ± 0.06	13,479 ± 145
0.02	7.2	57	120	2.00 ± 0.05	12,099 ± 302
0.02	10.8	56.8	120	2.13 ± 0.04	11,325 ± 178
0.05	10.8	55	140	2.36 ± 0.02	10,223 ± 71
0.5	10.8	54	150	3.12 ± 0.04	7752 ± 95
1.0	10.8	54	150	3.21 ± 0.06	7519 ± 221

Orientation in the induction period

Figure 2A shows an induction period at the three lowest concentrations (7 × 10⁻⁵, 5 × 10⁻⁴, and 1 × 10⁻³ mg/ml) with induction times of ≈4 × 10³, 1.5 × 10³, and 1 × 10² s, respectively. Because of the earliest time measurement of the XRR (≈3.6 × 10³ s), the induction period can only be probed by XRR for the lowest concentration. For 7 × 10⁻⁵ mg/ml, the surface concentration is plotted as a function of time in Fig. 4A at hour separations with the first point in time lying inside and near the end of the induction period of ≈4 × 10³ s. The tension at this point in time is the clean surface value (72.5 mN/m). The other two measurements of Γ in time at this bulk concentration are at longer surface ages (second and third hours) and lower tensions (70 and 67 mN/m). The surface concentrations steadily increase over the 3-hour period.

Fig. 4. Surface concentration of adsorbed mAb, surface tension, and bulk mAb concentration.

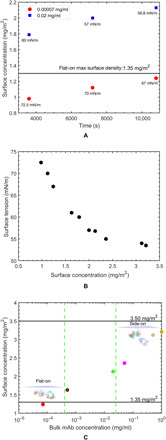
(A) XRR measurements of the surface concentration as a function of time for bulk concentrations of 7 × 10⁻⁵ and 2 × 10⁻² mg/ml. The horizontal line indicates the maximum packed density of the flat-on orientation ${\mathcal{A}}_{\parallel }$, 1.35 mg/m². (B) Dependence of the surface tension on the surface concentration and (C) quasi-equilibrium surface concentrations as a function of bulk concentration (adsorption isotherm). The horizontal lines indicate the maximum packing densities of the flat-on ${\mathcal{A}}_{\parallel }$, 1.35 mg/m², and side-on ${\mathcal{A}}_{\perp s}$, 3.50 mg/m², orientations. The error bars for surface concentration in (A) to (C) are smaller than the marker size and therefore are not visible in the plot. The actual error bars for surface concentration are shown in Table 1.

The measured surface concentration and thickness of the adsorbed layer just before the end of the induction period for 7 × 10⁻⁵ mg/ml are Γ = 0.98 ± 0.03 mg/m² (𝒜 = 24,582 ± 656 Ų per molecule), and the thickness is d = 70 Å. This measurement provides information about the orientation of the adsorbed mAbs during the induction period. The homology model of the IgG mAb used in this study calculates the size for the antibody Y shape of 150 Å by 125 Å by 55 Å with the Fab and Fc fragment thicknesses equal to 40 and 55 Å, respectively (Fig. 1A and the Supplementary Materials). For an mAb adsorbed in a flat-on orientation (Fig. 1B), the area per molecule would be 𝒜_∥ ≈ 18,750 Ų (150 Å by 125 Å, 1.35 mg/m²) at maximum packing and a thickness d_∥ ≈ 55 Å. mAbs in their end-on and side-on configurations (Fig. 1B) would have a thickness d_⊥e ≈ 125 Å and d_⊥s ≈ 150 Å and an area per molecule at maximum packing of 𝒜_⊥e ≈ 8250 Ų (150 Å by 55 Å, 2.80 mg/m²) for end-on and 𝒜_⊥s ≈ 6875 Ų (125 Å by 55 Å, 3.50 mg/m²) for side-on. The area per molecule at the end of the induction period, 24,582 Ų per molecule, is more than the theoretical area per molecule of the mAb in its flat-on orientation at maximum packing (𝒜_∥ = 18,750 Ų), indicating that the adsorbed mAb molecules are lying flat down and with a lower density than the maximum packing value 𝒜_∥. This orientation is also supported by the fact that the thickness, 70 Å (Table 1), is slightly larger than the homology model thickness of the Fc fragment. As the surface age increases for this lowest bulk concentration and the tension decreases past the induction period, the area per molecule decreases to 19,508 ± 661 Å. This value, which corresponds to the quasi-equilibrium surface concentration for c_o = 7 × 10⁻⁵ mg/ml, is still larger than 𝒜_∥, and the thickness remains at 70 Å. Thus, for this bulk concentration, at quasi-equilibrium, maximum packing of the flat-on configuration has not been achieved.

These measurements of area per molecule and thickness are consistent with measurements provided by Lu and colleagues (31, 38) who have used NR to obtain the layer thickness and surface concentration of an IgG mAb at quasi-equilibrium for a range of bulk concentrations for which the surface tension is near the clean surface value (i.e., remaining in the induction period). Lu and colleagues (31, 38) measured thicknesses of approximately 50 Å̊, indicating that the adsorbed layers were monolayers in a flat-on orientation, and the measured areas per molecule varied from values larger than 𝒜_∥ at low bulk concentrations to values just below 𝒜_∥ for higher bulk concentrations, indicating only the surface density of the flat-on orientation was increasing with bulk concentration for the quasi-equilibria realized within the induction period.

As a comparison, Fig. 4A shows the surface concentration as a function of time at hourly intervals for c_o = 2 × 10⁻² mg/ml. For this high bulk concentration, the mAb transport to the interface is so rapid that the induction period is not evident on the scale of the 1-s time resolution of the pendant bubble tensiometer (cf. Fig. 2A), and the tensions at the hourly points in time at which the XRR measurements are taken are much lower than the corresponding values for c_o = 7 × 10⁻⁵ mg/ml and are beyond this higher concentration’s subsecond induction period. The surface concentrations increase in time and are all larger than the surface concentrations at the same times for the lower concentration. These values, which range from 1.79 to 2.13 mg/m², are larger than the maximum packing on the flat-on configuration (1.35 mg/m²), which can be achieved if the mAbs adsorb in an end-on or side-on configuration, leading to more efficiently packing of the mAbs and results in the observed higher surface concentration. Furthermore, in the homology modeling part of this study, we show that the reorientation of the mAb populations can be mixed with both flat-on and end-on or side-on configurations. In time, as the surface concentration increases from 1.79 to 2.13 mg/m², the fraction of the flat-on configuration decreases (figs. S3 and S4). In addition to reorientation, the possible partial unfolding of the proteins on the surface can recruit additional proteins from the bulk to the surface leading to an increase in surface concentration. In the homology modeling section, we present evidence for this reorientation by examining in detail the modeling of the first peak in the XRR data, which is shown to correspond to β sheets at the interface. The thickness of the adsorbed layer for the hourly points in the condensation region is around 110 to 120 Ų. As the size of the Fc fragment is 55 Å, a second layer, with both layers in flat Y shape of the antibody, in the condensation region is a possible permutation, but our homology modeling of the EDP indicates strongly that the mAbs adsorb in end-on and side-on orientations in a mixed population with mAbs adsorbed in a flat-on state. This reorientation explains that the increase in thickness as a layer of mAbs adsorbed in end-on or side-on configurations would have a thickness corresponding to the lengths of the longer sides of the mAb, i.e., 125 to 150 Å. For the higher concentrations in which the surface concentrations are even higher, the monolayer thickness approaches the length of the longer side of the Y-indicating reorientation to the side-on configuration. This reorientation from flat-on to a side-on or end-on orientation for antibodies adsorbed at a fluid interface has only been demonstrated in an early study of an IgG antibody spread and compressed on a Langmuir trough (46).

Relationship between surface tension and surface concentration

From the results reported in Table 1, the tensions can be correlated directly with the surface concentrations irrespective of the time that the tensions are recorded. The direct correlation of the tension with surface concentration is shown in Fig. 4B and demonstrates that the mAb tension is determined uniquely by the surface concentration. This behavior has implications regarding the effect of unfolding on the adsorption process. For the evolving adsorbed layer, a critical surface concentration is achieved at longer surface ages for the lower bulk concentration c_o. As the surface ages to achieve the critical surface concentration, the mAb has an increasingly longer time to unfold, and the adsorbed mAb spends more time in an environment of low surface density, allowing a greater opportunity to unfold (19, 24–27, 47). Thus, at lower bulk concentrations, the critical surface concentration is developed over longer times, and these “aged” interfacially adsorbed mAbs are more unfolded. Conversely, mAbs at higher bulk concentration would, in principle, be structurally different, where the critical surface concentration is reached in much shorter times. The tensions corresponding to the same critical surface concentration would then be different because of the difference in structures. As the tension is uniquely defined from the concentration (Fig. 4B), suggesting that the unfolding does not contribute a structural change to the adsorbed layer affects the tension at least for the range of surface ages (a few hours) examined in this study (31, 38).

Adsorption isotherm and reorientation in the condensation region of the quasi-equilibrium tension-bulk concentration curve

In Fig. 4C, the quasi-equilibrium surface concentration is plotted as a function of bulk concentration from the data in Table 1 for the value of Γ at the quasi-equilibrium time of 10.8 × 10³ s. The surface concentrations corresponding to maximum packing of the flat-on (𝒜_∥ ≈ 18,750 Ų, 1.35 mg/m²) and side-on (𝒜_⊥s ≈ 6875 Ų, 3.50 mg/m²) orientations are also demarcated (Fig. 1C). At quasi-equilibrium, the surface concentration increases with the bulk concentration, and the values of Γ range from values just below 1.35 mg/m² to just below 3.50 mg/m², indicating the reorientation of the mAbs in the adsorbed layer from lying in a flat-on configuration at the surface to an orientation resembling the side-on configuration. This transition is also reflected in the thicknesses of the adsorbed layer at quasi-equilibrium, as recorded from Table 1. For a bulk concentration of 7 × 10⁻⁵ mg/ml, the thickness is equal to 70 Å̊, and the thickness of the Y shape of the mAb, indicating a flat-on configuration in agreement with the surface concentration approximating the theoretical maximum packing of the flat-on configuration, is 1.35 mg/m². For bulk concentrations equal to 5 × 10⁻³ and 2 × 10⁻² mg/ml, the thicknesses are 110 and 120 Å, respectively, resembling the length of the shorter end of the Y shape, indicating a more end-on or side-on arrangement of the mAb. These dimensions are consistent with the fact that the surface concentrations for these bulk concentrations lie above the concentration for maximum flat-on packing (1.35 mg/m²) but below the maximum packing for either the end-on (2.80 mg/m²) or side-on (3.50 mg/m²) configurations.

At the highest concentrations of 5.0 × 10⁻² to 1.0 mg/ml, the thicknesses increase to 140 to 150 Å, the length of the longer axis of the mAb, and the surface concentrations range from just below the maximum packing for the end-on configuration (2.80 mg/m²) to below the maximum packing of the side-on configuration (3.50 mg/m²). In terms of mAb bulk concentration at these highest concentrations, the mAb concentration chosen for reflectivity measurements is in steps of orders of magnitude as the transition to side-on or end-on orientations has already occurred at 5 × 10² mg/ml. In addition, the surface tension value corresponding to mAb concentrations (5.0 × 10⁻² to 1.0 mg/ml) for which the XRR measurements are performed is nearly of the same value (54 to 55 mN/m; Table 1). Notably, since the thickness of the adsorbed layer at these high bulk concentrations is ≈140 to 150 Å, the length of the longer axis of the mAb, there is no indication of a second layer forming at the highest bulk concentrations studied. Hence, at these higher bulk concentrations, the molecular picture of the adsorbed molecules is mAbs arranged in a spaced-out, end-on, or side-on configuration. This same conclusion was reached in our earlier study of this mAb [Kanthe et al. (37) in which the mAb was referred to as mAb-1], which examined, using XRR, the competitive adsorption of a surfactant excipient to the air/water surface at an mAb concentration of 0.5 mg/ml and presented data for the protein adsorption alone at this single concentration. Given the fact that the surface concentrations for bulk concentrations in the range of 5 × 10⁻² to 1 mg/ml are close to the maximum packing values for side-on and end-on orientations, the preferred orientation cannot be conclusively determined. NR reflectivity studies of the surface adsorption and thickness by Lu and colleagues (31, 38) and Wagner and colleagues (39) at high bulk concentrations of an mAb under quasi-equilibrium recorded similar surface concentrations either just below [≈2.50 mg/m² (31, 38)] or equal [≈2.82 mg/m² (39)] to the maximum packing for the end-on configuration. In these studies, the measured thicknesses of ≈55 Å (31, 38) and ≈110 Å (39) are less than the thickness measured in this study (140 to 150 Å̊) at the high concentrations, although these larger thickness measurements suggest a more side-on or end-on orientation.

Indicated in Fig. 4C are the delimiters, in the bulk concentration, of the plateau region in the surface tension/bulk concentration curve in which the tension is approximately constant (5 × 10⁻³ mg/ml <c_o< 2 × 10⁻² mg/ml; cf. Fig. 2B). The surface concentrations measured for this tension plateau region in the bulk concentration correspond to the end points of the region where the surface concentration increases from 1.63 to 2.13 mg/m², and the orientation changes from a flat-on to a more end-on or side-on orientation. This change in orientation accommodates the increase in surface concentration and allows the tension to change only marginally (Fig. 2B) since the end-on or side-on arrangement condenses the layer without increasing the surface pressure. After the plateau region, the tension decrease (and surface concentration increase) with bulk concentration, indicating that the adsorbed layer, with the molecules arranged side-on, is increasing their surface density and corresponding increasing the surface pressure. Hence, the high concentration region is dominated by an increase in density rather than a condensation from a flat-on to a side-on arrangement.

The separation of the surface tension–bulk concentration curve into three regions in the c_o space (Fig. 2B), as well as the corresponding monotonically increasing behavior in the surface concentration across this space (Fig. 4C), resembles the quasi-equilibrium tension/bulk concentration and adsorption isotherms of LYZ as measured by Miller and colleagues (20) using the pendant bubble tensiometer for tension and ellipsometry for surface concentration. A condensation region was observed in which the quasi-equilibrium tension remained constant and the surface concentration increased, and from the thickness and surface concentration measurements, this tension plateau was interpreted as a realignment of the LYZ prolate form from a flat to a vertical orientation at the surface. Because of the reorientation in the condensation region, fitting the data of Figs. 2B and 4 (B and C) to adsorption isotherms and equations of state (tension as a function of the surface or bulk concentration) requires the incorporation of the both flat-on and end-on or side-on states on the surface, as was undertaken by Miller and colleagues (20). The similarity between this IgG mAb and LYZ may reflect the similarities in the rigidity and shape of the proteins: LYZ is a “hard” globular hydrocolloid with a stiff tertiary structure due to four disulfide bonds, a large free energy for unfolding and a low foamability (2, 29). In this respect, LYZ is similar to this mAb IgG in which the disulfide linkages in the hinge region impart structural rigidity. Both proteins are anisotropic in shape (LYZ is a prolate spheroid and the mAb IgGs are flat Y shape) and can align either parallel to the interface for low densities or perpendicular for higher packing, explaining that both undergo a transition in orientation from flat to side at increased adsorption, which explains the condensation region. One difference, however, is that Miller and colleagues (20) present ellipsometric data at bulk concentrations larger than the condensation region that yields a second layer, while for this mAb IgG, the thickness measurement only indicates a monolayer.

Simulated EDPs using a rigid homology model construct for the mAb

The mAb surface concentrations and adsorbed layer thicknesses that are calculated from the experimental EDP (Fig. 3B and Table 1) provide a guide on the orientation of the adsorbed antibody at the surface as a function of the surface tension. More detailed information can be obtained by first constructing a 3D structural model of the native mAb and then locating and orientating this model at the interface in different configurations to directly compute the EDPs for comparison with the experimental profiles. While the primary structure (sequence of amino acids along the polypeptide chain) of the heavy and light chains of the mAb is known, a high-resolution construction of its native 3D structure using x-ray crystallography or nuclear magnetic resonance spectroscopy has not been obtained. Therefore, standard homology (comparative) modeling is used, in which amino acid sequences in the mAb are aligned to templates of similar sequences with known structures to create a static 3D model (see Material and Methods and the Supplementary Materials). The homology construct is shown in Fig. 5D and fig. S2. The structural model is then positioned at a flat interface (Cartesian axes x and y along the surface and z normal to the surface) (Fig. 5D) and oriented relative to the surface through rigid body rotation and translation of the coordinates of the atoms of the homolog. Beginning with the orientation shown in Fig. 5C, with the mAb completely beneath the air/water interface plane z = 0, the construct is first rotated around the y axis (θ) and then (at that orientation) rotated around the x axis (ϕ) (the rotations are undertaken in steps of 5° for both θ and ϕ from 0° to 180°). For each θ, ϕ, water molecules are then placed around the open regions in the interior and exterior of the homolog, which lie below the interface. The coordinates of the atoms of the 3D model are then processed to compute a simulated 1D EDP in the normal (Z) direction to the surface by summing electrons in slabs of thickness ΔZ. A third rotation, around the z axis, is not considered because of the rotational symmetry of the simulated EDP about this axis. For a particular θ and ϕ, a residual sum of squares (RSS) is calculated on the basis of the difference between the simulated and experimental EDPs. Retaining the θ and ϕ orientation, the z position of the center of mass of the mAb is moved relative to the interface in steps of a few angstroms, the water molecules are readjusted to lie below the surface, and the simulated EDP and RSS are again computed. The process is repeated to obtain a minimum RSS value, and, in this way, the mAb is located relative to the interface. Color maps of θ, ϕ at minimized RSS are shown in Fig. 5 (A to C) for low, intermediate, and high surface coverages. The closed lines on the maps identify contours in which the RSS is equal to 5%. The interior regions of these contours correspond to RSS values less than 5% and, therefore, demarcate regions in the θ, ϕ space of high-probability orientation. Configurations within these interiors are shown as A to G in Fig. 5D.

Fig. 5. Depiction of the rigid homology model for the mAb with protein rotational parameters (θ and ϕ).

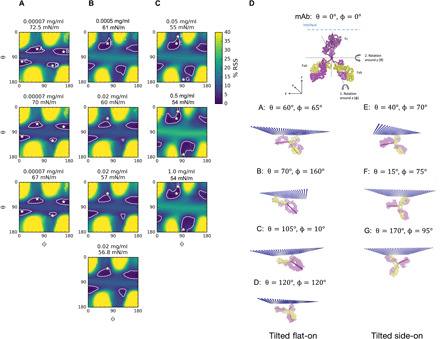
The variable and constant domains of the light and heavy chains are shown in yellow and magenta, respectively. A stick model is overlaid onto the detailed mAb structure to represent the Fab (yellow) and Fc (magenta) domains of the Y-shaped mAb molecule. Maps of the (minimized) RSS between the simulated and experimental EDPs for rotations θ, ϕ at mAb concentrations of (A) 0.0007 mg/ml (72.5, 70, and 67 mN/m); (B) 0.0005 mg/ml (61 mN/m) and 0.02 mg/ml (60, 57, and 56.8 mN/m); and (C) 0.05 mg/ml (55 mN/m), 0.5 mg/ml (54 mN/m), and 1.0 mg/ml (54 mN/m). The white contour lines in the maps correspond to 5% RSS that represent the optimum θ and ϕ pairs for mAb orientation. The asterisks (A to G) marked in the white contour lines demarcate representative orientations within the interior spaces, and these orientations are shown visually in (D). Orientations A to D correspond to tilted flat-on, and orientations E to G correspond to tilted side-on in (D).

In arriving at the results reported in Fig. 5, two notable facts emerge. The first concerns the minimization of the RSS by the vertical positioning of the mAb. For all the θ, ϕ orientations reported in Fig. 5, the minimized RSS corresponds to vertical positions in which the mAb is nearly completely below the surface and the coordinates of the atoms of the mAb closest to the interface, Z = 0, are within a few angstroms on either side. This minimum is sharp with respect to Z, and thus, the RSS data clearly indicate a strong preference of the mAb to lie just above or underneath the surface. For this reason, the configurations shown in A to G of Fig. 5D depict the mAb as immersed in the liquid phase. The second fact concerns the comparison of the experimental and simulated EDPs in the computation of the RSS. Figure 6 illustrates a low surface coverage example from Fig. 5A for a bulk concentration of 7.0 × 10⁻⁵ mg/ml and a surface tension of 70 mN/m. The dashed line in the figure corresponds to the experimental EDP curve for this bulk concentration and tension and demonstrates the sharp peak noted earlier at ≈5 to 10 Å below the interface. A simulated EDP that minimizes the difference with the experimental profile is also shown and corresponds to a flat-on orientation (“B”) in Fig. 5D.

Fig. 6. β Sheet formation at the air/water interface.

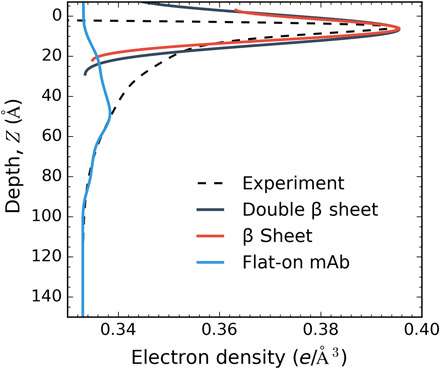
The simulated EDP for a β sheet represents the first 6-Å peak of the experiment EDP. A comparison of the β sheet (red), double β sheet (black), and flat-on mAb (blue) is included for comparison purposes to show that the broad EDP profiles do not represent the first peak of experimental EDP.

Figure 6 makes clear that while the calculated EDP can simulate the experimental profile for Z > 50 Å, it cannot reproduce the increase in electron density corresponding to the first 6-Å peak. No orientations in the θ, ϕ space can simulate this peak, and this is true for all the XRR experimental profiles in Fig. 5. These results are similar to the results of Yano et al. (26) on XRR investigations of the food proteins LYZ, myoglobin, and bovine serum albumin. Yano et al. (26) also observed the sharp first peak in the experimental EDP. In Yano et al. (26), 3D models of the native structure of the food proteins from x-ray crystallographic data are configured at the interface in a few orientations that position hydrophobic patches on the model surface toward the air side. The EDPs calculated in this way are not able to reproduce the first peak immediately underneath the surface. In addition, as with the results of Fig. 6, Yano et al. (26) found that the experimental profile is in agreement with the simulated EDP for distances further from the interface (i.e., >50 to 100 Å), particularly for LYZ and myoglobin. The congruence in these results between the food hydrocolloids and the mAb IgG of this study suggests that there is a common change in the native structure of these proteins, an unfolding, on adsorption to an air/water interface to account for the fact that the first peak cannot be fit with the native model. As the first peak reflects structure nearest to the interface, this reorganization in the native structure involves an unfolding of the part of the adsorbed protein nearest the interface. IRRAS studies of Lad et al. (47) and Postel et al. (27) and CD studies of Damodaran (48) suggest that the part of LYZ nearest the surface unfolds to β sheets, and this, as suggested by Yano et al. (26), represents one possibility to explain that the native structure cannot fit the first peak. The favorability of the β sheet configuration at the air/water interface is also suggested by studies that show the structuring of peptides into β conformations at an aqueous/hydrophobic solid interface, which would be analogous to the air/water interface as the air side is nonpolar (49). LYZ has a high α-helical content [≈40% (2)], and the IRRAS and CD studies note that the β sheet formation may be caused by an unraveling of the α helices. IgGs have a large β sheet content relative to LYZ β sheet (67%) and β turns (18%) and a small fraction of α helices (3%) and random coil (12%), so it is more likely that β sheets of the IgG may reposition at the interface to give rise to the first peak. To illustrate this possibility, a β sheet is cut from the mAb homology model and oriented flat, and just underneath the surface, and the EDP is calculated. This EDP is shown in Fig. 6 alongside a second curve corresponding to two stacked β sheets. The localization of β sheets at the interface is able to account for the first peak. β Sheets upon unfolding can expose hydrophobic amino acid residues (isoleucine, leucine, valine, phenylalanine, and alanine) and will therefore have a high propensity for relocating to the air/water interface where the sheet configuration allows these residues to be exposed to the air side of the interface. Thus, our XRR evidence suggests that the driving force for the mAb to adsorb to the surface is the energetic benefit derived from the hydrophobic residues of the β sheet relocating to the air side of the interface, and this relocation creates a large β sheet electron density at the surface. This evidence of unfolding of this IgG mAb agrees with the fluorescence evidence of the increase in surface hydrophobicity with adsorption of an IgG mAb relative to the native structure in the bulk (41). However, the IRRAS studies of an IgG adsorbed at an air/aqueous interface by Koepf et al. (36) demonstrated only a minor shift in the amide I peak—the peak is sensitive to the hydrogen bonding in the secondary structure—relative to the spectra of the native structure. In the case of LYZ, this shift is considerable (27, 47) and is consistent with the suggestion of a larger change in the secondary structure from α helix to β sheet. In the case of the IgG, with an already large β sheet content, the localization of the β sheet to the interface may incur only minor changes in the hydrogen bonding structure and thereby account for the small shift in the IRRAS spectra.

The RSS maps in the θ, ϕ space in Fig. 5 provide more information about the orientation of mAbs adsorbed to the interface. Consider first the three maps corresponding to the adsorption at the lowest concentration (7.0 × 10⁻⁵ mg/ml) (Fig. 5A) for increasing surface age (1, 2, and 3 hours; cf. Table 1) and adsorption. Each of the figures in Fig. 5A show four regions in θ, ϕ that correspond to the most likely orientations for the time sequence. The demarcated orientations inside these four regions (A to D) are shown pictorially in Fig. 5D with the interface depicted as a dotted surface. From Table 1, we have already noted that for this low concentration, the mAbs lie flat-on (Fig. 1B) during and past the induction period because the thickness of the interface (70 Å) is measured to be just larger than the thickness of the Fab fragment (55 Å̊), and the area per molecule is larger than the maximum packing of the mAb in the flat-on configuration (𝒜_∥). Note from Fig. 5D that a perfect flat-on geometry would correspond to θ = 90° for all ϕ (cf. Fig. 5D). The RSS maps in θ, ϕ (Fig. 5A) make clear that the regions of high probability are located at a tilted configuration from the flat-on geometry, i.e., two regions with θ = 70° ± 10° and two with θ = 110 ° ± 10° as shown by A to D. The RSS does not vary significantly for θ in these two horizontal strips in the θ, ϕ space, although RSS values less than 5% are obtained inside the contours as defined by a particular range of i. These correspond to adjustments in the relative positioning of the Fc and Fab fragments relative to the interface to minimize the difference between the experimental and theoretical EDPs.

Consider next the three RSS maps in the θ, ϕ space in Fig. 5C, corresponding to the quasi-equilibria in the surface adsorption at the highest bulk concentrations, 5.0 × 10⁻², 5.0 × 10⁻¹, and 1.0 mg/ml. In bulk concentration space, these points lie at values larger than the values that define the condensation region and correspond to increasing surface concentrations and decreasing surface tensions with c_o (Fig. 4C and Table 1). The RSS maps indicate that the regions of high probability have progressively shifted relative to the low concentrations of Fig. 4A. Two types of shifts are evident. The first concerns the two regions bordering near the vertical line ϕ = 90° (i.e., those containing either A or D). For the region containing A, the shift is toward the vertical ϕ = 90° line and lower values in θ→ 0°. For the region containing D, the shift is toward the vertical line and higher values in θ→ 180°. Note that a perfect side-on configuration would correspond to θ = 0° or 180° and ϕ = 90°. Thus, the shifting of the A and D regions corresponds to a reorientation to a side-on configuration that is tilted from ϕ = 90° and also tilted in θ. The orientations in the new shifted regions are characterized by configurations E, F, and G as shown in Fig. 5D, and examination of these configurations shows pictorially the tilting of the side-on configuration. The second type of shift concerns the regions bordering either ϕ = 0° or 180° (those containing C and B, respectively). These regions shift, either downward θ→ 180° remaining on the ϕ = 0° border (C-containing region) or upward θ→ 0° remaining on the ϕ = 180° border (B-containing region). These corners of the θ, ϕ space represent end-on orientations (Fig. 1B), with the Fab fragment up θ = 180°, ϕ = 0° and θ = 0°, ϕ = 180°, and these two relocated high-probability areas represent tilt orientations from these purely end-on configurations. Hence, the conclusion from the information provided from the θ, ϕ plots of orientation probability for these high concentrations beyond the condensation zone is that the adsorbed mAbs are in either tilted side-on or end-on configurations. As noted earlier, these orientations are consistent with the measured film thicknesses for these concentrations (140 to 150 Å̊) and with the surface concentrations ranging from 2.36 to 3.21 mg/m² below the maximum packing for the end-on state (2.08 mg/m²) to below the maximum packing for the side-on state (3.50 mg/m²; see Fig. 4C and Table 1).

Next, consider the two RSS maps in Fig. 5B corresponding to the quasi-equilibrium at the bulk concentrations of 5.0 × 10⁻⁴ mg/ml (61.0 mN/m) and 2.0 × 10⁻² mg/ml (56.8 mN/m). These quasi-equilibrium values define the borders of the condensation region in bulk concentration where the tension remains relatively constant but the surface concentration increases (Figs. 3B and 4C). Comparison of the maps of Fig. 5B with the maps of Fig. 5A show that the four regions of high probability still appear but have shifted in location with the top two regions (containing points A and B) moving up (θ→ 0°) and the two lower regions (containing C and D) moving down (θ→ 180°). The two regions bordering either ϕ = 0° or ϕ = 180° remain on the borders as they move up or down, while the two in the middle move toward ϕ = 90°. These trends continue for the higher bulk concentrations of the maps of Fig. 5C, which characterize a quasi-equilibrium for concentrations greater than the range of the condensation region. However, because, in Fig. 5B, the regions in the center have not migrated sufficiently toward ϕ = 90° and θ toward either 0° or 180°, they do not correspond to tilted, side-on configurations as they do in Fig. 5C. Similarly, the regions bordering ϕ = 0° (ϕ = 180°) have not moved far enough to θ = 0° (θ = 180°) to be characterized as tilted end-on as they have in panel (C). Rather than assuming intermediate orientations in the condensation region, one way of interpreting the RSSs of Fig. 5B is to assume that there are two surface populations, one in the flat-on configuration and one in a more vertical arrangement, e.g., either side-on or end-on. This interpretation follows from the fact that the mAb molecule is rigid. As higher bulk concentrations drive increased surface adsorption, adsorbed molecules “flip” to accommodate the increase in concentration. Thus, in the condensation zone, at the low concentration border, the mAbs are mostly flat-on, and, at the high concentration border, end-on or side-on begin to dominate. The flipping allows the surface pressure (tension) to remain constant although the surface density is increasing. For the food protein LYZ, with a rigid, elongated prolate shape, the existence of two populations (major axis of the prolate form along or perpendicular to the interface) has been proposed to explain the condensation region observed for LYZ for adsorption at the air/water surface (50).

The homology construct to examine the possibility of two populations with a theoretical EDP is computed assuming a population of a flat-on configuration (θ = 80° and ϕ = 160°) with population fraction X and a population with orientation θ and ϕ and fraction (1-X) (fig. S3 and, for more details, see the Supplementary Materials). The contour map as a function of the assumed θ, ϕ orientation of the second population is given in Fig. 7A for the two bulk concentrations [5.0 × 10⁻⁴ mg/ml (61 mN/m) and 2.0 × 10⁻² mg/ml (56.8 mN/m)], and the percentage of flat-on at the minimum for the θ, ϕ orientation of the second population is given in Fig. 7B.

Fig. 7. Fitting the EDP in the condensation region using the homology construct and assuming two populations of adsorbed mAbs, one with a flat-on configuration (θ = 80° and ϕ = 160°) and a second with configuration angles θ and ϕ (for details, see fig. S3).

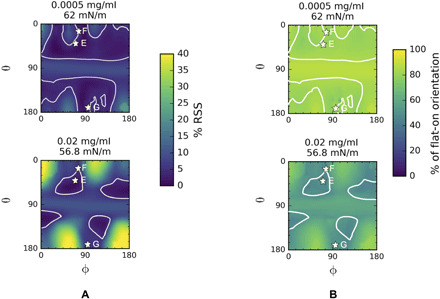
(A) Minimized RSS map in θ, ϕ space corresponding to the orientation of the second population. The RSS has been minimized in the relative fractions of the populations. (B) θ, ϕ Maps of the percentage fraction of the flat-on configuration corresponding to the minimized RSS in (A). At concentrations of 0.0005 mg/ml, which is the start of the condensation regime, the mAb adopts a higher percentage fraction of the flat-on configuration as compared to 0.02 mg/ml. This indicates that as mAb concentration increases in the condensation regime, a second population of mAb (side-on) evolves yielding fewer mAb molecules in flat-on orientation. The white contour lines in the maps correspond to 5% RSS that represent the optimum θ and ϕ pairs for mAb orientation. The asterisks (E to G) correspond to the second population indicating tilted side-on orientations of Fig. 5D.

For the lower concentration, 5.0 × 10⁻⁴ mg/ml (61 mN/m), which demarcates the beginning of the condensation, the regions with minimum RSS (<5%) lie above and below the horizontal lines θ = 70° and θ = 110° but are spread out in ϕ. Thus, while the tilted side-on orientations—e.g., E, F, and G—lie within these regions, tilted end-on configurations (Fab up), regions near θ = 0° and ϕ = 180° and θ = 180°, ϕ = 0° are not excluded. Therefore, the second population can be identified with the side-on and end-on (Fab up) orientations found in the postcondensation region (Fig. 5C). Characteristic values for the percentages of the two populations (flat-on and either side-on or end-on) can be obtained by averaging across the regions of minimum RSS as demarcated by the contours outlined in Fig. 7B. For the quasi-equilibrium at the beginning of the condensation, 5.0 × 10⁻⁴ mg/ml (61 mN/m), the flat-on configuration percentage is high—80%.

At the opposite end of the condensation region, 2.0 × 10⁻² mg/ml (56.8 mN/m), the minimum RSS in Fig. 7A clearly indicates that the regions of high probability are more localized in ϕ and coincide with the high-probability regions of the RSS in Fig. 5C for the side-on and end-on configurations realized for the adsorbed mAbs at the highest concentrations. Thus, the second population at the end of the condensation region is clearly the side-on and end-on orientations identified for the highest concentrations. From Fig. 7B, the average fraction of the flat-on population has decreased from 80 to 48% as is also clear from the shading in the interiors of the high-probability regions. This part of the homology modeling indicates that the condensation region can be captured with two populations—flat-on and either side-on or end-on—and in quasi-equilibrium, as the bulk concentration increases, the population transforms from the flat-on to the vertical orientation. Similarly, the two-population fits for 2.0 × 10⁻² mg/ml at two early times (1 hour, 60 mN/m and 2 hours, 57 mN/m) show that the average percentage of the flat-on configuration has decreased from 72% (1 hour) to 60% (2 hours), with the quasi-equilibrium percentage at 3 hours equal to 48% (figs. S3 and S4 and the Supplementary Materials). As these two datasets have tensions and surface concentrations that lie in the range of those in the condensation region, they support the hypothesis that the adsorbed layer could consists of two populations, i.e., flat-on and either side-on or end-on.

The adsorption of an IgG mAb from bulk aqueous solution to an air/water interface is studied using pendant bubble tensiometry and XRR. For a range of bulk concentrations, the EDP of the mAb at the interface and the surface concentration and adsorbed layer thickness is measured as a function of the surface age and tension. The quasi-equilibrium equation of state (tension versus bulk concentration) and adsorption isotherm is obtained. In addition, a homology model of the mAb has been constructed and placed in different (rigid body) rotational orientations at the interface to simulate the measured EDP and understand, in conjunction with the surface concentration, the orientation of the mAb at the interface and whether the mAb unfolds. Our aim is to understand how the interfacial properties are determined by the rigid, flat, Y-shaped architecture of the antibody, which can adsorb in two principal orientations (see Fig. 1). The first is the flat-on configuration with a thickness d_∥ and an area per molecule 𝒜_∥. The second are vertical orientations, either end-on with the Fab fragment (up or down) with thickness d_⊥,e and area per moleucle 𝒜_⊥,e or side-on with Fab on the side resulting in a slightly larger thickness d_⊥,s and smaller area per molecule 𝒜_⊥,s.

The primary conclusions are as follows:

1) For low bulk concentrations, the adsorption proceeds with an induction period in which the tension remains close to the clean surface value. The molecules adsorb flat-on during the induction with a thickness d_∥ and low density 𝒜 > 𝒜_∥.

2) The quasi-equilibrium relationship between the tension and the bulk concentration (from the pendant bubble) and the adsorption isotherm (from the XRR), together, exhibit three distinct behaviors (regions) as the bulk concentration increases. First, there is a substantial tension reduction in which the mAb adsorbs flat-on and the surface coverage is sparse (𝒜 > 𝒜_∥) but sharply increases with bulk concentration with the layer thickness remaining equal to d_∥. Second, a plateau is observed in the tension in which the mAbs reorient from a flat-on to side-on or end-on orientations, and the thickness increases to values within the range d_⊥,e to d_⊥,s. This reorientation condenses the layer with a moderate increase in overall surface density (𝒜_⊥,e < 𝒜 < 𝒜_∥). Third (the range of highest concentrations), the surface density of the vertically oriented mAbs increases (𝒜_⊥,s < 𝒜 < 𝒜_⊥,e) with a moderate reduction in tension. The thickness of the adsorbed layer remains in the range d_⊥,e to d_⊥,s, indicating that a second layer does not form.

3) The simulated EDPs using the homology construct show that the flat-on orientations are tilted with respect to the horizontal with the surface and the vertical orientations tilted with respect to the interface’s normal and with the Fab fragment of the mAb up. In the condensation region, the population can be described as containing a mix of flat-on and side-on populations with the percentage of the flat-on decreasing as the condensation proceeds.

4) The XRR results indicate that the overall structure of the mAb is retained on adsorption since the thicknesses of the adsorbed layer coincides with the thicknesses of the flat-on or side-on and end-on orientations. However, the simulated EDPs indicate that the first peak in the experimental profile cannot be reproduced for any of the surface concentrations, indicating a common rearrangement of the secondary structure of the mAb on adsorption. Additional simulation of the EDP of a β sheet at an interface reproduces this peak and suggests an alignment of β sheet(s) of the mAb at the interface.

MATERIALS AND METHODS

Materials

The mAb used is provided as a stock solution of 5 mg/ml by Bristol Myers Squibb (BMS), New Brunswick, NJ, USA. Histidine and NaOH for pH adjustments are purchased from Sigma-Aldrich and Thermo Fisher Scientific. The buffer solutions are filtered using 0.22-μm polytetrafluoroethylene filters. A series of dilute solutions of mAb are made using a 20 mM l-histidine/l-histidine monohydrochloride formulation buffer at pH 5.8 for the experiments, and the concentration is determined on the basis of the extinction coefficient at 280 nm provided by BMS (1.75 ml/mg per centimeter). The solutions are frozen using liquid nitrogen and are thawed as required. All sample dilutions are performed using Milli-Q ultrapure deionized (DI) water (Millipore Corp.; resistivity, 18.2 milliohm·cm).

Dynamic tension measurements

An Attension Theta (Biolin Scientific, Stockholm, Sweden) pendant bubble tensiometer is used to measure the dynamic surface tension relaxations of mAb solutions. Briefly, a pendant bubble of ≈22-μl volume is formed using an inverted hollow needle (16 gauge) placed in the mAb solution and connected via tubing to the syringe. A Hamilton gas tight syringe is used to push air through the tubing and the needle. A feedback control loop is used to ensure that the bubble volume remained constant throughout the duration of the experiment. The bubble images are recorded for 6.5 frames/s (fps) for the first 5000 s of the measurement and later, at a frame rate of 3.5 fps for the remaining 5000 s. The shape of the bubble is fit to the Young-Laplace equation to obtain the surface tension values as a function of time. The syringe, needle, and the solution cell are rinsed and cleaned using DI water, followed by sonication for 60 min. Before each measurement, the surface tension of the clean air/water interface using DI water is performed to confirm that the tension was in the range of 72.5 ±0.3 mN/m, the reference value of water at 20^∘C. All mAb surface tension measurements are performed at room temperature (20°± 3°C).

X-ray reflectivity

XRR measurements are performed at the National Science Foundation (NSF)’s ChemMatCARS, station 15-ID-C experimental hutch at the Advanced Photon Source in Argonne National Laboratory (Argonne, IL) (44, 51, 52). Custom-built mini-Teflon trough inserts (7 cm by 3 cm by 0.1 cm) are used to fit into the existing XRR setup at the beamline hutch. These minitroughs also ensured that the mAb solution sample requirement is minimal (≈5 ml). All solutions are freshly prepared, and the buffer is degassed for at least 1 hour before the setup. The trough is contained within a hermetically sealed aluminum box under helium, ensuring that the oxygen level is <1% (v/v) to reduce beam damage and atmospheric scattering of x-rays. The experimental setup is placed on a vibrational isolation table, and the reflected signal is collected using a PILATUS 100K area detector. All the measurements are carried out at room temperature (20°±3°C).

Simulated EDP

The construction of the homology model for the mAb is based on the MOE (Molecular Operating Environment) software (53), and the method for calculating the EDPs for two rotational degrees of freedom of the construct at the interface follows Tietjen et al. (54). For additional details, refer to the “Simulated EDPs using a rigid homology model construct for the mAb” section.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/35/eabg2873/DC1