Abstract
Using daily data of novel coronavirus pneumonia (COVID-19) covering 118 countries from January 1 to April 13, 2021, this research examines the relationship between the government response stringency index (GRSI) and COVID-19 pandemic. The empirical results show that GRSI significantly negatively impacts confirmed cases, and the effects are especially larger around 14 to 21 days after the implementation of the government response. These results are robust through analysis with sub-samples of Asian countries and non-Asian countries, proving that public prevention policies of being isolated for 14 days and being observed for 7 days are effective. The Dumitrescu-Hurlin causality test uncovers a statistically significant bi-directional correlation between government response stringency and COVID-19 pandemic when analyzing the full samples. In terms of the sub-samples, a bi-directional relationship exists between government response stringency and confirmed cases, while one-way causality runs only from government response stringency to deaths in Asian countries. We offer a policy implication that countries all over the world should continue to carry out public prevention policies, and governments in non-Asian countries should be more concerned about confirmed cases.
Key words: Government response stringency index, COVID-19 pandemic, Augmented Mean Group Estimator, Causality test
1. Introduction
After the first cases were identified in December 2019, COVID-19 quickly struck the world with exceptional speed. On March 11, 2020, the World Health Organization (WHO) declared it a pandemic and by December 20, 2020, over 9 million people in more than 100 countries had been infected and nearly 470,000 people had lost their lives. The COVID-19 pandemic has had a huge impact on humans’ health and lives as well as the global economy. The International Labor Organization estimates that 309 million people became unemployed in the second quarter of 2020 due to the COVID-19 pandemic, and most self-employed enterprises were impacted by prevention policies, such as lockdowns (Ceylan et al., 2020). Global income in 2020 is now forecasted to drop 6.7% year-on-year (McKibbin and Fernando, 2020).
Faced with such a severe pandemic and the negative effects it has brought about, governments are scrambling about what should they should do. The existing literature shows that governments play important roles in dealing with public emergencies, such as natural disasters and severe pandemics (Fredriksson et al., 2004; Vowles, 2008; Chang et al., 2018). Therefore, the implementation of a public health policy is inseparable from the government and greatly influences health systems and population health (Lakshminarayanan, 2011). Studies show that a government can influence and change health-related behaviors through various measures (Diepeveen et al., 2013), such as setting new standards for the public, which bring about changes that individuals on their own cannot make in order to safeguard the public health (Jochelson, 2006). The development of a national health system through expanded governmental health programs substantially improves the health status in both developed and developing countries (Roemer and Roemer, 1990).
Governments from different regions should also play critical roles in pandemic prevention and control (Stock, 2020). Most governments have responded rapidly with various measures taken to deal with the emergency pandemic, including school closures, workplace closures, canceling of public events, emergency investments in healthcare facilities, and so on (Hale et al., 2020). In general, measures taken by governments can be categorized as two main principal types: one is aimed at strengthening the capacity of the hospital system, such as setting up temporary hospitals; the other one targets to reduce the probability of contracting the virus, such as a lockdown (Alfano and Ercolano, 2020). Many scholars have investigated the influence of recent government measures, and their main concerns are the impacts of specific measures on the spread of the COVID-19 pandemic and economic development (Yilmazkuday, 2020; Elgin et al., 2020). Hussain (2020) believes that people's restricted mobility to school and workplaces can slow down the spread of the virus and flatten the curve of the COVID-19 pandemic, which is consistent with the view of Alfano and Ercolano (2020). Elgin et al. (2020) analyze the relationship between public health controls and economic responses and find that governments’ economic responses are affected by public health controls. Ceylan et al. (2020) compare known epidemics, evaluate the potential economic effects of COVID-19, and assume that the negative effects of COVID-19 are related to severe unemployment, which may result in poverty and insecurity. McKibbin and Fernando (2020) also hold the point that government response stringency does hinder economic activities and result in widespread factory closures. There are many research studies on the effectiveness of non-pharmaceutical interventions. Flaxman et al. (2020) analyze the effect of major interventions in 11 European countries and find that major non-pharmaceutical interventions, especially lockdowns, can reduce transmission effectively. Haug et al. (2020) and Brauner et al. (2021) estimate the effects of non-pharmaceutical interventions on COVID-19 transmission using different samples and come to a similar conclusion.
Previous scholars, however, have not investigated a linkage among a comprehensive indicator of government responses and COVID-19 pandemic. How does the severity of the COVID-19 pandemic affect governments’ policy-making? How do governments’ prevention policies hinder the transmission of the COVID-19 pandemic? These are questions worth answering. Moreover, a specific policy can only reflect the role of a certain measure, while the comprehensive index contains various policies and can better reflect the stringency of government response to the pandemic.
This research thus chooses the government response stringency index (GRSI), which is built by researchers from University of Oxford, to measure the stringency of prevention policies taken by governments to reduce the transmission of the COVID-19 pandemic. The level of response stringency to the pandemic depends on the importance attached by the governments and differs among Asian countries, such as China and Vietnam that have adopted stringent mitigation policies to tackle the spread of the COVID-19 pandemic and achieved good results from pandemic prevention and control, while non-Asian countries, such as Netherlands and Italy, have chosen to follow a less stringent policy and the pandemic is still very severe (Anderson et al., 2020).
Strict government response policies generally may slow down the spread of the COVID-19 pandemic and reduce the acute rise of daily new affected numbers, but there are few studies in the literature analyzing the influence of policy implementation on the spread of the pandemic (Jayatilleke et al., 2020). How does a government response stringency affect the spread of the COVID-19 pandemic? Does a higher level of government response stringency reduce the numbers of confirmed and deaths in a country? What determines the stringency of a government response? Will more confirmed cases and death cases compel governments to increase the stringency of government response? Is there any difference between the effects of Confirmed and Death on government response stringency? Are the relationships between GRSI and COVID-19 cases similar among different regions? As there are scant papers in the literature studying these problems, we try to investigate these problems through a series of empirical research.
Based on previous studies, we believe that government response stringency reduces Confirmed and Death, but there exists heterogeneity between different regions. At the same time, the numbers of confirmed cases and deaths may affect the decision-making of a government and influence the level of government response stringency. The panel cointegration test can reveal a long-run co-movement among variables. For instance, Chang et al. (2018) employ panel data of 31 OECD countries from 1994 to 2014 to study the panel cointegrated relationship between energy efficiency and government efficiency, during which the panel cointegration test proposed by Pedroni (2004) is adopted. Feng et al. (2021) utilize the Johansen cointegration test to examine the cointegration between natural gas price and natural gas production based on monthly data of 16 states in the U.S. between January 2007 and December 2016. Empirical results show that there is a reliable cointegration relationship between natural gas price and gross production. In this analysis, given that the cointegration relationship describes the long-run co-movement among variables (Chang et al., 2018; Feng et al., 2021), the severe spread of the COVID-19 pandemic has impelled governments to implement pandemic prevention policies, and if GRSI can hinder its spread, then we can assume that there should be cointegration between GRSI and Confirmed as well as Death. Therefore, we investigate the long-run relationship between GRSI and Confirmed as well as Death. As a cointegration test only reveals the correlations and not causality, thus it cannot reflect the influence directions between GRSI and Confirmed as well as between GRSI and Death. The Dumitrescu-Hurlin (D-H) panel causality test can be used to confirm panel causality, and it has the advantages of taking cross-section dependency into consideration, ensuring the cross-section irrelevance of time and size dimension. The null hypothesis of the D-H causality test is there is no causal relationship and if the null hypothesis is rejected, then there is a causal relationship in at least one cross-section unit. The causality between variables can then be calculated using the Wald test for each of the cross-section units (Dumitrescu and Hurlin, 2012). Aydin (2019) employs the D-H panel causality test to examine the relationship between electricity consumption and economic growth, with results revealing that there exists bidirectional causality between non-renewable electricity consumption and economic growth. Referring to Aydin (2019), we utilize the D-H panel causality test to also investigate the direction of causality between GRSI and Confirmed as well as between GRSI and Death.
The sample analyzed in this paper covers 118 countries. As countries may be related by economic development and by region (Kar et al., 2011), if cross-sectional dependence is ignored during analysis, then the estimated results will be incredible (Abban et al., 2020), and so we consider the problem as cross-sectional dependence in our empirical work. We first utilize the cross-sectionally dependent augmented dickey fuller (CADF) approach, which is proposed by Pesaran (2007), as well as the CIPS test, to test the dependence and stationarity of variables. According to the results of the panel unit root test, we then explore the relationship between GRSI, Confirmed, and Death using Westerlund and Edgerton (2007) bootstrap method, moreover, Augmented Mean Group Estimator (AMG) estimator is adopted to analyze the long-run cointegrated parameters of variables.
Second, as the outbreak of the COVID-19 pandemic hit Asian countries earlier than that in non-Asian countries, prevention policies were also implemented earlier in the former than that in the latter. In addition, research show that Asian countries generally adopted more stringent mitigation policies to tackle the spread of the COVID-19 pandemic than non-Asian countries (Anderson et al., 2020). Therefore, we divide the whole sample into sub-samples of Asian countries and non-Asian countries to test the heterogeneity of the effects of GRSI on the COVID-19 pandemic.
Finally, faced with the spread of COVID-19, governments from all the world have taken stringent measures to restrain the pandemic, such as lockdown and travel bans (Covello and Hyer, 2020). Existing research has proved that government response policies produce a negatively significant long-run effect on the confirmed cases and deaths (Achuo, 2020; Wijngaards et al., 2020). Therefore, the greater Confirmed and Death are, the more governments are faced with heavier pressure to increase the intensity of their responses. At the same time, when GRSI reduces Confirmed and Death, what is the causal path between GRSI and Confirmed as well as with Death? We use the D-H causality test to reveal these causal paths.
This paper contributes to the literature in several aspects. (1) It is the first to investigate the long-run cointegration between GRSI and the numbers of confirmed cases as well as deaths caused by COVID-19, by employing data from 118 countries. The estimations incorporate potential cross-section dependence. (2) This study utilizes the AMG estimator, a newly developed panel data model, to investigate the long-run causal link from GRSI to Confirmed as well as from GRSI to Death. We include different levels of lag for GRSI into our estimation such as 7th, 14th, and 21st lags, in accordance with the characteristic of COVID-19. The empirical results show that the public prevention policies of being isolated for 14 days plus being under observation for 7 days are effective. (3) We further study the bi-directional causal link between GRSI and COVID-19 cases based on the D-H causality test, confirming that there is a statistically significant bi-directional correlation between GRSI and Confirmed as well as the relationships between GRSI and Death. The effects of a government's epidemic prevention and control policy on the spread of the COVID-19 pandemic are significant and the numbers of confirmed cases and deaths do affect its decision-making. (4) Aside from the full sample, we further carry out investigations on the two sub-samples of Asian and non-Asian countries to explore whether the relationships between GRSI and COVID-19 pandemic vary among different countries. While the directions of causality in the sub-samples differ from that in the full sample, a bi-directional relationship exists between GRSI and Confirmed, a unidirectional relationship exists between GRSI and Death in Asian countries, a bi-directional relationship exists between GRSI and Death, and a unidirectional relationship exists between GRSI and Confirmed in non-Asian countries.
The remainder of the paper runs as follows. Section 2 explains the methodology employed in the empirical analysis. Section 3 describes the data. Section 4 presents the empirical results. Section 5 concludes and offers policy implications.
2. Methodology
Panel data have several advantages in dealing with data analysis, such as greater variability among variables and checking the heterogeneity between groups (Abban et al., 2020). Thus, a panel data model is employed to conduct our analysis. The empirical models and tests used in this paper are as follows.
(1) Cross-sectional dependence
Countries are related at their regional level and economic development, and if there exists panel data correlation among cross-sectional data, then deviations will exist and the unit root test will be debatable (Pesaran, 2007; Zhang and Chang, 2020; Zheng et al., 2020). Therefore, cross-section dependence (CD) should be conducted to test whether there exists panel data correlation cross-sectionally. Following Pesaran (2004), we use the CD test to test whether there exists cross-sectional dependence.
The basic panel data model is defined as Eq. (1).
| (1) |
Here, i represent the cross-sectional dimension; t indicates time series dimension; i = 1, 2, 3……N, where N is the sample size; t = 1, 2 ……T, and T is the time period; denotes the explanatory variable; means the vector of explanatory coefficients; and is the regression residual.
The CD test proposed by the Pesaran (2004) statistic is calculated by Eq. (2).
| (2) |
Here, is the product correlation errors of countries i and j. It is calculated by Eq. (3).
| (3) |
We note that is the ordinary least squares estimate of .
Pesaran (2015) proposes the weak cross-sectional dependence test, which is suitable for small samples and can be applies with a heterogenous slope. In this dependence test, the null hypothesis is that errors are weakly cross-sectional dependent. The statistics of CD in Pesaran (2015) are similar with that of Pesaran (2004), whereby:
| (4) |
Here, are the scaled residuals defined by:
| (5) |
We note that is OLS residuals from the country-specific regressions, and .
(2) Panel unit root test
As cross-sectional dependence is taken into consideration in the cross-sectionally dependent augmented dickey fuller (CADF) test and the results are more reliable (Pesaran, 2007), we now use CADF to examine data stationarity. The test can be calculated by Eq. (6).
| (6) |
Here, , and the average is used to represent the effect of an unobserved common factor. Moreover, is intercept parameters; stands for the coefficient of first lag, , , and stand for the individual specific effect, individual linear trend, and common time effect for all individuals, respectively; and is the error term. For the data to be stable, including separate and joint stationarity, it depends on the t-value of in the stationarity test.
Aside from the CADF unit root test, we further carry out the Cross-section Im-Pesaran- Shin (CIPS) test to study the stationarity of variables (Pesaran, 2007). Similar to the Im-Pesaran- Shin (IPS) statistics, the CIPS test provided by Pesaran (2007) is given as:
| (7) |
(3) Panel cointegration test
If there exists cross-sectional correlation, then the traditional test is not equipped to deal with cross-sectional dependence (Westerlund and Edgerton, 2007). A bootstrap panel cointegration test, which is proposed by Westerlund and Edgerton (2007), can deal with the correlation both within and between cross-sectional units and reduce distortions, thus obtaining robust critical values. Moreover, in order to examine the long-run relationships of variables, two statistics based on Durbin-Hausman principle are put forward. Four residual test methods are constructed to test the null hypothesis of no cointegration: two of these statistics are panel statistics (Pt and Pa) and two of these statistics are group statistics (Gt and Ga) (Westerlund, 2008). The panel statistics test is used to check whether the data are cointegrated at least at one unit, and the group statistics test is used to examine whether the panel as a whole is cointegrated. The model is built as Eq. (8).
| (8) |
Here, is the k-dimensional vector being I (1); Dit is the break dummy variables; Dit =1 if t > and zero otherwise; and is the break for individual i.
(4) Panel long-run parameters estimations
When faced with heterogeneity, non-stationarity, and cross-stationarity, the traditional first-generation panel data model will be invalid when estimating (Ahmad et al., 2019). The second-generation panel data model, which is called augmented means group (AMG), is independent of non-stationarity and is suitable for heterogeneous panel data (Eberhardt and Teal, 2010). The empirical analysis shows that the results are robust at handling cross-sectional dependence and non-stationarities (Ma, 2015; Balcilar et al., 2019). The AMG estimator is calculated as follows:
| (9) |
| (10) |
Eberhardt and Bond (2009) point out that the term denotes year dummies and are included in an additional regressor, which represents the common dynamic process. When is subtracted from the dependent variable, it means that the general-purpose procedure is applied to each set of unit coefficient. The AMG estimates are then taken as the average of an individual country. First, the regression model for the group should be adjusted with or , and then the average group-specific parameters can be calculated. Thus, models (9),(10) are re-written as:
| (11) |
| (12) |
(5) Causality estimation method
As AMG estimation cannot provide a causal path, we utilize a causality test to reveal the casual relationship between variables. The Dumitrescu-Hurlin (D-H) causality test proposed by Dumitrescu and Hurlin (2012) is employed during our analysis. This test has the advantage of correcting the empirical critical values produced by Grange causality tests and incorporating potential cross-sectional dependence, taking the heterogeneities of both the regression model and causality relationships into consideration. The model can be defined as Eq. (13).
| (13) |
Here, n represents the length of the lag term; i refers to cross-section; t denotes the time period; and and are the coefficients of autoregressive parameters for the dependent variable and independent variables, respectively.
3. Data description
The government response stringency index (GRSI): The government response stringency index is used to measure the variation in a government's response to the COVID-19 pandemic. The index is published by the Oxford COVID-19 Government Response Tracker in the Blavatnik School of Government. GRSI is a comprehensive measure based on specific policy and response categories - i.e., school closures, workplace closures, cancellations of public events, restrictions on gatherings, closing of public transport, public information campaigns, stay at home mandates, restrictions on domestic movement, and international travel controls. The value represents the intensity of the government response and ranges from 0 to 100; a higher score means a more stringent government response to the COVID-19 pandemic; if the value equals 100, then the government response is the strictest.
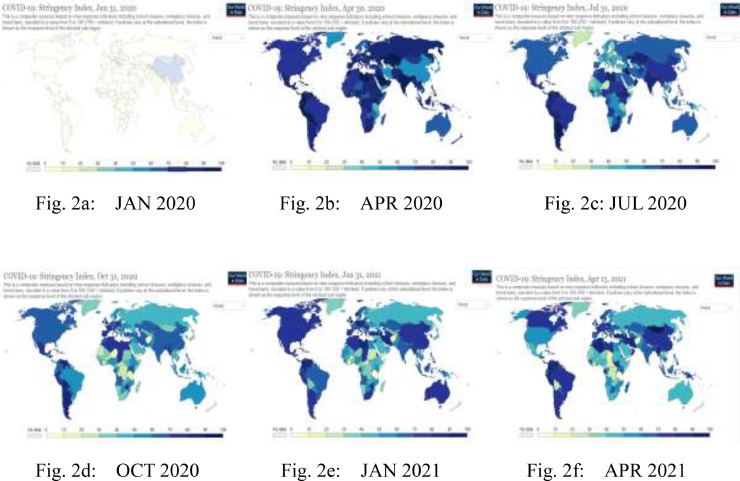
Fig. 1 shows the trend of GRSI in the world from January 1, 2020 to April 13, 2021. One can see that government response stringency to COVID-19 presents significant differences and heterogeneity especially among different areas. The governments of Asian countries, especially China, responded strictly in January and February, while governments in other regions barely took notice. However, after March, the COVID-19 pandemic quickly spread around the world and many countries initiated emergency response measures. The GRSI levels of European countries, such as Italy, Austria, and Czech Republic, gradually increased. After April, pretty much all governments had taken measures to prevent the spread of the COVID-19 pandemic.
Fig. 1.
Worldwide trend of GRSI, Note: these maps for GRSI are sourced from Our World in Data, whose website is: https://ourworldindata.org/covid-stringency-index.
Daily new confirmed cases (Confirmed): Due to differences in countries’ population base, daily new confirmed cases cannot be compared directly. Thus, we take the differences in population size among countries into consideration and deal with the data with a standardized measurement. Thus, daily new confirmed cases of COVID-19 per million people is used to measure daily new confirmed cases. The index is published by the European Centre for Disease Prevention and Control.
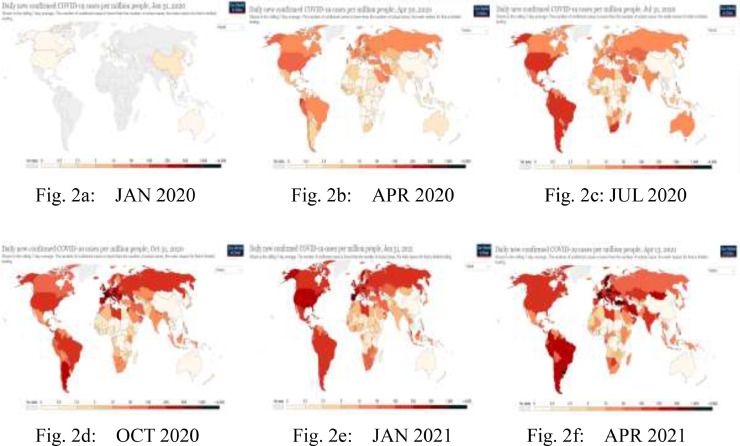
Fig. 2 shows the worldwide trend of daily confirmed cases per million. The cases of COVID-19 began at the end of December 2019, and by the beginning of January 2020, the number of such cases increased gradually. The COVID-19 outbreak reached an outbreak stage around January 20, and the China government took a series of measures to prevent and control the spread of it, such as lockdowns, restrictions on gatherings, school closures, and so on. The control measures achieved good effects at preventing the spread of COVID-19, which has been well controlled in China. Confirmed has gradually decreased in China. After COVID-19 broke out all over the world after March, Confirmed began to increase rapidly in Italy, Spain, France, Germany, Finland, Sweden, and so on. After April, the pandemic continued to worsen, and confirmed cases turned severe in the U.S., Canada, and almost all European countries and African countries.
Fig. 2.
Worldwide trend of daily confirmed cases per million, Note: these maps for daily confirmed cases are sourced from Our World in Data, whose website is: https://ourworldindata.org/covid-cases.
Daily new death cases (Death): Similar to Confirmed, we use daily new confirmed deaths due to COVID-19 per million people to eliminate the impact of population size among different countries. The index is published by the European Centre for Disease Prevention and Control. The trend of Death is very close to that of Confirmed.
All the data used in our analysis span from January 1, 2020 to December 3, 2020 and originate from the website https://ourworldindata.org/grapher/daily-cases-covid-19. Table 1 presents descriptive statistics of the variables.
Table 1.
Summary of descriptive statistics.
| Variable | N | Mean | SD | Min | Median | Max | |
| ALL | GRSI | 55342 | 2.51 | 2.12 | 0.00 | 2.37 | 8.26 |
| Confirmed | 55342 | 0.50 | 0.74 | 0.00 | 0.09 | 5.39 | |
| Death | 55342 | 3.57 | 1.37 | 0.00 | 4.11 | 4.62 | |
| ASIA | GRSI | 15946 | 2.17 | 2.03 | 0.00 | 1.82 | 7.23 |
| Confirmed | 15946 | 0.27 | 0.46 | 0.00 | 0.03 | 3.96 | |
| Death | 15946 | 3.64 | 1.29 | 0.00 | 4.11 | 4.62 | |
| NON-ASIA | GRSI | 39396 | 2.64 | 2.15 | 0.00 | 2.55 | 8.26 |
| Confirmed | 39396 | 0.59 | 0.80 | 0.00 | 0.14 | 5.39 | |
| Death | 39396 | 3.54 | 1.40 | 0.00 | 4.11 | 4.62 | |
From Table 1 for all the sampled countries, the mean of GRSI is 2.51, and the standard deviation is 2.12. In the samples of Asian countries and non-Asian countries, GRSI has Mean=2.17 and SD=2.03 as well as Mean=2.64 and SD=2.15, respectively. This result indicates that GRSI is on average higher in Asian countries than that in non-Asian countries. Confirmed is on average at 0.50 with a standard deviation of 0.74 for all sampled countries. Considering Confirmed among the groups of Asian countries (Mean=0.27, SD=0.46) and non-Asian countries (Mean=0.59, SD=0.80), it is on average higher in the latter than that in the former. In regards to Death, for all sampled countries (Mean=3.57, SD=1.37), Asian countries (Mean=3.64, SD=1.29), and non-Asian countries (Mean=3.54, SD=1.40), it is higher in non-Asian countries than in Asian countries. In other words, Confirmed is on average higher in non-Asian countries than that in Asian countries, while Death and GRSI is on average lower in non-Asian countries than that in Asian countries. Therefore, we further explore the relationship between GRSI and Confirmed as well as Death in the full samples and the two sub-samples.
4. Empirical results
4.1. Cross-sectional dependence test
Since cross-sectional dependence is a common problem when we carry out panel estimations, the CD-test is first used to examine whether cross-sectional dependence exists within each panel data (Pesaran, 2004). To further test for weak correlation, we conduct the CD-test for weak cross-sectional dependence, by referring to Pesaran (2015). The statistics of the CD-test and the corresponding provability are in Table 2 .
Table 2.
Cross-section dependence tests.
| Model |
Pesaran (2004) |
Pesaran (2015) |
|||||
|---|---|---|---|---|---|---|---|
| Sample | Variable | CD-test | p-value | Corr | abs(corr) | CD | P |
| ALL | GRSI | 1600.23⁎⁎⁎ | 0.000 | 0.889 | 0.889 | 1771.924⁎⁎⁎ | 0.000 |
| Confirmed | 896.88⁎⁎⁎ | 0.000 | 0.498 | 0.518 | 1399.796⁎⁎⁎ | 0.000 | |
| Death | 459.24⁎⁎⁎ | 0.000 | 0.255 | 0.288 | 893.532⁎⁎⁎ | 0.000 | |
| ASIA | GRSI | 431.52⁎⁎⁎ | 0.000 | 0.841 | 0.841 | 5.3.372⁎⁎⁎ | 0.000 |
| Confirmed | 203.05⁎⁎⁎ | 0.000 | 0.396 | 0.456 | 353.807⁎⁎⁎ | 0.000 | |
| Death | 81.40⁎⁎⁎ | 0.000 | 0.159 | 0.222 | 194.594⁎⁎⁎ | 0.000 | |
| NON-ASIA | GRSI | 1175.43⁎⁎⁎ | 0.000 | 0.919 | 0.919 | 1263.062⁎⁎⁎ | 0.000 |
| Confirmed | 694.21 ⁎⁎⁎ | 0.000 | 0.543 | 0.547 | 1041.819⁎⁎⁎ | 0.000 | |
| Death | 36.299⁎⁎⁎ | 0.000 | 0.302 | 0.318 | 701.597⁎⁎⁎ | 0.000 | |
Note: ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
All CD-tests in Table 2 are statistically significant at the 1% level, strongly rejecting the null hypothesis of cross-sectional independence. Hence, there exists cross-sectional dependence in the data, and the countries within our analysis are relevant to some extent. As all the variables contain cross-sectional dependence, it is necessary to test the stability of variables (Abban et al., 2020).
4.2. Panel unit root test
Because the CD tests show that there exists cross-sectional dependence for all three variables, we then employ the panel unit root test proposed by Pesaran (2007) such as CADF and CIPS to examine the stationaries of the variables. The results of CADF and CIPS are in Table 3 .
Table 3.
Results from the CADF and CIPS panel unit root tests.
| Group | GRSI | ΔGRSI | Confirmed | ΔConfirmed | Death | ΔDeath |
| ALL | ||||||
| CADF | -2.311 | -6.203⁎⁎* | -2.289 | -6.404⁎⁎* | -2.178 | -6.420⁎⁎* |
| CIPS | -2.295 | -5.980⁎⁎* | -2.381 | -6.175⁎⁎* | -2.474 | -6.190⁎⁎* |
| ASIA | ||||||
| CADF | -2.504 | -6.412⁎⁎* | -2.153 | -6.420⁎⁎* | -2.288 | -6.409⁎⁎* |
| CIPS | -2.326 | -6.190⁎⁎* | -2.077 | -6.190⁎⁎* | -2.519 | -6.185⁎⁎* |
| NON-ASIA | ||||||
| CADF | -1.970 | -6.234⁎⁎* | -2.225 | -6.396⁎⁎* | -2.047 | -6.420⁎⁎* |
| CIPS | -1.967 | -6.019⁎⁎* | -2.442 | -6.168⁎⁎* | -2.363 | -6.190⁎⁎* |
Notes: The statistic of CADF is t-bar, the critical value of t-bar for the CADF test for the ALL sample at the 1%, 5%, and 10% levels is -2.620, -2.550, and -2.500, respectively; while that for the ASIA sub-sample is -2.770, -2.650, and -2.590, respectively; and that for the NON-ASIA sub-sample is -2.650, -2.570, and -2.520, respectively; The critical value for the CIPS test for the ALL sample at the 1%, 5%, and 10% levels is -2.62, -2.55, and -2.51, respectively; while that for the ASIA sub-sample is -2.77, -2.65, and -2.59, respectively; and that for the NON-ASIA sub-sample is -2.65, -2.57, and -2.52, respectively. ⁎⁎⁎
, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
It is easy to see that the tests are statistically insignificant at the level and statistically significant at the 1% level in their first difference, which means that the results of the tests reject the null hypothesis of a unit root existing in their first difference, but they do not reject the null hypothesis at the level. This indicates that all the variables (i.e., GRSI, Confirmed, and Death in the whole sample, Asian countries and non-Asia countries) have unit roots at the level and have no unit roots in their first difference. Thus, all variables are stationary at I (1), making it appropriate for the next analysis via the panel cointegration test.
4.3. Panel cointegration test
Once the stationarity of all variables is confirmed, we next examine whether there exists a long-term association between variables using the bootstrap panel cointegration test proposed by Westerlund and Edgerton (2007), which can allow for dependence both within and between the cross-sectional unit. The results are in Table 4 . We conclude that most G τ and G α as well as Pτ and Pα are significant at the 5% level and reject the null hypothesis of no panel cointegration. Therefore, clear evidence shows that there exists a long-term cointegration relationship between GRSI and Confirmed as well as between GRSI and Death in the whole sample. The same conclusions can be derived from the sub-samples of Asian countries and non-Asian countries.
Table 4.
Panel Cointegration Test (Westerlund and Edgerton, 2007).
| Model | Gτ | Gα | Pτ | Pα | ||||
| value | p-robust | value | p-robust | value | p-robust | value | p-robust | |
| ALL | ||||||||
| Confirmed-GRSI | -3.368⁎⁎⁎ | (0.000) | -45.007⁎⁎⁎ | (0.000) | -47.930⁎⁎⁎ | (0.000) | -44.245⁎⁎⁎ | (0.000) |
| Death-GRSI | -4.365⁎⁎⁎ | (0.000) | -71.180⁎⁎⁎ | (0.000) | -44.353⁎⁎⁎ | (0.000) | -41.737⁎⁎⁎ | (0.000) |
| ASIA | ||||||||
| Confirmed-GRSI | -2.710⁎⁎⁎ | (0.000) | -24.175⁎⁎⁎ | (0.000) | -16.706⁎⁎⁎ | (0.000) | -18.063⁎⁎⁎ | (0.000) |
| Death-GRSI | -4.983⁎⁎⁎ | (0.000) | -84.155⁎⁎⁎ | (0.000) | -17.725⁎⁎⁎ | (0.000) | -23.792⁎⁎⁎ | (0.000) |
| NON-ASIA | ||||||||
| Confirmed-GRSI | -3.634⁎⁎⁎ | (0.000) | -53.439⁎⁎⁎ | (0.000) | -44.071⁎⁎⁎ | (0.000) | -52.765⁎⁎⁎ | (0.000) |
| Death-GRSI | -4.116⁎⁎⁎ | (0.000) | -65.929⁎⁎⁎ | (0.000) | -38.580⁎⁎⁎ | (0.000) | -44.265⁎⁎⁎ | (0.000) |
Note: ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
4.4. Long-run estimation analysis
As long-run cointegration is confirmed, we next study the long-run effect of GRSI on Confirmed and Death. The endogenous problem caused by the hypothesis of strong exogeneity of independent variables cannot be resolved (Perman and Stern, 2003), and short data span may lower the power of the unit root and cointegration tests, leading to a biased estimation of causality (Harris and Tzavalis, 1999). Lee and Chang (2006) point out that the long-run relationship can be distinguished through combining the information of both time series and cross-section data. Because the AMG estimator can account for cross-section dependence and explain the unobservable variables with economic relevance (Eberhardt and Teal, 2010), we use the AMG estimator to check the long-run effect of GRSI on Confirmed and Death. Due to COVID-19 exhibiting dynamic progress and possessing long latency of around 14 days or more, we incorporate the lag term of COVID-19 cases, as well as 7th, 14th, and 21st lags of GRSI into our regression. The results are in Table 5 .
Table 5.
Results of the AMG panel data estimation method.
| Confirmed |
Death |
|||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| L.dependent | 0.609⁎⁎⁎ | 0.621⁎⁎⁎ | 0.614⁎⁎⁎ | 0.593⁎⁎⁎ | 0.482⁎⁎⁎ | 0.484⁎⁎⁎ | 0.479⁎⁎⁎ | 0.465⁎⁎⁎ |
| (21.32) | (20.92) | (21.13) | (20.56) | (4.94) | (5.02) | (4.90) | (4.62) | |
| GRSI | -0.206⁎⁎⁎ | -0.020⁎⁎⁎ | ||||||
| (-13.18) | (-4.03) | |||||||
| L7. GRSI | -0.282⁎⁎⁎ | -0.031⁎⁎⁎ | ||||||
| (-17.76) | (-6.05) | |||||||
| L14. GRSI | -0.273⁎⁎⁎ | -0.019⁎⁎⁎ | ||||||
| (-16.76) | (-3.84) | |||||||
| L21. GRSI | -0.268⁎⁎⁎ | -0.018⁎⁎⁎ | ||||||
| (-15.18) | (-3.61) | |||||||
| Trend | -0.008⁎⁎⁎ | -0.008⁎⁎⁎ | -0.008⁎⁎⁎ | -0.007⁎⁎⁎ | -0.002⁎⁎⁎ | -0.002⁎⁎⁎ | -0.002⁎⁎⁎ | -0.002⁎⁎⁎ |
| (-30.34) | (-28.93) | (-27.05) | (-24.59) | (-22.64) | (-21.61) | (-20.56) | (-19.93) | |
| Cons | 5.739⁎⁎⁎ | 5.963⁎⁎⁎ | 0.143⁎⁎⁎ | 0.051* | 1.470⁎⁎⁎ | 1.506⁎⁎⁎ | 1.450⁎⁎⁎ | 1.447⁎⁎⁎ |
| (364.87) | (348.57) | (6.81) | (1.84) | (315.57) | (316.07) | (266.99) | (190.22) | |
| N | 55224 | 54516 | 53690 | 52864 | 55224 | 54516 | 53690 | 52864 |
| RMSE | 0.772 | 0.776 | 0.783 | 0.799 | 0.131 | 0.132 | 0.133 | 0.136 |
| Chi2 | 457.533 | 494.490 | 490.652 | 463.725 | 38.797 | 58.989 | 37.163 | 33.133 |
Note: ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
L7. GRSI, L14. GRSI and L21. GRSI represent 7-day, 14-day and 21-day lag term of GRSI, respectively.
Table 5 presents a long-term statistically negative effect of GRSI on Confirmed as well as on Death. The one-period lag term of Confirmed has a significantly positive effect on Confirmed; i.e., the more confirmed cases there are for day X, the more new confirmed cases there will be on day X+1. Death does not present such a feature, and the main reason is that confirmed cases are highly infectious, and numbers of COVID-19 deaths are determined by medical care and treatment. RMSE can explain how accurately the model predicts the response variable, and a smaller RMSE stands for higher efficiency of the model (Abban et al., 2020). Thus, we conclude that each model is fitted for estimation.
We first analyze the effects of GRSI on Confirmed, which appear in columns 1 to 4. The coefficients of GRSI on Confirmed are negative and statistically significant at the 1% level, indicating that countries with a strong government response should have fewer confirmed cases. Moreover, the effects of GRSI increase exponentially with the passing of time. In the current period, when GRSI increases by one unit, Confirmed decreases by 0.609 units. The coefficients of 7-day, 14-day, and 21-day lag terms of GRSI are -0.282, -0.273, and -0.268, respectively, and the coefficients are significant at the 1% level. Particularly, the effect of the 7-day lag term of GRSI has the largest size, suggesting that it is most effective at reducing the number of confirmed cases 7 days after a government takes measures to prevent the spread of COVID-19. The effects of the 14-day and 21-day lag terms of GRSI are also very large, and so our results are also in line with Achuo (2020), who has shown that government stringent responses produce a negative significant long-run effect on the number of confirmed cases. The analysis supports the effectiveness of current public prevention policies that implement lockdowns for 14 days plus observations for 7 days in preventing the spread of COVID-19.
We now analyze the effects of GRSI on Death, which we present in columns 5 to 8. Similar to the effects of GRSI on Confirmed, the coefficients of GRSI on Death are statistically significant at the 1% level, indicating that countries with a strong government response should show fewer death cases. In the current period, when GRSI increases by one unit, Death decreases by 0.02 units. The effects of GRSI increase exponentially with the passing of time. The coefficients of 7-day, 14-day, and 21-day lag terms of GRSI are -0.031, -0.019, and -0.018, respectively, and all the coefficients are statistically significant at the 1% level. In consistent with the effect of GRSI on Confirmed, the effect of the 7-day lag term of GRSI has the largest size, and the effect of 14-day is close to that of 21-day lag term, which again indicates that it is most effective at showing how deaths drop 7 to 21 days after a government takes measures to prevent the spread of COVID-19.
Combining the analysis above, we can conclude that all the lag terms are significant both on Confirmed and Death. Though the effect of the 7-day lag term has the largest size, the effects of the 14-day and 21-day lag terms are significant and the values of coefficients are also large, suggesting that government response is most effective at reducing the number of the confirmed and death cases 7 days after a government takes measures to prevent the spread of COVID-19, and the impact stays significantly effective during 14 to 21 days after the measures are initiated by governments. The reason may be that unlike traditional infectious diseases, COVID-19 has a long latent period during which it still is strongly contagious without significant symptoms, and the incubation period mostly appears in 7 days (Achuo et al., 2020). Thus, the measures taken by governments to control the pandemic produce a lasting effect. Moreover, the impact of GRSI on Confirmed is greater than that on Death, because the main function of prevention policies implemented by governments is to prevent the spread of COVID-19; however, death cases mainly come from confirmed cases, and so the lag term with the effect of the largest size on Death is longer than that on Confirmed. The empirical results also prove that the policy taken up by governments to require lockdowns of 14 days plus observations for 7 days is effective, especially at reducing the number of new confirmed cases (Alfano and Ercolano, 2020).
4.5. Long-run estimates for sub-samples
Governments in Asian countries responded to the COVID-19 pandemic earlier than those of non-Asian countries. Moreover, confirmed cases are mainly in Asian countries from January to March, while they are from April to December in Europe, and so it is necessary to conduct analysis by different regions. We next divide the whole samples into two sub-samples - i.e., Asian countries and non-Asian countries - and take Confirmed as an example to investigate the effects of a government response in different sub-samples. The results of the AMG panel data estimation method for the two sub-samples are in Table 6 .
Table 6.
Results of the AMG panel data estimation method for sub-samples.
| Confirmed |
||||||||
| ASIA |
NON-ASIA |
|||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| L.dependent | 0.751⁎⁎⁎ | 0.769⁎⁎⁎ | 0.770⁎⁎⁎ | 0.763⁎⁎⁎ | 0.549⁎⁎⁎ | 0.555⁎⁎⁎ | 0.540⁎⁎⁎ | 0.510⁎⁎⁎ |
| (13.99) | (14.02) | (15.88) | (16.76) | (16.86) | (16.55) | (16.26) | (15.56) | |
| GRSI | -0.171⁎⁎⁎ | -0.209⁎⁎⁎ | ||||||
| (-7.32) | (-10.13) | |||||||
| L7.GRSI | -0.259⁎⁎⁎ | -0.267⁎⁎⁎ | ||||||
| (-11.16) | (-12.83) | |||||||
| L14.GRSI | -0.269⁎⁎⁎ | -0.241⁎⁎⁎ | ||||||
| (-11.74) | (-11.68) | |||||||
| L21.GRSI | -0.280⁎⁎⁎ | -0.217⁎⁎⁎ | ||||||
| (-11.94) | (-9.67) | |||||||
| Trend | -0.007⁎⁎⁎ | -0.007⁎⁎⁎ | -0.007⁎⁎⁎ | -0.006⁎⁎⁎ | -0.008⁎⁎⁎ | -0.008⁎⁎⁎ | -0.008⁎⁎⁎ | -0.008⁎⁎⁎ |
| (-18.10) | (-17.97) | (-18.23) | (-17.97) | (-24.29) | (-22.97) | (-21.12) | (-18.99) | |
| Cons | 4.984⁎⁎⁎ | 5.243⁎⁎⁎ | 0.175⁎⁎⁎ | 5.103⁎⁎⁎ | 5.974⁎⁎⁎ | 6.148⁎⁎⁎ | 6.038⁎⁎⁎ | -0.002 |
| (241.63) | (225.68) | (6.75) | (158.95) | (307.32) | (297.73) | (226.80) | (-0.05) | |
| N | 15912 | 15708 | 15470 | 15232 | 39312 | 38808 | 38220 | 37632 |
| RMSE | 0.337 | 0.333 | 0.321 | 0.314 | 0.949 | 0.960 | 0.980 | 1.004 |
| Chi2 | 199.322 | 237.040 | 297.130 | 330.744 | 284.867 | 284.081 | 275.258 | 251.830 |
Note: ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
L7. GRSI, L14. GRSI and L21. GRSI represent 7-day, 14-day and 21-day lag term of GRSI, respectively.
We first analyze the effects in Asian countries. From columns 1 to 4 in Table 6, the effects of GRSI and its 7-day, 14-day, and 21-day lag terms are negative and statistically significant at the 1% level, which is consistent with the whole sample. While the effect of the 21-day lag term of GRSI has the largest size, this is different from the results of the whole sample. Comparing the coefficients of GRSI, we find that though the effect of the 21-day lag term of GRSI has the largest size, differences between the values of the 7-day, 14-day, and 21-day lag terms are not huge, while the coefficient of current period is significantly less than that of the lag periods, meaning that the effects of GRSI on reducing the numbers of confirmed cases are effective 7 to 21 days after a government takes measures to prevent the spread of COVID-19.
We now analyze the effects in non-Asian countries. From columns 5 to 8, the effects of GRSI on Confirmed in non-Asian countries are similar with those in the whole sample. The coefficients are negative and statistically significant at the 1% level. Particularly, the effect of the 7-day lag term of GRSI has the largest size, which is different from that in Asian countries. This may be because the first COVID-19 confirmed case was in Asia, and people did not carry out prevention policies very well until they realized the severity of it and then began to implement effective policies. In non-Asian countries, people became aware of the severity of COVID-19 once governments implemented a prevention policy that was carried out immediately. It should be noted that the effects of the 14-day and 21-day lag terms of GRSI are also very large, suggesting that government response is most effective at reducing the number of confirmed cases 7 days after a government takes measures to prevent the spread of COVID-19, and the impact stays significantly effective during 14 to 21 days after the measures taken by governments. The results are the same with the conclusion drawn by the whole sample and further prove that the policy taken by governments to require lockdowns of 14 days plus observations for 7 days is effective.
4.6. Dumitrescu and Hurlin (D-H) panel causality test
In addition to the analysis above, we ask the following: Is there any difference between governments’ responses to the numbers of confirmed cases and deaths? AMG estimation can only reveal a long-run relationship for the variables, but does not propose the direction of causality. The Dumitrescu and Hurlin (2012) (D-H) causality test is used to conduct this analysis. The results of the causality test are reported in Table 7 .
Table 7.
D-H causality.
| Model | W-bar | Z-bar | P | Lag | Conclusion |
|---|---|---|---|---|---|
| ALL | |||||
| GRSI Confirmed | 13.269 | 61.210⁎⁎⁎ | 0.000 | 2 | Two-way |
| Confirmed GRSI | 0.992 | -5.474⁎⁎⁎ | 0.000 | 2 | |
| GRSI Death | 6.793 | 26.037⁎⁎⁎ | 0.000 | 2 | Two-way |
| Death GRSI | 0.312 | -5.281⁎⁎⁎ | 0.000 | 1 | |
| ASIA | |||||
| GRSI Confirmed | 8.436 | 18.766⁎⁎⁎ | 0.000 | 2 | Two-way |
| Confirmed GRSI | 0.563 | -1.799* | 0.071 | 1 | |
| GRSI Death | 6.514 | 22.738⁎⁎⁎ | 0.000 | 1 | Two-way |
| Death GRSI | 0.168 | -3.426⁎⁎⁎ | 0.000 | 1 | |
| NON-ASIA | |||||
| GRSI Confirmed | 15.225 | 60.608⁎⁎⁎ | 0.000 | 2 | One-way: GRSI Confirmed |
| Confirmed GRSI | 0.904 | -0.619 | 0.535 | 1 | |
| GRSI Death | 7.927 | 27.163⁎⁎⁎ | 0.000 | 2 | Two-way |
| Death GRSI | 0.370 | -4.079 ⁎⁎⁎ | 0.000 | 1 | |
Note: ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively.
As can be seen from Table 7, D-H causality settings uncover a statistically significant bi-directional process between GRSI and Confirmed as well as with Death when analyzing the whole sample, indicating the importance of government action in pandemic control. Furthermore, GRSI is statistically significantly affected by Confirmed and Death, which means governments did respond strongly to the numbers of confirmed cases and deaths caused by COVID-19. If Confirmed and Death increase in a country, then the government can raise GRSI to prevent the spread of the pandemic.
When analyzing the sub-samples, the results of the D-H causality test show clear differences between Asian countries and non-Asian countries. In Asian countries, there is a statistically significant bi-directional correlation between GRSI and Confirmed, GRSI and Death. In non-Asian countries, there is a statistically significant bi-directional correlation between GRSI and Death, but the causality only runs uni-directional from GRSI to Confirmed. The results reveal that governments in Asian countries are concerned about both Confirmed and Death. When the number of confirmed cases and deaths increase, governments should take more stringent measures to control the pandemic. However, governments in non-Asian countries care more about Death and pay little attention to Confirmed. When the numbers of deaths increase, governments should take more stringent measures, but the numbers of confirmed cases do not have a significant influence on government policy-making. As confirmed cases are highly infectious, governments in non-Asian countries do not attach importance to them, and this may be one of the reasons why the spread of COVID-19 was faster in non-Asian countries than in Asian countries. In the next stage, governments in non-Asian countries should pay closer attention to Confirmed and take effective measures to reduce their numbers.
5. Conclusions and policy implications
The COVID-19 pandemic spread throughout the world starting in January 2020. Governments then began to initiate various policies to prevent the spread of the virus, such as workplace closures, stoppages of public transport, international travel controls, and so on. These prevention policies have controlled the spread of COVID-19 effectively, but the pandemic is still severe.
In order to analyze the relationship between GRSI and Confirmed as well as Death, we conduct an empirical analysis using daily data covering 118 countries during the period from January 1, 2020 to April 13, 2021. To control the influence of potential cross-sectional dependence and endogeneity, we utilize several estimations such as the cointegration test of Westerlund and Edgerton (2007), Augmented Mean Group (AMG) estimation, and the causality test provided by Dumitrescu and Hurlin (2012). Once the long-term relationships between GRSI and Confirmed as well as those between GRSI and Death are confirmed, we further divide the whole sample into two sub-samples (Asian countries and non-Asian countries) to study whether the relationships between GRSI and COVID-19 are constant between different regions.
Our research overall draws the following conclusions. First, the descriptive analysis shows that GRSI of Asian countries, especially China, is the strongest in January and February, while after March, GRSI of non-Asian countries gradually increases. Second, the results of the Westerlund and Edgerton (2007) test support the cointegration relationship between GRSI and confirmed cases as well as that between GRSI and deaths for the full sample. Similar findings are obtained for the Asia and non-Asia sub-samples. Third, the results of the long-run estimation show that GRSI significantly reduces confirmed cases and deaths, and the 7-day lag term has the largest size. Finally, the causality test uncovers a statistically significant bi-directional process between GRSI and confirmed cases as well as between GRSI and deaths in Asian countries, while in non-Asian countries, there exhibits a statistically significant bi-directional process between GRSI and deaths and a unidirectional process between GRSI and confirmed cases. The results reveal that governments in non-Asian countries are more concerned about deaths, while governments in Asian countries concentrate both on confirmed cases and deaths.
According to the conclusions above, we offer a summary of policy implications and suggestions as follows.
(1) Continue to carry out public prevention policies and enhance the government response stringency. Empirical results show that policy effects reach their maximum approximately 14 to 21 days after a government response. Our analysis demonstrates that public prevention policies of being isolated for 14 days plus observation for 7 days are indeed effective. Governments all over the world should continue to attach importance to this pandemic and take effective measures to decelerate the spread of COVID-19 based on the trends of its pandemic in their country. Prevention policies of lockdown for 14 days plus observation for 7 days should be continued to be implemented in both Asian and non-Asian countries. In this way, COVID-19 can be completely controlled before a proper vaccine can be developed. At the same time, governments should invest in medical facilities for the long run. The evidence of co-integration supports a long-run co-movement relationship between GRSI and Confirmed as well as Death. The stringency of a government's pandemic prevention and control policies is conducive to slowing down the spread of COVID-19. Therefore, the role of a government in pandemic prevention and control should be fully involved and the stringency of government response should be improved, especially for countries with an on-going severe pandemic.
(2) Propagate the practices of some Asian countries and encourage countries with a severe pandemic to use them as a reference. Many Asian countries and regions, such as China, Japan, South Korea, Singapore, and Taiwan, have implemented strict prevention policies of lockdowns for 14 days plus observations for 7 days and have achieved excellent results at controlling COVID-19. Therefore, these countries should be taken as examples by the World Health Organization (WHO), and their experiences should be used as a reference by countries with a more severe COVID-19 pandemic.
CRediT authorship contribution statement
Qi-Cheng Yang: Conceptualization, Formal analysis, Writing – review & editing, Data curation, Writing – original draft. Xia Chen: Writing – review & editing, Validation. Chun-Ping Chang: Writing – review & editing, Writing – original draft, Supervision. Di Chen: Writing – original draft, Project administration, Formal analysis. Yu Hao: Conceptualization, Methodology, Funding acquisition, Supervision.
Acknowledgments
The authors acknowledge financial support from the National Natural Science Foundation of China (72073010, 71761137001, 71521002), the key research program of the Beijing Social Science Foundation (17JDYJA009), and the Special Fund for Joint Development Program of the Beijing Municipal Commission of Education. The authors are also very grateful to two anonymous reviewers and Managing Editor Prof. Dr. Mario Pianta for their insightful comments that helped us sufficiently improve the quality of this paper. The usual disclaimer applies.
References
- Abban O.J., Wu J., Mensah I.A. Analysis on the nexus amid CO2 emissions, energy intensity, economic growth, and foreign direct investment in belt and road economies: does the level of income matter? Environ. Sci. Pollut. Res. 2020;27(10):11387–11402. doi: 10.1007/s11356-020-07685-9. [DOI] [PubMed] [Google Scholar]
- Achuo E.D. How efficient are government stringency responses in curbing the spread of the covid-19 pandemic? Int. J. Res. Innov. Soc. Sci. 2020;4(8):629–635. [Google Scholar]
- Achuo E.D., Dinga G.D., Njuh C.J., Ndam N.L. The socioeconomic impacts of the COVID-19 pandemic in Africa. Int. J. Progress. Sci. Technol. 2020;22(2):01–10. [Google Scholar]
- Ahmad M., Zhao Z.Y., Li H. Revealing stylized empirical interactions among construction sector, urbanization, energy consumption, economic growth and CO2 emissions in China. Sci. Total Environ. 2019;657:1085–1098. doi: 10.1016/j.scitotenv.2018.12.112. [DOI] [PubMed] [Google Scholar]
- Alfano V., Ercolano S. The efficacy of lockdown against COVID-19: a cross-country panel analysis. Appl. Health Econ. Health Policy. 2020 doi: 10.1007/s40258-020-00596-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet N. Am. Ed. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aydin M. Renewable and non-renewable electricity consumption–economic growth nexus: evidence from OECD countries. Renew. Energy. 2019;136:599–606. [Google Scholar]
- Balcilar M., Gungor H., Olasehinde-Williams G. On the impact of globalization on financial development: a multi-country panel study. Eur. J. Sustain. Dev. 2019;8(1):350. 350. [Google Scholar]
- Brauner J.M., Mindermann S., Sharma M., Johnston D., Salvatier J., Gavenčiak T., Kulveit J. Inferring the effectiveness of government interventions against COVID-19. Science. 2021;371(6531) doi: 10.1126/science.abd9338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceylan R.F., Ozkan B., Mulazimogullari E. Historical evidence for economic effects of COVID-19. Eur. J. Health Econ. 2020;1 doi: 10.1007/s10198-020-01206-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C.P., Wen J., Dong M., Hao Y. Does government ideology affect environmental pollutions? New evidence from instrumental variable quantile regression estimations. Energy Policy. 2018;113:386–400. [Google Scholar]
- Chang C.P., Wen J., Zheng M., Dong M., Hao Y. Is higher government efficiency conducive to improving energy use efficiency? Evidence from OECD countries. Econ. Model. 2018;72:65–77. [Google Scholar]
- Covello V., Hyer R. Association of State and Territorial Health Officials; Arlington, Virginia: 2020. COVID-19: Simple Answers to top Questions, Risk Communication Guide. July 12, 2020. [Google Scholar]
- Diepeveen S., Ling T., Suhrcke M., Roland M., Marteau T.M. Public acceptability of government intervention to change health-related behaviors: a systematic review and narrative synthesis. BMC Public Health. 2013;13(1):756. doi: 10.1186/1471-2458-13-756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumitrescu E.I., Hurlin C. Testing for Granger non-causality in heterogeneous panels. Econ. Model. 2012;29(4):1450–1460. [Google Scholar]
- Eberhardt, M. and Bond, S. (2009). Cross-section dependence in nonstationary panel models: a novel estimator.
- Eberhardt M., Teal F. University of Oxford; 2010. Productivity analysis in global manufacturing production. Economics Series Working Papers. [Google Scholar]
- Elgin C., Basbug G., Yalaman A. Economic policy responses to a pandemic: developing the COVID-19 economic stimulus index. COVID Econ. 2020;1(3):40–53. [Google Scholar]
- Feng G.F., Wang Q.J., Chu Y., Wen J., Chang C.P. Does the shale gas boom change the natural gas price-production relationship? Evidence from the US market. Energy Econ. 2021 [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., Bhatt S. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020;584(7820):257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- Fredriksson P.G., Vollebergh H.R., Dijkgraaf E. Corruption and energy efficiency in OECD countries: theory and evidence. J. Environ. Econ. Manag. 2004;47(2):207–231. [Google Scholar]
- Hale, T., Petherick, A., Phillips, T. and Webster, S. (2020). Variation in government responses to COVID-19. Blavatnik school of government working paper, 31.
- Harris R.D., Tzavalis E. Inference for unit roots in dynamic panels where the time dimension is fixed. J. Econom. 1999;91(2):201–226. [Google Scholar]
- Haug N., Geyrhofer L., Londei A., Dervic E., Desvars-Larrive A., Loreto V., Klimek P. Ranking the effectiveness of worldwide COVID-19 government interventions. Nat. Hum. Behav. 2020;4(12):1303–1312. doi: 10.1038/s41562-020-01009-0. [DOI] [PubMed] [Google Scholar]
- Hussain, A.H.M. (2020). Stringency in policy responses to Covid-19 pandemic and social distancing behavior in selected countries. Working paper (April 20, 2020).
- Jayatilleke, A.U., Dayarathne, S., de Silva, P., Siribaddana, P., Abeygunawardana, R.A., Nieveras, O. and de Silva, J. (2020). COVID-19 case forecasting model for Sri Lanka based on stringency index. MedRxiv.
- Jochelson K. Nanny or steward? The role of government in public health. Public Health. 2006;120(12):1149–1155. doi: 10.1016/j.puhe.2006.10.009. [DOI] [PubMed] [Google Scholar]
- Kar M., Nazlıoğlu Ş., Ağır H. Financial development and economic growth nexus in the MENA countries: bootstrap panel granger causality analysis. Econ. Model. 2011;28(1-2):685–693. [Google Scholar]
- Lakshminarayanan S. Role of government in public health: current scenario in India and future scope. J. Fam. Commun. Med. 2011;18(1):26. doi: 10.4103/1319-1683.78635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C.C., Chang C.P. Social security expenditure and GDP in OECD countries: a cointegrated panel analysis. Int. Econ. J. 2006;20(3):303–320. [Google Scholar]
- Ma B. Does urbanization affect energy intensities across provinces in China? Long-run elasticities estimation using dynamic panels with heterogeneous slopes. Energy Econ. 2015;49:390–401. [Google Scholar]
- McKibbin, W.J. and Fernando, R. (2020). The global macroeconomic impacts of COVID-19: seven scenarios.
- Pedroni P. Panel cointegration: asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis. Econometric theory. 2004;20(3):597–625. [Google Scholar]
- Pesaran, H.M. (2004). General diagnostic tests for cross-sectional dependence in panels. University of Cambridge, Cambridge Working Papers in Economics, 435.
- Pesaran M.H. A simple panel unit root test in the presence of cross-section dependence. J. Appl. Econom. 2007;22(2):265–312. [Google Scholar]
- Pesaran M.H. Testing weak cross-sectional dependence in large panels. Econom. Rev. 2015;34:1089–1117. 6-10. [Google Scholar]
- Perman R., Stern D.I. Evidence from panel unit root and cointegration tests that the environmental Kuznets curve does not exist. Aust. J. Agric. Resour. Econ. 2003;47(3):325–347. [Google Scholar]
- Roemer M.I., Roemer R. Global health, national development, and the role of government. Am. J. Public Health. 1990;80(10):1188–1192. doi: 10.2105/ajph.80.10.1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stock J.H. National Bureau of Economic Research; 2020. Data Gaps and the Policy Response to the Novel Coronavirus (No. w26902) [Google Scholar]
- Vowles J. Does globalization affect public perceptions of ‘who in power can make a difference’? Evidence from 40 countries. Elect. Stud. 2008;27(1):63–76. 1996–2006. [Google Scholar]
- Westerlund J., Edgerton D.L. A panel bootstrap cointegration test. Econ. Lett. 2007;97(3):185–190. [Google Scholar]
- Westerlund J. Panel cointegration tests of the Fisher effect. J. Appl. Econom. 2008;23(2):193–233. [Google Scholar]
- Wijngaards I., de Zilwa S.C.S., Burger M.J. Extraversion moderates the relationship between the stringency of COVID-19 protective measures and depressive symptoms. Front. Psychol. 2020;11 doi: 10.3389/fpsyg.2020.568907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yilmazkuday, H. (2020). Stay-at-home works to fight against COVID-19: international evidence from Google mobility data. Available at SSRN 3571708.
- Zhang L.W., Chang C.P. Do natural disasters increase financial risk? An empirical analysis. Bul. Ekon. Monet. Dan Perbank. 2020;23:61–86. [Google Scholar]
- Zheng M., Feng G.F., Wen J., Chang C.P. The influence of FDI on domestic innovation: an investigation using structural breaks. Prague Econ. Pap. 2020;29(4):403–423. [Google Scholar]