Abstract
We predicted water-octanol partition coefficients for the molecules in the SAMPL7 challenge with explicit solvent classical molecular dynamics (MD) simulations. Water hydration free energies and octanol solvation free energies were calculated with a windowed alchemical free energy approach. Three commonly used force fields (AMBER GAFF, CHARMM CGenFF, OPLS-AA) were tested. Special emphasis was placed on converging all simulations, using a criterion developed for the SAMPL6 challenge. In aggregate, over 1000 μs of simulations were performed, with some free energy windows remaining not fully converged even after 1 μs of simulation time. Nevertheless, the amount of sampling produced logPow estimates with a precision of 0.1 log units or better for converged simulations. Despite being probably as fully sampled as can expected and is feasible, the agreement with experiment remained modest for all force fields, with no force field performing better than 1.6 in root mean squared error. Overall, our results indicate that a large amount of sampling is necessary to produce precise logPow predictions for the SAMPL7 compounds and that high precision does not necessarily lead to high accuracy. Thus, fundamental problems remain to be solved for physics-based logPow predictions.
Keywords: molecular dynamics, solvation free energy, OPLS-AA force field, AMBER force field, CHARMM force field, ligand parametrization, free energy perturbation, octanol-water partition coefficient, SAMPL7
1. Introduction
One of the goals of physics-based molecular simulations is the accurate prediction of thermodynamic observables from atomic-scale interactions. The accuracy of predictions, i.e., how well the prediction matches the experimentally known value, depends on how well the physics of the molecular interaction is modelled and how well different thermodynamically relevant configurations of the system (or more broadly, its phase space) are sampled. A rigorous approach to improving accuracy requires that simulations first have sampled all relevant regions of phase space sufficiently in order to obtain precise estimates for the observables because only then does it become possible to attribute inaccuracies to the model for the interactions and not to random chance [1]. Establishing that a system has sampled sufficiently (and that an observable is truly converged to its infinite sampling/infinite time equilibrium value) is challenging. Here we present, in the context of the SAMPL7 challenge [2], precise predictions for a non-trivial observable, the octanol-water partition coefficient Pow for a set of small molecules (Fig. 1). As the model for interactions we use classical force fields, namely three widely used force fields, AMBER/GAFF, CHARMM/CGenFF, OPLS-AA (with LigParGen parameters); additionally, we also generated “classic” OPLS-AA parameters with the same in-house approach that we had employed in previous challenges [3–6].
Fig. 1:
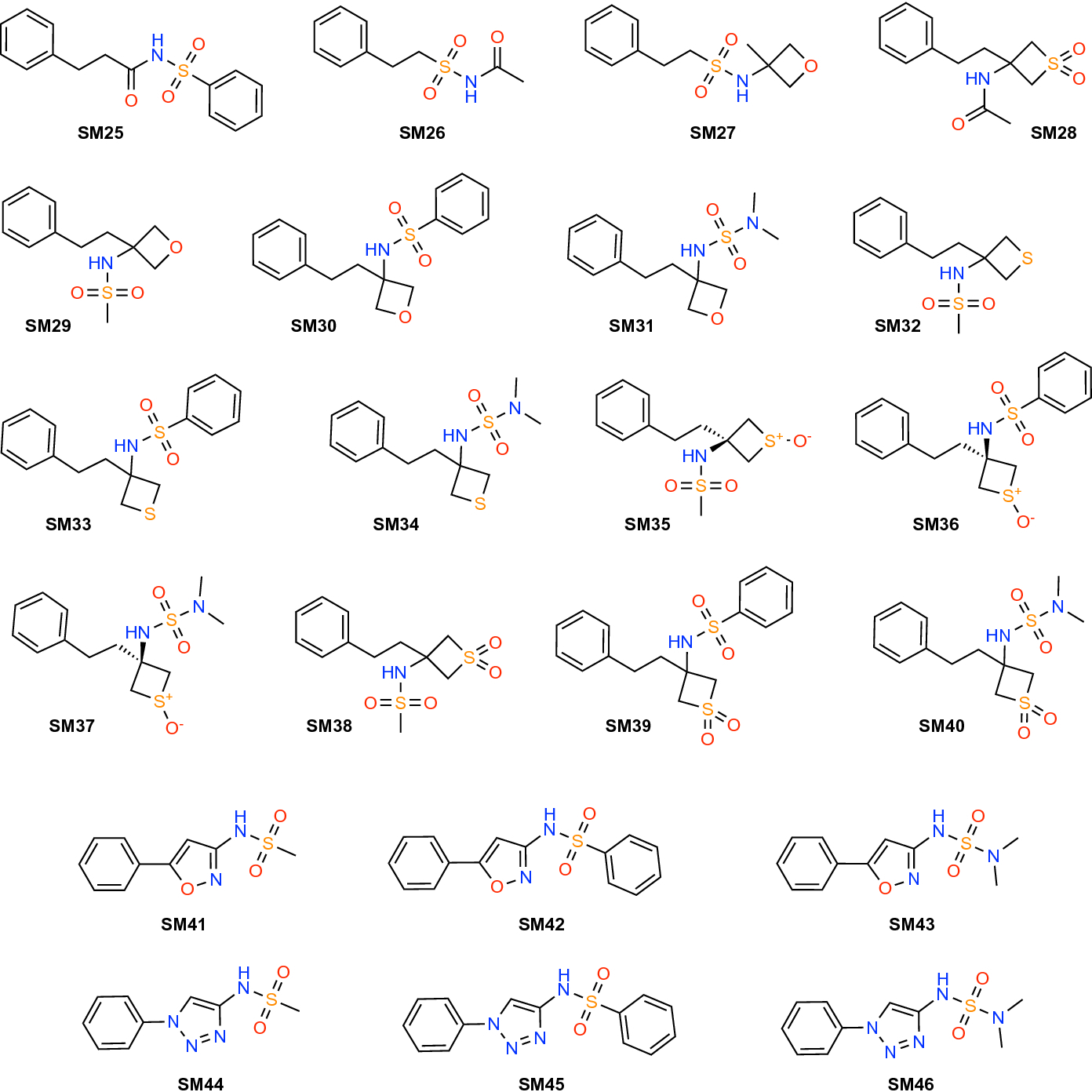
Chemical structures of the SAMPL7 physical properties data set.
In order to sample configuration space (the momentum part of phase space is not relevant) we use molecular dynamics (MD) simulations with the same approach as for previous solvation-free energy based challenges [3–6]. The logarithm of the partition coefficient logPow is computed from the solvation free energies of the solute in the two solvents (ΔGw in water and ΔGo in 1-octanol) as
| (1) |
where R = 8.31446261815×10−3 kJ·mol−1 ·K−1 is the universal Gas constant (i.e., Boltzmann’s constant for 1 mol), T is the temperature, and e Euler’s number.
2. Methods
As in our previous SAMPL participations [3–6] we calculated solvation free energies with explicit solvent all atom MD simulations and classical force fields. In particular, the protocol that used our MDPOW Python package (https://github.com/Becksteinlab/mdpow/) followed closely the one from SAMPL6 [6], which we briefly summarize below for completeness.
We generally followed our standard stratified alchemical free energy calculation protocol [5, 6], with classical explicit solvent MD simulations in the NPT ensemble for water and 1-octanol solvents. For the SAMPL6 challenge we had not observed any particular improvement in prediction accuracy by including water in the octanol simulations [6]. Therefore, only pure octanol was used as a solvent. For all 22 SAMPL7 molecules SM25-SM46 (Figure 1), absolute solvation free energy calculations were carried out using topologies generated with CHARMM/CGenFF (CGenFF), standard OPLS-AA atom types with fixed charges (referred to as OPLS-AA (mol2ff) or simply OPLS-AA), OPLS-AA with variable 1.14*CM1A charges (OPLS-AA (LigParGen) or just LigParGen), and AMBER/GAFF (GAFF). All logPow values were computed from the solvation free energies according to Eq. 1.
The detailed results for logPow presented in Section 3 used the same methodology as the submitted SAMPL7 results, the only difference being that the simulations presented here were run much longer. In the SAMPL7 submissions, all λ windows were of 50 ns length regardless of their convergence status, except for CGenFF simulations of compounds SM25-SM34 in which each window was extended until convergence was reached or the simulation time exceeded 1 μs. In the results included in this paper, these criteria are fulfilled for all windows of CGenFF and OPLS-AA (mol2ff) simulations and partially in the case of GAFF and OPLS-AA (LigParGen). Overall, more than 1000 μs were simulated to obtain precise predictions.
2.1. Force field parameters
Force field parametrization for the molecules included in the SAMPL7 physical properties data set (Figure 1) started with the three dimensional coordinates that were generated with CORINA version 4.2.0 (http://www.molecular-networks.com) from the corresponding SMILES strings provided by the SAMPL7 challenge organizers. No other tautomers were evaluated, as we considered that these are the most stable forms.
For OPLS-AA [7–13] we generated parameters in two different ways: The OPLS-AA (mol2ff) data set was parametrized with transferable charges using our in house MOL2FF algorithm (O. Beckstein and B. I. Iorga, unpublished), based on the CACTVS Chemoinformatics Toolkit (http://www.xemistry.com/) [14]. The OPLS-AA (LigParGen) data set with non-transferrable charges was generated with CM1A charges (scaled with a factor of 1.14 for neutral molecules) using the LigParGen web server [15] (http://zarbi.chem.yale.edu/ligpargen/). CHARMM/CGenFF force field [16] parameters were obtained from the CGenFF server (https://cgenff.umaryland.edu/) using the CGenFF program version 2.2.0 and CGenFF 4.0 [17, 18] with mol2 files as inputs. The resulting CHARMM files were converted to GROMACS files with the Python script cgenff_charmm2gmx.py (downloaded from http://mackerell.umaryland.edu/download.php?filename=CHARMM_ff_params_files/cgenff_charmm2gmx.py, copyright notice from 2014). AMBER/GAFF [19] parameters were generated with AM1-BCC charges using AmberTools15 (http://ambermd.org) with version 1.7 of GAFF and ACPYPE [20]. The force field parameter files are available as will be described in the Section 2.5.
The OPLS-AA hydration free energies simulations were performed using the TIP4P water model [21], the CHARMM/CGenFF [16] simulations used the CHARMM TIP3P water model [22], and the AMBER/GAFF [19] simulations were carried out using the standard TIP3P water model [21] — all of which are the water models used for the development of the corresponding force fields, respectively. For simulations in pure 1-octanol we used the parameters that we developed and validated for SAMPL6 [6].
2.2. Solvation free energy and partition coefficient calculation
Solvation free energies were calculated as described previously [6] via stratified all-atom alchemical free energy perturbation (FEP) MD simulations with the MDPOW Python package (https://github.com/Becksteinlab/mdpow/, 0.7.0 development version) with the GROMACS 2020.3 [23] MD package. Autocorrelation analysis and the multistate Bennett acceptance ratio (MBAR) [24] were performed with the ALCHEMLYB Python package (https://github.com/alchemistry/alchemlyb), release 0.3.0 [25] as integrated into MDPOW.
Each compound molecule was solvated in a periodic cubic simulation cell with a minimal distance of 1.5 nm to the nearest box surface. Simulations were performed in the NPT ensemble at T = 300 K with Langevin dynamics (integration time step 2 fs) for temperature control with the friction coefficient for each particle computed as mass/0.1 ps [26]. An isotropic Parinello-Rahman barostat [27] with relaxation time constant τp = 1 ps and compressibility κT = 4.6×10−5 bar−1 was used to simulate at constant average pressure 1 bar. Van der Waals (i.e., Lennard-Jones) interactions were calculated up to a cutoff of 1 nm without force-switching for OPLS-AA and AMBER simulations and a cutoff of 1.2 nm with a force-switching cutoff of 1.0 nm for CHARMM simulations. A dispersion correction was applied to energy and pressure to account for van der Waals interactions beyond the cutoff in a mean field manner [1] for OPLS-AA and AMBER. Coulomb interactions were evaluated with the SPME method [28] with an initial short range cutoff of 1 nm, 0.12 nm Fourier grid spacing, sixth order spline interpolation, and a relative tolerance of 10−6. Each simulation was run on 8–20 CPU cores. All bonds containing hydrogen atoms were constrained with the P-LINCS algorithm [29] using a twelfth order expansion with a single iteration. Simulation parameters for water and octanol simulations were identical.
Solvated systems were energy minimized and relaxed with a short NPT MD simulation with a time step of 0.1 fs and duration of 5 ps. An initial NPT equilibrium simulation at constant temperature and pressure (T = 300 K, P = 1 bar) with time step 2 fs was carried out for 15 ns. The convergence of the potential energy U was then evaluated with the criterion Rc < 0.05 (Eq. 16) for a relative value of ε/[maxt U(t)−mint U(t)] = 0.05 (see Section 2.4); simulations that were not converged were extended until convergence was reached or total simulation time exceeded 1 μs.
The last frame of the equilibrium simulation served as the starting configuration for the windowed alchemical free energy calculations in the NPT ensemble. Coulomb interactions (partial charges) were linearly switched off over five windows (coupling parameter λCoul ∈ {0, 0.25, 0.5, 0.75, 1}) for water simulations, and seven windows (coupling parameter λCoul ∈ {0, 0.125, 0.25, 0.375, 0.5, 0.75, 1}) for octanol simulations, while the van der Waals (Lennard-Jones) interactions were maintained (i.e. λvdW = 0); sixteen windows were used to switch off the Lennard-Jones term for the uncharged solute (λCoul = 1 and λvdW ∈{0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1}). The van der Waals calculations used soft core potentials with the values [26] α = 0.5, power 1, and σ = 0.3 nm. The calculations made use of the “couple-intramol = no” feature in GROMACS [23, 30, 31], which maintains intramolecular interactions while decoupling all intermolecular ones.
Each λ window was simulated for at least 50 ns at which point convergence of the derivative of the Hamiltonian H with respect to the coupling parameter λ, , was quantified as described below in Section 2.4. Convergence was assessed with ε = 4 kJ/mol (see Eq. 15) and the criterion
| (2) |
where Rc is defined in Eq. 16. For the CGenFF and OPLS-AA (mol2ff) parametrizations, windows that were not converged were extended until convergence was reached or total simulation time exceeded 1 μs. The GAFF and OPLS-AA (LigParGen) simulations were not run to convergence although GAFF simulations were substantially extended (see Supplementary Fig. S1).
Uncorrelated samples of energy differences ΔUi,j (for free energy calculations) and (for convergence analysis) were obtained by autocorrelation analysis [32, 33]. For a time series of N samples, the autocorrelation function of the observable at a given time frame i was computed as
| (3) |
The integrated autocorrelation time τac (measured in trajectory frames) was calculated as
| (4) |
and the statistical inefficiency g was given by
| (5) |
where we conservatively took the ceiling. Once the statistical inefficiency was found, every gth sample of the original data set was selected at regular intervals to build up a set of uncorrelated samples. In practice, we used as the observable . Solvation free energies and statistical errors for the discharging and decoupling process were calculated with the multistate Bennett acceptance method (MBAR) [24]. The MBAR estimator [24] in ALCHEMLYB requires uncorrelated data for its uncertainty estimates.
The total solvation free energy (transfer from gas phase to aqueous phase at the 1M/1M Ben-Naim standard state)
| (6) |
was calculated as the sum of the Coulomb and van der Waals contributions, with the minus sign originating from the convention in GROMACS that λ = 0 corresponds to the fully coupled (solvated) state while λ = 1 describes a fully decoupled (gas-phase) solute.
In principle, the partition coefficient contains contributions from multiple tautomers with significant populations. To simplify the calculations, we only picked for each compound a single uncharged tautomer (see structures in Figure 1), and calculated the octanol-water partition coefficients logPow (Eq. 1) for one fixed state of the compound via the solvation free energies (Eq. 6).
2.3. Error analysis
As described in our previous study [6], the error δ on logPow was computed by error propagation from the errors of the individual free energies in Eq. 1 as
| (7) |
For each of the N compounds, labeled with its identification code α =SM25,SM26,..., the difference between experimental and computed octanol-water coefficients (called “signed error”), was computed as
| (8a) |
| (8b) |
The uncertainty δΔ of Δ in Eq. 8b was determined as the standard error from propagating the experimental and simulation errors (Eq. 7) through Eq. 8a. The root mean square error (RMSE) was computed from the individual errors Δ as
| (9) |
the absolute unsigned error (AUE) as
| (10) |
and the signed mean error (ME, also named the “mean signed error”, MSE) as
| (11) |
The standard errors of the RMSE, AUE, and ME were estimated via error propagation of the individual uncertainties Eq. 8b through Eqs. 9–11 as
| (12a) |
| (12b) |
Eq. 12a followed the derivation of RMSE from Ref. [34], but is more conservative by not including a correction factor of .
2.4. Convergence analysis
For the previous SAMPL6 challenge we introduced a convergence analysis, which built on previous work on time-reversed convergence plots[32, 35], to quantitatively assess non-equilibrated regions in individual λ windows and complete sets of free energy calculations [6]. In brief, we calculated the time-forward average and time-reversed average of by
| (13) |
| (14) |
For a simulation with a time length of T, the convergence time tc was defined as the smallest time t for which both the forward and the reverse average after this time point were within ε of the value computed over all T,
| (15) |
To make the time point of convergence easily comparable, we defined the convergence time fraction Rc as
| (16) |
Rc denotes the fraction of the simulation time from which onwards the system appears to be equilibrated. Thus, Rc = 0 indicates that the system is well equilibrated right from the beginning while Rc = 1 signifies that the whole trajectory is not equilibrated. In other words, Rc is the fraction of the trajectory that is not well equilibrated, so smaller values of Rc are better.
With Rc as a measure of convergence, we can analyze a complete set of λ windows by computing Rc(λ) for each window and then plot a cumulative probability distribution function
| (17) |
of these values, which measures the fraction of windows that has at least the given Rc. For a perfectly equilibrated FEP calculation, resembles a unit step function near Rc = 0 because all windows have Rc(λ) ≈ 0. For a poorly equilibrated calculation, rises steeply near Rc = 1. The area Ac under the cumulative distribution ,
| (18) |
defines a quantitative quality measure for the convergence of a whole set of λ windows in the form of a single number. Ac is a number between 0 and 1 that can be interpreted as the ratio of the total equilibrated simulation time to the whole simulation time for a full set of simulations. Ac = 1 means that all simulation time frames in all windows can be considered equilibrated (with the meaning of Eq. 15), while Ac = 0 indicates that nothing is equilibrated.
2.5. Data sharing
Data related to this work are shared in the GitHub repository Becksteinlab/SAMPL7_logP_data that is archived on Zenodo at DOI 10.5281/zenodo.4650632. Input files for GROMACS 2020, the results in CSV format and the SAMPL7 submissions are included. The submission codes for our logPow predictions using LigParGen, CGenFF (ranked), GAFF and OPLS-AA are 54, 55, 56 and 57, respectively. The submission code for the pKa prediction is 15 (which was part of the challenge but is not discussed further).
3. Results and Discussion
3.1. Convergence
Our work in SAMPL6 indicated that sufficient equilibration of the equilibrium simulation and λ windows could be crucial for accurate results [6]. However, these simulations were likely still too short to be converged and fully sampled. We therefore specifically aimed to generate converged and precise estimates for free energies and logPow in order to separate sampling issues from force field accuracy, following a similar philosophy as Shirts et al [1] in their work on precises free energy calculations of amino acid side chain analogs.
We assessed convergence in two ways. Firstly, we used convergence of as a proxy to assess the sampling of individual windows using the Rc measure (Eq. 16). We chose ε = 4kJ/mol ≈ 1kcal/mol for Eq. 15 and considered a λ window converged when Rc ≤ 0.05 (see Eq. 2). This convergence criterion implies that at least 95% of the data of any converged window are well-sampled, with the fluctuations in remaining in a ±4kJ/mol band around the mean. Roughly speaking, the fluctuations in , expressed as the variance , are related to the fluctuation in the free energy estimate by , where νλ is the number of independent samples in window λ (and by the definition of the Riemann sum of the thermodynamic integral, ). Thus, for ν = 104 independent samples in each window, the uncertainty in the final free energy estimate would be about 0.04 kJ/mol.
Secondly, the convergence of the observable itself (logPow) was established through post-hoc analysis of the calculated logPow as a function of data used, which is expressed as the maximum simulated time across all window simulations that are needed to compute the free energies for Eq. 1 with the MBAR estimator.
3.1.1. Rc and Ac
The advantage of the criterion Eq. 2 is that it can be calculated for a running simulation without requiring knowledge of any other simulations for other λ values. We therefore used this criterion to dynamically extend simulations for individual windows (for the CGenFF and OPLS-AA (mol2ff) data sets) until they fulfilled Eq. 2 or exceeded a run length of 1 μs. The total simulated time per λ window showed a characteristic dependence on λ for the fully converged simulations. For both CGenFF (Fig. 2) and OPLS-AA (mol2ff) (Fig. 3) water and octanol simulations behaved in a specific manner: The Coulomb windows for water typically converged in less than 400 ns whereas the octanol windows required close to 1000 ns at the beginning of the λ range (Figs. 2a and 3a). The Lennard-Jones (van der Waals) decoupling typically converged faster (200 ns or less), except around λ ≈ 0.7 (water) or 0.9 (octanol) where simulations took more than 600 ns to converge (Figs. 2b and 3b) — a pattern that seemed directly related to the fact that (with our soft core parameters) exhibits a minimum in the same region. In all cases there existed windows that did not converge within 1 μs, as seen by the distribution of the data points in the figure.
Fig. 2:

Convergence of CGenFF simulations. (a) and (b): Total simulated time for each λ window. Lines connect the means of data for each λ and the shaded band indicates the standard deviation over all times for a given λ. Simulations that are not converged according to the criterion Eq. 2 are shown as larger symbols. (c) For each SAMPL7 compound, the Ac convergence measures for each of the four free energy calculations that are needed to compute logPow are shown to indicate specific free energies that are potentially insufficiently sampled.
Fig. 3:
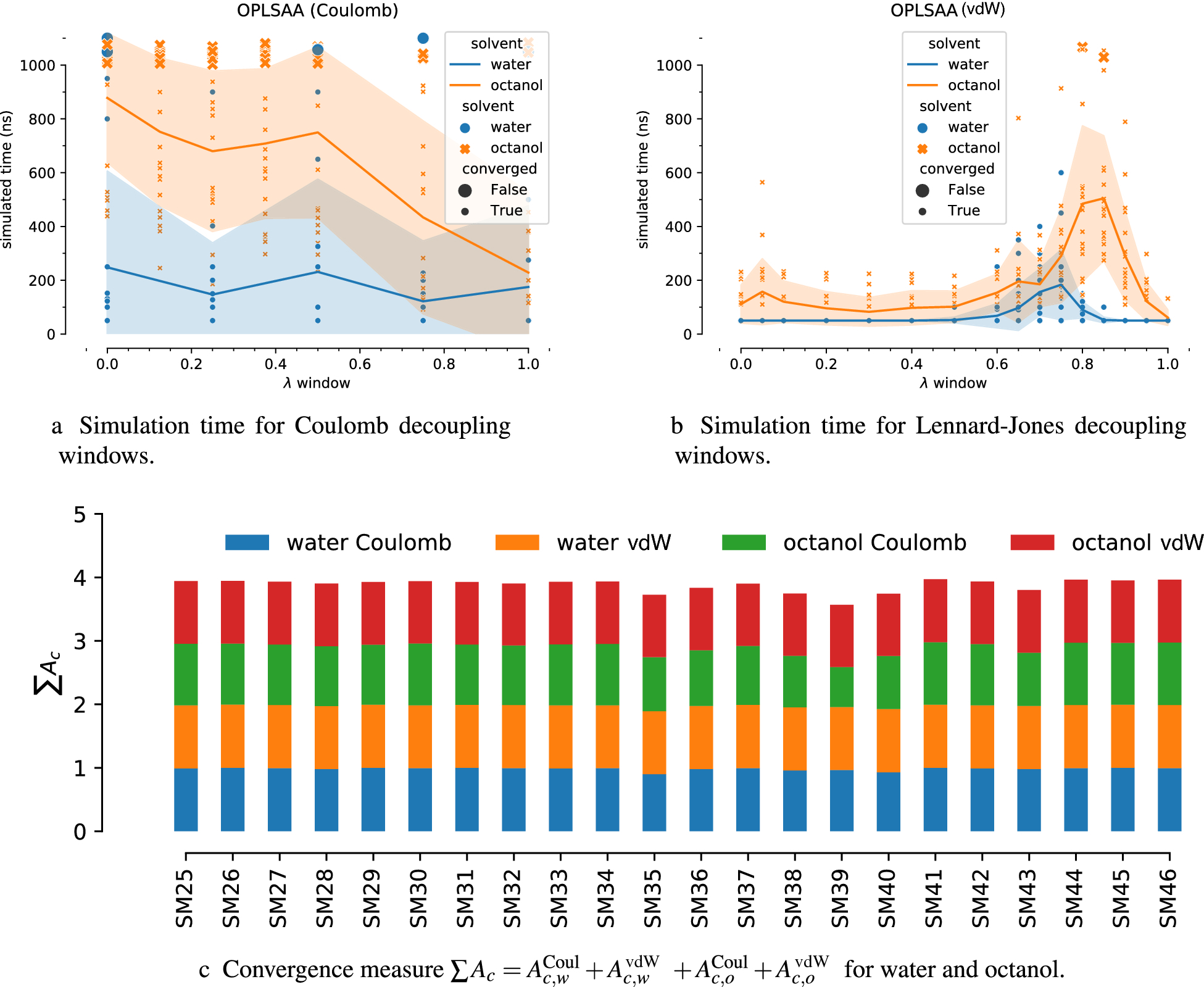
Convergence of OPLS-AA (mol2ff) simulations. (a) and (b): Total simulated time for each λ window. Lines connect the means of data for each λ and the shaded band indicates the standard deviation over all times for a given λ. Simulations that are not converged according to the criterion Eq. 2 are shown as larger symbols. (c) For each SAMPL7 compound, the Ac convergence measures for each of the four free energy calculations that are needed to compute logPow are shown to indicate specific free energies that are potentially insufficiently sampled.
Based on the Rc for all λ windows, the summary convergence measure Ac (Eq. 18) was determined for the Coulomb and Lennard-Jones interaction decoupling steps in the water and octanol simulations. Because Ac is a number between 0 and 1 (where 1 means all simulations that contribute to a free energy estimate are fully converged) a rough quality measure of convergence is the sum of the four values
| (19) |
with a total value ∑Ac = 4 indicating full convergence. By this measure, all of the CGenFF (Fig. 2c) simulations were well converged (> 0.9 for each Ac), with only SM36 showing some deficits in the Coulomb decoupling with octanol (, see Table 2). The OPLS-AA (mol2ff) dataset (Fig. 3) was also generally well converged although a few compounds also had octanol Coulomb free energies that were not fully converged with (Table 3). For comparison, Fig. S3 shows the data for the GAFF dataset. Because fewer GAFF simulations were run to convergence, the distribution of the run times per window were skewed towards the length of the non-converged simulations and the trends seen in Supplementary Figs. S3a and S3b might change with longer run times. Nevertheless, the breakdown by Ac is informative (Supplementary Fig. S3c) and clearly shows that the GAFF simulations were less converged than the CGenFF and OPLS-AA (mol2ff) ones, especially with a majority of octanol Coulomb values in the range (Table 5).
Table 2:
Calculated (log Pow) and experimental () octanol-water partition coefficients with error estimate and convergence measures Ac for the CGenFF resultsa,
| id | Ac,w b | Ac,o b | Exp. | Calculated | |||
|---|---|---|---|---|---|---|---|
| Coul | VDW | Coul | VDW | log Pow | Δ c | ||
|
| |||||||
| SM25 | 0.985 | 0.983 | 0.946 | 0.978 | 2.67(1) | 4.84(8) | 2.17(8) |
| SM26 | 1.000 | 0.988 | 0.968 | 0.981 | 1.04(1) | 1.83(4) | 0.79(4) |
| SM27 | 0.980 | 0.991 | 0.904 | 0.980 | 1.56(11) | 2.43(6) | 0.87(12) |
| SM28 | 0.985 | 0.991 | 0.925 | 0.975 | 1.18(8) | 1.94(5) | 0.76(9) |
| SM29 | 0.990 | 0.984 | 0.911 | 0.981 | 1.61(3) | 1.90(6) | 0.29(6) |
| SM30 | 0.990 | 0.994 | 0.939 | 0.980 | 2.76(19) | 4.10(4) | 1.34(19) |
| SM31 | 0.990 | 0.986 | 0.971 | 0.978 | 1.96(14) | 3.00(6) | 1.04(15) |
| SM32 | 0.980 | 0.988 | 0.964 | 0.981 | 2.44(17) | 4.39(8) | 1.95(18) |
| SM33 | 0.975 | 0.972 | 0.975 | 0.980 | 2.96(21) | 5.48(6) | 2.52(21) |
| SM34 | 0.995 | 0.970 | 0.954 | 0.975 | 2.83(20) | 4.48(5) | 1.65 (20) |
| SM35 | 0.990 | 0.994 | 0.918 | 0.988 | 0.88(2) | 1.62(4) | 0.74(4) |
| SM36 | 0.985 | 0.997 | 0.818 | 0.977 | 0.76(5) | 3.09(6) | 2.33(7) |
| SM37 | 0.995 | 0.994 | 0.929 | 0.980 | 1.45(10) | 2.18(5) | 0.73(11) |
| SM38 | 0.985 | 0.995 | 0.921 | 0.981 | 1.03(7) | 2.16(7) | 1.13(9) |
| SM39 | 0.990 | 0.989 | 0.925 | 0.981 | 1.89(13) | 3.61(7) | 1.72(14) |
| SM40 | 0.985 | 0.992 | 0.936 | 0.981 | 1.83(5) | 2.98(6) | 1.15(7) |
| SM41 | 1.000 | 1.000 | 0.975 | 0.986 | 0.58(2) | 2.72(2) | 2.14(2) |
| SM42 | 1.000 | 0.998 | 0.968 | 0.984 | 1.76(3) | 5.21(2) | 3.45(3) |
| SM43 | 1.000 | 1.000 | 0.964 | 0.989 | 0.85(1) | 3.62(2) | 2.77(2) |
| SM44 | 0.995 | 0.995 | 0.964 | 0.994 | 1.16(3) | 1.19(2) | 0.03(3) |
| SM45 | 0.995 | 0.995 | 0.936 | 0.989 | 2.55(4) | 3.62(4) | 1.07(5) |
| SM46 | 1.000 | 0.998 | 0.943 | 0.986 | 1.72(1) | 2.27(2) | 0.55(2) |
| RMS Error (RMSE)d | 1.65(3) | ||||||
| Absolute Unsigned Error (AUE)d | 1.42(2) | ||||||
| Mean Error (ME)d | 1.42(2) | ||||||
Preliminary data related to these simulations (only 50 ns for the FEP windows of compounds SM35-SM46) were submitted to the SAMPL7 challenge with the code 55 (see Section 2.5 for the availability of raw submission files).
The convergence measure 0 ≤ Ac ≤ 1 (Eq. 18) is provided for each of the separate free energy calculations that are necessary for log Pow, namely for water (Ac,w) and octanol (Ac,o) with the separate Coulomb (“Coul”) and Lennard-Jones (“VDW”) decoupling steps. Higher Ac are better and indicate that a larger fraction of the λ windows is converged according to the criterion Eq. 2.
Table 3:
Calculated (log Pow) and experimental () octanol-water partition coefficients with error estimate and convergence measures Ac for the OPLS-AA (mol2ff) resultsa.
| id | Ac,w b | Ac,o b | Exp. | Calculated | |||
|---|---|---|---|---|---|---|---|
| Coul | VDW | Coul | VDW | log Pow | Δ c | ||
|
| |||||||
| SM25 | 0.990 | 0.994 | 0.971 | 0.986 | 2.67(1) | 3.81(3) | 1.14(3) |
| SM26 | 1.000 | 0.997 | 0.961 | 0.986 | 1.04(1) | 1.36(2) | 0.32(2) |
| SM27 | 0.995 | 0.994 | 0.954 | 0.991 | 1.56(11) | 1.77(2) | 0.21(11) |
| SM28 | 0.980 | 0.992 | 0.943 | 0.989 | 1.18(8) | 1.96(6) | 0.78(10) |
| SM29 | 1.000 | 0.994 | 0.946 | 0.988 | 1.61(3) | 1.22(4) | −0.39(5) |
| SM30 | 0.995 | 0.991 | 0.975 | 0.978 | 2.76(19) | 4.43(3) | 1.67(19) |
| SM31 | 1.000 | 0.992 | 0.950 | 0.984 | 1.96(14) | 4.00(3) | 2.04(14) |
| SM32 | 0.995 | 0.994 | 0.939 | 0.975 | 2.44(17) | 3.54(4) | 1.10(17) |
| SM33 | 0.990 | 0.994 | 0.961 | 0.986 | 2.96(21) | 5.33(2) | 2.37(21) |
| SM34 | 0.995 | 0.989 | 0.968 | 0.983 | 2.83(20) | 5.89(4) | 3.06(20) |
| SM35 | 0.900 | 0.992 | 0.850 | 0.983 | 0.88(2) | 1.46(8) | 0.58(8) |
| SM36 | 0.980 | 0.995 | 0.879 | 0.981 | 0.76(5) | 3.88(9) | 3.12(10) |
| SM37 | 0.995 | 0.997 | 0.929 | 0.981 | 1.45(10) | 4.31(6) | 2.86(11) |
| SM38 | 0.960 | 0.994 | 0.811 | 0.981 | 1.03(7) | −1.80(6) | −2.83(9) |
| SM39 | 0.965 | 0.994 | 0.629 | 0.981 | 1.89(13) | 1.01(5) | −0.88(13) |
| SM40 | 0.930 | 0.997 | 0.836 | 0.981 | 1.83(5) | 3.12(10) | 1.29(11) |
| SM41 | 1.000 | 0.994 | 0.986 | 0.992 | 0.58(2) | 2.30(2) | 1.72(2) |
| SM42 | 0.990 | 0.995 | 0.964 | 0.984 | 1.76(3) | 4.97(4) | 3.21(5) |
| SM43 | 0.980 | 0.995 | 0.839 | 0.986 | 0.85(1) | 4.82(6) | 3.97(6) |
| SM44 | 0.995 | 0.995 | 0.982 | 0.991 | 1.16(3) | 2.74(2) | 1.58(3) |
| SM45 | 1.000 | 0.994 | 0.975 | 0.983 | 2.55(4) | 5.54(2) | 2.99(4) |
| SM46 | 0.995 | 0.994 | 0.986 | 0.991 | 1.72(1) | 5.18(2) | 3.46(2) |
| RMS Error (RMSE)d | 2.20(2) | ||||||
| Absolute Unsigned Error (AUE)d | 1.89(2) | ||||||
| Mean Error (ME)d | 1.52(2) | ||||||
Preliminary data related to these simulations (only 50 ns for all FEP windows) were submitted to the SAMPL7 challenge with the code 57 (see Section 2.5 for the availability of raw submission files).
The convergence measure 0 ≤ Ac ≤ 1 (Eq. 18) is provided for each of the separate free energy calculations that are necessary for log Pow, namely for water (Ac,w) and octanol (Ac,o) with the separate Coulomb (“Coul”) and Lennard-Jones (“VDW”) decoupling steps. Higher Ac are better and indicate that a larger fraction of the λ windows is converged according to the criterion Eq. 2.
Table 5:
Computed (log Pow) and experimental () octanol-water partition coefficients with error estimate and convergence measures Ac for the GAFF resultsa.
| id | Ac,w b | Ac,o b | Exp. | Calculated | |||
|---|---|---|---|---|---|---|---|
| Coul | VDW | Coul | VDW | log Pow | Δ c | ||
|
| |||||||
| SM25 | 0.980 | 0.989 | 0.746 | 0.928 | 2.67(1) | 3.62(12) | 0.95(12) |
| SM26 | 0.965 | 0.986 | 0.921 | 0.984 | 1.04(1) | 1.27(6) | 0.23(6) |
| SM27 | 0.935 | 0.983 | 0.839 | 0.981 | 1.56(11) | 2.24(11) | 0.68(15) |
| SM28 | 0.795 | 0.989 | 0.796 | 0.989 | 1.18(8) | 2.61(14) | 1.43(16) |
| SM29 | 0.900 | 0.961 | 0.714 | 0.989 | 1.61(3) | 2.97(12) | 1.36(12) |
| SM30 | 0.900 | 0.969 | 0.821 | 0.952 | 2.76(19) | 3.92(13) | 1.16(23) |
| SM31 | 0.935 | 0.991 | 0.925 | 0.967 | 1.96(14) | 3.27(8) | 1.31(16) |
| SM32 | 0.800 | 0.972 | 0.807 | 0.959 | 2.44(17) | 3.50(17) | 1.06(24) |
| SM33 | 0.815 | 0.987 | 0.829 | 0.964 | 2.96(21) | 4.18(12) | 1.22(24) |
| SM34 | 0.970 | 0.978 | 0.918 | 0.970 | 2.83(20) | 4.04(9) | 1.21(21) |
| SM35 | 0.870 | 0.995 | 0.746 | 0.958 | 0.88(2) | 2.44(18) | 1.56(18) |
| SM36 | 0.905 | 0.995 | 0.725 | 0.973 | 0.76(5) | 3.76(13) | 3.00(13) |
| SM37 | 0.990 | 0.995 | 0.871 | 0.970 | 1.45(10) | 2.86(13) | 1.41(16) |
| SM38 | 0.985 | 0.997 | 0.796 | 0.980 | 1.03(7) | 2.60(16) | 1.57(17) |
| SM39 | 0.955 | 0.995 | 0.736 | 0.980 | 1.89(13) | 4.02(14) | 2.13(19) |
| SM40 | 0.980 | 0.995 | 0.589 | 0.844 | 1.83(5) | 3.71(21) | 1.88(21) |
| SM41 | 0.995 | 0.995 | 0.686 | 0.944 | 0.58(2) | 2.70(14) | 2.12(14) |
| SM42 | 0.985 | 0.995 | 0.707 | 0.898 | 1.76(3) | 4.21(10) | 2.45(10) |
| SM43 | 0.965 | 0.997 | 0.771 | 0.905 | 0.85(1) | 3.11(14) | 2.26(14) |
| SM44 | 0.995 | 0.997 | 0.729 | 0.955 | 1.16(3) | 2.22(11) | 1.06(11) |
| SM45 | 0.990 | 0.997 | 0.754 | 0.902 | 2.55(4) | 3.76(9) | 1.21(9) |
| SM46 | 0.975 | 0.997 | 0.764 | 0.897 | 1.72(1) | 3.08(15) | 1.36(15) |
| RMS Error (RMSE)d | 1.60(3) | ||||||
| Absolute Unsigned Error (AUE)d | 1.48(4) | ||||||
| Mean Error (ME)d | 1.48(4) | ||||||
Preliminary data related to these simulations (only 50 ns for all FEP windows) were submitted to the SAMPL7 challenge with the code 56 (see Section 2.5 for the availability of raw submission files).
The convergence measure 0 ≤ Ac ≤ 1 (Eq. 18) is provided for each of the separate free energy calculations that are necessary for log Pow, namely for water (Ac,w) and octanol (Ac,o) with the separate Coulomb (“Coul”) and Lennard-Jones (“VDW”) decoupling steps. Higher Ac are better and indicate that a larger fraction of the λ windows is converged according to the criterion Eq. 2.
The OPLS-AA (LigParGen) windows were only run to a maximum of 150 ns and consequently most of them did not converge and the patterns discernible for the better converged simulations were not apparent (Supplementary Figs. S2a and S2b). The overall poor convergence was immediately visible in the Ac analysis (Supplementary Fig. S2c) where especially octanol and water Coulomb windows were not sufficiently sampled.
3.1.2. Convergence of logPow
Here we focused on the CGenFF and the OPLS-AA (mol2ff) datasets because only those were run until most windows were converged (or had accumulated 1 μs of simulated time) as discussed in Section 3.1.1. Therefore, the maximum amount of time to be included across all simulation windows was 1 μs and the value of logPow for 1 μs was taken as the reference value. Convergence was assessed by looking at the difference Δ logPow between logPow(T) computed from shorter trajectory slices up to a time T ≤ 1 μs and the reference value logPow(T = 1μs).
For CGenFF, at least 250 ns were required so that the observable was within less than 0.25 units of the final value (Figure 4a). In some cases, convergence of logPow was not steady and only after 800 ns the value approached the reference. The statistical error of the prediction, δ (Eq. 7), steadily decreased with increasing amount of data used (Fig. 4b).
Fig. 4:

Convergence of logPow in CGenFF simulations as a function of the maximum amount of simulation time used across all λ windows. In (a) the difference to the value for 1000 ns is plotted. Black dashed lines indicate ±0.25 units from 0.
Convergence of logPow for OPLS-AA (mol2ff) was more varied than for CGenFF. Although many simulations also converged after about 250 ns, a subset of simulations required between 500 ns and about 700 ns to approach the final value to within 0.25 units (Figure 5a). The more difficult convergence was reflected in how the statistical error δ decreased less steadily (SM39) or even increased before decreasing near 1000 ns (SM40), as seen in Fig. 5b.
Fig. 5:
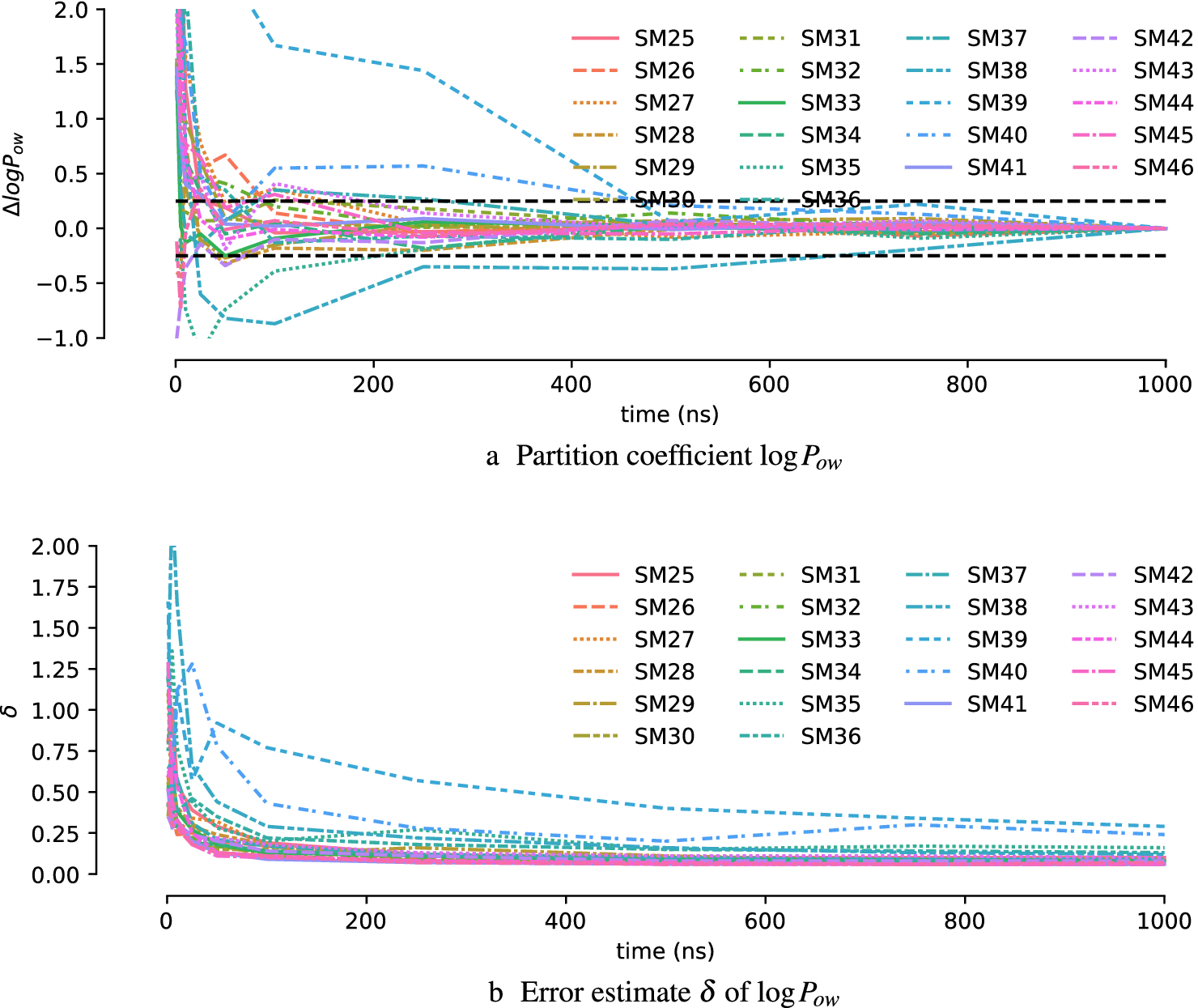
Convergence of logPow in OPLS-AA (mol2ff) simulations as a function of the maximum amount of simulation time used across all λ windows. In (a) the difference to the value for 1000 ns is plotted. Black dashed lines indicate ±0.25 units from 0.
The analysis of convergence established that at least our CGenFF and OPLS-AA (mol2ff) dataset were sufficiently well sampled so that the resulting logPow predictions should not suffer from a sizable sampling error. Similar analysis for the GAFF dataset also showed good convergence for > 250 ns (Supplementary Fig. S4). The resulting error estimate of logPow, which used the statistical inefficiency (Eq. 5) to obtain decorrelated, independent samples, should therefore be a good measure of the precision of our results. Thus, any differences between prediction and experiment, as discussed in the next section, should be due to the force field parametrization and/or the simulation protocol.
3.2. Partition coefficients
The predicted logPow values were compared to the experimental values that were made available by the SAMPL7 organizers. In addition to RMSE, AUE, and ME, the Pearson correlation coefficient r and the Kendall rank correlation coefficient τ were calculated, with a summary for all four data sets listed in Table 1. In the following we discuss in more detail the individual data sets with our converged simulations, sorted by force field parametrization. Table 1 also contains the summary statistics for our ranked submission (ID 55) as computed by the SAMPL organizers. Additional discussion of the difference between submitted predictions and analysis of simulations with established convergence behavior can be found in Supplementary Information.
Table 1:
Summary statistics (RMSE, AUE, ME, Pearson correlation coefficient r and Kendall rank correlation coefficient τ) for the log Pow predictions from long simulations.
| force field | RMSE | AUE | ME | r | τ |
|---|---|---|---|---|---|
|
| |||||
| CGenFFa | 1.62 | 1.41 | 1.38 | 0.54 | 0.523 |
|
| |||||
| CGenFF | 1.65(3) | 1.42(2) | 1.42(2) | 0.715 | 0.521 |
| OPLS-AA (mol2ff) | 2.20(2) | 1.89(2) | 1.52(2) | 0.536 | 0.351 |
| OPLS-AA (LigParGen)b | 2.35(6) | 2.05(5) | −1.51(5) | 0.207 | 0.134 |
| GAFFc | 1.60(3) | 1.48(4) | 1.48(4) | 0.660 | 0.521 |
Ranked submission with submission ID 55
OPLS-AA (LigParGen) simulations are not converged with respect to the convergence criterion Eq. 2.
The GAFF dataset contains many more non-converged simulations than CGenFF and OPLS-AA (mol2ff).
3.2.1. CGenFF
The CGenFF dataset was well converged according to our convergence analysis. The calculated error for the logPow was 0.08 log units or less (Table 2) and so our predictions were very precise, consistent with the convergence analysis. Compared to experimental data, the accuracy was modest with an RMSE of 1.65±0.03, a value comparable with the average performance of SAMPL7 submissions (RMSE ranging from 0.55 to 3.97). The correlation plot (Fig. 6) showed that the logPow was systematically overestimated, which was reflected in the ME and AUE being the same value of 1.42±0.02. The correlation between experimental and computed values was relatively good, with a Pearson correlation coefficient of r = 0.715 (with r = 1 indicating perfect correlation, 0 no correlation, and −1 perfect anti-correlation). The first ranked SAMPL7 submission had a Pearson correlation coefficient of r = 0.746, which would have made the converged CGenFF dataset the second best result. Thus, in the context of SAMPL7, r > 0.7 should count as a high value. The Kendall rank correlation coefficient τ quantifies the ability to rank-order the data; a value of τ = 1 indicates that the simulations predict the same ranking of compounds by logPow as the experimental data whereas if the rankings were completely reversed τ would obtain the value −1 and if the simulations produced random results, a value close to 0 would be expected. For CGenFF, a Kendall τ = 0.521 indicated a relatively modest ability to correctly rank order compounds. However, this value would have been among the top scorers in SAMPL7, not very different from the best submission, which showed a Kendall rank correlation coefficient τ of 0.575.
Fig. 6:
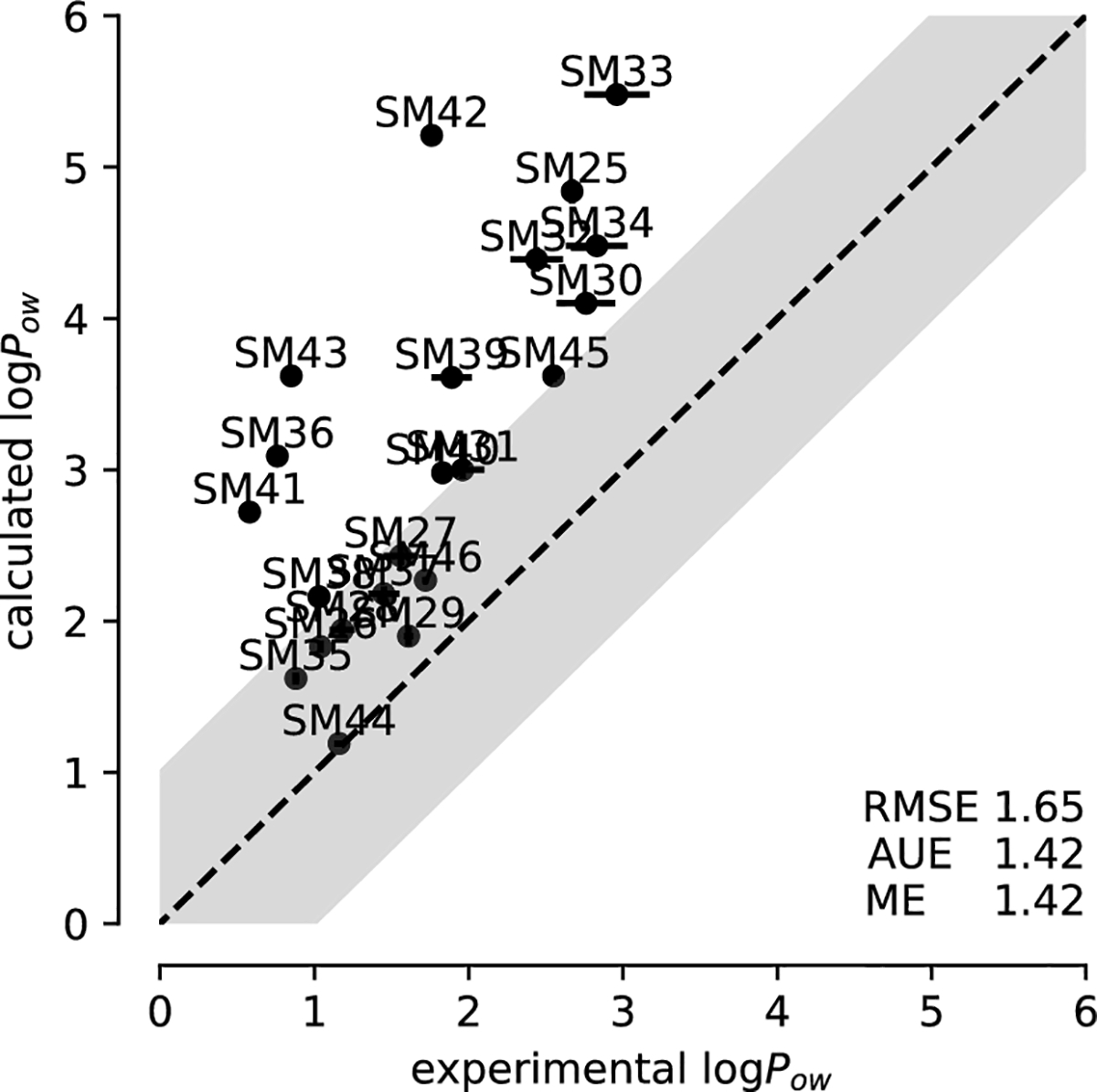
Correlation between experimental and computed octanol-water coefficients logPow for simulations performed with CGenFF parameters.
In the previous SAMPL6 logPow challenge, we had achieved best agreement with experiment with CGenFF (RMSE 1.42±0.06) and those earlier predictions did not suffer from any obvious systematic error as seen in a ME of −0.10±0.06 [6]. On the other hand, the SAMPL6 results were overall poorly correlated with experiment (r = 0.27, τ = 0.29). For the SAMPL7 compounds, the agreement with experiment was worse and displayed a systematic large positive shift, even though the correlation measures were stronger. The SAMPL6 CGenFF data set was not as well sampled as the SAMPL7 simulations and was smaller with only eight compounds so comparisons are somewhat difficult. However, the new SAMPL7 results showed clearly that CGenFF also exhibits a systematic positive shift of logPow compared to experiment, similar to OPLS-AA and GAFF here (see below) and in SAMPL6 [6].
3.2.2. OPLS-AA (mol2ff)
The OPLS-AA (mol2ff) dataset was well converged, similar to the CGenFF dataset. The calculated logPow were very precise with a maximum error of 0.10 log units (Table 3). However, the predictions were not accurate as seen by the RMSE 2.20±0.02. As for CGenFF, the logPow was systematically overestimated as indicated by the systematic positive shift of the predicted values in the correlation plot (Fig. 7) and the positive ME (1.52±0.02). The correlation between experimental and computed values was worse than for CGenFF with a Pearson correlation coefficient of r = 0.536. The Kendall τ = 0.351 indicated relatively poor ability to rank order compounds.
Fig. 7:

Correlation between experimental and computed octanol-water coefficients logPow for simulations performed with OPLS-AA (mol2ff) parameters. The gray band indicates ±1 log-units from ideal correlation, shown by the dashed line. The root mean square error (RMSE), the absolute unsigned error (AUE), and the (signed) mean error (ME) are indicated. Error bars represent the error in the experiments or the error on the mean, derived from the simulations. SM38 is outside the plotting area with a calculated logPow = −1.80±0.06.
The results for SAMPL7 were consistent with our SAMPL6 results, which were slightly worse with RMSE 2.79±0.05 and slightly better with r = 0.41 and τ = 0.60 [6]. As before, the logPow were too positive, which we previously hypothesized to be due to undersolvation in the aqueous phase due to under-polarization of the force field [6].
3.2.3. OPLS-AA (LigParGen)
The OPLS-AA (LigParGen) dataset, i.e., OPLS-AA with non-transferable charges, was not converged. As discussed in Section 3.1.1 and shown in Supplementary Fig. S2c, the converged fraction Ac for some free energy calculations—especially the octanol Coulomb part—was less than 0.5 (Table 4), which lead to larger statistical errors of up to 0.65 (Table 4). The accuracy was similar to the OPLS-AA (mol2ff) simulations with RMSE 2.35±0.06. Unlike any of the other parametrizations, logPow was systematically shifted to more negative values compared to experiment (Fig. 8), resulting in a ME of −1.51±0.05. Correlation with experiment and the ability to rank order compounds correctly was poor (r = 0.207, τ = 0.134).
Table 4:
Calculated (log Pow) and experimental () octanol-water partition coefficients with error estimate and convergence measures Ac for the OPLS-AA (LigParGen) resultsa.
| id | Ac,w b | Ac,o b | Exp. | Calculated | |||
|---|---|---|---|---|---|---|---|
| Coul | VDW | Coul | VDW | log Pow | Δ c | ||
|
| |||||||
| SM25 | 0.875 | 0.972 | 0.704 | 0.950 | 2.67(1) | 1.42(10) | −1.25(10) |
| SM26 | 0.815 | 0.984 | 0.868 | 0.986 | 1.04(1) | 1.36(12) | 0.32(12) |
| SM27 | 0.890 | 0.984 | 0.761 | 0.970 | 1.56(11) | −1.39(6) | −2.95(12) |
| SM28 | 0.635 | 0.981 | 0.679 | 0.981 | 1.18(8) | 0.96(16) | −0.22(17) |
| SM29 | 0.855 | 0.975 | 0.832 | 0.945 | 1.61(3) | −1.88(8) | −3.49(8) |
| SM30 | 0.685 | 0.972 | 0.675 | 0.942 | 2.76(19) | −0.68(16) | −3.44(24) |
| SM31 | 0.780 | 0.798 | 0.189 | 0.347 | 1.96(14) | −0.29(40) | −2.25(42) |
| SM32 | 0.790 | 0.986 | 0.629 | 0.917 | 2.44(17) | 0.26(8) | −2.18(18) |
| SM33 | 0.890 | 0.970 | 0.654 | 0.958 | 2.96(21) | 1.83(10) | −1.13(23) |
| SM34 | 0.675 | 0.720 | 0.329 | 0.386 | 2.83(20) | −2.01(19) | −4.84(27) |
| SM35 | 0.860 | 0.967 | 0.507 | 0.950 | 0.88(2) | −2.67(10) | −3.55(10) |
| SM36 | 0.465 | 0.967 | 0.436 | 0.911 | 0.76(5) | −1.85(30) | −2.61(30) |
| SM37 | 0.465 | 0.355 | 0.307 | 0.138 | 1.45(10) | −0.98(65) | −2.43(65) |
| SM38 | 0.715 | 0.980 | 0.554 | 0.909 | 1.03(7) | −1.32(12) | −2.35(13) |
| SM39 | 0.790 | 0.953 | 0.571 | 0.906 | 1.89(13) | 2.53(13) | 0.64(18) |
| SM40 | 0.650 | 0.572 | 0.211 | 0.344 | 1.83(5) | −0.99(28) | −2.82(28) |
| SM41 | 0.895 | 0.984 | 0.736 | 0.967 | 0.58(2) | 1.98(5) | 1.40(5) |
| SM42 | 0.885 | 0.978 | 0.511 | 0.939 | 1.76(3) | 3.70(7) | 1.94(7) |
| SM43 | 0.910 | 0.992 | 0.746 | 0.945 | 0.85(1) | −0.93(3) | −1.78(3) |
| SM44 | 0.870 | 0.995 | 0.775 | 0.964 | 1.16(3) | 1.86(6) | 0.70(6) |
| SM45 | 0.935 | 0.987 | 0.711 | 0.872 | 2.55(4) | 3.49(4) | 0.94(5) |
| SM46 | 0.830 | 0.988 | 0.500 | 0.898 | 1.72(1) | −0.09(32) | −1.81(32) |
| RMS Error (RMSE)d | 2.35(6) | ||||||
| Absolute Unsigned Error (AUE)d | 2.05(5) | ||||||
| Mean Error (ME)d | −1.51(5) | ||||||
Preliminary data related to these simulations (only 50 ns for all FEP windows) were submitted to the SAMPL7 challenge with the code 54 (see Section 2.5 for the availability of raw submission files).
The convergence measure 0 ≤ Ac ≤ 1 (Eq. 18) is provided for each of the separate free energy calculations that are necessary for log Pow, namely for water (Ac,w) and octanol (Ac,o) with the separate Coulomb (“Coul”) and Lennard-Jones (“VDW”) decoupling steps. Higher Ac are better and indicate that a larger fraction of the λ windows is converged according to the criterion Eq. 2.
Fig. 8:
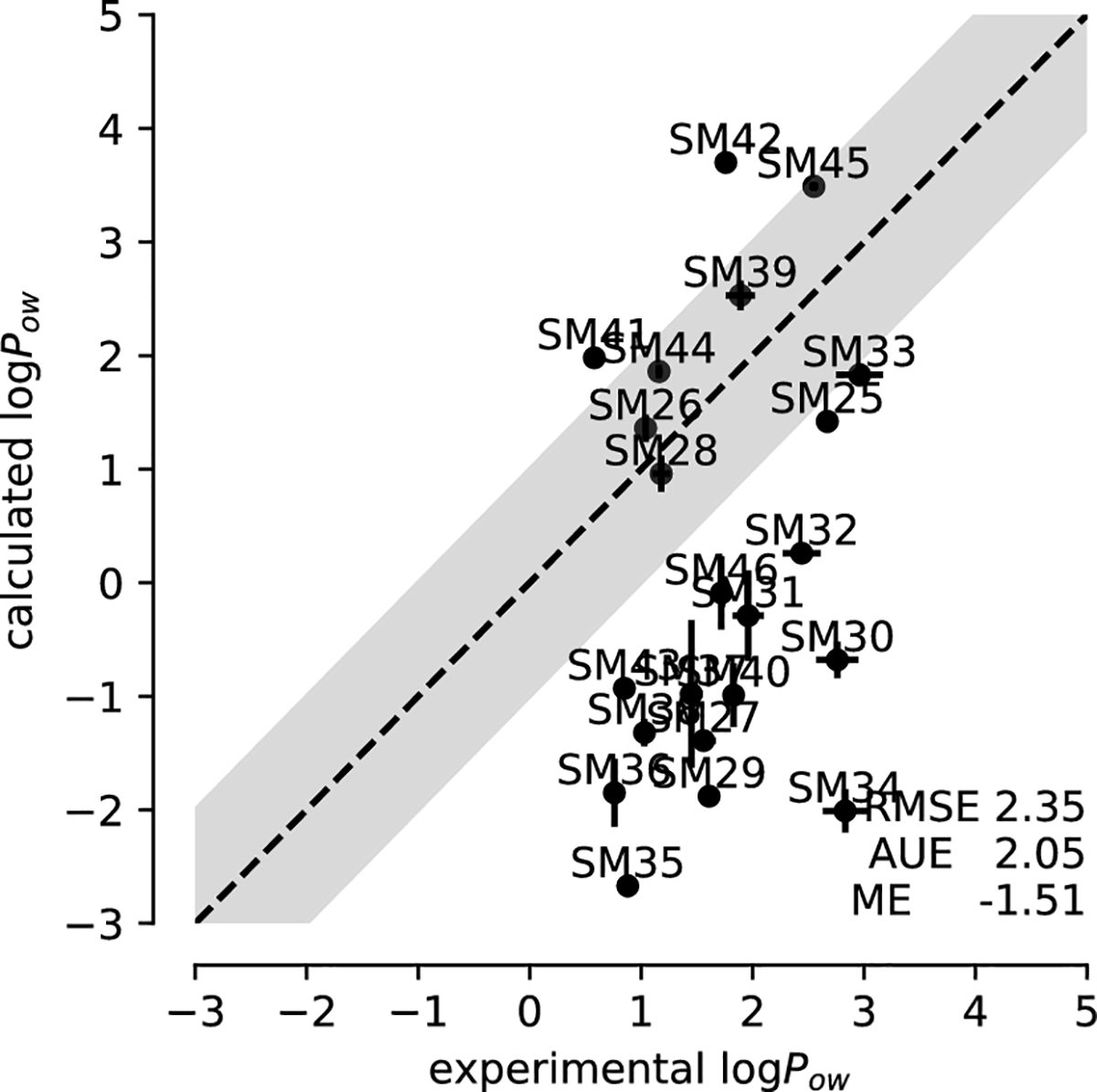
Correlation between experimental and computed octanol-water coefficients logPow for simulations performed with OPLS-AA (LigParGen) parameters.
The lack of convergence resulted in slightly larger errors of the statistical measures RMSE, ME, and AUE. However, the decrease in statistical uncertainty from e.g., 0.06 to 0.02 [for converged OPLS-AA (mol2ff)] would not seem to be worth the effort to run windows out to 1 μs. More important is the knowledge that for every individual compound the value is converged precisely so that for aggregate assessments on medium sized datasets one does not need to rely on averaging and effectively cancellation of errors to obtain a realistic measure of accuracy. In other words, the variance is reduced and results become more easily reproducible and comparable between different runs by different research groups.
Compared to our SAMPL6 results with OPLS-AA (LigParGen) (RMSE 1.71± 0.07, r = 0.78, τ = 0.64 [6]) the overall accuracy was much worse even though the previous simulations only sampled each λ window for 5 ns compared to 50–150 ns here. Unlike the previous simulations, the logPowwas systematically downshifted, leading to a qualitatively different behavior from the one observed before. Ultimately, it is difficult to draw firm conclusions for OPLS-AA (LigParGen) because the data are not converged so the results shown here may change with more sampling.
3.2.4. GAFF
The GAFF dataset was not fully converged but, according to our convergence analysis, appeared to be much better sampled than the OPLS-AA (LigParGen) dataset. The precision of the calculated logPow values was better than for LigParGen, with a maximum statistical error of 0.21 log units (Table 5) but worse than the 0.10 or better for CGenFF or OPLS-AA (mol2ff). The prediction accuracy was the best in our comparison with RMSE 1.60±0.03. The Pearson correlation coefficient r = 0.660 was of similar magnitude as seen for CGenFF and the Kendall rank correlation coefficient τ = 0.521 was also the same, indicating overall decent correlation with the experimental data. The logPow was systematically overestimated as shown by the systematic positive shift of the predicted values in the correlation plot (Fig. 9) and the positive ME (1.48±0.04), which equaled the AUE.
Fig. 9:
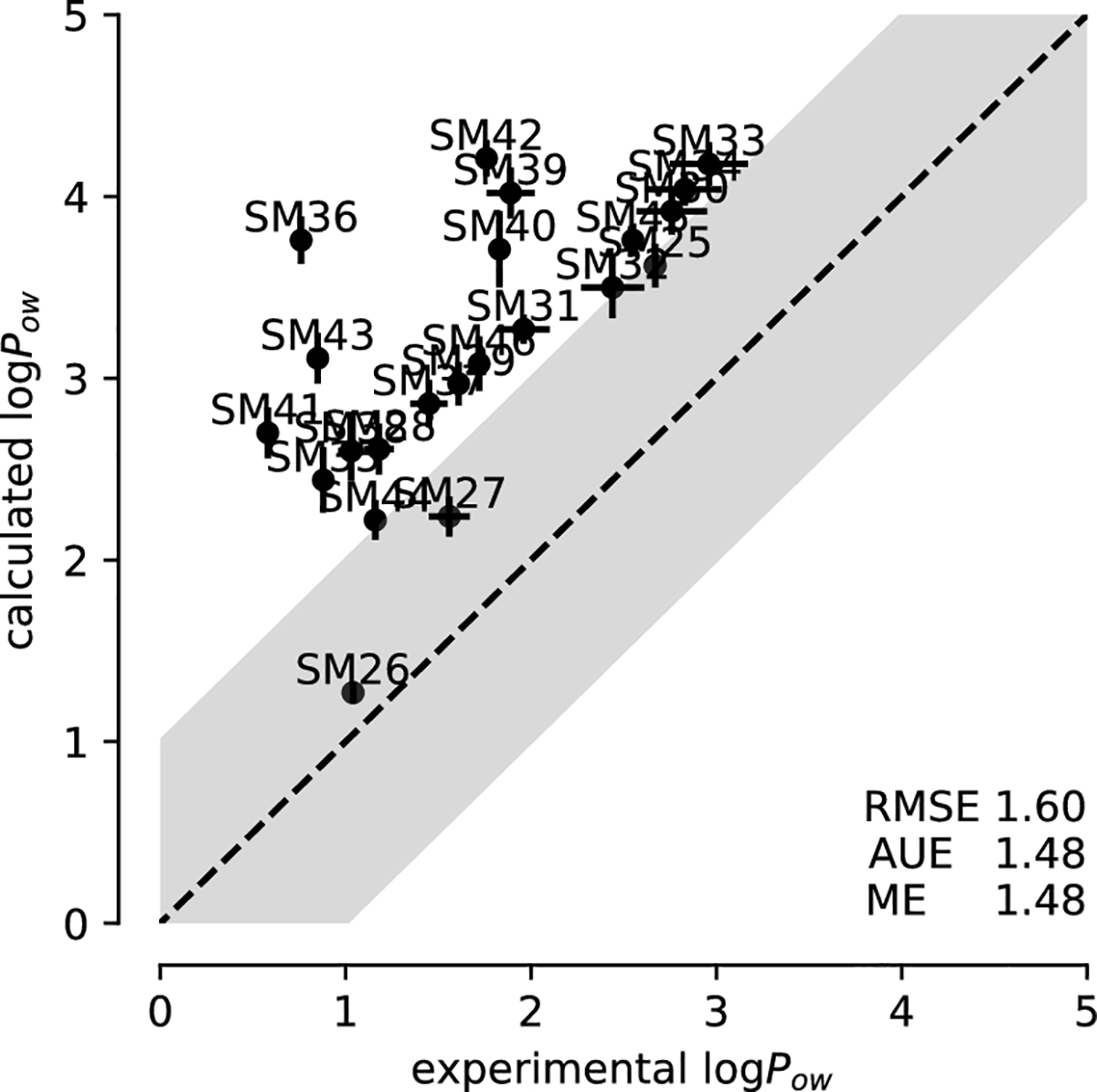
Correlation between experimental and computed octanol-water coefficients logPow for simulations performed with GAFF parameters.
The GAFF results for SAMPL7 were consistent with our previous SAMPL6 results (RMSE 1.52±0.08, r = 0.80, and τ = 0.53) [6], assuming that the two sets of simulations with different sampling quality can be compared directly. In both cases, logPow was systematically too positive, but overall the long GAFF simulations predicted logPow reasonably well.
3.3. Potential remaining sources of sampling errors
A possible reason for low accuracy results could be sampling problems that we did not explicitly address and that would not be captured by our convergence analysis. In general, such sampling problems relate to the sampling of regions of configuration spaces that are not easily accessible on our simulation time scales: As long as the simulation never sees another low free energy region, the simulation only samples the local free energy minimum and any convergence measure will report on good local sampling but completely miss out on the insufficient global sampling — such “unknown unknowns” [36] are the major challenges in solving the sampling problem for free energy calculations.
3.3.1. Insufficient gas phase sampling
We used an alchemical decoupling approach that started with the solute in solvent. Although all FEP windows were calculated independently and in parallel, each effectively started from the fully solvated equilibrated system. Furthermore, we only decoupled the solute-solvent interactions and therefore no explicit FEP simulation in the gas phase was needed; only the λCoul = 1, λVDW = 1 window sampled the gas phase. (The presence of the solvent in the gas phase simulations makes implementing the reverse approach of starting from an equilibrated gas phase system difficult because of clashes between solvent and solute.) The conformational space that is accessible to the solute in different solvents likely differs from the gas phase conformational space. It is therefore possible that starting from the solvated system may trap the gas phase conformation in different regions of conformational space, depending on the solvent. Because the gas phase free energy should exactly cancel in a transfer free energy calculation between two solvents, systematic errors in the free energies could arise due to insufficient overlap of the gas phase contributions.
In the Supplementary Information we discuss compound SM46 as an example because it only contains two main rotatable bonds (dihedrals) and could be expected to be well sampled. The OPLS-AA (mol2ff) simulations sampled a much larger range of dihedral values in the solvent phase than in the gas phase (Fig. S6). Water and octanol solvent simulations sampled all of dihedral space but the gas phase simulations of one of the two dihedrals only sampled around the dihedral angle that was dominant in each solvent. This dominant dihedral differed between the two gas phase simulations. Therefore, the SM46 gas phase simulations were trapped in different regions of conformational space, even though the Rc analysis indicated well sampled simulation [low Rc = 0.0006 (starting from water solvent) and Rc = 0.0168 (starting from octanol solvent)]. In this case, the Rc value was erroneously too small because in the available simulation time no other states were reached and conformational space was only locally well sampled but not globally. Without additional simulations we cannot ascertain if the low accuracy of the OPLS-AA (mol2ff) prediction for SM46 with an error of Δ = 3.46±0.02 (see Table 3) was due to insufficient gas phase sampling.
A potential technique for alleviating the trapping problem for transfer free energy calculations between solvents is to restrain the gas conformation and include the introduction of restraints in the alchemical free energy cycle. In this way, a welldefined (non-physical) reference state is created that is exactly canceled in the final difference between solvent to restricted-gas phase state. Alternatively, enhanced sampling approaches such as well-tempered meta dynamics [37] or Hamiltonian replica exchange [38] or Monte Carlo steps could be employed to improve exploration of slow dihedral degrees of freedom in the gas state and obtain correct solvent-gas phase transfer energies.
All 4 (force field parameters) ×2 (solvent) ×22 (compounds) = 176 simulations consistently showed fast convergence with low Rc for the gas phase window (see Figs. 2b, 3b and Fig. S3b in Supplementary Information) so it would be surprising if such trapping had occurred in all cases. Nevertheless, future work will examine more rigorously trapping of gas state simulations and its influence on the accuracy of the prediction.
3.3.2. Tautomers
A second potential problem consists in the presence of multiple tautomeric states even though we only simulate a single state. Compounds SM25 and SM26 may have multiple tautomeric states, in contrast with the other compounds that have a single stable tautomer, and we did not observe worse predictions specifically for SM25 and SM26. Therefore it is likely that the tautomer selection was not an issue, at least for the SAMPL7 data set.
4. Conclusions
We computed logPow for the 22 drug-like molecules from the SAMPL7 physical properties dataset. Using all-atom, explicit solvent MD simulations with three different classical force fields our free energy simulations sampled in total more than 1 ms of simulated time, guided by a convergence analysis for individual λ windows that indicated windows that needed to be extended further for convergence. For converged simulations, a clear pattern of required run length emerged. Early windows (small λ), where the Coulomb interaction is still strong, were difficult to converge, especially for octanol, where sometimes even 1 μs was not sufficient. For Lennard-Jones (van der Waals) decoupling, the longest convergence time was needed near regions where the graph has a minimum. In general, octanol simulations were slower to converge than water simulations. For CGenFF and OPLS-AA with transferrable charges we generated precise predictions for the water-octanol partition coefficient with statistical errors smaller than 0.1 log units. In SAMPL6, our best predictions came from CHARMM/CGenFF simulations [6]. In the present study, the best predictions were obtained from AMBER/GAFF simulations (RMSE 1.60 ± 0.03), although the CHARMM/CGenFF predictions performed similarly well (RMSE 1.65±0.03). The predictions using the OPLS-AA force field, with “classical” transferable charges were less accurate, with RMSE values of 2.2 ± 0.02; OPLS-AA simulations with LigParGen non-transferable charges were also less accurate (RMSE 2.35±0.06) but because these simulations were not converged, conclusions could change with better sampling.
The extension of the λ windows until convergence (or up to 1 μs simulation time) did not affect significantly the accuracy of CHARMM/CGenFF and OPLS-AA predictions, but had a tremendous effect on the AMBER/GAFF results, whose accuracy increased dramatically from RMSE 3.02 to 1.60; some compounds improved 3 units although a few became worse by about 1 unit (Supplementary Fig. S5d).
In summary, for CHARMM/CGenFF and OPLS-AA with transferrable charges (and to lesser degree for AMBER/GAFF) we computed precise predictions for logPowwhich allowed us to separate sampling issues from model issues although future work needs to address potentially low conformational overlap of gas phase simulations that can become trapped in an initial conformation. Within the context of the SAMPL7 compounds, both CGenFF and GAFF appear to be limited to an accuracy of about 1.6 in logPow while OPLS-AA seems limited to > 2. In all these three cases, a clear systematic positive shift in computed logPow was visible, consistent with previous observations [5, 6]. As noted previously [6], the likely reason for this shift is under-solvation of small molecules with classical force fields (i.e., the hydration free energy is too positive and unfavorable) because these force fields are known to be underpolarized [39, 40]. Although previously this effect was not apparent for CGenFF, our new, very precise logPow calculations show that CHARMM/CGenFF appears to suffer from the same problem as GAFF and OPLS-AA. Future work will focus on identifying the molecular causes of slow convergence in solvation free energy calculations; with a quantitative description of such slow degrees of freedom in hand, enhanced sampling approach could then be employed to improve the efficiency of such calculations. Our approach to selectively extend free energy windows that are not yet converged could already be used as part of free energy workflows to allocate scarce computing resources in an efficient manner and so help to eliminate incomplete sampling as one of the major obstacles to comparable and reproducible research in the area of quantitative molecular simulations.
Supplementary Material
Acknowledgements
We thank an anonymous referee for pointing out potential problems with gas phase sampling in our simulations. We appreciate the National Institutes of Health for its support of the SAMPL project via R01GM124270 to David L. Mobley (UC Irvine).
Research reported in this publication was supported by the National Institute Of General Medical Sciences of the National Institutes of Health under Awards Number R01GM118772 and R01GM125081, by GENCI–IDRIS (Grant 2020-A0080711524), by the French National Research Agency (ANR) through grants ANR-10-LABX-33 (LabEx LERMIT) and ANR-14-JAMR-0002–03 (JPIAMR), and by the Région Ile-de-France (grant DIM MAL-INF). Computing time on the Agave cluster of Research Computing at Arizona State University is gratefully acknowledged.
Contributor Information
Shujie Fan, Department of Physics, Arizona State University, P.O. Box 871504, Tempe, AZ 85287-1504, USA.
Hristo Nedev, Université Paris-Saclay, CNRS, Institut de Chimie des Substances Naturelles, UPR 2301, Labex LERMIT, 1 Avenue de la Terrasse, 91198 Gif-sur-Yvette, France.
Ranjit Vijayan, Department of Biology, College of Science, United Arab Emirates University, Al Ain PO Box 15551, UAE.
Bogdan I. Iorga, Université Paris-Saclay, CNRS, Institut de Chimie des Substances Naturelles, UPR 2301, Labex LERMIT, 1 Avenue de la Terrasse, 91198 Gif-sur-Yvette, France.
Oliver Beckstein, Department of Physics and Center for Biological Physics, Arizona State University, P.O. Box 871504, Tempe, AZ 85287-1504, USA.
References
- 1.Shirts MR, Pitera JW, Swope WC, Pande VS (2003) Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J Chem Phys 119(11):5740–5761, URL http://www.scopus.com/scopus/inward/record.url?eid=2-s2.0-0141990949&partnerID=40&rel=R5.6.0 [Google Scholar]
- 2.Bergazin TD, Zhang Y, Mao J, Gunner M, Francisco K, Ballatore C, Mobley DL (2021) Evaluation of logP, pKa, and logD predictions from the SAMPL7 blind challenge. J Comput Aided Mol Des [this issue] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Beckstein O, Iorga BI (2012) Prediction of hydration free energies for aliphatic and aromatic chloro derivatives using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 26(5):635–645, DOI 10.1007/s10822-011-9527-9 [DOI] [PubMed] [Google Scholar]
- 4.Beckstein O, Fourrier A, Iorga BI (2014) Prediction of hydration free energies for the SAMPL4 diverse set of compounds using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 28(3):265–276, DOI 10.1007/s10822-014-9727-1 [DOI] [PubMed] [Google Scholar]
- 5.Kenney IM, Beckstein O, Iorga BI (2016) Prediction of cyclohexane-water distribution coefficients for the SAMPL5 data set using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 30(11):1045–1058, DOI 10.1007/s10822-016-9949-5 [DOI] [PubMed] [Google Scholar]
- 6.Fan S, Iorga BI, Beckstein O (2020) Prediction of octanol-water partition coefficients for the SAMPL6-logP molecules using molecular dynamics simulations with OPLS-AA, AMBER and CHARMM force fields. Journal of ComputerAided Molecular Design 34:543–560, DOI 10.1007/s10822-019-00267-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kaminski G, Duffy E, Matsui T, Jorgensen W (1994) Free energies of hydration and pure liquid properties of hydrocarbons from the OPLS all-atom model. J Phys Chem 98(49):13,077–13,082, DOI 10.1021/j100100a043 [DOI] [Google Scholar]
- 8.Jorgensen WL, Maxwell DS, Tirado-Rives J (1996) Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc 118(45):11,225–11,236, DOI 10.1021/ja9621760 [DOI] [Google Scholar]
- 9.Damm W, Frontera A, Tirado-Rives J, Jorgensen W (1997) OPLS all-atom force field for carbohydrates. J Comput Chem 18(16):1955–1970, DOI [DOI] [Google Scholar]
- 10.Jorgensen WL, McDonald NA (1998) Development of an all-atom force field for heterocycles. Properties of liquid pyridine and diazenes. J Mol Struct THEOCHEM 424(1–2):145–155, DOI 10.1016/S0166-1280(97)00237-6 [DOI] [Google Scholar]
- 11.McDonald NA, Jorgensen WL (1998) Development of an all-atom force field for heterocycles. Properties of liquid pyrrole, furan, diazoles, and oxazoles. J Phys Chem B 102(41):8049–8059, DOI 10.1021/jp981200o [DOI] [Google Scholar]
- 12.Rizzo RC, Jorgensen WL (1999) OPLS all-atom model for amines: Resolution of the amine hydration problem. J Am Chem Soc 121(20):4827–4836, DOI 10.1021/ja984106u [DOI] [Google Scholar]
- 13.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL (2001) Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B 105(28):6474–6487, DOI 10.1021/jp003919d [DOI] [Google Scholar]
- 14.Ihlenfeldt W, Takahashi Y, Abe H, Sasaki S (1994) Computation and management of chemical properties in CACTVS: An extensible networked approach toward modularity and compatibility. J Chem Inf Comput Sci 34(1):109–116 (http://www.xemistry.com/) [Google Scholar]
- 15.Dodda LS, Cabeza de Vaca I, Tirado-Rives J, Jorgensen WL (2017) LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res 45(W1):W331–W336, DOI 10.1093/nar/gkx312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, Mackerell AD Jr (2010) CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comput Chem 31(4):671–90, DOI 10.1002/jcc.21367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vanommeslaeghe K, Raman EP, MacKerell AD (2012) Automation of the CHARMM General Force Field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. Journal of Chemical Information and Modeling 52(12):3155–3168, DOI 10.1021/ci3003649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vanommeslaeghe K, MacKerell AD (2012) Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing. Journal of Chemical Information and Modeling 52(12):3144–3154, DOI 10.1021/ci300363c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA (2004) Development and testing of a general AMBER force field. J Comput Chem 25(9):1157–74, DOI 10.1002/jcc.20035 [DOI] [PubMed] [Google Scholar]
- 20.Sousa da Silva AW, Vranken WF (2012) ACPYPE - AnteChamber PYthon Parser interfacE. BMC Res Notes 5:367, DOI 10.1186/1756-0500-5-367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML (1983) Comparison of simple potential functions for simulating liquid water. J Chem Phys 79(2):926–935, DOI 10.1063/1.445869 [DOI] [Google Scholar]
- 22.MacKerell AD, Wiorkiewicz-Kuczera J, Karplus M (1995) An all-atom empirical energy function for the simulation of nucleic acids. J Am Chem Soc 117(48):11,946–11,975, DOI 10.1021/ja00153a017, URL 10.1021/ja00153a017, 10.1021/ja00153a017 [DOI] [Google Scholar]
- 23.Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E (2015) GROMACS: High performance molecular simulations through multilevel parallelism from laptops to supercomputers. SoftwareX 1–2:19–25, DOI 10.1016/j.softx.2015.06.001 [DOI] [Google Scholar]
- 24.Shirts MR, Chodera JD (2008) Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys 129(12):124,105, DOI 10.1063/1.2978177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dotson D, Beckstein O, Wille D, Kenney I, shuail, trje3733, Lee H, Lim V, brycestx, Barhaghi MS (2019) alchemistry/alchemlyb: 0.3.0. Software, DOI 10.5281/zenodo.3361016, URL 10.5281/zenodo.3361016 [DOI]
- 26.Mobley DL, Dumont E, Chodera JD, Dill KA (2007) Comparison of charge models for fixed-charge force fields: Small-molecule hydration free energies in explicit solvent. J Phys Chem B 111(9):2242–2254, DOI 10.1021/jp0667442 [DOI] [PubMed] [Google Scholar]
- 27.Parrinello M, Rahman A (1981) Polymorphic transitions in single crystals: A new molecular dynamics method. J Appl Phys 52(12):7182–7190, DOI 10.1063/1.328693, URL http://link.aip.org/link/?JAP/52/7182/1 [DOI] [Google Scholar]
- 28.Essman U, Perela L, Berkowitz ML, Darden T, Lee H, Pedersen LG (1995) A smooth particle mesh Ewald method. J Chem Phys 103:8577–8592, DOI 10.1063/1.470117 [DOI] [Google Scholar]
- 29.Hess B (2008) P-LINCS: A parallel linear constraint solver for molecular simulation. J Chem Theory Comput 4(1):116–122, DOI 10.1021/ct700200b [DOI] [PubMed] [Google Scholar]
- 30.Hess B, Kutzner C, van der Spoel D, Lindahl E (2008) GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput 4(3):435–447, DOI 10.1021/ct700301q [DOI] [PubMed] [Google Scholar]
- 31.Páll S, Abraham MJ, Kutzner C, Hess B, Lindahl E (2015) Tackling exascale software challenges in molecular dynamics simulations with GROMACS. In: Markidis S, Laure E (eds) Solving Software Challenges for Exascale: International Conference on Exascale Applications and Software, EASC 2014, Stockholm, Sweden, April 2–3, 2014, Revised Selected Papers, Lecture Notes in Computer Science, vol 8759, Springer International Publishing, Switzerland, pp 3–27, DOI 10.1007/978-3-319-15976-8_1 [DOI] [Google Scholar]
- 32.Klimovich PV, Shirts MR, Mobley DL (2015) Guidelines for the analysis of free energy calculations. J Comput Aided Mol Des 29(5):397–411, DOI 10.1007/s10822-015-9840-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chodera JD (2016) A simple method for automated equilibration detection in molecular simulations. J Chem Theory Comput 12(4):1799–1805, DOI 10.1021/acs.jctc.5b00784 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Faber NKM (1999) Estimating the uncertainty in estimates of root mean square error of prediction: application to determining the size of an adequate test set in multivariate calibration. Chemometrics and Intelligent Laboratory Systems 49(1):79–89, DOI 10.1016/S0169-7439(99)00027-1 [DOI] [Google Scholar]
- 35.Yang W, Bitetti-Putzer R, Karplus M (2004) Free energy simulations: Use of reverse cumulative averaging to determine the equilibrated region and the time required for convergence. J Chem Phys 120(6):2618–2628, DOI 10.1063/1.1638996 [DOI] [PubMed] [Google Scholar]
- 36.Rumsfeld DH (2011) Known and Unknown: A Memoir. Penguin Group, New York [Google Scholar]
- 37.Barducci A, Bussi G, Parrinello M (2008) Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys Rev Lett 100:020,603, DOI 10.1103/PhysRevLett.100.020603, URL 10.1103/PhysRevLett.100.020603 [DOI] [PubMed] [Google Scholar]
- 38.Sugita Y, Okamoto Y (2000) Replica-exchange multicanonical algorithm and multicanonical replica-exchange method for simulating systems with rough energy landscape. Chemical Physics Letters 329(3–4):261–270, DOI 10.1016/S0009-2614(00)00999-4, URL http://www.sciencedirect.com/science/article/pii/S0009261400009994 [DOI] [Google Scholar]
- 39.Swope WC, Horn HW, Rice JE (2010) Accounting for polarization cost when using fixed charge force fields. II. Method and application for computing effect of polarization cost on free energy of hydration. The Journal of Physical Chemistry B 114(26):8631–8645, DOI 10.1021/jp911701h [DOI] [PubMed] [Google Scholar]
- 40.Lundborg M, Lindahl E (2015) Automatic gromacs topology generation and comparisons of force fields for solvation free energy calculations. J Phys Chem B 119(3):810–23, DOI 10.1021/jp505332p [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


