Automated clinical target volume delineation using deep 3D neural networks in radiation therapy of Non-small Cell Lung Cancer

Abstract

Background and purpose

Clinical targeted volume (CTV) delineation accounting for the patient-specific microscopic tumor spread can be a difficult step in defining the treatment volume. We developed an intelligent and automated CTV delineation system for locally advanced non-small cell lung carcinoma (NSCLC) to cover the microscopic tumor spread while avoiding organs-at-risk (OAR).

Materials and methods

A 3D UNet with a customized loss function was used, which takes both the patients’ respiration-correlated (“4D”) CT scan and the physician contoured internal gross target volume (iGTV) as inputs, and outputs the CTV delineation. Among the 84 identified patients, 60 were randomly selected to train the network, and the remaining as testing. The model performance was evaluated and compared with cropped expansions using the shape similarities to the physicians’ contours (the ground-truth) and the avoidance of critical OARs.

Results

On the testing datasets, all model-predicted CTV contours followed closely to the ground truth, and were acceptable by physicians. The average dice score was 0.86. Our model-generated contours demonstrated better agreement with the ground-truth than the cropped 5 mm/8 mm expansion method (median of median surface distance of 1.0 mm vs 1.9 mm/2.0 mm), with a small overlap volume with OARs (0.4 cm³ for the esophagus and 1.2 cm³ for the heart).

Conclusions

The CTVs generated by our CTV delineation system agree with the physician's contours. This approach demonstrates the capability of intelligent volumetric expansions with the potential to be used in clinical practice.

1. Introduction

Lung cancer is the second most common cancer and the most common cause of cancer death worldwide. Among all diagnosed lung cancers, the majority (~87%) are non-small cell lung cancers (NSCLC). Definitive radiation therapy concurrently with chemotherapy is the standard treatment for locally advanced unresectable NSCLC. Delineation of treatment volumes for NSCLC patients is a critical and complex process for radiation oncology departments worldwide, and is predicted to increase in the near future [1].

There are three main types of treatment target volumes used in radiation therapy planning: the gross target volume (GTV), the clinical target volume (CTV) and the planning target volume (PTV) [2], [3], [4]. The CTV of lung cancer encompasses direct microscopic spread in the lung parenchyma as well as potential microscopic extension around grossly involved hilar or mediastinal lymph nodes. To compensate for the patient specific motion, ICRU [4] recommends to form an internal target volume (ITV) as the union of CTVs in different locations (due to motion). However, there are different variations of this approach. For NSCLC patients treated in our institute, the internal gross target volume (iGTV) is contoured from the GTVs in the different breathing phases to include the patient-specific respiratory motion, and then expanded to the CTV to form an iCTV.

Among these three types of volumes, the CTV is the most difficult one to define [5] because microscopic tumor spread is invisible. Therefore, the CTV delineation heavily depends on the clinician’s judgement, literature on patterns of failure and clinical experience. In common practice, this can be done by laborious manual contouring by clinicians in a slice-by-slice manner. This process accounts for a high workload for the radiation oncology departments worldwide [1]. Furthermore, there is significant intra- and interobserver variability [4].

To approximate the extent of the microscopic spread, many institutes generate the CTV by an automatic geometric expansion of the GTV. These auto-expansion tools, which are included in commercial contouring software and most treatment planning system (TPS), are generally geometric-based expansions (either isotropic or anisotropic in three dimensions). The expanded contours can be cropped at OARs. While this approach reduces the manual contouring time, it does not accurately reflect the details of tumor biology, anatomic patterns of spread, and thus may not accurately reflect the geometry of microscopic disease. Thus, for the centers that want specialist-designed patient-specific CTV contours (e.g. those institutions following ESTRO ACROP guidelines [1]), there is a need to develop a more intelligent CTV delineation tool.

With the rapid developments of deep learning in recent years, there have been pioneering studies on applying deep learning techniques to automatically and intelligently delineate CTVs [6], [7], [8], [9]. These neural-network based approaches can be categorized into two classes: one- and two-step approaches. The one-step approach learns CTV and nearby anatomic sites from images in one step [6], [8], [9]. The two-step approach learns anatomical barriers explicitly first from the anatomic images and then the CTV definition is formed by expanding the GTV while avoiding the anatomical barriers [7].

Although there are existing studies on automation of CTV delineation for radiation therapy, little has been done for NSCLC CTV delineation. Furthermore, most existing approaches need post-processing and/or hyperparameter tuning. Therefore, the aim of this study is to devise an automated intelligent CTV delineation network for locally advanced NSCLC that needs minimal human intervention, or none if possible.

2. Methods and materials

2.1. Patient image preparation

In this study, we selected 84 patients with locally advanced NSCLC, who were treated with standard chemotherapy and radiation therapy in our center from 2012 through 2017. All patients who satisfied the following two selection criteria were included in our study: 1) stage 3 NSCLC patients with no tumor removal surgery before the radiation treatment, and 2) the patient dataset had both iGTV and CTV contoured on the corresponding CT images. This study was approved by the Institutional Review Board (IRB). 4D CT images were acquired using the same scanning protocol for all patients. If the tumor movement was less than 15 mm, iGTVs were created from the 4D CT as the union of the GTVs in all different breathing phases and drawn on the average CT images derived from the full 4DCT scans. For the patients with large respiratory motion or if the 4D CT was not representative of the motion, the final iGTV contours were created on the exhale phase of the 4DCT images and the patients were treated with gated beam delivery. Then on the same set of CT images where final iGTVs were contoured, CTVs were delineated by clinicians with specialty expertise in thoracic radiation oncology. Per longstanding institutional practice, the CTV was generated by an automatic at least 5 mm expansion of the iGTV followed by manual editing. This included removal of overlap with anatomical structures such as heart, great mediastinal vessels, and vertebral bodies that were not judged to contain invisible microscopic tumor spread. The CTV was also edited to minimize overlap with the esophagus in order to facilitate contralateral esophagus sparing [10], [11]. While comprehensive elective nodal irradiation was not performed, CTVs were expanded on a case-by-case basis to include small, PET negative lymph nodes or other areas judged to be at high risk for lymphatic spread.

Although all planning CT scans were acquired with the same imaging protocol with a slice thickness of 2.5 mm, the exact slice pixel size varied between 0.72 mm and 1.27 mm based on the required field of view (FOV) to encompass the entire patient. To reduce the learning complexity, we used MIM’s (MIM Software Inc, Beachwood, OH, USA) resampling function to interpolate all the images to the same voxel size of $0.98\times 0.98\times 2.5$ mm³.

Among all 84 patients, 56 patients had the tumor volume located in the right lung and 28 in the left lung. We randomly selected 40 right lung patients and 20 left lung patients as training datasets. The remaining 16 right lung and eight left lung patients were used as testing datasets. Also, the validation datasets of 10 patients were randomly selected from the training datasets.

To compare our model-generated CTV with auto-expansion, auto-expansion-based CTV contours were generated for each testing dataset using MIM: the generated contours were uniformly expanded from the iGTV and then the OARs were manually contoured for exclusion (cropped). The vertebral bodies without visible microscopic spread were also cropped out. Two expansion amounts of 5 mm and 8 mm were used to represent two extreme cases of the expansions as specified in RTOG 1308 protocol and other guidelines. In the rest of paper, we call these two sets 5 mm/8 mm cropped expansions.

2.2. Image augmentation

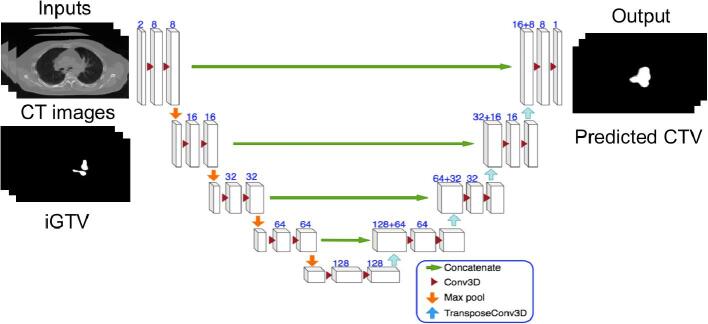
The network architecture is shown in Fig. 1. It took the CT images and iGTV masks as inputs and produced the predicted CTV masks. All the 3D convolutions and transposed convolutions had the kernel size of $3\times 3\times 3$. Besides the network architecture, data augmentation was another important step to train deep networks with limited training data sets. A properly designed augmentation teaches the network to focus on robust features for a good generalization. For the model training in our study, CT images, iGTV masks and CTV masks were augmented 20 times using a 2D elastic deformation algorithm based on [9], [12]. We chose 2D deformation with the consideration that the CTVs were contoured based on the image information on each 2D slice. In each augmentation, a 3 × 3 grid of random displacements was drawn from a Gaussian distribution ($\mu =\left(0,0\right)$ pixels and $\sigma =\left(10,10\right)$ pixels). Then the displacements were interpolated to the pixel level. All the 2D slices of a training data, including the simulation CT image, the iGTV masks and the CTV mask) were deformed using the same displacements and a spline interpolation. Since the interpolation results in blurred mask boundaries, a threshold, 0.5, was applied to binarize them.

Fig. 1.

The schematic diagram of our deep 3D Unet-based network. The input has two channels, the CT images and corresponding iGTV masks, which were cropped to the size of 416 × 288 × 128. Each 3D block represents a feature map with the number of channels denoted in the picture. All the Conv3D and TransposeConv3D have the kernel size of $3\times 3\times 3$. The pool sizes in the Maximum pooling and the stride sizes in TransposeConv3D are $2\times 2\times 2$.

2.3. Loss function

A popular loss function choice for UNet-based network is binary cross entropy $\mathrm{B}\mathrm{C}\mathrm{E}\left({\widehat{y}}_{i,}{y}_i\right)={\widehat{y}}_i\mathrm{l}\mathrm{n}{y}_i+\left(1-{\widehat{y}}_i\right)\mathrm{l}\mathrm{n}\left(1-y_i\right)$, where $y_i$ and $\widehat{y_i}$ are the predicted and ground-truth probability of being inside the CTV for the $i$-th voxel, respectively. Unfortunately, BCE does not work well in situations of high imbalance between foreground (CTV) and background (non-CTV). This is due to accumulated small losses from background voxels, which can overpower the foreground contributions and result in a biased estimation. A typical way to address this issue is to introduce weighted binary cross entropy (WBCE), which introduces a hyperparameter $w$ to reduce the loss contribution of background voxels: $\mathrm{W}\mathrm{B}\mathrm{C}{\mathrm{E}}_w({{\widehat{y}}_i,y}_i,)={\widehat{y}}_i\mathrm{l}\mathrm{n}{y}_i+w(1-{\widehat{y}}_i)\mathrm{l}\mathrm{n}(1-y_i)$. This approach works in situations where the balance ratio between the foreground and background was relatively fixed, but it does not work well when the ratio varies dynamically among patients. To solve this problem, we propose to use an AM-GM inequality based loss function,

$$\begin{array}{c}L=1-\frac{2}{N}\frac{{\sum }_{i=1}^N{y}_i\widehat{y_i}}{{\sum }_{i=1}^N(y_i^2+{\widehat{y}}_i^2)}\#\left(1\right)\end{array}$$

where $N$ is the total number of voxels in the simulated CT. The intuition behind this design is that the AM-GM based loss focuses more on the foreground by zeroing out the contribution from background voxels, which avoids the challenges of balancing foreground and background.

2.4. Training and metrics

Our code was implemented in python using Keras with Tensorflow as back-end. All the CT images and corresponding contour masks were cropped to the size of 416 × 288 × 128 in order to fit into the 12 GB GPU memory. Our model was trained end-to-end by back propagation and Adam optimizer with a learning rate of 10⁻⁴. It took about 3 days to finish training on a single NVidia Titan XP GPU card. The model was trained with a mini-batch size of 32. During the training, 200 epochs were run. The validation metrics were the AM-GM inequality based metrics, and the model weights were selected from the earliest epoch when the validation reached saturation.

The predicted CTVs from the trained model were compared to the physician ground-truth volumes by calculating differences in volumes ($\mathrm{\Delta }V$), precision, recall, and dice. Precision is defined as the ratio of the predicted volume that overlaps with the ground-truth volume, relative to the predicted volume: $\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}=\frac{V_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}\cap V_{\mathrm{g}\mathrm{t}}}{V_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}}$, whereas recall is defined as the overlap relative to the ground-truth volume: $\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}=\frac{V_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}\cap V_{\mathrm{g}\mathrm{t}}}{V_{\mathrm{g}\mathrm{t}}}$.

The surface distance between the model prediction and physicians’ ground truth was calculated as another measure of shape similarity. Here, four values are compared: the Hausdorff distance, the mean distance, the median distance, and the 95-percentile distance.

The esophagus and the heart are the two most relevant OARs. One important measure is the overlap volume (OV) between the CTV and the OARs: $\mathrm{O}\mathrm{V}=V_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}\cap V_{\mathrm{C}\mathrm{T}\mathrm{V}}$.

For simplicity, we assumed both the shape similarity metrics and OV have normal distributions, so that the results are represented by the mean and standard deviations in Table 1. More robust estimations should refer to the box plots of those measures in Fig. 3, Fig. 4. The surface distances are represented by median values to reduce the influence from few outliers with large surface distances.

Table 1.

The comparison between our ML-based model, the two cropped expansions and Ground-truth CTV on all testing samples. The values of the overlapping volume, OV, with OARs were calculated only when the OARs are within the 8 mm vicinity of the corresponding iGTVs. The CTV volumes were summarized as the mean value with minimum and maximum values over all testing datasets.

	ML-predicted CTV	Ground truth CTV	Cropped 5 mm expansion CTV	Cropped 8 mm expansion CTV
DSC	$0.86\pm 0.03$	N.A.	$0.81\pm 0.10$	$0.83\pm 0.04$
Precision	$0.89\pm 0.04$	N.A.	$0.86\pm 0.10$	$0.76\pm 0.06$
Recall	$0.84\pm 0.05$	N.A.	$0.77\pm 0.10$	$0.92\pm 0.04$
Median surface distance [mm]	1.0	N.A.	1.0	$2.0$
Hausdorff surface distance [mm]	8.6	N.A.	$9.1$	$12.6$
95% surface distance [mm]	3.9	N.A.	$4.5$	$6.1$
*OV with the esophagus [cm3]	$0.4\pm 0.3$	$0.1\pm 0.2$	$0.0\pm 0.0$	$0.0\pm 0.0$
*OV with the heart [cm3]	$1.2\pm 0.6$	$0.8\pm 0.6$	$0.0\pm 0.0$	$0.0\pm 0.0$
**CTV Volume [cm3]	95.2 [31.7, 290.2]	101.1 [27.5, 314.0]	88.0 [17.2, 282.0]	120.6 [44.1, 356.4]
Contouring Time	3.8~4.0 s	5~20 min	5~20 min	5~20 min

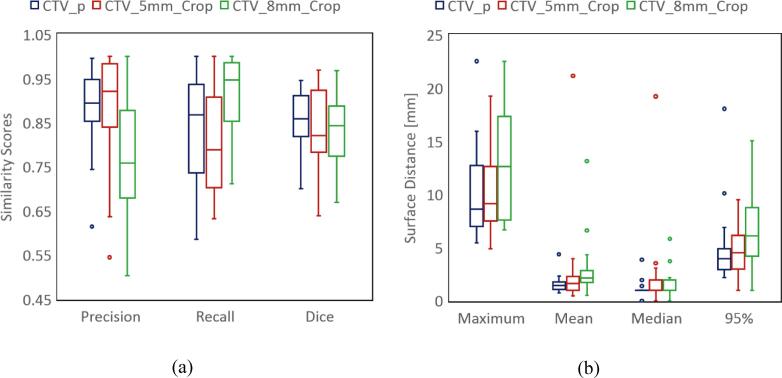
Fig. 3.

Contour shape similarity with ground-truth contours. The box plots in (a) show the three metrics for performance evaluation: precision, recall, and dice score. The dark blue color stands for our trained model prediction, the red color represents the 5 mm cropped expansion, and the green color the 8 mm cropped expansion. We also calculated four measures of the surface distances from the physician contours, as shown in Fig. 3(b): Hausdorff (maximum), mean, median, and 95-percentile of the surface distance. The color coding is as in Fig. 3(a). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

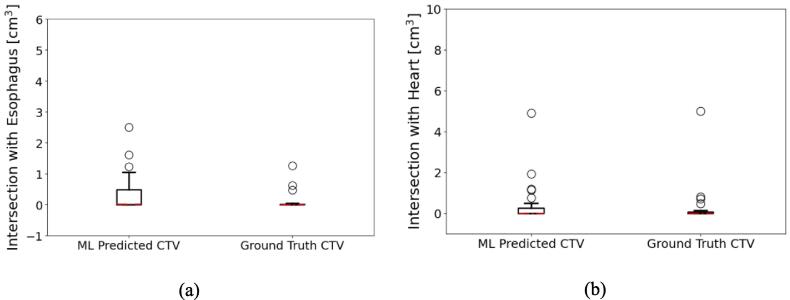
Fig. 4.

Comparisons of intersections with OARs. (a) and (b) are the intersection volumes (OVs) in unit of cm³ for the esophagus, and the heart. When the OAR is not available for the patient, the case is excluded from both plotting and the mean value calculation.

2.5. Ablation studies

The concept of the ablation study was introduced to the computer vision community by Sun [13] in 2010 as a way to understand some components’ impact on the overall system. Since then the ablation study has become a norm in the field of machine learning and computer vision. In our case, the standard 3D UNet is the baseline system, which has the BCE loss function and no elastic deformation. Our model uses the 3D UNet with the AM-GM inequality based loss function and the elastic deformation in the image augmentation. To understand the contribution of those two components to the overall system, ablation studies were performed for the following three scenarios: 1) standard 3D U-Net; 2) 3D U-Net with the AM-GM inequality loss function without elastic deformation; 3) 3D U-Net with BCE loss function and elastic deformation.

3. Results

3.1. Similarity metrics

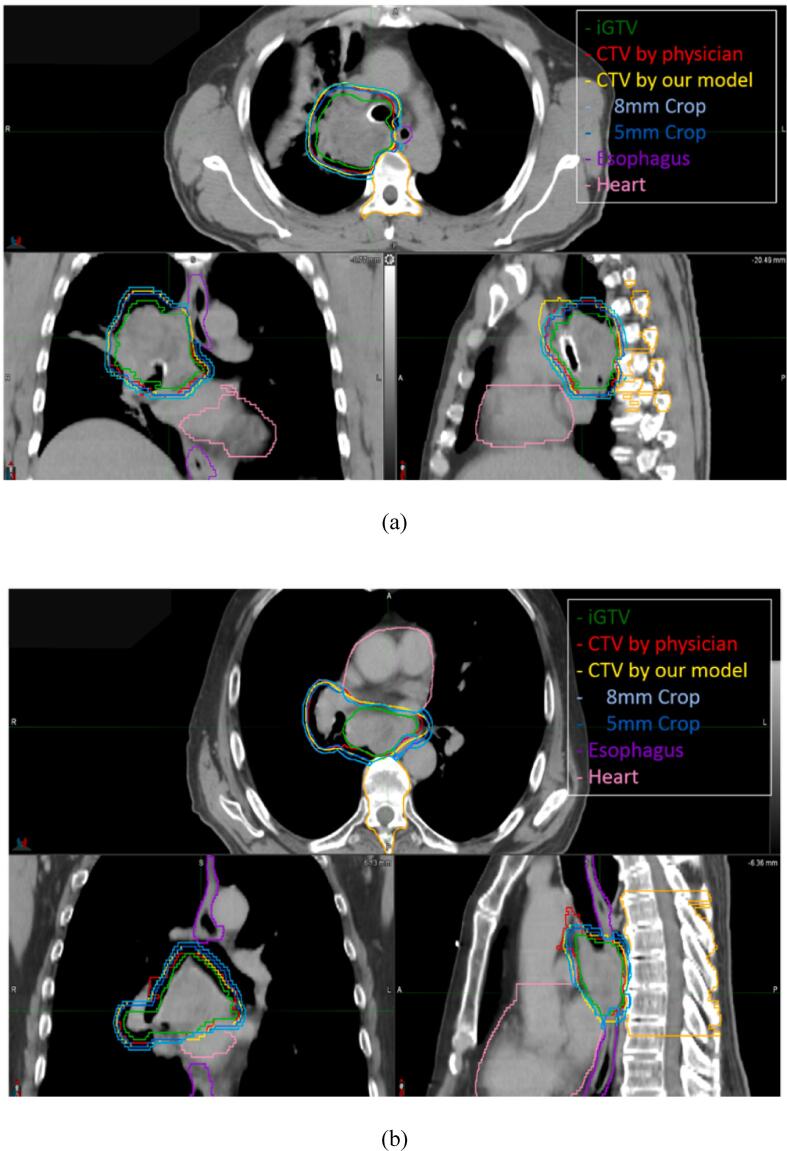
The CTV contours predicted by our model were visually closer to the ground-truth contours than the cropped expansion method. Fig. 2 shows two examples of CTV predictions from our model overlaid on the patient CT scan.

Fig. 2.

Two typical examples of the CTV delineation generated by our model overlaid on the patient CT scan with tumor in a) the upper lobe and b) the lower lobe. The yellow lines stand for the automated predicted CTV. The red and green lines are the CTV and corresponding iGTV drawn by the physicians, respectively. The blue, purple, and pink lines are the cropped expansion CTV, the esophagus contour, and the heart contour, respectively. As shown in the axial view of b), our predicted CTVs, similar to the physician’s contoured CTVs, have less expansion in the anterior direction from iGTV to avoid the heart. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Our model achieved a mean precision of 0.89, mean recall of 0.84, and mean dice score of 0.86, which means a higher DSC and smaller difference between recall and precision than the two cropped expansions, as shown in Fig. 3 (a).

3.2. Surface distances

In the test group, the median values for the Hausdorff distance, the mean, the median, and the 95-percentile, were 8.6 mm, 1.4 mm, 1.0 mm, and, 3.9 mm, for our model predicted CTVs respectively. For the 5 mm cropped expansions, the mean values were 9.1 mm, 1.6 mm, 1.0 mm, 4.5 mm, while the values for the 8 mm cropped expansions were 12.6 mm, 2.2 mm, 2.0 mm, and 6.1 mm. Compared to both cropped expansions, our ML model predictions have smaller distances. The results are plotted in Fig. 3(b) and summarized in Table 1.

3.3. Overlapping volumes with OARs

We compare the intersection with OARs of our model predicted CTV contours with the ground-truth CTVs for both the esophagus and the heart, which were important organs in the chest. The overlapping volumes (OVs) with the esophagus and the heart are 0.4 ± 0.3 cm³ and 1.2 ± 0.6 cm³ for the ML-predicted CTVs. The ground truth CTVs have 0.1 ± 0.2 cm³ and 0.8 ± 0.6 cm³ OV with the esophagus and the heart, respectively. The OVs are zero for both cropped expansion CTVs by definition. All results are shown in Fig. 4 and summarized in Table 1.

3.4. Ablation studies

The model performance under the ablation study was evaluated using the same evaluation metrics as defined in Section 2.4. The standard 3D UNet achieved a mean value of 0.84 for the DSC, 0.91 for the precision, and 0.81 for the recall. The mean values of the DSC, the precision and the recall are 0.85, 0.89, and 0.82 for the model trained with BCE loss fuction with elastic augmentation, and 0.85, 0.88, and 0.84 for the model trained with AM-GM loss function without elastic augmentation. All those results are summarized in Table 1 in the supplementary material.

4. Discussion

In our study, a 3D UNet based neural network model was trained with 60 datasets that were randomly selected from 84 available datasets. The remaining 24 datasets were used for model testing. The model’s performance was evaluated using the shape similarities and the OAR sparing between our model and the physician’s contours.

Using the 3D UNet architecture and a modified loss function, our approach resulted in an automated CTV delineation system which is trainable in an end-to-end fashion and capable to approximate the physician contoured CTVs. As shown in the results session, our model on NSCLC had similar performance as existing deep-learning based approaches applied to other sites (0.86 mean DSC, 1.5 mm the median mean surface distance (MSD)). Cardenas [14] had the mean DSC values ranged from 0.843 to 0.909 for different lymph node levels. The achieved mean MSD values were from 1.0 mm to 1.3 mm, and mean Hausdorff surface distance (HD) values from 5.5 mm to 8.6 mm. Men [15] achieved mean DSCs from 62.3% to 82.6% with a deep deconvolutional neural network (DDNN) for target segmentation of the nasopharyngeal cancer. In terms of OAR overlap, our trained model behaved similarly to physicians: the overlapping volume was at the same magnitude as the ground-truth by physicians in terms of the intersection volumes.

Unlike the existing approaches applied to the other sites, our approach on NSCLC required little manual intervention: no hyper-parameters tuning or post-processing steps. For example, Cardenas [14] needed to tune a hyper parameter to combine the “DSC” (in fact, it is an AM-GM inequality loss) and the “FND” (false-negative AM-GM inequality loss).

For the ablation study, we also implemented the standard 3D UNet. The model trained from the standard 3D U-Net did suffer the problem of bias to high precision and low recall. Our model with the AM-GM inequality loss and elastic deformation augmentations out-performed the standard 3D U-net with a 3% higher recall, 1% better DSC, and 0.1 mm smaller median mean surface distance. It also showed that the AM-GM inequality based loss function resulted in an estimation less bias to the background (or less difference between precision and recall). As shown in Supplementary Table 1, the AM-GM inequality based loss function accounts for 2% improvement of the recall (reduces the problem of the underestimation). In the other words, this AM-GM inequality based function alone handled imbalance well. Similar to our approach, a dice coefficient based loss function to replace BCE for UNet was reported in [16], [17].

One advantage of using our ML-based CTV delineation was the reduced contouring time for those who wanted to follow our institutional approach. Once the model was trained, it typically took less than a minute per patient to generate the whole 3D CTV contour from input images and GTV contours. Then physicians can examine the predicted contour lines in each 2D plane overlaid on the patient’s CT images in all three views (axial, sagittal, and coronal) with minimal adjustments. This automation has the potential to be used in a clinical setting to free physicians from the labor-intensive process and allow them to handle more complex cases. For our patients, using the center of the CT images as the region center for our model is sufficient without cropping the patient anatomy. This operation was nearly instantaneous (<1 ms) on a Dell 8930 PC. Therefore, adding this cropping time wouldn’t affect the contouring time of our model in Table 1.

Another advantage of using the ML-based automated CTV prediction was the smoothness of the generated contours in the superior-inferior direction. This result was expected because of the 3D convolution kernels used in this study. Similar results were reported in [17] even with a semi 3D approach. Different from clinicians (or uniform-expansion in TPS) who handle the CT images and delineate the CTV contours slice-by-slice, our trained model took the full 3D volumetric information into account and naturally enforced the smoothness of the predicted contours in axial direction. This greatly reduced artificial contour shape changes across slices.

The biological considerations behind our CTV delineation practice is that the microscopic tumor spread depends on tumor’s environment, e.g. the nearby anatomical structures. This means that the expansion could vary in all directions on each slice, which is individualized for each patient. In this sense, fitting this anisotropic expansion pattern using the deep learning approach is reasonable and cannot be done by the simple uniform expansion with cropping OARs.

Shown in Table 1, when compared to the 8 mm cropped expansion method, although our model had a little lower recall, it had more balanced scores in all the other similarity measures to the ground truth contours. When compared to the 5 mm cropped expansion, our model had a higher recall. In other words, the 8 mm cropped expansion method was biased to recall, which meant that this expansion includes larger amounts of normal tissues and could lead to unnecessary dose delivered to those normal tissues. On the other hand, the 5 mm cropped expansion was biased to precision, which meant that some target volumes were excluded which could affect the tumor local control and the patient survival rate. There were a few outliers with large HD and 95-percentile, which were outside the scales shown in the Y-axis in Fig. 3(b). Those outliers resulted in much larger mean values than the median values in Table 1.

In this study, we presented the first study on CTV delineation using a deep 3D convolutional neural network for NSCLC patients. Since our physicians contoured the patient specific CTVs based on each individual’s case, when our model was trained, those clinical variables were learned implicitly. Trained from a dataset of limited size, the model demonstrated the capability of intelligent CTV delineation with consideration of patient anatomy and clinical variables (e.g. the tumor location, the distances to the OARs, tumor biology, etc) for NSCLC patients. Our model showed better shape similarity and smaller surface distances to the ground-truth CTVs than the standard 3D U-net. Compared with a simple cropped expansion algorithm, our trained model matched the physician-drawn contours better, while it only slightly increased the overlap with the OARs.

Conflict of interest notifications

None.

Funding statement

None.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: