Abstract
This paper presents a new stochastic-based method for modelling and analysis of COVID-19 spread. A new deterministic Susceptible, Exposed, Infectious, Recovered (Re-infected) and Deceased-based Social Distancing model, named SEIR(R)D-SD, is proposed by introducing the re-infection rate and social distancing factor into the traditional SEIRD (Susceptible, Exposed, Infectious, Recovered and Deceased) model to account for the effects of re-infection and social distancing on COVID-19 spread. The deterministic SEIRD(R)D-SD model is further converted into the stochastic form to account for uncertainties involved in COVID-19 spread. Based on this, an extended Kalman filter (EKF) is developed based on the stochastic SEIR(R)D-SD model to simultaneously estimate both model parameters and transmission state of COVID-19 spread. Simulation results and comparison analyses demonstrate that the proposed method can effectively account for the re-infection and social distancing as well as uncertain effects on COVID-19 spread, leading to improved accuracy for prediction of COVID-19 spread.
Keywords: COVID-19 modelling, Stochastic epidemiological model, Social distancing, Re-infection, And extended kalman filter
1. Introduction
At the end of 2019, the novel coronavirus, SARS-CoV-2 (COVID-19), firstly appeared in Wuhan, the city of Hubei province in the People's Republic of China and spread rapidly around the world. The pathogenesis of the virus is characterized by respiratory tract infection, which directly leads to pneumonia showing ground glass alveolar angiography. The COVID-19 virus is contagious from the people infected even though they may not show symptoms (asymptomatic infections). Although China, United States, Italy, Australia and other countries have successively adopted various containment and detection measures, the cumulative number of diagnoses is still increasing every day. The occasional rebound has also hampered the implementation of economic recovery plans. In order to better control and monitor the epidemic, mathematical modelling of COVID-19 becomes an area of active research.
Predictive mathematical models for epidemics are essential to understand the propagative characteristics of COVID-19 and to implement the intervention and preparedness measures for controlling the disease spread. The current existing research efforts on prediction of infectious diseases are mainly dominated by the agent-based and compartmental models. The agent-based model involves a complex process to define agent behaviours together with their associated interaction mechanisms and intervention rules, leading to expensive computations. Chang et al. developed an agent-based model to study the effect of social distancing (SD) compliance on COVID-19 spread [28]. Kerr et al. proposed a methodology of COVID-19 agent-based simulator, which is used to explore different intervention scenarios [29]. However, both methods depend on a large number of samples and rules, leading to the difficulty of parameter identification. They also require an expensive sensitivity analysis to determine the prediction robustness. Therefore, these two methods can only use a relatively small number of agents for COVID-19 modelling, leading to the limited modelling accuracy.
Comparing to the agent-based model, the compartmental model is simple and correlated to observation [28]. It involves a dynamic process based on how the population is divided into different compartments to describe the transmission state [1]. The SIR (Susceptible, Infectious and Recovered) model divides the population into the susceptible, infectious and recovered compartments to describe the state of disease spread, where people who are susceptible to infection will possibly be infected, and the infected people will be recovered with a certain rate. The SEIR (Susceptible, Exposed, Infectious and Recovered) model introduces the exposed compartment into the SIR model to describe the intermediate state between the susceptible and infected people. Since the ferocity of the epidemic has claimed many lives, its lethality cannot be ignored. However, neither SIR nor SEIR considers the lethality of the disease. The deceased compartment is thus introduced in parallel to the recovered compartment to describe the possibility of disease transmission from infected people via the transmitting rate from the infected to deceased compartment [2]. The SIRD (Susceptible, Infectious, Recovered and Deceased) model introduces the deceased compartment into the SIR model to consider the fatal condition. Similarly, the SEIRD (Susceptible, Exposed, Infectious, Recovered and Deceased) model introduces the deceased compartment into the SEIR model to describe disease transmission between humans.
Since the outbreak of COVID-19 pandemic, especially in the absence of vaccines, various SD measures such as flight restriction, school closure, indoor activity restrictions and quarantine [28] have been widely adopted by governments to reduce the cross-infection possibility [3,4]. Therefore, it is necessary to account for the effect of SD compliance on COVID-19 spread in epidemiological modelling. Further, patients cannot develop the lifelong immunity after recovery and the SARS-CoV-2 virus mutates over time, causing immune evasion [5,8]. Therefore, it is also necessary to take into account the deceased compartment and the re-infection rate from the recovered to susceptible compartment into epidemiological modelling. Hagger et al. studied a social cognition model by taking into account the distance between individuals in the SEIR model [6]. However, this model does not consider the deceased people and re-infection effect. Malkov studied how the possibility of reinfection shapes the epidemiological dynamic based on the SEIR model [31]. However, the lethality of COVID-19 is not considered. Further, all containment measures are integrated into the transmission rate, unable to characterize the effects of various kinds of containment measures on COVID-19 spread.
Distinct from other infectious diseases, COVID-19 has a randomly variable incubation period. It mutates with varying infectivity and pathogenicity (e.g. the B.1.1.7 and B.1.617.2 variants have increased infectivity and shorter incubation period of about 24 h), making the incubation period of COVID-19 and its associated infection rate involve randomness [8,27]. Moreover, since the potential sources of infection are unknown, asymptomatic infections are difficult to detect, resulting in uncertainties in reported infection cases [7]. The inadequate contact tracing, lack of population-wide PCR testing and short-term policy changes also cause the uncertainties in reported data on COVID-19 [32]. However, the existing studies on COVID-19 modelling are dominated by deterministic epidemiological models for describing the epidemiological evolution deterministically via ordinary differential equations, unable to model the stochastic behaviours of the COVID-19 epidemic [9,10]. Therefore, it is also necessary to develop a stochastic epidemiological model to account for random or stochastic events involved in the COVID-19 transmission system.
In addition to an epidemiological model, dynamic modelling of COVID-19 pandemic also requires a real-time algorithm to estimate the transmission state online. The recursive least square (RLS) is a traditional method for online parameter estimation in epidemiological modelling [1,11]. It can generate optimal state estimation via minimizing the linear least-squares cost function related to system observations. As an improvement of RLS, the Kalman filter (KF) introduces the system state equation in RLS to calculate the propagation of system state via a prediction process. It can achieve optimal state estimation in the accuracy of minimum mean square error, even in the absence of observations. Kumar et al. developed a KF based on a linear forest regression model that describes the correlations between infected individuals to predict the future trend of COVID-19 [11]. Arroyo-Marioli et al. used KF to estimate the basic reproduction number of COVID-19 based on a linearized form of the SIR model [2]. Nevertheless, RLS and KF can be applied to linear systems only [12], while the existing epidemiological models for COVID-19 forecast are nonlinear. The constrained least-squares (CLS) [13] and Markov chain Monte Carlo (MCMC) [14] are the commonly used estimation method for nonlinear epidemiological models. However, since CLS and MCMC are based on maximum posteriori estimates of probability density function, the accuracy of both methods heavily depends on the sample size [13]. Further, both methods also involve expensive computations and can only be conducted in an offline manner. Accordingly, they are unsuitable for characterising random uncertainties involved in epidemiological model parameters for COVID-19 prediction.
As an improvement of KF for nonlinear systems, the extended Kalman filter (EKF) dynamically linearizes the nonlinear system model to employ the traditional KF for online state estimation. Comparing to CLS and MCMC, EKF is a simple iterative algorithm with significant computational efficiency for nonlinear epidemiological modelling [15,16]. So far, there has been very limited research on using EKF for epidemiological modelling, especially in COVID-19. Just recently, Hassan et al. developed an EKF based on the SEIR model for modelling of COVID-19 spread, but without considering the exposed patients and incubation period [17]. Younes and Hassan developed an EKF based on the Lotka-Volterra model to estimate COVID-19 spread [18]. However, the predator-prey interaction mechanism described by the Lotka-Volterra model has a very limited capacity to model the complex characteristics of the natural transmission process of COVID-19. Song et al. studied a novel maximum likelihood based EKF to estimate COVID-19 spread [9]. However, since this method is based on a deterministic epidemiological model, it is incapable of characterizing the stochastic characteristics of COVID-19 spread. Further, it does not consider the re-infection and SD effects either.
This paper presents a new stochastic-based method for estimation and prediction of COVID-19 spread. This method introduces the deceased compartment with the death rate, and the re-infection rate that characterizes the transmission from the infected back to susceptible compartment, into the SEIRD model, leading to a new deterministic Susceptible, Exposed, Infectious, Recovered (Re-infected) and Deceased-based Social Distancing model, named SEIR(R)D-SD, to account for both re-infection and the SD effects of COVID-19. Subsequently, the stochastic version of the deterministic SEIR(R)D-SD model is constructed according to the probabilities of independent random changes occurred in the system to account for the stochastic characteristics of COVID-19 spread. Based on this framework, an EKF algorithm is developed for online estimation of the spreading behaviours of COVID-19, where the system state equation and system observation equation are constructed and the model parameters of SEIR(R)D-SD are also augmented into the system state to simultaneously estimate both model parameters and system state. Simulation results are consistent with the COVID-19 epidemic in Australia, where the multiple outbreak waves are accurately captured by the proposed method [33]. They also reveal that SD restriction can postpone the COVID-19 outbreak and the re-infection rate can reflect the non-lifelong immunity characteristic of COVID-19.
2. Methodology
2.1. SEIR(R)D-SD model
The SEIRD model has an additive deceased compartment associated with the death rate [19,20]. It constitutes the following time-continuous deterministic system
| (1) |
where S, E, I, R and D denote the susceptible, exposed, infectious, recovered and deceased compartments, is the total population; and , , and are the model parameters, where is the infection rate which is the inverse of the incubation period, is the exposing rate, is the recovery rate, and is the death rate. For simplicity and consideration of the limited immigration-emigration effect on population due to border restriction policies, is generally considered as a constant for COVID-19 modelling [30,33].
Suppose that the community of all the compartments is closed, i.e.,
| (2) |
By introducing the SD factor into the deterministic SEIRD model to study the SD effect and by introducing a factor in S and R to represent the rate from the recovered to susceptible compartment to account for the re-infected population [20], the deterministic SEIR(R)D-SD model can be written as
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where is the re-infection rate, and is the SD factor which is dynamically changed with the compliance levels of various SD policies such as travel restriction, lockdown or semi-lockdown, self-quarantine and school closures [28].
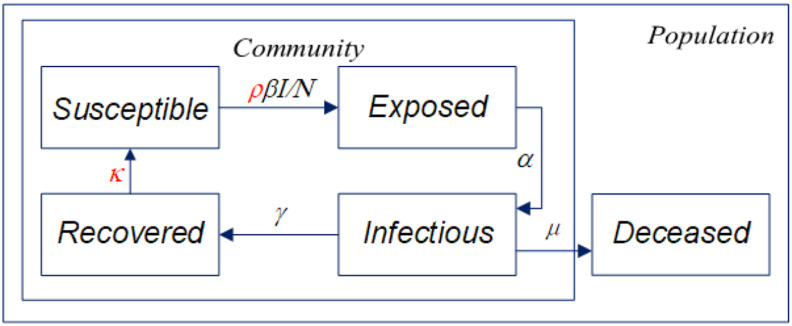
Fig. 1 illustrates the structure of the SEIR(R)D-SD model. The deceased compartment is outside the loop of disease spread to leave the community with the death rate , while the rest of the compartments form a loop, where the susceptible compartment which is initially presumed as the total population size, is transferred to the exposed compartment with the exposing rate and the SD factor , and the recovered compartment will return to the susceptible compartment to cyclically transmit the disease in the community.
Fig. 1.
Structure of the SEIR(R)D-SD model.
2.2. Stochastic SEIR(R)D-SD model
In this section, we discuss how to convert the above deterministic SEIRD(R)D-SD model into a stochastic model according to the possibilities of all the independent random changes occurred in the system.
According to (2),
| (8) |
Substituting (8) into (3)–(7), the deterministic SEIR(R)D-SD model becomes
| (9) |
| (10) |
| (11) |
| (12) |
Equation (9), (10), (11), (12) can be combined into the following form
| (13) |
where is the four-dimensional system state consisting of the susceptible, exposed, infected and death compartments, and is the nonlinear system function.
Discretizing (13) in time domain, we can have the following discrete-time SEIR(R)D-SD model
| (14) |
where is the system state at time point k.
The deterministic discrete system (14) involves four random changes with each occurred to at least one of the state parameters. Define the jth random change as
| (15) |
where denotes the probability of the jth change and denotes the transition of the system state under the jth change, both of which are obtained from (9), (10), (11), (12) and given in Table 1 .
Table 1.
Random changes involved in the SEIR(R)D-SD model where denotes the time step.
| Transition of change | Probability |
|---|---|
By summing each random change for the system state, a simple stochastic form of (14) can be written as
| (16) |
where it is known from (15) that obeys the normal distribution with expectation and variance .
Approximating the random changes using a normal random vector via the central limit theorem [21,22] yields
| (17) |
where , and which is subject to the Gaussian distribution.
2.3. System state and observation equations
Simplifying (17) yields
| (18) |
where and is the system noise.
Since the reported data are in terms of the infectious, recovered and dead compartments only, the system observation is constructed as
| (19) |
where is the system observation (i.e., the reported data); is the observation noise which is assumed to be white noise with covariance and is independent of ; and is the observation matrix which is expressed as
| (20) |
The nonlinear function can be linearized as
| (21) |
where is the Jacobian matrix, which is expressed as
| (22) |
Since the epidemiological model parameters are random unknowns, they must also be estimated in the filtering process to account for their randomness. Accordingly, we augment the model parameters into the system state as
| (23) |
where is the augmented system state and . collects the model parameters including the infection rate α, exposing rate , recovery rate , death rate , re-infection factor and SD factor .
Correspondingly, the system state equation (18) becomes
| (24) |
where is the process noise which is assumed as a white noise with covariance , and is the augmented system function which is represented as
| (25) |
where is the unit matrix.
The EKF procedure for estimating the model parameters and transmission state involves the following steps:
-
i)
Set the initial system state and its associated covariance
| (26) |
| (27) |
-
ii)
Calculate the predicted state and its associated covariance
| (28) |
| (29) |
-
iii)
Calculate the Kalman gain
| (30) |
-
iv)
Update the estimated state and its associated covariance
| (31) |
| (32) |
-
v)
Repeat (28)–(32) until all iterations are processed.
3. Performance evaluation
Simulations were conducted to comprehensively evaluate the performance of the proposed method for COVID-19 modelling in terms of the following aspects: (i) the effectiveness of the proposed deterministic SEIR(R)D-SD model in comparison with the classical SEIRD model; (ii) the effectiveness of the proposed EKF based on the stochastic SEIR(R)D-SD model in comparison with the numerical solution of the deterministic SEIR(R)D-SD model; and (iii) the effectiveness of the proposed EKF based on the stochastic SEIR(R)D-SD model in comparison with the numerical solution of the classical SEIRD and the proposed deterministic SEIRD(R)D-SD models based on CLS parameter identification for modelling of the pandemic in Australia from daily reported data. It should be noted that the COVID-19 pandemic in Australia is considered for verification and validation purposes only, while the proposed method is generic and independent of application cases and thus it can also be used to predict COVID-19 pandemics in any other countries/regions.
The modelling accuracy is evaluated in terms of the root mean-squares error (RMSE), which is defined as
| (33) |
where denotes the ground truth and N the number of samples.
3.1. Deterministic SEIR(R)D-SD model
Simulation tests were conducted to evaluate the performance of the deterministic SEIR(R)D-SD model in comparison with the classical SEIRD model. The simulation time was set to 200 days. The model parameters are given in Table 2 .
Table 2.
The values of the model parameters.
| SEIRD model | 0.14 | 0.6 | 0.12 | 0.01 | 0 | 0 |
| Deterministic SEIR(R)D-SD model | 0.14 | 0.6 | 0.12 | 0.01 | 0.005 | 0.6 |
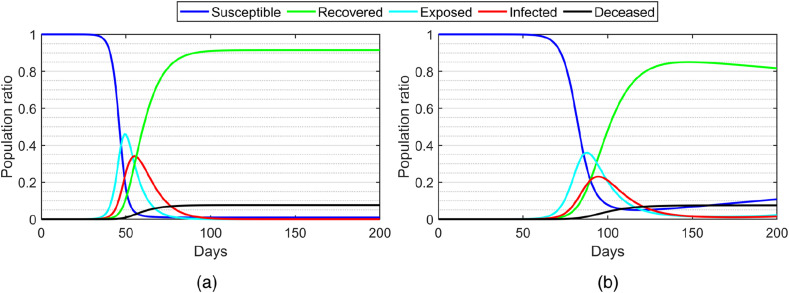
Fig. 2(a) illustrates the numerical solution of the classical SEIRD model. The susceptible population decreases and the recovered population increases exponentially from day 40–100, whereas both exposed and infected populations quickly increase and then decrease after day 50. After day 100, the populations of all the compartments remain stable, where the susceptible, infected and exposed populations decrease to zero while the deceased population remains at a constant. For the deterministic SEIR(R)D-SD model, as shown in Fig. 2(b), due to the SD effect, the peaks of the exposed, infected and recovered populations are lower than those of the classical SEIRD model.
Fig. 2.
The population ratios of the susceptible, exposed, infected, recovered and deceased compartments calculated by the numerical solutions of (a) the classical SEIRD model; and (b) the proposed deterministic SEIR(R)D-SD model ( and ).
Despite the steep drop, the susceptible population does not drop to zero and slightly increases after day 100 due to the re-infection effect. Due to the SD effect, the peaks of the exposed and infected populations are delayed from day 50–100, comparing to those of the SEIRD model. Due to the transfer from the recovered to infected compartment via the re-infection rate, the infected population gradually increases after the steep decrease from day 50–100, while the recovered population gradually decreases after the steep increase from day 50–100. The results show that SD restriction can postpone the disease outbreak and the re-infection rate can reflect the non-lifelong immunity characteristic of COVID-19.
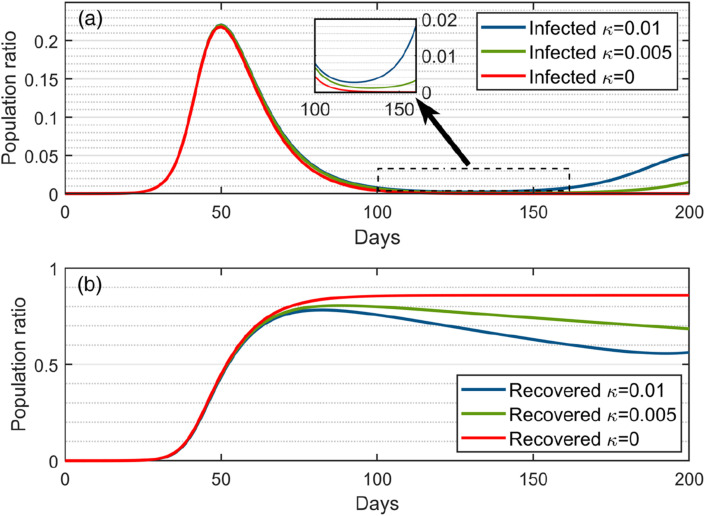
Simulations were also conducted to evaluate the effects of the re-infection rate and SD factor .
Fig. 3(a) illustrates the variations of the infected populations under three different values, i.e., , and , without involving the SD effect (i.e. the natural spread case of ). In the case of (lifelong immunity), the infected population rises steeply from zero to the peak and then quickly reverts to zero and eventually remains at zero after day 120. In the case of , the infected population has a similar trend as that in the case of . before day 140, while it gradually increases after day 140 since the re-infected people cause the disease to spread in the community. In the case of , the infected population has a similar trend as in the cases of and before day 130, whereas it gradually increases again after day 130. It can be seen that the larger the value is, the more the infected population will rebound, leading to the higher chance that the disease will break out again in the future.
Fig. 3.
The population ratios of the infected (a) and recovered (b) compartments calculated by the numerical solution of the deterministic SEIR(R)D-SD model under three different re-infection rates (, and ).
Fig. 3(b) illustrates the trends of the recovered population ratio under the three different re-infection rates. Before day 50, the recovered populations for all the three cases have a similar trend and all rise quickly. This is because the recovered population is too small at the beginning of disease spread, leading to a similar re-infection effect for the three cases. After day 50, the recovered population becomes stable for the cases of , while the recovered populations for both cases of and gradually decrease, where the decrease in the case of is almost the twice of that in the case of . The larger the re-infected rate is, the more the recovered population will decrease. The resultant increase of the infected population and the resultant decrease of the recovered population after day 130 indicate that future COVID-19 outbreaks may occur.
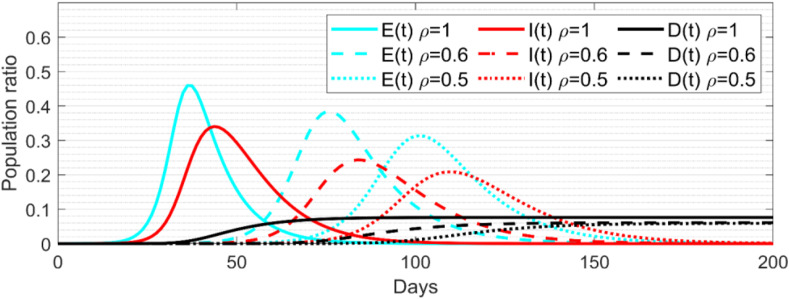
Simulation tests were also conducted to evaluate the SD effect. As shown in Fig. 4 , both exposed and infected populations decrease significantly, and their peaks are also postponed when the SD factor is changed from 1 to 0.5. The peak population ratios for both populations in the case of are only about 20% and 40% smaller than those in the case without SD restriction (i.e., ). Further, in the case of , the ratios of both populations are about 40% and 50% smaller than those in the case of natural spread (i.e., ). This is because SD restriction directly reduces the transmission rate from the susceptible to exposed compartment. However, since SD restriction does not affect the total exposed population, the cases of SD restriction (i.e., and ) postpone the peaks of both exposed and infected populations for about 40 days and 60 days comparing to the case without SD restriction (i.e., ). It can be seen from the results that the smaller the SD factor is, the lower the risk of disease outbreak will be. However, SD restriction can only keep the transmission rate from the susceptible to exposed compartment at a low level to delay disease outbreaks, while unable to prevent them.
Fig. 4.
The population ratios of the exposed, infected and deceased compartments calculated by the numerical solution of the deterministic SEIR(R)D-SD model.
3.2. EKF based on stochastic SEIR(R)-D model
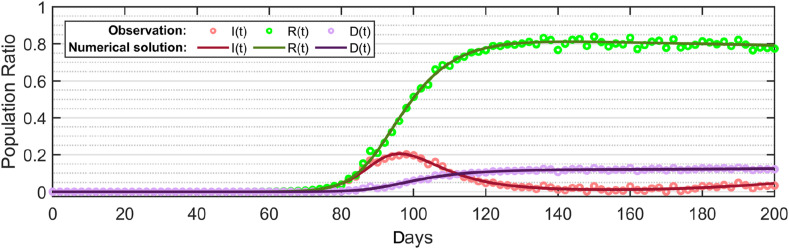
To evaluate the stochastic SEIR(R)D-SD model and its associated EKF, the observation data were generated by adding a random white noise of covariance in the numerical solution of the deterministic SEIR(R)D-SD as shown in Fig. 2(c) to simulate the actual reported data of COVID-19 spread that involve uncertainties.
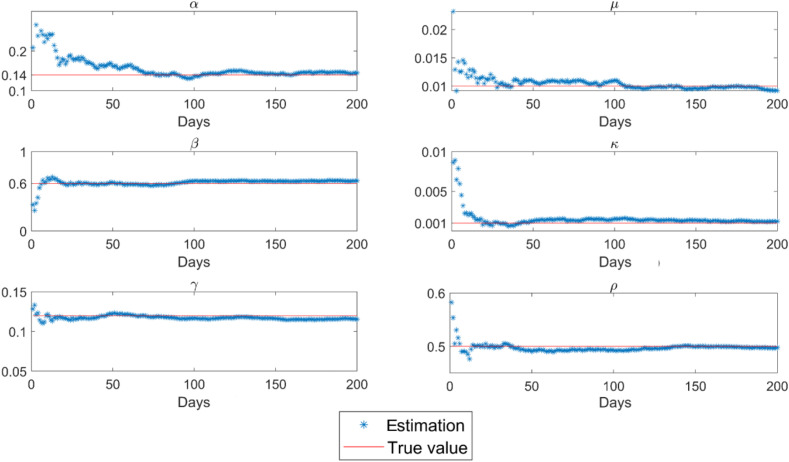
Based on the observation data shown in Fig. 5 , both model parameters and transmission state are estimated by the proposed EKF based on the stochastic SEIR(R)D-SD model. Fig. 6 illustrates the model parameters estimated by EKF with reference to their true values given in Table 2. It can be seen that the EKF estimations of the model parameters closely approximate their true values. As shown in Table 3 , the estimation RMSEs (Root Mean Square Errors) are 0.0032, 0.011, 0.0018, 0.00085, 0.0036 and 0.012 for parameters , , , , and , respectively, demonstrating that the proposed EKF based on the stochastic SEIR(R)D-SD model can effectively estimate the model parameters.
Fig. 5.
Simulated observation data generated by adding a white noise in the numerical solution of the deterministic SEIR(R)D-SD model.
Fig. 6.
Model parameters estimated by the proposed EKF based on the stochastic SEIR(R)D-SD model.
Table 3.
RMSEs of the model parameters estimated by the proposed EKF based on the stochastic SEIR(R)D-SD model.
| α | β | γ | μ | κ | ρ | |
|---|---|---|---|---|---|---|
| EKF | 0.0032 | 0.011 | 0.0018 | 0.00085 | 0.0036 | 0.012 |
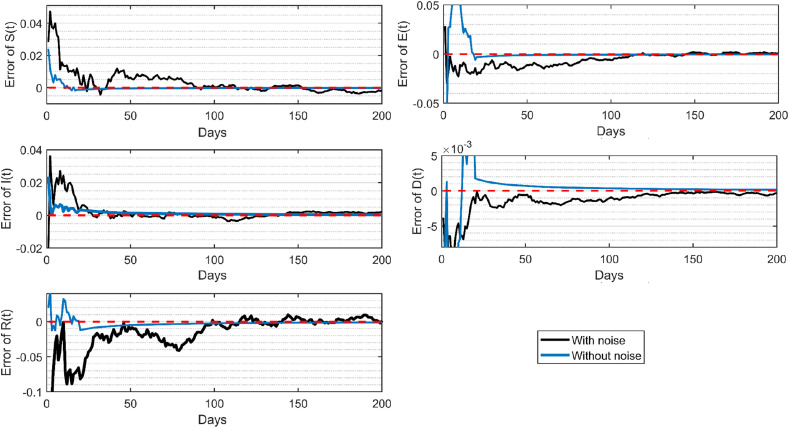
Fig. 7 illustrates the errors of the compartment populations estimated by the proposed EKF from the noisy observation data. The estimations of each compartment population resulted from the noisy observation data converge to their true values quickly, with the RMSE of 0.0032 for the susceptible, 0.0021 for the exposed, 0.0035 for the infected, and 0.00064 for the deceased population. This demonstrates that the proposed EKF based on the stochastic SEIR(R)D-SD model can effectively predict the transmission state from noisy observation data.
Fig. 7.
Estimation error by the proposed EKF based on the stochastic SEIR(R)D-SD model.
To further evaluate the stochastic SEIR(R)D-SD model, the non-noisy measurement data, i.e., the numerical solution shown in Fig. 2(b), were also used as observations to estimate the compartment populations by the proposed EKF based on the stochastic SEIR(R)D-SD model. As shown in Fig. 7, the estimations of each compartment population from the non-noisy observation data converge to their true values within a very short time period, demonstrating the stochastic SEIR(R)D-SD model is a particular case of the deterministic SEIR(R)D-SD model in the ideal condition. Table 4 lists the RMSEs of the compartment populations estimated by the proposed EKF based on the stochastic SEIR(R)D-SD model from both noisy and non-noisy observation data.
Table 4.
RMSEs of the proposed EKF based on the stochastic SEIR(R)D-SD model.
| Susceptible | Exposed | Infected | Recovered | Deceased | |
|---|---|---|---|---|---|
| Without noise | 3.2 × 10−3 | 2.1 × 10−3 | 1.2 × 10−3 | 3.5 × 10−3 | 6.4 × 10−4 |
| With noise | 8.2 × 10−3 | 4.4 × 10−3 | 3.1 × 10−3 | 5.5 × 10−3 | 1.2 × 10−3 |
3.3. COVID-19 pandemic in Australia
In Australia, a hotspot of the COVID-19 pandemic, as of September 30, 2020, the Australian government reported 27,078 total confirmed cases and 886 deaths [23]. The pandemic started in January and reached the first peak on April 6, 2020. Its second wave started at the end of June 2020 and reached the peak on 9th August. The Australian government adopted a series of SD measures such as travel restriction policies, school closure, indoor activity restrictions and quarantine to control the virus spread. The infected cases were almost vanished in the mid of June 2020. However, when the compliance level of SD restriction was relaxed at the end of May 2020 due to a good progress in controlling the first outbreak and the urgent desire for economic recovery, the second outbreak occurred at the end of June 2020.
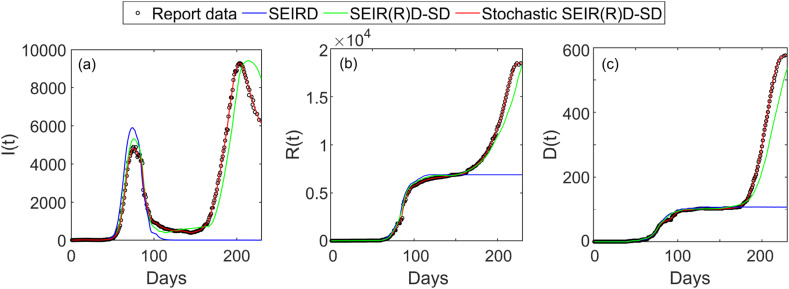
Simulation trials were conducted by tracking and analysing the COVID-19 spread in Australia during the outbreak period of 230 days from 22nd January to September 8, 2020. According to the report of United Nations Population Division [24], the Australian population were about 25.5 million during the COVID-19 pandemic. We collected the reported cases within 230 days from 22nd January to September 8, 2020 from the World Health Organization (WHO) Novel Coronavirus Situation Report [25]. As shown by the reported data in Fig. 8 , the COVID-19 spread in Australia has two outbreaks from 22nd January to September 8, 2020, where the first outbreak was occurred on about day 75 and the second outbreak started from day 160.
Fig. 8.
The infected, recovered and deceased populations by the numerical solutions of the SEIRD and deterministic SEIR(R)D-SD models based on CLS and the estimation solution of the proposed EKF based on the stochastic SEIR(R)D-SD model for the COVID-19 pandemic in Australia: (a) the infected population; (b) the recovered population; and (c) the deceased population.
Since the true values for the actual cases are unknown, the reported data were taken as reference for calculation of estimation error. The initial state and noise covariances were set based on the observation data on the first day of the simulation analysis. The initial values of the model parameters are given in Table 5 . For comparison analysis, the transmission state was also calculated from the SEIRD and deterministic SEIR(R)D-SD models based on parameter identification via the offline CLS algorithm [1,26] under the same conditions.
Table 5.
The initial values of the model parameters for the COVID-19 pandemic in Australia.
| Parameters | ||||||
|---|---|---|---|---|---|---|
| Value | 0.63 | 0.24 | 0.03 | 0.01 | 0.001 | 0.5 |
Fig. 8 illustrates the infected, recovered, and deceased populations calculated by the numerical solutions of the SEIRD model and deterministic SEIR(R)D-SD models based on CLS as well as those estimated by the proposed EKF based on the stochastic SEIR(R)D-SD model. As shown in Fig. 8(a), the numerical solution of the SEIRD model presents only one peak (i.e., only one outbreak). The maximum infected population calculated from the SEIRD model is about 850 more than and about 10 days earlier than that in the report data. Further, the infected population quickly drops to zero after the only peak, leading to a significant error. Different from that of the SEIRD model, the numerical solution of the deterministic SEIR(R)D-SD model for the infected population presents two outbreaks. Although the first outbreak is occurred closely to that in the report data, due to the inability to account for uncertainties involved in COVID-19 spread, the numerical solution of the deterministic SEIR(R)D-SD model for the infected population involves an obvious error, leading to the second outbreak with a delay of about 20 days and a deviation of 1237 infections comparing to that in the reported data. In contrast, the solution of the proposed EKF based on stochastic SEIR(R)D-SD model for the infected population is much closer to the report data than that of the deterministic SEIR(R)D-SD model, and the estimated two outbreaks are in a good agreement with those in the report data.
As shown in Fig. 8(b) and (c), the solutions of the recovered and deceased populations by the three methods have a similar trend as those of the infected population. The numerical solutions of the SEIRD model for the recovered and deceased populations remain at a constant value after day 120 and 110, respectively, both of which miss the second outbreak. Although the solutions from the deterministic and stochastic SEIR(R)D-SD models follow the report data and present the two outbreaks, the solution estimated by the proposed EKF based on the stochastic SEIR(R)D-SD model approximates the reported data more closely than the numerical solution of the deterministic SEIR(R)D-SD model for both recovered and decreased populations.
The RMSEs for the infected, recovered and deceased populations are shown in Table 6 . The RMSEs of the infected, recovered and deceased populations obtained by the numerical solution of the SEIRD model are 5064, 6614 and 311. The corresponding RMSEs of the deterministic SEIR(R)D-SD model are 472, 556 and 35, which are about 10 times smaller than those of the SEIRD model, whereas the corresponding RMSEs of the proposed EKF based on the stochastic SEIR(R)D-SD model are 203, 225 and 17, which are more than twice smaller than those of the deterministic SEIR(R)D-SD model and more than 20 times smaller than those of the SEIRD model. Thus, it is evident that the proposed EKF based on the stochastic SEIR(R)D-SD model has much higher accuracy than the SEIRD and deterministic SEIR(R)D-SD models for modelling of COVID-19 spread. Table 6 also compares the prediction means of the three methods with reference to the means of the reported data, which further verifies the above conclusion.
Table 6.
RMSEs and prediction means of the infected, recovered and deceased populations by the numerical solutions of the SEIRD and deterministic SEIR(R)D-SD models based on CLS as well as the proposed EKF based on the stochastic SEIR(R)D-SD model for the COVID-19 pandemic in Australia.
| Compartments |
Numerical solution of the SEIRD model based on CLS |
Numerical solution of the deterministic SEIR(R)D-SD model based on CLS |
EKF based on the stochastic SEIR(R)D-SD model |
Report data |
|||
|---|---|---|---|---|---|---|---|
| RMSE | Mean | RMSE | Mean | RMSE | Mean | Mean | |
| Infected | 5064 | 800 | 472 | 1484 | 203 | 1631 | 1649 |
| Recovered | 6614 | 3466 | 556 | 4028 | 225 | 4254 | 4203 |
| Deceased | 311 | 64 | 35 | 92 | 17 | 101 | 103 |
4. Conclusion
This paper presents a new method for COVID-19 modelling. The novelties of this method are: (i) a deterministic SEIR(R)D-SD model is developed to account for the re-infection and SD effects on COVID-19 spread; (ii) a stochastic SEIR(R)D-SD model is developed from the deterministic SEIR(R)D-SD model to account for uncertainties involved in COVID-19 spread; and (iii) based on the stochastic SEIR(R)D-SD model, an EKF algorithm is developed to simultaneously estimate both model parameters and transmission state. Simulations and comparison analyses demonstrate that the proposed method can effectively account for the re-infection and SD effects as well as uncertainties on COVID-19 spread, leading to increased accuracy for COVID-19 modelling.
The future research work will focus on improvement of the proposed method to account for the vaccination effect especially due to the vaccination rollout on COVID-19 spread. A new compartment and its associated rate will be introduced into the proposed SEIR(R)D-SD model to characterize the behaviours of vaccination, leading to a new stochastic epidemiological model and its associated real-time estimation algorithm for COVID-19 modelling.
CRediT authorship contribution statement
Xinhe Zhu: Formal analysis, Writing – original draft. Bingbing Gao: Writing – original draft. Yongmin Zhong: Writing – original draft. Chengfan Gu: Writing – original draft. Kup-Sze Choi: Formal analysis.
Declaration of competing interest
The authors whose names are listed immediately below certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.
References
- 1.Sameni R. 2020. Mathematical Modeling of Epidemic Diseases; a Case Study of the COVID-19 Coronavirus. arXiv preprint arXiv:2003.11371. [Google Scholar]
- 2.Marioli F.A., Bullano F., Rondón-Moreno C. Tracking R of COVID-19: a new real-time estimation using the Kalman filter. PloS One. 2020;16(1) doi: 10.1371/journal.pone.0244474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hsiang S., Allen D., Annan-Phan S., Bell K., Bolliger I., Chong T., Druckenmiller H., Huang L.Y., Hultgren A., Krasovich E., Lau P., Lee J., Rolf E., Tseng J., Wu T. Publisher Correction: the effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature. 2020;585(7824):E7. doi: 10.1038/s41586-020-2691-0. [DOI] [PubMed] [Google Scholar]
- 4.Ramezani S.B., Amirlatifi A., Rahimi S. A novel compartmental model to capture the nonlinear trend of COVID-19. Comput. Biol. Med. 2021;134:104421. doi: 10.1016/j.compbiomed.2021.104421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shi Y., Wang Y., Shao C., Huang J., Gan J., Huang X., Bucci E., Piacentini M., Ippolito G., Melino G. COVID-19 infection: the perspectives on immune responses. Cell Death Differ. 2020;27(5):1451–1454. doi: 10.1038/s41418-020-0530-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hagger M.S., Smith S.R., Keech J.J., Moyers S.A., Hamilton K. Predicting social distancing intention and behavior during the COVID-19 Pandemic: an integrated social cognition model. Ann. Behav. Med. 2020;54(10):713–727. doi: 10.1093/abm/kaaa073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hu Z., Song C., Xu C., Jin G., Chen Y., Xu X., Ma H., Chen W., Lin Y., Zheng Y., Wang J., Hu Z., Yi Y., Shen H. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. Sci. China Life Sci. 2020;63(5):706–711. doi: 10.1007/s11427-020-1661-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Korber B., Fischer W.M., Gnanakaran S., Yoon H., Theiler J., Abfalterer W., Hengartner N., Giorgi E.E., Bhattacharya T., Foley B. Tracking changes in SARS-CoV-2 Spike: evidence that D614G increases infectivity of the COVID-19 virus. Cell. 2020;182(4):812–827. doi: 10.1016/j.cell.2020.06.043. e819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Song J., Xie H., Gao B., Zhong Y., Gu C., Choi K.S. Maximum likelihood-based extended Kalman filter for COVID-19 prediction. Chaos, Solit. Fractals. 2021;146:110922. doi: 10.1016/j.chaos.2021.110922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Khataee H., Scheuring I., Czirok A., Neufeld Z. Effects of social distancing on the spreading of COVID-19 inferred from mobile phone data. Sci. Rep. 2021;11(1) doi: 10.1038/s41598-021-81308-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kumar S., Singh K.K., Dixit P., Kumar Bajpai M. Kalman filter based short term prediction model for COVID-19 spread. Appl. Intell. 2020;51(5):2714–2726. doi: 10.1007/s10489-020-01948-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gao B., Hu G., Zhong Y., Zhu X. Cubature rule-based distributed optimal fusion with identification and prediction of kinematic model error for integrated UAV navigation. Aero. Sci. Technol. 2020:106447. [Google Scholar]
- 13.Marzouk Y., Xiu D. A stochastic collocation approach to bayesian inference in inverse problems. Comput. Phys. Commun. 2009;6(4):826–847. [Google Scholar]
- 14.Gatto M., Bertuzzo E., Mari L., Miccoli S., Carraro L., Casagrandi R., Rinaldo A. Spread and dynamics of the COVID-19 epidemic in Italy: effects of emergency containment measures. Proc. Natl. Acad. Sci. U.S.A. 2020;117(19):10484–10491. doi: 10.1073/pnas.2004978117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Diniz P.S.R. Springer International Publishing; Cham: 2020. Kalman Filters. Adaptive Filtering: Algorithms and Practical Implementation; pp. 431–456. [Google Scholar]
- 16.Zhu X., Gao B., Zhong Y., Gu C., Choi K.S. Extended Kalman filter for online soft tissue characterization based on Hunt-Crossley contact model. J. Mech. Behav. Biomed. Mater. 2021;123:104667. doi: 10.1016/j.jmbbm.2021.104667. [DOI] [PubMed] [Google Scholar]
- 17.Hasan A., Susanto H., Tjahjono V.R., Kusdiantara R., Putri E.R.M., Hadisoemarto P., Nuraini N. 2020. A New Estimation Method for COVID-19 Time-Varying Reproduction Number Using Active Cases. arXiv preprint arXiv:2006.03766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bani Younes A., Hasan Z. COVID-19: Modeling, prediction, and control. Appl. Sci. 2020;10(11) [Google Scholar]
- 19.Korolev I. Identification and estimation of the SEIRD epidemic model for COVID-19. J. Econom. 2021;220(1):63–85. doi: 10.1016/j.jeconom.2020.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Salman A.M., Ahmed I., Mohd M.H., Jamiluddin M.S., Dheyab M.A. Scenario analysis of COVID-19 transmission dynamics in Malaysia with the possibility of reinfection and limited medical resources scenarios. Comput. Biol. Med. 2021;133:104372. doi: 10.1016/j.compbiomed.2021.104372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gelman A., Carlin J.B., Stern H.S., Dunson D.B., Vehtari A., Rubin D.B. CRC press; 2013. Bayesian Data Analysis. [Google Scholar]
- 22.Allen E. vol. 22. Springer Science & Business Media; 2007. (Modeling with Itô Stochastic Differential Equations). [Google Scholar]
- 23.Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.United Nations . Department of Economic and Social Affairs, Population Division; 2019. World Population Prospects 2019: Highlights. [Google Scholar]
- 25.World Health Organization . vol. 3. 2020. (Novel Coronavirus (2019-nCoV) Situation Reports). [Google Scholar]
- 26.Loli Piccolomini E., Zama F. Monitoring Italian COVID-19 spread by a forced SEIRD model. PloS One. 2020;15(8) doi: 10.1371/journal.pone.0237417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rao S., Singh M. An evolving public health crisis caused by the rapid spread of the SARS-CoV-2 Delta variant. DHR Proceedings. 2021;1(S4):6–8. [Google Scholar]
- 28.Chang S.L., Harding N., Zachreson C., Cliff O.M., Prokopenko M. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020;11(1) doi: 10.1038/s41467-020-19393-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kerr C.C., Stuart R.M., Mistry D., Abeysuriya R.G., Rosenfeld K., Hart G.R., Klein D.J. Covasim: an agent-based model of COVID-19 dynamics and interventions. PLoS Comput. Biol. 2021;17(7) doi: 10.1371/journal.pcbi.1009149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nouvellet P., Bhatia S., Cori A., Ainslie K.E.C., Baguelin M., Bhatt S., Boonyasiri A., Brazeau N.F., Cattarino L., Cooper L.V., Coupland H., Cucunuba Z.M., Cuomo-Dannenburg G., Dighe A., Djaafara B.A., Dorigatti I., Eales O.D., van Elsland S.L., Nascimento F.F., Donnelly C.A. Reduction in mobility and COVID-19 transmission. Nat. Commun. 2021;12(1) doi: 10.1038/s41467-021-21358-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Malkov E. Simulation of coronavirus disease 2019 (COVID-19) scenarios with possibility of reinfection. Chaos, Solit. Fractals. 2020;139:110296. doi: 10.1016/j.chaos.2020.110296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Keeling M.J., Hollingsworth T.D., Read J.M. Efficacy of contact tracing for the containment of the 2019 novel coronavirus (COVID-19) J. Epidemiol. Community. 2020;74(10):861–866. doi: 10.1136/jech-2020-214051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bickley S.J., Chan H.F., Skali A., Stadelmann D., Torgler B. How does globalization affect COVID-19 responses? Glob. Health. 2021;17(1):57. doi: 10.1186/s12992-021-00677-5. [DOI] [PMC free article] [PubMed] [Google Scholar]