Statistical Guidelines for Handling Missing Data in Traumatic Brain Injury Clinical Research

Abstract

Missing data is a persistent and unavoidable problem in even the most carefully designed traumatic brain injury (TBI) clinical research. Missing data patterns may result from participant dropout, non-compliance, technical issues, or even death. This review describes the types of missing data that are common in TBI research, and assesses the strengths and weaknesses of the statistical approaches used to draw conclusions and make clinical decisions from these data. We review recent innovations in missing values analysis (MVA), a relatively new branch of statistics, as applied to clinical TBI data. Our discussion focuses on studies from the International Traumatic Brain Injury Research (InTBIR) initiative project: Transforming Research and Clinical Knowledge in TBI (TRACK-TBI), Collaborative Research on Acute TBI in Intensive Care Medicine in Europe (CREACTIVE), and Approaches and Decisions in Acute Pediatric TBI Trial (ADAPT). In addition, using data from the TRACK-TBI pilot study (n = 586) and the completed clinical trial assessing valproate (VPA) for the treatment of post-traumatic epilepsy (n = 379) we present real-world examples of typical missing data patterns and the application of statistical techniques to mitigate the impact of missing data in order to draw sound conclusions from ongoing clinical studies.

Introduction

Traumatic brain injury (TBI) research is entering a new phase of data-intensive studies that expands the horizon for knowledge-based discovery. This special issue of the Journal of Neurotrauma focuses on data analysis and statistical concerns attendant to this era of big data, as part of the International Traumatic Brain Injury Research (InTBIR) Initiative. In this article, we focus on the issue of missing data and discuss its implications for clinical inference and outcome prediction in TBI research. Missing data is a major and largely unrecognized factor that likely helps explain imprecision in TBI research, contributing noise to outcome prediction and limiting the likelihood of sensitive and accurate detection of therapeutic efficacy in clinical trials.¹ We will discuss the brief history of missing data as a topic of statistical science, and provide a review of best practices for measuring the impact of missing data and of mitigation approaches that help ensure the robustness of statistical inferences made in the face of missing data. Using concrete examples from real-world TBI data, this review focuses on practical application of statistical methods, rather than intensive mathematics, with the goal of offering TBI researchers guidelines and best practices for dealing with missing values.

The field of missing data as a statistical problem is fairly young, having only been developed since the early 1970s, when computer programs began to help statisticians carry out complex calculations unapproachable by hand. This gave rise to a set of methods known collectively as missing values analysis (MVA). The seminal research for MVA was first described by Rubin in 1976,² followed by a comprehensive set of guidelines for application of methods for MVA in 2002.^3,4 Since its inception, MVA has been widely adopted to make sense of population statistics when portions of the data are missing.

There are only a handful of published studies discussing MVA's application to missing data specifically for TBI. Childs and coworkers attempted to describe and categorize why data were missing in TBI patients who were monitored for both brain temperature and intracranial pressure (ICP), and identified several etiologies, including sensor failures resulting from disconnections.⁵ A second article by Feng and coworkers assessed the feasibility of dealing with missing brain temperature and ICP data, focusing on the potential value of re-using old monitoring data that had previously excluded from analyses because they were not complete.⁶ A third article by Zelnick and coworkers focused on imputing outcome data as measured by the Glasgow Outcome Scale Extended (GOS-E) in order to maximize the usefulness of the GOS-E as a primary outcome even if participants dropped out.⁷ A very recent systematic review by Richter and coworkers revealed that TBI clinical research rarely addresses the issue of missing data despite the fact that missing data are common.⁸ Accordingly, the latest edition of the highly cited clinical prediction modeling textbook by Steyerberg devotes two chapters to dealing with missing data, including a general overview with references to TBI, and a chapter devoted to a case study of MVA in TBI from the International Mission for Prognosis and Analysis of Clinical Trials in TBI (IMPACT-TBI) study.^9,10 The present article complements this prior work and reviews additional approaches for dealing with missing data. In addition, we illustrate the impact of missing data using participant-level analysis of two recent TBI studies, a clinical trial of valproate (VPA) and the Transforming Research And Clinical Knowledge for TBI Pilot study (TRACK-TBI Pilot).

Here, we ask readers to imagine a scenario in which patients are enrolled in a clinical study to develop prediction models for prognosis and long-term outcome following TBI based on factors that are inherent both in an individual's pre-existing medical history, and aspects of the neurocritical care received after admission to the emergency room. Throughout the course of this study, some data are missing for nearly every patient. Common problems include loss to follow-up, comorbid conditions that prevent data collection for a specific time point, and instrumentation problems, among others. Some of these sources of missingness may be random, such as lack of follow-up data resulting from unforeseen circumstances in patients' lives. Examples of this from the TRACK-TBI Pilot study included participants who were homeless and therefore either unwilling to come in for follow-up testing, or could not be reached. Others may be systematic, such as lack of follow-up care caused by infrastructure problems at the hospital (e.g., insufficient staff coverage, equipment failures, or magnetic resonance imaging (MRI) scanner out of service ). Failure to account for the explanation of the missing data could introduce bias, limiting both the generalizability and reproducibility of the findings, and in fact, may be problematic for deriving conclusions about the primary outcomes: prognoses and long-term outcome. At the completion of the study, how should one handle the missing data? How may we assess the significant missing patterns in our study while maximizing the contribution that may otherwise be lost when patients are excluded simply because some of their data are missing?

Diagnosing Missingness and MVA

The initial steps in any approach are to analyze whether data are missing at random (MAR) or completely at random (MCAR), or, most commonly in TBI research, whether data are missing not at random (MNAR). The first incidence of missing data is flagged using the “missingness” label and coded as a binary variable (yes = 1 vs. no = 0). MCAR indicates that missingness is uncorrelated with other variables in the data set. MAR indicates that missingness is correlated with some variables, but not key variables of interest to analysis. NMAR indicates that missingness is associated with key variables (e.g., outcome). Many studies have simply described data MNAR as being “problematic,” with no clear guidelines for how to fill in the missing data patterns, other than by modeling.¹¹ More frequently, MNAR is simply overlooked and unreported.

The Little's test is a descriptive analytic tool to assess whether data are MCAR.¹² A variable (e.g., cognitive outcome) with MCAR has a pattern of missingness that is not associated with other variables (e.g., age, gender, socioeconomic status, or poor function), but is rather a random occurrence of missingness that cannot otherwise be explained. Commonly used statistical software packages, such as SPSS (IBM, Inc.), have MVA modules for determining whether the data are MCAR. To run a Little's test in SPSS, the variables of interest are selected within the missing values analysis module, and analyzed using the expectation maximization (EM) function. The resulting output will return a significance test under the EM means generated. If p < 0.05, then the data fail the Little's test and the data are not MCAR. If this is the case, some statisticians have recommended that nothing more be done to fill in the missing data patterns, and that only complete-case analyses can be used.¹³ This is potentially problematic, however, because it can introduce bias in the data set by not accounting for the reason for the missingness, and violating assumptions about the sample population being studied.¹⁴ Alternative models known as sensitivity analyses¹⁵ can be performed when data are not missing at random (NMAR), which will be discussed subsequently.

If the data are MCAR or MAR, data modeling approaches help test whether missing values impact statistical results (discussed in detail subsequently). Simple methods include t tests or logistic regression analyses on incidence of missingness to determine if variables such as early poor performance, age, gender, or education level can explain differences about whether data were collected or not. More advanced methods involve using non-missing values to predict individual missing values. Noise is added to the predicted value to avoid awarding unwarranted precision to the values. This is done multiple times, with the analyses repeated on each set; the final analysis takes into account both the individual tests and how much they differ from one another.^12,16 This enables researchers to indirectly measure the probability that missing values impact the statistical results.

Methods for Handling Missing Data for Analysis

Once missingness has been diagnosed, a number of methods exist to mitigate the impact of missing values (Table 1). Richter and coworkers put together a practical decision tree helping researchers handle missing data.⁸ Our Table 1 provides recommondations that align with this decision tree; however, we extend this prior work with examples of additional methods reviewed subsequently in detail.

Table 1.

Summary of Missing Values Analyses (MVA) Recommended for Traumatic Brain Injury (TBI) Clinical Research

Type of MVA	Assumptions	Recommended for TBI
Complete-case analysis	None	No
Partial deletion	MCAR or MAR	No
Mean or mode substitution	MCAR or MAR	No
Expectation maximization (EM)	MCAR or MAR	No
Multiple imputation (MI)	MCAR or MAR	Yes, combined with appropriate modeling through SA
Sensitivity analysis (SA)	NMAR	Yes
Inverse probability weighting (IPW)	NMAR	Yes, with appropriate modeling of confounders of missingness

MCAR, missing completely at random; MAR, missing at random; NMAR, not missing at random.

Complete-case analysis

The simplest way to analyze data that have missing values is to drop any patients who do not have the complete set of variables collected, and test the patterns of the raw data. This approach, known as “listwise deletion,” is the default for most statistical packages when researchers apply traditional analytics including regression approaches, analysis of variance, t tests, and odds-ratios tests among others. Although this type of analysis appears straightforward, it creates a biased sampling of the population based on potential latent variables or patterns that could explain the source/cause for the missing data, if the data are MAR or NMAR. Because listwise deletion is the default for most statistical analyses, it is likely that researchers are often unaware of biases introduced by complete-case analyses. This method of data analysis is not recommended for TBI clinical research, and can lead to biased and unreliable findings.

Partial deletion

Partial deletion approaches may be useful to maximize the raw data by only including variables that have the most complete data across the study population. Most statistical software packages have an option for most types of statistical tests to delete cases in either a listwise or a pairwise fashion. Listwise deletion will automatically drop patients from the analysis if they are missing one or more data points from the list of variables included in the model, whereas pairwise deletion will still include patients who may have some missing data points in the included variables. The analysis will exclude those variables when the data are missing, while still completing analysis of other variables and cases with complete data. However, partial deletion approaches make the assumption that the data are either MCAR or MAR and does not apply for data that are NMAR.

Mean and mode substitution

Other methods involve replacing missing values based on observed values; for example, using mean or mode substitution. The reliability of these methods to accurately model the missing data is questionable, as they may skew the data if the values that are missing do not truly fall within the same distribution of the group mean or mode of the variable. This type of method does not rely on the relationships in the covariance matrix of the existing data patterns, but rather replaces any missing values within each variable with either the mean or mode value for that variable. This is problematic for the following reasons.

Here, we ask readers to imagine that there are data missing on the same 6-month outcome measure—the Wechsler Adult Intelligence Scale (WAIS)—from two different patients for different reasons. One of the patients may not have data because that individual was so low functioning as to be unable to perform the WAIS assessment, and, therefore, no data were collected. The other patient may have been so high functioning that the individual had no interest in returning for follow-up assessment and therefore also does not have WAIS data collected. If only the data within WAIS are taken into account when filling in the missing data, either based on the mean or the mode, both patients would get the same score, despite that had their data been collected, they would have scored very differently from each other.

Multiple imputation (MI)

When it is determined that the data are MCAR or MAR, EM can be used for a partial imputation of the data. The benefit of a more rigorous approach, known as MI, is that missing values are replaced with data based on the known relationships that exist in the completed data. These relationships are then used to make assumptions about how specific patients would score on the missing measures, compared with how the patient population performed collectively.

As noted, EM is a method that iterates through the data to find the maximum likelihood estimation that can estimate the parameters of a statistical model, given specific observations in the data. This method assumes that unobserved latent variables are in the model, and the combination of expectation and maximization of the log-likelihood is used to derive the latent variable distribution (e.g., the missing data). However, if a complete imputation is desired, MI can be performed to fill in missing information in order to boost the analytical sample size. Investigators may then potentially infer what value the missing data may have.

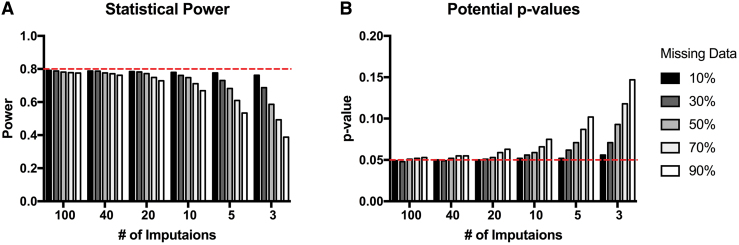
Previous recommendations for multiple imputation originally described by Rubin⁴ suggested that approximately three to five imputations are sufficient in order to fill in missing data. Although imputing data with only three to five iterations may not change the sample mean or standard error and the general inferences that can be drawn from the imputed results, others have suggested that if effect sizes in the data set are low, having fewer total imputations runs the risk of decreasing the statistical power of the analyses, and therefore reducing the ability to detect statistical significance between groups.¹⁷ Additionally, the proportion of missing data is a factor in deciding how many imputations to use to maximize efficiency and yield accurate inferences for power and effect sizes. Monte Carlo simulations were performed by Graham and colleagues¹⁷ to estimate the appropriate number of imputations needed, based on the proportion of missing data, to yield results approaching the power that the study would have were there no missing data (Fig. 1). Theoretically, it is possible to include data that are missing at high percentages of the total data, but in order to maximize power, the number of necessary imputations increases according to the amount of data missing. Multi-level modeling approaches such as modern linear mixed-effect models provide mechanisms to extend imputation to multi-level nested designs, in which missingness may occur in the pattern of higher-order interactions. A full review of these methods is beyond the scope of the present review, but we refer interested readers to prior work by Goldstein and colleagues.¹⁸ Similarly, advanced methods exist to assess latent trajectory classes in time series data that apply mixture modeling to missingness in time series data, and these approaches have recently been applied to TBI outcomes.¹⁹ Extended discussion of these approaches is beyond the scope of the current review, but we refer interested readers to prior work.²⁰

FIG. 1.

Monte Carlo simulations for number of imputations needed to maximize effect sizes based on percentages of missing data (adapted from Graham and coworkers¹⁷). Color image is available online.

Sensitivity analyses

Sensitivity analysis is an in silico method used in clinical trials to assess whether certain aspects of the study results can be altered simply by arbitrarily changing a single parameter of the experimental design.¹⁵ For example, here we ask readers to consider a hypothetical TBI study that finds that hyperthermia produces worse outcome, while controlling for common covariates such as sex. Sensitivity analysis may involve statistically correcting for sex, and assessing whether this dramatically alters the pattern of significance. If sensitivity analysis reveals that the sex covariate dramatically changes the observed relationship, this would suggest that the results are highly sensitive to the sex variable and may not generalize to another population with a different distribution of males versus females.

A similar method is useful when there may be biases as to why data are missing. Here, sensitivity analysis involves using a mixture modeling approach to compare data distributions when data are missing and non-missing. First, variables are imputed using the MAR assumption by applying machine learning tools such as EM or regression modeling to estimate and fill in missing data points.³ Then, the data distributions and descriptive statistics for significant differences between the raw, unimputed data set and the imputed data set^2–4 are tested. Significant differences between imputed and non-imputed data sets indicate that missing data cannot be ignored, establishing that they are NMAR. This analysis can be expanded by introducing variables affected by imputation as covariates to test their impact as candidate NMAR mechanisms and establish the threshold at which data cannot be imputed. In TBI, for example, if blood pressure has a significant impact on functional recovery, but blood pressure data are known to be NMAR, a model can be developed to determine the threshold at which blood pressure data can be imputed that both doesn't significantly change the data distributions and maintains precision in outcome prediction. The Multivariate Imputation by Chained Equations (MICE) package in R can be used for these purposes, where mulitiple imputation can be nested within a sensitivity analysis to test for these sensitivity thresholds when performing MI.^21,22 Unfortunately, the results of these types of analyses are not prominently reported in medical journals in general, and even less so in randomized controlled clinical trials.¹⁵ However, multiple experts in the field of MVA agree that when data are NMAR, which is the case in most clinical trials and research, performing sensitivity analysis is crucial to reduce unintended bias.²³ This procedure can be implemented in combination with MI, provided that the influence of the missing data and its source can be accurately modeled.^24,25

Inverse probability weighting

Inverse probability weighting allows inverse weighting to be applied to certain patients in the data set who are skewing results because of missingness and/or dropout. If the source of the missing or confounding data is known, it can be used to weight the data similarly to regression analyses to remove the influence on the study results.^26,27 This is also similar to sensitivity analysis. These approaches look at confounding when comparing groups that differ in incidence of missingness, and the missingness is related to both group assignment and outcome (i.e., NMAR).

Practical Application of MVA to Real-World TBI Participant-Level Clinical Research Data

Although the modeling approaches we recommend (sensitivity analysis, inverse probability weighting, and, to a lesser extent, multiple imputation) may be applied post hoc, the optimal method, described subsequently, is to provide detailed codes regarding why data is missing at each stage of the study so that they can be included in statistical models that aim to account for the impact that the missing confounders have on outcome.

In this section, we present data from real-world examples of missing values analysis applied in the context of past and ongoing TBI clinical studies. We first explore missing data patterns in the TRACK-TBI Pilot study,²⁸ in which the cause of missing data patterns was not known. The second example tests hypotheses about the potential causes of missing data in the completed clinical trial assessing VPA for the treatment of post-traumatic epilepsy,²⁹ in which similar outcomes were collected and specific coding was included in the study design to account for why data were not collected for each patient at each phase of the study.

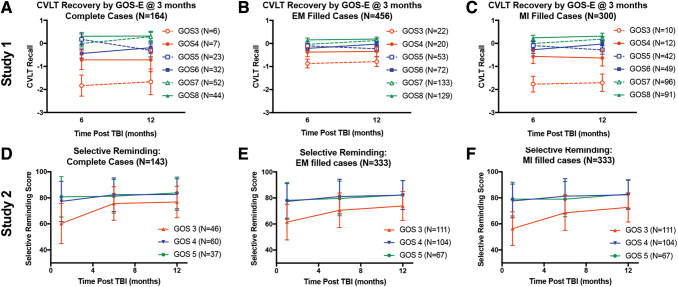
Figure 2 shows how patients recover on measures of verbal learning either measured by the California Verbal Learning Task (CVLT) in the TRACK-TBI Pilot study, or the Selective Reminding Task in the VPA study, blocked by their initial score on the GOS or GOS-E in the TRACK-TBI Pilot. Patients are also grouped based on changes in GOS(E) over the course of each study. There is a similar pattern of recovery between the two studies, providing a rationale for potential conclusions to be drawn about patient recovery, and potential sources of missingness. For this analysis of neurocognitive outcomes, we limited the analysis to GOS(E) scores beyond persistent vegetative state (GOS[E] >2). Comparisons are shown in Figure 2 for how these recovery curves differ between either complete case analysis (Fig. 2A,D), EM-filled data (Fig. 2B,E), or MI-filled data (Fig. 2C,F). The results demonstrate important features of missing values analysis: (1) the method used to impute data can have a large potential impact on the estimated variance as well as the estimated means (Fig.2B vs. Fig.2C), and (2) multiple imputation can recapitulate fundamental patterns in raw data while reducing error variance, which has the potential to boost statistical power (Fig.2A vs. 2C). However, the findings also raise cautionary points. By compairing the percent missing (Fig. 3) with the filled case analysis (Fig.2C, F) it is clear that EM and MI approaches assigned values for some patients who were untestable for central nervous system (CNS) reasons (or death). In this sense, the MI glossed over the poor functioning of this subset of subjects. Indeed, the primary authors of Study 2 report that if the examiners gave the word list and waited a minute for the person to respond, most of the GOS 3s who were untestable for CNS reasons would have recalled none of the words and recieved a score of 0. It is worth mentioning that the original analysis of this study assigned 1 (CNS) or 2 (Death) points less than the worst observed score, to acknowledge the poor functional level of these patients, and ranked analysis was used. This reflects a powerful alternative approach for handling missing data, which reflects deep domain knowledge and a priori planning for handling missing data at the study design stage.

FIG. 2.

Recovery curves for cognitive function as measured by verbal learning tasks grouped by first reported measure of Glasgow Outcome Scale (GOS). (A–C) Top row are data from Study 1 (Transforming Research and Clinical Knowledge in Traumatic Brain Injury [TRACK-TBI] pilot) assessing neuropsychological testing measured by the California Verbal Learning Task (CVLT) normative data, blocked by their first GOS-Extended (GOS-E) rating at 3 months post-TBI, looking at either complete case analysis (A), or with missing data filled in by either expectation maximization (EM) (B), or multiple imputation (MI) (C). The bottom row are data from Study 2 (valproate [VPA]) using similar outcomes, in which the verbal learning was assessed using a Selective Reminding task and an older version of the GOS in which functional deficits were previously grouped into single categories for mild (green), moderate (blue), and severe (red) disability, with similar comparisons across complete case analysis (D), or EM-filled (E) or MI-filled (F) data sets. Color image is available online.

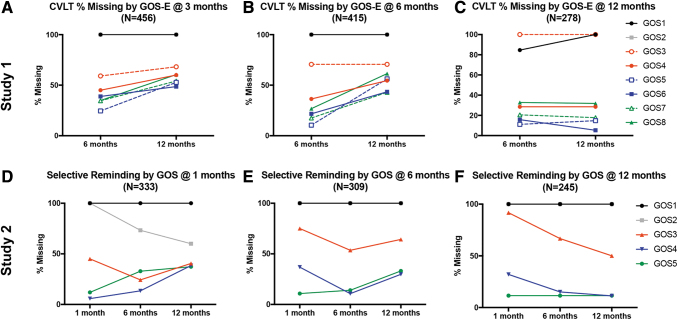
FIG. 3.

Missing data patterns for verbal learning tasks blocked by Glasgow Outcome Scale (Extended) (GOS[E]) score at each of the three time points for each study. (A–C) Percent of missing data for the California Verbal Learning Task (CVLT) in study 1 (Transforming Research and Clinical Knowledge in Traumatic Brain Injury [TRACK-TBI) Pilot) between 6 and 12 months based on GOS-E scores at either 3 months (A), 6 months (B), or 12 months (C) post-TBI. (D–F) Percent of missing data for Selective Reminding in study 2 (valproate [VPA]) among 1, 6, and 12-months post-TBI based on GOS scores at those same time points. Patients with less disability (green lines) show a marked increase in missing data at the final time point when blocked by their GOS(E) at 1, 3, or 6 months, with a flat line at the 12-month mark indicating that the higher functioning patients did not have data for the final time point. Also of note are the black and gray lines that represent patients who either died (GOS[E] 1) or were in a vegetative state (GOS[E] 2) before the first time point and therefore show no change in missing data over time, with the exception of more data being collected over time for patients starting out at a GOS score of 2 at 1 month, and presumably improving and therefore being able to have Selective Reminding assessed. +GOS scores 3, 4, and 5 are an older version of the GOS-E, where 3/4, 5/6, and 7/8 have since been extended, respectively. Color image is available online.

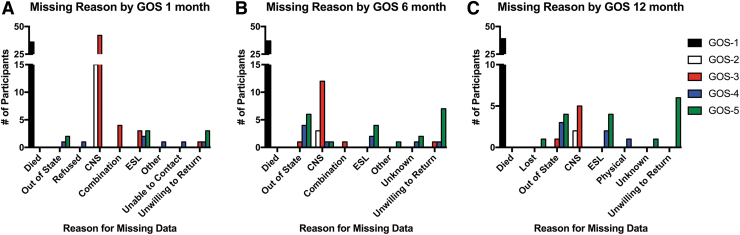
Figure 3 shows the proportion of missing data at each time point for each study on the verbal learning task data blocked again by disability severity measured on the GOS(E). Again, we see similar patterns between the two studies, suggesting that we may be able to make predictions about the cause of missing data in the TRACK-TBI Pilot that were not specifically coded, as was done in the VPA study. This is explored in Figure 4, where specific codes were documented regarding the reason for missing data on the Selective Reminding task at each phase of the study. Reasons included death, inability to perform the task because of either physical or CNS complications, being unreachable or unwilling to return for follow-up, and English being a second language (ESL), thus preventing subjects from accurately performing the task in English. The studies' similar patterns for recovery curves and rates of missing data from global disability and verbal learning measures may permit us to retrospectively perform sensitivity analyses on the TRACK-TBI Pilot data to more accurately model the confounding factors contributing to missing data patterns and, in turn, help fill in missing data. Examples include assumptions about patients with a higher score on the GOS-E (7 or 8) presumably performing very well on the CVLT at 6 and 12 months when data are otherwise missing because patients are unwilling to return for follow-up. Conversely, lower scores on the GOS-E (3 or 4) may include assumptions about poor performance resulting from underlying brain pathology causing CNS complications so severe that the patients are unable to perform the task, providing more information about the pathophysiology of their injuries.

FIG. 4.

Study 2 (valproate [VPA]) had codes for the reason for the missing data measured at 1 month (A), 6 months (B), and 12 months (C) to confirm hypotheses about why outcome data were missing for different groups of patients in the Transforming Research and Clinical Knowledge in Traumatic Brain Injury (TRACK-TBI) Pilot, blocked by Glasgow Outcome Scale (GOS) severity. As expected, patients from the VPA study who were higher functioning (green) were less likely to participate in follow-up care, potentially a as a result of a lack of interest in staying in the study because they did not have a measurable disability. Whereas patients with severe disability (red) were more likely to have missing data because of central nervous system (CNS) problems preventing them from performing the task. Patients who started in a vegetative state (white) at 1 month generally could not be assessed because of CNS complications, with, presumably, patients moving to either the red category (out of a vegetative state, severe disability), or into the black category (dead). Color image is available online.

Conclusion

In conclusion, careful attention to TBI trial design to prevent, as far as possible, missing data from occurring, is ideal, but planning ahead with detailed coding protocols to account for the reasons for missingness acknowledges and mitigates the reality of human research. When possible, sensitivity analysis should be conducted to account for confounding factors that are contributing to the missing data and thus impacting outcome. Being able to specifically label why data are missing allows that information to be included in the statistical models where confounding variables can be corrected for, and additional meaningful sources of missingness can be considered as their own outcomes. This is particularly so when they affect patients' ability to be helped or harmed by their treatment and participation in the research.²³ As with TBI clinical care, prevention is the key to future success.

TRACK-TBI Investigators

Opeolu Adeoye, University of Cincinnati; Neeraj Badjatia, University of Maryland; Kim Boase, University of Washington; Yelena Bodien, Massachusetts General Hospital; M. Ross Bullock, University of Miami; Randall Chesnut, University of Washington; John D. Corrigan, Ohio State University; Karen Crawford, University of Southern California; Ramon Diaz-Arrastia, University of Pennsylvania; Sureyya Dikmen, University of Washington; Ann-Christine Duhaime, MassGeneral Hospital for Children; Richard Ellenbogen, University of Washington; V Ramana Feeser, Virginia Commonwealth University; Adam R. Ferguson, University of California, San Francisco; Brandon Foreman, University of Cincinnati; Raquel Gardner, University of California, San Francisco; Etienne Gaudette, University of Southern California; Joseph Giacino, Spaulding Rehabilitation Hospital; Dana Goldman, University of Southern California; Luis Gonzalez, TIRR Memorial Hermann; Shankar Gopinath, Baylor College of Medicine; Rao Gullapalli, University of Maryland; J Claude Hemphill, University of California, San Francisco; Gillian Hotz, University of Miami; Sonia Jain, University of California, San Diego; Frederick K. Korley, University of Michigan; Joel Kramer, University of California, San Francisco; Natalie Kreitzer, University of Cincinnati; Harvey Levin, Baylor College of Medicine; Chris Lindsell, Vanderbilt University; Joan Machamer, University of Washington; Christopher Madden, UT Southwestern; Geoffrey T. Manley, University of California, San Francisco; Alastair Martin, University of California, San Francisco; Thomas McAllister, Indiana University; Michael McCrea, Medical College of Wisconsin; Randall Merchant, Virginia Commonwealth University; Pratik Mukherjee, University of California, San Francisco; Lindsay Nelson, Medical College of Wisconsin; Laura B. Ngwenya, University of Cincinnati; Florence Noel, Baylor College of Medicine; David Okonkwo, University of Pittsburgh; Eva Palacios, University of California, San Francisco; Daniel Perl, Uniformed Services University; Ava Puccio, University of Pittsburgh; Miri Rabinowitz, University of Pittsburgh; Claudia Robertson, Baylor College of Medicine; Jonathan Rosand, Massachusetts General Hospital; Angelle Sander, Baylor College of Medicine; Gabriella Satris, University of California, San Francisco; David Schnyer, UT Austin; Seth Seabury, University of Southern California; Mark Sherer, TIRR Memorial Hermann; Murray Stein, University of California, San Diego; Sabrina Taylor, University of California, San Francisco; Nancy Temkin, University of Washington; Arthur Toga, University of Southern California; Alex Valadka, Virginia Commonwealth University; Mary Vassar, University of California, San Francisco; Paul Vespa, University of California, Los Angeles; Kevin Wang, University of Florida; John K. Yue, University of California, San Francisco; Esther Yuh, University of California, San Francisco; Ross Zafonte, Harvard Medical School.

Funding Information

This work was supported by: Department of Defense (DoD) grants W81XWH-13-1-0441 (G.T.M.), W81XWH-14-2-0176 (N.R.T.), National Institutes of Health/National Institute of Neurological Disorders and Stroke (NIH/NINDS) grants NS069409 (G.T.M.), NS069409-02S1 (G.T.M.), NS106899 (A.R.F.), NS088475 (A.R.F.), MH116156 (J.L.N.), and CTSA UL1 TR002494.

Author Disclosure Statement

No competing financial interests exist.