Satellite data and machine learning reveal a significant correlation between NO₂ and COVID-19 mortality

Abstract

The Coronavirus disease 2019 (COVID-19) pandemic has officially spread all over the world since the beginning of 2020. Although huge efforts are addressed by scientists to shed light over the several questions raised by the novel SARS-CoV-2 virus, many aspects need to be clarified, yet. In particular, several studies have pointed out significant variations between countries in per-capita mortality. In this work, we investigated the association between COVID-19 mortality with climate variables and air pollution throughout European countries using the satellite remote sensing images provided by the Sentinel-5p mission. We analyzed data collected for two years of observations and extracted the concentrations of several pollutants; we used these measurements to feed a Random Forest regression. We performed a cross-validation analysis to assess the robustness of the model and compared several regression strategies. Our findings reveal a significant statistical association between air pollution (NO₂) and COVID-19 mortality and a significant role played by the socio-demographic features, like the number of nurses or the hospital beds and the gross domestic product per capita.

1. Introduction

The novel coronavirus SARS-CoV-2 is responsible of the pandemic disease, named Coronavirus disease 2019 (COVID-19), which has rapidly spread throughout the world since its first identification in December 2019 in Wuhan, China (Zhu et al., 2020). By February 2020, the diffusion of the virus to all the globe has manifestly shown its pandemic behavior (Phan et al., 2020; Chinazzi et al., 2020; Lu et al., 2020; Onder et al., 2020), until on March 11, 2020 the World Health Organization (WHO) officially declared the pandemic (Cucinotta and Vanelli, 2020).

Several clinical and demographic factors affecting the COVID-19 mortality have been thoroughly investigated (Ji et al., 2020; Dietz and Santos-Burgoa, 2020; Promislow, 2020; Baud et al., 2020; Leffler et al., 2020); in particular, many studies have addressed the sources of variation between countries in per-capita mortality due to environmental factors, such as temperature and humidity (Ma et al., 2020), meteorological factors (Sarkodie and Owusu, 2020), air quality (Setti et al., 2020a).

The role of pollutants in easing the virus diffusion or increasing its severity after prolonged exposure has been independently confirmed from many studies (Setti et al., 2020b; Berman and Ebisu, 2020; Comunian et al., 2020; Azuma et al., 2020; Gatti et al., 2020). Nonetheless, these studies have analyzed limited regions, usually not exceeding national boundaries, and often focused on retrospective considerations such as the impact of lockdown on pollution levels (Yao et al., 2020; Adams, 2020; Li et al., 2020; Metya et al., 2020) more than the assessment of an association between the presence of high levels of pollution and an increased severity of the disease and its effects.

The prolonged exposure to fine particulate matter has been statistically associated with COVID-19 mortality by several studies (Wu et al., 2020a; Setti et al., 2020a; Marquès et al., 2020; Becchetti et al., 2020). In general, two different perspectives arise: on the one hand, some studies emphasize the statistical association between pollution exposure and COVID-19 mortality as a matter of causal inference; on the other hand, other studies explore the possibility for pollutants to be effective vectors of contagion and therefore attempt to explain the increase in mortality and severity in terms of dynamics.

A major issue discouraging the investigation of the relationships between pollution and COVID-19 severity is the difficulty to collect a sufficiently robust base of knowledge based on on-ground measurements. However, thanks to remote sensing imagery and specifically thanks to the satellite Sentinel-5 Precursor (S-5p) (Veefkind et al., 2012) it is possible to find a workaround, at least for some specific pollutants. In fact, thanks to the TROPOspheric Monitoring Instrument (TROPOMI) spectrometer, the S-5p missions allow the observation of key atmospheric constituents, such as ozone (O₃), nitrogen dioxide (NO₂), carbon monoxide (CO), sulfur dioxide (SO₂), methane (CH₄), formaldehyde (CH₂O), aerosols and clouds. Although, the S-5p worldwide coverage allows the investigation of pollutants’ concentrations through the whole globe, this study focuses on the European region, which provides a roughly homogeneous area for geographic, climatic and socio-economic features, therefore excluding factors which could potentially blur the association between pollutants and COVID-19 mortality.

Thus, in this work, we collected and analyzed the data acquired by S-5p missions since June 2018 to feed a regression model explaining the variation of COVID-19 mortality throughout all European countries; in particular our analysis focused on administrative regions of about 50–70, 000 km² The main goal of this work was the assessment of a (significant) statistical association between pollution and COVID mortality. A not secondary aspect of this work was identifying and evaluate the role played by the different features in this association. In particular, we evaluated to which extent pollutants are relevant in increasing the pandemic severity. Our findings reveal that the differences in pollution levels can explain the observed differences in mortality on the continental scale and the major role is played by NO₂.

2. Materials

The Copernicus S-5p mission is the first Copernicus mission dedicated to the monitoring of the Earth's atmosphere and, specifically, air quality, climate and the ozone layer in the timeframe 2015–2022. S-5p is the result of the collaboration between ESA, the European Commission, the Netherlands Space Office, industry, data users and scientists. The satellite's single payload instrument is the TROPOMI spectrometer, which, thanks to its wide field-of-view (~ 2600 km), allows a daily coverage of the globe. The TROPOMI four different detectors provide high resolution (typically 7 × 7 km²) spectral measurements of eight distinct bands in the ultraviolet (UV), visible (VIS), near infrared (NIR) and shortwave-infrared (SWIR) range, see Table 1 .

Table 1.

Main characteristics of S-5p acquisition bands.

Detector	UV		VIS		NIR		SWIR
Band	1	2	3	4	5	6	7
Range (nm)	270–300	300–320	310–405	405–500	675–725	725–775	2305–2385
Resolution (nm)	1	0.5	0.55	0.55	0.5	0.5	0.25
Spatial Sampling (km2)	21 × 28	7 × 7	7 × 7	7 × 7	7 × 7	7 × 7a	7 × 7

^aThis resolution can be reduced to 1.8 × 1.8 km².

The information provided by the spectral bands yields the estimation of concentrations for several pollutants. For the purposes of the present study which aims at investigating the association between pollution and COVID-19 mortality, only the concentrations of O₃, NO₂, CO, CH₄ SO₂, aerosol, CH₂O and Cloud were considered. Besides, thanks to the European Centre for Medium-Range Weather (ECMRW) data which produces the ECMWF Re-Analysis (ERA), we obtained a thorough coverage of climatic variables across Europe since 1979. Currently, the fifth generation ECMWF reanalysis, called ERA5, provides an horizontal resolution (~ 51 km) and an hourly estimation, among the most significant improvements compared to previous releases (Hersbach et al., 2020). In this study, among ERA5 measures we considered only AH_2m.

From the daily coverage, we retrieved the mean values for the concentrations of the selected pollutants. Furthermore, it is worth noting that, given the spatial sampling properties of S-5p, countries with tiny geographical extensions (below 50 km²) had to be excluded from this study. A comprehensive overview is provided in Table 2 .

Table 2.

Outline of the features investigated in this study.

Variable Type	Symbol/Acronym	Description
Pollution	NO2 (mol/m2)	Tropospheric vertical column of NO2
	SO2 (mol/m2)	Tropospheric vertical column of SO2
	CO (mol/m2)	Vertically integrated CO column density
	HCHO (mol/m2)	Tropospheric HCHO column number density
	AER AI	Prevalence of coarse aerosols in the atmosphere
Climate	AH2m (Kg/m3)	Absolute humidity at 2 m height
	Cloud	Retrieved effective radiometric cloud fraction
Socio-Demographic	Life expectancy (yr)	Life expectancy at birth
	GDP per capita ($)	Gross domestic product per capita in US dollars
	ESCH (yr)	Expected years of schooling of child aged 6
	MSCH (yr)	Mean years of schooling of population aged 25 and older
	Pop	Population
	max(d)	Max population density
	avg(d)	Average population density
	First death	First death by COVID-19
	Age-70	Share of people aged 70 and older
	Beds	Hospital beds per thousand of inhabitants
	Smoke	Share of smokers
	Diabetes	Share of people affected by diabetes
	Nurses	Nurses per thousand of inhabitants
	Phys	Physicians per thousand of inhabitants

Data about COVID-19 mortality were collected from the Joint Research Centre (JRC) (https://github.com/ec-jrc/COVID-19). The website provides a monitoring in the European area of sub-national data (administrative level-1 regions which represent the largest administrative subdivision of a country) in terms of COVID-19 fatalities for million of inhabitants; these data are directly collected from National Authoritative sources. Along with mortality data, we collected the date of the recorded first deaths, a useful information to normalize the epidemic diffusion from a temporal perspective. Finally, social and economic data were collected from online repositories last accessed in December 2020. Specifically, through the Global Data Lab1 we obtained socio-economic data like life expectancy and gross domestic product; from the Google Cloud Platform2 we accessed other socio-economic data like the number of nurses and physicians; finally, we collected COVID-19 data from a dedicated github initiative3 We obtained a full description in terms of the considered variables for 202 regions.

Each administrative region was represented by 21 features, the aforementioned variables, and 1 target variable, the mortality, thus resulting in a 202 × 22 data matrix.

3. Methods

3.1. Methodological overview

The main goal of this study is to evaluate the existence of a statistical association between the exposure to pollutants and COVID-19 mortality. For this purpose, we collected three distinct types of data, pollutants’ concentrations were retrieved from S-5p data, climatic data were collected from ERA5 while data characterizing the socio-economic context, including COVID-19 mortality were collected from several online repositories which on their turn gathered the data officially released from National authorities. Thus, the whole dataset was exploited through a learning framework to evaluate the statistical association between COVID-19 mortality and the collected variables. We investigated several multivariate regression models, such as Random Forests (RF), Multi-Layer Perceptron (MLP), Support Vector Machine (SVM) and a simple linear regression (LR) model. From the comparison of these models we were able to assess the statistical association between pollutants and COVID-19 mortality, to which extent this association was independent from the adopted model and which features were the most important in predicting the outcome variable. Furthermore, extensive sensitivity analyses were performed to ensure the robustness of the models. An overview of the study is presented in Fig. 1 .

Fig. 1.

Schematic flowchart of the proposed procedure. Three different data sources are explored. These data are processed to obtain a spatial map of administrative level-1 regions, the case of an Italian region (Lombardy) is shown. Finally, a regression model evaluates the association between COVID-19 mortality and pollutants.

In the following paragraphs, a detailed description of all procedures (preprocessing, temporal averaging for pollution exposure, spatial normalisation and learning) is presented.

3.2. Preprocessing and flowchart

In this work, we exploited a base of knowledge consisting of three distinct pillars: pollutants’ concentrations, climatic variables, socio-demographic descriptors in order to provide a quantitative framework for the assessment of COVID-19 impact, measured in terms of registered deaths per million of inhabitants.

Firstly, we collected data about pollutants’ concentrations and climatic variables from Google App Engine (Gorelick et al., 2017), in particular we computed their yearly averages for a simple but effective denoising. The socio-demographic descriptors, instead, were downloaded from the previously mentioned online repositories in a data-table format. We collected data related to the latest year available, in general 2017–2020. Finally, we collected the time series of COVID-19 deaths per million of inhabitants for all available administrative units of the countries adhering to the JRC. Our data are updated until 21 November 2020. Thus, preliminar preprocessing and data harmonization were performed before regression analyses.

The yearly average pollutants’ concentrations and the meteorological data were downloaded from Google App Engine in raster format. The concentrations were obtained from the collections of Offline Sentinel-5p L3 products acquired over Europe during the year 2019. These data were merged into one large mosaic. The Sentinel-5p outcomes are acquired along different directions, so that the grids of two distinct Sentinel-5p products usually has two different orientations. Therefore, it was necessary to spatially normalize the data using a unique regular grid. We built the new grid by area-averaging within each pixel the values of original pixels overlapping. Climatic variables downloaded from Google App Engine underwent an analogous preprocessing, see Fig. 2 for an example about humidity.

Fig. 2.

Absolute humidity over Europe; January 1 – December 2019.

Once the data were spatially normalized, we estimated the yearly exposure to pollutants by clipping each average raster by the administrative boundaries and then computing the spatial average weighted by the NASA density population layer. Accordingly, we estimated the values of each climatic variables within an administrative region.

Next, we included the socio-demographic and COVID-19 mortality data to the features describing each administrative region. These data, already in a tabular format, did not require a specific preprocessing or a harmonization technique. Finally, before the learning phase, (i) we cleaned our data from missing values (each missing entry was replaced using the median value of that feature) and (ii) we explored the pairwise Pearson's correlation among the considered features to exclude the presence of correlated variables.

3.3. Regression models and feature importance

Several studies have attempted to model and evaluate the association between COVID-19 mortality and pollution exposure. Although, there are no guarantees that the variables employed in such studies were independent and, more importantly, there is no evidence that the relationships between these variables had to be linear, the vast majority of proposed models were linear. On the contrary, we refuse here any a priori assumptions about the data and, therefore, we consider a more general approach which is Random Forests (RF) regression (Breiman, 2001). RF exploits an internal cross-validation to avoid biased estimates; thanks to this, RF tend to be generally robust with performance unaffected by over-training issues.

It is demonstrated that the accuracy of RF models substantially depends on two parameters, the number of sampled features f and the number of the forest trees. Accordingly, RF is probably the simplest non-linear model in terms of hyperparameters to be tuned and one of the most efficient in terms of computational requirements. In this work we adopted the R 3.6.2 implementation with a standard configuration (500 trees and one third of features for each random split).

However, the most striking advantage is undoubtedly the possibility to use out-of-bag estimates to assess the importance of each feature. In this study, we aim at providing a quantitative evaluation of both (i) the association between COVID-19 mortality and pollution exposure and (ii) the influence of each feature of the model in driving the pandemics or aggravating its effects. RF models can evaluate and rank the importance of each feature in terms of two distinct metrics: mean decrease accuracy and Gini index.

Mean decrease accuracy (MDA) measures how the regression performance changes if a specific feature is removed from the model. Gini index evaluates the nodal purity (in the case of regression using the residual sum of square). The latter is not recommended for mixed models, i.e. including both discrete and continuous variables (Strobl et al., 2007); accordingly, in this study we used MDA values for feature importance.

A standard least-squares linear regression approach or linear model (LM) was employed. It assumes a Gaussian distribution of the dependent variable and a linear relationship between the input variables and the output variable. Linear regression was developed in the field of statistics and was studied as a model for understanding the relationship between input and output numerical variables. It gained popularity due to its simplicity, however it may suffer when dealing with moderate to high multi-collinearity in data.

For further comparison, we evaluated the results of other machine learning approaches, namely support vector machines (SVMs) and Multi-layer Perceptrons (MLPs). SVMs are learning algorithms (Cortes and Vapnik, 1995) which can be proficiently used with non-linearly separable observations, provided the existence of a higher dimensional space where linear separation can be achieved with a suitable kernel function. Geometrically determining a separation hyperplane is equivalent to determining a number of observations, called support vectors, best representing the classes of the problem. In this study, the e1071 (v.1.7 − 3) R package was used (Meyer et al., 2019). A radial basis function kernel with the default configuration C = 1 and γ = 1/M was adopted, where M is the number of input features.

MLPs are instead composed by three basic structures: an input layer fed by the features, hidden inner layers combining the output vectors of previous layers with linear combinations and a final output layer which yields the classification result. During the training phase, a backpropagation algorithm (Le Cun, 1986; Hecht-Nielsen, 1992; Rumelhart et al., 1986) measures the classification error according to the given nodal weights and rearrange the weights in order to minimize the error. In this study, the h2o package R implementation (v.3.28.0.4) of MLP was used (LeDell et al., 2020). In this study, a simple architecture with one hidden layer and 7 neurons (one third of input features) was employed; for the sake of simplicity, no regularization or dropout were considered. For the activation function we adopted the basic choice offered by a Rectified Linear Unit (ReLu).

3.4. Performance evaluation

To evaluate the performance of the RF regression we adopted two metrics: Pearson's correlation (r)

$$r=\frac{{\sum }_{i=1}^N(y_i-\overline{y})({\widehat{y}}_i-\overline{\widehat{y}})}{\sqrt{{\sum }_{i=1}^N{(y_i-\overline{y})}^2{\sum }_{j=1}^N{({\widehat{y}}_i-\overline{\widehat{y}})}^2}}$$ (1)

and Mean Absolute Logarithmic Error (MALE)

$$MALE=\frac{1}{N}\sum _{i=1}^N\left|{\log }_{10}\left(\frac{y_i}{{\widehat{y}}_i}\right)\right|$$ (2)

where y _i and ${\widehat{y}}_i$ are the actual mortality and its RF prediction; $\overline{y}$, $\overline{\widehat{y}}$ their averages and N the available observations.

As previously explained, RF models generally ensure a robust performance evaluation thanks to their internal validation. Nevertheless, we adopted a 5−fold cross-validation framework to further strengthen the robustness of our estimates and minimize overfitting issues, in fact, a rigorous application of cross-validation is important to minimize the bias affecting the model performance (Maggipinto et al., 2017). Accordingly, we randomly divided the data in training (80%) and validation (20%) sets; the procedure was repeated 5000 times to ensure a sufficient statistical power.

3.5. Feature importance

Feature selection strategies are usually employed for data reduction purposes; reducing the data dimensionality also reduces the computational burden of machine learning algorithms and, in some cases, can improve the model performance. Another important aspect, which becomes of fundamental importance in this case, concerns the possibility to distinguish which variables are significantly related to the target variable.

Although one of the main advantages of RF is the mentioned possibility to measure and rank the features according to their importance, this measure provides continuous values which, unless special situations do, cannot distinguish between variables statistically associated or not to the target.

Several approaches have been proposed; they can be generally divided into three categories (Tangaro et al., 2015): filter, wrapper and embedded methods. Filter methods are generally univariate approaches which explore the existing relationship between features and target variables, an example generally adopted in regression is Pearson's correlation. The weakness of univariate filter approaches is that they cannot account for multivariate relationships; it is not uncommon that two features which singularly taken provide a poor association with the target when combined can account for significant effects (Duda et al., 1973).

Wrapper and embedded methods exploit a learning model (both for classification and regression) to assess the importance of available features. The main difference is that in embedded methods classification is performed internally, e.g. RF. Boruta (Kursa and Rudnicki, 2010) is a wrapper method whose basic idea relies in comparing the importance of a feature with unimportant features, called shadow features. A model is fed with a subset of features, based on its performance it is possible to add or remove features from the subset until an optimal set is defined. Among wrapper methods, Boruta main advantages are that (i) it can find the subset of all the relevant input variable for a given regression task without requiring any a priori discrimination threshold and (ii) it provides a measure of statistical significance for the adopted features.

Boruta consists of the following 4 main steps:

• 1.Random shuffled copies of the available features, called shadow features, are created;
• 2.A RF is trained and the importance of each feature is computed;
• 3.It is checked whether a real feature is more important or not than the most important shadow feature, accordingly it is kept or removed;
• 4.Iterations are repeated until importance is assigned to all features or the algorithm has reached a previously set limit of iterations.

In Boruta algorithm, features do not compete among themselves but they compete with randomized variables, which, by definition, cannot be considered “important”.

4. Results

4.1. Correlation analysis

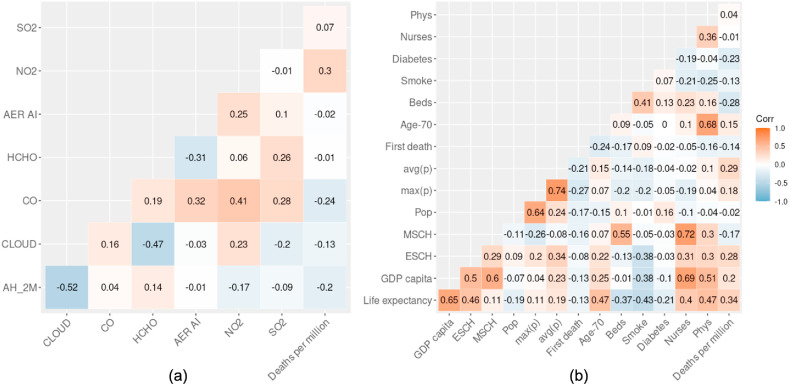
Before examining the accuracy our model and assessing the statistical association between pollutants' concentrations and COVID-19 mortality, we performed a correlation analysis to exclude the presence of strong correlations between the variables included in the model. Firstly, we evaluated the correlations among pollutants’ concentrations retrieved from remote sensing data, see the panel (a) of Fig. 3 .

Fig. 3.

Correlation matrices for socio-demographic, climate and pollution features and COVID-19 mortality.

In absolute terms, we observed the highest correlation r between humidity and cloud fraction, in fact these variables were anti-correlated (r = −0.52). We judged that the observed correlations were not preventing the use of any of these variables. Accordingly, we kept all the pollution variables within the model. Analogously, we investigated the correlations between climate and socio-demographic variables, Fig. 3 panel (b).

Even in this case, we observed that the two most correlated variables (r = 0.68) were the number of physicians and the people with age over 70. Correlations ranging from 0.6 to 0.8 are generally considered moderate, therefore we did not exclude any socio-demographic variable from the analysis. From both correlation analyses, we also concluded that COVID-19 mortality was weakly linearly correlated with the variables considered in our study. The strongest correlations were observed with NO₂ (r = 0.3) and life expectancy (r = 0.34). The same correlation analysis was carried out by pooling all the available variables but even in this case no strong correlation was detected, thus no variable should be removed.

4.2. Statistical association between pollution and COVID-19

We estimated the statistical association between COVID-19 mortality and the proposed descriptors using a RF regression, the results obtained by 5000 cross-validation rounds were averaged to obtain a unique representation, see Fig. 4 for the average results.

Fig. 4.

RF average predictions over 5000 iterations against COVID-19 mortality (deaths per million).

The previous Fig. 5 shows the scores obtained by averaging the scores of 5000 iterations performed against the actual deaths per million caused by COVID-19. We quantitatively assessed the model performance in terms of median and standard deviation; we obtained Pearson's correlation r = 0.75 ± 0.09 and Mean Absolute Logarithmic Error MALE = 0.217 ± 0.031.

Fig. 5.

Comparison of the different regression models for the COVID-19 mortality prediction in terms of Pearson's correlation (left panel) and Mean Absolute Logarithmic Error (right panel).

4.3. Comparison between models

To evaluate to which extent the regression accuracy was affected by the choice of a particular model, we compared the RF performance with other methods: a linear model (LM), a neural network model, specifically a multi-layer perceptron (MLP), and a Support Vector Machine (SVM) regression, see Fig. 5.

RF resulted the best performing method in terms of both metrics (r = 0.76 ± 0.09 and MALE = 0.217 ± 0.031) followed by the LM (r = 0.72 ± 0.11 and MALE = 0.231 ± 0.034), SVM (r = 0.69 ± 0.10 and MALE = 0.217 ± 0.029) and MLP (r = 0.65 ± 0.12 and MALE = 0.258 ± 0.036). RF resulted the best performing method both in terms of correlation and MALE, the observed differences (between RF and the other methods) were statistically significantly with p-value p < 0.01 according to a Wilcoxon test.

Besides, we investigated the agreement of the four proposed models. The goal of this analysis was to evaluate whether different models were prone to misclassify different examples and therefore to evaluate the possibility to consider a combination to improve the overall performance. Results can be visually inspected in Fig. 6 .

Fig. 6.

RF predictions (y-axis) against the MLP (left), SVM (top right) and LM (bottom right) predictions (x-axes).

Despite these significant differences, all these models yield predictions with moderate/strong correlations; the correlation between RF and SVM is strong r(RF − SVM) = 0.86, while the ones between RF and MLP or LM are moderate, r(RF − MLP) = 0.79 and r(RF − LM) = 0.68, respectively. Interestingly, the minimum correlation is obtained for the best performing methods.

4.4. Feature importance

To evaluate the importance of all available features and rank them accordingly we exploited the Boruta method. The analysis was performed over the whole set using a sufficiently high number of iterations (1000) allowing the algorithm to reach a definite decision about all the features; we implemented Boruta with 100 auxiliary shadow variables, the results are presented in Fig. 7 .

Fig. 7.

Feature Importance measured by the Boruta analysis.

The most important features resulted life expectancy, followed by the number of nurses, the absolute humidity and the NO₂ concentration with substantially equal importance. The socio-demographic variables were generally more important than the other features.

4.5. Remote sensing vs demographic

Feature importance analysis demonstrated how COVID-19 mortality is statistically associated with socio-demographic and climatic variables, although one pollutant, NO₂, resulted the third feature by importance. One could wonder if the contribution of pollutants and climatic variables (remote sensing-based measurements) is relevant or not. Accordingly, we performed a further analysis by separating remote sensing variables from socio-demographic features and trained the same model as before, see Fig. 8 .

Fig. 8.

Comparison of the different regression models for the COVID-19 mortality prediction in terms of Pearson's correlation (left panel) and Mean Absolute Logarithmic Error (right panel).

The models trained using only remote sensing variables or only socio-demographic features showed a significant loss of accuracy, both in terms of correlation and MALE.

5. Discussion

This work presents a first attempt to extensively evaluate the statistical association between pollution and COVID-19 mortality over the European region using remote sensing imagery. Using S-5p data for pollutants’ concentrations and online repositories for climatic and socio-demographic data, we used a RF to model COVID-19 mortality in terms of these features. This study can be considered an extension of previous ecological studies conducted in Europe for at least three different reasons (Wu et al., 2020b; Ogen, 2020; Cole et al., 2020; Liang et al., 2020; Fiasca et al., 2020; Cazzolla Gatti et al., 2020). First of all, previous studies reached (according to different experimental design and different data) not conclusive findings about the association between pollution and COVID-19 mortality; the database considered here examined several months of observations, thus extending the temporal range of our study and granting increased robustness to the analyses. Another major difference here is the use of socio-demographic variables, which have been previously used only at smaller scales or in studies over the USA. Finally, and most importantly, this is the first machine learning study including a Boruta feature importance evaluation to quantify the role played by predictors.

On the one hand, our findings show that NO₂ and life expectancy are weakly correlated to the target variable, the COVID-19 mortality, therefore a linear relationship between these factors and the target should be excluded. On the other hand, we observed that COVID-19 mortality can be accurately predicted (r = 0.74 ± 0.09 and MALE = 0.217 ± 0.031) with a RF model, thus suggesting the presence of non-linear interactions between the features considered in the study and the target.

These findings are also confirmed when using other regression strategies: LM (r = 0.70 ± 0.11 and MALE = 0.231 ± 0.034), SVM (r = 0.68 ± 0.10 and MALE = 0.217 ± 0.029) and MLP (r = 0.63 ± 0.12 and MALE = 0.258 ± 0.036). In fact, we observed that the accuracy of predictions slightly depended on the choice of the adopted model and all the investigated models yield predictions moderately or strongly correlated; this would suggest that the association between COVID-19 mortality and our features is not a statistical occurrence. The simplicity of a linear model could make this model preferable over the slightly (but significant) performance improvement of RF which comes at the cost of huge computational requirements and less interpretability. Although linear models could be preferred, for the sake of interpretability (Gibson et al., 2019), it should also kept in mind that RF is a robust choice and it does not require any a priori assumption. Besides, combining RF with the Boruta feature importance makes the framework completely intelligible.

We also performed a feature importance analysis, according to which life expectancy resulted the most important feature to predict COVID-19 mortality. This result confirms findings from other studies (Cole et al., 2020; Chaudhry et al., 2020) independently from the adopted methodologies. This result reasonably confirms the increment of COVID-19 mortality with age. Although, life expectancy grows with a nation's wealth and therefore its capability to take care of elder people, other sources of heterogeneity, like the different sanitary systems or policies, prevent this variable to reliably account for the overall morality.

According to this study, other important features were the number of physicians, nurses and hospital beds which are likely to be good proxy for the capacity of the health systems in the administrative units. These findings would enforce the robustness of our study as the same results were independently observed by other studies which, at a country level, showed how the capacity of a health system affects mortality (Fisher et al., 2000; Karaca-Mandic et al., 2020). Although some authors (Wu et al., 2020b) find these conclusions controversial, our findings suggest that these features are accordingly important predictors for COVID-19 mortality. Analogously, socio-demographic features like gross domestic product per capita, mean years of schooling of population aged 25 and expected years of schooling for children aged 6 were confirmed to be important; other studies suggested that accounting for the development level of the sanitary systems and the population mobility (Chaudhry et al., 2020) these variables can play an important role during pandemic.

Regarding the association between air pollution and Covid-19 mortality, NO₂ tropospheric column was the most important feature; on the contrary SO₂, CO, HCHO and AER AI were rejected. Interestingly, these results would suggest to neglect the majority of pollutants, except for NO₂, but we also demonstrated that the combination of pollutants with climatic and socio-demographic features ensures an accuracy otherwise inaccessible. Regarding the association between exposition to NO₂ and COVID-19 mortality, it should always kept in mind that our study cannot assess any causality by design. If a causality exists, this might be related to the role of NO₂ in contributing to the development of asthma and respiratory infections, causing a range of harmful effects on lungs (Pilotto et al., 1997; Gamble et al., 1987; Kubota et al., 1987). Moreover, premature deaths are attributable to long-term air pollution exposure (Khomenko et al., 2021). On the other hand, the statistical association with NO₂ be confounded by an omitted-variable bias.

Minor effects can also be imputed to humidity and diabetes. According to other studies, these contributions are still unclear (Mecenas et al., 2020; Rashed et al., 2020; Lin et al., 2020; Shi et al., 2020; Hussain et al., 2020). Among these, a particular mention is deserved by the average population density. We found this feature to be the least important among the selected variables. In literature, opposite conclusions are presented (Wu et al., 2020b; Rashed et al., 2020; Kadi and Khelfaoui, 2020), thus confirming the elusiveness of such association.

It is important to acknowledge some limitations of the present study. It is worth noting that the models adopted here present two main sources of bias affecting the interpretation of the results, namely omitted-variable bias and multicollinearity (Jargowsky, 2005; Cinelli and Hazlett, 2020; Rinella et al., 2020). The omission of a variable cannot be treated as it depends on the contingency of the study design and eventually on the available data, for example in the present study no demographic breakdown was considered. Besides, multicollinearity leads learning models, such as Random Forests, to spread feature importance across collinear variables (Strobl et al., 2008), so that these findings should be considered cum grano salis. Similarly, a linear regression model could flip a coefficient's sign and increase its variance (Greene, 2003; Belsley et al., 2005). Finally, both linear regression and negative Bernoulli model results can be unstable against removing or adding additional variables (especially when fed with data having small cardinality).

The importance of pollutants in modeling the COVID-19 severity has been thoroughly investigated from several perspectives. For example, a remote sensing investigation on a regional scale has already revealed the association between NO₂ levels and COVID-19 mortality (Ogen, 2020). However, some aspects should be considered with caution. First of all, correlation does not imply causation and, therefore, it should always kept in mind that these findings reveal a statistical association between COVID-19 and pollution not a causal relationship. Besides, the use of S-5p data for the purpose of measuring ground level pollution has intrinsic limitations: NO₂ is mainly a street-level pollutant and the concentration measured in the total column could be affected by a considerable uncertainty (Pisoni and Van Dingenen, 2020).

6. Conclusions

In this work, we presented a machine learning framework combining pollutants’ concentrations, climatic variables and socio-demographic features to model COVID-19 mortality. As far as we know, this is the first work to attempt such a goal on a continental scale. We considered European administrative units and used a RF model to predict COVID-19 mortality. The resulting model was characterized by both accuracy and robustness. Besides, we were able to evaluate and rank the importance of the variables included in the model and found that the four key factors for modeling the mortality were life expectancy, number of nurses, absolute humidity and NO₂ concentration. However, uncertainty about street-level concentrations of pollutants should be considered as a potentially limiting factor weakening the role played by NO₂; accordingly, further studies, possibly involving street-level measurements should be taken into account.

Statement authors

NA: Conceptualization, Methodology, Project Administration, Supervision, Visualization, Writing - original draft, Writing - review & editing. RC: Data Curation, Formal Analysis, Methodology, Software, Writing - original draft. TM: Writing - review & editing. AM: Methodology, Writing - original draft, Writing - review & editing. ST: Writing - review & editing. RB: Resources, Supervision, Writing - review & editing. Conceptualization, N.A. and R.C.; Methodology, N.A. and R.C.; Software, R.C.; Formal analysis, R.C.; writing--original draft preparation, N.A.; writing--review and editing, all the authors; Visualization, N.A. and R.C.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.