Induced fit versus conformational selection: From rate constants to fluxes… and back to rate constants

Abstract

Induced fit‐ (IF) and conformational selection (CS) binding mechanisms have long been regarded to be mutually exclusive. Yet, they are now increasingly considered to produce the final ligand‐target complex alongside within a thermodynamic cycle. This viewpoint benefited from the introduction of binding fluxes as a tool for analyzing the overall behavior of such cycle. This study aims to provide more vivid and applicable insights into this emerging field. In this respect, combining differential equation‐ based simulations and hitherto little explored alternative modes of calculation provide concordant information about the intricate workings of such cycle. In line with previous reports, we observe that the relative contribution of IF increases with the ligand concentration at equilibrium. Yet the baseline contribution may vary from one case to another and simulations as well as calculations show that this parameter is essentially regulated by the dissociation rate of both pathways. Closer attention should be paid to how the contributions of IF and CS compare at physiologically relevant drug/ligand concentrations. To this end, a simple equation discloses how changing a limited set of “microscopic” rate constants can extend the concentration range at which CS contributes most effectively. Finally, it could also be beneficial to extend the utilization of flux‐ based approaches to more physiologically relevant time scales and alternative binding models.

IF always increases with increasing ligand concentration, [L], but minimum may vary from one case to another. A flux‐based approach shows that a limited number of rate constants suffice to describe the curve.

Abbreviations

CS

conformational selection

IF

induced‐fit

1. INTRODUCTION

The pharmacokinetic properties as well as the binding kinetics of a drug/ligand are nowadays considered to direct the selectivity and duration of its clinical action.¹, ² In this respect, induced‐fit (IF) binding is often evoked as a means to achieve its long residence time at the target. Traditionally, this mechanism comprises fast binding of the ligand, L, to the free target, T, to yield a transient TL complex, followed by slow transconformation thereof into a more stable T*L species (Figure 1).³, ⁴, ⁵, ⁶ This model represents a compromise between the classical “Occam's razor” principle, which favors a reversible one‐step binding, and increasing experimental evidence for a model in where TL experiences multiple small conformational adjustments.⁷, ⁸, ⁹ Conformational selection (CS) constitutes a well‐known counterpart to IF. Traditionally, this mechanism implies that a slow conformational change between free T and T* precedes a fast but highly selective binding step.⁵, ⁶, ¹⁰, ¹¹, ¹²

FIGURE 1.

Schematic representations and equations. (A) Schematic representation of the explored IF‐CS‐ based thermodynamic cycles and parameters for individual pathways. Left side: The “ground state” of the target, T, undergoes a conformational change before the binding of the ligand, L, (to yield T*) according to the conformational selection, CS, model. According to the induced‐fit, IF, model, the binding (to yield TL) precedes the conformational change of the complex. Both pathways give rise to the same final T*L complex. Mid‐ and right side: Schematic representation of individual pathway with focus on the microscopic rate constants (denoted as k₁…₄) and microscopic fluxes (denoted as F₁…₄). (B) Top: Relationship between the macroscopic forward and reverse fluxes (i.e., F_on for T to T*L and F_off for T*L to T) and the microscopic fluxes such as presented by Hammes et al..¹⁹ Bottom: Relationship between the macroscopic fluxes and the conditional rates.²¹ (Supporting Information Section S2). Those distinct formulations are mathematically equivalent at equilibrium only (Supporting Information Section S8‐G)

CS‐ binding has often been opposed to IF⁶, ¹³, ¹⁴ and, in this respect, Copeland¹⁵, ¹⁶ asserted a decade ago that most of the drugs with high clinical efficacy act via IF. This conclusion was essentially based on the shape of k_obs versus [L] plots: i.e., a hyperbolic increase for IF and a hyperbolic decrease for CS.⁴, ⁵ However, this strict distinction has been challenged by bio‐mathematical considerations showing that CS may also bring about increasing plots.¹⁷, ¹⁸ Hence, some previously qualified IF‐ binders could actually bind via CS.¹⁴

Such explicit distinction between IF‐ and CS‐binders is now also increasingly regarded to be a false dichotomy.¹⁹, ²⁰, ²¹, ²² Indeed, they are now rather considered to “compete” with one another for producing the final T*L complex within a thermodynamic cycle. This viewpoint benefited from the introduction of binding fluxes, F, as a tool for analyzing the behavior of such cycle.¹⁹ Analogous to the rate of product formation in enzymology, a binding flux refers to the rate by which one target species converts into another. As such, it relies on the concentration of a target species as well as on the rate constant for its transformation into the other species. While, a reversible one‐step mechanism only necessitates a “forward” and a “reverse” flux, a two‐step mechanism such as IF and CS already requires four “microscopic” fluxes: i.e., two for each step (Figure 1, and Supporting Information Section S1). The overall conversion of T into T*L and back can also be expressed in terms of “macroscopic” forward‐ and reverse fluxes, F_on and F_off. In essence, they approximate the lowest of the intervening microscopic fluxes (Figure 1B). In this respect, Hammes et al.¹⁹ evaluated the relative contribution of IF, Rc_‐IF, and CS to T*L within a cycle by comparing their F_on‐ values at equilibrium. This approach is now also adopted by many others.¹³, ²⁰, ²³, ²⁴, ²⁵, ²⁶ The emerging picture is that Rc_‐IF invariably increases with [L]. This usually allows CS to dominate at low [L], but not always.¹⁹, ²⁴

Prior estimation/knowledge of all the microscopic rate constants is required for calculating F_on. The presently available sets of constants are not only theoretical¹³, ²³, ²⁷ but also based on molecular dynamics simulations and experimental observations.¹⁹, ²⁴, ²⁵, ²⁶ In this respect, it is striking that many of the published sets depart from the traditional frame of reference (Section 2.4 and Supporting Information Section S2). Moreover it is still little know that F_on and/or Rc_‐IF can also be directly calculated based on the microscopic rate constants without invoking concentration of each target species (e.g., Ref. [21]) and that relevant Rc_‐IF‐ estimates can also been obtained by comparing by how much T*L accumulates via each pathway ²⁶, ²⁷ (Supporting Information Section S1).

Binding flux‐ based concepts may appear quite exotic for many pharmacologists who are more acquainted with rate constants. This study aims to partly fill this gap by providing more vivid and applicable insights into this emerging field. Attention is first paid to the link between F_on and the microscopic forward fluxes for IF and CS separately. The impact of the rate of each step of the thermodynamic cycle on the Rc_‐IF–[L] relationship is examined next. The role of the most influential microscopic rate constants is finally highlighted.

2. MATERIALS AND METHODS

2.1. Nomenclature

The rate constants that govern the individual steps in two‐step binding models are commonly referred to as “microscopic” are denoted as for IF k₁ (in M⁻¹·min⁻¹) and k₃ (in min⁻¹) when moving forward from T to T*L and as k₂ (in min⁻¹) and k₄ (in min⁻¹) when reverting to T. (Figure 1A). The “macroscopic” constants are denoted as k_on and k_off, respectively.²⁸ To keep the same type of nomenclature, we refer to fluxes that are associated with the individual steps as the “microscopic” F₁…F₄ and those that account for the “macroscopic” fluxes as F_on and F_off (Figure 1A). To distinguish between the IF and CS pathways of a thermodynamic cycle, those notations are appended by the appellation of each pathway in question. To distinguish between the notations for conventional IF binding (i.e., for which k₃ < k₂) and bivalent‐ like binding (i.e., for which k₃ > k₂)²⁹ the latter are appended by “Biv” (Supporting Information Section S2).

2.2. Definitions

For a mono‐ molecular binding step (e.g. from T to T*), F_1‐CS amounts to the product of [T] and the associated first‐order rate constant k_1‐CS and, for a bimolecular step (e.g. from T* to T*L), F_3‐CS amounts to the product of [T*], [L] and the associated second‐order rate constant k_3‐CS. Hence, all fluxes can be expressed in % of [T_total] × min⁻¹ (Figure 1A). The “competition” between IF and CS in a thermodynamic cycle is presently quantified by the relative contribution (also often denoted as dominance, prevalence...) of IF: i.e., Rc_‐IF = F_on‐IF/(F_on‐IF + F_on‐CS).¹⁹ When based on how much each pathway has contributed to the accumulation of T*L, Acc, after a given time span (such as proposed by Ordabayev et al.²⁶), Rc_‐IF = Acc_‐IF/(Acc_‐IF + Acc_‐CS) (Supporting Information Section S1). Please note that Rc_‐CS equals 1−Rc_‐IF, that the pathway with the highest Rc value is considered to “dominate” and that both pathways contribute equally when their Rc = 0.5. Finally, it is only at equilibrium that F_on and F_off of each pathway can also be expressed in terms of their conditional rates (Figure 1B).²¹, ³⁰ While those also act as composite first order rate “constants” (Supporting Information Section S2), they should not be confounded with k_obs.

2.3. Simulations

Microscopic rate constants are provided for each investigated case in Supporting Information Section S3. Accumulation of T*L at time t’ via a given pathway is obtained by integrating the fluxes of the last microscopic step thereof,²⁶ such as shown Supporting Information Section S1. The sum of both yields the total [T*L]. In general, numerical solutions for the differential equations are achieved by consecutively solving all their segments in parallel over very small time intervals.³¹ All simulations take account of the pre‐existing equilibrium between [T] and [T*]. Simulated data are analyzed by non‐linear regression analysis with GraphPad Prism^® (GraphPad Software Inc.).

2.4. Paradigms

Simulations are also based on the widely adopted paradigm according to which [L] vastly exceeds [T_tot] so that [L] remains constant throughout. This is often the case for drug‐ binding.¹⁷, ¹⁹, ²¹, ²³, ³², ³³, ³⁴ The transconformation step should significantly contribute to the ligand's affinity for genuine IF binding, i.e., k_3‐IF > k_4‐IF (so that [T*L] exceeds [TL] at equilibrium). Also, [T*] should also only represent a small fraction of the initial unbound targets, i.e., k_2‐CS > k_1‐CS.¹³, ¹⁸ The microscopic rate constants should comply with the classical “rapid equilibrium” paradigm according to which the binding proceeds faster than the conformational change for both pathways, i.e., k_2‐IF > k_3‐IF ²⁹ and k_4‐CS > k_1‐CS.⁵, ¹³, ¹⁷, ¹⁸, ¹⁹ Yet, exceptions to those rules are nowadays tolerated, and those are here also taken into consideration. Finally, ratios between microscopic fluxes are only equivalent to the ratios between their constituent rate constants when they “originate” from the same target species and when they do not, or equally depend on [L]. This only concerns the F_2‐IF/F_3‐IF and F_4‐IF/F_4‐CS ratios.

Since the difference in Gibbs free energy between T and T*L needs to be rigorously the same for the two pathways of a thermodynamic cycle, their thermodynamic K_D’s (i.e., the k₂·k₄/k₁·k₃‐ ratios) need to be equal as well. This constraint has been referred to as the “detailed balance rule“.²¹ When only approximate rate constants are provided in the literature, one of them needs to be adjusted to conform to this rule. Also, when starting from a compliant situation, it is only permitted to change two (or more) of them in parallel, such as when changing the forward and reverse rate constants of a single step equally (Figures 5 and 6). On the other hand, the two forward (or reverse) rate constants of a single pathway have to changed oppositely and so on.

FIGURE 5.

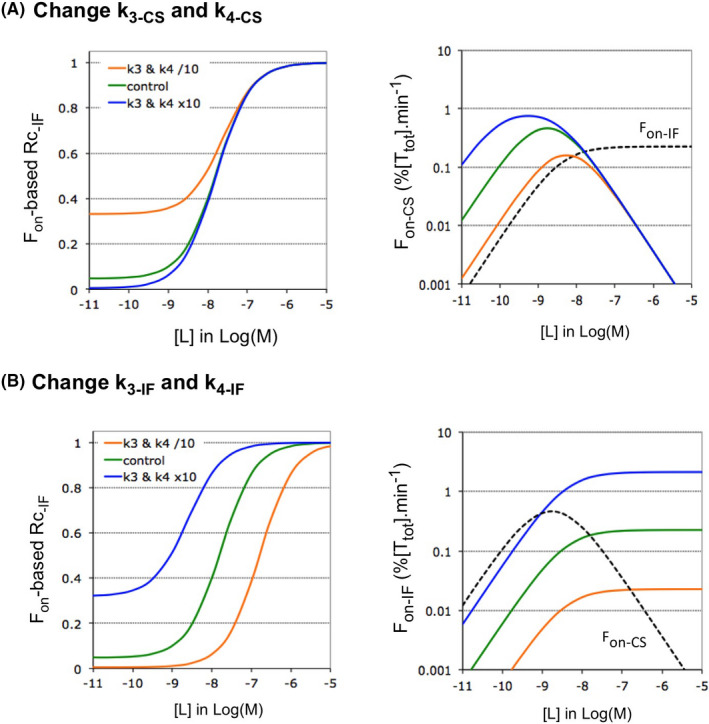
Impact of the rate of the second step of each pathway on Rc_‐IF at equilibrium. Microscopic rate constants k₃ and k₄ are changed 10‐fold in tandem (to keep the K_D unchanged) for a single pathway. The impact thereof on the Rc_‐IF versus [L] plots is here shown for Case A (as control). Similar outcomes are also observed for Case B (Supporting Information Section S5). While Case A allows a better appreciation of the horizontal shifts, Case B allows a better appreciation of the vertical ones. (A) Left side: Decreasing or increasing the value of the k_3‐CS–k_4‐CS tandem does not affect the ascending portion of the Rc_‐IF versus [L] plots but shifts Rc_‐IF at low [L] in the opposite way. Right side: This shift can be related to the ability of changing k_3‐CS to produce a similar change of F_3‐CS at low [L] (not shown) and thus also of F_on‐CS. Hence, the F_on‐IF/F_on‐CS ratio changes in the opposite way. (B) Left side: Decreasing or increasing the value of the k_3‐IF–k_4‐IF tandem shifts the ascending portion of the Rc_‐IF versus [L] plots in the opposite way (i.e., to higher and lower [L], respectively) but shifts Rc_‐IF at low [L] in a similar way. Right side: This latter shift can be related to the ability of changing k_3‐IF to produce an alike change of F_on‐IF (via F_3‐IF) and thus also of the F_on‐IF/F_on‐CS ratio at low [L]. The more complex link between k_3‐IF and the horizontal shifts is documented in Supporting Information Section S6

FIGURE 6.

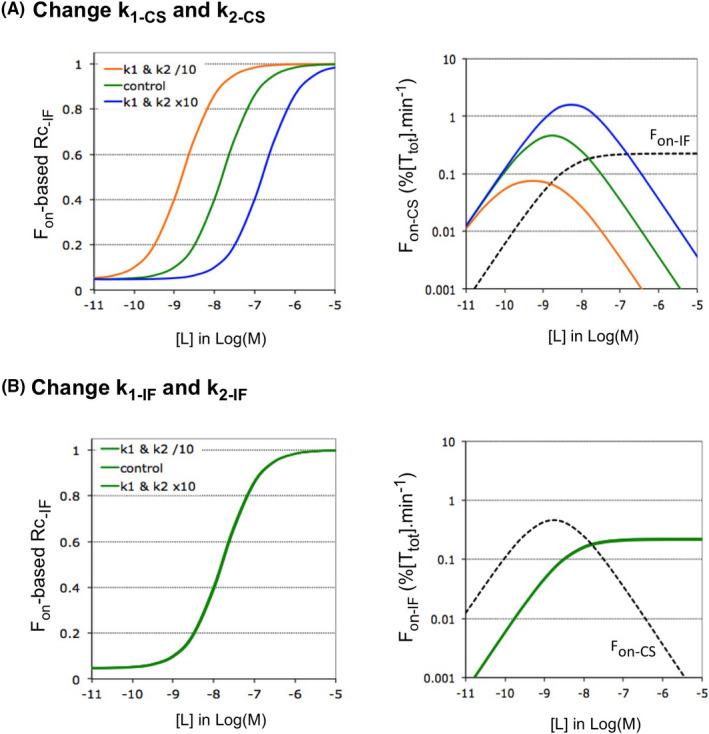
Impact of the rate of the first step of each pathway on Rc_‐IF at equilibrium. Microscopic rate constants k₁ and k₂ are changed 10‐fold in tandem for a single pathway of Case A. The impact thereof on the Rc_‐IF is also shown for Case B in Supporting Information Section S5. (A) Left side: Decreasing or increasing the value of the k_1CS–k_2‐CS tandem shifts the ascending portion of the Rc_‐IF versus [L] plots in the same way (i.e., to lower and higher [L], respectively) without affecting Rc_‐IF at low [L]. Right side: The horizontal shifts can be related to the ability of F_on‐CS to start descending at lower and higher [L], respectively. The more complex link between k_1CS and the shifts is further documented in Supporting Information Section S6. (B) Left side: Decreasing or increasing the value of the k_1IF–k_2‐IF tandem does not affect the Rc_‐IF versus [L] plots. Left side: the F_on‐IF versus [L] plots are not affected either

2.5. Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY,³⁵ and are permanently archived in the Concise Guide to PHARMACOLOGY 2019/20.³⁶, ³⁷

3. RESULTS

3.1. Bivalent‐like‐ (Biv) versus genuine IF binding

It is of note that some authors have also classified as ‘IF’ cases that deviate from the classical “rapid equilibrium binding”‐ premise (i.e., with k₃ < k₂) by allowing the transconformation to proceed equally fast (i.e., k₃ = k₂)¹⁹ or even faster than the dissociation (i.e., k₃ > k₂).¹⁴ Kinetically speaking, the latter act like genuine bivalent ligands (Supporting Information Section S2) and are therefore abbreviated as ‘biv’. Here we show that this k₃/k₂ ratio also determines the microscopic step that mostly impacts F_on.

The simulated plots in Figure 2 gradually move from Biv‐ (left side) to classical IF binding (right side) by lowering k₃ and k₄. (i.e., to keep the K_D constant and because the slow dissociation of IF binders is linked to a low k₄ ⁵). Alike previous observations,²⁹ Figure 2A shows that binding equilibrium is reached faster for Biv‐ than for IF binding at equal [L]. Figure 2B compares how the microscopic forward fluxes for each step—F₁ and F₃—evolve with time. Although both change considerably early on, they eventually reach a plateau when equilibrium is approximated and this takes again less time for Biv‐ than for IF binding. This difference also applies to the macroscopic F_on (Figure 2C).

FIGURE 2.

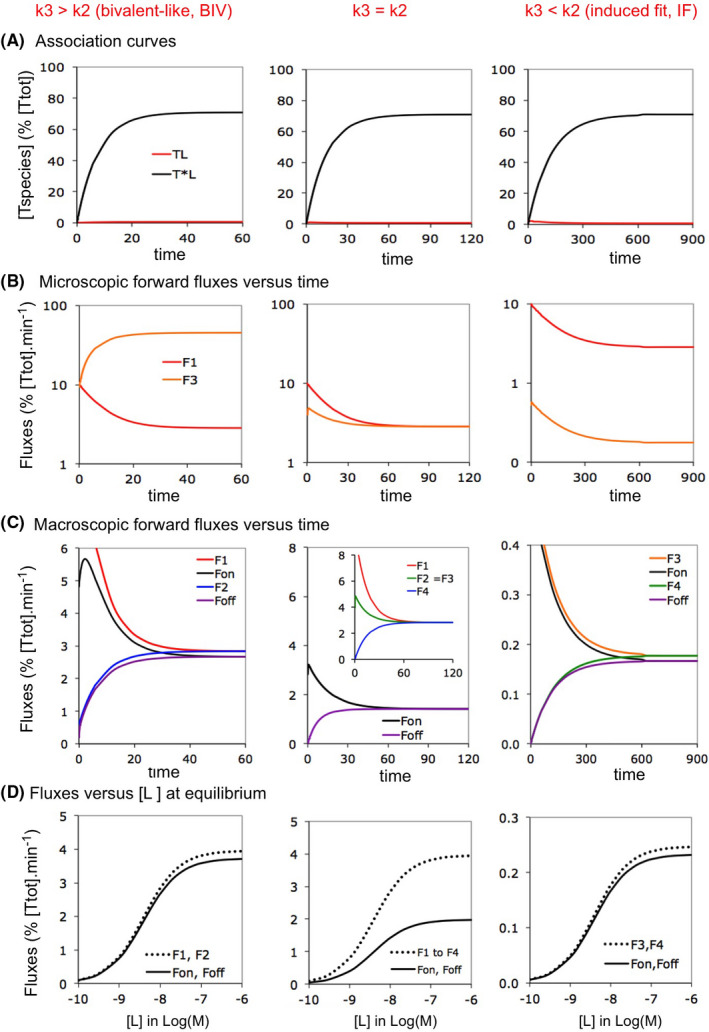
Fluxes for Biv‐ versus IF binding: implication of the k₃/k₂ ratio. Bivalent‐like, “Biv” refers to IF binding in where the conformational change proceeds faster than the binding, i.e., with k₃ > k₂ compared to k₃ < k₂ for classical IF. It is only from the kinetic viewpoint that such Biv‐ binding behaves similarly as genuine bivalent ligand binding (More information in Supporting Information Section S2). Simulations refer to isolated pathways. From left to right: the binding shifts from a Biv‐ to an IF pattern when the k₃/k₂ ratio decreases. Data for t = 0 not presented. (A) Simulated association/”accumulation” plots of the bound target species (i.e., TL for the intermediate complex and T*L for the final complex) as a function of the incubation time. Microscopic rate constants are provided in Supporting Information Section S3 and comply with the classical frame of reference for each model. [L] = 2.5 × K_D for each example. Please note that [TL] still remains minimal (i.e., <1% of [T_tot]) at all times. It is only at higher [L] that transient rises in [TL] become significant for IF (not shown). (B) Evolution of the microscopic forward fluxes with time. Note that, at equilibrium, F₁ < F₃ for Biv and F₁ > F₃ for IF. (C) Evolution of the macroscopic F_on and F_off with time. Note that at equilibrium, all forward and reverse fluxes cancel out, that F_on is dictated by the smallest microscopic forward flux for Biv and IF and that F_on equals half of the microscopic forward fluxes for the intermediate situation in where F₁ = F₃. (D) The above considerations apply to all [L] at equilibrium

At equilibrium, F₃ predominates for Biv binding, F₁ and F₃ are equal for the intermediate case (i.e., with k₂ = k₃) and F₁ predominates for IF binding. As expected, F_on is largely determined by the smallest of the microscopic fluxes (i.e., F₁ for Biv and F₃ for IF) (Figure 2C). Similar relationships apply to the reverse fluxes. Figure 2C,D show that F_off always equals F_on at equilibrium and that this rule also applies to the microscopic fluxes (Figure 1A). Finally, the intermediate case (Figure 2C‐mid) represents a special situation: the microscopic fluxes are all equal at equilibrium and F_on only equals 50% thereof. Figure 2D further shows that, at equilibrium, F_on increases with [L] until a plateau value for all three cases. Interestingly, the proportionality between F_on and its most influential microscopic flux (or fluxes) remains constant throughout. This invariance owes to fact that the F₂/F₃ ratio always equals the k₂/k₃ ratio (see Section 2.4).

3.2. CS binding

Hyperbolically decreasing k_obs versus [L] plots were regarded to be a hallmark for CS binding.⁴, ⁵ Yet, this shape only applies when k₄ > k₁ (Supporting Information Section S4). Otherwise (i.e., when k₄ < k₁), the plots rather increase hyperbolically.¹⁷, ³² In spite of this, all the forward (and reverse) fluxes still respond in the same way to increasing [L] for those two cases.

Figure 3 depicts the time‐wise evolution of the forward fluxes for both cases at low‐ (left side) as well as at high [L] (mid). Here also, they tend to reach a standstill when equilibrium is approximated. All the connected forward and reverse fluxes then become equal as well (not shown). However, it is noteworthy that F₁ predominates at low [L] while F₃ predominates at high [L]. This shift is gradual such as shown by the bell‐shaped profile of the F_on versus [L] plots (right side). This shape reflects the fact that F_on is governed by the lowest of the microscopic fluxes (i.e., from F₃ to F₁ when [L] increases). From the strict viewpoint of fluxes, increasing [L] allows CS‐ binding to shift from an IF‐ like‐ profile to a Biv‐ like profile.

FIGURE 3.

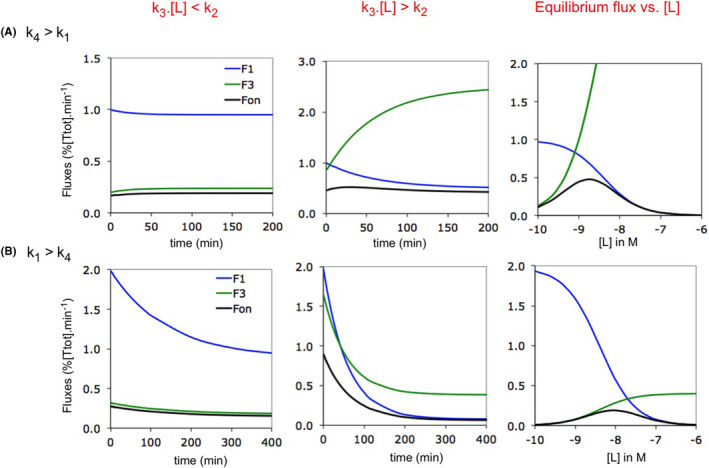
Forward fluxes for CS binding: implication of the ([L]·k₃)/k₂ and k₄/k₁ ratios. Simulated plots are for isolated CS binding. Microscopic rate constants are provided in Supporting Information Section S3. Data for t = 0 not presented. (A) The model complies with the traditional “rapid equilibrium binding” paradigm (i.e., with k₄ > k₁). Left side: forward fluxes versus time at low [L] = 0.2 nM. Such as for IF (Figure 2C), F_on is essentially dictated by F₃ at all times. Mid: forward fluxes versus time at higher [L] = 4 nM. F_on becomes essentially dictated by F₁ (i.e., Biv‐like, Figure 2C) as time goes by. Right side: forward fluxes versus [L] at equilibrium. The F_on versus [L] plot adopts a bell‐shaped pattern with a F₃‐ dictated ascending portion and a F₁‐ dictated descending portion. (B) Plots such as in (A) for the alternative CS binding model¹⁴, ¹⁷, ³² in where the conformational change proceeds faster (i.e., with k₄ < k₁). Low [L] = 5 nM and high [L] = 100 nM. The observations are quite similar as for the traditional model in (A). This contrasts with the hyperbolically decreasing k_obs versus [L] plot for the traditional model and hyperbolically decreasing plot for the alternative model (Supporting Information Section S4). Finally, F_on is not maximal when the F₁‐ and F₃ versus [L] plots intersect because of their different curvature (right side)

3.3. Thermodynamic cycles: from macroscopic to microscopic fluxes

Next, we evaluate the contribution of the IF‐ and CS‐ pathways to T*L within a thermodynamic cycle. To this end, Figure 4 focuses on three cases with a distinct relative contribution of IF, Rc_‐IF, at low [L] and at equilibrium. Although this difference received little attention until now, it offers a key to a better understanding of how this relative contribution is related to some of the microscopic rate constants.

FIGURE 4.

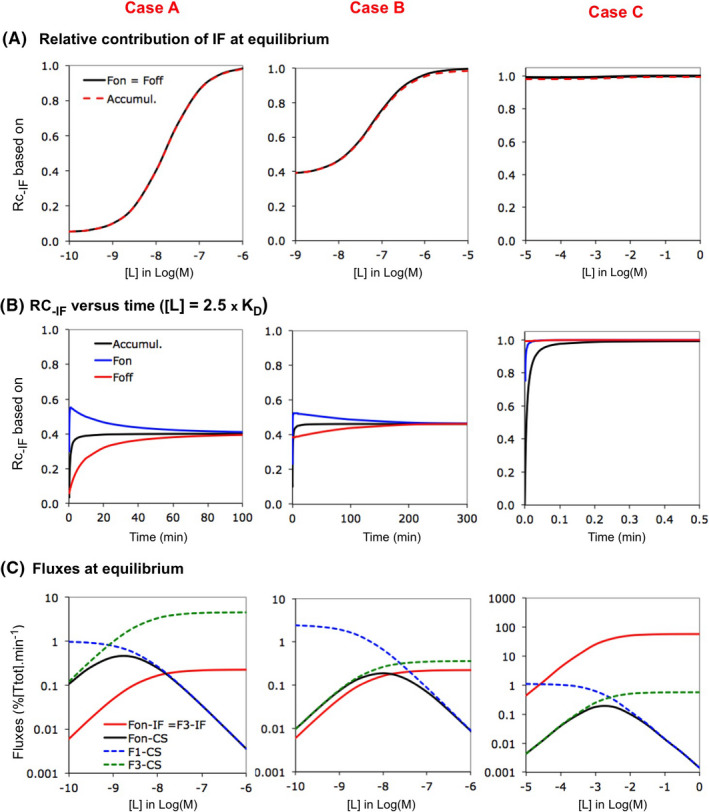
Competition between pathways of a thermodynamic cycle: IF versus CS. Competition between IF and CS is evaluated for three Cases. Both pathways comply with the classical frame of reference for Case A (see “Definition”). The two other cases diverge. The conformational change proceeds faster than the binding for CS For Case B (such as in Figure 3B) and Case C is based on kinetic data provided by Zhou et al.²⁴ The latter values are 10⁶‐ fold lower for the sake of comparison. Please see Supporting Information Section S3 for microscopic rate constants and important ratios thereof. (A) The relative contribution of IF to T*L, “Rc_‐IF” increases with [L] for the three Cases at equilibrium. Rc_‐IF can be expressed in terms of F_on (i.e., Rc_‐IF = F_on‐IF/(F_on‐IF + F_on‐CS)), F_off and the accumulation of T*L (same type of equations). These three modes of calculation yield nearly‐ overlapping plots for each Case (hence only one color. Rc_‐IF at very low [L] differs among the Cases: i.e., from <0.5 (CS‐ dominant) for Case A to nearly 1 (outspokenly IF‐ dominant) for Case C.²⁴ (B) The evolution of Rc_‐IF with time is shown for the three cases for [L] = 2.5 × K_D. Note that, while the three approaches provide different Rc_‐IF‐ values early on for each given case, they become closely the same at equilibrium. (C) Evolution of microscopic and macroscopic fluxes at equilibrium as a function of [L]. Such as for the individual pathways in Figures 2 and 3, F_on is dominated by F₃ for both IF and CS at low [L]. Hence, the different Rc_‐IF values low [L] relates to F_3‐IF << F_3‐CS for Case A, F_3‐IF ≈ F_3‐CS for Case B and F_3‐IF >> F_3‐CS for Case C. The bell‐shaped F_on versus [L] profile for CS is preserved when moving from the isolated CS pathway (Figure 3) to the cycle and the drop of F_on‐CS at higher [L] permits Rc_‐IF to increase

Figure 4A compares their Rc_‐IF versus [L] plots. The microscopic rate constants for each case and their compliance with the classical frame of reference are related in Supporting Information Section S3. Case A represents the conventional model. For this and several other cases in the literature (e.g., Refs. [23, 26, 27]), CS largely dominates at low [L] and Rc_‐IF increases gradually with [L] until full IF‐ dominance. Such as for the two examples by Hammes et al.,¹⁹ Rc_‐IF already resides well above baseline at low [L] for Case B. Case C relies on molecular dynamics simulation‐ based rate constants for MDM2 binding to the intrinsically disordered transactivation domain of the tumor suppressor p53 protein.²⁴ This case represents an extreme situation in where IF always overwhelmingly dominates at low [L]. Interestingly, the F_on‐, the F_off‐ and the accumulation‐ based approaches²⁶ yield nearly alike plots for each of the three cases (Figure 4A). Yet, Rc_‐IF‐ values may differ from one another for each case early on (Figure 4B). We will only deal with equilibrium binding below.

Comparing how F_on is related to its constituent microscopic fluxes offers better insight into why Rc_‐IF may be so different at low [L] (Figure 4C). Although both pathways now act in unison (so that they can potentially influence one another), the relationships that applied to the separate pathways (Figures 2 and 3) remain largely preserved. In particular, F_on‐CS is limited by F_3‐CS at low [L] only while F_on‐IF is always limited by F_3‐IF. The differences between the three cases can thus be explained as follows: IF is marginal for Case A because F_3‐CS exceeds F_3‐IF, both pathways contribute almost alike for Case B because F_3‐IF and F_3‐CS are nearly equal and IF dominates for Case C because F_3‐CS exceeds F_3‐IF (Figure 4C).

3.4. Link between Rc_‐IF and the rate of individual steps

Ideally, it should be of interest to examine the impact of each rate constant on the Rc_‐IF versus [L] plots separately. Unfortunately, the “detailed balance rule“ (Section 2.4) requires two (or more) rate constants to be changed in parallel. We here compare how changing the two rate constants of each step affect those plots.

Figure 5 focuses on the k₃‐ and k₄ values for Case A. Decreasing or increasing those values for CS prompts an inverse change of Rc_‐IF at low [L] (Figure 5A). This is to be expected since changing k_3‐CS produces an identical change of F_3‐CS and F_on‐CS (right side) and thus an opposite change of the F_on‐IF/F_on‐CS ratio. Hence, decreasing k_3‐CS favors IF while increasing this constant favors CS. This effect is even more explicitly illustrated for Case B (Supporting Information Section S5). In contrast, changing the k_3‐IF‐ k_4‐IF tandem produces an alike change of the F_on‐IF/F_on‐CS ratio and thus also of Rc_‐IF at low [L] (Figure 5B). However, changing this tandem also prompts an appreciable horizontal shift of the Rc_‐IF versus [L] plot, i.e., a decrease thereof allows CS to remain efficacious until higher [L] whereas an increase narrows this concentration range. As shown at the right side, those horizontal shifts reflect the ability of k_3‐IF to change the amplitude of the F_on‐IF versus [L] plot (see also Supporting Information Section S6).

Figure 6 focuses on the k₁‐ and k₂ values for Case A. Here, decreasing or increasing this tandem for CS produces a (respectively) left‐ and rightward shift of the Rc_‐IF versus [L] plot (Figure 6A). In essence, these shifts reflect the ability of k_1‐CS to change the overall shape of the biphasic F_on‐CS versus [L] plot (right side). Please see also Supporting Information Section S6 for more detailed information. Finally, Figure 6B shows that increasing or decreasing the k_1‐IF–k_2‐IF tandem does not affect those plots.

Taken together, the present observations disclose the diversity of outcomes that that can be obtained by changing the overall rate of each step. In particular, they shed light on the ability of both transconformation steps to modulate the ligand's concentration range within which CS remains most efficacious (Figures 5B and 6A) and also on the ability of both k₃–k₄ tandems to modulate Rc_‐IF at low [L] (Figure 5A,B). Comparable outcomes are also observed for Case B (Supporting Information Section S5) and the above principles can also be applied for transforming the IF‐ dominated situation for Case C (Figure 4C) into a situation in where CS remains dominant for an extended range of ligand concentrations (Supporting Information Section S7).

3.5. What do equations tell?

In line with the common practice, the previous figures essentially referred to forward fluxes. Yet, it is of note that substituting the forward fluxes by their reverse counterparts yields equivalent outcomes at equilibrium. Moreover, this special condition also allows F_on and F_off to be expressed by mathematically equivalent conditional rate‐ based equations (e.g., Refs. [21, 30]) (Figure 1B and Supporting Information Section S8‐G). As a major advantage, these allow the Rc_‐IF–[L] relationship to be expressed in terms of the eight microscopic rate constants and [L] as only input (Figure 7A). This relationship can also be resolved in terms of ^minRc, i.e., the minimal value of Rc_‐IF (for [L] = 0, Figure 7B); [L]_0.5, the ligand concentration at which IF and CS contribute equally²¹ (Figure 7C) and [L]_med, the median/midpoint of the sigmoidal plots (Figure 7D). Elaboration of all the equations is shown in Supporting Information Section S8. Taken together, those equations shed light on two major aspects.

FIGURE 7.

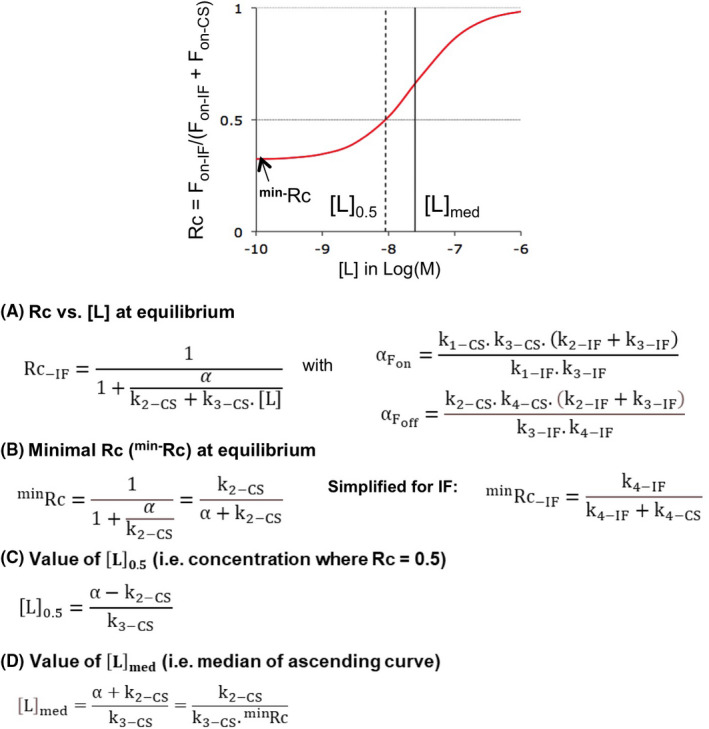
All equations refer to equilibrium binding and, unless explicitly specified, Rc applies to IF as well as to Biv (Supporting Information Section S2). The graph at the top shows the parameters that define a Rc versus [L] plot: ^minRc for the minimal value of Rc (i.e., when [L] reaches 0), [L]_med for [L] at which the ascending portion of the plot is half‐maximal and [L]_0.5 for [L] at which IF and CS contribute equally (i.e., when Rc = 0.5). Please see Supporting Information Section S8 for the elaboration of the equations. They are all based on the conditional rate‐ based equations for F_on and F_off (Figure 1B).²¹ (A) Equations for Rc at all [L]: The F_on‐ and F_off‐ based approaches yield the same value for the recurrent parameter, α. (B) ^minRc: The conditional rate‐ based equations can be simplified when [L] = 0 (see also Supporting Information Section S2). Simplification of the F_off‐ based equations discloses the implication of k_4‐IF and k_4‐CS for IF‐CS‐ based cycles. (C) IF and CS contribute equally at [L]_0.5. The presented equation is mathematically equivalent to the one in.²¹ Those do obviously not apply when ^minRc exceeds 0.5. (D) [L]_med refers to “Median” value of [L], i.e., at which the Rc versus [L] plot is half‐maximal between ^minRc and 1. Please see Table 1 for numerical values

First, it is only for a genuine IF–CS combination that the equation for ^minRc draws attention to a major impact of the two k₄ values (Figure 7B and Supporting Information Sections S2 and S8‐C). Indeed, the calculations and simulations also reveal that the role of k_4‐IF is taken over by the “k_1‐Biv.K_D ^” product for a Biv–CS combination (Supporting Information Sections S2, S8‐D and S9). This shift corroborates with the fact that F_on‐Biv is largely dictated by F_1‐Biv instead of F_3‐Biv at low [L] (Figure 2).

Second, the surprisingly simple expression of [L]_med as k_2‐CS/(k_3‐CS. ^minRc) implies that only a limited set of—largely CS related—microscopic rate constants suffices to quantify the concentration range of the ligand for which CS remains most efficacious. As shown in Table 1, the so‐ calculated values of [L]_med correspond to those that are based on the simulations in Figures 5 and 6. Among others, this equation also provides a straightforward explanation for why [L]_med is unaffected by varying the rate of ligand association for IF (Figure 6B). It also links the only minimal effect of the association rate for CS (Figure 5A) to the opposite contributions of ^minRc and k_3‐CS.

TABLE 1.

[L]_med and related parameters for Case A

Parameters	minRc‐IF (approximated)	k3‐CS/k2‐CS in nM	[L]med in nM (calculated)	[L]med in nM (simulated)a
	0.0476	0.8	16.8	16.9
Fold‐ shift in Figures 5 and 6 by changing
k3‐CS and k4‐CS
×0.1	×7.0	×10	×1.43	×1.43
×10	×0.104	×0.1	×0.96	×0.96
k3‐IF and k4‐IF
×0.1	×0.104	×1.0	×9.57	×9.52
×10	×7.0	×1.0	×0.143	×0.148
k1‐CS and k2‐CS
×0.1	×1.0	×0.1	×0.1	×0.1
×10	×1.0	×10	×10	×10
k1‐IF and k2‐IF
×0.1	×1.0	×1.0	×1.0	×1.05
×10	×1.0	×1.0	×1.0	×1.0

The ascending portion of the sigmoidal Rc_‐IF versus Log[L] plot is half‐maximal at [L]_med. This median/midpoint is calculated via equation 25 in Supporting Information Section S8 (also presented in Figure 7D) based on the k_2‐CS/k_3‐CS ratio and the simplified expression of the baseline value of the relative contribution of IF (i.e., ^minRc_‐IF as k_4‐IF/(k_4‐IF + k_4‐CS)) for Case A and variations thereof such as shown in Figures 5 and 6. Those calculated [L]_med values are already in excellent agreement with those that are obtained by non‐linear regression analysis with GraphPad Prism^® (Graphpad Software Inc.) of the F_on‐ based Rc_‐IF versus Log[L] plots (in where F_on‐ values are based on the microscopic rate constants and simulated concentrations of the different target species at equilibrium, such as related).¹⁹

^a A perfect fit between both [L]_med‐ values is obtained when expressing ^minRc_‐IF by its unabridged equation in Figure 7B (not shown). Other parameters: Please see Figure 1.

Finally, please note that the present differential equation‐ and conditional rate‐ based calculations provide closely the same Rc_‐IF versus [L] plots as the reported ones for cases whose input data were based on molecular dynamics simulations and experimental observations¹⁹, ²⁴, ²⁶ (not shown). Conclusions about the impact of microscopic rate constants on those plots (see Discussion) remain pertinent as well.

4. DISCUSSION

IF and CS pathways are increasingly considered to operate alongside within a thermodynamic cycle. This allows both of them to contribute to the final T*L complex instead of being mutually exclusive. The notion by Hammes et al.¹⁹ that binding fluxes are more appropriate than rate constants for evaluating this contribution is also gaining ground. The present article aims to provide better insight into the basic aspects of this new approach, with special focus on the connection between such fluxes and their constituent rate constants (Figure 1).

Although the concept of binding‐ or “reactive” fluxes is already pretty ancient,³⁸ the equations that were presented by Hammes et al.¹⁹ have the merit to express the “macroscopic” fluxes of each pathway (F_on for T to T*L) in terms of the “microscopic” fluxes of the intervening steps (e.g., F_1‐IF for T to TL) under equilibrium‐ as well as under non‐equilibrium conditions. The present simulations show such relationships as a function of time, the ligand concentration and of the kinetic properties of each pathway. While they confirm that F_on is chiefly dictated by the lowest of the microscopic fluxes (Figures 2 and 3), they also call attention to differences between IF and CS at equilibrium. F_on‐IF is governed by the flux of the transconformation step (F_3‐IF) at all [L] whereas F_on‐CS is successively controlled by the binding step (F_3‐CS) and the transconformation step (F_1‐CS) when [L] increases. This shift is gradual and confers a bell‐shaped profile to the F_on‐CS versus [L] plots.

The relative contribution of both pathways to T*L within a cycle is now also customary evaluated by comparing their F_on‐ values at equilibrium (here referred to as R_c‐IF = F_on‐IF/(F_on‐IF + F_on‐CS). Like all previous reports, Figure 4A shows that R_c‐IF increases with [L] until IF fully dominates for three distinct Cases. However, matching profiles can also be obtained by the accumulation‐ based approach²⁶ (Supporting Information Section S1). This correspondence is especially striking because both approaches embody different perceptions of the term “contribution”. Indeed, the former refers to a macroscopic flux at a given time point which, by definition, has to originate from T. Alternatively, the accumulation‐ based approach plays the role of an “archivist” by adding up all the net contributions each pathway to T*L during a given time frame.

Figure 4 also clearly shows that the positive relationship between R_c‐IF and [L] does not imply that CS necessarily dominates at low [L]. It is therefore of interest to find out how this parameter is governed by microscopic fluxes and even rate constants. To this end, comparing the Cases in Figure 4C, changing the k₃–k₄ tandems for each pathway (Figure 5) as well as simplifying the conditional rate‐ based equations (Figure 7B and Supporting Information Sections S2 and S8‐D) shed light on a major impact of the two k₄‘s on the baseline value of R_c‐IF (^minR_c‐IF) for a genuine IF–CS‐ composed cycle. Taken together, ^minR_c‐IF can be approximated as F_3‐IF/(F_3‐IF + F_3‐CS), such as already hinted at in Figure 4C, but also as F_4‐IF/(F_4‐IF + F_4‐CS) and even as k_4‐IF/(k_4‐IF + k_4‐CS). This owes to the equivalence between the forward‐ and reverse fluxes for each step at equilibrium as well as to the equivalence between the F_4‐IF/F_4‐CS‐ and k_4‐IF/k_4‐CS ratios. In this respect, it is of note that the ratios between the F₃‐ and the more elemental k₃‐ values are not equivalent (see Section 2.4).

Because of the limiting role of the k₄’s with respect to the dissociation of T*L via both IF and CS,⁵ it can be inferred that R_c‐IF at low [L] is essentially controlled by the rates of the bidirectional transit between T and T*L. In other words, it implies that the fastest pathway dominates. Such conclusion was previously also reached for heterobivalent ligand binding³⁹ and it is also central to a model in where TL to T*L transition goes along with the formation of a ‘lid’ that occludes bound L from the aqueous surrounding.¹⁵, ⁴⁰, ⁴¹ This shielding is considered to greatly impair the spontaneous escape of the ligand so that its dissociation is most prone to proceed via a retrograde IF mechanism.

The most effective contribution of CS can also be perceptibly extended to higher [L] by changing the transconformation rates of IF and CS (Figures 5B and 6A). Although this issue has only been scantly addressed in previous studies ⁴² it also merits particular attention since it relates to how much each pathway is able to contribute to T*L within a physiological range of [L]. While horizontal shifts of the Rc_‐IF versus [L] plots (left side) are quite arduous to interpret in terms of microscopic fluxes (right side), this is not the case when turning to the conditional rate‐ based equations. Indeed, these allow the Rc_‐IF–[L] relationship to be expressed in terms of the microscopic rate constants and [L] only (Figure 7A, see also¹³) and they also allow the median/midpoint of such plots, [L]_med, to be calculated. This equation is even surprisingly simple since it only embraces ^minRc_‐IF and the k_2‐CS/k_3‐CS ratio (Figure 7D). Those parameters fully account for the shifts of L_med in Figures 5 and 6 (Table 1) and, since F_1‐CS and F_2‐CS are equal at equilibrium, it can be inferred that k_2‐CS/k_3‐CS ratio corresponds to [L] at which the F_1‐CS‐ and F_3‐CS plots do intersect in Figure 3.

The present binding flux‐ based approaches provide better insight into how the microscopic rate constants of IF and CS pathways affect their relative contribution to T*L at equilibrium. Relying on this special condition is now common practice since it facilitates comparative studies by getting rid of time‐ related variations. Also, it is only at equilibrium that R_c‐IF can be expressed in terms of simple equations. On the backside, it is obvious that equilibrium binding is only rarely met in real‐ life situations.⁴¹ This important consideration pleads for extending the use of the present—as well as additional flux‐related approaches to more physiologically relevant time scales.²⁷, ⁴³

Ligand‐target interactions are still often classified as either IF or CS based on the shape of their k_obs versus [L] plots (e.g., Ref. [44]). Yet, while the already many reported hyperbolically decreasing plots do still point at CS, increasing plots are nowadays considered as inconclusive.¹⁷, ⁴⁵ Interestingly, the thermodynamic cycle model allows them to be biphasic (i.e., with an initial decrease and subsequent increase)²³, ²⁷ and such pattern has also been observed experimentally (e.g., Refs. [46, 47, 48, 49, 50]). Structural biology provides complementary information. Refinements in molecular dynamics simulations and in experimental techniques like nuclear magnetic resonance‐ and fluorescence spectroscopy already provided the kinetic parameters for some of the reported relative contributions of IF and CS.¹⁹, ²⁴, ²⁶ They also greatly improved our insight about the conformational plasticity of many targets. In this respect, it is now considered that CS‐ binding can take place when the unbound target is already able to adopt a “binding‐competent” conformation⁵¹ and especially when ligand binding increases the population thereof. On the other hand, IF is to be preferred when new conformations are produced. Based on a mixed profile, Sušac et al.⁵² recently concluded that agonist‐mediated adenosine A_2A receptor activation might utilize both mechanisms. The constitutive activity of many wild‐type and mutant G protein‐ coupled receptors, the existence of inverse agonists¹² and the results from above‐ mentioned simulations and measurements⁵³, ⁵⁴, ⁵⁵ point to the ability of such receptors to perform highly dynamic sampling between “inactive” and “active” conformations. Such CS‐ prone sampling has also been observed for other target proteins. The Hsp90 heat shock protein offers a striking example. Based on the ascending profile of its k_obs versus [L] plot, it was initially assumed that the antagonist geldanamycin binds to this protein via IF.¹⁵, ¹⁶, ⁵⁶ However, this profile has meanwhile been related to its conversion into a more potent species in the assay medium.⁵⁷, ⁵⁸ Instead, simulations and measurements now indicate that the involved N‐terminal domain can sample a wide range of conformations in between the fully open‐ and the ATP‐ bound closed ones⁵⁹, ⁶⁰, ⁶¹, ⁶², ⁶³ and recent kinetic considerations further suggest that the binding of related antagonists implicate both IF and CS.⁴⁵

In this respect, there is also increasing awareness that conformational changes can take place within a large range of timescales and that the energy landscape of a binding process may be funnel‐like with rapidly interconverting conformations at each bottom.⁹, ¹⁶, ⁶⁴, ⁶⁵, ⁶⁶ While some authors opted to neglect such fast transconformations,³², ³³ others rather opted to extend the CS model to an increasingly popular one in where a fast CS‐ binding precedes a slower IF‐ like conformational change of the complex.⁶⁷, ⁶⁸, ⁶⁹ Since this hybrid model is thought to allocate high selectivity (via CS) and high affinity (via IF) to drug binding,²² it could be of particular interest to pay more attention to this model in terms of fluxes.

DISCLOSURES

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

AUTHOR CONTRIBUTIONS

G. Vauquelin: conception and design of this work, generation of data and writing of this manuscript. D Maes: design of this work, generation of mathematical data and writing of this manuscript.

ETHICS APPROVAL STATEMENT

N/A.

Supporting information

Supplementary Material

Vauquelin G, Maes D. Induced fit versus conformational selection: From rate constants to fluxes… and back to rate constants. Pharmacol Res Perspect. 2021;9:e00847. 10.1002/prp2.847

DATA AVAILABILITY STATEMENT

No data have been shared.