Abstract
Molecular dynamics (MD) simulations have become an indispensable tool to investigate phase separation in model membrane systems. In particular, simulations based on coarse-grained (CG) models have found widespread use due to their increased computational efficiency, allowing for simulations of multicomponent lipid bilayers undergoing phase separation into liquid-ordered and liquid-disordered domains. Here, we show that a significant temperature difference between molecule types can artificially arise in CG MD membrane simulations with the standard Martini simulation parameters in GROMACS. In particular, the linear constraint solver (LINCS) algorithm does not converge with its default settings, resulting in serious temperature differences between molecules in a time step-dependent manner. We demonstrate that the underlying reason for this behavior is the presence of highly constrained moieties, such as cholesterol. Their presence can critically impact numerous structural and dynamic membrane properties obtained from such simulations. Furthermore, any preference of these molecules toward a certain membrane phase can lead to spatial temperature gradients, which can amplify the degree of phase separation or even induce it in compositions that would otherwise mix well. We systematically investigated the effect of the integration time step and LINCS settings on membrane properties. Our data show that for cholesterol-containing membranes, a time step of 20 fs should be combined with at least lincs_iter = 2 and lincs_order = 12, while using a time step of 30 fs requires at least lincs_iter = 3 and lincs_order = 12 to bring the temperature differences to a level where they do not perturb central membrane properties. Moreover, we show that in cases where stricter LINCS settings are computationally too demanding, coupling the lipids in multiple groups to the temperature bath offers a practical workaround to the problem, although the validity of this approach should be further verified. Finally, we show that similar temperature gradients can also emerge in atomistic simulations using the CHARMM force field in combination with settings that allow for a 5 fs integration step.
I. Introduction
Membranes play a central role in biology because they enable the structuring of cells into different compartments, such as the endoplasmic reticulum or the cell nucleus. Moreover, the plasma membrane (PM) separates the interior of living cells from its environment. It is now also clear that cellular membranes, consisting of hundreds of different lipid types and crowded with proteins, are laterally heterogeneous and contain transient membrane domains with specific biophysical properties.1−3 Moreover, these different lipid environments can have distinct roles in regulating cellular processes.4,5
To study membrane heterogeneity, complex lipid mixtures present in biological systems are not absolutely necessary. Simpler mixtures of three components are sufficient to observe differentiated phases or smaller-scale heterogeneity. Ternary mixtures of two lipid species with high and low melting temperatures (Tm) together with cholesterol (CHOL) are of particular interest, as they mimic substantially more complex biological compositions; depending on the mixture and temperature, they can undergo phase separation into liquid-ordered (Lo) and liquid-disordered (Ld) phases, the former of which is enriched in CHOL and the high-Tm lipid. These simpler mixtures have been studied extensively by means of experiments as well as theory.1−6 From a modeling perspective, molecular dynamics (MD) simulations are the obvious method of choice to study the biophysics of membrane phase separation.6,7 However, even with the currently available computing performance, demixing of lipids into Ld- and Lo-like domains by means of atomistic MD simulations is hard to achieve due to size and time scale limitations. Only a few studies have recently managed to glimpse such phenomena using all-atom models.8,9 Instead, coarse-grained (CG) MD simulations more readily provide access to the required long simulation times and large system sizes, where domain or phase boundaries do not constitute a majority of the studied membrane. This allows for systematic studies of factors affecting membrane heterogeneity at various scales.10−14
For reliable simulations of biomembranes, both the structural behavior of their constituents and the thermodynamic properties of the whole system have to be described with adequate accuracy. Temperature in an MD simulation can be controlled by coupling the system to a temperature bath, for example, using a stochastic velocity rescaling algorithm.15 The entire simulation box can be coupled to the same temperature bath; however, this can cause artifacts in heterogeneous systems.16,17 This is known as the “cold solute–hot solvent problem” where, for example, a cold protein is surrounded by an overheated solvent. To avoid such undesired artifacts, a widely accepted solution is to couple the components of systems with stable phases, such as lipid bilayers and the surrounding water, to separate temperature baths with the same target temperature. Then, the question arises as to whether coupling all membrane components inside the stable phase to the same bath ensures the correct target temperature on the whole membrane. This is especially critical when considering phase-separated membranes, where artifacts or modeling inaccuracies may influence the temperatures of certain moieties differently.
In this work, we report an artificial temperature heterogeneity in membranes that phase-separate when using CG force fields in GROMACS. These anomalies are demonstrated to affect simulations of simple ternary model membranes and a complex PM model when using the CG Martini model with its standard simulation settings.18 We show that the culprit is the presence of molecular moieties with constraints to be solved by the linear constraint solver (LINCS).19 In our case, the lipid mixtures contained cholesterol, a critical building block of biomembranes, whose Martini representation contains multiple constraints. The cooling of cholesterol due to LINCS observed in our simulations significantly impacts the degree of phase separation as well as other membrane properties. We show that the current case is not a cold solute–hot solvent problem but rather another artifact caused by inadequately converged constraints. As demonstrated in the present work, a straightforward remedy for this issue is to sacrifice some computing time to reach better convergence of the constraint equations. In cases where more stringent LINCS settings are not feasible because the associated increase in computational costs is unreasonable, using multiple temperature coupling groups may provide a potential workaround. Finally, we show that the issue with the convergence of the LINCS algorithm also compromises the validity of other simulation models that rely heavily on constraints, such as recent versions of the atomistic CHARMM force field that rely on hydrogen mass repartitioning (HMR) or virtual sites (VIS) to enable large time steps.
II. Simulation and Analysis Methods
II.I. Coarse-Grained Simulations
All simulations were performed with the CG force field Martini 220,21 and the GROMACS program package (versions 2018 and 2020).22 For cholesterol, the most recent Martini model with two virtual sites was employed.23
The ternary lipid bilayer system with a size of 30 × 30 nm2 was generated with the program insane.py,(24) and it contained 1276 dipalmitoyl-phosphatidylcholine (DPPC), 950 dilinoleoyl-phosphatidylcholine (DLiPC), and 912 cholesterol molecules (0.42/0.28/0.30 molar ratio) in a random distribution. The bilayer was solvated in a 0.15 M NaCl solution resulting in 38 917 CG water beads (of which 10% were antifreeze water beads) and 428 NaCl ion pairs. The potential energy of this initial conformation was minimized using a steepest descent algorithm, followed by two equilibration runs for 5 ps using a 1 fs time step and 500 ps using a 10 fs time step, respectively. The production run of 15 μs was performed with a time step of 20 fs. Large membrane undulations were suppressed by weak harmonic position restraints in the direction of the membrane normal applied to the DLiPC lipids of the upper leaflet. The force constant was 2 kJ mol–1 nm–2. The cutoff values for the nonbonded terms, as well as the dielectric constant, were chosen according to the recent and suggested simulation settings (the “New-RF” set).18
LINCS was used to solve the constraints with lincs_order = 4 and lincs_iter = 1. Briefly, this means that a single iteration was performed to correct for rotational lengthening of the bonds, whereas the first four terms were used in the series expansion to approximate the inverse of the coupling matrix. It is also noteworthy that GROMACS detects the triangular constraints in the CHOL topology and automatically doubles the value of lincs_order for these constraints involved.25 However, in this article, we refer to the lincs_order values set by the user, i.e., the doubling by GROMACS is not taken into account. See the original publications, refs (19) and (25), for further details on the LINCS algorithm.
The pressure was controlled using a Parrinello–Rahman barostat26 at a pressure of 1 bar (semi-isotropic coupling) using a coupling constant of τp = 12.0 ps and a compressibility of β = 3 × 10–4 bar–1. During equilibration, a Berendsen barostat27 (τp = 3.0 ps) was applied. The temperature was kept at 310 K using a velocity rescaling thermostat15 with a coupling constant of τT = 1.0 ps. The solvent beads (water, antifreeze, and ion beads) were grouped together in a single temperature coupling group. For the lipids, two different choices for the temperature coupling groups were tested. In the first case, all lipids were grouped together so that the whole system was divided into two temperature coupling groups. In the second case, each lipid type was put in an individual temperature coupling group, resulting in a total of four groups. We also performed two additional tests with either (1) a more conservative set of LINCS settings using lincs_order = 8 and lincs_iter = 2 or (2) switching the thermostat to the Nosé–Hoover one28,29 with a coupling constant of τT = 12.0 ps. For these tests, all lipids were coupled to the same thermostat.
Finally, to provide guidelines on which LINCS settings result in satisfactory small temperature gradients, we performed additional simulations on the ternary lipid mixture with various LINCS settings and integration time steps. In these simulations, all of the lipids were coupled to the same thermostat. The initial structure of the membrane corresponds to a phase-separated configuration of the main simulation after 10 μs (see the description above). We simulated the membrane for an additional 5 μs with combinations of lincs_order = 4, 6, 8, 10, or 12, lincs_iter = 1 or 2, and the integration time step = 10, 20, or 30 fs. We also simulated lincs_order = 12, lincs_iter = 3, and the integration time step = 30 fs. Again, the internal doubling of lincs_order is not taken into account here. The simulation inputs and outputs are available at DOIs 10.5281/zenodo.4453216, 10.5281/zenodo.4445341, and 10.5281/zenodo.4445314.
A complex PM model consisting of 63 different lipid types and with 30 mol % CHOL was set up in accordance with Ingólfsson et al.30 The patch size was ≈84 × 84 nm2 containing ≈27 000 lipids. The system was neutralized and solvated with a 0.15 M NaCl solution resulting in ≈417 000 CG water beads (10% antifreeze water). The simulation settings were identical to the ones of the ternary mixture described above. The production run was performed for 53.4 μs using one temperature coupling group for the lipids. The final configuration was then simulated further for 8.2 μs (cumulative simulation time of 61.6 μs) using seven temperature coupling groups for the lipids that were separated in phosphatidylcholine (PC) lipids, phosphatidylethanolamines, phosphatidylserines, gangliosides, sphingomyelins, cholesterol, and other remaining lipids such as phosphatidylinositols.
II.II. Analysis of the Coarse-Grained Simulations
The temperature calculation of the different groups of lipids was performed with the gmx traj tool specifying the option -ot using trr trajectory files that contain velocities. The obtained values for DPPC and DLiPC were readily used, as the topologies of these lipids do not contain any constraints, and thus they both have the expected 3N degrees of freedom. For the latest Martini model for cholesterol,23 the eight CG beads of CHOL would result in 3N = 24 degrees of freedom. However, the three massless virtual particles with 9 degrees of freedom do not contribute to the kinetic energy, and in addition, five constraints are present in the CHOL topology. Thus, in fact, the CHOL molecules only have 10 degrees of freedom. Since this is not taken into account by gmx traj -ot, the resulting temperature value has to be scaled by 24/10 = 2.4. The final value is in agreement with the temperature calculated with the gmx energy tool that uses the correct number of degrees of freedom. The same holds true for the temperature calculated by gmx mdrun during propagation. Similarly, a scaling factor has to be applied to some other lipid types in the PM model that also contain constraints in their topologies.
To provide a more in-depth analysis of the temperature gradients in the simulated systems, the lateral distribution of temperature was calculated by an in-house Python script using the MDAnalysis library.31 The kinetic energy was obtained from the velocities v contained in the trajectory through EK = mv2/2, where m is the mass of the particle. After using T = 2/3·EK/(kBNDoF) to calculate the temperature, where kB is Boltzmann’s constant and NDoF is the constraint-corrected number of degrees of freedom, the resulting values were binned into a two-dimensional (2D) histogram and normalized. As a check, the average temperatures per molecule type matched those calculated by gmx traj. For the sake of representation, the 2D temperature distributions were averaged along the axis parallel to the boundary between the high- and low-temperature regions, i.e., the Ld and Lo regions.
Most of the analyses of the ternary mixture were performed for the last 2 μs, but for clarity, all used time windows are given for the averaged values in the tables or figure captions. The area per lipid (APL) was calculated using the FATSLiM program.32 The area compressibility, lipid tail order, and the CHOL flip–flop rate were calculated using in-house programs. The bilayer thickness was evaluated for the PO4 beads using the gmx distance tool. The gmx mindist tool was applied for the calculation of the number of contacts between different lipid types using a cutoff distance of 0.7 nm. For the PM model, the temperature was evaluated for the last 5 μs of each temperature coupling scheme. The CHOL densities were averaged over the last 100 ns. The calculation was performed based on the position of the ROH bead (representing the CHOL hydroxyl group), which was broadened with a Gaussian kernel (σ = 3 nm)33 using the Python library MDAnalysis.31
Lateral diffusion coefficients were calculated for the simulations with different LINCS settings. First, a center of mass (COM) trajectory was created with gmx traj -oxt. Then, the mean squared displacement (MSD) of the COMs was extracted as a function of lag time (Δ), i.e., the MSD data were time-averaged and further averaged over each lipid type. The lateral motion was measured with respect to that of the entire bilayer, thus eliminating any possible drift. The MSD data were fitted in the lag time interval between 100 and 200 ns by MSD = 4DΔ, where D is the diffusion coefficient. In this interval, the MSDs are linear,34 and the sampling is still adequate for convergent results. An overview of the simulation and analysis times, as well as the screened settings, is provided in Table S1 in the Supporting Information (SI).
II.III. Atomistic Simulations and Analysis
A pure palmitoyloleoylphosphatidylcholine (POPC) membrane and a POPC membrane with 20% cholesterol were set up using the CHARMM-GUI web portal.35 These membrane patches were equilibrated and joined into a single membrane, which thus had a heterogeneous distribution of cholesterol with a CHOL-containing and a CHOL-depleted end (see Figure 1). This gradient was also maintained during the fairly short simulations. The membrane contained a total of 320 (160 + 160) POPC and 40 (40 + 0) cholesterol molecules, and it was hydrated by 50 water molecules per lipid. Water was modeled as the CHARMM-variant of the TIP3P model,36 and for the POPC and CHOL lipids, we used three variants of CHARMM36, each with its own simulation parameters: (1) Standard CHARMM36,37,38 (2) CHARMM36 model with hydrogen mass repartitioning (HMR)39 available in CHARMM-GUI with GROMACS outputs,40 and (3) CHARMM36 model with hydrogens modeled as virtual sites (VIS).41,42 For standard CHARMM36, we used the standard simulation parameters optimized for GROMACS35 with a 2 fs time step and constraints applied to bonds with hydrogen atoms. This simulation was 200 ns long. For HMR and VIS, we used constraints on all bonds, a time step of 5 fs, and the simulations were 500 ns long. For HMR, the simulation parameters were obtained from CHARMM-GUI,35 except that to maintain the nstcalcenergy parameter value, the thermostat coupling time constant was increased from 1 to 2 ps to avoid a warning in gmx grompp. For VIS, we used simulation parameters provided in DOI 10.5281/zenodo.1240161. In all cases, the lipids together and the solvent were coupled to two independent thermostats, and the first 10 ns of simulation were omitted from the analyses. The input and output files from atomistic simulations are available online at DOI 10.5281/zenodo.4475605.
Figure 1.
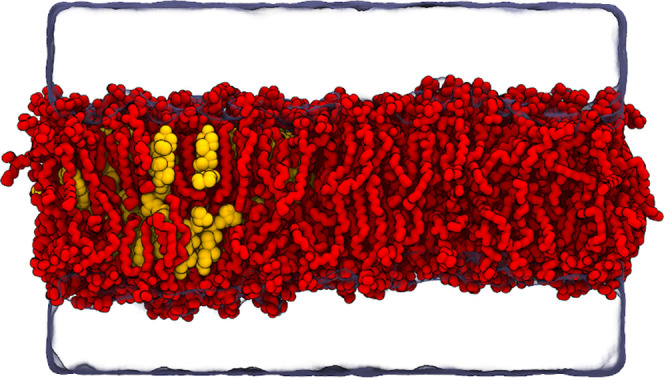
Snapshot of the atomistic system with one half of the box consisting solely of POPC (red) and the other half consisting of a mixture of POPC and cholesterol (yellow). Water is rendered as a transparent surface and all hydrogens are omitted for clarity.
The temperatures of POPC and CHOL were extracted with gmx traj -ot. All three used models have a substantial and different amount of constraints, leading to different numbers of degrees of freedom. The temperatures of each lipid type were thus corrected by the ratio of the real number of degrees of freedom reported by gmx grompp and the constraint-free value of 3 × N for a lipid group with N particles (atoms or virtual sites). The mean corrected temperature per degree of freedom of the lipid types agreed with the output of gmx energy.
III. Results and Discussion
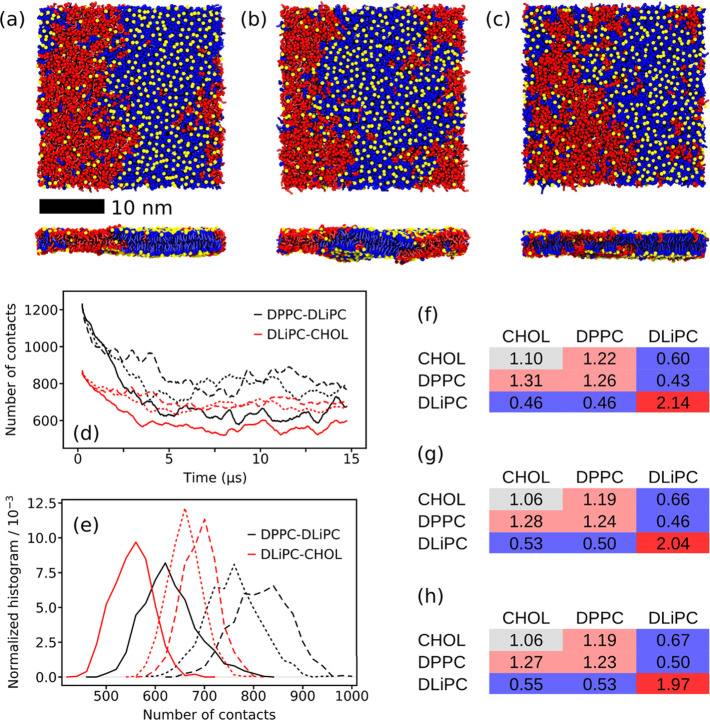
The ternary lipid mixture DPPC/DLiPC/CHOL in the ratio 0.42/0.28/0.30 shows a strong Lo/Ld phase separation in simulations with the CG Martini force field.10,33Figure 2a depicts a typical snapshot of the membrane after establishing a stable phase separation. Here, all lipids were coupled together to the temperature bath, as was the solvent, i.e., water and ions. Table 1 shows that the temperature of the whole patch is slightly lower than the reference temperature Tref = 310 K of the velocity-rescale thermostat. A closer look at the individual lipid types however reveals that their temperatures differ dramatically. While DPPC and CHOL have a lower temperature of 303.3 ± 0.2 and 302.5 ± 0.4 K, respectively, the unsaturated DLiPC has an increased temperature of 316.9 ± 0.8 K. This large difference between the two phospholipids of ≈13 K indicates that the Lo and the Ld phase must have different temperatures because they mainly consist of DPPC/CHOL and DLiPC, respectively. The temperature difference is strongly reduced when using three temperature coupling groups (see Table 1), but a small difference of ≈1 K still remains. Also, with these settings, CHOL has the lowest temperature of 306.2 ± 0.5 K in the membrane. The temperature of water is 309.5 ± 0.1 K for both simulation settings indicating a slight energy loss due to the simulation time step of 20 fs. The use of stricter LINCS settings (lincs_iter = 2 and lincs_order = 8 as recommended in ref (23)) also results in a reduced temperature difference between the lipid types (see Table 1), and the temperature difference between the whole patch and the Tref is lower than that with other settings. To check if the temperature difference with loose LINCS settings also appears with other thermostats, we performed a 15 μs long simulation using the Nosé–Hoover thermostat and only one temperature coupling group for the lipids. A temperature difference between the lipid types was again observed (see Table S2), indicating that the issue is independent of the thermostat.
Figure 2.
Membrane organization of the ternary lipid mixture DPPC/DLiPC/CHOL. (a–c) Top and side views of the DPPC (blue)/DLiPC (red)/CHOL (yellow) membrane after 15 μs of simulation. The simulations were performed using (a) one and (b) three temperature coupling groups for the lipids, respectively. In (c), stricter LINCS settings (lincs_order = 8 and lincs_iter = 2) were applied. The phospholipid headgroups are omitted for clarity, and CHOL is represented by the ROH bead only. (d) Number of contacts between DPPC–DLiPC (black) and DLiPC–CHOL (red) analyzed for the linker beads of the phospholipids and the ROH bead of CHOL. The solid lines were obtained with one temperature coupling group, the long dashed lines with three temperature coupling groups, and the short dashed lines with lincs_order = 8 and lincs_iter = 2. (e) Histograms of the number of contacts depicted in (d) calculated from the last 5 μs of simulation. Colors and line styles are identical with (d). Relative neighboring data using (f) one temperature coupling group, (g) three temperature coupling groups, and (h) lincs_order = 8 and lincs_iter = 2, respectively, calculated for the last 2 μs of simulation. Errors are below 0.01 in (f)–(h).
Table 1. Membrane Properties of the Ternary Lipid Mixture DPPC/DLiPC/CHOL Simulated Using Either One or Three Temperature Coupling Groups for the Lipids with Loose LINCS Settings (First Two Columns) or the More Conservative LINCS Options with One Coupling Group for the Lipids (the Last Column)c.
| lincs_iter = 2 | |||
|---|---|---|---|
| single temperature coupling group | three temperature coupling groups | lincs_order = 8 | |
| average membrane temperature (K)a | 308.1 ± 0.4 | 308.2 ± 0.2 | 309.3 ± 0.2 |
| temperature DPPC (K)a | 303.3 ± 0.2 | 308.0 ± 0.2 | 308.7 ± 0.2 |
| temperature DLiPC (K)a | 316.9 ± 0.8 | 309.1 ± 0.2 | 310.4 ± 0.2 |
| temperature CHOL (K)a | 302.5 ± 0.4 | 306.2 ± 0.5 | 308.9 ± 0.3 |
| temperature water(K)a | 309.6 ± 0.1 | 309.6 ± 0.1 | 309.5 ± 0.1 |
| average APL (nm2)b | 0.737 ± 0.003 | 0.736 ± 0.003 | 0.738 ± 0.003 |
| average area compressibility (mN/m)b | 377 ± 11 | 314 ± 7 | 335 ± 9 |
| average tail order DPPCb | 0.633 ± 0.003 | 0.602 ± 0.002 | 0.607 ± 0.002 |
| average tail order DLiPCb | 0.238 ± 0.001 | 0.249 ± 0.001 | 0.246 ± 0.001 |
| average bilayer thickness (nm)b | 4.07 | 4.07 | 4.07 |
| CHOL flip–flop rate (106 s–1)a | 5.12 ± 0.07 | 4.69 ± 0.04 | 4.93 ± 0.06 |
Averaged over the last 10 μs
Averaged over the last 2 μs.
All errors are standard errors and they were omitted if <0.001.
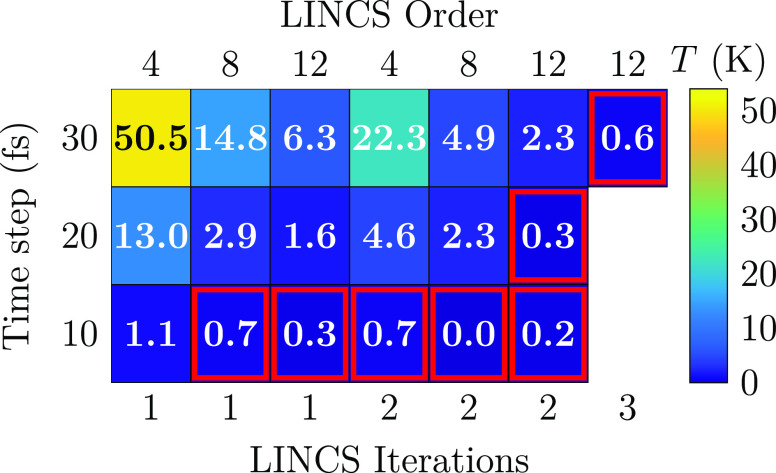
Although it is possible to minimize the temperature difference by coupling each lipid type to a different thermostat, this merely masks the underlying problem, as the thermostat forces the recovery of any lost energy. This is supported by the average temperature of the entire membrane patch being closer to Tref in the case of the stricter LINCS settings. The superiority of the use of stricter LINCS settings instead of separate coupling groups was also recently demonstrated using Martini-derived lipid models for a ternary lipid mixture.43,44 We also performed a systematic check on how different LINCS settings (lincs_iter and lincs_order) and integration time steps affect the temperature difference that builds up in the simulations of the ternary mixture. We initiated the 5 μs long simulations with various settings from a phase-separated membrane that contained a cool Lo phase consisting mainly of DPPC/CHOL, as well as a warmer DLiPC-rich Ld phase (see Section II).
The temperatures of the different lipid types stabilized quickly with the different settings. In Figure 3, we show this temperature difference between the DPPC and DLiPC lipids in the presence of cholesterol and with various tested LINCS settings and time steps. It is evident that both of these factors have a significant effect on the temperature difference of the lipids. Notably, the commonly used settings (lincs_iter = 1, lincs_order = 4) lead to a large temperature difference with the commonly used time steps of 30 fs (50.5 K) and 20 fs (13.0 K). Moreover, even the parameters recommended for the virtual site cholesterol model (lincs_iter = 2 and lincs_order = 8)23 lead to temperature differences of 4.9 and 2.3 K with the same time steps. Based on Figure 3, the larger the time step, the larger the temperature difference. Similarly, the smaller the values of the lincs_iter and lincs_order parameters, the larger the difference. Thus, the best representation of the NPT ensemble is obtained with the maximal lincs_order and lincs_iter values and minimal time steps. For the case of 10 fs, the trends are not that evident due to the error of ≈0.2 K associated with the temperatures calculated for the different lipid types. Since the DPPC-rich Lo phase contains some DLiPC and vice versa for the Ld phase, the spatial temperature differences might be underestimated by the analysis shown in Figure 3. Indeed, as demonstrated in Figures S1 and S2 in the SI, the local temperatures can vary by up to 70 K. In both figures, the temperatures are averaged over the axis parallel to the phase boundary, which is the vertical axis in Figure 2a–c.
Figure 3.
Temperature difference of DPPC and DLiPC lipids with selected LINCS settings in the ternary DPPC/DLiPC/CHOL mixture. The last 4.9 of the 5 μs long simulations were used for the analysis. For a complete set of data, see Figure S3 in the SI. The error estimates for the lipid temperatures from block averaging are of the order of 0.2 K (10 fs), 0.3 K (20 fs), and 0.4 (30 fs).
In addition to scanning the different LINCS settings and time steps, we also performed two additional checks with the same protocol. First, we repeated the simulation with lincs_order = 4. lincs_iter = 1 and a time step of 20 fs with the original Martini cholesterol model.20,45 The temperature difference between DPPC and DLiPC again built up to ≈20 K, indicating that the virtual sites on the new CHOL model23 are not the ones causing the energy conservation issue, but rather it has persisted in every Martini simulation containing CHOL (and likely some other molecules with similar complex constraint constructions). Second, we repeated the simulation once more with a time step of 20 fs and using the SHAKE46 constraint algorithm. SHAKE is not particularly handy in modern simulations due to the challenges in its parallelization.47 Importantly, with SHAKE, no temperature difference was observed between DPPC and DLiPC, indicating that the differences observed in other simulations are solely due to the LINCS algorithm and the low values used for lincs_order and lincs_iter. With these settings, the constraints are not converged, and thus the amount of virtual work they perform is not zero, as expected from a properly converged constraint algorithm.48
However, the fundamental reason for performing CG simulations is that they are computationally efficient. Therefore, the time step should be as large as possible, and the constraint algorithm should not lead to major computational overhead. Fortunately, based on our benchmarks across desktop computers and computer clusters using various numbers of computing nodes, the overhead of LINCS even with the strict settings (lincs_iter = 2, lincs_order = 12) resulted in ≈4–6% performance loss depending on the number of computing nodes used, with a single node providing the smallest performance penalty. When GPUs were used, we observed losses as large as ≈23% with the probed LINCS settings. As shown in Figure 3, the temperature differences are further suppressed by increasing lincs_iter to 3 while keeping lincs_order equal to 12. For these settings, we observed a performance loss of 10% with a single computing node. However, the performance certainly depends on the computing architecture used and the simulation system and should therefore be benchmarked separately for each study. In all, our results suggest a fairly modest performance hit, indicating that there is no LINCS-related reason not to use the maximum time step at which the simulation is stable, as a reasonable convergence of constraints can be achieved by modifying the LINCS settings likely without sacrificing all of the gains of an increased time step. A key question then is regarding the level of temperature difference that is acceptable. This naturally depends on the property of interest, and a few examples are provided below.
Figure 2a depicts the bilayer patch simulated with one temperature coupling group for all lipids and the loose LINCS settings (lincs_iter = 1 and lincs_order = 4). Upon visual inspection, the bilayer shown in Figure 2b appears to be slightly less phase-separated than the one in Figure 2a. Except for the temperature coupling of the lipids, the simulations were performed with identical settings. Here, the three lipid types were coupled separately to the temperature bath. By analyzing direct lipid–lipid contacts as well as neighboring lipids, we will get a quantitative picture to see if the impression from Figure 2a and b holds. The distributions of the DPPC–DLiPC and DLiPC–CHOL contacts are depicted in Figure 2e. Both distributions clearly show an increase in the number of contacts. The average DPPC–DLiPC contacts increase by 29% from 640 ± 27 to 828 ± 46 and the average DLiPC–CHOL contacts by 25% from 563 ± 13 to 702 ± 5 (see Table S3). The shift of the number of contacts is also reflected in the normalized numbers of neighbors. They are depicted in Figure 2f and g for both systems and show a consistent change toward reduced phase separation. This means all numbers are closer to a random statistical distribution of 1. Altogether, the contact analysis and the number of neighbors show that a lower degree of phase separation is obtained when each lipid type is coupled separately to a temperature bath ensuring the correct temperature in both phases. A similarly lower degree of phase separation coupled with a smaller temperature difference among the lipid types is obtained with stricter LINCS settings of lincs_iter = 2 and lincs_order = 8 (Figure 2c–e, and h).
A look at other structural membrane properties shown in Table 1, namely, the APL, area compressibility, tail order, and bilayer thickness, reveals different sensitivities to the different temperatures in the lipid phases. While the average APL of the membrane and the bilayer thickness do not reveal any changes, the picture changes for the area compressibility and the tail order. The area compressibility becomes lower using three temperature coupling groups, i.e., when the lipid temperatures are closer to Tref. This indicates that the compressibility of the Ld phase majorly formed by DLiPC dominates the compressibility observed for the whole membrane patch. The tail order is sensitive to the temperature changes as well and changes in the expected way. Thus, the order increases with reduced temperature and vice versa.
The cholesterol flip–flop rate is a dynamic property, which behaves unexpectedly at first sight. While the CHOL temperature increases and the DPPC tail order decreases with separate temperature coupling groups for the lipid types, the CHOL flip–flop rate decreases by 8% from 5.12 ± 0.07 to 4.69 ± 0.04 μs–1. However, several MD simulation studies showed that the flip–flop preferably occurs in the disordered Ld phase due to a lower free energy barrier.49−51 The decrease of the flip–flop rate observed here is perfectly in line with the flip–flop taking place in the vicinity of DLiPC, since DLiPC becomes more ordered in contrast to DPPC, because the lipids are coupled separately to a thermostat.
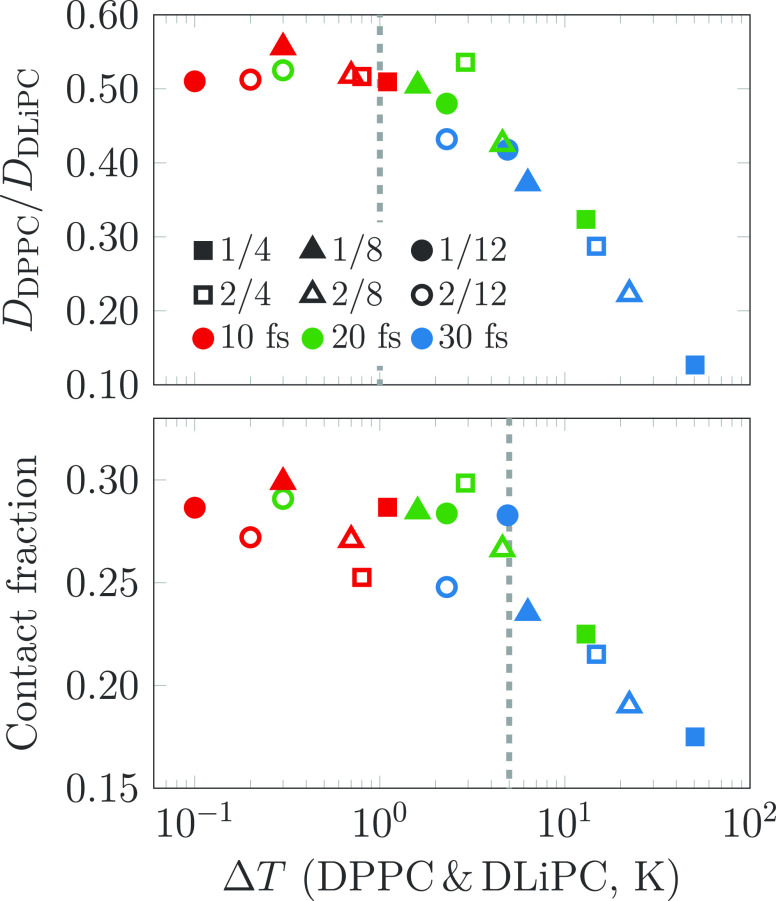
We also studied the effect of temperature differences between DPPC and DLiPC caused by different time steps and various LINCS settings on selected membrane properties. The contact fraction,100 describing the degree of phase separation, is shown as a function of the temperature difference between DLiPC and DPPC (ΔT) in the bottom panel of Figure 4, whereas the ratio of the diffusion coefficients of DPPC and DLiPC is shown in the top panel. Diffusion coefficient ratios seem to converge only at ΔT < 1 K, whereas contact fractions are unaffected up to ΔT values of 4 K. This highlights the requirement for a properly converged constraint algorithm. The LINCS settings that fulfill the requirement for the stricter threshold of 1 K are highlighted in red in Figure 3; with a time step of 30 fs, lincs_iter = 3 and lincs_order = 12 are required, whereas with a time step of 20 fs, lincs_iter = 2 suffices. Thus, the large energy drain observed in simulations with constraints has possibly affected the properties extracted from numerous Martini simulations containing molecules with complex constraint constructions, as the looser LINCS settings (lincs_iter = 1, lincs_order = 4) have been commonly used.
Figure 4.
Contact fraction, describing lipid mixing, and the ratio of the lateral diffusion coefficients of DPPC and DLiPC as a function of the temperature difference of DLiPC and DPPC. The diffusion coefficients and contact fractions were extracted from the last 2 and 1 μs of the 5 μs simulations, respectively. The temperature difference is due to the loose settings of LINCS, which has far-reaching consequences regarding the static and dynamic properties of the simulated systems. All of the tested LINCS settings are shown in Figure S4 in the SI. We estimate that the diffusion coefficient ratios converge at temperature differences below 1 K, whereas the contact fractions are less sensitive, and even temperature differences of 4 K do not seem to affect the results significantly. These estimates are highlighted by dashed lines. The LINCS settings that fulfill the stricter criterion of the 1 K difference are highlighted in red in Figure 3.
In the simulation of the complex PM model, different temperatures emerge for different groups of lipids similar to the ternary lipid mixture. Figure 5a shows the temperatures of seven groups of lipids for the last 5 μs of simulation using one and seven temperature coupling groups, respectively. The average temperatures of CHOL and the gangliosides (GM lipids) are about ΔT = 11 K below Tref = 310 K (see Figure 5b). An analysis of the CHOL density depicted in Figure 5c demonstrates that here also, the formation of heterogeneities in the patch is sensitive to the temperatures of the lipid groups. While the formation of regions that are strongly enriched and depleted in CHOL can be observed in the case of the one temperature coupling group (left in Figure 5c), the density is much more homogeneous with seven temperature coupling groups (right in Figure 5c).
Figure 5.
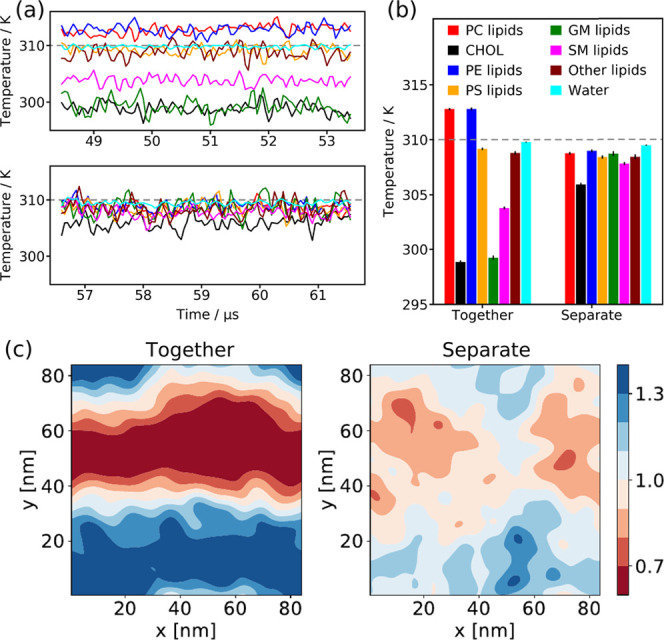
Impact of the temperature coupling groups on large-scale PM simulations. (a) Temperature of the different lipid groups (for the color scheme, see (b)) simulated with one (top) and seven (bottom) temperature coupling groups, respectively. In addition, the water temperature is plotted. The gray dashed line indicates Tref = 310 K. (b) Average temperature of the different lipid groups and water depicted in (a). (c) Cholesterol density in the outer PM leaflet averaged over the last 100 ns of simulation with the lipids coupled together (left, one group) and separate (right, seven groups) to the temperature bath. The color scale shows the enrichment and depletion of CHOL relative to the average CHOL concentration in the outer leaflet.
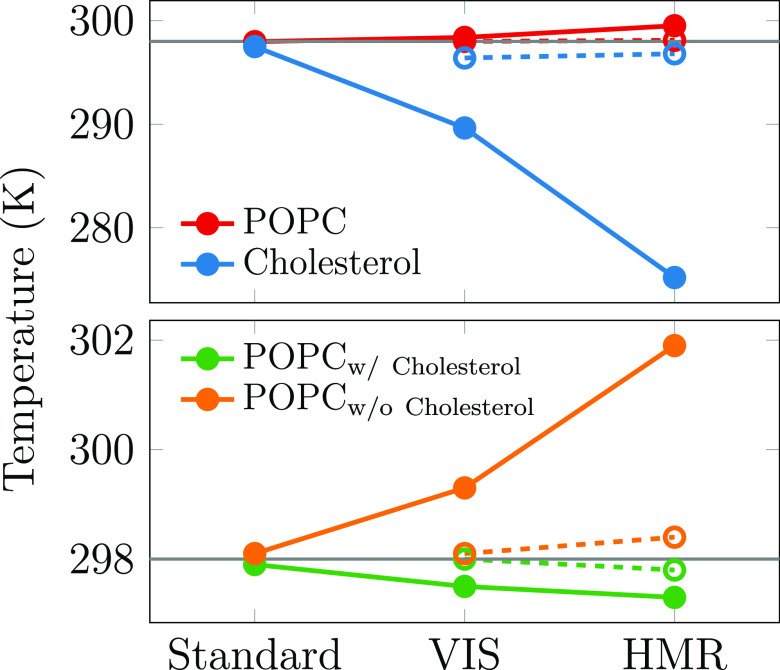
Finally, we also performed atomistic simulations of a cholesterol/POPC membrane using (1) the CHARMM36 force field with standard models and simulation parameters,37,38 (2) the CHARMM36 model with hydrogen mass repartitioning (HMR)39 available in CHARMM-GUI with GROMACS outputs,40 and (3) the CHARMM36 model with hydrogens modeled as virtual sites (VIS).41,42 The latter two apply plenty of constraints and thus allow for an increase of the simulation time step to 5 fs, whereas the standard CHARMM36 model uses fewer constraints and a 2 fs time step. As demonstrated in Figure 6, the HMR and VIS approaches lead to uneven temperatures of different molecule types. CHOL molecules are on average 24.3 K (HMR) or 8.7 K (VIS) cooler than the POPC lipids in the respective systems. When more strict LINCS settings of lincs_iter = 2 and lincs_order = 8 are used for HMR and VIS models, the temperature difference is suppressed, as demonstrated by the empty circles and the dashed lines in Figure 6. However, with the standard CHARMM36 force field, this temperature difference drops to a mere 0.5 K even with the default LINCS settings of lincs_iter = 1 and lincs_order = 4. In the membrane with a CHOL-free and a CHOL-containing side, the poorly convergent constraints on CHOL molecules also affect other lipids in their neighborhood, akin to what happens to CHOL-associated DPPC in the CG simulations. Indeed, we observe a spatial temperature gradient with the POPC molecules with and without nearby CHOL. The temperature difference is 4.6 K for VIS, 1.8 K for HMR, and 0.2 K for the standard CHARMM36 with the default LINCS settings, yet the HMR and VIS models again behave reasonably well with stricter LINCS parameters. This demonstrates that the issue is not only limited to the molecules with inadequately behaving constraints but that it can also affect the temperatures of other molecules in their vicinity. In systems containing a heterogeneous lipid distribution, this can lead to spatial temperature gradients. In all of the described atomistic simulations, gmx energy reports a mean lipid temperature of 298.0 K, and the mean temperature of a degree of freedom calculated from the values in Figure 6 are within 0.2 K of this value. These simulations thus also highlight another important, and so far scarcely checked, property of converged equilibrium simulations, that is, the uniform spatially and moleculewise distributed temperature.
Figure 6.
Temperatures of (all) POPC and cholesterol molecules (top panel) and the POPC molecules in cholesterol-containing and cholesterol-depleted ends of the simulated membrane (bottom panel). The open symbols and dashed lines show values for VIS and HMR models simulated with lincs_iter = 2 and lincs_order = 8. The gray line shows the target temperature of 298 K.
IV. Summary and Conclusions
Our CG MD simulations of a ternary DPPC/DLiPC/CHOL mixture with the Martini force field showed a temperature difference between the Lo-favoring DPPC and the Ld-favoring DLiPC of ΔT ≈ 13 K when using the common loose LINCS settings of lincs_iter = 1 and lincs_order = 4 and coupling the lipids to a single thermostat. We identified the loosely solved constraints in the cholesterol topology as a source of the temperature difference. As a consequence, the temperature of the Lo phase is reduced and that of the Ld phase is greatly increased. Our systematic investigation of the interplay between the time step and the LINCS settings revealed that this can be remedied by modifying the lincs_iter and lincs_order parameters. For a time step of 20 fs, at least lincs_iter = 2 and lincs_order = 12 should be chosen, whereas for a 30 fs time step, the even higher settings of lincs_iter = 3 andlincs_order = 12 are required to suppress the temperature difference between the lipid types to less than 1 K. This 1 K threshold was selected based on the convergence of lipid dynamics, but not all of the studied properties are equally sensitive. Updated GROMACS mdp files will be provided for Martini users at www.cgmartini.nl.
Of course, the proper convergence of the constraint algorithm comes at an additional computational cost; in the ternary lipid patch tested here, lincs_iter = 2 and lincs_order = 12 result in a ≈6% performance loss on a single node with 128 CPU cores, whereas for the lincs_iter = 3 and lincs_order = 12 settings, this increases to ≈10%. The numbers seem to increase somewhat upon parallelization to multiple nodes, and with the use of GPUs, even 20% performance hits were observed. Thus, in systems with many more constraints such as polymer melts,52,53 stricter LINCS settings might not be computationally feasible. An alternative, though not ideal, workaround is the use of multiple temperature coupling groups. We showed that a consistent temperature in the phase-separated membrane can be recovered when coupling the saturated and unsaturated lipid types and cholesterol to individual temperature baths.
For cholesterol-containing lipid bilayers, we demonstrated that the degree of phase separation is affected by the temperature difference. This is not only the case for the ternary mixture but also for more complex systems such as a large-scale PM lipid mixture. Here, the enrichment and depletion in CHOL is much more pronounced if one temperature coupling group for the lipids is used, which results in a reduced temperature of primarily CHOL and gangliosides, both enriched in Lo domains. In addition, our analysis revealed that besides the degree of phase separation, the lipid tail order, area compressibility, and the CHOL flip–flop rate are also affected. In contrast, the overall APL and the bilayer thickness remain unchanged. Previously, we demonstrated that the temperature difference can even induce phase separation in models that do not show any demixing when the temperature is evenly distributed among lipid types.44
Importantly, not only CG MD simulations but also atomistic simulations with many constraints such as VIS or HMR where larger time steps of 5 fs are used suffer from uneven temperatures of different molecule types when loose LINCS settings are applied. To avoid artificial temperature gradients in the future, we recommend monitoring the temperature of different components in the system. In case a temperature gradient develops, stricter LINCS settings or the workaround of multiple temperature coupling groups should be considered.
Finally, it is worth asking why the coarse-grained CHOL poses such a difficulty for the LINCS algorithm. Nonconverged constraints, regardless of the algorithm, lead to the loss of energy19,25,54,55 and subsequently to cooling. For instance, Table 2 of ref (19) shows a negative energy drift during 4 ps long simulations of a 32 residue peptide, which increases with reduced accuracy of the constraint algorithms LINCS and SHAKE. Similar results were observed for a villin headpiece,25 a box of SPC water,54 and ubiquitin.55 The Martini CHOL parametrization contains two obtuse triangles that share an edge. This configuration results in highly coupled constraints that in the LINCS algorithm lead to high eigenvalues of the constraint coupling matrix (see original papers for details of the LINCS implementation in refs (19) and (25)). For example, typical sp3- and sp2-hybridized bonds present in all-atom systems give eigenvalues of around 0.4, which allow for the convergence of the LINCS algorithm with the standard settings of lincs_iter = 1 and lincs_order = 4.25 However, with an eigenvalue of 1.0, LINCS fails to converge entirely regardless of the values of lincs_iter and lincs_order used. Unfortunately, the eigenvalues of the coarse-grained CHOL are very close to this value. Importantly, the use of a smaller time step such as 10 fs leads to a smaller energy drift, although without affecting the convergence of LINCS per se. The resulting smaller energy drifts are better handled by a temperature bath.
Acknowledgments
The authors thank Prof. Berk Hess for a fruitful discussion regarding the workings of LINCS. M.J., H.M.-S., and B.F. acknowledge the support from the Czech Science Foundation (EXPRO grant 19-26854X). M.J. thanks CSC, IT Center for Science, for computational resources and the Emil Aaltonen foundation for funding. S.T. acknowledges the support from the Alfons und Gertrud Kassel foundation, the Dr. Rolf M. Schwiete foundation, and the Center for Multiscale Modelling in Life Sciences (CMMS) sponsored by the Hessian Ministry of Science and Art. S.T. and S.J.M. thank the Center for Information Technology of the University of Groningen for providing access to the Peregrine high performance computing cluster and the National Computing Facilities Foundation (NCF) of The Netherlands Organization for Scientific Research (NWO) for providing access to the Dutch national supercomputer Cartesius.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.1c03665.
Details about the simulation times, analysis times, and screened simulation settings; spatially resolved temperature gradients; results with a Nosé–Hoover thermostat; average number of contacts in the ternary lipid mixture; and details about the temperature difference and the membrane properties with different LINCS settings (PDF)
Author Contributions
∥ S.T. and M.J. contributed equally to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Sezgin E.; Levental I.; Mayor S.; Eggeling C. The mystery of membrane organization: composition, regulation and roles of lipid rafts. Nat. Rev. Mol. Cell Biol. 2017, 18, 361. 10.1038/nrm.2017.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veatch S. L.; Cicuta P.; Sengupta P.; Honerkamp-Smith A.; Holowka D.; Baird B. Critical fluctuations in plasma membrane vesicles. ACS Chem. Biol. 2008, 3, 287–293. 10.1021/cb800012x. [DOI] [PubMed] [Google Scholar]
- Moon S.; Yan R.; Kenny S. J.; Shyu Y.; Xiang L.; Li W.; Xu K. Spectrally resolved, functional super-resolution microscopy reveals nanoscale compositional heterogeneity in live-cell membranes. J. Am. Chem. Soc. 2017, 139, 10944–10947. 10.1021/jacs.7b03846. [DOI] [PubMed] [Google Scholar]
- Cheng X.; Smith J. C. Biological membrane organization and cellular signaling. Chem. Rev. 2019, 119, 5849–5880. 10.1021/acs.chemrev.8b00439. [DOI] [PubMed] [Google Scholar]
- Doktorova M.; Symons J. L.; Levental I. Structural and functional consequences of reversible lipid asymmetry in living membranes. Nat. Chem. Biol. 2020, 16, 1321–1330. 10.1038/s41589-020-00688-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink S. J.; Corradi V.; Souza P. C.; Ingólfsson H. I.; Tieleman D. P.; Sansom M. S. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. 10.1021/acs.chemrev.8b00460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingólfsson H. I.; Arnarez C.; Periole X.; Marrink S. J. Computational ‘microscopy’ of cellular membranes. J. Cell Sci. 2016, 129, 257–268. 10.1242/jcs.176040. [DOI] [PubMed] [Google Scholar]
- Hakobyan D.; Heuer A. Phase separation in a lipid/cholesterol system: comparison of coarse-grained and united-atom simulations. J. Phys. Chem. B 2013, 117, 3841–3851. 10.1021/jp312245y. [DOI] [PubMed] [Google Scholar]
- Gu R.-X.; Baoukina S.; Tieleman D. P. Phase separation in atomistic simulations of model membranes. J. Am. Chem. Soc. 2020, 142, 2844–2856. 10.1021/jacs.9b11057. [DOI] [PubMed] [Google Scholar]
- Risselada H. J.; Marrink S. J. The molecular face of lipid rafts in model membranes. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 17367–17372. 10.1073/pnas.0807527105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baoukina S.; Rozmanov D.; Tieleman D. P. Composition fluctuations in lipid bilayers. Biophys. J. 2017, 113, 2750–2761. 10.1016/j.bpj.2017.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingólfsson H. I.; Bhatia H.; Zeppelin T.; Bennett W. D.; Carpenter K. A.; Hsu P.-C.; Dharuman G.; Bremer P.-T.; Schiøtt B.; Lightstone F. C.; et al. Capturing biologically complex tissue-specific membranes at different levels of compositional complexity. J. Phys. Chem. B 2020, 124, 7819–7829. 10.1021/acs.jpcb.0c03368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackerman D. G.; Feigenson G. W. Multiscale modeling of four-component lipid mixtures: domain composition, size, alignment, and properties of the phase interface. J. Phys. Chem. B 2015, 119, 4240–4250. 10.1021/jp511083z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X.; Lorent J. H.; Skinkle A. D.; Levental K. R.; Waxham M. N.; Gorfe A. A.; Levental I. Domain stability in biomimetic membranes driven by lipid polyunsaturation. J. Phys. Chem. B 2016, 120, 11930–11941. 10.1021/acs.jpcb.6b06815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Cheng A.; Merz K. M. Application of the nosé- hoover chain algorithm to the study of protein dynamics. J. Phys. Chem. A 1996, 100, 1927–1937. 10.1021/jp951968y. [DOI] [Google Scholar]
- Lingenheil M.; Denschlag R.; Reichold R.; Tavan P. The “hot-solvent/cold-solute” problem revisited. J. Chem. Theory Comput. 2008, 4, 1293–1306. 10.1021/ct8000365. [DOI] [PubMed] [Google Scholar]
- De Jong D. H.; Baoukina S.; Ingólfsson H. I.; Marrink S. J. Martini straight: Boosting performance using a shorter cutoff and GPUs. Comput. Phys. Commun. 2016, 199, 1–7. 10.1016/j.cpc.2015.09.014. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; De Vries A. H. The martini force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Tieleman D. P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Melo M.; Ingólfsson H.; Marrink S. Parameters for martini sterols and hopanoids based on a virtual-site description. J. Chem. Phys. 2015, 143, 243152 10.1063/1.4937783. [DOI] [PubMed] [Google Scholar]
- Wassenaar T. A.; Ingólfsson H. I.; Böckmann R. A.; Tieleman D. P.; Marrink S. J. Computational lipidomics with insane: a versatile tool for generating custom membranes for molecular simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. 10.1021/acs.jctc.5b00209. [DOI] [PubMed] [Google Scholar]
- Hess B. P-lincs: A parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 2008, 4, 116–122. 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Berendsen H. J.; Postma J.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
- Hoover W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
- Ingólfsson H. I.; Melo M. N.; van Eerden F. J.; Arnarez C.; Lopez C. A.; Wassenaar T. A.; Periole X.; de Vries A. H.; Tieleman D. P.; Marrink S. J. Lipid organization of the plasma membrane. J. Am. Chem. Soc. 2014, 136, 14554–14559. 10.1021/ja507832e. [DOI] [PubMed] [Google Scholar]
- Gowers R. J.; Linke M.; Barnoud J.; Reddy T. J. E.; Melo M. N.; Seyler S. L.; Domanski J.; Dotson D. L.; Buchoux S.; Kenney I. M.. et al. MDanalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations; Los Alamos National Laboratory: Los Alamos, NM, 2019.
- Buchoux S. Fatslim: a fast and robust software to analyze md simulations of membranes. Bioinformatics 2017, 33, 133–134. 10.1093/bioinformatics/btw563. [DOI] [PubMed] [Google Scholar]
- Thallmair S.; Ingólfsson H. I.; Marrink S. J. Cholesterol flip-flop impacts domain registration in plasma membrane models. J. Phys. Chem. Lett. 2018, 9, 5527–5533. 10.1021/acs.jpclett.8b01877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Javanainen M.; Hammaren H.; Monticelli L.; Jeon J.-H.; Miettinen M. S.; Martinez-Seara H.; Metzler R.; Vattulainen I. Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes. Faraday Discuss. 2013, 161, 397–417. 10.1039/C2FD20085F. [DOI] [PubMed] [Google Scholar]
- Lee J.; Cheng X.; Swails J. M.; Yeom M. S.; Eastman P. K.; Lemkul J. A.; Wei S.; Buckner J.; Jeong J. C.; Qi Y.; et al. Charmm-gui input generator for namd, gromacs, amber, openmm, and charmm/openmm simulations using the charmm36 additive force field. J. Chem. Theory Comput. 2016, 12, 405–413. 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Klauda J. B.; Venable R. M.; Freites J. A.; O’Connor J. W.; Tobias D. J.; Mondragon-Ramirez C.; Vorobyov I.; MacKerell A. D. Jr.; Pastor R. W. Update of the charmm all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim J. B.; Rogaski B.; Klauda J. B. Update of the cholesterol force field parameters in charmm. J. Phys. Chem. B 2012, 116, 203–210. 10.1021/jp207925m. [DOI] [PubMed] [Google Scholar]
- Balusek C.; Hwang H.; Lau C. H.; Lundquist K.; Hazel A.; Pavlova A.; Lynch D. L.; Reggio P. H.; Wang Y.; Gumbart J. C. Accelerating membrane simulations with hydrogen mass repartitioning. J. Chem. Theory Comput. 2019, 15, 4673–4686. 10.1021/acs.jctc.9b00160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y.; Lee J.; Smith I. P. S.; Lee H.; Kim S.; Qi Y.; Klauda J. B.; Widmalm G.; Khalid S.; Im W. Charmm-gui supports hydrogen mass repartitioning and different protonation states of phosphates in lipopolysaccharides. J. Chem. Inf. Model. 2021, 831. 10.1021/acs.jcim.0c01360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loubet B.; Kopec W.; Khandelia H. Accelerating all-atom md simulations of lipids using a modified virtual-sites technique. J. Chem. Theory Comput. 2014, 10, 5690–5695. 10.1021/ct500100f. [DOI] [PubMed] [Google Scholar]
- Olesen K.; Awasthi N.; Bruhn D. S.; Pezeshkian W.; Khandelia H. Faster simulations with a 5 fs time step for lipids in the charmm force field. J. Chem. Theory Comput. 2018, 14, 3342–3350. 10.1021/acs.jctc.8b00267. [DOI] [PubMed] [Google Scholar]
- Carpenter T. S.; López C. A.; Neale C.; Montour C.; Ingólfsson H. I.; Di Natale F.; Lightstone F. C.; Gnanakaran S. Capturing phase behavior of ternary lipid mixtures with a refined martini coarse-grained force field. J. Chem. Theory Comput. 2018, 14, 6050–6062. 10.1021/acs.jctc.8b00496. [DOI] [PubMed] [Google Scholar]
- Javanainen M.; Fabian B.; Martinez-Seara H.. “Comment on” Capturing Phase Behavior of Ternary Lipid Mixtures with a Refined Martini Coarse-Grained Force Field. 2020, arXiv:2009.07767. arXiv.org e-Print archive. https://arxiv.org/abs/2009.07767.
- Marrink S. J.; de Vries A. H.; Harroun T. A.; Katsaras J.; Wassall S. R. Cholesterol shows preference for the interior of polyunsaturated lipid membranes. J. Am. Chem. Soc. 2008, 130, 10–11. 10.1021/ja076641c. [DOI] [PubMed] [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Elber R.; Ruymgaart A. P.; Hess B. Shake parallelization. Eur. Phys. J.: Spec. Top. 2011, 200, 211–223. 10.1140/epjst/e2011-01525-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray S.; Shamanna J. On virtual displacement and virtual work in lagrangian dynamics. Eur. J. Phys. 2006, 27, 311. 10.1088/0143-0807/27/2/014. [DOI] [Google Scholar]
- Bennett W. F. D.; MacCallum J. L.; Hinner M. J.; Marrink S. J.; Tieleman D. P. Molecular view of cholesterol flip-flop and chemical potential in different membrane environments. J. Am. Chem. Soc. 2009, 131, 12714–12720. 10.1021/ja903529f. [DOI] [PubMed] [Google Scholar]
- Bennett W. F. D.; Tieleman D. P. Molecular simulation of rapid translocation of cholesterol, diacylglycerol, and ceramide in model raft and nonraft membranes. J. Lipid Res. 2012, 53, 421–429. 10.1194/jlr.M022491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu R.-X.; Baoukina S.; Tieleman D. P. Cholesterol flip-flop in heterogeneous membranes. J. Chem. Theory Comput. 2019, 15, 2064–2070. 10.1021/acs.jctc.8b00933. [DOI] [PubMed] [Google Scholar]
- Barnoud J.; Rossi G.; Marrink S. J.; Monticelli L. Hydrophobic compounds reshape membrane domains. PLoS Comput. Biol. 2014, 10, e1003873. 10.1371/journal.pcbi.1003873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alessandri R.; Uusitalo J. J.; de Vries A. H.; Havenith R. W. A.; Marrink S. J. Bulk heterojunction morphologies with atomistic resolution from coarse-grain solvent evaporation simulations. J. Am. Chem. Soc. 2017, 139, 3697–3705. 10.1021/jacs.6b11717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alessandri R.; Grünewald F.; Marrink S. J. The martini model in materials science. Adv. Mater. 2021, 2008635 10.1002/adma.202008635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kräutler V.; van Gunsteren W. F.; Hünenberger P. H. A fast shake algorithm to solve distance constraint equations for small molecules in molecular dynamics simulations. J. Comput. Chem. 2001, 22, 501–508. . [DOI] [Google Scholar]
- Eastman P.; Pande V. S. Energy conservation as a measure of simulation accuracy. bioRxiv 2016, 083055 10.1101/083055. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.