Interphase Chromatin Undergoes a Local Sol-Gel Transition Upon Cell Differentiation

Abstract

Cell differentiation, the process by which stem cells become specialized cells, is associated with chromatin reorganization inside the cell nucleus. Here, we measure the chromatin distribution and dynamics in embryonic stem cells in vivo before and after differentiation. We find that undifferentiated chromatin is less compact, more homogeneous and more dynamic than differentiated chromatin. Further, we present a noninvasive rheological analysis using intrinsic chromatin dynamics, which reveals that undifferentiated chromatin behaves like a Maxwell fluid, while differentiated chromatin shows a coexistence of fluid-like (sol) and solid-like (gel) phases. Our data suggest that chromatin undergoes a local sol-gel transition upon cell differentiation, corresponding to the formation of the more dense and transcriptionally inactive heterochromatin.

Material properties of the genome are critical for its proper function and organization inside the cell nucleus. Chromatin, the functional form of DNA in cells, consists of DNA polymer and associated proteins [1, 2]. About two meters of DNA are packed inside a human cell nucleus, which is ~ 10 μm in diameter [3]. Chromatin serves as the template for cellular processes such as gene expression and genome replication [1], hence its rheological behavior directly impacts the timescales and length scales of all biological processes [4].

In multicellular organisms, major reorganization of chromatin occurs during cell differentiation: Stem cells, which are undifferentiated, become specialized, i.e. differentiated, such as neurons or blood cells [5, 6]. During this process, rheology of the entire cell changes, nuclear size increases, nuclear compliance decreases, while the genome size remains unchanged [7–11]. Chromatin is rearranged from a homogeneous to heterogeneous distribution in the nucleus, forming patches of dense heterochromatin surrounded by less dense euchromatin, containing inactive and active genes, respectively [12, 13]. How this affects genome’s physical properties remains unclear.

In this work, we posit that the physical reorganization of chromatin occurring during cell differentiation leads to changes in its rheology. To test this hypothesis we monitor chromatin distribution and dynamics in mouse embryonic stem cells (ESCs) and their differentiated progeny, and seek dynamical and rheological signatures of a phase transition. Such a phase transition could strongly impact gene regulation by affecting the local accessibility of the genome upon cell differentiation.

To visualize chromatin distribution and dynamics before and after cell differentiation, we first observe ESCs with fluorescently labeled chromatin (histone H2B-GFP) using spinning disc confocal microscopy and perform Displacement Correlation Spectroscopy (DCS) [14]. Next, we differentiate ESCs using retinoic acid, which promotes formation of neuronal cells, and carry out the same measurements (see Supplemental Material [15–17]). The observed differences upon differentiation are striking: Chromatin becomes less mobile and its distribution visibly heterogeneous. We present evidence that upon differentiation chromatin undergoes a local sol-gel transition, leading to the formation of solid-like (gel) heterochromatin patches immersed in a fluid-like (sol) euchromatin.

First, we evaluate chromatin distribution in both undifferentiated and differentiated cells by analyzing their H2B-GFP signal, which is a reliable marker of chromatin position and its relative compaction [14, 20]. The difference between the undifferentiated and differentiated states is stark: While the former exhibits a more homogeneous H2B-GFP signal with only a few small higher intensity areas [Fig. 1(a)], the latter displays a strong ‘patchiness’ of H2B-GFP signal [Fig. 1(c)].

FIG. 1.

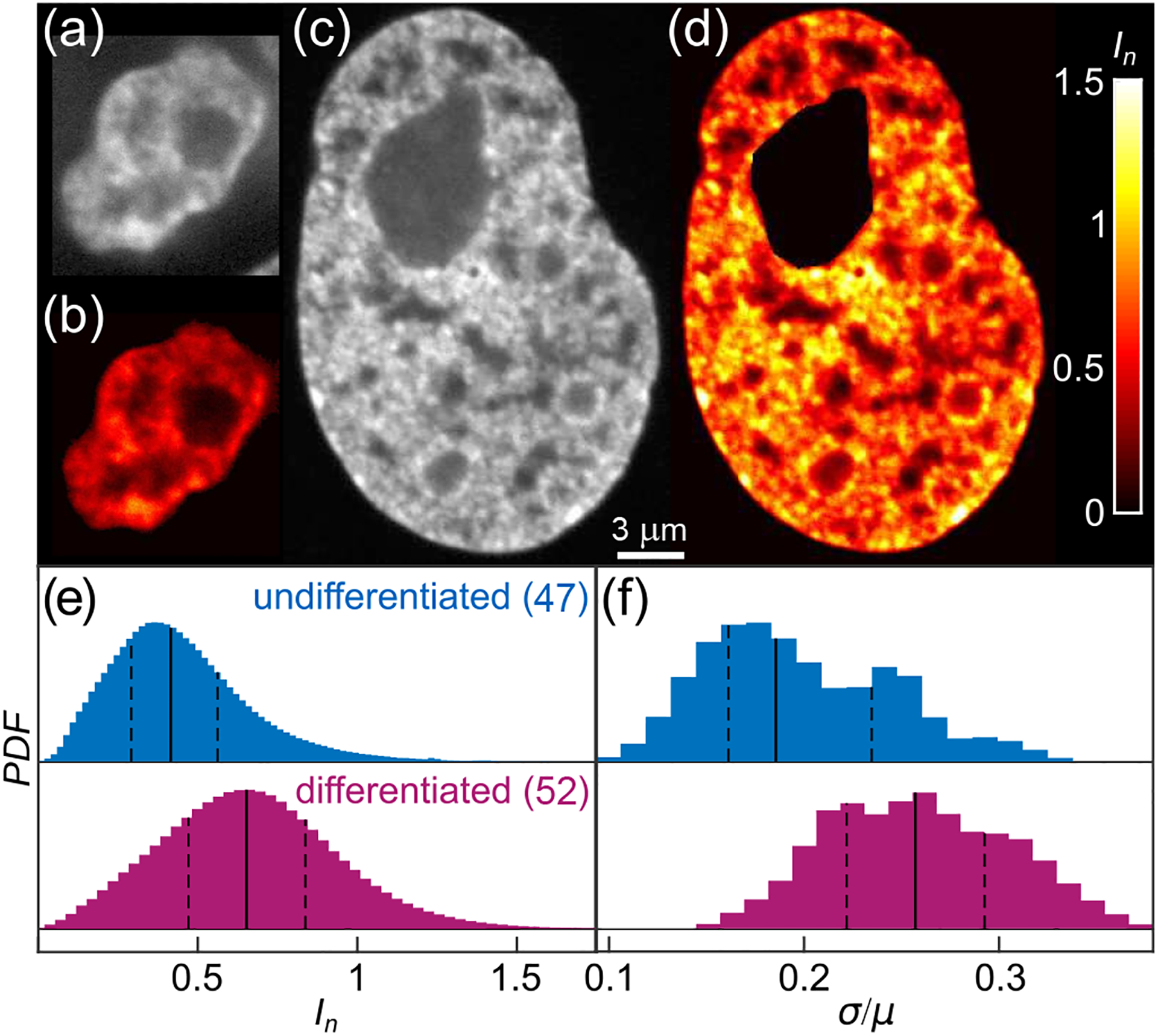
Chromatin distribution before and after cell differentiation. (a) & (c) Micrographs of (a) an undifferentiated (ESC) and (c) a differentiated nucleus with fluorescently labeled chromatin (H2B-GFP). (b) & (d) Color-coded normalized pixel intensities I_n (color bar, black to white) for (b) nucleus from (a), and (d) nucleus from (c). (e) Distribution of normalized pixel intensities I_n for 47 undifferentiated and 52 differentiated nuclei. (f) Distribution of σ/μ for population of undifferentiated (blue) and differentiated (magenta) nuclei. Solid and dashed lines correspond to the median and quartiles of the distribution, respectively.

To quantify the observed differences in chromatin distribution, we analyze the H2B-GFP intensity I at every pixel. When clearly visible, large organelles such as nucleoli are removed [21]. For each nucleus we obtain the distribution of I, its minimum I_min, mean μ and standard deviation σ. One way to facilitate comparison across different nuclei is to compute the normalized pixel intensities I_n = (I − I_min)/μ for each nucleus, accounting for the biological variation in the H2B-GFP expression across cells. Figure 1(e) shows the I_n distributions across 47 undifferentiated (blue) and 52 differentiated (magenta) nuclei. The former is shifted towards smaller I_n values, suggesting that the undifferentiated chromatin is on average less compact than the differentiated one (p-value of 10⁻¹⁶). When we visualize I_n using a heat map, we find regions of high compaction (heterochromatin, yellow) to be sparse in undifferentiated chromatin [Fig. 1(b)] but abundant in the differentiated case [Fig. 1(d)]. Upon evaluation of σ/μ for single nuclei, we find that the σ/μ-distributions for undifferentiated (blue) and differentiated (magenta) nuclei are shifted with respect to each other (p-value of 10⁻⁷) [Fig. 1(f)]. Our data show that the undifferentiated chromatin is less compact and more homogeneous than the differentiated chromatin. This is consistent with earlier observations of undifferentiated chromatin being more accessible to nuclear enzymes and lacking the more dense heterochromatin [22].

The difference in spatial distributions of undifferentiated vs. differentiated chromatin may hint at a change in its material properties upon cell differentiation. To explore this hypothesis, we develop a new method to investigate the rheological behavior of chromatin in live cells. We use intrinsic chromatin dynamics, employing histones H2B-GFP as native rheological probes, and measure the spatiotemporal evolution of the H2B-GFP signal by Displacement Correlation Spectroscopy (DCS)[14]. Using the analytical framework of passive microrheology [23–25], we then extract chromatin rheology from the DCS measurements. It is important to note that the passive microrheology approach assumes that the observed particle motion is thermally driven and thus obeys the fluctuation-dissipation theorem [23–26]. In contrast, many processes in live cells, including chromatin dynamics, have been shown to be actively driven by ATP [14, 27–30]. Our rheological analysis uses an effective temperature to account for the chromatin activity.

Specifically, we record streams of images over 25 s with high spatial (~65 nm in x, y) and temporal resolution (250 ms), which we analyze using DCS [14]. DCS is a time-resolved image correlation analysis that maps chromatin dynamics simultaneously across an entire live cell nucleus in real time. It provides us with chromatin displacement maps $\overrightarrow{d}(\overrightarrow{r},\Delta t)$ over time intervals Δt, while sampling all time intervals (and thus time scales) accessible experimentally [14]. Here, we sample Δt = 0.25–17.5 s. Figure 2 shows DCS maps at Δt = 0.25 s for the undifferentiated [Fig. 2 (a)] and differentiated [Fig. 2 (b)] nucleus from Fig. 1. To assess chromatin motions across the nucleus we computed their average local speed $v(\overrightarrow{r})={\langle \left|\overrightarrow{d}(\overrightarrow{r},\Delta t)/\Delta t\right|\rangle }_t$ at Δt = 0.25 s averaged over all time frames [Fig. 2 (c–d)]. Moreover, at each $\overrightarrow{r}$ we computed the local spatial correlation of chromatin displacements $C_l(\overrightarrow{r},\Delta \overrightarrow{r})=\langle \overrightarrow{d}(\overrightarrow{r},\Delta t),\overrightarrow{d}(\overrightarrow{r}+\Delta \overrightarrow{r},\Delta t)\rangle$ at Δt = 0.25 s over all times. We then fit the radially and time averaged ${\langle C_l(\overrightarrow{r},\Delta \overrightarrow{r})\rangle }_t$ to an exponential decay yielding the local correlation length $l(\overrightarrow{r})$. Fig. 2 (e–f) show nucleus-wide maps of the time averaged $l(\overrightarrow{r})$. Our data reveal that differentiated nuclei contain patches where chromatin motions are slower [Fig. 2 (d), yellow] and correlated [Fig. 2 (f), yellow], surrounded by chromatin that moves faster and in uncorrelated fashion, hinting at presence of two different chromatin phases. This is in contrast to undifferentiated nuclei, which display only one chromatin phase with larger [Fig. 2 (c)] and uncorrelated [Fig. 2 (e)] local displacements.

FIG. 2.

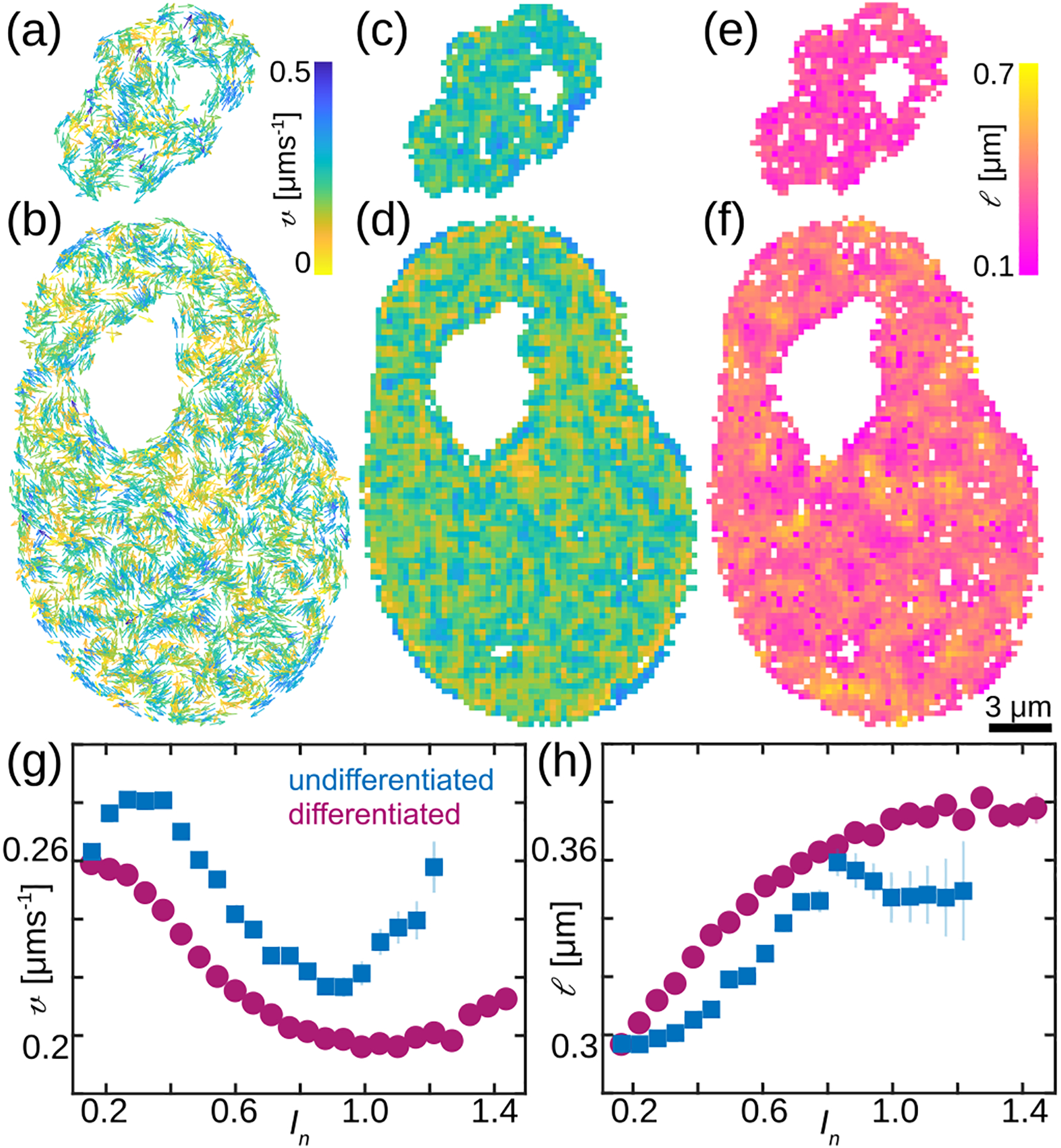
Chromatin dynamics before and after cell differentiation. (a–b) DCS maps $\overrightarrow{d}(\overrightarrow{r},\Delta t)$ for nuclei from Fig. 1, vectors are color-coded by their magnitude, Δt = 0.25 s. (c–d) Heat maps of the average local speed v at Δt = 0.25 s averaged over all time frames. (e–f) Heat maps of local correlation length l of chromatin motion measured at Δt = 0.25 s. (g) The average local speed v as a function of the normalized pixel intensity I_n for 47 undifferentiated and 52 differentiated nuclei. (h) The local correlation length l as a function of I_n for population of undifferentiated (blue) and differentiated (magenta) nuclei. Error bars show standard error.

We then evaluate local average speed $v(\overrightarrow{r})$ and local correlation length $l(\overrightarrow{r})$ as a function of local chromatin compaction as measured by the normalized pixel intensity $I_n(\overrightarrow{r})$ for 47 undifferentiated and 52 differentiated nuclei [Fig. 2 (g–h)]. We find that both v and l are strongly correlated with chromatin compaction I_n. The former decreases, while the latter increases with increasing chromatin compaction in differentiated nuclei [Fig. 2 (g–h), magenta]. This reveals distinct dynamics of heterochromatin (I_n > 1), which is not present in undifferentiated nuclei [Fig. 1 (e)]. Our results uncover that undifferentiated chromatin behaves like a fluid, with no significant spatial differences in local chromatin compaction, displacements and their correlations. Conversely, upon cell differentiation we discover emergence of a local solid-like (gel) phase, corresponding to highly compact heterochromatin, which shows reduced speeds and moves in a correlated fashion. The gel phase coexists with the liquid-like (sol) phase that corresponds to euchromatin.

To further compare dynamics of undifferentiated and differentiated chromatin, we compute the mean square network displacement $\mathit{\text{MSND}}(\Delta t)=\langle |\overrightarrow{d}(\overrightarrow{r},\Delta t){|}^2\rangle$ [14], averaging over 47 undifferentiated [Fig. 3(a), blue squares] and 52 differentiated nuclei [Fig. 3(a), magenta circles], respectively. As a negative control, we measure MSND for cells fixed in formaldehyde [Fig. 3(a), black solid line], confirming that measured values are well above the noise floor. We find that undifferentiated chromatin undergoes larger displacements than the differentiated one consistently across all timescales. Next, we fit the MSND to a power law, MSND(Δt) = A + BΔt^α, which allows us to evaluate the type of chromatin motion (e.g. diffusive, subdiffusive and superdiffusive) at the time scale of our measurement. As shown in earlier studies [14, 19], the constant A accounts for a possibility of an additional fast motion at time scales below our time resolution. We find that while we obtain similar values for A and B for differentiated (d) and undifferentiated (u) chromatin, with A_d = (3.8 ± 0.1) ×10⁻³ μm², A_u = (4.5 ± 0.1) × 10⁻³ μm², B_d = (1.2 ± 0.1) × 10⁻³ μm²s^−α and B_u = (1.3 ± 0.1) × 10⁻³ μm²s^−α, the exponents α are measurably different, with α_d = 1.02 ± 0.02 and α_u = 1.20 ± 0.02 (p-value < 10⁻¹²). Our data suggest that differentiated chromatin moves by an apparent free diffusion, while when undifferentiated, it behaves superdiffusively at the timescales of few seconds. This may be due to different levels of gene expression in ESCs and differentiated cells, the former being hyperactive, the latter having parts of the genome silenced [13].

FIG. 3.

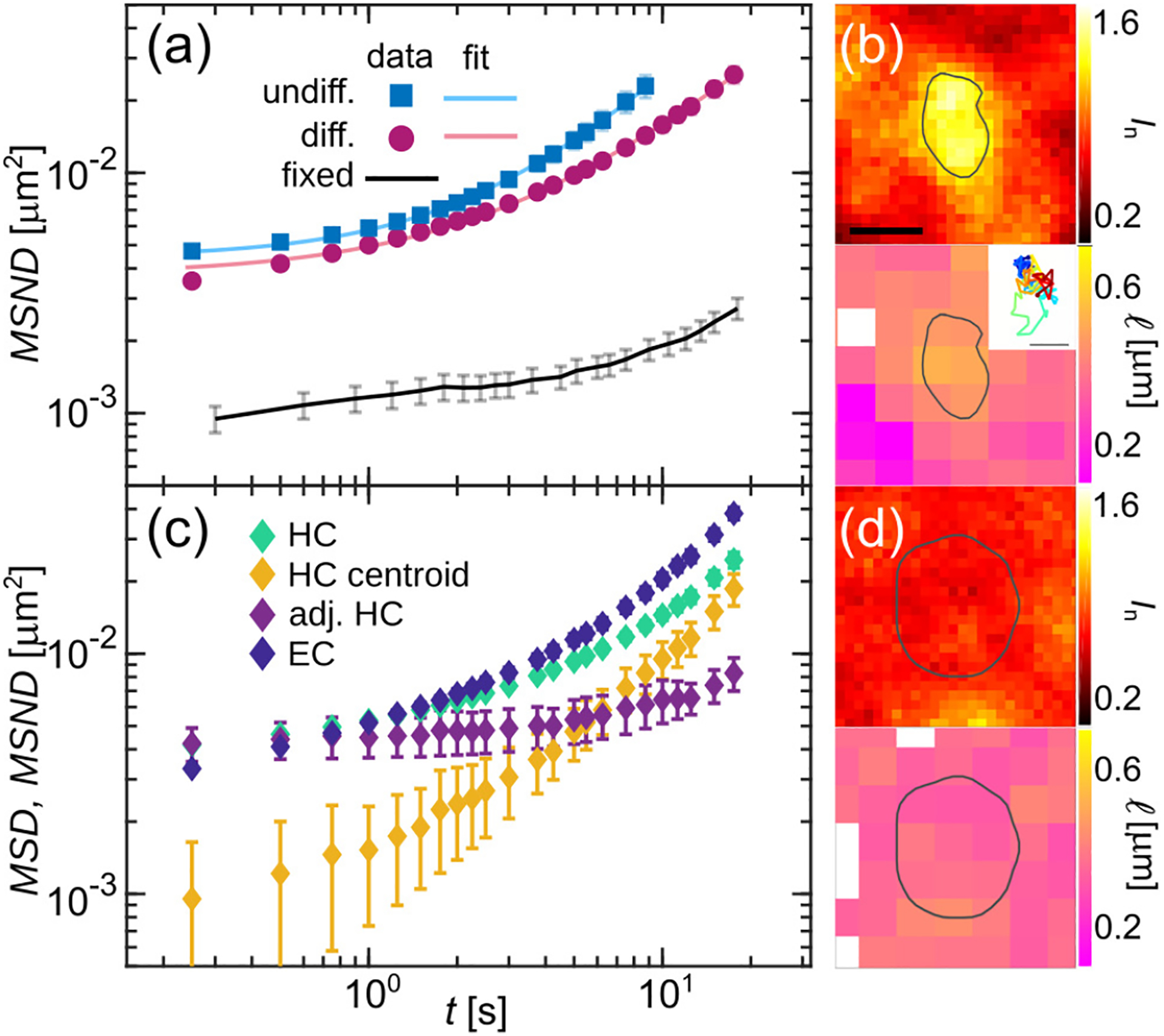
Analysis of chromatin dynamics before and after cell differentiation. (a) Average MSND for chromatin in 47 undifferentiated (blue squares) and 52 differentiated (magenta circles) nuclei and their fits (solid lines) to MSND(Δt) = A + BΔt^α. Black line presents the MSND of formalehyde-fixed cells establishing the noise floor. (b) Heat maps of normalized intensity I_n and local correlation length l in and around HC region outlined by grey contour. Inset shows the HC region trajectory. (c) Average MSND for heterochromatin (HC) regions (N = 93, green markers) and euchromatin (EC) regions (N = 72, blue markers). Yellow markers show the average MSD of the HC centroids and purple markers present the HC MSND corrected for the HC region motion and averaged over all HC regions. (d) Heat maps of I_n and l in and around EC region outlined by grey line. Error bars show standard error. Scale bar, (b) & (d) 500 nm, inset 50 nm.

Our spatially resolved DCS maps allow to selectively analyze dynamics within heterochromatin and euchromatin in differentiated nuclei. To this end, we identified heterochromatic (HC) regions by their high intensity I_n (see Supplemental Material). Fig. 3(b) shows I_n and high correlation length l within an HC region outlined by a grey contour. We analyzed chromatin displacements within 93 HC regions over 52 differentiated nuclei by computing their MSND [Fig. 3(c), green markers] and found it to be similar to that of the bulk differentiated chromatin [Fig. 3(a), magenta markers]. However, we observed that HC regions move as rigid bodies over time, thus their translation contributes to the measured HC displacements. Indeed, tracking HC regions over time reveals significant motion as illustrated by their trajectories [Fig. 3(b), inset] and the mean square displacement MSD of the HC region centroids [Fig. 3(c), yellow markers]. To reveal true chromatin displacements inside the HC regions, we need to correct for their translatory motion. Strikingly, the MSND for adjusted HC motions shows strongly reduced motions within HC [Fig. 3(c), purple markers], when compared to the bulk differentiated chromatin [Fig. 3(a), magenta markers]. Our data reveal that heterochromatin motions are strongly confined, with a constant displacement amplitude at short times, consistent with a solid-like gel phase.

Similarly, we performed analysis of the chromatin displacements in euchromatin (EC), within which the HC regions are embedded. We identified EC by its compaction (see Supplemental Material) and selected EC regions of size comparable to that of HC regions. Fig. 3(d) shows an EC region highlighted by a grey line, manifesting its low compaction (I_n), and lack of motion correlations (l). We analyzed chromatin displacements within 72 EC regions over 52 differentiated nuclei and computed their MSND [Fig. 3(c), blue markers]. We found that EC displacements are larger than those of bulk differentiated chromatin [Fig. 3(a), magenta markers], resembling dynamics of undifferentiated chromatin [Fig. 3(a), blue markers]. Moreover, their MSND monotonously increases, which is in agreement with a fluid-like sol phase.

The measured chromatin dynamics directly reflects chromatin rheology in undifferentiated and differentiated state, revealing fluid-like nature of the former and coexistence of sol and gel phases in the latter. We assess their frequency-dependent bulk rheology by computing the complex viscoelastic modulus $\widehat{G}(s)$ from the MSND(Δt) using a generalized Stokes-Einstein relation [23–26]:

$$\widehat{G}(s)=\frac{k_{B}T}{\pi as\langle \Delta {\widehat{r}}^2(s)\rangle }$$ (1)

where T is effective temperature, a the tracer particle size and $\langle \Delta {\widehat{r}}^2(s)\rangle$ the Laplace transform of MSND(Δt). Since short wavelength chromatin fluctuations were shown to be thermal-like and isotropic noise to capture active chromatin dynamics [31–34], we assume that T is frequency-independent. For each complex frequency s = iω we obtain G*(ω) = G′(ω) + iG″(ω), where G′ and G″ are the storage and loss moduli, i.e., the elastic and viscous response of chromatin, respectively. Moreover, T and a are multiplicative constants impacting the absolute values but not the frequency-dependence of G′ (ω) and G″(ω). Since T and a are unknown, we compute G′(ω)a/T, G″(ω)a/T, examining the frequency-dependence of G′(ω) and G″(ω) for undifferentiated and differentiated chromatin [Fig. 4]. We find that both G′(ω) and G″(ω) for the two states show clear differences (p-value ~ 10⁻¹²).

FIG. 4.

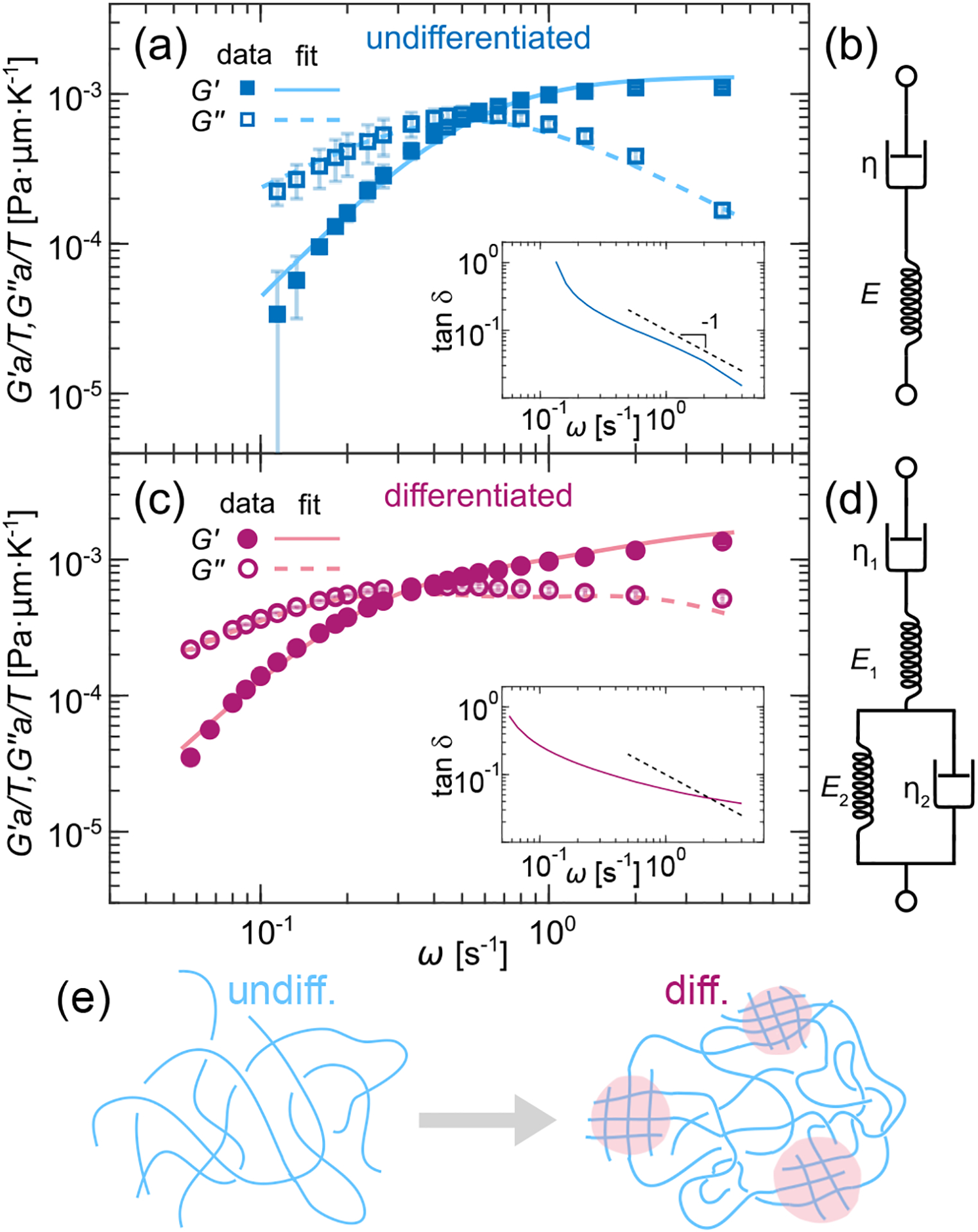
Rheological models of undifferentiated and differentiated chromatin. (a) G′ and G″ measured for undifferentiated chromatin (blue markers) and fitted to the Maxwell fluid model (blue lines). Inset shows tan(δ) = G″/G′, dashed line represents ω⁻¹. (b) Diagram of the Maxwell fluid as a spring-dashpot system. (c) G′ and G″ measured for differentiated chromatin (magenta markers) and fitted to the Burgers model (magenta lines). Inset shows tan(δ) = G″/G′, dashed line indicates ω⁻¹. (d) Diagram of the Burgers model as a spring-dashpot system. (e) Cartoon illustrating the fluid-like (blue) state of undifferentiated chromatin and the emergence of local solid-like phase (magenta) upon differentiation. Error bars show standard error.

We assess the relative fluidity of undifferentiated and differentiated chromatin by evaluating their respective loss tangent tan(δ) = G″(ω)/G′(ω) [Fig. 4(a) & (c), insets]. Remarkably, we find that at most frequencies tan(δ) ~ ω⁻¹ for ESC chromatin [Fig. 4 (a), inset], which is in agreement with a Maxwell fluid [35]. Encouraged by our observations, we fit G′(ω)a/T and G″(ω)a/T obtained for undifferentiated chromatin to those of a Maxwell fluid, the complex viscoelastic modulus of which is defined as [35]:

$$G_M^{*}(\omega )=E\frac{\omega \tau }{\omega \tau -i}$$ (2)

where $\tau =\frac{\eta }{E}$, with η and E being the viscosity and the elastic modulus, respectively. Figure 4(a) shows G′(ω)a/T and G″(ω)a/T (blue markers) and the corresponding fits to the Maxwell fluid (blue lines). The agreement across all ω is striking. Indeed, ESC chromatin can be well described by the Maxwell fluid, a simple viscoelastic fluid with a single relaxation time, which can be mechanically represented by a single spring and dashpot in series [Fig. 4(b)]. Our fit yields a relaxation time τ = 1.9 ± 0.1 s.

Conversely, G′(ω)a/T and G″(ω)a/T for differentiated chromatin cannot be fit to the Maxwell fluid, suggesting a more complex rheology. Indeed, our dynamical measurements identified a coexistence of fluid-like and solid-like phases [Fig. 3]. When looking for a minimal model, we find that differentiated chromatin can be well described by the Burgers model, a combination of a Maxwell fluid and a Kelvin-Voigt solid [35]. Mechanically, the Burgers model can be represented by springs and dashpots in both series and parallel, representing a composite material with two relaxation times [Fig. 4(d)]. As shown in Fig. 4(c), we fit G′(ω)a/T and G″(ω)a/T obtained for differentiated chromatin experimentally (magenta markers) to those of the Burgers model (magenta lines), the complex viscoelastic modulus of which is defined as [35]:

$$G_B^{*}(\omega )=E_1\frac{i\omega {\tau }_1-{\omega }^2{\tau }_1{\tau }_2}{1+i\omega \left({\tau }_1+{\tau }_2+{\tau }_1\frac{E_1}{E_2}\right)-{\omega }^2{\tau }_1{\tau }_2}$$ (3)

where ${\tau }_i=\frac{{\eta }_i}{E_i}$, η_i is viscosity and E_i is elastic modulus. The data and fit are in excellent agreement, suggesting that the biphasic nature of the differentiated chromatin can be well captured by two relaxation times of the Burgers model. From our fit we obtain two relaxation times τ₁ = 2.3 ± 0.1 s and τ₂ = 0.8 ± 0.1 s.

Using the Maxwell and Burgers models, we can estimate absolute values of the elastic moduli E and viscosities η for the respective systems by approximating temperature T and particle size a. Specifically, we use an effective temperature of 300°C, which was previously found for the nucleus in live human cells [36]. With respect to the tracer particle size a, we examine length scales ranging from size of a single nucleosome (~ 10 nm) to larger chromatin regions (~ 100 – 1000 nm). Depending on a, the Maxwell model yields for the undifferentiated chromatin E = 0.8–80 Pa and η = 1.5–150 Pa·s. Similarly, for the differentiated chromatin the Burgers model provides us with E₁ = 1 – 100 Pa, E₂ = 1.8 – 180 Pa, η₁ = 2.3–230 Pa·s and η₂ = 1.4–140 Pa·s. The order of E and η compare favorably with previous point-wise microrheology measurements in differentiated cells [21, 37–40]. Our method characterizes the chromatin rheology across the entire nucleus, over a wide range of timescales and in both differentiated and undifferentiated cells.

The fact that undifferentiated chromatin can be described by a simple Maxwell fluid corroborates its homogeneity and viscoelastic nature. It relaxes applied stresses at single characteristic timescale, consistent with a solution of free polymer chains [Fig. 4(e)]. In contrast, differentiated chromatin is a heterogeneous polymer solution, containing dense chromatin patches of cross-linked polymers (heterochromatin) within a less dense chromatin solution of free polymers (euchromatin), resembling a composite material comprised of solid-like (gel) and fluid-like (sol) phases [Fig. 4(e)]. The Burgers model captures this composite nature of the differentiated chromatin, accounting for both euchromatin and heterochromatin relaxation timescales. Indeed, this model has been applied before to describe rheology of artificial biocomposites [41, 42].

Overall, our findings suggest that during stem cell differentiation chromatin rheology and dynamics change dramatically. Chromatin undergoes a phase transition from originally a homogeneous fluid-like state in stem cells into a biphasic state comprised of a fluid-like (eu-chromatin) and a solid-like (heterochromatin) phase in differentiated cells. The solid-like phase is more elastic and less viscous than the surrounding solution, implying a ‘patchy’ (local) sol-gel transition leads to formation of heterochromatin patches. Such a transition might be facilitated by the liquid-liquid phase separation of the nucleoplasmic HP1 proteins, which was implicated in the heterochromatin formation [43, 44]. Indeed, it was previously shown in differentiated cells, fibroblasts, that a decrease in their heterochromatin content softened the nuclei [45]. Furthermore, a recent study in differentiated cells, B-lymphocytes, found the motion of the immunoglobulin gene to be consistent with its localization at a sol-gel boundary [46]. More broadly, we speculate that the patchy sol-gel transition of chromatin could play a direct role in the genome compartmentalization and gene regulation by altering the local rheology as well as accessibility of the genome.

In summary, our approach is noninvasive, it uses natural probes and their intrinsic dynamics. This allows us to study rheology in systems like chromatin in ESCs, where probe injection is not feasible, and thus its rheological characterization was until now missing. In addition, using DCS we map chromatin dynamics across the entire nucleus measuring both local and global chromatin rheology, in contrast to traditional microrheology, which probes rheology only in the vicinity of an injected probe. Hence, our approach opens new avenues in investigating rheological behavior of the cell and its constituents.