Abstract
We introduce a compartmental model SEIAHRV (Susceptible, Exposed, Infected, Asymptomatic, Hospitalized, Recovered, Vaccinated) with age structure for the spread of the SARAS-CoV virus. In order to model current different vaccines we use compartments for individuals vaccinated with one and two doses without vaccine failure and a compartment for vaccinated individual with vaccine failure. The model allows to consider any number of different vaccines with different efficacies and delays between doses. Contacts among age groups are modeled by a contact matrix and the contagion matrix is obtained from a probability of contagion per contact. The model uses known epidemiological parameters and the time dependent probability is obtained by fitting the model output to the series of deaths in each locality, and reflects non-pharmaceutical interventions. As a benchmark the output of the model is compared to two good quality serological surveys, and applied to study the evolution of the COVID-19 pandemic in the main Brazilian cities with a total population of more than one million. We also discuss with some detail the case of the city of Manaus which raised special attention due to a previous report of We also estimate the attack rate, the total proportion of cases (symptomatic and asymptomatic) with respect to the total population, for all Brazilian states since the beginning of the COVID-19 pandemic. We argue that the model present here is relevant to assessing present policies not only in Brazil but also in any place where good serological surveys are not available.
Keywords: Epidemiological model, Non-linear ODE, SARS-CoV-2, COVID-19
1. Introduction
The present COVID-19 pandemic initiated in the end of 2019 in the city of Wuhan in China, and was first reported to the World Health Organization in January 2020 as an outbreak of pneumonia of undetermined origin. The etiologic agent was identified as the new coronavirus SARS-CoV-2 [1]. The resulting disease caused until the present day more than four million deaths in the whole world, with a reported number of 190 million cases [2]. Waves of the pandemic occurred at different moments of time and in all countries, prompting mitigation measures, that were widely adopted, such as social distancing and mask wearing [3]. During the year of 2020 a few vaccines were developed and approved, with only a small number of countries having vaccinated a significant part of the population [4]. Since then an ongoing effort was taken to gain knowledge has been accumulated on how the virus act and how it spreads, with mathematical modeling one of the tools deployed to predict possible future outcomes [5].
The mathematical modeling of infections diseases has a long tradition starting from the seminal work by Kermack and McKendrick that introduced a SIR (Susceptible, Infectious,Recovered) model to estimate for the epidemic outbreak threshold [6]. Different approaches were developed afterwards to study many diseases, emphasizing different aspects of the epidemic evolution [7], [8], [9]. Since the beginning of the COVID-19 pandemic a substantial number of works were devoted at its modeling, ranging from SIR and SEIR mean-field models and variants [10] to agent-based models [11] and meta-population based models [12] (for reviews of different forecasting models used for COVID-19 see [13] and [14]). The main limitation relies in model calibration due to the lack of reliable data resulting from the emergency situation caused by a pandemic [15], mainly during its initial period, that must be used with care [16]. Despite that, models have a been valuable planning tool in predicting possible future scenarios [5].
We present here a SEIARHV (Susceptiblem Exposed, Infected symptomatic, Asymptomatic, Recovered, Hospitalized, Vaccinated) model, with age structure, that uses known epidemiological parameters to model the evolution of the COVID-19 pandemic by fitting the time dependent transmission rate using real data available from official sources. We implement the model for the main Brazilian cities (municipalities) and all its 27 states.
Since the beginning of 2021 Brazil has received great attention due to a strong second wave, resulting in overcrowded hospitals, a lack of basic medical supplies for a proper treatment in ICUs, and even people dying asphyxiated with lack of oxygen, as occurred in the city of Manaus [17]. The lack of a centralized coordinated effort to mitigate the pandemic allowed for a rapid circulation of the virus in a country with the sixth largest population in the world, resulting in one more hotbed for variants. After more than a year of pandemic some variants of concern have emerged. The variants of concern currently are [18]: (B.1.1.7 from the United Kingdom), (B.1.351 from South Africa), (P1 from Brazil), (B.1.427-9 from the US), and more recently the variant, from India, which in now prevalent in India, the UK and other localities. Those variants are more transmissible by a factor from 1.5 to 2.5 than the original strain, and possibly able to reinfect individuals with a former infection by the original variant [19]. This makes the analysis and predictions of possible outcomes even more difficult, as base epidemiological parameters change over time.
The official figures for the total number of cases, and also for the number of deaths although to a lesser extent, are underestimated all over the world [20], [21], and also in Brazil [22] due to a very small number of tests per million inhabitants (), at the 120-th position among all countries [23]. Due to the large proportion of non-identified cases we fir our model using the time series for deaths in each locality, as it is more reliable and representative of the situation of the pandemic at each moment of time. On the other hand, a realistic estimate of the number of people already infected by the virus is of great relevance for implementing and evaluating mitigation policies, such as determining the degree of social distancing and which sectors to close or reopen, as well as for predicting possible outcomes of the pandemic in each locality. For that purpose serological surveys for detecting SARS-CoV-2 antibodies were implemented in many countries worldwide [24]. Among good quality surveys there are two in Brazil: an estimate of the attack rate (proportion of total real number of symptomatic and asymptomatic cases in the population) in the state of Rio Grande do Sul, based on a serological survey in ten municipalities [25], and the SoroEpi MSP in the city (municipality) of São Paulo [26]. The former covered a time span from April, 1 to May, 11 2020, while the survey in São Paulo reported five surveys from April 2020 to January 2021. We use these two surveys as benchmarks for our model.
The paper is structured as follows: The model, all the required parameters, and how it fitted from data, are presented in Section 2. Section 3 contains the benchmark analysis with the serological surveys and the results for the attack rate (proportion of already infected individuals) for all the Brazilian states and cities with a population of over a million inhabitants. We discuss with a greater length the city of Manaus where the pandemic was particularly intense, ans present some prognostics for the evolution of the pandemic with the arrival of the variant. We close the paper with some discussion and concluding remarks in Section 4.
2. Model
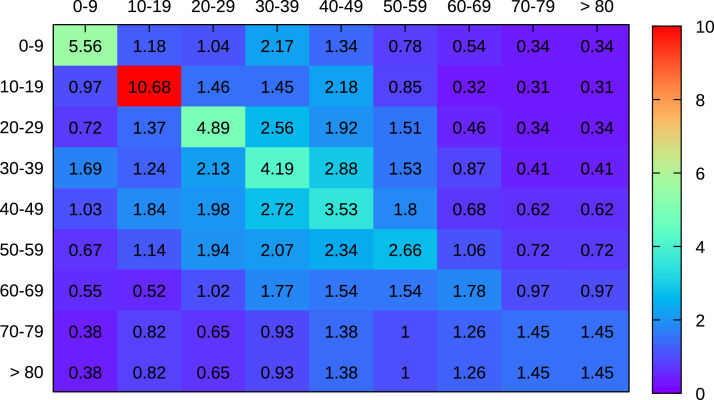
The SEIAHRV model (Susceptible, Exposed, Infected, Asymptomatic, Hospitalized Recovered and Vaccinated), is an extension of the model used in [27], with compartments for individuals vaccinated with one and two doses, and for different vaccines, each with a known efficacy with one and two doses, respectively, and a time delay between the two, each vaccine type denote by the superscript, without primary vaccination failure. A compartment is also introduced for individuals with primary vaccination failure . The model assumes homogeneous mixing and age groups with different number of contacts between each group. The variables are given as proportion with respect to the total population at the initial time. The decomposition of the compartments into age groups enables to incorporate the estimated contact structure in a given population, represented here by a contact matrix with the average number of contacts per day of a single individual of age group with any individual of age group . Up to the authors knowledge there is no estimation for the contact matrix in Brazil, so we use the results by Mossong et al. [28] for eight European countries, taking the average of the contact matrix for all countries, and adapting the result to the age distribution for each cities and state considered here. This is a reasonable assumption due to cultural similarities between Europe and Brazil. The age groups represented in the model are: 0 to 9, 10 to 19, 20 to 29, 30 to 39, 40 to 49, 50 to 59, 60 to 69, 70 to 79 and 80 years of age and more. The contact matrix obtained in this way for Brasília (capital of Brazil) is shown in Fig. 3.
Fig. 3.
Estimated contact matrix for Brasília (see supplementary material) with the average number of contacts of an individual of a given age group (column) with any individual of age group (row).
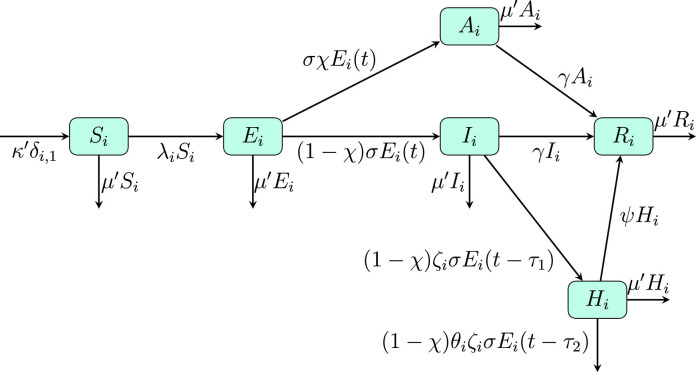
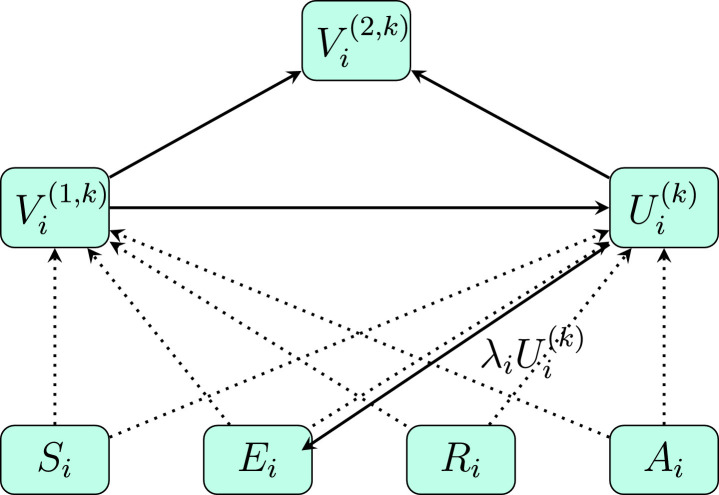
Required epidemiological parameters are given in the literature in Refs. [29], [30], [31], [32], [33], [34] and shown in Tables 1 and 2 . The transfer diagram for the model is shown in Figs. 1 and 2 , and the corresponding non-linear differential equations with time-delay are given by:
| (1) |
where all variables are calculated at time except where explicitly indicated. The time delay is due to the average time between first symptom and hospitalization and first symptom and death. In Eq. (1) and are the number of individual vaccinated per unit of time for the first and second dose, respectively, for the age group and vaccine type , and the efficacy of vaccine of type with one and two doses, respectively, , with the number of different vaccines. In order to consider the time for a dose to reach full efficacy we assume a linear growth of the protection and suppose the vaccine is given at half this time interval. We also define and , with , , and the initial population, current population, birth and natural mortality rates, respectively, with the mortality rate distributed homogeneously through all age groups. The aging rate from the -th to the -th age group is denoted by and given by the inverse of the time span of the -th age group, with . The force of infection is given by
| (2) |
with
| (3) |
is the infection rate matrix, with the proportion of the population in age group and the infectiousness of an asymptomatic individual with respect to a symptomatic one, the contagion probability per single contact, assumed to be age independent.
Table 1.
Epidemiological parameters required by the SEIAHRV model.
| Parameter | Definition | Value [Ref] |
|---|---|---|
| Recovery rate from hospitalization | [29], [30] | |
| Inverse of incubation time | [31] | |
| Recovery rate for non hospitalized individuals | [32] | |
| Fatality rate among hospitalized individuals | ||
| (see Table 2) | ||
| Median time from first symptoms | 3.3 [31] | |
| to hospitalization | ||
| Average time from first symptoms to death | 16.8 [29] | |
| Proportion of asymptomatic cases | [33] | |
| Contagiousness of asymptomatic with respect | [32] | |
| to symptomatic individuals | ||
| Average birth rate in Brazil | [34] | |
| Average natural mortality rate in Brazil | [34] |
Table 2.
Infection fatality ratio (IFR) and hospitalization probability for each age group as obtained by Linton et al. [31].
| Age group | ||
|---|---|---|
| 0 – 9 | ||
| 10 – 19 | ||
| 20 – 29 | ||
| 30 – 39 | ||
| 40 – 49 | ||
| 50 – 59 | ||
| 60 – 69 | ||
| 70 – 79 | ||
| 80 |
Fig. 1.
Transfer diagram for the SEIAHRV epidemiological model.
Fig. 2.
Transfer diagram for the vaccination component of the model in Fig. 1. Dotted lines indicate a flow between different compartments due to vaccination, according to the effectiveness of each vaccine type, with one and two doses.
The knowledge of the Infection Fatality Ratio(IFR) according to age-group is central in our approach. We use the values obtained by Linton et al. (see Table 2) from a statistical analysis of data from and outside Wuhan,China up to January, 31 2020 [31]. It is important to notice that this analysis does not consider the proportion of asymptomatic cases and therefore the fatality is relative only to the symptomatic cases, as implemented in our model. An estimate of for the proportion of true asymptomatic cases was obtained from the follow up of cases on the Diamond Princess cruise ship, as reported in [33]. The passengers were kept quarantined on board of the ship, which allowed a fully controlled groups, which resulted in a more realistic estimate for .
As discussed in the introduction, the time series of total deaths reported in each locality is a more reliable data than the number of cases [20], [21], [22], and therefore is better suited for determining the (time dependent) probability of contagion . Different functional forms are possible, and we use here a piece-wise function, with constant values in 14 days intervals and varying among different intervals. These values are determined by minimizing the square error function:
| (4) |
where is the number of data points to fit, and are the real and model values for the cumulative number of deaths, respectively. The fitted parameters are the values of in each interval and the number of infectious individuals in the older age group at the initial time (which age group represents the seed becomes irrelevant after a few generations). The minimization process is performed using a simplex algorithm with adaptative parameters [35]. The time varying contagion probability is a result of changes in behavior, social distancing, and other mitigation policies.
All COVID-19 data for each municipality in Brazil is publicly available at the Brazilian Health Ministry COVID-19 website [36]. Estimates of population by age-group for 2020 are available at the Brazilian Institute for Geography and Statistics [37] and from DATASUS system of the Ministry of Health [34]. Detailed data on each vaccine shot applied in Basil is publicly available on the at Brazilian Health Ministry [38]. All the data considered here span the period from February, 26 2020 (first case in Brazil) up to July, 18 2021.
The fatality ratio in ICUs varied according to the region in Brazil, from to in the southeast and north regions, respectively [39]. The IFR values for each age group are then corrected accordingly, with the IFR in the Southeast region, the one with the best health infrastructure, used as reference and changing the values for other regions accordingly to the proportion of increase reported in [39].
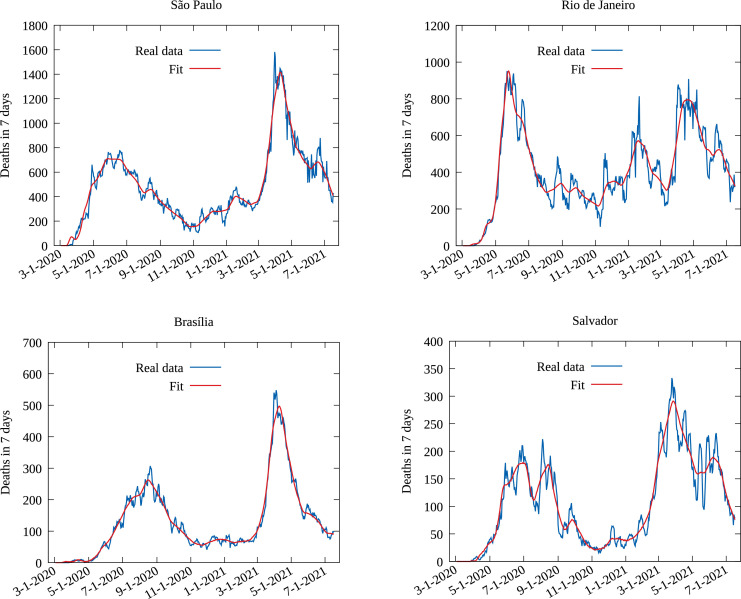
Fig. 4 shows the resulting fit for the four more populous Brazilian cities. Although the series for total deaths was used in the fitting, We display the results in the form deaths per week to facilitate the visualization of the quality of the fit. Once the model is fitted to the data, the attack rate is computed from the cumulative number of individual entering the exposed compartment since the beginning of the pandemic.
Fig. 4.
Number of deaths per week from real data and the fitted model data for the four more populous cities in Brazil: São Paulo, Rio de Janeiro, Brasília and Salvador.
For a comparison purpose, we also estimate the total number of cases from the average IFR obtained as:
| (5) |
where is the population in age group , the total population and the IFR for age group . The number of new cases at day can then be estimated by
| (6) |
where is the distribution for the time between first symptom and death [32] and the numbers of new deaths in day .
3. Results
3.1. Comparing model results to serological surveys
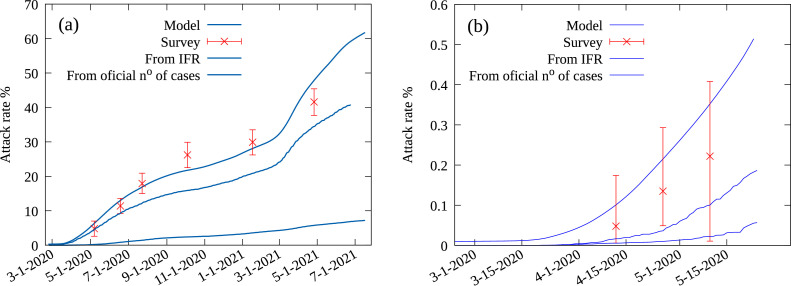
As a benchmark for the present approach, we first compare the attack rate obtained from for our model to the surveys for São Paulo and Rio Grande do Sul. The results are shown in Fig. 5 , alongside values obtained from official number of cases, the results from the serological surveys, and estimates obtained from the averaged IFR as given by Eq. (6). The serological survey for the Rio Grande do Sul state was obtained from data for the ten largest cities in the state, and is not necessarily representative of the whole state [25], but the attack rate obtained from our model is well within the confidence intervals. We note that the time span considered in this survey corresponds to the very beginning of the pandemic in the state, with a small number of cases and deaths, which resulted in greater estimated errors. In the case the SoroEpi MSP survey in city of São Paulo our model yields a good agreement.
Fig. 5.
a) Attack rate from the total number of cases (symptomatic and non-symptomatic) as obtained from the epidemiological model (solid line), and data from the SoroEpi MSP serological survey [26]. The dotted line gives the total number of cases estimated from the average IFR using Eq. (S4), and the dashed line is obtained from the official number of cases as reported by the Brazilian Ministry of Health [36]. b) Attack rate for the state of Rio Grande do Sul from the epidemiological model and IFR estimates, official number of cases and serological survey [25].
The SEIAHRV model considers explicitly the social contact structure expressed by the contact matrix among individuals of different age groups and thus is a better representative of how the virus spreads than estimates obtained from the IFR average. The difference between the IFR estimate and the surveys is at least in part due to the proportion of asymptomatic individuals. Indeed, a direct computation from the data here presented implies that the result from Eq. (6) would imply a value for the proportion of asymptomatic individuals of , CI , which is compatible with the result reported in [33] and considered in our model. Emerging variants may result in an increase in mortality, and thence an overestimation of the total number of cases [40], [41], [42]. This is not expected to play a major role in São Paulo up to January 2021, but most certainly the case latter, with the arrival of the and other variants. We now extend our analysis to the main cities and all the 27 states in Brazil.
3.2. Main Brazilian cities
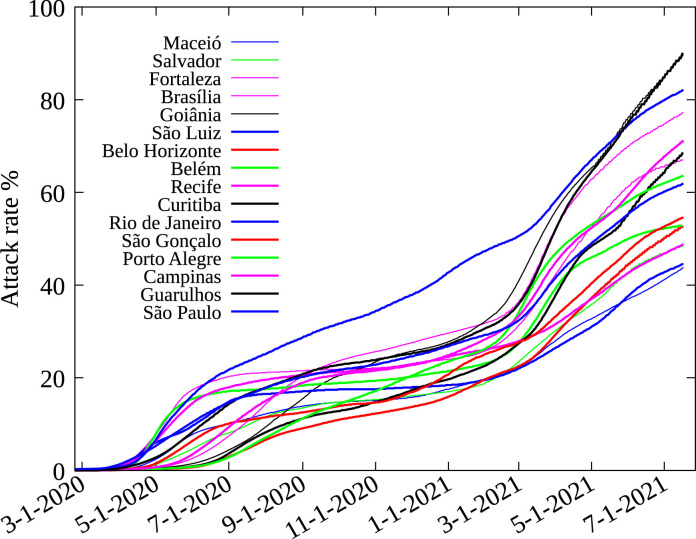
We consider the Brazilian cities (municipalities) with a population of at least one million inhabitants (population between parenthesis): Macei (1018948), Curitiba (1933105), Manaus (2182763), Rio de Janeiro (6718903), Salvador (2872347), São GonȺalo (1084839), Fortaleza (2669342), Porto Alegre (1483771), Goinia (1516113), Campinas (1204073), São Luís (1101884), Guarulhos (1379182), Belo Horizonte (2512070), São Paulo (12252023), BelȨm (1492745), Brasília (3055149) and Recife (1645727). The time evolution of the attack rate obtained for these cities is shown in Fig. 6 . The case of the city of Manaus must be considered with more care, and is discussed separately.
Fig. 6.
Model estimates for the attack rate for Brazilian cities with more than one million inhabitants (except Manaus).
The attack rate by July, 18 2021 in all cities in the interval from 35% to 90%, showing a great heterogeneity of the current situation. This is mainly due to different adherence to mitigation measures adopted locally. The cases with a very high attack rate, above , must be explained as they are above the herd immunity predicted for SARS-CoV-2. The second wave of the pandemic was very intense in Brazil, with overcrowded hospitals in many localities, resulting in an increase of the IFR, which at its turn implies an overestimation of the total number of cases. Also after more than a year in the pandemic the natural immunity by a previous infection may start to wane, allowing for a substantial proportion of reinfections [43], [44]. Future research for gathering more data is important to clarify this point.
3.3. The case of Manaus
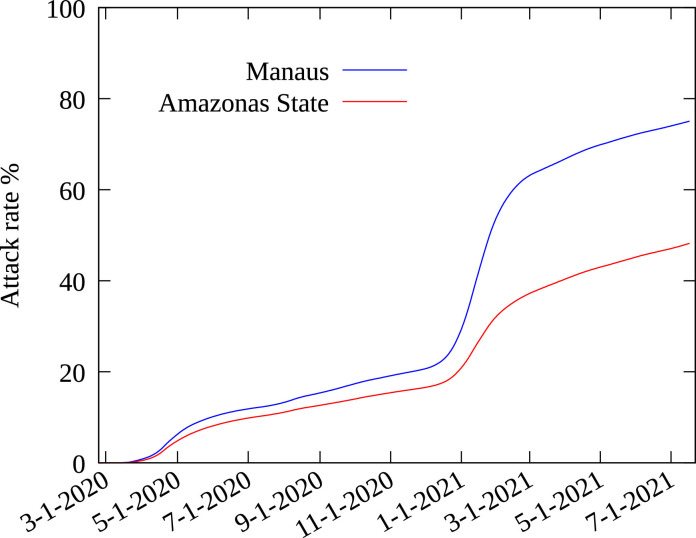
Results for Manaus and the Amazonas state are shown in Fig. 7 , with the attack rate for the city of Manaus and for the Amazonas state in July, 18 2021 are and , respectively. This result must be interpreted with due care. The Amazonas state is the largest state in Brazil, with , of the Brazilian territory, but only of its population. The state capital Manaus has inhabitants, a little more than half the population of the state, and the second largest city has a population of only 101 thousand. Almost all medical facilities, including ICUs, are in Manaus. As a consequence most of the critical patients, with a higher probability of dying, are transferred there. This explains why of the deaths in the state occurred in Manaus, while only of the official number of cases were reported there. This flow of critical cases to Manaus was even more pronounced during the second wave, the deadliest observed in Brazil until now, which overwhelmed all medical facilities. Therefore, fitting the model with the time series of deaths in Manaus is unrealistic. The attack rate in the city is most probably closer to the one estimated for the whole Amazonas state. Such peculiarities do not occur, at least not in the same intensity, for the other cities considered here. The occurrence of the P1 variant in the Amazonas state could also explain a higher value of the attack rate due to possible reinfections, as claimed in [42], but not the asymmetry of the number of deaths compared to the total number of cases between Manaus and the rest of the state.
Fig. 7.
Model estimates for the attack rate for the Amazonas state and Manaus municipality.
A previous estimate by Bussi et al. [45], based on a survey of samples from blood donors, obtained an attack rate in Manaus of in October, 1st 2020. Therefore the important second wave that occurred in January 2021 would imply a high proportion of reinfection among new cases, possibly caused by the more contagious P1 variant. Nevertheless this value for the attack rate is highly at variance with our finding of for the whole state and for the city of Manaus in January, 15 2021. This significant difference can be explained out by two facts: Bussi and collaborators considered a model for seroconversion with an exponential decay to estimate the expected real number of already infected individuals. Although the results obtained by Bussi et al. for São Paulo are close to those from the SoroEpi MSP survey, we note that small errors are exponentially increased, which could lead to large errors in the estimate, while the SoroEpi MSP survey relied on a blood test with negligible seroconversion during the time span considered. The second fact is that using samples from blood donors introduces a strong bias, which is even more important if one considers that blood donations in the state of Amazonas are only possible in Manaus, and that the family of hospitalized individuals are often asked to donate blood, and that it is a common practice for people from other Amazonas cities to register in the hospital using the address of a relative living in Manaus. As a consequence, many donors in Manaus have been in recent contact with hospitalized individuals from all over the state.
3.4. Brazilian states
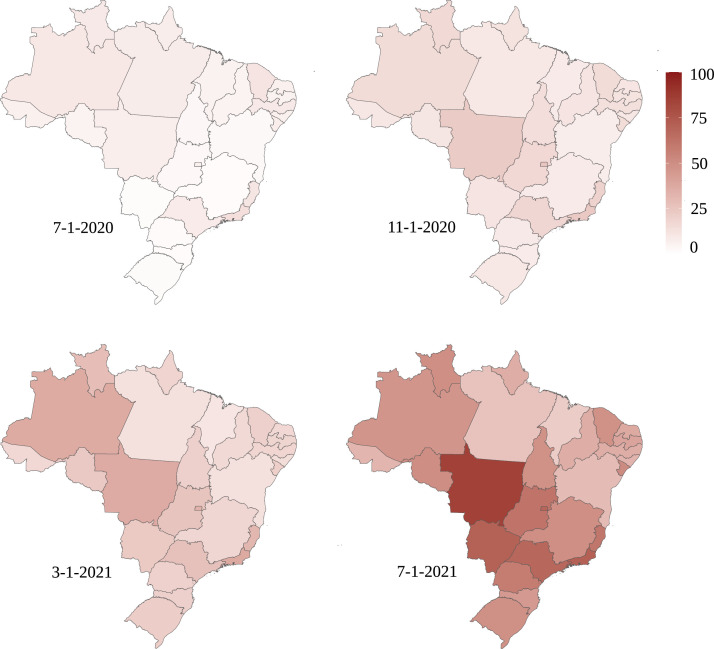
We also obtain estimates for the attack rate in each Brazilian state by considering the time series for the cumulative number of deaths for the whole state. Population and COVID-19 data are obtained from the same sources. Results for the attack rate in intervals of four months starting in July, 2020 are shown as heat maps in Fig. 8 , where the great impact and rapid increases during the second wave starting by the end of 2020 is clearly visible, but with different intensities in each state.
Fig. 8.
Heat map with the model estimates of the attack rate in % for each Brazilian state for four different dates.
3.5. Using the model for prognostics
In order to demonstrate how our model can be used to predict future outcomes for the pandemic, we show how to model an increase in the transmission probability due to a more contagious variant. Our intent is not to provide an complete set of possible outcome for the pandemic, but to show how our model can be used to model the evolution under different circumstances. New variants become dominant in an area only if it is more transmissible than the original strain. In Brazil the currently predominant variant is roughly 70% to 140% more contagious than the original strain. The variant, first observed in the United Kingdom, is 50% to 100% more contagious and the variant from India is estimated to be 64% more contagious than the variant, i. e. roughly 50% more contagious than the Brazilian variant [18]. With this estimate, we perform a few prognostics for the evolution of the pandemic in Brazil by considering the current situation in each state as given by the last computed value of the transmission probability in Eq. (3). The variant is present in Brazil but not yet dominant, which means that its prevalence will raise in a amount of time that depends on the circulation of the virus, which is high in Brazil in July 2021. we suppose that this results in an increase of given by a logistic function of the form:
| (7) |
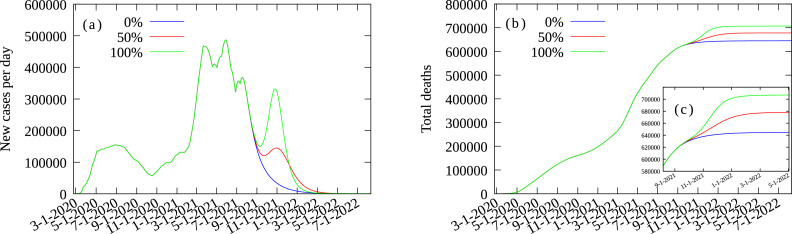
with and constants chosen such that at present time (July, 12 2021) the probability increases from and reaches a value of after an estimated time of 90 days, which is compatible with what was observed in places where the variant became predominant [46]. Following the discussion above we use the values 0.0 (no increase in , 0.5 and 1.0 for . We also suppose that vaccination will proceed in Brazil with a number of doses for each type of vaccine equal to the average during the months of May and June 2021, with of the population in each age-group being fully vaccinated proceeding from the eldest to the youngest, including children. The results for the epidemic curve (cases per day) and the cumulative number of deaths ares shown in Fig. 9 . We see that the arrival of the variant which is already present in Brazil, can produce another wave with an intensity depending on how much it contagious, and the vaccine coverage, among other factors.
Fig. 9.
Prognostics for Brazil in three different scenarios: (no change in current situation), (a increase in the contagiousness) and (the new variant is twice as contagious as the current dominant variant). a) New cases per day; b) Deaths per day; c) Zoom over (b).
Predicting the future for a pandemic is always an intricate task, as it depends on many factors such as the degree of social isolation, the compliance to mask use and to other measures, the possibility of new yet unknown variants. Despite that, a well calibrate model is an important tools for assessing the current situation, foe evaluations of previous mitigation measures, and for predicting possible scenarios of evolution that can be helpful for evaluating the effect of different policies for reducing the already immense impact of the current pandemic.
4. Concluding remarks
We have shown that the SEIARHV model here introduced can be calibrated with data from the time series for the number of deaths in each locality, with very good results when compared with two good quality serological surveys. For that it is important to have good quality estimates for the infection fatality rate according to the age group, and for the proportion of asymptomatic individuals. In fact, our results corroborate the estimate for obtained in [33]. An additional complication comes from new variants of the SARS-CoV-2 virus, which are more transmissible and also more lethal, which was overcome by estimating the increase in mortality during the second-wave in Brazil from data for the number o official cases and deaths. Of course, this may lead to a change over time of some of the epidemiological parameters used in our model, and must be taken into account if sufficient information is available. The same applies for new variants as data is gathered on them. A different approach would be to use the series for cases and deaths to determine how the parameters change [15], but then this would require that the data used is reliable which, as discussed above, is not currently the case for the COVID-19 pandemic [20], [21], [22], so one has to chose which information is more appropriate to use for model calibration.
We applied our approach to study the current, and previous, state of the pandemic in Brazil, one the most attacked countries in the World. Since there was no centralized policy for controlling the pandemic in Brazil, each state and sometimes each municipality had to implement his own mitigation measures. This explains the widely different attack rates in each one, and also shows how the present approach can describe them if properly adjusted. In our case we chose to use the series of deaths as reliable data. The attack rate in most of Brazil is still well below herd immunity, estimated at the initial stages of the pandemic close to [44]. The advent of more transmissible variants raise significantly this value. Some Brazilian states and cities are approaching or even surpassing this value. This fact was properly discussed in the text, but requires more data to be gathered for a more precise interpretation. The attack rate in the cities presented here are higher than in the corresponding states, as the pandemics started in the bigger cities, with the main airports and more intense inter-cities traveling. The pandemic then spread to smaller cities, meaning that more important outbreaks are most likely to be expected there.
It is expected that future results of serological surveys can shed some light on the possibility of a greater proportion of reinfections, and we hope that the present approach can be used as an important tool in this analysis. Our approach can be extended straightforwardly to other cities and countries with reliable data, usually on the number of deaths but not for the number of cases as under-reporting is important almost anywhere [20], [21], [22]. Where good serological surveys are not available the current approach is an alternative tools to asses the current and past situation, and to prepare for what is still ahead. It can also be directly applied to other diseases than are modeled by SEIR type models, such as measles.
The simplifying assumption that the transmission probability is age independent can also be readily improved by considering a probability that depends on the age of the infecting or being infected individual, provided that data on the time series of deaths is publicly available. One can also fit the model with the number of cases if the data is reliable, which is usually not the case by far for the current COVID-19 pandemic.
It is yet not clear how long natural immunity will last, and how much current vaccines protect against transmission. The arrival of more contagious variants casts many doubts on the real relevance of herd immunity. The determination of the attack rate is important for guiding and correcting public policies as a criterion to estimate its results. The model used in the present work is also a useful tool in estimating the evolution of the present pandemic from the current situation, if good estimates for the IFR and for the characteristics of new variants exist.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work received financial support from the National Council of Technological and Scientific Development - CNPq (grant numbers 302449/2019-1 FAS, 309617/2020-0 ACGA, 305291/2018-1 MAM), Bahia State Research Support Foundation (BOL0723/2017 AJAC) (Brazil) and i3N (grant numbers UIDB/50025/2020 & UIDP/50025/2020) - Fundacão para a Ciencia e Tecnologia/MEC (Portugal).
References
- 1.Zhu N., Zhang D., Wang W., Li X.W., Yang B., Song J.D., et al. A novel coronavirus from patients with pneumonia in china. 2019. N Engl J Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU).https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html/bda7594740fd40299423467b48e9ecf6 Accessed on July, 19 2021.
- 3.Ayouni I., Maatoug J., Dhouib W., Zammit N., Fred S.B., Ghammam R., Ghannem H. Effective public health measures to mitigate the spread of COVID-19: a systematic review. BMC Public Health. 2021;21:1015. doi: 10.1186/s12889-021-11111-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.The New York Times Coronavirus Vaccine Tracker. https://www.nytimes.com/interactive/2020/science/coronavirus-vaccine-tracker.html.
- 5.Vespignani A., Tian H., Dye C., Lloyd-Smith J.O., Eggo R.M., Shrestha M., et al. Modelling COVID-19. Nat Rev Phys. 2020;2:279. doi: 10.1038/s42254-020-0178-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kermack W., McKendrick A.G.. A contribution to the mathematical theory of epidemics. Proc Royal Soc London Series A 197(115):700.
- 7.Hethcote H.W. The mathematics of infectious diseases; SIAM Rev. 2000;42:599. [Google Scholar]
- 8.Brauer F., Driessche P., Wu J.. Mathematical epidemiology. 2008 Springer-Verlag Berlin Heidelberg
- 9.Keeling M.J., Rohani P.. Modeling infectious diseases in humans and anumals;. 2008 Princeton University Press;
- 10.Estrada E. COVID-19 And SARS-CoV-2. modeling the present, looking at the future. Phys Rep. 2020;869:1. doi: 10.1016/j.physrep.2020.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lorig F., Johansson E., Davidsson P. Agent-based social simulation of the covid-19 pandemic: a systematic review. J Artif Soc Soc Simul. 2021;24:5. [Google Scholar]
- 12.Coletti P., Libin P., Petrof O., Willem L., Abrams S., Herzog S.A. A data-driven metapopulation model for the belgian COVID-19 epidemic: assessing the impact of lockdown and exit strategies. BMC Infect Dis. 2021;21:503. doi: 10.1186/s12879-021-06092-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xiang Y J., Chen L., Guo L., Shu B., Long E. COVID-19 Epidemic prediction and the impact of public health interventions: a review of COVID-19 epidemic models. Infect Dis Modell. 2021;6:324. doi: 10.1016/j.idm.2021.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rahimi I., Chen F., Gandomi A.H.. A review on COVID-19 forecasting models. Neural Comput Appl10.1007/s00521-020-05626-8 [DOI] [PMC free article] [PubMed]
- 15.Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect Dis Modell. 2020;5:271. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.James L.P., Salomon J.A., Buckee C.O., Menzies N.A. The use and misuse of mathematical modeling for infectious disease policymaking: lessons for the COVID-19 pandemic. Med Decis Making. 2021;41:379. doi: 10.1177/0272989X21990391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Taylor L. Covid-19: is manaus the final nail in the coffin for natural herd immunity? BMJ. 2021;372 doi: 10.1136/bmj.n394. [DOI] [PubMed] [Google Scholar]; N394. https://www.bmj.com/content/372/bmj.n394
- 18.Otto S.P., Day T., Arino J., Colijn C., Dushoff J., Li M. et al.The origins and potential future of SARS-cov-2 variants of concern in the evolving COVID-19 pandemic. To appear in: Current Biology10.1016/j.cub.2021.06.049 [DOI] [PMC free article] [PubMed]
- 19.Callaway E. Delta coronavirus variant: scientists brace for impact. Nature. 2021 doi: 10.1038/d41586-021-01696-3. [DOI] [PubMed] [Google Scholar]
- 20.Jrahmandad J., Lim T.Y., Sterman J.. Behavioral dynamics of COVID-19: estimating under-reporting, multiple waves, and adherence fatigue across 92 nations. MedRXiv10.1101/2020.06.24.20139451 [DOI] [PMC free article] [PubMed]
- 21.Docherty K.F., Butt J.H., de Boer R.A., Dewan P., Kober L., Maggioni A.P. et al.Excess deaths during the Covid-19 pandemic: An international comparison10.1101/2020.04.21.20073114MedRXiv
- 22.Veiga e Silva L., MPA A.H., AMTB S., CAM T., VHM G., EHS C. COVID-19 Mortality underreporting in brazil: analysis of data from government internet portals. J Med Internet Res. 2020;22 doi: 10.2196/21413. [DOI] [PMC free article] [PubMed] [Google Scholar]; E21413.
- 23.2021. Worldometers. https://www.worldometers.info/coronavirus/countries. Accessed July, 19.
- 24.Chen X., Chen Z., Azman A.S., Deng X., Sun R., Zhao Z. Serological evidence of human infection with SARS-cov-2: a systematic review and meta-analysis. Lancet Glob Health. 2021;9 doi: 10.1016/S2214-109X(21)00026-7. [DOI] [PMC free article] [PubMed] [Google Scholar]; E598
- 25.Silveira M.F., AJD B., Horta B.L., Pellanda L.C., Victora G.D., Dellagostin O.A. Population-based surveys of antibodies against SARS-cov-2 in southern brazil. Nat Med. 2020;26:1196–1199. doi: 10.1038/s41591-020-0992-3. [DOI] [PubMed] [Google Scholar]
- 26.Soroepi MSP: Serial soroepidemiological survey to monitor the prevalence of SARS-cov-2 infection in the municipality of são paulo, SP, brazil. 2020. https://www.monitoramentocovid19.org/. Accessed April, 28 2021.
- 27.Rocha Filho T.M., JFF M., Murari T.B., Nascimento Filho A.S., AJA C., Ramalho W.M. et al.WHO vaccination protocol can be improved to save more lives. research square, january 18. 2021. Preprint Available at https://www.researchsquare.com/article/rs-148826/v1.
- 28.Mossong J., Hens M., Jit M., Beutels P., Auranen K., Mikolajczyk R., Massari M. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5 doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]; E74.
- 29.Zhou T., Liu Q., Yang Z., Liao J., Yang K., Bai W. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. 2020;13:3–7. doi: 10.1111/jebm.12376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Verity R., Okell L.C., Dorigatti I., Winskill P., Whittaker C., Imai N. Estimates of the severity of coronavirus disease 2019: a model-based analysis. Lancet Infect Dis. 2020;20:669–677. doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Linton N.M., Kobaiashi T., Yang Y., Hayashi K., Akhmetzhanov A.R., Jung S. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: astatistical analysis of publicly available case data. J Clin Med. 2020;9:538. doi: 10.3390/jcm9020538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lauer S.A., Grantz K.H., Bi Q., Forrest K., Zheng Q., Meredith H.R. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med. 2020;172:577–583. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mizumoto K., Kagaya K., Zarebski A., Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the diamond princess cruise ship, yokohama, japan, 2020. Euro Surveill. 2020;25:2000180. doi: 10.2807/1560-7917.ES.2020.25.10.2000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.DATASUS. 2021. http://tabnet.datasus.gov.br/cgi/deftohtm.exe?popsvs/cnv/popbr.def. Accessed April, 28.
- 35.Gao F., Han L. Implementing the nelder-mead simplex algorithm with adaptive parameters. Comput Optim Appl. 2012;51:259–277. doi: 10.1007/s10589-010-9329-3. [DOI] [Google Scholar]
- 36.COVID19 Painel Coronavírus- Ministério da Saúde da República Federativa do Brasil- DATASUS. https://covid.saude.gov.br/
- 37.2021. Instituto Brasileiro de Geografia e Estatística (IBGE). https://brasilemsintese.ibge.gov.br/populacao/. Accessed April, 28
- 38.OpenDATASUS. Ministério da Saúde do B.. https://opendatasus.saude.gov.br/dataset/covid-19-vacinacao.
- 39.Ranzani O.T., LSL B., JGM G., Marchesi J.F., Baião F., Hamacheri S., Bozza F.A. Characterisation of the first 250 000 hospital admissions for COVID-19 in brazil: a retrospective analysis of nationwide data. Lancet Respir Med. 2020;9:322–324. doi: 10.1016/S2213-2600(20)30560-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.ARR F., DRQ L., Beckedorff A.O., LPG C., Siqueira A.M., CRS M., ENC B. The increase in the risk of severity and fatality rate of covid-19 in southern brazil after the emergence of the variant of concern (VOC) SARS-cov-2 p.1 was greater among young adults without pre-existing risk conditions. medRxiv. 2021 doi: 10.1101/2021.04.13.21255281. [DOI] [Google Scholar]; MedRXiv
- 41.Tuite A.R., Fisman D.N., Odutayo A., Bobos P., Allen V., Bogoch I.I. et al.COVID-19 hospitalizations, ICU admissions and deaths associated with the new variants of concern. science briefs of the ontario COVID19 science advisory table. 2021. 1, 1–10, 10.47326/ocsat.2021.02.18.1.0
- 42.PMM B., Lorenz C., Aguiar B.S., Failla M.A., Barrozo L.V., Chiaravalloti-Neto F.. Spatio temporal dynamic of COVID-19 mortality in the city of sao paulo, brazil: shifting the high risk from the best to the worst socio-economic conditions. ArXiv: 2008.02322 [STAT.ap], August 5, 2020; arXiv https://arxiv.org/abs/2008.02322.
- 43.Lavine J.S., Bjornstad O.N., Antia R. Immunological characteristics govern the transition of COVID-19 to endemicity. Science. 2021;371:741. doi: 10.1126/science.abe6522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fontanet A., Cauchemez S. COVID-19 Herd immunity: where are we? Nat Rev Immunol. 2020;20:583–584. doi: 10.1038/s41577-020-00451-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bussi L.F., Prete Jr C.A., CMM A., Mendrone Jr A., Salomon T., Almeida-Neto C. Three-quarters attack rate of SARS-cov-2 in the brazilian amazon during a largely unmitigated epidemic. Science. 2021;371:288–292. doi: 10.1126/science.abe9728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Alizon S., Haim-Boukobza S., Foulongne V., Verdurme L., Trombert-Paolantoni S., Emmanuel L., et al. Rapid spread of the SARS-CoV-2 delta variant in some french regions, june 2021. Euro Surveill. 2021;26:2100573. doi: 10.2807/1560-7917.ES.2021.26.28.2100573. [DOI] [PMC free article] [PubMed] [Google Scholar]