Linear and nonlinear profiles of weak behavioral and neural differentiation between numerical operations in children with math learning difficulties

Abstract

Mathematical knowledge is constructed hierarchically during development from a basic understanding of addition and subtraction, two foundational and inter-related, but semantically distinct, numerical operations. Early in development, children show remarkable variability in their numerical problem-solving skills and difficulties in solving even simple addition and subtraction problems are a hallmark of math learning difficulties. Here, we use novel quantitative analyses to investigate whether less distinct representations are associated with poor problem-solving abilities in children during the early stages of math-skill acquisition. Crucially, we leverage dimensional and categorical analyses to identify linear and nonlinear neurobehavioral profiles of individual differences in math skills. Behaviorally, performance on the two different numerical operations was less differentiated in children with low math abilities, and lower problem-solving efficiency stemmed from weak evidence-accumulation during problem-solving. Children with low numerical abilities also showed less differentiated neural representations between addition and subtraction operations in multiple cortical areas, including the fusiform gyrus, intraparietal sulcus, anterior temporal cortex and insula. Furthermore, analysis of multi-regional neural representation patterns revealed significantly higher network similarity and aberrant integration of representations within a fusiform gyrus-intraparietal sulcus pathway important for manipulation of numerical quantity. These findings identify the lack of distinct neural representations as a novel neurobiological feature of individual differences in children’s numerical problem-solving abilities, and an early developmental biomarker of low math skills. More generally, our approach combining dimensional and categorical analyses overcomes pitfalls associated with the use of arbitrary cutoffs for probing neurobehavioral profiles of individual differences in math abilities.

Introduction

Mathematical knowledge is constructed hierarchically from symbolic representations of quantity and rules to manipulate them by adding and subtracting items to and from numerical sets. Although the symbolic representations of these operations differ only minimally in their perceptual format, they differ considerably at the cognitive-semantic level (Campbell & Alberts, 2009). Crucially, knowledge of basic addition and subtraction problems lies at the core of successful acquisition of more complex mathematical skills during development, and poor performance on these two basic arithmetic operations is a defining phenotypical and clinical feature of learning disabilities and math learning difficulties (MLD) more generally. Here, we use novel quantitative analyses to investigate whether two foundational arithmetical operations, namely addition and subtraction, share overlapping neural representations, and whether an inability to form distinct representations is associated with poor problem-solving abilities in children during the early stages of math-skill acquisition. A key aspect of our approach is that we combined dimensional and categorical analyses to uncover linear and nonlinear neurobehavioral profiles of heterogeneity in MLD.

Addition and subtraction differ minimally in surface format and are highly inter-related operations, by virtue of the fact that subtraction is the mathematical inverse of addition. Perceptually the two operations are virtually identical as they differ only by a single vertical line: ‘+’ vs. ‘−’. However, they are highly dissimilar in terms of cognitive processes and efficiency (Barrouillet et al., 2008). Behavioral studies have shown that while single-digit addition problems are typically solved by memory retrieval (Barrouillet et al., 2008; Thevenot et al., 2007; Thevenot & Barrouillet, 2020) or fast procedural strategies (Ashcraft, 1992; Y. Chen & Campbell, 2018), related subtraction problems are far less likely to be solved by direct retrieval, and they place greater demands on working memory and cognitive control, particularly in children with weaker problem-solving skills (Caviola et al., 2014; Hayashi et al., 2000). Typically-developing children initially use inefficient strategies such as finger counting, slow mental counting and eventually learn to retrieve solutions to simple addition problems from memory with high efficiency; however, they continue to solve subtraction problems with more elaborate algorithmic procedures, such as counting and multi-step calculation (Barrouillet et al., 2008; G. Peters et al., 2014). While typically developing children engage distinct strategies when starting to master addition and subtraction problems, children with poor math abilities continue to rely on laborious procedural computations for both operations (Ostad, 1999). These behavioral findings suggest that the two operations rely on dissimilar cognitive processes, but the extent to which they engage distinct brain representations, and the underlying neurobehavioral sources of individual variability are poorly understood.

Neuroimaging studies have shown that children with poor math abilities show aberrant brain responses and connectivity during the processing of both addition and subtraction problems (Ashkenazi et al., 2012; Iuculano et al., 2015; Lowe, 2011; Rosenberg-Lee et al., 2015; Rykhlevskaia, 2009). Surprisingly, despite slower and less accurate performance, children with low math skills show significant hyper-activity in multiple parietal, occipito temporal and prefrontal regions during arithmetic problem solving (De Smedt et al., 2011; Iuculano et al., 2015; L. Peters & De Smedt, 2018) as well as hyper-connectivity between parietal and prefrontal cortices (Rosenberg-Lee et al., 2015). Yet, although extant brain imaging studies have identified the anatomical and functional bases of deficits in children with different levels of math difficulties, it remains unclear how these aberrancies may relate to behavioral difficulties in arithmetic processing, and for different types of numerical problems and operations. Examining patterns of neural representations, rather than activations, could potentially provide a neurobiological mechanism to probe sources of heterogeneity in math processing, and thereby identify novel biomarkers of impairments in children at the lower end of the distribution of abilities. Furthermore, it is unknown whether aberrant patterns of neural representations exist along a continuum of math abilities or whether children with most severe difficulties represent information in a fundamentally different manner. To date, few studies have examined individual variation in children with low math skills and the neural mechanisms associated with these differences, creating a significant challenge to our understanding of heterogeneity in math problem-solving skills during its formative stages, particularly in children falling at the lower end of the distribution of abilities. Notably, in order to develop effective interventions for those with low math skills, the neurobiological basis of the deficits need to be well characterized using robust quantitative approaches. Thus far, research into these causes has been hindered by variable selection/cut-off criteria used to define individuals with lower math abilities (Geary, 2011, 2013). To address this challenge, we leverage both dimensional and categorical analyses to probe neural representations underlying distinct numerical operations in the brains of children with poor math abilities, using multiple levels of analyses (Figure 1).

Figure 1. Multi-level analytical framework for investigation individual differences in behavioral, cognitive and neural profiles of differentiation between distinct numerical operations.

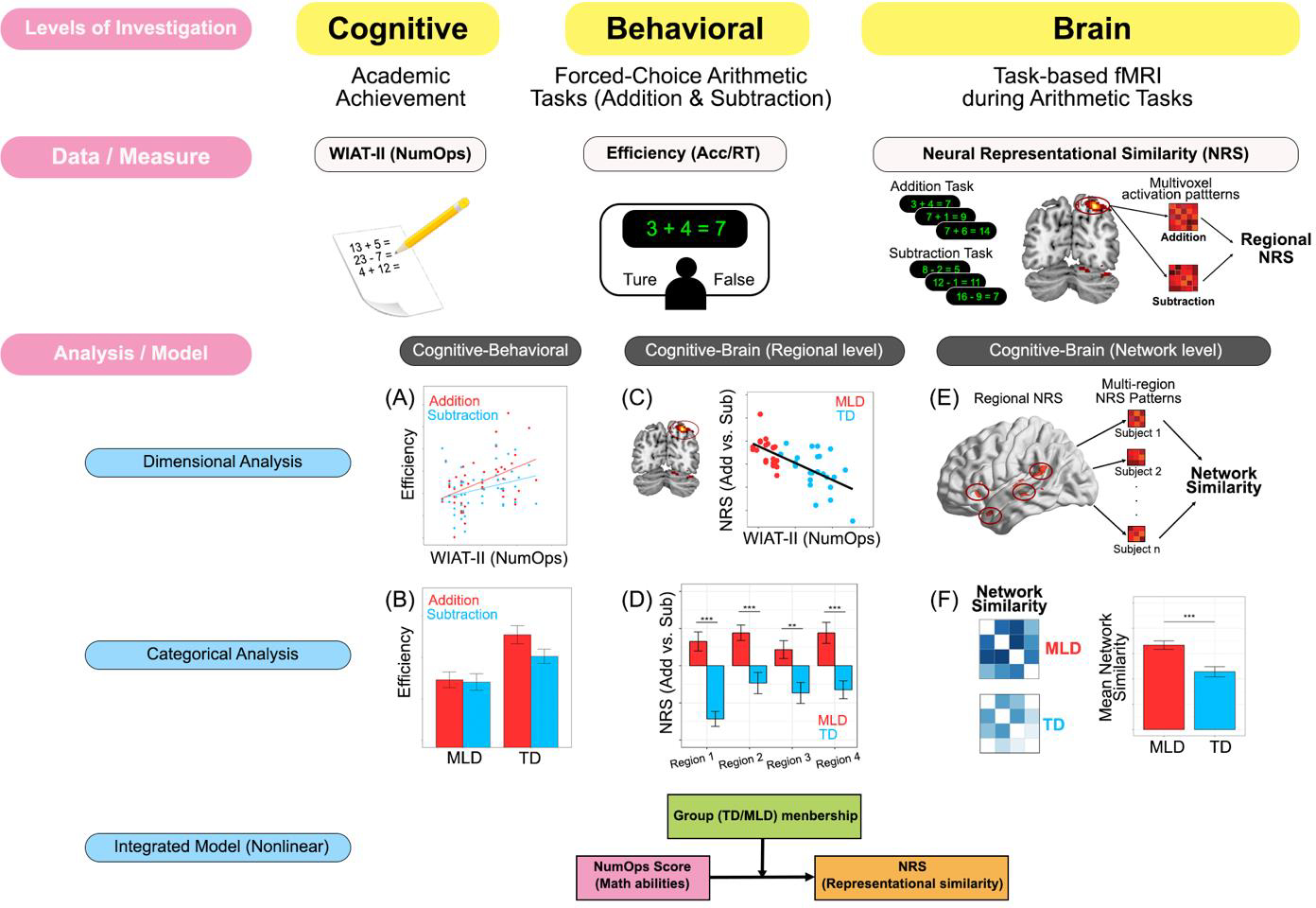
(A, B) Analysis of cognitive-behavioral relationship using dimensional and categorical approaches. (C, D) Analysis of cognitive-brain relationships using dimensional and categorical approaches. (E, F) Inter-regional network similarity analysis to probe integration of neural representations in pathways important for manipulation of numerical quantity.

The first aim of our study was to investigate behavioral and cognitive profiles associated with arithmetic problem-solving involving addition and subtraction operations in children with low math abilities (Figure 1A&B). We used both dimensional and categorical approaches to determine whether children with low proficiency are impaired on both operations, and whether performance on the two operations is less differentiated in children with poor math skills compared to their typically developing (TD) peers (Bruyer & Brysbaert, 2011). In addition to overt behavioral measures, we evaluated latent decision-making processes by jointly modelling accuracy and reaction time using a hierarchical drift diffusion model (HDDM) in which a drift-process accumulates evidence over time until it crosses one of the two response boundaries (Froehlich et al., 2016; Oganian et al., 2016; Ratcliff & McKoon, 2008; Ratcliff & Smith, 2004). Drift-rate, the speed with which the accumulation process approaches the decision boundaries, represents the relative evidence for or against a particular response (Wiecki et al., 2013), and previous work has suggested that a lower drift-rate could indicate worse performance on math tasks involving addition problem solving (Iuculano et al., 2020). Therefore, we investigated whether the rate of evidence accumulation to a decision threshold was a potential mechanism underlying weak problem-solving skills and tested the hypothesis that, compared to their peers with higher math skills, children with poor math skills would show a lower speed of evidence accumulation, for both addition and subtraction operations.

The second aim of our study was to characterize neural representations between addition and subtraction operations, and to test the hypothesis that children with poor problem-solving abilities show weak neural differentiation between the two distinct operations. Different from mapping brain activation levels, neural representational similarity (NRS) analysis assesses whether cognitive processes share similar neural features, and identifies brain areas that are most sensitive to distinctions between mental states evoked by specific task conditions (Kriegeskorte et al., 2008; Kriegeskorte & Kievit, 2013). Neural representational similarity reflects similarities in population-based coding and is therefore ideal for examining neurocognitive processes underlying addition and subtraction problems, given their close perceptual similarity but semantic dissimilarity. A previous study found that children with MLD tended to show less differentiated neural representations between addition problems of different levels of difficulty (Ashkenazi et al., 2012). Whether such lack of differentiation extends to distinct numerical operations is currently not known. We hypothesized that children with low math abilities would show less differentiated neural representations between two operations because they are likely to engage inefficient strategies for both (Ostad, 1999). An alternative hypothesis is that if children with lower math abilities engaged entirely different cognitive processes for addition and subtraction problems (Barrouillet et al., 2008; G. Peters et al., 2014), they would show more differentiated neural representations than their TD peers. Here, we test these competing hypotheses to gain insights into neurocognitive processes associated with basic problem-solving skills in children with MLD.

In an advance over previous work, we used both dimensional and categorical approaches to characterize linear and nonlinear relationships of math skills and neural representations of addition and subtraction, the two arithmetic operations during a crucial age for math skill acquisition in children (Figure 1C&D). A dimensional approach was used to assess linear changes along a continuum of arithmetic abilities, while a combination of dimensional and categorical approaches was used to assess distinct profiles in children at the lower end of the distribution of abilities, including those with MLD, in contrast to the profiles observed in their TD peers. This two-pronged approach was used to identify brain systems that show weaker- or stronger-than-expected profiles in children with MLD.

The third and final aim of our study was to probe disruptions in communication of neural representations across brain regions in children at the lower end of the distribution of abilities, including those with MLD (Figure 1E&F). In a further advance over previous research in the field, we examined representational similarity at a network level and determined impairments in co-occurring patterns of deficits across multiple brain regions (Anzellotti & Coutanche, 2018; Pillet et al., 2020). This approach was used to characterize the organization of multivariate representational networks in children with low math skills and determine specific pathways of impaired communication. Using an NRS-based network analysis, we specifically examined whether: (a) weak differentiation of neural representations at the regional level is also manifested at the network level; and (b) integration of neural representations in the ventral (i.e., number form system) and dorsal (i.e., quantity information system) pathways (Battista et al., 2018; Evans et al., 2015; Menon, 2014) are aberrant in children with poor math abilities.

We hypothesized that children with poor math abilities would show less differentiated behavioral, cognitive, and neural representational profiles between addition and subtraction problems. We further hypothesized that aberrant neural representations would be detected in distributed brain areas, including parietal areas associated with visuo-spatial attention, temporal lobe regions involved in language and semantic processing, as well as prefrontal cognitive control systems, consistent with a multicomponent model of math learning disabilities and developmental dyscalculia (Fias et al., 2013; Iuculano, 2016). We demonstrate that our novel quantitative approaches provide a more comprehensive understanding of how distinct numerical operations are represented in the brains of children, elucidate linear and nonlinear profiles of neural representations associated with individual differences in children’s math abilities, and reveal weak operation-specific pruning of distributed neural circuits. Our findings are relevant for understanding both typical and atypical development of problem-solving skills and has the potential to inform targeted interventions in children with math learning difficulties.

Method

Participants

A total of forty-six children in their 2^nd or 3^rd grade of schooling (ages 7 to 9) were recruited from multiple school districts in the San Francisco Bay area. Informed written consent was obtained from the legal guardian of the child and all study protocols were approved by the Stanford University Review Board. All participants were volunteers and were treated in accordance with the American Psychological Association “Ethical Principles of Psychologists and Code of Conduct”. The participants had no history of medical, neurological or psychiatric illness. All participants had Full-scale IQ (FS-IQ) scores > 80 (range: 84–128; Table 1), as assessed by the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999). Math skills of children were assessed by the Numerical Operations (NumOps) subtest of the Wechsler Individual Achievement Test Second Edition (WIAT-II; Wechsler, 2001) given that weak arithmetic ability represents one of the most distinctive behavioral features of impaired problem-solving skills in children, and it is a hallmark of MLD (Butterworth, 2005). On this test, a wide range of math skills was observed (range: 77–131). One participant with an invalid NumOps subtest score due to administrator error was then excluded, resulting in a final sample of 45 children (25 Females; mean age = 8.37 years old).

Table 1.

Demographic and cognitive profiles of the whole sample and the TD/MLD subgroups.

	The whole sample			TD	MLD
	N	Range	Mean (SD)	Mean (SD)	Mean (SD)
Gender (Female/Male)	25F/20M			12F/12M	13F/8M
Grade (2nd/3rd)	15/30			7/17	8/13
Age	45	7.14–9.92	8.37 (0.64)	8.40 (0.64)	8.34 (0.65)
WASI
VIQ	45	79–138	110 (12.47)	111.88 (12.46)	107.86 (12.43)
PIQ	45	77–145	108.38 (12.8)	109.38 (12.71)	107.24 (13.12)
FSIQ	45	84–128	110.2 (10.5)	111.83 (10.26)	108.33 (10.69)
WIAT-II
Word Reading	45	77–130	106.29 (11.26)	110.38 (9.36)	101.62 (11.64)
Numerical Operations	45	77–131	98.73 (15.01)	110.75 (9.6)	85.00 (4.29)
Reading
Comprehension	45	88–124	106.73 (10.06)	109.04 (10.19)	104.10 (9.45)
Math Reasoning	45	50–130	104.69 (14.78)	109.17 (15.64)	99.57 (12.16)
WMTB-C
Digit Recall	45	73–145	106.47 (16.57)	107.42 (16.3)	105.38 (17.22)
Block Recall	44	64–114	93.55 (11.72)	96.21 (11.39)	90.35 (11.6)
Count Recall	45	56–117	85.38 (18.82)	88.04 (20.03)	82.33 (17.31)
Digit Backward Recall	45	70–131	96.29 (16.53)	100.42 (15.4)	91.57 (16.88)

Notes: WASI = Wechsler Abbreviated Scale of Intelligence; WIAT-II = Wechsler Individual Achievement Test (Second Edition); WMTB-C = Working Memory Test Battery for Children.

Using a norm-based criterion, namely below-grade-level scores (the 25^th percentile. i.e., a standardized score below 90) on the WIAT-II NumOps subtest, 21 children were classified as having math learning difficulties (MLD group), while 24 children whose scores were at or above 90 on the same test formed the TD group (Table S1). The 25^th percentile was chosen based on the extant literature of cohorts identified as having math learning difficulties (Lambert & Spinath, 2018; Schwartz et al., 2018; Skeide et al., 2018; Swanson et al., 2018; Tolar et al., 2016; Wong & Chan, 2019). We also chose this criterion to ensure an appropriate N of children falling within the low-end of the distribution of abilities (N = 21) in order to conduct categorical analysis of nonlinearity-effects associated with individual differences in math problem-solving skills, and to ensure that individuals with low math abilities did not have comorbid disabilities in general cognitive functions, such as low IQ or impaired working memory compared to TD. The MLD and TD groups did not differ on age, FSIQ, Verbal and Performance IQ, and standardized Working Memory (WM) measures (Working Memory Test Battery for Children, WMTB-C; Pickering & Gathercole, 2001). The MLD had significant lower NumOps, Math Reasoning and Word Reading scores than the TD group (see Table S1).

Standard assessments of math and reading abilities

Children’s mathematical and reading abilities were assessed using the WIAT-II (Wechsler, 2001). This achievement battery includes nationally standardized measures of academic skills and problem-solving abilities for Grades K to 12, which are normed by grade and time of academic year (Fall, Spring, or Summer). The Numerical Operations was used to assess participants’ mathematical skills and assign children into MLD or TD groups, and measures number writing and identification, rote counting, number production and simple addition, subtraction, multiplication and division. Additionally, the Mathematical Reasoning subtest was also administered (see Table 1). This subtest measures counting, geometric shape identification, and single- and multi-step word problem-solving involving time, money, and measurement. In this subtest, students are given unlimited time to solve written math problems and the problems are organized with increased progression of task difficulty. The participant is required to solve problems with whole numbers, fractions or decimals, interpret graphs, identify mathematical patterns, and solve problems of statistics and probability. The WIAT-II (i.e. Word Reading and Reading Comprehension subtests) was also used to assess reading abilities in both cohorts.

Experimental procedures

Functional MRI (fMRI) tasks

The fMRI experiment examined single-digit arithmetic problem-solving skills in children and consisted of one run of addition and one run of subtraction. Within each run, there were four task conditions: (i) Complex arithmetic, (ii) Simple arithmetic, (iii) Symbol-finding and (iv) Passive fixation/rest. In the Complex addition task, participants were presented with an equation involving two addends and were asked to indicate, via a button press, whether the presented answer was correct (e.g. “3 + 4 = 8”). The first operand ranged from 2 to 9, the second from 2 to 5 (tie problems, such as “5 + 5 = 10”, were excluded), and correct answers appeared in 50% of the trials. Incorrect answers deviated by ± 1 or ± 2 from the correct sum. The Simple addition task was identical except that one of the addends was always ‘1’ (e.g. “3 + 1 = 4”). In the Complex subtraction task, the first operand ranged from 3 to 14 and the second operand from 2 to 5. In the Simple subtraction task, the first operand ranged from 2 to14 and the second operand was always ‘1’. As in the addition task, incorrect answers deviated by ± 1 or ± 2 from the actual difference, with the constraint that actual and presented difference was always greater than zero. All subtraction problems were the inverse of addition problems and matched on problem size. In the symbol-finding condition, participants were asked to decide whether the digit “5” was present in a string of symbols, e.g., “3 @ 5 ( 9” or “4 ( 7 @ 2”. In the passive fixation block-periods the symbol “*” appeared at the center of the screen and participants were asked to focus their attention on it.

During the task, stimuli were presented in a block fMRI design in order to optimize signal detection (Friston et al., 1999). In each task, stimuli were displayed for 5 seconds with an inter-trial interval of 500 ms. There were 18 trials for each task condition, broken into 4 blocks of 4 or 5 trials (2 blocks of 4 trials and 2 blocks of 5 trials, resulting in a total of 18 trials), thus each block lasted either 22 or 27.5 seconds. The total length of each experimental run was 6 minutes and 36 seconds. The order of blocks was randomized across participants with the following constraints: in every set of four blocks, all conditions were presented, and the Complex and Simple arithmetic condition-blocks were always separated by either a symbol-finding (not examined here) or a passive-fixation condition-block. We focused on the contrast between Complex and Simple arithmetic conditions, rather than the symbol-finding condition, to best equate (and thus control for) low-level perceptual, motor and decision-making processes involved in arithmetic problem solving. Previous research has shown that ‘N+1′ and ‘N−1′ arithmetic problems are solved by incremental, or decremental, counting (Campbell & Metcalfe, 2007) with higher accuracy and faster reaction times relative to more complex addition (and subtraction) problems (Cho et al., 2011). Hence, this choice of contrast allowed us to best isolate processes involved in arithmetic problem-solving across addition and subtraction tasks, reflecting overall arithmetic problem-solving efficiency with different strategies in children.

Behavioral performance on mental arithmetic tasks

We determined accuracy (%) and Reaction Times (RTs) associated with performance of addition and subtraction problem-solving tasks during fMRI scanning in each participant. To overcome accuracy-speed trade-off issues (Bruyer & Brysbaert, 2011), we used composite efficiency scores (ES) calculated as: accuracy % / mean RTs of correct responses, to examine task performance so higher ES values reflect better performance. We used this measure because a speed-accuracy trade-off has been systematically reported to be a phenotypic characteristic of poor math performance across a range of math abilities, including MLD (Butterworth, 2005; Geary et al., 1991; Iuculano et al., 2008; G. Peters et al., 2014; L. Peters & De Smedt, 2018; Rosenberg-Lee et al., 2015).

Cognitive modeling of behavior

The addition and subtraction verification processes (2-choice) were modeled as a drift diffusion process, in which evidence accumulates over time resulting in a forced-choice selection, when a decision threshold is reached. We developed a hierarchical drift diffusion model (HDDM) to determine the drift rate, decision threshold, response bias, and non-decision time. The drift rate parameter characterizes evidence accumulation, with higher values characterizing a greater proportion of correct responses, and higher absolute values of the drift rate characterizing faster responses. The decision threshold parameter captures the degree of evidence required to conclusively evaluate the answers. For each individual, the threshold, bias, and non-decision time parameters were allowed to vary for addition and subtraction, and for simple versus complex problems. The drift rate was hierarchically inferred by adding an item-response model that allowed the drift rate to be a combination of item-level difficulty that was inferred at a group level (TD and MLD) individually for each unique item, and individual level ability, separately for addition and subtraction. The model was implemented within a Bayesian inference framework using JAGS (Plummer, 2003).

Functional MRI data acquisition

Functional brain images were acquired on a 3T GE Signa scanner (General Electric, Milwaukee, WI) using a custom-built head coil at the Stanford University Lucas Imaging Center. Cushions were placed around participants’ heads to minimize head movement. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the anterior commissure-posterior commissure line and covering the whole brain were acquired using a T2* weighted gradient echo spiral-in/spiral-out pulse sequence (Glover & Lai, 1998) with the following parameters: TR = 2 sec, TE = 30 ms, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring fMRI scans (Kim et al., 2002).

Functional MRI data preprocessing

Data were analyzed using SPM12 (http://www.fil.ion.ucl.ac.uk/spm). The first 5 volumes were discarded to allow for signal equilibration. Images were reconstructed, by inverse Fourier transform, for each of the time points into 64 × 64 × 28 image matrices (voxel size 3.125 × 3.125 × 4.5 mm). Images were first realigned to the first scan to correct for motion and slice acquisition timing. A linear shim correction was applied separately for each slice during reconstruction using a magnetic field map acquired automatically by the pulse sequence at the beginning of the scan (Glover & Lai, 1998). Translational movement in millimeters (x, y, z) was calculated based on the SPM12 parameters for motion correction of the functional images in each subject. To correct for deviant volumes resulting from spikes in movement, we used de-spiking procedures similar to those implemented in AFNI (Cox, 1996). Deviant volumes were identified as having either total displacement from the initial volume greater than half of a voxel size (1.562 mm) or change in global signal greater than 5%. The frame-wise displacement was then computed as the square root of the sum of both translational and rotational displacement by first converting rotational displacement from degree to millimeters, assuming a brain radius of 65mm. Deviant volumes were then interpolated using the two adjacent scans. Furthermore, translational movement parameters (x, y, z), rotational movement parameters (roll, pitch, yaw), and framewise displacement did not differ between MLD and TD groups for either addition or subtraction tasks (all ps > .05, see Table S6). No participants had more than 0.5 mm frame-to-frame mean displacement. After the interpolation procedure, images were spatially normalized to standard stereotaxic space (based on the Montreal Neurologic Institute – MNI – coordinate system), resampled every 2 mm using sinc interpolation, and smoothed with a 6mm full-width half-maximum Gaussian kernel to decrease spatial noise prior to statistical analysis.

Functional MRI data analysis

1^st-level analyses

Task-related brain activation in response to each condition (complex arithmetic, simple arithmetic, symbol-finding, fixation) and each task (addition, subtraction) was first modeled at the individual subject-level using the General Linear Model (GLM) implemented in SPM12. For each subject we modeled task-related regressors as boxcar functions corresponding to the epochs during which each condition was presented, and for each task, and convolved with a hemodynamic response function. The six head motion parameters generated in the realignment procedure were also included in the model as regressors of non-interest. Voxel-wise contrasts and t-statistics images were then generated by contrasting Complex versus Simple problems in each task. We focused on the contrast of Complex versus Simple since behavioral research suggests that the simple (n ± 1) trials are solved by incremental or decremental counting (Campbell & Metcalfe, 2007), and performance on this task is characterized by higher accuracy and faster reaction times compared to complex problems (Cho et al., 2012; Iuculano et al., 2014; Rosenberg-Lee et al., 2011; Young et al., 2012). Moreover, because stimuli in the Simple condition have the same format as in the Complex condition, it provides a high-level control for sensory and number processing, as well as decision-making and response selection. All trials were included in the analysis to ensure similar number of trials across participants.

Multi-voxel Representational Similarity Analyses (MRSA)

A whole brain searchlight MRSA (Kriegeskorte et al., 2008) was used to assess the similarity of spatial activity patterns associated with two arithmetic tasks: addition and subtraction at the individual subject level. At each voxel, a 6mm radius sphere was used to define a searchlight region. The Pearson correlation coefficient between t-scores for addition and subtraction problems was then computed for each region after removing mean brain activity. Then, correlation coefficients were normalized using Fisher’s r-to-Z transform: Z = 0.5 * ln((1+r)/(1−r)) and entered into group-level analyses. First, we used the NRS z-score in a one-sample correlational analysis to identify brain regions showing multivoxel representation similarity between addition and subtraction that was associated with individual differences in math skills using NumOps scores. In order to ensure an independent analysis for the nonlinear approach, we then investigated brain regions showing different relationships of NRS and NumOps between the MLD and TD groups to characterize any nonlinear patterns between NRS and NumOps. Significant NRS clusters were determined using a voxel-wise height threshold of p < .005, FDR-corrected for multiple spatial comparisons at p < .01 (cluster extent 87 voxels), based on Monte Carlo simulations (Cho et al., 2012; Iuculano et al., 2014).

Multi-region network similarity analysis

In order to further investigate how neural representations were related to individual differences in math skills in children at a network level, we conducted a series of analyses based on the NRS score from the local regions which showed significant correlations – in terms of less differentiated neural representations – and math skills across individuals (Table 2 and Figure 3). We characterized the multi-region network similarity in MLD and TD groups separately. Based on the regional NRS of the same set of identified regions from the GLM results, we first calculated the Manhattan Distance of these brain regions across all subjects with MLD or across all subjects in the TD group, and then converted the Distance matrix into a similarity matrix by normalization, 1-(D-min(D))/range(D), in which D is the distance matrix. We then used independent sample t-tests to examine group difference (MLD vs TD) in the mean values of the lower triangles of the multi-region similarity matrix. To test the hypothesis of deficits in ventral-dorsal integration in MLD, we selected three regions from the GLM results for this analysis: (i) the posterior fusiform gyrus (pFG) as a seed, and examined the similarity of the right pFG with a (ii) dorsal target superior parietal lobe/intraparietal sulcus (SPL/IPS) and a (iii) ventral target superior anterior temporal cortex (sATC) as a comparison control). We chose these regions as they are core regions for representing the number form, manipulation of numerical quantity, and semantic knowledge of numerical operations (Fias et al., 2013; Iuculano, 2016; Menon, 2014; L. Peters & De Smedt, 2018). The significance testing was conducted by subsampling and permutation. In each permutation, we subsampled 80% of subjects in the MLD and TD groups separately, and conducted the same multi-region similarity analysis and the hierarchical clustering based on the similarity matrix. We recorded the distance of pFG with SPL/IPS and sATC in MLD and TD groups. After 10,000 permutations of this procedure, we established distributions of pFG-SPL/IPS and pFG-sATC distances in both MLD and TD. Finally, we conducted a two-way ANOVA to examine the interaction between Group (MLD vs. TD) and Target (dorsal vs. ventral).

Table 2.

Brain regions showing significant effects of NRS associated with NumOps scores and Group (MLD vs. TD)* NumOps interaction.

Main effect of NumOps (linear)
	MNI Coordinates
Region	x	y	z	Max Z	Cluster Size
Negative effect
Left STS/ Heschl’s gyrus	−42	−22	2	5.72	414
Right IPL/IPS	26	−72	52	5.45	318
Right Ventral Striatum	26	−10	2	4.79	316
Right ventral insula	32	6	−12	4.14	200
Right SPL/IPS	46	−40	52	3.79	112
Left TPJ/SMG	−64	−44	22	3.74	192
Left sATC	−50	12	−22	3.56	90
Right cerebellum	38	−64	−24	3.5	274
Right FG	36	−62	−12	3.21
Positive effect
No significant clusters
Interaction between Group*NumOps (nonlinear)
TD > MLD
Left dlPFC	−30	36	28	3.74	97
Left IPS	−28	−72	42	3.76	89
Right Cerebellum	14	−50	−22	4.30	103
MLD > TD
No significant clusters

Figure 3. Higher Neural Representational Similarity (NRS) in children with low math abilities.

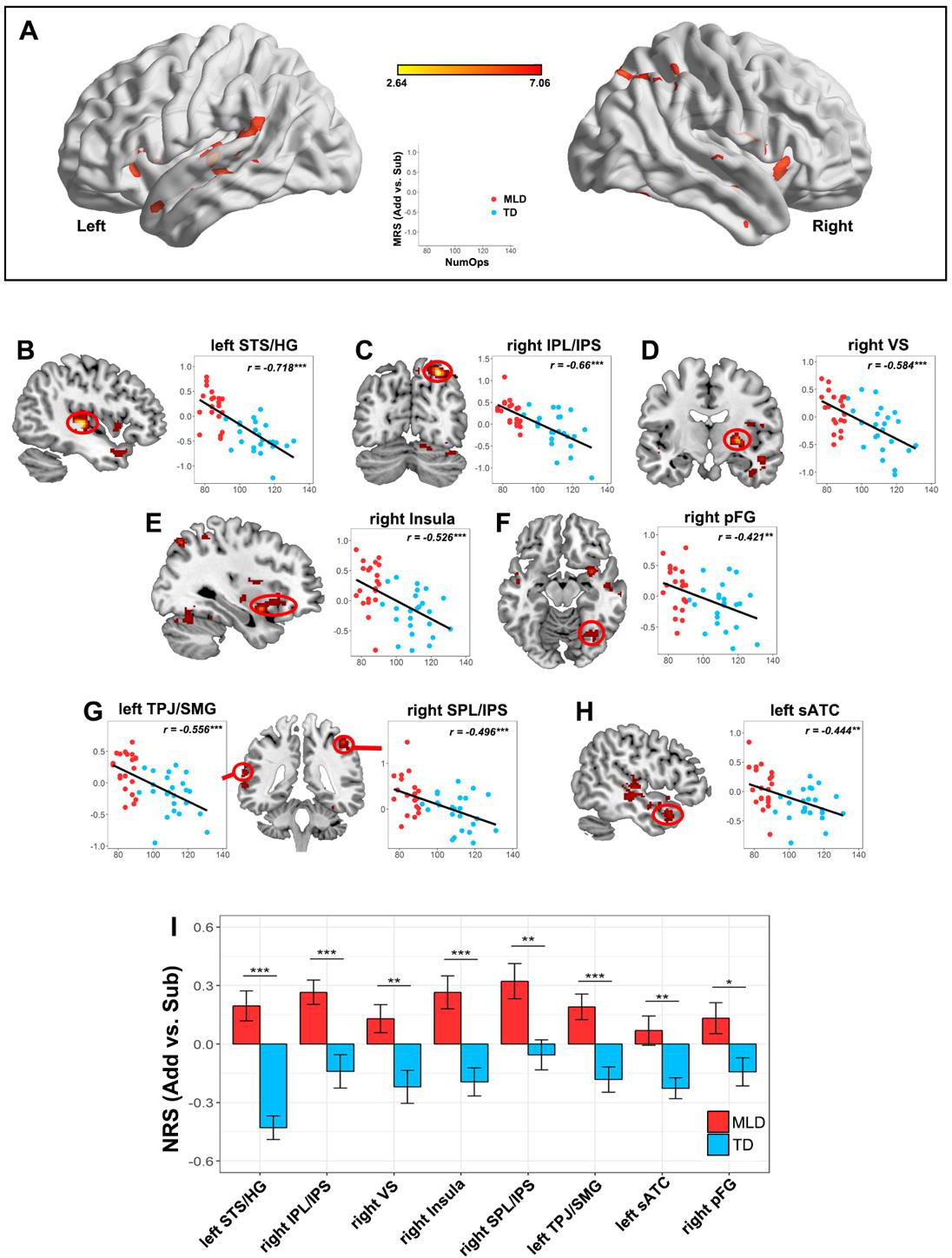
(A) Brain regions showing significant negative correlation between NRS and Numerical Operations (NumOps) subscores of the WIAT-II. (B-H) Children with low math abilities show higher NRS in multiple parietal, temporal and prefrontal cortical regions (I) Children with MLD show higher NRS than TD children (ROIs were chosen to visualize the MRS difference in a categorical approach). Note: Statistical testing and analysis were conducted using a stringent threshold (height, p < 0.005; FDR-corrected for cluster extent p < 0.01); to facilitate visualization activation maps are shown at p < 0.01 (height) (FDR-corrected for cluster extent p < 0.01). STS/HG = Superior Temporal Sulcus and Heschl’s gyrus; IPS = Intraparietal Sulcus; VS = Ventral Striatum (putamen/pallidum); pFG= posterior Fusiform Gyrus; TPJ/SMG = Temporoparietal Junction and Supramarginal Gyrus; SPL/IPS = Superior Parietal Lobule and Intraparietal Sulcus; and sATC = superior Anterior Temporal Cortex.

Results

Performance on addition and subtraction operations is correlated with individual differences in math abilities

We investigated the relation between performance on addition and subtraction tasks, undertaken during fMRI scanning, and Numerical Operations (NumOps) subscores of the WIAT-II, a standardized measure of math abilities (see Table 1) (Wechsler, 2001). Behavioral performance was assessed using efficiency scores (Iuculano et al., 2008), a composite measure obtained by dividing accuracy by mean reaction time (RT) in each participant (Bruyer & Brysbaert, 2011). Efficiency scores in both addition (r = 0.447, p < .01) and subtraction (r = 0.299, p < .05) were correlated with NumOps, suggesting that children with lower math abilities performed worse on both arithmetical operations (Figure 2A). Although the overall difference in slopes was not significant (p > 0.05), children at the lower end of performance tended to show smaller differences in efficiency between the two operations. Additional analyses with accuracy and RT measures, separately, are shown in the Supplementary Information (see Figure S1 and Tables S1 & S2).

Figure 2. Behavioral performance during problem-solving involving addition and subtraction operations.

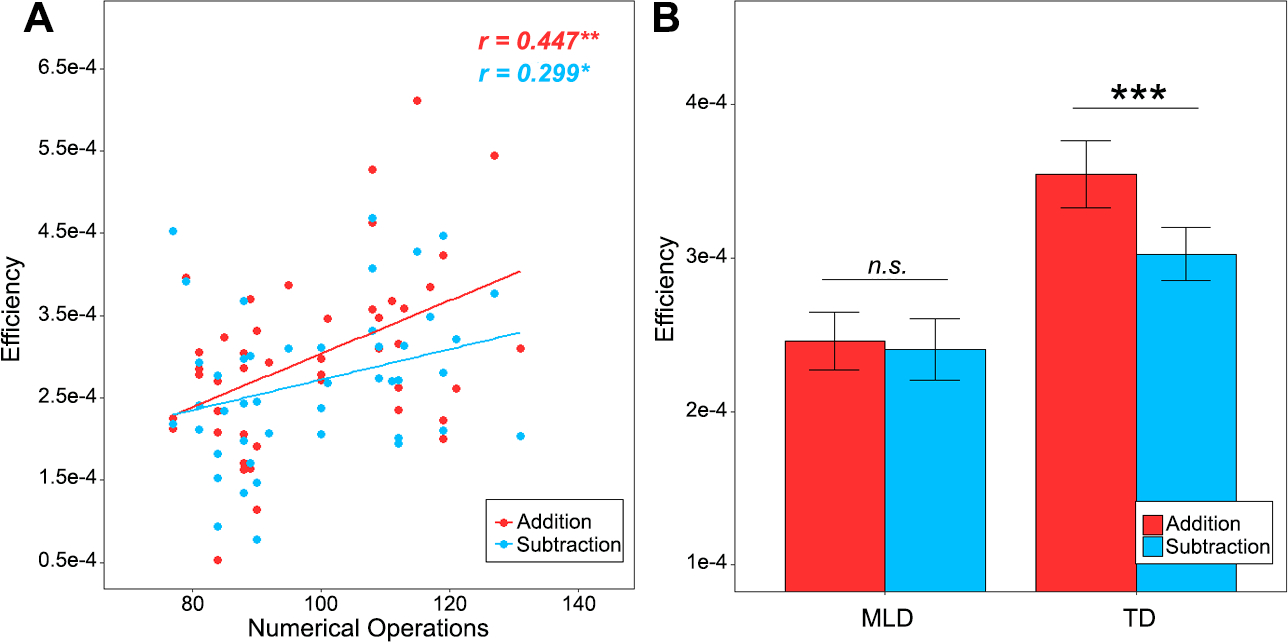
(A)Numerical Operations subtest scores were significantly correlated with performance efficiency (accuracy/reaction time) in both addition and subtraction tasks; (B) Lower efficiency in children with MLD compared to TD children in both addition and subtraction tasks. A significant difference between addition and subtraction operations was observed in TD, but not in MLD children.

Less differentiated performance in children with MLD

Next, we used a categorical approach to investigate whether children with MLD show poorer performance overall, when compared to TD controls, and crucially, whether they show less differentiated performance between the addition and subtraction operations (Table S3). A two-way mixed ANOVA on performance efficiency with between-subject factor Group (MLD vs. TD) and within-subject factor Operation (Addition vs. Subtraction) revealed a significant interaction between Group and Operation (F(1,43) = 4.647, p <0.05). Main effects of Group (F(1,43) = 11.22, p <.01) and Operation (F(1,43) = 8.062, p <0.01) were also significant. Further analysis revealed that in the MLD group, there was no significant difference between performance on addition and subtraction (t(20) = 0.3085, p = 0.76), whereas the TD controls showed significantly better performance in the addition task compared to the subtraction task (t(23) = 4.376, p < 0.001) (Figure 2B). It is unlikely that the lack of statistically significance in the MLD group was due to sample size because the sample size of n =21 (i.e. MLD group) had a large a-priori power = 95% assuming the same effect size in TD (d = 0.83), at the α = 0.05 level.

Decision-making associated with addition and subtraction problem solving is impaired in children with low abilities

Next, we investigated latent decision-making processes associated with arithmetic problem solving by combining hierarchical drift diffusion modeling (Ratcliff & McKoon, 2008; Ratcliff & Smith, 2004) with item-response based modeling to account for differential item level difficulty. We found that NumOps scores were positively correlated with the drift rate on addition (r = 0.341, p < 0.05) and subtraction (r = 0.347, p < 0.05) problems. No other model parameters – decision threshold, non-decision time, or response bias – showed a significant correlation with NumOps (Table S4). Comparison of children with MLD and their TD peers revealed that the drift rate on addition and subtraction problems differed in the TD group (M_Add = 0.91 vs. M_Ssub = 0.80, p < 0.05), but not in the MLD group (M_A = 0.68 vs. M_S = 0.60, p > 0.05; a- priori power = 46% at α = 0.05 assuming a similar effect size in TD as d = 0.43) (Figure S2).

Less differentiated neural representations in children with lower math abilities

We next sought to determine whether low math abilities are associated with weaker differentiation between neural representations for addition and subtraction problems, using a whole-brain searchlight algorithm (Ashkenazi et al., 2012; Bugden et al., 2019; Misaki et al., 2009). We found that NumOps scores were negatively correlated with NRS between addition and subtraction problems in multiple parietal-temporal-prefrontal areas, including intra-parietal sulcus, posterior superior temporal sulcus and anterior temporal cortex, and anterior insula (Table 2 and Figure 3A–H). No brain regions showed a positive correlation between NRS and NumOps scores. These results suggest that more distinct NRS is a hallmark of higher math skills.

Less differentiated neural representations in children with MLD

A categorical approach was used to further demonstrate that children identified as MLD in our study did show aberrant neural representations in the same set of regions that were revealed in the dimensional analysis. Two-sample t-tests between the MLD and TD groups showed a significant group difference in each of the parietal, temporal and prefrontal cortex regions identified above, with the MLD group showing significantly higher NRS values between addition and subtraction problems (all ps < .05; Figure 3I and Table S5).

Nonlinear profile of less differentiated neural representations in children with MLD

Next, we investigated whether any brain regions showed nonlinear profiles of neural representations in children with MLD, compared to TD controls. This analysis allowed us to identify brain areas that showed worse- or better-than-expected profiles in children with MLD. Adding group membership (MLD, TD) as a moderator (Figure 4A), we found a significant interaction between Group and NumOps scores on NRS in the left superior part of the anterior temporal cortex (sATC; Figure 4B). Additionally, the independent whole-brain NRS analysis, which examined the interaction between Group and NumOps on NRS, identified two other brain regions: the left dorsolateral prefrontal cortex (dlPFC) and intraparietal sulcus (IPS) showing a moderation effect of group on the relationship between NumOps scores and NRS values (height threshold p < .005; FDR-corrected for multiple spatial comparisons at p < .01). Specifically, we found that lower NumOps scores were associated with higher NRS values in the MLD group only (ps < 0.05; Figure 4C&D), but no such relationship was found in the TD group. More surprisingly, the relationship between NumOps and NRS was positive in the TD group in left dlPFC (p <.001).

Figure 4. Nonlinear relationship between math ability and Neural Representational Similarity (NRS).

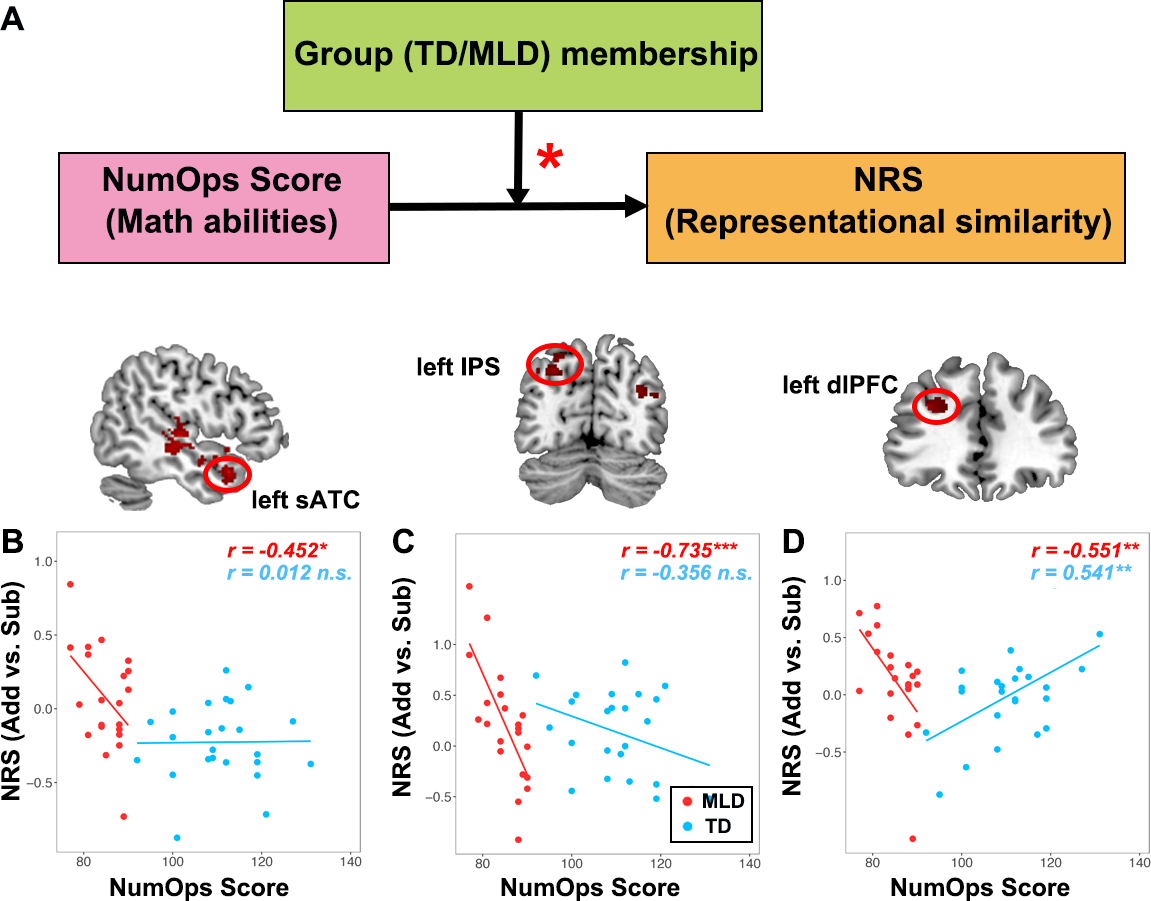
(A) Model to test effect of group membership on the relationship between NumOps and NRS. (B-D) NRS in the superior part of the left anterior temporal cortex (sATC), left intraparietal sulcus (IPS), and left dorsolateral prefrontal cortex (dlPFC) was associated with lower math skills in children with MLD, but not in TD children.

Aberrant multi-region network similarity in children with MLD

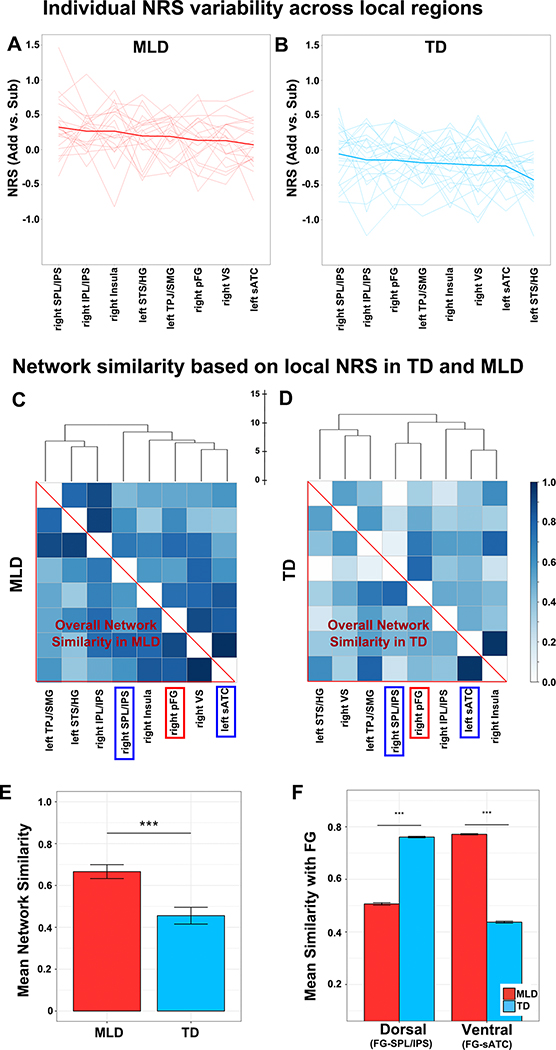
As noted above, we found a significant relationship between math abilities and NRS values in multiple brain regions. We extended this analysis to determine whether aberrant neural representations at the local level are also manifested at the network level. We first noted that when we averaged NRS values across the eight brain regions shown in Figure 3 and tested their association with NumOps, we observed a significant negative relationship: r(43) = −0.82, p < .001. This result is not surprising given the linear relationship between NumOps scores and NRS values found in individual brain regions. The consistent pattern across these brain regions can be seen in Figure 5A&B. Furthermore, we also observed that the multi-region NRS values across individuals seemed to be more similar (or consistent) in the MLD group, i.e., the individual lines showed similar patterns around the group averaged line, compared to the TD group. This observation suggested that NRS across multiple brain regions (i.e., multi-region network similarity) could provide a novel aspect of neural representational similarity at a network level.

Figure 5. Aberrant inter-regional network similarity in children with MLD.

(A, B) Individual and group-averaged NRS across brain regions in children with MLD and TD children. (C, D) Network similarity matrix based on NRS in eight brain areas that showed higher regional NRS in MLD, compared to the TD group. (E) The average Network similarity was higher in MLD compared to TD children; (F) NRS similarity between the fusiform gyrus and intraparietal sulcus (FG-IPS) nodes was lower in children with MLD, compared to TD children. In contrast, NRS similarity between fusiform gyrus and anterior temporal cortex (FG-sATC) nodes was higher in children with MLD, compared to TD children. Error bars and significance were estimated using subsampling and permutation testing.

To further quantify the consistent patterns of NRS across multiple brain regions and its relationship to arithmetic abilities, we examined whether children with MLD showed different patterns of network-level similarity compared to TD controls. To calculate the multi-region network similarity, we first derived a distance matrix between regional NRS values across participants in the MLD and TD groups separately. We then converted the group-specific distance matrices to a similarity measure wherein ‘0’ indexed lowest similarity (i.e., largest distance) and ‘1’ highest similarity (i.e., shortest distance; for more details see Method). We found that children with MLD showed higher multi-region network similarity compared to TD children (Figure 5C&D). Permutation tests with 10,000 subsampling procedures revealed a significant difference in the multi-region network similarity matrix between MLD and TD groups (M_MLD = 0.66, M_TD = 0.43; p < .001; Figure 5E).

Aberrancies in neural representations in the ventral-dorsal pathway in children with MLD

To further investigate the structure of multi-region network similarity, we applied hierarchical clustering to the similarity matrix in the MLD and TD groups, separately. This analysis revealed that the multi-region representations between the posterior fusiform gyrus (pFG) and Superior Parietal Lobule/Intra-Parietal Sulcus (SPL/IPS) were clustered at a higher level of hierarchy in children with MLD compared to TD children. In contrast, multi-region representations between the pFG and the anterior temporal cortex were clustered at a higher level of hierarchy in TD children. Using permutation testing across 10,000 subsamples, we confirmed that neural similarity between pFG and SPL/IPS representations was significantly lower in the MLD group, compared to the TD group, while similarity between the pFG and anterior temporal cortex showed a reverse pattern (p < .001; Figure 5F).

Discussion

We examined whether addition and subtraction, the two foundational numerical operations, are represented differently in children with low math abilities, compared to their TD peers. Both dimensional and categorical approaches revealed less differentiated neural representations in children with low math abilities in multiple neurocognitive systems including the parietal visuo-spatial attention, lateral temporal lobe language-semantic, and prefrontal cognitive control systems. Furthermore, a nonlinear profile characterized by a worse-than-expected profile of deficits in children with MLD was detected in parietal attention and anterior temporal cortex language-semantic systems. Analysis of multi-region network similarity patterns revealed weak communication of neural representations across pathways linking the fusiform gyrus with parietal regions important for manipulation of quantity and numerical problem-solving. Together, these findings point to weak pruning of local and distributed neural circuits in children with poor math abilities, and identify less differentiated neural representations as a potential neurobiological signature of MLD.

Weak behavioral differentiation between numerical operations in children with low mathematical skills

The first aim of our study was to investigate behavioral performance and decision-making associated with problem-solving involving addition and subtraction operations in children with low math abilities. Not surprisingly, children with poor math abilities showed lower efficiency in solving addition and subtraction problems. Critically, children with lower math skills were similarly impaired in problem-solving efficiency of both operations. In contrast, compared to their TD peers who performed better on addition than subtraction problems, children with MLD showed no such distinction. Children with low math abilities showed less differentiated performance on the two numerical operations, suggesting the engagement of similar – and inefficient – computational – strategies for both addition and subtraction operations/problems.

Computational modeling of latent decision-making processes during problem-solving revealed that lower math abilities were related to slower drift rate (v) for both addition and subtraction problems on a continuous scale. At a group level, TD children, compared to children with MLD, showed better differentiation on drift rate (v) between addition and subtraction problems. This suggests that decision-making processes between operations are better differentiated in TD children compared to the MLD group. Our results indicate that lower problem-solving efficiency in children with impaired math abilities may stem from weak evidence-accumulation, partly on account of poor item discrimination, leading to impaired decision-making. In TD children, the rate of evidence accumulation differed significantly between addition and subtraction problems, and therefore, it is reasonable to assume that at this developmental stage, TD children may rely on different strategies, processes, or representations for solving addition and subtraction problems (Barrouillet et al., 2008; Geary et al., 1991; Jordan et al., 2003; Ostad, 1999), and children with MLD did not show such a distinction. Further studies with larger samples and analysis of strategy-use are needed to elaborate on the observed patterns.

Previous research has suggested that children with poor math abilities fail to use retrieval strategies even for simple addition problems, and they adopt suboptimal strategies for both operations (Ostad, 1999). During the early stages of formal math learning, children use a wide range of inefficient strategies, such as finger counting, verbal counting and some forms of decomposition, for solving both operations (Barrouillet et al., 2008; Siegler, 1987; Siegler & Shrager, 1984). With increased practice, operation-specific shifts take place, and by 3rd grade, neurotypical children start applying more efficient retrieval strategies for addition problems while continuing to rely on more laborious mental manipulation strategies for subtraction problems (Barrouillet et al., 2008; Geary et al., 1991; Jordan et al., 2003; Ostad, 1999). Our findings converge on these observations, and suggest that children with low math abilities may rely on similar, indistinct, and suboptimal cognitive processes for solving the two distinct operations.

Neural representations are less distinct in children with low math abilities

The second aim of our study was to determine the neural underpinnings related to weak behavioral differentiation in children with poor math abilities. Specifically, we examined whether children with low math abilities showed weak neural differentiation during problem-solving associated with the two numerical operations. We found that children with low math abilities displayed less distinct neural representations in posterior parietal, prefrontal and lateral temporal cortices including the intraparietal sulcus (IPS), anterior insula, fusiform gyrus, and anterior temporal cortex. Interestingly, no brain region showed lower neural representational similarity, i.e. more differentiated representations, in children with weak math abilities. These results provide novel insights into the neurobiological basis of behavioral learning difficulties in math problem-solving, highlighting a distinctive brain-based feature of impairment in relation to two foundational arithmetical operations, deficits in which are are known to be a defining phenotypic feature of MLD.

It is noteworthy that the format of numerical problems presented to participants was perceptually identical across the two problem types: the two strings of presented problems differ only by a single vertical line ‘+’ vs. ‘−’. Thus, as expected, no individual differences or aberrancies in neural representations were found in primary visual cortex, consistent with the view that the lack of distinct representations arises at the semantic level, rather than at the low-level perceptual processing.

Less differentiated neural representations between addition and subtraction problems associated with lower math skills were observed in the IPS/SPL, a brain region that plays a critical role in quantity judgement and manipulation (Dehaene et al., 2003; Holloway et al., 2013; Schel & Klingberg, 2016). The IPS/SPL is a critical locus of numerical processing deficits in children and adults with MLD (Arsalidou & Taylor, 2011; Ashkenazi et al., 2012; Chang et al., 2016; De Smedt et al., 2011; Houdé et al., 2010; L. Peters & De Smedt, 2018; Rosenberg-Lee et al., 2015). Less differentiated representations associated with lower math skills were also detected in the fusiform gyrus. The fusiform gyrus in the ventral-occipital cortex is involved in high-level visual processing of complex visual objects, including words and numbers (Cantlon et al., 2009; Shum et al., 2013; Vogel et al., 2017). Taken together, this pattern of weak neural differentiation of addition and subtraction problems in the dorsal (IPS/SPL) and ventral visual stream (fusiform gyrus) is consistent with impaired core-systems for representing and manipulating numerical quantity, highlighting a less tuned representation of these problems in terms of their core features of symbols processing and numerosity manipulation.

Weak differentiation was also observed in the anterior temporal cortex, a region crucial for integrating cross-modal semantic information (L. Chen et al., 2017; Lambon Ralph et al., 2016), and for processing abstract concepts (Binney et al., 2016; Hoffman et al., 2015; Rodd et al., 2010; Sabsevitz et al., 2005). Lesions in the anterior temporal cortex are associated with semantic dementia and furthermore specifically with deficits in arithmetic problem-solving (Cappelletti et al., 2012; Julien et al., 2008). These observations point to aberrant representations in brain areas important for processing semantic knowledge in children with MLD.

Children with low math abilities also showed weak differentiation in brain regions involved in phonological processing, including the superior temporal sulcus, superior temporal gyrus, and supramarginal gyrus (De Smedt et al., 2011; Prado et al., 2014). Differential engagement of language-related systems have been reported in relation to distinct arithmetical operations, reflecting task and operation-specific specializations (Archibald et al., 2013; De Smedt et al., 2011; Hecht et al., 2001; L. Peters & De Smedt, 2018; Prado et al., 2014). Critically, verbalization during arithmetic problem solving has been linked to language systems (Zarnhofer et al., 2013). Higher neural representational similarity between addition and subtraction problems within language-processing regions may therefore stem from similar reliance on immature and effortful verbally-mediated strategies for both types of arithmetic problems. We suggest that children with low math abilities may rely on the same language-based strategies to solve both types of problems, consequently resulting in higher neural representational similarity, and lower neural differentiation, across the two operations.

Children with low math abilities also showed higher neural representational similarity in the anterior insular cortex, a region important for cognitive control during cognition in general, and numerical problem-solving in particular (Supekar & Menon, 2012). The strength of causal signals from the anterior insular cortex to parietal and prefrontal regions has been associated with better performance during arithmetic problem-solving (Supekar & Menon, 2012). Meta-analysis of brain imaging studies points to the insula as a region showing a consistent profile of deficits in children with low math abilities (Arsalidou et al., 2018). Compared to addition problems, subtraction problems require more effortful processing, resulting in different levels of cognitive control demands for the two operations (Caviola et al., 2014; Hayashi et al., 2000). Our results indicate, for the first time, that children with low math abilities may not appropriately engage this prefrontal control region for operation-specific numerical problem-solving.

In sum, both dimensional and categorical approaches revealed that neural patterns associated with the two basic operations were less distinct in children with poor math abilities across multiple functional brain systems, further supporting the hypothesis of dysfunctions in multiple functional brain systems in the neurobiological characterization of MLD (Fias et al., 2013; Iuculano, 2016). Notably, our findings suggest that neural dysfunction in MLD arises not just at the level of task-related activation (Iuculano et al., 2015; Rosenberg-Lee et al., 2015), but also at the level of multivariate pattern representations in multiple brain systems (Iuculano, 2016; Iuculano et al., 2015). This pattern of enhanced neural representational similarity is consistent with hyperactive responses observed in children with MLD (Jolles et al., 2016; Rosenberg-Lee et al., 2015), and together points to weak operation-specific tuning of neural circuits as a putative mechanism of poor math abilities in these children. More generally, the distributed nature of the deficits uncovered here provides further support for a multi-componential deficit model of math difficulties, including MLD (Fias et al., 2013; Iuculano, 2016).

Nonlinear, worse-than-expected, profile of weak neural representations in children with MLD

The next aim of our study was to characterize nonlinear profiles of neural representations in children integrating dimensional and categorical approaches. While most brain areas showed a continuous linear profile of neural representational similarity associated with poor math skills, the left anterior temporal cortex and left IPS showed a nonlinear profile characterized by a significant negative relation in the MLD group and no variation in the TD group (Figure 4). These results suggest that children with MLD show a unique neural profile, characterized by weaker than expected differentiation of problem representations in two left hemisphere regions important for semantic knowledge of numerical operations (Julien et al., 2008) and their manipulation (Cappelletti et al., 2012). Our findings identify a novel locus of impairments in children with MLD and are noteworthy because they converge on studies of patients with semantic dementia (Julien et al., 2008) which have suggested that aberrancies in the anterior temporal cortex result in difficulty with identifying arithmetic signs as well as conceptual understanding of quantity.

Our analysis also revealed a worse than expected profile in the dorsolateral prefrontal cortex. However, in this case, while the MLD group showed a negative relationship between neural representational similarity and math abilities, as seen in the parietal-temporal-prefrontal areas consistently identified above, this relationship was instead positive in the TD group. This result suggests that children with MLD engage the dorsolateral prefrontal cortex differently from TD children, and further highlights a dissociation in representations encoded by this brain region. Notably, children at the lowest and highest end on the ability scale show similar overlap in representations, but for entirely different reasons. The dorsolateral prefrontal cortex plays a key role in selective manipulation of information in working memory (Barbey et al., 2013; Curtis & D’Esposito, 2003). One interpretation of our findings is that children with high math abilities engage the dorsolateral prefrontal cortex with similar efficiency for both operations, whereas children with MLD at the lowest end of the abilities (Figure 4C) engage this region with a similar level of inefficiency for both operations. This interpretation is also consistent with previous findings showing that adults with better arithmetic skills display higher neural representational similarity between addition and subtraction operations in the dorsolateral prefrontal cortex compared to typically-developing children (Chang et al., 2015).

Together, these results identify brain areas with a nonlinear profile, characterized by worse-than-expected aberrations in neural representations, and thus, areas of particular vulnerability in the most severe cases of children with poor math skills.

Less differentiated neural representations at the network level in children with MLD

The final goal of our study was to characterize network similarity across brain regions (Anzellotti & Coutanche, 2018; Pillet et al., 2020) showing lower differentiation in neural representational similarity values as a function of math abilities. We used a novel computational approach to determine multi-region representational similarity patterns, and assessed whether these patterns could differentiate children with MLD from their TD peers. Analysis of network similarity revealed that children with MLD showed higher multi-region representational similarity compared to their TD peers, suggesting that less differentiated neural representations are manifested not only at the regional level (Figure 3I) but also at the network level (Figure 5E). Notably, this analysis also highlights weaker integration of representations between the fusiform gyrus and intraparietal sulcus in children with MLD. These brain regions are crucial for representing and manipulating numerical quantity (Ansari, 2008; Cantlon et al., 2009), and the functional connectivity between these two regions has been shown to be associated with the successful acquisition of numerical abilities (Battista et al., 2018; Evans et al., 2015). In contrast, children with MLD showed higher integration of neural representations between the right fusiform and the left anterior temporal cortex, likely reflecting the greater need to access semantic representations for solving both problem types. More generally, these results highlight impairments in co-occurring patterns of deficits across multiple brain regions in children with MLD (Fias et al., 2013).

A developmental model of operation-specific changes in neural representation with age and math skills

Our findings inform putative developmental models of how distinct neural representations may develop across ages and different levels of math abilities (Figure 6). Behavioral studies have characterized distinctive strategies used to solve addition and subtraction operations at different developmental stages. School-age children apply efficient retrieval strategies to solve addition problems 65% of the time – with lower rates in children with poor math abilities – while only 19% of subtraction problems are solved using this strategy by the 3^rd grade (Barrouillet et al., 2008). Consistent with these behavioral results we found less distinct neural representations between addition and subtraction problems children with high math abilities. In contrast, adults solve 76% of addition problems by retrieval and use this strategy during subtraction 58% of the time (Campbell & Xue, 2001). These differences in retrieval-rates suggest that with development, there is a shift from effortful counting to efficient fact retrieval, leading to a convergence of problem-solving strategies across the two operations. In this case, we would predict increased overlap in neural representations between the two operations in adults. Thus, we predict that, paradoxically, children with poor math abilities and adults would show similar levels of neural representational similarity across distributed frontal, parietal, and temporal regions, but for different reasons (Figure 6). Specifically, in children with poor math abilities, similar NRS patterns reflect the use of inefficient strategies for both operations, while in proficient adults, similar NRS patterns reflect the use of efficient strategies for both operations (Chang et al., 2015). Furthermore, our data also hints at the possibility that linear versus non-linear patterns of neural representational similarity may reflect different sub-types of math difficulties, such that children following a linear trajectory may be classified as having a developmental delay, while non-linear profiles may reflect more severe forms of math difficulties, including children commonly classified as having severe forms of learning disabilities. Future studies using longitudinal designs are needed to assess how neural representations change over time heterogeneous groups of children with MLD.

Figure 6.

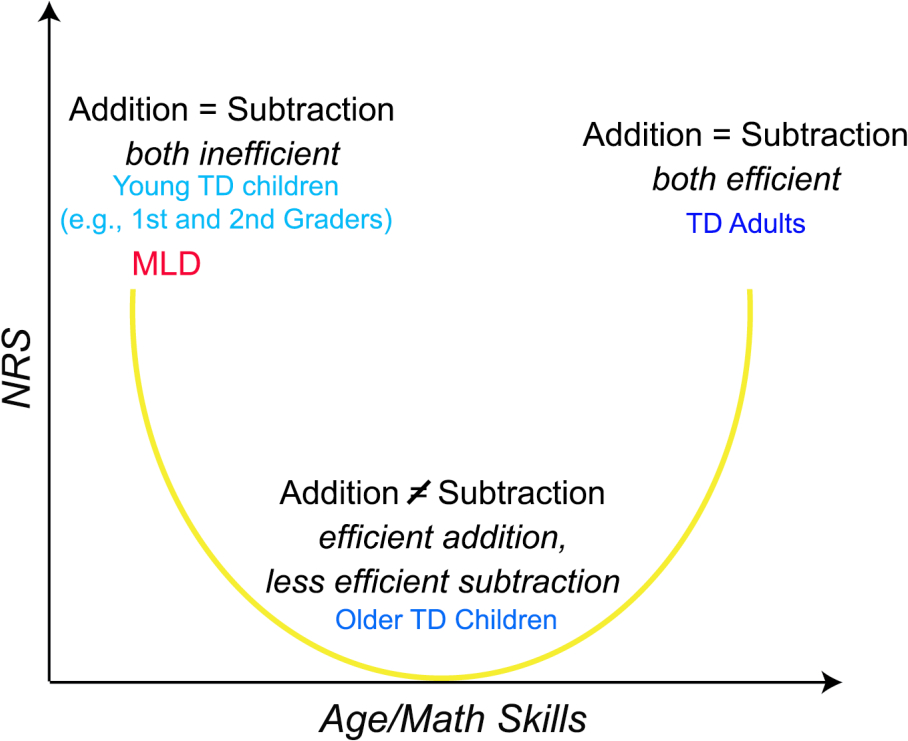
Proposed developmental model of operation-specific shifts in neural representations with age and math skills. This model predicts that there is a shift from effortful counting to efficient fact retrieval, leading to a convergence of problem-solving strategies across the two operations. Therefore, we would predict increased overlap in neural representations between the two operations in adults. Paradoxically, children with poor math abilities would also show high levels of neural representational similarity across distributed frontal, parietal, and temporal regions as in adults, because they tend to use inefficient strategies for both operations.

Conclusions

The present study identifies distinct neural representations as a novel neurobiological feature for individual differences in math abilities, and a potential neurobiological marker of poor math skills in an inability to form distinct neural representations for different numerical operations. Less differentiated neural representations for addition and subtraction problems associated with poor arithmetic abilities were evident in widely-distributed cortical regions related to quantity representations and their manipulation, as well as in prefrontal regions involved in cognitive control, and those engaged in the semantic and phonological aspects of language processing. Our findings identify a novel distributed locus of information processing and representational deficits in children at the lower end of the distribution of math abilities. Moreover, network-level analysis revealed that poor mathematical skills were associated with not only less differentiated representations at the regional level but also with manifested overlapping representations at the network level. Critically, the present study is the first to show that failure to properly differentiate between arithmetical problem-types may be a hallmark of math difficulties. Notably, lack of representational differentiation was not evident in perceptual, but rather in cognitive-semantic processing brain systems. The approach and methods developed here may be useful for future studies of neural representational features in other learning disabilities, such as developmental dyslexia. Finally, our approach provides a template for probing typical and atypical developmental changes associated with cognitive problem-solving and skill acquisition, overcoming pitfalls associated with use of arbitrary cutoffs for probing neurobehavioral profiles of heterogeneity in learning disabilities.

Research highlights.

• Children with low math abilities showed less differentiated performance on addition and subtraction operations and their low efficiency stemmed from weak evidence-accumulation during problem solving.

• Children with low math abilities showed less differentiated neural representations between the two operations in cortical areas important for quantity judgement, cognitive control, attentional processing, semantic, and phonological processing.

• Less differentiated neural representations between two operations were specific to children with math learning difficulties.

• Children with math learning difficulties also showed less differentiated neural network-level representations.

Data availability statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.