Ymir: A 3D structural affinity model for multi-epitope vaccine simulations

Summary

Vaccine development is challenged by the hierarchy of immunodominance between target antigen epitopes and the emergence of antigenic variants by pathogen mutation. The strength and breadth of antibody responses relies on selection and mutation in the germinal center and on the structural similarity between antigens. Computational methods for assessing the breadth of germinal center responses to multivalent antigens are critical to speed up vaccine development. Yet, such methods have poorly reflected the 3D antigen structure and antibody breadth. Here, we present Ymir, a new 3D-lattice-based framework that calculates in silico antibody-antigen affinities. Key physiological properties naturally emerge from Ymir such as affinity jumps, cross-reactivity, and differential epitope accessibility. We validated Ymir by replicating known features of germinal center dynamics. We show that combining antigens with mutated but structurally related epitopes enhances vaccine breadth. Ymir opens a new avenue for understanding vaccine potency based on the structural relationship between vaccine antigens.

Graphical abstract

Highlights

• •Fast in silico antibody-antigen affinities to simulate multivalent vaccine response
• •Ymir recapitulates affinity jumps, cross-reactivity, and epitope accessibility
• •Possibility to simulate multivalent vaccine response using antigen PDB structure
• •Combining antigens with structurally related epitopes enhances vaccine breadth

Molecular Structure; Immunology; Biocomputational method; Computer simulation

Introduction

Vaccines poorly target highly mutating pathogens like human immunodeficiency virus (HIV), hepatitis C virus, or influenza, and elicited antibodies do not necessarily protect against the next mutated strain. Strikingly, a few individuals naturally develop broadly neutralizing antibodies (bnAbs) against a large range of strains, and injecting these bnAbs is protective against future infections in certain contexts (Shingai et al., 2014), demonstrating their therapeutic potential.

Meeting the requirements for the induction of bnAbs in vivo, especially in humans or primates, would support better vaccine design and the development of new bnAbs that are functional but not self-reactive. Antibody responses and ultimately the generation of bnAbs happen in anatomical structures called germinal centers (GCs), where B cells selectively mutate their B-cell receptors (BCRs) through somatic hypermutation (SHM), which are later secreted as antibodies. High-affinity B cells are selected for survival and proliferation at the expense of low-affinity B cells. Consequently, the affinity of the antibodies increases over time, a process called affinity maturation (AM).

The GC’s response to single well-defined antigens has been studied in vivo. Many single-antigen predictive mathematical models have been developed on abstract antigen-antibody affinities in a probabilistic manner: a mutation is an improvement or decrease in affinity to the single target antigen (Keşmir and De Boer, 2003; Meyer-Hermann et al., 2012; Perelson and Oster, 1979; Wang et al., 2016; Zhang and Shakhnovich, 2010). However, at the scale of multiple or complex antigens, new layers of complexity are not covered by these models. Firstly, mutating pathogens evolve multiple antigenic variants that differ in their accessible epitopes, their frequency, and the amino acid (AA) sequences of their accessible sites. Secondly, during a chronic HIV infection, the epitopes recognized inside the GCs evolve over time and different B-cell clones expand successively toward different epitopes (Gao et al., 2014). Thirdly, it has been reported that antibodies produced by GC-derived plasma cells can diffuse back to the GCs themselves and compete for epitope binding of GC B cells (Zhang et al., 2013), potentially changing the immunodominance landscape of the response (Meyer-Hermann, 2019).

A major question in the vaccine field is to understand how B cells carrying BCRs cross-reactive to multiple strains are expanded or not in the GC. For instance, germline BCRs for the broadly neutralizing antibody VRC01 show a very low frequency among naive B cells (Abbott et al., 2017). GCs are permissive to low affinity B cells (Kuraoka et al., 2016) depending on their frequency (Abbott et al., 2017), and the VRC01 germline has been shown to participate in GC reactions (Huang et al., 2020). It then remains unclear why the large majority of HIV-infected patients fail to mount broadly neutralizing antibodies and how to modulate the GC reaction to specifically expand them. Targeted amplification of cross-reactive BCR sequences is a fundamental question that can be mathematically explored provided a physiological expression of mutation-induced affinity jumps toward multiple antigens.

Recent mathematical models have accounted for the quantitative properties of AM toward multiple antigens and compared different vaccine strategies such as simultaneous cocktail immunizations or sequential vaccinations (Robert et al., 2018). Such models require taking assumptions on how mutations are linked with a change in affinity toward the antigens, based on their own abstract model of binding affinities. These representations include the abstract N-dimensional shape-space model (Perelson and Oster, 1979); the size of longest substrings between proteins taken from a finite alphabet (Luo and Perelson, 2015); binary proteins with a clone-specific accessibility profile (Nourmohammad et al., 2016); binary proteins with position-dependent residue strength sampled from predefined affinity distributions (Wang et al., 2015); abstract matching between epitopes and binary receptors using the NK model (Kauffman and Weinberger, 1989); AA interaction potential of facing residues (Murugan et al., 2018); and a structural representation of cubic-folded lattice proteins carrying AAs (Raoof et al., 2013; Shakhnovich and Gutin, 1990). We have previously reported (Robert et al., 2018) that these representations carry different levels of cross-reactivity. Only some can incorporate differential epitope accessibility, key mutations, or shielding, and it is not easy to translate a real antigen or structure into any of them. A recent study (Amitai et al., 2020) generated antibody affinities by sampling binding off-rates from a predefined distribution, while pre-calculating on-rates as a coefficient per epitope using coarse-grained molecular dynamics to model differential accessibility between epitopes. This approach is suitable for unrelated epitopes with independent effects of antibody mutation but does not incorporate changes in cross-reactivity following mutation, especially to mutated epitope variants. A physically grounded, structural encoding of antibody-antigen affinity would overcome these limitations, and the physiological properties would naturally emerge without the necessity to add them manually.

Several prediction tools can simulate protein folding thermodynamics for new antibody sequences, typically with prior knowledge of the few known antibody-antigen structures. Full prediction tools like Rosetta have reached powerful binding accuracy at the expense of few hundreds of computational hours for a single calculation (Brown et al., 2019). One GC typically contains 10,000 cells at its peak. Through mutations and high turnover between proliferation and death, a GC will typically explore 10⁵ to 10⁶ mutations during a single reaction (Meyer-Hermann, 2014). Therefore, the current available prediction techniques for structural antigen-antibody binding are unable to achieve a single GC simulation in feasible time.

Since the outcome of the GC reaction is determined by the relative affinity of the competing BCRs to the antigens, any model predicting physiological affinity changes upon mutation and preserving global properties of cross-reactivity and structural relationship between antigens would be sufficient to capture the main forces behind the emergence of cross-reactivity in GCs.

Here, acknowledging that accurate antibody-antigen binding calculations are not feasible at the precision of the above mentioned atom-scale methods for GC simulations, we decided to use a simplified coarse-grained model of protein binding that can represent general structural features of protein antigens, including their AA composition. To this end, we develop a new hybrid model of antigen-antibody binding that simulates the best folding of the complementarity determining region (CDR) 3 of the antibody heavy chain (CDRH3) around a predefined antigen structure on a 3D lattice. Real AA sequences are used, up to 12 AAs for the CDR loop, and with complex antigen structures up to 1000 AAs for the antigen. The interaction between neighboring AAs is based on experimentally measured potentials (Miyazawa and Jernigan, 1996). The hybrid model can derive binding energies in computational times suitable for GC simulations (a few minutes for 1000 affinity calculations). Key properties naturally arise from this representation: polyreactivity, cross-reactivity, accessibility and shielding effects, and mutations inducing affinity jumps.

As a proof of concept, we show that multivalent affinity maturation can successfully be studied using Ymir with synthetic toy antigens with desired structural features. We adapted and ran GC simulations from an in silico model (Meyer-Hermann et al., 2012) with this structural antigen representation. The model showed physiological GC dynamics and proper AM and allows using lattice representation of protein data bank (PDB) antigen structures. We show that the use of cocktails of similar antigens generated favorable conditions for cross-reactivity. Sequential immunizations also raised higher cross-reactivity using cocktails of antigens. GC simulations combined with the 3D affinity model presented here are suitable for testing vaccine strategies and predicting therapeutic methods to modulate immunodominance in realistic computational time. We freely provide the C++ implementation, “Ymir”, of the presented structural model. Further, we validated the presented model on the physiological relevance of somatic hypermutation in GCs, showing it is suited for the physiological scale than more general receptor-ligand interactions.

Results

A fast computational model for lattice-based antigen-antibody binding

Calculations of antibody-antigen binding energy were so far either simplified to an unphysiological degree or so expensive in computational time that they could not be used in real-world problems involving many interactions. Here, we describe a fast algorithm that still captures important physiological properties.

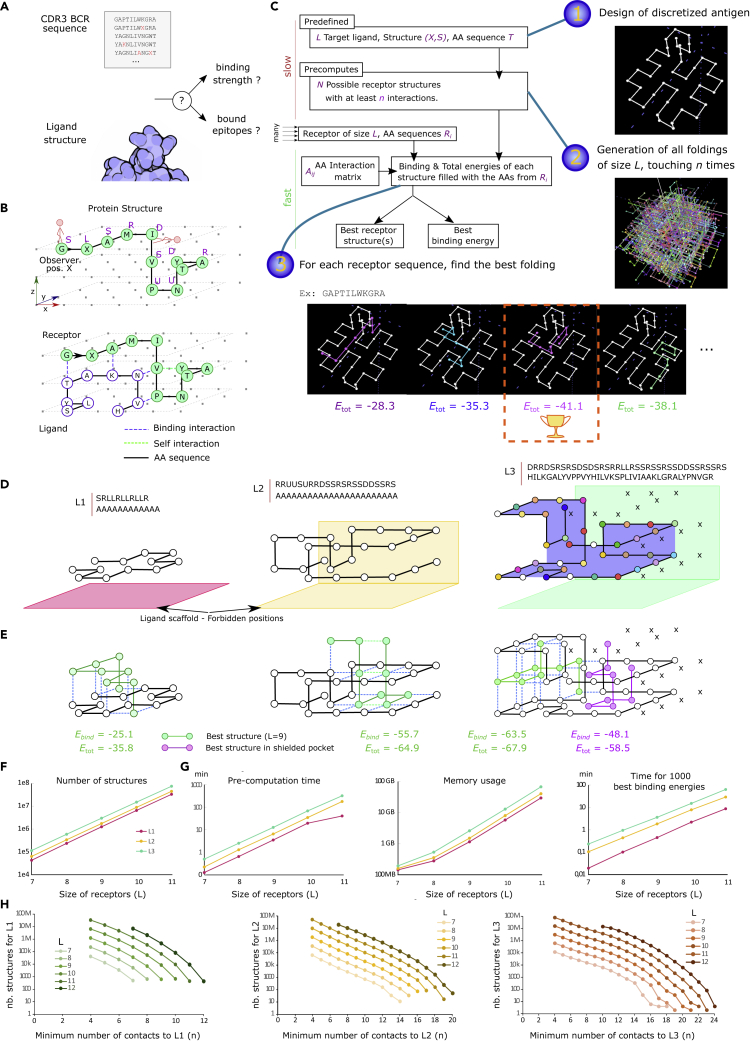
GC simulations need access to affinity changes by somatic hypermutations. Given a predefined antigen structure (the “ligand”), binding energy and affinity have to be computed for a large number of mutated binding regions of the antibody (the “receptor”) (Figure 1A).

Figure 1.

Fast computation of antibody-antigen structural binding on a 3D lattice

(A) Aim: given an antigen, generate a binding landscape of thousands of mutated antibody binding regions.

(B) Proteins are a path in a 3D lattice (black line). Interactions happen between non-covalent neighboring AAs. The receptor binding energy E_bind sums interacting bonds (blue), and the total energy E_tot additionally includes intrinsic bonds (green).

(C) Workflow for the computation of binding energies. (1) A ligand structure is predefined. (2) Possible receptor folding structures are stored. (3) For a receptor sequence, E_bind and E_tot are derived from each structure, and the “best binding energy” E_best is returned (see STAR Methods).

(D) Toy model ligands: a simple one with alanines only (L1), one with tail and pocket (L2), and a third one with diverse AAs, a hook, and a pocket covered by shielded residues ‘X’ (L3). Alanine in white; other residues are colored.

(E) Best folding structures (green); and reaching the pocket of L3 (purple) of a random receptor of size 9.

(F) The number of precomputed structures depending on receptor length L, when at least n= 4 contacts are required.

(G) Time and memory requirements for pre-computation and best energy of 1000 receptor sequences.

(H) The number of structures as a function of n.

We defined a regular lattice, on which residues can occupy predefined positions on a grid (Figure 1B). Real AA sequences are used, consecutive AAs are on neighboring points, and only one AA is allowed on each grid point. A protein structure is represented as a list of relative moves, namely Straight, Up, Down, Left, and Right (Figure 1B; STAR Methods). All covalent bonds are equal and are neglected. Neighboring but non-covalently linked AAs are assumed to contribute to the binding strength. Their binding energy has been previously estimated from structural databases for each pair of AAs (Miyazawa and Jernigan, 1996). For two interacting proteins, the binding energy E_bind is estimated as the energetic sum of individual bonds between the two proteins. The total energy E_tot of one protein is the energetic sum of inter-molecular interactions (interacting bonds) and intra-molecular interactions (intrinsic bonds), thus including intrinsic bonds as a stabilization factor of the protein structure (see STAR Methods). We assume that the antigen has a stable conformation, which is not impacted by the bound antibody, and the intra-molecular interactions of the antigen are therefore neglected because they are constant. Instead, the CDRH3 loop of the antibody folds onto it. For each CDRH3 sequence, a folding has to be generated and the folding structure around the antigen with lowest total energy has to be found (Figure 1C).

Because of the exponentially high number of possible foldings, it is unrealistic to compute all foldings for each CDRH3 sequence at every time step in a dynamic computer simulation of GCs. We developed an optimized algorithm that pre-computes only the “interesting” possible foldings of CDRH3 loops of realistic length L between 7 and 14 AAs. Starting from a predefined antigen structure, a recursive algorithm enumerates all possible foldings of the not yet specified CDRH3 sequence, with the constraint of touching the antigen at least n times (Figures 1C, 6D, and 6E; STAR Methods). This considerably reduces the amount of structures to be enumerated and stored in the memory. For each CDRH3 sequence to be evaluated, all the previously enumerated foldings are taken one by one and filled with the AA sequence of the CDRH3. The binding and total energies are calculated. As a result, the “best binding energy” is the binding energy of the most stable structure, i.e., the structure with optimal total energy. We confirmed in Figure S1 that the ensemble of structures with low energy according to the Boltzmann weight is well represented by the best structure, and we further only use the best binding energy. Of note, the enumeration of folding, calculation of energies, and identification of best binding structure are completely deterministic.

Figure 6.

Representation of proteins and enumeration of receptor foldings

(A) A protein structure is described as a list of “moves” (see Figure 1B) that are relative to the observer coordinates $\left(\overrightarrow{Ox},\overrightarrow{Oy},\overrightarrow{Oz}\right)$. For each move, the new coordinates are given $\left(\overrightarrow{O{x}^{\prime }},\overrightarrow{O{y}^{\prime }},\overrightarrow{O{z}^{\prime }}\right)$ and $\overrightarrow{O{z}^{\prime }}=\overrightarrow{O{x}^{\prime }}ˆ\overrightarrow{O{y}^{\prime }}$.

(B and C) (B) Example of the structure “SURLDUULURS” (C) “Absolute”, with a starting position in space, or “Relative” after translation and rotation representation of structures.

(D) We define a “first position of contact” for a receptor-ligand interaction. One of the two receptor tails does not interact with the ligand.

(E) Recursive rules for enumerating all possible receptors from a “first contact position”. All possible structures for the two tails are enumerated separately. Each combination of structures from both tails is tested as a fusion to get a full, non-self-colliding receptor. The recursive function generate tail (GT) of length l from a position P without contacts (red ‘x’) calls itself from the neighboring positions with length l– 1. Similarly, the function GT of length L − l with at least k contacts calls itself from neighboring positions with length L-l-1 and k or fewer minimum contacts, depending on the number of contacts gained.

(F) Graphical illustration of (E).

As an example, we show three typical antigen structures (Figure 1D): one simple accessible and flat antigen (L1), one antigen with an accessible tail and a hidden pocket (L2), and an antigen with both an accessible hook and a pocket and additional inaccessible shielded positions, marked X (L3). We assume that positions below the antigens (and on the side of L2 and L3) are inaccessible to receptors to reflect the antigen scaffold (shown as filled planes). For a randomly chosen CDRH3, the best binding structures are shown in Figure 1E, together with the binding energy E_bind and the total energy E_tot. As expected, the best receptor structure around L2 is located in the accessible pocket. Similarly, the best receptor structure around L3 binds the accessible hook. For comparison, the best structure that would bind the shielded pocket of L3 is shown in purple (Figure 1E) and has much worse binding energy.

For larger CDRH3 sequences, up to 75 million folding structures exist (Figure 1F). The pre-computation time still did not exceed a few hours (Figure 1G) and has to be performed and saved only once. Thousands of CDRH3 can be evaluated for best binding energy to these antigens in less than one hour on a single central processing unit (CPU) (Figure 1G), implying that it becomes possible to simulate a full GC within a few hours. By increasing n, the required minimum number contacts to the antigen, calculations are further speeded up (Figure 1H). For instance, for ligand L3, receptors of length 11 lead to 75 million structures with four contacts, which can be brought down to only 5.6 million by requiring nine contacts. Thus, the structural model for antibody-antigen binding has the capacity to model complex antigens with an efficiency suitable for GC simulations.

The model reflects physiological structural properties

The model reflects antibody specificity

Thousands of random receptor sequences of length 7 to 11 AAs were sampled. The best binding energy of the receptors varied according to a broad Gaussian distribution with average in the range of 20, 40, and 50 kT for L1, L2, and L3, respectively (Figure 2A), thus generating different binding landscapes for each sequence. Despite millions of possible folding patterns, some receptors did bind this antigen with low affinity in comparison to others. Thus, the calculated best binding energy contains structural information about the receptor sequences. The best binding energy of receptors increased linearly with their length (Figure 2A) because they have more options for binding and a bigger folding ensemble. Therefore, we do not recommend comparing energies between receptors of different lengths, unless a correction coefficient is added.

Figure 2.

Distributions of receptor binding energies

(A–C) The best binding energy of 2500 randomly sampled receptors (A) of length 7 to 11 to ligands L1, L2, and L3; (B) of length 9 to ligands L1, L4, and L5; and (C) to L6 and L7. Dashed box: length used for future simulations. The structures of the ligands L2 and L3 are as depicted in Figure 1D.

(D) Histogram of best binding energies induced by all possible single point mutations for eight selected receptor sequences with different best binding energies for L6.

Steric hindrance of epitope access

The impact of the antigen structure onto the binding energies was investigated on a bigger version of ligand L1 with a similar flat shape. It induced a global increase in binding (Figure 2B), due to more available positions, especially corners where three AAs are accessible from the same point. In the case of L3, we first created a more physiological variant L6 where the hole in the pocket was filled (green arrow) to avoid receptors going through it. We then monitored the contribution of the shielded pocket by removing it in ligand L7 (Figure 2C). The distribution of best binding energies remained similar because the receptor structures accessing the pocket were not favored. This shows that the model is a suitable tool for studying the effect of steric hindrance of epitopes such as HIV GP120 protein.

Antigen AA complexity

Changing the AA composition of L1 from alanine only to diverse AAs (L5) induced a strong improvement of the best binding energy (Figure 2B). Indeed, if an antigen contains only one type of AAs, receptors do not benefit from different folding structures. Therefore, surface AA composition impacts on the simulated binding energies.

Point mutations

In the GC, somatic hypermutation generates point mutations that lead to increased or decreased best binding energies. All receptor sequences for L6 displayed best binding energies between −90 and −45 kT (Figure 2C). We tested all possible point mutations for eight sequences of length 9 with different best binding energies to L6 (Figure 2D). Mutations could always do both, increase or decrease the best binding energy, even when starting from sequences with very high (green) or very low (purple) energy. Large energetic shifts of ± 15 kT were possible by single mutations.

GC simulations show affinity jumps and clonal bursts

In order to predict AM and ultimately the efficiency of multivalent vaccines from the structural properties of the antigens, the next step was to simulate full-scale GC reactions. We incorporated the structural binding model into an agent-based model for GC dynamics, where B cells and T cells are explicitly modeled to move, interact, be selected, proliferate, die, or exit in 3D space (Meyer-Hermann et al., 2012; Robert et al., 2017) (see STAR Methods). The best binding energies derived from the structural binding model were mapped to an affinity [see STAR Methods, Equation (6)]. In the simulation, the affinity between the BCR and the antigen is identical to the probability of capturing the antigen, which is needed later to survive T-cell selection. Although the calculation of affinities using Ymir is deterministic, the agent-based model for GC dynamics captures the stochastic nature of antibody responses due to the random selection of founder cell sequences within a predefined affinity range, the persistent random walk of cells, and probability-based cellular decisions (Meyer-Hermann et al., 2012; Robert et al., 2017).

With suitable values for the two parameters linking binding energy to affinity (see STAR Methods), realistic GC dynamics and AM for a single complex target antigen L6 were found (Figure 3A). The number of B cells over time in single GCs expands first and reaches a maximum at day 8, followed by slow decay. Starting randomly from cells with at least 0.0001 affinity, the average affinity of B cells reached 0.3 to 1 after 21 days. The average number of mutations of cells leaving GCs was around six mutations at day 21. As a comparison, single-cell sequencing of GC B cells from single GCs has found cells to be typically mutated 4 to 7 times at day 15 after immunization (Tas et al., 2016), which translates to day 12 after GC. We observed an average of 4.4–6.8 mutations in GC B cells at this time point, depending on the antigen. The high affinity receptor sequences from five GCs were different (Figure 3B), in contrast to most abstract affinity models for which the high affinity sequence is unique (Robert et al., 2018).

Figure 3.

Full-scale in silico GC simulations and mutation histories of high-affinity cells

(A) Dynamics of 25 GC simulations against antigen L6 without shielding residues. The number of GC B cells (left), the mean affinity of GC B cells (middle), and the distribution of mutations per GC output cell (right).

(B) The best and consensus BCR sequences emerging from 5 GCs with very high affinity (> 0.75).

(C) Network (forest) of BCR sequences representing the mutation histories of the cells (alive or dead) that existed during a single GC simulation. Edges connect mother and daughter sequences by mutation. Each panel shows the progeny sequences of one founder sequence (one clone), starting from the biggest progeny. High-affinity cells (> 0.5, dark red) and total number of cells are quantified beneath each founder dynasty.

(D) A founder progeny showing a burst and 3 futile founder progenies staying at low affinity.

(E) Lineage history of high-affinity sequences (> 0.5) from (D), annotated with affinity increases from the founder sequence to the burst.

(F) Same as (E), after merging identical sequences, indicating their first time of appearance.

(G) Progeny of high-affinity cells back to the founder cell for different GC clones. (C–G) Node size and gradual colors represent affinity: < 0.3 (light blue), 0.6 (red), 0.9 (purple), and ≥ 1.0 (black).

Next, we analyzed all receptor sequences generated by mutations during 21 days of a GC reaction. We retrieved all (around 70,000) mutations that occurred in selected or dead cells and found that more than one GC founder cell achieved high affinity (Figure 3C), thus pointing to parallel AM of multiple founder cells in silico. This is in accordance with the observation that some GCs are dominated by single clones while others display coexistence of multiple founder clones with high affinity (Tas et al., 2016).

To characterize the mutation history of high-affinity cells back to the founder cell, we selected the mutation cluster of a winning or losing founder cell in Figure 3D. The former showed an explosive expansion of a sequence into many mutated daughter sequences with high affinity. More bursts (hubs in the trees) happened within both the winning and losing clones (Figure 3C). The history of affinity changes during AM leading to high-affinity sequences revealed that increases and decreases of affinity happened, typically by 2- to 10-fold, before expansion of the high affinity sequence (see founder with affinity 0.009 in Figure 3E). In the simulations, not exclusively advantageous sequences are selected, which well reflects the stochastic nature of selection observed in Kuraoka et al. (2016) and Tas et al. (2016).

In the tree representation, the same sequence can occur in different nodes with a different order of mutations. We simplified the graph by merging identical sequences around the bursting cell (Figure 3F). Strikingly, single point mutations inducing a 74-fold increase in affinity were observed, similar to key mutations like the acquisition of L33 in antibodies against ovalbumin. Thus, our model captures key mutations.

The comparison of the history of winning founder cells from different GC simulations (Figure 3G) illustrates how different mutation patterns can be. All of them show clonal bursts to rather different degrees. Few reports have studied single-cell sequences inside a single GC. Interestingly, these bursts have been observed experimentally in a subset of GCs (Tas et al., 2016) in response to protein antigens. This indicates that our structural model reflects several non-trivial physiological properties of GCs.

Using a discretization pipeline that we developed in Robert et al. (2021), we converted a PDB structure into a lattice antigen preserving its topology and AA composition in the lattice world (see STAR Methods) and simulated the GC dynamics to this lattice antigen (Figure S3), showing that Ymir can be used on antigens with complex topologies reminiscent of real antigens of interest. Using 159 different discretized antigens, we have shown in Robert et al. (2021) that Ymir reproduces well immunogenic regions of antigens, compared with experimental binding structures.

Antigen cocktails with high similarity promote cross-reactivity

Next, we simulated GCs with two antigenic variants with same structure (L6) but a modified epitope with different number of point mutations (Figure 4A). We refer to them as different “epitope” variants from the same antigen. Interestingly, the GC dynamics and AM were not impacted by the addition of the second epitope variant. GC with two epitopes distant of Hamming distance (HD) = 4 showed increased antibody sequence diversity and slightly increased amount of produced output cells without increase in affinity compared to the other epitopes (see Figures 5C and S2 for statistics, by comparing conditions “A” and “AB”). For two similar epitopes, the simulated GCs could be classified in four groups according to cell affinity to both epitopes at day 11 (Figure 4B). In some GCs, highly cross-reactive cells emerged (GC2), and in others, the GCs matured to one epitope only (GC1). In most cases, cross-reactive cells were enriched compared with the cells recognizing only one epitope (GC3, 4). Therefore, high variability could be observed between GCs, and the overall affinity to the best epitope did not reflect the success to generate high cross-reactivity.

Figure 4.

Dynamics and cross-reactivity of GCs with two or four epitopes

(A) Dynamics of GC and affinity maturation for two epitopes variants of the antigen structure L6 that differ by one or two point mutations.

(B) Affinity of single cells in four different GC simulations to two similar epitopes, which differ by two mutations, at day 11.

(C) GC dynamics with two or four similar epitopes (differing by two mutations).

(D) Affinity of single cells in a single GC to pairs of epitopes at day 11.

(E) Average affinity to each epitope of single GCs with two or four similar epitopes. The epitopes are sorted from the highest (Epi1) to lowest (Epi2 or 4) average affinity in each GC.

(F) Average cross-reactivity of single GCs raised with two or four similar epitopes, defined as the minimum affinity to the two best-recognized epitopes, for each cell (among the two or four epitopes present in the GC). As a comparison, the cross-reactivity between the same two or four epitopes is shown when only one epitope was present in the GC (red), and the average cross-reactivity between any pair of GC epitopes is shown (right).

(G) Affinity of GC B cells or output cells to a similar epitope that was not present in the GC (external epitope) but similar (HD = 2) to one of the GC epitopes (see Table S1 for the combinations of two or four GC epitopes with the external epitope). (A) and (C) show 10 replicates per curve. For (E) to (G), distributions were non-normal and compared using Wilcoxon tests (40 replicates for 4 epitopes and 38 replicates for 2 epitopes, as listed in Table S1).

Figure 5.

Affinity maturation of antibodies in sequential versus single immunization schemes

(A) Immunization schemes: for two epitope variants A and B of the same antigen, single GCs with A, B or A and B are compared with secondary GCs for which 5% of the founder cells are randomly taken from the output of a primary GC, provided their affinity to one of the GC epitopes is above the threshold to enter a GC. Five cases are considered with two (related) epitopes that differ by four point mutations (see Table S1 for their AA sequence).

(B–F) Dynamics of the secondary GC (or single GC) on the example of case 3 (A = F2, B = F3). Each row compares conditions with the same epitope in the secondary GC. Each condition was simulated 10 times with new sampled 5% injected founder cells each time; the shaded area represents the standard deviation between the 10 simulations. (B) Affinity of GC B cells to the epitope present in the GC. (C) GC volume: the number of B-cells in the GC. (D) The number of (accumulated) produced output cells from the GC. (E) The number of different antibody sequences in one GC. (F) Distribution of mutations in output cells at day 21.

(G and H) Statistical analysis of affinity and cross-reactivity of GC B cells and output cells at day 13, after pooling the 10 replicates of each case (50 simulations per condition in total). Significance is shown based on the Wilcoxon test. (G) Affinities have been normalized for each case separately, relative to the average affinity to epitope A in the single GC with epitope A only (condition A). (H) Conditions that were symmetrical in view of the cross-reactivity were pooled according to their generic name to have more points per condition.

Increasing the number of similar epitopes to four did not induce major changes in the GC characteristics (Figure 4C) except a higher affinity to the best recognized epitope. B cells developed high reactivity to typically two but not all epitopes (Figure 4D). In order to quantify this effect, we calculated the average B-cell affinity to each epitope for individual GCs with two or four similar epitopes, starting from the best recognized epitope in each GC (Figure 4E). The concomitant use of four similar epitopes induced a slightly higher affinity to the two best recognized epitopes as compared to GCs with only two similar epitopes. Further, we assessed the average cross-reactivity of each cell for each GC, measured as the minimum affinity to the two best recognized epitopes (Figure 4F). The average cross-reactivity was slightly increased by the combination of four similar epitopes instead of two, but these two measures of cross-reactivity are not directly comparable when taking the two best recognized epitopes among two or four epitopes, respectively. By adding a control where only one epitope was present in the GCs, the best cross-reactivity of GCs with four epitopes was not significantly different than using only one epitope. The average cross-reactivity of GC B cells between each pair of epitopes was not decreased by using four instead of two epitopes. A key problem in vaccine design is to raise antibodies against antigenic variants to which a person has not been exposed. GC raised with four epitopes showed a slightly higher (although not significant) recognition of an “external” related epitope that was not present in the GC (Figure 4G). Therefore, adding more similar epitopes is not harmful for cross-reactivity but rather supports better recognition of the epitopes.

The model shows that using combination of similar epitopes enhances the chance of generating cross-reactive antibodies, even if less GC founder cell recognizes each epitope. We believe this will support the design of better vaccines toward poly-reactivity, conserved recognition, or broad neutralization.

Cocktail sequential immunizations induce highest affinity and cross-reactivity

To mimic the prime and boost vaccine steps, we used Ymir to predict the relative effect of single versus sequential GCs with one or two related antigen epitope variants named A and B (Figure 5A). We used epitopes with HD = 4 as a “harder task” than HD = 2. The mechanisms behind the induction of secondary GCs did not reach a consensus yet. In particular, it is not clear whether and to which extent memory B cells generated by a first GC are able to seed secondary GCs (Dogan et al., 2009; Mesin et al., 2020; Turner et al., 2020; Wong et al., 2020). Here, we simulated a secondary response by including only 5% of output cells generated by a primary simulated GC onto the founder cells of the secondary GC, provided they pass the affinity threshold to enter a GC, while the remaining 95% founder cells are freshly generated random naive sequences. This 5% fraction is a lower boundary to test the effect of very few re-engaged memory B cells. Secondary GCs (Figures 5B–5F) displayed a faster GC dynamics than the primary GCs, with higher GC volume and higher affinity to the epitope present, and output cells showed less numbers of mutations compared to primary GCs. The affinity and cross-reactivity to A and B are shown for each epitope combination in Figures S2A and S2B. Some antigens showed higher GC response than others; therefore, further analyses of affinity to A have been normalized for each epitope combination by the average affinity raised by a single GC to A. Cross-reactivities to A and B were not normalized.

The affinity of GC B cells and output cells to epitope A (relative to the single GC with only epitope A) was higher in the secondary GCs containing epitope A (Figure 5G, conditions “A→A”, “B→A”, “AB→AB”). Among all tested conditions, the sequence “AB→AB” (sequential cocktail GCs) showed the highest affinity. Conditions “A→A” and “AB→AB” raised equally high affine antibodies to A, showing that immunizations to A are permissive to the presence of the related epitope B. Affinity to A in secondary GCs containing only B were similar in output cells (and slightly lower in GC B cells) than the control primary GC with only A, showing that a secondary GC with epitope B was not “erasing” the primary response to A. The condition “B→B” raised similar affinity to A as “B→A”, suggesting that sequential GCs, with the same or two different related epitopes between primary and secondary GC, raise antibodies with similar affinity to both epitopes (i.e., that output cells from A or B are compatible to a secondary response to A).

Cross-reactivity between A and B (Figure 5H) was increased using a single cocktail GC compared to single GCs with A or B only (confirming the trends observed in Figures 4C and 4F for GC B cells), while sequential GCs showed higher cross-reactivity in comparison with single GCs, and the condition “AB→AB” raised the highest cross-reactivity.

The slight statistical differences between affinities of GC B cells and output cells can be explained by a delay in output cell affinities (Figures S2C and S2D) because they contain all cells accumulated over the GC history (i.e., they contain many cells produced early with lower affinity and need more time to attain a high average affinity). For instance, GC B cells in the condition “AB” reach higher cross-reactivity than the sequential GC conditions but only at late time points, and this is therefore not visible in the output cells. The conditions with sequential GCs were faster at raising high affinity in the secondary GC, and therefore, output cells had higher affinity than the “AB” condition at day 21.

Therefore, the inclusion of as few as 5% of founder cells from a primary GC significantly increases the affinity raised by secondary GCs. We tested the quantitative impact of a scenario in which more cells (20% and 90%) could re-enter secondary GCs (Figures S2E and S2F). More re-entry further increased affinity to A after the secondary GC if A was present in the primary or the secondary GC (“A→A”, “A→B”, “B→A”, and “AB→AB”) but had a very minor impact in the condition “B→B”. In the “A→B” condition, 20% of re-entry (or more) was necessary to provide an increased affinity to A compared to “B→B”. This suggests that the percent of memory cells entering secondary GC can tune the strength of boost response and the recall of affinities to the primary GC epitopes. Here, A and B were related epitopes (HD = 4), possibly explaining that higher re-entry in the “B→A” condition improved affinity to A (i.e. memory cells raised to B helped to respond to A later). In the context of less similar epitopes, the extent of re-entry could modulate the trade-off between recall of the first epitope and affinity maturation to the second epitope, in which case there might be an optimal amount of re-entry.

We wondered which type of injected founder cells were responsible for the high affinity and cross-reactivity induced by the “AB→AB” condition and separately injected 5% mono-specific (single reactive to A or B) or cross-reactive cells from a primary “AB” GC (Figure S3). Interestingly, the features of the secondary GCs observed in “AB→AB” (faster dynamics, faster diversification) were recapitulated already by single-reactive founders to A or B, although cross-reactive founders induced higher affinity and cross-reactivity. This suggests that memory B cells generated against an epitope A can efficiently be used in a secondary GC with a related epitope B.

Discussion

We presented a realistic representation of antibody-antigen binding that can be simulated efficiently on regular computers. For the first time, an affinity directly derived from a structural in vivo-like folding was used in full-scale GC simulations of AM. Affinity changes induced by mutations were depending on whether they start from already low or high-affinity CDR sequences, which increases physiological relevance compared with models using predefined distributions of energetic jump for each mutation. The mutation history and AM can directly be linked to the structural properties of the antibody-antigen binding in silico. This representation encompasses the complex topology of real antigens and simulates vaccination with either one antigen with complex combination of antigen epitopes or cocktails of many related epitopes. The implementation of the structural affinity model Ymir is modular and not restricted to GCs. It can be easily transferred to other receptor-ligand applications like thymic selection.

Critical features and behavior of antibody-antigen recognition are well captured in our system: The binding energy of each individual AA pair is taken from an experimentally derived energy potential (Miyazawa and Jernigan, 1996). Many non-trivial properties of antibody-antigen binding were successfully reproduced, like less easy recognition of hidden pockets and the emergence of many unrelated antibody sequences binding an antigen with high affinity. AM was correctly simulated at the scale of a complex 3D GC reaction. Realistic dynamics of individual GC cell numbers and affinity could be obtained. A substantial variation could be observed between simulated GCs, ranging from monoclonal bursts to polyclonal co-existence of clones, which is in line with the stochastic nature of GCs (Tas et al., 2016). Each GC produced a different antibody sequence with high affinity, and some GCs performed better than others. The mutation path to high-affinity cells was not stringent and allowed for intermediate reductions of affinity. Along the path to high affinity, typical affinity jumps of 2- to 10-fold and up to 74-fold were observed, which is associated with key mutations in real GCs (Mesin et al., 2016). These results together provide evidence that the structure-related affinity landscape is sufficiently complex for studying structural implications of antibody development.

The endpoints of the CDR loops are rooted on conserved parts of the antibody structure and cannot reach the target antigen [except in very rare cases, see Akbar et al. (2021a)]. This could be implemented by removing the endpoints (one or more AAs) of a sequence before calculating its energy. Here, we did not explicitly model a CDRH3 (whose length typically vary between 5 and 25 AAs) but rather CDR sub-sequences of a fixed size (a pre-requisite to compare binding energies between them, see Figure S1) that can access the antigen. Therefore, Ymir implicitly simulates a part of the CDRH3, and we have chosen here only sequences of size L = 9. Ymir can directly be used to process CDRH3 sequences by removing AAs at its endpoints, calculating the binding energy of each subsequence of size L (here, L = 9 AAs), and keeping the subsequence with the lowest binding energy as the binding paratope of the CDRH3, as done in Robert et al. (2021). We did not assess the concomitant binding of multiple loops (for instance, the CDRH3 and the CDRL3), which became computationally infeasible due to the combinatorial explosion of binding positions for both loops, and the need to check for collision between each pair of them. As an approximation, it could be possible to first simulate CDRH3 binding and then simulate the CDRL3 binding by excluding the positions taken by the CDRH3, but this would neglect the distance constraints between the CDRL3 and CDRH3 rooting residues to the antibody structure, which would make the simulation less biologically relevant.

Thanks to new methods for enumerating and clustering possible peptide backbone structures (Malliavin et al., 2019), it will become possible to adapt the present algorithm to more realistic space conformations by discarding improper angles using rotamer libraries on finer lattices (Koliński, 2004) and using approximate scoring functions for receptor-ligand affinities, as for protein docking.

We observed a high use of hydrophobic residues in amplified sequences from GC simulations (Figure 3B), as well as unpaired cysteines, which are very infrequently observed in antibody sequences. To test whether these improper sequences come from the randomly selected founder sequences, we simulated single-epitope GCs using 9-AA substrings of experimental human CDRH3 sequences as founder cells (Table S2). Albeit still preferentially using L and F, the amplified sequences showed higher AA usage diversity and shorter stretches of hydrophobic residues. Therefore, the AA bias can be improved by using experimentally derived founder sequences. Since the GC model does not contain counter selection mechanisms (such as tolerance-based deletion of clones), it is still possible that some amplified sequences in the simulation would have been deleted in vivo because they are degenerate or cross-reactive to self if they contain too many hydrophobic residues. In the future, the use of nucleotide sequences would allow including out-of-frame and SHM hotspots into nucleotide sequences.

Affinity calculations with Ymir require the knowledge of an antigen structure to start with. The use of toy antigens with minimal complexity in this manuscript allows us to control the simulation settings and understand the effect of structural similarity or specific mutations without « noise » from more complex structures. However, we have shown that GC simulations can be performed on lattice antigens discretized from real PDB structure (Figure S4), preserving the complex topology and AA surface composition (Robert et al., 2021). The discretization pipeline allowed us to incorporate the presence of glycans from the surface of the PDB antigen to its lattice representation, and it could impact the affinity of antibody sequences to the antigen with the glycan (Robert et al., 2021). Antigens with mutated sequences can be simulated using the same lattice structure. However, to account for (potentially buried) mutations that would impact the antigen surface structure, the new structure would need to be known and re-discretized into the lattice. When only a few mutated antigens are considered, it could be envisionable to perform molecular dynamics simulations of the mutated antigen from the original antigen structure to estimate the new structure before discretizing it.

Several studies have used phylogenetic mutation trees of B-cell repertoires as readout of selection signatures (Dunn-Walters et al., 2018). The robustness of those methods may be improved using Ymir by generating affinity matured repertoire benchmarks (Davidsen and Matsen IV, 2018) with structurally related antigens and proposing the appropriate size and time points of sequencing data sets to be analyzed (Uduman et al., 2014).

Vaccine development is hindered by the hierarchical immunodominance of some epitopes over others, on the same or different antigens (Angeletti and Yewdell, 2018). Some epitopes may be accessible and easily targetable, while others are hidden in pockets (Ward and Wilson, 2017). By reflecting accessible, shielded, and hidden epitopes, Ymir is suitable to study causes of immunodominance. We have modeled residue shielding (for instance due to glycans) as inaccessible positions to the CDR3 of the antibody that could represent the anchor of the glycans to the protein rather than their flexible tail. Alternately, different flexible glycan configurations could be enumerated in the lattice and transformed into multiple possible shielding conformations of the same antigen to calculate the binding energy.

Immunodominance can also evolve over time, as observed during HIV vaccination (Forsell et al., 2017). Antibody feedback has been proposed to contribute to hiding immunodominant epitopes (Meyer-Hermann, 2014). Our model can easily be extended to account for antibody feedback: The B-cell antibody sequence and an earlier produced antibody can compete to bind to the full antigen using mass action kinetics at equilibrium provided their target structures overlap, although such antagonism might be more complex (Alanine et al., 2019). In this setting, time shifting of immunodominance will emerge naturally.

Vaccines against highly mutating pathogens like the hepatitis C virus, dengue fever, influenza, or HIV need to raise antibodies against many strains at the same time, ultimately toward the holy grail of broad neutralization. For instance, HIV envelope accessible regions are highly variable, while the conserved core pocket is harder to target (Ward and Wilson, 2017). The accessible immunodominant region diverts the immune system into recognizing regions that can escape easily without impact on viral function. Broad neutralization can be achieved by antibodies recognizing the conserved region like the CD4 binding site of HIV Env protein or influenza hemagglutinin, thus binding most strains (conserved cross-recognition); but also cross-reactivity of antibodies that recognizes slightly mutated regions (promiscuous cross-reactivity) (Pancera et al., 2017) or completely unrelated antigen epitopes (poly-reactivity) (Bournazos et al., 2016) on various strains have the potential of broad neutralization. It is obvious that the best vaccination strategy depends on the antigen structure and the associated kind of cross-reactivity.

Simulations have the potential to inform the best vaccination strategy. Earlier works have simulated cross-recognition of conserved region using abstract affinities with a penalty for recognition of a shielding pocket (Wang et al., 2015). Here, we have shown that GC simulations can be performed with antigens of variable and controllable structure and mutation landscape. This enables predictions of vaccine efficacy with cocktails of antibodies with any structural or mutation relationship not only in the case of conserved recognition.

Further, by simulating waves of mutant viruses over a long period of time, it has been proposed (De Boer and Perelson, 2017) that the breadth of recognition by Tfh cells in GCs can determine the emergence of broadly neutralizing antibodies. More generally, Ymir could be used to simulate the co-evolution of virus protein and GC B cells and T cells, as was performed at the repertoire level (Nourmohammad et al., 2016). Altogether, Ymir paves the ground for computer simulations of AM and conditions that favor the development of bnAbs, thus providing an advance in the field of in silico design of antibody-related immunotherapies.

Limitations of the study

Several assumptions were made to achieve efficient computational time. The antigens and receptors were discretized on a 3D grid lattice. Instead of enumerating receptor structures and docking them, we perform both simultaneously, allowing us to discard huge amounts of possible structures. We do not pretend to simulate the exact affinity of antigen-antibody interactions: Real affinities will not be captured by simulation of the folding of a single CDR loop around a pre-folded antigen but is influenced by many other surrounding factors. Further, the coarse grained simulation naturally reduce the extremely large ensemble of possible binding conformations, making it impossible to relate a lattice binding structure back to an atom-scale antibody-antigen complex. As all previous mathematical models for GC response were based on even more abstract representations of antibody-antigen affinity, we argue that a phenomenological affinity function that preserves major features of antibody binding on physically grounded bases is sufficient and the best we can do so far to predict vaccine response to multivalent vaccines.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Ymir	This paper	Data S1 – maintained at https://gitlab.com/Sporistos/Ymir
hyphasma (GC simulations)	(Meyer-Hermann, 2019)	https://gitlab.com/germinalcentres/bnab
Absolut (Antigen discretization)	(Robert et al., 2021)	https://github.com/csi-greifflab/Absolut

Resource availability

Lead contact

Philippe A. Robert, philippe.robert@ens-lyon.org.

Materials availability

No experimental data were generated.

Data and code availability

We include as supplementary file the Ymir C++ package for simulating the structural affinities. No library is required. Commands are minimal, as follow:

#include "Ymir.h"

#include <string>

std::string structure = "DUUSURUSLDDUUDDUDDSUUSRDDRUDDUUDDUDDSUULS";

std::string AAsequence = "YFHGCARRATLNTTISWEYVSVDMEKIRVGGNEWFNHTMYVT";

int receptorSize = 8; // the receptor size is defined in bonds in the code (8 bonds: L=9 AAs)

int minNbContacs = 4;

double kT = 1.0;

affinityOneLigand T = affinityOneLigand(structure, AAsequence,

 lattice::idFromPosisition(31,30,34), receptorSize, minNbContacs, -1, kT);

double bestAffinity = T.affinity("AGNALIVN").first;

double statAffinity = T.affinity( " AGNALIVN " ).second;

Newer versions of Ymir will be made available and maintained on https://gitlab.com/Sporistos and the antigen discretization pipeline is available at https://github.com/csi-greifflab/Absolut.

Methods details

3D-lattice representation of proteins

Proteins structures are represented on a 3D Euclidean grid inspired from previous single-protein lattice models (Mann et al., 2012; Shakhnovich and Gutin, 1990). Successive AAs occupy neighboring positions in the grid (Figure 1B). Only a single AA can occupy the same position. Starting from a grid point, a protein structure is represented as a sequence of moves on the grid, namely straight (S), up (U), down (D), left (L) or right (R), as a plane pilot would follow. The first move can also be backwards (B). From predefined observer coordinates, each move is made relative to the previous observer coordinates and turns the observer in a new direction, except for a straight move (Figures 6A and 6B).

For each structure, a unique ‘absolute structure’ is defined by (1) a starting position and (2) a string built on the alphabet [SUDLRB], where B can only be the first letter. The ‘relative structure’ is defined as the group of absolute structures identical by translation or symmetry (Figure 6C). This is achieved by forcing the first move to be ‘S’ and the first turn to be ‘U’, thereby removing the 'B'. Relative structures follow the regular expression: 'S∗ | S[S]∗U[SUDLR]∗' and do not need a start position on the grid.

The use of relative structures has several advantages. It allows enumerating and manipulating possible structures by generation of random strings according to the regular expression. The representation is compact (an alphabet of five letters) and direct collisions (two AAs at the same position) among three successive AAs are avoided by removal of ‘B’. Rotations around a covalent bond are performed by changing a single letter, inducing a turn of the observer coordinates and propagating changes of the turn names according to the new coordinates, but without computing the new spatial positions of the AAs. It is also easy to fuse two proteins into a longer one: All possible structures resulting from the fusion, according to different rotations, can be found by fusing the sequences and performing turns of the observer coordinates. It has to be noted that a structure is oriented; the same protein structure can be described from both ends, and the sequence of a relative structure can be easily reversed to describe it by starting from the other end.

Binding and total energies between two proteins

For two proteins (as in Figure 1), an interaction is defined by a pair of two non-consecutive AAs occupying nearest neighbor positions in the lattice. One AA in a peptide can therefore have 1 to 5 interactions (since the covalent bond is not counted as an interaction). Interactions can be within a protein (folding) or between two proteins (binding). To distinguish the notions of 'empty' structure and 'protein (that is a structure with AAs), we introduce the operator P(R,S) that represents the protein of structure S and AA sequence R (both sharing the same length).

The binding energy E_bind between a receptor protein P(R,S) of length L and an antigen protein P(G,K) of length L_G, is the strength of the interaction between the two proteins, and is calculated as the sum of all interaction potentials between them:

$$E_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\left(P\left(R,S\right),P\left(G,K\right)\right)={\sum }_{k=1}^{L_{\mathrm{G}}}{\sum }_{j=1}^L\mathrm{T}\mathrm{o}\mathrm{u}\mathrm{c}\mathrm{h}\left(S_j,K_k\right)A\left(R_j,G_k\right).$$ (Equation 1)

The i_th grid positions of a structure S is denoted by S_i, irrespective of the type of AA at this position. The operator Touch(S_j,K_k) returns 1 if the residues Sj and K_k are non-covalent neighbors. A(R_j,G_k) is the interaction potential between the residues types given by Miyazawa and Jernigan (1996).

The folding energy E_fold of a protein P(R,S) of length L, is the sum of intrinsic interactions between its own interacting AAs:

$$E_{\mathrm{f}\mathrm{o}\mathrm{l}\mathrm{d}}(P(R,S))={\sum }_{j=1}^L{\sum }_{k=1}^L\mathrm{T}\mathrm{o}\mathrm{u}\mathrm{c}\mathrm{h}(S_j,S_k)A(R_j,R_k).$$ (Equation 2)

As we assume a static conformation of the antigen, we can define the ‘total energy’ E_tot of S around the antigen P(G,K) as the sum of its binding and total energies (neglecting the antigen folding energy because it is constant):

$$E_{\mathrm{t}\mathrm{o}\mathrm{t}}(P(R,S),P(G,K))=E_{\text{fold}}\left(P(R,S)\right)+E_{\text{bind}}(P(R,S),P(G,K)).$$ (Equation 3)

Energies are negative and calculated in kT units. Strong binding implies low energies. For the sake of simplicity, we took a linear model of energies, summing all interactions irrespective of whether an AA was interacting with 1, 2 or more residues. It could be possible to derive other energy models that give more or less weight to AAs with many binding partners.

Combinatorial enumeration of all possible foldings

From a predefined ligand, we explicitly enumerate all the possible 3D structures of the receptor of length L with at least n ≥ 1 interactions with the ligand. Starting from the first receptor residue, a first interaction point with the ligand is localized (Figure 6D). By definition, further interactions with the ligand have to be behind this point.

From a particular empty grid point X that is neighbor of a ligand residue, it is possible to recursively enumerate all receptor structures with X the first contact point to the ligand. All structures without interaction until X and all structures that may interact with the ligand behind position X are enumerated. Next, each pair of starting and finishing structures are checked for collisions with each other and for the right total length L (Figure 6E).

The recursive algorithm ‘GenerateTails’ (Figure S5) shows how to get a starting or finishing structure, and the algorithm ‘GenerateReceptors’ (Figure S6) shows how to enumerate all possible receptor structures around a ligand, with a minimum number of interactions between receptor and ligand. In order to improve efficiency, the GenerateTails function will be called multiple times from the same point, and the result of each call is stored in memory, avoiding excessive recomputing and explaining why memory usage reaches a few GB (Figure 1G).

Note that each starting point X describes a set of mutually exclusive structures if we assume oriented receptor structures (first to last residue). Indeed, every structure, if not oriented, would be enumerated twice, once from each end. Figure S6 is still valid in the particular case of n = 1 because the structures will be enumerated twice in lines 18-23.

Finally, in order to minimize the computational time, a list of structures can be compressed into a list of binding pairs of positions on the receptor and AAs on the ligand. Some structures produce the same list of binding pairs. By keeping track of which structures have which binding pairs in a dictionary, only the binding pairs need to be stored and evaluated for further exploration of the binding energies of concrete receptor sequences. This step leads to a three- to four-fold increase in computational speed.

The best binding energy of a receptor sequence to the ligand

Given the pre-computed list of possible 3D receptor structures with at least n interactions to the pre-defined ligand, the binding energy and total energy between the two AA sequences is calculated for each structure with the receptor AA sequence. The ‘best binding energy’ E_best is the average binding energy of all optimal structures in terms of ‘total energy’ E_tot (around a small ε = 0.001 to account for rounding errors), with

$$E_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}(R,P(G,K))=\begin{array}{c}\underset{\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{s}S}{\mathrm{A}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}}(E_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\left(P\right(R,S),P(G,K\left)\right),\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}S\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\\ E_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(P(R,S),P(G,K)\right)<\stackrel{n_{\mathrm{S}}}{\underset{i=1}{\mathrm{m}\mathrm{i}\mathrm{n}}}\left(E_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(P\right(R,S_i),P(G,K\left)\right)\right)+\epsilon )\end{array}$$ (Equation 4)

Self-folding can contribute to stabilize a structure and therefore the best structure is not necessarily the one binding with highest strength, but with lowest total energy. R is the receptor sequence, G the antigen sequence, K the antigen structure, S are the possible enumerated receptor structures, and n_S is the number of these structures. If a receptor sequence folds on itself with better energy than the total energy around the ligand, no binding is assumed and the energy is NAN (Not A Number).

Alternatively, a ‘statistical energy’ can be computed by applying a Boltzmann weight to each protein structure P(R,S_i) according to its total energy:

$$\begin{array}{l}{E}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}}(R,P(G,K))=\frac{1}{Z}\sum _{i=1}^{n_{\text{S}}}{E}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}(P(R,S_i),P(G,K))\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_{\mathrm{t}\mathrm{o}\mathrm{t}}(P(R,S_i),P(G,K))}{kT}\right)\\ Z=\sum _{i=1}^{n_{\text{S}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_{\mathrm{t}\mathrm{o}\mathrm{t}}(P(R,S_i),P(G,K))}{kT}\right),\end{array}$$ (Equation 5)

with kT the Boltzmann coefficient and S_i the i^th structure. Z is the sum of weights among all possible structures, and is used as normalization coefficient. Many structures could co-exist with good but not optimal total energy, and this may not be described well by the set of optimal structures alone in E_best. The statistical energy takes into account the ensemble of possible receptor conformations, and calculates a weighted energy that is the contribution of each binding structure with its probability as weight (probability being an exponential function of energy).

Choosing the minimal number of contacts

A high required number of contacts n allows to discard thousands of structures expected not to have a competitive energy in comparison with structures with many more contacts, while it increases the chance to miss the optimal structure if it contained strong bonds. We took n = 4 (non-stringent value) to ensure that the optimal structure is enumerated. In theory, the Boltzmann distribution should be distributed according to all possible receptor structures, rather than only with respect to a particular minimum number of interactions n, even including those that do not interact with the ligand (self-foldings). In the context of sequences of size 9 AAs, structures with n < 4 had a negligible contribution to Z because these come with a small weight. We also computed all the possible self-foldings for different receptor sizes L, and found that the influence of self-foldings on Z was negligible because the number of possible self-folding structures was small compared to large number of foldings around the ligand. This justifies to discard self-foldings. Higher values of n may be used to increase speed, as shown in Figure 1F, provided that there is still no impact on Z.

Transforming energy into affinity and binding probability

The best binding energy between receptor and ligand was calculated for short receptor structures. The real antibody–antigen affinity needs to include the contribution of the full antibody, with two binding regions and the scaffold. Further, inside a GC, the affinity of a BCR to the antigen translates into capture and internalization of the antigen, a process that depends on many other factors. Therefore, an affinity cannot be drawn easily. We define an empirical ‘re-scaled affinity’ a, of a receptor AA sequence R, to represent the probability of binding the antigen:

$$a(R,P(G,K))=\text{exp}\left(-\frac{E_{\text{max}}-E_{\text{best}}(R,P(G,K))}{C}\right)$$ (Equation 6)

E_max is the binding energy at which the antigen capture probability becomes 1. The binding energy was re-scaled with a coefficient C because the best structures were dominant in the affinity and GC simulations did not develop because of low antigen binding. In Figures 3 and 4 the affinity of L2, L5, and L6 and receptors with L = 9 were calculated with: E_max = -100 and C = 2.8. The coefficient C determines the ‘spread’ of sequences into ranges of affinity. C = 2.8 was chosen as a trade-off to minimize the average affinity of random sequences (such that only few cells are above the threshold of 0.0001 to enter the GC) while still allowing a 1000 to 10000 fold increase in affinity inside GCs (i.e. that some GCs reached affinities higher than 0.5 and the GC did not collapse). E_max and C have to be adapted if using a different length L.

GC simulations

GC simulations were performed on an agent-based model programmed in C++ in the lab, for which the algorithm was described in Meyer-Hermann et al. (2012) and Robert et al. (2018). The model explicitly simulates the movement and encounters of B- and T-cells, capture of antigen by B-cells, T-cell help, proliferation, recirculation, death and exit from the GC. The model was validated on experimental datasets for GC dynamics (Meyer-Hermann et al., 2012), B cell migration in the GC (Binder and Meyer-Hermann, 2016), and successfully recapitulates clonal dominance (Meyer-Hermann et al., 2018; Tas et al., 2016). The model settings with constant inflow of founder cells and a single B-cell - T-cell interaction for B-cell selection were used (Meyer-Hermann et al., 2012). Parameters values are detailed in Robert et al. (2018).

The structural affinity model (Ymir) replaced the shape space affinity model in this framework. A mutation is a random change in the AA located at a randomly picked position of the BCR. Selection parameters had to be adapted: Antigen uptake is limited in the model by a 'refractory time' between two attempts of antigen capture. This time was reduced to 3.6 seconds. The simulation time-step had to be lowered to 0.001 hours accordingly.

In the model, the individual number of B-cell divisions upon T-cell selection is derived from a Hill-function depending on the amount of captured antigen. We observed that the appearance of high affinity B-cells happened slower with the structural space compared to the shape space. We needed to lower the Hill-coefficient from 2.0 to 1.4. This value was also supported in Binder and Meyer-Hermann (2016). With a higher slope, cells with intermediate affinity did not expand.

Each founder B-cell entering the GC carries a randomly picked BCR of length L = 9 AAs and with a minimum affinity of 0.0001 to at least one antigen epitope variant, potentially allowing for an increase in affinity by a factor of 10,000 in a GC reaction. If we lower this ‘entry’ threshold further, the simulated GCs collapse and the mutations do not reach reasonable affinities.

In the model, Follicular Dendritic Cells (FDC) occupy a set of positions in space, and display a certain amount of epitopes at each of position to the B-cells. When using multiple epitopes, the same total amount of epitopes in the simulation is used as for single epitope simulations, meaning two epitopes are used each with half-amount, etc. Each FDC position was initially filled with an equal amount of each epitope. At each position, B-cells can access all of the epitopes simultaneously. The antigen capture probability was determined by the highest affinity to any of the epitopes at this position, and this highest affinity epitope is removed by one epitope unit at this position. Other epitopes are not captured.

Computation times are given for simulations on a single Intel Xeon CPU core (model E5-2690 v3 at 2.6 GHz). The antigen sequences used for Figure 4 are given in Table S1.

GC simulations from PDB antigen structure

We developed a discretization pipeline in Robert et al. (2021) that transforms a PDB antigen structure into a Ymir lattice representation (initially for benchmarking machine learning antibody-antigen prediction methods (Akbar et al., 2021b)). Briefly, the PDB structure of the protein chains or interest is converted into a lattice using the LatFit software (Mann et al., 2012), that iteratively tries multiple possible lattice reconstructions of the 3D PDB structure, and returns the lattice structure minimizing the distance (dRMSD) between original and discretized residues. We used the coarse-grained representation of the centers of all atoms of each residue, and a lattice resolution of 5.25 Å between neighboring residues, as it was shown to maximize the quality of discretization (Robert et al., 2021).

Graph analysis

Each founder sequence was assigned a unique ID. For every mutation, a new unique ID is assigned to the mutated sequence, even if this sequence already exists in another cell. The mutation history network of one GC is created with sequence IDs as nodes and mutations as edges. It is a forest, where each founder dynasty is a tree. The network was analyzed with Cytoscape (Figure 3). To represent the network, the default Prefuse Force directed layout was used, which showed a cluster for each founder in a convenient way. For Figures 3C and 3G, a cluster was manually selected, the nodes with an affinity of more than 0.5 were selected and their parents were included up to the founder sequence. The Prefuse Force directed layout was used to represent the graph. For Figure 3F, the tree in Figure 3E was selected, the nodes with identical sequences were merged and the network was shown again. The sequence logos (consensus) of Figure 3B were generated using Skylign (skylign.org).

Quantification and statistical analysis

The Wilcoxon non-parametric test was used as shown individually in the Figure legends.

Published: September 24, 2021