Abstract
Within the past few decades, the application of light scattering techniques to a broad range of scientific disciplines has increased significantly, especially in the field of analytical chemistry. The resulting interest in and use of light scattering methods suggests the need for an easily understood introduction and review of material for those new to the method as well as for current users in need of a refresher. In many respects, the theory and its applications may appear so overwhelming for many studying the field for the first time, that they rarely can spend the time just needed to understand the basic measurements and their interpretations. A variety of applications in analytical chemistry especially have resulted in a greater understanding of many of the macromolecular processes themselves from molar mass distributions, to the macromolecular interactions responsible for aggregation processes, to determinations of structure and function. The use of such analytical processes to obtain a better understanding of nanoparticle structure and function has become almost universal.
Keywords: Differential light scattering, dLS, Molar mass, Molecular size, Asymmetric flow field flow fractionation (A4F), Zimm plots, MALS
Graphical abstract
Highlights
-
•
Deriving the distribution of fractionated macromolecules by light scattering.
-
•
Deriving the distribution of fractionated nanoparticles by light scattering.
-
•
Deriving the masses of fractionated macromolecules from their scattered light.
-
•
Deriving the size of nanoparticles from the angular variation of scattered light.
-
•
Deriving bacterial size and structure by light scattering.
1. Introduction
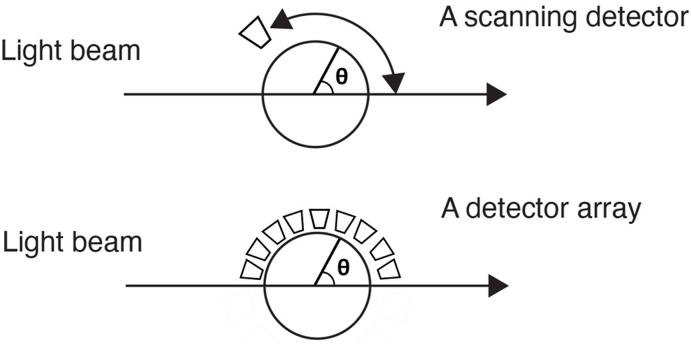
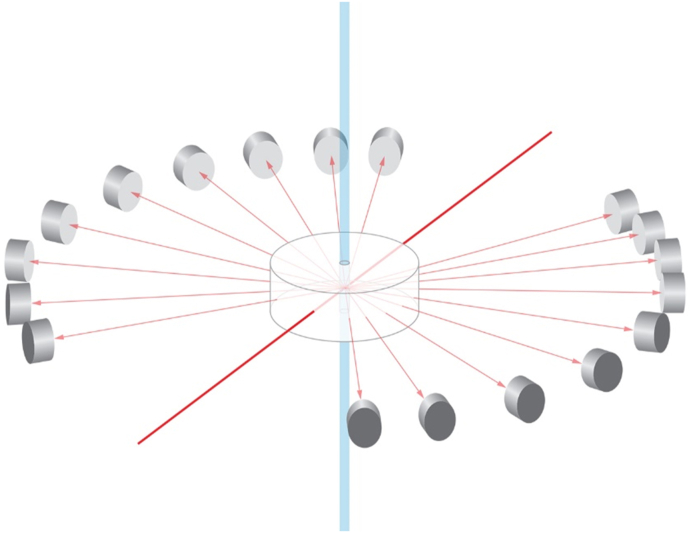
Most of the measurements and their interpretations presented in this article are based upon differential Light Scattering (dLS). Such dLS measurements generally refer to the process of measuring in a plane the intensity, I(θ), of light scattered by a sample (for example a particle, or ensemble of particles) as a function of angle, θ, with respect to the direction of incident beam of light. Historically, this geometry shown schematically in Fig. 1a, includes a light source, its passage through a sample, and a detector that may rotate about the sample through the range of angles between 0° and 180°. Although this geometry is fine for stationary samples, when the sample-containing fluid is changing in time, the single rotating detector must be replaced by a set of individual detectors placed over a range of angles surrounding the sample, such as shown in Fig. 1b. In this manner, the angular variation of the scattered light corresponding to the changes of the scattering solution are collected simultaneously at a set of specific angles at each selected time interval. Eventually, of course, each so-collected set thus forms the basis of the continuous dLS function that a scanning detector would have measured were the sample unchanged. Since the mass/size of the molecules or particles contained in a solution/solvent whose size/masses are sought, the final dLS function must derived from the scattering of the solution in excess of the scattering form the pure solvent or particle bearing fluid.
Fig. 1.
Classical measurement of a sample contained in a cylindrical glass cell.
Indeed, this multiangle detection concept has become the basis of modern dLS measurements. However, in order that such measurements be used to determine both mass and size, key measurements at 0° as well as the dLS slope at 0° were essential. The means by which these two important values are derived from a set of collimated detectors that collect light scattered into them at specific angles with respect to the incident beam, forms the basis of the general dLS concept. As we shall see from the discussion that follows, measurements of the light scattered by a sample into a set of n discrete scattering angles (between 0 and 180 degrees) are collected. The data are then fit by least squares means to a polynomial (the dLS function) in of the order m < n throughout the angular range from 0 to 180 degrees. The intercept of this polynomial at yields the particle mass, and its slope at the intercept yields its so-called mean square radius to be described/defined later.
Generally, such measurements are made in a plane containing a fine incident laser beam polarized perpendicular to it. Most commonly available laser sources produce linearly polarized monochromatic light and are, therefore ideally suited for this purpose. Surrounding the sample is an array of scattered light detectors, each subtending the same solid angle. The dLS concept, has a long history with its origins reaching back to early studies in nuclear physics measurements [1,2] as well microbiology [[3], [4], [5]]. Yet its more recent applications of the past few decades, to determine molar masses of a variety of molecules and sizes of various nanoparticles, have become its most extensive.
The first few sections of this article are presented for readers who may have little experience with light scattering processes. They are intended to provide sufficient historical material (hopefully, interesting as well as educational!) so that even those with no familiarity of the subject will be able to understand and appreciate the majority of its applications. Naturally, those having some experience in the field (and its history!) may easily skip such material. Companion anecdotal items often supplement the presentations of formulas and applications, perhaps of a historical nature, by which means the author hopes the materials may be more easily learned and recalled.
A review article [6] of many years ago discussed the then-recent practical developments of light scattering as an analytical means to measure the molar mass and size of molecules. Its focus, at the time, was synthetic polymers. Since then, there has been significant emphasis on measurements of proteins and other biological macromolecules including viruses such as those associated with COVID-19. In addition, the importance of characterizing nanoparticles, such as single wall carbon nanotubes, as well as gold particles, complexes of small particles, and other structures, has resulted in further applications of light scattering measurements and the associated means for their interpretation [7].
Historically, light scattering measurements involve samples of rather broad molar mass and size range. With the discovery of means to fractionate samples into their size constituents, analytical processes to measure each such fraction were developed and refined. The processes by which such fractionations are achieved will be described also for a variety of techniques and their characteristic sample types.
The measurements presented and discussed will focus on the general needs of an analytical laboratory whose broad responsibilities include determinations well beyond that of molar mass alone. With the tremendous increase in applications for protein and associated vaccine characterization, as well as remarkable phenomena such as gene delivery by means of so-called adeno-associated viruses [8], the instrumentation available to make such measurements continues to evolve. The growing significance of nanoparticles and their applications add more reason to study and understand light scattering measurements to determine the size and structure of such particles.
2. A little history (and why the sky is blue)
As most of this article focusses on the application of light scattering measurements to determine various physical properties of relatively small molecules/particles, it is important to emphasize that the field extends well beyond such needs of the analytical chemist. As mentioned in the Introduction, the reader of this article is not assumed to have seen or even have been aware of the remarkable historical results of the British physicist James Clerk Maxwell. His formulation of the theory of electromagnetic radiation, brought together for the first time electricity, magnetism, and light as different manifestations of the same phenomenon. The scientist, who even indirectly makes use of light scattering as an analytical tool, should have some familiarity with the work of this remarkable scientist, often ranked among the greatest physicists the world has ever known. Indeed, Einstein [9] described Maxwell's work as “… the most important event in physics since Newton’s time ….”
The remarkable four equations developed by Maxwell resulted in his deduction that electromagnetic waves existed and moved with an extraordinary velocity. But how could that be possible when there was no medium through which such waves could move? In his article on the Wave Theory of Light in the 9th Edition (effectively, its 100th anniversary) of the Encyclopedia Britannica, Lord Rayleigh (J. W. Strutt) [10] emphasized this apparent quandary stating: “… For although the evidence is overwhelming in favor of the conclusion that light is propagated as a vibration, we are almost entirely in the dark as to what it is that vibrates and the manner of vibration …..”
There are few examples of light scattering more familiar (though perhaps most often misunderstood) than the blueness of the sky on a clear day. It was only after Maxwell expressed the then-known phenomena of electricity and magnetism with a set of four equations, that Lord Rayleigh was able to explain the blueness quantitatively. Considering the scattering of monochromatic light of wavelength λ by a spherical particle of refractive index n and diameter d, much smaller than λ, he showed from Maxwell’s equations that the total scattering,from such a particle was
| (1) |
In other words, small particles such as the molecules of air, where scatter light inversely as the 4th power of the incident wavelength. Thus the blue light components of sunlight would be scattered much more than their longer wavelength companions (red, green, yellow, …). If you have a sheet of Polaroid and look at the sky away from the sun, you should notice that the blue sky light is highly polarized in a plane perpendicular to the earth. Fig. 2, a photograph of the horizon at sunrise, shows vividly the scattering of the sun’s various colors. As the sun is below the horizon, the light most scattered into the atmosphere is farthest from the horizon and is clearly blue with colors towards the red undergoing the least scattering.
Fig. 2.
Horizon at dawn. The sun is below the horizon.
3. Early measurements of molar mass
In the early 1940s, following his joining the faculty at Cornell University, Peter Debye [11] derived the following expression for the turbidity τ at the wavelength λ of a solution containing N particles of refractive index n per cm3:
| (2) |
where is the refractive index of the solvent. Thus from the number of particles per ml and their concentration (grams/ml), the molar mass of one particle (grams/particle) follows immediately. Two specific measurements are needed: the turbidity and the refractive index difference between the solution and the solvent. The turbidity may be determined directly by passing a fine monochromatic light beam through a solution contained in a cell of diameter w. If is the beam intensity entering the cell, then the intensity I of the beam exiting the cell is just Thus and when [Some additional corrections must be made for the small interface scattering events at the walls of the (generally glass) container. In addition, a differential refractometer is required to measure the difference of refraction of solution and solvent.] In summary once more: if we know the concentration, c, of the particles (e.g. grams/cm3) and the number of particles per cm3, N, then we know the mass of a single particle, c/N.
Although the method described above is interesting and perhaps useful for very small molecules such as proteins, the procedure is cumbersome and certainly of little use if the particular sample contains aggregates or is disperse. Debye did confirm, however, that the procedure and results for a 1% solution of the protein ovalbumin, studied earlier by Putzeys and Brosteaux [12], did produce the correct molar mass. These latter authors made measurements of 4 proteins of molar masses ranging from 3 × 104 to 5 × 108 (g/mol). Assuming a spherical structure and the formula, Eq.(1), for scattering developed by Rayleigh, they confirmed the molar mass values derived.
4. Interpreting the angular variation of scattered light, Zimm, and some further historical background
As the need to determine the molar mass of more complex and larger molecules developed, a more detailed analysis using light scattering became necessary. For larger molecules, the scattering of light incident upon them would show a variation of intensity with scattering angle. Such variation then had to be interpreted to obtain the molar mass and size/shape of the scattering particles. This interpretation, that will form a major part of this article, is based almost entirely upon the so-called Rayleigh-Gans approximation described in the following.
In this approximation, the refractive index of the particle is almost the same as the refractive index of its surrounding fluid. Thus, if the refractive index of the fluid in which the molecules/particles (of average diameter 2a) are measured is , and n is the average refractive index of the molecules/particles, the approximation is valid when
| (3) |
where and For virtually all molecules/particles that the reader of this article will encounter, the derivation of their scattering properties begins with this approximation. Accordingly, most of this article will focus on such measurements and their interpretations. There have been tremendous improvements in the instrumentation and software needed for the analytical interpretation of the scattering data collected since the great physical chemist Bruno Zimm first began developing the theory and his special instrumentation for this purpose in the late 1940s. It is a basic objective of this article to discuss some of them.
The great interest in large polymer molecules spurred this work throughout the 1950’s and 60’s resulting in the award of a Nobel Prize to Paul Flory in 1974 “… for his fundamental achievements, both theoretical and experimental, in the physical chemistry of the macromolecules.” An excellent paper by Oster [13] reviews well the early application and importance of light scattering processes to analytical chemistry, including Zimm’s work, anisotropic particles, large particles, and many other scattering systems. It is truly one of the outstanding papers of its era on light scattering. By the time of Flory’s Nobel Prize, Zimm [[14], [15], [16]], had already contributed significantly to the early analytical studies by which means the molar masses and sizes of such molecules could be determined graphically. For purposes of the present paper, let us focus on a most important equation, developed by Zimm, whose understanding will make the subsequent materials more apparent.
Though rarely mentioned, it is important to emphasize that Zimm’s measurements were made on solutions of molecules assumed to be nearly monodisperse whose average mass was M. Without an a priori knowledge of the actual mass distribution, the measured values cannot be interpreted easily. The graphical methods implicit in Zimm plots are still in frequent use to examine the molar mass properties of a solution. In addition, such computer-based implementations are particularly useful to confirm other experimental results, as well as for use for educational purposes. Off-line molar mass and mean square radii (size) may be needed to determine whether polymers have degraded during chromatographic separation. In addition, second virial coefficient A2 values derivable from Zimm plots may be needed to ascertain the thermodynamic quality (“goodness”) of a solution.
Following Zimm, we define the excess Rayleigh ratio, R(θ), as the intensity of light scattered by a suspension of molecules of mass M at a concentration c into the angle in excess of that scattered by the pure solvent in which the molecules/particles are suspended, i. e.
| (4) |
where is the measured intensity of the light scattered from the sample into angle θ, is the corresponding intensity of light scattered by the pure solvent, is the incident light intensity per unit area of the scattering volume V, and f is an absolute calibration constant derived from the geometry of the scattering apparatus. Throughout this article, all scattering measurements are assumed to be made in a plane perpendicular to the polarization of the incident (plane-polarized) light.
The relation between the excess Rayleigh ratio, , and the properties of the molecules/particles being measured (to concentration order c2) was shown by Zimm [15] to be
| (5) |
The scattering form factor , a known function of scattering angle θ, contains the structural features of the scattering molecules/particles. The function is the dLS function I(θ) discussed in the introduction. It will play a major role relating the dLS measurements to the physical properties of mass and size of the scattering molecules and nanoparticles that we seek. Further details may be found in Kratochvil’s excellent text [17]. The 2nd virial coefficient, , is a measure of the interaction between the molecules themselves in the solution. It is derived from measurements at higher concentrations and small scattering angles.
The constant K* is given by
| (6) |
where is Avogadro’s number, the refractive index of the solvent, dn/dc the differential refractive index increment (change of solution refractive index with a change of molecular concentration), and is the wavelength of the incident light in vacuum.
For example, for a homogeneous spherical molecule of radius a, it may be shown [18] that
| (7) |
where and , as defined in Eq.(7), is the spherical Bessel function of order unity. It is easily shown that and
Many of Zimm’s early studies [16] involved linear coiling molecules of uniform degree of polymerization, p, light of wavelength λ, and effective bond length b. For such molecules, it was shown that
| (8) |
where The wavelength in the surrounding medium of refractive index is . The scattering form factors for several other molecule/particle shapes will be presented later.
Returning now to early measurements, Zimm believed the precision of his measurements at smaller angles would be improved from the analysis of the reciprocal of viz.
| (9) |
To solve this equation for M graphically, measurements over a range of scattering angles and concentrations were needed. However, we note that as and, as the concentration, c, becomes very small, Thus at very small concentrations, and by the use of graphical means to extrapolate experimental measurements to very small scattering angles, Zimm was able to derive the mass directly. Similarly, from such graphs, the “size” (also referred to as the mean square radius,) was derived from the slope of at very small angles. (This will be discussed further in Sec.6.) In order to determine such slopes, R(θ) had to be measured over a range of small angles and, at each angle, measurements over a range of concentrations were required. To change the concentration, the entire thermostated instrument had to be disassembled, and, once reassembled (the sample chamber now containing the new concentration), recalibrated. Because of the great care required to measure samples at different concentrations, many of Zimm’s results were derived from only two or three different concentrations. Though easily stated, the work and time required to perform these measurements, using the instruments and graphical methods developed by Zimm, were very great.
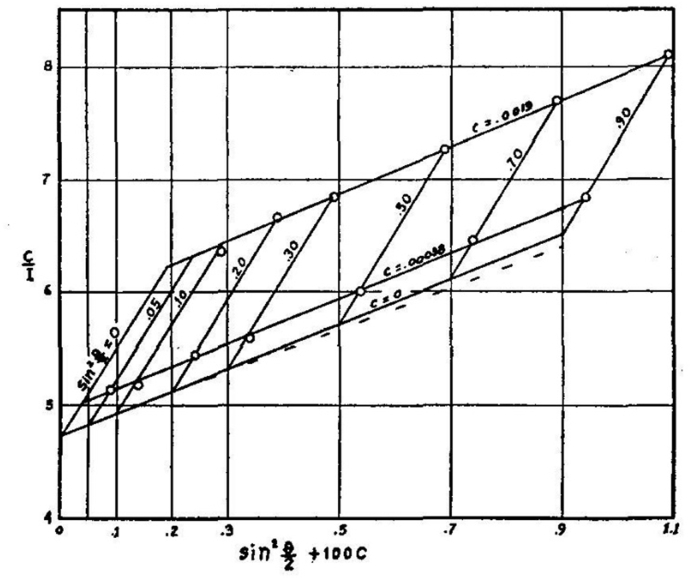
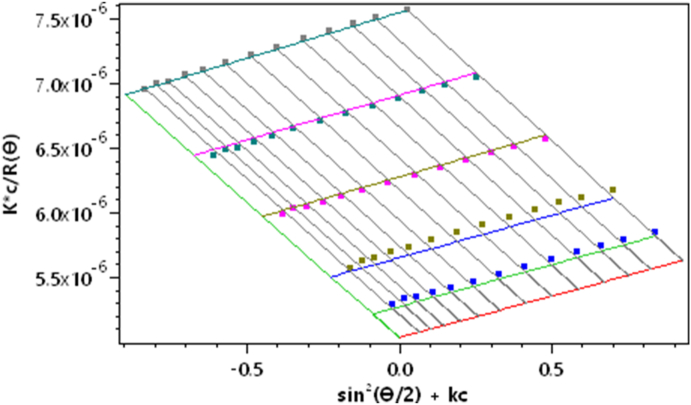
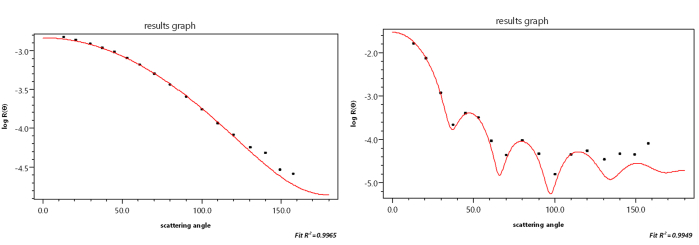
Fig. 3 shows an early example [16] of a Zimm plot. The data were collected from measurements at 7 angles (90°, 70°, 50°, 30°, 20°, 10°, and 5°) and 2 concentrations. The angular measurements were extrapolated to 0° and the concentration data were extrapolated to 0 to yield a value proportional to the reciprocal molar mass. Although such plots are rarely used to determine molar mass and size, their modern implementation, such as shown in Fig. 4 as a so-called “Global fit”, is a useful means to examine and present the collected data. As we shall see later, the dLS data are collected for each specific concentration injected.
Fig. 3.
An early Zimm plot.
Fig. 4.
A global fit Zimm plot.
With the development of new forms of chromatography for the separation and measurement of molecules and nanoparticles in solution, a rather rapid change in instrumentation occurred. Traditional measurements of unfractionated samples, of the type studied by Zimm, were simplified using instruments able to make “on-line” measurements of injected samples, at discrete concentrations. Adding to these improved measurements was the increased sensitivity of the instrumentation itself, permitting thereby measurements at far lower concentrations than accessible during the early years of the techniques introduced by Zimm. At such very low concentrations, of course, the dLS function of Eq. (5) takes on the simpler form
| (10) |
In 1969 the first light scattering photometer [19] was introduced that incorporated a laser. Its objective was the measurement of bacterial suspensions contained in a simple cylindrical cuvette. A scanning detector rotated about the cuvette providing the signal plotted on a simple Hewlett Packard X–Y recorder. No Zimm plot measurements made with the instrument are known to have been published.
5. Measuring the size of molecules/particles
Before addressing the specifics of current instrumentation and measurements and the required instrument capabilities needed to do so, we must address in some detail how such measurements relate to the structure of the molecules/nanoparticles themselves. Certainly, the equations that follow may seem somewhat foreboding at first glance, but spending a few minutes studying them is well worth the small effort required. If ones interest will always be restricted to molecules whose size is much smaller than, say, 1/100 of the wavelength of the incident light source used, this material may not be of importance. However, if particle/molecule size and shape will ever be of importance or interest, the few-minutes’ effort expended will be well-rewarded by the new insights it provides.
Accordingly, let us begin with a molecule/particle of mass M and volume V composed of n identical elements of mass m and density ρ. Let the distance between element i and element j be hij. We define to be the square of this distance over all its possible configurations. The mean square radius of the particle (referred to earlier and derived initially by a graphical means from a Zimm plot) is defined [16] as
| (11) |
Equation (11) may be reduced [16] to the more familiar form
| (12) |
where is the distance of the i-th element from the particle/molecule’s center of mass (the subscript “g” referring to the center of gravity, i. e. center of mass). Accordingly, setting a mass element to be of volume , and density ρ, we have Thus
| (13) |
where is the distance of the mass element from the particle center of mass.
As a simple example, consider a homogeneous sphere of radius a. Equation (13) yields
| (14) |
(For practice and to reinforce your understanding of the materials presented so far, calculate the mean square radius of a dimer comprised of two touching identical spheres of radius a.)
Following Kratohvil [17], of Eq. (5) or (10) may be written explicitly as
| (15) |
where Notice that the distance from element i to element j is the same as the distance from element j to element i. Equation (15) is obtained by expanding the sine function into its Taylor series. Since , the form of Eq. (15) follows. Since, furthermore,, we may now rewrite Eq. (15) as
| (16) |
where and Differentiating Eq. (16) with respect to yields the relation between the mean square radius and the variation of with respect to ξ, viz.
| (17) |
If we now restrict Eq. (17) to the initial slope of i.e. we obtain the very important result for the mean square radius
| (18) |
Before leaving this section to consider the measurement process itself, we should look more closely at the meaning of Eq. (18). It shows that from measurement of the scattered light variation at small angles (from a suspension of molecules/particles), we can derive their mean square radius, and from this, once we know the shape of the scattering particles/molecules, we can derive their size [20]! There does remain, unfortunately, a very simple question: how is the scattering variation at small angles actually measured? Or even more importantly, how is the purportedly differentiable function R(θ) obtained ab initio from the actual experimental measurements?
We’ll answer that question as we go into more details of the actual light scattering measurements later in this article but, for now, we at least see how light scattering measurements at discrete angles are fit by a simple function whose initial slope at may be easily calculated. Once we know the structure of the scattering particles, whose mean square radii have been determined, we may determine their associated sizes [20]. Historically, the light scattering measurements associated with the determination of molecule/particle size, shape, and mass have always been referred to as Differential light scattering.
6. Separation/fractionation of samples
As most samples of molecules and nanoparticles are not monodisperse, methods for determining the distributions of their molar mass and size required that the samples first be fractionated/separated before light scattering analyses, such as developed by Zimm, be used to determine molar mass distributions. Traditional samples, however, often contain broad ranges of masses, so suitable quantities of monodisperse fractions would be difficult to obtain for this purpose. Some means to separate a sample into its component monodisperse fractions was needed.
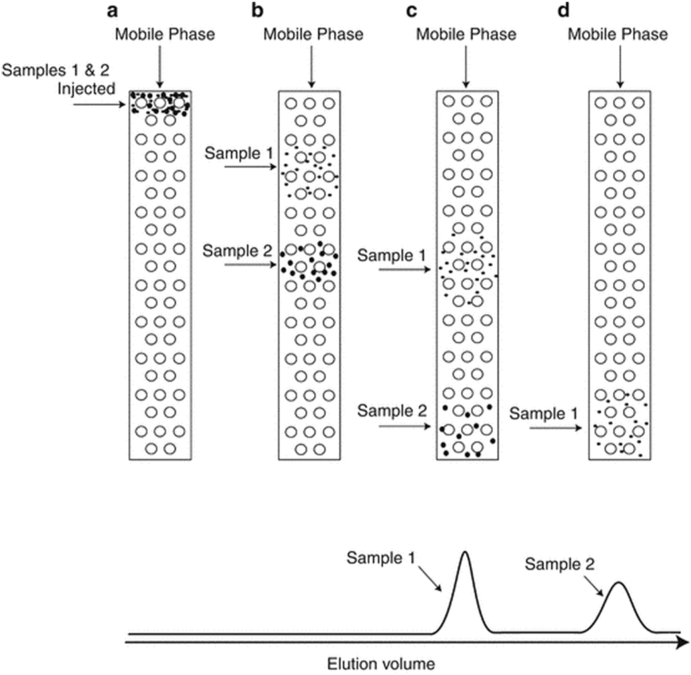
A major breakthrough occurred in 1955 with the invention by Lathe and Ruthven [21] of gel filtration chromatography. There were some earlier discoveries of such processes, but the Lathe/Ruthven concept was the most widely acknowledged and readily adopted. The concept they developed is the same as implemented in processes such as GPC (gel permeation chromatography) and SEC (size exclusion chromatography). Samples are dissolved in a suitable solvent (the “mobile” phase) and then flowed through rigid columns which are tightly filled with an insoluble (relative to the mobile phase used) porous stationary material. As the mobile phase carrying the sample flows through the column, the depth of penetration by sample molecules/particles flowing through it becomes greater as the size of the particles become smaller. Thus the larger the particles, the more rapidly will they elute. Fig. 5 shows the elution of a separation in time of a sample comprised of just two sizes. As the smaller particles can penetrate and be retained by the stationary substrates more readily, the first particles to elute will be the larger fraction. As a packing medium, Lathe and Ruthven used swollen starch or cellulose packings as a means to fractionate samples of proteins and similar biopolymers. In 1971 they were awarded the prestigious John Scott Award. This remarkable award, presented since 1822, is given to " ‘the most deserving’ men and women whose inventions have contributed in some outstanding way to the ‘comfort, welfare and happiness’ of mankind ”. Recipients have included such exceptional scientists as Mme. Curie, Thomas Edison, the Wright brothers, Sir Alexander Fleming, Alan Heeger (a professor at the University of California, Santa Barbara), Gordon Gould (inventor of the laser), Buckminster Fuller, Wallace H Coulter, and Jonas Salk [22].
Fig. 5.
Elution of a two-component sample through a porous stationary packing.
Almost a decade later, John C. Moore [23] of the Dow Chemical Corporation described a similar process for fractionating disperse polymer samples based on columns packed with cross-linked polystyrene gel. For Moore, of course, the mobile phase was an organic solvent such as toluene or THF. Moore’s implementation represented a major development for the analyses of organic polymers. The invention of Lathe and Ruthven was never referenced in their article or associated patent [24]. Within months of Moore’s paper, John Waters became the exclusive licensee of the method and began his corporation to exploit this application. Under his leadership, size exclusion chromatography (SEC) was now to become a major method for the study of petrochemical polymers. As the process became refined further, other terms such as HPLC (high performance/pressure liquid chromatography) were used to characterize the separation process. Its subsequent commercialization by Waters Corporation, in particular, resulted in immediate benefits for a broad range of polymer chemistry research.
Without companion scattered light measurements available, such columns were “calibrated” using well-defined mass standards whose specific elution times through such columns were associated with specific sizes or masses. Such calibration standards formed the basis of size exclusion chromatography for many years despite the availability of early light scattering instrumentation.
One of the more recent developments in SEC occurred in 2005 with the successful introduction by Waters of ultra-high pressure liquid chromatography [25]. This extension of HPLC resulted in analyses often ten times faster than the best HPLC/SEC using as little as 1/10th of a traditional sample size. Accessible molecular sizes, however, were further restricted to the smaller sizes appropriate for the special columns developed for such separations. Although the technique has proven exceptional for the analysis of proteins as well as some of their associated fragments [26], its high cost have minimized its impact significantly.
Differential light scattering measurements may be applied for the interpretation of samples fractionated by other chromatographic methods such as ion exchange [27], as well as, reverse phase chromatography [28].
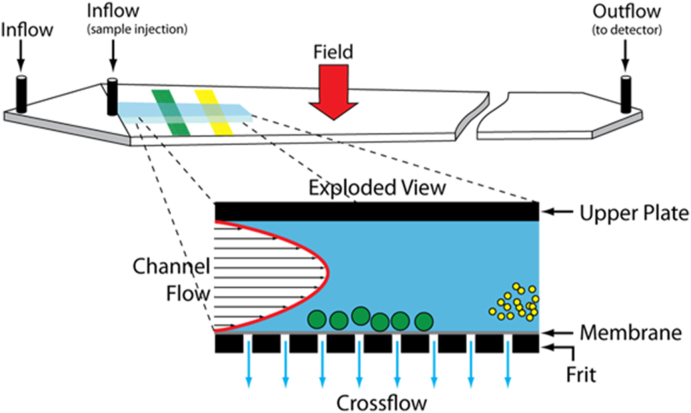
A completely different method for fractionating molecules and particles was introduced by J. Calvin Giddings in his pioneering Separation Science paper [29] of 1966. This method was based upon separation by a single phase process where fluid flow within a column is subjected to a force perpendicular to its direction of flow. (In this regard, note that SEC requires two phases: the column packing material and the eluting fluid passing through it.) Molecules/particles flowing through such a system would elute dependent upon their size, with larger particles, forced closer to the membrane because of their larger size, eluting later. The most used and successful system was invented by Wahlund [30,31] and is illustrated in Fig. 6. This system is usually referred to as asymmetric flow field flow fractionation, or simply A4F. The mobile phase (usually aqueous though it may be organic if measurements of organic polymers are to be made) enters the channel at the first inflow at the left. The sample is introduced at the sample injection inflow location shown. There it is held against the membrane, lying on top of a permeable frit, by the cross flow passing through the membrane while the outflow is reversed to balance the inflow. This produces a sample restricted to a confined linear region close to the membrane and perpendicular to the length of the channel. Once the outflow is restored, the sample is released and acted upon by the channel flow and the perpendicular cross flow component flowing through the membrane. Larger molecules/particles equilibrate more closely to the membrane than smaller molecules/particles and this separation/fractionation process continues as the sample flows through the crossed flow fields (channel flow and crossed flow through the membrane) of the channel. Smaller molecules/particles elute before their larger companions as they diffuse more easily against the cross flow and are swept through more rapidly by the increased channel flow with distance above the membrane.
Fig. 6.
Structure of an asymmetric flow field fractionation channel (A4F).
There are several other types of field flow fractionation [32] using different fields applied perpendicular to the direction of flow such as electrical, thermal, and even gravitational.
7. Differential light scattering instrumentation and the measurement of molar mass
Until the late 1960s, the Waters use of SEC dominated the market of polymer analysis. By 1973, Wilber Kaye [33] and colleagues at Beckman Instruments had developed a laser-based instrument connected directly to an SEC-based chromatograph and a differential refractometer to measure dn/dc, and from that, the concentration. Such a device was able to measure the light scattered by a sample at a very small scattering angle. Accordingly, one only needed to make light scattering measurements as a function of concentration at an angle as close as possible to 0° and the answer is there! From the analyses of Zimm, the molar mass could then be determined directly at values extrapolated to zero concentration. No size information was derivable. This concept and associated instrument design were sold by Beckman Instruments to Chromatix Corporation (later purchased by LDC/Milton Roy) who then commercialized what would be known as LALLS, or low angle laser light scattering. The idea conveyed by such terminology was that because a laser beam has a very small diameter passing exactly through 0°, measurements of scattered light from laser-illuminated samples could be made at angles very close to 0°. This was achieved by means of annuli allowing the detection of light scattered into discrete small angles. From Eq. (8) at a very low concentration and with a serial measurement of the sample refractive index from an on-line differential refractometer, the device could determine the sample’s molar mass directly. Throughout the 1980s and well into the 1990s, these instruments dominated the use of light scattering to the field of liquid chromatography then based almost entirely on size exclusion chromatography. Their major shortcoming, of course, was the fact that only the molar mass could be determined and, only then, if the samples contained no debris or aggregates. Columns also had to remain pristine with no shedding. No sizes were derivable.
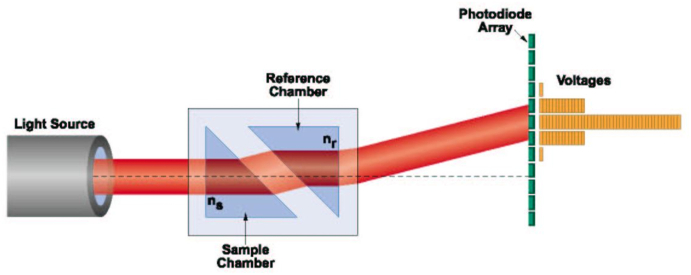
Fig. 7 is a schematic illustration of a differential refractometer needed to determine the refractive index increment, dn/dc, of a sample. The reference chamber contains the pure solvent of refractive index and the sample chamber contains the sample solution. As the concentration of the sample changes, the refractive index of the solution in the sample chamber changes. Thus the light source beam passing through the sample chamber changes its angle of refraction at the glass separating it from the pure solvent in the reference chamber, passes through the reference chamber and falls at a different position on the photodiode array detector.
Fig. 7.
A differential refractometer.
As discussed briefly in Sec. 1, the concept of dLS measurements at a plurality of scattering angles (for SEC separated samples) began to be adopted with a custom system delivered to S. C. Johnson and Son in 1986. The commercialization of laser-based differential light scattering instrumentation using a discrete set of detectors within the 0 to 180 degree range was confirmed with Amoco becoming the first major petrochemical firm to adopt the process for research in polymer chemistry in 1986.
We now have to use the individually collected scattered light intensities from the array of detectors to generate the dLS function R(θ) and, from that, determine its intercept [Eq. (16)] and incident slope [Eq. (18)]. This is achieved by fitting the data collected at every angle to an appropriate polynomial within the entire 0 to 180 degree range, taking into account, of course, that each datum is weighted appropriately by its associated reciprocal measurement error. For certain simple structures, the dLS functional variation is known initially and, in the Rayleigh-Gans approximation, the data would be fit directly to such a function instead of a more general polynomial. Thus, were the molecules/particles known to be spheres, their scattering would be fit [18] to the function
| (19) |
where The radius a of such molecules/particles would be derived, therefore, from the dLS fit to Eq.(19) of the collected data at each of the angles being measured.
Although homogeneous spherical molecules/particles are measured easily by the procedure just described, what about more “interesting” shapes such as simple aggregates (e. g. dimers of spheres, ellipsoids, disks, coated spheres, rods, tubes, etc.)? Those structures require more than a simple fitting of the collected scattering data to a single variable. If the structure of the molecules/particles is known, then the target of such measurements is chosen as the slope of the derived dLS function at the origin, θ = 0. Of course, that yields the mean square radius of Eq. (18).
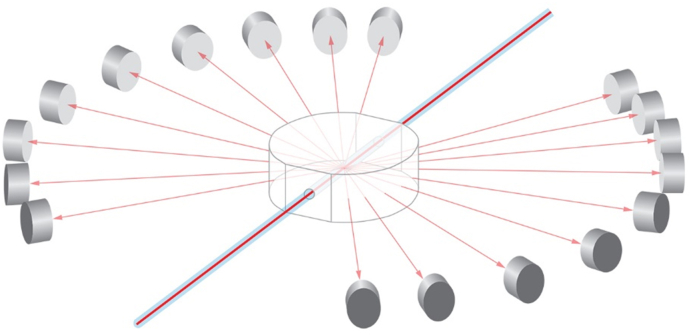
Since dLS measurements used for the determination of molar mass and size now dominate both the research and commercial fields focused on polymers, proteins, and nanoparticles, the specific instruments that are able to make such measurements are of somewhat different structures. The system shown in Fig. 8 measures light scattered from the sample-carrying flow stream within a cylindrical capillary illuminated by a laser beam perpendicular to it. In the system of Fig. 9, the laser beam is coaxial and within the sample-carrying flow stream, with detectors also co-planer with the laser beam. Despite the apparent similarity of the measurements made by the devices of Fig. 8, Fig. 9, the cylindrical geometry of Fig. 8 affects significantly the ability to measure scattering at smaller angles. For molecules/particles much smaller than the wavelength of light, simple 3-detector dLS systems are equally effective for both structures. As the configuration of Fig. 9 is most frequently referenced in the literature, its use is assumed in the discussions that follow.
Fig. 8.
Scattering detection geometry for scattering perpendicular to the flow.
Fig. 9.
Scattering detection geometry for scattering parallel to the flow.
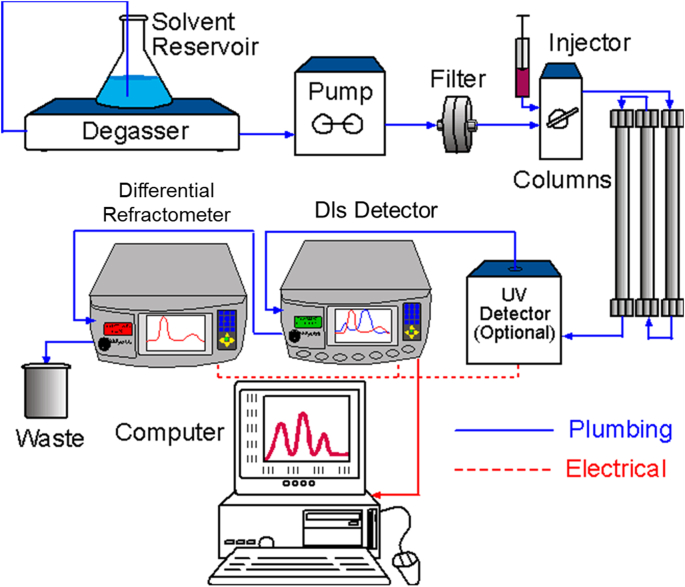
In addition to the dLS system, other components include a chromatography pump with solvent reservoir, an injection port, a size exclusion column (see below), and a differential refractometer to measure dn/dc. These elements and their sequential placement are shown in Fig. 10. Typically, an aliquot of a molecular sample (for example bovine serum albumin, or simply BSA) is injected, at a concentration of about 2.0 mg/ml, into the solvent (e.g. an isotonic saline solution) flowing at about 1 ml/min. The sample then passes through the columns where it is fractionated (remember larger molecules come out first!) and then passes through the dLS detector array and the downstream differential refractometer. The scattered light received simultaneously at each angular detector (as well as the sequential refractometer signal) are usually collected every second or half second, converted into numeric values, and stored for subsequent analysis. Each set of data collected at all angles is referred to as a “slice.” Thus, the molar mass at each slice is calculated from the ratio of the dLS signal, extrapolated to 0°, to the RI signal.
Fig. 10.
Sample measurements using dLS detector.
The first instrument incorporating the concept of differential light scattering with component detectors at several angles was a device [34] built and tested for the Food and Drug Administration in 1976 to detect antibiotic residues in meat products. David T. Phillips, who directed much of the instrumentation developed for this project, introduced additional detectors at different angles to improve the precision of the measurements and, thereby, ushered in the concept of determining the dLS function by means of the use of many detection angles spanning the accessible range between 0° and 180°. The simultaneous dLS detection concept was based in part on the instrumentation proposed [35] in 1971 to measure the scattering simultaneously at a distinct set of scattering angles by means of a plurality of detectors. Commercial light scattering systems (e. g. the familiar DAWN® systems), able to generate the dLS function from the simultaneous measurement of light scattered by molecules/particles at multiple angles from solutions flowing through them, have been available commercially since 1986.
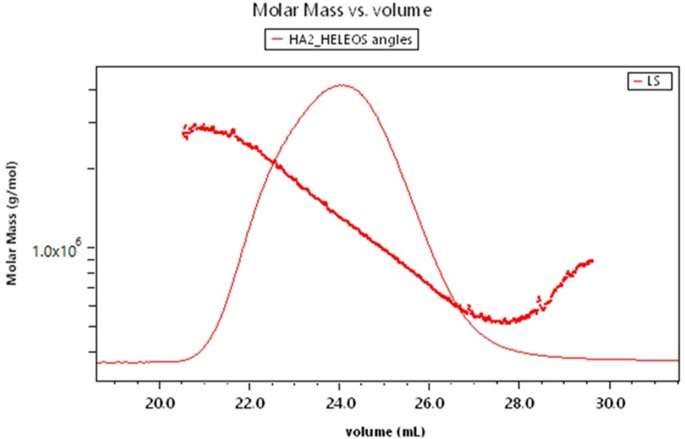
Let us now use the instrumentation of Fig. 10 to measure an amylopectin sample undergoing fractionation as it passes through an SEC column. At a flow rate of 0.5 ml/min, the system collects data from the RI detector and each dLS scattering angle each second. Each such collection is said to correspond to a “slice.” Fig. 11 shows the calculated molar mass as a function of the eluting volume superimposed over a graph of the 90° scattering as a function of time. Between 20 ml and about 27.5 ml, the sample appears to be eluting normally (smaller molecules retained longer than their larger companions), following passage through the size exclusion column. Beyond that limit, the molar mass begins to increase! This anomalous result has been hypothesized by Podzimek to arise because the sample probably contains some branched molecules [36] whose affinity for the column components results in their far longer retention. Podzimek has made an extensive study of these column interactions and related anomalies associated with the SEC fractionation of branched and other molecular structures, confirming that specific interactions between the sample and column constituents could produce such anomalous results. We shall return to this important subject later.
Fig. 11.
Amylopectin molar mass as a function of elution volume.
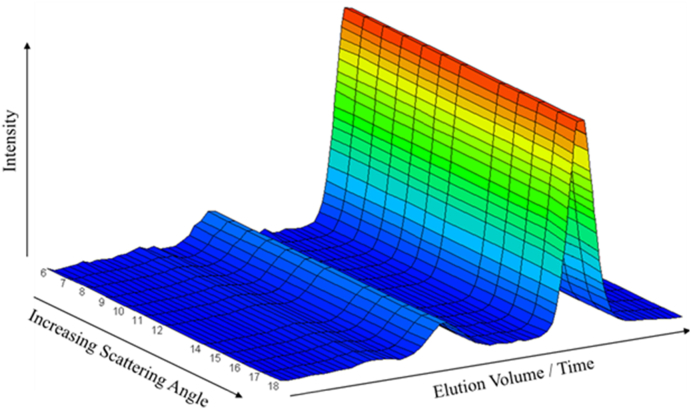
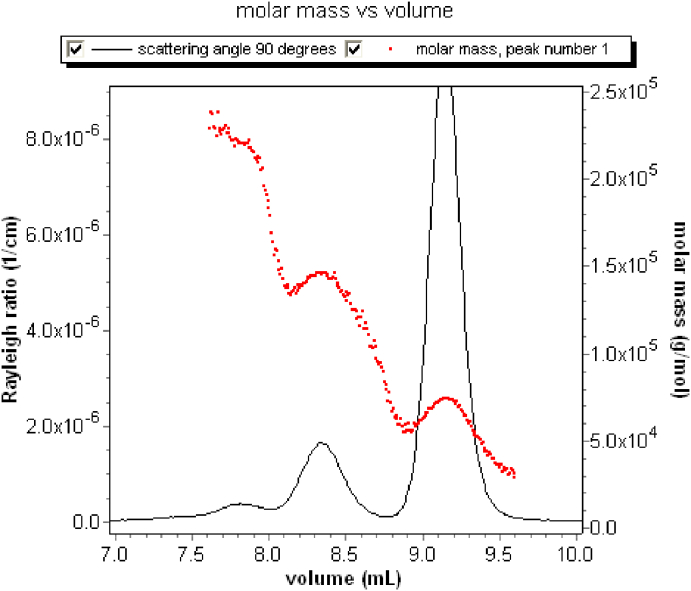
As a further example of an SEC fractionated sample and its dLS measurements, consider the well-referenced protein, BSA (bovine serum albumin). Its molar mass is known as 66.5 kDa for which a suitable SEC column is selected. This well-characterized protein is readily available from a variety of commercial sources. An aliquot of the BSA sample is injected as indicated earlier for the analysis of amylopectin in Fig. 11. As the separated sample passes through a dLS detector of the type shown in Fig. 10, each detector records the signal of light scattered into it. As we shall see soon from these measurements, this particular sample contains some aggregates. Since the size of each such aggregate is larger than the BSA monomer, they will elute first (Recall, for example, from Fig. 5, that larger molecules are more readily excluded from entering into the smaller pores of the column packings.). Note also that as the molecules leave the dLS detection region, they pass through a differential refractometer measuring the contribution to the refractive index of the solute whose concentration is calculated at each slice, based on the known value of dn/dc. Fig. 12 presents composite plot of the dLS values collected with the elution time on one axis and associated scattering angles on the other. Note the presence of larger components appearing at earlier elution volumes. (Recall again that larger molecules penetrate the column substrates less than smaller particles. Thus larger particles spend less time in the columns and elute earlier than their smaller companions.)
Fig. 12.
Scattering as a function of angle and time from a fractionated BSA sample.
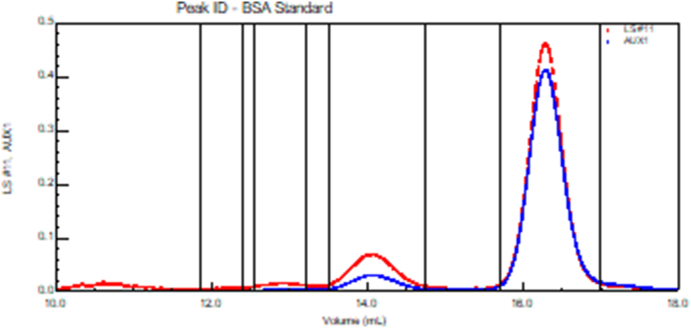
Fig. 13 presents the collected scattering data at 90° (upper trace in red, detector 11 of Fig. 12) and the differential refractive index (lower trace in blue) as a function of elution volume. Data collected at the other scattering angles are shown collectively in Fig. 12. Note that there are 3 distinct peaks produced for this purportedly monodisperse molecule. From the data, we may calculate the molar mass of each eluting fraction (slice), i. e. the molar mass is proportional to the ratio of the scattered intensity to the differential refractive index. These results are shown in Fig. 14. Look at this figure carefully. Each point shown corresponds to a different slice. The three regions of slices from right to left correspond to the monomer and two aggregate fractions: dimer and trimer. (The collected data at each slice includes all the associated dLS angles as well as the RI measurement. There is a corresponding value at every dLS detector in addition to the 90° data shown in Fig. 13.)
Fig. 13.
Scattered intensity at 90° (red) and corresponding dRI signal (blue) from BSA. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Fig. 14.
The uncorrected BSA molar mass vs. elution volume.
A further disturbing feature of the measurements shown is that each peak appears to correspond to a variable distribution of mass. How can this be possible? At the very least, the monomer of BSA has been well-measured for so many years, and yet here is a measurement made with light scattering at variance with reality. This “problem” with light scattering measurements, as well as other measurements involving SEC and the two detectors (differential refractive index and light scattering or, even, viscosity if such a detector is included) needed to characterize the separations, has long existed with associated discussions [37,38] to describe and, hopefully, correct, this so-called phenomenon of “band” broadening (BB). Such efforts were never successful [39] until the breakthrough of Steven Trainoff [40] who solved the problem analytically in a remarkable fashion.
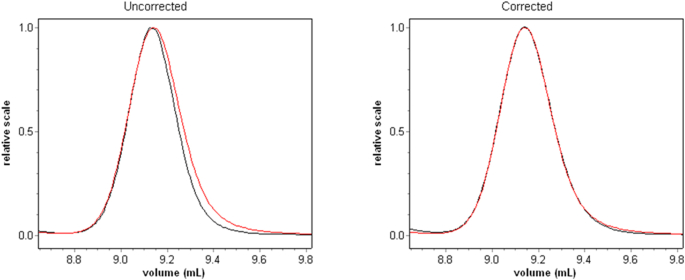
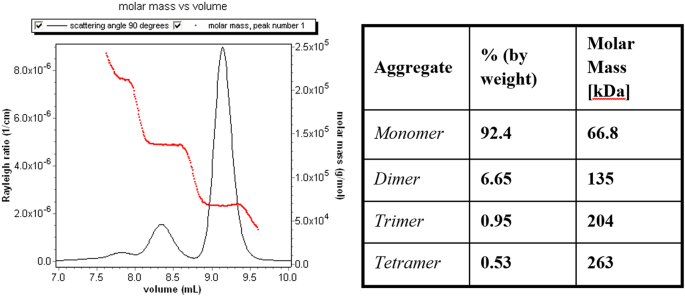
As many before him, Trainoff noted that the volume between detectors causes the downstream sample to broaden as it travels through sequential detectors (dLS and dRI) and then, uniquely, determined how to correct the effect. At the left of Fig. 15, we see the uncorrected profile of an injected sample at the 90°detector (black) and its profile at the sequential (and later) RI detector (red). Note that the RI signal is broader. In order to combine properly the scattered light signals with the associated RI signal, the former must be broadened. This “correction” for the 90° scattering is shown in the graph at the right. By this procedure, the band broadened artifact data shown for each angle are corrected to yield the graphs shown in Fig. 16. At the plateaus shown for these data, we obtain the results shown in the adjacent table. Note that the slices making up the monomer are (after correction for BB) indeed monodisperse as are those corresponding to the dimer and higher order aggregates. The regions between the plateaus, of course, correspond the slight overlap of the unseparated peak regions. Trainoff also showed that band broadening could be corrected by narrowing the associated RI signal. Such an approach turned out to produce inferior results and had other problems as well.
Fig. 15.
The Trainoff procedure for correcting the effects of band broadening.
Fig. 16.
The band broadening corrected BSA molar mass sample.
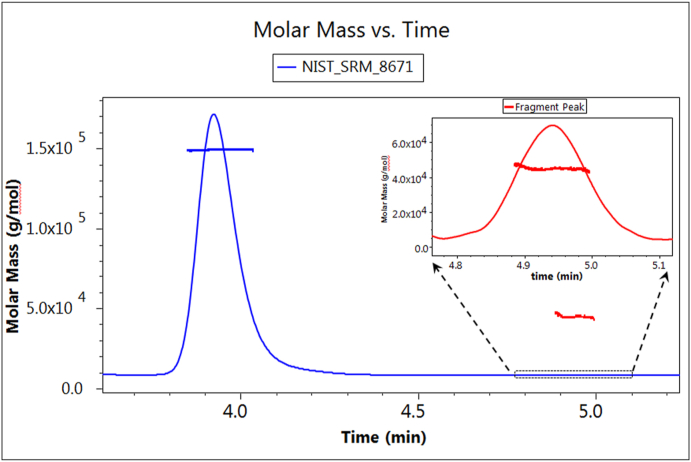
The fractionation of protein samples by SEC and their subsequent dLS measurement represent one of the most successful applications of the light scattering technique. For even smaller molecules, an extremely rapid SEC fractionation process was developed. This technique, known as ultra-high-performance liquid chromatography, or UHPLC [41], requires very small sample size and special columns. Fig. 17 shows a UHPLC measurement of the NIST reference monoclonal antibody RM 8671. An extremely small cylindrical cell of Fig. 9 structure is required to make these measurements [42] with an injected mass of only about 1 μg. The speed of these UHPLC measurements is almost ten times faster than a typical corresponding SEC measurement.
Fig. 17.
SE-UHPLC measurement of NIST RM 8671.
Although the pristine protein analyses of Fig. 16 (as well as those of Fig. 17) were of the greatest importance in elucidating the significance of band-broadening, they told us very little of significance about the concept of dLS itself. The BSA discussions above were concerned with a clean chromatography of very small molecules and the band broadening corrections needed. Nevertheless, the particular measurements presented are based on the derivation of a dLS function from scattering data collected at 12 angles. Are so many angles required for the measurement of SEC-separated molecules? Obviously, dLS measurements yield greater precision and are applicable to a greater range of samples including particles as well as analyses of aggregations and branching. Most importantly, with the dLS function generated from more angles, there is a built-in redundancy and less sensitivity to debris in the chromatographic system. The type of commercial instrumentation that a user might consider for the generation of the dLS function range from a single angle detector to as many as 20 or even more.
A frequent question associated with dLS measurements is, of course, how many angles are required to produce accurate (or sometimes just satisfactory) results? Commercial instrumentation is available with detectors at only three angles as well as implementations spanning a broad range of even 18 angles and more between 0° and 180°. In general, increasing the number of angles results in dLS functions of increased precision with an associated reduction in the system’s sensitivity to debris that may be present in the chromatography system. In addition, the incorporation of measurements from more detector angles results in greater measurement versatility of the derived dLS function including the ability to measure proteins, particles, branching phenomena, as well as complex aggregates of the molecules/particles measured. In a 1993 unpublished report, Dr. David W. Shortt did a thorough study of this problem of how many angles are needed to produce a dLS function. His conclusions were:
-
i.
Fewer angles make an instrument less expensive to build, and could therefore be sold at a price less than an instrument with more angles.
-
ii.
More angles improve the precision of the dLS determination by approximately the square root of the number of angles. For example—all else being equal—one would expect an 18-angle instrument to be more than twice as accurate as a 3-angle instrument.
-
iii.
Angles closer to zero degrees allow a better theoretical projection to zero and improve the accuracy of the molar mass and size determination. This consideration becomes more important as the molecular size increases. It is unimportant for molecular radii less than about 10 nm, very important for radii greater than about 50 nm, and moderately important in between.
-
iv.
Since dust and particles inevitably present in chromatography scatter much more at low angles than at high ones, angles farther from zero tend to show less noise and thus are more useful in the determination of molar mass and size. This consideration is important for organic-solvent chromatography when considering angles less than about 30°, and very important in any discussion of aqueous chromatography, in which dust and particles are more prevalent.
Although most of the dLS measurements presented in this article were made with instruments containing as many as 18 detectors, one should note from the above discussion that less expensive instruments containing only 3 detectors and the simplified structure of Fig. 8 could have produced comparable results for very small molecules of sizes less than 10 nm, such as many proteins.
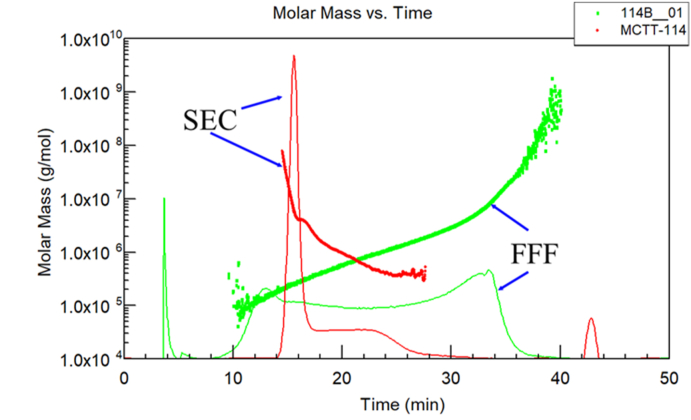
Although the aforementioned examples of SEC separations confirm the importance of the technique, there remain significant problems, as we have seen, if the molecules interact with the column materials themselves, as illustrated earlier with Fig. 11. In addition, SEC separations have some maximum size limits that will depend upon the effective pore sizes of the columns used. Usually these are limited to sizes well below 300 nm though with proper care macromolecules as large as 500 nm have been separated by SEC. What about the single-phase separation technique asymmetric flow field flow fractionation, A4F, discussed earlier? The superior resolution of A4F permits the separation of high molar mass samples more effectively than SEC while permitting also the ability to measure and characterize particles, often larger than 1000 nm. Fig. 18 compares the separation of some protein polysaccharide conjugates by SEC (dark red) and A4F (dark green). (The corresponding refractive index signals are indicated by the lighter traces of each color pair.) We note that A4F has superior resolution and is able to differentiate high molar mass samples more effectively and over a far broader range than SEC. The maximum sizes separated by SEC generally cannot exceed about 100 nm, whereas A4F can separate samples whose sizes often exceed 1000 nm. A4F separations have shown to be very useful for the characterizations of a variety of protein and bio-particle samples [43,44]. Care must be taken during the so-called focusing step (of the A4F process) to prevent the formation of protein aggregates.
Fig. 18.
Comparison of SEC and A4F fractionations of protein-polysaccharide conjugates.
There can be little doubt that many conventional separations of biopolymers and branched polymers that may undergo interactions with the SEC columns are separated more effectively and reliably using A4F techniques. In Fig. 11, for example, we saw an example of the effect of branched polymers interacting with the column materials themselves. Podzimek [36] has shown an even more vivid example of branched polymer SEC column interactions by means of side-by-side measurements of a highly branched polymer shown in Fig. 19. The extraordinary SEC elution (small circles) shows dramatically the effects of column interaction in contrast to the A4F elution (black dots) providing a simple and more traditional linear variation of size with mass. (An example of this anomaly appeared in the original referenced article [6] at which time its origin was not understood!) Although the cost of an A4F system is considerably greater than that of a corresponding SEC column, sample preparation times are comparable and channel flushing prior to use with a new sample are much faster than flushing an SEC column. Of course, channels never have shedding problems! The costs and complexity associated with A4F measurements certainly should fall significantly in the years ahead. Also of note is the fact that A4F techniques and apparatus are not able to operate in the UHPLC regime shown, for example, in Fig. 17.
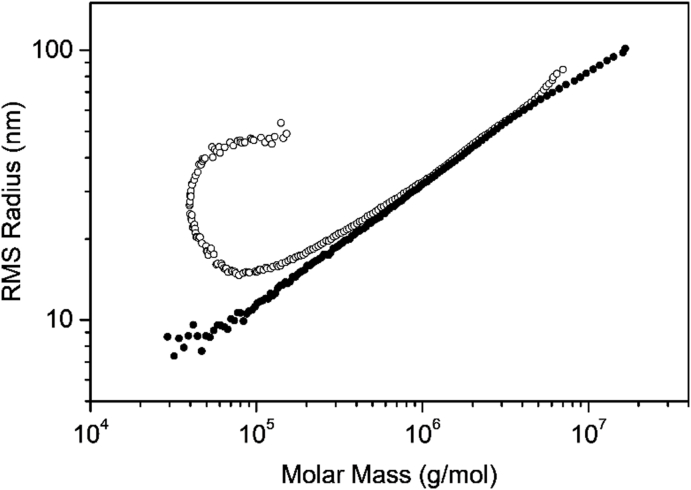
Fig. 19.
Comparison of an SEC and A4F (dark points) separated randomly branched polystyrene.
8. The structure of molecules/particles
During the discussions of SEC and A4F means for sample fractionation, and the associated measurements of molar masses derived from the subsequent dLS measurements, some mention had been made of the particle/molecular sizes derivable from such measurements. The earlier discussion of a Zimm plot following Eq. (9) and shown in the derivation of a size from measurement of the slope of at very small angles. Following Eq. (10), a rather lengthy mathematical discussion concerning size measurements of molecules and particles was presented. That was followed with an appeal that the reader to take some time out, from learning about the achievements of the dLS measurements, to study how such measurements are used to derive size information. In summary, that section showed that measurement of the very small-angle variation (slope) of the scattered light intensity (from an ensemble of molecules/particles) as a function of scattering angle could provide a measure of particle/molecule size! As we have seen, measurement of this slope at very small angles produces, the mean square radius, as discussed following Eq. (9).
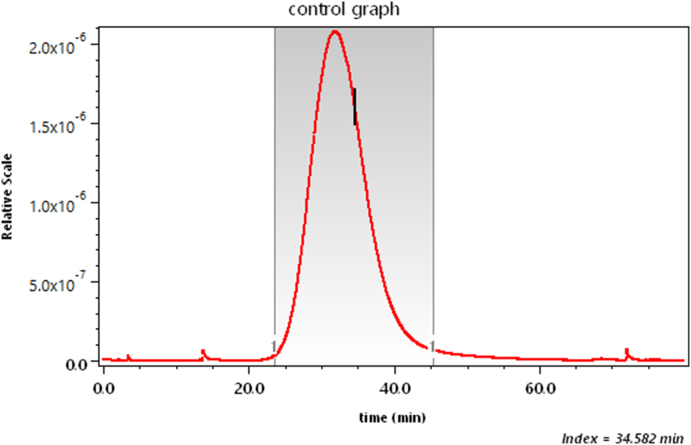
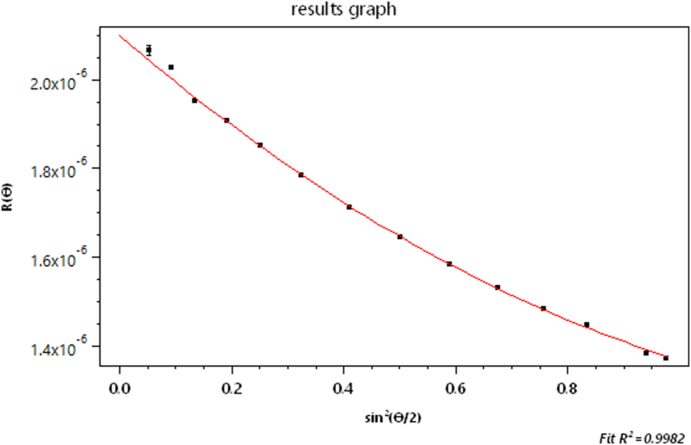
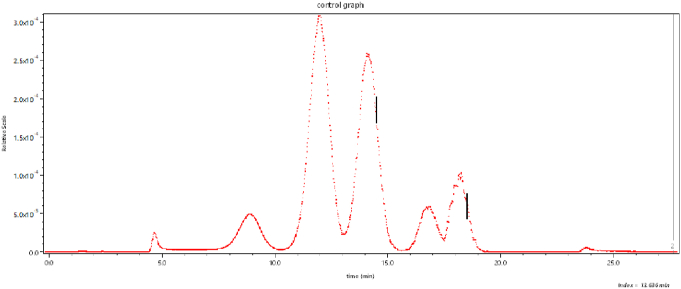
We have said very little about measurement of the size of the scattering particles/molecules. Recall that Zimm plots that generally produced a measure of molecular size through measurements of the function R(θ). Consider now an example of such measurements of a polysaccharide (cellulose) sample comprised of fibers/rods of length in the range of 100 to 150 nm. The refractive index of cellulose is about 1.47 at the laser wavelength of 658 nm, so such particles in a water-based solvent satisfy the Rayleigh-Gans approximation requirements of Eq. (3). Fig. 20 shows a SEC elution profile of the sample as a function of elution time. The vertical line shown at about 34.6 min (slice # 1044) corresponds to the dLS data at that slice shown in Fig. 21. From the initial variation (slope) of this curve with respect to , we can calculate the corresponding root mean square radius, rg, following Eq. (17). Its value is 48.6 ± 0.5 nm.
Fig. 20.
The elution of a cellulose sample as a function of time.
Fig. 21.
The scattered intensity for the slice indicated in Fig. 22.
Assuming that the individual cellulose rods are of length l and radius a, their mean square radius may be shown [20] to be
| (20) |
Therefore, the root mean square radius.
For infinitely thin rods, a = 0, and For later elution times, the individual eluting slices of Fig. 20 confirm the sample has even larger rods/molecules. By 40 min, the eluting rods exceed a length of 256 nm.
The fractionation of molecules/particles whose size exceeds about 50 nm often cannot be achieved effectively by size exclusion chromatography. Indeed, we have already noted in the discussion associated with Fig. 11 that even branched molecules of relatively smaller sizes can become “entangled” in the SEC column packings. Thus field flow fractionation processes become the most reliable means for the fractionation of larger molecular and particulate samples.
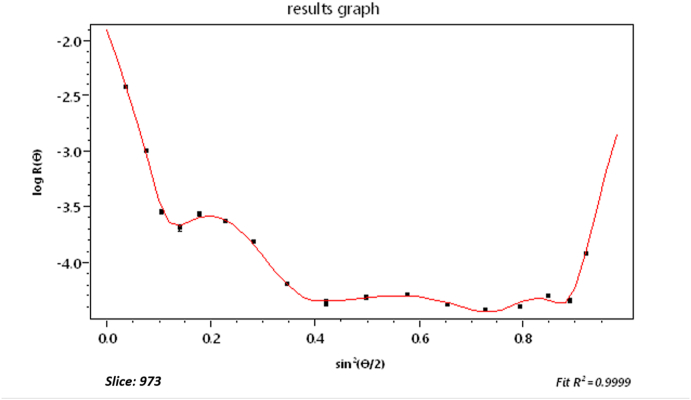
Many classes of particles are spherical whose unique scattering properties were explained in 1890 by the Danish scientist Ludvig Lorenz [45] and later, independently in 1908, by G. Mie [46]. For homogeneous spheres, for example, given their size and refractive index, the angular variation of their scattering may be calculated/predicted. Conversely, given their angular scattering patterns and their refractive index, their size may be determined rapidly. These scattering patterns depend, of course, on the polarization of the incident light and the detected scattered light. As stated earlier in this article, traditionally all measurements are made in a plane perpendicular to the polarization of the incident plane-polarized light source. Furthermore, A4F separation (fractionation) may be applied to molecules and particles that are too large for separation by SEC columns. The method is particularly useful for particles as demonstrated quite vividly by Dr. Wei Gao of the Dow Chemical Company. She considered a mixture of monodisperse polystyrene latex spheres of radii of approximately 50, 100, 150, 250, and 500 nm. Fig. 22 shows the 90° scattered intensity as a function of elution time for the fractionated sample. All 5 sizes are shown as being fractionated, i.e. separated according to size.
Fig. 22.
Scattered intensity of the eluting sample at 90° as a function of elution time.
Notice, of course, that unlike SEC separations the smallest particles elute first. A specific slice (870) from peak 3 (150 nm radii) and specific slice 1117 from peak 5 (500 nm radii) are marked by vertical lines. The best fits to the collected data for those two slices to the Lorenz-Mie theory are shown in Fig. 23 and yield radii of 145.3 ± 0.5 nm for slice 870 (peak 3) and 501.3 ± 5.5 nm for slice 1117 (peak 5). As the Lorenz-Mie theory is quite complex, its use to derive a best size from the data collected from a suspension of homogeneous spherical particles requires the determination of the value of radius that provides the best fit to the theory at each slice. Associated with each data point (scattering angle) is an associated measurement error that plays its own role in the analytical processes that follow. Although such Lorenz-Mie-fitting software packages are readily available and generally provided by the instrumentation manufacturers, not surprisingly, the question often comes up “Isn’t there a simpler theory whose results are reasonably accurate?” An obvious candidate, of course, would be the Rayleigh-Gans approximation for a sphere, viz. Eq. (19).
Fig. 23.
Characteristic scattering curves from the slices in the 90° peaks shown in Fig. 22.
The refractive index of the spheres at the wavelength of the incident 658 nm laser source is 1.59. Note that the requirements of Eq. (3) are not satisfied, i. e. the particles do not have a refractive index ratio such that , which is certainly not ≪1. Nevertheless, let us see how well the approximation really is when the refractive index of the particles (in this case, nanoparticles) is quite large. Fitting the data of slice 870 and slice 1117 to the sphere model produces the fits shown in Fig. 23 with corresponding radii of 155 ± 0.4 nm and 537 ± 19 nm, respectively. The values of 145 ± 0.5 nm and 501 ± 5.5 nm generated from the Lorenz-Mie theory are well within the particle size range of the latex particles as provided by their manufacturer. Thus, for these examples, we may confirm that the significant simplifications of the Rayleigh-Gans approximation can provide reasonably accurate results for particles well beyond the strictures of Eq. (3).
Not surprising, therefore, application of Eq. (17) can yield good approximations for a variety of important nanoparticles of a variety of structures [47] even though their refractive index is at variance with the strictures of Eq. (3).
9. Bacteria
Historically, an early application of light scattering measurements was in the field of microbiology [48] and, eventually, clinical microbiology and the need to monitor the susceptibility of various bacterial strains/isolates to various antibiotics. All of those studies were made using batch measurements (Fig. 1a). There were no attempts to monitor the size and morphological changes, such as might be produced by the presence of antibiotics. No measurements were made on flowing samples. The new types of dLS instrumentation and their measurement capabilities, however, are expected to provide many new opportunities, especially in the field of early treatment of bacterial infections. Whereas the historic batch measurements [49] presented the ability to observe the morphological changes in time following incubations with antimicrobials, the new dLS techniques discussed throughout this paper are expected to provide data even more rapidly and more easily interpreted permitting, thereby, improved diagnostic results both with respect to speed and precision.
Fig. 24 shows a fit to a slice from a dLS measurement of an E. coli bacterial suspension. The slope at θ = 0, is equal to the sample’s mean square radius per Eq.(18). Its square root yields a root mean square radius of 366.1 ± 9.5 nm. The shape of E. coli bacteria is well characterized as an ellipsoid of revolution with semi-axes a and b. The mean square radius of an ellipsoid is given by Ref. [50]:
| (21) |
Fig. 24.
Polynomial fit to scattering by the bacteria E. coli in suspension.
Therefore,
| (22) |
Setting a = 250 nm, corresponding to a characteristic diameter of 500 nm, we solve Eq. (20) for b and derive a value of about 738 nm, for a cell length (2b) of about 1.5 μm This values is slightly smaller than the range of sizes expected for a young culture.
In any event, the applications of dLS in microbiology are expected to be significant in the years ahead. This will be of particular importance for the early detection of in vitro antimicrobial effects and, therefore, play a major role in the rapid selection of appropriate antimicrobial agents for early treatment of infections.
10. Concluding remarks
The author hopes that this review of Differential light scattering and exposure to some of its new applications will provide a sufficient introduction of the subject to permit an early understanding of its use for the characterization of molecules and nanoparticles in solution. In addition, of course, is the hope that it has stimulated an interest in the subject, and conveyed enough of its details and new applications, to encourage the reader to try to make some light scattering measurements in their own labs.
The subject of quasi-elastic light scattering (often referred to as dynamic light scattering, or simply DLS) was not addressed as its applications are quite different in the context of this review. There is a broad range of DLS applications including the determination of particle size and motion distributions directly, without the fractionation processes that have been discussed in this paper. Although the precision of DLS may be inferior to dLS measurements of similar samples, its speed and simplicity are particularly important for a variety of applications.
In closing, mention should be made of other common terms and abbreviations that are found often in the literature. Certainly, the most frequently seen is the phrase multi-angle light scattering, or simply MALS. It became a popular term to differentiate instruments from the original Beckman single low angle laser light scattering (LALLS) measurements discussed earlier in Section 8. As the MALS abbreviation itself conveys no details of how the scattering data collected by such multi detectors produce the classical dLS function, the dLS term alone is sufficient. Historically, of course, (3,4,5) dLS was always referred to with the capital letters DLS, but with tremendous increase of quasi-elastic light scattering measurements (or more properly PCS, photon correlation spectroscopy) the phrase dynamic light scattering, or just plain DLS became the dominant use of the capital letter sequence.
Declaration of competing interest
The author declares that he has known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
It is certainly unusual that an acknowledgement section begin with a dedication. However, were it not for Dr. David T. Phillips, many of the remarkable instrumentation innovations responsible for the expanding use of light scattering measurements might never have been developed so rapidly. An early member of our founding group, his brilliance and innovations persist to this day. He died too soon.
Many thanks especially to my colleagues at Wyatt Technology Corporation including, especially, Dr. Steve Trainoff, Dr. Michelle Chen, Dr. Sigrid Kuebler, Dr. Dan Some, and Dr. Christoph Johann.Many thanks, as well, to Dr. Camille Lawrence for her many comments and suggestions. The additional contributions of former colleagues Dr. Stepan Podzimek and Dr. Vincent Hsieh were invaluable. The very early work of Dr. David Shortt formed the foundation for much of the analytical software in current use. Professor Bruno Zimm and Professor Edward Adelberg, both long-time members of our Scientific Advisory Board, Professor Walter Stockmayer, Dr. Patricia Cotts, Dr. Wallace Yau, Dr. Gary Janik, and, of course, my hardworking assistant and an undergraduate chemistry major, Jaime Hernandez.
Biography

Dr. Philip J. Wyatt received his undergraduate education at the University of Chicago and Christ's College, Cambridge University. He completed his graduate education in nuclear physics at the University of Illinois/Champaign-Urbana (M.S.) and the Florida State University (Ph. D.). His research interests have included electromagnetic scattering theory, laser light scattering, clinical microbiology, macromolecular characterization, aerosol science, and a variety of bioassay techniques for the detection of toxicants in the environment.
He is the Founder and Board Chairman of Wyatt Technology Corporation, a leading developer and manufacturer of scientific instruments for the characterization of molecules and particles. He initiated the development of the first commercial light scattering instrumentation incorporating a laser source. They are used in over 50 countries by most of the world’s major chemical and pharmaceutical companies, universities, and government agencies. At the date of this article’s publication, there are over 16,500 scientific journal articles and books that cite the use of the Company’s instruments
He is a Fellow of the American Physical Society, the Optical Society of America, and the American Association for the Advancement of Science. In his earlier years, he was selected by the National Academy of Science as one of the 15 finalists of the Nation’s first Scientist Astronaut program, but remained behind on Earth.
References
- 1.Wyatt P.J. Florida State University; 1959. A Complex Non-local Diffuse Boundary Independent Particle Model of Nucleon-Nuclear Scattering and Bound State Phenomena. (Ph.D. dissertation) [Google Scholar]
- 2.Wyatt P.J., Wills J.G., Green A.E.S. Nonlocal optical model for nucleon-nuclear interactions. Phys. Rev. August 1960;119:1031. [Google Scholar]
- 3.Carbonari M. In: Apoptosis—A Laboratory Manual of Experimental Methods. Boraschi D., Bossù P., Cossarizza A., editors. GCI Publications: L'Aquila; Italy: 1998. Differential light scattering and CD45 membrane fluorescence. [Google Scholar]
- 4.Mao D., Wallace B.A. Differential light scattering and absorption flattening optical effects are minimal in the circular dichroism spectra of small unilamellar vesicles. Biochemistry. 1984;23(12):2667–2673. doi: 10.1021/bi00307a020. [DOI] [PubMed] [Google Scholar]
- 5.Vacca G., Morgan R.D., Laughlin R.B. Differential light scattering: probing the sonoluminescence collapse. Phys. Rev. 1999;E60:R6303. doi: 10.1103/physreve.60.r6303. [DOI] [PubMed] [Google Scholar]
- 6.Wyatt P.J. Light scattering and the absolute characterization of macromolecules. Anal. Chim. Acta. 1993;272:1–40. [Google Scholar]
- 7.Wyatt P.J. Measurement of special nanoparticle structures by light scattering. Anal. Chem. 2014;86:7171–7183. doi: 10.1021/ac500185w. [DOI] [PubMed] [Google Scholar]
- 8.Selvaraj N., Wang C., Bowser B., Broadt T.L., Shaban S., Burns J. Detailed protocol for the novel and scalable viral vector upstream process for AAV gene therapy manufacturing. Hum. Gene Ther. 2021 doi: 10.1089/hum.2020.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Einstein A., Infeld L. Cambridge University Press; 1938. The Evolution of Physics. [Google Scholar]
- 10.Rayleigh J W Strutt ( Wave theory of light. Encyclopedia Britannica. 1888;24 [Google Scholar]
- 11.Debye P. Light scattering in solutions. J. Appl. Phys. 1944;15:338–342. [Google Scholar]
- 12.Putzeys P., Brosteaux J. The scattering of light in protein solutions. Trans. Faraday Soc. 1935;31:1314–1325. [Google Scholar]
- 13.Oster G. The scattering of light and its applications to chemistry. Chem. Rev. 1948;43:319–365. doi: 10.1021/cr60135a005. [DOI] [PubMed] [Google Scholar]
- 14.Zimm B.H. Molecular theory of the scattering of light in fluids. J. Chem. Phys. 1945;13:141–145. [Google Scholar]
- 15.Zimm B.H. The scattering of light and the radial distribution function of high polymer solutions. J. Chem. Phys. 1948;16:1093–1099. [Google Scholar]
- 16.Zimm B.H. Apparatus and methods for measurement and interpretation of the angular variation of light scattering; preliminary results on polystyrene solutions. J. Chem. Phys. 1948;16:1099–1116. [Google Scholar]
- 17.Kratochvil P. Elsevier; Amsterdam: 1987. Classical Light Scattering from Polymer Solutions. [Google Scholar]
- 18.van de Hulst H.C. Dover Publications; New York: 1981. Light Scattering by Small Particles. [Google Scholar]
- 19.Phillips D.T. Evolution of a light scattering photometer. Bioscience. 1971;21:865–867. [Google Scholar]
- 20.Wyatt P.J. Measurement of special nanoparticle structures by light scattering. Anal. Chem. 2014;86:7171–7183. doi: 10.1021/ac500185w. [DOI] [PubMed] [Google Scholar]
- 21.Lathe G.H., Ruthven C.R.J. The separation of substances and estimation of their relative molecular sizes by the use of columns of starch in water. Biochem. J. 1956;60:665–674. doi: 10.1042/bj0620665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.University of Pennsylvania The John Scott Award. www.garfield.library.upenn.edu/johnscottaward.html
- 23.Moore J.C. Gel permeation chromatography. I. A new method for molecular weight distribution of high polymers. J. Polym. Sci. 1964;2A:835–843. [Google Scholar]
- 24.J C Moore, Separation of Large Polymer Molecules in Solution, US Patent # 3,326,875 (1967).
- 25.Swartz M.E. UPLC™: an introduction and review. J. Liq. Chromatogr. Relat. Technol. 2005;28:1253–1263. [Google Scholar]
- 26.Wyatt P.J. In: Encyclopedia of Biophysics. Roberts G.C.K., editor. Springer; Berlin, Heidelberg: 2013. Multiangle light scattering from separated samples (MALS with SEC or FFF) [Google Scholar]
- 27.Amartely H., Avraham O., Friedler O., et al., Coupling multi angle light scattering to ion exchange chromatography (IEX-MALS) for protein characterization, Sci. Rep. 8. [DOI] [PMC free article] [PubMed]
- 28.Gentiluomo L., Schneider V., Roessner D. Coupling multi-angle light scattering to reverse-phase ultra-high-pressure chromatography (RP-UPLC-MALS) for the characterization monoclonal antibodies. Sci. Rep. 2019;9 doi: 10.1038/s41598-019-51233-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Giddings J.C. A new separation concept based on a coupling of concentration and flow nonuniformities. Separ. Sci. 1966;1:123–125. [Google Scholar]
- 30.Wahlund K.-G., Weingarner H.S., Caldwell K.D., Giddings J.C. Improved flow field-flow fractionation system applied to water-soluble polymers: programming, outlet stream splitting, and flow optimization. Anal. Chem. 1986;58:573–578. doi: 10.1021/ac00294a018. [DOI] [PubMed] [Google Scholar]
- 31.Litzen A., Wahlund K.-G. Improved separation speed and efficiency for proteins, nucleic acids and viruses in asymmetrical flow field flow fractionation. J. Chromatogr. 1989;476:413–421. doi: 10.1016/s0021-9673(01)93885-3. [DOI] [PubMed] [Google Scholar]
- 32.Schimpf M., Caldwell K., Giddings J.C. Wiley & Sons, Inc; NJ: 2000. Field-Flow Fractionation Handbook. [Google Scholar]
- 33.Kaye W., Havlik A.J. Low angle laser light scattering—absolute calibration. Appl. Opt. 1973;12:541–550. doi: 10.1364/AO.12.000541. [DOI] [PubMed] [Google Scholar]
- 34.Maldarelli L.V., Phillips D.T., Proctor W.L., Wyatt P.J., Urquhart T.C. Programmable action sampler system. U. S. Patent #. 1979;4:18. 140. [Google Scholar]
- 35.Wyatt P.J. Microparticle analyzer employing a spherical detector array. Patent #. 1971;3(624):835. [Google Scholar]
- 36.Podzimek S. Wiley & Sons, Inc; NJ: 2011. Light Scattering, Size Exclusion Chromatography and Asymmetric Flow Field Flow Fractionation: Powerful Tools for the Characterization of Polymers, Proteins and Nanoparticles. [Google Scholar]
- 37.Yau W.W., Kirkland J.J., Bly D.D. Wiley; New York: 1979. Modern Size-Exclusion Liquid Chromatography. [Google Scholar]
- 38.Wyatt P.J., Papazian L. The interdetector volume in modern light scattering and high performance size-exclusion chromatography. LC GC. 1993;11:862–872. [Google Scholar]
- 39.Bressau R. In: Cazes J., editor. vol. 2. M. Dekker; N.Y.: 1980. Problems in multiple detection of GPC eluents; pp. 73–93. (Liquid Chromatography of Polymers and Related Materials). [Google Scholar]
- 40.S.P. Trainoff, Method for correcting the effect of interdetector band broadening, Patent #7,386,427 (2003).
- 41.Bouvier E.S.P., Koza S.M. Advances in size-exclusion separations of proteins and polymers by UHPLC. Trends Anal. Chem. 2014;63:85–94. [Google Scholar]
- 42.Hsieh V.H., Wyatt P.J. Measuring proteins with greater speed and resolution while reducing sample size. Sci. Rep. 2017;7:10030. doi: 10.1038/s41598-017-09051-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yohannes G., Jussila M., Hartonen K., Riekkola M.-L. Asymmetrical flow field-flow fractionation technique for separation and characterization of biopolymers and bioparticles. J. Chromatogr. A. 2011;1218:4104–4116. doi: 10.1016/j.chroma.2010.12.110. [DOI] [PubMed] [Google Scholar]
- 44.Cao S., Pollastrini J., Jiang Y. Separation and characterization of protein aggregates and particles by field flow fractionation. Curr. Pharmaceut. Biotechnol. 2009;10:382–390. doi: 10.2174/138920109788488978. [DOI] [PubMed] [Google Scholar]
- 45.Lorenz L. Vidensk Selsk Skr T. 1890;6:405–529. [Google Scholar]
- 46.Mie G. Beiträge zur Optik Trüber Medien, speziell Kolloidaler Metallösungen. Ann. Phys. 1908;25:377–452. [Google Scholar]
- 47.Wyatt P.J. Measuring nanoparticles in the size range to 2000nm. J Nanopart Res. 2018;20:322–340. doi: 10.1007/s11051-018-4397-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wyatt P.J. Cell wall thickness, size distribution, refractive index ratio, and dry weight content of living bacteria (Staphylococcus aureus) Nature. 1970;226:277–279. doi: 10.1038/226277a0. [DOI] [PubMed] [Google Scholar]
- 49.Stull V.R. Clinical laboratory use of differential light scattering. I. Antibiotic susceptibility testing. Clin. Chem. 1 August 1973;19(Issue 8):883–890. [PubMed] [Google Scholar]
- 50.Holtzer A.M., Benoit H., Doty P. The molecular configuration and hydrodynamic behavior of cellulose trinitrate. J. Phys. Chem. 1954;58:624–634. [Google Scholar]