Mechanical competition alters the cellular interpretation of an endogenous genetic program

This paper shows that adjacent cells with similar genetic capabilities to change their own shape enter a tug of war that determines which cell shrinks and which expands. For a cell to contract, its neighbors must yield, requiring a nonlinear stress–strain response in the mechanism governing its physical properties.

Abstract

The intrinsic genetic program of a cell is not sufficient to explain all of the cell’s activities. External mechanical stimuli are increasingly recognized as determinants of cell behavior. In the epithelial folding event that constitutes the beginning of gastrulation in Drosophila, the genetic program of the future mesoderm leads to the establishment of a contractile actomyosin network that triggers apical constriction of cells and thereby tissue folding. However, some cells do not constrict but instead stretch, even though they share the same genetic program as their constricting neighbors. We show here that tissue-wide interactions force these cells to expand even when an otherwise sufficient amount of apical, active actomyosin is present. Models based on contractile forces and linear stress–strain responses do not reproduce experimental observations, but simulations in which cells behave as ductile materials with nonlinear mechanical properties do. Our models show that this behavior is a general emergent property of actomyosin networks in a supracellular context, in accordance with our experimental observations of actin reorganization within stretching cells.

Introduction

Epithelial tissues are shaped during animal development by changes in the geometry, number, or relative positions of their constituent cells. Cells change their shape by actively generating intracellular forces or by passively responding to external forces; from within the organism, such as neighboring cells; or by forces from outside the body (Halbleib and Nelson, 2006; Leerberg et al., 2014; Bailles et al., 2019; Münster et al., 2019). The actomyosin meshwork underlying the plasma membrane is the major source of morphogenetic forces (Lecuit and Lenne, 2007; Röper, 2013; Salbreux et al., 2012), which can be transmitted over larger, supracellular distances via cell junctions. The functioning of the cytoskeleton itself can be influenced by external mechanical forces (Latorre et al., 2018). In some systems, we are beginning to understand how forces act on a tissue scale (Shyer et al., 2013), but we know much less about the interplay of active forces and passive deformation and their genetic and molecular bases. Understanding the actomyosin contraction patterns in the individual cells that make up a tissue is unlikely to be sufficient to explain all the force changes and deformations within the entire tissue. For example, for a delaminating neuroblast to constrict its apical surface efficiently, the surrounding epithelial cells need to be able to relax their surfaces (Simões et al., 2017).

One example of epithelial morphogenesis is the formation of the ventral furrow during Drosophila gastrulation, an epithelial folding event that internalizes the future mesoderm, driven by active forces generated in an autonomous manner in the central part of the mesoderm (Leptin and Roth, 1994). Many studies have focused on these cells and their contractile actomyosin meshwork. We understand the major mechanisms that act within each cell: The proteins that are specifically activated in these cells change the location of the adherens junctions and recruit an active actomyosin meshwork to the apical cell cortex, which undergoes a series of pulsatile contractions until the apical surface is fully constricted (Dawes-Hoang et al., 2005; Martin et al., 2009, 2010).

To allow the furrow to internalize the mesoderm without causing disruptions elsewhere in the embryo, other parts of the embryonic epithelium obviously must respond or contribute to the movement. The cells outside the mesoderm appear not to contribute actively to furrow formation (Leptin and Roth, 1994), but their compliance is later required for the furrow to invaginate fully (Rauzi et al., 2015). The most important cells that enable the furrow to form are the mesodermal cells adjacent to the initial indentation. While central cells constrict, lateral cells expand their apical surfaces (Turner and Mahowald, 1977; Leptin and Grunewald, 1990; Sweeton et al., 1991; Oda and Tsukita, 2001; Rauzi et al., 2015).

In spite of their distinct behaviors, the constricting and expanding cells of the mesoderm share the same developmental program. They express the same genes, albeit with quantitative differences, but no known genes are absolutely restricted to one or another population (Karaiskos et al., 2017). There is a graded expression of important gene products from the center to the edges of the mesoderm (Fig. 1, A and B), in particular for the genes necessary for myosin activation (fog, t48, and mist) and junction remodeling (traf4), which are deployed under the control of the dorsal–ventral patterning system (Parks and Wieschaus, 1991; Costa et al., 1994; Kölsch et al., 2007; Mathew et al., 2011; Lim et al., 2017). While their quantitative differences have prompted the question whether the two populations should be considered distinct “subdomains,” each relevant gene has a different expression boundary, so they together cannot be seen as defining a genetic domain (Lim et al., 2017).

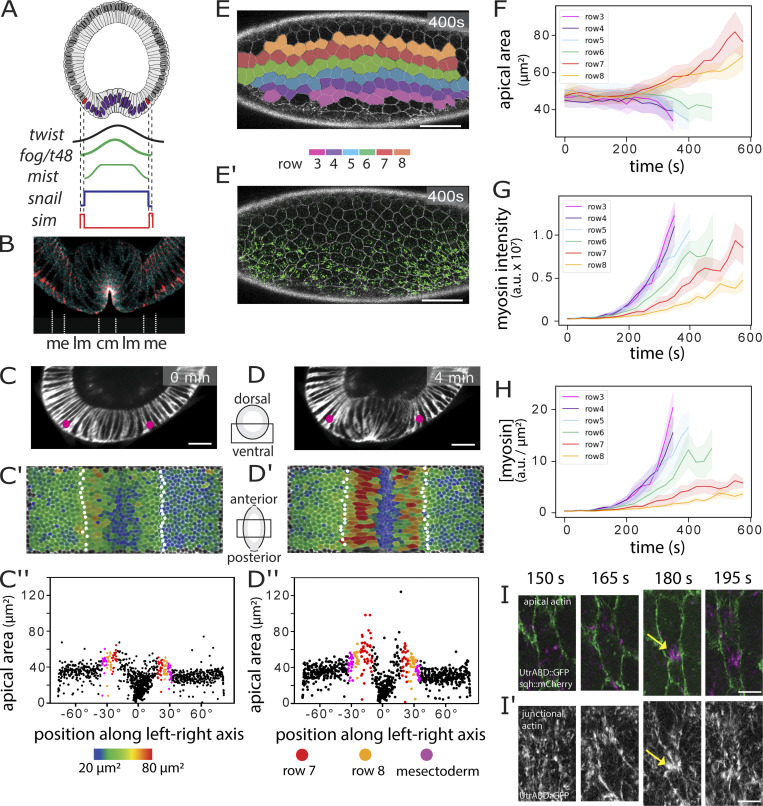
Figure 1.

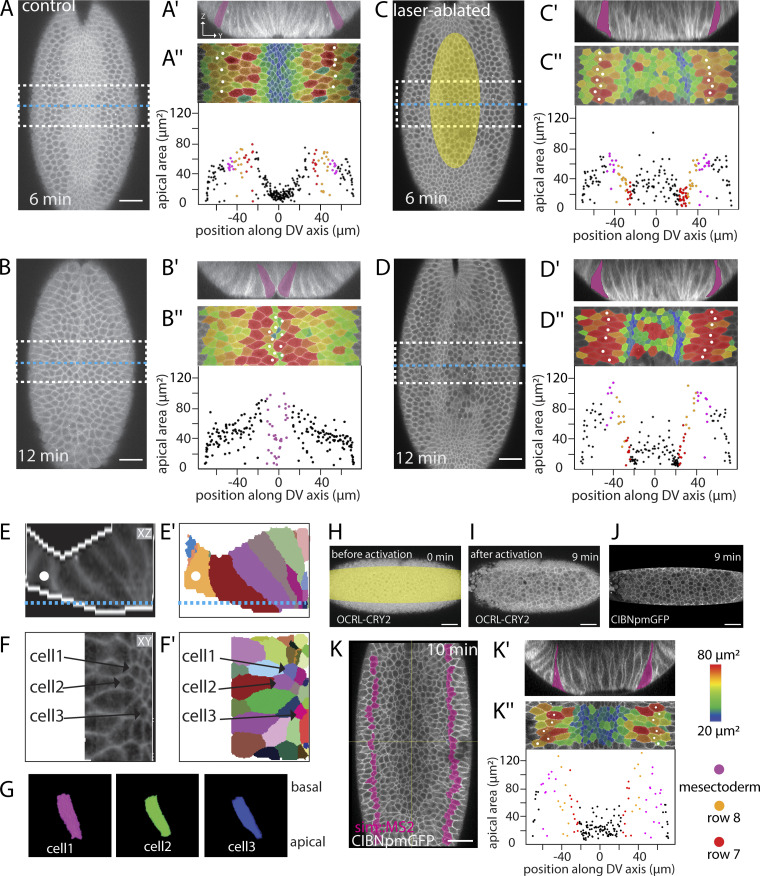
Cell activities during ventral furrow formation. (A) Genes expressed ventrally at the onset of gastrulation. Top: Diagram of a cross-section through an embryo at the beginning of gastrulation. Mesodermal nuclei expressing Snail (blue) and mesectodermal nuclei with single-minded (red) are shown. Bottom: Schematic of gene expression levels. Twist (black) and Snail (blue) regulate the genes that control shape changes (fog, T48, mist). (B) Section of an embryo stained for β-catenin/armadillo to visualize adherens junctions (pink) and myosin (blue). Junctions in the central (cm) and lateral (lm) mesoderm are apical, the mesectodermal (me) cell has one apical and one subapical junction, and ectodermal junctions are subapical (Kölsch et al., 2007). (C and D) Cross-sectional views at two time points from a MuVi SPIM recording of an embryo expressing GAP43::mCardinal (membrane). Pink dots: mesectoderm; scale bar: 25 µm. A time series is shown in in Fig. S1. (C′ and D′) Apical surface “peels” with color-coded apical cell areas. Mesectoderm: white dots. (C″ and D″) Apical area from C′ and D′ plotted against cell position (0° is the ventral midline). Each dot represents one cell. Color code for rows 7 and 8 is as in E; mesectoderm is shown in magenta (n = 836 cells). (E and E′) Ventrolateral views of a confocal recording of an embryo expressing Spider::GFP (white) and sqh::mCherry (green) at a confocal Z-plane 3 µm below the surface (Video 2). Scale bar: 5 µm. Cells were segmented using Spider::GFP and assigned to color-coded rows. (F–H) Apical areas, total myosin amount (i.e., total sqh:mCherry pixel intensity), and myosin concentration (amount over apical area) plotted per row against time (mean and SD). Tracks for ventral rows stop early because the cells are lost from the imaging plane (n = 16–21 cells per row). (I and I′) Example of a lateral mesodermal cell at four time points in an embryo expressing utrABD::GFP (subapical for cell outlines in I, green; apical in I′; white) and sqh::mCherry (magenta) during formation of a myosin focus. Yellow arrows: local cortical deformation. Scale bar: 5 µm.

Current models for cell shape determination in the ventral furrow (Conte et al., 2008, 2009; Hočevar Brezavšček et al., 2012; Spahn and Reuter, 2013; Polyakov et al., 2014) assume that changes in apical surface area correlate with the force generated by contractile actomyosin. In the first phase of invagination, the degree of apical constriction mirrors the graded distribution of apical myosin, with absence of myosin having been correlated with lack of constriction of lateral cells (Rauzi et al., 2015; Heer et al., 2017; Perez-Mockus et al., 2017).

It is not clear by what mechanism the quantitative differences in gene expression can cause dramatic qualitative differences in cell behavior: any two immediately adjacent cells in the mesoderm primordium have similar gene expression profiles. Thus, in the absence of any known genetic correlations for the pronounced differences, there must be other explanations for how these behaviors arise. Specifically, we need explanations for how the smooth and graded differences in expression levels of effector molecules are converted into a step difference in cell behavior.

We compare here, in a quantitative manner, the cellular activities in the mesoderm, contrast them with existing models, and propose and test a new model that explains qualitative differences in cell behavior. Our results suggest that two distinct cell behaviors emerge not from strict differences in genetic control, but from tissue-wide mechanical interactions.

Results

Cell shape evolution across mesoderm and neighboring populations

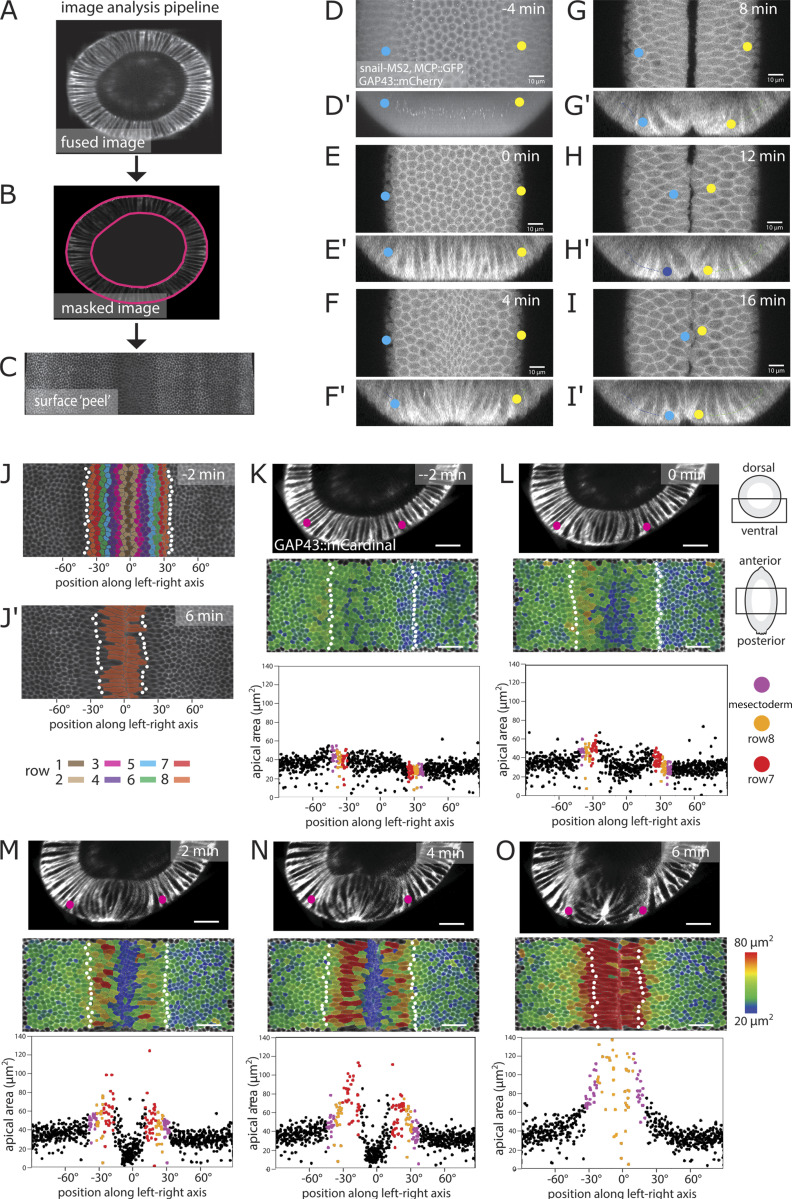
Analyses of shape changes in the prospective mesoderm (hereafter simply called “mesoderm”) often focus on the 10-cell-wide central band of cells that form the initial furrow. The lateral cells are less well studied, partly because the forces for folding are generated in central cells but also because their rapid displacement and extreme shape changes make them difficult to image (Fuse et al., 2013; see also Video 1, a full 3D segmentation and reconstruction of the ventral half of an embryo during the process of furrow formation). We extracted faithful 2D views of the apical surface of the entire mesoderm (surface “peels” [Bhide et al., 2020]; Fig. S1, A–C) for quantitative analysis. The breadth of the mesoderm varies along the anterior–posterior (AP) axis and between embryos; we therefore define the cell rows operationally from row 1 at the midline to row 8 as the outer row adjacent to the mesectoderm (Fig. S1, J and J′).

Video 1.

Part I: Cross-sectional (top) and ventral (bottom) views of 3D segmented ventral half of an embryo expressing GAP43::mCherry and imaged with SPIM. Each color marks a unique cell that is tracked in time. Part II: 3D volume rendering shown over time for three cells: one central and two (left and right) lateral mesodermal cells. The video illustrates the volume transited by the cells during ventral furrow formation. The tip of the left cell moved out of the imaging volume during the period. Apical side is up. Frame rate: 20 frames per second.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202104107.v1/source

Figure S1.

Image analysis and identification of the edge of the mesoderm. (A) Embryos were imaged using MuVi SPIM. The resulting datasets were fused into a single 3D stack for each time point. Ventral side is at top left. (B and C) Apical (outside) and basal surface masks were defined semiautomatically. These masks were then used to extract the apical surface of the embryo (Bhide et al., 2020). (D and D′) Maximum-intensity projections along the apical–basal (D) and AP (D′) directions of an embryo coexpressing GAP43::mCherry, Snail-MS2, and MCP::mCherry 4 min before the initiation of ventral furrow formation. The white spots represent sites of snail::MS2 RNA in the nuclei of mesodermal cells. Yellow and blue dots mark the positions of the adjacent mesectodermal cell rows. (E–I) Confocal Z-plane 2 µm from the surface and Z-sections (E′–I′) over the course of furrow invagination. The mesectodermal cell rows meet at the midline. Backtracing from this time point can be used to determine the edge of the mesoderm in unmarked embryos. Scale bars in A–J: 10 µm. (J and J′) Surface peels extracted from MuVi SPIM images at −2 and 6 min from initiation of ventral furrow formation. White dots indicate the mesectodermal cells as determined by backtracing. Cell rows are color coded with numbering coordinated operationally around row 6, which is the last nonstretching row and easily identifiable in all videos, regardless of imaging angle. The width of the mesoderm varies along the AP axis, with a width <18 cells in some areas. (K–O) Each panel is from one time point from a MuVi SPIM recording of an embryo expressing GAP43::mCardinal, with three of the three images showing first, cross-sectional views; second, apical surface “peels” extracted from the ventral half of the central one-third of the embryo; and third, the apical areas plotted against cell position along the left–right axis. (The center, 0°, is the ventral midline of the embryo.) Each dot represents one cell. Apical cell areas measured from segmented images were color coded and overlaid on the original image. Mesectodermal cells are marked as white dots in the surface peels and as magenta dots in the plots. For the description in this figure, we define t = 0 min as the time when cells in the central four rows have constricted by at least 20%, on average. Scale bar: 25 µm.

Furrow formation starts with cells in rows 1–6 constricting in a stepwise and stochastic manner (Martin et al., 2009; Kam et al., 1991). The last cells to constrict are those in row 6, while rows 7 and 8 expand their surfaces anisotropically (Leptin and Grunewald, 1990; Sweeton et al., 1991; Parks and Wieschaus, 1991; Heer et al., 2017; Fuse et al., 2013), stretching toward the midline. Mesectodermal cells also stretch slightly, but beyond them, the ectoderm remains inert. Thus, mesodermal cells can either constrict or stretch, with initially indistinguishable neighbors in rows 6 and 7 taking on dramatically different developmental paths. In addition, rows 7 and 8 do not respond equally to the force from the center. Row 7 expands first and most strongly, followed by row 8 and finally the mesectoderm (Fig. 1, C–C′′ and D–D′′; and Fig. S2, A–C, A′–C′).

Figure S2.

Further examples of embryos and quantifications. Further examples of embryos expressing GAP43::mCardinal (A–C and A′–C′) imaged by MuVi SPIM and embryos expressing Spider::GFP (white) and sqh::mCherry (green; D–H) imaged by confocal microscopy. MuVi SPIM analysis with (A and A′) cross-section, (B and B′) ventral peel with cell sizes and mesectoderm marked, and (C and C′) quantification of cell sizes. All details are as in Fig. 1, C and D. Scale bar: 25 µm. (D–L) Confocal (D) images and per-row (E) analysis and quantification of cell sizes (F), myosin concentration (G), and comparison of cell-intrinsic versus neighborhood myosin levels (H). (I–L) All details are as in Fig. 1, E–H; and Fig. 3, G–L. Scale bar = 25 µm. Number of cells analyzed per row in F, G, K, and L: 17–47.

Theoretical models and simulations based on bell-shaped contractility gradients create epithelial shape changes with highly constricted cells in the center and cell sizes increasing in a graded manner with distance from the center (Rauzi et al., 2015; Spahn and Reuter, 2013; Polyakov et al., 2014; Heer et al., 2017; Doubrovinski et al., 2017). Inverted patterns of stretching have so far been obtained in computational models only for stepwise gradients, where peripheral cells have no contractility (Spahn and Reuter, 2013; Odell et al., 1981; Pouille and Farge, 2008). To investigate this inconsistency, we examined actomyosin in lateral cells.

Actomyosin gradient as a predictor for cell shape behavior

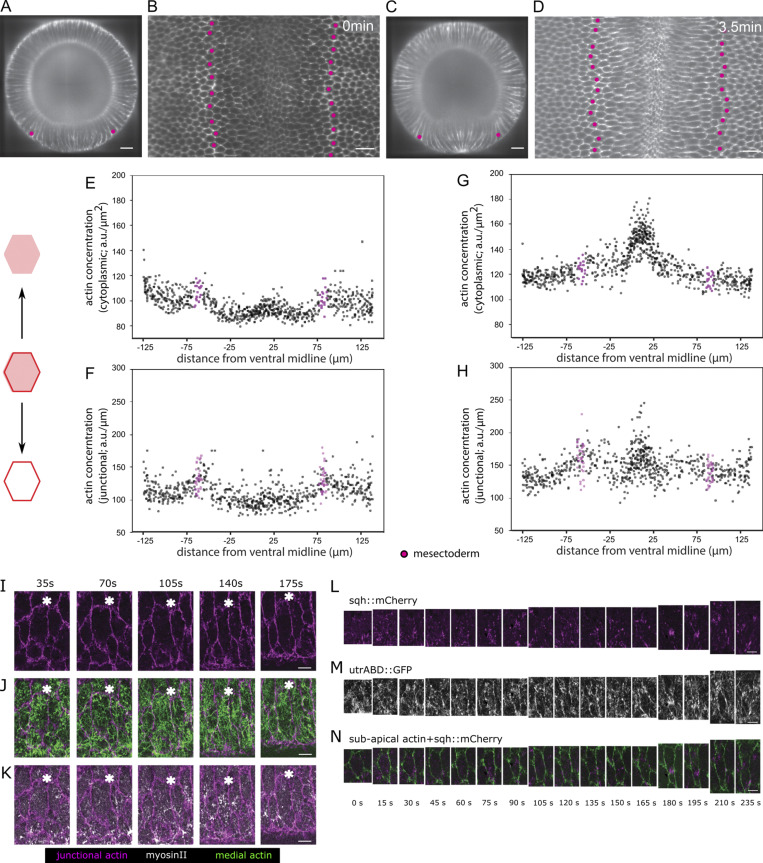
F-actin is present in two distinct but interacting pools with different morphological functions in the early embryonic epithelium: a fine meshwork underlying the apical cortex and a large pool associated with apical junctions and basolateral cell membranes (Martin et al., 2009; Heer et al., 2017; Morize et al., 1998; Fox and Peifer, 2007; Sawyer et al., 2009; Mason et al., 2013; Jodoin et al., 2015). Junctional actin is reduced in the mesoderm in unison with the relocation of adherens junctions before shape changes begin (Mason et al., 2013, 2016; Denk-Lobnig et al., 2021; Fig. S3, A–H). The apical meshwork changes along the entire dorsoventral (DV) axis around the time of gastrulation but remains present during furrow formation as a fibrous network in both central and lateral mesodermal cells (Rauzi et al., 2015; Fig. S3, I–K).

Figure S3.

Distribution of apical F-actin in the mesoderm. (A–H) Data from MuVi SPIM recordings of an embryo expressing UtrABD::GFP to visualize F-actin. The rows of mesectodermal cells (identified by backtracing) are marked in magenta. Scale bar: 25 µm. (A and C) Cross-sectional view at ∼50% egg length and (B and D) subapical peel extracted 2 µm below the apical surface. (E–H) From the segmented subapical peel, the F-actin mean cytoplasmic concentration (sum of all pixel intensities divided by area) and mean junctional intensity (sum of all pixel intensities divided by length of the junction) are plotted for every cell in the area shown. The mean cytoplasmic intensity and the mean junctional intensity are lower in the mesodermal cells than the ectodermal cells at the onset of furrow formation and increase slightly as furrow formation proceeds. (I–K) Apical actomyosin meshwork in an expanding lateral cell. Ventrolaterally mounted embryo (same as shown in Fig. 1, I and I′) expressing UtrABD::GFP and sqh::mCherry to visualize F-actin and myosin. (I) Junctional actin in a confocal section 3 µm from the surface. (J) Apical cortical actin meshwork (green; sum intensity Z-projection of confocal sections within 1 µm from surface) and subapical junctional actin (magenta) to visualize cell boundaries. (K) Sum intensity Z-projections of confocal sections within 1 µm from the surface for apical myosin (red) subapical junctional actin (magenta) to visualize cell boundaries. The white asterisks serve as reference points. Scale bar: 5 µm. (L–N) Pulsatile actomyosin meshwork in a lateral mesodermal cell. Example of a stretching lateral mesodermal cell in a ventrolaterally mounted embryo (same as shown in Fig. 1, I and I′) expressing UtrABD::GFP (white) and sqh::mCherry (magenta). Scale bar: 5 µm. (L and M) Sum intensity projections of myosin (L) and apical actin (M) in the first 2 µm below the surface. (N) Subapical cortical F-actin (2.5 µm below the surface; green) marks the cell boundaries. Actomyosin foci form twice (75 s and 180 s) and create a constriction in the AP direction.

We focused our further analyses on myosin, on which the contractile forces in the mesoderm depend. The amount of myosin regulatory chain (encoded by the gene sqh in Drosophila) within the apical cortex has been used as a proxy for the contractile actomyosin meshwork (Martin et al., 2009; Rauzi et al., 2010; Vasquez et al., 2014; Kerridge et al., 2016; Streichan et al., 2018). When the central cells begin to constrict, practically no apical myosin is seen in the lateral cells (Heer et al., 2017; Fig. 1, E and E′; and Video 2). Levels of total apical myosin (measured as the sum of all pixel intensities) rise over the next few minutes, reaching values seen in central cells at earlier points, when the cells constrict. For example, the level in row 7 at 525 s resembles that in rows 3 and 4 at 325 s. We also calculated the concentrations (sum of pixel intensities over apical cell area) and still found that row 7 at 525 s reaches concentrations similar to those of rows 3–5 at 275 s (Fig. 1, F–H). Thus, apical myosin levels alone are not sufficient to explain why lateral cells do not constrict.

Video 2.

Ventrolateral view of two embryos (parts I and II) expressing shq::mCherry (magenta; myosin) and Spider::GFP (green; membrane) showing the dynamics of apical area and myosin during ventral furrow formation and lateral cell expansion. t = 0 in both movies is defined as 100 s before the first appearance of myosin in central mesodermal cells. 25-s time steps are shown (Figs. 1 and 3). Frame rate: 7.5 frames per second.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202104107.v2/source

Another possibility is that in spite of having sufficient myosin, lateral cells cannot assemble a functional contractile meshwork. Epithelial apical actomyosin meshworks normally show a strong dynamic behavior characterized by fluctuations or “pulses” of myosin foci that correlate with periods of apical constriction (Martin et al., 2009; Rauzi et al., 2010; Blanchard et al., 2010; Simões et al., 2017). We see myosin foci forming, moving, and disappearing in lateral cells in a manner similar to that in central cells (Fig. 1, I and I′; Fig. S3, L–N). Myosin pulses in lateral cells are less frequent and less persistent (Denk-Lobnig et al., 2021). However, we now see that they are nevertheless able to pull on nearby plasma membranes, thereby narrowing the cell (Fig. S3, K and N), indicating an active, force-generating actomyosin meshwork. Thus, in terms of being able to generate contractile, morphogenetically active forces, lateral cells are not qualitatively different from central cells.

Viscoelastic model of the mesoderm

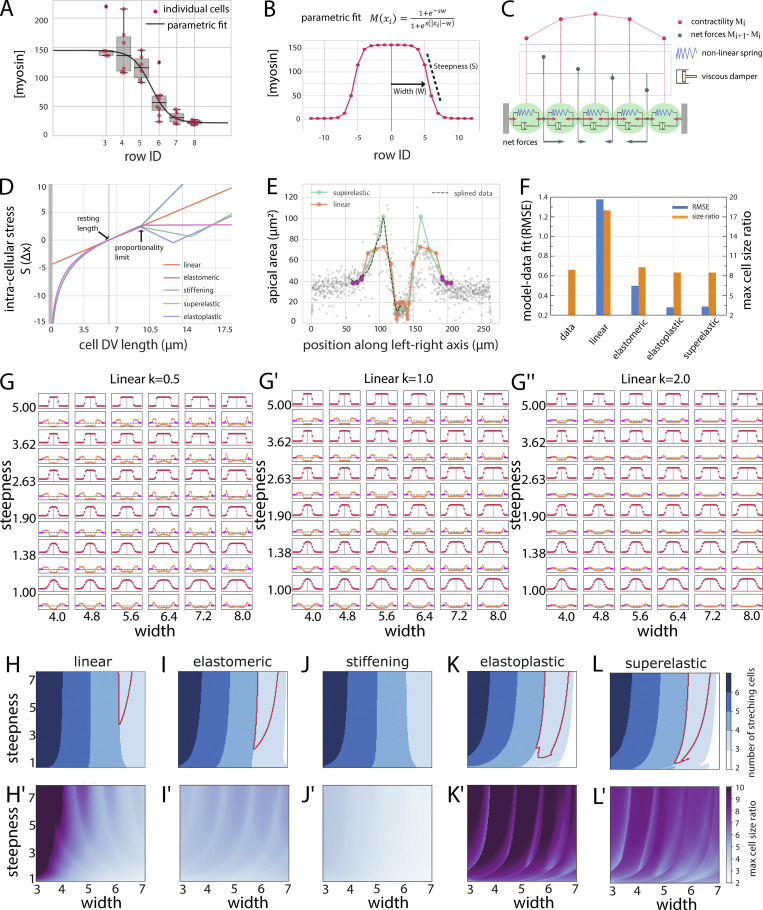
To learn what might be the basis for the cells diverging in behavior in spite of having contractile actomyosin, we explored in a computational model whether a simple contractility gradient could explain the observed in vivo behaviors, namely the bifurcation into constriction and expansion, the inverted pattern of stretching, and the apical cell size ratios. With a mathematical description of our myosin measurements per cell row (Fig. 2, A and B), we modeled the mesoderm and mesectoderm as a line of 19 viscoelastic “cells” bordered by three stiffer “ectodermal” cells on each side. The final equilibrium size of each “cell” in the model depends on the forces acting on its boundaries, which in turn depend on the difference of the myosin levels in the cells on either side of the boundary (Fig. 2 C). We tested the system with different types of stress–strain responses (Fig. 2 D). For a linear stress–strain response, the simulation showed constriction in central cells and stretching in lateral cells, but not with the pattern and size ratios observed in the embryo (Fig. 2, E and F). This might be explained by the measured myosin concentration not accurately reflecting the situation in vivo. However, a parameter scan in which we systematically varied the width and steepness of the myosin profile also did not reveal any curves that resulted in outputs corresponding to the in vivo data, nor did changes in the slope of the linear stress–strain curves (Fig. 2, G–G′′). The linear model could reproduce either the cell size ratios or the pattern of stretching cells but never both for the same set of parameters (compare Fig. 2 H and Fig. 2 H′). Allowing myosin concentrations to gradually accumulate over time did not affect the outcome, because the final state of the system in a linear model is determined by the final shape of the myosin profile.

Figure 2.

Viscoelastic model representing a line of cells. (A) Measurements of the myosin concentration per cell row (with 0 corresponding to the ventral midline and 9 the mesectodermal cell row) from the embryo shown in Fig. 1 E. t = 400 s. Solid lines correspond to the parametric fit shown in B. (B) Parametric fit (Eq. 2) of the measured myosin profile in vivo used in the viscoelastic and actomyosin simulations. (C) Cells are modeled as a series of Kelvin-Voigt viscoelastic elements with damping coefficient (η) and spring constant (k). Cell size changes depend on the contractile forces within cells (red arrows “pulling” on connection points) and movement of the connecting points, which is determined by the differential forces (gray arrows) acting on them. The model is driven by an explicit contractility value for each cell. The “steepness” is the slope between minimal and maximal values; the “width” is the approximate location of the inflection point between those two values (Eq. 2). (D) Graphs for five stress–strain relationships (linear elastic, elastomeric, superelastic, elastoplastic, and stiffening) that are imposed on the spring constants in the model. The resting length of the cell is set to L = 6.2 µm. Deviation from the resting length causes either expansion (positive stress) or constriction (negative stress). (E) Final cell lengths for linear elastic and superelastic spring constants superimposed on measured cell sizes. Magenta dots represent the stiffer ectoderm. (F) Quantitative comparison of results from models with experimental data. Blue bars indicate the RMSE between experimentally observed and simulated cell size distributions as a function of DV position for each stress–strain response. Orange bars indicate the measured and simulated cell size ratios between the most expanded and the most constricted cells. Model parameters are as in Table S3. (G–G″) Parametric scan of the myosin profile with varying steepnesses and peak widths for a linear response curve. The myosin profiles (M(x)) are shown in red, and the resulting final cell sizes are shown below in orange. The stiffer “ectodermal” cells are marked in pink. The viscoelastic elements have linear elasticity with constant k = 0.5, 1, and 2. (H–L and H′–L′) Parametric maps for myosin concentration curves with varying widths and steepnesses for the different stress–strain curves. (H–L) Number of stretching cells (denoted by blue shades). Red outline: Conditions where the three outer cells expand with an inverted pattern of stretching that qualitatively matches experimental observations. (H′–L′) Ratio of the most expanded to the most constricted cells. Magenta: Largest size differences; light blue: minimal size differences. The only conditions where three cells stretch in an inverted pattern and the size ratios between the most constricted and most stretched cells are reached are those for superelastic and elastoplastic responses. Error bars represent the 1.5× interquartile ranges.

We therefore tested whether the assumption of a linear stress–strain response in the cells was wrong, as also seems to be the case in other instances (Latorre et al., 2018; Jia et al., 2017; Fernández et al., 2006; Hoffman et al., 2006). We considered four classes of nonlinear stress–strain responses (Fig. 2 D): a stiffening response (like biopolymer networks) with increased stiffness (higher slope in the stress–strain graph) after the proportional limit; elastomeric (like rubber or silicon), with a decrease in stiffness after the proportional limit (but still positive; the material still experiences higher stress with increasing strains); superelastic (like nickel-titanium alloys), with strain softening beyond the proportional limit (reflected in a negative slope in the stress–strain graph; the material experiences reduced stress with increasing strains) followed by strain hardening while remaining elastic; and elastoplastic (like aluminum), with a similar stress–strain relationship but permanent deformation (yielding).

A quantitative comparison of the resulting cell size profile for each condition with the cell sizes observed in vivo showed that the closest matches were achieved with superelastic- and elastoplastic-like stress–strain responses (Fig. 2, E and F). Unlike the linear models, nonlinear models with strain softening (superelastic and elastoplastic; i.e., cases where stress reduces with increasing strain) reproduced the stretching pattern of lateral cells for a wide range of myosin profiles (Fig. 2, K, K′, L, and L′). The elastomeric-like response also reproduced the stretching pattern for a wide range of myosin profiles, but, unlike the two strain-softening responses, it was unable to reproduce the observed cell size ratios between largest and smallest cells (Fig. 2, I and I′). While inert materials and cultured cells can respond to strain also by stiffening (Gardel et al., 2004; Storm et al., 2005; Fernández et al., 2006; Hoffman et al., 2006), our simulations with strain stiffening curves did not reproduce our in vivo observations (Fig. 2, J and J′).

These results suggest then that the stretching cells must show a nonlinear strain response. Given that the cytoskeleton is the main determinant of cell shape and cell mechanical properties, we reexamined its behavior in lateral cells. We assumed that strain softening would most likely manifest as reorganization (permanent or reversible) of the cytoskeletal network.

Organization of actomyosin networks in lateral cells

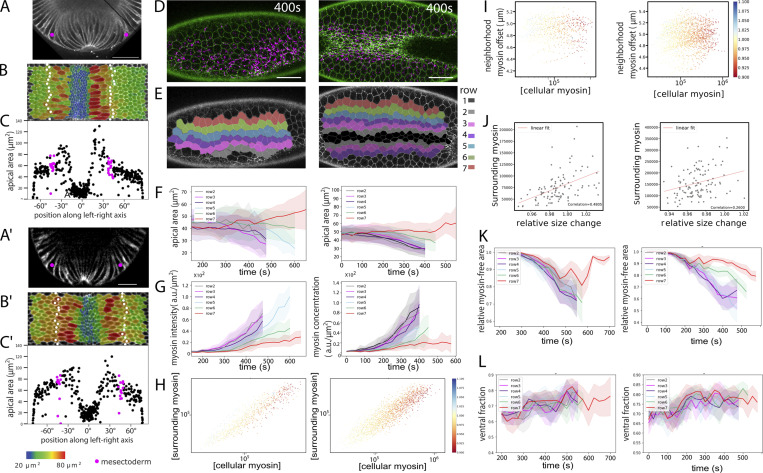
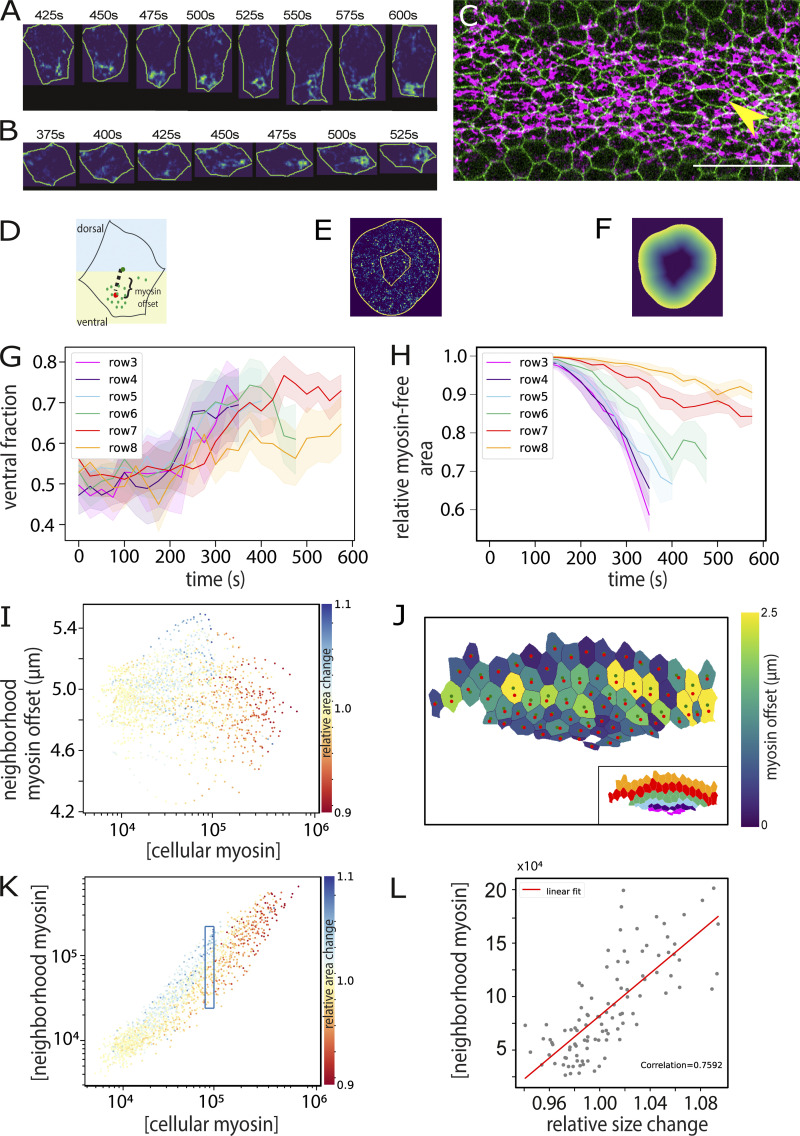
We had noticed that local constrictions in lateral cells occurred primarily in the AP axis (Fig. S3, K and N), pointing to a possible role for overall actomyosin distribution. We analyzed the distribution of apical myosin and found preferential segregation toward the ventral side in each cell, with the distance of displacement being greater in lateral cells (Fig. 3, A, G, and J). In addition, lateral cells have larger areas without myosin (Fig. 3 H). This local thinning out or dilution of myosin may reflect the strain-softening or yielding behavior predicted to be necessary by the model and explain the cells’ inability to constrict efficiently. This resembles the asymmetric distribution of RhoA in expanded central cells in concertina mutants, which has been proposed as an explanation for the cells’ inability to overcome the expansile forces acting on them and constrict (Xie et al., 2016). The reason for the asymmetry may be the initial myosin gradient. For every cell along the gradient, the ventral neighbor constricts earlier than its dorsal neighbor. Recent simulations showed that the ability of the cell cortex to yield to contractile forces feeds back on the orientation of the contractile network inside the cell, which becomes depleted near “softer” membranes and enriched near “stiffer” membranes (Chanet et al., 2017). More generally, if constriction of a cell affects the localization of myosin in its neighbors, then one might expect a difference in myosin offset in areas surrounding constricting and nonconstricting cells, and this is indeed what we observed (Fig. 3 I). In mesodermal cells, the least yielding should be the ventral side, which experiences stronger forces from the ventral neighbor than the other side does from the dorsal neighbor.

Figure 3.

Subcellular myosin distribution and actomyosin model. (A) Example of myosin dynamics in a single cell from row 8 in the embryo shown in Fig. 1 E. Cell contours and myosin signal pixels were isolated using individual cell segmentation masks. Myosin intensity values increase from blue to yellow. (B) Example of an incompletely constricted central mesodermal cell in the embryo shown in C (yellow arrow). (C) Embryo imaged from a ventral view. Green: membranes; magenta: myosin. Scale bar: 25 µm. (D–F) Diagrams to explain measurements in G–L. (D) Representation of myosin spatial distribution in a cell. “Offset” (shown in J) is the Euclidean distance between the cell centroid (red dot) and the intensity-weighted centroid of the myosin signal (green dot); “DV asymmetry” (shown in G) is the ratio of myosin pixels in the ventral half of the cell to the total number of myosin pixels in the cell. (E) The ratio of cell-internal versus neighboring myosin is the comparison between the sum of the pixel values within the cell and that in an area of a 70-pixel radius around the cell, each normalized to the measured area. (F) The myosin offset in the environment of a cell (shown in I) was calculated by weighting the value of each myosin pixel in E by its distance from the edge of the cell. Thus, the values in E were multiplied by the values in F. This gives pixels that are distant from the cell higher values. (G) Average proportion of myosin in the ventral half of the cell, plotted over time for each row. (H) Proportion of the myosin-free cell area as detected by classifying myosin pixels from background (see Materials and methods). As myosin levels rise, the myosin-free proportion drops. In lateral cells, large areas remain myosin free, even though the total amount of myosin rises to high levels (Fig. 1 G). (I) Asymmetry of myosin distribution in a cell’s environment. For each cell, the myosin in a surrounding 70-pixel (8.5 µm)-wide ring (outer region in E) was assessed. Each myosin pixel intensity value was weighted with a value for its distance from the cell’s outer boundary (represented graphically in F), yielding the “offset” for each point. The averaged offset for each cell was then plotted against the cell’s own myosin concentration and cell area change denoted in color. Lower offset values mean more of the myosin in the surrounding ring is close to the cells. For any given intrinsic myosin concentration, a constricting cell (red) has more myosin close to its perimeter than the expanding cells (red). (J) Myosin concentration within a cell plotted versus surrounding myosin concentration in a ring around the cell (E), with the change in cell size over two consecutive frames indicated in color (n = 1,883 cells). All segmented cells at 25 time points from the embryo in Fig. 1 E are represented. (K) A subset of cells from J with internal myosin concentrations at values ∼10⁵ (boxed in J) with surrounding concentration plotted against size change (n = 110 cells). (L) Myosin offset in cells at 550 s, calculated as shown in D and with the colored dots in the cells the same as in D and color coding the degree of offset. The inset shows the same cells with rows color coded as in G and H.

If the extent to which a cell at any moment expands or shrinks is influenced by its neighbors, then the amount of myosin in a cell’s environment (i.e., in the adjacent cells) should correlate with the cell’s size changes. Measuring these parameters and correlating them to each cell’s size change over two time points first showed, unsurprisingly, that concentration of myosin within a cell in general correlated highly with the concentration in its neighbors (Fig. 3 K). Second, cells with high concentrations (>120,000) always constricted (red values in Fig. 3 K), and at low concentrations (<8,000), all cells remained inert (relative change, 1.0; yellow values in Fig. 3 K). However, in the range between these values, for any given cell-internal myosin concentration, the cells that expanded were always those for which the neighbors had the highest myosin levels (Fig. 3 L). Fig. 3 L shows all those cells from Fig. 3 K with myosin concentrations of ∼100,000 (boxed region) and compares their neighbors’ myosin concentrations against their own expansion or constriction (x axis). For the expanding cells (size change >1; blue in Fig. 3 K), the neighbors’ myosin levels are high; for the constricting ones, they are low. This shows that forces acting on each cell from its neighbors have an important role in determining the cell’s behavior, confirming that the cells’ behavior is not determined exclusively by their own intrinsic genetic program.

Actomyosin model of the mesoderm

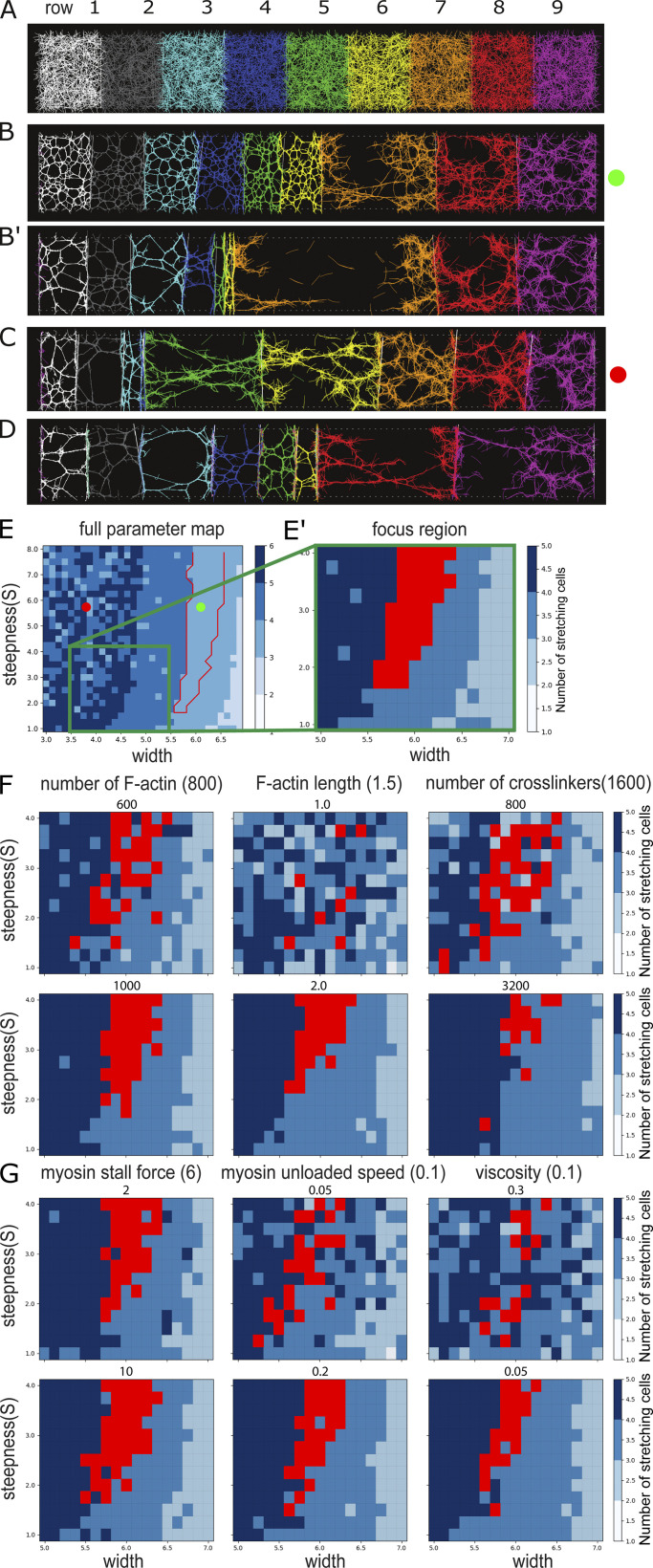
We do not know whether the correlation between actomyosin distribution and cell stretching reflects causality or whether both are effects of external forces (i.e., pulling by neighbors). We used cytosim, a microscopic, filament-based model (Belmonte et al., 2017; Nedelec and Foethke, 2007), to test under what conditions cells containing contractile actomyosin show the behaviors we observe in the embryo. We modeled half of the mesoderm as a chain of “membrane”-separated elements with fixed outer boundaries (Fig. 4 A). Each “cell” contained a constant number of actin filaments and cross-linkers at concentrations we previously found to be able to make a contractile meshwork (Belmonte et al., 2017) and added attachment points for filaments on the membranes. The biophysical parameters of the filaments, cross-linkers, and myosin were chosen on the basis of available biochemical data in the literature (Table S3). We varied the number of active myosin motors according to the same profiles as those we tested in the viscoelastic model (examples of outcomes in Fig. 4, B–D; and Video 3).

Figure 4.

Actomyosin model of a line of cells with a contractile actomyosin meshwork. (A) Initial condition of the system with randomly distributed actin, cross-linkers, and myosin motors within each cell (shown with different colors). (B and B′) Two time points from a simulation with a myosin profile that qualitatively reproduces experimental results. (C and D) Examples of simulations where the myosin profile was wider (B) or narrower (C). (E) Parametric map for myosin concentration curves with varying peak widths and steepnesses. Blue shades: Number of expanding cells. Red outline: Conditions where the three right cells expand with an inverted pattern of stretching that qualitatively matches experiments. The coordinates used for the simulations shown in B and C are marked. D is not within the range shown here. (E–G) Sensitivity analysis of the actomyosin model. (E and E′) We focused our analysis on a small region of the parametric map shown in E to test how variations in six parameters of the simulations affect the output of the model. (F and G) Results after variation of six simulation parameters. Reference values are indicated in parentheses next to the name of the parameter, tested values (both higher and lower than reference) are shown immediately above each map. Red regions indicate parameter sets that reproduce experimentally observed patterns of stretching. Results for each parameter set were averaged over three simulations.

Video 3.

Actomyosin simulation of a row of cells. Central (left-most cell) cell has 16,000 myosin motors, and the mesectodermal cell (right-most cell) has 1,600 myosin motors with intermediate amounts between cells determined by Eq. 3 with w = 6.25 and s = 5.5. All other parameters are as in Table S3. Frame rate: 10 frames per second.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202104107.v3/source

A set of profiles was able to generate constriction of six cells and stretching of three cells, of which a subset reproduced the qualitative behavior seen in vivo, with an inverted pattern of stretching (red region in Fig. 4 E). For such profiles, “cell 7” stretches until its actomyosin network tears apart (Fig. 4, B and B′), a result characteristic of a plastic (permanent) deformation. A sensitivity analysis of six model parameters for which the available literature information is scarce or where we expect higher impact on actomyosin behavior shows that the results are robust to small changes around our chosen values (Fig. 4, E–G).

In conclusion, without a priori assumptions, this model gives an output consistent with our experimental observations and is indicative of nonlinear (yielding) behavior, showing that such behavior can emerge directly from the properties of the network components and the myosin concentrations. The striking similarity between the parameter maps of the myosin profiles in the two unrelated models (actomyosin and viscoelastic) that yield the same outcomes (Fig. 2, K and L; and Fig. 4 E) illustrates the generality of the results and suggests that contractile meshworks in vivo can, in theory, do the same. Rapid cell expansion due to strain softening has also been observed in elegant mammalian tissue culture experiments. In these cells, persistent intermediate filaments allowed reestablishment of connectivity and the cell recontracting (Latorre et al., 2018). Our results here are the first demonstration of an equivalent process occurring in a physiological situation in vivo.

Intrinsic versus externally imposed behaviors of mesodermal cells

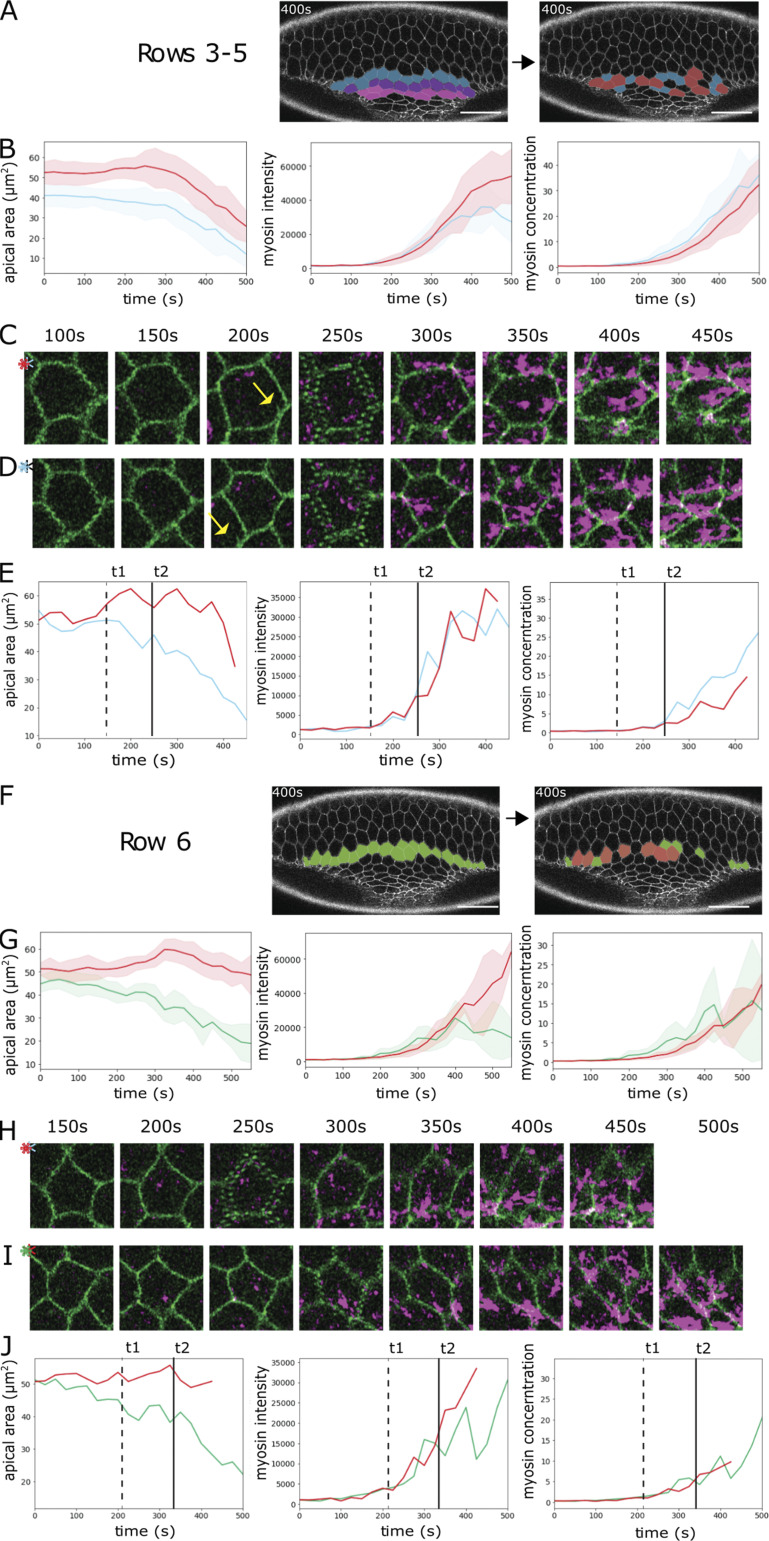
Our results so far show that cell-intrinsic genetic regulation or myosin levels alone cannot explain the difference between constricting and stretching. We also compared the role of myosin levels among cells at the same position in the gradient. Many central cells expand transiently before constricting, and some are internalized without constricting (Yevick et al., 2019; Fig. 3, B and C; Fig. S4). We tested whether myosin levels correlated with these behaviors by categorizing cells from all rows as either “transiently expanding” or “constricting.” In rows 3–5, transiently expanding cells started out with slightly larger surfaces but with the same myosin concentrations as contracting cells. During the transient expansion (200–250 s), neither myosin amounts nor concentrations are pronouncedly different from those in the contracting cells (Fig. S4, A–E). Myosin amounts in row 6 also rose simultaneously in both populations during the expansion period, the slight divergence in concentration therefore coinciding with but not preceding expansion (Fig. S4, F–J). Thus, myosin levels did not predict constriction versus transient expansion. Finally, central cells that remain unconstricted often have highly asymmetric myosin foci (Fig. 3, B and C), much like laterally expanding cells, showing that skewed myosin is determined neither by the cell’s position in the genetic gradient nor by its intrinsic myosin values. Together these results suggest that whether a cell constricts does not depend primarily on myosin levels, but it depends at least in part on what its neighbors do and in part on stochastic variation in its actomyosin organization.

Figure S4.

Myosin concentration in constricting and transiently expanding cells. Analysis of the embryo shown in Fig. 1 E expressing Spider::GFP (green) and Sqh::mCherry (magenta). Cells in the indicated rows were sorted into bins, defining cells as “transiently expanding” (red) if they increased their apical areas by >10% of their initial area for at least three consecutive time points and as contracting (blue for rows 3–5, green for row 6) if they decreased their apical areas over 10% of their initial area for at least 10 time points. (A–E) Constricting rows 3–5. (F–J) Transition row 6. (A and F) Image at t = 400 s. Left: Coloring shows rows; right: coloring indicates the individual cells that were analyzed (red, transiently expanding; blue or green, constricting). (B and G) Cell apical area, total apical myosin per cell, and apical myosin concentration (amount over area) of constricting and transiently expanding cells plotted against time, shown as mean (solid line) and SD (shaded area). (C–E) Analysis of a transiently expanding (C) and a constricting (D) cell from the constricting rows. (C and D) Snapshots of the two cells at the indicated time points. The two cells are adjacent to each other: The yellow arrow at 200 s points to a feature of the expanding cell that is also seen in the panel below. (E) Apical cell area, total apical myosin amount per cell, and myosin concentration of the cells in C (red) and D (blue) plotted against time. t1 (dashed line) marks the divergence of the cells in the apical area, and t2 (solid line) marks the divergence in myosin concentration. (H–J) Analysis of a transiently expanding (H) and a constricting (I) cell. (H and I) Snapshots of the two cells at the indicated time points. (J) Apical cell area, total myosin amount, and myosin concentration of the cells in H (red) and I (green) plotted against time. t1 (dashed line) marks the divergence of the cells in apical area, and t2 (solid line) marks the divergence in myosin concentration. Scale bars: 25 µm.

We therefore propose a model where all mesodermal cells have an endogenous program that gives them the capacity to constrict in principle, but the interpretation of the program is also influenced by neighbors. Cells that accumulate active actomyosin earlier or at higher levels than neighboring cells have a greater chance of sustaining their contraction. This hypothesis makes two testable predictions: (1) preventing central cells from constricting early should allow lateral cells to constrict, and (2) making lateral cells constrict early should affect the ability of central cells to constrict.

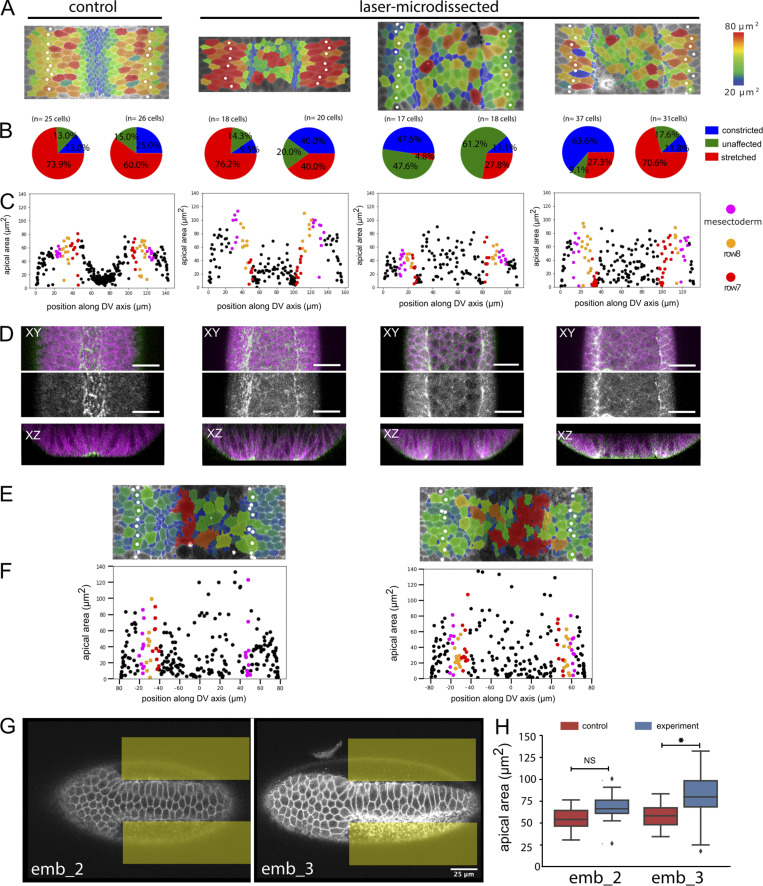
To test these predictions, we manipulated apical contractility by laser microdissection and optogenetic methods. We first inhibited constriction in central cells by transient severing of the actomyosin meshwork (Fig. 5 C, area marked in yellow; and Video 4) with a pulsed infrared laser (Rauzi et al., 2015). We compared the sizes in a central tranche of untreated (Fig. 5, A and B) and experimental (Fig. 5, C and D) embryos. This showed reduced apical constriction specifically in the illuminated area (marked yellow in Fig. 5), and, at the same time, some (though not all) cells in rows 7 and 8 now constricted their apical sides (Fig. 5, D, E, and G; and Video 5). Because these manipulations are made at a time before the precise extent of the mesoderm is visible, they are usually not precisely symmetric, and lateral cells on only one side are affected (Fig. S5). We also used an optogenetic tool to interfere with the cortical actomyosin network. The inositol polyphosphate 5 phosphatase OCRL dephosphorylates the phosphoinositol moieties that act as plasma membrane anchors for actin and can be used to release actomyosin from the membrane (Guglielmi et al., 2015). Optogenetically releasing the actomyosin meshwork in a band of central cells yielded the same results as the laser microdissections: Constriction in the illuminated cells was inhibited, and several cells in rows 7 and 8 constricted (Fig. 5, H–K′′; and Table S7). Thus, these results confirm the first prediction of the model.

Figure 5.

Effects of restricting apical constriction in central cells. (A–D) Two time points from confocal recordings of control (A and B) and laser-manipulated (C and D) embryos expressing GAP43::mCherry (cell outlines). The experimental embryo was exposed to repeated illumination with an infrared laser in the region marked in yellow in C. The embryos were recorded until the time when the furrow closed in the untreated embryo, surface peels were extracted, and cell sizes within the middle region of the embryo (dashed white outlines in A–D) were determined and are shown color coded in the peels in A′′–D′′ and plotted against positions along the circumference of the embryo in A′′′–D′′′. Snail-MS2 and MCP::mCherry (see Fig. S1 D) were used to determine the extent of the mesoderm; the mesectoderm is marked by magenta fill in A′–D″ and white spots in A″–D″. 0 s is the point when the apical–basal length of the central rows is 35 µm. Scale bar: 25 µm. See also Videos 4 and 5. Two further embryos are shown in Fig. S5. (A–D) Confocal Z-planes 15 µm below the ventral surface (a level that captures both rows 7 and 8) showing positions of Z-sections in A′–D′ marked by yellow lines and the region of the apical surface peels in A″–D″ by white boxes. (A′–D′) Z-sections at the positions indicated in A–D. (A″–D″) Apical surface peels of regions marked in A–D. The same markings as in Fig. 1 are shown, with quantification of the apical areas of the cells plotted against their position. The same representation of cell size as in Fig. 1 is shown. Note data points at the sides include artifactually small values because cells at the edge are not full size. (A′′′–D′′′) Apical area in the field shown above plotted against cell position (0° is the ventral midline). Each dot represents one cell. (E–G) 3D segmentation of individual cells from the embryo shown in D. (E) Z-section showing cell outlines and the binary mask used for segmentation (white edges). Blue line indicates the position of the Z-section shown in F. Mesectoderm: White spot. (E′) Segmentation results. (F and F′) Z-plane and segmentation results. The numbers indicate the cells shown in 3D below. (G) 3D renderings of the three cells marked above in F and F′. For viewing 3D rendering, see Video 5. (H–K) Optogenetic inactivation of cortical actomyosin in a ventrally mounted embryo coexpressing OCRL-CRY2::mCherry, CIBN::pmGFP, simMS2, and MCP::GFP to mark the mesectoderm. The illuminated region corresponds to the region in which GFP is visible as shown in J. Scale bar: 25 µm. (H–J) Confocal Z-planes 5 µm below the surface before and after release actomyosin from the apical cortex by illumination of the area marked in yellow. Illumination leads to recruitment of OCRL-CRY2 to the plasma membrane (compare H and I) via membrane-associated CIBN::pmGFP. (K) Z-plane 25 µm below the ventral surface (to capture both rows 7 and 8) 10 min after laser treatment to show the position of the edge of the mesoderm. The mesectoderm is shown in magenta. This level does not show the apical surface. (K′) Cross-section showing nonstretched cells adjacent to the mesectoderm (magenta). (K″) Apical surface peel and quantification of apical cell areas. Same markings as above.

Video 4.

Ventral view of an embryo expressing GAP43::mCherry (magenta; membrane) and sqh::GFP (green; myosin). MCP::mCherry and Snail::MS2 (not shown) were used to mark the mesoderm boundary. The embryo is illuminated repeatedly in the area marked by a red ellipse in frame 1. During the laser illumination experiment, images were captured every 2 s. The last three frames are single confocal sections from a 3D stack taken at intervals of 38 s (Fig. 5). Frame rate: 20 frames per second.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202104107.v4/source

Video 5.

3D reconstructions of lateral mesodermal cells from row 7 in an embryo where apical constriction of the central mesodermal cells was inhibited by laser ablation. Apical is down, and basal is up. The magenta and green cells fail to expand, and the blue cell constricts apically. See Fig. 5, E and F, for the location of cells in the embryo. Frame rate: 45 frames per second.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202104107.v5/source

Figure S5.

Quantifications and examples of laser-microdissected and optogenetically manipulated embryos. (A–D) Control embryo (first column) and laser-microdissected embryos with quantification of constricting cells in rows 7 and 8. The control embryo and the embryo in column 2 are the same as in Fig. 4, A–D; the two right columns show two additional laser-dissected embryos and their quantification. All experimental details are as in Fig. 5, A–D. (A) Surface peels with cell size shown in color and the mesectoderm marked by white spots. (B) Pie charts of the cell surface areas in the two cell rows adjacent to the mesectoderm, in each case for the left and right sides. Because the embryos are mounted for microscopy and laser treatment at a time point before visible differentiation along the DV axis, no visual cues exist to ensure perfect positioning. The illuminated area is therefore not perfectly symmetrical, and the effect does not always reach precisely to the edge of the mesoderm. As a result, in all of the manipulated embryos, one side is abnormal (large numbers of constricted or unstretched cells), and the other is unaffected. The number of cells counted and precise numbers for the proportions shown in the pie charts are listed in Table S7. (C) Quantification of cell sizes from the peels. (D) Distribution of myosin in laser-manipulated embryos. Confocal image with cell outlines (marked with GAP43::mCherry) shown in magenta, myosin in green in the top row, myosin only in the second row, and a Z-section in the third row. Scale bar: 25 µm. (E and F) Surface peels and cell size quantification of two embryos in which the actomyosin had been released optogenetically. All details are as in Fig. 5 K. (G and H) Two embryos in which constriction had been induced optogenetically in the lateral mesoderm (illuminated areas marked in yellow). (G) Confocal section showing stretched cells in the center of the mesoderm. Scale bar: 25 µm. (H) Quantification of average cell surface areas in the central regions of the mesoderm in the experimental and control areas in each embryo. All experimental details are as in Fig. 6, C and E. n = 20–40 cells per condition per embryo; NS, P = 0.4781; *, P = 0.00015).

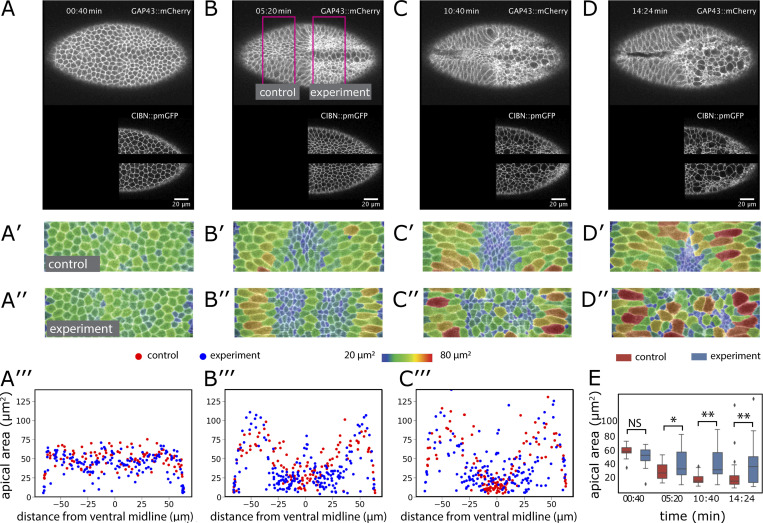
To test whether the central cells can be stretched, we optogenetically induced premature constriction (Izquierdo et al., 2018) in lateral cells. While genetic complexities prevent us from visualizing the previously demonstrated effects on myosin (Izquierdo et al., 2018) in these experiments, the activated cells constricted and affected the behavior of central cells. We activated regions on both sides of the central two rows (Fig. 6, A–D, bottom; and Video 6). We restricted the manipulation to the posterior half of the embryo, retaining the anterior half as a control. In the control half, central cells constricted, and lateral cells stretched normally (Fig. 6, A′–D′). In the experimental half, the illuminated cells constricted. At the same time, many of the cells near the ventral midline now expanded their apical surfaces (Fig. 6, A′′–C′′ and E). Thus, central cells failed to undergo their normal morphogenetic program, even though they themselves had not been manipulated, showing that external forces were able to override their genetic instruction to constrict.

Figure 6.

Effect of ectopic myosin recruitment. (A–D) Confocal Z-planes 5 µm below the surface of an embryo coexpressing GAP43::mCherry, CIBN::pmGFP, and RhoGEF2-CRY2. Scale bar: 20 µm. The embryo was continuously illuminated to induce membrane recruitment of RhoGEF2-CRY2 to the membrane-associated CIBN::pmGFP (shown in the lower panel). Magenta lines in B show the control and experimental areas that were analyzed quantitatively. (A′–D′ and A″–D″) Apical surface peels of the regions marked in B overlaid with a color code representing relative apical areas. (A′′′–C′′′) Apical areas of the cells in the control (red dots) and experimental (blue dots) parts of the embryo plotted against their positions (top) and size distribution of cells in the nonilluminated central area of the mesoderm compared with the corresponding control area (bottom chart). (E) Apical areas of central cells. The apical areas in the nonilluminated region in the posterior part of the embryo (blue) and an area of the same size and in the same ventral position but in the anterior control port of the embryo (red) are plotted for the time points shown above. Number of control and experimental cells for each time point: 9, 14; 24, 21; 34, 22; 25, 15. *, P < 0.01; **, P < 0.001. Error bars represent the 1.5× interquartile ranges. Two further embryos are shown in Fig. S5.

Video 6.

Ventral view of embryo expressing GAP43::mCherry (membrane, top), CIBN::pmGFP (membrane; bottom), and RhoGEF2-CRY2. Myosin is ectopically activated by illuminating the area as seen in the bottom half of the video. (Fig. 6). Frame rate: 10 frames per second.

https://movie.rupress.org/media/by_doi/10.1083/jcb.202104107.v6/source

Discussion

Following from the above, an explanation is needed for why lateral cells normally do not constrict, even though they reach sufficient myosin levels. The simplest explanation is that the external forces acting on them are greater than those acting on the early-constricting central cells. While different external forces are likely part of the explanation, in the absence of precise measurements at a subcellular level (an extremely challenging task, given the cells’ small size and rapid movement), we must also consider other possibilities.

According to the viscoelastic model, a nonlinear stress–strain relationship with strain softening is necessary for the inverted pattern of stretching of lateral cells, which could not be reproduced with previous computational models. This is in accordance with experimental work on reconstituted F-actin networks that shows the presence of a strain-softening response to large strains (Wagner et al., 2006; Åström et al., 2008; Semmrich et al., 2008; Lee et al., 2010; Gurmessa et al., 2017). The strong stretching, also documented in epithelia in vitro (Latorre et al., 2018), was best recapitulated by a superelastic response. The nonlinearity emerging from the actomyosin model, however, resembles elastoplasticity (irreversible strain), but the simulations do not include actin turnover, which would facilitate recovery from yielding of the cytoskeletal network and thus reverse the stretching, typical of superelastic materials. Allowing myosin concentrations to accumulate gradually over time may favor one nonlinear model over the other but will not change the main conclusion that linear models recapitulate the observed data less well than the nonlinear ones.

It is currently not feasible to determine experimentally whether cells in the embryo behave like elastoplastic or superelastic materials (as seen in vitro [Latorre et al., 2018] and in simple organisms [Jia et al., 2017]). Other possible explanations for the same output include dissipation through viscosity (Doubrovinski et al., 2017; D’Angelo et al., 2019) or external friction (Bailles et al., 2019; Münster et al., 2019) or a nonproportional causal relationship between myosin concentration and constriction forces. The former cannot explain single-cell stretching in the central mesoderm, while the latter is unlikely, given that myosin levels alone predict a wide range of morphogenetic movements in Drosophila (Streichan et al., 2018).

The most probable source of the nonlinear relationship between force (for which we use myosin as a proxy) and cell size is the actomyosin cytoskeleton, which is the main mechanical determinant of mesodermal cells and acts at the observed time scales of our experiments. Other components that could in principle contribute to the nonlinearity of the stress–strain response might be the viscosity of the cytosol, or the plasma membrane. However, stress responses of fluids to shear are usually in the direction of increasing stiffness and rarely, if ever, with shear thinning. The same is mostly true for colloidal solutions.

The mode by which actomyosin networks mediates the nonlinear response may be through a failure in assembling its component into an arrangement that efficiently supports constriction. Pulsatile apicomedial actin meshworks need to be tightly connected to junctional complexes to function (Martin et al., 2010; Kanesaki et al., 2013; Fox and Peifer, 2007; Spahn and Reuter, 2013; Krueger et al., 2020), relying also on an underlying nonpulsatile actin meshwork (Dehapiot et al., 2020). Despite the homogeneous actin meshwork in stretching cells, the areas that are free of active myosin occupy a large proportion of the apical surface, similar to ectodermal or amnioserosa cells in which the connection of pulsatile foci to the underlying actin meshwork is lost (Dehapiot et al., 2020). The observation that a skewed myosin distribution is not restricted to cells with low myosin but can occur even in central cells at the highest myosin concentrations underscores the conclusion that all aspects of this phenotype are externally imposed rather than intrinsically determined by myosin levels.

Dilution of cortical myosin may compromise a cell’s ability to make sufficient physical connections, in particular along the DV axis, so that even if sufficient force is generated, it cannot shorten the cell in the long dimension. In other words, even though the cells have enough myosin to create force, the system is not properly engaged, and its force is not transmitted to the cell boundary. In this model, the skewed myosin distribution is both a result of external forces and also part of the cause of a cell’s failure to constrict. By a feedforward mechanism, an initial expansion induced by constricting neighbors dilutes or distorts the apical actomyosin, giving these cells a lower chance of generating or sustaining a contraction. This mechanism, which we propose corresponds to the nonlinear behavior predicted by the models, would apply both to central and to lateral cells, with a catastrophic “flip” being stochastic and rare in central cells but reproducible in lateral cells because of the genetically determined temporal and spatial gradient in which contractions occur.

Materials and methods

Plasmid for membrane-associated mCardinal

To generate the plasmid attB-tubulin_promoter–growth-associated protein 43 (GAP43)::mCardinal-K10 plasmid, the attB–upstream activation sequence promoter (UASp)-K10 plasmid (provided by Anne Ephrussi, European Molecular Biology Laboratory, Heidelberg, Germany) was modified by replacing the UASp by a tubulin promoter sequence that was amplified from the plasmid pCasper4-tubulin (provided by Stefano De Renzis, European Molecular Biology Laboratory, Heidelberg, Germany). The mCardinal coding sequence was amplified from mCardinal-H2B-C-10 (Addgene; plasmid 56162) using a forward primer with the sequence encoding the first 20 aa of the GAP43 protein from Bos taurus (Table S5). The GAP43::mCardinal fragment was inserted into the attB-tubulin-promoter-K10 plasmid using NotI and BamHI enzymes.

Generation of fly stocks

To generate the fly transgenic lines p[mat tub>GAP43::mCardinal]/CyO and p[mat tub> GAP43::mCardinal]/TM6, Tb, the attB-tubulin_promoter-GAP43::mCardinal-K10 plasmid was inserted into landing sites on the second and third chromosomes (landing sites VK18 [BDSC-9736] and VK33 [BDSC-9750]) by BestGene Inc. Only the insertion on the second chromosome was used in this study, because it was brighter than the insertion in VK33.

Sample preparation

Embryos were collected according to standard procedures on apple juice agar plates. Plates were changed after a 1-h embryo collection and kept at 25°C for 2.5 h. Individual midcellularization to late cellularization embryos were hand selected under halocarbon 27 oil (Merck; H8773). The stage-selected embryos were devitellinized with 50% bleach and washed thoroughly with distilled water. For confocal microscopy, the embryos were then mounted on a glass-bottomed microwell dish (Matek; P35G-1.5-10.C) with the ventral or ventral-lateral side facing the glass and covered with PBS. For multiview selective plane illumination microscopy (MuVi SPIM), the embryos were mounted in 1% Gelrite (Merck; G1910) inside a glass capillary, and multiple views were registered and fused (Rauzi et al., 2015).

Confocal microscopy

For visualizing 3D cell shapes using two-photon illumination, a femtosecond-pulsed infrared laser (Chameleon Compact OPO Family; Coherent) tuned at 950-nm emission wavelength and coupled with a Zeiss LSM 780 confocal microscope was used. The region of interest was defined with the ZEN “Regions” interface, and the embryos were illuminated with 20–25% laser power. A volume of 200 × 500 × 60 µm³ was imaged, where the dimension of 200 µm is along the AP axis of the embryo, centered around the central region; 500 µm is along the left–right axis; and 60 µm is the depth in the z axis.

Two-color imaging was performed at RT with a Zeiss 880 Airyscan microscope, a 40×/1.4 NA oil-immersion objective, an argon ion laser, and a 561-nm diode laser. Image stacks were acquired every 25 s.

SPIM

Imaging was performed on a custom-built MuVi SPIM setup (Krzic et al., 2012) with Nikon 10×/0.3-W objective lenses for illumination and Nikon 20×/1.0-W objective lenses for detection. An additional 1.5× magnification tube lens produced an effective image pixel size of 0.19 µm × 0.19 µm. Optical sections were recorded with a typical spacing of 0.75–1 µm. For observing cell shape changes, GAP43::mCardinal embryos were imaged from two opposing directions simultaneously and successively from two directions with 90° apart. Registration of the four views was performed as previously described.

Identification of mesodermal cells

To identify unambiguously the lateral borders of the mesoderm, we used two methods (Fig. S1, D–J′): (1) backtracing mesectodermal cells from the point where the meet at the ventral midline after the mesoderm is fully internalized or (2) using the MS2 stem loop/MS2 RNA coat protein (MCP)-GFP system to visualize the expression of the genes singleminded (Bothma et al., 2015) in mesectodermal cells or snail in the mesoderm (Viswanathan et al., 2019).

Laser microdissection and illumination

Laser-based actomyosin meshwork ablation was performed as previously described (Rauzi et al., 2015) using a femtosecond-pulsed infrared laser (Chameleon Compact OPO Family; Coherent) tuned at 950-nm emission wavelength and coupled to an LSM Zeiss 780 confocal microscope. The ZEN “Bleaching” interface was used to create the region of interest and was illuminated at 65–70% laser power. We began illumination when the myosin first became visible on the apical surface of ventral cells, and we repeated illumination every time new fluorescent apical myosin reappeared (every ∼60 s). Two-photon illumination covered a depth of a single z-step (i.e., <1 µm). For this experiment, a C-Apochromat 63× magnification water immersion Zeiss objective with 1.1 NA was used (infrared corrected). The laser treatment does not kill cells or permanently damage the cytoskeleton, as shown by the fact that cells reconstrict and continue to participate in furrow formation once the illumination stops.

Optogenetic manipulations

Embryos were prepared in a room where the blue spectrum of visible light was filtered out (Izquierdo et al., 2018; Guglielmi et al., 2015). The ZEN “Regions” interface was used to create the region of interest, and the embryos were illuminated with 15–20% laser power with pixel dwell time between 0.8 and 1.27 ms. The embryos were illuminated when the ventral cell height reached ∼35 µm. Illuminations were then repeated at 10-s intervals until the end of the experiment. The depth of illumination was 4–5 µm. For this experiment, a C-Apochromat 40× magnification water immersion Zeiss objective with 1.2 NA (infrared corrected) and an infrared laser (Chameleon Compact OPO Family; Coherent) tuned to 950-nm emission were used.

Image processing

Apical surface extraction and cell segmentation from SPIM images

The middle 30% of the embryo along the AP axis was cropped in Fiji (Schindelin et al., 2012). A custom MATLAB software was then used to extract the apical surfaces (Bhide et al., 2020). A binary mask around the embryo was generated semiautomatically by defining the apical and basal surfaces. Using these masks, distance transformation was used to define a 1- to 2-pixel “peel,” typically 2–3 pixels below the binary mask. Along the AP axis of the embryo, pixels along the surface were traced and mapped onto a line. This process was performed on every stack to map the apical surface of the embryo onto a 2D plane. These 2D images were then segmented using TissueAnalyzer (Aigouy et al., 2016).

For 3D segmentations in Video 1, binary masks were generated (see above) to first segment foreground from background. Then, the cells were segmented in 3D and corrected as described (Bhide et al., 2020; Stegmaier et al., 2018).

Myosin measurements

Images were deconvolved in the ZEN software using AiryProcessing. The Spider:GFP images represent confocal slices 3 µm below the apical cortex. sqh:mCherry images represent sum Z-projections of an apical section of the same depth upon background myosin subtraction. Background sqh:mCherry intensity was measured in single subapical confocal slices, and mean + 2 SD values were subtracted from each slice before Z-projecting to obtain apical myosin intensity. The cells were segmented and tracked using TissueAnalyzer (Aigouy et al., 2016). The segmentation output was used to extract cell areas and pixel intensities. Total sqh:mCherry intensity (used as a measure of total myosin amount) within a cell was measured as a sum intensity of all pixels in a cell. Myosin concentration was calculated as myosin intensity/cell area.

For measuring myosin-free apical cell areas, the myosin signal was segmented from background by training a classifier using Ilastik. For generating a binary mask for myosin signal, pixels with >0.80 probability values were used. For Fig. 3, I–L, myosin concentration and cell size values for every cell were smoothed along the time axis using a 1D gaussian filter (Virtanen et al., 2020) with Σ = 3. For every cell at each of 25 time points, 3 values were taken: its myosin concentration; the myosin concentration in the area of 70 pixels around the cell boundary; and the relative size change, calculated as the cell size in the next time frame divided by the cell size in the current one.

A viscoelastic model for the mesoderm

We modeled the mesoderm as a 1D series of points (cell boundaries) connected by viscoelastic units (cells). Each cell behaves as a Kelvin-Voigt material made of a spring and dashpot in parallel connecting two adjacent cell boundaries (at positions $x_i$ and $x_{i+1}$). All cells have the same damping coefficient ($\eta$) and stress–strain response [$S\left(\Delta x\right)$]. We added three cells with a higher stiffness at each side of the 19 mesodermal cells to simulate the rigid ectodermal cells. Each cell contains a defined amount of “myosin” (M), which exerts a force at each cell membrane position $x_i$ that is directly proportional to the local gradient of “myosin” around that point [$\nabla M\left(x_i\right)$]. The system evolves over time according to the following deterministic equation:

$$\frac{d^2}{d{t}^2}{x}_i={\displaystyle \sum _j{k}_{ij}S}(x_i-x_j-L_0)-\eta \frac{d}{dt}{x}_i+\nabla M(x_i),$$ (1)

where the sum is over the two adjacent point coordinates, the function $S$ is the stress–strain response (defined below), $L_0$ is the resting length of the cells in the DV axis, and the myosin profile (M) is modeled as a symmetric sigmoidal function around the midline, described by the equation:

$$M(x_i)=\frac{1+e^{-sw}}{1+e^{s(x_i\vee -w)}},$$ (2)

where $w$ and $s$ are parameters describing the width and steepness of the function, respectively, and $x_i=0$ corresponds to the midline (central) position of the mesoderm.

We considered five types of stress–strain response models. The first corresponds to a simple linear elastic-like model, where stress increases proportionally with the strain. The other four models are nonlinear, with the same stiffening response to compressive strains ($\Delta x=x_i-x_j-L_0<0$), and four different types of responses to extensive strains: (1) an elastomer-like model, corresponding to an elastic response but with a decreased stiffness after the proportionality limit; (2) a stiffening model, with an increased stiffness after the proportionally limit; (3) a superelastic model, corresponding to a material that undergoes strain softening after the proportionality limit, followed by strain hardening; and (4) an elastoplastic model, with a similar curve as before but undergoing plastic (permanent) deformation after a certain yielding stress. For simplicity, all stress–strain curves are continuous functions, with a repulsive response for compressive strains ($\Delta x<0$) to prevent cells from having zero areas and made of connected linear segments with varying slopes (stiffness) for different ranges of extensive strains ($\Delta x>0$). Table S1 contains a mathematical description of each curve, and Table S2 lists the parameter values used in our simulations. All stress–strain curves are linear for extensive strains ($\Delta x>0$) lower than the proportionality limit ($x_{pl}$), with some curves (elastoplastic and superelastic) undergoing a strain-softening to strain-hardening change after a given strain-hardening limit ($x_{sh}$). By definition, $0>x_{pl}>x_{sh}$, and we chose their values to be within the observed ranges of dorsal–ventral lengths of stretching cells. We systematically explored the outcomes of the five models by varying the parameters controlling the myosin profile (Eq. 2).

Comparison between models and data

To determine how each stress–strain response compared with our data, we used three criteria. We calculated a root mean square error (RMSE) goodness of fit between each model distribution of cell sizes over the dorsal–ventral direction and the corresponding experimental data. To reduce noise, we splined the data points (i.e., fitted them with segmented polynomials) and used those values for the RMSE calculation (Fig. 2, E and F). We also checked whether models were able to reproduce the observed pattern of constriction and stretching (only the last three cells stretching, with the inner cell stretching the most and the outer cell stretching least; Fig. 2, H–L) and the observed ratios between the size of the most stretched cell and the most constricted cell (Fig. 2 F and Fig. 2, H′–L′).

Actomyosin model for the mesoderm

We modeled a line of cells from the ventral midline to the mesectodermal cell as a series of sequentially connected actomyosin networks with varying amounts of myosin motors. Each network is a 2D mesh of 800 actin filaments 1.5 µm long, randomly distributed within a rectangular region of 7 × 8 µm. The cells have periodic boundary conditions along the “anteroposterior” direction (top to bottom in the graphic representation) and are separated by rigid but movable “membranes.” The row is bounded by unmovable walls on each end to simulate the ectoderm and the ventral midline. Each membrane has 800 transmembrane connecting points for the filaments on each side. Actin filaments of adjacent cells do not interact except through the membrane connectors. Each cell has 1,600 cross-linkers and between 1,600 and 16,000 myosin motors (with a minimum level that was sufficient, in principle, to contract the network). Both connectors are modeled as pointlike objects with two independent hands that can bind and bridge two nearby filaments pertaining to the same cell. Once bound, motor hands move toward the plus end of the filaments until they unbind or reach and detach from their ends.

The quantities of motors, actin filaments, cross-linkers, and transmembrane connectors were chosen on the basis of our previous work (Belmonte et al., 2017; Wollrab et al., 2018) to ensure that all cells had a sufficiently connected network to generate contractile forces and transmit forces between cells. The amount of actin filaments was the same in each cell, in accordance with our measurements (Fig. 4, E–G; see also Mason et al., 2016); the numbers of cross-linkers and transmembrane connectors were assumed to be uniform, and the number of motors varies between cells in a manner similar to that in the viscoelastic model according to the equation:

$$M(c_i)=1,600+16,000\frac{1+e^{-sw}}{1+e^{s(c_i\vee -w)}},$$ (3)

where $c_i$ is the cell number with $c_i=0$ being the central cell and $c_i=8$ being the mesectodermal cell. Other parameter values, such as the on-off rates, movement kinetics, and stiffness/persistence lengths of the modeled cytoskeletal components, were based on biochemically determined values for α-actinin, myosin, and F-actin (see Table S3).

To test how sensitive the results are to the parameters of the cytoskeletal model, we varied the amounts of cytoskeletal components and the parameters controlling their dynamics. Due to the high computational costs associated with this model, we performed a sensitivity analysis on six parameters for which the available literature information was not sufficiently clear or for where we expect higher impacts on the results of the model (Fig. 4), namely the number of F-actin units per cell, F-actin lengths, number of cross-linkers, myosin stall force, myosin unloaded speed, and viscosity. For each parameter, we tested values above and below the reference values (Table S3; and Fig. 4 E, right) and explored a reduced region of the myosin profile map (Fig. 4 E′). We saw no major shifts of the region that reproduced the previous qualitative observations, although the results on parameter variations that likely altered network connectivity (such as reduced lengths or amounts of F-actin) became visibly noisier. All data points shown in each map were averaged over three simulations.

All filament-based simulations were done with CytoSim (Nedelec and Foethke, 2007), a cross-platform simulation engine designed to handle large systems of flexible filaments and associated proteins. CytoSim uses a Brownian dynamics approach to simulate the cytoskeleton, where each element is individually represented in either 2D or 3D space. The number, spatial location, and physical properties of each element are determined at the start of the simulation, and the system evolves according to the laws of mechanics and stochastic reaction kinetics.

Data analysis and plotting

All graphs were plotted using either MATLAB (MATLAB_R2015a) or Python (version 3.7). Matplotlib (Hunter, 2007), Pandas (McKinney, 2010), Scikit-image (van der Walt et al., 2014), and NumPy (Harris et al., 2020) packages were used. The figures were compiled using Adobe Illustrator CS6 (version 16.0.0) and Inkscape 1.1.

We analyzed a large number of embryos, but here we present only those that provided the most extensive data. It is difficult to obtain absolutely “perfect” embryos at high resolution for full quantification over long periods. “Perfect” means that the embryos are mounted in such a way that they are imaged from an angle of 45° off the DV axis, so that initially mesodermal rows 3–7 are seen, and then, as furrow formation progresses, the more lateral rows move through the field of vision. It is difficult for two reasons: the shape of the embryo means that balancing in this position is not favored, but the embryo tends to fall back on its side. Second, the embryo has to be mounted at a time point before visible differentiation along the DV axis, so no visual cues exist for the correct positioning. This means that many of our recordings lack either the more ventral or the lateral cell rows. The numbers of complete recordings are therefore not high, but multiple shorter recordings provide a body of results that support the findings, even though they are not easily comparable statistically. We include three fully analyzed, end-quantified examples for each condition.

Cell sizes and myosin values were measured for all cells in each row for each time point, and their means and SDs were plotted against time. Testing for statistical significance was performed using the SciPy module (Virtanen et al., 2020) in Python 3.7. We used the independent two-sample t test to generate all reported P values.

Online supplemental information

Fig. S1 shows the results of image analysis and identification of the edge of the mesoderm. Fig. S2 shows further examples of embryos and quantifications. Fig. S3 displays the distribution of apical F-actin in the mesoderm. Fig. S4 shows the myosin concentration in constricting and transiently expanding cells. Fig. S5 shows quantifications and examples of laser-microdissected and optogenetically manipulated embryos. Video 1, part I, shows cross-sectional and ventral views of the 3D segmented ventral half of an embryo expressing GAP43::mCherry and imaged with SPIM. Video 1, part II, shows 3D volume rendering over time for three cells: one central and two lateral mesodermal cells. Video 2 shows a ventrolateral view of two embryos (parts I and II) expressing shq::mCherry and Spider::GFP depicting the dynamics of apical area and myosin during ventral furrow formation and lateral cell expansion. Video 3 shows actomyosin simulation of a row of cells. Video 4 shows a ventral view of an embryo expressing GAP43::mCherry and sqh::GFP. Video 5 shows 3D reconstructions of lateral mesodermal cells from row 7 in an embryo where apical constriction of the central mesodermal cells was inhibited by laser ablation. Video 6 shows a ventral view of an embryo expressing GAP43::mCherry, CIBN::pmGFP, and RhoGEF2-CRY2. Table S1 describes equations used for the viscoelastic stress–strain responses. Table S2 lists parameters used in the viscoelastic models. Table S3 lists parameters used in the actomyosin simulations. Table S4 lists fly stocks used. Table S5 lists primers used. Table S6 lists genotypes of embryos and imaging methods used in experiments. Table S7 lists numbers of constricting lateral cells after laser and optogenetic manipulations.

Supplementary Material

Table S1

describes equations used for the viscoelastic stress–strain responses.

Table S2

lists parameters used in the viscoelastic models.

Table S3

lists parameters used in the actomyosin simulations.

Table S4

lists fly stocks used.

Table S5

lists primers used.

Table S6

lists genotypes of embryos and imaging methods used in experiments.

Table S7

lists numbers of constricting lateral cells after laser and optogenetic manipulations.

Data availability

Apart from the third-party software tool SEGMENT3D (Stegmaier et al., 2018), all described algorithms were implemented in MATLAB and are available from https://github.com/stegmaierj/CellShapeAnalysis/ (Apache License 2.0), and the code for myosin analysis is available from https://github.com/sourabh-bhide/tissue2cells.