Evaluating Vaccine Efficacy Against Severe Acute Respiratory Syndrome Coronavirus 2 Infection

Abstract

Although interim results from several large, placebo-controlled, phase 3 trials demonstrated high vaccine efficacy (VE) against symptomatic coronavirus disease 2019 (COVID-19), it is unknown how effective the vaccines are in preventing people from becoming asymptomatically infected and potentially spreading the virus unwittingly. It is more difficult to evaluate VE against severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection than against symptomatic COVID-19 because infection is not observed directly but rather is known to occur between 2 antibody or reverse-transcription polymerase chain reaction (RT-PCR) tests. Additional challenges arise as community transmission changes over time and as participants are vaccinated on different dates because of staggered enrollment of participants or crossover of placebo recipients to the vaccine arm before the end of the study. Here, we provide valid and efficient statistical methods for estimating potentially waning VE against SARS-CoV-2 infection with blood or nasal samples under time-varying community transmission, staggered enrollment, and blinded or unblinded crossover. We demonstrate the usefulness of the proposed methods through numerical studies that mimic the BNT162b2 phase 3 trial and the Prevent COVID U study. In addition, we assess how crossover and the frequency of diagnostic tests affect the precision of VE estimates.

We show how to estimate potentially waning efficacy of coronavirus disease 2019 vaccines against severe acute respiratory syndrome coronavirus 2 infection using blood or nasal samples collected periodically from clinical trials with staggered enrollment of participants and crossover of placebo recipients.

Enormous progress has been made in the development of vaccines against severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Within 1 year after the emergence of this novel infection that caused a global pandemic, vaccine targets were identified, vaccine constructs were created, and phase 1 through phase 3 testing was conducted. Interim results from several large-scale, phase 3, randomized, placebo-controlled clinical trials have demonstrated high vaccine efficacy (VE) against symptomatic coronavirus disease 2019 (COVID-19) [1–4]. However, very little is known about VE against possibly asymptomatic SARS-CoV-2 infection.

It is critically important to assess VE against SARS-CoV-2 infection because reduction of infection and community transmission is the key to halting the pandemic. Fortunately, most phase 3 trials have collected blood samples that can be used to identify SARS-CoV-2 seroconversion [1–4]. For economic and logistical reasons, however, blood samples can only be drawn infrequently, such that seroconversion is only known to occur between 2 clinic visits that are weeks or months apart. It is more difficult to analyze such interval-censored seroconversion data than potentially right-censored symptomatic disease data, especially when VE changes over time. (An event time is said to be interval-censored if it is only known to lie in a time interval; an event time is said to be potentially right-censored if it is either observed exactly or known to be longer than the duration of follow-up [5].) Additional challenges arise when community transmission varies over time and when participants are vaccinated on different dates because of either staggered enrollment of participants or crossover of placebo participants to the vaccine arm before the end of the trial.

SARS-CoV-2 infection is commonly diagnosed by reverse-transcription polymerase chain reaction (RT-PCR) on nasal swabs. Most phase 3 trials have collected nasal swabs at the enrollment and crossover visits [1, 2, 4]. Such infrequent swab samples will miss many infections because a person may be RT-PCR–positive for only a few days or weeks after infection [6]. Some phase 3 trials have taken nasal swabs more frequently (eg, twice a week) on a subset of participants, and the newly launched Prevent COVID U study takes nasal swabs every day; however, frequent RT-PCR testing increases trial cost. How does the RT-PCR testing schedule affect the estimation of VE against infection (defined as viral RNA above a minimum threshold)?

Here, we show how to evaluate potentially waning VE against SARS-CoV-2 infection, defined by seroconversion or detectable viral RNA, using blood or nasal samples taken at varying levels of frequency under the conditions of time-varying community transmission, staggered enrollment of participants, and possible crossover of placebo volunteers to the vaccine arm before the end of the study. We demonstrate the usefulness of the proposed methods through extensive simulation studies that mimic the BNT162b2 phase 3 trial [1] and the Prevent COVID U study. In addition, we investigate how the frequency of diagnostic tests and the characteristics of crossover (blinded vs unblinded, immediate vs gradual) affect the precision of VE estimation.

METHODS

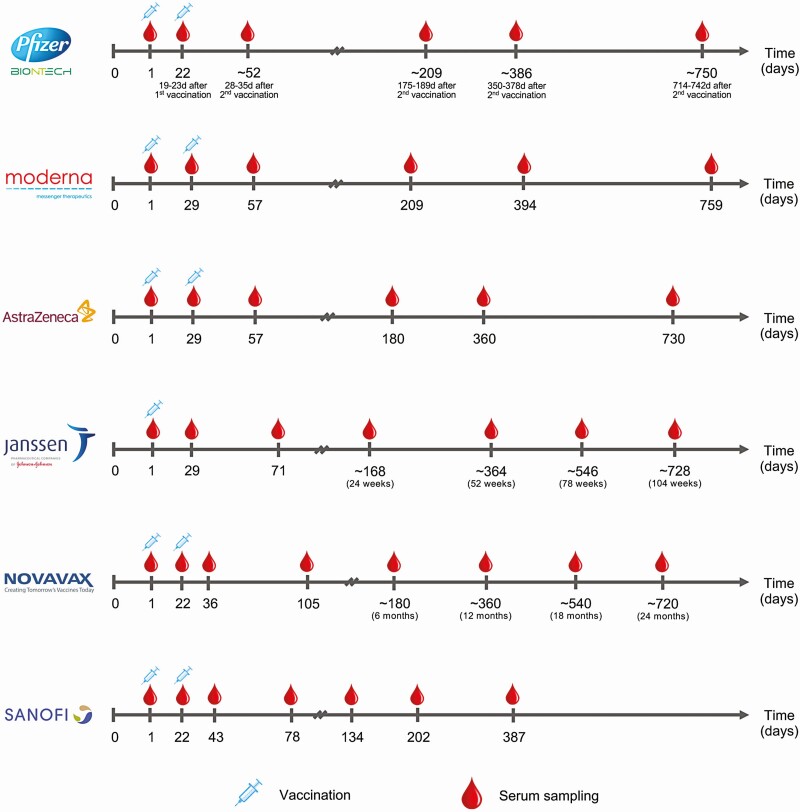
Figure 1 displays the blood sampling schedules for several phase 3 vaccine trials. For the 3 vaccines that have received the US Food and Drug Administration’s (FDA’s) emergency use authorization (EUA), blood samples are also taken at the crossover visits [1, 2, 4].

Figure 1.

Serum sampling schedules in 6 phase 3 coronavirus disease 2019 vaccine trials. The sampling time points are measured from the day of enrollment.

We are interested in time to SARS-CoV-2 infection assessed by seroconversion, which is only known to occur between 2 blood draws and is thus interval-censored. We allow the risk of infection to vary over the calendar time and to depend on baseline risk factors, such as age, sex, ethnicity, race, occupation, and health conditions. We allow the effect of vaccine on infection to depend on the time elapsed since vaccination.

We consider the following 3 measures of VE as a function of time elapsed since vaccination: VE_h(t) is the percentage reduction in the hazard rate or instantaneous risk of infection at time t; VE_a(t) is the percentage reduction in the attack rate or cumulative incidence of infection over the time period (0, t]; and VE_a(t₁, t₂) is the percentage reduction in the attack rate over the time period (t₁, t₂]. Note that VE_h(t) and VE_a(t) pertain to instantaneous and cumulative vaccine effects, respectively, and that VE_a(t) is a special case of VE_a(t₁, t₂) with t₁ = 0 and t₂ = t. If the vaccine effect is constant over time, then the 3 VE measures are equivalent (provided that the infection rate is low) [7].

In Supplementary Appendix 1, we formulate the above ideas through an adaptation of the well-known Cox [8] regression model, in which each participant’s time to infection is measured from the start of the clinical trial, and the hazard ratio of infection for vaccine vs placebo depends on the time elapsed since vaccination. Because of staggered enrollment and staggered crossover, the serum sampling time points are scattered randomly over the calendar time, providing valuable information about the infection-time distribution. We express VE_h and VE_a as appropriate functions of the time-varying hazard ratio. We derive the maximum likelihood estimator for the time-varying hazard ratio based on the interval-censored infection time data and provide the corresponding estimators of VE_h and VE_a.

The above framework also applies to RT-PCR tests of nasal swabs. Because an infected person is RT-PCR–positive for a shorter period of time than they are seropositive (days/weeks vs months) [6, 9, 10], nasal swabbing needs to be done more frequently than serum sampling in order to capture the infections defined by detectable viral RNA. With very frequent RT-PCR, time to detectable viral RNA may be treated as a potentially right-censored event time. In our framework, potentially right-censored data are a special case of interval-censored data, with the exactly observed event time lying within an interval of 1 day.

RESULTS

We conducted a series of simulation studies that mimicked the BNT162b2 phase 3 trial [1] (Supplementary Appendix 2.1). We considered 40 000 participants who enter the trial at a constant rate over a 4-month period and are randomly assigned to vaccine or placebo in a 1:1 ratio. To reflect the increase of COVID-19 cases since summer 2020 and the downward trend in spring 2021, we let the risk of infection increase over the first 7 months and decrease afterward. In addition, we let the risk of infection depend on priority tier.

As in the BNT162b2 phase 3 trial [1], the vaccine in our simulation received an EUA from the FDA at the fifth month, after which placebo participants are sequentially crossed over to the vaccine arm. We considered the following two cases:

Priority-Dependent Crossover

Crossover starts at month 6, 7, 8, 9, or 10 of the study for participants with priority tier of 1, 2, 3, 4, or 5, respectively, each participant’s waiting time for the clinic visit following the exponential distribution with mean of 0.5 month.

Priority-Independent Crossover

Crossover starts at month 6 of the study for all participants, with the waiting time following the exponential distribution with mean of 0.5 month.

Note that crossover spreads over a much longer time period under priority-dependent crossover than under priority-independent crossover.

We considered both blinded and unblinded crossover. At blinded crossover, placebo participants receive the vaccine and vaccine participants receive the placebo; none of them are aware of the order of their treatments. At unblinded crossover, participants are notified of their original treatment assignments, and placebo recipients are vaccinated. In both types of crossover, all participants are followed until the time of analysis, which is 10.5 months since trial initiation. To avoid bias due to behavioral confounding, we discarded the data collected after unblinded crossover.

As shown in Figure 1, blood samples were scheduled to be drawn on day 1, day 22, day 52, and day 209 (during the first year) in the BNT162b2 phase 3 trial [1]. In our simulation, we allowed for small random deviations from the schedule. Blood samples were also drawn at the crossover visits. Because of staggered enrollment and staggered crossover, serum sampling points were scattered randomly over the study period, making it possible to estimate time-varying VE.

We also simulated a design under which there is no crossover before the time of analysis. Without crossover, placebo participants stay on placebo longer than with crossover, providing more information about long-term placebo-controlled VE. However, because crossover is 1 of the serum sampling points, there are fewer sampling points and thus fewer antibody tests under no crossover than under crossover.

Naturally, VE_h equals 0 at the first injection. We let VE_h increase from 0% to 80% at 4 weeks and then either stay constant or decrease gradually over time. We refer to these 2 situations as constant VE and waning VE, respectively. (Note that constant vs waning VE pertains only to the period after the first 4 weeks when VE is ramping up.)

In our first simulation scenario, we let VE_h stay at 80% after 4 weeks, and we analyzed the resulting interval-censored data using the proposed method with a log hazard ratio that decreases linearly between weeks 0 and 4 and stays constant after week 4. For comparison, we fit the same model by treating the time of the first positive antibody test as a potentially right-censored event time and performing maximum partial likelihood estimation with Efron’s method of handling ties [5, 8]. We refer to this as the naive method, which estimates the same VE parameter using the same data as the proposed method, the only difference being that it converts interval-censored event times to potentially right-censored event times.

Table 1 summarizes the results of these simulation studies. Using the proposed method, the VE estimates are unbiased, the standard errors are accurately estimated, and the confidence intervals have proper coverage probabilities. The standard error is lower under blinded than unblinded crossover and lower under priority-dependent than priority-independent crossover. The standard error is slightly higher under no crossover than under blinded priority-dependent crossover. (Note that there are fewer sampling points under no crossover than under crossover.) In comparison, the naive method overestimates the true VE under blinded crossover and underestimates the true VE under unblinded crossover, and the confidence intervals have lower coverage under blinded crossover than under unblinded crossover.

Table 1.

Estimation of Constant Vaccine Efficacy Based on Antibody Tests Under No Crossover (A), Blinded Priority-Dependent (B) and Priority-Independent (C) Crossover, and Unblinded Priority-Dependent (B’) and Priority-Independent (C’) Crossover When VE_h Stays at 80% After Week 4

	Proposed Method				Naive Method
Design	Mean (%)	SE (%)	SEE (%)	CP (%)	Mean (%)	SE (%)	SEE (%)	CP (%)
A	79.8	1.33	1.33	94	76.8	1.42	1.43	34
B	79.9	1.31	1.30	95	87.3	0.95	0.97	0
C	79.9	1.58	1.54	93	89.6	1.13	1.12	0
B’	79.8	1.41	1.38	95	76.9	1.49	1.47	40
C’	79.8	1.67	1.63	95	75.8	1.80	1.77	27

Mean and SE denote the mean and standard error of the vaccine efficacy estimator, SEE denotes the mean of the standard error estimator, and CP denotes the coverage probability of the 95% confidence interval.

Abbreviation, VE_h, vaccine efficacy on hazard rate.

In our second simulation scenario, we let VE_h stay at 80% after 4 weeks or let it decrease to 0 at 1 year. We implemented the proposed method (for interval-censored data) using a piecewise linear function for the log hazard ratio, with a change point placed at 4 weeks and with the 2 slopes estimated from the data. For comparison, we also implemented the naive method with the same piecewise linear function for the log hazard ratio.

Tables 2 and 3 show the simulation results on the estimation of VE_a over successive time periods under constant VE and waning VE, respectively. The proposed method yields unbiased VE_a estimates, with accurate standard error estimates and proper confidence intervals in virtually all cases. The naive method yields severely biased VE_a estimates.

Table 2.

Estimation of VE_a Over Successive Time Periods Based on Antibody Tests Under No Crossover (A), Blinded Priority-Dependent (B) and Priority-Independent (C) Crossover, and Unblinded Priority-Dependent (B’) and Priority-Independent (C’) Crossover When Vaccine Efficacy Does Not Wane Over Time

Design	Weeks	True VEa (%)	Proposed Method				Naive Method
			Mean (%)	SE (%)	SEE (%)	CP (%)	Mean (%)	SE (%)	SEE (%)	CP (%)
A	0–4	50.3	49.9	3.2	3.0	94	48.5	4.0	3.9	92
	4–16	80.0	79.7	2.2	2.1	94	77.6	3.3	3.2	86
	16–28	80.0	79.9	1.9	1.8	94	76.9	1.4	1.4	37
	28–40	80.0	79.7	4.6	4.2	92	75.8	3.4	3.3	74
B	0–4	50.3	50.1	2.2	2.2	94	59.9	1.7	1.7	0
	4–16	80.0	79.8	1.7	1.6	93	88.5	1.2	1.2	0
	16–28	80.0	80.0	1.6	1.6	95	87.0	1.0	1.0	0
	28–40	80.0	80.0	3.1	3.0	95	85.3	1.5	1.5	14
C	0–4	50.3	50.1	2.1	2.0	94	61.1	1.8	1.7	0
	4–16	80.0	79.9	1.7	1.7	94	89.9	1.2	1.2	0
	16–28	80.0	80.0	2.0	2.0	95	89.4	1.2	1.2	0
	28–40	80.0	79.9	3.6	3.5	95	88.7	1.7	1.7	2
B’	0–4	50.3	49.7	2.6	2.5	95	39.6	3.2	3.4	6
	4–16	80.0	79.6	1.8	1.8	95	70.9	2.8	2.9	5
	16–28	80.0	80.1	1.9	1.8	94	77.4	1.5	1.5	51
	28–40	80.0	80.2	3.9	3.8	94	82.3	2.1	2.1	82
C’	0–4	50.3	49.6	2.9	2.8	94	37.8	3.9	3.9	7
	4–16	80.0	79.6	1.8	1.8	94	70.8	2.9	2.9	4
	16–28	80.0	80.2	3.3	3.2	95	80.2	2.2	2.2	96
	28–40	80.0	80.1	6.9	6.5	94	86.3	3.4	3.3	62

Mean and SE denote the mean and standard error of the vaccine efficacy estimator, SEE denotes the mean of the standard error estimator, and CP denotes the coverage probability of the 95% confidence interval.

Abbreviation: VE_a, vaccine efficacy on attack rate.

Table 3.

Estimation of VE_a Over Successive Time Periods Based on Antibody Tests Under No Crossover (A), Blinded Priority-Dependent (B) and Priority-Independent (C) Crossover, and Unblinded Priority-Dependent (B’) and Priority-Independent (C’) Crossover When Vaccine Efficacy Wanes Over Time

Design	Weeks	True VEa (%)	Proposed Method				Naive Method
			Mean (%)	SE (%)	SEE (%)	CP (%)	Mean (%)	SE (%)	SEE (%)	CP (%)
A	0–4	50.3	50.3	3.1	2.7	91	58.3	3.6	3.5	42
	4–16	75.3	75.3	2.6	2.3	92	82.9	3.0	2.9	39
	16–28	62.9	62.9	2.7	2.9	96	68.0	1.9	1.9	26
	28–40	44.3	43.2	10.8	10.3	93	38.7	8.4	8.2	91
B	0–4	50.3	50.1	2.1	2.0	95	61.5	1.6	1.5	0
	4–16	75.3	75.2	1.9	1.9	94	87.6	1.2	1.2	0
	16–28	62.9	63.1	2.3	2.3	96	79.8	1.3	1.3	0
	28–40	44.3	44.7	6.6	6.5	94	66.8	2.8	2.8	0
C	0–4	50.3	50.2	1.9	1.9	94	62.5	1.6	1.6	0
	4–16	75.3	75.3	1.9	1.9	95	88.8	1.2	1.3	0
	16–28	62.9	63.0	3.1	3.0	95	82.2	1.7	1.7	0
	28–40	44.3	44.1	8.0	7.9	95	71.5	3.6	3.6	0
B’	0–4	50.3	49.9	2.3	2.3	95	43.5	2.7	2.9	28
	4–16	75.3	75.0	2.0	2.0	96	70.2	2.7	2.8	50
	16–28	62.9	62.9	2.6	2.5	95	66.4	1.8	1.9	56
	28–40	44.3	44.5	8.1	7.9	95	61.8	3.5	3.5	1
C’	0–4	50.3	49.7	2.6	2.6	95	41.7	3.4	3.4	23
	4–16	75.3	74.9	2.0	2.1	95	69.3	2.9	2.9	38
	16–28	62.9	63.1	4.8	4.8	94	68.5	2.7	2.8	56
	28–40	44.3	44.5	15.1	14.8	94	67.0	6.4	6.5	19

Mean and SE denote the mean and standard error of the vaccine efficacy estimator, SEE denotes the mean of the standard error estimator, and CP denotes the coverage probability of the 95% confidence interval.

Abbreviation: VE_a, vaccine efficacy on attack rate.

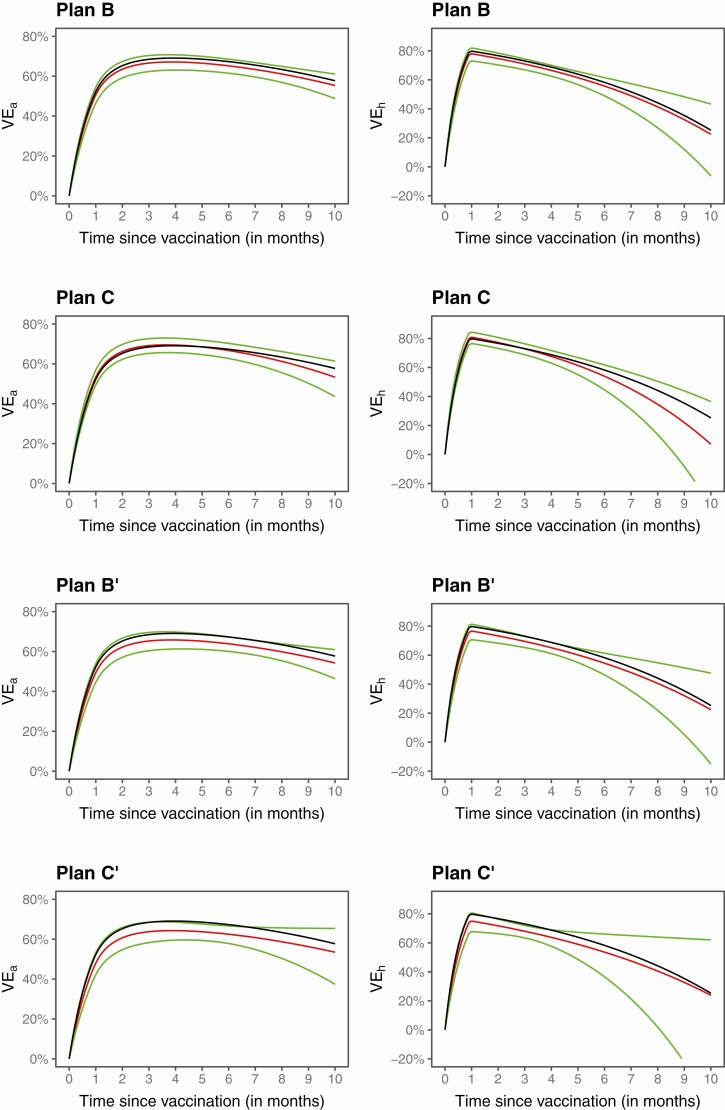
Figure 2 displays the estimation results produced by the proposed method in 1 of the trials simulated under waning VE. The estimated VE_h and VE_a curves are close to the truth, and the 95% confidence intervals nearly cover the entire true curves. As expected, the confidence intervals are the narrowest under blinded priority-dependent crossover and the widest under unblinded priority-independent crossover. In addition, the confidence intervals for VE_h are wider than the confidence intervals for VE_a at the right tail.

Figure 2.

Estimation of VE_a and VE_hin a clinical trial under blinded priority-dependent (B) and priority-independent (C) crossover and under unblinded priority-dependent (B’) and priority-independent (C’) crossover. The black curve pertains to the true value, the red curve pertains to the proposed estimate, and the green curves pertain to the 95% confidence intervals. Abbreviations: VEa, vaccine efficacy on attack rate; VEh, vaccine efficacy on hazard rate.

We also conducted a series of simulation studies that mimicked the Prevent COVID U study (Supplementary Appendix 2.2). A total of 12 000 participants enter the study at a constant rate over 1 month. Half of them are randomly selected to receive the Moderna vaccine at enrollment, and the other half get their first injection with a 4-month delay. We assumed a downward trend of infection over time; we adopted the VE patterns from the first series of simulation studies but placed the change point at 6 weeks instead of 4 weeks.

We explored various swabbing/RT-PCR testing schedules, ranging from every day to every 2 weeks. Each participant is followed for 4 months, and the study ends at month 5, when the last enrolled participant has been followed for 4 months. We also considered a scenario where 50% of the delayed-arm participants receive outside vaccines before the end of follow-up; in the analysis, we discarded the data collected after outside vaccination.

Table 4 summarizes the simulation results on the estimation of constant VE. The proposed method yields unbiased VE estimates, with accurate standard error estimates and proper confidence intervals in all cases. The standard error of the VE estimate tends to increase a little bit as RT-PCR testing becomes less frequent. There is a slight loss of precision in the VE estimates when the delayed-arm participants are allowed to receive outside vaccines. In comparison, the naive method shows results that are highly similar to those of the proposed method when RT-PCR testing is performed every day. However, as RT-PCR testing becomes less frequent, the naive estimate becomes more biased, with increasingly larger standard error than the proposed estimate. Exclusion of the events within the first 6 weeks substantially reduces the precision of VE estimates. (The substantial loss of precision is due to relatively high incidence in the first 6 weeks under decreasing background incidence over time and high VE. In the setting of constant background incidence with VE of 0.6 after 4 weeks, excluding the events within the first 4 weeks incurs about 13% loss of statistical efficiency.)

Table 4.

Estimation of Constant Vaccine Efficacy Under Different Reverse-Transcription Polymerase Chain Reaction Testing Schedules When VE_h Stays at 80% After Week 6

Outside Vaccines	Frequency of Tests	Proposed Method					Naive Method
		Mean (%)	SE (%)	SEE (%)	CP (%)	RE	Mean (%)	SE (%)	SEE (%)	CP (%)
No	Every day	79.5	3.44	3.49	95	1.36	79.5	3.44	3.46	95
	Every 2 days	79.4	3.52	3.51	95	1.35	79.1	3.54	3.50	94
	Every 4 days	79.5	3.49	3.52	95	1.38	78.7	3.53	3.53	93
	Every week	79.5	3.50	3.49	95	1.33	77.8	3.59	3.55	90
	Every 2 weeks	79.5	3.58	3.60	95	1.35	75.4	3.81	3.80	74
Yes	Every day	79.4	3.50	3.52	95	1.35	79.4	3.50	3.49	95
	Every 2 days	79.5	3.48	3.53	95	1.36	79.2	3.49	3.51	95
	Every 4 days	79.5	3.58	3.56	95	1.35	78.7	3.60	3.56	93
	Every week	79.5	3.53	3.52	95	1.34	77.9	3.59	3.56	91
	Every 2 weeks	79.4	3.69	3.64	95	1.35	75.7	3.85	3.79	76

Mean and SE denote the mean and standard error of the vaccine efficacy (VE) estimator, SEE denotes the mean of the standard error estimator, CP denotes the coverage probability of the 95% confidence interval, and RE is the variance of the VE estimator excluding the infections of the first 6 weeks divided by the variance of the VE estimator using all infections.

Abbreviation: VE_h, vaccine efficacy on hazard rate.

Table 5 presents the results on the estimation of VE_a over successive time periods when VE_h decreases to 0 at 1 year. The proposed method provides unbiased VE_a estimates, along with proper confidence intervals. The naive method performs well when RT-PCR testing is done daily but performs poorly when RT-PCR testing becomes infrequent.

Table 5.

Estimation of VE_a Over Successive Time Periods Under Different Reverse-Transcription Polymerase Chain Reaction Testing Schedules When Vaccine Efficacy Wanes Over Time

Outside Vaccines	Frequency of Tests	Weeks	True VEa (%)	Proposed Method				Naive Method
				Mean (%)	SE (%)	SEE (%)	CP (%)	Mean (%)	SE (%)	SEE (%)	CP (%)
No	Daily	0–6	50.3	49.3	4.60	4.61	95	49.3	4.60	4.56	95
		6–12	77.7	77.0	3.81	3.84	95	77.0	3.81	3.81	95
		12–18	72.4	72.1	7.69	7.57	95	72.1	7.69	7.57	95
	Every 4 days	0–6	50.3	49.4	4.61	4.66	95	48.0	4.68	4.68	92
		6–12	77.7	77.2	3.82	3.84	94	76.2	3.89	3.88	93
		12–18	72.4	72.3	8.21	7.99	95	72.9	7.86	7.65	95
	Weekly	0–6	50.3	49.4	4.44	4.61	96	46.5	4.61	4.73	88
		6–12	77.7	77.1	3.70	3.83	95	75.1	3.85	3.95	90
		12–18	72.4	72.2	7.61	7.50	96	73.3	7.05	6.99	96
Yes	Daily	0–6	50.3	49.3	4.52	4.62	95	49.3	4.52	4.56	95
		6–12	77.7	77.0	3.85	3.86	95	77.0	3.85	3.83	95
		12–18	72.4	72.0	7.90	7.81	95	72.0	7.90	7.80	95
	Every 4 days	0–6	50.3	49.4	4.67	4.65	94	47.9	4.73	4.67	92
		6–12	77.7	77.0	3.84	3.87	96	76.2	3.89	3.89	94
		12–18	72.4	71.8	8.41	8.34	95	72.8	7.94	7.89	95
	Weekly	0–6	50.3	49.4	4.56	4.61	96	46.5	4.70	4.73	88
		6–12	77.7	77.1	3.93	3.86	95	75.2	4.05	3.95	89
		12–18	72.4	72.0	7.82	7.84	96	73.6	7.10	7.11	96

Mean and SE denote the mean and standard error of the vaccine efficacy (VE) estimator, SEE denotes the mean of the standard error estimator, and CP denotes the coverage probability of the 95% confidence interval.

Abbreviation: VE_a, vaccine efficacy on attack rate.

We have assumed that VE ramps to an unknown peak level 4 weeks (or 6 weeks) after the first injection of the Pfizer/BioNTech vaccine (or the Moderna vaccine). We can allow uncertainty in this change point by including several change points in the analysis or by selecting the change point through the Akaike information criterion. We evaluated these strategies by extending the simulation studies reported in Table 1. We considered the following 2 scenarios: the true change point is 4 weeks and the true change point is 6 weeks. In both scenarios, the true VE increases from 0 at time 0 to 0.8 at the true change point and stays at 0.8 afterward. We implemented the following 2 methods: (1) place 3 change points at weeks 4, 6, and 8 and estimate the corresponding 3 slopes of the log hazard ratio and (2) calculate the likelihood with the change point placed at week 4, 6, or 8 and select the time point that yields the highest likelihood. As shown in Table 6, the first method performs very well, although the standard error is higher than using a single change point. The second method correctly selects the change point with high probability.

Table 6.

Estimation of Constant Vaccine Efficacy With Unknown Change Points Under No Crossover (A), Blinded Priority-Dependent (B) and Priority-Independent (C) Crossover, and Unblinded Priority-Dependent (B’) and Priority-Independent (C’) Crossover When VE_h Stays at 80% After the Change Point

	True Change Point = 4 Weeks					True Change Point = 6 Weeks
Design	Mean (%)	SE (%)	SEE (%)	CP (%)	Correct (%)	Mean (%)	SE (%)	SEE (%)	CP (%)	Correct (%)
A	79.9	1.50	1.47	94	73	79.9	1.46	1.47	94	65
B	80.0	1.42	1.42	95	80	79.9	1.43	1.42	95	73
C	79.9	1.78	1.70	94	82	79.9	1.73	1.69	95	78
B’	79.9	1.58	1.52	94	72	79.9	1.60	1.53	94	67
C’	79.9	1.96	1.90	94	70	79.9	1.91	1.91	95	67

Mean and SE denote the mean and standard error of the vaccine efficacy (VE) estimator, SEE denotes the mean of the standard error estimator, and CP denotes the coverage probability of the 95% confidence interval. Correct denotes the probability of correctly selecting the change point by the Akaike information criterion.

Abbreviation: VE_h, vaccine efficacy on hazard rate.

Discussion

We have demonstrated that it is possible to evaluate time-varying VE against SARS-CoV-2 infection using the blood samples collected in the ongoing phase 3 vaccine trials [1–4] or using the nasal samples collected in studies such as the Prevent COVID U study. We found that when antibody or RT-PCR tests are performed infrequently, the use of standard Cox regression for potentially right-censored data yields biased and imprecise VE estimates. The new methods provide valid and efficient estimation of 3 useful VE measures.

The model considered here is similar to that used in our previous work on evaluating VE against symptomatic COVID-19 [7]; however, here, the hazard ratio is piecewise log-linear rather than completely arbitrary. In addition, the estimation approach is more sophisticated because infection times are interval-censored rather than potentially right-censored. The proposed methodology is general enough to include potentially right-censored data as a special case and thus offers an alternative way to assess VE against symptomatic COVID-19. A major advantage of this approach is that it provides a unified framework for studying constant vs waning VE and produces confidence intervals for VE_h.

Another important contribution of this work is a careful treatment of the ramping VE after initial vaccination. The prevailing approach is not to count the events that occur within 4–6 weeks of the first injection [1, 2]. Discarding the first 4–6 weeks of follow-up data causes considerable loss of statistical efficiency, as shown in Table 4. In the case of blinded crossover, excluding the events that occur within 4–6 weeks of crossover will further reduce statistical efficiency, whereas including all the events will result in biased VE estimates.

We have not accounted for the measurement errors of antibody or RT-PCR tests in the analysis. The false-positive rate is negligible for RT-PCR testing and small for antibody testing. An infected person is seropositive for a longer period of time than they are RT-PCR–positive (several months vs several days or weeks) [6, 9, 10]. Thus, infrequent serology will capture more infections than infrequent RT-PCR. Some asymptomatic infections never seroconvert or have transient seroconversion that may be missed by infrequent serology [9, 10]. However, those who do not seroconvert tend to be less infectious than those who do, such that missed seronegative infections may be clinically less important. Likewise, an asymptomatic infection that is RT-PCR–positive for just a day or 2 is difficult to detect but may have little public health relevance.

For the Prevent COVID U study, the main reason for daily swabbing and testing is not to determine the timing of infection but rather to measure the full course of viral load for all infected participants. In particular, investigators wish to capture potential infectiousness by measuring the peak viral load, the duration of viral shedding, and the area under the viral load curve. If detecting the presence of viral RNA were the study’s only goal, then less frequent testing would be needed. The proposed methods (for interval-censored data) may be warranted in the case that a substantial number of swabs are not collected or are not usable (due to improper collection or storage).

Blood samples and nasal swabs provide complementary information about SARS-CoV-2 infection. Viral RNA can be detected sooner after infection than seroconversion, but antibody lasts longer than viral shedding [6, 9, 10]. There is considerable heterogeneity in the duration of both seropositivity and RT-PCR positivity, with the biggest driving factor being symptomatic vs asymptomatic infection [6, 9, 10]. Many studies collect both blood and nasal samples. For example, the Moderna phase 3 trial [2] performs RT-PCR testing at month 1 and at crossover in addition periodic serology. The Prevent COVID U study performs periodic (every 2 months) serology and frequent RT-PCR testing. The proposed methods can be applied to the 2 types of infection data separately or as a combined end point, depending on the objective of the analysis and the frequency of each type of test.

The monitoring times are assumed to be independent of the infection time (conditional on covariates). This assumption is satisfied for planned diagnostic tests but is unlikely to hold if SARS-CoV-2 infection is detected through symptom-prompted testing. We can apply the proposed methods (for interval-censored data) to planned tests and standard Cox regression with potentially right-censored data to symptom-prompted tests. The estimates for the 2 log hazard ratios have a joint normal distribution, which can be used to make simultaneous inference about VE against the 2 end points. If the planned RT-PCR testing is frequent, then the data from planned and symptom-prompted RT-PCR tests can be combined and standard Cox regression for potentially right-censored data can be adopted.

We have implemented the methods described in this article in an R package, which is available at https://dlin.web.unc.edu/software/idove/.

Supplementary Data

Supplementary materials are available at Clinical Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.

Notes

Financial support. This work was supported by National Institutes of Health grants R01 AI029168, R01 GM124104, P01 CA142538, and UM1 AI068635.

Potential conflicts of interest. All authors: No reported conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.